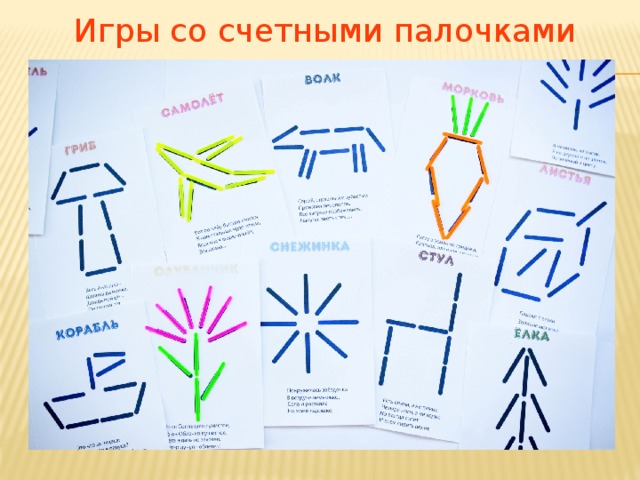
Работа со счетными палочками в 1 классе презентация: Презентация к внеурочному занятию в 1 классе “Игры со счетными палочками”
От простого к сложному. Счётные палочки
Похожие презентации:
Деятельность пришкольного лагеря с дневным пребыванием детей «Дружба» МОУ школа № 71
Моя будущая профессия: юрист
Развитие интеллектуальной одаренности детей Новосибирской области с использованием дистанционных образовательных технологий
Творческий проект «Планирование кухни-столовой»
Моя будущая профессия – военный
Кейсы (ситуации взаимодействия ребёнка и взрослого)
Творческий проект «мой профессиональный выбор»
Развитие связной речи у дошкольников
Технология В.А. Илюхиной «Письмо с открытыми правилами» для учащихся начальных классов
Технологии нейрокоррекции нарушений письменной речи младших школьников с тяжелыми нарушениями речи
МАДОУ «Центр развития ребенка – детский сад № 394» г. Перми
«От простого к сложному»
счётные палочки как средство интеллектуального развития
дошкольника с ЗПР
Стендовый доклад подготовили:
Катаева Светлана Петровна, учитель-дефектолог
Сятчихина Вера Евгеньевна, воспитатель
Пермь 2019
Интеллектуальное развитие дошкольников – важная
часть
общего психического развития ребёнка, его подготовки к
школьному обучению.
Для развития интеллектуальныхспособностей детей используются различные педагогические
приемы, в том числе и конструирование из счетных палочек.
Счётные палочки – незаменимый дидактический материал, его
основные особенности – абстрактность, универсальность,
высокая эффективность.
Работа с палочками помогает развивать ручную умелость,
координацию, конструктивные навыки, зрительное восприятие,
внимание, память, мыслительные операции сравнения, анализа,
синтеза,
пространственную ориентировку , воображение,
сообразительность.
В ходе решения каждой новой задачи ребёнок включается в
активную умственную деятельность, стремясь достичь конечной
цели – построить или видоизменить пространственную фигуру.
Цель:
развитие интеллектуальных способностей детей с ЗПР
посредством счётных палочек.
–
Задачи:
обучать технике конструирования из счетных палочек;
развивать зрительное восприятие, память, внимание,
воображение;
развивать мыслительные операции сравнения, анализа,
синтеза,
развивать мелкую моторику руки.
воспитывать настойчивость, умение доводить начатое
дело до конца.
Последовательность обучения детей
играм с палочками
(по степени сложности).
Задания на конструирование из палочек:
1. Образец схематичный, изображение контура в натуральную
величину (приложение 1)
а) детям со сложными нарушениями предлагается наложить палочки на
предъявленный образец.
б) в более лёгких случаях дети составляют изображение сначала сбоку
от образца, затем под образцом.
На этом этапе дети выкладывают изображение сначала сбоку от
образца, затем под образцом
3. Работа без
представлению.
образца,
дети
выкладывают
предмет
по
Задания на развитие памяти
Изображения, сложенные из палочек, можно использовать для
развития памяти. Картинка из палочек рассматривается ребёнком
в течение 30 секунд и затем выкладывается им по памяти, без
зрительного образца.
Задания на развитие наблюдательности, внимания
Изображения, выложенные палочками можно использовать для
выполнения заданий «Найди отличия», которые так любят дети.
Дети выкладывают изображение по образцу, затем педагог
показывает им карточку с небольшим отличием, которое дети
должны обнаружить и внести в свою конструкцию.
Игры– головоломки со счетными палочками
Дети старшего дошкольного возраста любят головоломки, игры
на смекалку.
Одним из наиболее доступных видов задач на смекалку
являются игры со счетными палочками. Их еще называют
задачами на смекалку геометрического характера, т. к. в ходе
решения идет создание различных форм и преобразование одних
фигур в другие.
В ходе таких игр дошкольники охотно
преодолевают трудности, возникающие по ходу выполнения
игровых задач.
Игры-головоломки со счетными палочками формируют такие
качества, как усидчивость, упорство в достижении цели,
находчивость, развивают конструктивные умения, умственную и
творческую активность.
Задания на составление заданной фигуры
из определенного количества палочек,
записанное схематично.
(Приложение 3)
8
Задания на преобразование фигур, путём
перекладывания палочек.
(Приложение 4)
В ходе решения задач, направленных на формирование умения детей
убирать или добавлять указанное количество палочек для получения
новой заданной фигуры развиваются творческая мыслительная
деятельность, гибкость ума.
ппп
Переложить 3 палочки так, чтобы из кораблика получить 4 треугольника
Задания на преобразование фигур путем удаления
или добавления заданного количества палочек.
(Приложение 3)
8 6 3 2 5
63 9 8
Из 7 палочек собери цифру 8.
-Подумайте, что надо сделать , что бы из цифры 8 сделать цифру 6?
(убрать , добавить или переложить палочки?)
– Что надо сделать, чтобы из цифры 6 получилась цифра 3? И т.д.
Из 5 палочек собери весы. Что изменится,
если на одну чашу положить
а
арбуз, а на другую яблоко?
Более сложный этап – коллективное решение общей
головоломки на трансформацию фигур из палочек. 4-5 детей
получают одно задание и общими усилиями ищут варианты
решения головоломки.
На этом этапе дети не только учатся логически мыслить, но и
могут работать в команде, выдвигать свои версии решения,
слушать товарища, радоваться общему успеху.
Из 8 палочек собери лошадку.
Лошадка поела траву и захотела пить. Переложи 3 палочки так, чтобы
лошадка повернулась к ведру.
Образцы изображений
в натуральную величину
(Приложение 1)
Уменьшенные
схематичные образцы
(Приложение 2)
Задания на преобразование
фигур путем удаления или
добавления заданного
количества палочек.
(Приложение 3)
Задания на преобразование фигур
путём перекладывания палочек.
(Приложение 4)
Задания на преобразование фигур
путём перекладывания палочек.
(Приложение 4)
Игра со счётными палочками – это занятие, которое способствует
развитию детей, а ещё доставляет им удовольствие и вызывает
Литература:
1.Р.И.Лалаева, А.Гермаковска Предупреждение нарушений в
овладении математикой у дошкольников: Профилактика
дискалькулии: Учебно-методическое пособие.
– СПб.: КАРО,2007. – 136с +32с.цв.вкл.
2.Л.Смирнова Палочки для пальчиков девочек и мальчиков.
Предшкольный портфель. Газета «Дошкольное образование»
№22-24/2009
3.О.А.Глушакова, С.И.Дедова Весёлые счётные палочки.Мозырь:Содействие, 2011.- 76 с: ил
Интернет-источники:
https://pandia.ru/text/80/609/371.php
English Русский Правила
Пальчиковые игры и игры на развитие мелкой моторики
Вы можете изучить и скачать доклад-презентацию на тему Пальчиковые игры и игры на развитие мелкой моторики. Презентация на заданную тему содержит 10 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас – поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Образование» Пальчиковые игры и игры на развитие мелкой моторики
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Пальчиковые игры и игры на развитие мелкой моторики Пальчиковые игры и игры на развитие мелкой моторики
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
«Шифр»
Чтобы враг не мог перехватывать сообщения из разных частей нашей армии, наши солдаты придумывали различные шифры.
Давайте и мы попробуем передать послание, используя шифр. Ритмическое упражнение “Шифр”. Задача малыша – посмотреть на карточку и отстучать послание таким образом, что на большую букву О мы делаем один длинный хлопок, на маленькую о – два маленьких хлопка.
Слайд 6
Описание слайда:
Работа со счетными палочками или ватными палочками А ты знаешь, что на Великой Отечественной Войне солдатам за проявленные смелость и мужество давали награды и ордена? А самый главный орден, орден Героя, был сделан в форме звезды, потому что звезда – это символ Красной армии. Давайте и мы попробуем выложить такую звезду. Так же можно предложить малышу выложить танк и корабль.
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Для того, чтобы фашистская военная техника не могла проехать, наши солдаты и простые люди сооружали противотанковые ежи.
Давайте мы тоже попробуем сделать такие. Нам понадобится шарик из пластилина, спички, зубочистки или счетные палочки. Задача ребенка – воткнуть палочки, спички или зубочистки в пластилиновые шарики. Мы получим противотанкового ежа.
Для того, чтобы фашистская военная техника не могла проехать, наши солдаты и простые люди сооружали противотанковые ежи. Давайте мы тоже попробуем сделать такие. Нам понадобится шарик из пластилина, спички, зубочистки или счетные палочки. Задача ребенка – воткнуть палочки, спички или зубочистки в пластилиновые шарики. Мы получим противотанкового ежа.
Слайд 9
Описание слайда:
Игра “Пограничный столб”
Рассмотрите с малышом карточки с изображением пограничных столбов или столб, сделанный из кубиков лего. Расскажите малышу, что именно такие столбы стояли на пути у наших врагов. “Посмотри, какого он цвета? Сколько красных и зеленых кубиков (полосок)?”.
Предложите малышу сделать (нарисовать, раскрасить) точно такой же столб (следующий слайд)
(Ребенок строит или раскрашивает столбик по образцу. Важно, чтобы ребенок в точности повторял последовательность цветов).
Слайд 10
Описание слайда:
Tags Пальчиковые игры и игры на развитие мелкой моторики
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
21 Упражнения и идеи по счету без пропусков для учащихся начальной школы математики
Счет без пропусков — это важный навык, который естественным образом приводит детей к умножению. Дети могут научиться пропускать счет наизусть, но они получат больше пользы, увидев, как эта концепция соотносится с реальной математикой. Попробуйте эти действия и идеи, чтобы помочь это осуществить!
1.
Спойте несколько песен со счетом. У мистера Р так много песен со счетом! Они гораздо веселее, чем просто повторять «пять, десять, пятнадцать, двадцать…». Найдите их все здесь.
РЕКЛАМНОЕ ОБЪЯВЛЕНИЕ
2. Прочтите книгу по подсчету пропусков.
Преподавание по учебной программе с помощью одной или нескольких из этих милых книжек с картинками, в которых подсчет пропусков является частью истории.
- 100-й день забот
- Отважные обезьяны на параде
- Сто разгневанных муравьев
- Одна улитка, десять краб
- Два способа счета до десяти
3. Превратите полоски предложений в настенную диаграмму.
Такой простой способ сделать красочную настенную диаграмму! (Нужны полоски с предложениями? Попробуйте этот хорошо зарекомендовавший себя набор на Amazon.)
Подробнее: This Reading Mama
4. Сгруппируйте объекты, чтобы представить концепцию.
Дошкольники и детсадовцы начинают осваивать этот навык с группировки предметов. Получите бесплатные страницы для печати для использования с этим занятием по ссылке.
Подробнее: File Folder Fun
5. Пропустить счет с отпечатками ладоней.
Используйте отпечатки ладоней ваших учеников, чтобы продемонстрировать счет пятерками и десятками. Такой милашка!
Узнайте больше: Место раннего обучения Лиз
6. Играйте в классики, пропуская счет.
Это классическое упражнение для подсчета пропусков. Начните просто, пометив блоки цифрами 2 или 5. Смешайте вещи, добавив некоторые варианты, чтобы сделать по пути.
Подробнее: Math Geek Mama
7. Кружевные тарелки по мере счета.
Это задание легко настроить, и дети могут даже переворачивать тарелки, чтобы проверить свои ответы! Узнайте, как их сделать, по ссылке.
Подробнее: 123Homeschool4Me
8. Решите лабиринт со счетом.
Пройдите лабиринт, чтобы попрактиковаться в счете. Получите бесплатные печатные формы по ссылке ниже.
Подробнее: Признания школьника
9. Сосчитай и соедини точки.
Соедините точки очень популярны, и вы можете найти множество доступных в Интернете. Сначала попробуйте эти бесплатные примеры — вашему классу они обязательно понравятся!
Подробнее: Рабочие листы сайта
10. Используйте скрепки на бумажной тарелке.
Готовы поспорить, что у вас остались бумажные тарелки после шнуровки, так что соедините их со скрепками, чтобы получить еще одну идею, которая также способствует развитию мелкой моторики.
Подробнее: Творческое семейное развлечение
11. Добавьте немного движения.
Вместо того, чтобы просто повторять цифры, поднимайте детей и двигайтесь, пока они пропускают счет! (Дополнительные математические идеи см. здесь.)
Узнайте больше: Обучение с Terhune
12. Пропускайте искусство счета.
Эта идея объединяет группировку с пуантилизмом, техникой создания искусства из крошечных точек. Все, что вам нужно, это ватные палочки и краска для плакатов.
Подробнее: Творческое семейное развлечение
13. Возьмите несколько кубиков LEGO.
Кто не любит использовать LEGO в классе? Различные размеры кирпичей идеально подходят для подсчета пропусков.
Подробнее: Royal Baloo
14. Наполните стаканчики кубиками.
Вы также можете использовать LEGO с этим или вытащить свои блоки Unifix. Дети строят стопки и наполняют стаканчики.
Подробнее: Powerful Mothering
15. Соберите деревянные палочки для рукоделия.
Деревянные палочки для рукоделия имеют множество применений в классе. Пометьте их цифрами и используйте для тренировки счета! Вы также можете попросить детей нарисовать одну палочку и попрактиковаться в счете в большую сторону от этого числа. (Возьмите эти красочные палочки для рукоделия с Amazon здесь.)
Подробнее: Simply Kinder
16. Поставьте на карту немного денег.
Пятаки и десятицентовики — отличные инструменты для счета, а дети также потренируются в деньгах.
Подробнее: Набор инструментов ОТ
17. Бросьте счетные кости с пропуском.
Попросите детей бросить кости, чтобы узнать, по какому числу они будут считать. Это дает практику вплоть до счета до 12.
Подробнее: 3 динозавра
18. Прикрепите прищепки к измерительной ленте.
Такое простое занятие — нужны только прищепки и сантиметровая лента!
Подробнее: Thriving STEM
19. Создание воздушных змеев для подсчета пропусков.
Эта идея для бесплатной распечатки делает воздушных змеев со счетными хвостами. Повесьте их в своем классе, когда закончите!
Подробнее: Рабочие листы и игры для детского сада
20. Соберите головоломку со счетом.
Головоломки подсказывают детям, нужна ли им помощь, но они действительно тайно учатся считать.
Подробнее: Life Over Cs
21. Сделать плакаты с цифрами.
Вы можете купить набор этих симпатичных цифр по ссылке ниже или разбить своих детей на группы и попросить их вырезать и подписать свои собственные для демонстрации.
Узнать больше: Блог из пруда
Десять фреймов — отличный инструмент для обучения счету в прыжках.
Найдите здесь 10 рамочных занятий и идей.
Включите больше математики во время чтения с этими 17 иллюстрированными книгами о математике.
Этот пост содержит партнерские ссылки Amazon. WeAreTeachers может получить очень небольшую комиссию, когда вы покупаете по этим ссылкам.
Манипуляторы в начальных классах
В отчете Ofsted за 2012 г. «Сделано на заказ» говорится, что, хотя манипуляторы используются в некоторых начальных школах для поддержки преподавания и обучения, они не используются так эффективно и широко, как могли бы быть. В этой статье рассматриваются некоторые исследования их использования и предлагаются некоторые предложения о том, как использовать
практический аппарат может поддерживать математическое мышление детей, рассуждение и решение проблем. Дженни опирается на свой собственный опыт наблюдения за использованием манипулятивных средств в классах венгерского языка и делает ссылки на некоторые сложные задания с веб-сайта.
Введение
В прошлом году я провел много времени, работая с учителями и детьми над тем, как лучше всего обучать арифметическим понятиям и процедурам детей в начальных школах. Это дало мне много времени, чтобы рассмотреть способы, которыми мы используем аппаратуру различного типа, чтобы помочь детям думать и помочь им следовать, иногда сложным, процедурам для решения арифметических задач. в моем собственном
обучая детей и учителей, моя главная задача всегда состоит в том, чтобы помочь им разобраться в математике, которую мы используем, и эта идея лежит в основе всего, что я делаю профессионально. Центральная важность этого осмысленного процесса была основным выводом моей диссертации, завершенной почти десять лет назад.
У нас есть тенденция принимать различные представления и артефакты в зависимости от их пригодности для определенного раздела математики, часто арифметической процедуры, и при этом лишать детей, которых мы учим, возможности, которые могут быть ценными для них, чтобы понять смысл конкретный ресурс в отношении их собственного понимания вовлеченных концепций.
Артефакт становится реквизитом
поддерживать следующие процедуры. Так не должно быть, да и в других культурах это не так.
Так что же говорят исследования о том, как используются практические устройства и изображения? Недавний метаанализ (Carbonneau, K.J., Marley, S.C. & Selig, J.P. 2013) исследований сравнил использование манипулятивных или практических практических инструментов в обучении математике с преподаванием, основанным только на абстрактных математических символах. Они нашли статистически значимые доказательства того, что
манипуляции оказали положительное влияние на обучение с размерами эффекта от малых до умеренных. Сосредоточив внимание на конкретных результатах обучения, исследование показало, что размеры эффекта были от среднего до большого в случае удержания, но небольшие в отношении решения проблем, переноса и обоснования. Это убедительное свидетельство в пользу использования манипулятивных средств, основанное на данных, собранных в 55 исследованиях.
с участием более 7000 учащихся от детского сада до школьного возраста. Однако, несмотря на то, что это исследование предполагает, что использование манипулятивных средств полезно для обучения математике, способы их использования также чрезвычайно важны.
Многие учителя, с которыми я работал в течение последнего года, были в замешательстве относительно того, какие манипулятивные средства использовать в определенных контекстах, и я видел довольно много практики, когда одно конкретное манипулятивное средство могло появиться, чтобы научить данному понятию, а затем исчезнуть. больше никогда не увидишь в классе. За
детей это может сделать практический аппарат довольно загадочным и побудить их думать, что каждое манипулятивное действие имеет определенную функцию по отношению к конкретной задаче: мы используем бусинки для счета вперед и назад по числовой прямой, но затем переключаемся на использование сотен в квадрате для считайте шагами по 10. Это вполне может означать, что дети путаются в том, как каждое манипулятивное действие
отражает аспекты системы счисления и рассматривать ее исключительно как дополнение к выполнению определенной процедуры.
(В качестве альтернативного подхода к сотне квадратов, который рассматривает его структуру и значение, вы можете попробовать это задание: 100 Square Jigsaw.)
манипуляторы в классе. Таким образом, это будет только начало для вас, как практикующих, но я надеюсь, что это даст вам возможность изучить свою собственную практику и изучить способы, которыми вы используете манипулятивные средства с детьми. Я, как всегда, буду рад узнать, как у вас дела. Моя собственная работа зависит от получения такой обратной связи, и вы можете связаться со мной через NRICH.
Что такое манипуляции и как они используются?
Итак, что я подразумеваю под манипулятивными действиями? Я имею в виду все практические приспособления, которые мы используем в наших классах, такие как многозвенные кубы, прибор Дьенеса, счетчики, счетчики разрядов, нитки для бус, стержни Кюизенера, палочки, разделенные на 10 равных секций, а также те, которые используют числа, такие как карточки разрядов, сто квадратов, цифровые карты, игральные кости, домино и так далее.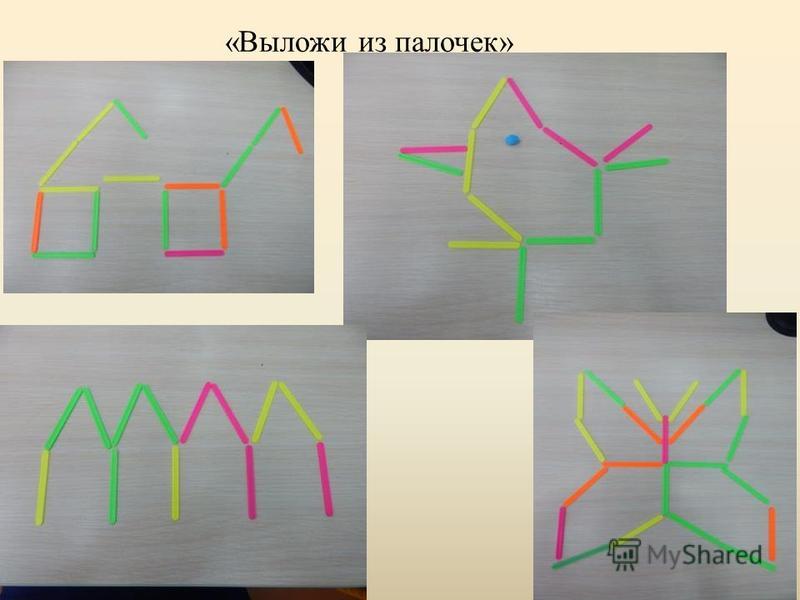
Этот список не является исчерпывающим, и я
конечно, вы можете добавить свои собственные избранные. Все они представляют собой практичные элементы набора, которые дети могут брать в руки и которыми они могут манипулировать, и которые имеют присущие им различные аспекты чисел и системы счисления, которые могут помочь детям справиться с очень абстрактными понятиями чисел, отношениями между ними и как они работают в системе счисления. При подготовке к написанию
В этой статье я прочитал много недавних исследований по этому вопросу, а также опирался на свои собственные исследования в Венгрии и Англии, и это привело меня к ряду выводов, которые, я надеюсь, помогут вам в ваших классах.
История использования манипуляторов в классе насчитывает более пятидесяти лет. Краткое историческое резюме этого предлагает Патрисия Мойер (2001). Она комментирует работу Жана Пиаже (1951), в которой предполагалось, что дети в возрасте от семи до десяти лет работают преимущественно конкретными способами и
что абстрактные понятия математики могут быть доступны им только через воплощение в практических ресурсах.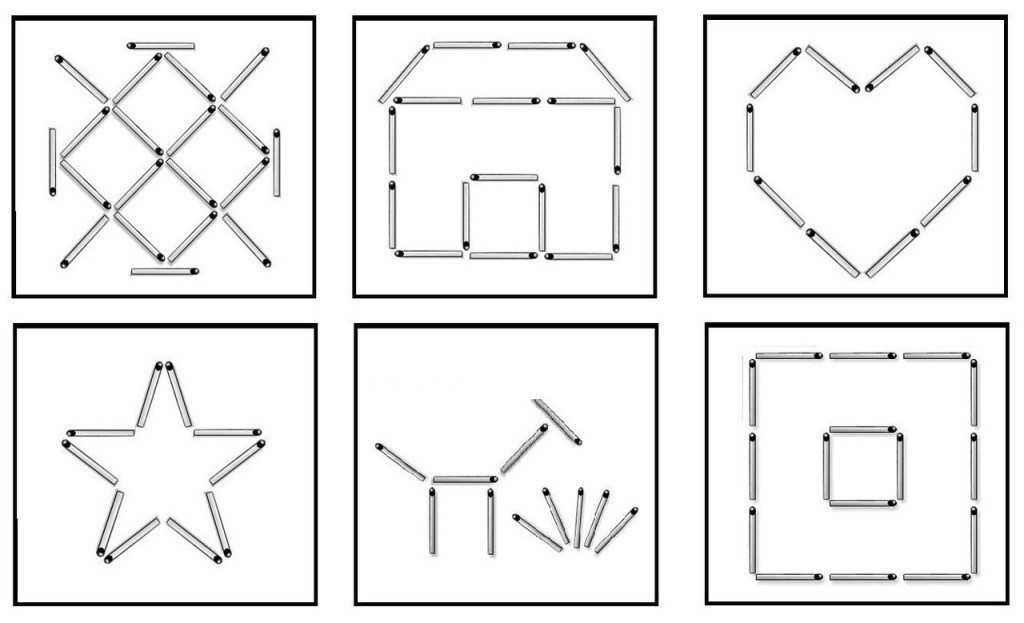
Позже это было развито Золтаном Динесом (1969), разработавшим свой базовый аппарат, а также Калебом Гаттеньо и Жоржем Куизенером (19).54) с их развитием стержней Кюизенера. Можно найти занятие с использованием стержня Кюизенера аналогично тому, как это делают сторонники Гаттеньо и Кюизенера.
здесь: Поезда одинаковой длины. Разработка Джеромом Брунером (1966) энактивных, иконических и символических способов работы привлекает дополнительное внимание к роли конкретного и репрезентативного в развитии абстрактной работы в символических сферах. Более поздние работы 80-х и 90-х годов развивают это дальше, используя конструктивистские теории для разработки идей обучения, которые
увидьте, как учащийся конструирует свои собственные значения, связывая конкретные манипуляции с абстрактными символами способами, которые имеют для них смысл. Мойер (2001) отмечает, что:
Манипулятивные материалы — это объекты, предназначенные для явного и конкретного представления абстрактных математических идей.
Они имеют как визуальную, так и тактильную привлекательность, и учащиеся могут манипулировать ими посредством практического опыта. (стр.176)
Далее она указывает, что часто студенты используют манипуляции, чтобы следовать заученной процедуре, не имея представления о том, как аппарат отражает математические структуры. Изучение того, как аппарат отражает и воплощает математическую структуру, имеет решающее значение для его эффективного использования и для процесса обеспечения прозрачности значения манипуляции для пользователя. Еще раз мы вернуться к понятию учащегося как создателя смысла в классе и необходимости предложить учащимся возможности понять как используемые манипулятивные средства, так и их отношение к математическим идеям и проблемам, для решения которых они используются.
Мойер также обращает внимание на необходимость знакомства учащегося с ресурсом, который используется в качестве инструмента, чтобы снизить когнитивные потребности при его использовании.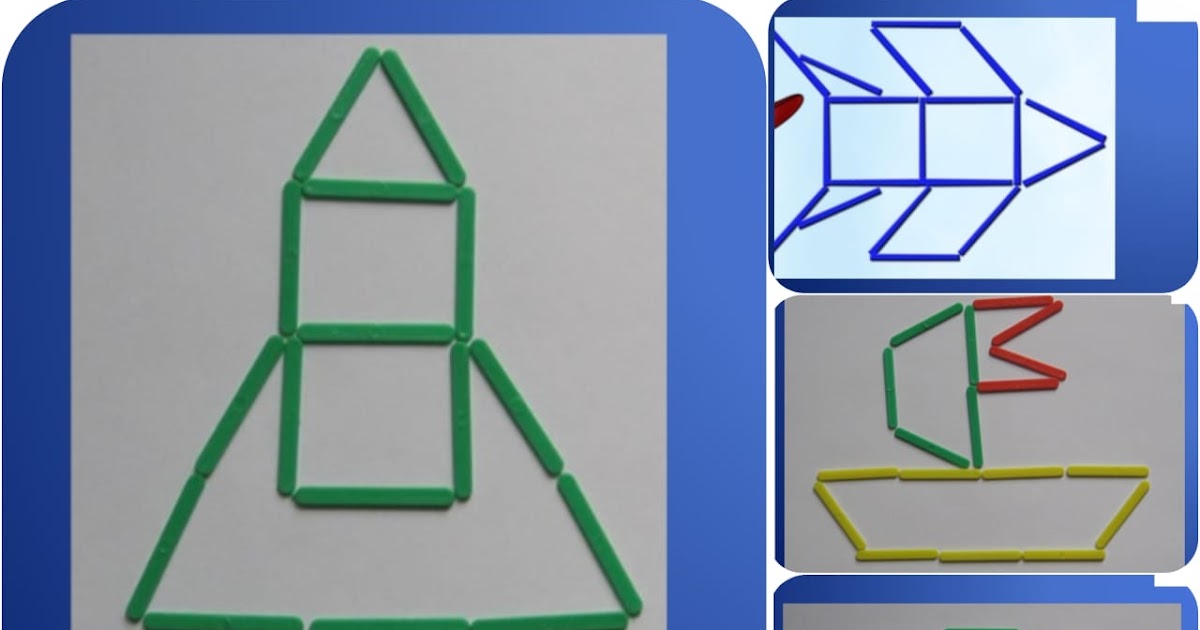
Если учащийся хорошо осведомлен о различных атрибутах ресурса, вряд ли это облегчит его использование в качестве представления конкретной математической структуры. Я, конечно, осознавал это в своем собственном обучении:
много играть с стержнями Кюизенера и знакомиться с пропорциональными отношениями между стержнями разных цветов, прежде чем учащиеся смогут использовать их для помощи в решении сложных вычислений, таких как сложение дробей. При более элементарном использовании желание строить стены из маленьких цветных палочек может помешать рассмотреть, какие пары стержней эквивалентны друг другу.
из которого могут быть получены числовые связи. В венгерских классах детям дошкольного возраста дается много возможностей свободно играть со стержнями до того, как их математическая структура и отношения будут выяснены, когда они пойдут в формальное школьное образование в возрасте семи лет. Одним из ресурсов, который я часто использую в работе над геометрией, являются петли из веревки, и я обнаружил, что если я не позволю изучающим какие-либо
В возрасте имеют возможность свободно поиграть со струной некоторое время, прежде чем ставить математическую задачу, они будут отвлекаться на желание поиграть и изучить различные свойства петли струны – обычно используя ее для игры в «Колыбель для кошки»!
Итак, как только учащиеся получат доступ к ряду манипулятивных средств, с которыми они знакомы и которые имеют присущие им определенные аспекты математической структуры, как мы должны помочь им в их использовании? Исследование Мойера является важным исследованием, в котором основное внимание уделяется фактическим наблюдениям за тем, как учителя используют манипулятивные средства, и вопросам, почему они используют их именно так.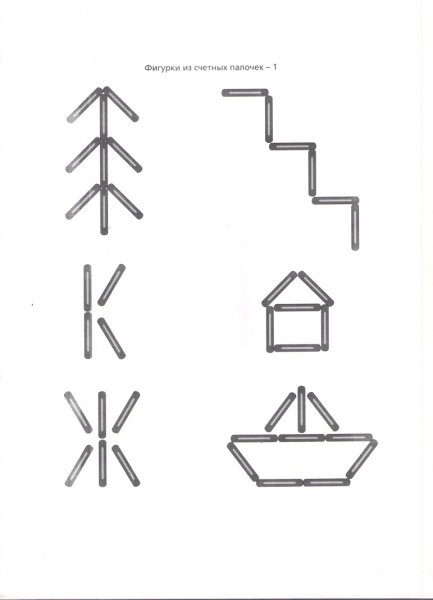
Все десять учителей участвовали в
программа обучения, которая предоставила им набор инструментов математических манипуляций для использования в их классах и предложила им некоторую профессиональную поддержку в этом.
Участвующие учителя приводили различные причины использования манипулятивных средств. Одним из них было то, что использовать их было приятнее, чем заниматься математикой, которая была исключительно абстрактной и символической. Это подтверждается наблюдениями исследователя о том, что учащиеся были активны, вовлечены и заинтересованы в занятиях при использовании манипулятивных средств. Удовольствие, которое испытывают учителя и учащиеся при использовании
манипуляции означали, что учителя, как правило, использовали их в качестве награды за хорошее поведение, а не только тогда, когда они были бы полезным дополнением к обучению. Некоторые учителя использовали манипуляторы только в конце недели, в конце года или когда у них было время. Похоже, они рассматривали их использование не как неотъемлемую часть основной части учебной программы, а скорее как дополнение, улучшающее
удовольствие.
Это резко контрастирует с использованием манипулятивных средств, которые я наблюдал в Венгрии. Там использование манипулятивных средств считается центральным элементом раннего развития математических идей, особенно у детей в возрасте до одиннадцати лет. Один урок, который я наблюдал, был посвящен знакомству детей с числом шесть, и в нем использовались следующие манипуляции: домино,
Жезлы Кюизенера, аналоговые циферблаты, венгерские цифры и домино. Позже на неделе также использовались монеты. Кроме того, дети считали наборы предметов, наборы из шести действий и определяли наборы из шести предметов по картинкам. Они показали рисунок пальца, обозначающий шесть, определили римские цифры, обозначающие шесть, и
наконец, сам символ 6. Это концентрированное представление множества репрезентаций и манипулятивных действий, раскрывающих «шестерку», позволило детям обобщить понятие «шестерки» по всем этим различным проявлениям и, я бы предложил, абстрагироваться от более глубокого понятия о качествах шестерки.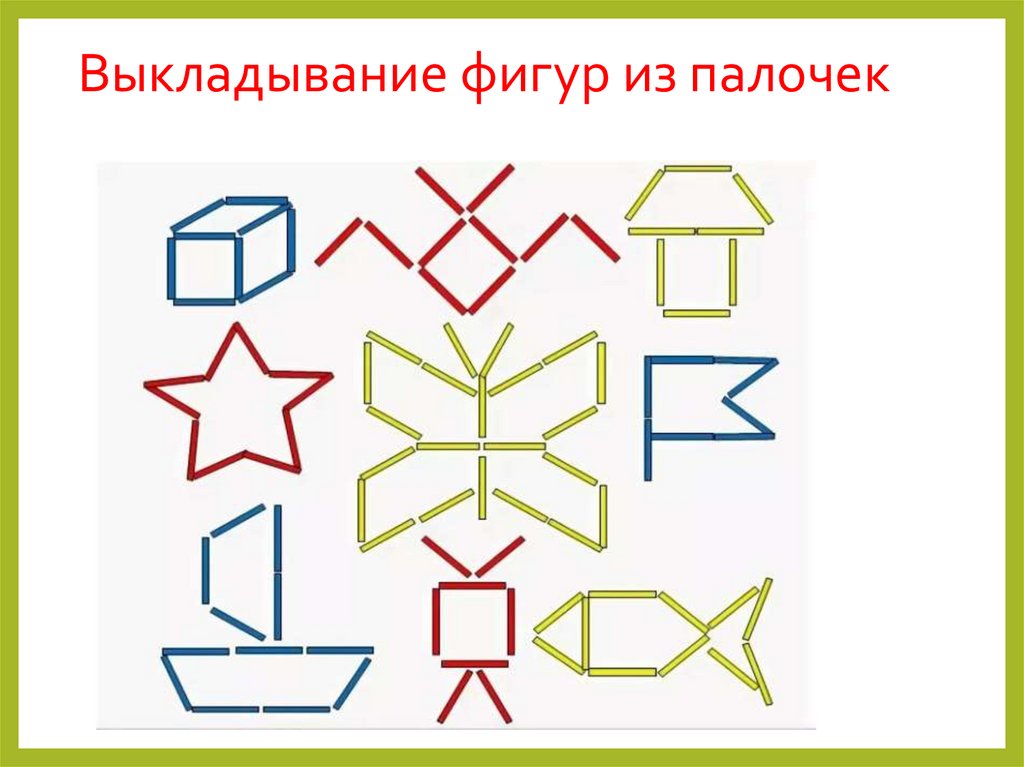
Они сделали стены из стержней Кюизенера той же длины, что и шесть стержней, и наборы домино.
с шестью пятнами на них и таким образом получили конкретный опыт того, как шесть можно разделить на два набора.
Этот урок описан в статье «От предметов и образов к математическим идеям». Связанные действия, ориентированные на несколько представлений, можно найти здесь: сопоставление чисел и сопоставление дробей. По моим наблюдениям, венгерские учителя предлагают маленьким детям такой широкий спектр конкретных математических занятий. концепций в надежде, что они будут обобщать их и абстрагировать центральный математический пункт, который делается.
Одно из исследований, которое произвело на меня наибольшее впечатление, было опубликовано Лио Москардини (2009 г.), в которой он анализирует использование аппарата при обучении вычитанию детей с умеренными трудностями в обучении. Хотя дети с особыми потребностями находятся в центре его внимания, его анализ и выводы не менее важны для всех учащихся.
Он проводит ценное различие между использованием
манипуляторы как инструменты и как костыли. Он предполагает, что манипуляторы можно рассматривать как костыли, когда дети используют их, не понимая, чтобы следовать заученной процедуре для решения математической задачи. В данном случае его исследование показало, что детское обучение невозможно перенести даже на абстрактную работу с символическими представлениями той же проблемы, не говоря уже о решении новой задачи.
задача поставлена по другому сценарию. В тех случаях, когда детям предлагалось разобраться в математике, используя манипуляторы в качестве инструментов для решения поставленных задач, они могли перенести свои знания в новые ситуации, а также решить проблемы, поставленные символически.
Тематические исследования, о которых рассказывает Москардини, показывают несколько поразительных примеров использования манипулятивных средств различными способами: от слепого следования процессу до использования манипулятивных средств для демонстрации результата однокласснику.
В одном примере, который он описывает, один учащийся объяснял другому решение проблемы владения мячом, которое одна команда имела в игре.
футбол, если первая сторона владела мячом 56 минут. Используя базовый аппарат Дьенеса, учащийся, выступавший в качестве наставника для одноклассника, смог продемонстрировать, что решение было 34, а не ответ 33, который получил его одноклассник, неправильно подсчитав количество баллов за свое решение. Решающим компонентом эффективного использования манипулятивных средств здесь, по-видимому, является акцент.
на возможности для детей понять аппарат и использовать его для поддержки своих собственных аргументов. У манипулятивных средств действительно есть место в качестве вычислительных инструментов для поддержки различных стратегий расчета и демонстрационных инструментов для объяснения процедуры, но только когда учащиеся сами используют артефакты для поддержки своих собственных процессов осмысления, они начинают видеть их силу.
как инструменты для вычислений, а не просто полагаться на них как на костыли, чтобы слепо следовать обученным процедурам.
Мое венгерское исследование подтверждает это. В течение последних трех учебных лет я слежу за успеваемостью одного и того же класса, а также изучаю практику воспитателя детского сада (дети 3-6 лет) и воспитателя 1/2 класса (дети 7-8 лет). лет). В недавний визит я наблюдал урок по дробям, на котором учитель использовал представления дробей с стержнями Кюизенера, как дроби различной формы, включая прямоугольники, круги и неправильные формы, как числа на числовой прямой, как пропорции параллельных стержней, чтобы можно было проводить сравнения. И снова в качестве дополнения к обобщению использовались манипуляции: на этот раз о природе дробей как чисел.
Что это значит для меня в моем классе?
Вот к чему ведут нас исследования; предполагается, что манипуляторы могут быть мощными инструментами для поддержки осмысления, математического мышления и рассуждений, когда они используются в качестве инструментов для поддержки этих процессов, а не в качестве дополнения к слепому следованию обученной процедуре для получения ответа.
Вопрос для нас, учителей, заключается в следующем: как мы можем использовать эти данные для развития практики?
в наших классах, которые поддерживают это? В контексте, когда основными целями новой учебной программы будет развитие беглости учащихся в математических процедурах, а также развитие способности решать проблемы и рассуждать математически, использование манипулятивных инструментов в качестве инструментов играет ключевую роль. Как это обычно бывает в математическом образовании, исследование показывает, что дело не только в том, что
мы используем то, что будет иметь значение для обучения наших учеников, но как мы это используем. У меня есть следующие предложения для вас по развитию вашего использования манипулятивных средств, чтобы дети начали рассматривать их как инструменты, а не костыли.
Во-первых, я бы открыл доступ ко всем ресурсам, к которым у вас есть доступ, и позволил бы детям свободно выбирать, что использовать для моделирования любой проблемы, которую они могут решить.
Я бы позаботился о том, чтобы дети всех возрастов имели такой доступ от 3 до 11 лет и старше. Я бы позаботился о том, чтобы спектр ресурсов был как можно шире, так как разные манипуляторы имеют разную силу для
различные проблемы и процедуры. Я знаю, что это может быть проблематично в некоторых контекстах, и, возможно, такое изменение необходимо вносить постепенно, позволяя детям не перегружаться выбором или вести себя «глупо» в отношении ресурсов, но как только культура класс принимает это во внимание, все это должно стать частью вашей классной рутины. Это может
также стоит проводить специальные уроки для детей, чтобы изучить конкретный манипулятор и изучить его силу и потенциал. Это может быть сосредоточено на том, что дети замечают в ресурсе и как он связан с числами и системой счисления.
Во-вторых, я бы начал давать детям больше возможностей демонстрировать вам и друг другу математические истины, используя ряд артефактов. Например, при рассмотрении вычисления 47-28 дети могут использовать бусины, аппарат Дьенеса, пустую числовую строку, квадрат 100, счетчики разрядов и наборы предметов.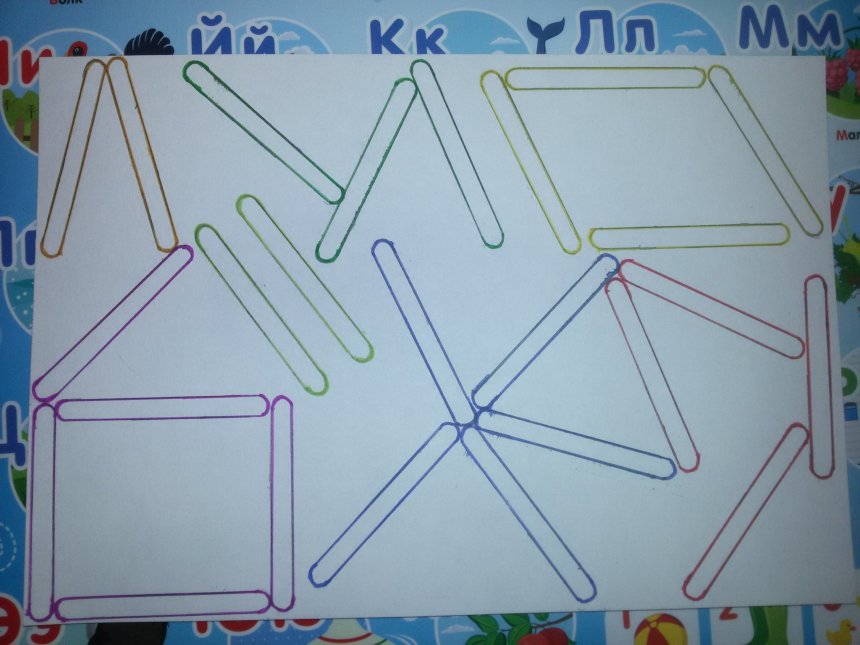
Сравнивая результаты, которые можно легко зафиксировать как
изображения на интерактивной доске с помощью веб-камеры или даже короткие видеоролики на DVD, дети могут изучить структуру вычисления и полезность манипуляторов как инструментов для его решения. Как различные артефакты помогают понять процесс расчета? Понятие задач «Покажи мне» также может стать частью культуры в классе.
В-третьих, использование манипуляторов может быть очень полезным для объяснения смысла и обоснования использования различных математических процессов, таких как компактные алгоритмы. Предлагая учащимся использовать манипуляторы для демонстрации результатов и доказательства их истинности, мы в некотором смысле развиваем их математическое мышление на глубоком уровне, необходимом для поддержки их концептуального понимания. В моем
В своей собственной работе в прошлом году я продемонстрировал, как можно раскрыть смысл алгоритма короткого деления, и несколько учителей, с которыми я поделился этим, сказали, как сильно это помогло им понять, почему работает то, чего они никогда до конца не понимали.
Однако сила не в демонстрации, а в возможности осмыслить процесс с помощью
манипулятивные ресурсы. Донна Лэнгли написала о своем опыте наблюдения и поделилась этим со своими коллегами в статье для Primary Mathematics.
Конечно, существует целый ряд виртуальных манипуляторов, доступных для поддержки развития математического обучения детей, и многие из них доступны на веб-сайте NRICH, например Cuisenaire Environment. Я бы рекомендовал их вам с оговоркой, что эти виртуальные ресурсы находятся на один шаг дальше от конкретных ресурсов и еще на один шаг на пути к символическим. представления. Я бы назвал их знаковыми в терминах Брунера. Таким образом, они не заменяют настоящую вещь, но могут предложить способ обмена результатами со всеми классами, а также для детей, чтобы продемонстрировать их на отдельных компьютерах, как только они познакомятся с конкретным манипулятивным средством.
В этой статье я сосредоточился исключительно на ресурсах для поддержки изучения арифметики и проигнорировал те, которые помогают с геометрическими темами, но те же аргументы справедливы, и есть аналогичные интерактивные ресурсы, связанные с ними.
Эта область должна быть предметом дополнительного письма. Итак, в заключение я предполагаю, что жизненно важно, чтобы при использовании
манипуляций с детьми, мы исходим из того, что эти инструменты будут полезны нашим учащимся в их стремлении стать математиками только в той мере, в какой мы позволяем им использовать манипуляции для понимания математики и обращаем их внимание на то, как они это делают.
Ссылки
Брунер, Дж. (1960) Процесс образования. Кембридж, Массачусетс: Издательство Гарвардского университета.
Карбонно, К. Дж., Марли, С. К. и Селг, С. К. (2013) Метаанализ эффективности обучения математике с использованием конкретных манипуляций. Журнал педагогической психологии. Vol 105 (2) pp380-400
Dienes, Z. (1969) Создание математики. Лондон: Hutchinson Education
Gattegno, C. & Cuisenaire, G. (1954) Цифры в цвете. Лондон: Хайннеман
Лэнгли, Д. (2013) Подразделение с Диенесом. Первичная математика 17 (2) стр. 13–15.