Примеры в 4 действия 3 класс: Карточки по математике на порядок действий 3 класс | Методическая разработка по математике (3 класс) на тему:

“Порядок действий в числовых выражениях”.

(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =
35 + (7 ∙ 4 + 47 – 25) : 10 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =

 

(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =

35 + (7 ∙ 4 + 47 – 25) : 10 =

18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =

80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =

(64 – 26) + (35 : 7 + 45) : 10 =

70 – (32 + 19) + 24 – (60 : 10 + 28) =

24 : 6 + 42 : 7 =

56 : 8 – 35 : 5 =

40 – 24 : 8 =

21 : 3 + 28 :7 =

 

(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =

35 + (7 ∙ 4 + 47 – 25) : 10 =

18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =

80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =

(64 – 26) + (35 : 7 + 45) : 10 =

70 – (32 + 19) + 24 – (60 : 10 + 28) =

24 : 6 + 42 : 7 =

56 : 8 – 35 : 5 =

40 – 24 : 8 =

21 : 3 + 28 :7 =

 

(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =

35 + (7 ∙ 4 + 47 – 25) : 10 =

18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =

80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =

(64 – 26) + (35 : 7 + 45) : 10 =

70 – (32 + 19) + 24 – (60 : 10 + 28) =

24 : 6 + 42 : 7 =

56 : 8 – 35 : 5 =

40 – 24 : 8 =

21 : 3 + 28 :7 =

 

(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =

35 + (7 ∙ 4 + 47 – 25) : 10 =

18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =

80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =

(64 – 26) + (35 : 7 + 45) : 10 =

70 – (32 + 19) + 24 – (60 : 10 + 28) =

24 : 6 + 42 : 7 =

56 : 8 – 35 : 5 =

40 – 24 : 8 =

21 : 3 + 28 :7 =

70 : 7 + 6 · 8 – 42 : 7 =

24 : 6 · 3 : 2 · 5 : 3 · 7 =

92 – (40 – 21 + 37) + 46 =

72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =

35 : 5 · 4 : 7 · 9 : 6 =

9 · 4 : 6 · 7 : 42 · 64 : 8 =

(4 ∙ 9 + 28) – (27 : 3 + 15) =

82 – 44 · 0 – 82 =

(31 + 61 – 47) · 0 =

18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =

 

70 : 7 + 6 · 8 – 42 : 7 =

24 : 6 · 3 : 2 · 5 : 3 · 7 =

92 – (40 – 21 + 37) + 46 =

72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =

35 : 5 · 4 : 7 · 9 : 6 =

9 · 4 : 6 · 7 : 42 · 64 : 8 =

(4 ∙ 9 + 28) – (27 : 3 + 15) =

82 – 44 · 0 – 82 =

(31 + 61 – 47) · 0 =

18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =

 

70 : 7 + 6 · 8 – 42 : 7 =

24 : 6 · 3 : 2 · 5 : 3 · 7 =

92 – (40 – 21 + 37) + 46 =

72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =

35 : 5 · 4 : 7 · 9 : 6 =

9 · 4 : 6 · 7 : 42 · 64 : 8 =

(4 ∙ 9 + 28) – (27 : 3 + 15) =

82 – 44 · 0 – 82 =

(31 + 61 – 47) · 0 =

18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =

 

70 : 7 + 6 · 8 – 42 : 7 =

24 : 6 · 3 : 2 · 5 : 3 · 7 =

92 – (40 – 21 + 37) + 46 =

72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =

35 : 5 · 4 : 7 · 9 : 6 =

9 · 4 : 6 · 7 : 42 · 64 : 8 =

(4 ∙ 9 + 28) – (27 : 3 + 15) =

82 – 44 · 0 – 82 =

(31 + 61 – 47) · 0 =

18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =

 

70 : 7 + 6 · 8 – 42 : 7 =

24 : 6 · 3 : 2 · 5 : 3 · 7 =

92 – (40 – 21 + 37) + 46 =

72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =

35 : 5 · 4 : 7 · 9 : 6 =

9 · 4 : 6 · 7 : 42 · 64 : 8 =

(4 ∙ 9 + 28) – (27 : 3 + 15) =

82 – 44 · 0 – 82 =

(31 + 61 – 47) · 0 =

18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =

34 · 2 – 48 : 8 =

56 : 7 + 42 : 6 =

5 · (18 : 3) + 58 =

8 ∙ 9 + (70 – 56) =

48 : 6 + 24 : 6 =

9 · (12 : 6) + 47 =

6 · 2 + (90 – 73) =

63 : 7 + 28 : 7 =

48 : 8 · 2 : 3 · 0 : =

56 : 8 + 7 · 7 =

 

35 · 2 – 32 : 8 =

45 : (33 – 24) ∙ 6 =

63 + 27 : (30 : 10) =

60 – 54 : 6 =

60 – 18 : 2 ∙ 3 =

96 – (35 – 5) : 6 =

49 : 6 ∙ 3 : 0 =

72 : 8 + 63 : 7 + 81 : 9 =

60 : 2 + 60 : 3 + 100 : 2 =

27 : 3 ∙ 2 : 6 ∙ 3 ∙ 4 =

 

81 : 9 + 72 : 8 =

54 : 6 – 15 : 15 =

0 : 12 + 13 ∙ 2 =

18 : 1 ∙ 0 + 99 =

56 : (24 : 4 · 3 : 9) + (40 – 25 : 25) =

64 – (80 – 38 – 29) + (90 – 46 + 17) =

4 · (71 – 58) – (60 – 40 : 4) =

46 + (91 – 76) + 19 – (63 – 38) =

35 + 57 – (62 – 29) – (71 – 48) =

56 – 8 – 9 – ( 7 + 24) =

 

54 + 6 ∙ 3 – 72 : 8 =

56 : (15 – 7) + 4 =

9 ∙ (5 + 4) : 9 =

13 + (60 – 6) : 9 =

42 : 6 + 7 ∙ 4 =

72 + (40 – 4) : 9 =

63 : 7 + (20 – 5) – (9 + 6) =

18 + 36 : 9 + 6 ∙ 8 – 50 =

5 ∙ (4 + 3) + 19 – 10 =

(18 + 36) : 9 + 6 ∙ 8 – 40 =

 

(78 – 24) : 9 + 3 · 7 =

7 · (18 : 3) – 32 : 4 =

67 – 9 : 3 · 9 + 28 =

45 : 5 + 12 : 4 ∙ 6 =

16 + 560 : 7 – 21 =

72 : (44 – 8) + 5 =

49 : 7 + 18 – 9 =

98 – 6 ∙ 4 + 17 =

630 : 7 + 40 : (4 ∙ 2) =

6 ∙ 4 : ( 560 : 70) ∙ 5 =

85 – 6 ∙ 8 : 4 =

(26 – 6) ∙ 5 : 4 =

7 ∙ 4 : 2 – 8 =

54 : 9 ∙ 7 – 20 =

420 : 7 · 8 – 24 : 6 =

47 – 30 : 5 + 7 · 7 =

20 : 4 ∙ 8 + 28 : 4 ∙ 7 =

14 + 12 : 6 · 8 – 45 : 5 =

6 · 2 : 3 · 7 – 81 : 9 =

18 + 27 : 3 · 8 – 8 · 8 =

 

35 : 5 – 16 : 4 + 9 ∙ 9 =

4 ∙ (18 : 9) ·7 – 64 : 8 =

7 · 3 + (28 + 8) : 6 · 5 =

80 – (25 : 5 + 9) : 2 – 13 =

2 · 9 – 36 : (3 · 8 : 6) =

4 · 4 : 2 + (30 – 15) : 3 =

(12 + 9 · 4) : 6 – 5 =

20 – 3 · 3 · 2 + 48 : 8 · 5 =

4 · 9 – 6 · 6 + 56 : 8 · 6 =

12 + (9 · 4 : 6 – 5) =

 

2 · 8 + 54 : 6 · 7 – 3 =

2 · 2 · 5 – 72 : 8 + 9 · 9 =

12 + 9 · 4 : (6 – 5) =

9 · 8 – (5 · 2 – 8) – 6 · 6 : 4 =

40 : 8 + 3 · 2 · 6 : 4 – 7 =

5 · (9 – 6) + 14 : 2 =

(5 · 5 – 7) : 9 + 7 · 8 – 81 : 9 =

3 · 3 · 7 – (7 · 2 – 1) + 28 : 7 =

5 · 9 – (6 + 14) : 2 =

5 · 3 + 5 · 6 + 5 · 7 =

 

81 : 9 + 3 ∙ 6 – 64 : 8 =

(9 ∙ 6 – 5) : 7 + 3 ∙ 3 ∙ 9 – 12 =

5 · 9 – (6 +14) : 2 =

62 + (7 · 4 + 4) : 8 – 54 : 6 ∙ 3 =

7 ∙ 4 + 28 – 17 + 32 : 8 + 7 =

(72 : 8 + 3) · (15 – 6) =

7 · 9 – 18 : 9 =

81 : 9 – 21 : 7 + 40 : 5 =

9 · 9 – 7 · 3 + 8 · 5 =

7 · 4 + (28 -170 + 32 : 8 + 7 =

 

8 · 3 + (42 – 7) : 5 · 6 =

5 · (27 : 9) · 10 – 640 : 80 =

5 · 50 : 10 + (45 – 15) : 3 =

9 · 4 – (35 + 14) : 7 · 3

6 · (36 : 40 ∙ 10 – 560 : 70 =

7 ∙ 4 – 32 : 4 + 10 =

6 ∙ 60 ∙ 10 + (65 – 5) : 6 ∙ 3 =

7 · 5 + 4 · 9 – 26 =

42 : 7 + 58 – 23 – 2 ∙ 7

32 + (74 – 20) : 9 ∙ 7 =

1 вариант

__________________________

37 – ( 24 – 20) х 2 = _____

( 50 : 5 – 5 ) х 3 = _______

27 : 3 + 4 х 2 = ________

 100 – 8 х 4 = __________

78 – 3 х 8  = ________

 

 

 

 

 

1 вариант

__________________________

37 – ( 24 – 20) х 2 = _____

( 50 : 5 – 5 ) х 3 = _______

27 : 3 + 4 х 2 = ________

 100 – 8 х 4 = __________

78 – 3 х 8  = ________

 

 

 

 

 

2 вариант

__________________________

24 : 3 +  5 х 3 _______

79 – 5 х 4 =    _______

30 : (2 х 5 ) + 68  = ________

 31 – 3 х 4 + 5  = __________

23 + 2 х 6  = ________

 

 

 

 

 

2 вариант

__________________________

24 : 3 +  5 х 3 _______

79 – 5 х 4 =    _______

30 : (2 х 5 ) + 68  = ________

 31 – 3 х 4 + 5  = __________

23 + 2 х 6  = ________

 

 

 

 

 

Порядок действий в математике 3 класс: примеры.

Что сначала

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).

2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком −­­­­­­ это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала — умножение или сложение?

Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:

• 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
• 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

• 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
• 50 + 50 – это кучки малолетних работников;
• 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Порядок действий без скобок

Установленный порядок арифметических действий без скобок:

1. Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
2. Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
3. Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):

Первый способ

• Каждое действие записывается отдельно со своим номером под примером.
• После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните! При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись “цепочкой”. Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните! Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий со скобками

Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.

В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.

Секрет безошибочного порядка действий

Всех людей, которые ловко решают примеры на смешанные действия, отличает одно свойство. Точнее даже — навык.

Они умеют «видеть» или воспринимать числа, стоящие по обе стороны от знака умножения или деления не как «отдельно стоящие циферки», а как «единое число» (выраженное в такой странной форме).

Говоря наглядно, в нашем примере:

2 + 6 — 8 : 2

человек «видит» не четыре числа, а только три:

• Двойка
• Шестерка и
• 8:2, которые воспринимает как единое число.

Как правило, это неосознанное, невербализованное восприятие. Мозг мгновенно производит эту операцию, и человек не замечает её.

Этот навык вырабатывается долгим «нарешиванием» огромного количества длинных примеров. К старшей школе уже у многих детей есть.

Но можно попробовать ускорить события.

Предложу вам упражнение для отработки такого «видения».

Примеры на порядок действий 3-4 класс для тренировки

Рассмотрим выражения, установим порядок действий и выполним вычисления.

Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

Узнаем, правильно ли определен порядок действий в следующих выражениях.

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М. А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Определи порядок действий в данных выражениях. Найди значение выражений.

***

Определи, в каком выражении такой порядок выполнения действий:

• умножение;
• деление;.
• сложение;
• вычитание;
• сложение.

Найди значение данного выражения.

***

Составь три выражения, в которых такой порядок выполнения действий:

• умножение; 2. сложение; 3. вычитание
• сложение; 2. вычитание; 3. сложение
• умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

• в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
• в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

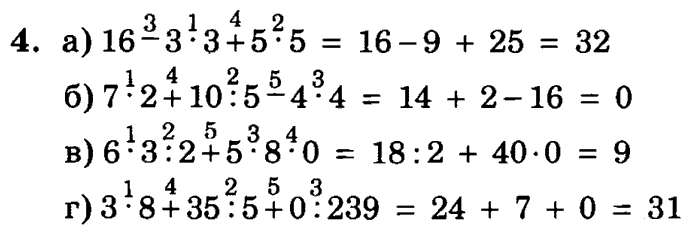
При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

• сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
• затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Сначала выполняем умножения:

2 · 5 = 10

3 · 3 = 9

затем вычитание:

10 – 9 = 1

Сначала выполняем действия в скобках:

16 – 2 · 7 + 4 = 16 – 14 + 4 = 6

2 + 5 = 7

Теперь выполняем остающиеся действия:

9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.

Выполняем действия в круглых скобках, имеем:

8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4

действия в квадратных скобках дают:
14 – 3 · 2 = 8

выполняя остающиеся действия скобках находим:

5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29

Порядок действий:

30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150

Расставь порядок действий. Найди значение выражения:

1. (12 – 0 : 4) : 3 – (7 — 7)*45 + (36 : 6) : (15 : 15)
2. 36 : (12 – 6 : 20 – (0 *5 + 3) – (7 * 8) : 14 : 4
3. (3 + 27 : 3) * 5 – 60 * 3 : 90 + 8 * (7 – 7) : 4
4. (630 : 7 + 4 * 9) : (5 + 5 : 5) + (8 – 8) : (35 * 7 + 49)
5. 5 * (48 : 6 + 2 : 2) – 280 : 20 * 3 + (50 – 32) : 9
6. 8040 : 6 + (109004 – 76048) : 7
7. (64000 : 80 * 3 + 600) : 15 – (3200 * 100) : 2000
8. 240400 – (5796 + 1803200 : 400) * 8
9. 345 * (250 * 125) * (8 * 400)
10. 56432 : 8 * 50 – (223956 + 882630 : 9)
11. (62456715 + 548185) : 700 – 300 * 80450 : 5000
12. 80 – (17 * 4) : (20 – 380 : 20) + 90 * 40 : 120
13. (1000 – 999) * 40 – 0 : 24 + 360 : (16 * 5 + 280 : 7)
14. (600000 – 538704) * 500 : 300
15. 280 : (60 : 15) – (25 + 3 * 8) : 7 + 3 * (720 : 80)
16. (250 * 840 – 145 * 1008) : 60
17. (1000 – 832) * 715 : 30 + (104402 – 58842 : 7)

Дополнительные примеры

В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.

Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.

Материалы по теме  Адаптация ребенка 3–4 лет к детскому саду

Например,

В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:

Вычисляем:

10 + 15 = 25

25 – 6 = 19

19 – 8 = 11

Полностью пример записываем так:

10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11

Например, 

В числовом выражении 3 арифметических действия: деление, умножение и деление.

Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:

Вычисляем:

15 : 5 = 3

3 • 4 = 12

12 : 6 = 2

Полностью пример записываем так:

15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2

Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.

15 : 3 = 5

6 • 8 = 48

10 – 5 = 5

5 + 48 = 53

Полностью пример записываем так:

10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53

Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.

Например,

В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.

Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.

25 – 10 = 15

15 : 3 = 5

6 • 8 = 48

5 + 48 = 53

Полностью пример записываем так:

(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53

Например,

В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.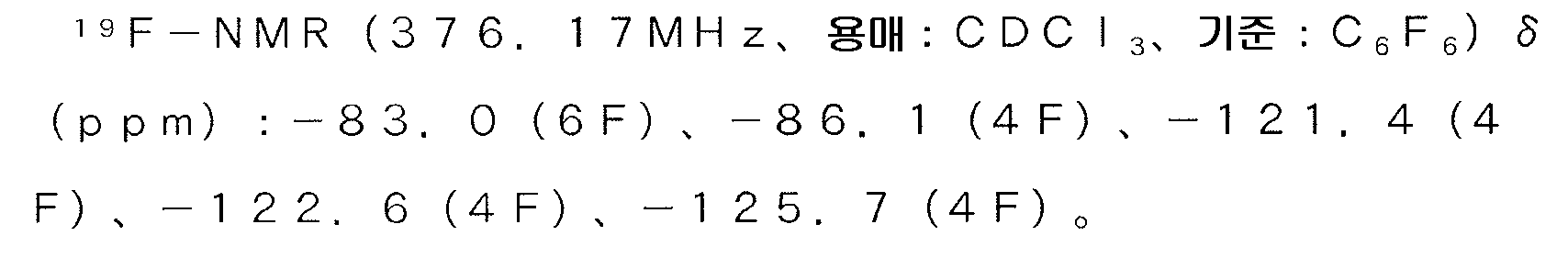

Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.

12 : 4 = 3

6 + 3 = 9

18 : 9 = 2

42 + 2 = 44

Полностью пример записываем так:

42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44

Добавление дробей

PGSG8gJWt1g

Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.

Чтобы сложить дроби, нужно выполнить три простых шага:

• Шаг 1: Убедитесь, что нижние числа ( знаменатели ) совпадают
• Шаг 2: Сложите верхние числа ( числителей ), поместите этот ответ в знаменатель
• Шаг 3: Упростите дробь (если возможно)

Пример:

1 4 + 1 4

Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.

Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:

.

1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4

Шаг 3 . Упростите дробь:

2 4 знак равно 1 2

На картинке это выглядит так:

1 4	+	1 4	=	2 4	=	1 2

. .. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)

 

Пример:

1 3 + 1 6

Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?

1 3	+	1 6	=	?

Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем добавить их вот так.

Число «6» в два раза больше «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 9. 0016 2 , например:

× 2

1 3

=

2 6

× 2

Важно: вы умножаете как сверху, так и снизу на одинаковую величину,
чтобы сохранить значение дроби одинаковым

Теперь дроби имеют одинаковое нижнее число (“6”), и наш вопрос выглядит так:

2 6	+	1 6

Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.

 

Шаг 2 : Сложите верхние числа и поместите их над одним и тем же знаменателем:

2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6

На картинке это выглядит так:

2 6	+	1 6	=	3 6

Шаг 3 : Упростить дробь:

3 6 знак равно 1 2

 

В графической форме весь ответ выглядит так:

2 6	+	1 6	=	3 6	=	1 2

 

С ручкой и бумагой

А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

 

Играй! Попробуйте сложить дроби.

Стихотворение, которое поможет вам вспомнить

♫ “Если вашей целью является сложение или вычитание,
нижние числа должны совпадать!
♫ “Измените низ, используя умножение или деление,
Но то же самое нужно применить и к верху,
♫ “И не забудьте упростить,
Пока не пришло время прощаться”

Пример:

1 3 + 1 5

Опять же, нижние цифры разные (ломтики разного размера)!

1 3	+	1 5	=	?

Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :

5 15	+	3 15

Первая дробь: умножив верх и низ на 5, мы получили 5 15 :

× 5

1 3

=

5 15

× 5

Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :

× 3

1 5

=

3 15

× 3

Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:

5 15	+	3 15	=	8 15

Результат настолько прост, насколько это возможно, поэтому ответ: 

1 3 + 1 5 знак равно 8 15

Делаем знаменатели одинаковыми

Откуда в предыдущем примере мы узнали, что нужно разрезать их на ¹ / ₁₅ тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).

Прочтите о двух основных способах приведения знаменателей в соответствие здесь:

• Метод общего знаменателя или
• Метод наименьшего общего знаменателя

Они оба работают, используйте тот, который вам больше нравится!

Пример: Кексы

Вы хотите испечь и продать кексы:

• Друг может предоставить ингредиенты, если вы дадите им ¹ / ₃ продаж
• Прилавок на рынке стоит ¹ / ₄ продаж

Сколько это вообще?

нам нужно добавить ¹ / ₃ и ¹ / ₄

1 3 + 1 4 = ? ?

Первые делают нижние числа (знаменатели) одинаковыми.

Умножить верх и низ ¹ / ₃ на 4 :

1×4 3×4 + 1

7 90 0

90 ?

и размножается верхняя и нижняя часть ¹ / ₄ на 3 :

1 × 4 3 × 40010 + 1 × 3 4 × 3 = + 1 × 3 4 × 3 = + 0007 ? ?

Теперь Сделайте расчеты:

4 12 + 3 12 = 4 + 3 12 = 7 12

9007. 7 12 сбываний идут в ингридиентах и ​​ценах рынка.

 

Добавление смешанных фракций

У нас есть специальная (более продвинутая) страница по добавлению смешанных фракций.

 

930 931, 1399 932, 1400 933, 1401, 1402, 3564, 3565

Умножение дробей – шаги, примеры

Умножение дробей начинается с умножения данных числителей, за которым следует умножение знаменателей. Затем полученная дробь еще больше упрощается и при необходимости сокращается до наименьших членов. Узнайте все об умножении дробей в этой статье.

1.	Как умножать дроби?
2.	Правила умножения дробей
3.	Умножение дробей с одинаковым знаменателем
4.	Умножение дробей с разными знаменателями
5.	Умножение дробей на целые числа
6.	Умножение дробей со смешанными числами
7.	Умножение неправильных дробей
8.	Часто задаваемые вопросы об умножении дробей

Как умножать дроби?

Умножение дробей не похоже на сложение или вычитание дробей, где знаменатель должен быть одинаковым. Здесь можно легко перемножить любые две дроби с разными знаменателями. Единственное, что нужно иметь в виду, это то, что дроби не должны быть в смешанной форме, они должны быть либо правильными дробями, либо неправильными дробями. Давайте научимся умножать дроби, выполнив следующие шаги:

• Шаг 1: Умножьте числители.
• Шаг 2: Умножьте знаменатели.
• Шаг 3: Сократите полученную дробь до наименьшего значения.

Давайте разберем эти шаги на примере.

Пример: Умножьте следующие дроби: 1/3 × 3/5.

Решение: Начнем с умножения числителей: 1 × 3 = 3, затем умножим знаменатели: 3 × 5 = 15. Это можно записать как: (1 × 3)/(3 × 5) = 3 /15. Теперь уменьшите это значение до самой низкой формы. 3 — это наибольший общий делитель (НОД) 3 и 15, поэтому разделите и 3, и 15 на 3, чтобы упростить дробь. Следовательно, 1/3 × 3/5 = 1/5.

Правила умножения дробей

При умножении дробей следует помнить следующие правила:

• Правило 1: Первое правило состоит в том, чтобы преобразовать смешанные дроби в неправильные дроби, если таковые имеются. Затем умножьте числители данных дробей.
• Правило 2: Умножьте знаменатели отдельно.
• Правило 3: Упростите полученное значение до наименьшего члена.

Эти три правила можно применить к любым двум дробям, чтобы найти их произведение. Теперь давайте изучим отдельные случаи умножения дробей с разными типами дробей.

Умножение дробей с одинаковым знаменателем

Умножение дробей с одинаковым знаменателем не меняет правила умножения дробей. Дроби, имеющие одинаковые знаменатели, называются дробями. Хотя сложение и вычитание одинаковых дробей отличается от сложения и вычитания разнородных дробей, в случае умножения и деления метод остается тем же. Мы умножаем числители, затем знаменатели, а затем дробь сокращается до наименьших членов.

Пример: Умножить 1/3 × 5/3

Решение: Мы можем умножить эти дроби, используя следующие шаги.

• Шаг 1: Умножьте числители, 1 × 5 = 5.
• Шаг 2: Умножьте знаменатели, 3 × 3 = 9.
• Шаг 3: Произведение, которое мы получаем, равно 5/9. Это не может быть уменьшено дальше, поэтому ответ 5/9.

Умножение дробей с разными знаменателями

Умножение дробей с разными знаменателями точно такое же, как умножение одинаковых дробей. Давайте разберемся в этом на примере.

Пример: Умножьте 4/12 × 16/24.

Мы можем умножить эти дроби, используя следующие шаги:

• Шаг 1: Умножьте числители, 4 × 16 = 64.
• Шаг 2: Умножьте знаменатели, 12 × 24 = 288.
• Шаг 3: Произведение, которое мы получаем, равно 64/288. Это может быть уменьшено до 2/9. Таким образом, 2/9 является ответом.

Альтернативный метод

Те же дроби можно умножить другим методом, в котором мы упрощаем дроби между собой, а затем умножаем числители, затем знаменатели, чтобы получить конечный продукт.

Пример: Умножьте 4/12 × 16/24.

Умножим данные дроби, используя следующие шаги:

• Шаг 1: Упростим данные дроби между собой. Другими словами, эти дроби можно сократить до 1/3 × 2/3.
• Шаг 2: Умножим числители, 1 × 2 = 2.
• Шаг 3: Теперь умножим знаменатели, 3 × 3 = 9.
• Шаг 4: Следовательно, произведение, которое мы получаем, равно 2/9.

Умножение дробей на целые числа

Умножение дробей на целые числа — простая идея. Поскольку мы знаем, что умножение — это многократное сложение одного и того же числа, этот факт можно применить и к дробям.

Умножение дробей на целые числа Визуальная модель

Рассмотрим следующий пример: 4 × 2/3. Это означает, что 2/3 добавляется 4 раза. Представим этот пример с помощью визуальной модели. Четырежды две трети представляются как:

Шаги умножения дробей на целые числа

Чтобы умножать дроби с целыми числами, мы используем простое правило умножения числителей, затем умножения знаменателей, а затем сокращения их до наименьших членов. Однако в случае целых чисел мы запишем их в дробной форме, поставив «1» в знаменателе. Давайте разберемся в этом на примере.

Пример: Умножить: 5 × 3/4.

Решение: Давайте используем следующие шаги, чтобы умножить данную дробь на целое число.

• Шаг 1: Здесь 5 — это целое число, которое можно записать как 5/1, а затем его можно умножить, как мы умножаем обычные дроби.
• Шаг 2: Это означает, что нам нужно умножить 5/1 × 3/4.
• Шаг 3: Умножьте числители, 5 × 3 = 15.
• Шаг 4: Умножьте знаменатели, 1 × 4 = 4.
• Шаг 5: В результате получается произведение 15/4, которое больше нельзя уменьшить.
• Шаг 6: Поскольку 15/4 — неправильная дробь, мы изменим ее на смешанную дробь, 15/4 = \(3\frac{3}{4}\).

Умножение дробей со смешанными числами

Смешанные числа или смешанные дроби — это дроби, состоящие из целого числа и правильной дроби, например \(2\frac{3}{4}\), где 2 — целое число, а 3/4 — правильная дробь. Для умножения смешанных дробей нам нужно преобразовать смешанные дроби в неправильную дробь перед умножением. Например, если число равно \(2\frac{2}{3}\), нам нужно изменить его на 8/3. Давайте разберемся в этом с помощью примера.

Пример: Умножьте \(2\frac{2}{3}\) и \(3\frac{1}{4}\).

Решение: Следующие шаги можно использовать для умножения дробей со смешанными числами.

• Шаг 1: Измените заданные смешанные дроби на неправильные, т. е. (8/3) × (13/4).
• Шаг 2: Умножьте числители неправильных дробей, а затем умножьте знаменатели. Это даст 104/12.
• Шаг 3: Теперь уменьшите полученную дробь до наименьшего значения, что сделает ее равной 26/3.
• Шаг 4: Далее, преобразуйте ответ обратно в смешанную дробь, которая будет \(8\frac{2}{3}\).

Умножение неправильных дробей

Теперь разберемся с умножением неправильных дробей. Мы уже знаем, что неправильная дробь — это та, у которой числитель больше знаменателя. При умножении двух неправильных дробей часто получается неправильная дробь. Например, чтобы умножить 3/2 × 7/5, две неправильные дроби, нам нужно выполнить следующие шаги:

• Шаг 1: Умножьте числители и знаменатели. (3 × 7)/(2 × 5) = 21/10.
• Шаг 2: Дробь 21/10 не может быть приведена к самому низкому значению.
• Шаг 3: Следовательно, ответ равен 21/10, что можно записать как \(2\frac{1}{10}\).

Советы и приемы умножения дробей

Вот несколько важных советов и приемов, которые помогут умножить дроби.

• Обычно учащиеся упрощают дробь после умножения. Однако, чтобы упростить расчеты, проверьте, не находятся ли две дроби, которые нужно умножить, в младших формах. Если нет, сначала упростите их, а затем умножьте. Например, 4/12 × 5/13 будет сложно умножить напрямую.
• Теперь, если мы сначала упростим дробь, мы получим: 1/3 × 5/13 = 5/39.
• Упрощение также можно выполнить для двух дробей. Если между числителем одной из дробей и знаменателем другой дроби есть общий множитель, можно их упростить и продолжить. Например, 5/28 × 7/9можно упростить до 5/4 × 1/9 перед умножением.

☛ Похожие темы

• Калькулятор умножения дробей
• Обратная дробь
• Умножение десятичных дробей
• Умножение и деление целых чисел
• Сложение дробей
• Вычитание дробей
• Деление дробей

 

Умножение дробей Примеры

1. Пример 1: Умножьте данные дроби: 1/4 × 5/8.

   Решение:

   Для умножения дробей с разными знаменателями, как указано в 1/4 × 5/8, мы начинаем с умножения числителей: 1 × 5 = 5. После этого мы умножаем знаменатели: 4 × 8 = 32. Это можно записать как: (1 × 5)/(4 × 8) = 5/32. Теперь эту результирующую дробь нельзя упростить, поэтому ответ равен 5/32.

2. Пример 2: Изменяет ли правило умножения дробей умножение дробей на целые числа? Обоснуйте свой ответ, умножив 4 × 6/5.

   Решение:

   Нет, умножение дробей на целые числа не меняет правила умножения дробей. Нам просто нужно записать целое число в форме дроби. В этом случае 4 будет записано как 4/1, и тогда мы будем использовать тот же метод. Итак, мы будем умножать 4/1 × 6/5. При умножении числителей мы получаем 4 × 6 = 24. При умножении знаменателей мы получаем 1 × 5 = 5. Следовательно, результирующее произведение равно 24/5, которое нельзя уменьшить дальше. Поэтому мы изменим эту неправильную дробь 24/5 на смешанную дробь, чтобы представить ее как ответ, который равен 24/5 = \(4\frac{4}{5}\).

3. Пример 3: Каким будет произведение 5/4 × 5/2 × 5/3?

   Решение:

   Чтобы умножить три дроби, мы сначала умножим все три числителя, а затем все три знаменателя. Затем мы упростим окончательный ответ.

   ⇒ 5/4 × 5/2 × 5/3

   ⇒ (5×5×5)/(4×2×3)

   ⇒ 125/24

   Следовательно, 5/4 × 5/2 × 5/3 = 125/24 или \(5\frac{5}{24}\)

перейти к слайдуперейти к слайдуперейти к слайду

Готовы увидеть мир глазами математика?

Математика — это жизненный навык. Помогите своему ребенку усовершенствовать его с помощью реального приложения.

Записаться на бесплатный пробный урок

Практические вопросы по умножению дробей

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об умножении дробей

Как умножать дроби?

Умножение дробей означает нахождение произведения двух или более дробей. Метод, используемый для умножения дробей, отличается от сложения и вычитания дробей. Чтобы умножить любые две дроби, мы следуем шагам, указанным ниже. Давайте умножим 7/8 × 2/6, чтобы понять шаги.

• Умножьте числители. Итак, 7 × 2 = 14,
.
• Умножьте знаменатели. Это означает, что 8 × 6 = 48,
.
• Полученная дробь равна 14/48. Упростите полученную дробь до наименьших членов. Упрощение дроби 14/48 дает нам 7/24. Следовательно, ответ 7/24.

Каковы правила умножения дробей?

Есть три простых правила умножения дробей. Сначала умножьте числители, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Затем нам нужно упростить полученную дробь, чтобы получить окончательный ответ. Это можно понять на простом примере → 2/6 × 4/7 = (2 × 4)/(6 × 7) = 8/42 = 4/21.

Как умножать дроби со смешанными числами?

Следующие шаги можно использовать для умножения смешанных дробей. Умножим 1/4 × \(3\frac{1}{2}\).

• Замените смешанную дробь на неправильную. Здесь \(3\frac{1}{2}\) станет 7/2. Итак, теперь нам нужно умножить 1/4 × 7/2.
• Умножьте числители, а затем знаменатели. Это означает, что (1 × 7)/(4 × 2) = 7/8.
• Убедитесь, что ответ указан в самом низком выражении. Поскольку 7/8 нельзя уменьшить дальше, ответом будет 7/8.

Как умножать дроби на целые числа?

Чтобы понять, как умножить дробь на целое число, возьмем простой числовой пример 2/7 × 3. Для начала перепишем целое число (в данном примере 3) в виде дроби 3/1. Теперь мы можем применить шаги, которые мы используем для умножения дробей. Это означает, что 2/7 × 3/1 = (2 × 3)/(7 × 1) = 6/7.

Как умножать дроби с одинаковыми знаменателями?

Умножение дробей с одинаковыми знаменателями аналогично умножению других правильных дробей. Давайте разберемся в этом на примере. Умножим 4/5 × 3/5. Умножаем числители, то есть 4 × 3 = 12. Затем умножаем знаменатели, то есть 5 × 5 = 25. Это даст нам произведение как 12/25. Поскольку это нельзя уменьшить дальше, ответом будет 12/25.

Как умножать дроби с разными знаменателями?

Умножение дробей с разными знаменателями не меняет правила умножения дробей. Давайте разберемся в этом на примере. Умножьте 2/6 × 3/4. Мы можем умножить эти дроби, используя следующие шаги:

• Умножьте числители, 2 × 3 = 6.
• Умножьте знаменатели, 6 × 4 = 24.
• Продукт, который мы получаем, 6/24. Это можно уменьшить до 1/4, следовательно, ответ 1/4.

Как умножить дробь на дробь?

Умножение двух дробей — простейшая форма арифметических операций между двумя дробями. Сначала умножаются числители обеих дробей, а затем умножаются знаменатели. Затем полученная дробь при необходимости упрощается до наименьших членов.

Чем умножение дробей отличается от сложения дробей?

Сложение дробей отличается от умножения дробей. При умножении сначала умножаются числители двух дробей, затем умножаются знаменатели, чтобы получить результирующую дробь. Однако в процессе сложения дробей нам сначала нужно сделать знаменатели обеих дробей равными, а затем сложить числители, чтобы получить результирующую дробь. Кроме сложения или вычитания дробей, мы не складываем и не вычитаем знаменатели отдельно.

Как умножать десятичные дроби?

Чтобы умножить дроби на десятичные, мы преобразуем десятичное число в дробь, а затем используем те же правила умножения дробей. Например, давайте умножим 5/7 × 0,6.

• Здесь мы преобразуем 0,6 в дробную форму, что составит 6/10.
• Теперь умножим 5/7 × 6/10 обычным способом.
• Умножим числители, 5 × 6 = 30.
• Умножим знаменатели, 7 × 10 = 70.
• Таким образом, результирующая дробь будет 30/70.
• Упростив полученную дробь, мы получим произведение как 3/7.

Как научить умножению дробей?

Умножению дробей можно научиться так же, как умножению целых чисел. Важным аспектом перед умножением дробей является преобразование смешанной дроби в неправильную дробь. После этого шага мы умножаем числители обеих дробей, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Для обучения умножению дробей можно использовать следующие способы:

• Максимально используйте визуальные модели для представления концепции.