Примеры со скобками для 4 класса: Математика :”Порядок выполнения действий в примерах без скобок и со скобками.” (4 класс)

Решение примеров со скобками

Метки

Математика Мозг Ум Цифры Школа

Решение примеров со скобками дети проходят уже во втором классе. И хотя все эти знания впоследствии многократно закрепляются при решении всё более сложных примеров, но иногда ощутимого результата это не дает. И ребенок так и не усваивает главные принципы решения. А потому и во взрослом возрасте не может с такими заданиями совладать.

Сегодня редакция «Так Просто!» предлагает решить несколько примеров со скобками. Попутно вспомним, каких правил в этом деле следует придерживаться. Да и в целом такая небольшая математическая разминка довольно полезна для ума. А потому советуем регулярно решать интересные задачки и примеры как взрослым, так и детям.

© Depositphotos

1. Первое задание кажется довольно простым. Однако скобки способны запутать даже признанных хорошистов, не говоря уже о троечниках, тем более двоечниках. Постарайся пошагово решить этот пример, не сделав ни единой ошибки.

2. Во втором задании снова-таки есть и скобки, и деление, и умножение. Однако похоже, что выполнять математические операции придется в другом порядке. Попробуй вспомнить необходимые правила, которых нужно придерживаться в этой ситуации. И помни, что правильный ответ только один.

3. Третий пример выглядит более сложным. Но если знать, какие действия в каком порядке выполнять, то и здесь легко найти правильный ответ. Также не забудь свериться с нашими объяснениями и ответами во второй части статьи.

Объяснения и ответы

В первую очередь напомним простые правила, о которых многие взрослые люди уже вполне могли забыть. Если в примере отсутствуют скобки, то все математические операции выполняются слева направо. Но при этом деление и умножение выполняем сразу, а сложение и вычитание позже.

В примерах со скобками всё чуть сложнее, но не намного. Тут сперва выполняем всё в скобках (как описано выше), а затем выполняем все математические операции слева направо, учитывая, что деление и умножение снова-таки имеют более высокий приоритет.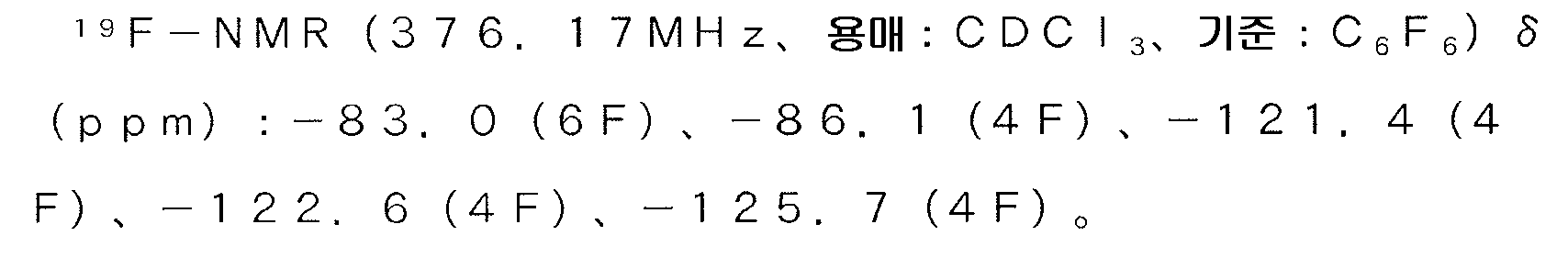

© Depositphotos

1. Учитывая описанные алгоритмы, в первом задании сначала выполняем действия в скобках, потом делим, а только в самом конце умножаем. Таким образом получаем: 10 ÷ 5 × 2 = 2 × 2 = 4.
2. Во втором примере сначала выполняем действия в скобках, потом умножаем, а только напоследок делим. В итоге наш пример приобретает следующий вид: 10 × 4 ÷ 2 = 40 ÷ 2 = 20.
3. Теперь последний пример наверняка уже не кажется читателю таким страшным, как прежде. Сперва высчитываем, что в скобках у нас 10 – 2 × 3 = 10 – 6 = 4. Тогда весь пример решается так: 4 + 2 × 4 = 4 + 8 = 12.
   © Depositphotos

Надеемся, что теперь решение примеров со скобками не будет представлять для тебя трудную задачку. А если же эти задания считаешь слишком простыми, то попробуй решить более сложные примеры, которые мы публиковали совсем недавно. Сможешь не наделать ошибок? Не забудь поделиться своими решениями в комментариях.

Поделиться

Страница 18 – ГДЗ Математика 4 класс.

Моро, Бантова. Учебник часть 1

1. Главная
2. ГДЗ
3. 4 класс
4. Математика
5. Моро, Бантова. Учебник
6. Что узнали. Чему научились.
7. Страница 18. Часть 1

Вернуться к содержанию учебника

Что узнали. Чему научились.

Вопрос

1.

32 + (96 – 64) : 8 • 2	(400 – 160 : 8) : 2
32 + (96 – 64) : (8 • 2)	(400 – 160) : 8 : 2
(32 + 96 – 64 : 8) • 2	(400 – 160) : (8 : 2)

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

2.

900 – 2 • 50 + 140	120 – 75 : 3 • 4 + 65	342 : 3
600 + 90 : 3 – 200	200 – 80 : 4 • 5 – 35	564 : 2
700 – 25 • 2 + 100	108 – 54 : 9 • 6 + 58	721 : 7

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

3. Сравни числа.

796 и 800

312 и 320

1000 и 999

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4.

36 + 60 : 4 • 2 + 34	(760 + 100) – (430 + 230)
42 + 54 : 3 • 2 – 18	(970 – 340) + (250 + 120)

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5.

Вычисли и проверь деление умножением.

624 : 6	482 : 2	135 : 3	248 : 8	728 : 7
963 : 3	147 : 7	825 : 5	616 : 2	453 : 3

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

6.

346 + 458	832 – 456	503 + 204	603 – 28
157 + 484	621 – 241	308 + 106	204 – 39

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

7.

318 • 3	207 • 4	824 : 4	234 : 9	434 : 7
247 • 4	108 • 6	565 : 5	632 : 8	984 : 8

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

8. Запиши выражения и найди их значения.

1) Сумму чисел 960 и 40 уменьшить в 10 раз.

2) Частное чисел 500 и 100 увеличить на 25.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

9. На поездку в магазин и обратно мальчик затратил 1 ч 10 мин. Туда он ехал на велосипеде 25 мин, в магазине пробыл 15 мин. Сколько минут мальчик ехал обратно?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

10. Из 28 м ткани сшили 7 одинаковых платьев. Сколько потребуется ткани, чтобы сшить 12 таких платьев? Сколько таких платьев можно сшить из 60 м ткани?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

11.

1) Выпиши названия всех многоугольников.

2) Найди периметр и площадь квадрата ABCD.

3) Сравни площадь прямоугольника AMKD и площадь треугольника ABC.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Продолжи ряды чисел.

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

Что такое скобки? Определение, правила, примеры

Что такое круглые скобки?

Скобки или «круглые скобки» — это знакомые ( ) символы, которые используются парами для группировки элементов или указания порядка операций в уравнении.

В математике вам часто придется использовать скобки при создании или решении уравнений. Они помогают группировать числа и определять порядок операций. В таких случаях используются три типа скобок:

• Круглые скобки или ( )
• Квадратные или квадратные скобки или [ ]
• Фигурные скобки или угловые скобки или { }

Скобки всегда идут парами, и если есть открывающая скобка, должна быть и закрывающая скобка. Открывающие скобки: (, [  и {. Соответствующие им закрывающие скобки: ), ] и }.

 В этой статье мы изучим правила использования скобок в математике.

Как использовать скобки в математике?

В математике вы можете использовать скобки для разделения чисел. Например, вы можете использовать их для упоминания отрицательных чисел при написании уравнения сложения.

Вот пример, чтобы лучше понять это:

3 + (-5) = -2

Второй способ использования скобок в математике — умножение чисел. Если в уравнении нет арифметической операции, наличие скобок означает, что вы должны применить умножение.

Разберем это на примере:

6 (4 + 2)

можно записать как 6 х (4 + 2)

Следовательно, ответ 6 х 6 = 36.

Третий и последний скобки в математике используются для группировки чисел и определения порядка операций.

Порядок операций

Скобки изменяют порядок операций.

Вот порядок, которому вы можете следовать, когда в уравнении присутствует несколько символов:

Если вы столкнетесь со скобками в уравнении, вы сначала посмотрите на термины, присутствующие в них.

Давайте лучше разберемся на примере.

Возьмем задачу: 9 – 10 ÷ 5 – 3 x 2 + 7

Давайте решим ее, используя изученный вами порядок операций.

= 9 – 10 ÷ 5 – 3 x 2 + 7

= 9 – 2 – 3 x 2 + 7 (сначала вы делите)

= 9 – 2 – 6 + 7 (затем умножаете)

= 7 – 6 + 7 (Затем вычесть)

= 1 + 7 (Затем вычесть)

= 8 (И, наконец, сложить)

Теперь давайте рассмотрим ту же задачу со скобками: 

9 – 10 ÷ (5 – 3) x 2 + 7

Сначала нужно вычислить числа в скобках.

= 9 – 10 ÷ 2 x 2 + 7 (Решите выражение в скобках)

= 9 – 5 x 2 + 7 (Разделить)

= 9 – 10 + 7 (Умножить)

= –1 + 7 (Сложить)

= 6

Вы заметили? Ответ на то же уравнение изменился, потому что в уравнении присутствовали круглые скобки!

Помните: если внутри других скобок есть скобки, сначала нужно решить внутреннее выражение.

Давайте разберем это на примере:

Упростим выражение (2 + (3 x 4))

Здесь мы сначала решим внутреннюю скобку.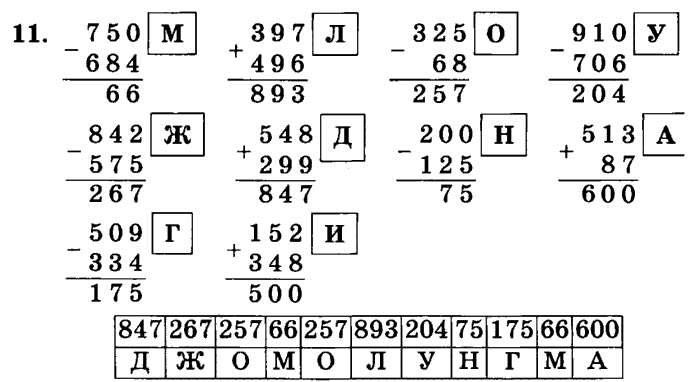

Таким образом, выражение примет вид (2 + 12) = 14

Решенные примеры

Пример 1: Упростим выражение: (2 + 4 x 6) – 4 + (2 x 3)

Решение . Начните с решения выражений в скобках.

= (2 + 24) – 4 + 6 (умножить в скобках)

= 26 – 4 + 6 (решить члены в скобках)

= 22 + 6 (сложить)

= 28

Пример 2: Упростите выражение: ( 2 x (7 – 5)) – ((6 ÷ 3) + 4)

Начните с решения самых внутренних скобок

= (2 x 2) – (2 + 4)

= 4 – 6

= –2

Пример 3: Упростите выражение: 2 (3 + 5) + 8 (4 – 1)

Сначала решите выражения в скобках.

Здесь скобки также обозначают знак умножения.

= 2 x 8 + 8 x 3

= 16 + 24

= 40

Практические задачи

1

Упростим выражение: (3 + 2 x 8) – 4 + (5 x 7)

45

50

24

5 Мы знаем, что правильный ответ 9

9000 уравнение в скобках решается первым.
Итак, 19 – 4 + 35 = 50

2

Упростим выражение: ( 4 x (6 – 2)) – ((8 ÷ 2) + 5 )

7

2

17

5

Правильный ответ: 7
Мы знаем, что сначала решается уравнение в скобках.
Итак, (4 x 4) – (4 + 5)
16 – 9 = 7

3

Упростим выражение: 4 (3 + 2) + 4 (7 – 2)

10

50

20

40

Правильный ответ: 40
Мы знаем, что скобки также обозначают умножение.
Итак, 4 x 5 + 4 x 5
20 + 20 = 40

Часто задаваемые вопросы

Что такое скобки в математике?

Скобки используются для группировки чисел или переменных в математике. Они могут изменить решение выражения и, следовательно, ответ.

Круглые скобки — это то же самое, что фигурные скобки?

Нет. Скобки, обозначенные ( ), отличаются от фигурных скобок { }. Они имеют различные применения в математике. Они используются во вложенных выражениях. Вы узнаете о них больше позже.

Есть ли другое название для скобок?

Да. Иногда скобки также называют круглыми скобками.

Что такое скобки в математике? Определение, типы, примеры и использование

Что такое скобки?

Вы, должно быть, видели в учебниках по математике различные символы, подобные этим: (, ), [ ], { и }. Эти символы называются скобками. Скобки в математике служат очень важной цели; эти символы помогают нам сгруппировать различные выражения или числа вместе. Скобки подразумевают, что вещь или выражение, заключенное в них, должно иметь более высокий приоритет по сравнению с другими вещами.

Различные виды скобок

Обычно в математике используются три вида скобок:

• Скобки или круглые скобки, ( )
• Фигурные или скобки { }
• Квадратные или квадратные скобки [ ]
900en Скобки

Они также известны как круглые скобки и записываются как ( ). Это самые распространенные виды брекетов. Они используются для группировки различных значений и уравнений вместе.

При использовании просто вокруг чисел круглые скобки обозначают умножение. 9{-3}$

Примеры: (2 + 4), 5(111), 25 – (12 + 8) и т. д.

Фигурные скобки

Как и скобки, фигурные скобки также используются для группировки различных математических компонентов; однако фигурные скобки также используются для обозначения множеств или для написания вложенных выражений. Примеры: 

[4 + [3 $\times$ (- 2)] – [{(4 $\times$ 6) + (14 $\div$ 7)} – (- 3)],

 [{ 12 − (12 − ​​2) } + (5 − 7)] + 9 и т. д.

Квадратные скобки

Квадратные скобки обычно используются для различения подвыражений сложного математического выражения.

Примеры: [100 – (3 – 1) + (7 x 8)], 10 x [(4 – 2) x ( 4 x 2)] и т. д.

Порядок операций скобок

При оценке математическое выражение, состоящее из разных скобок, мы должны следовать определенным правилам.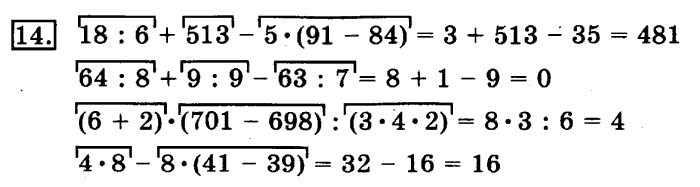 Это называется правилами работы или порядком работы скобок.

• Общий порядок работы скобки может быть проиллюстрирован как [ { ( ) } ]; это означает, что в данной задаче вам придется сначала упростить значения в самой внутренней скобке. Это означает, что будут решены первые ( ) скобки, затем будут решены { } скобки и, наконец, [ ] скобки.
• Второй шаг в решении этих задач — найти показатель степени; если есть, решите сначала.
• На третьем этапе мы ищем выражения с операторами умножения или деления. Если оба оператора присутствуют, мы проверяем выражение слева направо. Какой бы оператор ни пришел первым, мы сначала решим этот оператор.

Например, в выражении 10 6 ÷ 5 мы проверяем слева направо, поскольку сначала идет умножение, поэтому мы сначала решаем умножение, а затем деление.

10 $\times$ 6 ÷ 5 

= 60 ÷ 5

 = 12

• На четвертом и последнем шаге мы ищем числа, которые нужно сложить или вычесть. Мы следуем той же инструкции, если присутствуют оба оператора, мы смотрим слева направо в выражении, и какой бы оператор ни был первым, мы решаем это выражение первым. Но если операции в скобках, мы всегда сначала решаем скобки, так как скобки имеют наивысший приоритет.

Чтобы запомнить упомянутые выше шаги, мы можем использовать аббревиатуру PEMDAS,

P – Скобки,

E – Экспоненты

M – Умножение

D – Деление

A – Сложение

S – Вычитание.

давайте воспользуемся pemdas для вычисления выражения Следуйте порядку решения круглых скобок ( ), затем фигурных скобок { }, а затем квадратных скобок [ ].

= 100 − [(2) + (56)]

= 100 − 58

Шаг 2: В данном выражении нет показателя степени.

Шаг 3: В данном выражении нет ни умножения, ни деления.

Шаг 4: Решите вычитание.

= 100 − 58

= 42

Решаемые примеры

Вопрос 1: Найдите значение выражения: (5 + 4) − (3 − 2).

Ответ: Данное выражение:

(5 + 4) − (3 − 2),

Шаг 1: Решение значений в скобках,

−

(9) (1),

Таким образом, ответ равен (9) − (1) = 8.

Вопрос 2: Найдите значение выражения: {(7 − 2) × 3}  ÷ 5

Ответ : Заданное уравнение:

{(7 − 2) × 3}  ÷ 5 

Шаг 1: Решение скобок 

{(7 − 2) × 3}  ÷ 5 

= {5 × 3} ÷ 5

Решение фигурной скобки
= {15} ÷ 5

= 15 ÷ 5 

= 3 

Вопрос 3: Найдите значение выражения: (12 ÷ 6) × (4 − 2)

Решение:

Данное уравнение:

(12 ÷ 6) × (4 − 2)

Решение значений в скобках 2) x (2)

Таким образом, ответ: (2) x (2) = 4

Вопрос 4: Найдите значение выражения: [120 + { (3 x 4) + (4 − 2) − 1 } + 20]

Ответ: Следуя правилу PEMDAS, сначала 

Шаг 1: Найдем значения в скобках ( ),

[120 + { (3 x 4) + (4 − 2 ) – 1 } + 20 ]

= [ 120 + { (12 ) + ( 2 ) – 1 } + 20 ],

Теперь вычисляем значения в скобках { } ,

= [ 120 + { 13 } + 20 ],

153 490

492

494

500

Правильный ответ: 492
Шаг 1: Решите все скобки, учитывая приоритет.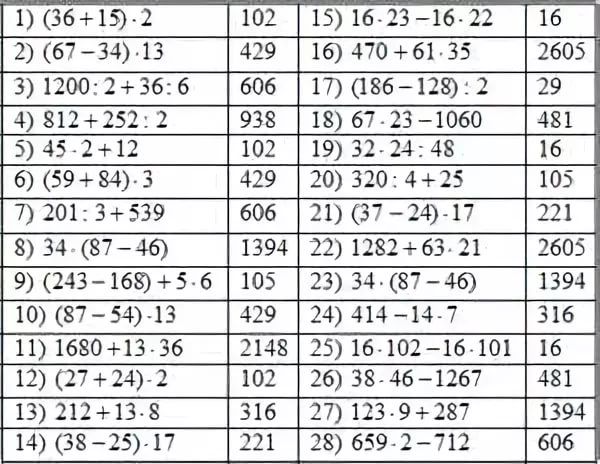 2$ 9{2} = 4,096 $

4

Решите это выражение, 12 + (5 + 3),

18

20

16

8

Правильный ответ: 20
. Правильный ответ – 20.

8

Часто задаваемые вопросы

Почему скобки важны в математике?

Скобки — очень важные части математического уравнения; они отделяют разные математические выражения друг от друга и помогают установить приоритет для выражений, которые необходимо решить в первую очередь.

Является ли PEMDAS единственным методом решения проблем со скобами?

BODMAS — это другой аббревиатур от PEMDAS, где B означает скобки, O — числа или экспоненты, D — деление, M — умножение, A — сложение и S — вычитание. Любое выражение считается правильно решенным, если оно соответствует правилу PEMDAS или BODMAS.

Есть ли еще виды кронштейнов?

Угловые скобки также используются в различных математических выражениях; они представлены с〈 〉.