Примеры со скобками 3 класс по математике: Карточки по математике 3 класс «Порядок действий»

Урок 10. порядок выполнения действий в числовых выражениях – Математика – 3 класс

Математика, 3 класс

Урок №10. Порядок выполнения действий в числовых выражениях

Перечень вопросов, рассматриваемых в теме:

– В какой последовательности выполняются действия в выражениях без скобок?

– В какой последовательности выполняются действия в выражениях со скобками?

Глоссарий по теме:

Если в выражение без скобок входят только сложение и вычитание или умножение и деление, то действия выполняются по порядку: слева направо.

Если в выражение без скобок входят не только сложение и вычитание, но и умножение или деление, то сначала выполняются по порядку умножение и деление, а затем сложение и вычитание также по порядку.

Если в выражение есть скобки, то сначала выполняются действия в скобках, а затем в установленном порядке сначала умножение и деление, затем сложение и вычитание

Основная и дополнительная литература по теме урока:

1.

Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 24.

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 15.

Теоретический материал для самостоятельного изучения

Выполним вычисления устно и расставим значения выражений в порядке возрастания.

Подсказка: Он должен быть в доме, в шкафу, на столе и даже в портфеле ученика.

В результате вычислений получилось:

Действительно во всём должен быть порядок и в математике тоже.

Выполняя задания, мы пользуемся законами и правилами математики. Эти правила и законы и поддерживают математический порядок.

Выполняя устные вычисления, мы выполняли действия по порядку. В выражениях использовали действия умножения и деления.

Рассмотрим выражения:

6 ∙ 3 + 4 : 2; 27 : 3 – 2 ∙ 2; 2 ∙ (5 + 4).

Это числовые выражения. Для их составления использовали числа и знаки действий.

Использовали не только умножение и деление, но и сложение, вычитание. В каком порядке будем выполнять действия?

В выражении 76 – 27 + 9 – 10 использовали знаки сложения и вычитания. Выполнять действия нужно по порядку: слева направо.

В выражении 80 : 8 ∙ 2 использовали знаки умножения и деления. Выполнять действия нужно также по порядку: слева направо.

Вывод: Если в выражениях только сложение и вычитание или умножение и деление, то действия выполняются по порядку слева направо.

Выражения могут содержать сложение и вычитание, и умножение, и деление. В этом случае сначала выполняются деление и умножение по порядку. В математике эти действия считаются сильными. А затем сложение и вычитание тоже по порядку.

В математике есть способ, который позволяет выделить какое-то действие. Это постановка скобок. Скобки показывают, что действие внутри них, выполняется в первую очередь.

Действия в числовых выражениях выполняются в следующем порядке:

1. Действия записанные в скобках;
2. Умножение иделение по порядку: слева направо;
3. Сложение и вычитание по порядку: слева направо.

Знания этих математических правил позволит правильно находить значения выражений и не нарушать порядок.

Порядок действий в выражениях особый. 
И в каждом случае, помните, он свой. 
В порядке все действия выполняйте.

Сначала в скобках все посчитайте.

Потом чередом, умножайте или делите.

И, наконец, вычитайте 

или сложите.

Тренировочные задания.

1. Выберите действие, которое будет в выражение первым.

38 + 4 ∙ 7 + 19

Правильный ответ: умножение.

2. Выберите действие, которое в выражение будет последним.

40 : 5 + 12 – 8 : 2

Правильный ответ: вычитание.

Конспект урока по математике “Порядок действий. Скобки” 3 класс

Урок по математике во 3 классе с применением

технологии проектной деятельности на тему «Порядок действий. Скобки»

Цель: формирование вычислительных навыков, умения находить значение выражения со скобками.

Задачи:

– познакомить с записью и чтением выражений со скобками, с порядком выполнения действий в выражениях со скобками;

– развивать логическое мышление, грамотность математической речи;

– формировать умение анализировать содержание задания, планировать свою деятельность, делать выводы, давать оценку своей работы и работы одноклассников, работать в группах и парах.

Планируемые результаты: учащиеся научатся читать и записывать выражения со скобками, выполнять действия в выражениях со скобками.

Оборудование: таблицы, памятки, презентация.

Ход урока.

1. Организационное начало урока.

2. Актуализация и фиксирование индивидуального затруднения в пробном действии.

1) Устный счет.

Найдите значение выражений.

19-10-2

18-12-10

Задача. На полке стояло 8 книг. В первый день взяли 2 книги, а во второй 3. Сколько книг осталось?

У трех мальчиков 18 значков. У одного 5 значков. У другого 6 значков. Сколько значков у третьего мальчика?

2) Разделите выражения на две группы:

8+1+4

(Учащиеся распределяют выражения по группам.)

I группа

– Чем выражения первой группы отличаются от второй?

– Примеры второй группы содержат скобки.

– Найдите значения выражений первой группы.

(Ответы детей.)

– Найдите значения выражений второй группы.

(Ответы детей. Ребята не умеют ещё читать выражения со скобками, поэтому называют только значения выражений

.)

3. Выявление места и причины затруднения. Построение проекта выхода из затруднения.

– Почему у вас получились разные ответы?

– Потому что мы не знаем, как находить значение выражений со скобками.

– Сформулируем тему урока.

– Порядок действий в выражениях со скобками.

– Чему мы будем учиться на уроке?

– На уроке мы будем учиться находить значение выражений со скобками.

4. Реализация построенного проекта.

– Запишите выражение: (6-2) +4

– Чтобы научиться правильно читать выражения со скобками надо:

1. Посмотреть на знак в скобках и сказать, что записано в скобках – сумма или разность.

2. Посмотреть на второй знак действия и сказать, что надо сделать – прибавить или вычесть.

Короче это можно записать так:

Чтение выражений со скобками.

1. Скобки ( ) – сумма или разность.

2. Второй знак – прибавить или вычесть.

Читаем: к разность чисел 6 и 2 прибавить 4. Найдите значение этого выражения.

(6-2)+4=8

– Запишите выражение: из числа 6 вычесть сумму чисел 2 и 4 и найдите значение выражения.

6-(2+4)=0

– Сравните выражения. Что интересного заметили?

– Числа и знаки одинаковые, но скобки расставлены по разному.

– Почему получились разные значения выражений?

– Действия выполнялись в разном порядке: первое действие в скобках.

– Сформулируем правило порядка выполнения действий в скобках.

– Действие, записанное в скобках выполняется первым.

– Откройте учебник математики на с. 38 и прочитайте правило. Запомните его.

5. Физкультминутка.

(групповая физкультминутка, дети повторяют все то, о чем говорится в стихотворении)
Мы – веселые мартышки,
Мы играем громко слишком.
Все ногами топаем,
Все руками хлопаем,
Надуваем щечки,
Скачем на носочках.
Дружно прыгнем к потолку,
Пальчик поднесем к виску
И друг другу даже
Язычки покажем!
Шире рот откроем,
Гримасы все состроим.
Как скажу я слово три,
Все с гримасами замри.
Раз, два, три! 

6. Первичное закрепление с проговариванием.

1. С. 38 № 1 (1 и 2 столбик с комментированием)

– Прочитайте и сравните выражения.

– Числа и знаки одинаковые, но скобки расставлены по разному.

-В каком порядке будем выполнять действия?

– Первым будем выполнять действие в скобках

– Найдите значение выражений.

2. С. 38 № 2

– Восстановим пропущенные скобки.

Методика работы:

1. Выражение списывается без скобок. (4-1+2)

2. Карандашом ставятся в скобки первые два числа, пример выполняется. Если ответ не совпадает, скобки стираются и карандашом в скобки заключаются второе и третье число, пример выполняется. Если ответ совпадает, скобки пишутся ручкой.

(4-1)+2=1

3 5

Таким образом выполняются все примеры.

7. Самостоятельная работа с самопроверкой.

– А теперь самостоятельно найдите значение выражений:

(19-10)-2=

8. Физкультминутка.

Ветер дует нам в лицо,
Закачалось деревцо.
Ветер тише, тише, тише.
Деревцо все выше, выше.
9. Включение в систему знаний и повторения.

1. С. 38 № 4. Устно.

2. С. 39 № 5. (1,2)

3. С. 39 № 7. Устно.

10. Домашнее задание, инструктаж по его выполнению.

Д /з: С. 38 № 1 (3ст.), № 2 (2 ст.)

С. 39 № 6

11. Рефлексия учебной деятельности на уроке (подведение итогов занятия).

– Ребята, с чем мы сегодня познакомились на уроке и чему мы учились на уроке?

– Сегодня на уроке мы познакомились с порядком выполнения действий выражений, содержащих скобки и учились находить значение выражений со скобками.

– Проверим, как вы усвоили новые знания. Выполним задание внизу на с. 39.

Вспомните, какое действие в выражении выполняется первым и найдите значения выражений, где порядок действий определён правильно.

2) 16+(20-10)=26

3. 45-(39+1)=5

 

7+3+5 6+2+8	10+9 7+8	20-9 16-7	15-(2+8)	9-1+2	4+6-8	12+(6+3)	II группа
8+1+4 9-1+2 4+6-8	15-(2+8) 12+(6+3)
1=5		Карандаш стираем.
4-(1+2)=1 3	1=1		Обводим скобки ручкой.
18-(12-10)=
(7+3)+5=
6+(2+8)=

Презентация к уроку математики 3 класс «Порядок выполнения действий»

Слайды и текст этой онлайн презентации

Слайд 1

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ
Внимательно слушайте – и всё услышите! Внимательно смотрите – и всё увидите! Думайте – и всё обязательно поймёте!
Удачи!

Слайд 2

20-8:2=6
20-8:2=16
(20-8):2=6
Сегодня на уроке фиксик Нолик предлагает нам рассказать ему о хитростях математических действий
?

Слайд 3

«Порядок действий в выражениях со скобками»

Слайд 4

Нолик считает, что день надо начинать с утренней гимнастики, а урок математики – с гимнастики ума.
Чем отличаются столбики примеров?
8 – 3 + 4 = 9 8 – (3+4) =1 18 – 8 + 9 =19 18 – (8+9) =1 20 – 5 + 3 = 18 20-(5+3)=12

Слайд 5

Как же правильно выполнять действия в выражениях со скобками?

Слайд 6

Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:
Если в выражении нет скобок, то сложение и вычитание выполняют по порядку слева направо. Если выражение содержит действия сложения, вычитания, умножения и деления и в нем нет скобок, то сначала выполняют действия умножения и деления, потом – действия сложения и вычитания слева направо. Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2)

Слайд 7

Каждое выражение задает программу своего вычисления. Она состоит из команд.
Определяю порядок выполнения действий в числовом выражении. Выполняю действие в скобках. Выполняю слева направо сложение (вычитание). Читаю значение выражения.

Слайд 8

Фиксики предлагают вам физкультминутку – фиксипелку.

Слайд 9

Во всем нужна сноровка, закалка, тренировка. №2 (с. 38).
Решите первый пример. Проверьте, получим ли мы нужный результат, если вычисления будем выполнять по порядку. Измените порядок действий. Какое действие выполним первым? Вычислите. Получился ли у вас нужный результат? Поставьте скобки.
(Не получим.)
(Сложение.)
(Да.)

Слайд 10

Семь раз отмерь – один отрежь

Слайд 11

Проверь себя!
100 – 60 = 40 (м) Ответ: 40 метров осталось проплыть Коле.
60 + 40 = 100 (м) Ответ: 100 метров длина дорожки в бассейне.

Слайд 12

Над какой темой мы работали?
Удалось ли решить поставленную задачу? В чём испытывали трудности? Над чем еще надо работать? «Проверь себя» стр.39 ПОСТАВИМ ОЦЕНКИ ЗА УРОК.
Молодцы!!!

Слайд 13

Домашнее задание (по выбору):
Учебник: № 6 (с. 39). Тетрадь с печатной основой: № 27 (с. 37).

примеры по математике 2 класс на сложение и вычитание со скобками

Image Wallpaper and More collection of примеры по математике 2 класс на сложение и вычитание со скобками contain 30+ more images free download Конспект урока математики во 2 классе Тема: Сложение и

ГДЗ (решебник) по математике 2 класс Петерсон часть 1, 2, 3 – РЕШАТОР!

Как расставить действия в примере. Порядок выполнения действий …

Порядок решения примера сначала умножение потом деление. Конспект …

Решать примеры на 2 плюс. Примеры со скобками, урок с тренажерами

Примеры по математике 2 класс в игре :: nalreiloove

Рецензия покупателя на “3000 примеров по математике. Цепочки …

Занимательная математика командной строки / Хабр

КСП по математике 1 класс Тема:Порядок действий в выражениях со …

2

Конспект урока математики во 2 классе Тема: Сложение и

Кулаков А. А.: Математика. Все цепочки примеров для устных и …

Сложение и вычитание в пределах 100

О. В. Узорова, книга 3000 примеров по математике. Цепочки примеров …

Иллюстрация 7 из 24 для Математика. 3 класс. Цепочки примеров …

Иллюстрация 6 из 11 для 3000 примеров по математике. Цепочки …

Порядок выполнения действий в выражениях без скобок и со скобками …

Иллюстрация 1 из 24 для Математика. 3 класс. Цепочки примеров …

3000 примеров по математике. Цепочки примеров. 2 класс (Ольга …

Рецензии покупателей на “3000 примеров по математике. Цепочки …

реши примеры задания по математике

Математические раскраски для 2 класса с примерами. Распечатайте!

Иллюстрация 11 из 11 для 3000 примеров по математике. Цепочки …

СЛОЖЕНИЕ И ВЫЧИТАНИЕ.

Книга Математика – купить в Томске, Северске

Математика. 2 класс (страница 2)

Иллюстрация 6 из 24 для Математика. 3 класс. Цепочки примеров …

Порядок действий» ( 2 класс, М.И. Моро)

3000 примеров по математике. 4 класс. Цепочки примеров. Умножение …

Примеры по математике 2 класс в игре :: nalreiloove

Иллюстрация 2 из 24 для Математика. 3 класс. Цепочки примеров …

Математические раскраски для 2 класса с примерами. Распечатайте!

Порядок действий в выражениях со скобками (2 класс, Петерсон

Сложение и вычитание в пределах 100

Примеры по математике со скобками

Рецензии покупателей на “3000 примеров по математике. Цепочки …

Примеры со скобками, урок с тренажерами. | Kid-mama

Математика. 2 класс. Все цепочки примеров для устных и письменных …

Примеры в столбик для 2 класса hfccgtxfnfnm :: biocicacon

Книга «Математика. 3 класс. 3000 примеров. Цепочки примеров» Ольга …

Calaméo – математика 2 класс

примеры по математике 2 класс на сложение и вычитание со скобками Images Collection Порядок действий в выражениях со скобками (2 класс, Петерсон 2 Сложение и вычитание в пределах 100

Страница 25 – ГДЗ Математика 3 класс.

Моро, Бантова, Бельтюкова, Волкова, Степанова. Учебник часть 1

Вернуться к содержанию учебника

Порядок выполнения действий

Вопрос

3. Рассмотри выражения, установи порядок выпол­нения действий и выполни вычисления.

76 – 27 + 9 – 10	80 : 8 : 2	75 – (35 – 30) • 2
43 – (20 – 7) + 15	21 : 7 • 9	60 : (4 + 6) • 3

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

4. В книге 48 страниц. Даша читала книгу втече­ние трёх дней, по 9 страниц ежедневно. Сколь­ко страниц ей осталось прочитать?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

5. Брат и сестра хотят купить несколько каранда­шей по цене 3 р. за карандаш. У брата есть 5 р., а у сестры — 7 р. Сколько карандашей они могут купить на все деньги?

Подсказка

Повтори, как решать задачи на нахождение стоимости.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

6. На сколько миллиметров один из отрезков длиннее другого?

Подсказка

Чтобы узнать, на сколь­ко сантиметров один отрезок длиннее другого, нужно совме­стить начало первого отрезка с началом второго отрезка и измерить расстояние от конца ко­роткого отрезка до конца длинного отрезка или измерить длины отрезков и сравнить их, из большего числа вычитая меньшее.

Вспомни, сколько миллиметров в одном сантиметре.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

7. Выпиши и реши те уравнения, которые решают­ся сложением.

х – 18 = 29	64 – а = 52	х – 23 = 57
х + 15 = 25	17 + b = 28	48 – x = 20

Подсказка

Решить уравнение – это значит найти такое значение неизвестного числа, при котором это равенство станет верным.

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

8. В хозяйстве 8 комбайнов, 12 тракторов, а гру­зовиков на 5 больше, чем комбайнов и тракто­ров вместе. Сколько … ?

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

32 + 9 • (19 – 16)

27 : 3 • 4

2 • 9 – 18 : 3

Ответ

Поделись с друзьями в социальных сетях:

Вопрос

Ребусы:

Подсказка

Внимательно рассмотри примеры в столбик и вставь пропущенные цифры.

Ответ

Поделись с друзьями в социальных сетях:

Вернуться к содержанию учебника

---

© budu5.com, 2021

Пользовательское соглашение

Copyright

Карточки по математике. Тема “Примеры на порядок действий (примеры с несколькими действиями)” 3 класс | Школьные годы с родителями

Карточки по математике. Тема “Примеры на порядок действий (примеры с несколькими действиями)” 3 класс

Примеры с несколькими действиями вызывают затруднения у детей. Чтобы допускать меньше ошибок, нужно запомнить в каком порядке выполнять действия и быть внимательным при вычислении.

Сначала выполняется действие в скобках по порядку слева направо, сначала умножение и деление, затем сложение и вычитание.

Если скобок нет, то действие выполняется также по порядку слева направо, сначала умножение и деление, затем сложение и вычитание.

Для удобства проставьте над примером порядок действий, а внизу пример разделите на части, чтобы не потерять данные расчета.

Карточки по математике. Тема “Примеры на порядок действий (примеры с несколькими действиями)” 3 класс

Предлагаю примеры на порядок действий для тренировки (с ответами):

1) (82 – 74) : 2 • 8 + 5 • 6 – 19 + (93 – 57) : 4 =

2) (560 – 480) • 3 : 4 + 560 : 7 =

3) 720 : 8 + (401 + 199) : 6 + 180 • 5 =

4) 810 : 90 • 5 + 8 • (18 : 3 + 15 : 15) + (25 : 5) • 100 =

5) 6 • (630 : 9 – 12 : 2) – 720: 60 • 5 + (100 – 36) : 8 =

6) 953 000 – 45 544 + (1 000 • 65) – 15 110 =

7) (500 – 230) : 3 + 60 • 9 – 15 • 2 – (325 – 225 ) • 6 =

8) (9 • 3 – 2 • 4 + 49 : 7) + (92 – 88) • 7 – 11 =

9) (169 – 145) : 3 • 20 + (43 – 34) • 9 =

10) 534 000 + 11 523 – 122 000 + 150 : 5 =

Ответы:

1) 52

2) 140

3) 1090

4) 601

5) 452

6) 957 346

7) 0

8) 43

9) 241

10) 423 553

Эти же примеры размещаю в виде “картинки”, можно сохранить и распечатать.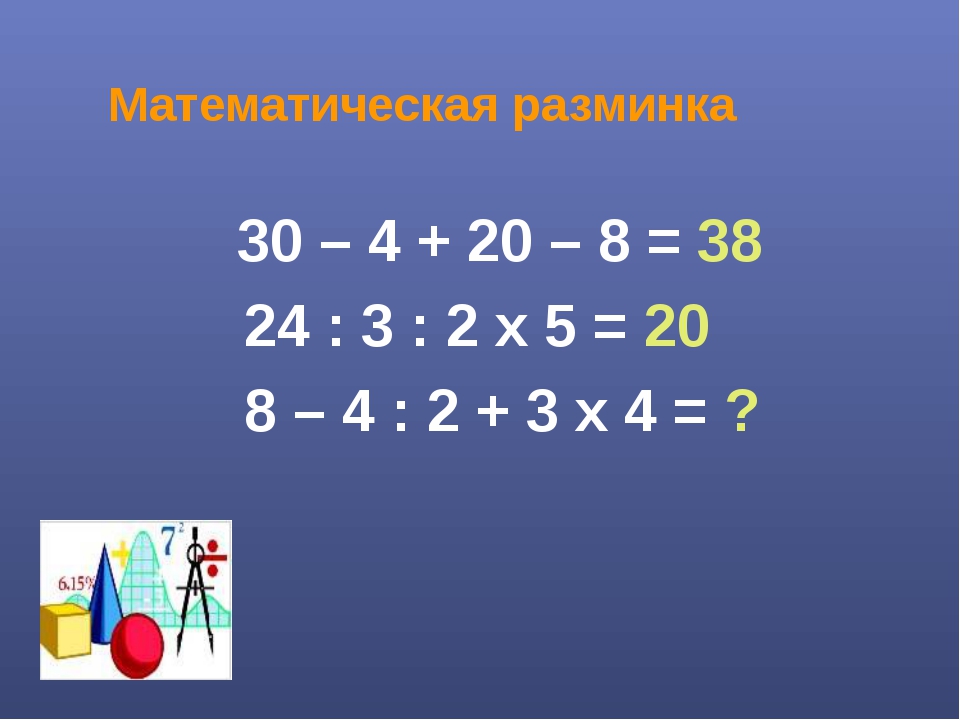 Может так удобнее…

Карточки по математике. Тема “Примеры на порядок действий (примеры с несколькими действиями)” 3 класс

На моем канале еще есть тренировочные задания на темы “Меры длины” и “Меры веса”.

И еще сделала для дочки Карточки для развития внимания. Они состоят из примера на порядок действий и упражнения на внимание.

Решение примеров на порядок действий учат ребенка сосредотачиваться и не отвлекаться.

Ставьте лайк, если эта публикация стала для вас полезной. Пишите, если еще нужны примеры для дополнительных занятий.

Математика урок 3 класс – начальные классы, уроки

Математика

Тема: Порядок выполнения арифметических действий со скобками и без скобок.

Цель: Познакомить с правилом порядка выполнения действий в выражениях, содержащих арифметические действия со скобками и без них;

 – совершенствовать вычислительные навыки;

– развивать

– воспитание доброжелательности, самостоятельности, аккуратности при работе в тетради.

Ход занятия

1.Организационный момент

2.Актуализация опорных знаний

– арифметический диктант + самопроверка

1. Произведение чисел 5 и 4 2.

2. Частное чисел 24 и 3

3. Первое слагаемое 40 и второе слагаемое 40, найдите сумму

4. Уменьшаемое 25, вычитаемое 20, чему равна разность

 – Чтобы записать примеры, какие арифметические знаки использовали? / повторение арифметических знаков и их обозначение /. А ещё есть скобки / показ /. Кто догадался, чем сегодня мы будем заниматься на уроке? / ответы учеников /.

3.Сообщение темы и цели урока

Существуют правила порядка выполнения арифметических действий, которые надо строго соблюдать

4. Усвоение материала

№1Определи порядок действий

37+12:6 27+6-3 12:6*3 (6+10):2+5

5*2+4:2 54-14-7 18:9*5 50+(98-90)*2

Правило

1.Сначала выполни действие в скобках

2. Затем * или : по порядку

3.Потом + или – по порядку

№1(б) Исправь ошибки

5. Физ.минутка

6. Закрепление материала

Работа по учебнику/ стр. 44 № 2

№3 Задачи

Красных роз 8р.по4кус.

Белых роз 23кус.

Всего-?роз

(8*4)+23=55роз

Лиственных д.-179с.

Хвойных д.-186с.

Высадили-?с.

Осталось -145с.

(179+186)-145=220с.

7.Повторение

№4 Реши уравнения

– Какие компоненты неизвестны?

-Как найти множитель? Делимое? Делитель?

Х*5=10 Х:6=2 14:Х=7 8*Х=16

Х=10:5 Х=2*6 Х=14:7 Х=16:8

Х=2 Х=12 Х=2 Х=2

2*5=10 12:6=2 14:2=7 8*2=16

Работа в парах

№6 Расставь скобки так, чтобы равенства были верными

(3+5)*4=32 (3+5)*4-2=30

3+(5*4)=23 3+5*(4-2)=13

Взаимопроверка

8. Итог урока

– Что узнали нового?

9.Задание на дом №2 (3,4 строчки)стр.44

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

3+5*4=32 3+5*4-2=30

3+5*4=23 3+5*4-2=13

ПРИЛОЖЕНИЕ

Задание № 1 / на голубом листе /

700 + 200 – 600 =

200 + 80 + 120 =

300 – 200 – 50 =

90 – 40 + 500 =

Задание №2 / на ярко – жёлтом листе /

( 98 – 8 ) – 50 =

100 + ( 4 + 6 ) =

( 1 + 9 ) – 5 =

50 – ( 25 – 20 ) =

Задание № 3 / на розовом листе /

24 : 4 : 1 =

8 × 0 × 7 =

10 : 2 × 5 =

7 × 3 : 21 =

Задание № 4 / на бледно- зелёном листе /

25 : ( 1 × 5 ) =

( 6 × 3 ) : 18 =

24 : ( 12 : 3 ) =

( 9 × 4 ) × 1 =

Задание № 5 / на оранжевом листе /

5 × 2 + 60 =

42 – 4 : 2 =

60 : 1 – 12 × 0 =

20 : 4 + 5 × 3 =

Задание № 6 / на белом листе /

( 15 + 35) : 5 =

8 × ( 9 – 4 ) =

( 2 + 8 ) × 3 – 20 =

( 5 + 5 ) : ( 11 – 1 ) =

ОСУД « Порядок действий в выражениях, содержащих 4 арифметических действия и скобки » 3 класс

ЕСЛИ В ВЫРАЖЕНИИ

ТОЛЬКО

+ и –

ЕСЛИ В ВЫРАЖЕНИИ

ТОЛЬКО * и :

ЕСЛИ В ВЫРАЖЕНИИ

+ и – , * и :

ЕСЛИ В ВЫРАЖЕНИИ

ОДНА ИЛИ НЕСКОЛЬКО ( )

все действия по порядку

все действия по порядку

1. * или :

по порядку

1.сначала действия

в скобках

2.+ или –

по порядку

2.* или : по порядку

3.+ или – по порядку

КГУ « ОШ № 2 акимата города Шахтинка »

ТЕМА:

« Порядок выполнения арифметических действий

в числовых выражениях без скобок и со скобками,

состоящими из 2-3 действий »

Урок математики по теме “Порядок выполнения действий в выражениях без скобок и со скобками”. 3-й класс

Разделы: Начальная школа

Ход урока

I. Оргмомент (звучит песня “Дважды два четыре”). СЛАЙД

Презентация.

– Ребята, кто из вас любит математику? Почему вы её любите? Математику любят наши знакомые Миша и Маша, ученики 3 класса. Сегодня они как всегда с нами на уроке.

“Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели. ” (А. Маркушевич)

СЛАЙД “Математику уже затем изучать нужно, что она ум в порядок приводит”

Михаил Васильевич Ломоносов, русский учёный, энциклопедист, поэт.

II. Устная работа.

1. Повторение табличных случаев умножения и деления. Работа в группах с использованием ноутбуков.

– Как вы считаете, какое задание, выполняемое нами на каждом уроке приводит наш ум в порядок? (повторение таблицы умножения и деления)

– Проверим, чья группа первая справится с этим заданием. Если вы ошибаетесь в ответе, вас компьютер возвращает к началу теста, и вы выполняете задание заново.

– Прекрасное начало урока! Рада, что вы все справились с заданием!

2. Игра “Да или нет”

– Поиграем в игру “Да или нет”. Если вы согласны с моим высказыванием, то показываете “Да” (скрещенные пальчики), если не согласны – “Нет” ( один указательный пальчик). Договорились?

– При умножении любого числа на 1 получается 1 (да).

– При умножении любого числа на 1, получается 1 (да).

– Чтобы разделить на 10, достаточно дописать 0 (нет, отбросить).

– Умножать на 0 нельзя (нет, можно).

– Чтобы найти делимое, нужно значение частного умножить на делитель (да).

– Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).

– В выражениях без скобок все действия выполняются по порядку слева направо (нет, сначала умножение и деление, потом вычитание и сложение).

– С каждым уроком у вас получается всё лучше! Просто замечательно!

3. Логические упражнения.

Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль) Предлагаю выполнить логические задания. Вы готовы?

– Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)

– Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)

– Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)

– На руках 10 пальцев. Сколько пальцев на 6 руках? (30)

– У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)

– Сколько хвостов у семи котов?

– Сколько носов у двух псов?

– Сколько ушей у 5 малышей?

– Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.

III. Актуализация знаний.

“Чтобы переварить знания, надо поглощать их с аппетитом.” (А.Франц)

– Вы готовы поглощать их с аппетитом? Тогда внимание!

– Посмотрите, пожалуйста, внимательно на доску. Как вы считаете, какое задание предполагается? (Указать арифметические действия, которые выполняются в заданном порядке)

– Проговорите правило, которое подходит к данной схеме.

В выражениях без скобок, содержащих только сложение и вычитание – действия I ступени, или умножение и вычитание – действия II ступени, действия выполняются в том порядке, как они записаны : слева направо.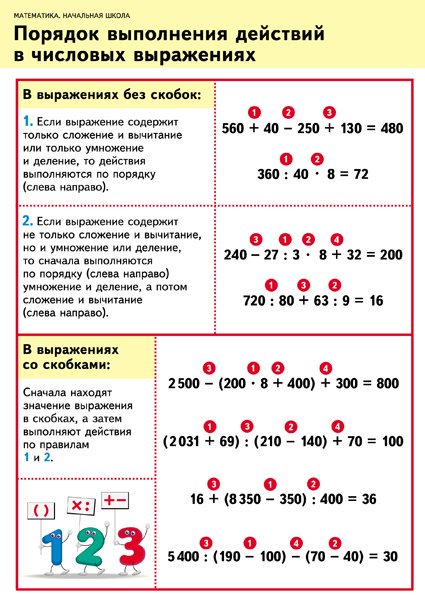

В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.

В выражениях со скобками сначала вычисляют значения выражений в скобках. Затем по порядку слева направо выполняется умножение или деление.

– Озвучьте тему нашего урока. (“Порядок выполнения действий в выражениях со скобками и без скобок”)

– Просто умницы, ловко справились, умело.

VI. Целеполагание.

– Ребята, как вы считаете, достаточно ли хорошо отработана нами тема “Порядок выполнения действий в выражениях”?

– На что нам сегодня необходимо обратить внимание? Над чем поработать? (Упражняться в нахождении значений выражений, содержащий действия разных ступеней со скобками и без них. Познакомиться с видами выражений, в которых можно допустить ошибки)

– И в этом разобрались. Я думаю, достаточно поставленных задач на сегодняшний урок.

V. Постановка проблемной ситуации. Работа в группах. (карточки)

– Ребята, послушайте, пожалуйста, что говорил французский математик Д. Пойя: “Лучший способ изучить что-либо – это открыть самому”. Вы готовы к открытиям?

СЛАЙД– Даны выражения, посмотрите, как справились с заданием Маша и Миша.

– Кто выполнил задание верно: Маша или Миша? (ответы детей)

– К кому из наших друзей можно отнести следующее высказывание Р. Декарта “Мало иметь хороший ум, главное – хорошо его применять? (К Мише, потому что он ошибся)

– Какие ошибки допущены Мишей?

СЛАЙД – Давайте проверим!

– Я знала, что это задание вам было под силу!

VII. Разрешение проблемной ситуации.

СЛАЙД – В данной ситуации кто является КП – “кислой парочкой”? (Миша и выражения)

– Как разрешить проблему?

(Миша должен САМ найти значения выражений

– Какие у него есть для этого ресурсы? (Память, чтобы запомнить правило, старание, тренировка, учебник,

Выражения САМИ должны быть решены, для этого ресурсы: Маша, учитель, родители)

– Какое ИКР вы бы выбрали? Почему?

– А если Миша воспользуется ИКР2? Это будет хорошо или плохо, давайте поиграем!

Игра “Хорошо-плохо”

– Если за него выполнят задание, то будет хорошо, потому что. ..(ему не нужно будет долго сидеть за уроками, не нужно будет думать, у него появится свободное время…)

– Если за него выполнят задание, то будет плохо…(сам не научится решать, не будет трудолюбивым, не усвоит тему, будут проблемы в учёбе…)

“Величие человека – в его способности мыслить.” (Б. Паскаль)

– Ребята, у вас получилось лучше, чем я могла бы подумать!

– А ещё вам предлагается новый способ записи решения. В чём он заключается? (Нужно выписывать все действия ниже данного выражения)

– Вот в этом мы сейчас с вами и поупражняемся.

VIII. Нахождение значений выражений. (№228) – у доски 3 выражения.

“Счет и вычисления – основа порядка в голове.” (Песталоцци)

IX. Самостоятельная работа № 228, 3 выражения.

– Я горжусь вами, что вам удалось выполнить задание почти без ошибок.

X. Решение задачи №227.

“Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. ” (Д.Пойа)

У всех учащихся второго класса 39 ручек. У шести учеников по одной ручке, у пяти по три, а у остальных по две. Сколько учеников имеют по две ручки? Маша записала решение этой задачи выраженим так: 39-1 * 6+3 * 5. Миша – так: 39-(1 * 6+3 * 5) Кто прав: Миша или Маша?

– Прочитайте установку и ответьте на вопрос. Кто прав Миша или Маша?

– Самостоятельно запишите решение задачи и ответ.

– Назовите ответ.

СЛАЙД – Давайте проверим!

– Поздравляю, это правильный ответ!

XI. Работа по алгоритму.

– Что такое алгоритм? (Порядок выполнения действий)

СЛАЙД – Выполните действия по алгоритму.

– “Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.”, говорил М.В. Остроградский. Вот и мы сейчас вспомним то, что изучали на уроках информатики.

– Какая фигура получилась? (прямоугольник)

– Ниже начертите фигуру, площадь которой в 6 раз больше.

– Что примите за единичный отрезок? (2 клетки)

– Вы на верном пути!

СЛАЙД – Из скольких мерок состоит ваша фигура?

– Внимание на слайд! Вас ждёт сюрприз, если правильно найдёте значения выражений.

XII. Нахождение значений выражений. (СЛАЙД)

– Именно этого мы с вами и ждали! (на слайде появляется фото класса)

XIII. Итог урока.

– Выполнили ли мы поставленные цели урока? Что планировали? Всё ли у нас получилось? Над чем необходимо поработать?

– Вы сегодня просто умнички, много сделали. Работать с вами просто радость!

XIV. Рефлексия.

– Оцените работу вашей группы, насколько успешно работали, аргументируйте свой выбор (карточки с цифрами).

XV. Домашнее задание.

– Что необходимо закрепить дома? (порядок выполнения действий в сложных выражениях) № 234 (1 столбик), №230.

– “Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)

Муниципальное бюджетное  общеобразовательное учреждение

Целинная средняя общеобразовательная школа № 14 Урок математики 2 класс

Тема: « Порядок выполнения действий. Скобки УМК «Школа России»

   Автор : учитель начальных классов  Котюшева В.Н

Цели: познакомить с порядком выполнения действий при вычислениях; учить находить значения выражений со скобками; развивать умение решать текстовые задачи и задачи логического характера; совершенствовать вычислительные навыки.

УУД:

Познавательные :учащиеся научатся соблюдать порядок действий при вычислениях; находить значения выражений, содержащих скобки;

Регулятивные: использовать графические модели при решении задач;

Коммуникативные: слушать собеседника и вести диалог;

Личностные: оценивать себя и товарищей.

        Ход урока:

1. Мотивация (самоопределение) к учебной деятельности.

Прозвенел звонок и смолк-

Начинается урок.

Вы за парты тихо сели,

На меня все посмотрели.

Пожелайте успехов глазами

И вперёд за новыми знаниями!

 

– Работать сегодня мы будем коллективно и в парах. Вспомните правила работы в парах.(Прислушиваться к мнению соседа, работать дружно, помогать друг другу)

В конце урока каждый из вас оценит свою работу.

 

1. Актуализация и фиксирование индивидуального затруднения в пробном действии.

(На доске записаны примеры.)

20-9+8=19

20-9+8=3  

-Рассмотрите примеры. Сравните. Чем они похожи? Чем отличаются?

-Какое равенство верно? (Первое.)

– Как выполняли действия?  (Сначала выполнили вычитание, а потом сложение.)

– В каком порядке нужно выполнить действия во втором равенстве, чтобы оно стало верным? (Сначала сложить 9 и 3, а затем из 20 вычесть их сумму. )

3. Выявление места и причины затруднения.

– Мы поняли, как нужно решать эти примеры. А как показать это другим?

– Чего мы не знаем?  (Как показать, в каком порядке нужно выполнять действия в некоторых примерах.)

 

1. Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)

– О чём сейчас говорили?  (О порядке выполнения действий.)

– Какая тема урока?  (Порядок выполнения действий.)

-Какова цель нашего урока? (Научиться обозначать в записи порядок действий.)

5.Поиск решения проблемы.

-Посмотрите, чем отличаются столбики примеров?

8-3+4=9                      8-(3+4)=1

18-8+9=19                  18-(8+9)=1

20-5+3=18                  20-(5+3)=12

(В первом столбике нет скобок, а во втором есть.)

– Зачем же они нужны?

-Как выполняли действия в первом столбике? (По порядку.)

-Как будем выполнять действия во втором столбике, чтобы получить эти значения выражений? (Сначала выполним действие в скобках.)

-Сравните порядок выполнения действий в первом и во втором столбиках. Что вы можете сказать? ( В первом столбике мы выполняли действия по порядку, а во втором  сначала в скобках.)

-Что нам поможет указать на порядок выполнения действий?  (Скобки.)

-Сформулируйте правило, как правильно выполнять действия в выражениях со скобками. (Сначала выполняются действия в скобках, а потом по порядку)

Первичное закрепление с проговариванием во внешней речи

– Мы получили новое знание. Проверим, правильно ли мы сделали выводы.

Сравним наше новое знание с научным в учебнике. Прочитайте на с.38 выделенное в рамочку.

-Попробуем применить наше новое знание на практике.

№ 1 (с. 38).

(Коллективное выполнение с комментированием.)

Физкультминутка

 

1. Самостоятельная  работа в парах  с самопроверкой по эталону.

№2 (с. 38).

-Решите первый пример. Проверьте, получим ли мы нужный результат, если вычисления будем выполнять по порядку. (Не получим.)

-Измените порядок действий. Какое действие выполним первым? (Сложение.)

-Вычислите. Получился ли у вас нужный результат? (Да.)

–Поставьте скобки.

(Остальные примеры  разбираются аналогично.  Следует обра­тить  внимание учащихся на то, что, если скобки не меняют порядок  действий,  их можно не ставить.)

1. Включение в систему знаний повторение.

№3 (с. 38).

(Один ученик выполняет на доске с комментированием,  остальные— в тетрадях.)

№4 (с. 38).

-Рассмотрите рисунок.

( Составьте задачу по первому решению. (В лодке плыли 5 де­тей и 1 взрослый. Сколько всего человек плыло в лодке ?)

( Составьте задачу по второму решению. (В лодке было 6 че­ловек. На берег вышли 2 человека. Сколько человек осталось и лодке?)

Можно ли задачи назвать обратными? (Нет.)

-Решите задачи.

(Ученик, решивший задачу первым, записывает решение и ответ на доске. Проверка. Тем, кто справится с заданием быстрее других, дополнительно можно предложить составить ко второй задаче обратные задачи.)

№5 (с. 39).

(Самостоятельное выполнение. Проверка по образцу на ли сточке, который находится у учителя.)

8. Рефлексия.

– Итак, над какой темой мы работали? Удалось ли решить поставленную задачу?

– В чём испытывали трудности?

(«Проверь себя» (учебник, с.39). Самостоятельное выполнение. Коллективная проверка. Самооценивание.

– Я поздравляю Вас, вы поднялись ещё на одну ступеньку знаний вверх Молодцы. Спасибо за урок.

9.Домашнее задание (по выбору).

 

 

 

 

 

Круглые скобки – математика для 3-го класса

Узнайте о скобках () в уравнениях

Во 2-м классе вы научились решать такие многоступенчатые уравнения:

15 + 20 + 10 =?

30 – 12 – 6 =?

Но иногда вы можете увидеть такие уравнения:

13 + ( 12 + 8 ) =?

Это уравнение содержит пару круглых скобок (), называемых круглых скобок.

Что такое круглые скобки?

Скобки – это пара скобок () , которые говорят вам, что решить в первую очередь.

Всегда сначала решайте задачи в скобках . 👍

👉 Скобки очень важны, потому что они могут изменить ответ на ваше уравнение!

Посмотрим как.

Посмотрите на это уравнение.

27-10 + 7 = ?

Если мы заключим в скобки первые два числа , какой ответ мы получим?

(27-10) + 7 = ?

Сначала решаем выражение внутри скобок .

Совет: переписывайте уравнение после каждого шага.

17 + 7 = 24

Отличная работа!

Теперь давайте попробуем заключить в круглые скобки последние два числа , вместо первых двух.

27 – (10 + 7) = ?

Когда мы решаем это уравнение, получаем ли мы такое же значение?

27 – 17 = 10

Ответ изменился с 24 на 10!

Добавление скобок изменило ответ.Это число скобок в степени . 💪

Решение уравнений в круглых скобках

Попробуем решить некоторые уравнения со скобками.

Пример 1

14 + (19-13) = ?

🤔 Какую операцию вы решите в этом уравнении в первую очередь – сложение или вычитание?

Верно! 👍

✅ Поскольку вычитание заключено в круглые скобки, мы должны сначала решить его.

Давайте теперь решим уравнение.

Как вы теперь знаете, мы должны сначала решить скобки .

14 + (19–13) = 14 + 6

Теперь давайте сложим два числа , которые у нас есть.

14 + 6 = 20

Отличная работа! 👏

__

Попробуем еще один пример.

Пример 2

(30-20) + (9 + 6) – 3 = ?

Какие части уравнения вы решите в первую очередь?

Очень хорошо! 👌

✅ Части в скобках должны быть решены в первую очередь.

Во-первых, давайте решим первые скобки .

😺 Совет: переписывайте уравнение после каждого шага.

Теперь давайте решим другие скобки .

Давайте теперь решим оставшуюся часть уравнения.

10 + 15 – 3 = 25 – 3

25 – 3 = 22

Отлично! 😎

Смотри и учись

Вы отлично справились с уроком! 👏 Теперь попробуйте самостоятельно освоить круглые скобки.

Порядок операций – урок для 3 класса

Это полный урок для третьего класса с обучением и упражнениями по порядку операций . Упражнения касаются только скобок, сложения, вычитания и умножения (но не деления). Студентам предлагается обвести первую операцию, которую нужно сделать, в пузыре или воздушном шаре – это может сделать ее интересной! Наконец, они решают забавную головоломку, выясняя, какие операции делают данные уравнения верными.

---

Порядок операций 1) Сначала мы вычисляем, что находится в скобках (). 2) Затем мы МНОЖЕСТВЕННО перед сложение или вычитание. 3) Наконец, мы ДОБАВЛЯЕМ и ВЫЧИТАЕМ слева направо.

Пример. 4 × (2 + 3) Сначала мы вычисляем 2 + 3, потому что оно заключено в круглые скобки. Итак, получаем 4 × 5. То есть 20.

1. Сложить и вычесть. Помните круглые скобки! Обведите операцию, для которой требуется
делать СНАЧАЛА в «пузыре» или воздушном шаре.

а. 20 + 6 – 3 б. 20 + (6–3)

г. 20-6 + 3 г. 20 – (6 + 3)

e. 80-30 – (30 + 20) ф. 80 – (30-30) + 20

2. Рассчитайте. Обведите в кружок операцию, которую нужно выполнить в первую очередь. Скобки → умножить → сложить / вычесть.

а. 3 + 5 × 2	б . 5 × (3 + 1)	г. 4 × (4-2)
г. 3 × 6 – 11	e. 25 – 5 × 2	ф. (2-3) × 6
г. (4 + 2) × 2	ч. 3 × 5 + 2 × 4	и. 50 – (7-2) × 4

3.Обведите «пузырем» операцию, которую нужно выполнить первой!

4. Теперь смотрите внимательно! Вам потребуется больше шагов.

а. 3 × 4 – 2 × 3	б. 6 + 7 × (4–2)
г. 2 × (5 + 4) + 5	г. 30 – 2 – 7 × 2

5. Решите. Написать числовое предложение для каждой проблемы. Не просто напишите ответ.

а. Десять человек собираются обедать. Одна из них – маленькая Ханна. Есть две тарелки на всех, кроме Ханны только одна тарелка. Сколько тарелок на столе?

г. В маленьком ресторане пять столов на двоих и четыре стола для четырех человек.Сколько человек может сидеть в ресторане?

Какие операции сделают числовые предложения верными? Из этого можно сделать игру. Заранее составьте задачи и используйте любую настольную игру с кубиками, Правило состоит в том, что вы можете бросить кубик, только если сначала правильно ответите на вопрос.

См. Также

Математический сейф
Веселая игра на логическое мышление, в которой вам нужно использовать четыре заданных однозначных числа и любую из четырех операций, чтобы достичь заданного числа, а затем сейф откроется! Он практикует использование всех четырех операций, а также порядок операций.Игра подходит лучше всего для 4 классов и выше.

Выберите игру с математическими операциями
Выберите математические операции, чтобы числовое предложение было верным. Практикуйте роль нуля и единицы в основных операциях или операциях с отрицательными числами. Помогает развить чувство числа и логическое мышление.

Бесплатные рабочие листы для порядка работы
Бесплатные распечатываемые рабочие листы для порядка операций в форматах PDF и html.Выберите из пяти операций и скобок. Вы можете настроить рабочие листы, выбрав используемый диапазон номеров, количество проблем и т. Д.

---

Авторские права HomeschoolMath.net.

---

Круглые, фигурные и квадратные скобки в математике

Вы встретите много символов в математике и арифметике. Фактически, язык математики написан символами, с некоторым текстом, вставленным по мере необходимости для пояснения. Три важных и связанных символа, которые вы часто будете видеть в математике, – это круглые, квадратные и фигурные скобки, которые вы часто будете встречать в предалгебре и алгебре.Вот почему так важно понимать, как эти символы используются в высшей математике.

Использование круглых скобок ()

Круглые скобки используются для группировки чисел или переменных, или того и другого. Когда вы видите математическую задачу, содержащую круглые скобки, вам нужно использовать порядок операций для ее решения. Например, возьмем задачу: 9-5 ÷ (8-3) x 2 + 6

Для этой проблемы вы должны сначала вычислить операцию в круглых скобках, даже если это операция, которая обычно выполняется после других операций в задаче.В этой задаче операции умножения и деления обычно выполняются перед вычитанием (минус), однако, поскольку 8–3 попадают в круглые скобки, вы должны сначала решить эту часть задачи. Как только вы позаботитесь о вычислениях, которые попадают в круглые скобки, вы удалите их. В этом случае (8 – 3) становится 5, поэтому вы должны решить проблему следующим образом:

9-5 ÷ (8-3) x 2 + 6

= 9–5 ÷ 5 х 2 + 6

= 9 – 1 х 2 + 6

= 9 – 2 + 6

= 7 + 6

= 13

Обратите внимание, что в соответствии с порядком операций вы должны сначала работать с тем, что указано в круглых скобках, затем вычислять числа с показателями, а затем умножать и / или делить и, наконец, складывать или вычитать.Умножение и деление, а также сложение и вычитание занимают одинаковое место в порядке операций, поэтому вы выполняете их слева направо.

В приведенной выше задаче, позаботившись о вычитании в круглых скобках, вам нужно сначала разделить 5 на 5, получив 1; затем умножьте 1 на 2, получив 2; затем вычтите 2 из 9, получив 7; а затем сложите 7 и 6, получив окончательный ответ 13.

Круглые скобки также могут означать умножение

В задаче: 3 (2 + 5) круглые скобки говорят вам умножать.Однако вы не будете умножать, пока не завершите операцию в круглых скобках – 2 + 5 – поэтому вы решите проблему следующим образом:

3 (2 + 5)

= 3 (7)

= 21

Примеры скоб []

Скобки также используются после скобок для группировки чисел и переменных. Обычно вы используете сначала круглые скобки, затем скобки, а затем фигурные скобки. Вот пример проблемы с использованием скобок:

4–3 [4–2 (6–3)] ÷ 3

= 4 – 3 [4 – 2 (3)] ÷ 3 (Сначала выполните операцию, указанную в скобках; скобки оставить.)

= 4 – 3 [4 – 6] ÷ 3 (Выполните операцию в скобках.)

= 4 – 3 [-2] ÷ 3 (Скобка советует вам умножить число внутри, которое составляет -3 x -2.)

= 4 + 6 ÷ 3

= 4 + 2

знак равно 6

Примеры скобок {}

Фигурные скобки также используются для группировки чисел и переменных. В этом примере задачи используются круглые, квадратные и фигурные скобки. Скобки внутри других скобок (или скобок и фигурных скобок) также называются «вложенными скобками».”Помните, когда у вас есть круглые скобки внутри скобок и фигурных скобок или вложенные круглые скобки, всегда работайте изнутри:

2 {1 + [4 (2 + 1) + 3]}

= 2 {1 + [4 (3) + 3]}

= 2 {1 + [12 + 3]}

= 2 {1 + [15]}

= 2 {16}

= 32

Примечания относительно круглых, квадратных и фигурных скобок

Круглые, квадратные и фигурные скобки иногда называют «круглыми», «квадратными» и «фигурными» скобками соответственно.Подтяжки также используются в наборах, например:

{2, 3, 6, 8, 10 …}

При работе с вложенными круглыми скобками всегда будут скобки, скобки, фигурные скобки в следующем порядке:

{[()]}

Порядок операций: примеры

Purplemath

Большинство проблем с упрощением использования порядка операций проистекают из вложенных круглых скобок, показателей степени и знаков «минус».Итак, в следующих примерах я продемонстрирую, как работать с такого рода выражениями.

(Ссылки приведены для дополнительного обзора работы с негативами, группировочными символами и полномочиями.)

• Упростить 4–3 [4–2 (6–3)] ÷ 2.

MathHelp.com

Я буду упрощать изнутри: сначала круглые скобки, затем квадратные скобки, помня, что знак «минус» на цифре 3 перед скобками идет вместе с цифрой 3. Только после того, как группировка будет завершена, я смогу сделайте деление с последующим добавлением 4.

4–3 [4–2 (6–3)] ÷ 2

4–3 [4–2 (3)] ÷ 2

4–3 [4–6] ÷ 2

4 – 3 [–2] ÷ 2

4 + 6 ÷ 2

4 + 3

7

Помните, что в leiu символов группировки, говорящих вам об обратном, деление идет перед сложением, поэтому это выражение в конечном итоге упростилось до «4 + 3», а не до «10 ÷ 2».

(Если вы не чувствуете себя комфортно со всеми этими знаками «минус», просмотрите «Негативы».)

---

• Упростить 16-3 (8-3)

  ² ÷ 5.

Я должен не забыть упростить в скобках перед квадратом I, потому что (8 – 3) ² – это , а не , то же самое, что 8 ² – 3 ² .

16-3 (8-3) ² ÷ 5

16-3 (5) ² ÷ 5

16-3 (25) ÷ 5

16-75 ÷ 5

16–15

1

---

Если вы узнали о переменных и объединении «похожих» терминов, вы также можете увидеть такие упражнения, как это:

• Упростить 14

  x + 5 [6 – (2 x + 3)].

Если у меня возникают проблемы с вычитанием через круглые скобки, я могу превратить его в умножение отрицательной единицы через круглые скобки (обратите внимание на выделенную красным цифру «1» ниже):

14 x + 5 [6 – (2 x + 3)]

14 x + 5 [6 – 1 (2 x + 3)]

14 x + 5 [6 – 2 x -3]

14 x + 5 [3–2 x ]

14 x + 15-10 x

4 x + 15

---

• Упростить – {2

  x – [3 – (4 – 3 x )] + 6 x }.

Мне нужно не забывать упрощать на каждом этапе, комбинируя похожие термины, когда и где я могу:

– {2 x – [3 – (4 – 3 x )] + 6 x }

–1 {2 x – 1 [3 – 1 (4 – 3 x )] + 6 x }

–1 {2 x – 1 [3 – 4 + 3 x ] + 6 x }

–1 {2 x – 1 [- 1 + 3 x ] + 6 x }

–1 {2 x + 1-3 x + 6 x }

–1 {2 x + 6 x – 3 x + 1}

–1 {5 x + 1}

–5 x – 1

(Дополнительные примеры такого рода см. В разделе «Упрощение с круглыми скобками».)

---

Выражения, содержащие дробные формы, тоже могут вызывать путаницу. Но пока вы работаете с числителем (то есть сверху) и знаменателем (то есть снизу) отдельно, пока они сначала полностью не упростят, а только потом объедините (или уменьшите), если возможно, тогда вы все должно быть в порядке. Если дробная форма добавляется или вычитается из другого члена, дробного или иного, убедитесь, что вы полностью упростили и уменьшили дробную форму, прежде чем пытаться выполнить сложение или вычитание.

• Упростить [45] / [8 (5 – 4) – 3] + [3 (2)

  ² ] / [5 – 3]

Прежде чем я смогу добавить два термина, я должен упростить.

[45] / [8 (5 – 4) – 3] + [3 (2) ² ] / [5 – 3]

[45] / [8 (1) – 3] + [3 (4)] / [2]

[45] / [8–3] + [12] / [2]

[45] / [5] + 6

9 + 6

15

---

• Упростить [(3–2) + (1 + 2)

  ² ] / [5 + (4–1)]

Это работает так же, как и в предыдущих примерах.Мне просто нужно работать над «верхом» и «низом» отдельно, пока я не получу дробь, которую я могу (возможно) уменьшить.

[(3–2) + (1 + 2) ² ] / [5 + (4–1)]

[(1) + (3) ² ] / [5 + (3)]

[1 + 9] / [8]

10/8

5/4

(Примеры с множеством экспонент см. В разделе Упрощение с экспонентами.)

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении порядка операций. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Упростить» или «Оценить» во всплывающем окне, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

---

Боковое форматирование и умножение на сопоставление

В следующем примере показана проблема, которая почти никогда не возникает, но когда она возникает, спорам, кажется, нет конца. (Публиковать их в Facebook стало досадно.)

• Упростить 16 ÷ 2 [8 – 3 (4 – 2)] +1.

Упрощаю обычным способом:

16 ÷ 2 [8 – 3 (4 – 2)] + 1

16 ÷ 2 [8 – 3 (2)] + 1

16 ÷ 2 [8–6] + 1

16 ÷ 2 [2] + 1 (**)

16 ÷ 4 + 1

4 + 1

5

В приведенном выше расчете сбивает с толку то, как «16, разделенное на 2 [2] + 1» (в строке, отмеченной двойной звездой) становится «16, разделенное на 4 + 1» вместо «8 раз на 2 + 1 “.

Это потому, что, хотя умножение и деление находятся на одном уровне (поэтому должно применяться правило слева направо), скобки каким-то образом превосходят деление по рангу, поэтому первые 2 в строке, отмеченной звездочкой, часто рассматриваются как идущие с [ 2], которая следует за ним, а не с «16, разделенными на», которое предшествует ему. То есть умножение, которое указывается путем помещения в круглые скобки (или скобки и т. Д.), Часто рассматривается (научными деятелями) как «более сильное», чем «обычное» умножение, которое обозначается каким-либо символом, например как “×”.

Набор всей задачи в графическом калькуляторе подтверждает существование этой иерархии, по крайней мере, в некотором программном обеспечении:

Обратите внимание, что различных программных пакетов будут обрабатывать это выражение по-разному ; даже разные модели графических калькуляторов Texas Instruments будут обрабатывать это выражение по-разному. Общее мнение среди математиков состоит в том, что «умножение на сопоставление» (то есть умножение путем простого размещения элементов рядом друг с другом, а не использования знака «×») указывает на то, что сопоставленные значения должны быть умножены вместе перед обработкой других операций.Но не все программы запрограммированы таким образом, и иногда учителя смотрят на вещи иначе. Если сомневаетесь, спрашивайте! И, печатая что-то боком, будьте очень осторожны с скобками и проясните свой смысл, чтобы избежать именно этой двусмысленности.

(Пожалуйста, не присылайте мне электронное письмо с просьбой или предложением окончательного вердикта по этому вопросу. Насколько я знаю, такого окончательного вердикта нет. Если я скажу мне действовать по-вашему, , а не , решит проблему проблема!) (Для примера того типа писем, которые я получаю по этому поводу, перейдите на следующую страницу, которая также содержит больше примеров дробной формы.)

---

Филиал

---

---

URL: https://www.purplemath.com/modules/orderops2.htm

Скобки (скобки)

Скобки – это символы, используемые попарно для группировки предметов.

Типы кронштейнов включают: круглые скобки или «круглые скобки» () “квадратные скобки” или “квадратные скобки” [] фигурные скобки {} “угловые скобки” <> (Примечание. Угловые скобки могут сбивать с толку, поскольку они выглядят как знаки «меньше» и «больше»)

Когда мы видим что-то внутри скобок, мы делаем это в первую очередь (как описано в разделе «Порядок операций»).

Пример: (3 + 2) × (6-4)

Скобки группируют 3 и 2 вместе, а 6 и 4 вместе, поэтому они выполняются первыми:

(3 + 2) × (6-4)

= (5) × (2)

= 5 × 2

= 10

Без скобок сначала выполняется умножение:

3 + 2 × 6-4
= 3 + 12-4
= 11 (не 10)

При более сложной группировке хорошо использовать кронштейнов различных типов :

Пример: [(3 + 2) × (6–4) + 2] × 4

Скобки группируют 3 и 2 вместе, а 6 и 4 вместе, а квадратные скобки говорят нам выполнить все вычисления внутри них перед умножением на 4:

[(3 + 2) × (6–4) + 2] × 4

= [(5) × (2) + 2] × 4

= [10 + 2] × 4

= 12 × 4

= 48

Фигурные скобки

Фигурные скобки {} используются в наборах:

Пример: {2, 4, 6, 8}

Набор четных чисел от 2 до 8

скобок по математике: типы и примеры – видео и стенограмма урока

Скобки и группировка

Часто можно встретить математические скобки, используемые для группировки .Эти скобки могут включать:

При использовании для группировки скобки всегда идут парами. Будет открывающаяся скобка и закрывающая скобка .

Скобки используются для наглядности порядка операций , порядка, в котором несколько операций должны выполняться в математическом выражении.

Например, предположим, что у вас есть следующее выражение: 2 + 4 * 6 – 1. Несмотря на то, что вы могли прочитать на Facebook, есть только один правильный ответ на это выражение.Вы выполняете умножение и деление, двигаясь слева направо, прежде чем выполнять сложение и вычитание, также перемещаясь слева направо. Выполнив сначала умножение, вы получите 2 + 24 – 1 = 25.

Что, если вместо этого вы захотите сначала выполнить сложение и вычитание (а затем умножить результаты)? Используйте скобки. Теперь проблема принимает следующий вид: (2 + 4) * (6 – 1) = 6 * 5 = 30. В этом примере круглые скобки говорят вам сделать что-то отличное от обычного порядка операций.В других случаях они просто используются для визуальной ясности.

Несколько уровней группировки

Возможно, вы захотите выполнить группировку внутри группировки. Если так, то такие выражения сбивают с толку: 2 + (1 + (3 + 2 * (4 + 5))). Хотя нет ничего плохого в использовании нескольких уровней круглых скобок (а иногда в компьютерных приложениях у вас нет выбора), на это немного сложно смотреть.

Вместо этого вы можете использовать разные типы скобок для каждого уровня. В математике чаще всего используются круглые скобки для первого уровня (первая операция, которую вы должны выполнить), квадратные скобки для следующего уровня и фигурные скобки для последнего уровня: 2 + {1 + [3 + 2 * (4 + 5)]}.

В любом случае вы сначала выполняете внутреннюю группировку (4 + 5), а оттуда двигаетесь наружу, как показано ниже:

 2 + {1 + [3 + 2 * 9]} = 2 + {1 + [3 + 18 ]} = 2 + {1 + 21} = 2 + 22 = 24 

Это немного похоже на поиск выхода из особняка вашего дяди Джерома. Сначала вам нужно выбраться из гостевой комнаты, затем вы выберетесь с третьего этажа, а затем вы выберетесь из самого дома. Сначала вы начинаете с самой внутренней «загадки», а оттуда двигаетесь наружу.

Другое использование скобок

Однако иногда скобки используются не для группирования. Например, если вы работаете с функциями , тогда f ( x ) означает «функция f с x в качестве входных данных». В этом случае круглые скобки используются для обозначения аргументов, или входных данных функции.

Также круглые скобки могут использоваться для обозначения упорядоченной пары , например (3, -1). Вы часто будете видеть, что это используется для обозначения декартовых координат : если вы строите точку относительно осей x и y , (3, -1) будет конкретной точкой на декартовой плоскости, где x равно 3, а y равно -1.

Или скобки могут представлять обозначение интервала . (1,5) может означать все значения от чуть более одного до почти пяти. [4,6] может означать все числа от четырех до шести, включая четыре и шесть.

Фигурные скобки также часто используются для обозначения множеств. Например, {3, 4, 5, 6} означает набор, включающий числа 3, 4, 5 и 6. Угловые скобки, такие как <1,3>, могут указывать на внутренний продукт в продвинутой математике или физике. class, а квадратные скобки могут означать, что то, что находится внутри, является матрицей.

Итак, как узнать, что означают скобки, если их можно использовать по-разному? Точно так же вы узнаете, относится ли «синий» к цвету глаз вашего любимого человека или к ощущению, которое вы испытываете, когда он бросает вас ради лучшего друга – по контексту.

Краткое содержание урока

Математические скобки часто используются для группировки, чтобы указать порядок, в котором должен выполняться набор математических операций. Однако в некоторых случаях скобки используются для специальных математических целей.

Ключевые точки

• Группировка : скобки будут включать: (), [] & {}
• Открывающая скоба и закрывающая скоба : все скобки попарно
• Порядок операций : порядок, в котором несколько операций должны выполняться в математическом выражении
• Функции : в скобках используется f ( x ), что означает «функция f с x в качестве входных данных»
• Аргументы : круглые скобки используются для указания входных данных функции
• Упорядоченная пара : круглые скобки могут использоваться для обозначения пар, например (3, -1)
• Декартовы координаты : нанесение точки на оси x и y –
• Интервальное обозначение : (1,5) может означать все значения от чуть более одного до почти пяти
• Внутренний продукт : угловые скобки, такие как <1,3>; может указывать наборы в продвинутом классе математики или физики

Результаты обучения

Просматривая урок по использованию скобок, сделайте своей целью:

• Иллюстрировать математические скобки
• Приведите примеры использования скобок
• Выделите их использование для нескольких уровней группировки
• Обсудите роль скобок в сообщении аргументов и указании упорядоченных пар, а также в представлении обозначений интервалов и множеств.

Правило PEMDAS – ChiliMath

Правило PEMDAS (аббревиатура от «Прошу прощения, моя дорогая тетя Салли») представляет собой набор правил, определяющих порядок вычислений, то есть какую операцию выполнять в первую очередь.В противном случае можно получить несколько или разные ответы. Мы не хотим, чтобы это произошло.

Ниже показан пример, в котором есть два возможных ответа. Первое решение дает неправильный ответ, поскольку вычисляет числовое выражение слева направо. В то время как второе решение является правильным, потому что оно следует правилам Порядка операций.

Упростите числовое выражение.

Неправильное решение:

Правильное решение:

---

Порядок операций

Шаг 1 : В верхней части списка не забудьте ВСЕГДА упростить все внутри символов группировки.Примерами символов группировки являются круглые скобки (), квадратные скобки и фигурные скобки {}. Для вложенных группирующих символов проработайте это изнутри и снаружи.

Шаг 2 : Экспоненциальные выражения вычисляются или оцениваются перед выполнением любой из четырех основных арифметических операций, а именно: сложение, вычитание, умножение и деление.

Шаг 3 : Затем умножьте и / или разделите слева направо в зависимости от того, что наступит раньше, перед выполнением сложения и вычитания.Это говорит нам о том, что умножение и деление имеют более высокий уровень важности, чем сложение и вычитание.

Шаг 4 : Наконец, сложите и / или вычтите слева направо в зависимости от того, что идет раньше.

---

PEMDAS

PEMDAS – это мнемоническое устройство, которое может помочь нам запомнить порядок операций, который, как мы уже знаем, означает « P lease E xcuse M y D ear A и S ally».

P – Скобки

E – Экспоненты

M – Умножение

D – Отдел

A – Дополнение

S – Вычитание

Небольшое предупреждение: операции умножения и деления имеют одинаковый уровень приоритета.Чтобы решить, когда умножать или делить, всегда выполняйте первое слева направо.

Таким же образом сложение и вычитание равны по важности. Выполните первую операцию слева направо.

---

Примеры применения правила PEMDAS

Пример 1 : Упростите следующее выражение, используя Порядок операций.

Решение : Обратите внимание, что здесь задействованы три операции.В зависимости от порядка операций умножение имеет приоритет перед сложением и вычитанием, поэтому мы будем умножать в первую очередь. Затем вычтите, затем добавьте, так как операция вычитания выполняется перед сложением слева направо.

---

Пример 2 : Упростите следующее выражение, используя Порядок операций.

Решение : символ группировки имеет наивысший приоритет, что означает, что мы должны сначала упростить все внутри. В скобках указаны операции деления и умножения.Поскольку они имеют одинаковую важность, порядок их появления слева для записи будет определять, что будет первым. В этом случае мы сначала делим, а затем умножаем.

После упрощения выражения внутри скобок у нас останется вычитание и деление. Очевидно, что деление должно быть вычислено перед вычитанием.

---

Пример 3 : Упростите следующее выражение, используя Порядок операций.

Решение : упростите выражение в скобках, затем оцените степени (члены с показателями степени).После этого у нас будет более простое выражение, включающее сложение, умножение и деление. Просматривая слева направо, мы видим, что сначала нужно умножить, затем разделить и, наконец, сложить.