Примеры с тремя действиями по математике для 2 класса: Примеры на порядок действий для 2, 3 классов. | Тренажёр по математике (2, 3 класс) на тему:
Порядок действий в примерах со скобками: попробуйте решить простой пример
Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу. Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?
Юлиана Качанова Отвечаю за тесты
Twitter: 1RealMir
Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.
Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.
Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.
Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:
Не торопитесь давать ответ: правила хотя бы вспомните!
ВОПРОС 1 ИЗ 1
3
17
21
Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:
- Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
- Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
- Последними выполняются сложение и вычитание. Это действия второй ступени.

Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.
Для закрепления рассмотрим следующий пример действия со скобками:
5+(7−2⋅3)⋅(6−4):2
В этом сложном примере со скобками порядок действий будет точно таким же.
Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2
Давайте подставим решение примеров в скобках в первоначальное выражение:
5+(1)⋅(2):2 .
Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.
Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания. Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:
5+1⋅2:2=6
Таким образом первоначальный пример со скобками также будет равняться 6
5+(7−2⋅3)⋅(6−4):2=6.
Карточки примеры на порядок действий для 2 класса.
Карточки примеры на порядок действий для 2 класса.| 12+ Свидетельство СМИ ЭЛ № ФС 77 – 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Учебно-дидактические материалы
▪Обучающие карточки
Материал опубликовал
0
#2 класс #Математика #ФГОС #Учебно-дидактические материалы #Учитель начальных классов #Соответствие должности #Школьное образование #УМК «Школа России» #Обучающие карточки
Нажмите, чтобы скачать публикацию
в формате MS WORD (*. DOC)
DOC)
Размер файла: 31.31 Кбайт
7 • 4 + 24 : 3 =______ 15 + 35 + 3 • 6 =_______ 20 : 5 + 32 – 24 =______ 20 – 32 : 8 – 13 =_______ 70 – 9 • 4 + 18 =_______ 80 – 32 : 4 • 3 =_______ 52 – 24 : 6 • 8 =______ 79 + 13 – 3 • 7=______ 36 : 4 • 2 + 18 =______ 27 : ( 18 : 2) • 8 =______ 27 : 3 • 2 + ( 20 : 4)=___ | 7 • 4 + 24 : 3 =______ 15 + 35 + 3 • 6 =_______ 20 : 5 + 32 – 24 =______ 20 – 32 : 8 – 13 =_______ 70 – 9 • 4 + 18 =_______ 80 – 32 : 4 • 3 =_______ 52 – 24 : 6 • 8 =______ 79 + 13 – 3 • 7=______ 36 : 4 • 2 + 18 =______ 27 : ( 18 : 2) • 8 =______ 27 : 3 • 2 + ( 20 : 4)=___ | 7 • 4 + 24 : 3 =______ 15 + 35 + 3 • 6 =_______ 20 : 5 + 32 – 24 =______ 20 – 32 : 8 – 13 =_______ 70 – 9 • 4 + 18 =_______ 80 – 32 : 4 • 3 =_______ 52 – 24 : 6 • 8 =______ 79 + 13 – 3 • 7=______ 27 : ( 18 : 2) • 8 =______ 27 : 3 • 2 + ( 20 : 4)=___ |
7 • 4 + 24 : 3 =______ 15 + 35 + 3 • 6 =_______ 20 : 5 + 32 – 24 =______ 20 – 32 : 8 – 13 =_______ 70 – 9 • 4 + 18 =_______ 80 – 32 : 4 • 3 =_______ 52 – 24 : 6 • 8 =______ 79 + 13 – 3 • 7=______ 36 : 4 • 2 + 18 =______ 27 : ( 18 : 2) • 8 =______ 27 : 3 • 2 + ( 20 : 4)=___ | 7 • 4 + 24 : 3 =______ 15 + 35 + 3 • 6 =_______ 20 : 5 + 32 – 24 =______ 20 – 32 : 8 – 13 =_______ 70 – 9 • 4 + 18 =_______ 80 – 32 : 4 • 3 =_______52 – 24 : 6 • 8 =______ 79 + 13 – 3 • 7=______ 36 : 4 • 2 + 18 =______ 27 : ( 18 : 2) • 8 =______ 27 : 3 • 2 + ( 20 : 4)=___ | 7 • 4 + 24 : 3 =______ 15 + 35 + 3 • 6 =_______ 20 : 5 + 32 – 24 =______ 20 – 32 : 8 – 13 =_______ 70 – 9 • 4 + 18 =_______ 80 – 32 : 4 • 3 =_______ 52 – 24 : 6 • 8 =______ 79 + 13 – 3 • 7=______ 36 : 4 • 2 + 18 =______ 27 : ( 18 : 2) • 8 =______ 27 : 3 • 2 + ( 20 : 4)=___ |
5 • ( 71 – 68) = _____ 3 • ( 28 : 4 ) =_____ ( 25 + 11) : 9=______ 32 : 8 • 7 =______ ( 36 – 28 ) : 4 =______ 24 : 8 + 47 =______ 93 – 4 • 7 =______ 81 – 8 • 3 : 4 =_____ 18 + 24 : 8 • 9 =______ 16 : 4 + 6 • 4 =______ 42 – 45 : 5 =______ 70 – 40 : 8 =______ | 5 • ( 71 – 68) = _____ 3 • ( 28 : 4 ) =_____ ( 25 + 11) : 9=______ 32 : 8 • 7 =______ ( 36 – 28 ) : 4 =______ 24 : 8 + 47 =______ 93 – 4 • 7 =______ 81 – 8 • 3 : 4 =_____ 18 + 24 : 8 • 9 =______ 16 : 4 + 6 • 4 =______42 – 45 : 5 =______ 70 – 40 : 8 =______ | 5 • ( 71 – 68) = _____ 3 • ( 28 : 4 ) =_____ ( 25 + 11) : 9=______ 32 : 8 • 7 =______ ( 36 – 28 ) : 4 =______ 24 : 8 + 47 =______ 93 – 4 • 7 =______ 81 – 8 • 3 : 4 =_____ 18 + 24 : 8 • 9 =______ 16 : 4 + 6 • 4 =______ 42 – 45 : 5 =______ 70 – 40 : 8 =______ |
5 • ( 71 – 68) = _____ 3 • ( 28 : 4 ) =_____ ( 25 + 11) : 9=______ 32 : 8 • 7 =______ 24 : 8 + 47 =______ 93 – 4 • 7 =______ 81 – 8 • 3 : 4 =_____ 18 + 24 : 8 • 9 =______ 16 : 4 + 6 • 4 =______ 42 – 45 : 5 =______ 70 – 40 : 8 =______ | 5 • ( 71 – 68) = _____ 3 • ( 28 : 4 ) =_____ ( 25 + 11) : 9=______ 32 : 8 • 7 =______ ( 36 – 28 ) : 4 =______ 24 : 8 + 47 =______ 93 – 4 • 7 =______ 81 – 8 • 3 : 4 =_____ 18 + 24 : 8 • 9 =______ 16 : 4 + 6 • 4 =______ 42 – 45 : 5 =______ 70 – 40 : 8 =______ | 5 • ( 71 – 68) = _____ 3 • ( 28 : 4 ) =_____ ( 25 + 11) : 9=______ 32 : 8 • 7 =______ ( 36 – 28 ) : 4 =______ 24 : 8 + 47 =______ 93 – 4 • 7 =______ 81 – 8 • 3 : 4 =_____ 18 + 24 : 8 • 9 =______ 16 : 4 + 6 • 4 =______ 42 – 45 : 5 =______ 70 – 40 : 8 =______ |
Опубликовано
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
Верные, ложные и открытые предложения в математике
Ричард Бланкман Редактор в форме
- Твитнуть Твитнуть
Поделиться
Делиться- Штырь Сохранять
- Соединять Соединять
В этой статье мы исследуем, что представляет собой «предложение» в математике и как определить, является ли предложение истинным или ложным. Затем мы обсуждаем открытые предложения, в которых одно из значений в предложении не задано и учащийся должен его определить. Это один из способов представить основные идеи о переменных и алгебре.
Затем мы обсуждаем открытые предложения, в которых одно из значений в предложении не задано и учащийся должен его определить. Это один из способов представить основные идеи о переменных и алгебре.
Первоклассники узнают о истинных и ложных предложениях и уже решают открытые предложения, не зная терминологии. (Например: 6 и какое число составляет 10?) Приведенные ниже объяснения и задания больше всего подходят для учащихся 4–5 классов, но их можно адаптировать и для младших школьников.
- Ключевое утверждение «Я могу»: Я могу решить, является ли математическое предложение истинным или ложным; если математическое предложение открыто, я могу определить, какие значения делают его верным.
Что такое математическое предложение?
Подумайте, из чего состоит предложение на английском языке. Предложение — это законченная мысль, обычно содержащая как минимум подлежащее и глагол. В математике тоже могут быть предложения, хотя они выглядят немного по-другому. В математике предложение — это «полная идея», содержащая символ равенства или неравенства и выражение с каждой стороны. Ниже приведены все примеры математических предложений.
В математике предложение — это «полная идея», содержащая символ равенства или неравенства и выражение с каждой стороны. Ниже приведены все примеры математических предложений.
\[3+2=5\]
\[\frac{1}{2}+\frac{3}{4}\neq\frac{3}{2}-\frac{1}{3 }\]
\[10-1>3+\mathord{?}\]
Обратите внимание, что если бы не было символа равенства или неравенства, то комбинация математических символов образует выражение, а не предложение.
Что такое истинное математическое предложение?
Математическое предложение является истинным, когда формулировка, которую оно делает, математически точна. Например, это истинное предложение:
\[3+2=5\]
Однако большинство математических предложений, встречающихся в реальном мире, выглядят немного сложнее. Рассмотрим следующее предложение, которое также верно, поскольку обе стороны знака равенства равны 5.
\[17-12=\frac{12}{2}-1\]
Распространенным способом физического представления истинного уравнения является использование баланса, подобного показанному ниже. Когда баланс четный, то количества с обеих сторон равны. Вы можете представить истинное уравнение, имея одинаковое количество с обеих сторон (например, один 10-блок и десять 1-блоков) или имея равные веса (например, 9 кубиков, каждый из которых составляет один грамм, и один шар, который весит 9 граммов). ). Обратите внимание, что для представления неравенства на чашечных весах может потребоваться не только обратить внимание на то, равны ли обе стороны, но и на то, какая сторона меньше или больше.
Когда баланс четный, то количества с обеих сторон равны. Вы можете представить истинное уравнение, имея одинаковое количество с обеих сторон (например, один 10-блок и десять 1-блоков) или имея равные веса (например, 9 кубиков, каждый из которых составляет один грамм, и один шар, который весит 9 граммов). ). Обратите внимание, что для представления неравенства на чашечных весах может потребоваться не только обратить внимание на то, равны ли обе стороны, но и на то, какая сторона меньше или больше.
Что такое ложное математическое предложение?
Математическое предложение ложно, если математическое утверждение, которое оно делает, не точное. Так, например, это ложное предложение:
\[3+2=9\]
Как и в истинных уравнениях, может стать сложнее определить, является ли предложение ложным, когда обе части уравнения являются выражениями, требующими вычисления. . Вот еще одно ложное предложение, где левая часть равна 5, а правая нет.
\[3+2=\frac{13}{3}+2\]
Обратите особое внимание на то, насколько важен порядок операций при определении истинности предложения. Если учащиеся неправильно добавляют \(\frac{13}{3}\) и \(2\), чтобы получить \(\frac{15}{3}\), они могут ошибочно подумать, что приведенное выше предложение верно!
Если учащиеся неправильно добавляют \(\frac{13}{3}\) и \(2\), чтобы получить \(\frac{15}{3}\), они могут ошибочно подумать, что приведенное выше предложение верно!
Верные и ложные предложения в реальном мире
Если вы ищете, как понятие истинных и ложных математических предложений связано с реальным миром, подумайте о том, чтобы связать его с программированием. Один из способов объяснить, как компьютеры могут превращать строки кода в веб-сайты, приложения и игры, — это заявить, что компьютеры разбивают все на простые вопросы типа «истина/ложь», такие как «пользователь нажал эту клавишу?» или «игрок дошел до конца уровня?» Изучая истинные и ложные математические предложения, студенты становятся программистами!
Неудивительно, что истинные и ложные предложения в реальном мире могут иметь гораздо большее значение, чем предложения, используемые на уроках математики. Предложите готовым учащимся более сложные примеры и предложите учащимся сравнить различные способы, которыми они определили, что одно и то же предложение было ложным. Предложение ниже, например, может открыть дверь для богатой дискуссии о контрольных числах и непохожих знаменателях. Может ли кто-нибудь из учащихся объяснить, почему следующее предложение ложно, не вычисляя суммы дробей?
Предложение ниже, например, может открыть дверь для богатой дискуссии о контрольных числах и непохожих знаменателях. Может ли кто-нибудь из учащихся объяснить, почему следующее предложение ложно, не вычисляя суммы дробей?
\[\frac{1}{2}+\frac{3}{4}=\frac{3}{2}+\frac{1}{3}\]
Что такое открытое математическое предложение?
Теперь пора продолжить урок. Покажите уравнение с пропущенным значением. Вот пример, хотя обратите внимание, что при представлении этого учащимся вы можете заменить вопросительный знак открытой рамкой (или любой другой формой):
\[6+\mathord{?}=14\]
Спросите учащихся, что они могли бы заменить вопросительный знак на. Другими словами, спросите студентов, как решить открытых предложений, подобных этому. Учащиеся должны признать, что значение 8 делает уравнение верным. Покажите, что любое выражение, эквивалентное 8, также решает предложение, например \(\frac{16}{2}\) или \(4\times 2\), и предложите учащимся подумать о других возможных выражениях. Подобные предложения — с «открытыми» частями, которые можно заполнить, — называются открытыми предложениями.
Подобные предложения — с «открытыми» частями, которые можно заполнить, — называются открытыми предложениями.
Поделитесь со учащимися этими или подобными примерами открытых предложений по математике, обращая внимание на то, что вопросительный знак находится в разных местах.
\[2+4=5+\mathord{?}\]
\[0+\mathord{?}+\frac{1}{2}=\frac{1}{2}+\frac{ 1}{4}+0\]
\[3\div 7=\mathord{?}\times\frac{1}{7}\]
Если учащиеся готовы, вы можете ввести более сложные уравнения, чтобы показать что одно открытое предложение может иметь два значения, которые делают предложение истинным (в обоих приведенных ниже уравнениях решения равны 5 и –5).
\[\mathord{?}\cdot\mathord{?}=25\]
\[|3\cdot\mathord{?}|=15\]
Вы также можете показать, что открытые предложения могут иметь бесконечно много значений, которые делают предложение истинным. С более сложными предложениями, такими как эти, может помочь учащимся составить список всего, что может войти в неизвестное значение, и создать предположение.
\[10<3+\mathord{?}\]
\[19+\mathord{?}\neq 19+1\]
\[0\cdot 3=0\cdot\mathord{?} \]
И последнее замечание относительно этого урока, особенно если у вас есть ученики, говорящие на языках, использующих разные алфавиты. Обратите внимание на вопросительный знак. Спросите, какие другие формы или символы ваши ученики могли бы поставить на его место и какой заполнитель делает его наиболее понятным для них. Замените вопросительный знак другими переменными, включая символы из других алфавитов, и посмотрите, есть ли символы, которые ваши ученики предпочли бы использовать. Это также связывает открытые предложения в математике напрямую с алгеброй, где одно значение абстрагируется в диапазон возможных значений.
Упражнения для отработки правильных, ложных и открытых предложений
Упражнение 1. Определение истинных или ложных предложений
Убедитесь, что учащиеся ясно понимают, что означает, что математическое предложение является истинным или ложным.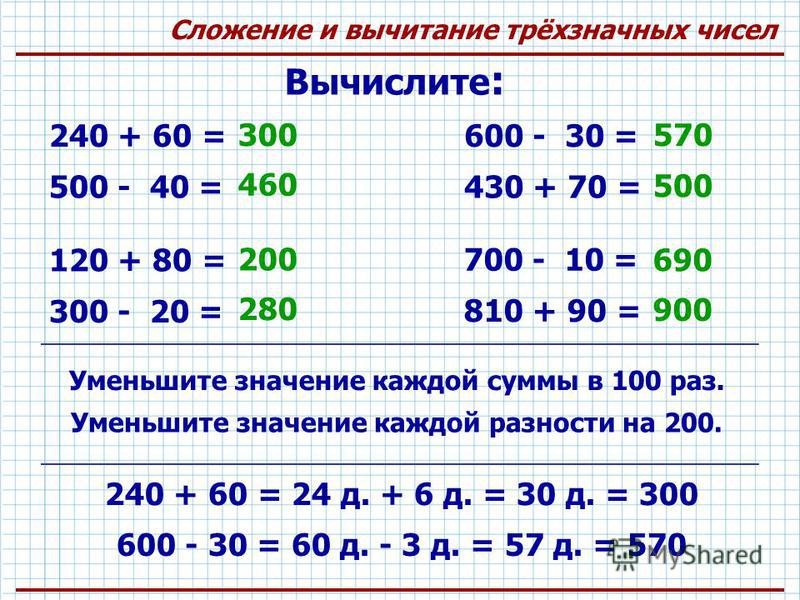 Подготовьте список из 5–10 предложений, которые соответствуют тому, чему вы сейчас учите. Простые примеры, такие как \(1+6=7\), позволяют использовать точки входа для всех учащихся и гарантируют, что учащиеся используют один и тот же словарный запас. Вы можете усложнить примеры, изменив величину (например, используя 4-значные числа), включив дроби или десятичные дроби или заставив выражения требовать больше шагов для вычисления.
Подготовьте список из 5–10 предложений, которые соответствуют тому, чему вы сейчас учите. Простые примеры, такие как \(1+6=7\), позволяют использовать точки входа для всех учащихся и гарантируют, что учащиеся используют один и тот же словарный запас. Вы можете усложнить примеры, изменив величину (например, используя 4-значные числа), включив дроби или десятичные дроби или заставив выражения требовать больше шагов для вычисления.
Проходя примеры предложений, поддерживайте дискуссию не только о том, истинны они или ложны математические утверждения, но и почему они истинны или ложны. Обратите внимание на то, как учащиеся подходят к решению задач. Подумайте над такими вопросами:
- На какую часть уравнения вы обратили внимание в первую очередь? Почему?
- Как проверить свою работу?
- Какое другое предложение означает то же самое, что и это предложение?
Упражнение 2: Предложите учащимся составить истинные и ложные предложения
Теперь попробуйте предложить учащимся составить свои собственные предложения. Поручите им составить три истинных предложения и три ложных предложения. Эта задача, в частности, имеет низкий пол и высокий потолок. Для тех учащихся, которые готовы, рассмотрите возможность включения дополнительных ограничений, таких как «должен использовать дробь», «должен содержать круглые скобки» или «все числа должны быть простыми».
Поручите им составить три истинных предложения и три ложных предложения. Эта задача, в частности, имеет низкий пол и высокий потолок. Для тех учащихся, которые готовы, рассмотрите возможность включения дополнительных ограничений, таких как «должен использовать дробь», «должен содержать круглые скобки» или «все числа должны быть простыми».
В зависимости от класса есть разные способы привлечь других учащихся и сделать занятие интерактивным. Студенты могут обменяться предложениями с партнером, который должен определить, какие предложения верны, а какие нет. В качестве альтернативы учащиеся могут написать каждое предложение на карточке, а затем положить все карточки в контейнер. Затем учащиеся могут по очереди вытягивать карточки и определять, являются ли они истинными или ложными.
Задание 3: Расскажите историю о математическом предложении
Рассказы — это способ, с помощью которого все ваши учащиеся могут связать математику с идеями и событиями, которые они считают важными. Вы можете смоделировать простые примеры, например, придумать историю для \(1+6=7\): «У Нары есть 1 тюбик с краской. У Люка 6 тюбиков с краской. Сколько тюбиков с краской у них будет, если они будут рисовать вместе?»
Вы можете смоделировать простые примеры, например, придумать историю для \(1+6=7\): «У Нары есть 1 тюбик с краской. У Люка 6 тюбиков с краской. Сколько тюбиков с краской у них будет, если они будут рисовать вместе?»
Затем вы можете либо предложить предложения (например, любой из примеров, показанных в этой статье), либо предложить учащимся составить свои собственные вместе с сопровождающим их рассказом. Поощряйте учащихся быть творческими и подробными в их рассказывании историй. Это возможность не только закрепить математику в реальном мире, но и потренировать у учащихся навыки грамотности.
***
Практикуйте уравнения, используя любое из наших математических решений, которые включают персонализированные уроки, математические видеоигры и тщательную оценку.
Математика 3-5 классы Мероприятия и уроки 1-2 классы
Будьте первым, кто прочитает последние новости из Shaped .
Похожие сообщения
14 стратегий обучения Дополнение
- Поделиться
- Твит
Стратегии сложения великолепны, потому что они предоставляют вашим учащимся инструменты, которые упрощают и ускоряют вычисления. Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.
Стратегии сложения : Kinder & 1st ClassДавайте начнем с краткого обзора стратегий сложения, которые внедряются в детском саду и первом классе. Эти первые две стратегии являются конкретными и манипулятивными.
Этот пост содержит партнерские ссылки Amazon.
1- Счетчики и манипуляции
Здесь большинство наших учеников начинают свои математические приключения. Лучшая часть этой стратегии в том, что ВСЁ может быть противодействием. Счетные чипы легко хранить и дезинфицировать, и они относительно дешевы. Эти милые счетные мишки всегда пользуются успехом. Тем не менее, не чувствуйте себя обязанным покупать что-то необычное. Фасоль, макароны, камешки, крышки от использованных клеевых стержней или крышки от бутылок могут быть фишками.
Лучшая часть этой стратегии в том, что ВСЁ может быть противодействием. Счетные чипы легко хранить и дезинфицировать, и они относительно дешевы. Эти милые счетные мишки всегда пользуются успехом. Тем не менее, не чувствуйте себя обязанным покупать что-то необычное. Фасоль, макароны, камешки, крышки от использованных клеевых стержней или крышки от бутылок могут быть фишками.
Научите своих учеников записывать уравнения и использовать счетчики для представления каждого слагаемого. Затем они считают их все, чтобы получить сумму. Не забывайте вводить и использовать термины «сложение», «сложение», «сумма» и «уравнение» как можно чаще. Знакомство с этими словами словарного запаса уровня 3 очень важно для наших студентов.
2- Стратегии сложения: подсчет баллов
Подсчет баллов вводится в детском саду, и в течение следующих нескольких лет этот навык совершенствуется. У нас есть отличный пост с видео, которые вы можете использовать в своем классе, чтобы помочь в обучении подсчету оценок. Манипуляции — отличный способ научить подсчету очков. Все, что прямое, можно использовать для отработки подсчета очков. Чтобы научить этому навыку, потренируйтесь преобразовывать однозначные числа стандартной формы в счетные метки, используя всевозможные забавные вещи, которые вы можете найти вокруг себя. Попробуйте палочки для эскимо, ватные палочки, палочки для кренделя или восковые палочки. Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.
Манипуляции — отличный способ научить подсчету очков. Все, что прямое, можно использовать для отработки подсчета очков. Чтобы научить этому навыку, потренируйтесь преобразовывать однозначные числа стандартной формы в счетные метки, используя всевозможные забавные вещи, которые вы можете найти вокруг себя. Попробуйте палочки для эскимо, ватные палочки, палочки для кренделя или восковые палочки. Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.
3- Стратегии сложения: десять фреймов
Причина, по которой мы обучаем наших студентов всем этим стратегиям сложения, заключается в желании развить более надежное чувство числа. Десять рамок помогают вашим ученикам визуализировать уравнения и дают им возможность попрактиковаться в субитизации. Десять кадров посвящены пониманию ценности чисел. После ознакомления вашего класса с тем, что такое десятичная рамка и как ее можно использовать , дайте каждому учащемуся свою собственную десятичную рамку для работы. Всей группой или небольшими группами потренируйтесь представлять уравнения с помощью десяти рамок и счетчиков. Моделирование можно выполнить, заполнив десятичную рамку по горизонтали, чтобы попрактиковаться в счете с пропуском на 5 секунд, или заполнив ее вертикально, чтобы попрактиковаться в счете с пропуском на 2 секунды.
После ознакомления вашего класса с тем, что такое десятичная рамка и как ее можно использовать , дайте каждому учащемуся свою собственную десятичную рамку для работы. Всей группой или небольшими группами потренируйтесь представлять уравнения с помощью десяти рамок и счетчиков. Моделирование можно выполнить, заполнив десятичную рамку по горизонтали, чтобы попрактиковаться в счете с пропуском на 5 секунд, или заполнив ее вертикально, чтобы попрактиковаться в счете с пропуском на 2 секунды.
Стратегии сложения: 1-й и 2-й класс
4- Подсчет
Числовые линии — прекрасный инструмент для ваших учеников. В первом классе хорошо начинать с помеченных и замкнутых числовых рядов. Научите своих учеников начинать с наибольшего числа и считать вперед.
По мере повышения уровня знаний учащихся в первом и втором классе можно вводить открытые числовые ряды. Обучение открытым числовым рядам может быть сложной задачей, но все дело в моделировании и метапознании. Поскольку открытые числовые ряды — это то, что многие взрослые уже делают в уме, разговор вслух о том, что вы делаете и почему, помогает учащимся понять, как использовать открытые числовые ряды. Студенты должны обладать прочной базой знаний о разрядных значениях, чтобы успешно использовать открытые числовые ряды. Если вы обнаружите, что ваши ученики борются с этим навыком, добавьте в свой блок по математике несколько упражнений с условными значениями.
Поскольку открытые числовые ряды — это то, что многие взрослые уже делают в уме, разговор вслух о том, что вы делаете и почему, помогает учащимся понять, как использовать открытые числовые ряды. Студенты должны обладать прочной базой знаний о разрядных значениях, чтобы успешно использовать открытые числовые ряды. Если вы обнаружите, что ваши ученики борются с этим навыком, добавьте в свой блок по математике несколько упражнений с условными значениями.
5- Zero Facts
В моем классе мы называем ноль «зеркалом». Чтобы ввести ноль фактов, у меня в классе есть овальное зеркало. Когда они смотрят в зеркало, что они видят? Сами себя! Все, что плюс ноль, есть само! Затем мы тренируемся с однозначными числами и становимся глупее, чтобы показать им, что прибавить ноль к чему угодно просто. Мои ученики ОБОЖАЮТ, когда я пишу смешное уравнение вроде 3 452 872 965 + 0= ? и попросите их решить ее.
6- Сложите 10
Будучи взрослыми, многие из нас автоматически складывают 10, чтобы создать более удобные числа для сложения в уме. Набрать 10 — такая мощная стратегия и для наших юных учеников. Второй уровень — это когда сложение действительно повышает уровень сложности, когда вводится сложение с перегруппировкой. Практика составления 10 и, в конечном счете, запоминание того, какие пары составляют десять, — это навык, к которому они будут прибегать, когда учатся складывать большие числа или когда они складывают вместе 3+ числа.
Набрать 10 — такая мощная стратегия и для наших юных учеников. Второй уровень — это когда сложение действительно повышает уровень сложности, когда вводится сложение с перегруппировкой. Практика составления 10 и, в конечном счете, запоминание того, какие пары составляют десять, — это навык, к которому они будут прибегать, когда учатся складывать большие числа или когда они складывают вместе 3+ числа.
Обучение этому навыку связано с возможностью попрактиковаться. Десять рамок — отличный способ поработать над созданием 10. Раздайте своим ученикам жетоны двух цветов. Попросите их найти как можно больше способов сделать десять, используя свои жетоны. В тетради по математике для 1-го класса: дополнение есть несколько замечательных интерактивных страниц, над которыми учащиеся могут работать. Веселые песни могут помочь вашим ученикам научиться делать десять! Когда учащиеся станут более опытными, не забудьте смоделировать, как использовать этот навык для решения более сложных уравнений сложения.
7- Doubles
Прежде чем мы перейдем к тому, как работают двойники, давайте сначала разберемся, почему. Механическое заучивание иногда имеет плохую репутацию. Исследования показывают, что, когда учащиеся развивают автоматизм в своих основных математических фактах, они освобождают место в своей рабочей памяти. Проще говоря, когда учащимся не нужно беспокоиться о базовых вычислениях, они лучше справляются с математикой более высокого уровня. У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач.
Так как же нам обучать двойников? Так же, как сделать 10, много возможностей для практики. В блокноте Addition Note есть действительно забавные интерактивные практические страницы. К ним относятся изображения, удобные для детей, в качестве наглядных пособий. Опять же, песни также являются действительно эффективным методом обучения. Нет ничего более приятного, чем слышать, как ваши дети напевают себе математические факты для развлечения.
Опять же, песни также являются действительно эффективным методом обучения. Нет ничего более приятного, чем слышать, как ваши дети напевают себе математические факты для развлечения.
8- Почти двойники
Как только ваши ученики зафиксируют двойные факты, переходите к почти двойникам. Это означает удвоение плюс один или два. Как и в случае со счетом 10, научить учащихся решать почти двойные числа — это моделирование. При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете.
Например, если вы используете уравнение 6+5, это может звучать так: «Я заметил, что это почти двойное уравнение. Число 6 всего на единицу больше, чем 5. Держу пари, я мог бы использовать свои двойные факты, чтобы решить эту проблему». Нарисуйте числовые связи, чтобы показать, что 6 равно 5+1, а затем продолжите: «Я заметил, что когда я разлагаю 6, я получаю еще 5! О, смотрите, 5+5 это 10, а потом у меня остался только один остаток. Я могу добавить это в моей голове! 10+1 равно 11». Проведите своих учеников через это шаг за шагом несколько раз, а затем попросите их попробовать вместе с вами. Выявление числовых связей очень полезно для многих учащихся.
Я могу добавить это в моей голове! 10+1 равно 11». Проведите своих учеников через это шаг за шагом несколько раз, а затем попросите их попробовать вместе с вами. Выявление числовых связей очень полезно для многих учащихся.
Если у вас есть ученики, которые все еще борются с трудностями, манипуляции, такие как счетчики, могут быть очень полезными, чтобы добавить больше физического элемента.
9- «Переворачивание фактов» или свойство перестановочности
Свойство перестановочности вводится в начале сложения, а затем возвращается к нему, когда учащиеся изучают умножение. Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения.
Творческий подход к обучению переворачиванию фактов — отличный способ повысить вовлеченность.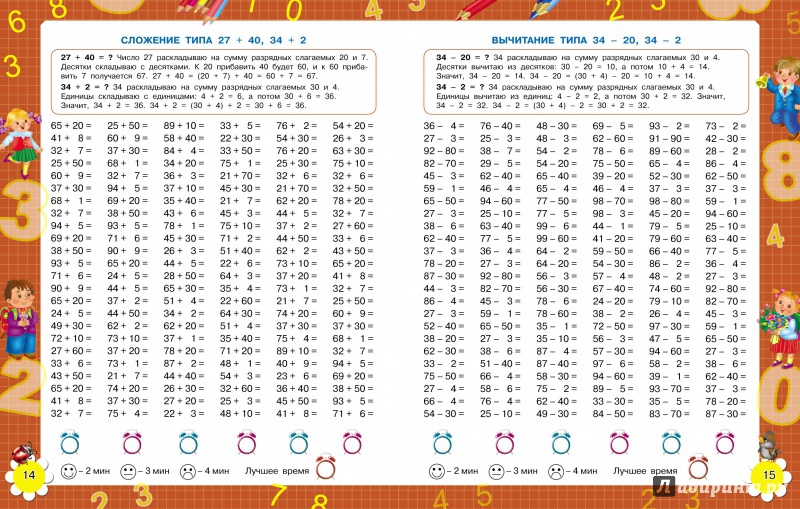 Коммутативное свойство помогает вашим учащимся понять значение чисел и, кроме того, перемещение слагаемых не влияет на сумму. Проще всего это сделать, нарисовав схему уравнения сложения для каждого ученика. Используйте пустые клетки для представления слагаемых и оставьте строку для ваших учеников, чтобы написать сумму.
Коммутативное свойство помогает вашим учащимся понять значение чисел и, кроме того, перемещение слагаемых не влияет на сумму. Проще всего это сделать, нарисовав схему уравнения сложения для каждого ученика. Используйте пустые клетки для представления слагаемых и оставьте строку для ваших учеников, чтобы написать сумму.
Раздайте прилавки любого вида: пластиковые прилавки, хлопья, фруктовые закуски, лего, слоеные шарики, все, что у вас есть под рукой. Начните с уравнения вроде 5 + 2. Попросите учащихся смоделировать это уравнение, поместив соответствующее количество манипуляций в соответствующее место. Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму?
Стратегии сложения: 2-й и 3-й классы
10- Расширенная форма
Учащиеся практикуются в написании чисел в различных формах — стандартной, расширенной, письменной и с основанием 10 в течение первых нескольких лет обучения в классе.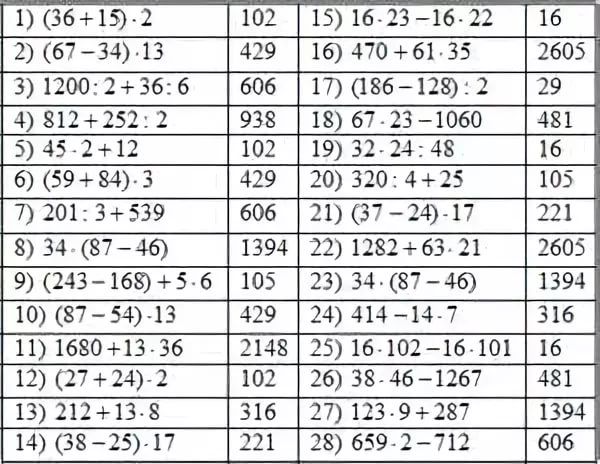 Способность разложить число в его расширенную форму показывает, что учащиеся действительно понимают значение чисел, с которыми они работают.
Способность разложить число в его расширенную форму показывает, что учащиеся действительно понимают значение чисел, с которыми они работают.
We Are Teachers опубликовали потрясающую статью о том, почему расширенная форма так важна. Прежде чем использовать расширенную форму в качестве стратегии сложения, убедитесь, что ваши ученики действительно понимают, как разбивать числа на их значения. В этом посте от Teach Junkie есть несколько хороших идей для практики. У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.
Ваши ученики получили развернутую форму. Как они используют его для решения уравнений сложения? Как только учащиеся начнут складывать двух- и трехзначные числа, они могут использовать расширенную форму для выполнения вычислений в уме. Например, давайте попробуем 64 + 42. Покажите учащимся, как решить эту задачу, используя числовые связи или десятичные блоки. 64 становится 60 + 4, а 42 становится 40 + 2. Старайтесь всегда моделировать свое мышление и произносите все, что делаете, вслух. Это может звучать так: « 64 становится 60+4, потому что 6 стоит в разряде десятков, поэтому его значение равно 60, а 4 — в разряде единиц, поэтому его значение равно 4. ” Привяжите другие стратегии, такие как упоминание о том, что 6 и 4 составляют 10, когда вы мысленно складываете 60 и 40. Для учащихся, которые борются с ментальной арифметикой, рисование или использование физических десятичных кубиков действительно хорошая поддержка.
Это может звучать так: « 64 становится 60+4, потому что 6 стоит в разряде десятков, поэтому его значение равно 60, а 4 — в разряде единиц, поэтому его значение равно 4. ” Привяжите другие стратегии, такие как упоминание о том, что 6 и 4 составляют 10, когда вы мысленно складываете 60 и 40. Для учащихся, которые борются с ментальной арифметикой, рисование или использование физических десятичных кубиков действительно хорошая поддержка.
11- Блоки с основанием 10
Сложение с использованием блоков с основанием 10 начинается в 1-м классе и используется, когда учащиеся изучают перегруппировку. Его также можно использовать в качестве поддержки для старших школьников, которые борются со сложением.
Скачать этот базовый десятичный мат | Скачать печатную версию базы десять блоков Учащиеся могут использовать пластиковые/деревянные или распечатанные бумажные кубики или рисовать их. В 1-м и начале 2-го класса иметь что-то конкретное для использования действительно полезно, но как только они станут более уверенными в рисовании блоков с основанием 10, это будет совершенно нормально.
12- Подсчет пропусков
Нельзя недооценивать важность подсчета пропусков. Иногда кажется, что пропуск счета откладывается на второй план для других «более важных» навыков, но так не должно быть! Подсчет пропусков основан на шаблонах и используется по-разному. Учащиеся используют его, когда считают деньги, определяют время и изучают умножение. У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете.
Счет в пропуске может быть сложным, но важным навыком, который нужно осваивать в первом, втором и третьем классе. Часто в учебной программе есть несколько уроков по подсчету пропусков, после чего ожидается, что учащиеся усвоят эту концепцию. Если вашим ученикам нужна дополнительная практика с пропуском счета по 5, вы можете получить эту распечатанную форму для подсчета пропусков бесплатно!
Загрузить эту игру При обучении учащихся тому, как использовать пропуск счета в качестве стратегии сложения, начните с открытых числовых рядов. Возьмите уравнение типа 25 + 32 и напишите число 25 в открытой числовой строке. Не забывайте моделировать все мысли вслух. Это может звучать так: «Я заметил, что 25 оканчиваются на 5. Когда число оканчивается на 5, я могу легко пропустить счет на 5 или 10. Теперь я смотрю на 32 и знаю, что в 32 3 десятка. Я собираюсь прыгнуть вперед на десятки. Начните с 25, прыгайте 10, 35, прыгайте 10, 45, прыгайте 10, 55. Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.
Возьмите уравнение типа 25 + 32 и напишите число 25 в открытой числовой строке. Не забывайте моделировать все мысли вслух. Это может звучать так: «Я заметил, что 25 оканчиваются на 5. Когда число оканчивается на 5, я могу легко пропустить счет на 5 или 10. Теперь я смотрю на 32 и знаю, что в 32 3 десятка. Я собираюсь прыгнуть вперед на десятки. Начните с 25, прыгайте 10, 35, прыгайте 10, 45, прыгайте 10, 55. Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.
13- Округление или «Понятные числа»
Учащиеся знакомятся с округлением в 3-м классе. В некоторых школах его преподают в начале года, а в некоторых предпочитают откладывать на конец. Проверьте карту своей учебной программы, чтобы узнать, когда она есть в вашем расписании. Если в вашей школе округление проводится в начале года, его можно использовать в качестве дополнительной стратегии в течение всего года.
Если в вашей школе округление проводится в начале года, его можно использовать в качестве дополнительной стратегии в течение всего года.
Вы наверняка слышали, что эту стратегию называют «дружественными числами», потому что именно этому мы учим наших студентов. Они учатся создавать числа, с которыми легче (более дружелюбно) работать в уме. Сложение 312+453 в уме может быть трудным, но округление этих чисел до 300 и 450 значительно облегчает работу с ними. Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.
Как только учащиеся поймут, почему они округляют перед сложением, пора практиковаться! Начните с двузначных чисел, таких как 34+29 (становится 30+30), и позвольте им потренироваться давать вам приблизительные ответы. Затем перейдите к трехзначным числам и попросите их округлить до ближайшей сотни 245+682 (становится 200+700). После того, как они овладеют этими двумя навыками, вы можете начать округлять трехзначные числа до ближайших десяти. Для студентов, которые действительно преуспевают, вы можете усилить строгость, дав им уже понятное уравнение, такое как 300 + 600, и попросив их привести примеры того, что могло быть первоначальными «недружественными» числами.
Затем перейдите к трехзначным числам и попросите их округлить до ближайшей сотни 245+682 (становится 200+700). После того, как они овладеют этими двумя навыками, вы можете начать округлять трехзначные числа до ближайших десяти. Для студентов, которые действительно преуспевают, вы можете усилить строгость, дав им уже понятное уравнение, такое как 300 + 600, и попросив их привести примеры того, что могло быть первоначальными «недружественными» числами.
14- Стандартный алгоритм
Во 2 классе вводится перегруппировка, а в 3 классе она пересматривается и совершенствуется. Стандартный алгоритм или, как многие его называют, «старая математика». Обычно стандартный алгоритм преподается после того, как студенты освоят некоторые другие стратегии. Благодаря чувству чисел, полученному во всех предыдущих стратегиях сложения, стандартный алгоритм становится больше направленным на применение того, что они знают, и меньше на запоминание рутины. Вот что такого замечательного в заполнении ящиков с математическими инструментами! К тому времени, как дети начинают перегруппировываться — брать и носить с собой, как это известно нам, старожилам, — они понимают, ПОЧЕМУ они перемещают эти числа в следующую колонку.
Когда дело доходит до обучения стандартному алгоритму, песнопения — отличный способ помочь учащимся запомнить шаги, которые им необходимо выполнить! Попробуйте два из перечисленных ниже способов со своими учениками.
- Дополнение с перегруппировочным пением: Десять или больше? Нести рядом. Девять или меньше? Пусть отдыхает!
- Вычитание с чатом перегруппировки: Еще сверху? Не нужно останавливаться! Больше на полу? Иди по соседству и возьми еще 10! номера одинаковые? Нулевая игра.
Не забывайте медленно выполнять инструкции. Студентам легко запутаться и в конечном итоге заимствовать и нести в незнакомых местах. Начните с двузначных чисел и переходите к трехзначным числам, когда учащиеся почувствуют себя уверенно и будут готовы к повышенной сложности. Для многих учеников вычитание через нули затруднено. Сохранение этого навыка напоследок может предотвратить разочарование.
Ресурсы для обучения дополнительным стратегиям
Если вы ищете комплексный пакет с МНОЖЕСТВОМ печатных и цифровых математических ресурсов для ваших учеников, включая десять рамок, счетчики, числовые линии, коврики «часть-часть-целое», ознакомьтесь с Lucky Little Toolkit в нашей библиотеке ресурсов полного доступа.