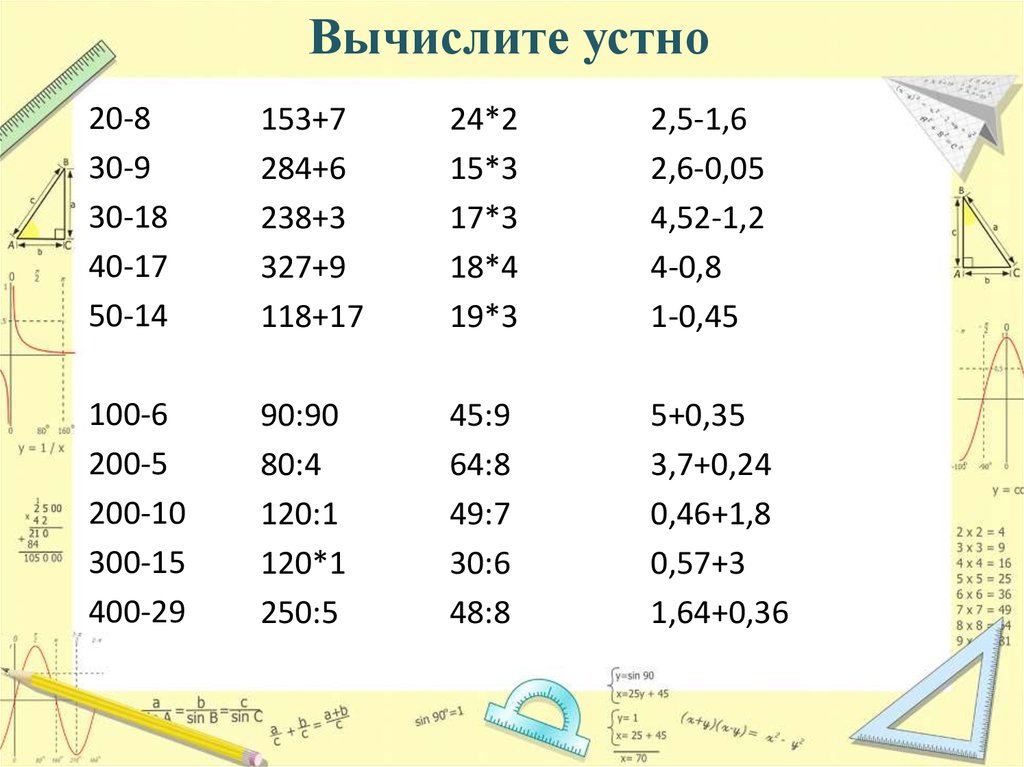
Примеры по математике для 4 класса сложные: Примеры. Математика 4 класс.

Примеры. Математика 4 класс.



Примеры. Математика 4 класс. 

Задачи по математике 4 класс

MAT-ZADACHI.RU





Математика 4 класс

• Математические диктанты
• Тесты
• Нестандартные задачи
• Логические задачи
• Задачи с ответами
• Примеры

Контрольные работы

1 четверть
• Числа, которые больше 1000. Нумерация
• Итоговая контрольная работа за 1 четверть

2 четверть
• Итоговая контрольная работа 1

Итоговая контрольная работа 2

3 четверть
• Контрольная работа 1

Контрольная работа 2

Итоговая контрольная работа

4 четверть
• Деление на двузначное число

Итоговые контрольные работы за курс начальной школы
• Контрольная работа 1

Контрольная работа 2





Математика 4 класс ->> Примеры

Чтобы увидеть решение, наведите на пример курсор мыши.

70 * 59 = 4130	792 – 168 = 624	9240 : 7 = 1320	336 + 655 = 991	8480 : 16 = 530
810000 : 60 = 13500	340000 : 340 = 1000	350 * 7 = 2450	348 – 224 = 124	810000 : 60 = 13500
509 – 446 = 63	34800 : 30 = 1160	712 + 274 = 986	7920 : 88 = 90	500 * 40 = 20000
9500 : 50 = 190	810 * 2 = 1620	999 – 949 = 50	49700 : 70 = 710	5 + 576 = 581
20200 : 200 = 101	228 + 604 = 832	45600 : 240 = 190	92 * 20 = 1840	951 – 18 = 933
410 * 40 = 16400	826 – 417 = 409409	2120 : 4 = 530	259 + 559 = 818	67200 : 840 = 80
542 – 70 = 472	544000 : 80 = 680	366 + 10 = 576	3880 : 97 = 40	80 * 70 = 5600
47300 : 430 = 110	46 * 50 = 2300	919 – 118 = 801	3600 : 600 = 6	71 + 733 = 804
68600 : 70 = 980	364 + 324 = 688	510000 : 34 = 15000	370 * 7 = 2590	855 – 648 = 207
4 * 470 = 1880	870 – 573 = 297	1920 : 3 = 640	80 + 790 = 870	24000 : 2 = 12000
542 + 324 = 866	15400 : 220 = 70	9000 * 70 = 630000	459 – 249 = 210	344000 : 20 = 17200
648 – 33 = 615	23200 : 80 = 290	24 + 407 = 431	2520 : 45 = 5656	5000 * 90 = 450000
384000 : 96 = 4000	670 * 9 = 6030	563 – 126 = 437	92000 : 800 = 115	41 + 657 = 698
637000 : 70 = 9100	292 + 443 = 735	58300 : 530 = 110	29 * 70 = 2030	472 – 430 = 42
320 * 6 = 1920	471 – 80 = 391	6550 : 5 = 1310	281 + 619 = 900	10000 : 50 = 200
338 + 372 = 710	30000 : 100 = 300	490 * 8 = 3920	883 – 593 = 290	63600 : 60 = 1060
921 – 436 = 485	18200 : 70 = 260	356 + 357 = 713	424000 : 530 = 800	7 * 430 = 3010
28000 : 35 = 800	160 * 70 = 11200	794 – 754 = 40	639000 : 30 = 21300	789 + 59 = 848
684000 : 600 = 1140	555 + 281 = 836	456000 : 380 = 1200	96 * 80 = 7680	926 – 736 = 190
880 * 20 = 17600	890 – 132 = 758	104000 : 80 = 1300	479 + 146 = 625	10200 : 510 = 20
372 + 313 = 685	306000 : 340 = 900	5200 * 50 = 260000	842 – 31 = 811	36400 : 700 = 52
226 – 134 = 92	5400 : 90 = 60	127 + 95 = 222	936000 : 520 = 1800	50 * 30 = 1500
55000 : 5 = 11000	35 * 80 = 2800	390 – 71 = 319	77400 : 90 = 860	351 + 458 = 809
112000 : 70 = 1600	100 + 823 = 923	64600 : 38 = 1700	77 * 90 = 6930	637 – 118 = 519
770 * 20 = 15400	281 – 39 = 242	2520 : 6 = 420	578 + 196 = 774	400 : 5 = 80
269 + 185 = 454	990000 : 99 = 10000	6600 * 30 = 198000	360 – 67 = 293	496000 : 80 = 6200
767 – 540 = 227	119000 : 70 = 1700	85 + 230 = 315	408000 : 680 = 600	620 * 90 = 55800
777000 : 370 = 2100	3 * 820 = 2460	772 – 536 = 236	4800 : 4 = 1200	378 + 532 = 910
231000 : 70 = 3300	29 + 384 = 413	60500 : 110 = 550	880 * 90 = 79200	815 – 370 = 445
4700 * 50 = 235000	293 – 46 = 247	57600 : 90 = 640	398 + 395 = 793	3300 : 33 = 100
373 + 250 = 623	770000 : 77 = 10000	200 * 9 = 1800	878 – 868 = 10	40800 : 30 = 1360
982 – 711 = 271	745000 : 500 = 1490	509 + 75 = 584	870 : 29 = 30	180 * 2 = 360
93600 : 12 = 7800	630 * 2 = 1260	315 – 175 = 140	2450 : 5 = 490	693 + 165 = 858
3630 : 3 = 1210	89 + 799 = 888	8730 : 97 = 90	990 + 4 = 994	712 – 97 = 615
4100 * 90 = 369000	420 – 383 = 37	96300 : 90 = 1070	96 + 94 = 190	612000 : 18 = 34000
815 + 38 = 853	7440 : 62 = 120	4300 * 90 = 387000	622 – 411 = 211	296000 : 80 = 3700
866 – 399 = 467	80000 : 40 = 2000	389 + 354 = 743	600000 : 50 = 12000	6200 * 80 = 496000
522000 : 870 = 600	99 * 90 = 8910	988 – 253 = 735	27900 : 900 = 31	219 + 198 = 417
462000 : 700 = 660	228 + 217 = 445	20800 : 520 = 40	30 * 30 = 900	567 – 408 = 159
590 * 6 = 3540	706 – 662 = 44	4640 : 4 = 1160	24 + 663 = 687	85200 : 71 = 1200
318 + 30 = 348	688000 : 430 = 1600	9 * 640 = 5760	610 – 8 = 602	160000 : 40 = 4000
839 – 506 = 333	60600 : 600 = 101	33 + 611 = 644	498000 : 830 = 600	3300 * 30 = 99000
29600 : 740 = 40	860 + 4 = 864	853 – 799 = 54	59600 : 400 = 149	181 + 361 = 542
39500 : 500 = 79	39 + 340 = 379	667000 : 23 = 29000	380 * 8 = 3040	512 – 40 = 472
910 * 4 = 3640	812 – 774 = 38	235000 : 500 = 470	208 + 557 = 765	962000 : 740 = 1300
67 + 808 = 875	2500 : 25 = 100	840 * 3 = 2520	924 – 179 = 745	50400 : 800 = 63
6100 * 80 = 488000	667 – 373 = 294	364000 : 700 = 520	62 + 728 = 790	87500 : 250 = 350
813 + 54 = 867	1000 : 25 = 40	560 * 60 = 33600	994 – 85 = 909	34500 : 30 = 1150
899 – 760 = 139	730000 : 500 = 1460	440 + 299 = 739	70400 : 44 = 1600	22 * 90 = 1980
59800 : 26 = 2300	940 * 60 = 56400	893 – 492 = 401	15000 : 300 = 50	26 + 947 = 973
____________________	____________________	____________________	____________________	____________________





Простые задачи

• Простые задачи на движение

Составные задачи

• Задачи на встречное движение
• Задачи на движение в одном направлении
• Задачи на противоположное движение
• Задачи на нахождение неизвестного по двум разностям
• Задачи на нахождение числа по доле и доли по числу
• Задачи на нахождение площади
• Задачи на сложение и вычитание многозначных чисел
• Задачи на умножение и деление многозначных чисел
• Задачи на приведение к единице и пропорциональное деление
• Задачи на определение цены, количества, стоимости



Читать онлайн «Математические диктанты.

Числовые примеры. Все типы задач. Устный счет. 4 класс», О. В. Узорова – ЛитРес

© Узорова О.В., Нефёдова Е.А.

© ООО «Издательство АСТ»

Предисловие

Материал пособия поможет сформировать навыки устного счёта по базовым темам программы по математике для 4 класса.

Диктанты распределены по четырём разделам:

«I четверть» (диктанты 1–14) – с. 4;

«II четверть» (диктанты 15–24) – с. 77;

«III четверть» (диктанты 25–38) – с. 132;

«IV четверть» (диктанты 39–46) – с. 212.

Каждый диктант представлен в двух вариантах и состоит из пятнадцати заданий – это не только простые примеры на сложение, вычитание, умножение и деление, но и задачи. Если решение задачи требует более трёх действий, по усмотрению учителя допускается записывать условия и некоторые промежуточные действия с ответами в самой работе или на черновике.

Работа над ошибками, размещённая после диктанта, может быть использована непосредственно по назначению или как дополнительный материал для урока.

Устный счёт – предметный навык, необходимый для успешного решения учебных и практических задач. Выполнение предлагаемых заданий развивает логическое и математическое мышление, память и внимание.

Пособие можно использовать на уроках математики для объяснения и закрепления изученного материала, для контроля знаний, в качестве заданий для отдельных учеников, а также для занятий дома.

I четверть

Диктант 1

Вариант 1

1. Уменьши 530 на 340.

2. На сколько надо увеличить 280, чтобы получить 460?

3. Какое число в 120 раз меньше 600?

4. Во сколько раз нужно увеличить 80, чтобы получить 560?

5. Сложи 722 и пятую часть от 80.

6. На сколько килограммов три четвёртых центнера больше одной второй центнера?

7. Во сколько раз 540 больше 27?

8. На сколько 540 больше 27?

9. Разность чисел 250 и 125 уменьши в 5 раз.

10. Из 240 м сатина сшили 80 одинаковых рубашек. Сколько метров пошло на 60 таких рубашек?

11. Раздели 72 на две части так, чтобы одна из них была в 8 раз больше другой; раздели 91 на две части так, чтобы одна из них была в 6 раз больше другой.

12. Увеличь 11 в 11 раз; увеличь 11 в 12 раз.

13. Уменьши 144 в 6 раз.

14. Поезд прошёл 150 км за 3 ч. За сколько часов он пройдёт 750 км?

15. В демонстрации приняли участие 1000 человек. Их разделили на группы по 125 человек в каждой. Сколько групп получилось?

Вариант 2

1. Уменьши 720 на 250.

2. На сколько надо увеличить 370, чтобы получить 530?

3. Какое число в 140 раз меньше 700?

4. Во сколько раз нужно увеличить 70, чтобы получить 490?

5. Сложи 633 и пятую часть от 70.

6. На сколько килограммов три пятых центнера больше двух четвёртых центнера?

7. Во сколько раз 580 больше 29?

8. На сколько 580 больше 29?

9. Разность чисел 450 и 250 уменьши в 5 раз.

10. Из 280 м ткани сшили 70 одинаковых брюк. Сколько метров пошло на 50 таких брюк?

11. Раздели 64 на две части так, чтобы одна из них была в 7 раз больше другой; раздели 96 на две части так, чтобы одна из них была в 7 раз больше другой.

12. Увеличь 9 в 13 раз; увеличь 9 в 14 раз.

13. Уменьши 161 в 7 раз.

14. Машина проехала 160 км за 2 ч. За сколько часов она проедет 640 км?

15. В празднике приняли участие 1080 человек. Их разделили на группы по 120 человек в каждой. Сколько групп получилось?

Работа над ошибками

1. 1) Уменьши 640 на 340.

2) Уменьши 530 на 160.

3) Уменьши 870 на 690.

2. 1) На сколько надо увеличить 370, чтобы получить 520?

2) На сколько надо увеличить 190, чтобы получить 460?

3) На сколько надо увеличить 460, чтобы получить 870?

3. 1) Какое число в 150 раз меньше 900?

2) Какое число в 160 раз меньше 800?

3) Какое число в 150 раз меньше 600?

4. 1) Во сколько раз нужно увеличить 70, чтобы получить 490?

2) Во сколько раз нужно увеличить 80, чтобы получить 720?

3) Во сколько раз нужно увеличить 30, чтобы получить 210?

5. 1) Сложи 633 и четвёртую часть от 56.

2) Сложи 455 и седьмую часть от 91.

3) Сложи 366 и четвёртую часть от 64.

6. 1) На сколько килограммов две четвёртых центнера больше одного центнера?

2) На сколько килограммов четыре пятых центнера больше трёх четвёртых центнера?

3) На сколько килограммов четыре пятых центнера больше одной второй центнера?

7. 1) Во сколько раз 570 больше 19?

2) Во сколько раз 480 больше 16?

3) Во сколько раз 850 больше 17?

8. 1) На сколько 720 больше 18?

2) На сколько 640 больше 16?

3) На сколько 950 больше 19?

9. 1) Разность чисел 970 и 130 уменьши в 7 раз.

2) Разность чисел 850 и 170 уменьши в 4 раза.

3) Разность чисел 620 и 280 уменьши в 2 раза.

10. 1) Из 140 м кожи сшили 70 одинаковых сапог. Сколько метров пошло на 30 таких сапог?

2) Из 210 м драпа сшили 70 одинаковых пальто. Сколько метров пошло на 60 таких пальто?

3) Из 720 г глины сделали 8 одинаковых чашек. Сколько граммов пошло на 10 таких чашек?

11. 1) Раздели 96 на две части так, чтобы одна из них была в 4 раза больше другой; раздели 125 на две части так, чтобы одна из них была в 5 раз больше другой.

2) Раздели 48 на две части так, чтобы одна из них была в 4 раза больше другой; раздели 128 на две части так, чтобы одна из них была в 8 раз больше другой.

3) Раздели 28 на две части так, чтобы одна из них была в 2 раза больше другой; раздели 108 на две части так, чтобы одна из них была в 6 раз больше другой.

12. 1) Увеличь 11 в 12 раз; увеличь 11 в 13 раз.

2) Увеличь 11 в 14 раз; увеличь 11 в 15 раз.

3) Увеличь 11 в 16 раз; увеличь 11 в 17 раз.

13. 1) Уменьши 144 в 9 раз.

2) Уменьши 135 в 9 раз.

3) Уменьши 128 в 8 раз.

14. 1) Ленивец прополз 120 см за 6 мин. За сколько минут он проползёт 400 см?

2) Велосипедист проехал 55 км за 5 ч. За сколько часов он проедет 121 км?

3) Вертолёт пролетел 690 км за 3 ч. За сколько часов он пролетит 460 км?

15. 1) У мастера было 1020 гвоздей. Он их разделил в коробки по 68 гвоздей в каждую. Сколько коробок получилось?

2) В палатке было 7 кг сахарного песка. Его расфасовали в пакеты по 500 г. Сколько пакетов получилось?

3) Собрали 240 редисок. Их связали в пучки по 5 редисок в каждом. Сколько пучков получилось?

Диктант 2

Вариант 1

1. Запиши число, в котором 53 десятка.

2. Какие числа стоят между числами 1597 и 1602?

3. Увеличь 400 в 2 раза, полученное произведение уменьши на 800, полученное число увеличь в 7 раз и прибавь 56.

4. Число 600 уменьши во столько раз, во сколько 84 больше 7.

5. 400 без 48.

6. На сколько разность чисел 800 и 250 меньше суммы чисел 1100 и 190?

7. Квадрат со стороной 7 дм 2 см. Найди периметр.

8. Парикмахерская работает с 10 часов утра до 9 часов вечера. Сколько часов открыта парикмахерская?

9. В первом доме 400 жильцов, а во втором на 150 жильцов меньше. Сколько жильцов в обоих домах?

10. В доме 72 квартиры, а в соседнем доме на 48 квартир больше. Сколько квартир в двух домах?

11. Увеличь 18 в 11 раз.

12. Уменьши 742 на 631.

13. Я задумал число, вычел его из 200, разность разделил на 11 и получил 11. Какое число я задумал?

14. В магазин завезли 112 кг картошки. В первый день продали половину, во второй 47 кг. Сколько килограммов картошки осталось?

15. Велосипедист ехал 4 дня по 5 ч в день со скоростью 12 км в час. Туристы прошли это же расстояние за 6 дней, причём они шли по 8 ч в день. Найди скорость туристов.

Вариант 2

1. Запиши число, в котором 68 десятков.

2. Какие числа стоят между числами 1498 и 1503?

3. Увеличь 350 в 2 раза, полученное произведение уменьши на 699, полученное число увеличь в 11 раз и прибавь 49.

4. Число 800 уменьши во столько раз, во сколько 64 больше 4.

5. 300 без 39.

6. На сколько разность чисел 700 и 350 меньше суммы чисел 1200 и 160?

7. Квадрат со стороной 6 дм 8 см. Найди периметр.

8. Химчистка работает с 9 ч утра до 8 ч вечера. Сколько часов открыта химчистка?

9. В первом доме 600 жильцов, а во втором на 240 жильцов меньше. Сколько жильцов в обоих домах?

10. В одном посёлке 63 дома, а в соседнем посёлке на 25 домов больше. Сколько домов в двух посёлках?

11. Увеличь 15 в 12 раз.

12. Уменьши 548 на 329.

13. Задумали число, вычли его из 200, разность разделили на 9 и получили 12. Какое число задумали?

14. В магазин завезли 132 кг моркови. В первый день продали половину, во второй 38 кг. Сколько килограммов картошки осталось?

15. Велосипедист ехал 3 дня по 6 ч в день со скоростью 10 км в час. Туристы прошли это же расстояние за 6 дней, причём они шли по 6 ч в день. Найди скорость туристов.

Работа над ошибками

1. 1) Запиши число, в котором 64 десятка.

2) Запиши число, в котором 75 десятков.

3) Запиши число, в котором 42 десятка.

2. 1) Какие числа стоят между числами 2396 и 2402?

 

2) Какие числа стоят между числами 3699 и 3708?

3) Какие числа стоят между числами 1998 и 2005?

3. 1) Увеличь 500 в 2 раза, полученное произведение уменьши на 700, полученное число увеличь в 6 раз и прибавь 61.

2) Увеличь 200 в 3 раза, полученное произведение уменьши на 500, полученное число увеличь в 5 раз и прибавь 92.

3) Увеличь 300 в 3 раза, полученное произведение уменьши на 400, полученное число увеличь в 2 раза и прибавь 56.

4. 1) Уменьши 800 во столько раз, во сколько 48 больше 3.

2) Уменьши 900 во столько раз, во сколько 105 больше 7.

3) Уменьши 600 во столько раз, во сколько 96 больше 8.

5. 1) 600 без 67.

2) 700 без 45.

3) 500 без 83.

6. 1) На сколько разность чисел 900 и 650 меньше суммы чисел 1200 и 150?

2) На сколько разность чисел 700 и 450 меньше суммы чисел 1000 и 690?

3) На сколько разность чисел 600 и 130 меньше суммы чисел 1300 и 270?

7. 1) Квадрат со стороной 5 дм 4 см. Найди периметр.

2) Квадрат со стороной 6 дм 3 см. Найди периметр.

3) Квадрат со стороной 3 дм 2 см. Найди периметр.

8. 1) Магазин работает с 8 часов утра до 7 часов вечера. Сколько часов открыт магазин?

2) Киоск работает с 7 часов утра до 6 часов вечера. Сколько часов открыт киоск?

3) Рынок работает с 9 часов утра до 8 часов вечера. Сколько часов открыт рынок?

9. 1) Фермер собрал 600 кг картофеля, а моркови на 270 кг меньше. Сколько всего килограммов овощей собрал фермер?

2) В музее 700 мужских портретов‚ а женских на 140 портретов меньше. Сколько всего портретов в музее?

3) Продали в партер 500 билетов, а в амфитеатр на 120 билетов меньше. Сколько всего билетов продано?

10. 1) В новом доме заселили 150 квартир, а пустует на 25 квартир больше. Сколько всего квартир в новом доме?

2) В хозяйственном магазине 68 газовых плит‚а электрических на 17 плит больше. Сколько плит в хозяйственном магазине?

3) Издательство в месяц выпускает 47 художественных книг‚ а учебников на 23 больше. Сколько всего книг выпускает издательство?

11. 1) Увеличь 16 в 11 раз.

2) Увеличь 11 в 11 раз.

3) Увеличь 15 в 11 раз.

12. 1) Уменьши 567 на 3351.

2) Уменьши 876 на 765.

3) Уменьши 954 на 342.

13. 1) Я задумал число, вычел его из 300, разность разделил на 11 и получил 12. Какое число я задумал?

2) Я задумал число, вычел его из 400, разность разделил на 11 и получил 13. Какое число я задумал?

3) Я задумал число, вычел его из 200, разность разделил на 11 и получил 14. Какое число я задумал?

14. 1) В «Детском мире» продавалось 246 мягких игрушек. В первый день продали половину, во второй 93 игрушки. Сколько игрушек осталось?

2) В магазине продавались 369 гвоздик. В первый день продали третью часть всех гвоздик, во второй 114 гвоздик. Сколько гвоздик осталось?

3) Было 400 м антенного кабеля. Одному мастеру выдали для работы половину всего кабеля, а другому 127 м. Сколько метров антенного кабеля осталось?

15. 1) Катер плыл 2 дня по 5 ч в день со скоростью 32 км в час. Лодка проплыла это же расстояние за 4 дня, причём она проплывала по 8 ч в день. Найди скорость лодки.

2) Мотоциклист ехал 3 дня по 6 ч в день со скоростью 60 км в час. Велосипедист проехал это же расстояние за 8 дней, причём он ехал по 9 ч в день. Найди скорость велосипедиста.

3) Повозка ехала 2 дня по 6 ч в день со скоростью 10 км в час. Туристы прошли это же расстояние за 3 дня, причём они шли по 8 ч в день. Найди скорость туристов.

Диктант 3

Вариант 1

1. На сколько надо увеличить 150, чтобы получить 280?

2. Увеличь 90 в 6 раз.

3. Что больше и на сколько: пятая часть от 90 или седьмая часть от 105?

4. От какого числа 40 составляет седьмую часть?

5. Запиши пятизначное число, в котором сумма цифр равна 9.

6. Уменьши 470 на 225.

7. Произведение чисел 10 и 6 увеличь на 36, полученное число раздели на 8 и умножь на 5.

8. Мальчик лёг спать в 10 часов вечера и проснулся в 8 часов утра. Сколько часов спал мальчик?

9. 117 кг помидоров разложили в 9 корзин поровну. Четыре корзины с помидорами продали. Сколько килограммов помидоров осталось?

10. Вычисли периметр прямоугольника со сторонами 2 дм 7 см и 59 см.

11. Увеличь 15 в 12 раз.

12. Уменьши 871 на 654.

13. Я задумал число, вычел его из 190, разделил на 12 и получил 12. Какое число я задумал?

14. В саду 43 груши, слив на 29 больше, чем груш, а яблонь в 5 раз больше, чем слив. Сколько яблонь в саду?

15. У Вити 75 марок, посвященных космосу, марок с автомобилями в 6 раз больше, а марок с животными на 49 меньше, чем марок с автомобилями. Сколько у Вити марок с животными?

Вариант 2

1. На сколько надо увеличить 140, чтобы получить 274?

2. Увеличь 72 в 8 раз.

3. Что больше и на сколько: шестая часть от 102 или восьмая часть от 128?

4. От какого числа 61 составляет шестую часть?

5. Запиши шестизначное число, в котором сумма цифр равна 11.

6. Уменьши 580 на 335.

7. Произведение чисел 11 и 7 увеличь на 43, полученное число раздели на 6 и умножь на 5.

8. Даша легла спать в 11 ч вечера и проснулась в 7 ч утра. Сколько часов спала девочка?

9. 152 кг абрикосов разложили в 8 корзин поровну. 5 корзин с абрикосами продали. Сколько килограммов абрикосов осталось?

10. Вычисли периметр прямоугольника со сторонами 3 дм 5 см и 73 см.

11. Увеличь 14 в 13 раз.

12. Уменьши 963 на 745.

13. Я задумал число, вычел его из 300, разность разделил на 13 и получил 11. Какое число я задумал?

14. В сквере 27 дубов, клёнов на 36 больше, чем дубов, а лип в 6 раз больше, чем клёнов. Сколько лип в сквере?

15. У Маши 67 открыток с цветами, открыток с собачками в 3 раза больше, а с кошечками на 55 меньше, чем с собачками. Сколько у Маши открыток с кошечками?

Работа над ошибками

1. 1) На сколько надо увеличить 230, чтобы получить 360?

2) На сколько надо увеличить 360, чтобы получить 450?

3) На сколько надо увеличить 450, чтобы получить 780?

2. 1) Увеличь 80 в 7 раз.

2) Увеличь 90 в 5 раз.

3) Увеличь 40 в 6 раз.

3. 1) Что больше и на сколько: седьмая часть от 117 или шестая часть от 114?

2) Что больше и на сколько: девятая часть от 135 или восьмая часть от 144?

3) Что больше и на сколько: восьмая часть от 152 или девятая часть от 162?

4. 1) От какого числа 30 составляет девятую часть?

2) От какого числа 50 составляет пятую часть?

3) От какого числа 70 составляет восьмую часть?

5. 1) Запиши пятизначное число, в котором сумма цифр равна 8.

2) Запиши пятизначное число, в котором сумма цифр равна 7.

3) Запиши пятизначное число, в котором сумма цифр равна 6.

6. 1) Уменьши 580 на 335.

2) Уменьши 690 на 115.

3) Уменьши 720 на 445.

7. 1) Произведение чисел 10 и 7 увеличь на 15, полученное число раздели на 5 и умножь на 8.

2) Произведение чисел 10 и 4 увеличь на 51, полученное число раздели на 7 и умножь на 4.

3) Произведение чисел 10 и 5 увеличь на 48, полученное число раздели на 7 и умножь на 6.

8. 1) Мама легла спать в 11 часов вечера и проснулась в 6 часов утра. Сколько часов спала мама?

2) Малыш заснул в 9 часов вечера и проснулся в 7 часов утра. Сколько часов спал малыш?

3) Выпускной вечер в школе начался в 10 часов вечера и закончился в 6 часов утра. Сколько часов продолжался выпускной вечер?

9. 1) 153 пирожка разложили на 9 противней поровну. Четыре противня поставили в духовку. Сколько пирожков осталось?

2) 126 пирожных разложили в 14 коробок поровну. 6 коробок с пирожными продали. Сколько пирожных осталось?

3) 126 тетрадей учительница разложила в 7 стопок поровну. 5 стопок тетрадей она проверила. Сколько тетрадей ей осталось проверить?

10. 1) Вычисли периметр прямоугольника со сторонами 3 дм 1 см и 59 см.

2) Вычисли периметр прямоугольника со сторонами 2 дм 7 см и 53 см.

3) Вычисли периметр прямоугольника со сторонами 7 дм 3 см и 27 см.

11. 1) Увеличь 11 в 12 раз.

2) Увеличь 12 в 12 раз.

3) Увеличь 13 в 12 раз.

12. 1) Уменьши 983 на 234.

2) Уменьши 761 на 345.

3) Уменьши 485 на 126.

13. 1) Я задумал число, вычел его из 210, разделил разность на 12 и получил 13. Какое число я задумал?

2) Я задумал число, вычел его из 180, разделил разность на 12 и получил 14. Какое число я задумал?

3) Я задумал число, вычел его из 170, разделил разность на 12 и получил 15. Какое число я задумал?

14. 1) За год прошло 32 научно-технических выставки, книжных на 18 выставок больше, а художественных выставок в 3 раза больше, чем книжных. Сколько художественных выставок прошло?

2) На спортивной базе 54 пары беговых лыж, слаломных на 15 пар меньше, а горных в 2 раза больше, чем слаломных лыж. Сколько пар горных лыж на спортивной базе?

3) В городке 9 проспектов, а улиц на 25 больше‚ а переулков в 2 раза больше‚ чем улиц. Сколько переулков в городке?

15. 1) Володя насчитал на карте 9 городов-героев, курортных городов в 6 раз больше, а промышленных на 12 меньше, чем курортных городов. Сколько промышленных городов насчитал Володя на карте?

2) В городе 65 магазинов, ларьков в 2 раза больше, чем магазинов‚ а небольших рынков на 58 меньше, чем ларьков. Сколько небольших рынков в городе?

3) В библиотеке 86 толковых словарей, орфографических словарей в 7 раз больше, чем толковых, а русско-английских на 73 словаря меньше, чем толковых. Сколько русско-английских словарей в библиотеке?

Диктант 4

Вариант 1

1. Найди частное от деления 1500 на 50.

2. На сколько 1 т больше 350 кг?

3. На сколько 1 км больше 340 м?

4. Найди шестую часть числа 3600.

5. Сколько сотен в числе 6490?

6. Напиши число, которое больше 15 в 200 раз.

7. Сколько килограммов в 5 ц 37 кг?

8. Во сколько раз частное от деления 480 на 4 больше частного от деления 76 на 19?

9. За 6 ч поезд проехал 420 км. Сколько километров с такой же скоростью он проедет за 8 ч?

10. Школьники работали на участке 3 ч 40 мин. Сколько это минут?

11. Раздели 780 на 4.

12. Увеличь 140 в 6 раз.

13. Я задумал число, разделил его на 15, потом умножил на 7, разделил на 6 и получил 23 и 2 в остатке. Какое число я задумал?

14. У Ромы в коллекции 125 открыток, а вкладышей в 5 раз меньше. У Димы вкладышей в 7 раз больше, чем у Ромы. Сколько вкладышей у Димы?

15. Между городами Касимов и Городец расстояние 560 км. Из этих городов одновременно навстречу друг другу выехали две машины и встретились через 4 ч на расстоянии 320 км от города Городец. С какими скоростями ехали машины?

Вариант 2

1. Найди частное от деления 1600 на 40.

2. На сколько 2 т больше 750 кг?

3. Во сколько раз 2 км больше 990 м?

4. Найди пятую часть числа 2500.

5. Сколько сотен в числе 7983?

6. Запиши число, которое больше 12 в 300 раз.

7. Сколько килограммов в 7 ц 24 кг?

8. Во сколько раз частное от деления 690 на 6 больше частного от деления 85 на 17?

9. За 9 ч поезд проехал 630 км. Сколько километров с такой же скоростью он проедет за 7 ч?

10. Туристы шли 5 ч 37 мин. Сколько это минут?

11. Раздели 678 на 6.

12. Увеличь 133 в 7 раз.

13. Я задумал число, разделил его на 20, затем частное умножил на 6, разделил на 5 и получил 24. Какое число я задумал?

14. У Миши в коллекции 138 марок, а открыток в 6 раз меньше. У Лены открыток в 8 раз больше, чем у Миши. Сколько открыток у Лены?

15. Между Китежградом и Цветочным городом расстояние 960 км. Из этих городов одновременно навстречу друг другу выехали две машины и встретились через 6 ч на расстоянии 540 км от Китежграда. С какими скоростями ехали машины?

Работа над ошибками

1. 1) Найди частное от деления 1200 на 30.

 

2) Найди частное от деления 1600 на 40.

3) Найди частное от деления 1800 на 90.

2. 1) На сколько 1 т больше 240 кг?

2) На сколько 1 т больше 360 кг?

3) На сколько 1 т больше 480 кг?

3. 1) Во сколько раз 1 км больше 500 м?

2) Во сколько раз 1 км больше 250 м?

3) Во сколько раз 1 км больше 125 м?

4. 1) Найди четвёртую часть числа 3600.

2) Найди третью часть числа 2400.

3) Найди шестую часть числа 1800.

5. 1) Сколько сотен в числе 2450?

2) Сколько сотен в числе 8760?

3) Сколько сотен в числе 5670?

6. 1) Напиши число, которое больше 14 в 200 раз.

2) Напиши число, которое больше 13 в 300 раз.

3) Напиши число, которое больше 12 в 400 раз.

7. 1) Сколько килограммов 6 ц 48 кг?

2) Сколько килограммов 4 ц 26 кг?

3) Сколько килограммов 7 ц 15 кг?

8. 1) Во сколько раз частное от деления 840 на 4 больше частного от деления 98 на 14?

2) Во сколько раз частное от деления 840 на 7 больше частного от деления 72 на 12?

3) Во сколько раз частное от деления 750 на 5 больше частного от деления 95 на 19?

9. 1) Бабочка-капустница за 6 с пролетела 24 м. Сколько метров с такой же скоростью она пролетит за 9 с?

2) Кит за 5 ч проплывает 35 км. Сколько километров с такой же скоростью он проплывёт за 7 ч?

3) Гончая собака за 4 с пробегает 120 м. Сколько метров с такой же скоростью она пробежит за 6 с?

10. 1) Дети работали на уроках 2 ч 45 мин. Сколько это минут?

2) Бабушка работала в огороде 3 ч 10 мин. Сколько это минут?

3) Витя гулял 4 ч 20 мин. Сколько это минут?

11. 1) Раздели 960 на 8.

2) Раздели 780 на 6.

3) Раздели 750 на 5.

12. 1) Увеличь 140 в 5 раз.

2) Увеличь 180 в 5 раз.

3) Увеличь 190 в 6 раз.

13. 1) Я задумал число, разделил его на 16, затем частное умножил на 8, разделил на 7 и получил 17 и 1 в остатке. Какое число я задумал?

2) Я задумал число, разделил его на 12, затем частное умножил на 2, разделил на 8 и получил 7 и 4 в остатке. Какое число я задумал?

3) Я задумал число, разделил его на 16, затем частное умножил на 4, разделил на 6 и получил 40. Какое число я задумал?

14. 1) В одной изостудии 72 набора с акварельными красками‚ а с масляными красками в 4 раза меньше. Во второй изостудии наборов с масляными красками в 2 раза больше‚ чем в первой. Сколько наборов с масляными красками во второй изостудии?

2) На одном предприятии 45 инженеров-механиков, а инженеров-конструкторов в 5 раз меньше. На другом предприятии инженеров-конструкторов в 2 раза больше, чем на первом предприятии. Сколько инженеров-конструкторов на втором предприятии?

3) В одной школе 32 учебных кабинета, а лингафонных кабинетов в 8 раз меньше. В другой школе лингафонных кабинетов в 2 раза больше, чем в первой школе. Сколько лингафонных кабинетов во второй школе?

15. 1) Расстояние между посёлками 240 км. Из этих посёлков одновременно навстречу друг другу выехали два мотоциклиста и встретились через 2 ч на расстоянии 140 км от одного из посёлков. С какими скоростями ехали мотоциклисты?

2) Расстояние между пристанями 210 км. От этих пристаней одновременно навстречу друг другу вышли два теплохода и встретились через 3 ч на расстоянии 120 км от одной из пристаней. С какими скоростями шли теплоходы?

3) Расстояние между станциями 180 км. От этих станций одновременно навстречу друг другу выехали два товарных поезда и встретились через 2 ч на расстоянии 80 км от одной из станций. С какими скоростями ехали товарные поезда?

Логические задачи для 4 класса — задания на логику по математике для 4 класса

Зачем развивать логическое мышление в 4 классе?

Чтобы успешно

реализовать себя в жизни

Критическое мышление, умение правильно задавать вопросы, с удовольствием учиться новому и использовать полученные знания пригодится не только в будущей профессии, но и в жизни.

Грамотно мыслить,

рассуждать и делать выводы

А ещё сравнивать, анализировать и выстраивать причинно-следственные связи — умения, которые необходимы каждому в течение всей жизни, в любой области знаний.

Различать правду и ложь

Логическое мышление помогает не только отыскивать ответы на свои вопросы в море информации, но и отделять главное от второстепенного, сопоставлять факты и отличать правду от вымысла.

Находить неординарные

способы решения задач

Креативность, без преувеличения, — одно из важнейших качеств современного человека. Её можно и нужно развивать, и чем раньше начать это делать, тем эффективнее будет результат.

Развитие логического мышления в 4 классе

вместе с Умназией

Навыки, необходимые

в реальной жизни

Математическая логика необходима не только для повышения успеваемости в школе или побед в олимпиадах. Она научит ребенка работать с информацией, моделировать ситуации, сравнивать и выбирать лучшие решения в реальной жизни.

Задания, которые не дадут заскучать

Ребенок решает логические задачи, проходя интерактивную сюжетную игру и помогая героям справиться с их проблемами. Задания требуют не только простого выполнения математических действий, но и смекалки, умения анализировать и просчитывать решение на несколько шагов вперед.

Нестандартные методы

решения задач

Решение логических задач, требующих творческого, «нешаблонного» подхода, гарантирует, что столкнувшись со сложной, не разрешимой на первый взгляд проблемой, ученик не опустит руки, а испробует несколько разных подходов к ее решению.

Примеры заданий на логику для 4 класса

Задача 1

Семья Чайниковых путешествует на теплоходе по городам Золотого кольца России. Посмотри на расписание теплохода на завтрашний день и на выводы, которые сделал из этого расписания Петя Чайников.
Все ли его выводы верны?

Решить задачу

Задача 2

Насекомые соревнуются в ловкости и скорости. И вот на финише трое: первым пришёл кузнечик, вторым — муравей, а третье место занял жук-навозник. Главный судья — уважаемый шмель — сел подписывать дипломы победителям, но не может вспомнить, как кого зовут!
Посмотри на факты, которые точно известны уважаемому шмелю и попробуй определить имена победителей.

Решить задачу

Задача 3

Робин Бобин, Винни-Пух, Карлсон и ученик 4 класса Петя Чайников участвовали в финале конкурса на скоростное поедание тортов. После соревнования финалисты сделали ряд заявлений. Выяснилось, что среди этих заявлений три верны, а одно неверно.
Кто из участников съел больше всех, а кто меньше всех?

Решить задачу

Решать задачи на логику для учеников 4 класса

Познакомьтесь с форматом курса “Математического мышления”. Пройдите сюжетную игру и решите три задачи на логику!

Решать задачи

Решать задачи

В УМНАЗИИ ДЕТИ РАЗВИВАЮТ МЫШЛЕНИЕ В ИГРОВОЙ ФОРМЕ, РЕШАЯ УВЛЕКАТЕЛЬНЫЕ СЮЖЕТНЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ

Продуманная программа

Курсы математического мышления разработаны на базе множества источников, экспертизы методистов и педагогов, разделены на 10 тем с теорией и игровыми заданиями с объяснением

Увлекательные задания

Ребенок решает сюжетные игровые задачи по математике для изучения новых тем и закрепления пройденного по каждому курсу. Никакой скуки! Ни одно задание не повторяется!

Дипломы и награды

В конце каждого курса математической логики ребенок решает тест или проходит игру, получая сертификат в случае успешного выполнения. Вы будете уверены в его знаниях!

Развитие логического мышления в 4 классе

Сложно переоценить значение развития логических навыков в начальной школе. Ориентироваться в потоке информации, отделять главное от второстепенного, постоянно развиваться, находить нестандартные решения и делать правильный выбор — навыки, которые одинаково важны и для успешной учебы, и для построения карьеры, и для комфортной повседневной жизни.

Развивать мышление ученика 4 класса эффективнее всего используя игровые методики, занимательные логические задачи и занятия, позволяющие ребенку проявить себя и увидеть реальный результат — например, программирование, работу с конструкторами, увлекательные физические и химические опыты и эксперименты.

Купите курс математики для детей со скидкой 40 % уже сейчас

Примеры заданий по математике 9-11 класс – уровень сложности Всероссийской олимпиады школьников по математике

Примеры заданий 1-го тура

Задание 1

Футбольная команда “Квадратный круг”состоит из 11 игроков, включая вратаря. Какое утверждение является верным?
1) Хотя бы два игрока команды родились в один день недели.
2) Хотя бы два игрока команды родились в понедельник.
3) Вратарь и один из полевых игроков родились в один день недели.

Посмотреть ответСкрыть ответ

1) Хотя бы два игрока команды родились в один день недели.

Задание 2

Свежесобранные ягоды черники содержат 99% воды. Через некоторое время эти же ягоды стали содержать 98% воды.
Как изменилась масса ягод?
1) Уменьшилась на 1%.
2) Уменьшилась в 98/99 раз.
3) Уменьшилась в 2 раза.

Посмотреть ответСкрыть ответ

3) Уменьшилась в 2 раза.

Задание 3

В треугольнике ABC известны длины двух сторон AB = π, BC = cos 30◦, а длина стороны AC является целым числом.
Найдите AC. Выберите верное утверждение.
1) Единственное возможное значение длины стороны AC равно 3.
2) Единственное возможное значение длины стороны AC равно 4.
3) Длина стороны AC может быть равна 3 или 4.

Посмотреть ответСкрыть ответ

3) Длина стороны AC может быть равна 3 или 4.

Задание 4

Длина дорожки легкоатлетического стадиона равна 400 м. Из одной точки одновременно в разных направлениях с постоянной скоростью выбежали два бегуна. Один бегун имеет скорость 5 км/ч, второй – 7 км/ч. Сколько раз бегуны встретятся за время получасовой тренировки? (Старт за встречу не считаем.)

Посмотреть ответСкрыть ответ

Ответ: 15

Задание 5

Решите уравнение \frac{\left|x-1\right|}{x-1}+\frac{\left|x\right|}{x}+\frac{\left|x+1\right|}{x+1}+(x-1)^2+x^2+(x+1)^2=a при всех значениях параметра a. 2-3xy+7y-23x+26=0.
В ответ запишите сумму произведений всех найденных значений (x; y).
(Например, найденные решения – это две пары (1; 1) и (2; 3), тогда в ответ следует записать число 7, потому что 1 · 1 + 2 · 3 = 7.)

Посмотреть ответСкрыть ответ

Ответ: 16

Задание 7

В равнобедренном треугольнике ABC AB = BC = 4, AC = 2, BH− высота. Вписанная в треугольник ABC окружность второй раз пересекает высоту BH в точке K. Найдите BK : KH.

Посмотреть ответСкрыть ответ

Ответ: 1,5

Задание 8

Точки L, E, F, T – последовательные вершины параллелограмма. На отрезке LT отмечена точка N такая, что LN : NT = 3 : 2. На отрезке LF отмечена точка O такая, что LO : OF = 2 : 3. Прямая NO пересекает отрезок EF в точке G. Найдите площадь четырехугольника LEGO, если площадь параллелограмма LEF T равна 100.

Посмотреть ответСкрыть ответ

Ответ: 23

Примеры заданий 2-го тура (11 класс)

Задание 1

Найдите последнюю цифру наибольшего по модулю решения уравнения

\left(x-6\cdot2019^{2020}\right)\left(x+8\cdot2019^{2020}\right)+5x-2\cdot2019^{2020}+6=0

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 1

Задание 2

Доктор Ай вырывает пациенту зуб за 10 минут, а доктор Ой делает это за 6 минут. Доктор Ай накладывает пациенту гипс за 13 минут, а доктор Ой делает это также за 6 минут. Доктор Ай заполняет документы для страховой компании за 14 минут, а доктор Ой делает это за 7 минут. Сколько времени потратят на пациента доктора Ай и Ой, работая совместно, если требуется вырвать зуб, наложить гипс и заполнить документы?

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 12

Задание 3

Найдите наименьшее целое значение параметра a, при котором неравенство

\sqrt{\frac{2x+a}{x-1}}-2\sqrt{\frac{x-1}{2x+a}}\le1

не выполняется ровно для 2222 целых значений x.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: -2224

Задание 4

В основании прямой призмы GUSG₁U₁S₁ лежит треугольник GUS со сторонами UG = US = 4, GS = 3, боковая сторона GG₁ = 5. Плоскость π проходит через точки U и S₁ и пересекает биссектрису SK треугольника GUS в точке M такой, что SM : MK = 2 : 1. Найдите периметр сечения призмы плоскостью π.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 15,36

Задание 5

При каком наименьшем целом значении параметра a система уравнений

имеет решение, удовлетворяющее условию |\sqrt{x}+y|>19? В ответ запишите значение y, соответствующее найденному значению a.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 19,26

Задание 6

На стороне BC прямоугольника ABCD со сторонами AB = 3, AD = 5 взяты точки K и N такие, что BK = 1, NC = 2. Вне прямоугольника ABCD построен прямоугольник KLMN со стороной KL = 1. Через точку D проходит прямая l, которая пересекает прямоугольник KLMN и делит его периметр в отношении 1 : 2. Найдите сумму тангенсов всех возможных углов между прямыми AD и l.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 2,4

Задание 7

В треугольнике ABC с площадью 100 на сторонах AB, BC и AC взяты точки K, L и M такие, что AK : KB = 1 : 5, BL : LC = 1 : 1 (точка L – середина стороны BC) и AM : MC = 2 : 1. Отрезки AL и BM пересекаются в точке F, BM и CK – в точке G, AL и CK – в точке E. Найдите площадь треугольника EFG.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 14,46

Задание 8

В классе на доске было записано некоторое четырехзначное число. {2020}+6=0

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 1

Задание 2

Доктор Ай вырывает пациенту зуб за 10 минут, а доктор Ой делает это за 6 минут. Доктор Ай накладывает пациенту гипс за 13 минут, а доктор Ой делает это также за 6 минут. Доктор Ай заполняет документы для страховой компании за 14 минут, а доктор Ой делает это за 7 минут. Сколько времени потратят на пациента доктора Ай и Ой, работая совместно, если требуется вырвать зуб, наложить гипс и заполнить документы?

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 12

Задание 3

Найдите наименьшее целое значение параметра a, при котором неравенство

\sqrt{\frac{2x+a}{x-1}}-2\sqrt{\frac{x-1}{2x+a}}\le1

не выполняется ровно для 3000 целых значений x.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: -3002

Задание 4

В основании прямой призмы GUSG₁U₁S₁ лежит треугольник GUS со сторонами UG = US = 4, GS = 3, боковая сторона GG₁ = 5. Плоскость \pi проходит через точки U и S₁ и пересекает биссектрису SK треугольника GUS в точке M такой, что SM : MK = 2 : 1. Найдите площадь сечения призмы плоскостью \pi.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 9,74

Задание 5

При каком наименьшем целом значении параметра a система уравнений

имеет решение, удовлетворяющее условию |\sqrt{x}+y|>19? В ответ запишите значение x, соответствующее найденному значению a.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 13,04

Задание 6

На стороне BC прямоугольника ABCD со сторонами AB = 3, AD = 5 взяты точки K и N такие, что BK = 1, NC = 2. Вне прямоугольника ABCD построен прямоугольник KLMN со стороной KL = 1. Через точку D проходит прямая l, которая пересекает прямоугольник KLMN и делит его периметр в отношении 1 : 2. Найдите тангенс наибольшего возможного угла между прямыми AD и l.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 1,4

Задание 7

В треугольнике ABC с площадью 100 на сторонах AB, BC и AC взяты точки K, L и M такие, что AK : KB = 1 : 5, BL : LC = 1 : 1 (точка L – середина стороны BC) и AM : MC = 2 : 1. Отрезки AL и BM пересекаются в точке F, BM и CK – в точке G, AL и CK – в точке E. Найдите площадь треугольника EFG.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 14,46

Задание 8

В классе на доске было записано некоторое четырехзначное число. Два ученика зашли в класс и подумали, что это пример на умножение двух чисел. Один из них умножал двузначные числа, другой – цифру и трехзначное число. (Например, было написано 2345, один умножил 23 на 45, другой – 2 на 345 или 234 на 5.) У ребят получились числа 1029 и 1926. Какое число было исходно записано на доске? Если подходящих чисел несколько, запишите их в порядке возрастания без пробелов. Если такого числа не существует, в ответ запишите 0.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 2149

Примеры заданий 2-го тура (9 класс)

Задание 1

Найдите последнюю цифру положительного решения уравнения

(x−6·2019^{2020})(x+8·2019^{2020})+5x−2·2019^{2020}+6=0

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 4

Задание 2

Доктор Ай вырывает пациенту зуб за 10 минут, а доктор Ой делает это за 6 минут. Доктор Ай накладывает пациенту гипс за 13 минут, а доктор Ой делает это также за 6 минут. Доктор Ай заполняет документы для страховой компании за 14 минут, а доктор Ой делает это за 7 минут. Сколько времени потратят на пациента доктора Ай и Ой, работая совместно, если требуется вырвать зуб, наложить гипс и заполнить документы?

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 12

Задание 3

Найдите наименьшее целое значение параметра a, при котором неравенство

\sqrt{\frac{2x+a}{x-1}}-2\sqrt{\frac{x-1}{2x+a}}\le1

не выполняется ровно для 2468 целых значений x.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: -2470

Задание 4

В прямоугольном треугольнике GUS с прямым углом U и сторонами UG = 3 и US = 4 проведена биссектриса GE, а на стороне GU взята точка V такая, что UE = UV . Биссектриса угла S треугольника GUS пересекает прямую EV в точке T. Найдите периметр треугольника GET.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 1,43

Задание 5

При каком наименьшем целом значении параметра a система уравнений

имеет решение, удовлетворяющее условию |\sqrt{x}+y|>19? В ответ запишите найденное значение a.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 8

Задание 6

На стороне BC прямоугольника ABCD со сторонами AB = 3, AD = 5 взяты точки K и N такие, что BK = 1, NC = 2. Вне прямоугольника ABCD построен прямоугольник KLMN со стороной KL = 1. Через точку D проходит прямая l, которая пересекает прямоугольник KLMN и делит его периметр в отношении 1 : 2. Найдите тангенс наименьшего возможного угла между прямыми AD и l.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 1

Задание 7

В треугольнике ABC с площадью 100 на сторонах AB, BC и AC взяты точки K, L и M такие, что AK : KB = 1 : 5, BL : LC = 1 : 1 (точка L – середина стороны BC) и AM : MC = 2 : 1. Отрезки AL и BM пересекаются в точке F, BM и CK – в точке G, AL и CK – в точке E. Найдите площадь треугольника EFG.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 14,46

Задание 8

В классе на доске было записано некоторое четырехзначное число. Два ученика зашли в класс и подумали, что это пример на умножение двух чисел. Один из них умножал двузначные числа, другой – цифру и трехзначное число. (Например, было написано 2345, один умножил 23 на 45, другой – 2 на 345 или 234 на 5.) У ребят получились числа 845 и 3078. Какое число было исходно записано на доске? Если подходящих чисел несколько, запишите их в порядке возрастания без пробелов. Если такого числа не существует, в ответ запишите 0.

Если Вы считаете, что для получения ответа не хватает данных, или задача составлена некорректно, в поле для ответа запишите −100 (минус сто).

Посмотреть ответСкрыть ответ

Ответ: 6513

Будь в курсе первым —
подпишись на рассылку!

Президентский физико-математический лицей № 239 (Санкт-Петербург)

Российский государственный педагогический университет им. А.И. Герцена

Санкт-Петербургский политехнический университет Петра Великого

Межрегиональный институт экономики и права при Межпарламентской ассамблее ЕврАзЭс

Институт программных систем РАН (Переславль-Залесский)

Сложные примеры – легкие решения

• Авторы
• Руководители
• Файлы работы
• Презентация
• Наградные документы

Татаурова Н. И. 1

---

1МБОУ Гимназия № 17 4 класс

Сунцова Е.В. 1

---

1МБОУ Гимназия № 17

---

---

Автор работы награжден дипломом победителя II степени

Диплом школьникаСвидетельство руководителяДиплом участника II этапаДиплом за подготовку участника II этапаДиплом лауреата II этапаДиплом за подготовку лауреата II этапа

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

ВВЕДЕНИЕ

Тема моей научно-практической работы – «Сложные примеры – легкие решения». Я выбрала эту тему для своей работы, так как для меня очень интересна и увлекательна математика. Чем дольше я учусь в школе и чем больше изучаю математику, тем чаще задаюсь вопросом: «Как можно решать такие сложные задачи и примеры быстро и, не прибегая к помощи калькулятора или компьютера». Интерес к этим вопросам побудил меня искать информацию в интернете, читать статьи и книги с этим связанные, спрашивать своих одноклассников и друзей, что они используют, чтобы облегчить себе изучение математики. Оказалось, что существует масса приемов устного счета, зная которые можно очень быстро считать в уме. Владение такими приемами не только облегчает изучение математики, но и значительно помогает в простой жизни. Мне захотелось поделиться со всеми найденной информацией, но для того, чтоб все легко запомнилось, появилась идея изложить в стихах алгоритмы решения примеров.

Цель моей работы – разработать свое пособие-напоминание, в котором изложены основные алгоритмы решения примеров на умножение и деление двузначных и трехзначных чисел. Это пособие выполнить в виде брошюры с примерами, объяснениями решений в стихах, которые я сочинила сама и иллюстрациями.

Моя гипотеза – с помощью моего пособия дети проявят большой интерес к математике, научатся быстро решать в уме сложные примеры, в том числе благодаря стихотворной форме изложения алгоритма.

Задачи моей работы:

Ознакомиться с алгоритмами решений сложных математических решений в уме.

Выяснить, что знают мои одноклассники о таких приемах.

Сочинить стих – объяснение про каждый пример, используемый в моем пособии.

Составить пособие и распечатать его в виде брошюры.

2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Каждый день каждый человек десятки, а то и сотни раз сталкивается с математикой. Начиная с момента пробуждения, мы весь день применяем в жизни наши математические навыки, иногда не замечая этого (как для приготовления завтрака и измерения пропорций), а иногда (как в магазине, например) вполне осознанно.

Чтобы что-то посчитать, человек применяет свои вычислительные навыки. И навыки эти нужно развивать. А развить их может каждый человек, независимо от его феноменальных математических способностей, хотя бы для того, чтобы не стать жертвой обмана в магазине или на рынке.

Развивать их можно, в том числе и с помощью применения различных техник и приемов устного счета. С давних времен люди изобретали или находили все новые такие приемы.

Когда я начала изучать этот вопрос, поняла, что мало знать о таких методах, их надо разобрать, запомнить, и тогда ты сможешь их активно применять в жизни. Разбираться с приемами устного счета оказалось не так уж сложно. Но вот запомнить столько различных задач сразу не удалось.

Так мне пришло в голову, что наиболее понравившиеся мне методы нужно зарифмовать. Ведь стихи запоминаются всегда лучше прозы. Пока я сочиняла стихи, все, используемые мной для работы математические примеры запомнились сами собой. Тогда и возникла идея поделиться своими стихами со своими друзьями, чтобы они тоже смогли легко запомнить алгоритмы решения сложных примеров.

Вас может удивит, но такая смесь математики и литературы дала очень хорошие результаты.

В ходе работы над своим проектом я ознакомилась со множеством подобных работ других учеников и пришла к выводу, что во всех случаях, когда ученики целенаправленно в счете использовали общеизвестные алгоритмы устного счета, скорость вычислений значительно увеличивалась, иногда даже в два раза. В просмотренных мною работах приводились таблицы с результатами таких экспериментов. Поэтому, я не стала доказывать в своей работе результативность применения различных методов устного счета. Это факт общепризнанный.

Моей задачей стало облегчить сам способ запоминания этих методов. Поскольку я очень люблю стихи и в повседневной жизни часто что-нибудь рифмую, выбор способа запоминания стал очевиден.

Вот что у меня получилось.

ПРАКТИЧЕСКАЯ ЧАСТЬ

3.1 Умножение на 11 числа, сумма цифр которого не превышает 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр.

63 х 11 = 693

26 х 11 = 286

Сложи числа две половинки

Помести их в серединку

3.2 Умножение на 11 числа, сумма цифр которого больше или равна 10.

Надо мысленно раздвинуть цифры этого числа и поставить между ними сумму этих цифр. Единицы числа записываем в середину, а десяток прибавляем к первой цифре.

78 х 11 = 858

64 х 11 = 704

Сложи числа две половинки

Помести их в серединку.

Про десяток не забудь,

Прибавь к началу, Умным будь!

3.3 Умножение на 111 (если сумма чисел множимого меньше 10).

Также мысленно раздвигаем цифры этого числа, находим сумму цифр данного двузначного числа и ставим ее в середину дважды.

36 х 111 = 3996

3 + 6 = 9

42 х 111 = 4662

4 + 2 = 6

Опять сложи две половинки

Помести их в серединку.

Только дважды повтори,

Так как единицы три.

3.4 Умножение на 111 (если сумма чисел множимого больше 10).

Опять мысленно раздвигаем это число, складываем цифры и вставляем их в середину числа. Но поскольку сумма цифр составляет двузначное число, прибавляем его к первым цифрам.

76 х 111 = 8436

(7+6=13)

7136

13

8436

И вновь сложи две половинки

Снова вставь их в серединку

Ну, а так как число двузначное

нужно вставить в ответ два раза

Мы прибавим его однозначно

К первым цифрам. И без отказа!

3.5 Умножение на 25.

Чтобы умножить число на 25 , надо данное число (36) умножить на 100 и произведение разделить на 4:

37 х 25 = 900

(37 х 100) : 4 = 925

Если множимое делится на 4, то сначала можно разделить множимое на 4 и полученное частное умножить на а 100.

48 х 25 = 1200

(48 : 4) х 100 = 1200

При умножении на двадцать пять

Число на сто нам надо умножать,

Потом разделим на четыре,

Вот и ответ мы получили

3.6 Деление на 25.

Чтобы разделить число на 25, надо разделить его на 100 (если делится на 100) и полученное частное умножить на 4, или сначала делимое умножить на 4, а потом полученное произведение разделить на 100:

800 : 25 = (800 : 100) х 4 = 32

225 : 25 = (225 х 4) : 100 = 9

Сделаем наоборот от предыдущего примера

При делении на двадцать пять

Число на сто нам нужно разделять

Потом уже умножим на четыре

Вот снова и ответ мы получили

А если разделить на сто нельзя

То мы пойдем другим путем, друзья

Сначала на четыре мы умножим

Потом на сто поделим и отложим.

3.7 Умножение чисел от 11 до 19.

Умножать такие числа можно используя следующую формулу, которую стоит запомнить.

100 + 10 х (а + в) + а х в

Где а и в это единицы множителей

Формула только на первый взгляд кажется сложной

Любое число из диапазона от 11 до 19 представляем как десятки и единицы.

Получаем формулу: (10+a)×(10+b).

Раскрываем скобки: 100+10×b+10×a+a×b.

Выносим за скобки общий множитель и получаем окончательную формулу, по которой можно считать и которую есть смысл запомнить: 100+10×(a+b)+a×b.

14 х 18 = 252

100 + 10 х (4 + 8) + 4 х 8 =

= 100 + 120 + 32 = 252

Чтобы перемножить два числа

Между десятью и двадцатью

Единицы перемножь сперва

И запомни как свою семью.

А еще сложи их и умножь

На десятку. Это тоже впрок.

Вот теперь сложи все результаты

И еще плюс сто. И весь урок.

3.8 Старинный русский способ умножения.

Умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа.

32 х 13

16 х 26

8 х 52

4 х 104

2 х 208

1 х 416

32 х 13 = 416

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Первое число дели на два,

Второе же, напротив, умножай.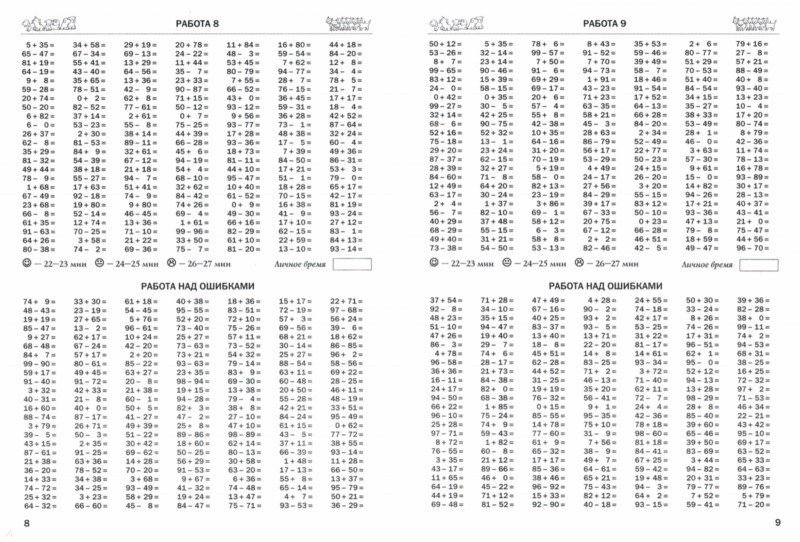

Дели до единицы и тогда

Записывай ответ и отдыхай!

Произведение не изменяется, если один множитель вдвое увеличить, а другой вдвое уменьшить.

Немного усложняется, если делимое нечётное число, то нужно откинуть единицу и делить остаток пополам, но в результате прибавить все те числа, которые стоят напротив нечётных чисел левого столбца.

19 х 17

((19-1):2) = 9 х 34

((9-1):2) = 4 х 68

2 х 136

1 х 272

19 х 17 = 272 + 17 + 34 = 323

А если разделить на 2 нельзя,

То просто единицу убирай

Все делать точно так же продолжай

А то, что не делил – к ответу прибавляй

3. 9 Умножение двузначных чисел на 9, 99, 999.

К первому множителю приписать столько нулей, сколько девяток во втором множителе, и из результата вычесть первый множитель.

28 х 9 = 280 – 28 = 152.

18 х 99 = 1800 – 18 = 1782.

23 х 999 = 23000 – 23=22977.

Так как 10а-а=9а, то для умножения числа а на 9 достаточно от увеличенного в 10 раз числа а отнять само число. Аналогично умножение на 99 и на 999. Число а умножают на 100 и на 1000 и отнимают само число.

Сколько девяток – столько нулей

Пусть даже три, ты не робей

Смело нули к числу припиши,

Ну, а потом, число отними.

3.10 Умножение трёхзначного числа на 999.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только на уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

385 х 999 = 384615

Но в принципе, здесь работает тот же принцип, что и в предыдущем примере.

385 х 999 = 385000 – 385 = 384615

Даже, если множитель трехзначный

Три нуля к нему прибавить можно

И само число из цифры этой

Вычесть для тебя совсем не сложно.

3.11 Умножение чисел от 91 до 99 друг на друга.

Первый множитель вычесть из 100, второй множитель вычесть из 100, результаты сложить. Сумму вычесть из 100 и записать ответ первыми цифрами ответа. Далее перемножить ответы и записать следующими цифрами ответа.

97 х 96 = 9312

100 – 97 = 3, 100 – 94 = 4.

4 + 3 = 7, 100 – 7 = 93, 4 х 3 = 12.

Из ста вычесть и второй и первый

Все сложить, поверьте, это верно.

Результат опять от ста отнимем

И началом для ответа примем.

А в конец ответа – очень просто,

Перемножим отнятое от ста.

3.12 Умножение трёхзначных чисел от 101 до 109.

Если к одному из чисел прибавить единицы второго числа, то это

будут первые цифры ответа, затем перемножить единицы – это будут

последние цифры ответа.

105 х 107=11235.

105 + 7 = 112, 5 х 7 = 35.

Целое число плюс единицы

И отправим их за знак «равно»

Только единицы перемножим

И поставим рядом заодно.

3.13 Умножение двузначного числа на 101.

Самое простое правило: припишите число к самому себе.

57 х 101 = 5757

На сто один умножить просто

Число ставь рядом как по росту.

3.14 Применение моего пособия.

Стихи получились не сложными и легкими в запоминании. Я раздала своим одноклассникам брошюры, в которых объясняются сами методы устного счета и рядом располагаются стихи для запоминания метода.

Спустя месяц, я провела исследование способом анкетирования и получила такие результаты. Из 29 опрошенных 20 человек сказали, что мои стихи им очень помогли в запоминании способов быстрого счета.

ЗАКЛЮЧЕНИЕ

В заключение я бы хотела сказать, что выбранная мной тема мне очень понравилась, мне было очень интересно искать разные возможности облегчения устного счета. Оказалось очень интересно и захватывающе самой разбираться в примерах, проверять и перепроверять работает ли алгоритм, сочинять стихи и разрабатывать свое пособие, а потом раздать его друзьям.

В ходе работы над проектом мне удалось кратко познакомиться с историей появления различных приемов устного счета и узнать, как человечество развивалось в этом направлении.

Цель моей работы было создание своего пособия по запоминанию некоторых методов устного счета. Указанное пособие основано на стихах про математические примеры, которые я сочинила сама. Цель моей работы достигнута.

После знакомства с моей брошюрой, ребята стали интересоваться математикой и, в частности, исследованием алгоритмов устного счета. А это, в свою очередь, развивает память, мышление, другие умственные способности, приучает к поиску решений в любых жизненных ситуациях. Таким образом, казалось бы простая тема получила большой отклик у моих одноклассников и все получили новые знания.

СПИСОК ЛИТЕРАТУРЫ

Арутюнян Е., Левитас Г. “Занимательная математика” -М.:АСТ-пресс,1999г.

Владимиров, А. И. Интересные способы быстрого счета / А. И. Владимиров, В. В. Михайлова, С. П. Шмелева. — Текст : непосредственный // Юный ученый. — 2016. — № 6.1 (9.1). — С. 15-17. — URL: https://moluch.ru/young/archive/9/633/ (дата обращения: 27.10.2020).

Гарднер М.  “Математические чудеса и тайны.”  М. 1978.

ГлейзерГ.И.” История математики в школе.” – М,1981.

“Библиотечка Первого сентября»,серия «Математика».Вып.3(15).  http//portfolio 1 September ru/subjest

ПРИЛОЖЕНИЕ

Просмотров работы: 1027

Рабочие листы по математике для 4-го класса, Рабочие листы по математике для 4-го класса

Преимущества рабочих листов по математике для 4-го класса

Обширные темы

Рабочие листы по математике для 4-го класса охватывают широкий спектр тем, от основных математических операций с большими числами до 7 цифр , четыре основные арифметические операции, простые числа, десятичные числа, делимость, множители и кратные, дроби, базовая геометрия, деньги, измерения, многоугольники и объемные фигуры, а также представление данных.

Упрощенные концепции

Рабочие листы по математике для 4 класса постарайтесь представить вашему ребенку учебную программу в максимально простом виде. В них используются пояснения, обозначения, забавные факты, таблицы и множество примеров, чтобы ваш ребенок мог изучать темы самостоятельно. Рабочие листы эффективно знакомят учащихся с темами и содержат вопросы разного уровня сложности.

Несколько заданий и игр

Онлайн-рабочие листы для 4 класса по математике содержат несколько типов заданий. Они включают в себя не оцениваемые действия, викторины, а также распечатываемые викторины и загадки. Есть также забавные игры и головоломки, чтобы вовлечь вашего ребенка в изучение основ математики.

Практические наборы для занятий дома и после школы

Рабочие листы по математике для 4 класса содержат различные учебные материалы, такие как планы уроков, практические листы, контрольные листы и задания. Эти ресурсы вовлекают и побуждают вашего ребенка создавать свои концепции, а затем помогают постепенно осваивать их.

Рабочие листы по математике для 4 класса с объяснением

Рабочие листы для сложения

Рабочие листы для сложения для 4 класса помогут вашему ребенку освоить сложение больших чисел до 4 и 5 цифр. Операция сложения не ограничивается натуральными числами. Есть рабочие листы для сложения десятичных знаков, а также дробей.

Рабочие листы по вычитанию

Рабочие листы по математике для вычитания охватывают различные аспекты уравнений вычитания, включая вычитание в уме и вычитание в столбцах. Кроме того, есть тренировочные суммы и текстовые задачи на нескольких уровнях сложности, включая вычитание дробей и десятичных чисел.

Рабочие листы по умножению

Рабочие листы по математике для четвертого класса по умножению предоставляют вашему ребенку практические уравнения, охватывающие различные аспекты операции умножения. Например, у них есть суммы умножения, начиная от простого умножения и заканчивая умножением трехзначных чисел на однозначные. Существуют также отдельные рабочие листы по умножению для 4 класса для умножения в столбцах и свойств умножения.

Рабочие листы на деление

ребенок может быстро освоить понятия операций деления как для умственного деления, так и для деления чисел в длинном столбце. Они научатся делить до 3-значных чисел с целым десятичным или целым делителем сотен, с остатком и без остатка.

Рабочие листы для дробей

Математические рабочие листы для дробей охватывают основные понятия, включая правильные и неправильные дроби, эквивалентные дроби, смешанные дроби, сравнение дробей и расположение дробей в порядке возрастания или убывания. Студенты также узнают о сложении и вычитании дробей и смешанных чисел, а также о том, как преобразовывать смешанные числа в неправильные дроби и наоборот.

Знакомство с десятичными числами

Рабочие листы по математике для 4-го класса с десятичными числами знакомят учащихся с десятичной системой счисления с помощью числовой строки. Дети учатся писать десятичные числа, сравнивать и упорядочивать их, а также использовать их в реальных задачах, таких как обмен денег и измерение. Они изучают десятичное сложение и вычитание, преобразование десятичных чисел в дроби и наоборот.

Единицы измерения

Математические рабочие листы для измерения предоставляют информацию как о метрической, так и о имперской системах измерения. Они учатся определять единицы длины, ширины, высоты, веса и даже температуры и использовать их в реальной жизни. Ваш ребенок не только научится правильно писать единицы, но и научится преобразовывать одни единицы в другие.

Площадь и периметр

Рабочие листы по математике для 4 класса включают вопросы по вычислению площади и периметра различных форм, таких как квадраты, прямоугольники, треугольники и сложные фигуры, такие как параллелограмм, ромб и т. д. 

Измерение углов

Математические рабочие листы по геометрии помогут вашему ребенку научиться измерять углы с помощью транспортира и классифицировать их как острые, прямые и тупые.

Все рабочие листы по математике для 4 класса подробно описаны. Они могут помочь вашему ребенку освоить математические концепции четвертого класса, а затем применять и практиковать их в легкой и увлекательной форме.

Часто задаваемые вопросы

Полезны ли рабочие тетради по математике для четвертого класса?

Эти онлайн-рабочие листы по математике для 4-го класса чрезвычайно полезны для учащихся, которые хотят улучшить свои математические представления, одновременно получая от них удовольствие. Эти интерактивные рабочие листы бывают трех разных уровней — легкий, средний и сложный. Основываясь на уровне знаний учащегося, они могут выбирать и практиковаться, чтобы повысить свой уровень, знания и почувствовать уверенность в своих математических навыках.

Какие понятия рассматриваются в этих листах по математике для 4 класса?

Понятия, описываемые в рабочих листах по математике для четвертого класса, включают понятия разрядности многозначных чисел, округление и сравнение многозначных чисел, сложение и вычитание многозначных чисел, умножение на однозначные и двузначные числа, деление многозначные числа, множители, кратные и шаблоны, определение простых и составных чисел, сложение и вычитание дробей, умножение целых чисел и дробей, понимание эквивалентности измерений, задачи о сумме периметра и площади, определение линий и углов различной формы и введение в линейная симметрия.

Каковы различные уровни этих математических листов для 4 класса?

Рабочие листы по математике для четвертого класса разделены на три уровня: простой, средний и сложный. Учащиеся могут выбрать любой уровень в зависимости от своего понимания математических концепций и степени уверенности в себе. Мы всегда рекомендуем учащимся попробовать все три уровня, чтобы получить всестороннее понимание математических концепций и, как следствие, получить ускоренные пути для изучения математики.

Рассчитаны ли листы по математике в четвертом классе?

Интерактивные или онлайновые задания по математике для четвертого класса рассчитаны на время. В первую очередь это делается для того, чтобы учащиеся лучше поняли, насколько они подготовлены к математическим понятиям, а последующие попытки выполнить тот же рабочий лист с новым набором вопросов могут помочь им не только улучшить свои знания, но и ускорить решение этих задач.

В каких форматах доступны рабочие листы по математике для четвертого класса?

Рабочие листы по математике для 4 класса доступны для учащихся в двух различных форматах. Рабочие листы для печати в формате PDF можно выполнять в автономном режиме после загрузки, в то время как другие технические интерактивные или онлайн-математические листы выполняются в онлайн-режиме с обратной связью в реальном времени и решениями при отправке.

Кто готовит вопросы для рабочих листов по математике в 4-м классе?

Вопросы в этих интерактивных математических таблицах подготовлены квалифицированными экспертами в предметной области, которые хорошо разбираются в предмете. Каждый вопрос проходит тщательную проверку и проверку качества, чтобы гарантировать, что каждый вопрос является инновационным и достаточно интересным для каждого учащегося.

Можно ли работать с рабочими листами по математике для 4 класса более одного раза?

Да, учащийся может практиковать математические понятия, используя бесплатные онлайн-рабочие листы по математике BYJU для четвертого класса, выполняя их более одного раза. Фактически, для каждой новой отправки студент может столкнуться с новым набором вопросов, чтобы попрактиковаться и улучшить свои знания и скорость.

Математические трудности – все виды мышления

Что может стоять на пути математического развития учащегося?
Математические трудности могут возникнуть практически на любом этапе школьного развития ребенка. Хотя очень мало известно о нейробиологических или экологических причинах этих проблем, многие эксперты связывают их со слабостью в одном или нескольких типах навыков, перечисленных ниже. Эти слабости могут существовать независимо друг от друга или могут возникать в комбинации. Все это может повлиять на способность ребенка прогрессировать в математике. 1. Неполное овладение числовыми фактами
Числовыми фактами (например, 9+ 3 = 12 или 2 x 4 = 8) — основные вычисления, которые учащиеся должны запомнить в самых первых классах начальной школы. Эффективное вспоминание этих фактов имеет решающее значение, поскольку позволяет учащемуся приблизиться к более сложному математическому мышлению, не увязая в простых вычислениях.

> Попробуйте сами. Попробуйте решить проблему с основными фактами.

2. Недостаток вычислений
Многие учащиеся выполняют вычисления непоследовательно. Несмотря на хорошее понимание математических понятий, они допускают ошибки, потому что неправильно читают знаки или неправильно переносят числа. Они могут писать цифры недостаточно четко или в правильном столбце. Эти учащиеся часто испытывают трудности, особенно в начальной школе, где основное внимание уделяется базовым вычислениям и «правильным ответам». Иногда они попадают в коррекционные классы, хотя у них может быть большой потенциал для математического мышления более высокого уровня.

3. Трудности с передачей знаний
Учащиеся могут испытывать затруднения, когда от них требуется связать абстрактные или концептуальные аспекты математики с реальностью. Понимание того, что символы представляют в физическом мире, важно для того, насколько легко ребенок запомнит понятие. Например, осмотр и сравнение одной трети стакана воды и половины стакана воды в мерном стакане будет иметь для ребенка гораздо больше смысла, чем просто сказать, что одна половина больше, чем одна треть.

4. Установление связей
Некоторым учащимся трудно устанавливать значимые связи внутри математического опыта и между ними. Например, учащийся может не сразу понять связь между числами и величинами, которые они представляют. Если такого рода связи не установлены, математические навыки могут быть не закреплены каким-либо осмысленным или релевантным образом. Это затрудняет их запоминание и применение в новых ситуациях.

5. Неполное понимание языка математики
Проблемы с математикой могут быть вызваны трудностями с языком. Дети также могут испытывать трудности с чтением, письмом и речью. В математике языковая слабость проявляется, когда дети сталкиваются со сложной лексикой, некоторые из которых они могут редко слышать за пределами математического класса. Эти учащиеся могут испытывать трудности с пониманием письменных или устных указаний или объяснений, а словесные задачи им особенно трудно понять.

6. Трудности с пониманием визуальных и пространственных аспектов и трудности с восприятием
Гораздо менее распространенная проблема — и, вероятно, самая серьезная — это неспособность эффективно визуализировать математические понятия. Студенты, которые борются с этим, могут испытывать трудности с оценкой относительного размера трех разных объектов (например, что выше: 1-дюймовая скрепка, 2-сантиметровый кусок веревки или 1,2-дюймовая травинка?).

У этой слабости есть очевидные недостатки, поскольку она требует, чтобы учащийся почти полностью полагался на механическое запоминание словесных или письменных описаний математических понятий, которые большинство людей считают само собой разумеющимися. Некоторые математические задачи также требуют, чтобы учащиеся сочетали мышление более высокого порядка с навыками восприятия (например, определение формы, которая получится при вращении сложной трехмерной фигуры).

> Попробуйте сами. Испытайте вызов визуализации.

---

Когда у ребенка проблемы с математикой, родители могут сделать следующие замечания.

Трудности с выводом
Учащийся с трудом выдает май

• быть не в состоянии вспомнить основные математические факты, процедуры, правила или формулы
• очень медленно извлекать факты или выполнять процедуры
• испытывают трудности с сохранением точности во время математической работы
• имеют трудности с почерком, которые замедляют письменную работу или затрудняют чтение позже
• с трудом запоминают ранее встречавшиеся шаблоны
• забыть, что он делает посреди математической задачи

Организационные трудности
Учащийся, борющийся с организацией, май

• испытывают трудности с последовательностью нескольких шагов
• запутаться в нескольких шагах или элементах проблемы
• недооценивать конечную цель и чрезмерно подчеркивать отдельные элементы проблемы
• не быть в состоянии идентифицировать существенные аспекты математической ситуации, особенно в текстовых задачах или других ситуациях решения задач, когда некоторая информация не имеет отношения к делу
• быть не в состоянии оценить уместность или разумность выработанных решений

Языковые трудности
Учащийся со слабыми языковыми способностями по математике май

• есть трудности со словарным запасом по математике
• быть сбитым с толку языком в текстовых задачах
• не знаю, когда включена нерелевантная информация или когда информация дается вне последовательности
• имеют проблемы с изучением или запоминанием абстрактных терминов
• с трудом понимают направление
• испытывают трудности с объяснением и общением по математике, включая задавание вопросов и ответы на них
• с трудом читают тексты, чтобы направлять собственное обучение
• испытывают трудности с запоминанием назначенных значений или определений в конкретных задачах

Проблемы с концентрацией внимания
Учащийся со слабым вниманием в математике, май

• отвлекаться или нервничать во время выполнения математических задач
• потерять место во время решения математической задачи
• кажутся умственно утомленными или чрезмерно утомленными при выполнении математических операций

Проблемы с визуальным пространством или упорядочением
Учащийся со слабыми зрительными, пространственными или последовательными аспектами математики 9 мая0007

• запутаться при изучении многошаговых процедур
• не могут упорядочить шаги, используемые для решения проблемы
• чувствует себя перегруженным, когда сталкивается с рабочим листом, полным математических упражнений
• не сможет правильно скопировать проблемы
• трудно читать стрелки на аналоговых часах
• испытывают трудности с интерпретацией геометрических конфигураций и управлением ими
• с трудом оценивают изменения объектов при их перемещении в пространстве

Трудности с несколькими задачами
Учащийся, пытающийся справиться с различными задачами по математике и/или объединить их, может

• трудно переключаться между несколькими требованиями в сложной математической задаче
• затрудняются сказать, когда задачи могут быть сгруппированы или объединены, а когда они должны быть разделены в многошаговой математической задаче
• Пытаться справиться со всеми требованиями сложной задачи, такой как проблема со словами, даже если он или она может знать факты и процедуры компонентов

ПРИМЕЧАНИЕ. Это не исчерпывающий список типов трудностей, которые могут возникнуть у учащегося с математикой, и его не следует использовать без учета всех сильных и слабых сторон ребенка. Если вас беспокоят трудности вашего ребенка с математикой или другие проблемы с обучением, прочтите дополнительные советы по оцениванию.

> Вернуться к началу

Вернитесь на главную страницу “Математика” или используйте навигацию выше, чтобы изучить другой раздел.

20 самых классных математических игр для 9-го класса0001

К четвертому классу дети овладели основами сложения, вычитания и умножения и готовы перейти к более сложным навыкам. Они начинают узнавать о делении, разложении на множители, дробях и десятичных дробях. В геометрии учащиеся начинают понимать понятия отрезков, углов и лучей. Чтобы помочь детям освоить этот широкий спектр навыков и получать от этого удовольствие, мы собрали самые классные математические игры для четвертого класса.

Выбирая игры для добавления в наш список, мы в первую очередь обращали внимание на академическое содержание и качество. Все игры в списке — это высококачественные игры, разработанные, чтобы помочь детям учиться. Конечно, дети тоже хотят развлекаться, поэтому мы сузили наш список, включив в него игры, которые также обладают высоким развлекательным фактором. Результат: двадцать действительно потрясающих игр, призванных помочь четвероклассникам изучать математику.

1. Сломанный калькулятор
Когда дети освоят базовые навыки сложения, вычитания и умножения, им нужно научиться использовать эти навыки более продвинутым способом. В этой игре детям предлагается найти альтернативные способы решения проблемы. Например, можете ли вы составить число 20, используя только клавиши 2, 3, +, x и = на калькуляторе?

2. Мосты
Это еще одна игра, в которой базовые навыки сложения выводятся на новый уровень. Дети должны соединить острова, строя мосты. На каждом острове есть число, обозначающее количество мостов, которые должны быть соединены с ним. Задача может показаться легкой, но на самом деле она довольно сложная.

3. Составь 15
Составление числа 15 путем сложения, вычитания, умножения или деления может показаться несложной задачей, но представьте, что у вас есть только три числа, с которыми можно это сделать. Это предпосылка этой игры, которая проверяет базовые математические навыки детей.

4. Поймай звезды: мультипликаторы
В этой веселой аркадной игре звезды падают с неба. Если звездочка кратна числу на ведерке, дети должны попытаться ее поймать. Поймать неправильный номер и потерять жизнь.

5. Math Lines: X Factor
Проверьте свои знания о множителях в этой увлекательной аркадной игре. В этой игре шарики путешествуют по дорожке. Цель состоит в том, чтобы шарики не попали в лунку. Чтобы остановить их, вы должны стрелять шарами, чтобы получить заданное число. Дети могут сосредоточиться на кратных от 12 до 72.

6. Бейсбол Batter’s Up
Три удара, и вы выбываете в этой веселой игре в бейсбол, которая помогает детям тренировать свои навыки умножения. Цель состоит в том, чтобы побить счет команды гостей. Дети делают это, решая задачи на умножение разного уровня сложности. Решить простую задачу? Получите сингл. Решить сложную задачу? Получите хоумран.

7. Пожиратели чисел
Эта игра похожа на популярную игру Пожиратели чисел , в которую дети играли в школе. Вы можете играть с задачами на сложение, вычитание, умножение или деление, а также с дробями. Во время игры старайтесь есть только те числа, которые относятся к данным инструкциям.

8. Дивизион Дерби
Отправляйтесь на скачки и предложите детям использовать свои навыки дивизиона во время многопользовательских скачек. Решайте задачи деления быстро и точно, чтобы выиграть гонку.

9. Drag Race Division
Еще одна игра, помогающая тренировать навыки разделения. Drag Race Division позволяет детям соревноваться друг с другом в гонке до финиша. Цель состоит в том, чтобы решить проблемы деления как можно быстрее. Однако важна и точность. Неправильно ответьте на задачу, и вы можете оказаться на дне жары.

10. Подразделение по сносу
Что может быть веселее, чем сносить вещи, решая проблемы с разделением?! В этой игре дети решают задачи на деление, чтобы помочь им взорвать танки. Игра позволяет детям устанавливать диапазон задач, с которыми они сталкиваются, что позволяет легко настраивать задачи для начинающих или для продвинутых учащихся.

11.  Героические муравьи
Сможете ли вы использовать свои знания об углах и траектории, чтобы доставить муравьев на новые земли? В этой игре, которая немного похожа на Angry Birds , дети запускают муравьев, чтобы посмотреть, как далеко они могут зайти. Это отличная игра, чтобы помочь им начать понимать углы.

12. Проект TRIG
В этой игре дети используют свои знания геометрии и углов во благо. Цель игры — доставить припасы в деревню, которая сейчас находится в осаде. Неправильно рассчитайте угол, и жители деревни не получат столь необходимые им припасы.

13. Мячи с числами
В этой игре детям предлагается расставить шарики по порядку от меньшего к большему. Однако некоторые из шаров содержат отрицательные числа, так что это не так просто, как может показаться.

14. Орбитальные целые числа
Включение целых чисел выводит задачи сложения на новый уровень. В этой игре дети соревнуются с другими игроками, решая задачи на сложение (включая положительные и отрицательные числа) быстро и точно.

15. Speedway. Добавление дробей
Еще один способ вывести задачи на сложение на новый уровень – включить дроби. Эта игра проверяет знание детьми дробей, заставляя их соревноваться в их сложении и вычитании.

16. Фракции Фредди
В этой игре детям нужно плыть по воде, чтобы собирать дроби. В начале каждого раунда детям даются некоторые рекомендации, например: «Собери дроби больше 2/6».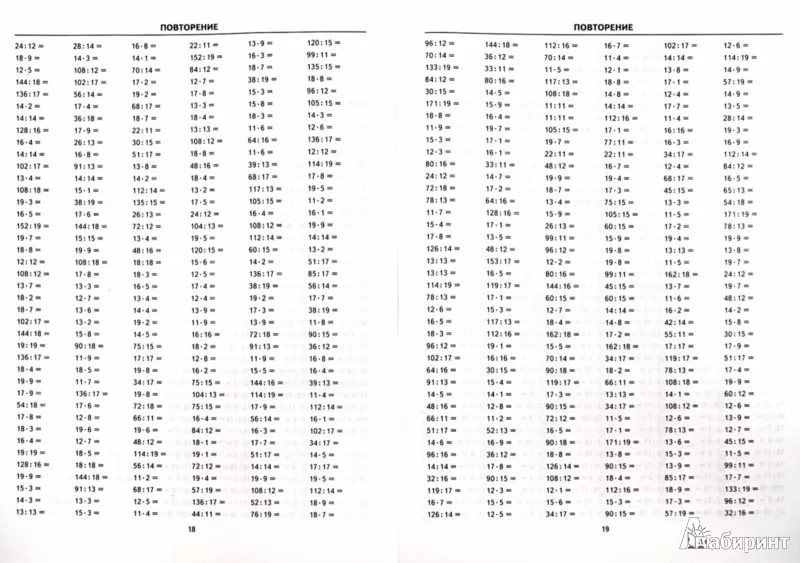

17. Знак дроби
Насколько хорошо вы знаете дроби? Проверьте свои знания о смешанных числах, дробях больше или равных единице и дробях меньше 1/2 в этой веселой игре.

18. Обезьяны дроби
В этой игре дети должны перетащить обезьян в нужное место на числовой прямой. Каждая обезьяна держит дробь. Сколько обезьян вы можете правильно разместить на линии?

19. Decention
Используйте свои знания о дробях, десятичных дробях и процентах, чтобы создавать команды пришельцев. В этой игре дети должны сопоставлять одинаковые числа, чтобы собрать команды из трех человек. Числа бывают разных форм.

20. Великая гонка пингвинов на каноэ
Что общего между каноэ, пингвинами и размножением? Все они являются частью Великой гонки пингвинов на каноэ. В этой игре дети учатся умножать двузначные числа, пытаясь выиграть гонку.

Если вам нравятся эти математические игры для четвертого класса, не забудьте просмотреть Math Game Time , чтобы найти больше бесплатных математических игр, а также бесплатные рабочие листы и видео, которые помогут развивать математические навыки в классах K-7.

Математика 4 класс Математика | GreatSchools.org

Чем хороша математика в четвертом классе, так это тем, что она идеально подходит для игр. Помогите своему ребенку измерить его скорость на скейтборде. Испеките два пирога и сделайте несколько воображаемых разрезов и кубиков, чтобы помочь вашему ребенку найти эквивалентные дроби или вычесть дроби с разными знаменателями (нижнее число). Развлечение математикой действительно поможет вашему ребенку в долгосрочной перспективе.

Вот 12 математических навыков, которые ваш ребенок должен освоить к концу четвертого класса:

• Решение многошаговых задач на сложение, вычитание, умножение и деление.
• Понимание того, что такое делители числа и как их найти.
• Значение разряда до 1 000 000.
• Умножение и деление двух двузначных чисел и умножение четырехзначного числа на однозначное.
• Решение задач на деление с остатком в ответе.
• Нахождение общих знаменателей (нижних чисел) двух и более дробей.
• Умножение дроби на целое число.
• Сложение и вычитание смешанных чисел с одинаковым знаменателем (например, 3 ¹ ⁄ ₂ + ¹ ⁄ ₂ ).
• Сравнение дробей с разными числителями (верхнее число) или знаменателями (нижнее число) или сравнение дробей с единичной дробью, например ¹ ⁄ ₂ .
• Сравнение двух десятичных долей с сотой.
• Понимание соотношения различных единиц измерения, таких как 12 дюймов = 1 фут.
• Изучение свойств различных фигур, в том числе измерение их углов.

4 операции

Четвертоклассники достаточно опытны, чтобы решать многошаговые текстовые задачи, используя любую из четырех операций — сложение, вычитание, умножение и деление — с уравнениями.

Например: у Кейли 272 бусины. Она покупает еще 38 бусин. Из 85 бусин она сделает браслеты, а из остальных — ожерелья. Ей нужно по 9 бусин на каждое ожерелье. Сколько ожерелий может сделать Кейли?

272 + 38 = 310. 310 – 85 = 225. 225 ÷ 9= 25 ожерелий

Реклама

Ваш ребенок научится находить пары множителей для целых чисел до 100. Это два числа, которые при умножении дают исходное целое число.

Например: 88 имеет 4 пары множителей: 2 x 44; 4 х 22; 8 х 11; и 88 x 1

Один на миллион

Четвертоклассники учатся читать, писать и понимать разрядное значение до 1 000 000. Начиная с единиц, каждое место слева в 10 раз больше.

Например: 987 654 = 900 000 + 80 000 + 7 000 + 600 + 50 + 4.

С таким пониманием разрядности ваш ребенок начнет работать с большими числами, включая сложение и вычитание целых чисел до 1 000 000, умножение два двузначных числа и умножение четырехзначного числа на однозначное число.

Например, :

 
Четвероклассники также учатся делить четырехзначное число на однозначное, но с изюминкой. В этом году они научатся делить с остатком, когда делимое (делимое число) нельзя разделить на равные части.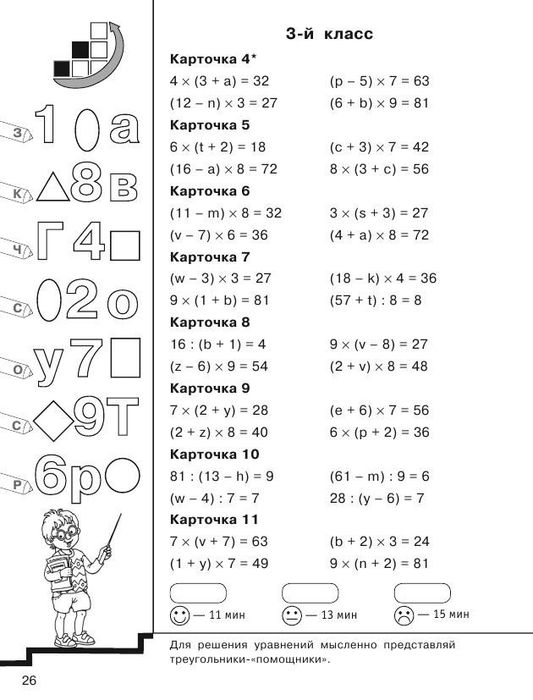

Например: 9 375 ÷ 7 = 1 339 остаток 2 или 1 339 R2.

Вычисление дробей

Четвертоклассники лучше понимают дроби. Они складывают и вычитают дроби с одинаковым знаменателем (нижнее число).

Например:

Они также складывают и вычитают смешанные числа с одинаковым знаменателем.

Например: 5 ¹ ⁄ ₃ + 8 ¹ ⁄ ₃ = 13 ² ⁄ ₃

10 ⁴ ⁄ ₅ – 5 ² ⁄ ₅ = 5 ² ⁄ ₅ = 5 ² ⁄ ₅ = 5 ² . Это помогает обучать учащихся эквивалентным дробям — дробям, имеющим одинаковое значение, — даже если их числители (верхние числа) и знаменатели (нижние числа) различаются.

Например: ¹ ⁄ ₂ равно ⁴ ⁄ ₈ .

 
Учащиеся также учатся умножать дроби на целые числа и понимают, почему произведение (ответ) меньше целого числа.

Например: 7 x ¹ ⁄ ₈ = ⁷ ⁄ ₈ . Его также можно записать как ⁷ ⁄ ₁ x ¹ ⁄ ₈ .

Ваш ребенок будет решать текстовые задачи, требующие сложения, вычитания или умножения целых чисел на дроби.

Например: Райан делает рюкзаки. На каждую из них он использует ¾ ярда ткани. Сколько всего ткани в ярдах израсходовал Райан на 6 рюкзаков? 6 x ³ ⁄ ₄ = ⁶ ⁄ ₁ x ³ ⁄ ₄ = ¹⁸ ⁄ ₄ = 4 ¹ ⁄ ₂ yards.

Четвертоклассники также узнают, как преобразовывать дроби со знаменателем 10 или 100 в десятичные и отображать их на числовой прямой.

Например: ⁹¹ ⁄ ₁₀₀ = 0,91

 

По любым меркам

Как долго эта игуана находится в вашей ванне? Один двор? Три фута? 36 дюймов? Да, да и да: это все вышеперечисленное.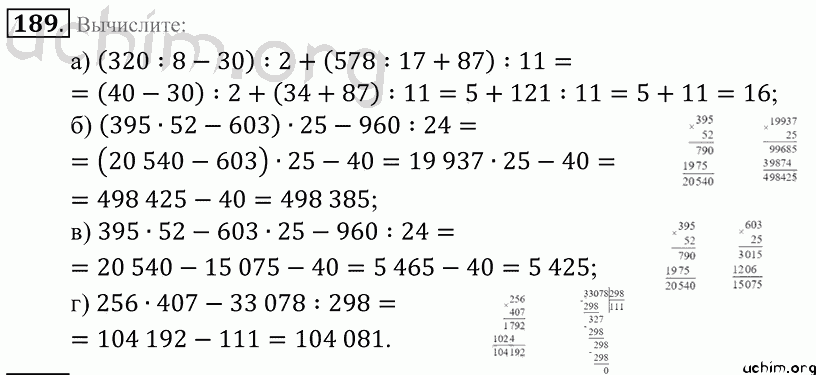 Четвертоклассники изучают взаимосвязь между различными единицами измерения в каждой системе. В США 12 дюймов равны одному футу, а три фута равны одному ярду. В метрической системе, основанной на 10, требуется, чтобы 10 миллиметров равнялись одному сантиметру, а 100 сантиметров равнялись одному метру.

В четвертом классе ваш ребенок будет использовать сложение, вычитание, умножение и деление для решения мировых задач, связанных со временем, расстоянием, объемом, массой и деньгами. Вопросы часто включают в себя дроби и десятичные числа и требуют, чтобы учащиеся проиллюстрировали проблему на диаграмме или числовой прямой.

Например: Сара едет со скоростью 60 миль в час в Сент-Луис, который находится в 100 милях от нее. Сколько минут потребуется, чтобы добраться туда? Сколько часов?

Площадь и периметр

Четвертоклассники учатся решать реальные задачи на определение периметра или площади фигуры, даже если длина одной стороны неизвестна. Они будут применять сложение, вычитание, умножение и деление к формулам площади и периметра.

Например: Площадь = длина x ширина
Периметр = сумма длин всех сторон.

Ваш четвероклассник изучит еще несколько свойств, используемых для классификации фигур, например наличие у фигуры перпендикулярных или параллельных линий. Дети также работают с углами в фигурах. Вы можете ожидать, что ваш ребенок будет использовать транспортир для измерения углов, определять прямой угол, когда он его видит, и знать, что сумма углов в треугольнике всегда равна 180 градусам, а в прямоугольнике — всегда 360 градусов.

Правда, здесь есть более продвинутые концепции. Если домашнее задание вашего ребенка по математике кажется вам немного сложнее, чем то, что вы помните, наберитесь мужества. Сохраняйте позитивное отношение к математике и постарайтесь весело провести время, помогая ребенку с математикой в ​​этом году.

Посмотрите, как выглядят четвероклассники, работающие на уровне класса с дробями, в наших видеороликах Milestones:

• Сравнение дробей

• Дроби в текстовых задачах

Math Worksheets: Free Printable Math Worksheet

Рабочие листы Brighterly предоставляют образовательные онлайн-ресурсы по математике для детей и их родителей.

Детский класс

• Дошкольный
• Детский сад
• 1 класс
• 2 класс
• 3 класс
• 4 класс
• 5 класс

Электронная почта родителей

Успешно отправлено

Математика — сложный предмет, который детям часто трудно понять. Родители должны искать способы помочь своим детям изучить предмет. Таким образом, наиболее подходящим решением для обеспечения того, чтобы ваши дети регулярно занимались математикой и улучшали свои математические навыки, является использование рабочих листов.

Рабочие листы по математике можно классифицировать по классам, уровням сложности и предметам, и вы всегда можете найти подходящие для детей всех возрастов. Студенты учатся подходить к решению задач шаг за шагом, признавать свои ошибки и улучшать свои математические способности с помощью рабочих листов.

Полностью бесплатные рабочие листы по математике от Brighterly’s Tutors

Бесплатные математические листы Brighterly охватывают математические понятия, такие как умножение, сложение и т. д., и помогают улучшить математические навыки детей. Родители и учителя могут использовать рабочие листы по математике для обучения детей и оценки их знаний. Бесплатные рабочие листы по математике от Brightelry для печати также помогают детям практиковать математику после школы, тем самым повышая их мастерство в предмете.

Бесплатные рабочие листы по математике структурированы в соответствии с способностями детей — ученики, которые быстро схватывают вещи, получают более сложные материалы, а другие — более простые учебные листы. Цель состоит в том, чтобы каждый учащийся получил пользу от использования этого типа учебного материала.

Преимущества использования рабочих листов по математике

Рабочие листы по математике в немалой степени влияют на развитие детей. Ниже приведены некоторые преимущества для детей, которые учатся с помощью рабочих листов:

Улучшение логического мышления

Вы можете улучшить способности детей решать задачи, побуждая их использовать арифметические рабочие листы. Рабочие листы по математике развивают рассуждения и логическое мышление детей, помогая им разрабатывать инновационные решения задач. Дети улучшают свои способности решать проблемы и повышают самооценку, работая с математическими таблицами.

Совместное обучение

Имитируя интерактивные игры, занятия и симуляции, рабочие листы по математике помогают детям учиться более эффективно. Вы можете использовать онлайн-таблицы по математике вместо бумажных. Позвольте вашему ребенку работать с рабочими листами в вашем физическом присутствии, чтобы удерживать внимание детей на предмете и не дать им потерять интерес к учебе. Когда класс увлекательный и интерактивный, дети более эффективно усваивают основные понятия, что позволяет им овладеть более сложной математикой.

Улучшение навыков управления временем

Плохое управление временем является распространенной причиной низкой успеваемости по математике. Сложность предмета и неспособность детей управлять временем часто лишают их возможности выполнить домашнюю работу по математике или сдать экзамены. Таким образом, страдают их оценки. Одним из решений являются математические рабочие листы.

Регулярное использование рабочих листов по математике может помочь учащимся научиться решать арифметические задачи быстрее и эффективнее. Кроме того, дети обретают уверенность в себе при решении математических задач, развивая при этом терпение, чтобы решать математические задачи.

Более глубокое понимание понятий

Учащиеся понимают арифметические понятия, работая с рабочими листами, которые разбивают каждую идею. Эти рабочие листы гарантируют, что дети понимают каждую тему и используют их в реальных сценариях. Это возможно, потому что в рабочих листах по математике используются самые простые броские и красочные примеры, которые вызывают интерес у детей.

Изучая эти листы, дети начинают решать фундаментальные математические задачи. Через некоторое время переходят к решению более сложных. Типичным результатом использования этой стратегии являются дети, которые все меньше и меньше нуждаются в вашем участии в изучении математики.

Лучшее понимание учебных материалов

Изучение основных арифметических понятий с помощью рабочих листов — отличный способ попрактиковаться и освежить навыки алгебры и тригонометрии ваших детей. Вы также можете использовать забавные математические рабочие листы, чтобы улучшить математические навыки детей за счет постоянной практики и повторения. Учащиеся, которые используют математические рабочие листы для обучения, с большей вероятностью сохранят представленные идеи и формулы. Кроме того, дети могут практиковаться в решении математических задач с комфортной скоростью и без беспокойства.

Повышенная концентрация

Дизайн многих математических листов для детей помогает детям изучать математику разных уровней сложности. Увлекательный характер рабочих листов гарантирует, что дети получат удовольствие от изучения математики. Следовательно, они полностью концентрируются, и по мере того, как дети лучше концентрируются, их математические способности улучшаются.

Рабочие листы по математике могут помочь детям сконцентрироваться на математических принципах, но ваше присутствие придаст им уверенности в том, что они смогут продолжить работу, когда задачи станут слишком сложными. Таким образом, родители или воспитатели должны направлять детей в процессе обучения и следить за тем, чтобы дети решали каждый вопрос в рабочем листе. Ваш ребенок не многого добьется, если сможет просто пропустить любое задание, которое не может решить.

Почему рабочие листы по математике важны для учащихся?

Рабочие листы по математике имеют решающее значение для роста и развития детей. Они облегчают понимание математических идей и помогают измерить, насколько быстро ребенок усваивает эти идеи.

В общем, обучение детей арифметике требует времени. Но с помощью математического листа вы можете научить своего ребенка решать математические задачи быстрее. С помощью этих рабочих листов вы воспитаете желание изучать математику у своих детей без присмотра, что сократит время, которое вы тратите на обучение детей.

Школы следуют установленной учебной программе, которую все учащиеся должны изучать и изучать. С другой стороны, дети по-разному усваивают понятия — одни не такие четкие, как другие, что может стать проблемой для учителя или родителей. К счастью, такие проблемы не относятся к обучению с рабочими листами, поскольку они позволяют учащимся решать задачи без ограничений по времени. Рабочие листы также позволяют детям потерпеть неудачу и попробовать снова, не опасаясь быть осмеянными или приобрести чувство неадекватности.

Рабочие листы по математике для увлекательного изучения математики

Математика — скучный предмет для многих детей; однако его сложность иногда объясняется структурой обучения, принятой в большинстве школ. В Brighterly учебный процесс и структура лекций ориентированы на ребенка. Дети изучают математику, используя бесплатные математические таблицы, занимательные задания и игры, которые помогают развить интерес к учебе.

В Brighterly обучение является тщательным, увлекательным и интерактивным. Пока ваш ребенок развлекается, он осваивает сложные уравнения и понятия. Например, ваш ребенок может освоить счет с помощью иллюстраций реальных объектов, которые он видит на рабочих листах. Таким образом, дети могут запомнить то, что они изучают и практикуют.

Как решать сложные математические задачи

Родитель одной из наших учениц написал сегодня о том, что его дочь иногда недовольна сложностью некоторых задач на наших курсах. Она отлично работает на наших курсах и легко входит в число самых лучших учеников в классе, который она брала со мной, и все же иногда она сталкивается с проблемами, которые не может решить.

Кроме того, у нее есть доступ к отличному учителю математики в ее школе, который иногда тоже не может помочь ей решить эти проблемы. (Это не мелочь для него — у меня есть ученики, которые тоже приносят мне задачи, которые я не могу решить!) Ее вопрос: «Почему это должно быть так сложно?»

Дело в том, что нужно делать трудные вещи

Мы задаем трудные вопросы, потому что многие жизненные проблемы, которые стоит решить, сложны. Если бы они были легкими, кто-то другой решил бы их до того, как вы до них доберетесь. Вот почему на занятиях в ведущих университетах есть тесты, по которым почти никто не набирает 70%, не говоря уже о том, чтобы получить высший балл. Они обучают будущих исследователей, и весь смысл исследования заключается в том, чтобы найти и ответить на вопросы, которые никогда не были решены. Вы не можете научиться этому, не сталкиваясь с проблемами, которые не можете решить. Если вы последовательно решаете каждую задачу в классе правильно, вы не должны слишком радоваться — это означает, что вы учитесь недостаточно эффективно. Вам нужно найти класс посложнее.

Проблема недостаточной сложности выходит далеко за рамки того, что вы не изучаете математику (или что-то еще) так быстро, как только можете. Я думаю, что многое из того, что мы делаем в AoPS, готовит учащихся к задачам, выходящим далеко за рамки математики. Те же самые стратегии, которые используются при решении очень сложных математических задач, могут быть использованы для решения очень многих задач. Я считаю, что мы учим студентов, как думать, как решать сложные проблемы, и что математика оказывается лучшим способом сделать это для многих людей.

Первый шаг в решении сложных проблем — принять и понять их важность. Не уклоняйтесь от них. Они научат вас гораздо большему, чем рабочий лист с простыми задачами. Блестящий «Ага!» мгновений почти всегда рождаются в умах, взращенных долгими периодами разочарований. Но без этого разочарования эти блестящие идеи никогда не возникнут.

Стратегии решения сложных математических задач и не только

Вот несколько стратегий решения сложных задач и разочарования, которое они вызывают:

Сделай что-нибудь . Да, проблема сложная. Да вы понятия не имеете, что делать, чтобы решить эту проблему. В какой-то момент вы должны перестать пялиться и начать пробовать что-то новое. Большая часть не будет работать. Примите тот факт, что многие ваши усилия будут потрачены впустую. Но есть шанс, что один из ваших ударов во что-то попадет, и даже если нет, усилия могут подготовить ваш разум к победной идее, когда придет время.

Мы начали разрабатывать учебную программу для начальной школы за несколько месяцев до того, как у нас появилась идея создать Академию Зверей. Наш ведущий разработчик учебной программы написал 100–200 страниц контента, придумав множество различных стилей и подходов, которые мы могли бы использовать. Ни одна из этих страниц не войдет в окончательную работу, но они породили множество идей для контента, который мы будем использовать. Возможно, что еще более важно, это подготовило нас к тому, что, когда мы, наконец, пришли к идее Академии Зверей, мы были достаточно уверены, чтобы следовать ей.

Упростите задачу . Попробуйте меньшие числа и особые случаи. Снять ограничения. Или добавить ограничения. Настройте свои цели немного ниже, а затем поднимите их, как только вы решите более простую проблему.

Подумай об успехах . Вы решили много проблем. Некоторые из них были даже трудными задачами! Как ты сделал это? Начните с проблем, похожих на ту, с которой вы столкнулись, но подумайте и о других, которые не имеют ничего общего с вашей текущей проблемой. Подумайте о стратегиях, которые вы использовали для решения этих проблем, и вы можете просто наткнуться на решение.

Несколько месяцев назад я играл с некоторыми задачами Project Euler и наткнулся на задачу, которая (в конце концов) сводилась к генерации целочисленных решений для c ² = a ² + b ² + ab эффективным образом. Теория чисел не моя сильная сторона, но мой путь к решению заключался в том, чтобы сначала вспомнить метод построения пифагорейских троек. Затем я подумал о том, как сгенерировать этот метод, и путь к решению стал ясен. (Я предполагаю, что некоторые из наших математически продвинутых читателей настолько усвоили процесс решения этого типа диофантова уравнения, что вам не нужно путешествовать с Пифагором, чтобы добраться до него!)

Сосредоточьтесь на том, что вы еще не использовали . Многие задачи (особенно задачи геометрии) имеют много движущихся частей. Оглянитесь на проблему и открытия, которые вы сделали до сих пор, и спросите себя: «Что я еще не использовал конструктивным образом?» Ответ на этот вопрос часто является ключом к вашему следующему шагу.

Работа в обратном направлении . Это особенно полезно при поиске доказательств. Вместо того, чтобы начинать с того, что вы знаете, и двигаться к тому, чего вы хотите, начните с того, чего вы хотите, и спросите себя, что вам нужно для этого.

Просить о помощи . Это тяжело для многих отличников. Вы так привыкли все делать правильно, быть тем, о ком все спрашивают, что вам трудно признать, что вам нужна помощь. Когда я впервые попал в программу математической олимпиады (MOP) на втором курсе, я был выше головы. Я мало что понимал из того, что происходило в классе. Однажды я обратился за помощью к профессору — очень трудно было набраться смелости сделать это. Я ничего не понял из того, что он сказал мне в течение 15 минут, когда он работал со мной наедине. Я просто не мог признать это и просить о дополнительной помощи, поэтому перестал просить. Я мог бы многому, гораздо большему научиться, если бы был более готов признаться людям, которых я просто не понимаю. (Отчасти поэтому в наших классах теперь есть функция, позволяющая учащимся задавать вопросы анонимно.) Преодолей это. Вы застрянете. Вам понадобится помощь. И если вы попросите об этом, вы добьетесь гораздо большего, чем если бы вы этого не сделали.

Начать рано . Это не очень помогает в тестах на время, но в случае более сложных заданий, которые являются частью учебы в колледже и жизни, это необходимо. Не ждите до последней минуты — сложные задачи достаточно сложны и без необходимости сталкиваться с нехваткой времени. Более того, для полного понимания сложных идей требуется много времени. Люди, которых вы знаете, которые кажутся чертовски умными и которые, кажется, придумывают идеи намного быстрее, чем вы могли бы, часто являются людьми, которые просто думали о проблемах гораздо дольше, чем вы. Я использовал эту стратегию в колледже с большим успехом — в первые несколько недель каждого семестра я продвигался вперед во всех своих классах. Поэтому к концу семестра я обдумывал ключевые идеи гораздо дольше, чем большинство моих одноклассников, что значительно облегчало экзамены и тому подобное в конце курса.

Сделай перерыв . Отвлекитесь на некоторое время от проблемы. Когда вы вернетесь к этому, вы можете обнаружить, что не полностью избавились от проблемы — фоновые процессы вашего мозга продолжают отключаться, и вы окажетесь намного ближе к решению. Конечно, намного легче сделать перерыв, если вы начнете рано.

Начать сначала . Отложите всю предыдущую работу, возьмите свежий лист бумаги и попробуйте начать с нуля. Ваша другая работа все еще будет там, если вы захотите извлечь из нее позже, и, возможно, она подготовила вас к тому, чтобы извлечь выгоду из идей, которые вы сделаете во время второго раунда.

Сдаться . Всех не решишь. В какой-то момент пришло время сократить свои потери и двигаться дальше. Это особенно верно, когда вы тренируетесь и пытаетесь узнать что-то новое. Одна-единственная трудная задача обычно научит вас большему за первый или два часа, чем за следующие шесть, а задач, на которых можно учиться, гораздо больше. Итак, установите себе ограничение по времени, и если вы все еще безнадежно застряли в его конце, то прочитайте решения и двигайтесь дальше.

Будьте самосозерцательны . Если вы сдаетесь и читаете решение, то читайте его активно, а не пассивно. Читая его, подумайте, какие подсказки в задаче могли привести вас к этому решению. Подумайте, что вы сделали не так в своем расследовании. Если в решении есть математические факты, которые вы не понимаете, идите исследовать. Я был совершенно сбит с толку, когда впервые увидел кучу материала о «модах» в олимпиадном решении — у нас тогда не было интернета, поэтому я не мог легко узнать, насколько проста модульная арифметика! Теперь у вас есть интернет, так что у вас нет оправдания. Если вы решили проблему, не хлопайте себя по спине. Подумайте о ключевых шагах, которые вы сделали, и о том, каковы были признаки того, что вы должны их попробовать. Подумайте о тупиках, которые вы исследовали на пути к решению, и о том, как вы могли их избежать. Эти уроки пригодятся вам позже.

Вернись . Если вы сдались и посмотрели на решения, то вернитесь и повторите попытку через несколько недель. Если у вас нет никаких решений, на которые можно было бы обратить внимание, сохраняйте проблему актуальной.