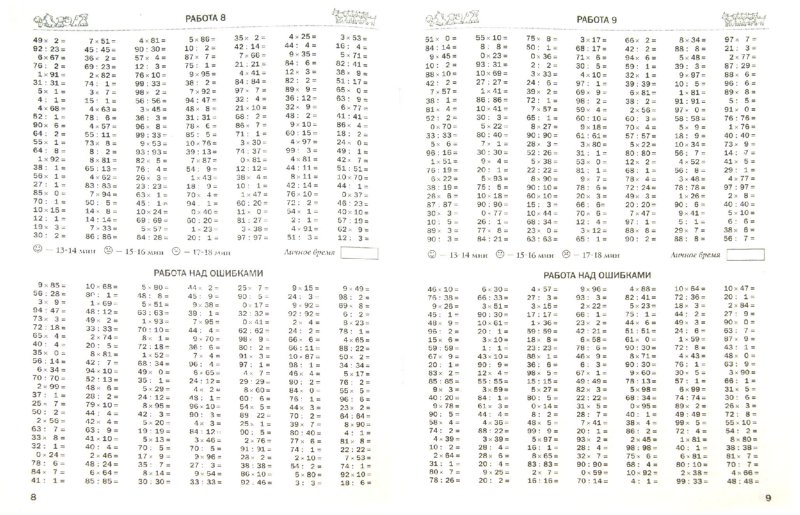
Примеры по математике 3 класс на умножение и деление решать двузначных: Математика. 3 класс. Умножение и деление двузначных чисел 📕
Математика: уроки, тесты, задания.
- Предметы
-
-
Пространственные и временные представления
-
Пары и группы предметов
-
Нумерация.
 Сколько? От 0 до 10
Сколько? От 0 до 10
-
Нумерация. Сколько? От 11 до 20
-
-
-
Точка, прямая линия, кривая и отрезок
-
Знаки сравнения, знаки действий и знак равенства
-
Сравнение чисел от 1 до 5
-
Примеры на сумму
-
Примеры на разность
-
Примеры на сложение и вычитание от 1 до 5
-
Сравнение чисел от 0 до 10 и выражений
-
Текстовые задачи (сумма)
-
Текстовые задачи (разность)
-
Задачи на смекалку (от 1 до 5)
-
Задачи на смекалку (от 0 до 10)
-
-
-
Счёт десятками
-
Сравнения чисел от 11 до 20
-
Таблица сложения.
 Числа от 1 до 9
Числа от 1 до 9
-
Задачи на смекалку (от 11 до 20)
-
-
-
Сложение и вычитание чисел в пределах 20 с переходом через десяток
-
Таблица сложения. Числа от 0 до 18
-
Ломаная линия
-
-
-
Числа от 20 до 100.
 Нумерация. Числа и цифры
Нумерация. Числа и цифры
-
Счёт десятками
-
Круглые числа
-
Сложение и вычитание чисел в пределах 100 без перехода через десяток
-
Сложение и вычитание чисел в пределах 100 с переходом через десяток
-
Сложение и вычитание чисел в пределах 100
-
Решение задач в два действия
-
Метр
-
-
-
Скобки.
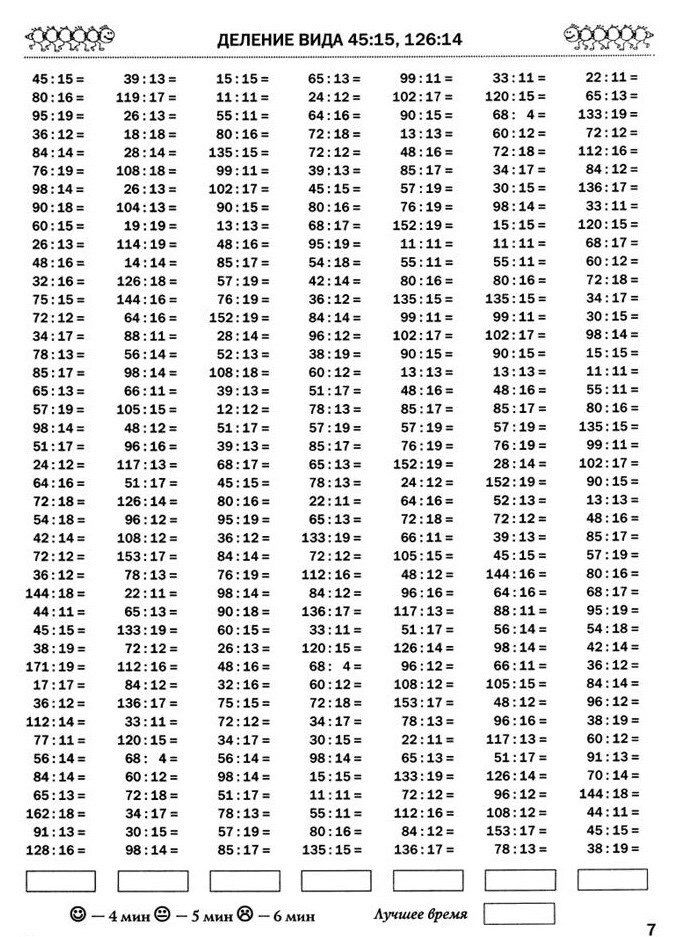 Сочетательный закон сложения
Сочетательный закон сложения
-
Выражения без скобок
-
Выражения со скобками
-
Луч
-
Угол
-
Прямой, тупой и острые углы
-
Квадрат, круг, прямоугольник, треугольник
-
Периметр
-
-
-
Понятие умножения
-
Деление
-
Чётные и нечётные числа
-
Переместительный закон умножения
-
Таблица умножения на 2
-
Таблица умножения на 3
-
-
-
Таблица умножения на 4
-
Таблица умножения на 5
-
Таблица умножения на 6
-
Таблица умножения на 7
-
Таблица умножения на 8
-
Таблица умножения на 9
-
Умножение и деление на 0, 1, 10.
 Деление числа на само себя
Деление числа на само себя
-
Увеличить на… Увеличить в… Уменьшить на… Уменьшить в…
-
Больше на… больше в… меньше на… меньше в…
-
Нахождение доли числа
-
Нахождение числа по доле
-
Сравнение долей
-
Уравнения (сумма)
-
Уравнения (разность)
-
Нахождение неизвестного множителя
-
Нахождение неизвестного делителя
-
Нахождение неизвестного делимого
-
Умножение суммы на число
-
Деление суммы на число
-
Деление круглого числа на круглое число
-
Умножение и деление круглого числа на однозначное число
-
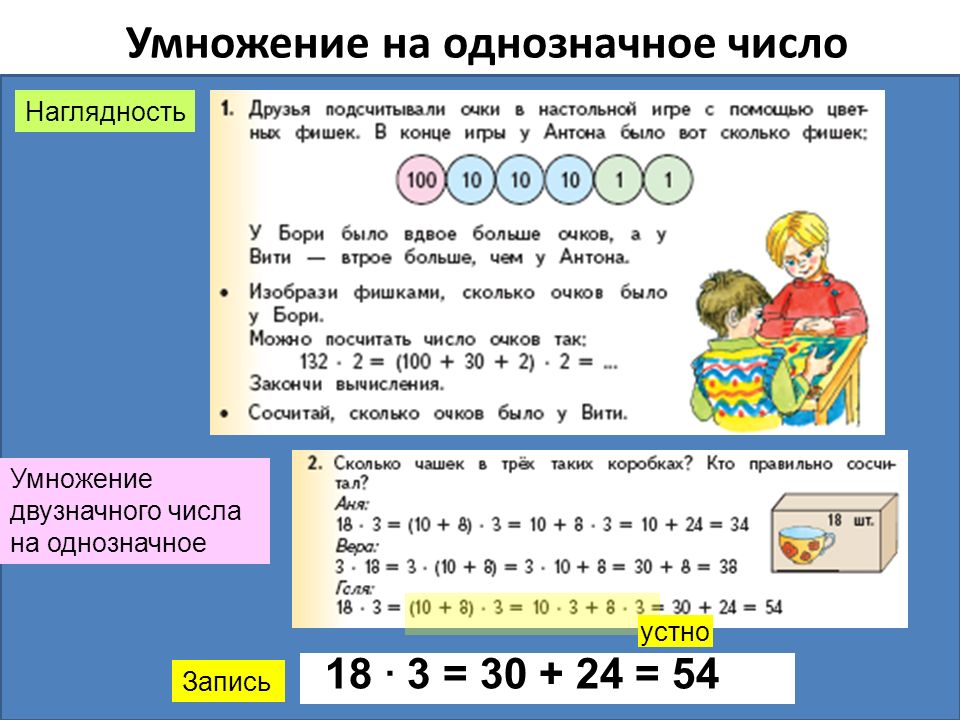
Умножение двузначного числа на однозначное число
-
Деление двузначного числа на однозначное
-
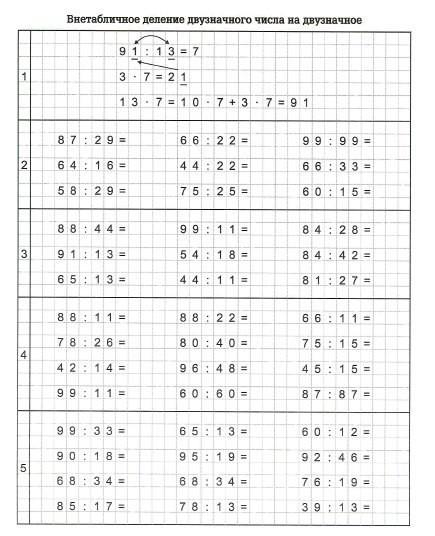
Деление двузначного числа на двузначное
-
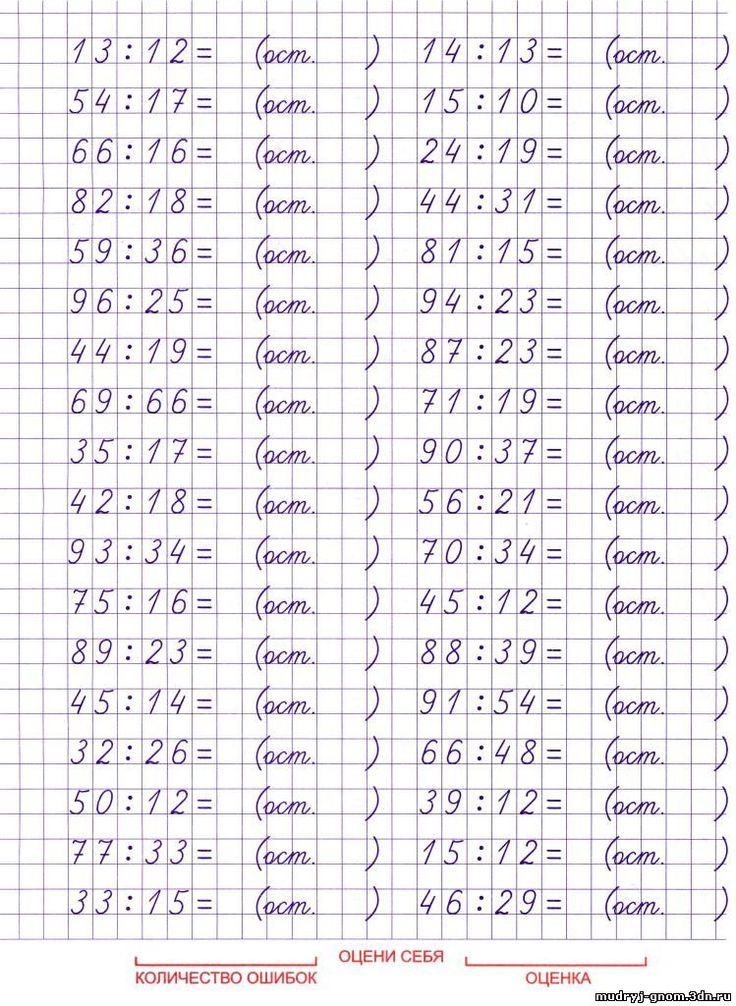
Деление с остатком
-
Треугольники
-
Час.
 Минута. Сутки
Минута. Сутки
-
-
-
Нумерация
-
Сложение и вычитание трёхзначных чисел
-
Умножение на однозначное число. Распределительный закон умножения относительно сложения
-
Умножение и деление трёхзначного числа на однозначное число
-
Километр
-
Килограмм
-
Связь между величинами
-
-
-
Миллиметр
-
Площадь фигуры.
 Площадь прямоугольника
Площадь прямоугольника
-
Единицы измерения площади
-
-
-
Умножение круглого числа на однозначное число
-
Деление круглого многозначного числа на однозначное
-
Умножение и деление чисел на 10, 100 и 1000
-
Умножение на круглое число
-
Умножение и деление круглых чисел
-
Умножение круглых чисел
-
Деление многозначного числа на однозначное число
-
Умножение на двузначное число
-
Деление трёхзначного числа на двузначное число
-
Деление многозначного числа на двузначное число
-
Умножение на трёхзначное число
-
Деление на трёхзначное число
-
Деление многозначного числа на 10, 100, 1000 с остатком
-
Деление круглого многозначного числа на круглое число
-
Деление многозначного числа с остатком на однозначное число
-
Деление трёхзначного числа на двузначное с остатком
-
Деление на двузначное число с остатком
-
Деление на трёхзначное число с остатком
-
Геометрические понятия: окружность и круг
-
-
Методические рекомендации по использованию в педагогической деятельности ЯКласс
-
-
Законы арифметических действий.
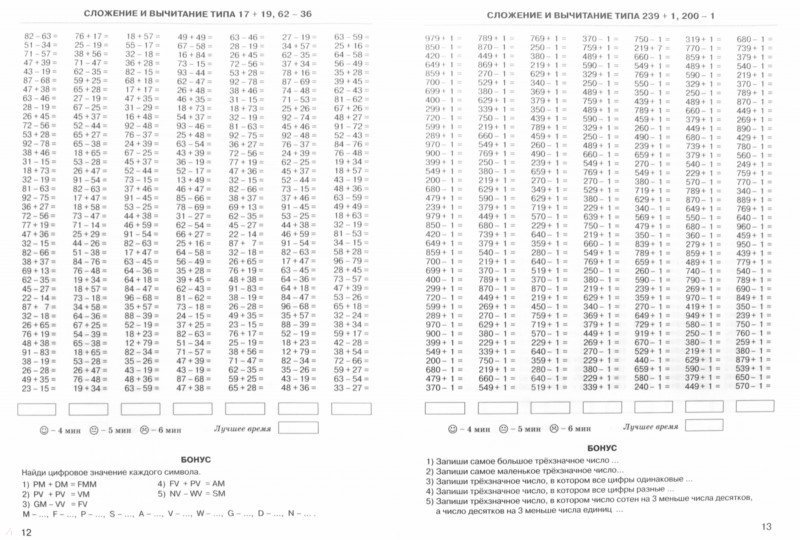 Вычисления с многозначными числами
Вычисления с многозначными числами
-
Координатный луч
-
Отношение “больше”, “меньше”, “равно” между числами на координатном луче
-
Сравнение натуральных чисел друг с другом
-
Округление чисел.
 Прикидка и оценка результатов вычислений
Прикидка и оценка результатов вычислений
-
Степень с натуральными показателями
-
Деление с остатком
-
Делители и кратные числа
-
Признаки делимости на 2, 3, 5, 9, 10
-
Простые и составные числа.
 Разложение натурального числа на простые множители
Разложение натурального числа на простые множители
-
Наибольший общий делитель и наименьшее общее кратное
-
Решение текстовых задач арифметическим способом
-
-
-
Числовые и буквенные выражения
-
Формулы.
 Уравнения. Упрощение выражений
Уравнения. Упрощение выражений
-
Математический язык и математическая модель
-
-
-
Понятие дроби
-
Правильные и неправильные дроби. Смешанные числа
-
Основное свойство дроби
-
Сравнение дробей
-
Сложение, вычитание, умножение и деление обыкновенных дробей и смешанных чисел
-
Среднее арифмитическое нескольких чисел.
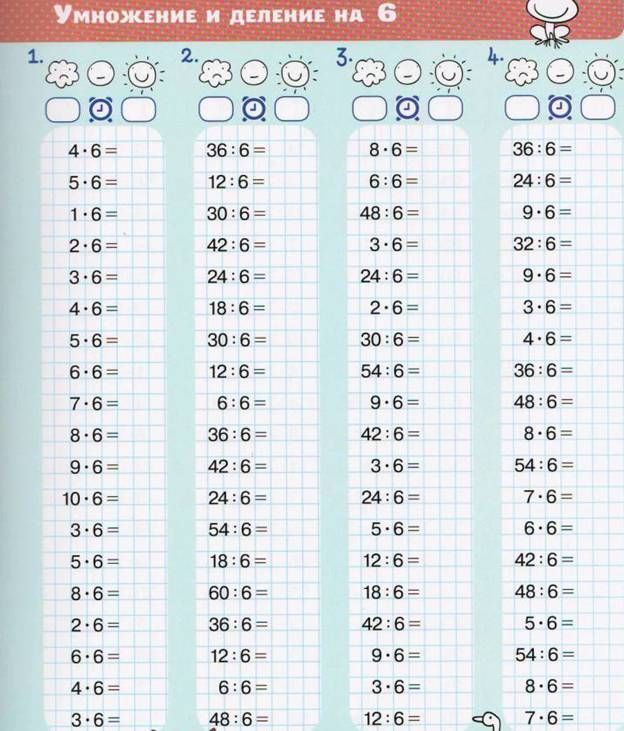 Задачи.
Задачи.
-
-
-
Начальные геометрические понятия: прямая, отрезок, луч, ломанная, прямоугольник
-
Угол. Измерение углов
-
Биссектриса угла. Свойство биссектрисы угла
-
Свойство углов треугольника.
 Размеры объектов окружающего мира (масштаб)
Размеры объектов окружающего мира (масштаб)
-
Расстояние между двумя точками. Масштаб
-
Параллельность прямых
-
Перпендикулярность прямых. Расстояние от точки до прямой. Серединный перпендикуляр
-
Треугольник.
 Площадь треугольника
Площадь треугольника
-
Прямоугольный параллелепипед
-
Развёртка прямоугольного параллелепипеда
-
Объём прямоугольного параллелепипеда
-
-
-
Угол.
 Измерение углов
Измерение углов
-
Биссектриса угла. Свойство биссектрисы угла
-
Параллельные и перпендикулярные прямые
-
Площадь прямоугольного треугольника и некоторых видов многоугольников.
-
Переход от одной единицы измерения площади к другой.
-
Прямоугольный параллелепипед
-
Объём прямоугольного параллелепипеда
-
-
-
Понятие десятичной дроби. Представление десятичной дроби в виде обыкновенной дроби и наоборот
-
Сравнение десятичных дробей
-
Рациональные числа.
 Периодические дроби
Периодические дроби
-
Сложение и вычитание десятичных дробей
-
Умножение десятичных дробей
-
Среднее арифметическое и деление десятичных дробей на натуральное число
-
Деление десятичной дроби на десятичную дробь
-
-
-
Положительные и отрицательные числа.
 Координатная прямая
Координатная прямая
-
Противоположные числа. Модуль числа
-
Сравнение чисел
-
Сложение рациональных чисел с помощью координатной прямой
-
Алгебраическая сумма и её свойства
-
Сумма рациональных чисел с одинаковыми знаками
-
Сумма рациональных чисел с разными знаками
-
Умножение и деление рациональных чисел
-
-
-
Координаты.
 Координатная плоскость. Координаты точки
Координатная плоскость. Координаты точки
-
-
-
Начальные понятия и факты курса геометрии
-
Окружность и круг. Число Пи. Длина окружности. Площадь круга
-
Осевая и центральная симметрия
-
-
-
Проценты.
 Задачи на проценты: нахождение процента от величины и величины по её проценту
Задачи на проценты: нахождение процента от величины и величины по её проценту
-
Отношения
-
Пропорция. Основное свойство пропорции
-
Решение задач с помощью пропорций
-
Прямая и обратная пропорциональность
-
Разные задачи на пропорции
-
Деление в столбик 3 класс.
 Примеры для тренировки и объяснения. Блог Кувырком
Примеры для тренировки и объяснения. Блог КувыркомТаблица умножения – это не самое трудное, с чем сталкивается младший школьник. Гораздо сложнее освоить деление в столбик. Многие дети без помощи родителей не могут понять этот процесс. Давайте разберёмся, как легко и без лишней нервотрёпки обучить ребёнка делить в столбик.
Что нужно знать, чтобы научиться делить в столбик?
Деление столбиком школьники обычно начинают изучать на уроках математики в третьем классе. Чтобы понять процесс деления и начать использовать его на практике, школьник должен уметь следующее:
- без труда решать примеры на сложение и вычитание;
- знать наизусть таблицу умножения;
- знать разряды чисел;
- уметь быстро считать в уме.
Если в этих знаниях у ребёнка есть пробел, ему трудно будет научиться делить столбиком. Поэтому перед началом обучения нужно обязательно повторить пройденный ранее материал, особенно таблицу умножения.
Учимся считать и считать вместе с КУВЫРКОМ
С чего начать учить ребёнка делению?
Прежде всего, объясните школьнику суть этого математического действия. Он должен понять, что деление – это процедура обратная умножению. Когда школьник усвоит, что эти два действия взаимосвязаны друг с другом, научиться делить будет несложно.
Он должен понять, что деление – это процедура обратная умножению. Когда школьник усвоит, что эти два действия взаимосвязаны друг с другом, научиться делить будет несложно.
Учить проще всего на практических, понятных детям примерах. Выдайте сыну или дочери конфеты и предложите разделить их между членами семьи. Вместо конфет можно использовать разрезанный на куски пирог. Главное, чтобы школьник уяснил суть действия: раздать угощение так, чтобы все получили поровну и без остатка.
Проявите фантазию, придумывая разные примеры, а затем запишите ваши действия в тетради, чтобы ребёнок увидел, как выглядит математическая запись деления (пока что не столбиком, а в строку).
Теперь возьмите таблицу умножения и выберите оттуда любой пример. Покажите сыну или дочери, что, если произведение разделить на один из множителей, результат такого действия будет равен второму множителю. Поэкспериментируйте с разными примерами из таблицы, чтобы школьник наглядно увидел эту закономерность.
Играем вместе с КУВЫРКОМ
Алгоритм деления в столбик
Для решения любых примеров на деление используется следующий алгоритм
:- Найдите в примере делимое (число, находящееся слева от знака деления, то есть число, которое нужно разделить) и делитель (число, находящиеся справа от знака, то есть число, на которое нужно разделить).
- Запишите первое число – делимое – слева, а второе – делитель – справа, а между ними нарисуйте «уголок».
- Определите неполное делимое, то есть часть первого числа, которую можно взять для первичного деления. Сначала возьмите первую цифру. Если она не подходит для деления, добавьте к ней следующую и т. д.
- Посчитайте, сколько раз второе число (делитель) помещается в неполном делимом.
- Для проверки правильности действия умножьте делитель на полученное число и запишите результат умножения под выбранную часть делимого. Это будет неполное частное.
- Вычислите разницу – это будет остаток.
- Повторяйте эти действия до тех пор, пока в остатке не получится 0.
Некоторые числа нельзя разделить так, чтобы в остатке получился 0. Примеры, в которых остаток больше нуля, называются делением с остатком.
Играем вместе с КУВЫРКОМ
Деление в столбик без остатка
Теперь применим этот алгоритм к конкретному примеру. Возьмём простой пример 35:5=?
Запишите делимое и делитель и нарисуйте между ними «уголок».
Попросите школьника найти неполное делимое – часть делимого, на которую можно разделить число 5 (делитель). Первая цифра в делимом – 3. Спросите у него, сколько пятёрок поместится в число 3? Ребёнок скажет, что ни одной. Значит, добавляем к тройке следующую цифру из делимого – пятёрку и получаем 35 (наше полное делимое).
Спросите у ребёнка, сколько троек поместится в число 35? Школьник, знающий таблицу умножения, без труда посчитает, что в 35 помещается 7 пятёрок. Число 7 записываем под «уголок». Это и будет ответ.
Это очень простой пример деления двузначного числа на однозначное без остатка. Результат можно проверить с помощью таблицы умножения. Потренируйтесь на подобных примерах, чтобы ребёнок хорошо усвоил алгоритм действий.
Теперь попробуйте решить пример с трёхзначным делимым. Возьмём пример 372:6=?
Запишите пример в столбик.
Попросите ребёнка определить неполный делитель. Первое число в делимом – 3. Сколько шестёрок (шестёрка – делитель) помещается в тройку? Ни одной. Значит добавляем к тройке следующее число из делимого – семерку. Получаем 37. Теперь смотрим, сколько шестёрок поместится в 37. Ребёнок, вспомнив таблицу умножения, без труда вычислит, что в 37 поместится шесть шестёрок и единица останется в остатке.
Значит добавляем к тройке следующее число из делимого – семерку. Получаем 37. Теперь смотрим, сколько шестёрок поместится в 37. Ребёнок, вспомнив таблицу умножения, без труда вычислит, что в 37 поместится шесть шестёрок и единица останется в остатке.
Запишите неполное частное (6) под делитель, а число 36 под делимое. Вычтите из 37 число 36. Получится 1 (это остаток). Запишите.
Теперь посмотрите, сколько шестёрок поместится в остаток (1)? Ни одной. Теперь добавьте к единице число, оставшееся в делимом – 2. Получилось 12. Сколько шестёрок поместится в 12? Две шестёрки. Добавьте двойку к уже имеющемуся у нас неполному частному 6. Получится 62. Из 12 вычтите 12. Получится 0. Запишите.
Предложите ребёнку попробовать решить примеры с четырёх-, пяти-, шестизначными делимыми, а также с двузначными делителями. Независимо от величины чисел принцип действий будет одинаковым.
Деление в столбик с остатком
Расскажите ребёнку, что некоторые числа нельзя разделить без остатка. Для лучшего понимания продемонстрируйте это действие на наглядном примере. Дайте сыну или дочери пять конфет и попросите разделить их между ним и вами. Ребёнок даст вам и себе по две конфеты и останется ещё одна.
Для лучшего понимания продемонстрируйте это действие на наглядном примере. Дайте сыну или дочери пять конфет и попросите разделить их между ним и вами. Ребёнок даст вам и себе по две конфеты и останется ещё одна.
Объясните ему, что так произошло потому, что число 5 не делится на 2 поровну. Остаётся одна конфета, которая и является в данном случае остатком. Дайте ребёнку больше конфет и снова попросите его разделить на троих, четверых, пятерых. Снова обратите внимание на то, что далеко не всегда конфеты можно разделить поровну.
После того как ребёнок поймёт суть такого деления, переходите к решению примеров в столбик. Решаются они по тому же принципу, только вместо нуля в остатке получается какое-либо другое число.
Почему ребёнку сложно освоить деление в столбик?
Деление – это наиболее сложное арифметическое действие из четырёх основных. Многие дети прекрасно справляются со сложением, вычитанием, умножением, но буксуют, когда дело доходит до деления. Проблема здесь заключается в том, что ребёнок не понимает сам принцип деления. Постарайтесь объяснить ему алгоритм этого математического действия как можно доходчивее. Если не получается, обратитесь за помощью к учителю.
Проблема здесь заключается в том, что ребёнок не понимает сам принцип деления. Постарайтесь объяснить ему алгоритм этого математического действия как можно доходчивее. Если не получается, обратитесь за помощью к учителю.
Если же ребёнок не умеет быстро считать в уме и плохо знает таблицу умножения, то с делением у него обязательно возникнут проблемы. В этом случает важно до автоматизма отточить навык сложения и вычитания и хорошо выучить таблицу умножения. На первых порах обучения делению столбиком можно держать таблицу при себе и изредка подсматривать в неё.
Не ругайте ребёнка, если у него не получается быстро освоить деление столбиком. Вспомните себя в его возрасте – наверняка у вас тоже были подобные проблемы. Наберитесь терпения и объясняйте правила столько раз, сколько требуется. Не ставьте цель научить сына или дочь делить столбиком за один вечер. Избыток информации утомит ребёнка и снизит его обучаемость. Занимайтесь в комфортном для него темпе и вскоре он научится решать примеры самостоятельно, без вашей помощи. Не забывайте хвалить и вознаграждать школьника за старание – это повысит его мотивацию.
Не забывайте хвалить и вознаграждать школьника за старание – это повысит его мотивацию.
Ход урока | Формирование УУД, ТОУУ (технология оценивания учебных успехов) | |
I. | 1. Организационный момент. Покажите с каким настроением вы пришли на урок математики. Я рада, что у вас хорошее настроение. Мы с вами сегодня снова отправляемся в путешествие, а на чём попробуйте отгадать загадку: В поле лестница лежит, Дом по лестнице бежит. (Поезд) слайд 1 Правильно. Нас ждёт поезд и океан математических знаний. Откройте тетради, подпишите число, классная работа. 2. Устный счёт. Давайте проверим, готовы ли вы к такому путешествию. Запишите только ответы: 1. 9 умножить на 4. 2. 9 увеличить на 4. 3. 27 разделите на 3. 4. 63 уменьшите в 9 раз. 5. Найдите произведение чисел 14 и 6. 6. Чему равно частное чисел 60 и 4. 7. 8. Сумму чисел 45 55 уменьшите в 4 раза. 9. Сыну 12 лет, а папе 48. Во сколько раз папа старше сына? 10. Чему равен периметр прямоугольника, длина которого 11 см, а ширина 6 см? Кто готов проверять? Проверьте.(ответы на слайде 2) У кого оценка 5? Учитель – вывод: Ученик – У меня была цель написать математический диктант. Мне удалось, я выполнил без ошибок, самостоятельно. Я могу поставить себе оценку 5. | Познавательные УУД Развиваем умения: 1 ориентироваться в своей системе знаний: самостоятельно предполагать, какая информация нужна для решения учебной задачи в один шаг. 2. – отбирать необходимые для решения учебной задачи источники информации среди предложенных учителем словарей, энциклопедий, справочников. |
II. Постановка проблемы (знакомимся…). | 1 2 Парно-групповая работа. Задание № 1, с. 74 Цель работы: – создание проблемной ситуации. А теперь откройте учебник на с. 74. Задание № 1. Прочитайте самостоятельно. Кто понял задание, поднимите руку? Поставьте № 1 и буквы а, б, в в столбик, запишите пример к каждой букве. ( 1 ученик у доски) Кто готов проверять, поднимите руку? Проверяем под буквой А: 20 * 3= 60 Как считали? ( дети объясняют) Проверяем под буквой Б: 78 : 6 = 13 Как считали? ( дети объясняют) Проверяем под буквой В: 780 : 6 = Какое число делим? (трёхзначное на однозначное) В каком случае вам было трудно? Почему? ( 780 : 6) Давайте подумаем, как можно решать такие примеры? Кто может? ( 780 ед. / \ 60 18 Какая тема нашего урока? (Умножение и деление трёхзначных чисел) слайд 3 Сформулируйте цель: научиться умножать и делить трёхзначные числа. Молодцы! | 3 – добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.). |
III. Открытие нового (узнаём…). | 2 3 4 Парно-групповая работа. 1. Задание № 2, с. 74 Прочитайте задание. Что нужно сделать? (решить задачи) Выполните самостоятельно. Запишите выражения для ответа на задачи. А) 840 : 4 = 210 (в) Б) 300 * 2 = 600 (м) А теперь проверим на доске, как выполнила задание Лика. Правильно ли она решила? (Да) 2. Текст со знаком ?! . 3. Задание № 3, с. 74 Цель работы: – на основе наблюдений над представленными способами вычислений сформулировать новое правило. – Объясните решения Лики. Как считала под буквой А? (840:4=84д.:4=21д.=210) А как считала под буквой Б?(300*2=3с.*2=6с.=600) Сформулируйте ответ на основной вопрос урока. 2. Работа с текстом в оранжевой рамке. Трёхзначные числа, запись которых оканчивается нулями, можно выразить в сотнях или десятках и выполнить умножение или деление этих сотен или десятков. Физкультминутка Мы немножко отдохнем, Встанем , глубоко вздохнем, Руки в стороны, вперед, Нас еще работа ждёт. Руки вниз, на пояс, вверх – Убегаем мы от всех. Головою повернем Сядем и писать начнем. | 4 – перерабатывать полученную информацию: сравнивать и группировать математические факты и объекты. 5 – делать выводы на основе обобщения умозаключений. 6 – преобразовывать информацию из одной формы в другую: – представлять информацию в виде текста, таблицы, схемы. 7 – переходить от условно-схематических моделей к тексту. |
IV. Первичное закрепление (применяем…). | 3 4 5 1 Работа в парах. Задание № 4, с. 74 Продолжаем работать. Найдите задание под №4. посмотрите на примеры первой строчки. Умеем мы их решать? (да) А примеры второй строчки? (Познакомились сегодня) Кто может самостоятельно решить нижнюю строчку? Выполните. Проверьте друг у друга, сошлись ли у вас ответы. Вывод? Ученики: Можно решать примеры, в которых трёхзначные числа оканчиваются нулями, можно выразить в сотнях или десятках и выполнить умножение или деление. Оцените свою работу. Работа на карточках. У вас на столах лежат карточки с заданиями. Задания двух уровней. Уровень А – лёгкий, Б средний по трудности. Вы можете выбрать любую карточку по своим силам. Уровень А. Реши примеры: Уровень Б 300 *2 = 600 : 3 = 100*8 = 240 : 8 = 400 : 5 = 120 : 4 = 320 : 8 = 210 : 7 = 120 * 8 = 420 : 6 = 500 * 13 = 90 0* 9 = 630 : 7 = 140 * 20 Кто готов проверять? (Ответы на слайде 4) Оцените себя. У кого одинаковые карточки проверяйте. Оцените товарища. Молодцы, и с этим заданием справились. | Регулятивные УУД: Развиваем умения: 1 – самостоятельно формули-ровать цели урока после предварительного обсуждения; 2 – совместно с учителем обнаруживать и формулировать учебную проблему; ТОУУ 3 – составлять план решения отдельной учебной задачи совместно с классом; |
V. | 6 7 5 Фронтальная работа. 1. Задание № 5, с. 75 Решение задач. 2. Задача № 6а, с. 75 – Прочитайте задачу. – Выделите все данные. – Смоделируйте условие задачи. (Схема). – Составьте план решения задачи. – Решите задачу. (1. 900 : 2 = 450 (сек.) – рассматривал камбалу; 2. 900 : 5 = 180(сек. – гнался за стаей скумбрий; 3. 900 – ( 450 + 180 ) = 270 (сек.)- наблюдал за черноморской акулой). Проверка решения. ( слайд 5) Вопросы к ученикам, выполнявшим работу: – Что вам нужно было сделать в задании? – Удалось ли правильно решить поставленные задачи? – Вы сделали всё правильно или были ошибки, недочёты? – Вы решили всё сами или с чьей-то помощью? – Какого уровня сложности было задание? – Оцените свою работу. – Есть ли у ребят какие-либо дополнения, замечания? Согласны ли вы с такой самооценкой? Вывод? Ученики: закрепляли умение решать текстовую задачу, в которой повторили умножение и деление, порядок действий, учились составлять и решать выражения и т.д. Тест. Молодцы! Вот мы и заканчиваем наше путешествие. Чтобы нам вернуться обратно попробуйте решить тест в группах. Если вы выполните правильно, у вас должно получиться слово. Но сначала вспомним правила работы в группах. Выполняйте. Тест 1.Как можно представить в виде произведения двух множителей число 24 ? а) 8 * 2 б) 7 * 3 м) 8 * 3 г) 3 * 6 2.Какое число делится на 6 ? а) 46 о) 42 в) 28 3.Какое число нужно подставить, чтобы равенство было верным ? 63 * = 9 л) 7 б) 6 в) 8 4.Частное каких чисел равно 4 ? а) 36 и 6 о) 24 и 6 в) 2 и 2 5. а) 6 и 3 б) 2 и 7 в) 3 и 5 д) 6 и 2 е) 4 и 3 6.На сколько надо разделить 48, чтобы получить 6 ? ц) на 8 б) на 7 в) на 6 7. На верхней полке было 18 книг, а на нижней – в 3 раза меньше, чем на верхней. Сколько книг было на нижней полке ? а) 9 книг ы) 6 книг в) 3 книги Молодцы! Оцените свою работу. Слайд 6 | 4 – работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки с помощью класса; 5 – в диалоге с учителем и другими учащимися учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев. Коммуникативные УУД Развиваем умения: 1.- доносить свою позицию до других: оформлять свои мысли в устной и письменной речи (выражение решения учебной задачи в общепринятых формах) с учётом своих учебных речевых ситуаций; ТОУУ 2 – доносить свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы; 3 – слушать других, пытаться принимать другую точку зре-ния, быть готовым изменить свою точку зрения; 4 – читать про себя тексты учебников и при этом: ставить вопросы к тексту и искать ответы; проверять себя; отделять новое от известного; выделять главное; составлять план; 5 – договариваться с людьми: выполняя различные роли в группе, сотрудничать в совместном решении проблемы (задачи). Личностные результаты: 1 – придерживаться этических норм общения и сотрудничества при совместной работе над учебной задачей; |
VI. Итог урока. | – Какая тема нашего урока сегодня была? Достигли мы своей цели на уроке? – Что нового вы узнали сегодня на уроке? – Чему научились? – Какие задачи решали? – Всё ли получалось? – Над чем ещё надо поработать? Сегодня за урок я могу поставить оценку… | 2. – в созданных совместно с педагогом на уроке ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, как себя вести. |
VII. Возможное домашнее задание. | Задания – запишите по выбору одно задание: – придумать и записать 4 выражения с подробной записью на изученную тему. – придумать задачу, с решением на изученную тему. |
Конспект урока по математике: «Внетабличное умножение и деление» (3 класс)
Ребята, ответьте на вопрос. Что находится в начале числовой линейки?
Правильно, нуль. Здравствуйте, ребята! Сегодня на уроке мы отправимся по математическому маршруту, где познакомимся с внетабличным делением и умножением.
Прокачайте уменья
В умноженье и деленье!
Примеры внимательно читайте –
Быстро, правильно считайте!
За старанье, прилежание
Цветную ленту получайте!
В конце урока вас ждет яркий сюрприз, но сейчас откройте тетради, возьмите ручки, начинайте выполнять задания.
Умножение и деление круглых чисел
Обратите внимание: круглым называется число, которое оканчивается нулем — 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Круглые числа похожи на десятки. Разряд единиц круглых десятков равняется нулю.
Прочитайте таблицу круглых чисел:
Умножение и деление круглого двухзначного числа на однозначное выполняется по определенным правилам. Познакомьтесь с этими правилами.
Деление круглых чисел
Рассмотрим пример внетабличного деления:
В примерах деления круглого числа делим количество десятков и дописываем в ответе нуль.
Делим на 10 — убираем в ответе нуль.
В частном не пишем нули, если делимое, делитель — круглые числа.
Умножение круглых чисел
А знаете ли вы, что за тысячелетия развития математики было придумано много вариантов умножения. Считалось, что для овладения искусством вычисление нужен талант. Итальянский математик 15 века Лука Пачоли приводит 8 способов. Познакомимся с некоторыми из них.
Рассмотрите прием внетабличного умножения.
Двадцать умножить на три равно шестидесяти.
Воспользуемся правилом перестановки множителей, получим пример, который умеем решать.
Прочитайте правило внимательно.
При умножении круглого числа на однозначное, надо умножить десятки на второй множитель, в ответ справа добавить нуль.
Увеличить в десять раз — это значит написать в значение произведения первый множитель и добавить к нему 0 справа.
Произведение семи и десяти равно семидесяти.
Воспользуйтесь правилами математики внетабличного умножения и деления для решения примеров:
Проверьте:
Ошибок нет, молодцы. Ваша первая награда — красная ленточка.
Впереди ждут новые открытия, не отставайте, думайте, решайте.
Умножение суммы на число
Задание. Посчитайте и запишите решение на вопрос: сколько квадратов в прямоугольнике?
Вариант 1. Рассуждайте так: в ряду шесть синих квадратов плюс три красных квадрата. Рядов 4. Значит, запишите решение:
Сумма в скобках равна девяти. 9 ∙ 4 = 36. Это табличное умножение.
9 ∙ 4 = 36. Это табличное умножение.
Вариант 2. Количество квадратов подсчитайте другим способом. Узнайте, сколько синих, потом, сколько красных, полученные результаты сложите.
Таким способом удобно умножать большие величины.
Любое двузначное число легко записать как сумму разрядных слагаемых: круглых десятков и единиц.
Умножайте сначала десятки, потом единицы, произведения складывайте.
Как это сделать, рассмотрите на примере.
Сумму десяти и пяти умножим на шесть.
Это распределительное свойство умножения суммы на число.
Правило умножения суммы на число запишите буквенным выражением.
За внимание награждаю вас оранжевой лентой.
Источник
Идите по маршруту дальше.
Умножение двузначного числа на однозначное
Сейчас будем решать вот такие примеры:
Они такие легкие, что мы разделаемся с ними на раз, два, три.
Устное умножение чисел двузначного на однозначное
Считать устно — это просто замечательно, я сам стараюсь обходиться без калькулятора. Но для того, чтобы это делать, нужно знать приемы устного счета. Это чудесная разминка для мозга.
Мы разберемся с примерами, когда двузначное число умножается на однозначное. Вы научились записывать сумму разрядных слагаемых, поэтому воспользуемся этим умением.
Давайте тренироваться:
Пример сложнее.
89 умножить на семь.
Ну как, простые примеры? По способу решения — да. А вот, если не знаете таблицу умножения, то не такие уж простые.
Умножение столбиком двузначного числа на однозначное
Это письменный прием вычислений. Такие примеры мы привыкли называть примеры в столбик или примеры столбиком. Давайте научимся правильно записывать такое решение.
Пусть надо 58 умножить на семь.
А теперь начните решать. Последовательно умножьте слева направо все цифры первого множителя на 7, пока они не закончатся. Умножаем 8 на 7, это 56. Что нам с ним делать? Смотрите, то, что единицы, мы так и записываем.
Последовательно умножьте слева направо все цифры первого множителя на 7, пока они не закончатся. Умножаем 8 на 7, это 56. Что нам с ним делать? Смотрите, то, что единицы, мы так и записываем.
Процесс умножения закончен. Читаем ответ — четыреста шесть.
Давайте посмотрим другой пример.
Запишите столбиком.
Проверьте, как записали.
Выполните вычисления. 5 ∙ 9 = 45. Пять записываем под девяткой. Четыре в уме.
4 ∙ 9 = 36. Да 4 в уме. 36 + 4 = 40. Записываем значение произведения. Читаем ответ — 405.
Проверьте свою запись.
Деление суммы на число
Прочитайте рассказ «Из истории символов».
Люди сначала умножали, делить научились позднее. В десятом веке ученый Герберт в математических трудах упомянул сложные правила «железного деления». Старинная итальянская поговорка гласила: «Трудное дело — деление». Оно и в самом деле было трудно, если принять во внимание утомительные методы, какими выполнялось тогда это действие.
В середине 18 века в странах Европы начали делить привычным для нас простым способом, который изобрели арабы. Он получил название «золотое деление».
Для записи действия применяются разные знаки:
В 17 веке в Англии и США чаще всего использовался обелюс. Символ в виде двух точек придумал немецкий математик Г. Лейбниц в 1684 году. На письме он очень похож на двоеточие.
Познакомимся со способом деления. Выполните задание.
Какие числа нужно вставить в «окошки», чтобы получились верные равенства?
Решение.
Рассуждаем: первое слагаемое — круглое число. В окошко нужно подставить слагаемое, которое делится на три без остатка.
Подсказка: вспомните результаты табличного умножения на 3. Например, 27.
Деление суммы чисел 30 и 27 на данное число 3 вычисляется так: каждое слагаемое делится на три и результаты складываются.
Запишите подробное решение:
Сформулируйте правило деления суммы на число:
Деление двузначного числа на однозначное
Ребята, вы меня узнали? Люблю наряжаться на маскарад. Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.
Вот прицепил такие усы, думал, что буду похож на фокусника. Чудеса начинаются.
Такие задания называют примерами с «усиками». Да, да, но усики носят не люди, кто делит, а сами примеры. Рисовать их нужно простым карандашом, а когда научитесь быстро считать, то просто представляйте в голове.
Устное деление двузначного на однозначное
Задание 1.
Пусть надо решить, сколько будет
К «усикам» запишем такие два слагаемых, которые делятся на 8, а в сумме дают 96.
Самое главное — это не ошибиться в подборе первого «усика». Надо запомнить, что он всегда больше, чем второй. Ищем его, умножая 8 на 10. Если не подойдет, то будем умножать на 20, на 30. Главное, чтобы было круглое число.
Все понятно? Будем тренироваться.
Задание 2.
Задание 3.
Попробуем разделить 90 на два. «Первый усик» явно не 20, тогда второй будет 70. Знаем, что «второй усик» не может быть больше первого.
Знаем, что «второй усик» не может быть больше первого.
Вижу, что не 60, потому что 30 разделить на два — это не табличный случай.
Следовательно, 2 ∙ 40 = 80. Значит «первый усик» предположительно 80. «Второй усик» тогда найдем вычитанием: 90 – 80 = 10. Десять разделить на два, это таблица.
Как думаете, вы справитесь с делением? Когда встречаете случаи, где двузначное число делится на однозначное, и примеры не относятся к таблице умножения, то решайте подбором «усиков». Разбивайте делимое на подходящие слагаемые. Их можно записать суммой в скобочках, а при делении использовать правило деления суммы на число.
Решите задачу.
Таня выполнила 96 примеров, а Коля в 4 раза меньше. Сколько примеров решил Коля?
Чтобы ответить на вопрос задачи, надо выполнить действие деления.
96 : 4 =
«Усиками» будут 80 и 16, получается сумма 80 + 16. Значит, каждое из этих слагаемых разделите на 4, а частные сложите.
Ответ: 24
Деление столбиком двузначное на однозначное
Письменное деление уголком просто невозможно усвоить без блестящего знания таблицы умножения. Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.
Это просто трата времени и нервов. В древности в римских школах ее заучивали хором на распев. Знаете ответы на «отлично», тогда переходите на примеры деления в столбик.
Задание 1.
Пусть надо 84 разделить на три. Посмотрите на запись. Такой значок означает деление уголком. Уголок имеет наверху делитель, на который делим. Под чертой — результат, который ищем. Он называется частным.
Нам надо узнать, чему равно частное. Но прежде определим, сколько цифр будет в результате. Это очень важный шаг, поэтому упускать его нельзя. Как мы будем это делать? Посмотрите на первую цифру. Это восьмерка. Восемь больше трех. Значит, она может дать нам полноценную цифру в частном. Ставим точку. После восьмерки еще одна цифра, это значит, что частное — двузначное число. Под чертой в уголке карандашом поставьте вторую точку.
Первое неполное делимое — восьмерка. Начинаем ее делить на три, ищем табличный случай. Легче всего уменьшать 8 на единицу.
8 – 1 = 7. В таблице нет деления семи на три.
В таблице нет деления семи на три.
Уменьшаем еще на 1.
7 – 1 = 6. Шесть делится на три, получается — по два. Записываем 2 в частное под чертой.
Теперь мы должны понять, сколько не разделили. Ведь разделили всего шесть.
А надо было разделить восемь.
Два осталось неразделенным. Это остаток. Он должен быть меньше делителя.
Давайте проверим: два меньше трех.
Да, действительно. Мы сделали все правильно. Этот шаг очень важен. Не забывайте сравнивать остаток с делителем.
После этого сносим следующую цифру с тем, чтобы получить новое неполное делимое. Обратите внимание: нужно писать каждую цифру в своей клетке. Получается неполное делимое 24.
Ответ: 28.
Задание 2.
Решите пример столбиком 96 : 4 =
Проверьте:
Ура! Наш математический маршрут пройден.
Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста,
напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.
Примеры на умножение и деление. Второе полугодие.
Примеры на умножение и деление. Второе полугодие. Задачи по математике 3 класс
MAT-ZADACHI.RU
Задачи для 3 класса
- Математические диктанты
- Комбинаторные задачи
- Нестандартные задачи
- Множество и его элементы
- Способы задания множеств
- Пустое множество
- Диаграмма Венна
- Диаграмма Венна. Часть 2
- Подмножество
- Множество. Задачи
- Скорость, время, расстояние
Числа от 1 до 100
- Сложение и вычитание
- Буквенные выражения
- Единицы длины
Контрольные работы
- Умножение и деление
- Итоговая контрольная работа
- 1 четверть
- 2 четверть
- Контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Контрольная работа 1
- Итоговые контрольные работы 3 класс
- Контрольная работа 1
Тесты. 3 класс.
3 класс.
- Тесты по математике 3 класс
- Табличное умножение и деление чисел
- Особые случаи умножения и деления
Примеры, уравнения
- Примеры
- Уравнения
- Кроссворды
| | Математика 3 класс ->> Примеры Первое полугодиеВторое полугодие |
| 49 : 7 = 7 | 117 : 9 = 13 | 8 * 16 = 128 | 72 : 9 = 8 | 90 : 6 = 15 | 24 : 24 = 1 |
| 23 * 7 = 161 | 6 * 17 = 102 | 171 : 9 = 19 | 11 * 4 = 44 | 48 : 2 = 24 | 13 * 2 = 26 |
| 85 : 5 = 17 | 16 : 8 = 2 | 49 : 7 = 7 | 10 * 22 = 220 | 35 : 7 = 5 | 32 : 8 = 4 |
| 24 * 2 = 48 | 56 : 7 = 8 | 189 : 9 = 21 | 12 * 5 = 60 | 4 * 22 = 88 | 126 : 9 = 14 |
| 28 : 7 = 4 | 198 : 9 = 22 | 3 * 21 = 63 | 26 : 2 = 13 | 21 * 5 = 105 | 17 * 2 = 34 |
| 138 : 6 = 23 | 90 : 5 = 18 | 8 * 16 = 128 | 20 * 10 = 200 | 115 : 5 = 28 | 10 * 17 = 170 |
| 192 : 24 = 8 | 3 * 14 = 42 | 54 : 9 = 6 | 75 : 15 = 5 | 48 : 6 = 8 | 4 * 23 = 92 |
| 18 : 3 = 6 | 198 : 22 = 9 | 9 * 24 = 216 | 12 * 3 = 36 | 7 * 24 = 168 | 12 * 4 = 48 |
| 7 * 15 = 105 | 36 : 12 = 3 | 24 : 3 = 8 | 140 : 20 = 7 | 14 * 8 = 112 | 7 * 16 = 112 |
| 207 : 9 = 23 | 16 : 4 = 4 | 135 : 9 = 15 | 56 : 7 = 8 | 20 * 9 = 180 | 19 * 6 = 114 |
| 55 : 5 = 11 | 72 : 8 = 9 | 30 : 2 = 15 | 12 * 9 = 108 | 6 * 6 = 36 | 99 : 9 = 11 |
| 50 : 5 = 10 | 114 : 6 = 19 | 15 : 5 = 3 | 42 : 3 = 14 | 0 * 25 = 0 | 13 * 4 = 52 |
| 65 : 5 = 13 | 66 : 6 = 11 | 9 * 9 = 81 | 12 * 8 = 96 | 8 * 17 = 136 | 51 : 17 = 3 |
| 144 : 6 = 24 | 11 * 8 = 88 | 24 * 7 = 168 | 95 : 19 = 5 | 207 : 23 = 9 | 5 * 21 = 105 |
| 15 * 4 = 60 | 114 : 19 = 6 | 48 : 24 = 2 | 17 * 9 = 153 | 18 * 6 = 108 | 152 : 8 = 19 |
| 45 : 3 = 15 | 63 : 3 = 21 | 176 : 8 = 22 | 20 * 3 = 60 | 7 * 16 = 112 | 70 : 14 = 5 |
| 91 : 13 = 7 | 9 * 22 = 198 | 18 : 3 = 6 | 32 * 6 = 192 | 110 : 5 = 21 | 41 * 3 = 123 |
| 168 : 7 = 24 | 78 : 13 = 6 | 161 : 7 = 23 | 12 * 17 = 204 | 19 * 4 = 76 | 21 * 8 = 168 |
| 115 : 23 = 5 | 56 * 3 = 168 | 32 * 5 = 160 | 27 * 3 = 81 | 207 : 23 = 9 | 60 : 3 = 20 |
| 144 : 16 = 9 | 85 : 5 = 17 | 48 : 12 = 4 | 13 * 10 = 130 | 52 * 2 = 104 | 31 * 4 = 124 |
| 21 : 3 = 7 | 24 : 12 = 2 | 95 : 19 = 5 | 40 * 2 = 80 | 92 * 2 = 184 | 39 * 4 = 156 |
| 72 * 3 = 216 | 124 : 2 = 62 | 147 : 21 = 7 | 77 : 7 = 11 | 126 : 18 = 7 | 3 * 62 = 186 |
| 102 : 17 = 6 | 72 : 4 = 18 | 12 : 4 = 3 | 45 * 3 = 135 | 19 * 6 = 114 | 31 * 2 = 62 |
| 36 : 3 = 12 | 168 : 21 = 8 | 126 : 21 = 6 | 84 : 12 = 6 | 41 * 5 = 205 | 12 * 9 = 108 |
| 33 * 3 = 99 | 85 : 17 = 5 | 77 : 7 = 11 | 114 : 19 = 6 | 32 : 2 = 16 | 44 * 2 = 88 |
| 96 : 3 = 32 | 21 * 6 = 126 | 32 * 7 = 224 | 14 * 7 = 98 | 133 : 7 = 19 | 92 : 4 = 23 |
| 152 : 8 = 19 | 216 : 9 = 24 | 18 * 11 = 198 | 53 * 3 = 159 | 12 * 9 = 108 | 38 : 2 = 19 |
| 49 * 4 = 196 | 0 * 15 = 0 | 12 * 6 = 72 | 48 : 8 =6 | 195 : 3 = 65 | 21 * 10 = 210 |
| 17 * 4 = 68 | 154 : 7 = 22 | 34 * 2 = 68 | 135 : 15 = 9 | 104 : 13 = 8 | 68 * 2 = 136 |
| 11 * 6 = 66 | 96 : 3 = 32 | 87 : 3 = 29 | 37 * 5 = 185 | 44 * 5 = 220 | 98 * 1 = 98 |
| _______________ | _______________ | _______________ | _______________ | _______________ | _______________ |
Простые задачи
- Задачи на умножение
- Задачи на деление по содержанию и на равные части
- Задачи на 1 действие
Составные задачи
- Задачи на нахождение суммы
- Задачи на нахождение уменьшаемого, вычитаемого, разности
- Задачи на 2 действия
- Задачи на 3 действия
- Задачи на разностное и кратное сравнение
Математика Приемы устных вычислений умножения и деления трехзначных чисел, которые оканчиваются нулями
Материалы к уроку
Приемы устных вычислений умножения и деления трехзначных чисел, которые оканчиваются нулями.doc”>45. Приемы устных вычислений умножения и деления трехзначных чисел, которые оканчиваются нулями.doc
68.5 KBСкачать45. Приёмы устных вычислений умножения и деления трёхзначных чисел, которые оканчиваются нулями.ppt
15.06 MBСкачать
Конспект урока
|
45. Приемы устных вычислений умножения и деления трехзначных чисел, которые оканчиваются нулями |
|
Организационный этап
Не стой в стороне равнодушно, Сегодня мы будем помогать сказочным героям выполнять различные задания. Вы готовы? |
|
Минутка чистописания
А дорога далека, Узнали героев? Для того чтобы попасть домой, Маша испекла пирожки. В корзину вмещаются пирожки только с трёхзначными числами. Назовите их………. Запишите их красиво в первой строчке…………
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Ах ты, Петя – простота, Узнали сказку? Ребята, нужно помочь спасти Петю. Но кот не знает, какой дорогой пошла лиса. Вы готовы ему помочь? |
|
Решите примеры. 6 ∙ 7 : 2 Проверьте себя. 6 ∙ 7 : 2 = 21
Красна девица грустна, Кто это? Проверьте себя. 305 903
Маленькая девочка весело бежит Кто это?
Проверьте себя. ABCO, OCDE, ABCF, FCDЕ Работа над новым материалом
Смышлёность этого мальчишки Помогите ему решить примеры. 170 ∙ 3 300 ∙ 3 Решали ли мы ранее такие примеры? Тема нашего урока «Приёмы устных вычислений умножения и деления трёхзначных чисел, которые оканчиваются нулями» Умножение и деление в таких случаях можно заменить действиями с сотнями и десятками. Рассмотрим пример 170 ∙ 3. В числе 170 сколько десятков? Рассмотрим пример 300 ∙ 3. В числе 300 сколько сотен? Запомните! Умножение и деление в таких случаях можно заменить действиями с сотнями и десятками. Давайте решим примеры. 240 ∙ 2 |
|
Проверьте себя. 240 ∙ 2 = 24 дес. ∙ 2 = 48 дес. = 480
Рассмотрим пример на деление. 180 : 3. В числе 180 сколько десятков? 600 : 2. В числе 600 – 6 сотен.
Решите примеры 560 : 7 Проверьте себя 560 : 7 = 56 дес. : 7 = 8 дес. = 80
|
|
Закрепление материала
Как выполняют умножение и деление трехзначных чисел, оканчивающихся 0? Вы готовы помогать дальше сказочным героям? У отца был мальчик странный, Верно, Буратино. Буратино очень хочет научиться решать примеры на умножение и деление трехзначных чисел, оканчивающихся 0.
Решите примеры устно. 900 : 3
|
|
Самостоятельная работа
-Нашей помощи ждет очередной сказочный герой. Вы любите котов? Я – да! Верно, это Кот в сапогах.
Давайте проверим. 1) 16 ∙ 2 = 32 метра в куске ткани Ответ: выйдет 8 платьев. |
|
Молодцы, ребята. Вы помогли Коту в сапогах, и он сможет спасти от бедности своего хозяина. |
|
Нашей помощи ждет Спящая красавица. Решите выражение, и вы разбудите ее. 400 : 8 ∙ 6 – 480 : (24 : 4) + 170 ∙ 4 Проверьте себя. 400 : 8 ∙ 6 – 480 : (24 : 4) + 170 ∙ 4=900
|
|
Этап подведения итогов
Наш урок заканчивается. На уроке мы научились. Пригодятся ли вам эти знания и умения в жизни? |
|
Рефлексия
Кто считает, что урок прошел для вас плодотворно, с пользой? |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Деление — значение, шаги, алгоритм, примеры
Деление — одна из четырех основных математических операций, три другие — сложение, вычитание и умножение. Проще говоря, деление можно определить как разбиение большой группы на более мелкие группы таким образом, чтобы в каждой группе было равное количество элементов. Это операция, используемая для равного группирования и равного распределения в математике. Давайте подробно узнаем об операции деления в математике в этой статье.
| 1. | Что такое дивизия? |
| 2. | Части отдела |
| 3. | Алгоритм деления |
| 4. | Как сделать Раздел? |
| 5. | Деление с остатками |
| 6. | Имущество отдела |
| 7. | Часто задаваемые вопросы по подразделению |
Что такое деление?
Деление — одна из основных арифметических операций в математике, при которой большее число разбивается на меньшие группы с одинаковым количеством элементов. Например, для спортивного мероприятия, если 30 студентов нужно разделить на группы по 5 человек, то сколько всего групп будет сформировано? Такие задачи легко решаются с помощью операции деления. Здесь нам нужно разделить 30 на 5. В результате получится 30 ÷ 5 = 6. Итак, будет 6 групп по 5 учеников в каждой. Вы можете проверить это значение, умножив 6 и 5, что даст вам исходное число 30.
Вы можете проверить это значение, умножив 6 и 5, что даст вам исходное число 30.
Деление Определение
Деление — это процесс повторяющегося вычитания. Это обратная операция умножения. Он определяется как акт формирования равных групп. При делении чисел мы разбиваем большее число на более мелкие так, чтобы умножение этих меньших чисел было равно большему взятому числу. Например, 4 ÷ 2 = 2. Это можно записать как факт умножения 2 × 2 = 4.
Символ деления
Деление обозначается математическим символом, состоящим из маленькой горизонтальной линии с точкой над каждой. и ниже линии. Есть два основных символа деления, которые обозначают деление двух чисел. их ÷ и /. Например, 4 ÷ 2 = 2 и 4/2 = 2.
Части отдела
Части деления означают названия терминов, связанных с процессом деления. Есть четыре части деления: делимое, делитель, частное и остаток. Давайте посмотрим на пример деления, приведенный ниже, и поймем значения этих четырех частей деления.
Здесь, когда мы делим 105 на 8, мы получаем значения делителя, делимого, частного и остатка. Посмотрите на таблицу ниже, чтобы понять значение этих терминов.
| Условия | Описания | Значения |
|---|---|---|
| Дивиденд | Число, которое нужно разделить | 105 |
| Делитель | Количество равных групп, которые необходимо составить, или число, на которое мы делим делимое | 8 |
| Частное | Значение/ответ, полученный после выполнения деления | 13 |
| Остаток | Оставшееся или пропущенное значение, не входящее ни в одну группу | 1 |
На изображении выше написано, что «Дивиденд = Делитель × Частное + Остаток». Это уравнение удовлетворяет приведенным выше значениям, но будет ли оно удовлетворять значениям делимого, делителя, частного и остатка при каждом делении? Давай выясним.
Алгоритм деления
Алгоритм деления представляет собой уравнение, которое формирует связь между всеми четырьмя частями деления. В любом факте деления произведение делителя на частное, прибавленное к остатку, всегда равно значению делимого. Таким образом, общая формула деления: Дивиденд = (Делитель × Частное) + Остаток . Это известно как алгоритм деления.
Приведенная выше формула помогает нам проверить значения частного и остатка, полученные после выполнения деления. Мы можем подставить значения частного, остатка и делителя в приведенное выше уравнение и проверить, совпадает ли результат с делимым или нет. Если мы получили дивиденд, значит, мы правильно выполнили шаги деления. Если нет, значит, в наших расчетах есть ошибка, которую нужно исправить. Давайте возьмем один пример и посмотрим, удовлетворяет ли он приведенному выше алгоритму деления или нет. Разделите 17 на 3. Разделив 17 на 3, мы получим 5 в частном и 2 в остатке.
Делимое = (Делитель × Частное) + Остаток
17 = (3 × 5) + 2
17 = 15 + 2
17 = 17
Следовательно, проверено.
Как сделать Раздел?
Однозначное деление можно выполнить с помощью таблицы умножения. Например, чтобы решить 24 ÷ 6, нам просто нужно посмотреть, что нам нужно умножить на 6, чтобы получить 24 в качестве ответа. Ясно, что 6 × 4 = 24, следовательно, 24 ÷ 6 = 4. Когда дело доходит до деления чисел на большие числа, то мы можем использовать метод деления в длину. Давайте возьмем пример 65, разделенного на 5, чтобы понять это. Выполните следующие действия, чтобы научиться выполнять деление:
- Шаг 1: Нарисуйте символ деления ⟌ и напишите делитель (5) слева от него и делимое (65), заключенное под этим символом.
- Шаг 2: Возьмите первую слева цифру делимого (6). Проверьте, больше ли эта цифра делителя или равна ему. [Если первая цифра делимого меньше делителя, то считаем первые две цифры делимого]
- Шаг 3: Затем разделите на делитель и запишите ответ сверху как частное. Здесь частное 6 ÷ 5 равно 1,
- Шаг 4: Вычтите произведение делителя и цифры, записанной в частном (5 × 1), из первой цифры делимого и запишите разницу ниже.
 Здесь разница 6 – 5 = 1.
Здесь разница 6 – 5 = 1. - Шаг 5: Запишите следующую цифру делимого (если она есть). Следующая цифра в делимом 5.
- Шаг 6: Повторяйте тот же процесс, пока не получите остаток меньше делителя.
Посмотрите на приведенное ниже изображение, показывающее вышеуказанные этапы деления.
Разделение с остатками
Не всегда обязательно иметь в остатке 0. Если делимое не кратно делителю, то получаем ненулевой остаток. Когда мы получаем ненулевой остаток при делении одного числа на другое, это называется делением с остатками. Возьмем пример раздачи 9 воздушных шаров 2 детям поровну так, чтобы у обоих детей было равное количество воздушных шаров. Можно ли это сделать, не получая остатка?
Разделив 9 на 2, мы получим 4 в частном и 1 в остатке. Мы можем сделать 2 группы по 4 шарика в каждой, но останется 1 шарик. Посмотрите на изображение ниже, на котором показано деление с остатком (9 ÷ 2).
Попробуйте ответить на следующие вопросы на деление и посмотрите, получится ли у вас ненулевой остаток или нет: 63 ÷ 9, 76 ÷ 13, 89 ÷ 8, 34 ÷ 5 и 27 ÷ 3.
Свойства отдела
Теперь давайте рассмотрим некоторые свойства операции деления, которые помогут вам лучше понять эту операцию. Ниже перечислены некоторые свойства деления:
- Деление на 1: Любое число, деленное на 1, дает само число. Другими словами, если делитель = 1, то делимое = частное.
- Деление на 0: Значение числа, деленного на 0, не определено, т. е. n/0 = не определено, где n — любое число.
- Деление само на себя: Если мы разделим число само на себя, мы всегда получим 1 в качестве ответа. Другими словами, если делимое = делителю, то частное = 1, .
- Деление 0 на любое число: 0 деление на любое число всегда дает 0. Некоторые примеры: 0 ÷ 4 = 0, 0 ÷ 9 = 0, 0 ÷ 5754 = 0 и т.
 д.
д. - Деление на 10: Если мы разделим число на 10, то цифра, стоящая на месте единиц, всегда будет остатком, а оставшиеся слева цифры будут частным. Например, 579 ÷ 10 = 57 р 9.
- Деление на 100: Если мы разделим число на 100, то число, составленное из разрядов единиц и разрядов десятков, всегда будет остатком, а оставшиеся слева цифры будут частным. Например, 8709÷ 100 = 87 р 9.
☛ Статьи по теме
Чтобы узнать больше о фактах разделения, ознакомьтесь с еще несколькими интересными статьями, перечисленными ниже, и изучите основы.
- Двоичный раздел
- Деление дробей
- Калькулятор длинного деления
Примеры разделов
Пример 1: У Лизы 2 щенка. Она купила 8 жевательных костей, чтобы накормить их обоих поровну. Сколько костей достанется каждому щенку?
Решение:
Дано, количество щенков = 2, а количество костей = 8.
 Таким образом, количество костей у каждого щенка = 8 ÷ 2 = 4. Таким образом, каждый щенок получит 4 кости.
Таким образом, количество костей у каждого щенка = 8 ÷ 2 = 4. Таким образом, каждый щенок получит 4 кости.Пример 2: Отец Евы испек для нее печенье. Пал и Эйкон, ее лучшие друзья, решили преподнести ей сюрприз, навестив ее без предупреждения. Если было 9 печенек, то сколько отец Евы дал Еве, Палу и Эйкону, чтобы они были разделены поровну? Используйте алгоритм деления, чтобы проверить свой ответ.
Решение:
Учитывая, что количество файлов cookie = 9, а количество людей, которым нужно поделиться файлами cookie = 3. Количество файлов cookie, разделенных поровну между Евой, Палом и Эйконом = 9 ÷ 3 = 3. Чтобы проверить деление, мы поместите значения в формулу, Делимое = (Делитель × Частное) + Остаток. Итак, 9 = 3 × 3 + 0 = 9. Значит, проверено.
Пример 3: Найдите значение частного и остатка при делении 75 на 3? Проверьте ответы, используя алгоритм деления.
Решение:
Здесь мы должны разделить 75 на 3.
 Таким образом, делимое = 75 и делитель = 3. Разделим 75 на 3, используя шаги деления.
Таким образом, делимое = 75 и делитель = 3. Разделим 75 на 3, используя шаги деления. Следовательно, мы получаем, Частное = 25 и Остаток = 0.
Чтобы проверить деление, мы подставим значения в формулу Делимое = (Делитель × Частное) + Остаток. Итак, 75 = 3 × 25 + 0 = 75. Значит, проверено.
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы отдела
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по подразделению
Что такое деление в математике?
В математике есть четыре основных арифметических действия: сложение, вычитание, умножение и деление. Среди этих четырех операций деление является одной из основных операций, которые мы используем в нашей повседневной деятельности. Это процесс разделения большой группы на равные меньшие группы. Например, разделите 25 на 5. Факт деления для этого примера будет 25 ÷ 5 = 5,9.0005
Это процесс разделения большой группы на равные меньшие группы. Например, разделите 25 на 5. Факт деления для этого примера будет 25 ÷ 5 = 5,9.0005
Какие существуют два типа разделения?
Подразделение разделено на две части: частичных и квотных моделей. Partitive используется при делении числа на известное количество слотов. Например, если мы разделим 4 на 2 слота, то сможем узнать, сколько предметов будет в каждом слоте. Quotative деление используется при делении числа на слоты измеряемой величины. Например, когда мы делим 4 на слоты по 2, мы можем определить, сколько слотов можно создать.
Что такое три части деления?
Тремя основными частями деления являются делимое, частное и делитель. В дополнение к этому, когда делитель не является делимым, мы получаем ненулевой остаток, который является четвертой частью деления.
Что такое метод длинного деления?
Метод длинного деления является наиболее распространенным методом, используемым для решения задач на деление. В этом процессе делитель записывается вне символа деления, а делимое помещается внутри. Частное пишется над чертой над делимым.
В этом процессе делитель записывается вне символа деления, а делимое помещается внутри. Частное пишется над чертой над делимым.
Каковы этапы отдела?
Шаги для деления перечислены ниже:
- Шаг 1: Возьмите первую цифру делимого. Проверьте, больше ли эта цифра делителя или равна ему.
- Шаг 2: Затем разделите на делитель и сверху напишите ответ.
- Шаг 3: Вычтите результат из цифры и запишите ниже.
- Шаг 4: Снова повторите тот же процесс.
Как делить, если делитель больше дивиденда?
В этом случае деления мы можем просто продолжать добавлять нули справа от делимого, пока не станет целесообразным дальнейшее деление. Кроме того, мы можем разделить частное на те же степени 10 для получения окончательного ответа, как только мы правильно выполним деление.
Как делить десятичные дроби?
Деление десятичных дробей так же просто, как и любое другое число. Все, что вам нужно сделать, это умножить десятичную дробь на степени десяти, пока не получите целое число. Затем вы можете выполнить обычный процесс деления. Получив окончательный ответ, обязательно разделите его на те же степени 10, на которые вы делили ранее.
Все, что вам нужно сделать, это умножить десятичную дробь на степени десяти, пока не получите целое число. Затем вы можете выполнить обычный процесс деления. Получив окончательный ответ, обязательно разделите его на те же степени 10, на которые вы делили ранее.
Как пользоваться калькулятором делений?
Калькулятор деления — это инструмент, который используется для быстрого решения задач на деление в течение нескольких секунд. Попробуйте сейчас калькулятор деления Cuemath для решения задач, основанных на делении, и получите ответы за считанные секунды одним щелчком мыши.
Какие правила умножения и деления целых чисел?
Ниже приведены правила умножения и деления целых чисел:
- Положительный ÷ / × положительный = положительный
- Отрицательный ÷ / × отрицательный = положительный
- Отрицательный ÷ / × положительный = отрицательный
- Положительный ÷ / × отрицательный = отрицательный
Что такое символ деления?
Есть два символа деления: ÷ и /. ÷ рисуется путем размещения двух маленьких точек сверху и снизу небольшой горизонтальной линии. И знак / используется в основном с дробями, отношениями и процентами.
÷ рисуется путем размещения двух маленьких точек сверху и снизу небольшой горизонтальной линии. И знак / используется в основном с дробями, отношениями и процентами.
Почему деление на ноль не определено?
Деление на ноль не определено, потому что нельзя делить любое число на ноль. Это потому, что когда любое число умножается на ноль, ответ равен 0. Теперь подумайте об обратном. 1/0 будет иметь бесконечное значение. Мы не можем количественно определить это значение в математике. Следовательно, деление любого числа на ноль неопределенно.
Что такое фактор? [Определение, факты и примеры]
Что такое фактор?
Множитель — это число, которое делится на другое число без остатка. Другими словами, если умножение двух целых чисел дает нам произведение, то числа, которые мы умножаем, являются делителями произведения, потому что они делятся на произведение.
Есть два метода нахождения множителей: умножение и деление. Кроме того, могут применяться правила делимости.
Пример: Рассмотрим число 8. 8 может быть произведением 1 и 8, а также 2 и 4. В результате делители 8 равны 1, 2, 4, 8. Следовательно, при нахождении или при решении задач на множители учитываются только положительные числа, целые числа и не дробные числа.
Общая формула, которую следует запомнить, состоит в том, что a и b являются множителями произведения ab.
2 ✕ 3 = 6. Следовательно, 2 и 3 являются делителями 6. При делении 6 на 2 или 3 остатка нет.
9 ✕ 3 = 27. Следовательно, 9 и 3 являются делителями 27. Здесь не дает остатка при делении 27 на 9 или 3.
7 ✕ 5 = 35. Следовательно, 5 и 7 являются делителями 35. При делении 35 на 5 или 7 остатка нет.
Пример: Найдите все множители числа 10.
Свойства множителей
- Множители никогда не бывают десятичными или дробными; это только целые числа или целые числа.
- Все четные числа имеют множитель 2.
- 5 — множитель для всех чисел, оканчивающихся на 0 и 5.

- Все числа больше 0 и оканчивающиеся на 0 имеют множители 2, 5 и 10.
- Факторинг — распространенный способ решения или упрощения алгебраических выражений.
Факторизация простых чисел
Когда мы записываем число как произведение всех его простых множителей, это называется факторизацией простых чисел. Каждое число в простой факторизации является простым числом. Чтобы записать число как произведение простых множителей, иногда нам, возможно, придется повторить и множители.
Пример: Чтобы записать простую факторизацию числа 8, мы можем записать 8 = 2 ✕ 2 ✕ 2, т. е. простой делитель 2 повторяется три раза.
Реальные приложения факторизации
Равное деление. Если шесть человек соберутся вместе, чтобы съесть целую пиццу, разрезанную на 24 ломтика, будет справедливо, если каждый получит равное количество ломтиков. Следовательно, эту пиццу можно разделить на равные доли, потому что 6 (количество людей) — это коэффициент 24 (количество кусочков пиццы). Когда вы делите 24 на 6, вы получаете 4, и каждый человек получает четыре ломтика!
Когда вы делите 24 на 6, вы получаете 4, и каждый человек получает четыре ломтика!
Факторинг и деньги. Обмен денег и их разделение на более мелкие единицы в значительной степени зависят от факторинга. Например, в Америке четыре четверти равны одному доллару. В Индии рупия делилась на 1 пайсу, 5 пайс, 10 пайс, 25 пайс и 50 пайс.
Решенные примеры
Пример 1: Найдите все делители числа 20.
Шаг 1: Запишите все числа от 1 до 20. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Шаг 2 : Теперь проверьте, какие из этих чисел делятся на 20 и не оставляют остатка.
20/1 = 20
20/2 = 10
20/3 = не делится.
Продолжите делить 20 на каждое из этих чисел.
S шаг 3 : Делители 20 равны 1,2,4,5, 10 и 20. Единственные два числа, которые полностью делят 31, это 1 и 31.
Таким образом, делители 31 равны 1 и 31.
Пример 3: Найти простые делители числа 144. Простые множители — это простые числа. Делителями таких чисел являются 1 и само число. Например, 13 — простое число, потому что делители этого числа равны 1 и 13.
Рассмотрим число 144. Начните с рассмотрения наименьшего возможного делителя, т. е. 2.
144 = 2 x 72 = 2 x 2 x 36 = 2 x 2 x 2 x 18 = 2 x 2 x 2 x 2 x 9 = 2 x 2 x 2 x 2 x 3 x 3
Таким образом, простые делители числа 144 равны 2 и 3, так как эти множители являются простыми числами.
SplashLearn сочетает наглядные материалы с теорией, чтобы представить сложные темы, такие как факторы, в удобном для запоминания формате. Посетите веб-сайт, чтобы узнать об интересных математических концепциях.
Практические задачи
1, 2, 5, 10
1, 2, 3, 7
3, 5, 9, 10
1, 3, 5, 10
Правильный ответ: 1, 2, 5, 10
Все остальные варианты имеют 3 в качестве одного из множителей, тогда как 3 не делит число 10 полностью. При делении 10 на 3 получается остаток.
При делении 10 на 3 получается остаток.
3, 9, 27, 1
1, 3, 9, 4
5, 9, 4, 0
2, 3, 5, 1
Правильный ответ: 3, 9, 27, 1
Варианты 2 и 3 имеют число четыре (4) как один из множителей числа 27, тогда как число 4 не делит 27 полностью. Вариант 4 имеет число 5 как один из множителей 27, что неверно, поскольку 5 не делит 27 полностью. Когда 27 делится на 4 или 5, мы получаем остаток, следовательно, 4 и 5 не являются множителями 27.
1, 3, 6, 7, 9
2, 6, 12, 1, 0
4, 3, 12, 9
1, 3, 4, 2, 6, 12
Правильный ответ: 1, 3, 4, 2, 6, 12
При делении 12 на 1, 3, 4, 2, 6 и 12 не остается остатка.
5, 10, 15, 1
1, 3, 5 , 15
3, 5, 7
1, 2, 3, 5
Правильный ответ: 1, 3, 5, 15
При делении 15 на 1, 3, 5 и 15 остатка не остается.
Часто задаваемые вопросы
Какие факторы?
Множитель — это число, которое можно умножить, чтобы получить определенное число в математике (например, 5 и 8 — это множители 40).
Как факторинг используется в реальной жизни?
Факторинг — ценный навык в реальной жизни. Типичные приложения включают в себя деление чего-либо на равные части, обмен денег, сравнение цен, определение времени и выполнение вычислений во время путешествий.
В чем важность изучения простых множителей?
Простые факторы важны для людей, которые пытаются построить (или взломать) секретные коды на основе чисел и должны знать о факторизации. Это известно как криптография или шифрование. Из-за сложности факторизации очень больших чисел, что может занять много времени у компьютеров.
Как найти множитель в математике?
Вот пошаговое руководство по нахождению множителя любого числа в математике. 1. Начните с рассмотрения наименьших натуральных чисел, таких как 2, 3 и т. д.
2. Разделите число на наименьшее натуральное число, на которое оно может быть разделено.
3. Продолжайте делить число на наименьшее возможное натуральное число, что даст в остатке 0.
4. Остановитесь, когда число будет полностью разделено, чтобы получить 1 в качестве частного.
5. Числа, которые вы использовали для деления исходного числа, являются делителями этого числа.
IXL | Изучайте математику в 3-м классе
IXL | Изучайте математику в 3 классе1
Четным или нечетным
2
Чет или нечет: шаблоны сложения
3
Чет или нечет: схемы умножения
4
Пропустить подсчет
5
Головоломки с пропуском счета
6
Последовательности чисел
7
Запишите числа словами
8
Римские цифры I, V, X, L, C, D, M
9
Сравните числа
10
Какое число больше/меньше?
11
Номера заказов
12
Сравнение: со сложением и вычитанием
13
Многоступенчатые неравенства
1
Размещение моделей до тысяч
2
Местоимения до тысяч
3
Местоимения до сотен тысяч
4
Значение цифры
5
Преобразование в/из числа
6
Преобразование между разрядными значениями
7
Преобразование из расширенной формы
8
Преобразование между стандартной и расширенной формой
9
Проблемы со значением места
1
Добавить два числа до трех цифр
2
Дополнительные таблицы ввода/вывода: до трех цифр
3
Сложите два числа до трех цифр: текстовые задачи
4
Завершите добавочное предложение: до трех цифр
5
Уравнения сложения баланса: до трех цифр
6
Используйте компенсацию для добавления: до трех цифр
7
Сложите три числа до трех цифр каждое
8
Сложите три числа до трех цифр каждое: текстовые задачи
9
Сложение до трех цифр: вставьте пропущенные цифры
10
Добавить два числа до четырех цифр
11
Сложите два числа до четырех цифр: текстовые задачи
12
Завершите дополнительное предложение: до четырех цифр
13
Сложите три числа до четырех цифр каждое
14
Сложите три числа до четырех цифр каждое: текстовые задачи
15
Сложение до четырех цифр: вставьте пропущенные цифры
16
Добавление шаблонов по возрастанию разрядных значений
17
Сложите два числа до шести цифр
1
Вычитание чисел до трех цифр
2
Таблицы ввода/вывода вычитания: до трех цифр
3
Вычитание чисел до трех цифр: текстовые задачи
4
Вычесть через нули
5
Завершите предложение вычитания: до трех цифр
6
Уравнения вычитания баланса: до трех цифр
7
Используйте компенсацию для вычитания: до трех цифр
8
Шаблоны вычитания по возрастанию разрядных значений
9
Вычитание чисел с четырьмя и более цифрами
10
Вычитание: вставь пропущенные цифры
1
Подсчитайте равные группы
2
Определите выражения умножения для равных групп
3
Напишите предложения на умножение для равных групп
4
Связать сложение и умножение для равных групп
5
Определение выражений умножения для массивов
6
Запишите предложения на умножение для массивов
7
Напишите два предложения умножения для массива
8
Создайте массивы для моделирования умножения
9
Запишите предложения на умножение числовых рядов.

1
Умножить на 0
2
Умножить на 1
3
Умножить на 2
4
Умножить на 3
5
Умножить на 4
6
Умножить на 5
7
Умножить на 6
8
Умножить на 7
9
Умножить на 8
10
Умножить на 9
11
Умножить на 10
12
Умножить на 11
13
Умножить на 12
1
Факты умножения на 2, 3, 4, 5 и 10
2
Факты умножения на 2, 3, 4, 5 и 10: правда или ложь?
3
Факты умножения на 2, 3, 4, 5 и 10: сортировка
4
Факты умножения на 2, 3, 4, 5 и 10: найти недостающий множитель
5
Факты умножения на 6, 7, 8 и 9
6
Факты умножения на 6, 7, 8 и 9: правда или ложь?
7
Факты умножения на 6, 7, 8 и 9: сортировка
8
Факты умножения на 6, 7, 8 и 9: найти недостающий множитель
9
Факты умножения до 10
10
Факты умножения до 10: правда или ложь?
11
Факты умножения до 10: сортировка
12
Факты умножения до 10: найти недостающий множитель
13
Факты умножения до 10: выберите недостающие множители
14
Умножение предложений до 10: правда или ложь?
15
Факты умножения на 12
16
Факты умножения до 12: правда или ложь?
17
Факты умножения до 12: найти недостающий множитель
18
Факты умножения до 12: выберите недостающие множители
19
Умножение предложений до 12: правда или ложь?
20
Умножьте на 0 или 1: завершите предложение
21
Квадраты до 10 х 10
- “>
1
Умножьте на кратное десяти, используя разрядное значение
2
Умножить на кратное десяти
3
Образцы умножения по возрастанию разрядных значений
4
Умножение чисел, заканчивающихся нулями
5
Таблицы ввода/вывода умножения
6
Таблицы ввода/вывода умножения: найти правило
7
Проблемы со словами на умножение
8
Проблемы со словами на умножение: найти недостающий множитель
9
Сравнивать числа с помощью умножения
10
Сравнивать числа с помощью умножения: текстовые задачи
11
Умножайте однозначные числа на подростковые числа, используя сетки
12
Умножение однозначных чисел на двузначные с использованием моделей площадей I
13
Умножение однозначных чисел на двузначные с использованием моделей площадей II
14
Умножение однозначных чисел на двузначные
15
Умножение однозначных чисел на двузначные: текстовые задачи
16
Умножать однозначные числа на трехзначные, используя модели площадей I
17
Умножение однозначных чисел на трехзначные с использованием моделей площадей II
18
Умножение однозначных чисел на трехзначные
19
Умножение однозначных чисел на трехзначные: текстовые задачи
20
Умножение трех и более чисел
21
Умножение трех и более чисел: текстовые задачи
22
Умножение решетки
1
Разделите, посчитав равные группы
2
Напишите предложения с разделением на группы
•
Новинка! Разделение предложений с 1 и 0
3
Связать умножение и деление для групп
4
Напишите предложения деления для массивов
5
Свяжите умножение и деление для массивов
1
Разделить на 1
2
Разделить на 2
3
Разделить на 3
4
Разделить на 4
5
Разделить на 5
6
Разделить на 6
7
Разделить на 7
8
Разделить на 8
9
Разделить на 9
10
Разделить на 10
11
Разделить на 11
12
Разделить на 12
1
Факты деления на 2, 3, 4, 5 и 10
2
Факты деления на 2, 3, 4, 5 и 10: правда или ложь?
3
Факты деления на 2, 3, 4, 5 и 10: сортировка
4
Факты деления на 6, 7, 8 и 9
5
Факты деления на 6, 7, 8 и 9: правда или ложь?
6
Факты деления на 6, 7, 8 и 9: сортировка
7
Факты деления до 10
8
Факты деления до 10: правда или ложь?
9
Факты деления до 10: сортировка
10
Факты деления до 10: найди пропущенное число
11
Факты деления до 10: выберите недостающие числа
12
Предложения с делением до 10: правда или ложь?
13
Факты деления до 12
14
Факты деления до 12: правда или ложь?
15
Факты деления до 12: найди пропущенное число
16
Факты деления до 12: выберите недостающие числа
17
Предложения с делением до 12: правда или ложь?
1
Шаблоны деления по возрастанию разрядных значений
2
Разделить числа, заканчивающиеся нулями
3
Таблицы ввода/вывода отдела
4
Таблицы ввода-вывода деления: найти правило
5
Проблемы со словами на деление
6
Разделить трехзначное число
7
Делим трехзначные числа: текстовые задачи
8
Разделите большие числа
9
Делим большие числа: текстовые задачи
10
Правила делимости на 2, 5 и 10
11
Правила делимости на 3, 6 и 9
12
Правила делимости на 4 и 8
1
Факты сложения, вычитания, умножения и деления
2
Завершите сложение, вычитание, умножение или деление предложения
3
Факты умножения и деления до 5: правда или ложь?
4
Факты умножения и деления до 10
5
Факты умножения и деления до 10: правда или ложь?
6
Факты умножения и деления до 12: правда или ложь?
7
Умножение и деление предложений до 12: правда или ложь?
8
Складывать, вычитать, умножать и делить
9
Добавлять и вычитать данные из таблиц
10
Словесные задачи на сложение и вычитание
11
Словесные задачи на умножение и деление
12
Задачи на сравнение слов: сложение или умножение?
13
Словесные задачи на сложение, вычитание, умножение и деление
14
Выполнение нескольких операций с целыми числами
15
Двухшаговые задачи на сложение и вычитание
16
Двухшаговые задачи на умножение и деление
17
Двухшаговые смешанные задачи со словами
1
Условия сложения, вычитания, умножения и деления
2
Скобки
3
Свойства дополнения
4
Завершите уравнение, используя свойства сложения
5
Добавить с помощью свойств
6
Свойства умножения
7
Распределительное свойство: найти недостающий множитель
8
Умножьте, используя распределительное свойство
9
Решите, используя свойства умножения
10
Соотнесите сложение и умножение
11
Связать умножение и деление
1
Определить уравнения
2
Решите для переменной: только сложение и вычитание
3
Решите для переменной: только умножение и деление
4
Решите для переменной
5
Напишите уравнения переменных для представления текстовых задач: только умножение и деление
6
Напишите переменные уравнения для представления текстовых задач
1
Округлите до ближайших десяти или сотен, используя числовую прямую
- г.

2
Округлите до ближайших десяти или сотен
3
Округлить до ближайших десяти или сотен в таблице
4
Округлить до наибольшего разряда
5
Круглые суммы денег с точностью до доллара
6
Головоломки с округлением
7
Оценить суммы округлением: до 1000
8
Оценить суммы округлением: до 1 000 000
9
Оцените суммы округлением: текстовые задачи
10
Оцените суммы, используя совместимые числа
11
Оценить разницу округлением: до 1000
12
Оценить разницу округлением: до 1 000 000
- г.

13
Оценить разницу округлением: текстовые задачи
14
Оцените различия, используя совместимые числа
15
Оценка для сравнения сумм и разностей
16
Оценить суммы и разности: текстовые задачи
17
Оценить продукты
18
Оцените коэффициенты
19
Двухэтапные задачи со словами: определите разумные ответы
1
Угадай число
2
Сделать наибольшее или наименьшее возможное число
3
Найти заказ
4
Возрастные пазлы
5
Найдите два числа по сумме и разности
6
Найдите два числа на основе суммы, разности, произведения и частного
1
Повторяющиеся узоры
2
Шаблоны выращивания
3
Найдите следующую фигуру в шаблоне
4
Завершите повторяющийся узор
5
Сделать повторяющийся узор
6
Найдите следующую строку в растущем шаблоне
1
Считайте монеты и купюры – купюра до 5 долларов
2
Сосчитайте монеты и купюры со словами – до 5 долларов
3
Покупки – хватит ли денег – до 10$
4
На какой картинке больше?
5
Правильная сумма сдачи
6
Внесение изменений
7
Неравенство с деньгами
8
Расположите денежные суммы по порядку
9
Складывать и вычитать денежные суммы
10
Сложите денежные суммы – словесные задачи
11
Прайс-листы
1
Сопоставьте часы и время
2
Сопоставьте аналоговые и цифровые часы
3
Чтение часов и запись времени
4
ЯВЛЯЮСЬ.
 или П.М.
или П.М.5
Время записи
6
Прошедшее время: найти время окончания
7
Найдите прошедшее время
8
Задачи на прошедшее время: найти время окончания
9
Задачи на прошедшее время: найти прошедшее время
10
Шаблоны времени
11
Преобразование между часами и долями часов
12
Соотнесите единицы времени
13
Читать календарь
14
Графики чтения
15
Хронология
1
Объекты на координатной плоскости
2
Координатные плоскости как карты
3
График точек на координатной плоскости
4
Интерпретация итоговых диаграмм
5
Читать таблицу
6
Интерпретация гистограмм
7
Используйте гистограммы для решения проблем
8
Создание гистограмм
9
Интерпретировать линейные графики
10
Создание линейных графиков
11
Создание линейных графиков с дробями
12
Интерпретировать пиктограммы
13
Создание пиктограмм
14
Интерпретировать линейные графики
15
Создание линейных графиков
16
Подсчет фигур на диаграмме Венна
17
Сортировка фигур в диаграмму Венна
18
Определенные, вероятные, маловероятные и невозможные
1
Определите равные части
2
Делайте половинки, трети и четверти
3
Сделайте шестые и восьмые
4
Сделайте половинки, трети, четверти, шестые и восьмые
5
Понимание дробей: столбцы дробей
6
Понимание дробей: модели площадей
7
Показать дроби: столбцы дробей
8
Показать дроби: модели площадей
9
Сопоставьте дроби с моделями: половинки, трети и четверти
10
Сопоставьте дроби единиц с моделями
11
Сопоставьте дроби с моделями
12
Запишите дроби, используя числа и слова
13
Доли числовых строк: дроби единиц
14
Доли числовых рядов: половинки, четверти и восьмые
15
Доли числовых строк
16
Определите дроби единиц на числовых линиях
17
Определите дроби в числовых рядах
18
Отображение дробей единиц измерения на числовых линиях
19
Графические дроби меньше 1 на числовых линиях
20
График дробей на числовых линиях
21
Отображение меньших или больших дробей на числовой прямой
22
Дроби группы: единичные дроби
23
Фракции группы
24
Дроби единиц: моделирование текстовых задач
25
Единичные дроби: текстовые задачи
26
Доли целого: моделирование словесных задач
27
Дроби целого: текстовые задачи
28
Дроби группы: текстовые задачи
29
Сопоставьте смешанные числа с моделями
30
Названия слов для смешанных чисел
•
Новинка! Найдите эквивалентные дроби, используя полоски дробей
1
Найдите эквивалентные дроби, используя модели площадей: две модели
2
Найдите эквивалентные дроби, используя модели площадей: одна модель
3
Определите эквивалентные дроби на числовых рядах
4
Найдите эквивалентные дроби, используя числовые линии
5
График эквивалентных дробей на числовых линиях
6
Определите эквивалентные дроби
7
Найдите эквивалентные дроби
8
Графические дроби, эквивалентные 1 на числовых линиях
9
Выберите дроби, эквивалентные целым числам, используя модели
10
Выберите дроби, эквивалентные целым числам
11
Найдите дроби, эквивалентные целым числам
12
Найдите эквивалентные дроби со знаменателями 10 и 100
13
Запишите дроби в меньших терминах
1
Сравните дроби с одинаковыми знаменателями, используя модели
2
Сравните дроби с одинаковыми числителями, используя модели
3
Сравните дроби, используя модели
4
Сравните дроби, используя числовые линии
5
Нарисуйте и сравните дроби с одинаковыми знаменателями на числовых линиях
6
График и сравнение дробей с одинаковыми числителями на числовых рядах
7
График и сравнение дробей на числовых линиях
8
Сравнивать дроби с одинаковыми знаменателями
9
Сравнивать дроби с одинаковыми числителями
10
Сравните дроби
11
Сравнивайте дроби в рецептах
12
Эталонные дроби
13
Сравните дроби, используя эталоны
14
График и порядок дробей на числовых линиях
15
Упорядочить дроби с одинаковыми знаменателями
16
Упорядочить дроби с одинаковыми числителями
17
Порядок дробей
1
Дроби числа – единичные дроби
2
Доли числа
3
Дроби числа – единичные дроби: текстовые задачи
4
Доли числа: текстовые задачи
5
Разложить дроби на единичные дроби
6
Сложите дроби с одинаковыми знаменателями, используя числовые строки
7
Вычитание дробей с одинаковыми знаменателями с помощью числовых линий
8
Складывать и вычитать дроби с одинаковыми знаменателями
9
Складывать и вычитать дроби с одинаковыми знаменателями: текстовые задачи
1
Читать термометр
2
Разумная температура
3
Измерьте с помощью дюймовой линейки
4
Проблемы со словами измерения
5
Какая обычная единица длины подходит?
6
Какая обычная единица веса подходит?
7
Какая обычная единица объема является подходящей?
8
Какая обычная единица подходит?
9
Сравнивайте и конвертируйте общепринятые единицы длины
10
Сравнивайте и конвертируйте обычные единицы веса
11
Сравните и конвертируйте обычные единицы объема
12
Таблицы преобразования – общепринятые единицы
13
Сравните обычные единицы, умножив
14
Какая метрическая единица длины подходит?
15
Какая метрическая единица веса подходит?
16
Какая метрическая единица объема подходит?
17
Какая метрическая единица подходит?
18
Сравните и конвертируйте метрические единицы длины
19
Сравните и конвертируйте метрические единицы веса
20
Сравните и конвертируйте метрические единицы объема
21
Таблицы преобразования – метрические единицы
22
Выберите подходящий измерительный инструмент
1
Определение двумерных фигур
2
Подсчитайте и сравните стороны и вершины
3
Открытые и закрытые формы
4
Это полигон?
5
Линии, отрезки и лучи
6
Углы больше, меньше или равны прямому углу
7
Параллельные, перпендикулярные и пересекающиеся прямые
8
Отражение, вращение и перевод
9
Определите конгруэнтные формы
10
Симметрия
1
Остроугольные, тупоугольные и прямоугольные треугольники
2
Разносторонние, равнобедренные и равнобедренные треугольники
3
Параллельные стороны в четырехугольниках
4
Определите параллелограммы
5
Определить трапеции
6
Определить прямоугольники
7
Определите ромбы
8
Классифицировать четырехугольники
9
Нарисуйте четырехугольники
1
Определять трехмерные фигуры
2
Подсчет вершин, ребер и граней
3
Определение граней трехмерных фигур
4
Формы повседневных предметов I
5
Формы повседневных предметов II
1
Периметр прямоугольников
2
Периметр четырехугольников
3
Периметр прямолинейных фигур
4
Периметр полигонов
5
Периметр: найти недостающую длину стороны
6
Периметр: словесные задачи
7
Найдите площади фигур, составленных из единичных квадратов.

8
Выбрать фигуры с заданной площадью
9
Выберите две фигуры с одинаковой площадью
10
Замостить прямоугольник и найти площадь
11
Умножьте, чтобы найти площадь прямоугольника, составленного из единичных квадратов.

12
Создание фигур с заданной площадью
13
Создание прямоугольников с заданной площадью
14
Найдите площади прямоугольников и квадратов
15
Найдите недостающую длину стороны прямоугольника
16
Найдите площадь прямоугольников, в которых отсутствуют единичные квадраты.

17
Найдите площадь прямоугольников: текстовые задачи.
18
Найдите площади сложных фигур, разделив их на прямоугольники.
19
Найдите площадь сложных фигур.

20
Найдите площадь между двумя прямоугольниками
21
Сравните площадь и периметр двух фигур
22
Использование площади и периметра для определения стоимости
23
Связь между площадью и периметром: найти периметр
24
Связь между площадью и периметром: найти площадь
Числовой смысл
- Значение места
- Запись чисел в развернутом виде
- Запись чисел в словесной форме
- Округление чисел
- Сравнение чисел
Сложение и вычитание
- Сложение с числовыми строками
- Многозначное сложение
- Вычитание с числовыми строками
- Многозначное вычитание
Умножение
- Умножение как многократное сложение
- Умножение с массивами
- Условия умножения
- Таблицы умножения
- Умножение кратных 10
- Квадратные числа
Отдел
- Разделение с помощью массивов
- Условия раздела
- Деление кратных 10
- Правила делимости
Недвижимость и смешанные операции
- Коммутативное свойство
- Ассоциативное свойство
- Распределительная собственность
- Свойство идентичности
- Семейства фактов
Дроби
- Обзор фракций
- Понимание дробей
- Модели фракционной площади
- Дроби на числовой прямой
- Фракции набора
- Эквивалентные дроби
- Сравнение дробей
Геометрия
- Виды четырехугольников
- Параллелограммы
- ромбы
- прямоугольники
- Квадраты
- Трапеции
- Воздушные змеи
- Правильные многоугольники
- Периметр
- Площадь прямоугольников
- Площадь сложных фигур
Данные и измерения
- Линейные графики
- Как сказать время
- Пройденное время
- Метрические единицы измерения
- Привычные единицы измерения
Использование разрядного значения для понимания умножения
Сегодня многие педагоги в какой-то степени согласятся с тем, что в математическом образовании произошел сдвиг на многих уровнях и во всех классах. Будучи студентом, человек должен часто демонстрировать понимание концепций математики, прежде чем его мозг в процессе развития сможет понять, что математика — это больше, чем процедуры или набор правил для достижения конкретного решения. Мозг младшего школьника еще только формируется, он постоянно впитывает информацию вокруг себя. Таким образом, ответ ребенка на математический запрос, как правило, основан на его или ее текущей информации, которая также может меняться в зависимости от деятельности.
Будучи студентом, человек должен часто демонстрировать понимание концепций математики, прежде чем его мозг в процессе развития сможет понять, что математика — это больше, чем процедуры или набор правил для достижения конкретного решения. Мозг младшего школьника еще только формируется, он постоянно впитывает информацию вокруг себя. Таким образом, ответ ребенка на математический запрос, как правило, основан на его или ее текущей информации, которая также может меняться в зависимости от деятельности.
По моему опыту работы учителем математики в четвертом классе, большинство моих учеников испытывают сильную неприязнь ко всему, что связано с умножением. Я привыкла к стонам и стонам, а также к крикам «это слишком сложно» или «это слишком долго» от моих учеников. Я часто задаюсь вопросом, почему мои ученики так себя чувствуют? Что еще более важно, как я могу помочь им чувствовать себя более уверенно в своей способности решать задачи на умножение? Что делает его слишком сложным или слишком длинным? Что вообще значит «слишком долго»? Имеют ли мои студенты в виду количество процедурных шагов, необходимых для получения продукта? На самом деле, некоторые из их чувств относительно этих навыков могут быть связаны с их общими чувствами к математике, которые могли быть повреждены негативным опытом с предыдущим учителем, взглядами родителей/опекунов на математику или отсутствием поддержки, или даже прошлой успеваемостью на уроках математики. в младших классах. В этих чувствах также могут быть элементы низкой самооценки и неуверенности в себе. Четвероклассники могут быть очень впечатлительными умами, ищущими одобрения сверстников.
в младших классах. В этих чувствах также могут быть элементы низкой самооценки и неуверенности в себе. Четвероклассники могут быть очень впечатлительными умами, ищущими одобрения сверстников.
Когда я думаю о своем личном опыте в начальной школе, я отчетливо вспоминаю учителя, который стоял перед классом и давал указания, показывал нам шаги по решению математической задачи дня, а затем давал классу решать задачи самостоятельно. Практически не было обучения в малых группах, передвижения по классу или использования технологий. Однако в классе был взрослый, который, как я искренне верил, заботился о моем успехе в ее классе, а также о моем общем росте в детстве. Я мог бы продолжать и продолжать о важности того, как отношение ученика к тому, как учитель относится к нему или к ней, может повлиять на успеваемость ученика в классе, но это привело бы к совершенно другому разделу.
Я надеюсь, что созданный мной учебный модуль уменьшит тревогу моих будущих учеников, когда мы углубимся в то, как основные принципы разряда могут помочь нам понять и решить задачи на умножение. Мы изучим систему счисления с основанием 10, роль разрядного значения в этой системе и то, как ясное и полное понимание того и другого необходимо для концептуализации параметров умножения, прежде чем можно будет тщательно применять процедуры, необходимые для исследования и решения многозначных уравнений. как того требует руководство штата, путем демонстрации учащимся того, что умножение является расширением навыков сложения, которыми они уже обладают. Я также продемонстрирую, как числа можно разбить на более удобные части, чтобы получить продукт, искомый в задаче, что поможет моим ученикам лучше визуализировать конечный результат. Я считаю, что более глубокое понимание концепций, лежащих в основе алгоритмов, повысит их общую уверенность, будет способствовать развитию мышления и повысит степень их исследования.
Мы изучим систему счисления с основанием 10, роль разрядного значения в этой системе и то, как ясное и полное понимание того и другого необходимо для концептуализации параметров умножения, прежде чем можно будет тщательно применять процедуры, необходимые для исследования и решения многозначных уравнений. как того требует руководство штата, путем демонстрации учащимся того, что умножение является расширением навыков сложения, которыми они уже обладают. Я также продемонстрирую, как числа можно разбить на более удобные части, чтобы получить продукт, искомый в задаче, что поможет моим ученикам лучше визуализировать конечный результат. Я считаю, что более глубокое понимание концепций, лежащих в основе алгоритмов, повысит их общую уверенность, будет способствовать развитию мышления и повысит степень их исследования.
После того, как будет заложена четкая основа, я сосредоточусь на требованиях Виргинских стандартов обучения для третьеклассников, включая умножение как однозначных, так и многозначных чисел. Хотя я не занимаюсь Стандартами обучения или стандартами Common Core по математике для третьеклассников, я считаю, что рассмотрение целей предыдущего года, а также более широко используемых стандартов может оказаться полезным для демонстрации того, как цели меняются из года в год. года и с чем должны были столкнуться учащиеся до прихода в четвертый класс. Наличие этой информации дает мне основу для доступа к предыдущим знаниям учащегося, а также для оценки того, как он усвоил знания, полученные в прошлом году.
Хотя я не занимаюсь Стандартами обучения или стандартами Common Core по математике для третьеклассников, я считаю, что рассмотрение целей предыдущего года, а также более широко используемых стандартов может оказаться полезным для демонстрации того, как цели меняются из года в год. года и с чем должны были столкнуться учащиеся до прихода в четвертый класс. Наличие этой информации дает мне основу для доступа к предыдущим знаниям учащегося, а также для оценки того, как он усвоил знания, полученные в прошлом году.
По мере того, как мы переходим от концептуализации умножения к применению и вычислениям, я углублюсь в несколько алгоритмов умножения. Я расскажу о трех методах умножения целых чисел: модели площадей, метод ящиков и традиционный американский алгоритм умножения (который я обычно называю «старой школой» в своем классе, поскольку он отдает дань уважения тому, как родители моих учеников и я учились умножению). Каждый из методов будет смоделирован для учащихся с упором на роль, которую играет значение места, и на то, что на самом деле означают цифры после того, как алгоритм будет введен в действие и решен.
Поскольку я хочу, чтобы мои ученики по-настоящему поняли, что математические связи могут быть установлены повсюду, я также планирую включить иллюстрированные книги по математике во введение каждого навыка. Например, книга Two Ways to Count to Ten: A Liberian Folktale 1 , пересказанная Руби Ди, показывает аудитории, что проще и быстрее пропустить счет, т. е. использовать умножение, а не считать единицами. Я могу использовать этот текст, чтобы ответить на жалобу моих учеников на то, что «требуется слишком много времени» для решения задач на умножение. Многие из вопросов, основанных на исследованиях, которые мы будем решать в классе, будут сосредоточены на повседневных событиях, с которыми мои ученики столкнутся в течение учебного года. (Примеры вопросов перечислены в разделе ресурсов)
Я перехожу на девятый год работы учителем четвертого класса в школу первого уровня. В течение нескольких лет, как и многие учителя начальной школы по всей стране, я весь год преподавал все основные предметы (чтение, письмо, математику, естественные науки и социальные науки/историю) одному классу учеников. Три года назад моя школа перешла на ведомственную модель для учащихся четвертого класса (пятый класс уже следовал этой модели). У нас есть три учителя четвертого класса, и каждый учитель проводит обучение по одному протестированному основному предмету для всего класса, а также науке (которая не является предметом государственной проверки в этом классе) в каждом соответствующем классе. Недавно я закончил второй год преподавания математики для всего класса. В прошлом учебном году я обучал около 80 учеников, которые были разбиты на три класса по 23-30 учеников, каждый из которых длился около 80 минут каждый день. Хотя моя школа не так подвержена кратковременности (учащиеся, которые переходят из школы в школу), как некоторые другие школы округа, в определенное время учебного года у нас случаются заметные всплески переменчивости, которые влияют на способность учащихся учиться. понятия основательно.
Три года назад моя школа перешла на ведомственную модель для учащихся четвертого класса (пятый класс уже следовал этой модели). У нас есть три учителя четвертого класса, и каждый учитель проводит обучение по одному протестированному основному предмету для всего класса, а также науке (которая не является предметом государственной проверки в этом классе) в каждом соответствующем классе. Недавно я закончил второй год преподавания математики для всего класса. В прошлом учебном году я обучал около 80 учеников, которые были разбиты на три класса по 23-30 учеников, каждый из которых длился около 80 минут каждый день. Хотя моя школа не так подвержена кратковременности (учащиеся, которые переходят из школы в школу), как некоторые другие школы округа, в определенное время учебного года у нас случаются заметные всплески переменчивости, которые влияют на способность учащихся учиться. понятия основательно.
У меня есть несколько причин, по которым я хочу написать этот модуль об использовании разрядного значения для понимания умножения. Во-первых, я хочу, чтобы мои студенты знали, как использовать основные принципы понимания чисел, чтобы помочь им в решении более сложных задач и продемонстрировать, как это понимание является движущей силой в их общем понимании математики в их будущих курсах. Смысл числа можно определить как:
Во-первых, я хочу, чтобы мои студенты знали, как использовать основные принципы понимания чисел, чтобы помочь им в решении более сложных задач и продемонстрировать, как это понимание является движущей силой в их общем понимании математики в их будущих курсах. Смысл числа можно определить как:
Способность человека использовать и понимать числа:
- зная их относительные значения,
- как их использовать для вынесения суждений,
- как их гибко использовать при сложении, вычитании, умножении или делении
- как разработать полезные стратегии при подсчете, измерении или оценке 2 .
Мои ученики испытывают большие трудности со всеми аспектами восприятия чисел. Создается впечатление, что учащиеся переходят из одного класса в другой без четкого понимания основ, что только увеличивает их общий дефицит по математике. Эти недостатки включают, помимо прочего, вычисления с базовым сложением, вычитание через нули и знание основных фактов умножения и деления. С такими недостатками в их фундаменте, как они могут успешно продвигаться к более сложным или ожидаемым уровням? Учащийся может бегло читать книгу, запоминать исторический вклад африканцев в поселение Джеймстаун и даже выполнять шаги научного метода, но как Пол Халмос 3 выражает это так: «Единственный способ выучить математику — это заниматься математикой».
С такими недостатками в их фундаменте, как они могут успешно продвигаться к более сложным или ожидаемым уровням? Учащийся может бегло читать книгу, запоминать исторический вклад африканцев в поселение Джеймстаун и даже выполнять шаги научного метода, но как Пол Халмос 3 выражает это так: «Единственный способ выучить математику — это заниматься математикой».
Во-вторых, для меня также жизненно важно, чтобы мои ученики начали чувствовать, что математика — это действительно то, что они могут делать, и что мы можем получать от этого удовольствие. За девять лет преподавания я имел удовольствие преподавать, наставлять и общаться с сотнями студентов ежегодно на разных уровнях в классе и за его пределами, но я не могу вспомнить ни одного студента, который просто сказал бы: «Я изучаю математику, мне легко». Многие ученики говорят: «Мне нравится математика, но я просто не понимаю ее». Самое распространенное утверждение: «Математика слишком сложна, поэтому мне она не нравится». Лично я принимаю все три утверждения такими, какие они есть, и я благодарен, что студент поделился со мной своими мыслями. Но при этом они знали, что я что-то сделаю с информацией. Я на 100% уверен в том, что знаю, что мои ученики верят, что я забочусь о них и хочу, чтобы они преуспели, и это большая честь, которой я всегда буду дорожить. Этот уровень доверия также позволяет мне доставлять им дискомфорт в отношении математики.
Лично я принимаю все три утверждения такими, какие они есть, и я благодарен, что студент поделился со мной своими мыслями. Но при этом они знали, что я что-то сделаю с информацией. Я на 100% уверен в том, что знаю, что мои ученики верят, что я забочусь о них и хочу, чтобы они преуспели, и это большая честь, которой я всегда буду дорожить. Этот уровень доверия также позволяет мне доставлять им дискомфорт в отношении математики.
В-третьих, слишком долго учащимся давали математические инструкции, основанные на простом получении решения, без понимания того, как они пришли к решению, и, что более важно, что означает решение с точки зрения исходной задачи. В этом модуле я хочу использовать эти компоненты, чтобы сделать понимание и применение моими учениками чувства числа полным кругом.
Система счисления с основанием 10
В системе счисления с основанием 10 используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.для формирования любого целого числа, а также для выражения десятичных дробей и дробей. Ноль в этой системе представляет собой заполнитель; например, 9099 означает, что в этом числе нет сотен. Чтобы правильно прочитать число, необходимо вставить ноль. Сьюзан Смит 4 утверждает, что десятичная система счисления — это позиционная система, в которой единица находится справа, а следующая позиция представляет основание, затем основание умножается на основание, и числа продолжаются таким образом. Это означает, что, поскольку основание нашей системы равно десяти, размер увеличивается в десять раз на каждом шаге или позиции. Другой важной особенностью системы счисления является то, что «значение целого числа есть сумма его частей или значение, приписываемое каждой цифре 9».3244 5 ». Когда вышеуказанные компоненты собраны вместе, мы можем использовать систему счисления для выполнения всех основных операций: сложения, вычитания, умножения и деления. Общая структура системы счисления с основанием 10, последовательность цифр, отношения цифр друг с другом в каждом числе обеспечивают нам основу для работы с числами связным образом.
Ноль в этой системе представляет собой заполнитель; например, 9099 означает, что в этом числе нет сотен. Чтобы правильно прочитать число, необходимо вставить ноль. Сьюзан Смит 4 утверждает, что десятичная система счисления — это позиционная система, в которой единица находится справа, а следующая позиция представляет основание, затем основание умножается на основание, и числа продолжаются таким образом. Это означает, что, поскольку основание нашей системы равно десяти, размер увеличивается в десять раз на каждом шаге или позиции. Другой важной особенностью системы счисления является то, что «значение целого числа есть сумма его частей или значение, приписываемое каждой цифре 9».3244 5 ». Когда вышеуказанные компоненты собраны вместе, мы можем использовать систему счисления для выполнения всех основных операций: сложения, вычитания, умножения и деления. Общая структура системы счисления с основанием 10, последовательность цифр, отношения цифр друг с другом в каждом числе обеспечивают нам основу для работы с числами связным образом. Howe и Epp 6 заявляют: «Мы надеемся, что раскрытие большего числа аспектов этой структуры улучшит концептуальное понимание и улучшит вычислительную гибкость, тем самым помогая сделать обучение математике более эффективным». Кроме того, понимание системы счисления с основанием улучшит способность учащихся понимать разрядное значение.
Howe и Epp 6 заявляют: «Мы надеемся, что раскрытие большего числа аспектов этой структуры улучшит концептуальное понимание и улучшит вычислительную гибкость, тем самым помогая сделать обучение математике более эффективным». Кроме того, понимание системы счисления с основанием улучшит способность учащихся понимать разрядное значение.
Место Значение
Значение разряда можно описать как предписывающее значение цифры на основе ее положения в числе. Другими словами, позиционное значение позволяет нам повторно использовать единую схему, которая назначает десять цифр в разных позициях в числе, чтобы сказать, сколько имеется каждой из групп. Например, 3 из 369 имеет значение 300, тогда как 3 из 39 имеет значение 30. Кроме того, прежде чем углубляться в математические концепции, мои ученики должны быть в состоянии надежно понять, что, когда кто-то спрашивает значение цифра 6 в числе 369это не 6 и не разряд десятков, а 60 или 6 десятков. Штейн и др. 7 повторяет, что «точное чтение и написание числительных, наряду с сильным концептуальным пониманием понятий разрядного значения, готовит учащихся к более сложным вычислениям и решению задач.
Howe-Reiter 8 представляет пять стадий понимания разрядности в помощь учителю начальной школы посредством подробного руководства о том, как обучение учащихся основам математики приводит к более глубокому концептуальному пониманию смысла чисел, что позволяет один, чтобы основываться на более строгих стандартах позже.
Пять стадий разрядности согласно Хоу и Райтеру следующие:
1. Напишите цифры-
369.
2. Признать, что число представляет собой сумму «частей разряда» или строительных блоков, которые явно показывают разрядность каждой цифры-
369 = 300 + 60 + 9.
3. Каждая единица разряда представляет собой произведение цифры, умноженной на единицу с основанием
.369 = (3 × 100) + (6 × 10) + (9 × 1).
4. Каждая единица с основанием десять является произведением некоторых копий основания (основание равно 10):
369 = 3 × (10 × 10) + 6 × 10 + 9 × 1.
Каждая десятичная единица является результатом умножения предыдущей на 10. Таким образом, десятичная единица равна 1, 10, 10 × 10 = 100, 10 × 10 × 10 = 1000 и так далее.
Таким образом, десятичная единица равна 1, 10, 10 × 10 = 100, 10 × 10 × 10 = 1000 и так далее.
5. Повторяющиеся произведения числа 10, которые часто называют степенями числа 10, можно удобно записать с использованием показателей степени:
369 = 3 × 10 2 + 6 × 10 1 + 9 × 10 0
Как выглядят пять стадий разряда в классе после решения задачи на умножение?
Если я куплю наггетсы из 4 и 6 штук в магазине Chick-fil-A для каждого ученика четвертого класса, сколько всего наггетсов у нас будет?
*количество студентов = 75 (только для демонстрационных целей)
1. Наггетсы из 4 и 6 частей = наггетсы из 10 штук; 75 студентов =
75 = 70 + 5 = 7 × 10 + 5 × 1, значит,
75 × 10 = (7 × 10 + 5 × 1) × 10 =
(70 × 10) × 10 + (5 × 1) × 10 =
7 × (10 × 10) + 5 × 10 =
700 + 50 =
750
Продукт в форме стоимости места будет выглядеть как оставшиеся этапы ниже:
2. 750 = 700 + 50 + 0
750 = 700 + 50 + 0
3. 750 = (7 х 100) + (5 х 10) + (0 х 1)
4. 750 = 7 х (10 х 10) + 5 х 10 + 0 х 1
5. 750 = 7 × 10 2 + 5 × 10 1 + 0 × 10 0
В четвертом классе мы обычно просматриваем и расширяем этап 1, поскольку учащиеся должны читать, писать и определять значение чисел до девяти цифр (что является увеличением по сравнению с требованием третьего класса, состоящим из шести цифр). Затем этот урок ведет ко второму этапу написания чисел в развернутой форме, и в большинстве классов мало что делается на этапах, следующих за этим этапом.
В моем классе было много раз, когда ученик читал число 66 как «шестьдесят шесть», но когда его просили написать число в развернутой форме, он писал «6 + 6». Еще одна ошибка, с которой я сталкивался на протяжении многих лет, заключается в том, что учащийся не демонстрирует понимания того, что положение цифры определяет ее значение. Это означает, что студент пишет 6009, когда его просят написать шестьсот девять, или 60029, когда его просят написать шестьсот двадцать девять. По мере того, как мы переходим к более крупным числам, на вопрос о значении цифры 4 в числе 430 516 802 703 студент может ответить «4» или «сто миллиардов» вместо «четыреста миллиардов». Эти простые, но критические ошибки служат мне сигналом тревоги. Как учитель, я знаю, что мне нужно вернуться назад и провести больше времени с этим учеником, чтобы улучшить его понимание отдельных частей разряда, которые составляют числа, перечисленные выше. Отсутствие времени в начальной школе для закрепления этого понимания приводит к тому, что учащийся еще больше упускает связь между разрядной стоимостью и вычислением.
По мере того, как мы переходим к более крупным числам, на вопрос о значении цифры 4 в числе 430 516 802 703 студент может ответить «4» или «сто миллиардов» вместо «четыреста миллиардов». Эти простые, но критические ошибки служат мне сигналом тревоги. Как учитель, я знаю, что мне нужно вернуться назад и провести больше времени с этим учеником, чтобы улучшить его понимание отдельных частей разряда, которые составляют числа, перечисленные выше. Отсутствие времени в начальной школе для закрепления этого понимания приводит к тому, что учащийся еще больше упускает связь между разрядной стоимостью и вычислением.
Проще говоря, разрядность — это то, что управляет всеми остальными арифметическими операциями. Понимание свойств операций также приводит к лучшему пониманию разрядного значения и вычислений. Мои ученики должны знать, почему мы объединяем эти числа, а затем разбиваем их на части и как это позволяет нам выполнять умножение. Они должны понимать, что единицы с основанием десять имеют разные размеры, и количество цифр говорит об этом размере, называемом порядком величины единицы 9. 3244 9 . Например,
3244 9 . Например,
9 = 9 × 1
30 = 3 × 10
300 = 3 × 100
3000 = 3 × 1000.
Из приведенной выше информации мы знаем, что 3000 означает 3 тысячи, потому что справа есть три позиции, заполненные нулями. Число 300 означает 3 сотни, потому что справа два разряда заполнены нулями, 30 означает 3 десятка или тридцать, так как справа один разряд или один ноль, а число 9 означает 9 единиц без оставшихся целых чисел. справа от цифры. 8
Если вы посмотрите на пять вышеприведенных стадий разрядного значения, станет совершенно ясно, что каждый этап основывается на предыдущем и связывает понимание разрядного значения со всеми арифметическими операциями.
Дополнение
В начальных школах США учителя постоянно говорят ученикам, что мы должны выстроить цифры, чтобы правильно складывать. Почему это важно делать? Проще говоря, мы должны добавить подобные единицы. К единицам следует прибавлять единицы, к десяткам – десятки, к сотням – сотни и т. д. до тех пор, пока не будут сложены все единицы цифр. На начальном уровне и для визуалов лучше всего использовать конкретные модели (блоки с основанием 10 и т. д.), чтобы продемонстрировать это, прежде чем переходить к концептуальному пониманию. Выстраивание цифр гарантирует, что мы добавляем одинаковые единицы.
д. до тех пор, пока не будут сложены все единицы цифр. На начальном уровне и для визуалов лучше всего использовать конкретные модели (блоки с основанием 10 и т. д.), чтобы продемонстрировать это, прежде чем переходить к концептуальному пониманию. Выстраивание цифр гарантирует, что мы добавляем одинаковые единицы.
Прежде чем перейти к умножению, я планирую кратко рассмотреть свойства сложения, поскольку они довольно хорошо связаны со свойствами умножения.
Переместительное свойство сложения гласит, что изменение порядка слагаемых не меняет сумму.
33 + 66 = 66 + 33
Ассоциативное свойство сложения утверждает, что способ группировки слагаемых не меняет сумму.
33 + (66 + 99) = (33 + 66) + 99
Свойство идентичности сложения утверждает, что сумма любого заданного числа и нуля эквивалентна этому числу.
99 + 0 = 99
Помня об этих основных свойствах, давайте сосредоточимся на звезде юнита.
Умножение
Умножение имеет свойства, параллельные свойствам сложения.
Коммутативное свойство умножения гласит, что можно умножать множители в любом порядке, и произведение не изменится.
369 × 33 = 33 × 369
Свойство коммутативности можно проиллюстрировать с помощью прямоугольного массива. Использование прямоугольного массива позволяет учащимся увидеть, как каждое пространство сетки представляет одну цифру и является результатом умножения строк на столбцы. Значение 6 строк, умноженных на 7 столбцов, эквивалентно 42 пробелам сетки. На приведенных ниже рисунках (а) представляет 7 × 6, а (б) представляет 6 × 7. Рисунок (б) является результатом поворота (а) на 90 градусов, и тем не менее на обоих рисунках одинаковое количество ячеек сетки, поэтому 6 × 7 эквивалентно 7 × 6,
Рисунок (а)
Рисунок (б)
Bennett et al 10 подчеркивает, что не менее важно отметить, что понимание свойства коммутативности практически вдвое сокращает количество основных фактов умножения, которые учащиеся должны усвоить. Предоставление учащимся этой основополагающей информации действительно поможет им в решении более сложных задач на умножение. Знание основных фактов умножения облегчает ученику умножение на степени десяти.
Предоставление учащимся этой основополагающей информации действительно поможет им в решении более сложных задач на умножение. Знание основных фактов умножения облегчает ученику умножение на степени десяти.
Другие важные свойства умножения
Ассоциативное свойство умножения гласит, что при умножении трех или более чисел произведение всегда одинаково, независимо от их группировки. Так, например
(5 × 14) × 19 = 70 × 19 = 1330 и 5 × (14 × 19) = 5 × (266) = 1330.
Свойство идентичности умножения утверждает, что любое число, умноженное на единицу, является этим числом.
369 × 1 = 369
Распределительное свойство — ключевое свойство арифметики, связывающее умножение и сложение. В нем говорится, что факт умножения может быть разбит на сумму двух фактов умножения. Мы можем разложить или «разбить одну из них на части, умножить каждую из частей на другую часть и сложить результаты 9».3244 11 ». Давайте смоделируем распределительное свойство, используя базовую задачу на умножение, которую мы использовали выше на рисунках (а) и (б).
7 × 6 также можно рассчитать как 7 × 3 + 7 × 3, поскольку 3 + 3 = 6.
Конечный результат поддерживает 7 групп по 6, что соответствует 42. 6 можно разбить и другими способами, например (5 и 1) или (4 и 2). Благодаря распределительному свойству продукт будет по-прежнему эквивалентен независимо от того, как распределяются факторы.
Свойство распределения можно моделировать с помощью массива. Я снова буду использовать 7 × 6 для демонстрационных целей.
В расширенном правиле распределения согласно Howe and Epp 12 говорится: «Если A и B являются суммами нескольких чисел, то произведение AB можно объединить, умножив каждое слагаемое B на каждое слагаемое A и сложив все полученные произведения. ».
Например, если A = a + b и B = c+ d + e, то
AB = (a + b) (c + d + e) =
ac + ad + ae + bc + bd +be
Рассмотрим это правило на примере: 45 × 239
(40 + 5)(200 + 30 +9) =
(40 × 200) + (40 × 30) + (40 × 9) +
(5 × 200) + (5 × 30) + (5 × 9) =
8000 + 1200 + 360 +
1000 + 150 + 45 =
9 560 + 1 195
= 10 755
Приведенный выше пример позволяет нам связать умножение и сложение с помощью расширенного правила распределения при умножении в форме с основанием 10. Каждая строка сетки является результатом умножения каждой единичной части одного фактора на каждую часть разрядной стоимости другого фактора, а затем сложения всех результатов.
Каждая строка сетки является результатом умножения каждой единичной части одного фактора на каждую часть разрядной стоимости другого фактора, а затем сложения всех результатов.
Распределительное свойство и его более общие версии, как в приведенном выше примере, являются ключом к выполнению многоразрядного умножения.
Нулевое свойство умножения гласит, что любое число, умноженное на ноль, равно нулю. Это правило является следствием правила идентификации для сложения и правила распределения.
369 х 0 = 0
Ноль — это цифра, которая часто представляется учащимся как не имеющая значения, а вместо этого занимающая роль заполнителя. Это может вызвать путаницу у учащихся при выполнении более сложных вычислений умножения, таких как умножение двухзначных чисел на двузначные числа. Ноль в этом контексте просто означает, что в этом месте ничего нет; мы примем во внимание, насколько легко это неправильное представление может изменить продукт в следующем примере.
Каждое из приведенных выше свойств предоставляет правила, помогающие решать задачи на умножение, которые всегда будут применяться к этим конкретным типам уравнений. Умение определять ситуации, в которых применяется свойство, было бы полезно для студента, который только изучает основы умножения.
«Когда учащиеся изучают понятия с основанием десять, они сочетают мультипликативное понимание (каждый разряд в десять раз больше значения разряда справа) с позиционной системой (каждый разряд имеет значение) — это трудно сделать до изучения об умножении». 13
Учащимся не менее сложно сразу перейти к решению задач на многозначное умножение, как того требуют стандарты четвертого класса в Вирджинии. Итак, прежде чем углубляться в многозначное умножение, давайте рассмотрим умножение однозначных чисел. Думая об однозначном числе и любой части разряда, мы можем легко написать: 3, 30, 300, 3000 и 30 000 и т. д., что эквивалентно:
.
3 × 1 = 3
3 × 10 = 30
3 × 100 = 300
3 × 1000 = 3000
3 × 10 000 = 30 000
Эти же принципы можно использовать для умножения однозначных чисел и чисел, кратных десяти. Например:
30 | 4 | |
6 × 30 | 6 × 4 | |
= 180 | = 24 | 6 |
180 + 24 = 204
6 × 34 = 204
В приведенном выше примере мы можем видеть, как распределительное свойство используется для умножения 6 на каждую из частей разряда 34, которые были записаны в расширенной форме.
По мере того, как учащиеся переходят от однозначных к двузначным умножениям, рекомендуется заранее познакомить их с числами, кратными 10 и 100. В Вирджинии это обычно вводится в третьем классе. Van de Walle 14 поясняет, что этот акцент поддерживает важность позиционного значения и акцент на числе, а не на отдельных цифрах. Глядя на число, учащийся сможет более четко видеть отдельные части разряда и, таким образом, соответствующим образом разложить число при работе с большими числами, если учащийся сможет отслеживать разрядное значение.
Глядя на число, учащийся сможет более четко видеть отдельные части разряда и, таким образом, соответствующим образом разложить число при работе с большими числами, если учащийся сможет отслеживать разрядное значение.
Например:
19 × 80 = 19 × (8 × 10) = (19 × 8) × 10 = 152 × 10 = 1520
Точно так же мы можем использовать позиционное значение, чтобы управлять вычислением умножения с участием более высоких степеней десяти:
19 × 800 = 19 × (8 × 100) = (19 × 8) × 100 = 152 × 100 = 15 200
Опять же, правило распределения вступает в силу, поскольку 19 умножаются на каждую единицу разряда, чтобы получить произведение для данного уравнения. Когда учащийся может визуализировать позиционные значения частей степеней десяти чисел, вычисления, как правило, легче для учащегося понять и применить эту концепцию к более реальным жизненным ситуациям.
При рассмотрении умножения двух цифр на две цифры и роли нуля, как в приведенном ниже примере, важность понимания каждой части разряда возрастает при вычислении произведения. Этот пример моделирует частое заблуждение среди студентов, которые не понимают роли нуля во второй строке частичных произведений, а также значения «1» в «13».
Этот пример моделирует частое заблуждение среди студентов, которые не понимают роли нуля во второй строке частичных произведений, а также значения «1» в «13».
Рисунок (с)
По сравнению с правильным алгоритмом:
Рисунок (г)
На рисунке (c) можно ясно увидеть понимание того, что «1» в множителе представляет одну десятку, что дает увеличенное значение общего продукта алгоритма, как показано на рисунке (d). Решение не идентифицировать «1» как один десяток заставило студента вместо этого умножить его на другую цифру единиц. Полное игнорирование разряда в этом примере является распространенным заблуждением среди учащихся этой возрастной группы. На рисунке (d) показано, как учащийся смог вставить «0» во второе частичное произведение, чтобы показать, что единица множителя уже была умножена на каждое число множимого.
Существует несколько типов одношаговых задач на умножение/деление в соответствии с тремя типами ситуаций, в которых используется умножение.
Равные группы
При умножении один множитель представляет количество равных групп, а другой множитель представляет количество или размер каждой группы. Результат является произведением суммы всех групп. Эта модель позволяет учащимся использовать конкретные элементы для визуализации умножения как продолжения сложения; умножение здесь сводится к сложению числа с самим собой несколько раз.
Массивы
Массив состоит из строки и столбца и укрепляет понимание коммутативного свойства, как указано выше (например, 7 строк и 6 столбцов создают массив 7 x 6).
Мультипликативные сравнения
Мультипликативное сравнение сравнивает две величины, говоря, что одна из них в несколько раз больше (или меньше), чем другая.
В приведенной ниже таблице приведены примеры каждого типа задач на умножение в форме словесных задач, в которых подчеркивается все неизвестное, поскольку эти типы задач требуют умножения для их решения и не включают типы умножения, которые требуют использования других операций. Примеры текстовых задач будут использоваться в сочетании со стратегиями обучения в демонстрационных целях.
Примеры текстовых задач будут использоваться в сочетании со стратегиями обучения в демонстрационных целях.
Тип задачи на умножение | Примеры |
Равные группы Всего Неизвестно | На столе 12 коробок кексов. В каждой коробке 24 капкейка. Сколько всего кексов? |
Целый массив Неизвестный | В национальном баскетбольном турнире принимают участие 18 баскетбольных команд. У каждой команды есть 12 баскетболистов, которые выступают за Государственный гимн. Сколько баскетболистов стоит вместе? |
Мультипликативное сравнение – результат неизвестен | На прошлой неделе Халил провел в тренажерном зале 55 минут. Джеральд был в тренажерном зале в четырнадцать раз дольше Халила в течение той же недели. Как долго Джеральд был в тренажерном зале? |
Мультипликативное сравнение — меньшее количество неизвестно | Essence пробежал 120 миль. |
Мультипликативное сравнение — коэффициент сравнения неизвестен | Тайя проехала 420 миль на танцевальное соревнование. Моней проехал 70 миль. Во сколько раз дальше проехала Тайя, чем Монай? |
Зональная модель
Использование модели площади для решения задачи на умножение может быть полезно учащимся при вычислении двузначного умножения на двузначное, поскольку оно основано на компонентах разрядного значения, поскольку каждое число разбивается на десятки и единицы. Нарисовав прямоугольники как можно ближе к масштабу, учащийся может понять, почему мы умножаем множители таким образом. Ван де Валле 15 подтверждает преимущество площадной модели, заявляя: «В площадной модели используется структура строк и столбцов для автоматической организации равных групп и визуальной демонстрации коммутативных и распределительных свойств».
— отличный инструмент для иллюстрации этой концепции, так как учащиеся могут подсчитать каждый квадрат, чтобы представить факторы, поскольку все квадраты имеют одинаковый размер, и было бы легко начертить модель области, которая представляет, например, 12 × 24. После того, как рамки обведены, учащийся может использовать блоки с основанием 10, чтобы закрыть соответствующую часть. Каждая часть с основанием 10 приводит к частичным продуктам, которые затем будут складываться вместе для вычисления продукта. При моделировании этого примера для моих учеников важно повторить, что каждая плоскость состоит из 10 стержней, что соответствует 10×10 = 100.
Используя равные группы, задачу с целым неизвестным словом из приведенной выше таблицы, я смоделирую шаги использования модели площади для решения задачи умножения двух цифр на две цифры. Как и в случае сложения, проблемы вычислений в значительной степени не зависят от типов задач. Учащиеся должны понимать контекст, в котором может использоваться умножение, а также то, как выполнять его с помощью вычислений.
Шаг 1: Напишите задачу.
12 (столбцов) × 24 (строк)
Шаг 2: Нарисуйте сетку в масштабе и запишите каждый фактор в развернутом виде.
20 | 4 | |
10 × 20 | 10 × 4 | 10 |
2 × 20 | 2 × 4 | 2 |
На этом шаге двузначные числа разлагаются на компоненты разрядности, и каждый компонент одного умножается на каждый компонент другого в соответствии с расширенным правилом распределения. Каждое произведение позиционных единиц легко вычислить, следуя приведенному выше обсуждению. Множимое 12 разбивается на 10 и 2, и каждый множитель умножается на каждую часть числа 24. На этом шаге также показано визуальное представление расширенного правила распределения, которое было объяснено ранее. Обратите внимание, что отрисовка прямоугольников в масштабе является ключевой особенностью площадной модели.
Шаг 3: Запишите числа в расширенной форме записи.
(10 + 2) × (20 + 4) =
(10 × 20) + (10 × 4) + (2 × 20) + (2 × 4) =
Важно отметить, что этот шаг иллюстрирует символическую версию расширенного правила распределения, в которой каждая часть разрядной стоимости одного фактора распределяется среди всех частей разрядной стоимости другого фактора.
Шаг 4: Выполните все указанные умножения в шаге 3 и добавьте частичные произведения.
200 + 40 + 40 + 8 = 288
Коробочный метод
Блочный метод — это абстрактная версия площадной модели. Учащиеся больше не рисуют пропорциональные прямоугольники для вычисления произведения, а рисуют прямоугольники одинакового размера, что более удобно для логики при умножении на большие числа. Было бы непрактично рисовать прямоугольники в масштабе для трехзначных чисел или больше. Кроме того, по моему опыту, студенты теряют драгоценное время, пытаясь нарисовать прямоугольники в масштабе при работе с большими числами, в отличие от рисования прямоугольников одинакового размера.
Давайте рассмотрим пример мультипликативной задачи сравнения результата неизвестного слова из таблицы выше.
На прошлой неделе Халил провел в тренажерном зале 55 минут. Джеральд был в тренажерном зале в четырнадцать раз дольше Халила в течение той же недели. Как долго Джеральд был в тренажерном зале?
Поскольку модель площадей и метод ящиков имеют некоторое сходство, шаги могут немного совпадать. Этот небольшой прогресс добавит учащимся общей уверенности, поскольку они будут расширять свое прежнее понимание вычисления двухзначного умножения на двузначное. Эта прогрессия также будет поддерживать принципы, лежащие в основе формирования мышления роста, позволяя учащимся увидеть, что рост — это непрерывный процесс. Кроме того, использование метода ящиков позволяет учащимся продолжать видеть разложение чисел на соответствующие им разрядные части.
Шаг 1: Запишите коэффициенты для умножения в развернутой форме.
Шаг 2: Нарисуйте прямоугольник с равными линиями сетки, которые соответствуют количеству слагаемых, полученных при записи факторов в развернутой форме. Поместите развернутую форму множимого горизонтально вдоль каждого поля, а развернутую форму множителя вертикально рядом с каждым полем.
Поместите развернутую форму множимого горизонтально вдоль каждого поля, а развернутую форму множителя вертикально рядом с каждым полем.
50 | 5 | |
10 | ||
4 |
Шаг 3: Используя сетку, умножьте каждое число множимого в верхней части коробки на каждое число множителя сбоку коробки.
50 | 5 | |
10 × 50 | 10 × 5 | 10 |
500 | 50 | |
4 × 50 | 4 × 5 | |
200 | 20 | 4 |
Шаг 4: Добавьте каждую часть продукта из коробок, чтобы получить общий продукт.
500
200
50
+ 20
——
770
Приведенный выше пример с методом ящика дополнительно иллюстрирует расширенное правило распределения, которое обсуждалось ранее, поскольку каждый фактор был объединен путем умножения каждого слагаемого. Кроме того, при рассмотрении метода ящика суммы по строкам частичных произведений дают сложения стандартного алгоритма, как показано в примере ниже. При суммировании по столбцам получаются сложения стандартного алгоритма, когда порядок множителей меняется на обратный: 14 × 55 (показано ниже).
Кроме того, при рассмотрении метода ящика суммы по строкам частичных произведений дают сложения стандартного алгоритма, как показано в примере ниже. При суммировании по столбцам получаются сложения стандартного алгоритма, когда порядок множителей меняется на обратный: 14 × 55 (показано ниже).
Стандартный алгоритм США
Стандартный алгоритм США для решения умножения может быть наиболее широко используемой стратегией, и можно также подозревать, что он наименее понятен учащимся в классах во всем мире. Многие учителя, как правило, вводят эту стратегию очень рано, когда обучают студентов умножению, когда они все еще пытаются понять, почему они перегруппировывают и вставляют «0» каждый раз, когда приходят к новому ряду частичных произведений.
Приведенный ниже пример представляет собой тот же алгоритм, который используется для описанного выше метода ящиков, чтобы наглядно показать, как части или результирующие частичные продукты в каждой стратегии эквивалентны.
Шаг 1: Умножьте цифру единиц в множимом (верхнее число) на цифру единиц в множителе (нижнее число). Поместите единицы на разряд единиц под чертой равенства и перегруппируйте десятки над разрядом десятков в множимом.
Поместите единицы на разряд единиц под чертой равенства и перегруппируйте десятки над разрядом десятков в множимом.
2
5 5
× 1 4
——
0
2
1 4
× 5 5
——
0
Важно отметить, что перегруппировка является результатом: 5 единиц × 4 единицы = 20 единиц и 20 единиц = 2 десятка и 0 единиц. Обязательно подчеркните язык с основанием десять, так как он указывает количество десятков и почему необходима перегруппировка.
Шаг 2: Умножьте цифру единиц множителя на цифру десятков множимого и добавьте перегруппированные десятки из шага 1. Запишите сумму рядом с «0» в разряде единиц.
2
5 5
× 1 4
——
220
2
1 4
× 5 5
——
70
Обратите внимание, что результат 220 представляет собой сумму двух сумм в нижней строке сетки, а 70 представляет собой сумму частичных произведений столбцов в методе Box для этого продукта.
Крайне важно, чтобы учащиеся умножали цифры перед перегруппировкой, поскольку умножение создает новое число десятков, которое затем нужно будет добавить к ранее созданному числу десятков из шага 1. Однако многие учащиеся совершают ошибку, добавляя 2 к 5 перед умножение на 4. Это означает, что 5 сетов по 4 равно 20; 20 плюс 2 десятка равно 22 десяткам или 2 сотням и 2 десяткам. Учащиеся, которые перегруппируются первыми, обычно делают это, имитируя процедуру сложения, добавляя перегруппированную цифру перед добавлением оставшихся цифр в этом столбце разряда.
Судя по моему опыту преподавания, многим учащимся трудно удерживать числа в порядке при использовании этого метода, который может легко исказить их конечный результат. Чтобы ограничить это, я предлагаю учащимся использовать бумагу с сеткой, в которой каждое число соответствует ячейке на бумаге, или учащиеся переворачивают бумагу своей тетради вертикально, чтобы числа уже были выровнены по строкам.
Шаг 3: Вставьте «0» во вторую строку частичных произведений, так как теперь мы будем умножать на десятки множителя.
2
5 5
× 1 4
——
220
0
2
1 4
× 5 5
——
70
0
Шаг 4: Умножьте разряд десятков множителя на разряд единиц множимого и запишите цифру рядом с «0».
2
5 5
× 1 4
——
220
50
2
2
1 4
× 5 5
——
70
00
Шаг 5: Умножьте разряд десятков множителя на разряд десятков множимого.
2
5 5
× 1 4
——
220
+550
2
2
1 4
× 5 5
——
70
+700
На этом этапе процесса я покажу учащимся, что второе слагаемое, 550, представляет собой сумму двух сумм в верхней строке сетки, а 700 — это сумма частичных произведений в левом столбце для Коробочный метод.
Шаг 6: Вычислите суммы частичных произведений, чтобы получить общий продукт.
2
5 5
× 1 4
——
220
+550
——
770
2
2
1 4
× 5 5
——
70
+700
——
770
Инструкция для всей группы/малой группы
Одна из стратегий, которую я буду использовать в своем классе, — это обучение всей группы/малой группы. В течение этого времени я буду давать прямые инструкции по стандарту дня, используя несколько способов (интерактивные заметки, книжки с картинками, вопросы-вопросы, создание складных материалов, видеодемонстрации и т. д.) для построения урока. Это время для студентов, чтобы узнать
В течение этого времени я буду давать прямые инструкции по стандарту дня, используя несколько способов (интерактивные заметки, книжки с картинками, вопросы-вопросы, создание складных материалов, видеодемонстрации и т. д.) для построения урока. Это время для студентов, чтобы узнать
явных способа решать математические задачи, пополнять словарный запас и расширять свое мышление за пределы того, чему их учили ранее, путем исследования в комфортной среде. Учащиеся увидят, что решение математического уравнения можно вычислить несколькими способами. Крайне важно, чтобы учащиеся учились в комфортных условиях и понимали, что ошибки являются частью учебного процесса. Все мои групповые занятия, как и весь мой класс, ориентированы на установку на рост, поэтому ученики создают классовые нормы, которым они соглашаются следовать, чтобы помочь нам добиться успехов в математике. Эта установка на рост моделируется при групповом обучении.
Подумай-пари-поделись
Эта стратегия дает учащимся возможность подумать над задачей индивидуально, а затем объединиться в пары с соседним сверстником, чтобы обсудить свои мысли, прежде чем поделиться со всей группой. Учащимся очень нравится эта стратегия, поскольку она дает им время поделиться своими идеями с кем-то еще, сводя к минимуму фактор запугивания, прежде чем поделиться своими мыслями или ответом со всем классом. Эта стратегия также способствует большому количеству математических разговоров, когда учащиеся общаются, используя конкретную лексику и математическое мышление, чтобы прийти к взаимно согласованному решению. Как учитель, я знаю, что учащиеся в этом возрасте легко отвлекаются и временами отходят от темы в своих разговорах, поэтому учащимся дается определенное время для разговора, чтобы свести это к минимуму.
Учащимся очень нравится эта стратегия, поскольку она дает им время поделиться своими идеями с кем-то еще, сводя к минимуму фактор запугивания, прежде чем поделиться своими мыслями или ответом со всем классом. Эта стратегия также способствует большому количеству математических разговоров, когда учащиеся общаются, используя конкретную лексику и математическое мышление, чтобы прийти к взаимно согласованному решению. Как учитель, я знаю, что учащиеся в этом возрасте легко отвлекаются и временами отходят от темы в своих разговорах, поэтому учащимся дается определенное время для разговора, чтобы свести это к минимуму.
Ученик в роли учителя
Еще одна стратегия, которую я использую в своем классе, заключается в том, чтобы ученик выступал в роли учителя. Я не использую эту стратегию в самом начале учебного года, так как ученики все еще пытаются приспособиться к своей новой среде и ролям четвероклассников. Однако, когда я реализую стратегию, даже самый упорный ученик хочет участвовать. По мере того, как ученики привыкают к ходу нашего класса, я постепенно передаю роль учителя ученику для небольшого задания. Во время этой смены ролей ученик, по сути, становится учителем, а я становлюсь одним из учеников. Они должны вести себя как знающие в классе и направлять учащихся к пониманию и выполнению поставленных задач. Я делаю мысленные заметки, какие ученики могут помочь в обучении, а также играю роль напуганного ученика, который просто не понимает, что делать в ситуации. По мере усложнения моих вопросов другие ученики в классе объединяют усилия со студентом-учителем, чтобы помочь мне понять концепцию. Командная работа, которая помогла мне понять концепцию, является еще одним преимуществом стратегии, потому что для меня важно, чтобы мои ученики знали, что мы семья и что мы все здесь, чтобы учиться и расти вместе.
По мере того, как ученики привыкают к ходу нашего класса, я постепенно передаю роль учителя ученику для небольшого задания. Во время этой смены ролей ученик, по сути, становится учителем, а я становлюсь одним из учеников. Они должны вести себя как знающие в классе и направлять учащихся к пониманию и выполнению поставленных задач. Я делаю мысленные заметки, какие ученики могут помочь в обучении, а также играю роль напуганного ученика, который просто не понимает, что делать в ситуации. По мере усложнения моих вопросов другие ученики в классе объединяют усилия со студентом-учителем, чтобы помочь мне понять концепцию. Командная работа, которая помогла мне понять концепцию, является еще одним преимуществом стратегии, потому что для меня важно, чтобы мои ученики знали, что мы семья и что мы все здесь, чтобы учиться и расти вместе.
Чтобы закрепить цели представленного материала, учащиеся выполнят несколько интерактивных заданий в классе. Для меня эти мероприятия могут служить как неформальными, так и формальными оценками. Упражнения также можно выполнять индивидуально или в небольшой группе. Основываясь на моем предыдущем опыте, я попрошу своих учеников выполнить первое задание, указанное ниже, в формате небольшой группы. Я ожидаю, что это поддастся большому количеству математических разговоров, которые еще больше способствуют пониманию навыка.
Упражнения также можно выполнять индивидуально или в небольшой группе. Основываясь на моем предыдущем опыте, я попрошу своих учеников выполнить первое задание, указанное ниже, в формате небольшой группы. Я ожидаю, что это поддастся большому количеству математических разговоров, которые еще больше способствуют пониманию навыка.
Игрушки R Математическая деятельность
В этом упражнении учащиеся будут иметь возможность делать покупки по рекламе магазина игрушек, созданной учителем. В рекламе будут представлены самые популярные и не очень популярные игрушки, которые нравятся учащимся этой возрастной группы. Студенты будут использовать умножение для завершения своих покупок, например, 2 контроллера Xbox One = 60 долларов США x 2 = 120 долларов США или 17 кубиков Zuru Fidget Cubes = 17 × 12 долларов США = 204 доллара США. Эта деятельность может быть дифференцирована в соответствии со способностями учащихся. Точно указав, сколько каждой игрушки должен купить учащийся, учащегося можно поддержать с помощью строительных лесов. Кроме того, я позволю учащимся использовать более открытый подход, основанный на запросах, предоставив им конкретный бюджет и поручив им посмотреть, насколько близко они могут подобраться, не выходя за рамки этого бюджета. Этот подход обеспечивает обогащение для студентов, которые нуждаются в большем количестве задач. Этот вариант заставляет студентов также проверять вычитание при совершении покупок. После того, как студенты завершили свои покупки, они должны выписать чек, чтобы покрыть стоимость своих товаров. Это, казалось бы, небольшое задание позволяет учащимся практиковать этот реалистичный навык в непугающей манере, одновременно повторяя, как читать, писать и определять числа как в стандартной, так и в словесной форме. Написание чека также дает студентам возможность попрактиковаться в написании своей подписи, что в наше время кажется забытым навыком. Как только все группы завершат свои транзакции, каждая группа затем расскажет всему классу о том, что они купили, и о методе, который они использовали для подсчета суммы.
Кроме того, я позволю учащимся использовать более открытый подход, основанный на запросах, предоставив им конкретный бюджет и поручив им посмотреть, насколько близко они могут подобраться, не выходя за рамки этого бюджета. Этот подход обеспечивает обогащение для студентов, которые нуждаются в большем количестве задач. Этот вариант заставляет студентов также проверять вычитание при совершении покупок. После того, как студенты завершили свои покупки, они должны выписать чек, чтобы покрыть стоимость своих товаров. Это, казалось бы, небольшое задание позволяет учащимся практиковать этот реалистичный навык в непугающей манере, одновременно повторяя, как читать, писать и определять числа как в стандартной, так и в словесной форме. Написание чека также дает студентам возможность попрактиковаться в написании своей подписи, что в наше время кажется забытым навыком. Как только все группы завершат свои транзакции, каждая группа затем расскажет всему классу о том, что они купили, и о методе, который они использовали для подсчета суммы.
Если я хочу расширить это задание, включив в него стандарты проверки, я могу попросить учащихся расположить общую сумму, потраченную различными группами, от наименьшего к наибольшему или наоборот. Учащиеся также могут сложить итоги, полученные каждой группой, чтобы составить итог класса, который затем можно было бы сравнить между тремя классами, которые я преподаю.
Чего не хватает?
Это занятие является игрой для скутеров. В скут-игры играют со всем классом одновременно, в которых учитель кладет карточку с вопросом на парту каждого ученика. Для игры ученики передвигаются по комнате от парты к парте, решая математические задачи. По мере того, как учащиеся перемещаются по классу, они должны будут либо завершить то, что отсутствует в модели сетки, а затем решить проблему, либо найти недостающий частичный продукт, который завершает метод коробки. (Примеры игровых карточек показаны ниже.) Поскольку учащиеся перемещаются по классу, это будет индивидуальное занятие. Чтобы предоставить учащимся возможность больше говорить о математике (стратегия «Думай-пары-разделяй»), они могут работать в парах или небольших группах в зависимости от расстояния между ними, что ограничит количество карточек, раздаваемых на каждой парте.
Чтобы предоставить учащимся возможность больше говорить о математике (стратегия «Думай-пары-разделяй»), они могут работать в парах или небольших группах в зависимости от расстояния между ними, что ограничит количество карточек, раздаваемых на каждой парте.
Это действие, как и предыдущее, можно дифференцировать. Глядя на три типа карт ниже, можно легко увидеть, что в каждом алгоритме отсутствуют различные аспекты, или карта требует, чтобы вы выполнили все шаги метода коробки, чтобы заполнить карту. Карточки можно отсортировать таким образом, чтобы конкретная группа или отдельные учащиеся последовательно решали только один тип задач, пока не будет достигнута уверенность и понимание, прежде чем применять другие типы карточек.
Образцы скут-карт
Математические рассказы в коробке
В этом упражнении учащиеся должны сложить чистый лист бумаги в четыре равных прямоугольника, как если бы они рисовали методом квадратов для биномов в своих интерактивных тетрадях. В каждой ячейке учащийся проиллюстрирует один из аспектов самостоятельно созданной задачи на мультипликативное сравнение слов. Затем учащиеся меняют коробки с историями в своей небольшой группе и повторяют задание до тех пор, пока у каждого учащегося не будет возможности поделиться своей историей. Чтобы обеспечить точность и еще больше установить связь между методом ящика и стандартным алгоритмом, учащиеся будут использовать метод ящика для решения текстовой задачи и стандартный алгоритм для проверки своей работы. Учащиеся должны будут понять сумму строк для частичного соединения продукта, как показано в примере ниже. По завершении каждая группа выберет одну историю, чтобы поделиться со всем классом. Группа должна коллективно научить класс (Стратегия «Студенты как учитель»), как решать задачу со словами, используя либо метод коробки, либо стандартный алгоритм.
В каждой ячейке учащийся проиллюстрирует один из аспектов самостоятельно созданной задачи на мультипликативное сравнение слов. Затем учащиеся меняют коробки с историями в своей небольшой группе и повторяют задание до тех пор, пока у каждого учащегося не будет возможности поделиться своей историей. Чтобы обеспечить точность и еще больше установить связь между методом ящика и стандартным алгоритмом, учащиеся будут использовать метод ящика для решения текстовой задачи и стандартный алгоритм для проверки своей работы. Учащиеся должны будут понять сумму строк для частичного соединения продукта, как показано в примере ниже. По завершении каждая группа выберет одну историю, чтобы поделиться со всем классом. Группа должна коллективно научить класс (Стратегия «Студенты как учитель»), как решать задачу со словами, используя либо метод коробки, либо стандартный алгоритм.
9 × 4, 353 = 9 × 4000 + 9 × 300 + 9 × 50 + 9 × 3 =
Коробочный метод Пример:
4000 | 300 | 50 | 3 | |
4000 × 9 = 36 000 | 300 × 9 = 2700 | 50 × 9 = 450 | 3 × 9 = 27 | 9 |
36 000 + 2 700 + 450 + 27 =
30 000 + 2 000 + 400 + 20
+ 6000 + 700 + 50 + 7 =
30 000 + 8 000 + 1100 + 70 + 7 =
30 000 + 9 000 + 100 + 70 + 7 = 39 177
Пример стандартного алгоритма США:
3 4 2
4353
× 9
———
39 177
Ключевым наблюдением здесь является то, что произведение цифры и значной части состоит не более чем из двух значных частей, одна из которых имеет ту же величину, что и исходная часть, а другая на одну величину больше. Числа в первой строке — это частичные продукты из сеток метода ящика. Во второй строке каждое число было разложено на разрядную часть той же величины, что и часть второго фактора, из которого оно получено, и разрядную часть следующей более высокой величины. Часть большей величины находится вверху, а меньшая – внизу. Это как если бы ящики были разделены на два подящика, причем больший по величине кусок помещался сверху, а меньший — снизу. Далее, чтобы получить 3 -й ряд , добавляются разрядные штуки того же порядка. Это похоже на добавление содержимого ящиков по диагоналям в более мелко разделенный ящик. Как указано в строке 4 th , перед записью окончательного ответа произошла дополнительная перегруппировка (справа в строке 4 th ).
Числа в первой строке — это частичные продукты из сеток метода ящика. Во второй строке каждое число было разложено на разрядную часть той же величины, что и часть второго фактора, из которого оно получено, и разрядную часть следующей более высокой величины. Часть большей величины находится вверху, а меньшая – внизу. Это как если бы ящики были разделены на два подящика, причем больший по величине кусок помещался сверху, а меньший — снизу. Далее, чтобы получить 3 -й ряд , добавляются разрядные штуки того же порядка. Это похоже на добавление содержимого ящиков по диагоналям в более мелко разделенный ящик. Как указано в строке 4 th , перед записью окончательного ответа произошла дополнительная перегруппировка (справа в строке 4 th ).
Если вы сравните это со стандартным методом, вы заметите, что суммы в верхних ячейках — это «переносы», числа, которые записываются в виде надстрочных индексов в стандартном методе и добавляются к продукту на следующем месте. Подобные действия и сравнение могут помочь учащимся понять, почему в каждом месте они должны сначала умножать, а затем прибавлять перенос к произведению, а не наоборот.
Подобные действия и сравнение могут помочь учащимся понять, почему в каждом месте они должны сначала умножать, а затем прибавлять перенос к произведению, а не наоборот.
Поскольку я буду делиться с учащимися книжками с местами и умножением (многоуровневый список книг, представленных в разделе ресурсов) на протяжении всего этого модуля, создание ими этих мини-историй повысит их способность применять математику для соединения чтения и письма. . Это также дает учащимся возможность проявить творческий подход к своим иллюстрациям, что иногда может быть редкостью для этого класса, особенно по математике.
Все вышеперечисленные действия соответствуют умножению 2 цифр на 2 цифры, поскольку это то, что требуют стандарты для моих учеников. Тем не менее, каждый пример также может быть расширен в большем масштабе за счет большего количества цифр в конце года для целей обогащения.
Алгоритм: пошаговый способ решения проблемы
массив: способ отображения объектов равными группами
декомпозиция: разделение числа на 2 или более частей
множителя: числа умножаются, чтобы получить произведение
.
кратное: любое число, умноженное на счетное число
.множимое: число, которое умножается на
умножение: операция, которая дает общее число при объединении равных групп
мультипликативное сравнение: сравнивает суммы, спрашивая или говоря, во сколько раз одна сумма больше другой
Множитель: число, на которое множимое умножается на
.порядок величины: число, присвоенное отношению двух величин, обычно выражаемое в десятичных степенях
Частичное произведение: произведение, которое получается при умножении на одну цифру за раз, которое составляет части общего числа
. Произведение: ответ в задаче на умножение
Соответствующие книги по математике с картинками
Книги уровня 1: иллюстрируют только математическую концепцию и не имеют прямой сюжетной линии
Строительные блоки умножения, Джозеф Мидтун и Сэмюэл Хити
Лучшие времена, Грег Танг
Гроздья математики, Грег Танг
Ноль – это листья на дереве, Бетси Франко
Сколько стоит миллион? Дэвид Шварц
Миллион точек , Майк Рид Эндрю Клементс
Ноль, это что-то? Это ничего? Клавдия Заславская
Большие числа, Эдвард Паккард
Теперь мой следующий номер, Маргарет Парк
Книги уровня 2: увлекательный сюжет, переплетенный с математикой
Завтрак в закусочной Дэнни, Джудит Стэмпер
7 x 9 = Проблемы, Клаудия Миллс
Таинственная банка для размножения Анно , Масаитиро и Мицумаса Анно
Слишком много кенгуру, чем заняться ! Стюарт Мерфи
Как сосчитать дюжину утят? Сон Че
Удивительный сон Аманды Бин, Синди Нойхвандер
В десять раз лучше, Ричард Майкельсон
Монстр умножения, Кимберли Гросс
Герой Зеро, Джоан Холуб
Место для нуля, Анджелина Спаранья LoPresti
За миллионом: удивительное математическое путешествие, Дэвид Шварц
Проблемы с обезьянами, Люси Равиш
Королевские уполномоченные, Синди Нойхвандер
Книги уровня 3: не специально математические, но могут быть использованы для установления связей
Город в цифрах, Стивен Джонсон
Два способа считать до десяти, Руби Ди
Примеры вопросов для исследования
- Сколько тебе дней?
- Сколько рулонов туалетной бумаги мы используем за учебный год?
- Сколько пакетов молока выпивает школа в месяц?
- Сколько миль проедет ваш школьный автобус до зимних каникул?
- Сколько секунд вам от роду?
- Как долго будут идти утренние объявления к концу учебного года?
- Если у нас есть 15-минутный перерыв каждый день, сколько времени вы проведете вне дома до весенних каникул?
- Сколько учеников потребуется, чтобы растянуть длинный зал?
- Сколько пар обуви потребуется, чтобы очертить периметр класса?
- Сколько ноутбуков потребуется, чтобы достичь потолка класса?
- Если мы все учащиеся 2-5 классов играли в Minecraft по 60 минут в неделю, сколько всего минут учащиеся будут играть за одну неделю? Через шесть недель?
Этот раздел учебной программы предназначен для обучения учащихся четвертого класса двузначному умножению на двузначное. Он соответствует недавно пересмотренным стандартам обучения 2016 года, представленным в рамках учебной программы, которые характерны для штата Вирджиния.
Он соответствует недавно пересмотренным стандартам обучения 2016 года, представленным в рамках учебной программы, которые характерны для штата Вирджиния.
Стандарты обучения Вирджинии (2016)
4.4 Студент будет
- продемонстрировать свободное владение фактами умножения до 12 x 12 и соответствующими фактами деления;
- оценивать и определять суммы, разности и произведения целых чисел;
- создавать и решать одноэтапные и многоэтапные практические задачи на сложение, вычитание и умножение, а также одноэтапные практические задачи на деление целых чисел.
Стандарты обучения 2016 года вводились поэтапно в течение 2017-2018 учебного года, поэтому учащиеся третьего класса были поставлены перед следующими задачами в качестве основы обучения в четвертом классе.
3.4 Студент будет
- представляют умножение и деление до 10 × 10, используя различные подходы и модели;
- создавать и решать одношаговые практические задачи на умножение и деление до 10 х 10; и
- продемонстрировать свободное владение фактами умножения 0, 1, 2, 5 и 10; и
- решают одношаговые практические задачи на умножение целых чисел, где один множитель равен 99 или меньше, а второй множитель равен 5 или меньше.

Важно знать уровень воздействия, с которым учащиеся сталкиваются до поступления в четвертый класс, так как это помогает направлять обучение.
Общие базовые стандарты
Вирджиния не является обычным основным штатом, но приведенные ниже стандарты также могут применяться к этому устройству.
CCSS.MATH.CONTENT.3.OA.A.1 Интерпретировать произведения целых чисел, например, интерпретировать 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
CCSS.MATH.CONTENT.3.OA.A.3 Использование умножения и деления в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, с использованием рисунков и уравнений с символом неизвестного числа представлять проблему.
CCSS.MATH.CONTENT.3.OA.A.5 Применение свойств операций как стратегий умножения и деления.2 Примеры. Если известно 6 × 4 = 24, то также известно 4 × 6 = 24. (Перестановочное свойство умножения.) 3 × 5 × 2 можно найти, если 3 × 5 = 15, тогда 15 × 2 = 30, или 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)
Если известно 6 × 4 = 24, то также известно 4 × 6 = 24. (Перестановочное свойство умножения.) 3 × 5 × 2 можно найти, если 3 × 5 = 15, тогда 15 × 2 = 30, или 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)
CCSS.MATH.CONTENT.3.OA.A.7 Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
CCSS.MATH.CONTENT.4.OA.A.1 Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте 35 = 5 × 7 как утверждение, что 35 в 5 раз больше 7 и в 7 раз больше 5. Представляйте словесные утверждения мультипликативных сравнений в виде уравнений умножения.
CCSS.MATH.CONTENT.4.OA.A.2 Умножение или деление для решения текстовых задач, связанных с мультипликативным сравнением, например, с использованием рисунков и уравнений с символом неизвестного числа для представления задачи, отличающей мультипликативное сравнение от аддитивного сравнения .
CCSS.MATH.CONTENT.4.OA.A.3 Решите многошаговые текстовые задачи, поставленные с целыми числами и имеющие целочисленные ответы, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.
CCSS.MATH.CONTENT.4.OA.A.5 Умножение целого числа, состоящего не более чем из четырех цифр, на однозначное целое число и умножение двух двузначных чисел с использованием стратегий, основанных на разрядности и свойствах операций . Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
По состоянию на 14 июля 2018 г. https://www.mathsisfun.com/definitions/number-sense.html. Этот веб-сайт дает четкое определение смысла числа математического термина.
По состоянию на 12 июля 2018 г. https://math.uchicago.edu/~chonoles/miscellany/quotations/. Этот веб-сайт предоставляет списки математических котировок, отсортированных по категориям.
https://math.uchicago.edu/~chonoles/miscellany/quotations/. Этот веб-сайт предоставляет списки математических котировок, отсортированных по категориям.
Беннетт, Альберт Б.-младший, Лори Дж. Бертон и Л. Тед Нельсон. Математика для учителей начальной школы Концептуальный подход . 8-е изд. Дубьюк, ИА: McGraw-Hill, 2010. 169.
Ди, Руби и Сьюзан Меддо. Два способа считать до десяти: либерийская народная сказка . Нью-Йорк: Square Fish, 2013.
.Хоу, Роджер и Гарольд Рейтер. «Пять стадий стоимости места». Учителя Индии. 26 сентября 2012 г. По состоянию на 10 мая 2018 г. http://www.teachersofindia.org/en/article/five-stages-place-value. Интернет-статья, в которой описываются пять стадий стоимости места и то, как они позволяют выполнять вычисления.
Хоу, Роджер. «Кратко о стоимости места». Неопубликовано. Рединг, Йельская национальная инициатива Йельского университета, 12 июля 2018 г. Эта статья полезна тем, что объясняет основы разрядной стоимости применительно к вычислениям.
Эта статья полезна тем, что объясняет основы разрядной стоимости применительно к вычислениям.
Роджер Хоу и Сюзанна Эпп, Серьезное отношение к ценности: арифметика, оценка и алгебра (Коннектикут), по состоянию на 6 июня 2018 г. Расширенное правило распределения, используемое в модуле, было получено из этой статьи.
Смолл, Мэриан. Взгляд на математику: визуальный подход к обучению математическим понятиям . 2012, 2013. 85.
Смит, Сьюзан Сперри. Математика для детей младшего возраста . Бостон: Пирсон, 2006. 153–154.
Штейн, Марси, Дайан Киндер, Кристен Рольф, Джерри Силберт и Дуглас В. Карнин. Математика прямого обучения . Пятое изд. Нью-Йорк, Нью-Йорк: Пирсон, 2018. 39.
Ван Де Валле, Джон А., Карен С. Карп, Дженнифер М. Бэй-Уильямс, Джонатан А. Рэй и Элизабет Тодд Браун. Математика в начальной и средней школе: обучение с учетом развития . Десятое изд. Нью-Йорк, Нью-Йорк: Пирсон, 2019.
Десятое изд. Нью-Йорк, Нью-Йорк: Пирсон, 2019.
- Ди, Руби и Сьюзан Меддо. Два способа считать до десяти: либерийская народная сказка .
- https://www.mathsisfun.com/definitions/number-sense.html
- https://math.uchicago.edu/~chonoles/miscellany/quotations/
- Смит, Сьюзан Сперри. Математика раннего детства.
- Смит, Сьюзен Сперри. Математика раннего детства.
- Роджер Хоу и Сюзанна Эпп, Серьезное отношение к ценности.
- Штейн, Марси, Дайан Киндер, Кристен Рольф, Джерри Силберт и Дуглас В. Карнин. Математика прямого обучения .
- Хоу, Роджер и Гарольд Рейтер. «Пять стадий стоимости места».
- Хоу, Роджер. «Кратко о стоимости места».
- Беннетт, Альберт Б.-младший, Лори Дж. Бертон и Л.
 Тед Нельсон. Математика для учителей начальной школы Концептуальный подход .
Тед Нельсон. Математика для учителей начальной школы Концептуальный подход . - Смолл, Мариан. глаза на математику: визуальный подход к обучению математическим понятиям.
- Роджер Хоу и Сюзанна Эпп, Серьезное отношение к ценности.
- Ван де Валле. Математика в начальной и средней школе: обучение в целях развития.
- Ван де Валле. Математика в начальной и средней школе: обучение в целях развития.
- Ван де Валле. Математика в начальной и средней школе: обучение в целях развития.
Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом неизвестного числа для представления задачи.
Экспорт
Распечатать
Связанные точки доступа
Альтернативная версия этого контрольного показателя для учащихся со значительными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Уроки STEM – Активность по моделированию
Chess Wish List:
Члены шахматного клуба 3-го класса составят два списка пожеланий о том, как потратить 75 долларов на материалы, связанные с шахматами. Затем они должны составить два новых списка пожеланий о том, как потратить 750 долларов на материалы, связанные с шахматами.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Выберите лучшего тренера по баскетболу:
Этот MEA 3-го класса предлагает учащимся работать в команде, чтобы выяснить, какой кандидат является лучшим кандидатом на роль тренера по баскетболу для мальчиков 8-го класса. Им придется проанализировать данные, выбрать процедуру и создать систему ранжирования, чтобы выбрать лучшего кандидата. Им также даются задачи на умножение и деление на основе данных.
Им придется проанализировать данные, выбрать процедуру и создать систему ранжирования, чтобы выбрать лучшего кандидата. Им также даются задачи на умножение и деление на основе данных.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Карнавальные аттракционы Купидона:
На этом уроке учащиеся рассмотрят различные карнавальные аттракционы и определят, какой из них принесет наибольшую прибыль, учитывая такие факторы, как количество билетов на аттракцион, стоимость билета, продолжительность поездка, количество часов, в течение которых поездка открыта, и стоимость эксплуатации поездки. Студенты должны будут использовать различные операции для решения задач и должны будут выполнять несколько шагов.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Florida Fish Aquarium Challenge:
В этом задании учащимся предлагается посмотреть на аквариумы трех разных размеров и определить, используя список данных, какие рыбы поместятся в этих аквариумах в зависимости от их размера. Им также нужно будет посмотреть на другие характеристики, чтобы определить, как группировать рыб вместе. Студентам придется умножать, делить или складывать несколько раз, чтобы найти разные решения о том, как разместить рыбу в аквариуме каждого размера.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Сколько длится ваш урок музыки?:
В этом MEA учащиеся третьего класса должны будут ранжировать пакеты уроков игры на музыкальных инструментах на основе продолжительности, частоты и качества уроков. Часть задания включает в себя определение учащимися прошедшего времени уроков на основе времени их начала и окончания. Им также необходимо будет рассчитать общую недельную стоимость уроков, исходя из количества предлагаемых уроков в неделю.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Выберите питомца:
В этом MEA учащиеся ранжируют домашних животных от наиболее подходящих для семьи до наименее подходящих для семьи, учитывая такие данные, как цена покупки, стоимость кормления, чистота и т. д., а также примечания, касающиеся физического описания животного. домашний питомец. Кроме того, студентам будет предоставлена информация о дополнительных домашних животных, а также информация о чистоте и продолжительности жизни. Учащимся, возможно, придется пойти на компромисс в отношении затрат на усыновление, кормление и проживание, а также ожидаемой продолжительности жизни, простоты уборки и т. д.
д., а также примечания, касающиеся физического описания животного. домашний питомец. Кроме того, студентам будет предоставлена информация о дополнительных домашних животных, а также информация о чистоте и продолжительности жизни. Учащимся, возможно, придется пойти на компромисс в отношении затрат на усыновление, кормление и проживание, а также ожидаемой продолжительности жизни, простоты уборки и т. д.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Формирующие оценки MFAS
Поиск неизвестного произведения:
Учащимся предлагается смоделировать задачу о равных группах и массиве, в которой произведение неизвестно, с помощью уравнений умножения или деления, а затем решить каждую задачу.
Определение размера группы:
Учащимся предлагается смоделировать равные группы и задачу с массивом, в которой размер группы неизвестен, с помощью уравнений умножения или деления, а затем решить каждую задачу.
Определение количества групп:
Учащихся просят смоделировать равные группы и задачу с массивом, в которой количество групп неизвестно, с помощью уравнений умножения или деления, а затем решить каждую задачу.
Задачи на измерения:
Учащимся предлагается смоделировать задачу на умножение и деление, включающую измеряемые величины с уравнениями умножения и деления, а затем решить каждую задачу.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом тесте.
Задачи решения проблем
Две интерпретации деления:
Оба вопроса решаются с помощью задачи деления 12÷3, но то, что происходит с лентой, в каждом случае разное. Задачу можно решить с помощью рисования ленточной диаграммы или числовой прямой. Для задачи 1 линия должна быть разделена на 3 равные части. Вторую задачу можно решить, последовательно вычитая 3 фута, чтобы узнать, сколько раз оно укладывается в 12.
Задачу можно решить с помощью рисования ленточной диаграммы или числовой прямой. Для задачи 1 линия должна быть разделена на 3 равные части. Вторую задачу можно решить, последовательно вычитая 3 фута, чтобы узнать, сколько раз оно укладывается в 12.
Тип: Задача на решение задач
Подарки от бабушки, Вариант 1:
Первая из них — задача на умножение с участием групп одинакового размера. Следующие две отражают две связанные проблемы деления, а именно: «Сколько групп?» и «Сколько в каждой группе?»
Тип: Задание на решение задач
Анализ задач со словами на умножение:
В этой задаче учащихся не просят найти ответ, а просят проанализировать задачи и объяснить свое мышление. В процессе они сталкиваются с различными способами мышления об умножении.
Тип: Задание на решение задач
Материалы для классных комнат:
Цель этого задания – помочь учащимся «Решить задачи, включающие четыре операции» (3. OA.A) и «Нарисовать график в масштабе и линейку в масштабе». график для представления набора данных с несколькими категориями» (3.MD.3).
OA.A) и «Нарисовать график в масштабе и линейку в масштабе». график для представления набора данных с несколькими категориями» (3.MD.3).
Тип: Задача решения проблем
Деятельность студенческого центра
Edcite: Математика 3 класс:
Учащиеся могут практиковаться в ответах на математические вопросы по различным темам. Имея учетную запись, учащиеся могут сохранять свою работу и отправлять ее учителю по завершении.
Тип: Деятельность студенческого центра
Руководство
Средняя высота этажа здания:
Используйте картинку и понимание умножения, чтобы решить задачу на деление слов. Остерегайтесь ненужной информации.
Тип: Учебник
Виртуальные манипуляторы
Ноги животных (умножение с помощью многократного сложения):
Учащиеся используют многократное сложение как стратегию решения задач на умножение.
Тип: Виртуальное манипулирование
Группы собак (умножение):
Учащиеся используют массивы, чтобы понять значение умножения.
Тип: Виртуальный Манипулятор
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом тесте.
Задачи решения проблем
Две интерпретации деления:
Оба вопроса решаются с помощью задачи деления 12÷3, но то, что происходит с лентой, в каждом случае разное. Задачу можно решить с помощью рисования ленточной диаграммы или числовой прямой. Для задачи 1 линия должна быть разделена на 3 равные части. Вторую задачу можно решить, последовательно вычитая 3 фута, чтобы узнать, сколько раз оно укладывается в 12.
Тип: Задача на решение задач
Подарки от бабушки, Вариант 1:
Первая из них — задача на умножение с участием групп одинакового размера. Следующие две отражают две связанные проблемы деления, а именно: «Сколько групп?» и «Сколько в каждой группе?»
Следующие две отражают две связанные проблемы деления, а именно: «Сколько групп?» и «Сколько в каждой группе?»
Тип: Задание на решение задач
Анализ задач со словами на умножение:
В этой задаче учащихся не просят найти ответ, а просят проанализировать задачи и объяснить свое мышление. В процессе они сталкиваются с различными способами мышления об умножении.
Тип: Задание на решение задач
Материалы для классных комнат:
Цель этого задания – помочь учащимся «Решить задачи, включающие четыре операции» (3.OA.A) и «Нарисовать график в масштабе и линейку в масштабе». график для представления набора данных с несколькими категориями» (3.MD.3).
Тип: Решение задач
Основные математические операции — сложение, вычитание, умножение и деление
Основные математические операции включают четыре основные операции:
● Сложение (+)
● Вычитание (-)
● Умножение (* или x) и
● Деление ( : или /)
Эти операции обычно называют
3 Арифметика — старейшая и наиболее элементарная ветвь математики.

В этом и других связанных уроках мы кратко объясним основные математические операции. Имейте в виду, хотя операции и примеры, показанные здесь, довольно просты, они обеспечивают основу даже для самых сложных операций, используемых в математике.
Сложение
Сложение — это математическая операция, объясняющая общее количество объектов при их объединении в коллекцию.
Например, предположим, что у Джимми 2 яблока, а у Лоры 3 яблока, и мы хотим узнать, сколько яблок у них вместе. Складывая их вместе, мы видим, что у обоих вместе есть 5 яблок (2 яблока Джимми + 3 яблока Лауры = всего 5 яблок). Как видите, добавление обозначается знаком «плюс (+)».
Сложение также можно использовать для выполнения операций с отрицательными числами, дробями, десятичными числами, функциями и т.д. Для сложения характерны несколько арифметических свойств:
1. Коммутативное свойство
2. Ассоциативное свойство
3. Свойство идентичности
Свойство идентичности
Вычитание
Вычитание — это арифметическая операция, обратная сложению. Вычитание используется, когда вы хотите узнать, сколько объектов осталось в группе после того, как вы уберете определенное количество объектов из этой группы.
Например, у Мэгги 5 яблок. Она дает 2 яблока своему другу Полу. Сколько яблок у нее? У нее 3 яблока (5 яблок, которые у нее были – 2 яблока, которые она отдала Полу = 3 яблока, которые у нее остались).
Как видите, вычитание определяется «символом минус (-)». Вычитание также можно использовать для выполнения операций с отрицательными числами, дробями, десятичными числами, функциями и т. д.
Умножение
Умножение — третья основная математическая операция. Когда вы умножаете два числа, это то же самое, что прибавлять число к самому себе столько раз, сколько равно значению другого числа. Подумайте об этом так: у вас есть 5 групп яблок, и в каждой группе по 3 яблока. Один из способов узнать, сколько у вас яблок, таков:
Один из способов узнать, сколько у вас яблок, таков:
3 яблока + 3 яблока + 3 яблока + 3 яблока + 3 яблока = всего 15 яблок
Вы можете видеть, что это слишком много работы (особенно если у вас есть большие числа), поэтому вы можете использовать умножение для решения этой задача:
5 групп яблок x 3 яблока в каждой группе = всего 15 яблок
Это может быть еще проще, если использовать таблицу умножения.
Умножение обозначается знаком умножения «х» и часто читается как «умножить» или «умножить на». Таким образом, если бы у вас было выражение типа «3 x 4», вы могли бы прочитать его как «3 умножить на 4» или «3 умножить на 4». Другими словами, выражение умножения означает, сколько раз одно число умножается на другое число.
$\ 3 * 4 = 12$ Число 3 умножается в этом уравнении 4 раза, и при умножении 3 на 4 получается число 12.
Деление
Деление — четвертая основная математическая операция. По сути, можно сказать, что деление означает разделение объектов на равные части или группы.
Например, у вас есть 12 яблок, которые нужно разделить поровну между 4 людьми. Итак, сколько яблок достанется каждому? Каждый получит по 3 яблока (12 яблок / 4 человека = 3 яблока на человека). Деление противоположно умножению:
$\ 3 * 4 = 12$
$\ 4 * 3= 12$
$\frac{12}{4} = 3$
$\frac{12}{3}=4$
Для облегчения понимания деления одного числа на другое используйте таблицу деления:
Основные математические операции
Основные математические операции — сложение, вычитание, умножение и деление. В зависимости от направления математической задачи вы можете увидеть разные слова:
- Сложение: добавление, добавление
- Вычитание: вычитание, вычитание
- Умножение: умножение, умножение
- Деление: деление, деление
В математике, когда вы выполняете вычислительные действия, вы должны помнить, что существует последовательность, которую необходимо соблюдать, чтобы делайте расчеты правильно.


 Слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения.
Слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения. Актуализация знаний.
Актуализация знаний. Запишите число, которое находится между числами: 198 и 200.
Запишите число, которое находится между числами: 198 и 200.
 : 6=78д.: 6= (60 + 18) : 6 = 10 + 3 = 13 д.=130 ед.
: 6=78д.: 6= (60 + 18) : 6 = 10 + 3 = 13 д.=130 ед.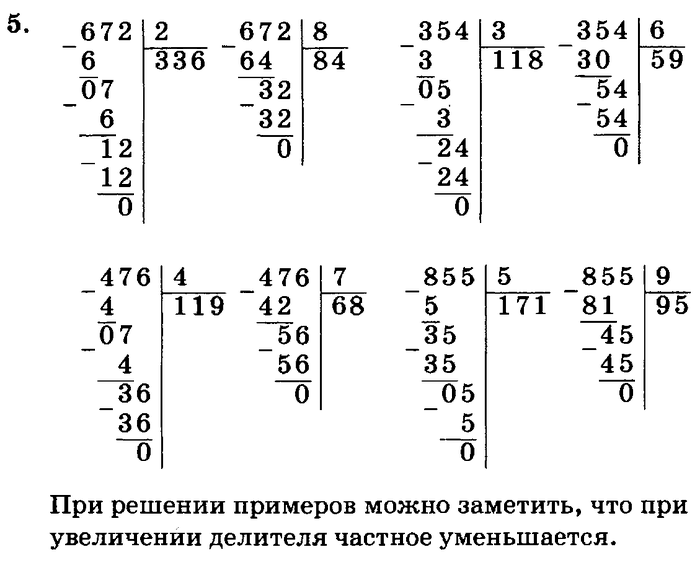 (№3)
(№3)
 Тренинг (выбираем…).
Тренинг (выбираем…).
 Найди числа произведение которых равно 12 ?
Найди числа произведение которых равно 12 ?
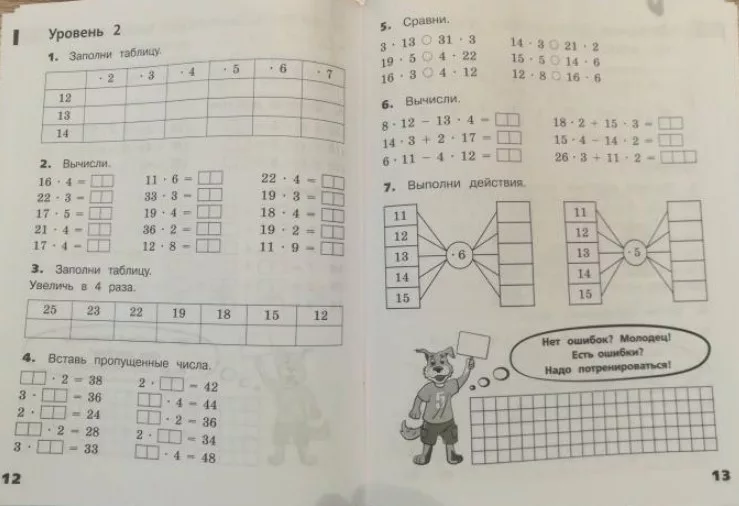
 100 999
100 999