Примеры на умножение столбиком 3 класс: Тренажер на умножение столбиком
Умножение чисел, в записи которых есть нули
Урок 45. Математика 4 класс ФГОС
На этом уроке будут рассмотрены случаи умножения, когда нули есть в первом множителе и стоят они или в конце числа, или в середине. А ещё разберётся и такой пример, в котором нули есть в обоих множителях. И, конечно, несколько числовых выражений подготовлено ребятам и для самостоятельного решения.
Конспект урока “Умножение чисел, в записи которых есть нули”
Привет, ребята!
Сегодня мы продолжим разговор об умножении многозначных чисел. И особое внимание уделим тем случаям, когда в записи первого множителя есть нули.
Некоторые случаи умножения трёхзначных чисел с нулями мы уже разбирали. Помните, как мы умножали семьсот пятьдесят два на триста девять?
752 · 309 = 232 368
А ещё шестьсот сорок три
умножали на четыреста тридцать.
643 · 430
А сейчас давайте разберём вот такой пример. Умножим четыре тысячи восемьсот на семьдесят шесть 4 800 · 76. Как записать это столбиком?
А вот как! Вы уже знаете, что, если многозначное число
оканчивается нулями, при записи умножения столбиком эти нули как бы остаются
справа. В данном примере мы сорок восемь сотен будем умножать на семьдесят
шесть и выполнять действие так, как оно выполняется при умножении двузначных
чисел. Восемью шесть – сорок восемь. Восемь пишем, четыре запоминаем. Четырежды
шесть – двадцать четыре. Да ещё четыре – двадцать восемь. Первое неполное
произведение записано. Умножаем первый множитель на семь десятков. Восемью
семь – пятьдесят шесть. Шесть пишем, пять запоминаем. Четырежды семь – двадцать
восемь. Да ещё пять – тридцать три. Теперь есть и второе неполное
произведение. Складываем их. Переносим нули из первого множителя вниз
и пишем справа от получившейся суммы.
Ну а если нули стоят не в конце, а в середине первого множителя, как вот в этом числовом выражении?
3 009 · 54
В данном случае все записываем как обычно – единицы под единицами, десятки под десятками. Умножаем на единицы. Девятью четыре – тридцать шесть. Шесть пишем, три запоминаем. Нуль умножаем на четыре – нуль. Да ещё три – получается три. И снова нуль умножаем на четыре – нуль. Трижды четыре – двенадцать. Записано первое неполное произведение.
Умножаем на пять десятков. Девятью пять – сорок пять. Пять пишем, четыре запоминаем. Нуль умножаем на пять – нуль. Пишем четвёрку, которую запомнили. Ведь мы её прибавляем к нулю. Вновь умножаем нуль и получаем нуль. Трижды пять – пятнадцать. Вот и второе неполное произведение. Складываем. Ответ: сто шестьдесят две тысячи четыреста восемьдесят шесть.
Ну а теперь попробуем перемножить два трёхзначных числа с
нулями в разряде десятков – шестьсот девять и двести семь.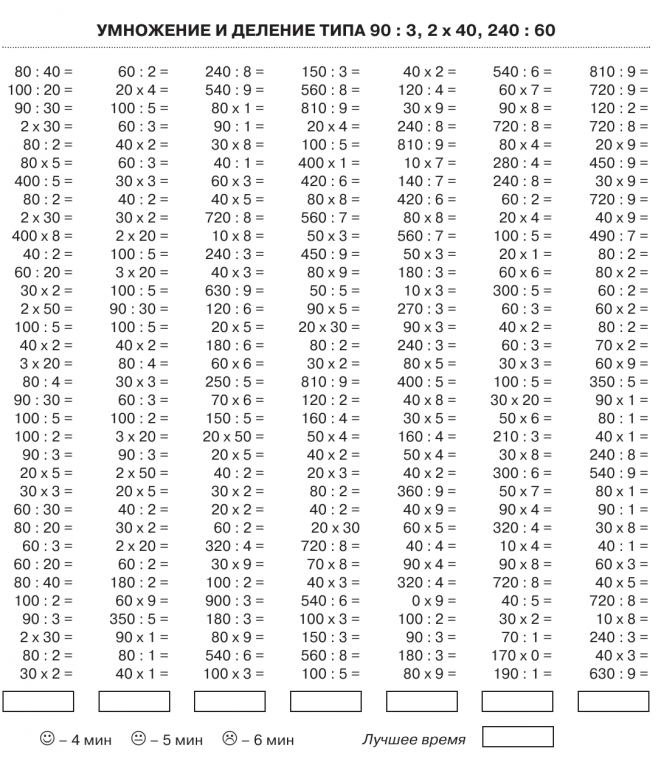
Записываем числа одно под другим. Умножаем шестьсот девять на семь единиц. Девятью семь – шестьдесят три. Три пишем под единицами, а шесть. Вы сейчас подумали: она скажет «запоминаем»! А вот и нет! Так как дальше умножать нужно нуль, и результат, конечно, тоже нуль, шестёрку можно не запоминать, а сразу писать в разряде десятков. А теперь шесть умножаем на семь и пишем сорок два. Первое неполное произведение готово.
На нуль умножать не будем.
Теперь шестьсот девять умножим на две сотни. И не забудьте!!! Писать начнём под сотнями. Девятью два – восемнадцать. Пишем восемь и. один – ведь впереди опять умножение нуля. Шестью два – двенадцать. Складываем неполные произведения. Ответ: сто двадцать шесть тысяч шестьдесят три.
Ну и последний пример. Умножаем два трёхзначных числа с нулями в разряде единиц.
Например, пятьсот восемьдесят и триста шестьдесят.
580 · 360
Так как нулей в обоих числах одинаковое количество, записываем
их точно одно под другим. А умножать будем так, как будто нам даны не трёхзначные, а двузначные
числа.
А умножать будем так, как будто нам даны не трёхзначные, а двузначные
числа.
Умножаем на шесть десятков. Восемью шесть – сорок восемь. Восемь пишем, четыре запоминаем. Пятью шесть – тридцать. Да ещё четыре – тридцать четыре.
Умножаем на три сотни. Восемью три – двадцать четыре. Четыре пишем, два запоминаем. Пятью три – пятнадцать, да ещё два – семнадцать.
Складываем неполные произведения. А теперь оба нуля переносим вниз и пишем справа от получившейся суммы
Ну вот и подходит к концу наша встреча. Но я думаю, что вы тоже хотите попробовать свои силы и решить примеры подобные тем, о которых я рассказала.
Решайте, а потом вы сможете проверить свою работу.
2670 · 36; 4190 · 27; 709 · 340; 902 · 506
Ребята, проверьте своё решение.
Я надеюсь, вы справились с заданием. Если, конечно, были внимательны и аккуратны.
А теперь я прощаюсь с вами! До новой встречи, друзья!
Предыдущий урок 44 Письменное умножение на трёхзначное число
Следующий урок 46 Письменное деление на двузначное число (без остатка и с остатком)
Получите полный комплект видеоуроков, тестов и презентаций Математика 4 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Умножение на однозначное число столбиком
МБОУ «Могилевская СОШ им.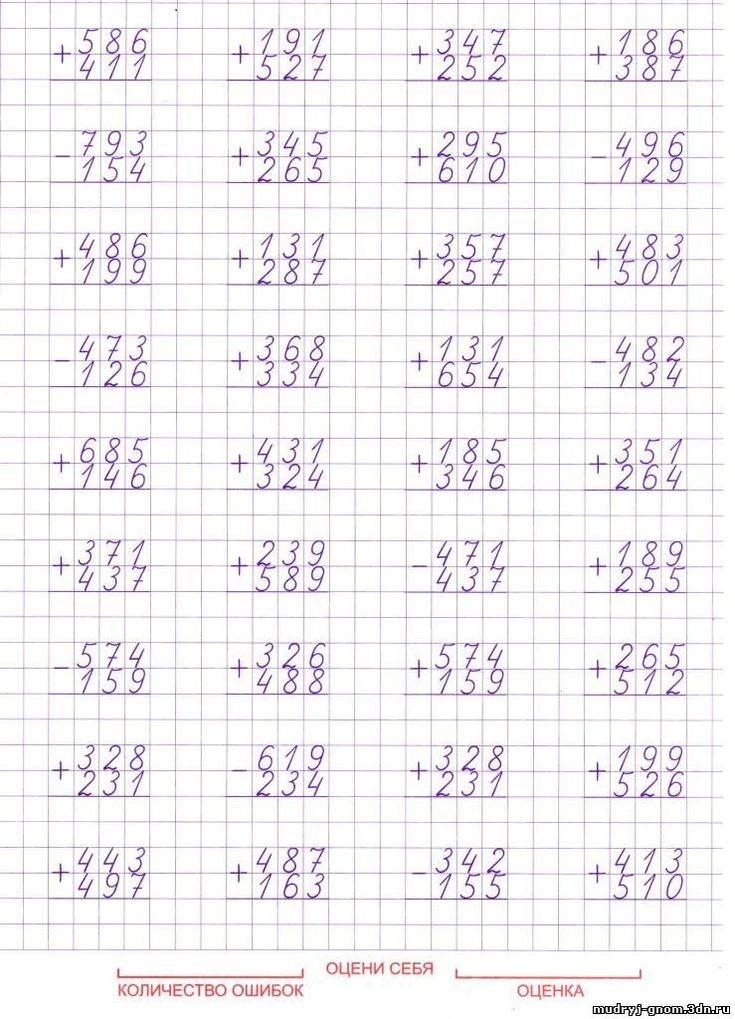 Н.У.Азизова»
Н.У.Азизова»
Конспект урока по математике «Умножение на однозначное число столбиком»
Класс: 4 УМК «Школа Росии»
Учитель начальных классов:Дадаева Марьям Касумовна.
Цели: выполнять умножение на однозначное число столбиком; совершенствовать вычислительные навыки; развивать логическое мышление, память и внимание.
Оборудование: карточки, таблица.
Ход урока
I. Организационный момент.
II. Устный счет.
Заполнить пропуски
Множитель | 20 | 50 | 12 | 14 | ||
Множитель | 70 | 15 | 40 | 16 | ||
Произведение | 240 | 840 | 720 | 960 |
2. Задача.
Мать старше дочери в три раза, а вместе им 48 лет. Сколько лет матери и дочери?
3. Рассмотрите чертеж.
Рассмотрите чертеж.
– Какие геометрические фигуры здесь изображены?
– Сколько треугольников на чертеже?
4. Индивидуальная работа у доски
Вырази в указанных единицах измерения.
6см8мм= мм5км700м= м.
5м6см= мм 8км 8м= м.
6дм6см= мм 6дм3см= см.
5см2= мм2 90м2= см2
8дм2 5см2= см2 8км2= м2
5м2 6см2= см2 7дм2 5см2= см2
III. Сообщение темы урока.
– Рассмотрите схемы на доске:
– Что обозначают данные схемы?
– Какие трудности у вас возникли?
– Сегодня на уроке будем учиться выполнять умножение на однозначное число столбиком.
IV. Работа по теме урока.
Задание 1.
– Проверьте, правильно ли выполнено умножение.
– Выпишите те случаи, в которых при поразрядном умножении не было перехода через разряд.
34 | 23 | 221 | 12 | 121 | 43 | 324 |
Х 2 | Х 3 | Х 4 | Х 3 | Х 4 | Х2 | Х 2 |
68 | 69 | 884 | 36 | 484 | 86 | 648 |
– Выпишите те случаи, в которых имел место переход через разряд.
Задание 2.
– Выполните умножение столбиком числа 273 на 3, отвечая на данные вопросы.
– Какое число получается при умножении в разряде единиц? (9.) Можно ли его сразу записать в разряд единиц результата? (Можно.)
– Какое число получается при умножении в разряде десятков? (21.) Сколько в 21 десятке содержится сотен и сколько еще десятков? (2 сотни 1 десяток.)
– Какую цифру мы записываем в разряд десятков результата? (2.) В какой разряд переходят 2 сотни? (В разряд сотен.)
– Какое число получается при умножении в разряде сотен? (6.) Сколько сотен перешло в этот разряд при выполнении умножения в предыдущем разряде? (2 сотни.)
– Сколько всего сотен получилось с учетом перехода? (8 сотен.) Какую цифру нужно записать в разряд сотен результата? (8.)
– В каком случае при поразрядном умножении не происходило перехода через разряд: когда результат являлся однозначным числом или двузначным? (Однозначным. )
)
Задание 3.
– Маша выполнила умножение числа 218 на число 4 столбиком.
– Что обозначает надписанная сверху в разряде десятков цифра 3? (Число десятков, которое запомнили.)
Задание 4.
– Выполните умножение числа 162 на число 4 столбиком.
– Объясните, как можно установить цифру каждого разряда результата. С какого разряда следует начинать вычисления? Почему? (Надо начинать умножение с разряда единиц.)
– К какому разряду следует переходить потом? (К разряду десятков.)
– Будет ли иметь место переход через разряд? (Да, запоминаем 2 сотни.)
Задание 5.
– Приведите примеры поразрядного умножения четырехзначного числа на однозначное, при выполнении которого дважды происходит переход через разряд: в разряде единиц и в разряде сотен.
1524 | 2514 | 1715 | 2415 |
Х 4 | Х 3 | Х 5 | Х3 |
6096 | 7542 | 8575 | 7245 |
Задание 6.
– Выпишите все трехзначные числа, при поразрядном умножении которых на число 5 не происходит перехода через разряд.
Задание 8.
– По данной схеме сформулируйте задачу, решить которую можно с помощью двух действий сложения или одного действия умножения.
– В одном ящике было 115 яблок, а в другом на 115 яблок больше. Сколько яблок всего? Для вычисления ответа задачи примените умножение столбиком.
Решение:
115 |
Х 3 |
345 |
Учащиеся выполняют умножение столбиком.
V. Итог урока.
– Как выполнить умножение многозначного числа на однозначное столбиком?
Домашнее задание. № 7.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/485423-umnozhenie-na-odnoznachnoe-chislo-stolbikom
Что такое коммутативная собственность? Определение, формула, примеры
Коммутативное свойство
Коммутативное свойство утверждает, что числа, с которыми мы работаем, можно перемещать или менять местами с их позиции без какого-либо изменения ответа.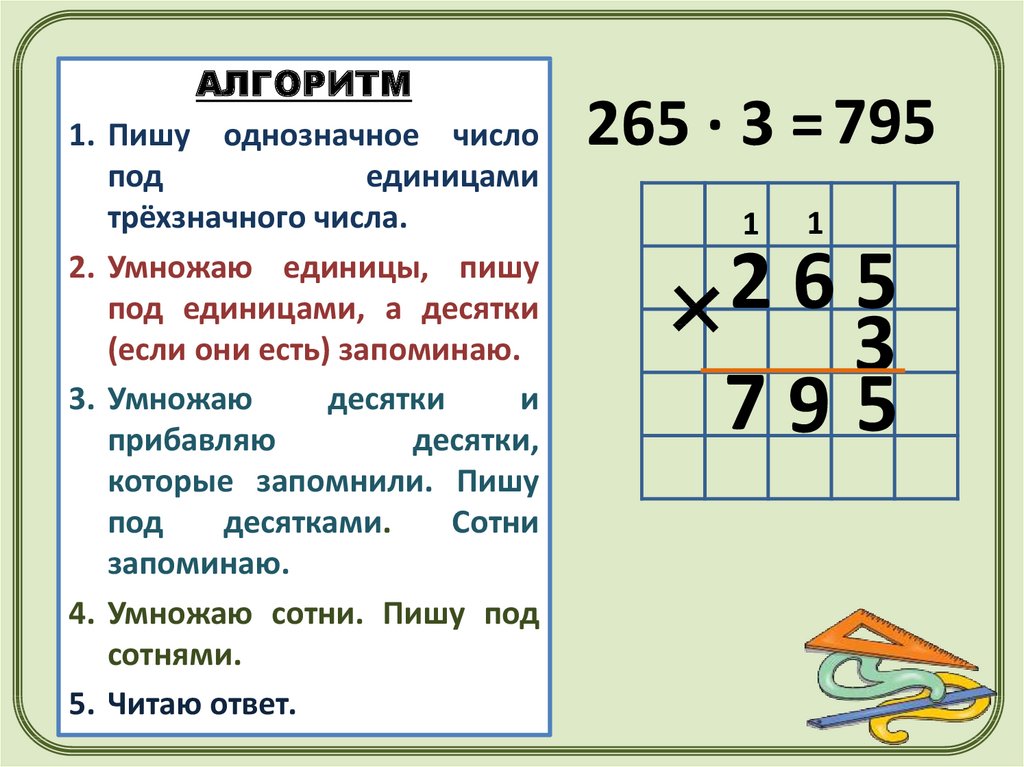 Это свойство справедливо для сложения и умножения, но не для вычитания и деления. Давайте посмотрим.
Это свойство справедливо для сложения и умножения, но не для вычитания и деления. Давайте посмотрим.
Приведенные выше примеры ясно показывают, что свойство коммутативности верно для сложения и умножения, но не для вычитания и деления. Итак, если мы поменяем местами числа в операторах вычитания или деления, это изменит всю проблему.
Итак, математически коммутативное свойство сложения и умножения выглядит так:
Родственные игры
Коммутативное свойство сложения:
a + b = b + a; где a и b — любые 2 целых числа
Связанные рабочие листы
Коммутативное свойство умножения:
a × b = b × a; где a и b — любые 2 ненулевых целых числа
Варианты использования коммутативного свойства
- У Майры 6 яблок и 2 персика. У Ким 2 яблока и 6 персиков. У кого больше фруктов?
Даже если у обоих разное количество яблок и персиков, у них равное количество фруктов, потому что 2 + 6 = 6 + 2.
- Сара покупает 3 упаковки булочек. В каждой упаковке по 4 булочки. Мила покупает 4 упаковки булочек, в каждой по 3 булочки. Кто купил больше булочек?
Даже если у обоих разное количество упаковок булочек, причем у каждого из них разное количество булочек, они оба купили одинаковое количество булочек, потому что 3 × 4 = 4 × 3.
Решенные примеры по свойству переместимости
Пример 1: Заполните пропущенные числа, используя свойство переместимости.
- _________ + 27 = 27 + 11
- 45 + 89 = 89 + _________
- 84 × ______ = 77 × 84
- 118 × 36 = ________ × 118
Решение:
- 11; по коммутативному свойству сложения
- 45; по коммутативному свойству сложения
- 77; по коммутативному свойству умножения
- 36; по коммутативному свойству умножения
Пример 2: Используйте 14 × 15 = 210, чтобы найти 15 × 14.
Решение:
Согласно свойству перестановочности умножения 15 × 14 = 14 × 15. 5
9 = 210, поэтому 15 × 14 также равно 210.Пример 3: Используйте 827 + 389 = 1,216, чтобы найти 389 + 827.
Решение:
= 389 + 827.Поскольку 827 + 389 = 1216, значит, 389 + 827 также равно 1216.
Пример 4: Используйте свойство коммутативности сложения, чтобы записать уравнение 3 + 5 + 9 = 17 в другой последовательности слагаемых.
Решение:
3 + 9 + 5 = 17 (поскольку 5 + 9 = 9 + 5)
5 + 3 + 9 = 17 (поскольку 3 + 5 = 5 + 3)
5 + 9 + 3 = 17 (потому что 3 + 9 = 9 + 3)
Точно так же мы можем переставить слагаемые и написать:
9 + 3 + 5 = 17
9 + 5 + 3 = 17
Пример 4: Бен купил 3 упаковки по 6 ручек в каждой. Миа купила 6 упаковок по 3 ручки в каждой. Они купили одинаковое количество ручек или нет?
Решение:
Бен купил 3 упаковки по 6 ручек в каждой.
Итак, общее количество ручек, которые купил Бен = 3 × 6
Миа купила 6 упаковок по 3 ручки в каждой.
Итак, общее количество ручек, которые купил Бен = 6 × 3
По свойству перестановочности умножения 3 × 6 = 6 × 3.
Итак, Бен и Мия купили одинаковое количество ручек.
Пример 5: У Лизы 78 красных и 6 синих шариков. У Бет есть 6 упаковок по 78 шариков в каждой. У них одинаковое количество шариков?
Решение:
Так как у Лизы 78 красных и 6 синих шариков.
Итак, общее количество шариков у Лизы = 78 + 6
У Бет 6 пакетов по 78 шариков в каждом.
Итак, общее количество шариков с Бет = 6 × 78
Очевидно, что сложение и умножение двух чисел дает разные результаты. (Кроме 2 + 2 и 2 × 2.
То есть 78 + 6 ≠ 6 × 78
Итак, у Лизы и Бет не одинаковое количество шариков.
Практические задачи
1
Какие следующее представляет коммутативное свойство сложения?0005
Правильный ответ: 8 + 5 = 5 + 8
Согласно свойству коммутативности сложения сумма не меняется при перестановке слагаемых. То есть а + b = b + а.
То есть а + b = b + а.
2
Что из следующего представляет коммутативное свойство умножения?
7 × $\frac{1}{7}$ = 1
7 × 1 = 7
7 × 3 = 3 × 7
7 × 0 = 0
Правильный ответ: 7 × 3 = 3 × 7
Согласно коммутативному свойству умножения, произведение остается тем же самым при замене местами множимого и множителя. То есть а × b = b × а.
3
Какое из следующих выражений будет следовать свойству коммутативности?
15 ÷ 3
15 × 3
15 – 3
3 ÷ 15
Правильный ответ: 15 × 3
Коммутативное свойство не выполняется для деления и вычитания.
4
Выберите набор чисел, чтобы утверждение было верным.
5 + _____ = 4 + ______
5, 5
4, 4
5, 4
4, 5
Правильный ответ: 4, 5
5 + 4 = 4 + 5
(по коммутативному свойству сложения)
Часто задаваемые вопросы
Можно ли применить коммутативное свойство сложения/умножения к трем числам?
Да. По определению коммутативность применяется к 2 числам, но результат остается тем же и для 3 чисел. Это потому, что мы можем применить это свойство к двум числам из 3 в различных комбинациях.
По определению коммутативность применяется к 2 числам, но результат остается тем же и для 3 чисел. Это потому, что мы можем применить это свойство к двум числам из 3 в различных комбинациях.
Какие операции не следуют свойству коммутативности?
Коммутативное свойство не применимо к вычитанию и делению.
Что такое ассоциативное свойство сложения (или умножения)?
Это свойство указывает, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается одинаковой независимо от группировки слагаемых (или множимых). То есть
(a + b) + c = a + (b + c)
(a × b) × c = a × (b × c), где a, b и c — целые числа.
Для каких операций выполняется свойство ассоциативности?
Ассоциативное свойство верно для сложения и умножения.
Какое распределительное свойство умножения?
Под распределительным свойством умножения над сложением мы подразумеваем, что умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждого слагаемого по отдельности на число, а затем сложение произведений вместе. То есть
То есть
a × (b + c) = (a × b) + (a × c), где a, b и c — целые числа.
3 способа понять умножение матриц | by Glenn Henshaw
Развивайте свою интуицию в умножении матриц с нуля Photo by Markus Spiske на UnsplashКогда я впервые узнал о умножении матриц, я был удивлен тем, как трудно мне было развить интуицию в отношении этой операции. Обычное определение матричного умножения скрывает множество интересных фактов, которые легче распознать, если посмотреть с разных точек зрения. В этом посте я опишу умножение матриц с трех точек зрения: столбцы, строки и их комбинации. Я также расскажу о некоторых простых фактах, которые помогут проверить вашу интуицию. Мы надеемся, что после прочтения вы получите более глубокое представление об умножении матриц, строках и столбцах. Этот пост был вдохновлен курсом линейной алгебры, который вел великий Гилберт Странг (MIT) .
В этом посте перечислены три способа интерпретации умножения матриц. Для каждой из этих интерпретаций мы обсудим следующее.
Для каждой из этих интерпретаций мы обсудим следующее.
- Интерпретация: Что это значит?
- Почему это работает?: Как эта интерпретация возникает из определения умножения матриц?
- Проверьте свою интуицию: Список фактов, которые вы можете использовать, чтобы проверить свою интуицию для интерпретации, которую мы рассматриваем.
Иногда я упоминаю понятия линейной комбинации , линейной зависимости , линейной независимости , скалярного произведения . Если вы хотите быстро освежить свою память по этим темам, посмотрите мою статью 3 основных понятия в линейной алгебре.
Пример. Допустим, у нас есть три завсегдатая: Ларс, Фатима и Джорджия. На вечеринке Ларс купил 2 пива и 1 коктейль, Фатима купила 1 пиво и 2 коктейля, а у Джорджии было 4 пива и никаких коктейлей. Пиво стоит 7 долларов, а коктейли — 10 долларов. Мы можем смоделировать их расходы на ночь с помощью матричного умножения.
Мы можем смоделировать их расходы на ночь с помощью матричного умножения.
Как были вычислены числа справа?
Наша цель — понять свойства умножения матриц в более общем виде, поэтому в этом посте мы будем рассматривать произведение матрицы 3×3 A и матрицы 3×2 B . . Результатом будет матрица 3×2 C .
Жак Филипп Мари Бине … признан первым, кто вывел правило умножения матриц в 1812 году. — Оливер Книлл
Обычный способ определить умножение матриц – это суммирование или, более компактно, скалярное произведение строк A и столбцов B. Скалярное произведение строки 1 A и столбца 1 B даст первую запись C.
В общем случае ij-я запись C представляет собой i-ю строку A , разделенную точками с j-м столбцом B .
Пример. Найдите третью строку и второй столбец произведения C .
Ответ: (1)(1)+(2)(2) +(3)(1) = 8. Попробуйте использовать определение, чтобы найти остальные записи С .
Интерпретация: Запись C является скалярным произведением строки A и столбца B . Нулевые записи в C соответствуют строке A и столбцу B , которые являются ортогональными (под прямым углом друг к другу).
Проверьте свою интуицию: С этой точки зрения некоторые факты становятся яснее .
- Количество столбцов A должно равняться количеству строк B . В противном случае суммы в определении не будут определены.
- Продукт AB будет матрицей с тем же количеством столбцов, что и A , и тем же количеством строк, что и B.

- соответствует ряду A и столбец B ортогональны. Ортогональные векторы линейно независимы . Но не все пары линейно независимых векторов ортогональны.
Первое, на что следует обратить внимание относительно AB = C , это то, что столбцы матрицы C связаны со столбцами матрицы A важным образом.
Интерпретация Каждый из столбцов C является матрицей A , умноженные на колонку B. Эффект этого состоит в том, что Колонны C – это Lineaear Combinations из 9024. столбцы B.
Почему это работает? Чтобы понять, почему столбцы C являются линейными комбинациями столбцов A , давайте внимательно посмотрим, как мы вычисляем первый столбец C.
Проверьте свою интуицию: С этой точки зрения некоторые факты становятся яснее .
- Матрица, умноженная на вектор, Ax , представляет собой просто линейную комбинацию столбцов a с элементами x. Таким образом, столбцы A линейно независимы тогда и только тогда, когда уравнение Ax = 0 имеет только нулевое решение.
- Мы можем просмотреть столбцы C как результат применения линейного преобразования, определенного B , к столбцам A .
- Предположим, что столбцы A линейно независимы. Тогда, если C имеет столбец нулей, B также должен иметь столбец нулей.
- Если столбцы C линейно зависимы и столбцы B линейно независимы, то столбцы A зависимы.
 This follows from that fact that if x is a non-trivial solution of Cx = 0 then Bx is a non-trivial solution of Ax = 0.
This follows from that fact that if x is a non-trivial solution of Cx = 0 then Bx is a non-trivial solution of Ax = 0. - Если уравнение Ax = b не имеет решения, то уравнение ABx = Cx = b не имеет решения. Ведь столбцы C – это просто комбинации столбцов A .
- Пролет колонн C содержится в пролете колонн A . Следовательно, ранг(AB) ≤ ранг(A) .
- Если B обратим с обратным B’ , то столбцы A и AB 9002 имеют одинаковый пролет. Мы можем доказать это из предыдущего факта, ранг(AB) ≤ ранг(A) в сочетании с тем фактом, что ранг(A) = ранг(AI) = ранг(ABB’) ≤ ранг(AB).

Итак, умножение матриц с точки зрения столбцов. Теперь перейдем к рядам?
Интерпретация Строки C являются строками A , умноженными на матрицу B . Следовательно, строки C являются линейными комбинациями строк B с весами, указанными в строках A.
Почему это работает? Чтобы понять, почему строки C являются линейными комбинациями строк B , давайте внимательно посмотрим, как мы вычисляем первую строку C , используя определение умножения матриц.
Проверьте свою интуицию: Давайте еще раз перечислим некоторые факты о строках, которые выводятся из этой интерпретации умножения матриц.
- Для AB = C , если строки C линейно независимы, то строки B линейно независимы.
 Предупреждение: обратное не обязательно верно.
Предупреждение: обратное не обязательно верно. - Если A имеет ряд нулей, то AB имеет ряд нулей.
- Диапазон строк B содержит диапазон строк C .
- Если E — обратимая матрица n×n , а B — любая матрица n×m . Тогда EB имеет то же место в строке, что и E . В частности, элементарные операции со строками сохраняют пространство строк.
Мы можем использовать интерпретацию строки и столбца, чтобы помочь набросать доказательство интересного результата о размерности пространства строки и пространства столбца m×n матрица. Размерность размаха столбцов матрицы называется ее рангом . Размер промежутка строк называется rowrank .
Претензия: Ранг и Rowrank из M × N MATRIX C4 4 4164.
Есть много m×r матриц A и r×n матрицы B такие, что C = AB. Выберите A и B так, чтобы r было минимальным. The r columns of A span the column space of C. The r строки B охватывают пространство строк C. Поскольку мы выбрали r как наименьшее такое число, rank(C) = rowrank(C) = r.
Претензия: , если A и B – квадратные матрицы, а AB = I Затем BA = I. Следовательно, B – это 2 A.
. Мы – 9023 9023. АВ = I . Поэтому столбцы A линейно независимы. Поэтому уравнение Ax = 0 имеет только тривиальное решение. умножьте первое уравнение справа на A , чтобы получить ABA = A . Тогда ABA-A = A(BA-I)=0 . Следовательно, ВА = I .Наша последняя интерпретация дает нам способ разложить произведение двух матриц на сумму матриц.
Интерпретация Матрица C представляет собой сумму матриц, состоящих из столбцов A , умноженных на строки B.