Примеры на состав числа до 10 распечатать: Примеры на состав числа до 10

Состав числа до 10

Правильный устный и письменный счет (и правильность выполнения заданий по математике в школе) зависит от того, насколько хорошо ребенок понимает состав числа. Усвоить, из чего состоят числа от единицы до десятки, малышу лучше в дошкольном возрасте. И учить его этому лучше в формате математической игры.

Содержание:

• Разбираемся в материале
• Упражнения на сложение
• Упражнения на вычитание

Разбираемся в материале

Состав любого числа – это пара любых слагаемых, которые в сумме дают этот результат. Например, число 10 можно получить как 5 + 5, как 3 + 7, как 1 + 9 и т.д. Для лучшего понимания материала рекомендуется сделать отдельные карточки из пар слагаемых для одной и той же суммы:

• 9 + 0 = 9
• 8 + 1 = 9
• 7 + 2 = 9
• 6 + 3 = 9
• 5 + 4 = 9 и т.д.

Карточки с цифрами можно использовать не просто для рассматривания и запоминания. С ними можно придумать множество игр, составляя примеры из счетных палочек, шашек или других предметов. Например, для карточки 1 + 3 = 4 ребенок должен составить правильную сумму из фруктов, поместив в миску 1 яблоко и 3 банана. Также можно выкладывать в ряд предметы разных цветов: 1 красную палочку и 3 зеленых или наоборот. Еще один вариант – раскрашивать нарисованные на бумаге деревья, домики, другие предметы в нужные цвета: два синих, четыре желтых и т.д.

Упражнения на сложение

Для занятий понадобятся карточки со слагаемыми, без цифр-ответов:

• 1 + 2;
• 1 + 3;
• 1 + 4;
• 1 + 5 и т.д., для всех чисел от 1 до 10.

Когда ребенок изучает состав определенного числа, например, 8, для закрепления материала ему выдаются карточки, где указан состав 8 и несколько других подобных: 1 + 6 = 7, 2 + 3 = 5 и т.д. Малыш должен выбрать из ряда карточек все примеры с составом нужного числа.

Также можно просто показывать ребенку произвольные карточки без ответов, чтобы он посчитал правильную сумму – сначала с помощью пальцев или других предметов, а затем устно. Отвечать можно устно, но также можно писать цифры-ответы на карточке.

Упражнения на вычитание

Сначала ребенку следует объяснить: если в сложении мы соединяем два числа и получаем сумму, то вычитание – это обратный процесс. При вычитании зная сумму и одно из слагаемых, мы находим второе из них. И если кроха назубок знает состав чисел от 1 до 10, неизвестное слагаемое ему долго высчитывать не придется – он его просто «припомнит».

К примеру, из каких слагаемых состоит 7, малыш уже выучил. Сначала нужно вспомнить все его вариации: пусть ребенок их перечислит. Теперь ставите семерку на первое место и вычитаете из нее одно из слагаемых. Второе получится в ответе. Аналогично пробуем другой пример: если 6 + 1 = 7, то сколько будет 7-6? Для занятий лучше приготовить несколько карточек на вычитание без ответов: 7–1, 7–2 и т.д.

Если вычитание у ребенка пока еще вызывает затруднения, приготовьте большие карточки, на которых приведите примеры состава чисел в следующем виде:

• 4 + 1 = 5
• 1 + 4 = 5
• 5 – 1 = ?
• 5 – 4 = ?

Это поможет малышу понять связь вычитания и сложения, что очень важно для решения уравнений в будущем. Если ребенок не усвоит этот материал, решать примеры с неизвестными в школе он будет с трудом.

Рейтинг: 5/5 – 1 голосов

Таблица сложения для детей распечатать. Как научить ребенка считать? Советуют педагоги

Подготовка к игре – настройки

1. Любые параметры и настройки могут быть изменены когда угодно, даже во время игры.
2. Изначально игра настроена так:
   • Тип вычисленией – Сложение до 10
   • Премия 1 – шоколадка, премия 2 – печенье
   • В игровой сессии 10 вычислений (арифметических примеров)
   • Процент примеров, которые надо решить правильно для получения Премии 1 – 90%
   • Процент примеров, которые надо решить правильно для получения Премии 2 – 70%
3. Вы можете выбрать любой другой тип вычислений – в зависимости от того, что ребенок знает и что проходит в школе в данный момент. Типы вычислений в игре:
   • Сложение, вычитание, сложение и вычитание (вперемешку):
     • До 10
     • До 20 (с переходом через десятку)
     • До 20 (с переходом через десятку и без)
     • До 30
     • До 100
   • Умножение, деление или любые комбинации -на 1, -на 2, -на 3…….и т. д. до 10
   • Сравнение чисел
4. Установите, сколько примеров будет в игровой сессии. Лучше начать с небольшого количества попыток – 5 или 10, чтобы не отбить у ребенка желание продолжать игру. Когда ребенок повысит надои:) улучшит показатели, можно переходить к серьезной игре с 100-200 примерами.
5. Внесите процент правильно решенных примеров, за который выдаются 1 и 2 премии. Для начала лучше понизить процент. Например выбрать 70 и 50 процентов для 1 и 2 премий, соответственно. Позже ставки можно увеличить до 90 – 70. Или даже до 98% – 95% для совсем уж жутко умных детей:). Вносите только цифры, без знака %!
6. Запишите премии, которые ребенок получит за 1 и 2 место.
7. Настройки будут сохранены с помощью cookie (небольшого скрипта) и восстановлены, когда вы следующий раз откроете в браузере страницу с игрой.

Теперь можно начинать игру!

1. Чтобы начать игру, нажмите кнопку СТАРТ
2. Когда на экране появится пример, ребенок должен внести ответ после знака “=”
3. Если играем в “сравнения”, нужно внести соответствующий знак: . Для этого удобнее всего пользоваться кнопками, которые появятся рядом с кнопкой ДАЛЬШЕ
4. После того, как внесен результат, нужно нажать на кнопку ОК (или ENTER на клавиатуре), чтобы проверить правильно ли был решен пример.
5. Если пример был решен правильно, на экране появится “Правильно”. Если нет, “Неправильно” и верный ответ. В то же время, игра посчитает процент правильно решенных примеров
6. Чтобы перейти к следующему примеру, нужно нажать кнопку ДАЛЬШЕ
7. Когда сессия закончится, на экране появится премия, которую выиграл ребенок (или “ничего не выиграл”) и процент правильно решенных за сессию примеров
8. Чтобы начать новую сессию, нажмите кнопку НАЧАТЬ СНАЧАЛА.

Большие надежды:)

Чего можно ожидать от этой игры? Большой помощи в прохождении школьной программы! Как правило за 5-7 дней, в которые ребенок играет по 30-40 минут, он твердо усваивает очередной тип вычислений (например, сложение до 20 с переходом через десятку). И практически перестает делать ошибки в классе.

Цели урока:

1. Обучающие:

• закреплять умение считать от 1-10 в прямом и обратном порядке;
• умение называть «соседей» числа, сравнивать числа;
• табличное сложение и вычитание 1, 2, 3;
• повторить состав числа 10;совершенствовать умение решать задачи на увеличение числа на несколько единиц;

2. Развивающие:

• развивать внимание, речь учащихся, мышление;

3. Воспитательные:

• воспитывать любовь к животным.

Оформление:

• фигурки животных – зайчика, белочки, ёжика; «брёвнышки» с примерами;
• лесная полянка – деревья, цветы;
• теремок;
• «печка»;
• корзинка с грибками;
• карточка на логическое мышление;
• индивидуальные карточки.

Ход урока

I. Организационный момент.

Солнце на небе проснулось,
Нам, ребята, улыбнулось.
Глазки тихо закрываем,
Руки к небу поднимаем.
Лучи солнышка возьмём
И к сердечку поднесём.

Вы чувствуете солнечное тепло?

Пусть сегодня на уроке будет тёплая, дружеская атмосфера.

На листочках нарисуйте солнышко.

II. Устные упражнения.

1. Счёт от 1 до 10, от 10 до 1.
2. Счёт через число.
3. Назвать «соседей» чисел: 2, 6, 5, 7, 1.
4. Сравнить числа: 5 и 3, 2 и 4, 6 и 7.
   Назвать самое меньшее число.
   Назвать самое большее число.
5. Прочитайте числа: 2, 5, 4, 8, 7.
   Увеличьте каждое число на 2.

III. Закрепление таблиц сложения и вычитания 1, 2, 3.

А сейчас мы отправимся в путь с нашими героями: Зайчиком, Белочкой и Ёжиком. Прослышали они, что на краю леса стоит чудо-теремок. Кто захочет, может в нём жить. Но с ними случилась беда. Нужно быстро им помочь.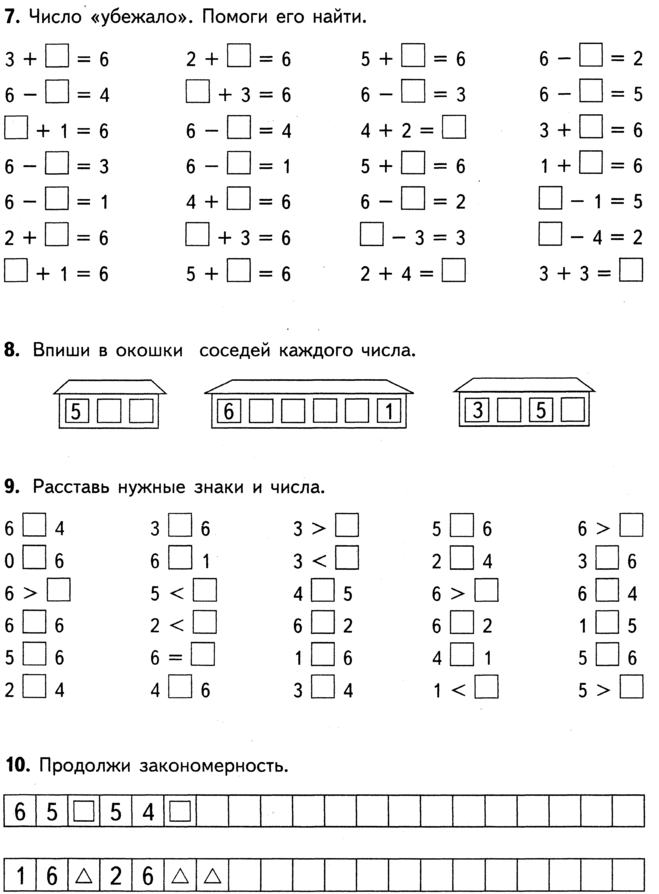

Скажите, какое время года сейчас наступило? По каким признакам определили?

Растаял снег, потекли ручейки. Речка вышла из берегов и всё кругом затопила. Это явление называется – половодье. Очень трудно приходится животным в это время. Они стараются спастись сами и в этом им помогают люди.Очень трудно приходится животным в это время. .удниковской гимназии, Ёжиком. ать умение решать задачи на увеличение числа на н

1. «Островок»

Оказались наши герои на островке. Нужно им построить мостик из брёвнышек. (На «брёвнышках» написаны примеры. Дети решают и строят мостик.)

2. «Чудо-дерево»

На этом дереве растут знаки и числа. Нашим героям нужно их расселить по своим квартирам.

Как ещё можно разделить?

б) Белка и Зайчик решили посоревноваться. (Белка собирает шишки, а Зайчик – морковки.)

Физминутка

Мы ногами – топ-топ.
Мы руками – хлоп-хлоп.
Мы глазами – миг-миг.
Мы плечами – чик-чик.
Раз – сюда, два – сюда,
Повернись вокруг себя.
Раз – присели, два – привстали,
Руки кверху все подняли.
Сели, встали,
Ванькой – встанькой словно стали.
Руки к телу все прижали
И подскоки делать стали,
А потом пустились вскачь,
Будто мой упругий мяч.
Раз-два, раз-два,
Заниматься нам пора!

4. Задание на логическое мышление.

Чтобы найти тропинку к теремку, нужно выполнить такие задания:

а) Логика.

На каждой полоске отметить крестиком две такие части, из которых можно составить круг.

б) Закрепление состава числа 10.

Найти «тропинку» к числу 10.

9 + 1		7 + 3		6 + 4
	7 + 2					5 + 5		10
8 + 1		8 + 2		5 + 4

(картинка «теремка»)

6. «Теремок».

Наши герои проголодались, а тут стоит печка.

Напекла я пирогов
Для друзей, не для врагов.
Дверку приоткрой,
Пирожочек будет твой!

Но пирогов они отведают только тогда, когда разрешат свой спор.

а) Решение задачи.

Спорят Ёжик и Зайчик. Зайчик говорит, что съест 4 пирожка, а Ёжик говорит, что съест на 2 пирожка больше. Сколько же пирожков съест Ёжик?

(Составление решения задачи в кассах.)

б) Составление задачи учащимися.

А Белка принялась за шишки. Составьте задачу про Белочку и про шишки.

И так, наши герои нашли теремок. Теперь им будет, где жить.

6. Работа на карточках.

Найти примеры с ответом 5 и раскрасьте красным карандашом, с ответом 8 – синим, 7 – зелёным, 6 – жёлтым.

IV. Итог урока.

• – За что вы себя можете похвалить?
• – Чем остались недовольны?
• -Нарисуйте солнышко, покажите какое у вас настроение.

Список литературы:

1. С. А. Лёвкина «Физминутки».
2. Учебник М.И. Моро 1 класс.
3. С.И. Волкова «Тетрадь с математическими заданиями».

Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу

Таблица сложения до 20 распечатать и скачать

Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.

Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.

Таблица вычитания до 20 распечатать и скачать

В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 – 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.

Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах.

Таблица вычитания без ответов распечатать и скачать

На основе макета таблицы вычитания с ответами в формате Excel при необходимости можно сделать и другие таблицы вычитания, например больших значений, до 20, до 30 и т.д.

Первый этап. Не используем запись числа

Первостепенная задача — научить считать до 10, н е используя соответствующие цифры.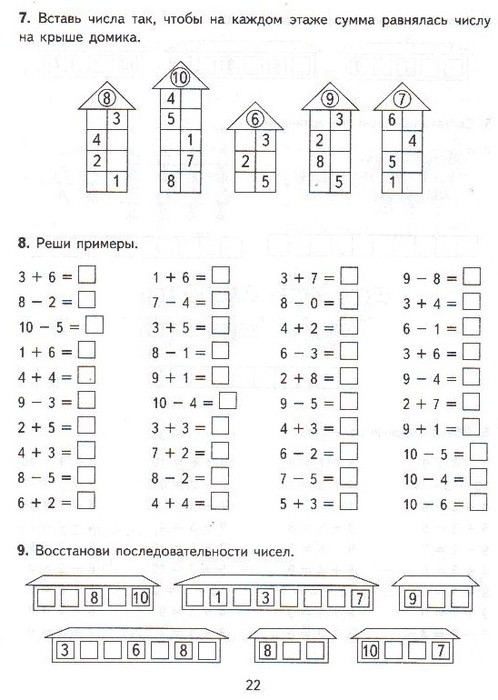 На первый план выходят действия с предметами. Например, была одна ложка, положили еще одну — стало две ложки. Потом можно увеличивать количество ложек, говоря название числа.

Помогут в решении этой задачи практические задания. Например, чаще спрашивать у ребенка о количестве чего-нибудь: сколько тарелок, сколько тапочек, сколько птиц на той ветке. Считать можно что угодно, даже ступеньки лестницы.

Второй этап. Знакомство с самими цифрами.

В первом классе сначала изучается цифра 1, 2, 0, а потом уже 3, 4, 5, 6, 7, 8, 9. Обусловлено положение нуля тем, что ученику на первых порах сложно понять, почему пустота обозначается цифрой. И тогда, когда уже практикуются действия с цифрами, становится понятно, зачем нужен нуль. Например, было пять яблок на столе, пять съели. Осталось — ничего, то есть ноль.

Еще вариант: Показываются эти рисунки, и спрашивает учитель у детей: «Что изменилось?». Они отметят: «Ничего».

На втором образце показано, что если в одном квадрате три точки убрать совсем, то будет пустой квадрат и точек вообще не останется.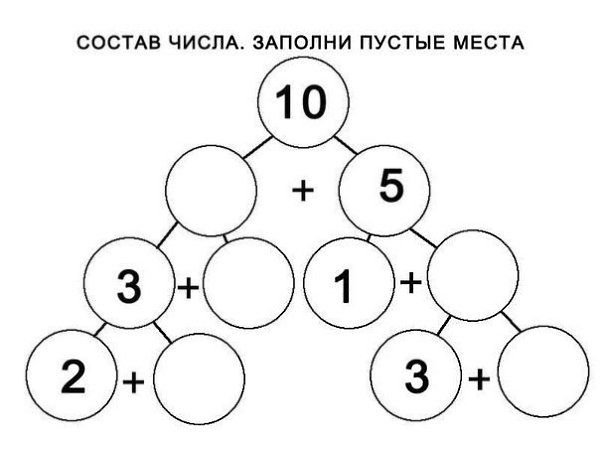

Главное правило, которые должны понять дети при счете до десяти: каждая цифра меньше последующей на один и больше прошлой цифры на один.

Приемы обучения счету до десяти:

• Игра в паровозик . Распространенная тренировка заучивания цифр, проводимая в первом классе. Выходит перед классом один ученик, он говорит, что он — вагон первый. После этого выходит еще один, и говорит: один и еще один будет два. И так продолжается до десяти. Потом операция делается в обратном порядке. Вагоны “распадаются” по одному. Цель этого упражнения — запоминание порядка чисел в прямом и обратном порядке.
• Показ на линейке . Это устаревший метод, основанный на механическом запоминании и наглядном доказательстве порядка чисел.
• Счет на пальцах . Традиционный и самый легкий для детей. Можно использовать на первой поре, пока ребенок не будет порядок цифр. Потом надо отучать от пальцев, рассказывая «секреты» превращений цифр.

• Использование смешных стихов и мультиков о числах . Интересно будет посмотреть мультик «Как козленок учился считать» или проговаривать считалки.

Стихотворения-запоминалки для изучения счета

Ягодный счет

По опушке шла лисичка:
— Раз, в корзинке земляничка,
Два — как небо голубика,
Три — румяная брусника,
А четыре — вот морошка,
Пять — смородины немножко,
Шесть — как бусинка калина,
Семь — как солнышко рябина,
Восемь — в лапке ежевика,
Девять — синяя черника,
Десять — сочная малина.
Вот и полная корзина!

Раз — рука, два — рука —
Лепим мы снеговика!
Три — четыре, три — четыре,
Нарисуем рот пошире!
Пять — найдем морковь для носа,
Угольки найдем для глаз.
Шесть — наденем шляпу косо.
Пусть смеется он у нас.
Семь и восемь, семь и восемь,
Мы сплясать его попросим.
Девять — десять — снеговик
Через голову — кувырк!
Ну и цирк!

Пошли пальчики гулять,
А вторые догонять,
Третьи пальчики бегом,
А четвертые пешком,
Пятый пальчик поскакал,
И в конце пути упал.

• Игра “Назови соседей числа” . Например, нужно назвать соседей числа 4.
• Упражнение «Цифры заблудились» . Нужно разложить по порядку беспорядочно разложенные картинки с цифрами. Есть другая интерпретация этого упражнения: Баба-Яга перепутала все цифры. Помоги расставить их правильно.

• Под забором было видно 10 лапок цыплят. Вопрос: сколько всего цыплят? — Счет двойками: 2, 4, 6, 8, 10 — пять цыплят.
• Сколько сапог надо подарить троим гусятам? Аналогично предыдущей задачке.
• Считать пятерками удобнее всего, наблюдая за часами.

Как выучить таблицу сложения и вычитания в пределах десяти?

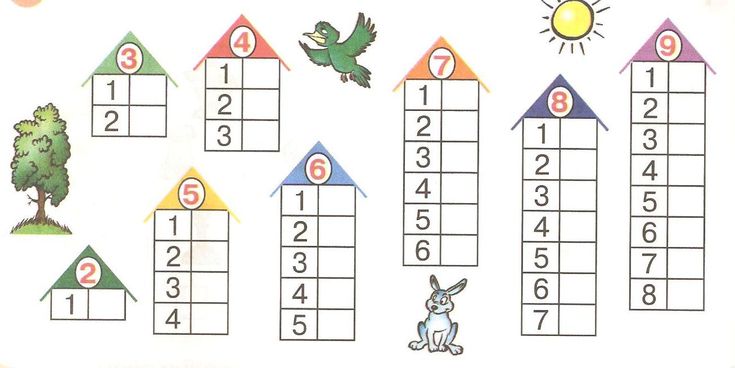
После того как ребенок знает порядок числительных, полезно применять задания на состав числа. Можно, конечно, зазубрить состав числа 5, например, но лучше использовать игровые действия с предметами с параллельной установкой на запоминание.

Например:

В одной тарелке было 4 апельсина, а в другой — 2. Сколько всего апельсинов? (Задача на нахождение суммы)

Всего 6 яблок, а друзей — трое. Разделите каждому поровну, одинаково.

Сочетать с простыми задачами можно и маленькие схемы, которые легко применять на уроке и дома.

На переместительный закон сложения не сложно привести такой пример: одна тарелка с двумя яблоками лежит на столе, а другая тарелка с четырьмя яблоками — лежит рядышком, если поменять их местами, то все равно общее количество яблок останется неизменным.

Как научить ребенка складывать и вычитать с переходом через десяток?

В приведенном ниже примере, чтобы сложить числа 8 и 5, второе слагаемое раскладывается так, чтобы дополнить первое слагаемое до десяти, а потом остаток прибавляется к десяти.

Что касается вычитания, то тут раскладывается уменьшаемое по разрядному составу. На примере 15 минус 8 мы видим, что число 15 раскладывается до своих разрядных единиц. В итоге всегда получается 10 и разрядные единички — 5. Теперь: вычитаемое надо разложить на слагаемые. Первым слагаемым будут разрядные единицы от 15-ти, а второе слагаемое подбирается (дети знают состав числа 8). Теперь остается от 10-ти отнять второе слагаемое от восьмерки. И ответ готов. Немного потренировавшись, можно будет легко решать подобные примеры в уме.

Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу

Таблица сложения до 20 распечатать и скачать

Таблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11.

Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.

Таблица вычитания до 20 распечатать и скачать

В качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 – 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ.

Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах.

Таблица вычитания без ответов распечатать и скачать

На основе макета таблицы вычитания с ответами в формате Excel при необходимости можно сделать и другие таблицы вычитания, например больших значений, до 20, до 30 и т. д.

Понимание списка Python (с примерами)

В этой статье мы узнаем о понимании списка Python и о том, как его использовать.

Понимание списка и цикл For в Python

Предположим, мы хотим разделить буквы слова человек и добавить буквы как элементы списка. Первое, что приходит на ум, это использование цикла for.

---

Пример 1. Перебор строки с использованием цикла for

 h_letters = []
для письма в «человеке»:
    h_letters.append(буква)
печать (h_letters) 

Когда мы запустим программу, вывод будет:

  ['h', 'u', 'm', 'a', 'n']  

Однако в Python есть более простой способ решить эту проблему с помощью понимания списка. Понимание списков — это элегантный способ определения и создания списков на основе существующих списков.

Давайте посмотрим, как вышеприведенная программа может быть написана с использованием списков.

---

Пример 2. Перебор строки с использованием понимания списка

 h_letters = [буква за буквой в 'человеке']
печать(h_letters) 

Когда мы запустим программу, вывод будет:

  ['h', 'u', 'm', 'a', 'n']  

В приведенном выше примере новый список назначается переменной h_letters , и список содержит элементы итерируемой строки ‘человек’.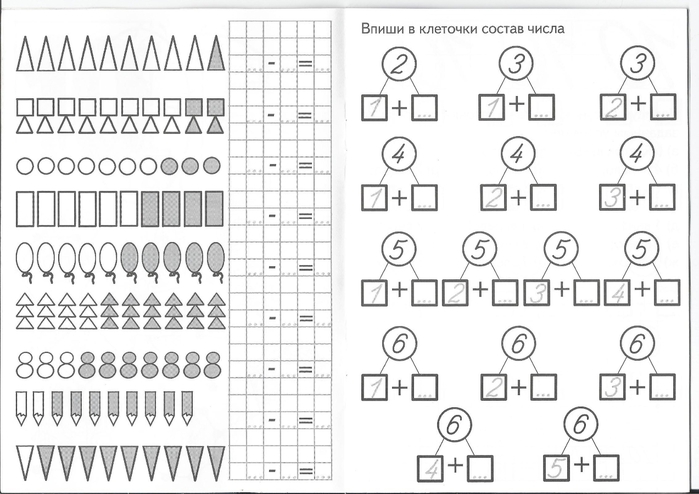 Мы вызываем функцию print() для получения вывода.

---

Синтаксис понимания списка

[выражение для элемента в списке] 

Теперь мы можем определить, где используются включения списков.

Если вы заметили, человек — это строка, а не список. Это сила понимания списка. Он может определить, когда он получает строку или кортеж, и работать с ним как со списком.

Это можно сделать с помощью циклов. Однако не каждый цикл можно переписать как понимание списка. Но по мере того, как вы изучаете и осваиваете понимание списков, вы обнаружите, что заменяете все больше и больше циклов этим элегантным синтаксисом.

---

Сравнение списков и лямбда-функций

Генерация списков — не единственный способ работы со списками. Различные встроенные функции и лямбда-функции могут создавать и изменять списки с меньшим количеством строк кода.

Пример 3. Использование лямбда-функций внутри List

 letter = list(map(lambda x: x, 'human'))
print(letters) 

Когда мы запустим программу, вывод будет

  ['h','u','m','a','n']  

Однако списковые включения обычно более удобочитаемы, чем лямбда-функции.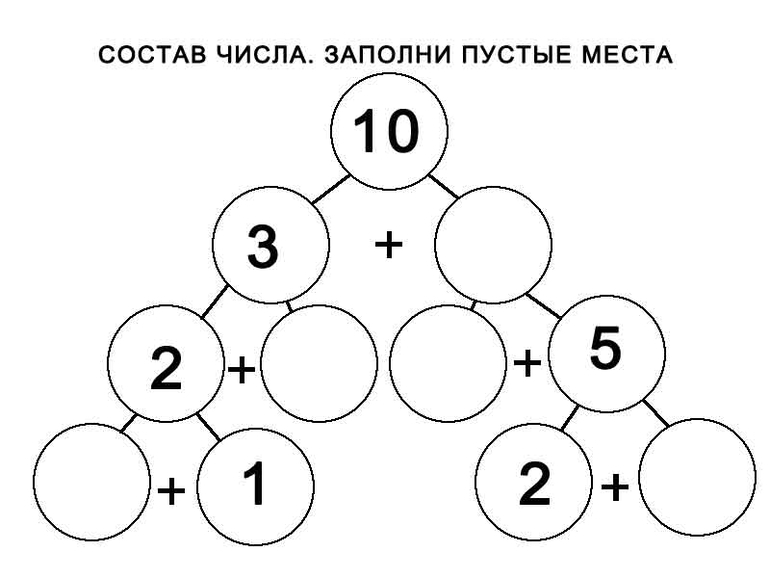 Легче понять, чего пытался достичь программист, когда используются списковые включения.

---

Условные операторы в распознавании списков

В генерациях списков может использоваться условный оператор для изменения существующего списка (или других кортежей). Мы создадим список, который использует математические операторы, целые числа и диапазон().

Пример 4: Использование if с пониманием списка

 number_list = [ x вместо x в диапазоне (20) if x % 2 == 0]
print(number_list) 

Когда мы запустим вышеуказанную программу, вывод будет:

  [0, 2, 4, 6, 8, 10, 12, 14, 16, 18]  

Список , number_list , будет заполнен элементами в диапазоне от 0 до 19, если значение элемента делится на 2. диапазон (100), если y % 2 == 0, если y % 5 == 0] print(num_list)

Когда мы запустим вышеуказанную программу, вывод будет:

  [0, 10, 20, 30, 40, 50, 60, 70, 80, 90]  

Здесь список проверок понимания:

1. Is y делится на 2 или нет?
2. Делится ли и на 5 или нет?

Если y удовлетворяет обоим условиям, y добавляется к num_list .

Пример 6: if…else с пониманием списка

 obj = ["Четный", если i%2==0 else "Нечетный" для i в диапазоне (10)]
print(obj) 

Когда мы запустим вышеуказанную программу, вывод будет:

  ['Четный', 'Нечетный', 'Четный', 'Нечетный', 'Четный', 'Нечетный', 'Четный', 'Нечетный', 'Четный', 'Нечетный']  

Здесь понимание списка проверит 10 чисел от 0 до 9. Если i делится на 2, то Четное добавляется к списку obj . Если нет, добавляется Odd .

---

Вложенные циклы в понимании списка

Предположим, нам нужно вычислить транспонирование матрицы, для которой требуется вложенный цикл for. Давайте сначала посмотрим, как это делается с помощью обычного цикла for.

Пример 7. Транспонирование матрицы с использованием вложенных циклов

 транспонировано = []
матрица = [[1, 2, 3, 4], [4, 5, 6, 8]]
для i в диапазоне (len (матрица [0])):
    транспонированная_строка = []
    для строки в матрице:
        transposed_row. append (строка [i])
    transposed.append(transposed_row)
печать (транспонирование) 

Вывод

  [[1, 4], [2, 5], [3, 6], [4, 8]] 
 

Приведенный выше код использует два цикла for для нахождения транспонирования матрицы.

Мы также можем выполнять вложенную итерацию внутри понимания списка. В этом разделе мы найдем транспонирование матрицы с использованием вложенного цикла внутри понимания списка.

Пример 8. Транспонирование матрицы с использованием понимания списка

 matrix = [[1, 2], [3,4], [5,6], [7,8]]
транспонировать = [[строка [i] для строки в матрице] для i в диапазоне (2)]
напечатать (транспонировать) 

Когда мы запустим приведенную выше программу, вывод будет:

  [[1, 3, 5, 7], [2, 4, 6, 8]]  

В приведенной выше программе у нас есть переменная матрица , которая имеет 4 строк и 2 столбцов. найти транспонирование матрицы . Для этого мы использовали понимание списка.

**Примечание: Вложенные циклы в понимании списка не работают как обычные вложенные циклы. В приведенной выше программе для i в диапазоне (2) выполняется перед row[i] для строки в матрице . Следовательно, сначала значение присваивается i , затем элемент, указанный row[i] , добавляется в переменную transpose .

---

Ключевые моменты, которые следует помнить

• Понимание списков — это элегантный способ определения и создания списков на основе существующих списков.
• Понимание списка, как правило, более компактно и быстрее, чем обычные функции и циклы для создания списка.
• Однако нам следует избегать написания очень длинных списков в одной строке, чтобы код был удобным для пользователя.
• Помните, что любое включение списка может быть переписано в цикле for, но каждый цикл for не может быть переписан в форме включения в список.

Изучение чисел для подростков в детском саду – KindergartenWorks

Лесли Симпсон · Около 5 минут, чтобы прочитать эту статью.

Обучение подростков числам в детском саду с использованием метода составления и разложения чисел. Учащиеся узнают значение разряда и быстро усваивают числа 11–19.

Вот урок математики, который я преподавал, и прелесть того, что дети снова и снова изучают концепции.

Учим числа для подростков в детском саду без простого “заучивания” путем визуализации!

В математике я действительно чувствую, что мы делаем большие успехи и нашли рутину и канавку, чтобы все это произошло! Последние три раза, когда я встречался со своими математическими группами, наше основное внимание было сосредоточено на ответах на вопрос: «Почему у подростков есть 1?»

“Почему у подростков 1?”

Первый день был почти жестоким, так как мы начали с обсуждения и не продвинулись очень далеко.

Мы использовали около десяти манипуляций с фреймами и сделали несколько подростковых чисел, чтобы попытаться выяснить, почему, но к концу нашего исследования, похоже, ничего не прижилось.

Мы использовали разлагающее выражение, чтобы записать то, что мы сделали, и, черт возьми, я сделал большое дело из этого номер один, который мы видели!

Это утверждение мы видим каждый день с начала школы   как часть нашей календарной процедуры, но теперь мы убрали наши пальцы, и радуга переместила число из утверждения на правильное значение места в первом поле.

Я не хочу сказать, что ожидал этого, но я полагал, что нам потребуется несколько раз нажать на это, чтобы действительно понять концепцию.

О боже. Некоторые из них, возможно, выглядели более растерянными, чем что-либо еще.

Сможем ли мы лучше узнать наших подростков, если поймем, почему число 13 выглядит именно так?

Это моя надежда. Я придерживался идеи, что могу лучше обучать подростков числам в детском саду, сосредоточив внимание на том, почему числа выглядят именно так, а не иначе.

Таким образом, мои ученики также могли понять, как составлять и разлагать 11-19, используя группы десятков и единиц, что является еще одним нашим стандартом.

Сможем ли мы лучше узнать наших подростков, если поймем, почему число 13 выглядит именно так?

Когда мы встретились во второй раз, они выглядели как олени в свете фар, когда я снова задал вопрос: «Почему у подростков есть 1?»

Но знаете ли вы, что почти один в каждой группе был в состоянии общаться достаточно, чтобы поделиться тем, что они поняли… как раз тогда, когда я думал никто не соединил точки.

Но это только 1 из 6 в группе! Итак, мы снова начали исследовать…

бесплатный разлагающийся лист

Используя десять ковриков из пеноматериала и фишки для бинго в качестве фишек, мы сделали числа подростков и исследовали числа большего размера (в зависимости от группы), чтобы понять, почему у них нет один. Что ж, от этого начал нарастать какой-то ажиотаж. Их глаза загорелись в трех из четырех групп, чтобы начать видеть, что они могут образовывать большие числа, считая десятками, а затем переключаясь на единицы. Используя наши хлопая в ладоши и щелкая они хотели соединить свои фишки и фишки партнера. Потом захотелось сложить их вместе с другим, а потом все соединить!

В течение одного дополнительного урока у нас было достаточно времени и практики, чтобы начать с малого и работать с большими числами (до 91), все время записывая наше разлагающее утверждение по ходу дела, что многие из них действительно выясняют это !

Все действительно начинает получаться

Все действительно начинает получаться, и они видят, почему за этой частью нашего календарного времени в наших собственных математических папках скрывается нечто большее, чем просто рутина ежедневного выполнения этого. Так что теперь они улыбаются, когда я спрашиваю: «Почему у подростков есть один?» потому что мы гордимся тем, что взломали код, поскольку мы узнаем больше об этих числах!

Десять кадров календаря

Я с нетерпением жду следующих недель, когда я поднимусь в декабрь, чтобы поработать над укреплением, проработкой неправильных представлений по мере их появления и продолжая увлекать их этими большими числами и использовать то, что они узнают о счете десятками и единицами. собрать все вместе!

Я делюсь этим, потому что это что-то другое. Я пробую в этом году вместо того, чтобы сначала изучать, как выглядит каждая цифра (я знаю, как сильно мы, добрые учителя, любим 11, 12, 13 и 15 {подмигивает}, а затем учимся их составлять, мы полагаемся на свой механический счет и навыки счета 1:1, чтобы сначала сделать это, а затем определить, почему это выглядит именно так, а не иначе.0238 Common Core Standards:

• K.NBT.1.a Составьте числа от 11 до 19 из группы из десяти единиц и дополнительных, используя предметы.
• K.NBT.1.b С помощью предметов разложить числа от 11 до 19 на группу из 10 единиц и дополнительных.
• K.CC.3.c. При появлении запроса печатать числа от 0 до 20
• K.CC.3.d. Распознавать числа от 11 до 20 не по порядку.
• К.СС.5.а. Сосчитайте до 20 предметов, которые находятся в порядке, отвечая на вопрос «сколько».

Позвольте мне помнить об этом в следующий раз, когда я захочу попробовать что-то новое, и мне кажется, что я пытаюсь загнать группу кошек на гору Синай.