Примеры на плюс и минус до 10: сложение и вычитание до 10. С пропусками. На листе А4 для печати.
Окно в Мир
| |||
15 примеров на лист. 6 листов.
15 примеров на лист. 6 листов.Сложение и вычитание до 10 – распечатать задания
Содержание
- Математическая радуга: состав числа 10
- Сложение пределах 10
- Математическая пирамида
- Вычитание в пределах 10
- Математический кроссворд
- Цветные задания
- Измерение линейкой
- Дополнительные материалы
- Стихи-задачи на сложение и вычитание до 10
Распечатать задания на сложение и вычитание до 10 для дошкольников и первоклашек.
Привычные и необычные задания: кроссворд, график, пирамида.
Математическая радуга: состав числа 10
Для чего нужна математическая радуга? Для запоминания дружественных пар чисел, сумма которых дает нам 10. Это и есть состав числа 10.
0 + 10 = 10 | 10 + 0 = 10
1 + 9 = 10 | 9 + 1 = 10
2 + 8 = 10 | 8 + 2 = 10
3 + 7 = 10 | 7 + 3 = 10
4 + 6 = 10 | 6 + 4 = 10
5 + 5 = 10
Вы можете распечатать различные варианты: цветной наглядный материал, задания для раскрашивания и подсчета, задание для составления таблицы состава числа 10.
Радуга хорошо объясняет состав числа 10: числа, расположенные на противоположных концах полоски одного цвета, в сумме дают 10.
Усвоение состава числа 10 – залог моментальных подсчетов. Быстрое сложение и вычитание до 10 напрямую зависит от этого урока.
Сложение пределах 10
Как только ребенок усвоит устный счет до 10 и написание цифр, ему можно предлагать решать несложные задачи на сложение и вычитание.
Арифметика в пределах первого десятка вполне по силам дошкольникам.
В заданиях, которые можно скачать и распечатать ниже, предлагаются простые арифметические задачи на сложение и вычитание, числовой кроссворд, математический график, математическая пирамида.
Математическая пирамида
Как решать математическую пирамиду: ее можно классифицировать как разновидность детского судоку. Задача состоит в том, чтобы решить математическую пирамиду путем сложения. Для быстрой проверки сложной трехуровневой пирамиды приложен лист с ответами!
Вычитание в пределах 10
Главное в вычитание – введение двух переменных: сколько было и сколько стало. Ребенок должен понять эти изменения, они не должны остаться абстрактными для него. Поэтому объяснения должны быть всегда на примерах.
Мальчику дали 7 печенек на тарелке. Он оставил его на столе и вышел за соком. Мальчик возвращается с ним к столу и видит, что на тарелке осталось всего два печенья.
– Кто съел мое печенье? – спросил мальчик.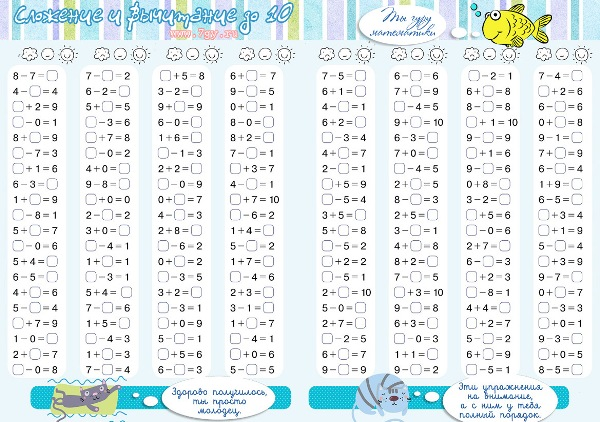
– Я съела, – говорит сестра. – Но всего три.
Сколько печенек получил тогда мальчик? А кто больше ел?
Математический кроссворд
Цветные задания
Тут необходимо заполнить все пропуски и раскрасить – как на образце.
Измерение линейкой
Пожалуй, изучение на практике – самый эффективный вид обучения. Однако тут следует воздержаться от смешивания настоящего и игрушечного. Возьмите обычную линейку с настоящими сантиметрами. Или с дюймами – это ведь тоже настоящая единица измерения, в которой измерялся и рост Дюймовочки!
В представленных ниже листах с заданиями линейка именно с дюймами. Вырежьте линейку и измерьте длину всех предметов на листе в дюймах. А потом возьмите сантиметровую линейку и сравните результат.
Если ребенку понравится это занятие, он сможет измерить все вещи в доме и со временем освоить не только счет до 10, но и до 100, 200 (тут придется взять папину рулетку), цифры, их написание, единицы измерения, развить пространственное воображение и математическое мышление.
Дополнительные материалы
- Задания для подготовки детей к школе,
- Красочные задания по математике для дошкольников,
- Счет до 20,
- Счет до 10.
Стихи-задачи на сложение и вычитание до 10
Если ребенок затрудняется с ответом, помогите ему понять задачу с помощью счетных палочек или пуговиц.
👇👇👇
Под кустами у реки
Жили майские жуки:
Дочка, сын, отец и мать.
Кто успел их сосчитать?
👇👇👇
Пять щенят в футбол играли,
Одного домой позвали.
Он в окно глядит, считает,
Сколько их теперь играет?
👇👇👇
Семь гусей пустились в путь.
Два решили отдохнуть.
Сколько их под облаками?
Сосчитайте, дети, сами.
👇👇👇
Шесть ворон на крышу село,
И одна к ним прилетела.
Отвечайте быстро, смело,
Сколько всех их прилетело?
👇👇👇
На крыльце сидит щенок,
Греет свой пушистый бок.
Прибежал еще один
И уселся рядом с ним.
(Сколько стало щенят?)
👇👇👇
Шьет себе котенок тапки,
Чтоб зимой не мёрзли лапки,
Но не может сосчитать:
Раз, два, три, четыре, пять…
👇👇👇
Я рисую кошкин дом:
Три окошка, дом с крыльцом.
Наверху еще окно,
Чтобы не было темно.
Посчитай окошки
В домике у кошки.
👇👇👇
Яблоки в саду поспели.
Мы отведать их успели:
Пять румяных, наливных,
Три с кислинкой.
Сколько их?
👇👇👇
Шесть веселых медвежат
За малиной в лес спешат.
Но один малыш устал —
От товарищей отстал.
А теперь ответ найди,
Сколько мишек впереди?
👇👇👇
У этого цветка
Четыре лепестка.
А сколько лепестков
У двух таких цветков?
👇👇👇
На плетень взлетел петух,
Повстречал еще там двух.
Сколько стало петухов?
У кого ответ готов?
👇👇👇
У меня есть три подружки,
У каждой по кружке.
Сколько кружек
У моих подружек?
👇👇👇
Барсучиха-бабушка
Испекла оладушки,
Пригласила трех внучат,
Трех драчливых барсучат.
Ну-ка, сколько барсучат
Ждут добавки и молчат?
Порядок действий – Элементарная математика
Уменьшение двусмысленности по договоренности
В общем, никто не хочет быть неправильно понятым.
В математике так важно, чтобы читатели понимали выражения именно так, как задумал автор, что математика устанавливает соглашения, согласованные правила для интерпретации математических выражений.
Означает ли 10 − 5 − 3, что мы начинаем с 10, вычитаем 5, а затем вычитаем еще 3, оставляя 2? Или это означает, что мы вычитаем 5 − 3 из 10?
Равно ли 2 + 3 × 10 50, потому что 2 + 3 равно 5, а затем мы умножаем на 10, или автор имеет в виду, что мы добавляем 2 к результату 3 × 10?
Чтобы избежать этих и других возможных неясностей, математика установила соглашения (соглашения) о том, как мы интерпретируем математические выражения. Одно из этих соглашений гласит, что когда все операции одинаковы, мы действуем слева направо, поэтому 10 – 5 – 3 = 2, поэтому автору, который хотел бы другую интерпретацию, пришлось бы писать выражение по-другому: 10 – (5). − 2). Когда операции не такие, как в 2 + 3 × 10, некоторым может быть отдано предпочтение перед другими. В частности, умножение выполняется перед сложением независимо от того, какое из чисел появляется первым при чтении слева направо.
Например, в 2 + 3 × 10 умножение должно быть выполнено первым, даже несмотря на то, что оно стоит справа от сложения, а выражение означает 2 + 30.
Полные правила порядка операций см. ниже.
Условные обозначения для чтения и записи математических выражений
Основной принцип: «более мощные» операции имеют приоритет над «менее мощными».
Использование числа в качестве показателя степени (например, 58 = 390625) имеет, как правило, «самый сильный» эффект; использование того же числа в качестве множителя (например, 5 × 8 = 40) дает более слабый эффект; сложение имеет, как правило, самый «слабый» эффект (например, 5 + 8 = 13). Хотя эти термины (мощный, слабый) в математике не употребляются, смысл сохраняется в языке «возведение 5 в 8-ю степень». Возведение в степень «мощно», поэтому оно на первом месте! Сложение/вычитание «слабые», поэтому они идут последними. Умножение/деление находится между ними.
Когда важно указать другой порядок , как это иногда бывает, мы используем круглые скобки для упаковки чисел и более слабую операцию, как если бы они представляли одно число.
Например, хотя 2 + 3 × 8 означает то же, что и 2 + 24 (поскольку умножение имеет приоритет и выполняется первым), (2 + 3) × 8 означает 5 × 8, поскольку (2 + 3) пакетное предложение, количество, которое необходимо выяснить перед его использованием. На самом деле (2 + 3) × 8 часто произносится как «два плюс три, количество, умноженное на восемь» (или «количество два плюс три, умноженное на восемь»).
Краткое изложение правил:
- Сначала скобки. Обращение к ним как к «пакетам» часто помогает детям вспомнить их цель и роль.
- Экспоненты рядом.
- Далее умножение и деление. (Ни один из них не имеет приоритета, и когда они идут последовательно, они выполняются слева направо.)
- Сложение и вычитание в последнюю очередь. (Опять же, ни один из них не имеет приоритета, и последовательная строка из них выполняется слева направо.)
Распространенные заблуждения
Многие учащиеся изучают порядок операций, используя PEMDAS (скобки, возведения в степень, умножение, деление…) в качестве вспомогательного средства для запоминания.
Это очень часто приводит к ошибочному представлению о том, что умножение предшествует делению, а сложение предшествует вычитанию. Понимание этого принципа, вероятно, является лучшим помощником в запоминании.
Двойное минус 1 — определение, пример, факты
Двойное минус 1
Различные стратегии сложения помогают нам лучше понимать числа и легко решать задачи. Это прививает нам способность складывать числа в уме. В этом уроке мы постараемся понять одну из таких стратегий сложения: удвоение минус один. Эта стратегия близка к фактам удвоения и известна как стратегия почти удвоения.
Связанные игры
Что такое двойные факты?
Чтобы удвоить число, мы можем дважды сложить одни и те же числа. Факт двойного сложения — это математический факт, когда мы складываем два одинаковых числа. Давайте рассмотрим факт удвоения от $1$$ до $$10$.
Заметим, что удвоение или сумма двух одинаковых чисел всегда четны.
Понимание концепции двойных фактов поможет нам манипулировать числами и использовать различные стратегии для решения различных математических задач.
Мы применяем этот факт, чтобы найти суммы для почти двойных фактов. Давайте погрузимся и узнаем, как складывать числа, используя стратегию удвоения минус 1.
Связанные рабочие листы
Что такое стратегия «двойной минус один»?
Теперь, когда мы распознали двойные числа, мы можем применить их для сложения двух последовательных чисел.
Давайте узнаем больше, помогая Чи. У Чи есть лоток с яйцами, в одном ряду которого 6 яиц, а в другом ряду 5 яиц. Помогите Чи найти, сколько яиц у него всего.
Чи хочет решить $6 + 5$. Мы можем найти общее количество, посчитав все яйца. Однако мы можем использовать наши знания о двойных фактах, чтобы быстро получить ответ.
Он знает, что когда в двух рядах лотков по шесть яиц, получается 12 яиц. Другими словами, 6 долларов + 6 = 12 долларов. Мы можем использовать этот «двойной факт», чтобы найти решение.
Мы знаем, что 5 на единицу меньше 6. Поскольку 6 + 6 = 12, 6 + 5 на единицу меньше, чем 6 + 6 или 12.
Итак, 6 + 5 на единицу меньше, чем 12 или 11. Следовательно, У Чи 11 яиц.
Мы можем сложить два последовательных числа, используя стратегию двойной минус один. Это делается путем добавления большего числа дважды или удвоения его и вычитания из него единицы, чтобы получить окончательный ответ.
Например, используйте $8 + 8 = 16$, чтобы найти сумму 8 и 7.
Поскольку 7 на единицу меньше, чем $8, 8 + 7 = 8 + 8$ $-$ $1 = 16$ $–$ $1 = 15$
Разница между удвоением и стратегией удвоения минус один
Когда мы говорим о удвоении, мы имеем в виду добавление числа к самому себе. Результирующий ответ, который мы получаем, называется двойным числом. Напротив, стратегия удвоения минус один — это способ получить сумму двух последовательных чисел. В этом процессе мы просто удваиваем большее из двух чисел и вычитаем из него единицу, чтобы получить сумму двух чисел.
Разница между удвоением плюс один и удвоением минус один
Мы также можем использовать стратегию почти удвоения для двух чисел, чтобы сложить их.
Стратегии «двойной плюс один» и «двойной минус один» выводят сумму двух последовательных чисел. Давайте поймем их разницу на следующем примере.
Решенные примеры
1. Найдите 4 + 3, используя следующий факт.0005 Так как 4$ + 4 = 8, 4 + 3 = 8$ $-$ 1$ = 7$. 2. C дополните следующее предложение. $12 + 11 = 12 + 12$ $– \underline{}$ Решение: Так как 11 на единицу меньше 12. , $12 + 11 = 12 + 12$ $-$ $1$. Следовательно, недостающее число равно 1. 3. Запишите двойной факт, который поможет вам решить следующую задачу. 7 уток плавали в пруду. К ним присоединились еще 6 уток. Сколько уток сейчас в пруду? Решение: Чтобы найти общее количество уток, нам нужно решить $7 + 6$. Поскольку $7 + 6$ на единицу меньше, чем $7 + 7$, мы можем использовать двойной факт: $7 + 7 = 14$, чтобы решить эту проблему. Так как $7 + 7 = 14, 7 + 6 = 14$ $-$ $1 = 13$ 1 $3 + 4$ $7 + 6$ $5 + 4$ $9 + 8$ Правильный ответ: $5 + 4$ 2 $14$ $–$ $1$ $14 + 1$ $14$ $–$ $6$ $14$ $–$ $7$ Правильный ответ: $14$ $–$ $1$ 3 $7 + 7$ $8 + 8$ $9 + 9$ $10 + 10$ Правильный ответ: $9 + 9$ 
Практические задачи
Какое из следующего можно решить, используя следующий двойной факт?
Так как $5 + 6$ на единицу больше, а $5 + 4$ на единицу меньше указанного факта. Мы можем использовать этот факт для решения $5 + 6$ и $5 + 4$. Если 7$ + 7 = 14$, что из следующего равно 7$ + 6$?
Поскольку $7 + 7 = 14, 7 + 6 = 7 + 7$ $–$ $1 = 14$ $–$ $1 = 13$ Какой факт удвоения поможет вам решить $9 + 8$, используя стратегию удвоения минус один?
$9 + 8$ на единицу меньше двойного числа $9$ или $9 + 9$.