Примеры деление на однозначное число столбиком: Примеры деления на однозначное число столбиком ( 4 класс) – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Деление многозначного числа на однозначное

Урок 24. Математика 4 класс ФГОС

Как можно многозначное число разделить на однозначное? Существует несколько способов: выполнить деление, раскладывая числа на разрядные слагаемые или на удобные для деления слагаемые. Но, конечно, гораздо легче выполнять деление столбиком. Решалочка объяснит способ записи простых случаев письменного деления многозначного числа на однозначное. В этих примерах каждый разряд делится на делитель. А ещё она напомнит, какой результат получается при делении на 1, и почему нельзя делить на 0.

Конспект урока “Деление многозначного числа на однозначное”

Привет, ребята!

Сегодня нам с вами предстоит вспомнить приёмы деления многозначного числа на однозначное. А ещё я напомню вам, как выполняется деление с числами нуль и один.

И начнём мы вот с такого примера.

624 : 2 =

Знаете ли вы, как устно разделить число шестьсот двадцать четыре на два? Да всё очень просто! В этом числе каждый разряд делится на два. Мы просто

разложим делимое на сумму разрядных слагаемых, потом каждое из них разделим на делитель. И полученные результаты сложим.

624 : 2 = (600 + 20 + 4): 2 = 600 : 2 + 20 : 2 + 4 : 2 = 312

Ну а если надо пятьсот семьдесят четыре разделить на семь?

574 : 7 = (560 + 14) : 7 = 560 : 7 + 14 : 7 = 82

Тут уж не получится делить каждый разряд. Поэтому мы будем раскладывать не на сумму разрядных слагаемых, а на сумму удобных для деления слагаемых.

Пять меньше семи, и разделить на семь мы его не сможем. Возьмём пятьдесят семь. Пятьдесят семь на семь не делится, зато делится пятьдесят шесть. Поэтому в качестве первого слагаемого мы берём пятьдесят шесть десятков – это число пятьсот шестьдесят. Остаётся один десяток и четыре единицы – это число четырнадцать.

Оно будет вторым слагаемым. Делим каждое из них на семь, складываем результаты. Ответ: восемьдесят два.

Попробуйте-ка вы сами, ребята, выполнить деление, раскладывая числа на разрядные или удобные для деления слагаемые.

Вот, например, найдите значения вот этих числовых выражений.

693 : 3 =

486 : 6 =

Ну, проверьте, так ли вы выполнили решение?

693 : 3 = (600 + 90 + 3) : 3 = 600 : 3 + 90 : 3 + 3 : 3 = 231

486 : 6 = (480 + 6) : 6 = 480 : 6 + 6 : 6 = 81

А теперь давайте вспомним, как трёхзначные числа делятся столбиком. Запишите решение этих же примеров столбиком.

Проверьте свои решения.

Я уверена, что и решение столбиком вы записали верно. А как вы думаете, друзья, всегда ли числа можно разделить нацело? Конечно, нет! Представьте себе такую ситуацию.

В школу привезли сорок три новые парты. Их надо разделить поровну между четырьмя классами. Сколько парт поставят в каждый класс?

Тааак. Парт 43. классов 4. 43 на 4 нацело не делится… ммм… А вот сорок – делится. Получается, что каждому классу достанется по десять парт. Да ещё три парты останутся. В резерве )).

43 : 4 =10 (ост. 3)

Ответ: каждому классу достанется по 10 парт, и ещё 3 парты останется.

А помните ли вы, как проверять деление с остатком? Надо частное умножить на делитель, и прибавить остаток. Вот как у меня:

Проверка:

10 ∙ 4 + 3 = 43

В результате получилось делимое, значит, деление с остатком было выполнено верно.

Ну и осталось нам вспомнить деление с числами нуль и один.

Я думаю, вы помните, что, если нуль делить на любое число, в ответе получится нуль.

Ведь, как говорится, на сколько бы частей дырку от бублика ни поделили, бублика отведать не получится.

А можно ли делить на нуль? Ну конечно же нет. Кто забыл, почему нельзя? Попробуйте выполнить обратное действие, умножение. Какое бы число ни получилось в ответе, а может быть только нулём и никаким другим числом. Ведь при умножении любого числа на нуль в ответе будет нуль. Но если а равно нулю, то и в ответе может быть только нуль. Других вариантов нет. Так что, мы просто должны помнить: на нуль делить не будем.

А вот с единицей всё гораздо проще. Если число делим на один

, то частное будет равно делимому. А если делимое и делитель равны, то частное будет равно числу один.

Ну и напоследок, я предлагаю вам решить несколько примеров, а потом мы их проверим.

58 : 26 =

0 : 514 =

317 : 1 =

568 : 568 =

Ребята, проверьте вашу работу.

58 : 26 = 2 (ост. 6)

0 : 514 = 0

317 : 1 = 317

568 : 568 = 1

Если вы всё сделали правильно, значит урок не прошёл мимо вас, и вы готовы к новым свершениям в нашей замечательной стране Математике.

Ну что же, сегодня нам пора прощаться. До встречи, друзья!

Предыдущий урок 23 Нахождение неизвестных множителя, делимого или делителя

Следующий урок 25 Приём письменного деления на однозначное число

Получите полный комплект видеоуроков, тестов и презентаций Математика 4 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Деление натуральных чисел столбиком | Математически правила деления

Определение

Деление столбиком — это стандартный математический метод для деления простых или сложных многозначных чисел изучаемый в 4 классе начальной школы. При делении столбиком, как и при обычном делении, первое число — это делимое, второе — делитель, а результат — частное.

В столбик можно выполнять как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.

Правила записи чисел при делении столбиком

Сначала делимое и делитель записываются в одну строку слева направо, после чего следует символ вида:

Например, если делимое равно 7439, а делитель 43, то правильная запись в столбце будет следующей:

Рассмотрим следующую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:

Рассмотрим общую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:

Из схемы выше видно, что частное будет написано под делителем, т.е. ниже горизонтальной линии, а промежуточные расчеты пишутся под делимым.

Деление столбиком на однозначное число

Практические навыки лучше всего отрабатываются на простых примерах. Поэтому делим числа 9 и 3 в столбик. Конечно, эту операцию легко проделать в уме или по таблице умножения, однако подробный разбор для наглядности будет полезен, хотя мы уже знаем, что 9 ÷ 3= 3. Итак, сначала запишем делимое и делитель по методу деления в столбик:

Далее определяем число делителей, имеющихся в делимом. Как определить? Поэтапно умножать делитель на 0, 1, 2, 3…, до тех пор, пока в итоге не получится число, равное или большее, чем делимое. Если в итоге сразу окажется число, равное делимому, под делителем запишем число, на которое делитель умножался.

Иными словами, когда получается число, большее делимого, под делителем записываем число, высчитанное на предпоследнем этапе. Вместо неполного частного записываем число, на которое делитель умножался на предпоследнем этапе.

\[3 \times 0=0 ; 3 \times 1=3 ; 3 \times 2=6 ; 3 \times 3=9\]

Итак, мы имеем число, равное делимому. Запишем его под делимыми, а вместо частного стоит число 3, на которое мы умножили делитель:

Теперь осталось вычесть числа под делителем (тоже методом столбца). В нашем случае 9 — 9 = 0.

Этот пример деления числа без остатка. Число после вычитания имеетс остаток от деления. Если он равен нулю, числа полностью делятся. Теперь рассмотрим пример деления числа с остатком.

Разделим натуральное число 7 на натуральное число 5.

При этом 5 последовательно умножается на 0, 1, 2, 3. ..получаем в результате:

\[5 \times 0=0<9 ; 5 \times 1=5<9 ; 5 \times 2=10>9\]

Под делимым запишем число, полученное на предпоследнем этапе. Под делителем пишем число 1 — неполное частное, полученное на предпоследнем этапе. Именно на 1 мы помножили делитель, когда получили 5.

В завершение операции вычитаем 5 из 7 и получаем:

Это пример деления числа с остатком. Неполное частное равно 1, а остаток равен 2. Теперь, после изучения простейших примеров, поделим многозначные натуральные числа на однозначные значения.

Изучим механизм деления столбиком на примере деления числа 140288 на число 4.

Понять суть принципа намного легче на практических примерах, и этот пример был избран неслучайно, так как описывает все вероятные аспекты деления натуральных чисел столбиком.

Алгоритм деления столбиком

Рассмотрим подробне алгоритм деления натуральных чисел в столбик. Для этого запишем числа совместно со знаком деления столбиком. Далее смотрим на первую цифру слева в записи делимого. Вероятны два случая: число, вычисляемое этой цифрой, больше делителя и наоборот. В первом моменте работаем с этим числом, во втором добавочно берем последующую цифру в записи делимого и работаем с подобающим двузначным числом. В соответствии с этим пунктом выберем в примере число, с которым будем работать первоначально. Это число 14, так как первая цифра делимого 1 меньше делителя 4.

Определите, сколько раз числитель входит в полученное число. Обозначим это число как x = 14 Последовательно умножаем делитель 4 на каждый элемент ряда натуральных чисел N, включая ноль: 0, 1, 2, 3 0, 1, 2, 3 и так далее. Мы делаем это до тех пор, пока результат не будет х или число больше, чем х. Когда результат умножения равен 14, мы записываем его под выбранным числом в соответствии с правилами вычитания столбца. Под делителем пишут множитель, на который умножался делитель. Если результатом умножения является число больше х, то под выбранным числом вписываем число, полученное на предпоследнем шаге, а вместо неполного частного (под делителем) вписываем множитель, на который производилось умножение на предпоследний шаг.

В соответствии с алгоритмом имеем:

\[4 \times 0=0<14;\\4 \times 1=4<14;\\4 \times 2=8<14;\\4 \times 3=12<14;\\14 \times 4=16>14.\]

Под отмеченным числом пишем полученное на предпоследнем шаге число 12. Вместо частного пишем множитель 3.

Вычтите 12 из 14 и запишите результат под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

Число 2 меньше числа 4, поэтому запишем под горизонтальной чертой после двойки число, находящееся в следующем числе делимого. Если в делимом больше нет цифр, то деление окончено. В нашем примере после числа 2, полученного в предыдущем пункте, пишем следующую цифру делимого — 0.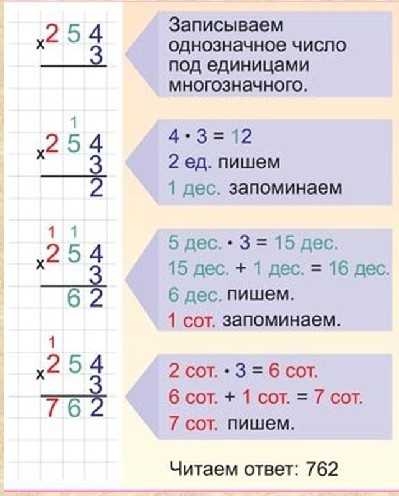 Соответственно, помечаем новое рабочее число — 20.

Важно

Пункты 2 − 4 циклически повторяются до окончания деления натуральных чисел.

Снова вычисляем, сколько содержится делителей в числе 20. Умножая 4 на 0, 1, 2, 3. . получаем: \[4 \times 5=20\]. Так как в результате мы получили число равное 20 , пишем под отмеченным числом, а вместо частного в следующем бите пишем 5 — множитель, на который производилось умножение.

Проведем вычитание: 20 − 20 = 0

Цифру ноль писать не будем, потому что этот шаг не является концом деления. Давайте просто запомним место, где мы могли его написать и рядом напишем число из следующего разряда делимого — в нашем случае это число 2.

Умножьте делитель на 0, 1, 2, 3.. и сравните результат с отмеченным числом:

\[4 \times 0=0<2;\\4 \times 1=4>2\]

Следовательно, под отмеченным числом пишем число 0, а под делителем в следующем разряде частного тоже пишем 0.

Выполняем операцию вычитания и записываем результат под чертой.

Справа, под чертой, прибавьте число 8, так как это следующая цифра делимого числа.

Следовательно, получаем новое рабочее число – 28, и снова повторяем пункты алгоритма.

Вычислив все по правилам, получаем результат:

Переносим последнюю цифру делимого 8 под черту. В последний раз повторяем шаги алгоритма 2 − 4 и получаем:

В нижней строке пишем число 0. Это число пишется только в последней фазе деления, когда операция завершена.

Рассмотрев алгоритм деления можно выделить общее правило деления натуральных чисел в столбиком:

Делим тысячи;
Делим сотни:
Делим десятки;
Делим единицы.

Рассмотрим другие примеры:

Пример №1

Выполним деление 7485 на 3:

Следовательно, 7485 : 3 = 2495

Проверка:

2495*3=7485

Пример № 2:

Разделим 318624 на 6:

Проверка: \[54104 \times 6=318624\]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Деление на многозначные натуральные числа столбиком

Алгоритм деления на многозначные числа столбиком весьма схож с ранее изученным механизмом деления многозначного числа на единичное число. Точнее, преобразования касаются только первого абзаца, а пункты 2-4 остаются без изменений. Если при делении на однозначное число мы смотрели только на первую цифру делимого, то сейчас будем смотреть на столько цифр, сколько их в делителе.Когда число, вычисляемое этими цифрами, больше делителя, мы берём это как рабочую цифру, иначе прибавляем лишнюю цифру из следующей цифры делимого. Далее следуем пунктам, изложенным в прошлом алгоритме. Изучим применение алгоритма многозначного деления на примере.

Пример №3

Разделим 5562 на 206.

В делителе три числа, поэтому в делимом сразу выбираем 556. Умножьте 206 на 0, 1, 2, 3.. и получаем:

\[206 \times 0=0<556;\\206 \times 1=206<556\\206 \times 2=412<556; \text { деление}\\206 \times 3=618>556\]

Следовательно, под делителем записываем результат предпоследнего действия, а под делимым — множитель 2.

Продолжаем вычисления:

В результате получаем число 144. Справа от результата под чертой пишем число из соответствующей цифры делимого и получаем новое рабочее число – 1442.

Повторяем пункты 2 − 4. Получаем:

\[\begin{gathered} 206 \times 5=1030<1442; \\ 206 \times 6=1236<1442; \\ 206 \times 7=1442,1442=1442 \end{gathered}\]

Под выделенным числом записываем 1442, а в следующий разряд частного записываем цифру 7- множитель.
Выполним вычитание в столбик, и поймем, что операция деления окончена: в делителе больше нет цифр, чтобы писать их справа от результата вычитания.
Ответ: 27
Пример № 4
Разделим 36261 на 153
Проверка: \[237 \times 153=36261\].
Ответ: 237
Пример № 5
Разделим 25725000 на 70
Проверка: \[367500 \times 70=25725000\].
Ответ: 367500
Примеры деления на многозначное число с остатком
Пример №6:
Разделим 14507 на 186
Проверка: \[186 \times 77=14507\].
Пример №7:
Разделим 300428 на 505
Проверка: \[505 \times 594=300428\].
Деление десятичной дроби на натуральное число
Деление десятичной дроби в столбик производится по правилам деления натуральных чисел.
Рассмотрим детальней на примере: \[1505,86 \div 43=35,02\].
Пример №8:
Разделим 5612,8 на 350,8
Проверка: \[350,8 \times 16=5612,8\]
Как выполнить длинное деление на одно число
В старые времена очень важно было уметь делить большие числа. Базовое деление в длинных по-прежнему полезно знать, поэтому следующие примеры покажут вам, как разделить однозначный делитель на другое число, а затем как найти остаток.
Вспомните, что делитель в задаче на деление — это число, на которое вы делите. Когда вы выполняете деление в длинные числа, вас больше всего беспокоит размер делителя: с маленькими делителями работать легко, а с большими — сплошная головная боль. Итак, здесь вы будете работать с красивым маленьким делителем, состоящим из одной цифры. Предположим, вы хотите найти 860. 5. Начните с написания задачи следующим образом:

В отличие от других операций «Большой четверки», длинное деление движется слева направо. В этом случае вы начинаете с числа в столбце сотен (8). Для начала спросите, сколько раз 5 входит в 8, то есть сколько будет 8 5? Ответ: 1 (с небольшим остатком), поэтому напишите 1 прямо над 8. Теперь умножьте 1 на 5, чтобы получить 5, поместите ответ прямо под 8 и нарисуйте линию под ним:
Вычтите 8–5, чтобы получить 3. (Примечание: после вычитания результат всегда должен быть меньше делителя. Если нет, вам нужно написать большее число над знаком деления.) Затем опустите 6, чтобы получилось новый номер 36:

Эти шаги представляют собой один полный цикл, и для завершения задачи вам просто нужно их повторить. Теперь спросите, сколько раз 5 входит в число 36, то есть сколько будет 36 5? Ответ 7 (с небольшим остатком). Напишите 7 чуть выше 6, а затем умножьте 7 на 5, чтобы получить 35; напишите ответ под 36:
Теперь вычтите, чтобы получить 36 – 35 = 1; уменьшите 0 рядом с 1, чтобы сделать новое число 10:
Еще один цикл завершен, поэтому начните следующий цикл, спросив, сколько раз 5 переходит в 10, то есть 10 5.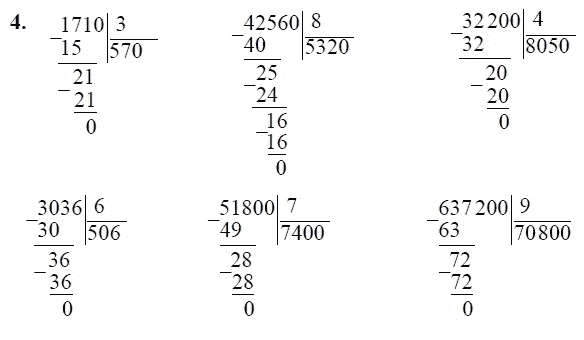 Ответ на этот раз 2. Запишите 2 в ответе над 0. Умножьте, чтобы получить 2 5 = 10, и напишите этот ответ ниже 10:
Теперь вычтите 10 – 10 = 0. Поскольку у вас больше нет чисел, которые нужно записывать, вы закончили, и вот ответ (то есть частное):

Итак, 860 5 = 172.
Эта задача делится поровну, но не многие. Следующие инструкции расскажут вам, что делать, когда у вас закончились номера, которые нужно сбить.
Деление отличается от сложения, вычитания и умножения тем, что возможно наличие остатка. Остаток — это просто часть, оставшаяся от деления.
Буква r указывает, что число, следующее за ним, является остатком.
Например, предположим, что вы хотите разделить семь шоколадных батончиков между двумя людьми, не разбив ни одного шоколадного батончика на кусочки (слишком беспорядочно). Таким образом, каждый человек получает три шоколадных батончика, и один шоколадный батончик остается. Эта проблема показывает вам следующее:
7 2 = 3 с остатком 1 или 3 r 1
В длинном делении остаток — это число, которое останется, когда у вас больше не будет чисел, которые нужно заносить. Следующее уравнение показывает, что 47 3 = 15 r 2:
Обратите внимание, что когда вы выполняете деление с небольшим делимым и большим делителем, вы всегда получаете частное 0 и остаток от числа, с которого вы начали:
1 2 = 0 р 1
14 23 = 0 р 14
2000 2001 = 0 r 2000
Что такое короткое деление? Разъяснение для начальной школы
Укороченное деление — это письменный способ деления, представленный в KS2. Важно, чтобы дети понимали концепцию деления до того, как научат этому методу, так как краткое деление — довольно абстрактный процесс.
Что такое короткое деление?
Сокращенное деление — это формальный метод деления, часто используемый при делении любого числа на однозначное число. Например, при делении 78 на 3 можно использовать короткое деление.
Вы также можете использовать короткое деление, когда делитель представляет собой двузначное число, где это двузначное число является знакомым делителем, как в этом примере для 168 ÷ 12.
Вы можете увидеть короткое деление, называемое методом автобусной остановки. разделения. Он отличается от метода длинного деления тем, что письменный метод более компактен.
См. ниже дополнительные примеры краткого деления, взятые из приложения 1 национальной учебной программы.
См. также: Что такое деление
Диагностический тест по умножению и делению
Загрузите этот бесплатный диагностический пакет по умножению и делению, чтобы выявить пробелы в обучении и помочь учащимся укреплять свои математические способности.
Как сделать короткое деление
Делимое (число, которое делится) помещается внутри «автобусной остановки»; делитель (число, на которое делится делимое) ставится слева от «остановки»; и частное (ответ) помещено выше. В отличие от методов сложения, вычитания и умножения, здесь мы работаем слева направо (от самой большой разрядной цифры до самой маленькой), чтобы решить задачу деления.
Пример 1: деление целых чисел
Начните с первой цифры делимого – в данном примере 9, что соответствует 9 десяткам. 9 десятков разделить на 7 равно 1 десятку (поместите эту цифру над 9, столбец десятков) с оставшимися 2 десятками (поместите эту цифру слева от следующей цифры в делимом). Эти 2 десятка представляют 20 единиц.
Переходим к следующей цифре делимого — в этом примере 8 (представляет 8 единиц), но у нас также есть 20 единиц из предыдущего деления, поэтому наш следующий шаг — 28 единиц, деленных на 7. Это 4, поэтому поместите 4 над 8, в колонке единиц. Это дает наше частное 14.
Пример 2: деление десятичных дробей
Короткое деление с остаткомКраткое деление также может использоваться для деления десятичных дробей. Как и во всех вычислениях с коротким делением, убедитесь, что все цифры выровнены правильно, и не забудьте десятичную точку в частном, а также делимое!
Короткое деление с остатком
Метод тот же, что и при делении с остатком, но остаток может быть выражен одним из трех способов – два из них представляют собой просто остаток (например, r1 в приведенном ниже примере) или дробь (например, \frac{1}{11} в приведенном ниже примере – остаток от 1 становится числителем дроби, а делитель 11 становится знаменателем).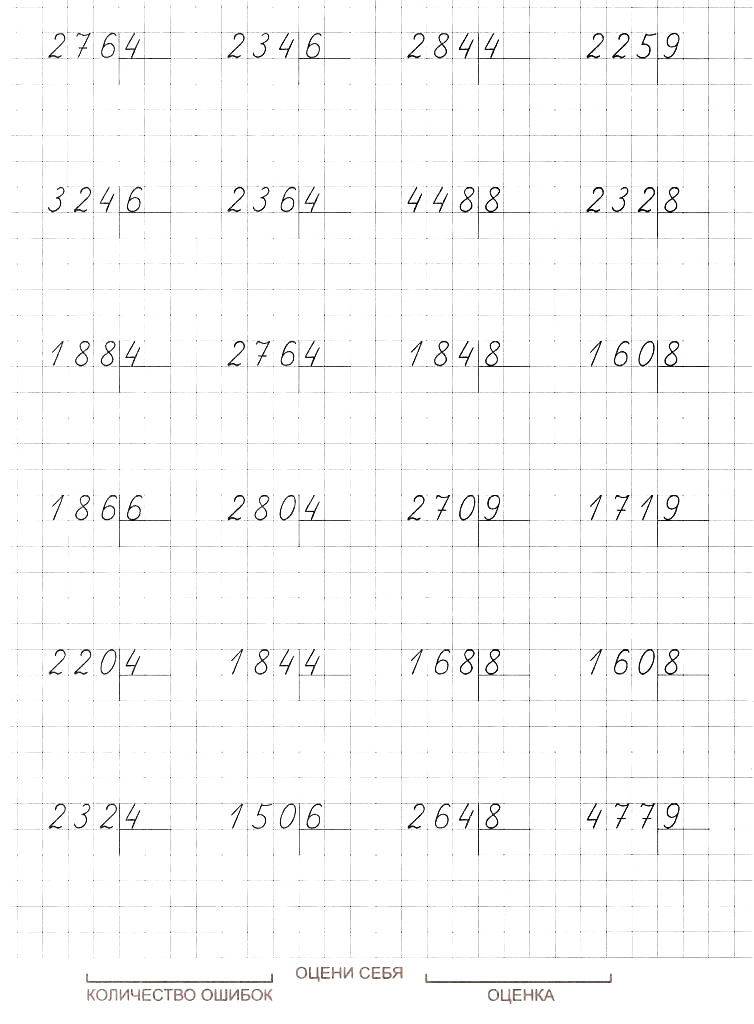
Третий способ — в виде десятичного числа — это может быть немного сложнее в зависимости от остатка. В первом примере ниже показано деление со стандартным остатком; второй показывает остаток, выраженный в виде десятичной дроби.
Метод такой же, как и выше, но после завершения деления разряда единиц добавьте десятичную точку и ноль в конце делимого, чтобы по существу «продолжить» деление.
В этом случае, после подсчета, что 32 единицы, разделенные на 4, составляют 6 единиц с 2 оставшимися, 2 оставшихся можно рассматривать как 20 десятых вместо этого. Затем мы можем разделить 20 десятых на 5, что равно 4 десятым, следовательно, частное равно 86,4. Это то же самое, что 86r2, так как при делении на 5 остаток от 2 равен ⅖, что эквивалентно 4 десятым.
Если десятичный остаток длиннее одного знака после запятой, продолжайте прибавлять 0 к делимому до тех пор, пока деление не завершится (или, если десятичные дроби продолжаются долго, просто округляйте!)
Как научить краткому делению
Возьмем 73 ÷ 3. Начав с конкретных материалов, таких как счетчики стоимости в приведенном ниже примере, продемонстрируйте разделение 73 на 3 равные группы. В этом случае 7 десятков можно разбить на 3 группы по 2 десятка, при этом 7-й десяток нужно обменять на 10 единиц. Затем у нас остается 13 штук, которые можно разделить поровну на 3 группы с 1 оставшейся. Это показывает, что 73 ÷ 3 = 24r1.
Затем мы можем перейти к графическому представлению этого, используя круги для обозначения десятков и точки для представления единиц (не забывая использовать инверсию для проверки!)
Наконец, мы можем показать это, используя абстрактный метод короткого деления: 7 десятков делится на 3 группы – 2 десятка, остается 1 десяток; 1 десяток обменов на 10 штук; 13 штук, разделенных на 3 группы, это 4 штуки с 1 оставшейся.
Подробнее о том, как учить краткое деление.
Когда дети узнают о кратком делении в школе?
В начальной школе формальный метод деления не преподается до KS2.
4-й класс, необязательное руководство: Учащиеся тренируются, чтобы свободно владеть формальным письменным методом краткого умножения и деления с точными ответами -значное число, используя формальный письменный метод краткого деления, и интерпретировать остатки в соответствии с контекстом.
Год 6: Учащихся следует учить делить числа до 4 цифр на двузначные числа, используя, где это уместно, формальный письменный метод краткого деления, интерпретируя остатки в соответствии с контекстом.
Как краткое деление связано с другими областями математики?
Короткое деление часто требуется при многоэтапном решении задач (задачи на деление слов часто требуют более одной математической операции, чтобы найти ответ).
В 6-м классе дети должны вычислять десятичные эквиваленты простых дробей. Например, чтобы вычислить десятичный эквивалент \frac{7}{8}, детям нужно разделить 7 на 8, что может потребовать метод короткого деления, но где делимое представляет собой одну цифру (в этом случае это может быть преобразовано в 7 000 ÷ 8, поскольку ответ имеет 3 знака после запятой!)
Как короткое деление связано с реальной жизнью?
Всякий раз, когда что-то нужно разделить поровну между двумя или более группами и разделить нельзя в уме, требуется короткое деление. Это может быть стоимость (например, счет в размере 174 фунтов стерлингов для четырех человек), расстояние (например, прохождение половины пути между двумя пунктами назначения), вес (17-килограммовый мешок картофеля, разделенный на шесть частей) или многое другое!
Примеры работы с коротким разделением
1. У меня есть 432 книги, которые мне нужно распределить поровну между 12 полками. Сколько книг можно разместить на каждой полке?
432, разделенное на 12, можно рассчитать с помощью приведенного ниже метода короткого деления:
Это показывает, что на каждую полку можно поставить 36 книг.
2. Фермер упаковывает яйца. В каждой коробке по шесть яиц. Фермеру нужно упаковать 980 яиц. Сколько ящиков может заполнить фермер, используя 980 яиц, и сколько яиц останется?
980, разделенное на 6, можно рассчитать с помощью приведенного ниже метода короткого деления:
Это показывает, что фермер может заполнить 163 ящика, оставив 2.
3. Саад отправляет три посылки. Почтовые расходы одинаковы для каждой посылки. Он расплачивается купюрой в 20 фунтов стерлингов. Его сдача составляет 14,96 фунтов стерлингов. Какова стоимость размещения одной посылки?
Это двухшаговая задача. Во-первых, нам нужно выяснить, сколько он заплатил, вычитая сдачу из 20 фунтов стерлингов, что составляет 5,04 фунта стерлингов. Затем нам нужно разделить это на 3, чтобы узнать, сколько стоит каждый пакет, что составляет 1,68 фунта стерлингов. (При делении десятичных дробей не забудьте включить десятичную дробь в частное вместе с делимым!)
Это показывает, что стоимость отправки одной посылки составляет 1,68 фунта стерлингов .
Учебные вопросы для коротких разделов
3,480 ÷ 8. Ответ: 435
Сколько 40,26 фунтов стерлингов поделили между 6 людьми? Ответ: 6,71 фунта стерлингов
3 ручки стоят столько же, сколько 2 линейки. Одна линейка стоит 1,35 фунта стерлингов. Сколько стоит одна ручка? Ответ: 90p
Ложка 5мл. Сколько ложек можно получить из бутылки объемом 275 мл? Ответ: 55
В Парковой школе учатся 275 детей. Они объединяются в группы по восемь человек. Какое наибольшее количество групп по восемь человек они могут составить? Ответ: 34
Third Space Learning предлагает широкий выбор математических заданий и рабочих листов, включая короткие рабочие листы и другие рабочие листы. Чтобы ознакомиться с полной библиотекой основных ресурсов по математике, посетите наш математический центр. В дополнение к учебным и обучающим ресурсам, Third Space Learning также предоставляет индивидуальные онлайн-репетиторы по математике, каждая программа адаптирована к конкретным потребностям каждого ребенка.
Пример слайда короткого урока разделения из онлайн-репетиторского занятия Third Space Learning.
Часто задаваемые вопросы о коротком делении
Что такое короткое деление и длинное деление?
Оба метода являются формальными методами деления, также известными как метод автобусных остановок. Короткое деление выглядит визуально более компактным, чем длинное, и используется, когда дети уверенно владеют методом автобусной остановки. Другой метод деления, о котором вы, возможно, слышали, — это «дробление», которое обычно ассоциируется с делением в длину.
Как объяснить ребенку краткое деление?
Дивиденд (число делится) помещается внутри «автобусной остановки»; делитель (число, на которое делится делимое) ставится слева от «остановки»; и частное (ответ) помещено выше.
В отличие от методов сложения, вычитания и умножения, здесь мы работаем слева направо (от наибольшего разряда разряда к наименьшему). Разделите каждую цифру делимого по одной на делитель — поместите ответ на каждый шаг деления над «автобусной остановкой», а все остатки перед следующей цифрой (см. примеры выше).
Продолжайте, пока ваше частное не будет завершено! Это может быть целое число или остаток, который может быть выражен в виде стандартного остатка, дроби или десятичной дроби.