Примеры 3 класс сложные: Тренажеры по математике 3 класс (задачи и примеры)

Порядок выполнения действий, правила, примеры. Порядок выполнения математических действий Примеры в 2 действия без скобок

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.

*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.

Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:

В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:

Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:

3 Примеры, в которых много действий

Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).

Эти знаки и будут делить наш пример на блоки:

Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.

А теперь закрепляем решение примеров на порядок действий на тренажерах!

Если у вас не открываются игры или тренажёры, читайте .

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот.

Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 – 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 – 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 – (20 – 7) +15

32 + 9 * (19 – 16)

Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 – 6: 2 * 3 =

18: (11 – 5) + 47=

7 * 3 – (16 + 4)=

Рассуждаем так.

37 + 9 – 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание.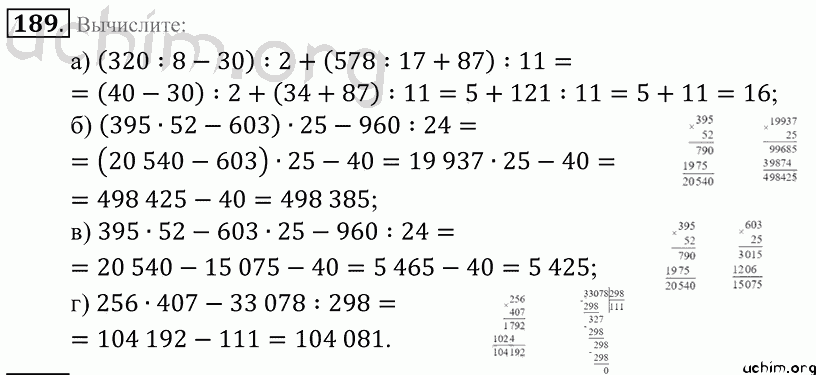 Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

1. Festival.1september.ru ().
2. Sosnovoborsk-soobchestva.ru ().
3. Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Сегодня мы поговорим о порядке выполнения математических действий . Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.

Итак, вспомним о том, что сначала вычисляются выражения в скобках

38 – (10 + 6) = 22 ;

1) в скобках: 10 + 6 = 16 ;

2) вычитание: 38 – 16 = 22 .

Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20 ;

Порядок выполнения действий :

1) слева направо, сначала деление: 10 ÷ 2 = 5 ;

2) умножение: 5 × 4 = 20 ;

10 + 4 – 3 = 11 , т.е.:

1) 10 + 4 = 14 ;

2) 14 – 3 = 11 .

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7

Порядок выполнения действий:

1) 18 ÷ 2 = 9 ;

2) 2 × 3 = 6 ;

3) 12 ÷ 3 = 4 ;

4) 9 – 6 = 3 ; т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7 ; т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54 , т.е.:

1) выражение в скобках: 13 – 9 = 4 ;

2) умножение: 6 × 4 = 24 ;

3) сложение: 30 + 24 = 54 ;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;

2) умножение и деление;

3) сложение и вычитание.

Если вы хотите получать анонсы наших статей подпишитесь на рассылку “ “.

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 – 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

• действия выполняются по порядку слева направо,
• причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Пример.

Выполните действия 7−3+6 .

Решение.

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Ответ:

7−3+6=10 .

Пример.

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Решение.

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

Ответ:

Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Пример.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Решение.

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 – значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

Ответ:

17−5·6:3−2+4:2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание – следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Определение.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Ответ:

5+(7−2·3)·(6−4):2=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Ответ:

4+(3+1+4·(2+3))=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Сложное предложение – примеры, схема и порядок частей (3 класс, русский язык)

4.6

Средняя оценка: 4.6

Всего получено оценок: 1443.

4.6

Средняя оценка: 4.6

Всего получено оценок: 1443.

Речь человека состоит из предложений, причем определить, о чем он говорит, зачастую можно, только найдя грамматическую основу этого предложения – подлежащее и сказуемое. Но что, если в предложении больше, чем одно подлежащее и сказуемое, если в нем говорится о разных предметах и явлениях? Ответ на этот вопрос даст очень важная тема, которую проходят в 3 классе.

Материал подготовлен совместно с учителем высшей категории Кучминой Надеждой Владимировной.

Опыт работы учителем русского языка и литературы – 27 лет.

Что такое сложное предложение и как с ним работать?

Сложное предложение – это такое предложение, которое состоит из двух или более простых предложений. Они могут соединяться между собой с помощью союзов, таких как а, но, и, а могут быть объединены только интонацией, что на письме выражается с помощью знаков препинания.

Вот примеры сложных предложений.

• Зима уже подходила к концу, а весна все не ощущалась.
• Он был голоден, но этот голод нельзя было утолить.
• Маша и Петя любили зверей, и мама отвела их в зоопарк.
• Дождь все шел, лужи сияли в свете фонарей.

На этих примерах можно увидеть, какие есть виды связи в сложных предложениях.

По сравнению с простым предложением их структура действительно более сложная, поскольку они не просто говорят о нескольких предметах или явлениях, но и соединяются при этом в одно целое по смыслу и грамматически. Простые предложения, которые входят в состав сложного, могут состоять только из грамматической основы или распространяться второстепенными членами.

Как сделать разбор сложного предложения

Чтобы составить схему сложного предложения, нужно сначала найти все его основы. Это поможет понять, сколько в нем частей, после этого можно будет найти, как они между собой связаны. Рассмотрим это на примере.

• Ребята гуляли допоздна, потом пошел снег.

В этом предложении две основы (ребята гуляли, снег пошел), которые соединены между собой интонацией, что на письме отражается в виде запятой. Союза между этими частями нет.

В сложном предложении не обязательно должно быть строго две грамматических основы: их может быть три и даже больше.

В основном порядок частей в сложном предложении последовательный: сначала идет главная часть, за ней следует та, которая связана с ней по смыслу. В предложениях, которые связаны интонацией и представляют собой просто перечисление событий, часто нет главной и присоединенной части – их порядок можно поменять местами и смысл предложения от этого совершенно не изменится.

Это легко понять, если сравнить два сложных предложения с одинаковыми основами, которые просто переставлены местами:

• Веет ветер, моросит дождик.
• Моросит дождик, веет ветер.

Очевидно, что от перестановки частей смысл предложения совершенно не поменялся: оно рассказывает о погоде, описывая ее с разных сторон.

Такой принцип роднит сложные предложения с максимально простой структурой с примерами на сложение, где от перестановки мест не изменяется итоговая сумма, что говорит о том, что язык в какой-то степени математичен.

Алгоритм разбора любого предложения, в котором две и больше основ, одинаковый: нужно найти эти основы и определить, соединены ли они только интонацией, то есть знаком препинания, или в установлении связи между ними участвовал союз.

Что мы узнали?

Определение сложного предложения само по себе достаточно простое: это такая единица языка, в которую входит не одна грамматическая основа, а несколько (как минимум две и больше). Эти части могут соединяться только интонацией (знаком препинания) или интонацией и союзом. Чтобы разобрать сложное предложение, нужно сначала найти все его основы, а потом определить, каким образом они соединены между собой. Это достаточно простой и понятный алгоритм.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 1443.

---

А какая ваша оценка?

Третий класс — Руководства для родителей — Семейные ресурсы

Руководство для родителей третьего класса по достижению успеха

Английский язык Искусство и грамотность

Третий класс — ключевой год для вашего ребенка. Обучение беглому и уверенному чтению послужит основой для требований к чтению в более поздних классах. Практикуя стратегии обучения чтению, ваш ребенок сможет уверенно понимать смысл многосложных слов в книгах. Он или она поймет, что слова имеют небуквальное значение (например, кусок пирога) и связаны с другими словами (например, компания и компаньон). Распознавание и понимание слов поможет вашему ребенку читать все более сложные рассказы и книги и расширять знания об окружающем мире. К концу года ваш ребенок также будет писать четкие предложения и абзацы по целому ряду тем, опираясь на расширяющийся словарный запас.

Пример того, над чем ваш ребенок будет работать в 3-м классе

• Внимательное чтение, чтобы найти основные идеи и вспомогательные детали в рассказе
• Описание логической связи между отдельными предложениями и абзацами в рассказах (например, первое, второе, третье; причина и следствие)
• Сравнение наиболее важных моментов и ключевых деталей, представленных в двух книгах на одну и ту же тему
• Написание мнений или объяснений, которые группируют связанную информацию и развивают темы с фактами и деталями
• Написание рассказов, создающих ситуацию и включающих детали и четкую последовательность событий, описывающих действия, мысли и чувства персонажей
• Самостоятельное проведение коротких исследовательских проектов, направленных на получение знаний по различным темам
• Задавать и отвечать на вопросы об информации, которую он или она слышит от говорящего или во время обсуждения в классе, предлагая соответствующие уточнения и детали, основанные на том, что сказали другие
• Бегло читать вслух рассказы и стихи, не останавливаясь, чтобы понять, что означает каждое слово
• Различение буквального и небуквального значений слов, например, что-то подозрительное и холодное отношение
• Правильное написание и обращение к словарям для уточнения значения слов 

Математика

В 3-м классе ваш ребенок узнает важные новые идеи и приобретет важные новые навыки. Одна из самых важных тем в этом году – умножение и деление. Другое дело дроби. Умножение, деление и дроби являются строительными блоками для многих жизненных навыков, которые учащиеся изучают в более поздних классах, таких как проценты. Учащиеся также должны освоить эти темы, чтобы быть готовыми к алгебре и высшей математике, поэтому очень важно хорошо начать изучение этих тем в 3-м классе.

Пример того, над чем ваш ребенок будет работать в 3-м классе

• Быстро и точно умножать и делить до 10 × 10, включая знание таблицы умножения по памяти
• Решение текстовых задач на сложение, вычитание, умножение и деление
• Начало умножения чисел, состоящих более чем из одной цифры (например, умножение 9 × 80)
• Понимание дробей и соотнесение их с знакомой системой целых чисел (например, признание того, что 3 ⁄1 и 3 — одно и то же число)
• Измерение и оценка веса и объема жидкости, а также решение текстовых задач, связанных с этими величинами
• Рассуждения о формах (например, все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами)
• Нахождение площадей фигур и отношение площади к умножению (например, почему количество квадратных футов для комнаты размером 9 футов на 7 футов определяется произведением 9 × 7?)

Помогите своему ребенку учиться дома

Английский язык Искусство и грамотность

• Сделайте чтение для развлечения частью повседневной жизни вашего ребенка. Выделите тихое время, без телефонов, компьютеров и других отвлекающих факторов, когда ваш ребенок может читать для удовольствия такие книги, как «Амос и Борис» Уильяма Стейга или «Огненный кот» Эстер Аверилл. Чтобы найти больше книг для вашего ребенка, посетите сайт www.corestandards.org/assets/Appendix_B.pdf.
• Предложите ребенку найти картинку в газете или журнале, вырезать ее, наклеить на бумагу и написать по ней рассказ.
• Создайте коробку или банку с семейным словарем. Попросите всех записать новые слова, которые они узнают, добавить их в рамку и использовать слова в разговоре.

Математика

Ищите «словные проблемы» в реальной жизни. Некоторые примеры 3-го класса могут включать:

• Обратите внимание на те повседневные случаи, когда вы ловите себя на использовании таблиц умножения, например, чтобы определить, сколько дней в четырех неделях. Спросите ребенка об ответе.
• Вовлекайте своего ребенка, когда заметите, что используете деление, чтобы «работать в обратном порядке» в таблице умножения — например, определить, сколько конфет получит каждый ребенок, если 36 конфет поровну разделить между девятью детьми на вечеринке, или определить, сколько шестидюймовых отрезки можно отрезать от нити длиной 18 дюймов.

 

Грамматика 3-го класса: основные навыки и рабочие листы

Третий класс является неотъемлемым годом начальной школы. Учащиеся используют навыки, полученные в детском саду, 1-м и 2-м классах, для развития навыков понимания прочитанного и письма. Правильное преподавание грамматических навыков является ключом к улучшению академических способностей третьеклассников. Учителя и родители могут убедиться, что учащиеся овладевают грамматическими навыками 3-го класса, ориентированными на Common Core, с помощью краткого обзора и бесплатных рабочих листов.

Грамматика 3 класса.

Реклама

Части речи и их функции

Государственные стандарты Common Core по грамматике для 3-го класса устанавливают требования к учащимся, знающим части речи. Узнав о частях речи в начальной школе, третьеклассники теперь готовы объяснить их определения и функции. Третьеклассники к концу учебного года должны знать следующие части речи:

• существительные
• местоимений
• глаголов
• прилагательных
• наречий

Прилагательные и наречия могут быть особенно сложными для 3-х классов. Они могут использовать рабочий лист по наречиям, чтобы прояснить любые недоразумения. Затем назначьте эти упражнения с прилагательными, чтобы закрепить разницу между этими двумя понятиями.

Просмотреть и скачать PDF

Правильные и неправильные существительные во множественном числе

Третьеклассники переходят от определения правильных и неправильных существительных к их использованию. Кроме того, проблема возрастает с понятием существительных во множественном числе. Используйте эти простые рабочие листы с существительными во множественном числе, чтобы закрепить как правильные, так и неправильные существительные во множественном числе в контексте предложений.

Реклама

Абстрактные существительные

В этом году учащиеся учатся расширять свое мышление с помощью абстрактных понятий. Сюда входят абстрактные существительные, такие как свобода или чрезвычайная ситуация . Третий класс — хорошее время для включения слова «идея» при описании существительного как «человека, места или вещи».

Правильные и неправильные глаголы

Если третьеклассники уже освоили правильные глаголы, пора переходить к следующему шагу. Использование неправильных глаголов — важный навык, который необходимо освоить, прежде чем 3-классники начнут формировать более сложные мысли. Назначьте лист с неправильными глаголами в качестве домашнего задания или работы в классе, чтобы закрепить эту концепцию.

Просмотреть и скачать PDF

Объявление

Времена простых глаголов

После того, как третьеклассники освоят правильные и неправильные глаголы, они смогут ставить их в разные времена. Ожидается, что учащиеся 3-го класса будут ставить глаголы в простые времена, включая прошедшее, настоящее и будущее время. Используйте полезный рабочий лист глаголов, который поможет 3-классникам практиковать каждое время.

Согласование подлежащего и глагола

Знают ли ваши третьеклассники правила правильного согласования подлежащего и глагола? Если нет, то это год, чтобы убедиться, что они делают. Попробуйте этот лист согласования подлежащего и глагола, чтобы закрепить важную грамматическую тему в 3 классе.

Местоимение-предшествующее соглашение

В 1-м и 2-м классах учащиеся работают над изучением и использованием местоимений. Но ожидается, что третьеклассники будут использовать в своей работе согласование местоимений и антецедентов, следя за тем, чтобы местоимения соответствовали существительным, которые они заменяют. Для дополнительной практики в этой области используйте эти упражнения на согласование местоимений и антецедентов в классе 3-го класса.

Просмотреть и скачать PDF

Реклама

Сравнительная и превосходная степени

Ваши 3-классники хорошо владеют грамматикой — теперь пришло время им стать лучшими! Третьеклассники должны уметь работать с прилагательными и наречиями в сравнительной и превосходной степени следующими способами:

• образование сравнительной и превосходной степени
• использование сравнительной и превосходной степени
• выбор использования сравнительной или превосходной степени (в зависимости от контекста)

Например, 3-классникам нужно знать разницу между хорошо, лучше и лучше , а так же как их правильно использовать. Дайте своим ученикам больше опыта с этими прилагательными и наречиями с помощью увлекательного плана урока в сравнительной и превосходной степени.

Сочинительные и подчинительные союзы

После изучения основ союзов в 1 классе учащиеся переходят к расширению своих знаний в 3 классе. Они должны знать:

• сочинительные союзы ( за, и, ни, но, или, еще, так )
• подчинительные союзы ( потому что, так как, хотя, в то время как , и так далее)

Помимо распознавания этих слов как союзов, третьеклассники должны использовать их в различных типах предложений. Практикуйте этот грамматический навык с помощью этих обучающих упражнений на союзы.

Простые, составные и сложные предложения

Теперь, когда третьеклассники могут успешно использовать союзы, они готовы составлять различные типы предложений. Они должны уметь образовывать:

• простые предложения (одно независимое предложение)
• сложные предложения (два независимых предложения, соединенные сочинительным союзом)
• сложные предложения (одно независимое предложение, соединенное с зависимым предложением подчинительным союзом)

Написание различных типов предложений помогает учащимся 3-х классов разнообразить их написание и развивать больше изощренные идеи. Развивайте этот навык с помощью рабочего листа по сочетанию предложений различными способами.

Просмотреть и скачать PDF

Реклама

Заглавные буквы

Может быть трудно понять, какие правила использования заглавных букв должны быть в центре внимания для 3-х классов. Но согласно языковым стандартам Common Core 3-го класса, они должны сосредоточиться на правильном использовании заглавных букв в названиях. Используйте план урока по использованию заглавных букв и упражнение, чтобы закрепить использование заглавных букв в 3-м классе. Вы также можете помочь учащимся освоить этот навык с помощью листа капитализации 3-го класса.

Просмотреть и скачать PDF

Реклама

Использование запятых в адресах

К 3-му классу учащиеся должны знать, как использовать запятые для различных целей в письменной форме. Но особый навык 3-го класса в этой области фокусируется на использовании запятых при написании адресов. Например, при написании «1183 West Pine Street, Seattle, Washington, 98101» третьеклассники должны уметь ставить запятую после названия улицы, города и штата.

Использование кавычек в диалоге

Творческое и повествовательное письмо является важным элементом элементарного письма. В 3 классе они должны уметь использовать кавычки при написании диалога. Дополнительно 3-классники должны знать правила употребления запятых в диалоге. Потренируйтесь с кавычками, прежде чем переходить к следующему грамматическому навыку.

Формирование и использование притяжательных существительных

Притяжательные существительные — это еще один тип существительных, которые должны знать третьеклассники. К концу учебного года они должны уметь распознавать, формировать и использовать притяжательные наклонения. Раздайте лист с притяжательными существительными для домашнего задания, работы в классе или даже для краткой оценки грамматики.

Просмотреть и скачать PDF

Реклама

Другие основные понятия словесности для 3-го класса

Это основные грамматические навыки, которые должны знать третьеклассники. Однако есть еще несколько языковых навыков, над которыми этим студентам следует поработать. Они включают в себя определенные навыки правописания, стратегии значения слов, отношения слов и навыки нюансировки слов.

Навыки правописания

В 3-м классе учащиеся работают над совершенствованием своих навыков правописания. Но это касается не только запоминания списков правописания. Третьеклассникам должно быть комфортно:

• использование общепринятых правил правописания высокочастотных слов
• добавление суффиксов к основным словам
• использование орфографических моделей и обобщений
• проверка правописания по справочным материалам

Каждая стратегия является продолжением того, что учащиеся над которыми работали во 2-м классе, и на шаг раньше того, что они должны будут выполнить в 4-м классе. Чтобы овладеть этими навыками, попробуйте эти печатные задания по правописанию.

Просмотреть и скачать PDF

Реклама

Правила письма

Третьеклассники вот-вот станут квалифицированными писателями. Они должны уметь выражать свои мысли, используя свои знания языка и письменной речи, уделяя особое внимание:

• выбору слов и фраз для эффекта
• пониманию различий между разговорным и письменным английским языком

Продвинутые писатели уже могут соответствовать этим стандарты. Однако ожидается, что к концу 3-го класса все учащиеся будут писать на этом уровне.

Определение значения слова

Помимо правописания, третьеклассники должны знать, как определять знакомые и незнакомые слова. Они могут сделать это следующим образом:

• используя контекстные подсказки на уровне предложения
• определяя новое слово после добавления аффикса
• определяя корень слова и используя его в качестве подсказки
• обращаясь к глоссариям или словарям

знают, как определять незнакомые слова указанными выше способами, они могут читать и понимать более сложный текст. Используйте таблицу префиксов и суффиксов, чтобы практиковать ценные словарные навыки в 3-м классе.

Формирование отношений слов

Знание того, как слова соотносятся друг с другом, является важной частью приобретения словарного запаса. Ожидается, что третьеклассники будут различать буквальное и переносное значение слов и фраз в зависимости от их контекста. Кроме того, они должны уметь устанавливать реальные связи между словами для лучшего понимания. Узнайте, как преподавать образный язык, укрепляя этот ценный навык языковых искусств.

Различение нюансов слов

К концу учебного года третьеклассники должны уметь определять конкретный оттенок того или иного слова. Эти оттенки значений включают состояния ума и степени неуверенности, которые можно найти в большинстве словарных списков 3-го класса.

Объявление

Подготовка 3-классников к старшей начальной школе

Поскольку 3-й класс — очень важный год в обучении ребенка, крайне важно, чтобы он освоил эти базовые грамматические навыки. Убедитесь, что ваши 3-классники могут справиться с задачей 4-го класса и выше с помощью этих учебных идей для 3-го класса.