Приемы запоминания таблицы умножения: Приемы запоминания таблицы умножения

Приемы запоминания таблицы умножения

Приемы запоминания таблицы умножения.

Создать мотивационную основу для дальнейшего изучения табличных случаев: для чего нам нужна таблица умножения?

На одном их первых уроков по данной теме, возможно, предложить детям такую задачу:
7 мальчиков пришли в школу учиться. Каждый из них принёс в кармане 6 полезных вещей (камешки, жёлуди, и т.п.). Сколько полезных вещей в школу принесли мальчики?
Рассуждая над задачей, дети приходят к выводу, что решить её возможно, если к 6 + 6 + 6 + 6 … и так далее  7 раз.
Выясняем:
– Удобно ли решать задачу таким способом? (Нет, потому что можно ошибиться в вычислениях).
– Можно ли её решить проще, более умно? (Наверное, можно)
– Нам нужно учиться решать УМНО – это позволит ЖИТЬ умно. Получается слово, обозначающее действие, с помощью которого можно решить эту задачу. (нужно умножить, то есть выполнить умножение).
– Сможем ли мы умножить 6 на  7? (Сами, без помощи калькулятора, нет.

Мы этому ещё не учились, этого мы не знаем.)

 

1. Прием счета двойками, тройками, пятерками.

   Прием обучения ребенка счету двойками, тройками, пятерками применяется до знакомства с действием умножения. Обучение ребенка свободному счету двойками, тройками, пятерками является подготовительным приемом к знакомству с умножением и таблицей умножения. Технологически этот прием соответствует приему заучивания состава однозначных чисел до знакомства с табличным сложением в первом классе. При хорошем усвоении таких способов счета ребенку будет легко освоить таблицы умножения чисел 2, 3 и 5. Знание этого базового объема табличных случаев поможет ребенку при освоении более сложных случаев.

2. Создать мотивационную основу для дальнейшего изучения табличных случаев: для чего нам нужна таблица умножения?

На одном их первых уроков по данной теме, возможно, предложить детям такую задачу:

7 мальчиков пришли в школу учиться. Каждый из них принёс в кармане 6 полезных вещей (камешки, жёлуди, и т. п.). Сколько полезных вещей в школу принесли мальчики?
Рассуждая над задачей, дети приходят к выводу, что решить её возможно, если к 6 + 6 + 6 + 6 … и так далее  7 раз.
Выясняем:
– Удобно ли решать задачу таким способом? (Нет, потому что можно ошибиться в вычислениях).
– Можно ли её решить проще, более умно? (Наверное, можно)
– Нам нужно учиться решать УМНО – это позволит ЖИТЬ умно. Получается слово, обозначающее действие, с помощью которого можно решить эту задачу. (нужно умножить, то есть выполнить умножение).
– Сможем ли мы умножить 6 на  7? (Сами, без помощи калькулятора, нет. Мы этому ещё не учились, этого мы не знаем.)

3. Прием последовательного сложения.

  Очень важный момент, который заключается в том, чтобы

дети поняли смысл умножения – замену суммы одинаковых слагаемых соответствующей записью и наоборот: что означает запись вида – 5 х 6 (по…. взять …… раз(а)).
 Прием последовательного сложения одинаковых слагаемых является основным приемом получения результатов табличного умножения. Данный прием связан со смыслом действия

умножения как сложения одинаковых слагаемых.

   Например: 6 * 7 = 6 + 6 + 6 + 6 + 6 + 6 + 6.  Рисовать рисунки.

 

4. Прием прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата).

   Данный прием, является вторым основным приемом получения результатов табличного умножения. Используется в том случае, если ребенок смог выучить хотя бы несколько

случаев из каждой таблицы. Это могут быть 3-4 первых самых легких случая, или 2-3 наиболее запоминающихся случая.

   Так, приведенный выше случай 6 * 7 является одним из наиболее плохо запоминающихся случаев. В то же время случаи 6 * 6 и 6 * 8 наиболее легко запоминаются из этой таблицы. Запомнив результат 6 * 6 = 36, ребенок может использовать прием прибавления 6 к предыдущему результату для получения значения случая 6 * 7. Запомнив случай 6 * 8, ребенок использует прием вычитания 6 из его результата. Для осознанного применения этого приема необходимо хорошее понимание смысла действия умножения и смысла каждого множителя в записи действия умножения:

чтобы получить 6 * 6 надо по 6 взять шесть раз, значит,

чтобы получить 6*7 надо по 6 взять семь раз,

т.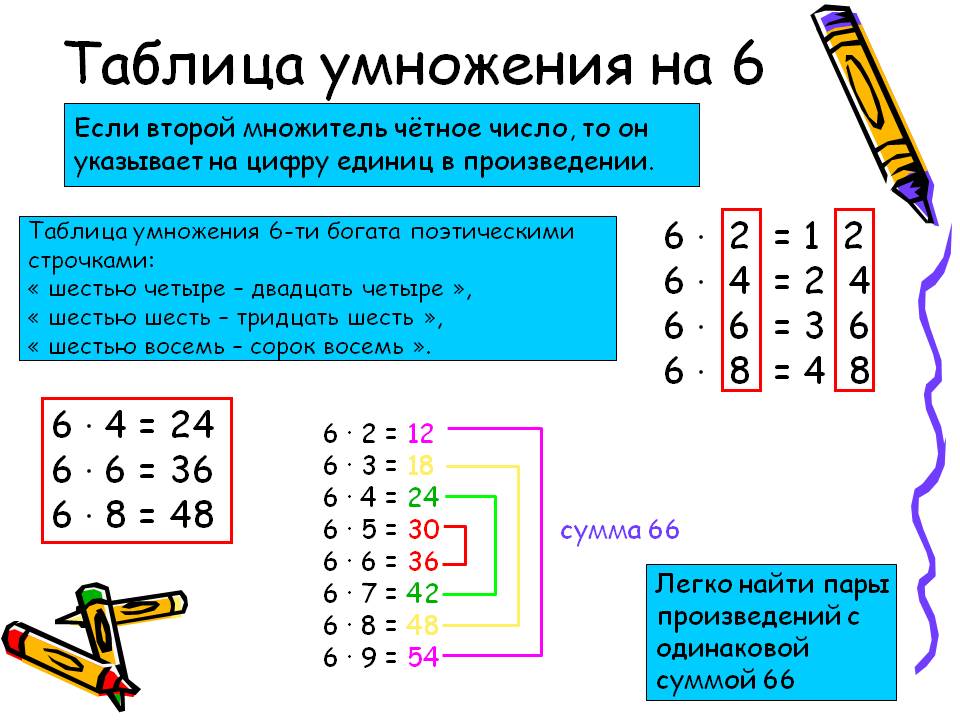 е. 6 * 7 = 6 * 6 + 6 = 36 + 6 = 42

или 6 * 7 = 6 * 8 – 6 = 48 – 6 = 42.

   Кроме того, необходимо уметь выполнять сложение и вычитание в пределах 100 в уме.

5. Прием взаимосвязанной пары: 2*6          6*2 (перестановка множителей).

 

   При хорошем понимании правила перестановки множителей ребенок заучивает в два раза меньше случаев табличного умножения, чем содержит полная таблица. Используя

перестановку множителей, все остальные случаи можно получить из имеющихся.

5. Прием запоминания последовательности случаев с ориентиром на возрастание второго множителя.

   Этот прием активно реализован в традиционном учебнике  по математике для 2 и 3 классов:

            3*2       3*3        3*4       3*5

   Эту же «серию» учитель предлагает детям для заучивания  к следующему уроку. На следующем уроке изучается новая     «серия»:

            3*6        3*7          3*8       3*9

   Эта же «серия» предлагается детям для заучивания.

В каждой серии задано последовательное увеличение второго  множителя. Ребенок фиксирует серию как визуально, так и  мнемонически (учит на память, глядя на запись). В

результате может получиться парадоксальный результат: от начала до конца, т. е. подряд ребенок «серию»

воспроизводит, а отдельные случаи вразбивку восстановить

не может (выучил как стихи).

6. Прием запоминающегося случая в качестве опорного.

   Например, 5 * 6 = 30, значит 5 * 7 = 30 + 5 = 35.

   Прием является производным от приема 3. Используются легко запоминающиеся случаи:

6*5,6*8,5*4,5*9,7*7,6*6,5*5 и т. п. Применяя затем прием прибавления или вычитания первого множителя, ребенок получает нужные результаты.

7. Прием внешней опоры.

   В качестве опоры используется рисунок или прямоугольная таблица чисел.

   Детям, которые обладают плохой механической памятью, можно на первых порах предложить использовать клетчатое поле тетради.

   Обводя на клетчатом поле прямоугольник с заданным количеством клеток в сторонах, ребенок использует эту модель для контроля полученного результата или просто подсчитывает клетки как умеет.

 

   Например:

   Задание:

Найди результаты умножения и проверь себя по рисунку:

8. Пальцевой счет при запоминании таблицы умножения.

   Прием пальцевого счета при получении значений  табличного умножения мало известен среди учителей  начальных классов, хотя является одним из древнейших  вычислительных приемов. Следует заметить, что многие учителя не признают правомочности приемов пальцевого счета при изучении табличного сложения и табличного умножения, придерживаясь мнения, что их результаты необходимо учить наизусть. На самом деле многие дети не могут твердо освоить весь объем таблицы умножения именно по причине неумения использовать приемы, помогающие ее освоению. Выучить всю таблицу наизусть могут не все дети. Учителя математики знают, что и среди школьников средних и даже старших классов имеется достаточное количество детей, плохо знающих таблицу умножения.

   Для детей младшего школьного возраста с преобладающим  кинестезическим восприятием и кинестезической памятью прием пальцевого счета при освоении таблицы умножения

может быть рекомендован как вспомогательный. Для того чтобы его эффективно использовать, следует знать результаты табличного умножения в пределах таблицы

умножения числа 4.

   Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, насколько каждый множитель больше, чем

пять.

   На двух руках отогнуто три пальца – это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой – четыре пальца эти числа перемножаем 3 * 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

   Еще один пример: необходимо умножить 8 на 9.

   Отгибаем на одной руке три пальца, а на другой руке

– четыре пальца (на столько каждый множитель больше,

чем пять).

   Отогнуто 7 пальцев – это десятки в искомом числе.

Перемножаем число загнутых пальцев обеих рук: 2 * 1 = 2.

Прибавляем это количество к числу десятков 70 + 2 = 72.

Таким образом, 9 * 8 = 72.

9. Мнемонические приемы при заучивании таблицы умножения.

   Мнемонические приемы при заучивании таблицы умножения   сходны с приемами заучивания иностранных слов. Это могут  быть карточки с записями табличных случаев, которые  ребенок носит в кармане и просматривает при любом удобном  случае (в транспорте, в очереди и т. п.).

   Карточки лучше делать двусторонними: с одной стороны

табличный случай, а с другой – ответ.

   Карточки с записью «порции» для заучивания можно  развешивать в местах, где ребенок их чаще увидит: над  его столом, в ванной у зеркала, в кухне возле его места  и т. п.

   В любом случае следует учесть, что процесс должен  быть распределен во времени, требует многократных  повторов и подкрепления любыми из приведенных выше  приемов, облегчающих заучивание таблицы.

Упражнение 1: “Запоминание чисел”

Система основана на использовании визуальных образов и их  элементов – контуров, форм, геометрических фигур, цветов и оттенков.

Каждой цифре присваивается свой визуальный код, например:

 

ноль – круг (или овал)

один – столб (кол, свеча)

два – близнецы (пара ботинок)

три – треугольник (трехколесный велосипед)

четыре – квадрат (4 лапы животного)

пять – звезда (пятиугольник)

шесть – коса (Белоснежка и семь гномов)

восемь – песочные часы (очки)

девять – улитка

десять пальцы двух рук

 

   Нетрудно связать такие образы в цепочку, соответствующую ряду

цифр, который нужно запомнить, например:

                        2*2=4

«Близнецы, стоящие в квадратном окне» или «Пара ботинок папы и

пара ботинок мамы стоят на квадратном  коврике».

 

Другой пример:       4+5=9

«В квадрате нарисована звезда, и по рисунку ползет улитка».

Упражнение 2:   Особый путь зубрежки

1. Повторение слова или фразы, которую надо запомнить, про себя.

2. Подождать 1 секунду и повторить снова.

3. Подождать 2 секунды и повторить снова.

4. Подождать 4 секунды и повторить снова.

Ожидание – это эмоционально загружено состояние. Удержание

информации в этом состоянии не дает ей выскочить, она бьется и

взбивает связи  с другими понятиями.

5. Повторите через 10 минут (необходимо для запечатления).

6. Для уверенного перевода в долговременную память повторить

через 2 – 3 часа.

7. При необходимости через 1 – 2 месяца; через 1 год.

 

 

1. Вычисли суммы и замени сложение умножением.

4 + 4 + 4 + 4 + 4
8 + 8 + 8 + 8
32 + 32 + 32
15 + 15 + 15 + 15 + 15

2. Выпиши только те примеры, где сложение можно заменить умножением.

9 + 9 + 9 + 9
5 + 5 + 5 + 5
7 + 4 + 47
12 + 12 + 12
28 + 82
8 + 5 + 9

№ 2

1. Прочитай выражения, вычисли их значения.

5 + 5 + 5
6 + 6
7 + 7 + 7 + 7
5 ´ 3
6 ´ 2
7 ´ 4

2. Запиши в виде суммы и выполни действия.

3 взять 4 раза
11 взять 3 раза
20 взять 2 раза
4 взять 5 раз

 

Приёмы запоминания таблицы умножения

Приёмы запоминания таблицы умножения

Подготовила: Власенко К. Е.

Приём счёта двойками, тройками, пятерками

Технологически этот приём соответствует приёму заучивания состава однозначных чисел. При хорошем усвоении таких способов счёта ребёнку будет легко освоить таблицы умножения чисел 2, 3 и 5. Знание этого базового объёма табличных случаев поможет ребёнку при освоении более сложных случаев.

Приём последовательного сложения

Приём последовательного сложения одинаковых слагаемых является основным приёмом получения результатов табличного умножения. Данный приём связан со смыслом действия умножения как сложения одинаковых слагаемых.

Приём прибавления слагаемого к предыдущему результату (вычитание из предыдущего результата)

Данный приём используется в том случае, если ребёнок смог выучить хотя бы несколько случаев из каждой таблицы. Это могут быть 3-4 первых самых лёгких случая, или 2-3 наиболее запоминающихся случая.

Случай 6 * 7 является одним из наиболее плохо запоминающихся случаев. В то же время случаи 6 * 6 и 6 * 8 наиболее легко запоминаются из этой таблицы. Запомнив результат 6 * 6 = 36, ребенок может использовать приём прибавления 6 к предыдущему результату для получения значения случая 6 * 7. Запомнив случай 6 * 8, ребёнок использует приём вычитания 6 из его результата. Для осознанного применения этого приёма необходимо хорошее понимание смысла действия умножения и смысла каждого множителя в записи действия умножения: чтобы получить 6 * 6 надо по 6 взять шесть раз, значит, чтобы получить 6 * 7 надо по 6 взять семь раз, т.е. 6 *7 = 6 * 6 + 6 = 36 + 6 = 42 или 6 * 7 = 6 * 8 – 6 = 48 – 6 = 42.

Приём взаимосвязанной пары (перестановка множителей)

При хорошем понимании правила перестановки множителей ребенок заучивает в два раза меньше случаев табличного умножения, чем содержит полная таблица. Используя перестановку множителей, все остальные случаи можно получить из имеющихся.

Художественный способ

• Предложить детям пофантазировать и представить, с чем у них ассоциируются цифры от 1 до 9.
• Попросить детей нарисовать ассоциации. Главное, чтобы эти образы были придуманы детьми.
• Далее нужно закрепить эти ассоциации, для этого вразброс показывайте вашему ученику нарисованные им картинки.
• Потом вместе сочините историю на каждый пример умножения.

В частности, 2*3=6. Одна девочка придумала рассказ: «Гулял как-то лебедь (2), встретил сердечко (3) и влюбился в него. Стал он ухаживать за сердечком. Увидел это клоун (6) и стал дразнить их: «Тили-тили-тесто, жених и невеста».

Литературный способ

Литературный способ (Андрей Усачёв, Таблица умножения в стихах)

Мнемонические приёмы при заучивании таблицы умножения.

Мнемонические приёмы при заучивании таблицы умножения сходны с приёмами заучивания иностранных слов. Это могут быть карточки с записями табличных случаев, которые ребёнок носит в кармане и просматривает при любом удобном случае (в транспорте, в очереди и т.п.).

«Мишени»

В самом центре – первый множитель (число изучаемое в таблице умножения), вокруг него написаны возможные вторые множители (от 1 до 10). В наружном кольце необходимо обозначить соответствующий результат умножения. 

«Цветок умножения»

Инновационная игра для запоминания таблицы умножения «Гусеница» (Х. Буреск)

Таблица умножения в магических цифрах

Закрашивание клеточек с числами – результатами таблицы умножения

Кроссворд по таблице умножения на 2

«Кидай до 100»

Учащимся даётся поле, в котором обозначены ячейки от 1 до 100, и два кубика. Ученик должен кинуть кубики и найти произведение цифр которые у него выпали, далее вычеркнуть получившийся результат.

«Собери картинку»

Подбери цвет соответствующий верному ответу умножения и закрась.

Таблица умножения на 9

«Числовая связь»

«Покрути, останови и закрась»

«Покрути и умножь»

«Брось, сложи и умножь»

«Раскрась результат»

«Поиск по умножению»

«Ритм чисел»

Игра – тренажёр

http://freedabest.ru/games/15t/index.html

Таблица Пифагора с использованием фигур для поддержания интереса учащихся

8 лучших трюков с таблицей умножения для учителей

Начальная математика

Если какие-то дети находят определенную таблицу умножения трудной задачей, всегда есть изящная уловка, которая может помочь, и эти видеоролики показывают некоторые из наших любимых

по Обучающий провод

Начиная со стихотворения «30 дней в сентябре» и заканчивая «Каждый хороший мальчик заслуживает футбола», в головах учителей, как правило, полно полезных приемов запоминания, которые дети могут использовать. И таблица умножения от этого не освобождается.

Откровенно говоря, многие советы и рекомендации для маленьких детей могут только запутать ситуацию, но они хороши в качестве резервной копии. Вы никогда не знаете, когда кто-то может пригодиться, чтобы заставить их мозги щелкнуть и помочь им преодолеть образовательный барьер.

Кроме того, многие из них просто показывают, какими удивительными могут быть числа и закономерности, что может помочь пробудить интерес к математике.

Мы продолжим и пропустим таблицы умножения на 1 и 2. Тогда мы тоже будем игнорировать 5, 10 и 11, если все согласны. В противном случае давайте умножим.

Таблица умножения на 3

Вам, вероятно, не понадобится помощь с таблицей умножения на три, но это руководство работает как предшественник для таблицы умножения на шесть позже, так что его стоит посмотреть.

Таблица 4 умножения

Это настолько просто, что вы удивитесь, почему вы сами до этого не додумались. Если только вы этого не сделали, в таком случае похлопайте себя по спине. Ты звезда.

Таблица умножения на 6

Итак, вы смотрели видео о таблице умножения на три числа, которое нам понравилось? Или вы пропустили это, как учитель-индивидуалист, которым вы являетесь? Эх ты.

Таблица 7 раз

‘Это не так уж сложно.’ Ты права, девушка на видео. Очаровательно выразился.

Таблица умножения на 8

Теперь, просто запомните, это 8, 7, 6, 5, 4, снова 4, 3, 2, 1, 0. Вот как вы считаете, дети. Хорошо, это не так, но это видео включает в себя крутых маленьких анимационных супергероев Определенно не Бэтмен и Совершенно не Человек-Паук (пожалуйста, не судитесь, DC и Marvel).

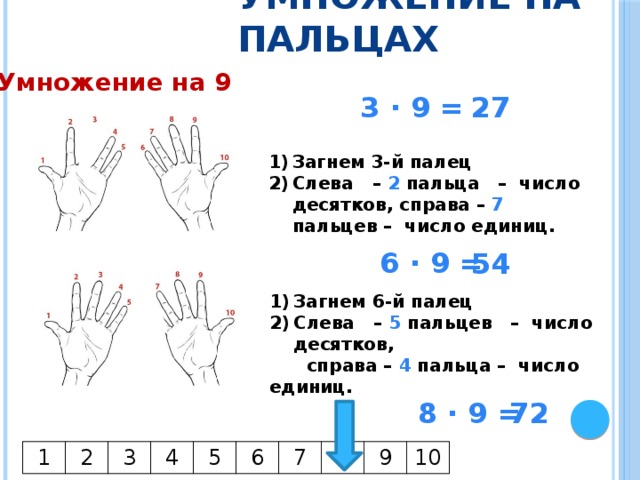
Таблица умножения на 9

Ах, старый трюк с пальцами. Вы, наверное, знаете это, но в этом видео ребенок по имени Мия дает инструкции, и Мия довольно крутая.

Таблица умножения на 12

Давайте проигнорируем эту Вещь из Семейка Аддамс использовала ненужный апостроф при написании «12» вверху страницы, и давайте просто будем впечатлены тем, что рука так хороша в умножении.

Бонус: умножение чисел от 6 до 10

Это один из тех трюков, которые, по вашему мнению, не могут сработать, пока вы не вспомните, что мы работаем в базе 10, потому что у нас так много пальцев (или, да, не будьте педантами, восемь пальцев и два больших пальца). Но кроме этого, мы не уверены, что черная магия не замешана.

20 умопомрачительных трюков с умножением, которые понравятся вашим детям

Не все дети могут выучить математические факты с помощью бездумного запоминания. Действительно, исследования показали, что механическое запоминание не помогает детям выучить связи между числами или понять правила умножения. К счастью, Помнящий   На помощь приходит математика с приемами умножения, помогающими детям выполнять математические действия в реальной жизни. Этот метод намного эффективнее, чем простое обучение математическим фактам или упор на запоминание.

Вот 20 трюков с умножением, которые научат детей творчески умножать.

1.

Правило девяток

Во-первых, у нас есть наши друзья, Девятки. Девятки похожи на вашего друга, у которого всегда есть немного правдоподобная теория заговора. У них обоих странные узоры, но, вероятно, это просто совпадение. Если вы посмотрите на левую часть столбца ответов, вы увидите, что в нисходящем столбце числа идут по порядку до 10. Затем прыгайте в правый столбец и поднимайтесь вверх, и числа также возрастают. Игнорируйте своего друга. Вселенная не пытается сказать вам что-то с помощью этого шаблона.

2 . Метод бабочки

Далее мы переходим к методу бабочки. Как и следовало ожидать, это метод перекрестного умножения, но для сложения и вычитания дробей. Сначала умножьте диагональ слева направо, затем умножьте диагональ справа налево. Эти два числа входят в антенну-бабочку. Вычтите их, и вы получите числитель. Умножьте два знаменателя, и вы получите знаменатель решения. Не забудьте сократить ответ!

3. Двузначный раунд

Один из моих личных фаворитов — двузначный раунд. Этот метод полезен для умножения двух двузначных чисел. Во-первых, подумайте о красивом круглом числе, к которому оба наших числа ближе всего. Возьмем, к примеру, 92 х 98. Оба числа близки к 100, поэтому мы вычтем их из 100, чтобы получить 8 и 2. Сложите их вместе, чтобы получить 10, и вот ваша разница! Вычтите 10 из 100, чтобы получить 90, что является первой частью нашего ответа. Помните 8 и 2? Умножьте их, чтобы получить 16. Следовательно, наш ответ — 9.016. Умно, правда?

4. Вспомните близнецов

Для следующего запомните, что все факты умножения имеют идентичных близнецов. Итак, если вы забудете 8×2, вы можете вспомнить, что 2×8 — это 16. Нам нравится это, потому что оно разрезает стол пополам!

5. Двойной двойной

Хорошо, давайте наберем обороты со следующими трюками. Удвоить, потом еще раз удвоить. 4×9: двойная 9 — это 18, двойная 18 — это 36, то есть 4×9.

6. В два раза больше 10

Разрезать пополам, затем умножить на 10. 5×6: половина от 6 будет 3, затем умножить на 10 будет 30. 

7. Шестерки любят эвенов

Шестерки смотрят на эвенов! 6x 2 = 1 2 , 6x 4 = 2 4 , 6x 6 = 3 6

8. Танцевой инструктор Трюк

7 ×. 7 и 8! 56 = 7 x 8

9. Трипл-дабл для восьмерок

(Примечание: это не заказ Dairy Queen!) Этот заказ работает только на 8 секунд. 8×6: удвоение 6 равно 12, удвоение 12 равно 24, удвоение 24 равно 48.

10. Умножить на 10, минус число (для 9)

На полпути! Давайте снова заглянем к нашим друзьям The Nines. 9 — это десятикратное число минус число. Например, 9 x 6 = 10 x 6 – 6 = 60 – 6 = 54. Не забывайте свой порядок действий (PEMDAS)!

11. Добавьте ноль к десяткам

Давайте поболтаем с нашим другом, и самое целое число, 10. Единственная реакция 10 — «поставить ноль после него». 10 x 2 = 2 0

12. 11s Повторять до 9

Хорошо, мы набрали 10; давайте перейдем к самому нечетному числу, 11. Конечно, 11 имеет повторяющиеся цифры до 11×9. 11×4=44. А что после 9?

13. Сумма между для 11s, 10-18

Для 11×10 до 11×18: сумма цифр между цифрами. Например, 11 × 15 = 1 (1 + 5) 5 = 165. 

14. Правило 12: 10 раз плюс 2 раза

12 — это весело, потому что это все подростковые гормоны без списка подростковых обязанностей ( может быть). Правило 12: 10-кратное число плюс 2-кратное число. Например, 12×4=40+8=48.

15. Правило 15s: Умножьте на 10, затем прибавьте половину, снова

15 умно с тем же методом, что и 12: умножьте на 10, затем снова прибавьте половину. 15×4=40+20=60. Мы любим 15-ки.

16. Правило 20-х: умножить на 10, затем удвоить

Хорошо, метод последней уникальной цифры. 20! Это как взросление, но не одновременно. Странный. Ладно, 20 умножаем на 10, потом удваиваем. 20×4=40+40=80 или 20×7 = 70+70 = 140. 

17. Цифры, разделенные цифрой 2

Если вы хотите что-то запомнить, начните с квадратов. Запомните каждое число, умноженное само на себя. Здесь нет шаблона; это просто важно. Но это не было бы 17-м номером, если бы у меня не было трюка. Когда числа, которые мы умножаем, разделены на 2 (пример 7 и 5), умножьте число в середине само на себя и вычтите единицу. Например, 5×5=25 на единицу больше, чем 6×4 = 24, а 6×6 = 36 на единицу больше, чем 7×5 = 35. 

18. Представьте с помощью объектов

Это одно из моих любимых заданий, потому что оно связывает математические факты с реальными объектами, а не с абстрактными идеями. Использование таких вещей, как кубики и маленькие игрушки, может помочь вашему ученику увидеть, что умножение — это способ складывать несколько групп одного и того же числа снова и снова. Например, в 6×3 попросите вашего ученика создать 6 групп по 3 блока в каждой. Тогда они увидят, что задача на самом деле состоит в том, чтобы мы собрали 6 групп по 3 человека.

Подсчет с пропуском на самом деле констатирует факты умножения 5s.