Правила 4 класса по математике: Сборник правил по математике. Система Л.В.Занкова | Методическая разработка по математике (4 класс) по теме:
Натуральные числа Числа, которые получают при счёте предметов, – называют натуральными числами 0-не натуральное число. Натуральный ряд чисел Если натуральные числа записаны начиная с числа 1 и каждое следующее число больше предыдущего на единицу ,такую запись называют натуральным рядом чисел. Чётные и нечётные числа Числа, которые делятся на 2 без остатка, называют чётными. Числа, которые делятся на 2 с остатком, называют нечётными. Натуральные числа: разряды и классы
Дробные и смешанные числа Числитель Целая часть 2 3 7 6 8
Знаменатель Дробная часть 1 | Число в записи дроби (над чертой) показывает, сколько частей взяли, называется числителем дроби. Число в записи дроби (под чертой), показывает, на сколько частей разделили, называется знаменателями дроби. Числа, которые состоят из натурального числа и дроби, называются смешанными числами. Дробь, в которой числитель меньше знаменателя, называют правильной дробью. Дробь, в которой числитель больше знаменателя, называют неправильной дробью. Правильная дробь меньше единицы, а неправильная дробь больше или равна единице.
Числовой (координатный) луч. Числовой (координатный ) луч- наглядное изображение расположения чисел относительно друг друга. Число, которое соответствует точке числового луча, называется её координатой. 0 1 2 3 4 Положительные и отрицательные числа Если перед числом стоит знак (-), его называют отрицательным.
5 Например:-352, -6 , 6 и т. Если перед числом стоит знак (+) ,его называют положительным. Числа, запись которых отличается только знаком + или – ,называются противоположными.
| Точные и приближённые числа. Числа, с которыми мы имеем дело в жизни, бывают двух видов. Одни в точности дают истинную величину, другие – только приблизительно. Первые называют точными, вторые – приближёнными. Если точное число заменяют приближённым или просто известно прибли- жённое число, используется знак ~. Он обозначает приближённо равно. 974 ~ 970, 974 ~ 980
Погрешность Значение разности между точным и приближённым числом называют погрешностью. 783 ~ 780, 783- 780 = 3
Округление чисел. Округлить число с точностью до десятков – это значит заменить его одним из ближайших чисел, у которых в разряде единиц нули. Округлить число с точностью до сотен – это значит заменить его одним из ближайших чисел, у которых в разрядах единиц и десятков нули. Если при округлении данное число заменяют меньшим, то говорят, что округление выполнено с недостатком. Если число заменяют большим , округление выполнено с избытком.
Среднее арифметическое Чтобы найти среднее арифметическое нескольких чисел, нужно найти значение их суммы и разделить его на количество слагаемых. (93+89+97+96+90):5=93 2 |
Выражение- это запись, в которой числа соединены знаками действий, но нет знаков сравнения.
Действия и их компоненты
Сложение Суммой чисел называют запись, в которой между числами стоит знак сложения(+).
Название чисел при сложении слагаемое слагаемое значение суммы 2 + 3 = 5 сумма Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое.
Вычитание Разностью чисел называют запись, в которой между числами стоит знак минус (-).
Название чисел при вычитании уменьшаемое вычитаемое значение разности 6 – 2 = 4 разность Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить значение разности. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности. | Умножение Выражение, в котором числа соединены знаком умножения, называется произведением.
Название чисел при умножении множитель множитель значение произведения 8 х 3 = 24 произведение Чтобы найти неизвестный множитель, нужно значение произведения разделить на известный множитель. Если один множитель равен 0, то и значение произведения равно 0.
Деление Выражение, в котором числа соединены знаком деления, называется частным.
Название чисел при делении делимое делитель значение частного 20 : 5 = 4 частное Чтобы найти неизвестное делимое, нужно делитель умножить на значение частного. Чтобы найти неизвестный делитель, нужно делимое разделить на значение частного. Если 0 разделить на любое натуральное число, получится 0. Делить на нуль нельзя: а : 0 При делении с остатком делимое равно произведению делителя на значение частного плюс остаток. 83 : 9 =9 (ост.2) 3 | Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее. Чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее. Уравнение-это равенство, содержащее букву, значение которой нужно найти. Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Решить уравнение – значит, найти его корни или установить, что корней нет/ При проверке правильности найденных корней их обязательно подставляют в исходное уравнение.
Действия с дробями. Действия с дробями с разными числителями и одинаковыми знаменателями Чтобы сложить дроби с одинаковыми знаменателями , нужно сложить их числители и записать тот же знаменатель. 5 3 8 14 + 14 = 14 Чтобы вычесть дробь с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемое и приписать тот же знаменатель. 9 4 5 12 12 = 12 Чтобы умножить дробь на натуральное число, нужно на него умножить числитель дроби, а знаменатель оставить без изменения 2 х 5 = 10 13 13 Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, получится дробь, равная данной.
|
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше. Если а> b, то a > b . Например: 5 > 3 c с 12 12 Если у дробей равные числители и разные знаменатели, то больше будет та дробь, у которой знаменатель меньше.
2 > 2 3 > 3 3 11 7 9 Возведение в степень
Умножение нескольких равных множителей можно заменить возведением в степень. 3 7 х 7 х 7 =7 3 7- показывает, какое число повторяется множителем, а – сколько таких множителей. 3 7 основание степени показатель степени 3 7 = 373
степень значение степени Любая степень чисел 0 и 1 равна этим же числам. 6 10 0 = 0 ; 1 = 1. 4
Величины и единицы их измерения
Длина Единицы измерения длины: миллиметр (мм), сантиметр(см), дециметр(дм), метр(м), километр(км). 1см = 10 мм 1дм = 10см =100мм 1м = 100см = 1000мм 1км = 1000м
Масса Единицы измерения массы: грамм (г), килограмм (кг), центнер (ц), тонна (т). 1кг = 1000г 1ц = 100кг =100 000г 1т = 10ц =1000кг =1000 000г
Ёмкость Литр (л)- единица измерения количества жидкостей. Когда узнают, сколько литров помещается в посуду, говорят, что измеряют её вместимость.
Время Единицы измерения времени: секунда (сек.), минута (мин), час(ч). сутки (сут.), неделя (нед.), месяц (мес.), год (г.), век (в.). 1мин = 60сек. 1нед. = 7 сут. 1ч = 60 мин = 3600сек. 1мес. 1сут. = 24 ч = 1440мин =86 400сек. 1год = 12мес.= 365 или 366 сут. 1век =100 лет Из четырёх лет подряд 3 года равны 365 суткам, а один год -366. Такой год называют високосным. |
Сложение вычитание – называют действиями первой ступени. Умножение и деление – это действия второй ступени. Порядок выполнения действий в выражении без скобок.
Если в выражении без скобок есть несколько действий одной ступени, их выполняют в том порядке, в котором они стоят слева направо. 1) 2) 1) 2) 75 – 37 +54 24 : 6 х 5 Если в выражении без скобок есть действия разных ступеней, сначала выполняют по порядку все действия второй ступени (умножение и деление),а затем все действия первой ступени (сложение и вычитание). 1) 3) 2) 4) 6 х 4 – 5 х 3 +38
Порядок выполнения действий в выражениях со скобками. Если в выражении скобки встречаются два раза, сначала выполняют действия в первых скобках, потом во вторых, а потом с получившимися в скобках числами. 1) 3) 2) (65 – 56 ) х (93 – 87) Если в выражении одни скобки находятся внутри других, сначала выполняют действия во внутренних скобках. 1) 2) 3) 4) (( 744 – 456) : 8 + 142) х 2 Порядок выполнения действий в выражениях, содержащих действие возведения в степень. 1) 2) 5) 3)4) 4 3 5 х 7 + 9 : 3 | Основные законы действий Сложение Переместительный закон сложения: От перемены мест слагаемых значение суммы не изменится. а +в = в +а Сочетательный закон сложения: Если при сложении нескольких чисел сумму рядом стоящих слагаемых заменить её значением, значение общей суммы не изменится. а+ в+ с=(а+в)+с= а+(в+с) Умножение Переместительный закон умножения: От перемены мест множителей значение произведения не изменится.
а х в = в х а Сочетательный закон умножения: Если при умножении нескольких чисел произведение рядом стоящих множителей заменить его значением, значение общего произведения не изменится. а х в х с= (а х в) х с = а х (в х с) Распределительный закон умножения относительно сложения: При умножении суммы на число значение выражения не изменится, если умножить на него каждое слагаемое и полученные результаты сложить.
(с + к ) х е = с х е + к х е
Деление Распределительный закон деления относительно сложения: При делении суммы на число значение выражения не изменится, если разделить на него каждое слагаемое и полученные результаты сложить. (а + в) : с = а : с + в : с 5 | Свойство вычитания числа из суммы: Если число нужно вычесть из суммы, его можно вычесть из одного слагаемого и результат сложить с другим слагаемым. (а +в) – с = (а – с) + в Свойство деления числа на произведение: Если число нужно разделить на произведение двух множителей, его можно разделить на один множитель, а получившийся результат разделить на другой множитель. а : (в х с )= а : в : с |
Величины и единицы их измерения
Длина Единицы измерения длины: миллиметр (мм), сантиметр(см), дециметр(дм), метр(м), километр(км). 1см = 10 мм 1дм = 10см =100мм 1м = 100см = 1000мм 1км = 1000м
Масса Единицы измерения массы: грамм (г), килограмм (кг), центнер (ц), тонна (т). 1кг = 1000г 1ц = 100кг =100 000г 1т = 10ц =1000кг =1000 000г
Ёмкость Литр (л)- единица измерения количества жидкостей. Когда узнают, сколько литров помещается в посуду, говорят, что измеряют её вместимость.
Время Единицы измерения времени: секунда (сек.), минута (мин), час(ч). сутки (сут.), неделя (нед.), месяц (мес.), год (г.), век (в.). 1мин = 60сек. 1нед. = 7 сут. 1ч = 60 мин = 3600сек. 1мес. 1сут. = 24 ч = 1440мин =86 400сек. 1год = 12мес.= 365 или 366 сут. 1век =100 лет Из четырёх лет подряд 3 года равны 365 суткам, а один год -366. Такой год называют високосным.
6 | Объём Объём показывает, сколько места занимает предмет в пространстве. Единицы измерения объёма: кубический миллиметр (мм ), кубический сантиметр (см ), кубический дециметр (дм ), кубический метр ( м ), кубический километр (км ). 3 1 куб. см. или 1см 3 3 1 см =1000 мм 3 3 3 1 дм =1000 см =1000 000 мм 3 3 3 1 м = 1000 дм =1000 000 см 3 3 1км = 1 000 000 000 м Площадь Площадь-это внутренняя часть какой-нибудь геометрической фигуры. Единицы измерения площади: квадратный миллиметр (мм ), квадратный сантиметр (см ), квадратный дециметр (дм ), квадратный метр(м ), квадратный километр (км ). 2 2 1см = 100мм 2 2 2 1дм =100см = 10 000мм 2 2 2 2 1м = 100 дм = 10 000 см = 1000 000 мм 2 2 1км = 1 000 000 м
Периметр. Формулы нахождения периметра. Периметр (Р) -это сумма длин сторон любой геометрической фигуры. Периметр фигуры измеряется в: миллиметрах, сантиметрах, дециметрах, метрах, километрах. Периметр прямоугольника Р= (а+b) x 2 или Р= а х 2+ b x 2 Периметр квадрата Р= (а х 4) |
Действия над величинами Чтобы действие между величинами было возможным, нужно их выразить в одну и ту же единицу измерения величины. Чтобы деление величины на величину было возможным. Делимое и делитель нужно выразить одной и той же единицей измерения этой величины. 24 м : 60 см = 2400см : 60см = 40см 18 кг : 75 г = 18000г :75 г = 240 г
Формулы определения объёма призмы Объём прямоугольной призмы равен значению произведения её длины, ширины и высоты. V=a x b x h , где V- объём прямоугольной призмы, a- её длина, b- ширина, h- высота. Объём произвольной прямой призмы равен значению произведения площади её основания и высоты. V= Sx h, где V-объём призмы, S-площадь её основания, h-высота.
Формулы определения площади: Прямоугольника Площадь прямоугольника можно узнать, перемножив длину на ширину. S=a x b Чтобы найти площадь прямоугольника, нужно основание (а) умножить на высоту(h). S= a x h Треугольника Площадь любого треугольника равна половине произведения длины его стороны и проведённой к ней высоты. S = (a x h) : 2 Квадрата S=a x a, где а-сторона квадрата
7 | Геометрические фигуры Плоскостные: точка, прямая, отрезок, луч, линии (замкнутые, незамкнутые, ломаные, кривые, прямые), углы (прямые, острые, тупые) , многоугольники, круги. Объёмные: шар, конус, цилиндр, призма, пирамида. Прямая-это линия, не ограниченная ни с одной, ни с другой стороны. Прямую линию можно мысленно продолжить в обе стороны безгранично. Прямую можно обозначить одной строчной латинской буквой или двумя заглавными. Отрезок-это линия, ограниченная с обеих сторон. Отрезок можно обозначить двумя заглавными латинскими буквами или одной строчной. Луч-это линия, с одной стороны ограниченная, а с другой стороны –нет. Луч можно обозначить двумя заглавными латинскими буквами или одной сторочной. Треугольник – геометрическая фигура, в которой три угла и три стороны. Треугольник можно обозначить заглавными латинскими буквами. В А С Треугольник, у которого есть прямой угол, называется прямоугольным. Треугольник, у которого есть тупой угол, называется тупоугольным. Треугольник, у которого все три угла острые, называется остроугольным. Равносторонним называют треугольник, у которого все стороны равны. Равнобедренным называют треугольник, у которого две боковые стороны равна. 0 Сумма углов треугольника равна 180 . Высота треугольника – это отрезок, соединяющий вершину треугольника с точкой его стороны или её продолжения и образующий с ней прямой угол. Любой треугольник имеет три высоты.
|
Четырёхугольник-это геометрическая фигура, у которой четыре угла и четыре стороны. Четырёхугольник можно обозначить четырьмя заглавными латинскими буквами.
В С
D А D Прямоугольник-это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника равны.
В С
А D
АВ=СD и AD=BC Квадрат-это прямоугольник, у которого все стороны равны. B К
A N Диагональ многоугольника – это отрезок, который соединяет вершины двух его углов, не имеющих общей стороны. P K
N M 8 | Линию, которая является границей круга, называется окружностью. Точка, вокруг которой чертят окружность,- центр окружности. Радиус- это отрезок, который соединяет центр окружности с любой точкой на окружности. Диаметр- это отрезок, проходящий через центр окружности и соединяющий две точки на этой окружности. Если вершиной угла является центр окружности, угол называют центральным углом.
Е
Т оооооо Стороны центрального угла являются радиусами окружности. Радиусы одной окружности равны между собой. Отрезок, который соединяет две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром. Диаметр – самая длинная хорда окружности. B C F A P Q D N |
Татьяна Яковлевна Балашова Страница не найдена
ПОЗДРАВЛЯЕМ!
Ноябрь11
Поздравляем Катю с 1 местом среди девочек и Семена с 3 местом среди мальчиков 2-х классов!!!
МЫ — МОЛОДЦЫ!!!
Сентябрь14
Дорогие мои девчонки и мальчишки!
Читать всю запись »
С Днем Рождения!
Сентябрь14
Дмитрия мы поздравляем
Счастья, радости желаем,
Жизни доброй без хлопот
И улыбок много-вот!
Пускай сбываются мечты
И распускаются цветы!
Пускай всегда твои друзья
Дарят теплые слова!
Пускай надежды водворятся
А ты всегда будешь смеяться!
С днем рождения!
Сентябрь7
Ярослав, прими наши поздравленья,
В твой личный праздник – день рожденья,
Пускай фортуна улыбается тебе всегда,
Пусть жизнь течёт, как полная река.
Пускай печали тебя не знают,
Пускай друзья надёжные окружают,
Пусть счастье тебе улыбается.
ПОЗДРАВЛЯЮ!
Сентябрь1
ПЕРЕХОДИМ ВО 2-ОЙ
Май26
Уважаемые родители!
Позади у нас сложный год — первый год обучения в школе. У нас было много радостей и трудностей тоже. Огромное спасибо вам за поддержку, понимание и сотрудничество! С наступлением летних каникул у вашего ребенка изменится режим дня. Он будет больше времени проводить на улице, общаться с друзьями. Это здорово! Но не забывайте о занятиях. Они несложные в выполнении, творческие, но требуют вашего контроля.
Читать всю запись »
Прощай, 1-й класс!
Май26
Выпускной у 11-х классов
Правила по математике
ЧИСЛА И ЦИФРЫ.
Числа – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.).
Для записи чисел используются специальные знаки – цифры.
Цифр – десять:
1 2 3 4 5 6 7 8 9 0
НАТУРАЛЬНЫЕ ЧИСЛА.
Числа, которые используются при счёте, называются натуральными.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, □
1 – самое маленькое число.
□ – самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число.
СРАВНЕНИЕ ЧИСЕЛ.
Правило 1.
Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:
…, 10, 11, 12, 13, 14, 15,
14 > 11
Правило 2.
Из двух натуральных чисел с разным количеством разрядов больше то число, в котором разрядов больше.
28 < 145 782 < 1263
Правило 3.
Из двух натуральных чисел с одинаковым количеством разрядов больше то, у которого больше цифра старшего разряда.
4 5 861 и 4 7 361
45 861 < 47 361 47361 > 45 681
СЛОЖЕНИЕ.
Сложение – это математическое действие.
Числа, которые складываются, называются слагаемыми.
Результат сложение называется суммой.
сумма |
a + b = c |
первое слагаемое второе слагаемое сумма |
2 + 3 = 5 |
сумма |
Правило 1.
Если одно из слагаемых равно 0, сумма равна второму слагаемому:
a + 0 = a 0 + a = a
5 + 0 = 5 0 + 5 = 5
Правило 2.
Если оба слагаемых равны 0, то и сумма равна 0: 0 + 0 = 0
ВЫЧИТАНИЕ.
Вычитание – действие, обратное сложению.
Правило 1.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Правило 2.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
ЗАКОНЫ СЛОЖЕНИЯ.
Закон 1.
Переместительный закон сложения.
От перемены мест слагаемых значение суммы не меняется:
a + b = b + a
4 + 2 = 2 + 4
Закон 2.
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел:
(a + b) + c = a + (b + c) = (a + c) + b
(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4
УМНОЖЕНИЕ.
Умножение – это сложение одинаковых слагаемых.
2 + 2 + 2 = 2 · 3 = 6
2 – слагаемое
3 – число, которое показывает, сколько раз повторяется слагаемое 2 (по два три раза)
· , × – знаки умножения.
a · b = a + a + a + … + a
b раз
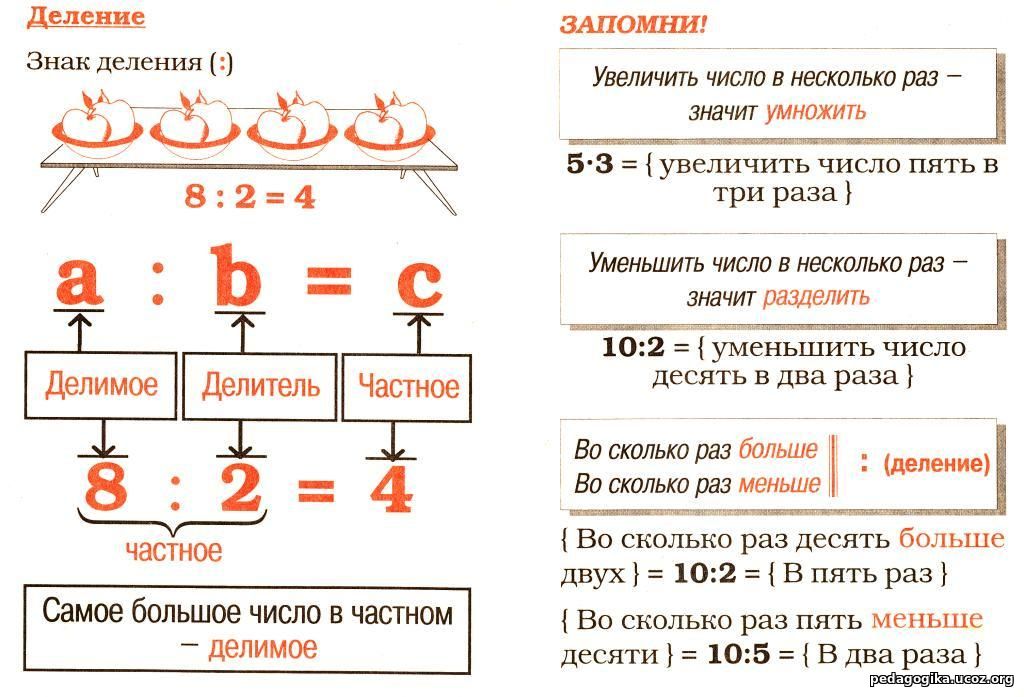
ДЕЛЕНИЕ.
Деление – это действие, обратное умножению.
6 : 2 = 3 6 : 3 = 2
ЗАКОНЫ УМНОЖЕНИЯ.
Закон 1.
Переместительный закон умножения.
От перестановки множителей произведение не меняется:
a · b = b · a
4 · 2 = 2 · 4
8 = 8
Закон 2.
Сочетательный закон умножения.
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел:
(a · b) · c = a · (b · c) = (a · c) · b
(2 · 4) · 8 = 2 · (4 · 8) = (2 · 8) · 4
Закон 3.
Распределительный закон умножения.
Относительно сложения
Произведение суммы на число равно сумме произведений каждого слагаемого на это число.
(a + b + c) · d = a · d + b · d + c · d
(2 + 5 + 3) · 2 = 2 · 2 + 5 · 2 + 3 · 2 = 20
Относительно вычитания
Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.
(a – b) · d = a · d – b · d
(15 – 5) · 4 = 15 · 4 – 5 · 4 = 60 -+ 20 = 40
СВОЙСТВА ДЕЛЕНИЯ.
Правило 1.
Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.
(a + b) : c = a : c + b : c
Правило 2.
Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное.
(a – b) : c = a : c – b : c
Правило 3.
Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число.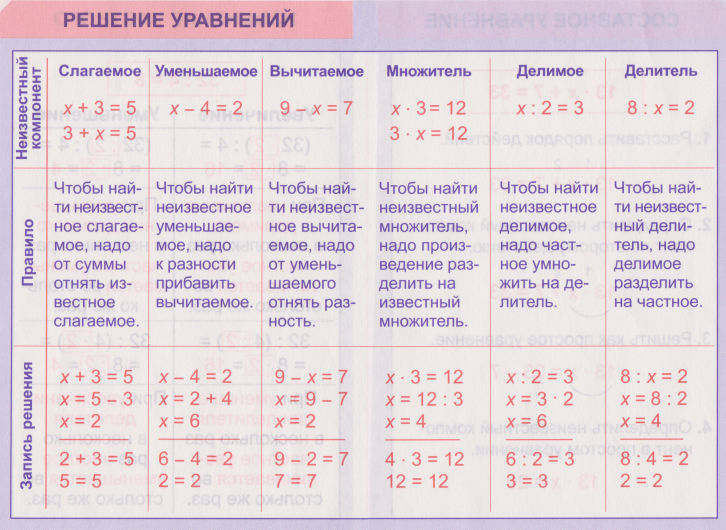
(a · b) : c = (a : c) · b = a · (b : c)
Правило 4.
Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель.
a · (b : c) = (a : b) · c
Правило 5.
Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат
Можно так же разделить делимое на это число, а полученный результат разделить на делитель.
(a : b) : c = a : (b · c)
или
(a : b) : c = (a : c) : b
НАХОЖДЕНИЕ КОМПОНЕНТОВ ДЕЛЕНИЯ.
Правило.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
a : ? = c ? = a : c
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
? : b = c ? = c · b
ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ.
a · 1 = a 4 · 1 = 4 | 1 · a = a 1 · 4 = 4 |
0 · a = 0 0 · 6 = 0 | a · 0 = 0 6 · 0 = 0 |
ОСОБЫЕ СЛУЧАИ ДЕЛЕНИЯ.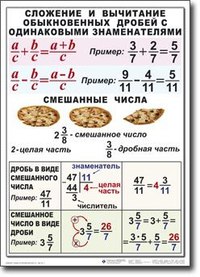
a : 1 = a 8 : 1 = 8 | 0 : a = 0 0 : 6 = 0 | a : a = 1 8 : 8 = 1 |
На нуль делить НЕЛЬЗЯ! a : 0 | ||
Нуль можно делить на любое число, получится 0.
ПРИЗНАКИ ДЕЛИМОСТИ.
На 2 делятся все чётные числа, то есть числа, которые оканчиваются цифрами 0, 2, 4, 6, 8.
На 3 делятся все числа, сумма цифр которых делится на 3.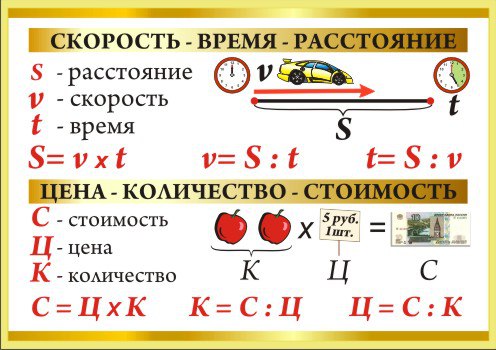
На 5 делятся все числа, которые оканчиваются на 0 или 5.
На 6 делятся числа, которые делятся одновременно и на 2, и на 3.
На 9 делятся числа, сумма цифр которых делится на 9.
ИМЕНОВАННЫЕ ЧИСЛА.
Именованные числа – это числа, полученные при измерении величин и сопровождающиеся названием единиц измерения.
Например: 2 кг, 4 см, 8 л
Именованные числа бывают простые и составные.
Простые именованные числа: 7 м, 18 т, 21 кг – в них входит только одн единица измерения.
Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м – в них входят несколько единиц измерения.
ПРЕОБРАЗОВАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Чтобы перейти от одних единиц измерения к другим, пользуйся таблицей величин.
Таблица величин.
Единицы измерения длины 1 см = 10 мм 1 дм = 10 см 1 м = 10 дм = 100 см = 1000 мм 1 км = 1000 м = 10000 дм = 100000 см |
Единицы измерения массы 1 кг = 1000 г 1 ц = 100 кг 1 т = 10 ц = 1000 кг |
Единицы измерения времени 1 мин = 60 с 1 ч = 60 мин = 3600 с 1 сутки = 24 часа 1 неделя = 7 дней 1 месяц = 30 или 31 день (в феврале 28 или 29 дней) 1 год = 12 месяцев = 52 недели = 365 или 366 дней 1 век (столетие) = 100 лет |
Единицы измерения площади 1 мм2 1 см2 = 100 мм2 1 дм2 = 100 см2 1 м2 = 100 дм2 = 10000 см2 1 км2 = 1000000 м2 1 ар (1 а) = 1 сотка = 100 м2 1 гектар (1 га) = 10000 м2 |
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Правило.
Складывать и вычитать можно именованные числа, выраженные в одинаковых единицах измерения.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Запомни!
При умножении и делении составные именованные числа сначала заменяют простыми, а затем выполняют вычисления. В ответе простое именованное число заменяют составным.
ВЫРАЖЕНИЯ.
Математическое выражение – это фраза, записанная с помощью чисел, знаков и букв.
Выражение, записанное только с помощью чисел и знаков, называется числовым.
Выражение, в котором кроме чисел и знаков есть буквы, называется буквенным.
Любое числовое выражение имеет значение. Найти значение числового выражения – значит найти его ответ.
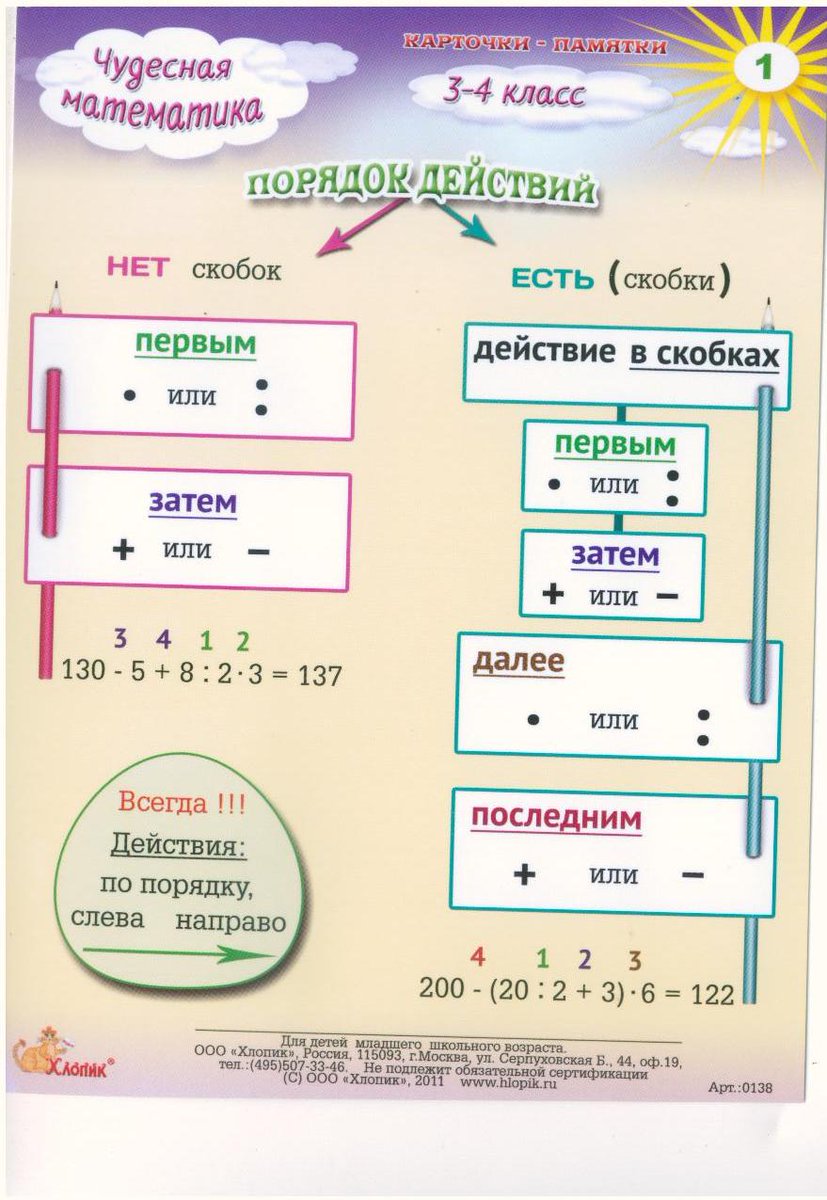
ПОРЯДОК ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ.
Правило 1.
В выражениях без скобок, где выполняются только сложение и вычитание, действия выполняются в том порядке, в котором они записаны (то есть слева направо).
1 2
70 – 26 + 10 = 54
1 2
90 – 20 – 15 = 55
1 2
42 + 18 – 19 = 41
Правило 2.
В выражениях без скобок, где выполняются только умножение и деление, действия выполняются в том порядке, в котором они записаны.
1 2
4 · 10 : 5 = 8
1 2
60 : 10 · 3 = 18
1 2
36 : 9 · 3 = 12
Правило 3.
В выражениях со скобками первым выполняется действие в скобках, затем умножение или деление и только потом сложение или вычитание.
1 2
80 – (46 – 14) = 48
1 2
6 · (30 – 20) = 60
1 2
90 : (2 · 5) = 9
Правило 4.
В выражениях, где есть действия первой и второй ступеней (то есть +, -, ·, :), сначала выполняются умножение и деление, а затем по порядку сложение и вычитание.
1 3 2
6 · 5 + 40 : 2 = 20
2 1 3
72 – 24 : 6 + 2 = 70
УРАВНЕНИЯ.
Уравнение – это равенство, которое содержит в себе неизвестное (переменную), значение которого нужно найти, чтобы равенство было верным.
x + 3 = 5 5 · x = 20 | y – 2 = 7 8 : a = 2 |
Решить уравнение – значит найти все значения переменной, при которых уравнение превращается в верное равенство.
x + 3 = 5
x = 5 – 3
x = 2
2 + 3 = 5
5 = 5
Значение переменной, при котором уравнение превращается в верное равенство, называется корнем уравнения: y – 2 = 7
y = 9 – корень уравнения, так как 9 – 2 = 7
РЕШЕНИЕ ПРОСТЕЙШИХ УРАВНЕНИЙ.
Правило 1.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
x + 3 = 5
x = 5 – 3
Правило 2.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
x – 3 = 5
x = 5 + 3
Правило 3.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
8 – x = 5
x = 8 – 5
Правило 4.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
x · 3 = 15
x = 15 : 3
Правило 5.
Чтобы найти неизвестное делимое, нужно к вычитаемому прибавить разность.
x : 3 = 5
x = 5 · 3
Правило 6.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
8 : x = 2
x = 8 : 2
УЧИМСЯ РЕШАТЬ ЗАДАЧИ.
Как работать над задачей.
1. Прочитай внимательно условие задачи и представь то, о чём идёт речь.
2. Запиши кратко задачу или сделай к ней рисунок, схему, чертёж.
3. Объясни, что означает каждое число.
4. Устно составь план решения задачи.
5. Реши задачу и найди ответ.
6. Проверь решение, составив обратную задачу.
7. Запиши ответ.
Знак | Действие | Знак | Действие |
+ | Увеличить на … | – | Найти разность |
– | Уменьшить на … | · (х) | Увеличить в несколько раз |
– | На сколько больше? | : | Уменьшить в несколько раз |
– | На сколько меньше? | : | Во сколько раз больше? |
+ | Найти сумму | : | Во сколько раз меньше? |
ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ ДВУХ ЧИСЕЛ.
Запомни!
Задачи этого вида решаются сложением, потому что находим сумму.
Задача.
Белочка припасла для маленьких друзей 4 гриба и 5 орехов. Сколько всего гостинцев приготовила белочка?
Краткое условие:
Грибов – □
Орехов – □
Решение:
4 + 5 = 9 (гост.)
Ответ: 9 гостинцев.
ЗАДАЧИ НА НАХОЖДЕНИЕ ОСТАТКА.
Запомни!
Задачи этого вида решаются вычитанием, потому что находим остаток.
Задача.
На ветке было 7 ягод рябины. Снегирь склевал 3 ягоды. Сколько ягод осталось?
Краткое условие:
Было – 7 яг.
Склевал – 3 яг.
Осталось – ? яг.
Решение:
7 – 3 = 4 (яг.)
Ответ: 4 ягоды.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА
НА НЕСКОЛЬКО ЕДИНИЦ.
Задача.
Во дворе гуляло 6 утят, а гусят на 2 больше. Сколько гуляло гусят?
Краткое условие:
Утят – 6 пт.
Гусят – ? пт., на 2 больше (>)
Решение:
6 + 2 = 8 (гус.)
Ответ: 8 гусят.
ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА
НА НЕСКОЛЬКО ЕДИНИЦ.
Задача.
На столе лежало 9 столовых ложек, а чайных на 3 меньше. Сколько чайных ложек лежало на столе?
Краткое условие:
Стол. – 9 лож.
Чайн. – ? лож., на 3 меньше (<)
Решение:
9 – 3 = 6 (лож.)
Ответ: 6 чайных ложек.
ЗАДАЧИ НА РАЗНОСТНОЕ СРАВНЕНИЕ ДВУХ ЧИСЕЛ.
Правило.
Чтобы узнать, на сколько одно число больше (меньше) другого, нужно из большего числа вычесть меньшее.
Задача.
В одной корзине 7 яблок, а в другой – 10 груш. На сколько груш больше, чем яблок?
Краткое условие:
Яб. – 7 шт.
Гр. – 10 шт., на ? шт. больше (>)
Решение:
10 – 7 = 3 (гр.)
Ответ: на 3 груши.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО СЛАГАЕМОГО.
Задача.
Два петушка нашли 8 червячков. Первый нашёл 5. Сколько червячков нашёл второй петушок?
Краткое условие:
1 пет. – 5 чер. 8 чер.
2 пет. – ? чер.
Решение:
8 – 5 = 3 (чер.)
Ответ: 3 червячка.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО.
Задача.
На тарелке лежали пряники. Когда дети взяли 4 пряника, на тарелке осталось 8. Сколько пряников было на тарелке?
Краткое условие:
Было – ? пр.
Взяли – 4 пр.
Осталось – 8 пр.
Решение:
8 + 4 = 12 (пр.)
Ответ: 12 пряников.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО.
Задача.
В вазе стояло 7 гвоздик. Когда несколько гвоздик отдали, в вазе осталось 5 гвоздик. Сколько гвоздик отдали?
Краткое условие:
Было – 7 гв.
Отдали – ? гв.
Осталось – 5 гв.
Решение:
7 – 5 = 2 (гв.)
Ответ: 2 гвоздики.
ЗАДАЧИ НА НАХОЖДЕНИЕ
ПРОИЗВЕДЕНИЯ ДВУХ ЧИСЕЛ.
Задача.
В одной коробке 6 карандашей. Сколько карандашей в 4 коробках?
Краткое условие:
1 кор. – 6 кар.
4 кор. – ? кар.
Решение:
6 · 4 = 24 (кар.)
Ответ: 24 карандаша.
ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТНОГО ДВУХ ЧИСЕЛ.
Задача 1.
ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ.
15 шариков раздали 5 ученикам поровну. Сколько шариков получил каждый ученик?
Краткое условие:
15 шар. – 5 уч.
Поровну шар. – 1 уч.
Решение:
15 : 5 = 3 (шар.)
Ответ: 3 шарика.
Задача 2.
ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ.
12 лимонов разложили в пакеты по 4 лимона в каждый. Сколько получилось пакетов с лимонами?
Краткое условие:
12 лим. – ? пак.
4 лим. – 1 пак.
Решение
12 : 4 = 3 (пак.)
Ответ: 3 пакета.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ.
Задача.
У Тани было 4 ириски, а карамелек в 2 раза больше. Сколько карамелек было у Тани?
Краткое условие:
Ириски – 4 шт.
Карамельки – ? шт., в 2 раза больше (>)
Решение:
4 · 2 = 8 (кар.)
Ответ: 8 карамелек.
ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА
В НЕСКОЛЬКО РАЗ.
Задача.
На одной полке стоит 12 книг, а на второй – в 3 раза меньше. Сколько книг на второй полке?
Краткое условие:
I – 12 кн.
II – ? кн., в 3 раза меньше (<)
Решение:
12 : 3 = 4 (кн.)
Ответ: 4 книг.
ЗАДАЧИ НА КРАТНОЕ СРАВНЕНИЕ ДВУХ ЧИСЕЛ.
Правило.
Чтобы узнать, во сколько раз одно число больше (меньше) другого, нужно большее число разделить на меньшее.
Задача.
Петя почистил 27 картофелин, а Коля – 9. Во сколько раз больше картофелин почистил Петя, чем Коля?
Краткое условие:
Петя – 27 кар. во ? раз больше (>)
Коля – 9 кар.,
Решение:
27 : 9 = 3 (гр.)
Ответ: в 3 раза больше.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО МНОЖИТЕЛЯ.
Задача.
20 яблок разложили в сетки по 5 яблок в каждую. Сколько потребовалось сеток?
Краткое условие:
1 сет. – 5 яб.
? сет. – 20 яб.
Решение:
1-ый способ: 20 : 5 = 4 (сет.)
2-ой способ: запишем решение задачи, составив уравнение.
х · 5 = 20
х = 20 : 5
х = 4 (сет.)
Ответ: 4 сетки.
ЗАДАЧИ В КОСВЕННОЙ ФОРМЕ.
Правило.
При решении задач в косвенной форме помни: если одна величина на несколько единиц (в несколько раз) больше, то другая на столько же единиц (во столько же раз) меньше.
Задача.
Брату 5 лет, он на 2 года старше сестры. Сколько лет сестре?
Краткое условие:
Брат – 5 лет, на 2 года больше (>)
Сестра – ? лет
Если брат старше на 2 года, значит, сестра на 2 года младше. Чтобы стало меньше, нужно вычитать.
Решение:
5 – 2 = 3 (г.)
Ответ: 3 года.
Задача.
У Нины 7 марок. Это на 4 марки меньше, чес у Тани. Сколько марок у Тани?
Краткое условие:
Нина – 7 мар., на 4 мар. меньше (<)
Таня – ? мар.
Если у Нины на 4 марки меньше, значит, у Тани на 4 марки больше. Чтобы стало больше, нужно прибавлять.
Решение:
7 + 4 = 11 (мар.)
Ответ: 11 марок.
Желаю успехов! | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Grade 4 Curriculum
Ниже приведены необходимые навыки со ссылками на ресурсы, которые помогут в освоении этого навыка. Мы также поощряем много упражнений и книжную работу. Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.
4 класс | Подсчет
☐ Счетчик пропусков по 1000
4 класс | Сложение
☐ Используйте различные стратегии для сложения чисел до 10 000
4 класс | Вычитание
☐ Используйте различные стратегии для вычитания чисел до 10 000
4 класс | Умножение
☐ Разберитесь в различных значениях умножения
☐ Используйте различные стратегии для умножения двузначных чисел на однозначные числа (с перегруппировкой и без нее)
☐ Используйте различные стратегии для умножения двузначных чисел на двузначные числа (с перегруппировкой и без нее)
☐ Научитесь умножать числа, кратные 10 и 100, на 1000
☐ Развивайте беглость речи с умножением до 10x
4 класс | Деление
☐ Используйте умножение и деление как обратные операции для решения задач
☐ Используйте различные стратегии для деления двузначных дивидендов на однозначные делители (с остатками и без остатков)
☐ Толковать значение остатков
☐ Разбираться в различных значениях деления
4 класс | Числа
☐ Развивайте понимание свойств нечетных / четных чисел в результате умножения
☐ Выбрать подходящие вычислительные и операционные методы для решения проблем
☐ Чтение и запись целых чисел в 10,000
☐ Округлить числа от 1000 до ближайшей десятки или до ближайшей сотни
☐ Сравните и закажите номера до 10,000
☐ Разберитесь в структуре разряда десятичной системы счисления: 10 единиц = 1 десять 10 десятков = 1 сотня 10 сотен = 1 тысяча 10 тысяч = 1 десять тысяч
☐ Распознавать эквивалентные представления чисел до четырех цифр и генерировать их путем разложения и составления чисел
☐ Узнайте, как расширить структуру значений разряда десятичной системы счисления, включив в нее десятичные дроби: десятые, сотые, тысячные…
☐ Округлить десятичные дроби до ближайшего целого числа.
Таблица правил делимости– 4 класс по математике
Овладейте 7 столпами успеха в школе
Повысьте оценки и снизьте уровень стресса
Общий основной стандарт: 4.OA.4 Математика 4-го класса
Связанные веб-сайты / Таблица правил делимости
делится даже на 2.
Итак, если число заканчивается на 0, 2,4,6,8 делится на 2. | ||
Номер | Делимый | Почему? |
66 | да | Заканчивается через 6, что является четное число |
203 | № | 3 не делится на 2 |
48 | да | Заканчивается на 8, что является делится на 2 |
Правила делимости для 6, 8, 9, 10,
Правила делимости для 2, 3.4 и 5
Чтобы число делилось на 6, оно должно быть четным. и,
Если сложить цифры, это число должно делиться на 3 | ||
Номер | Делится на 6? | Почему |
72 | Есть | 72 – четный номер и 7 + 2 = 9 – это делится на 3 |
357 | № | Цифра не четная. |
| 138 | Есть | Число четное и 1 + 3 + 8 = 12 делится на 3 |
Чтобы число делилось на 8, посмотрите на последние три цифры и если это число делится на 8, то все число делится на 8 | ||
Номер | Можно разделить на 8? | Почему |
3648 | Есть | 648/8 = 81, поэтому число, образованное последними тремя цифрами, делится на 8 |
5679 | № | 679 нет делится на 8, поэтому все число не делится на 8 |
Для того, чтобы число делилось на 9, просто сложите цифры и если это число делится на 3 и 9, то все число делится на 9 | ||
Номер | Можно разделить на 9? | Почему |
234 | Есть | 2 + 3 + 4 = 9, что делится на 3 и 9 |
897 | № | 8 + 9 + 7 = 24, что является не делится 9 |
561 | Есть | 5 + 6 + 1 = 12, что делится на 3 и 9 |
Чтобы число делилось на 10, оно должно заканчиваться на 0 . | ||
Номер | Делится на 10 | |
220 | Есть | Окончание 0 |
678 | Нет | Не заканчивается на 0 |
43780 | Есть | Окончание 0 |
Чтобы число делилось на 12, оно должно делиться на 3 и 4 | ||
Номер | Можно разделить на 12? | Почему |
1044 | Есть | Is число делимое на 3? 1 + 4 + 4 = 9, что делится на 3 и две последние цифры 44 делятся на 4 |
204 | Есть | 4 + 2 = 6, что является делится на 3, а последние две цифры 04 делятся на 4 |
878 | Нет | Сумма чисел 8 + 7 + 8 = 23 не делится на 3 |
Если последняя цифра заканчивается на 0 или 5, то это делится на 5 | ||
Номер | Делится на 5? | Почему |
55 | Есть | 55/5 = 11 До 5 |
456 | № | 456/5 = 91.2 Заканчивается через 6 |
650 | да | 650/5 = 130 Окончание 0 |
У вас есть два варианта: 1. Если сложить две последние цифры вместе, делится ли их сумма на 4? В таком случае все число делится на 4 .2.Разделите число на 2, и если сумма четная, то получится делится на четыре.
| ||
Номер | Делится на 4 ? | Почему |
56 | Есть | 56/2 = 28 и это даже |
786 | № | 786/2 = 393, что нечетно или 86 не делится на 4 |
128 | да | 128/2 = 64, что является даже или 28 делится на 4 |
Вам тоже понравится……
Используйте эту диаграмму правил видимости di , чтобы определить, делится ли одно число на на другое.
4-й класс по математике | Бесплатные онлайн-математические игры
1 класс
2 класс
3 класс
4 класс
5 класс
6 класс
Веселые игры для детей
Математические игры для 4-х классов
Обзор игры: Дивизион Дерби
Реклама | Без рекламыОперации и алгебраическое мышление
Пазлы с числами
Блоки мышления
Загадка глубоководной математики
Поиск сокровищ X
Сделайте число
Tug Team Multiplication
Пазлы с числами
Pony Pull Division
Дивизион Math Surpass
Сопряжение факторов
Музыкальный микс
PEMDAS Экспонат
Monster Mischief
Следы умножения
Схемы лент
Умножение Гран-при
Умножение метеоров
Умножение
Умножение
Удаленные функции
Дивизион Дерби
Math. Превосходит остаток
10 Маха, кратное
Demolition Derby
Дивизион дрэг-рейсинга
Пингвин в прыжке
Прогулка с монстрами X
Блоки продуктов
Коэффициенты превосходства по математике
Задачи по математическому слову
Выдры
Math Превосходя простое число
Таблица умножения
Candy Challenge
Умножение
Умножение
Число и операции в базе десять
Умножение недостающих цифр
Отдел пропущенных цифр
Один продукт
Добавление недостающих цифр
Вычитание отсутствующих цифр
Визуальный отдел
Canoe Penguins
Щенки каноэ
Пазл сложения
Дополнительное видео
Коммутативное видео
Ассоциативное видео
Распределительное видео
Видео умножения
Отдел видео
Видео большого дивизиона
Число и операции с дробями

 д.
д.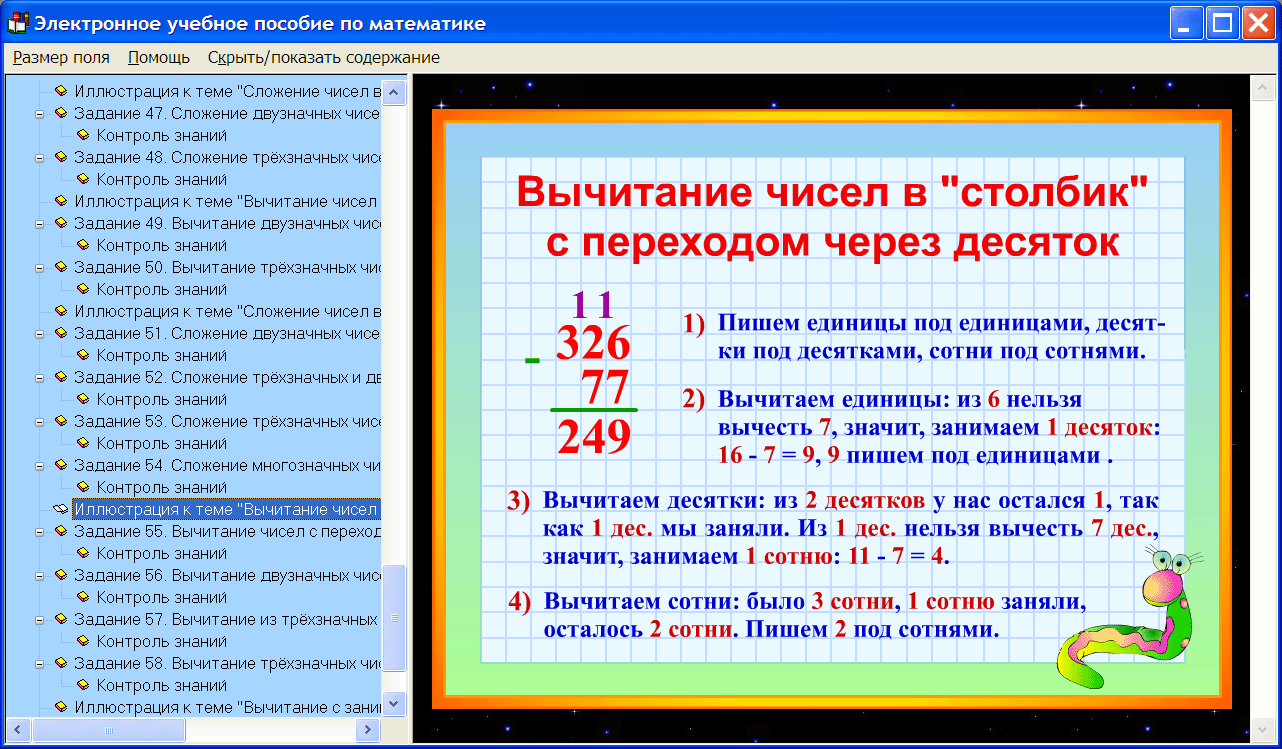







 = 28,29,30 или 31 сут.
= 28,29,30 или 31 сут.



 = 28,29,30 или 31 сут.
= 28,29,30 или 31 сут.