Повторение таблицы умножения: Таблица умножения на 6. В случайном порядке
Таблица умножения на 6. В случайном порядке
Тесты на проверку знаний табличного умножения и деления
Вам задается 10 вопросов по таблице умножения в разброс без ответов. Вопросы не повторяются.
Проверить знания
История решений
Таблица умножения на 2
Таблица умножения на 3
Таблица умножения на 4
Таблица умножения на 5
Таблица умножения на 6
Таблица умножения на 7
Таблица умножения на 8
Таблица умножения на 9
Таблица умножения до 2
Таблица умножения до 3
Таблица умножения до 4
Таблица умножения до 5
Таблица умножения до 6
Таблица умножения до 7
Таблица умножения до 8
Таблица умножения до 9
Таблица умножения на 2 по возрастанию
Таблица умножения на 3 по возрастанию
Таблица умножения на 4 по возрастанию
Таблица умножения на 5 по возрастанию
Таблица умножения на 6 по возрастанию
Таблица умножения на 7 по возрастанию
Таблица умножения на 8 по возрастанию
Таблица умножения на 9 по возрастанию
Таблица умножения на 2 по убыванию
Таблица умножения на 3 по убыванию
Таблица умножения на 4 по убыванию
Таблица умножения на 5 по убыванию
Таблица умножения на 6 по убыванию
Таблица умножения на 7 по убыванию
Таблица умножения на 8 по убыванию
Таблица умножения на 9 по убыванию
Таблица умножения огромная и скучная? Сокращаем её и учим всего за 2 дня!
Когда второклашка видит таблицу умножения, какая она большая и скучная, он учить ее не хочет.
Но его заставляют зубрить. Вроде и выучит кое-как, а в третьем классе зубрит заново. И каждый раз по новой. Да и в четвертом классе таблица умножения постоянно вылетает из головы.
А дело в зубрёжке и в непонимании сути таблицы умножения. Зачем её вообще учить? Ведь калькулятор в телефоне есть и есть обложка тетради по математике, где эта таблица написана.
Но таблицу умножения учить необходимо в обязательном порядке.
И сделать это можно буквально за 2 дня. Изучение делится на 2 этапа:
- Объясняем суть умножения
2. Учим без зубрёжки в форме игры
На первом этапе необходимо объяснить ребенку, для чего нужно знать таблицу умножения в жизни, и что такое вообще умножение. Для этого приводим пример из жизни, который ребенок поймёт. Например, конфеты на блюдцах, карандаши в коробках, монеты в кучках.
Например, рисуем четыре монеты в четырёх кучках. Спрашиваем у ребенка: «Сколько всего денег возьмёшь с собой в магазин?». Ребенок пересчитывает, отвечает, что всего 16.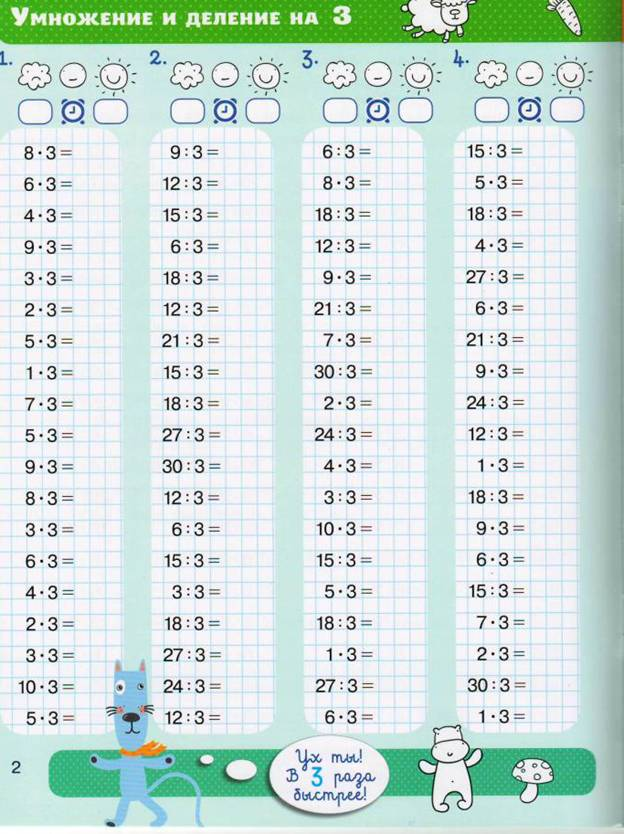
Говорим, что пересчитывание и сложение 4+4+4+4 можно заменить умножением 4×4. Далее даем более сложный пример — 7 монет в 5 кучках. Пересчитывать их долго, проще записать 7×5=35. Сразу же поясняем, что это всё равно что 5×7=35.
Таким образом выяснили суть таблицы умножения. Это всё равно, что сложение одинаковых слагаемых, но в магазине считать сложением деньги долго и можно сбиться или ошибиться. Для этого и придумали таблицу умножения, с ней проще решать примеры.
Переходим ко второму этапу. Учим без зубрёжки всё таблицу.
Если правильно объяснили ребенку в первом пункте суть таблицы умножения, то он понял, что есть зеркальные примеры: 7×8 = 8×7, 5×9 = 9×5 и т.д. Нам осталось взять тетрадь с таблицей и вычеркнуть из неё все эти примеры. Вычеркиваем зеркальные примеры. Например, 2×3 оставляем, а 3×2 вычеркиваем. Таким образом сокращаем таблицу умножения. Она становится маленькой и не такой тяжёлой, какой казалась нам вначале.
После всех зачеркиваний у нас остаётся только 36 примеров:
Согласитесь, что учить эти примеры легче, чем всю таблицу умножения целиком.
Можно разделить на 18 примеров и выучить их за 2 дня, а можно на 12 и выучить за 3 дня.
Метод «воронки».
Делаем карточки на эти 36 примеров таблицы умножения. Или покупаем готовые.
Читаем ребенку пример на карточке. Если он даёт правильный ответ, то забирает карточку себе. Если ответ неправильный или ребенок его не знает, то берём карандаши и тетрадки и рисуем монетки в кучках.
Ребенок рисует, например, 6 монет в 8 кучках, пересчитывает кружочки. Находит ответ, что 6×8=48.
Карточку с этим примером (который изначально ребенок не мог решить сам) надо положить в конец стопки. Позже ребенок вернётся к ней. Он снова будет рисовать кружочки, если даст неверный ответ.
Таким образом прорабатываем всю колоду. Решаем по одному примеру, а карточки с ошибками в конец стопки и возвращаемся к ним снова и снова, пока вся колода не окажется на руках ребенка.
Более подробно об этом методе в видео.
Этот метод считается эффективным, так как ребенок подключает все способы восприятия информации и свои органы чувств: слух, зрение, моторику, память.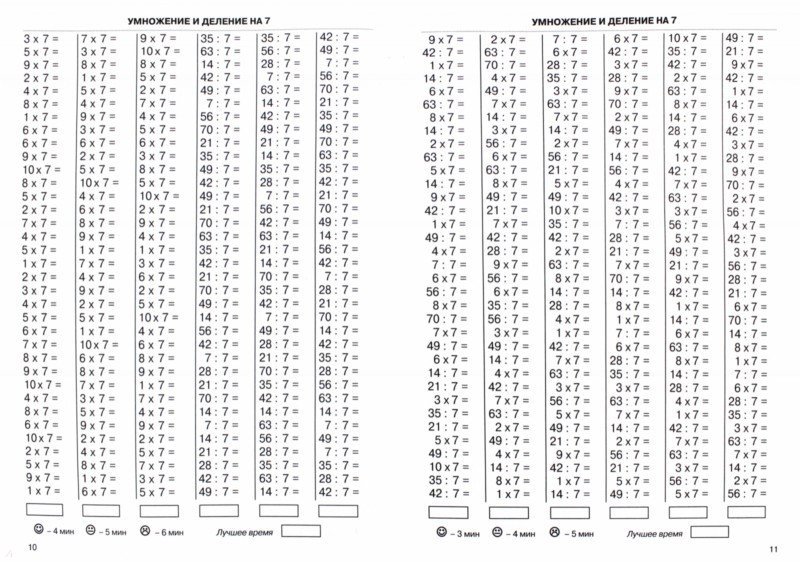
Плюс игровой момент, который помогает учить без зубрежки.
Закрепление, повторение таблицы умножения
Для закрепления таблицы умножения можно сделать математические раскраски. Купить настольную игру на таблицу умножения. Купить яркие пособия, рабочие тетради с интересными заданиями, скачать приложение на телефон.
Обучение мнемонике | Таблица умножения Таблица 101 – Дом сказок о временах!
Делиться:18 февраля 2021 г. ДЖЕННИ УИНТЕРС
Как завоевать таблицу умножения и полный почтовый ящик одним и тем же способом!
Вы родитель, который в настоящее время пытается помочь своим детям освоить таблицу умножения? Если это так, вы, скорее всего, слишком хорошо знакомы с неэффективностью механического заучивания путем повторения. Каждый день вы выполняете бесконечные упражнения с карточками, но, похоже, никогда не добиваетесь реального прогресса.
В один прекрасный день может показаться, что ваш ребенок “знает” ответ на свою таблицу умножения, но на следующий день он полностью забывает — это особенно верно, когда речь идет о страшных таблицах умножения. Сегодня я хочу поделиться с вами короткой историей о том, как я приручил своего «монстра входящих сообщений» — и как вы можете используйте ту же тактику , чтобы укротить « монстра умножения », пытаясь научить вашего ребенка таблице умножения.
My Nightmare Inbox Story:
До недавнего времени в моем почтовом ящике было ровно 7233 электронных письма. В течение последних двух лет я продолжал думать, что посвятил бы выходные своей силе кнопки удаления и НАКОНЕЦ-то приручил монстра. К сожалению, эти выходные так и не состоялись… Работа казалась слишком тяжелой! Каждый день я тратил немного времени на удаление новых писем, но так и не смог продвинуться вперед. Я застрял в бесконечном цикле повторения одного и того же каждый день, но на самом деле не добился никакого прогресса.
Несколько месяцев назад мой друг рассказал мне о приложении для организации электронной почты, которое сэкономит мне время и нервы после того, как я потратил первоначальный час на изучение того, как использовать программу. Я проверил веб-сайт, но сначала не заинтересовался, потому что не хотел тратить время.
Мой поворотный момент!
Однажды утром я посмотрел на этого монстра почтового ящика… и мне было достаточно. Пришло время действовать! Решительно я сел и понял, как управлять, удалять и упорядочивать своего почтового монстра. После нескольких лет беспокойства по поводу моего постоянно растущего почтового ящика я, наконец, покорил его! Потребовалось всего буквально час моего времени.
Какое отношение электронная почта имеет к завоеванию таблицы умножения?
Как соучредитель Times Tales, я слышал сотни историй от родителей, говорящих, что независимо от того, сколько месяцев (а иногда и лет ) они потратили на карточки для умножения и упражнения, их дети не могли выучить таблицу умножения.
вниз. Хотя мой «стресс из-за почтового ящика» не мог сравниться с разочарованием от наблюдения за тем, как ребенок борется с умножением, есть общий фактор для успешной победы над обоими «монстрами».
Решение!
Когда одно и то же снова и снова не удавалось добиться успеха, наконец сработал ДРУГОЙ ПОДХОД. Небольшие первоначальные затраты времени превращаются в МНОГО ВРЕМЕНИ, СЭКОНОМИРОВАННОГО в будущем.
Многие родители идут по пути и повторяют , когда нужно помочь своим детям выучить таблицу умножения просто потому, что они не знают, что есть лучший способ. Хорошая новость заключается в том, что ЕСТЬ гораздо более эффективный способ научить детей таблице умножения, и это превращает математику в увлекательное занятие! Использование мнемонического инструмента обучения (см. пример того, как он работает на картинке выше) упрощает процесс запоминания, потому что он заставляет эти математические факты фактически оставаться в банках памяти.
Когда я, наконец, завладел своим почтовым ящиком, я почувствовал огромное облегчение, которое длилось весь день! Многие дети испытывают такое же чувство выполненного долга и облегчения, когда они, наконец, могут освоить таблицу умножения НАВСЕГДА! Если вы родитель, у которого есть ребенок, который изо всех сил пытается, наконец, прибить таблицу умножения, пришло время попробовать Times Tales! Это может быть нетрадиционный подход к изучению таблицы умножения, но он действительно работает ИЗУМИТЕЛЬНО хорошо!
Посмотрите видео, чтобы узнать, как учить правополушарному умножению учащихся с дислексией и дискалькулией.
Times Tales® Deluxe: $39,95
Times Tales® Video (потоковое или DVD): $21,95
для протокола, у меня нет абсолютно никакого отношения, кроме того факта, что я ЛЮБЛЮ, как это упростило мой почтовый ящик!! 🙂
Дженни Уинтерс — создательница и соавтор книг Times Tales®, Pet Math, Memory Triggers и Zone Cleaning for Kids. Дженни — ветеран домашнего обучения, мать четырех детей, и теперь она любит проводить свое время за написанием нестандартных учебных материалов для детей. Когда Дженни не занимается разработкой новых продуктов, она любит рисовать, путешествовать и проводить время у озера с мужем.
*Эта запись в блоге взята из информационного бюллетеня Trigger Sisters и предназначена для продажи и продвижения Times Tales® и сопутствующих товаров.
Подано в: дискалькулия, дислексия, Запоминать таблицы умножения, умножение, таблицы умножения, таблица умножения, таблицы умножения, визуальная математика
Делиться: Предыдущая статья Умножение для визуалов Следующая статья Как сделать домашнее обучение летом интересным!Скрытая красота таблицы умножения
В этой статье мы исследуем некоторые симметрии, которые скрываются в таблице умножения положительных целых чисел.
Начнем со стандартной таблицы умножения. Таблица ниже содержит числа от 1 до 10 в первой строке и первом столбце. Любой другой квадрат содержит произведение первого числа в строке и первого числа в столбце.
Мы добавим строку вверху и столбец слева. Это по-прежнему дает непротиворечивую таблицу — первая строка и столбец содержат числа, кратные , вторая строка и столбец содержат числа, кратные , третья строка и столбец содержат числа, кратные и т. д. — и это обеспечит хорошую основу для наших шаблонов.
Далее мы будем раскрашивать квадраты таблицы умножения, которые соответствуют кратным числам для различных значений . И мы обнаружим несколько красивых симметрий.
Отдельные кратные
Начнем с: мы назначаем синий цвет каждому квадрату в таблице умножения, который кратен . (Число кратно , поэтому все квадраты синие.)
Здесь мы немного расширили таблицу, чтобы она шла до числа 15 в горизонтальном направлении.
Действительно, поскольку полная таблица умножения на натуральные числа бесконечна с двух сторон, мы продолжим
чтобы настроить размеры таблиц в дальнейшем, чтобы отобразить возникающие
узоры более четко.
Обратите внимание, что весь приведенный выше шаблон можно собрать вместе, используя основной строительный блок:
Основной строительный блок содержит ячейки таблицы умножения. Квадраты, определяемые белыми ячейками в шаблоне, состоят из
кл.
Ниже приведены еще два изображения, на которых числа, кратные числу, выделены синим цветом. Можете ли вы сказать, каково значение в каждом случае? Можете ли вы сказать, каковы основные строительные блоки, сколько ячеек они содержат и сколько ячеек составляют квадраты, определяемые белыми ячейками? Вы можете опубликовать свои ответы в поле для комментариев ниже — если вы не сможете их решить, мы опубликуем ответы через несколько недель.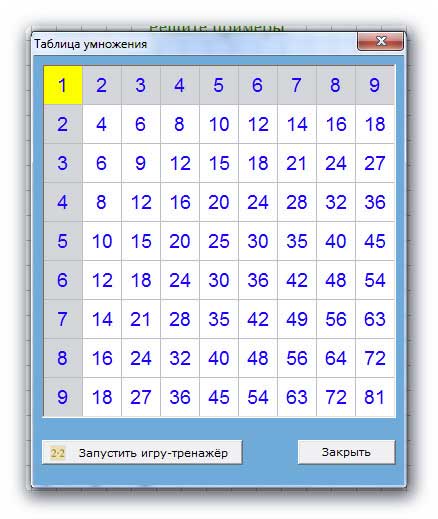
Несколько кратных последовательных чисел
Более интересная картина возникает, если мы используем несколько кратных и соответствующих им нескольких цветов. На следующем рисунке числа, кратные , окрашены в красный цвет, а числа, кратные , окрашены в оранжевый цвет (при этом оранжевый имеет приоритет над красным в случае кратных обоих и , то есть кратных ).
Это дает следующий шаблон.
Обратите внимание, что на этот раз наши основные строительные блоки состоят из маленьких квадратов, что имеет смысл, поскольку является наименьшим общим кратным и . Симметрия возникает из повторяющихся копий квадрата с хорошей четырехкратной симметрией.
Следующий рисунок делает это еще дальше, назначая красный цвет числам, кратным , оранжевый — числам, кратным , а желтый — числам, кратным . Если ячейка кратна двум из этих чисел (например, ), то ей будет присвоен цвет большего из этих двух чисел (оранжевый в примере).
Мы будем придерживаться этого соглашения до конца этой статьи.
На этот раз наши основные строительные блоки содержат ячейки, что опять же имеет смысл, учитывая, что это наименьшее общее кратное , и . Симметрия возникает из повторяющихся копий квадрата, состоящего из девяти маленьких квадратов, которые вместе создают прекрасную четырехкратную симметрию.
Мы можем продолжать играть в эту игру бесконечно. Следующие четыре цифры используют числа, кратные четырем, пяти, шести и семи последовательным числам соответственно, и четыре, пять, шесть и семь цветов соответственно. Какие закономерности вы можете различить? Можете ли вы найти какие-либо оси (отражательной) симметрии? Каковы должны быть размеры фундаментальных (повторяющихся) строительных блоков симметрии в каждом случае? Помните, что вы можете опубликовать свои ответы в поле для комментариев ниже, и если вы не сможете их решить, мы опубликуем ответы через несколько недель.
(Нажмите на изображение, чтобы увидеть его в большем размере.
)
Несколько непоследовательных чисел
Далее мы используем некоторые непоследовательные значения . На следующем рисунке синий цвет используется для чисел, кратных , а зеленый — для чисел, кратных .
(Нажмите на изображение, чтобы увеличить его.)
Основные строительные блоки теперь будут состоять из маленьких квадратов, как и наименьшее общее кратное для и . Тем не менее дополнительные симметрии внутри девяти квадратов, составляющих повторяющиеся квадраты, могут стать приятным сюрпризом. Можете ли вы найти им математическое объяснение?
Вот еще несколько узоров, которыми вы можете полюбоваться. В каждом случае мы окрашиваем кратные непоследовательные числа. Можете ли вы сказать, что это за числа, и описать закономерности, которые возникают? Помните, что вы можете опубликовать свои ответы в поле для комментариев ниже, и если вы не сможете их решить, мы опубликуем ответы через несколько недель.
(Нажмите на изображение, чтобы увидеть его в большем размере.
)
Остатки
Наконец, если мы зафиксируем число и зададим цвета ячейкам в зависимости от их остатка относительно , то все квадраты могут быть заполнены. Например, пусть кратные будут черными, числа с остатком относительно будут зеленый, числа с остатком по отношению к красному, числа с остатком по отношению к фиолетовому и числа с остатком по отношению к желтому; получается следующая цифра.:
(Нажмите на изображение, чтобы увеличить его)
Заключение
Мы обнаружили некоторые симметрии, которые скрываются в таблице умножения положительных целых чисел.
Эти закономерности легко создавать (например, с помощью Excel), и все их можно без особого труда объяснить, используя арифметику целых чисел и критерии делимости. Отображение этих симметрий с помощью цветов представляет новый аспект математики. Эти и другие изображения, созданные аналогичным образом, могут понравиться студентам, изучающим математику и искусство, и могут привести к новому сотрудничеству.