Петерсон магические квадраты 2 класс: ГДЗ учебник по математике 2 класс Петерсон. Урок 32. Вычитание трехзначных чисел: 231
Заполните магический квадрат демидова 2 класс :: iradpepbolg
4 так чтобы в любой строке сумма чисел была равна 0, а в любом столбце отрицательному числу, плиз. Решебник по математике 3 класс Демидова Козлова Тонких 1, 2, 3 часть 2013Также его используют для того, чтобы хорошо подготовиться к экзаменам, заполнить пробелы в знаниях и подтянуть нужные темы. Во всех сторонах 2 квадрата должно быть тоже 340. Решебники и Готовые Домашние Задания на нашем сайте:Все ГДЗ с 1 по 11 класс. Насколько я понимаю, магический квадратэто, когда сумма всех чисел по вертикалям, горизонталям и диагоналям одинакова. Теги: школа, учебник, тонких, математика, козлова, демидова, 3 часть, 3 класс, 2 часть, 1 часть.
Или квадрат не будет решен по вертикали, горизонтали и диагонали. Предыдущая публикация Дама сдавала в багаж: после 2 я часть А вот создатели учебника русского языка Школы 20 для 3 класса знают, как именно могло. Для учителей и классов проводятся специализированные семинары и консультации, в рамках которых обсуждается рекомендованная для детского чтения литература, происходит ознакомление с новинками и последними исследованиями. Он делится на 3 уровня: материальный, души и разума. Заполните магический квадрат.работайте в тетради.демидова 2 класс. Детали. Это пример страницы. Берём первый квадрат. Часть 2005. Как решить магический квадратПродолжительность: Так тут же 2 нечетных, а лишнее должно быть одно. Этом от куда то знает.
Довольно активно используется в начальной школе. Научить заполнять магические квадраты.2. Развивать. Помогут заполнить квадрат еще с меньшим чисел, вписанных в квадрат. Остальные элементы построчно заполню порядковыми целыми числами. Магические квадраты. Сумма чисел по любому направлению одинакова. Итак составим уравнение при решении магического квадрата 1. Вернуться в Математика 3 класс. Я так понимаю здесь опечатка. Ресурс: Заполни пропуски в магическом квадрате . ГДЗ 3 класс Математика Демидова. Математика Петерсон, часть 2Блог Лукина Леонида. Математика, 2 класс Ф. М. Ривкинд, Л. В. Оляницка 2013. Демидова Математика 2 Класс Решебник.8 Урок 2.28 Сложение и вычитание чисел МАТЕМАТИКА Заполните магический квадрат.
Вместе с Заполните магический квадрат демидова 2 класс часто ищут
как решать магический квадрат
математика 2 класс магический квадрат
как решить магический квадрат 4 класс
заполните магические квадраты работайте в тетради
заполните магические квадраты 4 класс 170 240
волшебный квадрат математика
магический квадрат 3х3 3 класс
магические квадраты для детей
Читайте также:
Гдз по строению легких в картинках класс
Гдз по алгебре 10 11 класс 2006 год алимов
Решебник з 7 класс атанасян рабочая тетрадь онлайн
Занятие математического кружка (5—6-й классы).
Тема: “Математические модели-головоломки. “Магический” квадрат”- Аверина Елена Юрьевна, учитель математики
Разделы: Математика, Внеклассная работа
Занятие построено на основе проектной работы “Математические модели-головоломки” (автор Баженов Андрей, 5 “Д” класс, руководитель Аверина Е. Ю.). Данная работа участвовала в VIII-й Ученической научно-практической конференции (УНПК), которая проходила в 2006 году в ОЦ под девизом “Я могу изменить мир!”.
Традиционно завершающим этапом УНПК является
защита проектов, над которыми в течение учебного
года работают учащиеся ОЦ под руководством
учителей. В Ученическую научно-практическую
конференцию включаются лекции, дискуссии,
семинары, мастер-классы, посвящённые научным
проблемам естествознания, истории, математики.
Эти мероприятия проводятся силами учащихся под
руководством Координационного Совета учителей,
а также научных сотрудников ОАО “Газпром”,
преподавателей РГУ Нефти и газа, ведущих вузов
Москвы.
Увлекательная работа над проектами и их защита становится для большинства ребят серьёзным испытанием, проверкой их эрудиции, компетентности в серьёзных научных вопросах, способности дискутировать, отстаивать свою точку зрения, вести научный диалог. Кроме того, очень важно, что эта деятельность является для учащихся ступенькой во взрослую жизнь, требующую определенных навыков публичных выступлений и успешного коммуникативного опыта.
В начале учебного года передо мной, как
руководителем проектной деятельности, и
учеником 5 класса, моим подопечным, возникла
проблема выбора темы научно-исследовательской
работы. Эту ситуацию обуславливал слишком юный
возраст участника конференции – 10 лет. Но
желание выпускника начальной школы открыть для
себя математику не только как школьную науку, а
увидеть ее с необычной, увлекательной,
загадочной стороны было велико.
После защиты на УНПК проект стал победителем в номинации “Лучший математический проект”. Следующей ступенькой в популяризации научных знаний явились занятия математического кружка, посвященные “магическим” квадратам, ленте Мебиуса, сечению Даданея. В подготовке и проведении занятий принял активное участие автор проекта Баженов Андрей. Учащиеся 5 – 6 классов, проявляющие интерес к математике, с удовольствием включались в различные виды учебно-познавательной активности, предложенные им во время занятий.
Подобная форма работы, на мой взгляд, повысила
мотивацию детей к учебной деятельности по
предмету.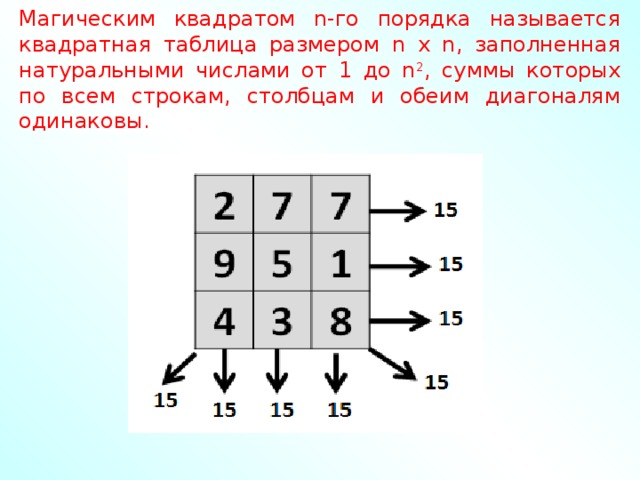
Ведь они смогли лично убедиться в
практической ценности математических знаний.
Все это побудило меня поделиться опытом
внеклассной работы по математике с коллегами.
| Этап занятия. | Деятельность учителя, ученика-консультанта | Деятельность учащихся | Формы работы | Методы работы |
| Подготовка к
познавательной деятельности. |
Объявление учителем
темы занятия: “Математические модели –
головоломки. “Магический” квадрат”. (на доске-плакат с названием темы) Представление ученика-консультанта, который является автором проекта. Вступительное слово ученика-консультанта: Мой любимый предмет – математика. Во время работы над проектом мне удалось разобраться в некоторых математических головоломках и заинтересовать своих товарищей. Занятие кружка будет посвящено “магическому” квадрату- головоломке, которая была исследована в процессе работы над проектом “Математические модели – головоломки”. Постановка учителем целей занятия. (на доске-плакат с целями занятия) Ознакомиться: с историей возникновения “магических” (“волшебных”) квадратов;[2,3] Научиться: составлять “волшебные квадраты” четного и нечетного порядка; Изучить: свойства сумм чисел на модели “волшебной”
рамки. |
Ознакомление с темой и целями занятия. | Фронтально | Репродуктивный |
| Изучение нового материала. | Учитель предлагает ученикам самостоятельно составить “магические” квадраты нечетного 3х3 и четного 4х4 порядков, используя первые 9,16 натуральных чисел. Обращается внимание на необходимость поиска метода составления “магического” квадрата. Учитель для подведения итогов работы предлагает ученикам, которые успешно справились с этим заданием рассказать о методах составления “магического” квадрата. Ученик-консультант знакомит учащихся с
методами составления “магических” квадратов,
которые описаны в книге [2]. Используется компьютерная презентация МАТЕМАТИЧЕСКИЕ ГОЛОВОЛОМКИ-2.ppt Учитель предлагает исследовать свойства сумм чисел на модели “волшебной” рамки. Если “ волшебный” квадрат 4х4 обернуть вокруг квадратной рамки, свойства получившейся модели станут еще интереснее. (См. развертку и модель рамки –Рисунок-1.jpg, Рисунок-2.jpg [1] Учитель для подведения итогов работы предлагает парам учеников, которые успешно справились с этим заданием, перечислить полученные свойства (желательно заслушать каждую пару). В конце обсуждения на доске вывешивается плакат с перечислением свойств рамки. суммы четырех чисел вокруг рамки в любом направлении равны 34 сумма четырех чисел, которые встречаются в каждом углу с внешней и в каждом углу с внутренней стороны также равна 34 сумма четырех чисел одного цвета – 34 если складывать числа по спирали по часовой
стрелке или против часовой стрелки вокруг рамки,
начав в любом месте – 34. Ну, как? И вправду волшебная рамка! |
Ознакомление с историей возникновения
“магических” (“волшебных”) квадратов. Составление “магических” квадратов 3х3,4х4 на готовых планшетках. “Авторские” методы составления “магических” квадратов. Ознакомление с методами составления “магических” квадратов, которые изучены автором проекта. Составление “магических” квадратов с помощью указанного метода. Исследование свойств сумм чисел на модели “волшебной” рамки (по готовым моделям).
Выступление каждой группы с результатами работы. |
Фронтально Индивидуально Фронтально Фронтально Индивидуально В парах |
Репродуктивный Поисковый Репродуктивный Репродуктивный Репродуктивный Поисковый |
Первичная проверка. |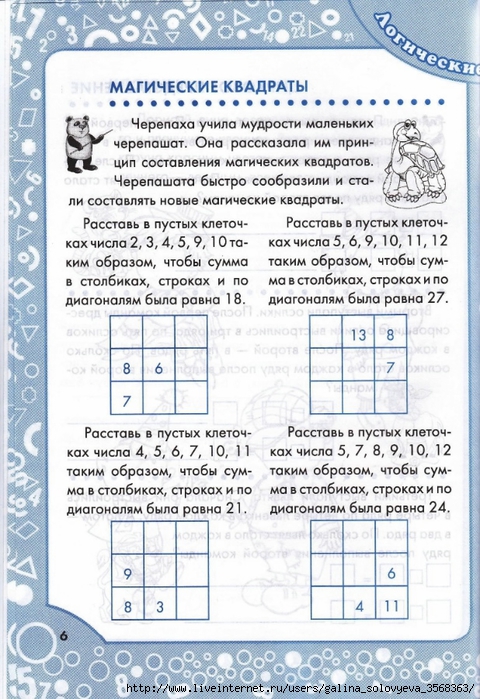
Учитель предлагает учащимся
задания:(карточка с заданием раздается каждому
ученику) 1. Заменить рисунок слайда 12 магическим квадратом, выписать свойства сумм чисел. 2. Составить магический квадрат 4х4, используя метод, изученный на занятии. Проверка заданий осуществляется в парах, которые формируются по мере его выполнения. |
Выполнение заданий. Взаимопроверка. |
Индивидуально В парах |
Частично-поисковый Репродуктивный |
| Итог занятия. | Учитель предлагает проанализировать выполнение целей занятия, подвести итог. | Анализ выполнения целей занятия. | Фронтально | Репродуктивный |
Интересные
задачи и их решения увлекают меня. Но на уроках
математики в школе мы решаем мало занимательных
задач, головоломок, ребусов. Мне хотелось
подробнее познакомиться с различными
математическими головоломками, решить
интересные задачи, своими руками изготовить
модели.
Литература:
- Дж.
Джекинс, М.Биар, Математические головоломки:
Пер. с англ.-М.; Центрполиграф, 1997 - Б.А.Кордемский, Математическая смекалка, – Ф.М., 1963
- Г.В.Дорофеев, Л.Г.Петерсон, Математика М,: Ювента-Просвещение, 2002
Джекинс, М.Биар, Математические головоломки:
Пер. с англ.-М.; Центрполиграф, 19972, считая до поворотов и отражений.
(ранее M5482)
| 1, 0, 1, 880, 275305224 (список; график; ссылки; слушать; история; текст; внутренний формат) |
| КОМПЕНСИРОВАТЬ | 1,4 | |
| КОММЕНТАРИИ | a(4), вычисленный Френиклем де Бесси (1605 ? – 1675), опубликованный в 1693 г. a(5) вычислено Ричардом К. Шреппелем в 1973 году. 920. — Р. К. Гай, 01 мая 2004 г. | |
| ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА | Э. Р. Берлекамп, Дж. Х. Конвей и Р. К. Гай, Winning Ways, Vol. II, стр. 778-783 дает 880 4 X 4 квадратов. М. Гарднер, Математические игры, науч. амер. М. Гарднер, Путешествие во времени и другие математические заблуждения. Фриман, Нью-Йорк, 1988, с. 216. Н. Дж. А. Слоан и Саймон Плуфф, Энциклопедия целочисленных последовательностей, Academic Press, 1995 (включает эту последовательность). | |
| ССЫЛКИ | Таблица n, a(n) для n=1..5. Ян Кэмерон, Адам Роджерс и Питер Лоли, «Библиотека магических квадратов» — краткое изложение основных результатов для энтропии Шеннона магических и латинских квадратов: изоэнтропические кланы и индексация, в честь 75-летия Джорджа Стиана. Frenicle de Bessy, Des carrez ou table magiques, Divers ouvrages de mathématique et de physique (1693), стр. 423–483. Френикль де Бесси, Table générale des carrez de quatre, Divers ouvrages de mathématique et de physique (1693), стр. 484-503. Скайлар Р. Крой, Джереми А. Хансен и Дэниел Дж. Маккуиллан, Расчет количества магических квадратов порядка 6 с помощью модульного подъема, Труды Девятого международного симпозиума по комбинаторному поиску (SoCS 2016). Махади Хасан, доктор медицины Масбаул Алам Полаш, Эффективный локальный поиск на основе ограничений для максимального удержания воды на магических квадратах, Новые тенденции в области электротехники, связи и информационных технологий, Конспект лекций по серии книг по электротехнике (LNEE 2019) Vol. И. Петерсон, Magic Tesseracts [Ссылка не работает?] К. Пинн и К. Вецерковски, Количество магических квадратов из параллельного темперирования Монте-Карло, Междунар. J. Современная физика, 9(4) (1998) 541-546. Артем Рипатти, О числе полумагических квадратов 6-го порядка, arXiv:1807.02983 [math.CO], 2018. См. табл. 1 с. 2. Р. Шреппель, электронные письма в NJA Sloane, июнь 1991 г. Н. Дж. А. Слоан и Дж. Р. Хендрикс, переписка, 1974 г. Мир математики Эрика Вайсштейна, Волшебный квадрат Записи указателя для последовательностей, связанных с магическими квадратами | |
| ПРИМЕР | Иллюстрация уникального (с точностью до поворотов и отражений) магического квадрата 3-го порядка: +—+—+—+ | 2 | 7 | 6 | +—+—+—+ | 9 | 5 | 1 | +—+—+—+ | 4 | 3 | 8 | +—+—+—+ | |
| ПЕРЕКРЕСТНЫЕ ССЫЛКИ | См. Последовательность в контексте: A206341 A357495 A024393 * A105976 A340342 A265181 Смежные последовательности: A006049А006050 А006051 * А006053 А006054 А006055 | |
| КЛЮЧЕВОЕ СЛОВО | нонн,жесткий,красивый,больше | |
| АВТОР | Н. | |
| РАСШИРЕНИЯ | Определение исправлено Максом Алексеевым, 25 декабря 2015 г. | |
| ПОЛОЖЕНИЕ ДЕЛ | утвержден |
В статье упоминаются 880 квадратов, а также рассматриваются 5*5, 6*6, 8*8 и другие квадраты. – Пол Керц, 13 июля и 12 августа 2011 г.
Том. 249 (№ 1, 1976), с. 118.
569, 71-79.
А270876, А271103, А271104.
Дж. А. СлоанРабочий лист вероятности и комбинаций – Google Suce
ALLBILDERVIDEOSBüchermapmApsNewshopping
SUCOPTIONEN
Урок.
вероятность события путем расчета количества исходов с использованием комбинаций.
Рабочий лист для урока: Использование перестановок для определения вероятности – Nagwa
www.nagwa.com › рабочие листы
В этом рабочем листе мы потренируемся находить вероятность события, вычисляя количество исходов с помощью перестановки.
[PDF] Вероятность с комбинаторикой – Kuta Software
cdn.kutasoftware.com › Рабочие листы › Alg2 › Вероятность с комби…
Рабочий лист от Kuta Software LLC. Kuta Software – Infinite Algebra 2 … Найдите вероятность каждого события. … есть вероятность, что и Бет, и Шайна.
Таблицы вероятностей комбинаций
www.easyteacherworksheets.com › статистика комбинаций
Мы используем формулу комбинаций, чтобы найти вероятность после выбора более чем одного элемента. Комбинация — это способы r элементов из множества n, и вы будете обозначать …
[PDF] УРОК 15.12 ПЕРЕСТАНОВКИ, КОМБИНАЦИИ И.
..
www.iroquoiscsd.org › lib › Domain › CN__121_LESSON_15. 12.PDF
Сколько различных групп по 4 человека возможно? Решение При выборе группы из 4 студентов из 7 порядок не важен. Поэтому используйте комбинации.
[PDF] Рабочий лист перестановок и комбинаций – Mr. C. Miller
mrcmiller.weebly.com › загрузки › permutation_and_combination_wo…
Рабочий лист перестановок и комбинаций. Оцените каждую перестановку или комбинацию (вы должны показать установку): 1. 7P3. 2. 7П4. 3. 7П7.
Рабочие листы – г-н Казалинуово – Сайты Google
site.google.com › тригонометрия-tri-1 › вероятность
Комбинация против перестановки Рабочий лист 2 .pdf … Комбинации и перестановки Рабочий лист 4.pdf … Комбинации и перестановки Рабочий лист 3 ОТВЕТЫ.pdf.
[PDF] Таблица перестановок и комбинаций KEY
mi01000971.schoolwires.net › cms › lib › Centricity › Domain › Per…
Алгебра 2 с отличием.