Онлайн калькулятор круги эйлера: Диаграммы Эйлера-Венна онлайн

Таблица истинности онлайн

Назначение сервиса. Онлайн-калькулятор предназначен для построения таблицы истинности для логического выражения.
Таблица истинности – таблица содержащая все возможные комбинации входных переменных и соответствующее им значения на выходе.
Таблица истинности содержит 2ⁿ строк, где n – число входных переменных, и n+m – столбцы, где m – выходные переменные.

• Решение онлайн
• Видеоинструкция

Инструкция. При вводе с клавиатуры используйте следующие обозначения:

Клавиша	Оператор
!	¬	Отрицание (НЕ)
|	|	Штрих Шеффера (И-НЕ)
#	↓	Стрелка Пирса (ИЛИ-НЕ)
*	&	Конъюнкция (И)
+	v	Дизъюнкция (ИЛИ)
^	⊕	Исключающее ИЛИ, сумма по модулю 2 (XOR)
@	→	Импликация (ЕСЛИ-ТО)
%	←	Обратная импликация
=	≡ (~, ↔)	Эквивалентность (РАВНО)

Логическое выражение: Вывод промежуточных таблиц для таблицы истинности
Построение СКНФ
Построение СДНФ
Построение полинома Жегалкина
Построение карты Вейча-Карно
Минимизация булевой функции методом Квайна

Например, логическое выражение abc+ab~c+a~bc необходимо ввести так: a*b*c+a*b=c+a=b*c
Для ввода данных в виде логической схемы используйте этот сервис. y).

Максимальное количество переменных равно 10.

Проектирование и анализ логических схем ЭВМ ведётся с помощью специального раздела математики – алгебры логики. В алгебре логики можно выделить три основные логические функции: “НЕ” (отрицание), “И” (конъюнкция), “ИЛИ” (дизъюнкция).
Для создания любого логического устройства необходимо определить зависимость каждой из выходных переменных от действующих входных переменных такая зависимость называется переключательной функцией или функцией алгебры логики.
Функция алгебры логики называется полностью определённой если заданы все 2ⁿ её значения, где n – число выходных переменных.
Если определены не все значения, функция называется частично определённой.
Устройство называется логическим, если его состояние описывается с помощью функции алгебры логики.
Для представления функции алгебры логики используется следующие способы:

• словесное описание – это форма, которая используется на начальном этапе проектирования имеет условное представление.
• описание функции алгебры логики в виде таблицы истинности.
• описание функции алгебры логики в виде алгебраического выражения: используется две алгебраические формы ФАЛ:
  а) ДНФ – дизъюнктивная нормальная форма – это логическая сумма элементарных логических произведений. ДНФ получается из таблицы истинности по следующему алгоритму или правилу:
  1) в таблице выбираются те строки переменных для которых функция на выходе =1.
  2) для каждой строки переменных записывается логическое произведение; причём переменные =0 записываются с инверсией.
  3) полученное произведение логически суммируется.
  Fднф= X₁*Х₂*Х₃ ∨ Х₁x₂Х₃ ∨ Х₁Х₂x₃ ∨ Х₁Х₂Х₃
  ДНФ называется совершенной, если все переменные имеют одинаковый ранг или порядок, т.е. в каждое произведение обязательно должны включаться все переменные в прямом или инверсном виде.
  б) КНФ – конъюнктивная нормальна форма – это логическое произведение элементарных логических сумм.
  КНФ может быть получена из таблицы истинности по следующему алгоритму:
  1) выбираем наборы переменных для которых функция на выходе =0
  2) для каждого набора переменных записываем элементарную логическую сумму, причём переменные =1 записываются с инверсией.
  3) логически перемножаются полученные суммы.
  Fскнф=(X₁ V X₂ V X₃) ∧ (X₁ V X₂ V X₃) ∧ (X₁ V X₂ V X₃) ∧ (X₁ V X₂ V X₃)
  КНФ называется совершенной
  , если все переменные имеют одинаковый ранг.

По алгебраической форме можно построить схему логического устройства, используя логические элементы.

Рисунок1- Схема логического устройства

Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении. Если число высказываний в логическом выражении N, то таблица истинности будет содержать 2^N строк, так как существует 2^N различных комбинаций возможных значений аргументов.

Операция НЕ — логическое отрицание (инверсия)

Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть и простое, и сложное логическое выражение. Результатом операции НЕ является следующее:

• если исходное выражение истинно, то результат его отрицания будет ложным;
• если исходное выражение ложно, то результат его отрицания будет истинным.

Для операции отрицания НЕ приняты следующие условные обозначения:
не А, Ā, not A, ¬А, !A
Результат операции отрицания НЕ определяется следующей таблицей истинности:

A	не А
0	1
1	0

Результат операции отрицания истинен, когда исходное высказывание ложно, и наоборот.

Операция ИЛИ — логическое сложение (дизъюнкция, объединение)

Логическая операция ИЛИ выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и сложное логическое выражение. Высказывания, являющиеся исходными для логической операции, называют аргументами. Результатом операции ИЛИ является выражение, которое будет истинным тогда и только тогда, когда истинно будет хотя бы одно из исходных выражений.
Применяемые обозначения: А или В, А V В, A or B, A||B.
Результат операции ИЛИ определяется следующей таблицей истинности:

A	B	А или B
0	0	0
0	1	1
1	0	1
1	1	1

Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложен тогда, когда аргументы А и В — ложны.

Операция И — логическое умножение (конъюнкция)

Логическая операция И выполняет функцию пересечения двух высказываний (аргументов), в качестве которых может быть и простое, и сложное логическое выражение. Результатом операции И является выражение, которое будет истинным тогда и только тогда, когда истинны оба исходных выражения.
Применяемые обозначения: А и В, А Λ В, A & B, A and B.
Результат операции И определяется следующей таблицей истинности:

A	B	А и B
0	0	0
0	1	0
1	0	0
1	1	1

Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях.

Операция «ЕСЛИ-ТО» — логическое следование (импликация)

Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия.
Применяемые обозначения:
если А, то В; А влечет В; if A then В; А→ В.
Таблица истинности:

A	B	А → B
0	0	1
0	1	1
1	0	0
1	1	1

Результат операции следования (импликации) ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.

Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)

Применяемое обозначение: А ↔ В, А ~ В.
Таблица истинности:

A	B	А↔B
0	0	1
0	1	0
1	0	0
1	1	1

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

Операция «Сложение по модулю 2» (XOR,

исключающее или, строгая дизъюнкция) Применяемое обозначение: А XOR В, А ⊕ В.
Таблица истинности:

A	B	А⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны.

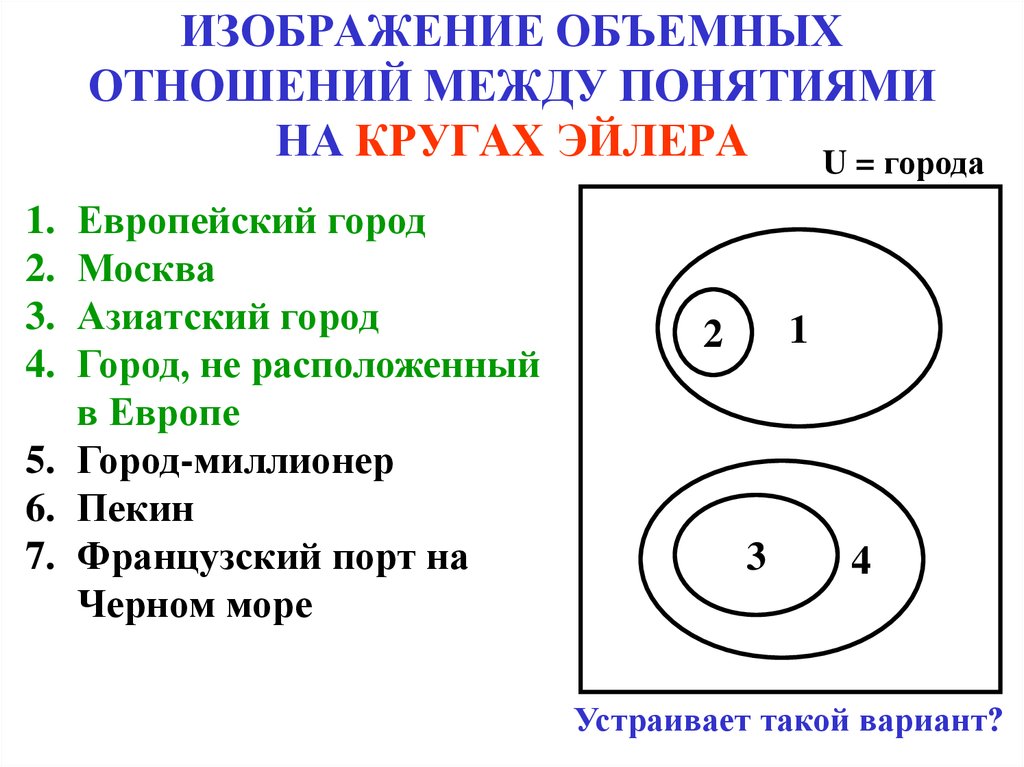
Приоритет логических операций

• Действия в скобках
• Инверсия
• Конъюнкция ( & )
• Дизъюнкция ( V ), Исключающее ИЛИ (XOR), сумма по модулю 2
• Импликация ( → )
• Эквивалентность ( ↔ )

Совершенная дизъюнктивная нормальная форма

Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:

1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x₁,x₂,…x_n).
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое не содержит переменную и её отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

СДНФ можно получить или с помощью таблиц истинности или с помощью равносильных преобразований.
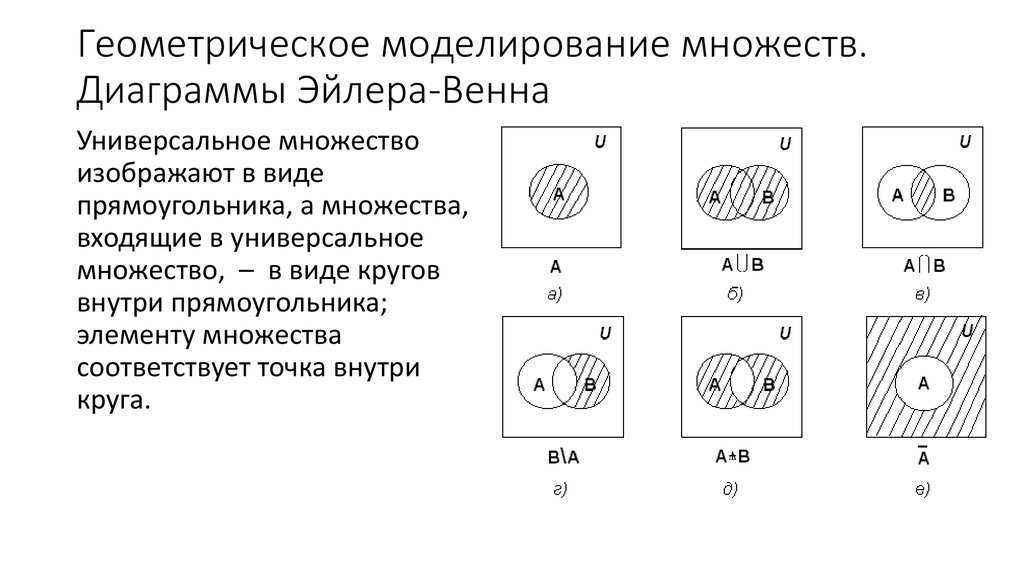
Для каждой функции СДНФ и СКНФ определены единственным образом с точностью до перестановки.

Совершенная конъюнктивная нормальная форма

Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:

1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x₁,x₂,…x_n).
2. Все элементарные дизъюнкции различны.
3. Каждая элементарная дизъюнкция содержит переменную один раз.
4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание.

Формула Пуассона онлайн

Закон Пуассона , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828.

Ряд распределения закона Пуассона имеет вид:

X	0	1	2	…	m	…
P	e-λ	λe-λ		…		…

Назначение сервиса. 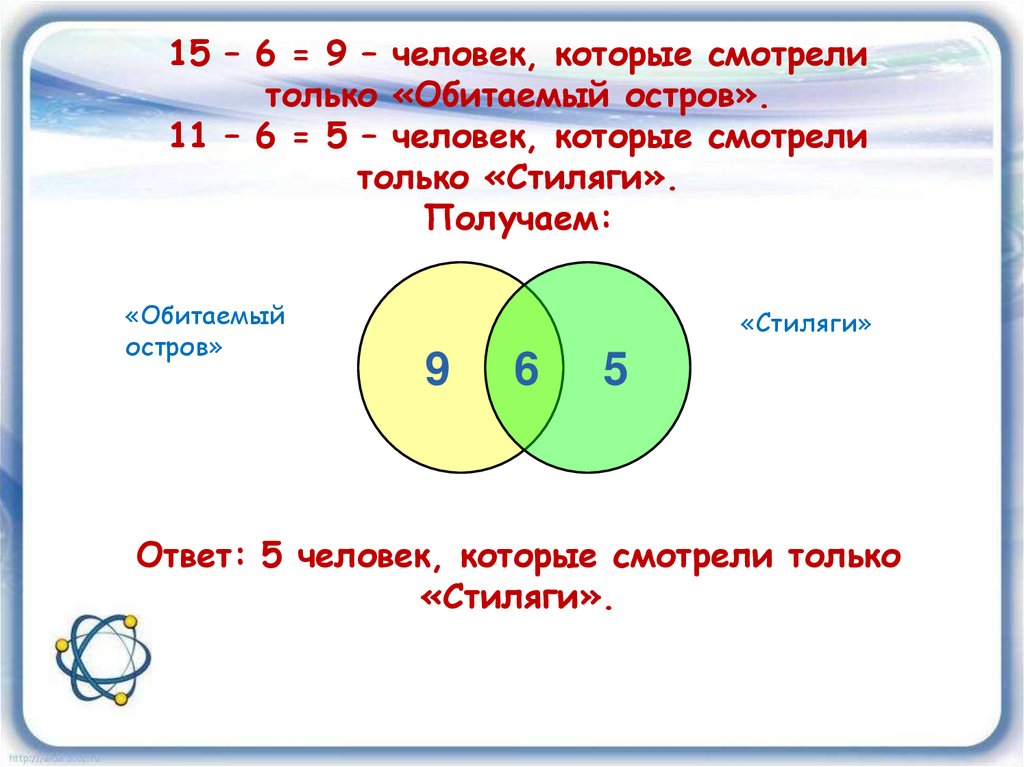Онлайн-калькулятор используется для построения Пуассоновского распределения и вычисления всех характеристик ряда: математического ожидания, дисперсии и среднеквадратического отклонения. Отчет с решением оформляется в формате Word.

• Решение онлайн
• Видеоинструкция

Число испытаний: n = , Вероятность p =
Вычислить вероятность для: m =
наступит раз
менее раз
не менее раз
более раз
не более раз
не менее и не более раз
наступит хотя бы один раз

В случае, когда n велико, а λ = p·n > 10 формула Пуассона дает очень грубое приближение и для расчета P_n(m) используют локальную и интегральную теоремы Муавра-Лапласа.

Математическое ожидание распределения Пуассона
M[X] = λ

Дисперсия распределения Пуассона
D[X] = λ

Пример №1.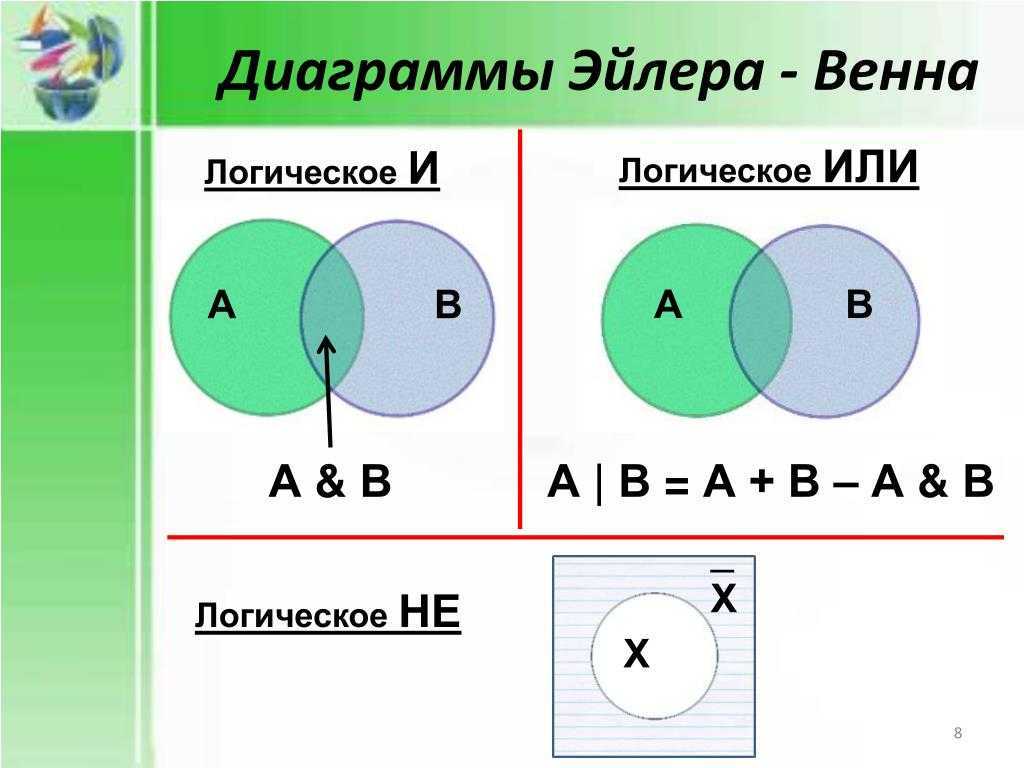 Семена содержат 0.1% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
Решение.
Вероятность р мала, а число n велико. np = 2 P(5) = λ⁵e^-5/5! = 0.03609
Математическое ожидание: M[X] = λ = 2
Дисперсия: D[X] = λ = 2

Пример №2. Среди семян ржи имеется 0.4% семян сорняков. Составить закон распределения числа сорняков при случайном отборе 5000 семян. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Математическое ожидание: M[X] = λ = 0.004*5000 = 20. Дисперсия: D[X] = λ = 20
Закон распределения:

X	0	1	2	…	m	…
P	e-20	20e-20	200e-20	…	20me-20/m!	…

Пример №3. На телефонной станции неправильное соединение происходит с вероятностью 1/200. Найдите вероятность того, что среди 200 соединений произойдет:
а) ровно одно неправильное соединение;
б) меньше чем три неправильных соединения;
в) больше чем два неправильных соединения.
Решение. По условию задачи вероятность события мала, поэтому используем формулу Пуассона (15).
а) Задано: n = 200, p = 1/200, k = 1. Найдем P₂₀₀(1).
Получаем: . Тогда P₂₀₀(1) ≈ e^-1≈ 0,3679.
б) Задано: n = 200, p = 1/200, k < 3. Найдем P₂₀₀(k < 3).
Имеем: a = 1.

в) Задано: n = 200, p = 1/200, k > 2. Найдем P₂₀₀(k > 2).
Эту задачу можно решить проще: найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем
P₂₀₀(k>2) = 1-P₂₀₀(k≤2) = 1-P₂₀₀(kРассмотрим случай, когда n является достаточно большим, а p — достаточно малым; положим np = a, где a — некоторое число. В этом случае искомая вероятность определяется формулой Пуассона:

Вероятность появления k событий за время длительностью t можно также найти по формуле Пуассона:
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.

Пример №4. Вероятность того, что деталь бракованная, равна 0.005. проверяется 400 деталей. Укажите формулу вычисления вероятности того, что больше 3 деталей оказались с браком.

Пример №5. Вероятность появления бракованных деталей при их массовом производстве равна p. определить вероятность того, что в партии из N деталей содержится а) ровно три детали; б) не более трех бракованных деталей.
p=0,001; N = 4500
Решение.
Вероятность р мала, а число n велико. np = 4.5 < 10. Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон.
Случайная величина X имеет область значений (0,1,2,… ,m). Вероятности этих значений можно найти по формуле:

Найдем ряд распределения X.
Здесь λ = np = 4500*0.001 = 4.5
P(0) = e^{– λ} = e^-4.5 = 0.01111
P(1) = λe^-λ = 4.5e^-4.5 = 0.04999

Тогда вероятность того, что в партии из N деталей содержится ровно три детали, равна:

Тогда вероятность того, что в партии из N деталей содержится не более трех бракованных деталей:
P(x<3) = P(0) + P(1) + P(2) = 0,01111 + 0,04999 + 0,1125 = 0,1736

Пример №6. Автоматическая телефонная станция получает в среднем за час N вызовов. Определить вероятность того, что за данную минуту она получит: а) ровно два вызова; б) более двух вызовов.
N = 18
Решение.
За одну минуту АТС в среднем получает λ = 18/60 мин. = 0,3
Считая, что случайное число X вызовов, поступивших на АТС за одну минуту,
подчиняется закону Пуассона, по формуле найдем искомую вероятность

Найдем ряд распределения X.
Здесь λ = 0.3
P(0) = e^{– λ} = e^-0.3 = 0.7408
P(1) = λe^-λ = 0.3e^-0.3 = 0.2222

Вероятность того, что за данную минуту она получит ровно два вызова:
P(2) = 0,03334
Вероятность того, что за данную минуту она получит более двух вызовов:
P(x>2) = 1 – 0,7408 – 0,2222 – 0,03334 = 0,00366

Пример №7. Рассматриваются два элемента, работающих независимо друг от друга. Продолжительность времени безотказной работы имеет показательное распределение с параметром λ1 = 0,02 для первого элемента и λ2 = 0,05 для второго элемента. Найти вероятность того, что за 10 часов: а) оба элемента будут работать безотказно; б) только Вероятность того, что за 10 часов элемент №1 не выйдет из строя:
Рещение.
P₁(0) = e^-λ1*t = e^-0.02*10 = 0,8187

Вероятность того, что за 10 часов элемент №2 не выйдет из строя:
P₂(0) = e^-λ2*t = e^{-0. 05*10} = 0,6065

а) оба элемента будут работать безотказно;
P(2) = P₁(0)*P₂(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P₁(0)*(1-P₂(0)) + (1-P₁(0))*P₂(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321

Пример №7. Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не больше 17?
Примечание: поскольку здесь n*p=1100*0.01=11 > 10, то необходимо использовать теорему Лапласа.

Формула Эйлера и калькулятор тождеств Эйлера

Ниже приведен калькулятор и интерактивный график, который позволяет вам исследовать концепции, лежащие в основе знаменитой и необычной формулы Эйлера:

e ^iθ = cos( θ ) + i sin( θ )

Когда мы устанавливаем θ = π, мы получаем классическое Тождество Эйлера:

e ^iπ + 1 = 0

Формула Эйлера используется во многих областях науки и техники. Это очень удобное тождество в математике, так как оно может значительно упростить выполнение многих вычислений, особенно связанных с тригонометрией. Мы видели часть этой концепции в произведениях и частных комплексных чисел ранее.

Леонард Эйлер был блестящим и плодовитым швейцарским математиком, чей вклад в физику, астрономию, логику и инженерию был неоценим. Он, безусловно, был одним из величайших математиков в истории. 9п

И формулу, и тождество можно использовать для выполнения вычислений, а также для графических функций. Калькулятор можно использовать для ввода комплексного числа и вычисления различных степеней этого числа, а также для построения графика функции. График можно увеличить или уменьшить, а комплексное число можно изменить, чтобы увидеть, как оно влияет на график.

Формула Эйлера и тождество очень полезны в математике и технике, поскольку они могут значительно упростить выполнение многих вычислений. Попробуйте поиграть с калькулятором и графиком, чтобы увидеть, что вы можете обнаружить!

Формула Эйлера, калькулятор тождества и график

На следующем графике реальная ось (обозначенная «Re») горизонтальна, а воображаемая ось (`j=sqrt(-1)`, обозначенная «Im») вертикальна, как обычно. У нас есть единичная окружность , и мы можем варьировать угол, образованный отрезком OP.

Точка P представляет комплексное число. Угол θ , разумеется, в радианах.

Чем заняться

1. Выберите, будут ли ваши углы выражаться десятичными знаками или числами, кратными π.
2. Выберите i или j в качестве символа мнимого числа. (Во многих учебниках используется и для символа мнимого числа, но в IntMath, как и во многих инженерных учебниках, используется j , чтобы попытаться уменьшить путаницу с символом тока в электронике.)
3. Вы можете перетащить точку P , чтобы изменить угол θ.
4. Когда вы установите θ = π, вы увидите (эквивалент) Тождество Эйлера: e ^iπ = − 1

Углы: кратные π

Мнимый символ: i j

Формула Эйлера

Прямоугольный и полярный эквиваленты

Некоторая справочная информация о том, что происходит, и дополнительные пояснения см. на предыдущих страницах,

Комплексные числа и полярная форма комплексного числа

См. также калькулятор полярного преобразования в прямоугольное и прямоугольного в полярное, на котором основано приведенное выше:

Онлайн-калькулятор полярных координат в прямоугольные

Комплексная экспоненциальная форма

В математике комплексная экспоненциальная функция — это функция вида f(z) = ea(z), где z — комплексное число, а a — произвольная комплексная константа. Функция целая, что означает, что она определена и дифференцируема для всех комплексных чисел z. В отличие от вещественно-показательных функций сложные показательные функции не являются взаимно однозначными; то есть два разных комплексных числа могут иметь одинаковый образ под функцией. 9{-би}.

Сложные функции

Комплексная функция — это функция вида f(z) = u(x, y) + iv(x, y), где z = x + iy — комплексная переменная, u и v — вещественнозначные функции две действительные переменные x и y, а i — мнимая единица измерения. В этой статье будут рассмотрены некоторые свойства сложных функций с упором на формулу Эйлера и тождество Эйлера.

Сложные функции имеют множество приложений в физике и технике, а также в чистой математике. В физике они используются для моделирования волновых явлений, а в технике — для проектирования электрических цепей. В чистой математике они изучаются сами по себе как красивые и интригующие объекты. 9(i*pi) + 1 = 0. Это уравнение важно, поскольку оно связывает вместе пять наиболее важных чисел в математике: e, pi, i, 1 и 0.

Дифференциальные уравнения чрезвычайно полезны в математическом моделировании и находят применение в самых разных областях, от физики до экономики. Следовательно, они являются важным инструментом для понимания и прогнозирования изменений.

Если у вас есть твердое понимание формулы Эйлера и тождества Эйлера, вы можете относительно легко выполнять широкий спектр вычислений. Это делает формулу бесценным инструментом для математиков, инженеров и других ученых.