Объяснение как писать цифру 6: “Число и цифра 6. Написание числа 6. “ – Всё о детях – беременность, воспитание, уроки для детей

Содержание

“Число и цифра 6. Написание числа 6. “

Цель: познакомить учащихся с новым числом 6 и соответствующей ему цифрой; формировать умения писать цифру 6; упражнять в сравнении чисел, составлении выражений на сложение в пределах 6 по предметным рисункам; закреплять знание состава числа 5. Развивать наблюдательность, зрительную и слуховую память, математическую речь, мыслительные операции у учащихся. Воспитывать культуру поведения, умение следить за ответом товарищей. Формировать здоровьесберегающую компетентность путём чередования различных видов деятельности и активного отдыха, создания комфортной и доверительной атмосферы в классе.

Тип урока: урок усвоения новых знаний.

ноутбук, электронная презентация, геометрические фигуры, индивидуальный набор цифр, образцы написания цифры 6, тетради с печ. основой, учебник, простой карандаш.

Слайд № 1

Организационный момент. 1. – Ребята, сегодня на нашем уроке присутствуют гости. Посмотрите, пожалуйста, на них. Поздоровайтесь.

Теперь глазки все на меня.
Встало солнышко давно, Заглянуло к нам в окно. На урок торопит нас, Математика сейчас.

2.Тренинг-настрой на урок.

– У вас хорошее настроение? – Радость, улыбка помогают нам жить, учиться и справляться с трудностями, быть здоровым. Ребята! Вы готовы помочь друг другу в преодолении трудностей? Тогда улыбнитесь друг другу. Поделитесь своим хорошим настроением. Я желаю вам успеха на уроке.

А теперь проверь, дружок: Ты готов начать урок? Все ль на месте, Все ль в порядке: Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят?

(обращение к Цветку порядка) Распускается1 лепесток

II. Актуализация знаний (развитие внимания, зрительной памяти)

– Посмотрите на доску. Как всё это можно назвать? Фигуры)

– Каким по счёту слева является ромб? (шестым)
– А справа, какая фигура является шестой? (треугольник)
– Какая фигура находится между кривой и квадратом? (круг)
– Какая фигура следует за треугольником? (ломаная)
– Какая фигура стоит перед кругом? (кривая)

– Сейчас я проверю, какие вы внимательные. Мы проведём игру на внимание «День-ночь». Запомните расположение фигур. Сфотографируйте глазками. Ночь (переставляю). День.

– Что изменилось?

Ночь (переставляю). День. – Что изменилось?
Ночь (переставляю). День. – Что изменилось? (появилась новая фигура)

– Как называется эта фигура? (шестиугольник)
– Почему вы так её назвали? (шесть углов)
– А ещё чего шесть в этой фигуре? (шесть сторон)

– Ребята, а для чего мы с вами выполняли это задание? – Продолжаем дальше учиться? Отвечайте хором. (Да).

III. «Открытие» нового знания, формулирование темы урока.
1.Разминка. (используем знак «ХОР»)
– Сколько углов у шестиугольника? (Шесть)
– Сколько звуков в слове задача? (Шесть)
-В корзине сидят котята. Но котят не видно, а видно 6 хвостиков. Сколько котят в корзине? (Шесть)
– Сколько глаз у 3 щенят? (Шесть)
— Что интересного вы заметили?
( В условии и ответе встречается слово шесть).
– Подумайте, что может это означать?
2. Определение темы урока.
Какова же сегодня тема урока? Выслушиваются ответы детей и выводится тема урока «Число и цифра 6». Слайд №2
(На слайде высвечивается тема урока).

4. Актуализация опорных знаний и постановка проблемы
– У вас имеется на парте набор цифр. Будете работать в парах. Работать надо дружно, сообща, не ссорясь. Слайд
1) Сосчитайте, сколько столов на рисунке и обозначьте их количество нужным числом. Положите карточку на середину парты. (1)
2) Сколько ящиков у тумбы? Найдите карточку с нужным числом. (4)
3) Сколько деток на поляне? Обозначьте нужным числом. (2)
4) Сколько зверят на лугу? Обозначьте их количество числом. (3)
5) Сколько шариков в небе? Положите карточку. (5)

– Молодцы. Вы были внимательные, не ошиблись.
– Посмотрите на числа. Что можете сказать? (стоят не по порядку)
– Измените последовательность так, чтобы они стояли по порядку. (1 2 3 4 5)
– Умницы. Можно ли продолжить этот ряд чисел? Какое число будет следующее? (6)
Слайд (познакомить с числом 6, развитие умения доказывать свою точку зрения).
– Посмотрите на доску. Здесь много разных знаков. Каким знаком можно обозначить число 6?
8 + 9 – < 6 VI ( на доске)
(1 ученик выбирает знак).
– А я бы выбрала вот этот знак 9. Посмотрите, он так похож, есть закругление и кружок.
– Как мне, ребята, запомнить знак цифры 6? (ответы детей)
– Найдите у себя на парте карточку с цифрой 6. Поверните её правильно.
– Посмотрите на свой числовой ряд. Куда мы поставим число 6?
– А никто не знает, есть ли ещё знак цифры 6?
– VI – вот этот знак – римская цифра 6.
– Ребята, а где мы уже сталкивались сегодня с числом 6? К чему новому привёл нас шестиугольник? Видите, какая замечательная фигура пришла к нам сегодня на урок!
Посмотрите на наш кабинет и назовите 6 предметов, находящихся в нём
Назовите 6 имен своих друзей

Где в жизни встречается число шесть?

V. Физкультминутка (рисуем цифры).

Работа по учебнику. (с. 26, № 2) Сравнения чисел.

Составление выражений на сложение в пределах 6 (Слайд)

– Откройте рабочие тетради на стр. 21
Я тетрадочку открою
И наклонно положу.
Я, друзья, от вас не скрою,
Ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.
– Сколько элементов у цифры 6? (2)
– Послушайте внимательно моё объяснение. (у детей локоть на парте)
– Сначала пишется большой левый полуовал, а затем малый правый. Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.
– Правильно возьмите ручки, спинки прямые. Напишите цифру 6 в воздухе. . Кто запомнил, как пишется цифра 6? (пишут самостоятельно. Кто не запомнил, пишу ещё раз).
-Какая цифра самая красивая? Подчеркните её простым карандашом.
– Для чего научились писать цифру 6? Кто знает числа, в записи которых есть цифра 6? (ответы детей).
– Кто может назвать это число? 16, 36, 66, 666. СЛАЙД
VII. Суперфизминутка (аудио- видео)

VIII. Закрепление изученного материала.
– Ребята, вы готовы работать дальше?
– Продолжение работы в тетради. № 3,4.

IX. Итог урока (формирование самооценки, самоконтроля).
Рефлексия

– Как вы себя чувствуете? – О чём бы вы хотели рассказать родителям? – Какие задания вам понравились больше всего? – Какое задание для вас было трудным?

-Поднимите руку у кого веселое настроение. – Объясните, почему у вас весёлое настроение? У меня всё получилось. Я хорошо отвечал. Я правильно выполнил все задания.

– А у кого грустное настроение? Почему? У меня не все получилось. Я не смог выполнить все задания правильно.

– Не нужно грустить, если что-то не получилось. На следующем уроке вы будете успешнее. Я в это верю. Ваше хорошее настроение- залог успеха в любом деле. Я желаю вам хорошего настроения на следующем уроке. – Урок окончен. Вы славно потрудились!

Прозвенел опять звонок
и закончился урок!
Вы, ребятки, отдохните,
силы новой наберите.

Просмотр содержимого документа
«”Число и цифра 6. Написание числа 6. ” »

Артемовская общеобразовательная школа І-ІІІ ступеней №18

Артемовского горсовета
Донецкой области







Рожанская Ирина Николаевна,

учитель начальных классов Артемовской общеобразовательной

школы І-ІІІ ступеней№18 Артемовского горсовета

Донецькой области

Квалификационнаа категория: специалист высшей категории

Год присвоения: 2003

2014 г.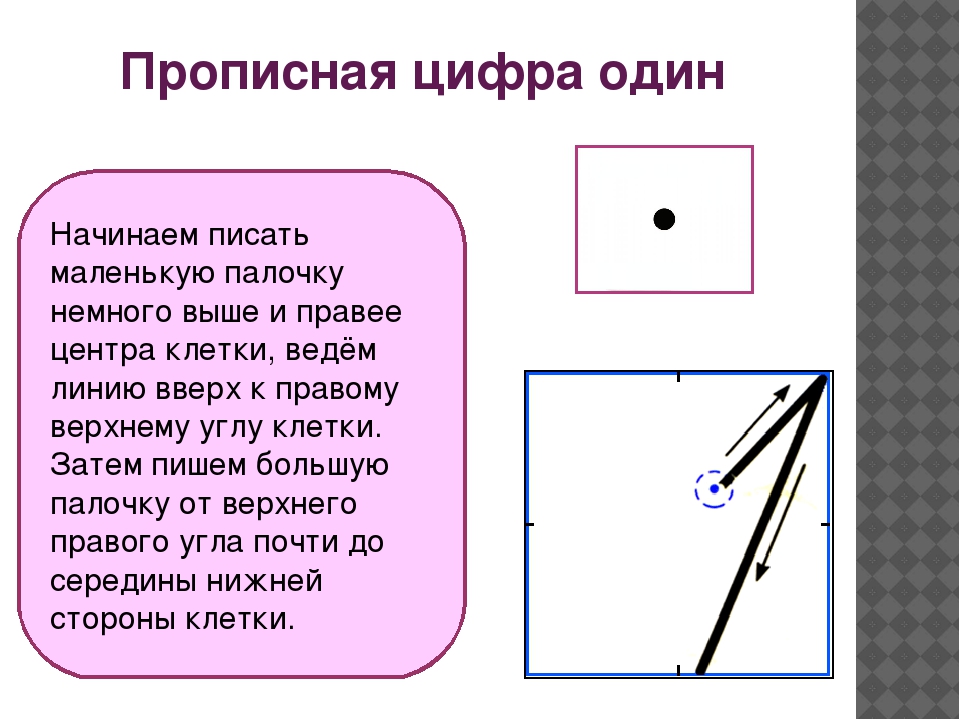

Урок математики в 1-ом классе

Тип урока: урок усвоения новых знаний.

Оборудование: ноутбук, электронная презентация, геометрические фигуры, индивидуальный набор цифр, образцы написания цифры 6, тетради с печ. основой, учебник, простой карандаш.

Слайд № 1

Организационный момент. 1. – Ребята, сегодня на нашем уроке присутствуют гости. Посмотрите, пожалуйста, на них. Поздоровайтесь.

2.Тренинг-настрой на урок.

(обращение к Цветку порядка) Распускается1 лепесток

II. Актуализация знаний (развитие внимания, зрительной памяти)

– Посмотрите на доску. Как всё это можно назвать? Фигуры)

– Что изменилось?

– Как называется эта фигура? (шестиугольник)
– Почему вы так её назвали? (шесть углов)
– А ещё чего шесть в этой фигуре? (шесть сторон)
– Ребята, а для чего мы с вами выполняли это задание? – Продолжаем дальше учиться? Отвечайте хором. (Да).

III. «Открытие» нового знания, формулирование темы урока.
1.Разминка. (используем знак «ХОР»)
– Сколько углов у шестиугольника? (Шесть)
– Сколько звуков в слове задача? (Шесть)
-В корзине сидят котята. Но котят не видно, а видно 6 хвостиков. Сколько котят в корзине? (Шесть)
– Сколько глаз у 3 щенят? (Шесть)
— Что интересного вы заметили?
( В условии и ответе встречается слово шесть).
– Подумайте, что может это означать?
2. Определение темы урока.
Какова же сегодня тема урока? Выслушиваются ответы детей и выводится тема урока «Число и цифра 6». Слайд №2
(На слайде высвечивается тема урока).

– Молодцы. Вы были внимательные, не ошиблись.
– Посмотрите на числа. Что можете сказать? (стоят не по порядку)
– Измените последовательность так, чтобы они стояли по порядку. (1 2 3 4 5)
– Умницы. Можно ли продолжить этот ряд чисел? Какое число будет следующее? (6)
Слайд (познакомить с числом 6, развитие умения доказывать свою точку зрения).
– Посмотрите на доску. Здесь много разных знаков. Каким знаком можно обозначить число 6?
8 + 9 – ( на доске)
(1 ученик выбирает знак).
– А я бы выбрала вот этот знак 9. Посмотрите, он так похож, есть закругление и кружок.
– Как мне, ребята, запомнить знак цифры 6? (ответы детей)
– Найдите у себя на парте карточку с цифрой 6. Поверните её правильно.
– Посмотрите на свой числовой ряд. Куда мы поставим число 6?
– А никто не знает, есть ли ещё знак цифры 6?
– VI – вот этот знак – римская цифра 6.
– Ребята, а где мы уже сталкивались сегодня с числом 6? К чему новому привёл нас шестиугольник? Видите, какая замечательная фигура пришла к нам сегодня на урок!
Посмотрите на наш кабинет и назовите 6 предметов, находящихся в нём
Назовите 6 имен своих друзей

Где в жизни встречается число шесть?

V. Физкультминутка (рисуем цифры).

Работа по учебнику. (с. 26, № 2) Сравнения чисел.

Составление выражений на сложение в пределах 6 (Слайд)

– Посмотрите на эти картинки. Попробуйте догадаться, как они связаны с числом 6?
– Есть печатная цифра 6 и письменная. На иллюстрациях какая? Почему?
– А вот это письменная (показать). Чем отличается письменная цифра от печатной?
– Может догадался кто-то о нашей следующей работе? (Будем учиться писать цифру 6)
– А для чего нам надо уметь её писать? (ответы детей)
Работа в тетрадях (знакомство с цифрой 6, формировать умение правильно писать цифру 6).
– Откройте рабочие тетради на стр. 21
Я тетрадочку открою
И наклонно положу.
Я, друзья, от вас не скрою,
Ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я возьмусь.
– Сколько элементов у цифры 6? (2)
– Послушайте внимательно моё объяснение. (у детей локоть на парте)
– Сначала пишется большой левый полуовал, а затем малый правый. Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.
– Правильно возьмите ручки, спинки прямые. Напишите цифру 6 в воздухе. . Кто запомнил, как пишется цифра 6? (пишут самостоятельно. Кто не запомнил, пишу ещё раз). -Какая цифра самая красивая? Подчеркните её простым карандашом.
– Для чего научились писать цифру 6? Кто знает числа, в записи которых есть цифра 6? (ответы детей).
– Кто может назвать это число? 16, 36, 66, 666. СЛАЙД
VII. Суперфизминутка (аудио- видео)

IX. Итог урока (формирование самооценки, самоконтроля).
Рефлексия

– А у кого грустное настроение? Почему? У меня не все получилось. Я не смог выполнить все задания правильно.

Прозвенел опять звонок
и закончился урок!
Вы, ребятки, отдохните,
силы новой наберите.

Урок математики «Число 6. Цифра 6». 1-й класс

2. Актуализация знаний и пробное учебное действие

– Вспомните наше путешествие по числовому отрезку.
– На какой станции мы остановились?
– Стоит ли нам продолжить наше путешествие по числовому отрезку?
– Для чего?
– Но для того, чтобы узнать новое необходимо повторить то, что мы уже знаем.

– Приготовьте карточки.
– Я задумала число, если к этому числу прибавить 1, то получится 4. Какое число задумала?
– Уменьшите это число на 2
– покажите следующее число за числом 3.
– Как получить следующее число? (+ 1)
– Назовите соседей числа 4.
– Составьте числовое выражение.
– Что вас удивило?
– Как быть?

На станции 5
Стоит

5 + 1 = ?

У детей карточки.

на доске запись:
3 + 2
1 + 4
2 + 2
5 + 1

3. Постановка проблемы

– Почему здесь возникло затруднение?
– А можем объяснить правильность решения по числовому отрезку?

– А ещё?
– Почему не смогли воспользоваться домиком?

Таких соседей нет ни в одном домике.

На нашем числовом отрезке нет числа шесть, значит надо найти место числу шесть на числовом отрезке.
Не умеем записывать цифру 6.
Такого домика нет. Надо познакомиться с составом числа шесть.

4. Построение проекта выхода из затруднения

Составим план на данный урок.
– Не умеем записывать цифру 6. Надо научиться писать цифру 6)
– Почему не можем объяснить правильность решения по числовому отрезку?
(надо найти место числу шесть на числовом отрезке )
– Почему не смогли воспользоваться домиком? (Такого “домика” нет, надо познакомиться с составом числа 6.
– Что в нашей жизни связано с числом шесть?
– Что в жизни бывает только 6?

Презентация. Слайд

Цифра 6.
Место на числовом отрезке.
Состав числа шесть.

6 материков, 6 ног у насекомых

5. Реализация построенного проекта

Открытие нового знания и формулирование темы урока.

– Давайте посмотрим на поставленные цели? Что предстоит выполнить вначале?

Знакомство с цифрой 6
Кирилл покажет фокус.

– Какая это цифра?

Это цифра – акробатка:
То шестёрка, то девятка.

– На что похожа цифра?
– Из каких элементов состоит цифра?

Цифра 6 состоит из большого левого и малого правого полуовалов. Начинают писать цифру немного ниже верхнего правого угла клетки. В правом верхнем углу клетки делают закругление, пишут большой левый полуовал, касаются середины нижней стороны клетки, ведут линию вверх, закругляя ее влево немного выше середины клетки.

Нет углов у цифры шесть,
Лишь дуга с кружочком есть.
Ты с дуги писать начни,
И кружочком оберни.
Цифру шесть писать легко:
Ни штришков, ни уголков!
За рукой своей следи,
Плавно линию веди!

– Попробуйте в воздухе обвести несколько раз цифру .
– А теперь в тетрадях научимся писать цифру 6

– Первый пункт мы выполнили? Научились писать цифру 6? Для чего научились?
– Переходим ко второму пункту: найти место на числовом отрезке.
– Чтобы найти место числу 6 на числовом отрезке, надо к 5 прибавить 1.
– Назовите предыдущее число числа 6.
Заселяем дом.
– Какой следующий пункт плана?

Работа в парах.
– Для данной работы приготовьте 6 кружков. Как можно разложить данные кружки. Результаты проговариваются в громкой речи и “заселяется домик № 6”
Аналогично работают с остальными вариантами.

Научиться писать

Полуовала

Самооценка.

Теперь сможем не только считать до 6, но записывать числа до 6.
Стрелочкой на числ.отр. показать направление), приложить единичный отрезок и подписать 6.

Состав числа.

(Вначале положим один кружок выше и пересчитаем, сколько осталось во втором ряду, получили 1 да 5, значит, на первом этаже находятся жители 1 и 5, следовательно, 6 – это 1 и 5) (Дети работают на доске и на партах).

Показ цифры 6.

Листочки с точками

6. Первичное закрепление с проговариванием во внешней речи

– Какую работу мы выполнили?
– Для чего необходимо знать состав числа?
– Значит, состав числа нужно быстрее выучить наизусть. Для этого мы ещё раз с помощью выражений вслух проговорим состав числа и заселим жильцов в “домик” № 6.
– Все ли поставленные цели мы выполнили?
Обращаясь к целям урока:
– Писать цифру научились?
– На числовом отрезке нашли место числу 6?
– С составом числа 6 поработали?
– Чем необходимо заняться теперь?
– Верно. Чтобы быстрей и лучше запомнить состав числа 6, давайте решим следующее задание
Посмотрим, какое задание нам предлагает учебник.

Составить равенства к 1 рисунку. 1 ученик у доски.

Познакомились с составом числа.
Чтобы быстро решать примеры.

Открыли число 6?
Работа в парах. На каждой парте – «домик», которое они заполняют.
1 пара у доски

1 и 5
2 и 4
3 и 3

Учимся писать цифру 6. Прописи для детей — буквы, цифры, игры

Знакомя ребенка с математикой в дошкольном возрасте, родители стараются привить любовь к этой науке. Прописи цифры помогут малышу научиться писать числа красиво и правильно. Написать цифры прописью вовсе не так легко. На освоение этого навыка в школе у непоседливого первоклассника часто не хватает времени и сил, поэтому к пятому классу его тетради по математике выглядят весьма печально. Как научить ребенка писать цифры, занимаясь с ним дома, чтобы занятия были в радость и на пользу?

Из этой статьи вы узнаете

Когда начинать

В каком возрасте лучше учить ребенка писать цифры прописью зависит не только от желания родителей. Многие хотят пораньше обучить своего малыша, как правильно писать цифры. Но если у ребенка еще неразвита мелкая моторика рук, он не умеет считать, и заниматься ему не очень хочется, покупать прописи с цифрами еще рано. Опытные педагоги не советуют предлагать прописи цифры для детей в три–четыре года по нескольким причинам:

формируются неправильные навыки письма, так как ребенок еще не способен оценить прием написания чисел;
у ребенка пропадает интерес осваивать новый материал в школе, если учитель объясняет то, что ему давно знакомо и успело надоесть;
ребенок должен получить начальную подготовительную базу, которая включает умение держать ручку, ровно сидеть за партой, быть аккуратным и внимательным;

Когда малыш сам выявит желание заниматься, заполняя пропись цифр, можно скачивать материал для обучения из интернета бесплатно. Скачать прописи для дошкольников и распечатать можно самые разные: с картинками раскрасками, с узорами из различных элементов, образец, который нужно обводить по точкам. Первые занятия должны проходить в игровой форме и не утомлять ребенка.

Упражнения для развития мелкой моторики

Распечатанный цифровой образец, который нужно обвести, является хорошим упражнением для развития мелкой моторики. Но в два или три года давать ребенку прописи еще рано. Начинать нужно с простых занятий аппликацией, лепкой из пластилина или соленого теста.

Можно делать самостоятельно или покупать в игрушечных магазинах сенсорные коробки с сыпучими материалами, фигурками зверей из пластика или резины, камешками разной формы и размера. Построение из элементов игры различных сценок будет способствовать развитию мелкой моторики рук ребенка с одного года.

С малышом старшего возраста можно заниматься нанизыванием бус на ниточку. В качестве бус могут служить большие пуговицы, крышечки от пластиковых бутылок, деревянные катушки из-под ниток.

Нужно делать с малышом пальчиковую гимнастику, рассказывая забавные стишки про сороку-ворону, которая кашу варила и деток кормила, про зайчиков и белочек, про мальчиков и девочек.

Можно устраивать театр теней при помощи рук, складывать оригами, плести макраме, делать фигурки и браслеты из резинок, вырезать новогодние снежинки, плести фигурки из крупного бисера. Собирание мелкого конструктора тоже прекрасно развивает мелкую моторику пальчиков, но старайтесь не давать мелкие детали деткам до трех лет, чтобы они их случайно не проглотили.

Важно научить ребенка правильно держать карандаш и ручку. Чтобы карандаш лежал на среднем пальце руки, будучи зажат большим и указательным пальцами, потренироваться придется долго. Не ругайте малыша, если он держит карандаш неправильно, раскрашивая картинки. Объясните, что если он хочет научиться рисовать и писать, карандаш нужно держать, так как это делает мама или папа. Хвалите ребенка за старание и малейшие успехи, стараясь не замечать промахов и ошибок.

Как проводить занятия

Учимся писать цифры играя. Урок письма должен стать не сухим заучиванием правил написания по клеточкам, а творческим занятием, развивающим воображение. Желательно, чтобы ребенок понимал то, что он пишет. Учить значение чисел можно с двух лет.

В пять лет можно начинать учить, как пишутся числа в прописях. Сначала необходимо объяснить ребенку, из каких частей состоит клетка в тетради. Где у нее верхняя сторона, где нижняя, правая и левая. Малыш должен сам находить центр клетки. Правильное написание цифр – это мамина гордость. Но нельзя торопить малыша.

Навык письма формируется по наблюдениям психологов в течение нескольких лет жизни. Привычка выполнять задание торопливо и небрежно, чтобы быстрее окончить урок и заняться более интересными делами – это нежелательное поведение, которое нужно сразу корректировать. Вносить в дошкольный период обучения элемент игры можно самыми разными способами.

Заполнение прописи

Заполняя с ребенком прописи пишем цифры правильно, чтобы в школе не пришлось переучиваться. Правила написания по клеточкам от 1 до 10 показывают малышу в виде небольших карточек со стрелками, так он лучше поймет движение ручки во время письма и запомнит.

Вариант для цифры 1

Письмо цифры 1 начинается почти от середины клетки. Рисуют короткую палочку до угла клеточки. Потом вниз из правого угла длинную палочку, которая опускается на сторону основание клеточки.

Вариант для цифры 2

Писать цифру 2 начинают выше центра клеточки. Рисуют плавный полукруг, который касается середины правой части верха клеточки и середины верхней части правой стороны клеточки. Плавно закругляясь в виде ровной палочки, полукруг числа два опускается на черту-основание клетки немного левее середины. Теперь рисуют хвостик, который красивой волной упирается в правую сторону клеточки недалеко от основания. На этом письмо цифры 2 окончено.

Вариант для цифры 3

Число три состоит из двух полуокружностей. Начинают писать из точки, которая находится немного ниже середины верхней грани клеточки. Закругляя, ведут полуовал, который соприкасается с верхней гранью и с правой, ближе к углу. Оканчивается верхний полуовал чуть выше и правее центра клетки. За ним рисуют второй полуовал, который опирается одним боком на правую сторону клеточки и, доходя до основания, оканчивается чуть левее его середины.

Вариант для цифры 4

Число четыре так же как один, не имеет симпатичных округлостей и плавных линий. Она состоит из прямых линий и углов. Письмо цифры 4 начинают из точки, лежащей на середине правой части верхней грани. Ведут линию до точки, которая находится немного ниже центра клеточки. Рисуют угол, со стороной параллельной основанию. Останавливаются, не доходя до правой стороны. Из точки, лежащей немного выше середины правой стороны, рисуют под наклоном линию до основания клеточки.

Вариант для цифры 5

У числа пять рисуют ровную палочку вниз, по направлению к центру, из точки немного правее середины верхней грани клеточки. Красивый полукруг, отходящий от палочки, соприкасается с правой стороной клеточки посредине и опускается на сторону основание клетки. В конце из начальной точки рисуют хвостик в виде полукруга, который упирается в угол клеточки.

Вариант для цифры 6

Число шесть похоже на девять, которое поставили на голову. Начинают писать шестерку из точки на правой стороне клеточки, недалеко от верхнего угла. Ведут полукруглый хвостик до нижней стороны клеточки. Против часовой стрелки рисуют овал, который занимает чуть больше одной четвертой части пространства.

Вариант для цифры 7

Число семь пишут почти так же, как один. Только начинают вести не ровную линию, а плавную, как волну, из точки немного ниже середины верхней грани клеточки. Потом из правого угла клетки рисуют ровную ножку до основания, немного правее середины. Перечеркивают ножку цифры посередине короткой ровной чертой слева направо.

Вариант для цифры 8

Писать цифру 8 проще простого. Рисуют полукруг, как для числа два, начиная вести из точки немного выше центра клетки. На основании закругляют линию и рисуют второй полукруг больше, возвращая ручку в первоначальную точку написания числа восемь.

Вариант для цифры 9

Писать цифру 9 нужно из точки, которая находится в середине верхней части правой стороны клетки. Нарисовав небольшой овал, который почти помещается в одной четвертой части клетки, возвращаются в первоначальную точку и рисуют полукруглую ножку у овала. Ножка овала, доходя до середины основания клетки, закругляется немного вверх.

Вариант для цифры 0

Ноль, похожий на круглый бублик, начинают рисовать из точки, которая лежит на верхней грани клетки, недалеко от правого угла. Движение идет против часовой стрелки, через центр клетки, опускается на ее основание посередине и возвращается в исходную точку, соприкасаясь с правой стороной клетки вверху.

Освоив, как красиво писать первый десяток чисел, не забывайте повторять с ребенком простые правила сложения и вычитания. Тогда красиво написанные числа в тетради по математике для 1 класса будут стоять в правильно решенных задачках.

В разделе «Прописи», Вы можете бесплатно скачать методические материалы для развития навыков письма, предназначенные для школьников и дошкольников. Также, с помощью прописей можно скорректировать свой собственный почерк или научиться писать другим почерком.

1 | | | |

Ю. Астапова

Прописи предназначены для подготовки детей дошкольного возраста к письму в тетради. Задания помогут развить мелкую моторику и координацию движений руки, формируют графические навыки и воображение ребёнка. Прописи помогут детям научится ориентироваться на листе бумаги в узкую косую линеку, задания разовьют зрительное восприятие, логическое мышление. Заниматься по настоящим прописям можно как индивидуально, так и в группе.

Н.В, Масберг

Перед вами прописи, упражняясь по которым малыш сможет натренировать мелкие мышцы руки и добиться правильной координации пальцев при письме.
Материал в прописях представлен в виде увлекательных заданий на внимательность, точность и координацию движений. Малыш должен научиться проводить различные фигурные и непрерывные линии ровно и красиво, и стараться не отрывать карандаш от бумаги. Выполняя такие задания, он научится аккуратно обводить по пунктирной линии, легко освоит первые навыки письма и рисования, приобретет ловкость при работе с ручкой и карандашом.

Астапова Ю.

Прописи предназначены для подготовки детей дошкольного возраста к обучению письму.
Задания тетради знакомят ребенка с конфигурацией букв русского алфавита. Дети запоминают название букв и их конфигурацию, учатся вписывать в рабочую строку форму буквы, соблюдая ее пропорции, писать буквы на равном расстоянии друг от друга, начинать работу в начале строки слева, соблюдать размеры строки, пользоваться гигиеническими правилами письма.

Издательство “Стрекоза”

Прописи-раскраска, которые призваны помочь развить мелкие мышцы руки и правильную координацию пальцев при письме у детей младшего возраста. Выполняя задания, ребенок освоит первые навыки рисования, письма, обводки, а также научится мыслить и фантазировать. Для учащихся начальных классов.

Трифонова Н.М., Романенко Е.В.

Подготовка этой выкладки заняла у нас немало времени. Мы постарались собрать здесь все известные нам прописи для дошкольника, которые когда-либо выпускались на рынок. Некоторые из них уже давно не используются в образовательных учреждениях., но это не делает их неэффективными в обучении детей письму.
С помощью прописей букв и цифр Ваш ребенок научится основам письма и грамоте, сможет самостоятельно выводить цифры на бумаге в клетку или линейку.

По математике (цифры)

Математические прописи – незаменимый помощник в ходе подготовки к школе. Практика показывает, что детки, с которыми родители занимались изучением того, как правильно писать цифры, чаще становятся отличниками и хорошистами в начальной школе.

Колесникова Е.В. для 5-7 лет по математике по клеточкам

Скачать

Колесникова Е.В. для 4-5 лет математические ступеньки

Ссылка для скачивания

Шевелев К.В. для 6-7 лет математические прописи

Часть 1
Часть 2

Перерсон Л.Г. и Суворина Е.А. – учимся писать числа 3-4 года и старше

Эта книга в двух частях от изветных авторов для бесплатного скачивания. В подготовительной группе детского сада она часто используется педагогами. Потренироваться с ребенком никогда не помешает.

Часть 1
Часть 2 Пособие научит ребенка правописанию цифр, что так необходимо для изучения математики в 5 классе. Также в нем присутствуют задания для развития графических навыков, а для математического уклона – геометрические фигуры.

Нефедова и Узорова 3000 упражнений для дошкольника

В этом пособии не только образец и пример, как должны выглядеть подобного рода пособия, но и полный цикл обучения правописанию цифр. Пожалуй, это лучшие прописи..
Скачать бесплатно и без регистрации

По русскому языку и грамоте (буквы)

Рабочая тетрадь по русскому для 5-6 лет в клетку

Данное пособие по грамоте предназначено для детей старшей группы детского сада. Веселые прописи для детей, главный герой в которых – утенок, помогут научить будущих первоклассников, как писать элементы букв. Весь алфавит в виде прописи перед нами.

Печатные и письменные буквы Федосова Н.А. для 5-7 лет

Эти прописи научат выводить и заглавные и прописные буквы любого ребенка. Они соответствуют ФГОС. Предназначены для работы в дошкольных образовательных учреждениях.

Лункина – подготовка к школе 5-7 лет обучение грамоте

В данных прописях автор Лункина занимательно учит детей грамоте. Сначала палочки и крючочки, а потом уже и вся азбука, затем соединения букв. И все это с рабочей тетрадью с заданиями.

Бунеев Р.Н., Бунеева Е.В., Пронин О.В. по письму

2 части учебного пособия от известных авторов для подготовки к школе. С их помощью можно научиться выводить печатные буквы. Мы и сами учимся писать буквы с их помощью.

Скачать и печатать часть 1
Скачать и напечатать часть 2

Развивающие письмо букв от Нянковской Н.Н.

Помогает сформировать графическое представление букв, их соединение. Интересное и развивающее пособие для дошкольников. Большая часть книги посвящена крючкам, черточкам, штриховке, галочкам, линиям. Только потом обучение переходит к буквам.

Первые и правильные! Со штриховкой

В данном пособии содержится целая азбука. 98 страниц для того, чтобы научиться писать все буквы русского алфавита. Все изображено достаточно крупно. Отличная идея, как для подготовки к школе, так и для младших дошкольников.

Денисова, Дорожкин для подготовительной группы

Уроки грамоты для малышей от метров отечественного издательства прописей.

Жиренко, Колодяжных – элементы букв, основы письма

Отличное пособие для формирования навыков письма у детей дошкольников.

Гласные и согласные буквы. Автор: Жукова

Прописи авторов Илюхиной, Козловой, Васильевой, Белых и Нищевой мы выкладывать не стали, в связи с тем, что уже наслышаны историями о жалобах правообладателей на сайты, где размещены файлы для скачивания. Надеемся на Ваше понимание и постоянно работаем над улучшением контента сайта.
В косую линейку

Прописи картинки (шаблоны)

Буквы русского алфавита

Буква А

Вы находитесь в категории раскраски Прописи цифры. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом “” Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски Прописи цифры и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему Прописи цифры развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.

Прописи – замечательная придумка взрослых, для развития навыков письма у детей. Использовать прописи можно с самого раннего возраста, начиная с 3 лет.

Сейчас можно найти огромное количество прописей. Главное, подобрать прописи для ребенка, соответствующие его возрасту. На этой странице вы сможете бесплатно скачать и распечатать прописи для детей 3-4 лет, 5-6 лет (дошкольников) и первокласcников.

Не стоит начинать занятия сразу с прописей цифр, букв и слов – это очень сложно. Малышам в 3-4 года будут интересны прописи с увлекательными заданиями на внимательность, точность и координацию движений.

Это прописи с достаточно простыми фигурами, линиями, различными завитками. Пусть малыш сначала потренирует руку, обводя фрагменты картинок, забавные крючочки и палочки.

Малыш должен научиться проводить различные фигурные и непрерывные линии ровно и красиво, стараться не отрывать карандаш от бумаги. Это не так просто.

Скачать прописи для малышей

Прописи И.Попова отлично подойдут малышам для самых первых занятий. Палочки и крючочки встроены в рисунки прописи. Сначала можно раскрасить рисунок, а потом перейти к “строчному письму”.

Скачать прописи для мальчиков

Веселые прописи для детей 5-6 лет

Для детей 5-6 лет возьмите прописи с более трудными заданиями. Используя такие прописи, ваш ребенок научится аккуратно обводить пунктирные линии, освоит первые навыки письма и рисования, приобретет ловкость при работе с ручкой и карандашом.

Скачать прописи для детей 5-6 лет

Скачать весёлые прописи для дошкольников

Прописи для дошкольника подготовят ребенка к письму, познакомят его с конфигурацией букв русского алфавита, научат писать буквы прописью. Используйте данные прописи, и ваш ребенок быстрее запомнит название и написание букв.

Скачать прописи – алфавит для дошкольников

Прописи по математике с цифрами и задачками помогут ребенку заранее научиться правильно писать цифры и познакомиться со счетом. Нажав на ссылку, вы можете скачать несколько видов прописей по математике быстро и бесплатно

Скачать прописи с цифрами

Прописи для школьников

Чтобы выработать красивый почерк, ребенку потребуется не мало времени. Но сейчас в школе очень мало уделяют внимания на правильное и каллиграфическое написание букв и цифр. Поэтому вы можете распечатать прописи с алфавитом для школьников и дополнительно заниматься. Эти прописи – без картинок, направлены на более серьезную работу по обучению письму. Кроме самих букв в прописях есть и отдельные элементы букв.

Скачать прописи для школьников “Алфавит прописью”

Тема урока: Число и цифра 6. Письмо цифры 6. | Материал (1 класс):

1. Организационный момент

– Долгожданный дан звонок

Начинается урок.

Встало солнышко давно,

Заглянуло к нам в окно.

На урок торопит нас

Математика у нас.

Пожелаем всем удачи.

За работу! В добрый час!

Приветствуют учителя

Личностные:

– положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся

2. Актуализация знаний

Устный счёт

Игра «Продолжай – не зевай»

Я назову число, вы мне следующее

У.- Один.

Д.- Два.

У.- Два.

Д.- Три.

2.К каждому числу предметов найди соответствующую цифру( на доске в ряд выставлены предметы нужно подобрать соответствующую цифру для каждого ряда)

3.Расставить числа в порядке возрастания

( на доске выставлены карточки с цифрами)

У меня возник вопрос. (Показывается карточка с изображением вопроса.) Я хочу поставить его сюда.

0 1 2 3 4 5 ?

– Как вы думаете, какой вопрос у меня возник?

-Это число будет меньше числа 5 или больше?

Воспринимают задание, наблюдают, анализируют, выполняют, предъявляют результат.

Дети вставляют ответы ,

ученики работают на доске

Расставляют числа в порядке возрастания

Меняются работами, проверяют и оценивают друг друга.

Отвечают на вопрос

-Какое число следует за числом 5

Познавательные:

– осознавать познавательную задачу

Коммуникативные:

– вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения;

– задавать вопросы, слушать и отвечать на вопросы других, формулировать собственные мысли, высказывать и обосновывать свою точку зрения

3. Целеполагание

Сейчас я загадаю вам загадку , которая поможет вам узнать это число

– Отгадайте загадку

Черен, да не ворон,

Рогат, да не бык,

Шесть ног без копыт.

Летит – воет,

Упадет – землю роет. (Жук.)

– Какое число вы услышали в загадке?

– Кто же догадался, о чем пойдет речь сегодня на уроке?

Дети отгадывают загадку

Число 6

Ответы учащихся

Коммуникативные:

– строить небольшие монологические высказывания

4. Сообщение темы и цели урока

5. Открытие новых знаний

Физминутка

6. Формирование и отработка графического навыка по написанию цифры

7. Раскрытие порядкового смысла числа 6

8. Выполнение логического задания

9. Рефлексия. Итог урока

-Давайте откроем учебник на нужной странице (стр.68) и прочитаем тему нашего урока

– Какова тема нашего урока?

– Каковы будут задачи нашего урока?

– К нам сегодня на урок пришли наши друзья Маша и Миша.

По дороге к нам они нашли жука, который не успел спрятаться от холодов

1.Работа по учебнику

Задание № 1

Учитель читает текст к заданию по учебнику

– Как называется число «пять и еще один»? (6)

– Как еще можно было посчитать количество

ног у жука (3+3)

(Рассматриваются варианты: 5 и 1, 3 и 3, 4 и 2)

2.-А сейчас давайте выполним задание «Засели жильцов»

на листочках (организуется взаимопроверка)

Далее учитель демонстрирует карточку с цифрой 6

– Посмотрите, как выглядит цифра, с помощью которой записывают число шесть

3.Работа по учебнику.

Задание № 2

– Найдите в задании 2 среди знаков цифру 6

– Сколько раз вам встретилась цифра 6? (5 раз.)

– На что похожа цифра 6?

На трубку деда, так и есть.

Г. Виеру

Цифра шесть – дверной замочек:

Сверху крюк, внизу кружочек.

С. Маршак

красивую цифру 6

Раз – подняться, подтянуться.

Два – согнуться, подтянуться.

Три – в ладоши три хлопка.

На четыре – руками шире.

Пять – руками помахать.

Шесть – за парту тихо сесть.

1.Работа по учебнику.

Задание № 3

С помощью звёздочек нужно определить на каком рисунке изображено 6 предметов

Выполняют задание на внимание

2.Работа по учебнику.

Задание № 4

Рассмотри, как пишется цифра 6. Сколько элементов необходимо для написания цифры 6?

-Где будем выполнять данное задание?

– Приготовимся писать цифру 6

Я тетрадь свою открою,

И наклонно положу.

Я друзья от вас не скрою,

Ручку правильно держу.

Сяду прямо, не согнусь,

За работу я возьмусь.

(Учитель подробно объясняет написание цифры, сопровождая показом на демонстрационной клетке. Дети имитируют написание «в воздухе»

Послушайте внимательно моё объяснение. – Сначала пишется большой левый полуовал, а затем малый правый. Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.

3.Работа по учебнику

Задание № 5

При выполнении задания учащиеся продолжают знакомство со сказкой про Козленка

Учитель читает отрывок:

– А у самой дороги, в загоне, спала большая жирная Свинья.

– Хрю-хрю-хрю! Куда это вы все? – спросила любопытная Свинья и пустилась трусцой вслед за другими.

Тогда Козленок сосчитал и Свинью.

– Один – это я, два – это Теленок, три – это Корова, четыре – это Бык, пять – это Конь, шесть – это Свинья. Один, два, три, четыре, пять, шесть!

– Рассмотрите рисунок. Кто шестым подошел к козленку?

– Сколько всего животных на рисунке?(6)

4. Работа в учебнике

-Задание № 6

-Слева направо найдите 6 доску и раскрасьте её

Теперь найдите справа налево 6 доску и

раскрасьте её.

– С каким числом мы сегодня познакомились ?

Какой цифрой мы будем обозначать

число 6 ?

-За каким числом следует число 6 ?

– Молодцы, ребята, вы хорошо потрудились

– Оценим свою работу . Перед вами лежат звёздочки , если вы все задания выполнили легко, то звёздочку красного цвета положите в красный кармашек, если были трудности, но вы справились, то звёздочку зелёного цвета положите в зелёный кармашек.

Урок закончен

Ответы учащихся

Научимся писать цифру 6, считать до 6.

Отвечают на вопросы учителя, опираясь на жизненный опыт (в пословицах и поговорках, сказках)

Рассматривают иллюстрацию в учебнике стр.68

Дети высказывают свои предположения

Ребята выполняют задание на состав числа, затем меняются листочками и проверяют работы

Ребята отвечают на вопрос

Сравнивают с образцом, анализируют, делают вывод.

Анализируют изображения на рисунке

Делают вывод: на среднем рисунке изображено 6 предметов

Работают устно по учебнику

Выполнение заданий по печатной тетради № 1 стр.76

Фронтальная работа

Учащиеся прописывают цифру 6

Работают на доске, выделяя только правильные цифры

Выполняют упражнения

Отвечают на вопросы

Работу выполняют в паре

Сверяют результаты своей работы с предложенным решением.

Высказывания учащихся

Проговаривание критериев оценки

Самооценка, складывают звёздочки по кармашкам

Коммуникативные:

– вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения

Личностные:

– осознавать свои трудности и стремиться к их преодолению, осваивать новые виды деятельности, участвовать в творческом, созидательном процессе;

– осознание себя как индивидуальности, способность к самооценке своих действий

Познавательные:

– понимать информацию, представленную в изобразительной, схематичной, модельной форме, использовать знаково-символичные средства для решения различных учебных задач

Коммуникативные:

Личностные:

– осознание себя как индивидуальности, способность к самооценке своих действий

Регулятивные:

– планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану;

– контролировать процесс и результаты деятельности, вносить необходимые коррективы; адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления

Познавательные:

– осознавать познавательную задачу;

– читать и слушать, извлекая нужную информацию, а также самостоятельно находить её в материалах учебников, рабочих тетрадей;

Личностные:

– осознание себя как индивидуальности, способность к самооценке своих действий

Коммуникативные:

– вступать в учебный диалог с учителем, участвовать в общей беседе, соблюдая правила речевого поведения;

Урок математики в 1 классе на тему ” Число 6. Цифра 6″

Работа с учебником

– Заглянем в наш учебник. Откройте его на странице 70 и рассмотрите рисунок.

– Сколько цыплят было? (5)

– Сколько цыплят стало? (6)

– Как получили 6 цыплят? (к 5 прибавили 1)

– Какое время показывают часы? Как вы узнали? (6ч., т.к. большая стрелка смотрит вверх, а маленькая показывает на цифру 6)

– Из каких частей состоит множество? (5 и 1)

– Сколько всего элементов во множестве? (6)

– Как получили число 6?

– Сколько элементов останется, если мы уберем часть 1? (5)

– Если уберем часть 5? (1)

Физпауза

Голубой аэропланчик сел на белый одуванчик.

(Что это ?)

Утром стрекоза проснулась, (Потерли кулачками глаза.)

Потянулась, улыбнулась. (Руки через стороны вверх, потянулись.)

Раз росой она умылась,

(Потерли ладонями щеки.)

Два – изящно покружилась, (Покружились на месте.)

Три – нагнулась и присела, (Присели.)

На четыре – дружно полетела. (Помахали руками вверх – вниз.)

У реки остановилась, (Легкий бег на месте.)

Над водою закружилась. (Присели.)

1.Письмо цифры 6

– Есть печатная цифра 6 и письменная.

– Чем отличается письменная цифра от печатной?

– Кто догадался, что мы будем делать дальше? (Будем учиться писать цифру 6)

Нет углов у цифры 6,

Лишь дуга с кружочком есть.

Ты с дуги писать начни

И кружочком оберни.

Цифру 6 писать легко:

Ни штришков, ни уголков.

За рукой своей следи,

Плавно линию веди.

Просмотр написания цифры 6.

– Послушайте внимательно моё объяснение.

– Начинаю писать большой полуовал немного ниже верхнего правого угла клетки, закругляю, касаясь верхней стороны клетки и веду вниз, закругляя, касаясь нижней стороны клетки и веду вверх, затем закругляю влево, немного выше середины клетки.

– Правильно возьмите ручки, спинки прямые.

– Напишите цифру 6 в воздухе вместе с экраном.

2.Работа в парах:

-На карточках найдите на какой полочке стоят 6 предметов.

-Раскрасте их.

-Чем они отличаются?

-Составить выражения и записать в тетрадь.

3.Восстановить порядок в строю.

Пока мы считали и работали по теме числа устроили чехарду и теперь здесь куча-мала.

А число 6 говорит, что она стоит первой.

– С каким числом мы сегодня познакомились?

– Как получить число 6?

– Какое задание вам понравилось больше всего? Почему?

– Что особенно запомнилось?

Продолжи:

Я научился…….

Я сомневаюсь………

А теперь похлопаем себе! Все хорошо работали!

Как помочь ребенку запомнить графическое изображение цифр

Как помочь ребёнку запомнить

графическое изображение цифр?

Очень часто бывает так, что ребёнок прекрасно считает от 1 до 10, но самостоятельно найти цифру, изображённую на картинке, никак не может. Графический образ цифры для него – это сложное абстрактное понятие. Развитие абстрактного мышления не простой процесс, как считают детские психологи. И без помощи взрослых здесь не обойтись.

Часто дети путают цифры, немного похожие друг на друга, например 6 и 9, 3 и 8, 4 и 7. И эту проблему ни в коем случае нельзя упускать. Детям нужно помочь разобраться в таких сложных для его восприятия графических образах. Ребёнку будет гораздо легче запомнить цифру, если он сможет найти её сходство с каким-нибудь предметом или животным: 2 – лебедь, 8 – очки.

Если педагог в детском саду или мама смогут подобрать интересные стихотворения о цифрах, то процесс запоминания будет ещё более лёгким. Главное, не стоит сердиться на детей, если они не схватывает всё “на лету”. Это для вас, взрослых, всё легко и просто, а для детей, только приступивших к овладению цифрами и счётом, всё очень сложно. Любой педагог подтвердит, что самым действенным способом запоминания нового материала для детей послужат игровые занятия по математике.

Рекомендую почитать своему ребёнку эти забавные стихотворения и, возможно, обучение пойдет быстрее и легче.

Цифры живут на различных предметах:

В календарях и трамвайных билетах,

На циферблатах часов, на домах,

Прячутся цифры в книжных томах,

И в магазине, и в телефоне,

И на машине, и на вагоне…

Цифры повсюду, цифры кругом.

Мы их поищем и сразу найдём.

Стихи про цифру 0

Эту цифру знать изволь:

На баранку похож ноль.

Ноль похож на колобок.

Он пузат и круглобок.

На него похожа кошка,

Если сложится в клубок.

Цифра 0 похожа на кольцо или баранку. Внутри кольца ничего нет — пусто. Цифра ноль обозначает число ноль, т.е. когда ничего нет — пусто.

Стихи про цифру 1

Вот один, иль единица,
Очень тонкая, как спица. С. Маршак

Похожа единица на крючок,

А может, на обломанный сучок.

Г. Виеру

Стихи про цифру 2

Два похожа на гусенка

С длинной шеей,

Шеей тонкой. Г. Виеру

А вот это цифра два.

Полюбуйся, какова:

Выгибает двоййка шею,

Волочится хвост за нею.

С. Маршак

Стихи про цифру 3

А вот это – посмотри,

Выступает цифра три.

Тройка – третий из значков –

Состоит из двух крючков.

С. Маршак

Стихи про цифру 4

Цифру 4 можно написать с помощью нескольких прямых линий. Сначала сверху вниз проведем карандашом самую левую наклонную линию, затем перекладинку, а потом правую вертикальную линию.

Смотри – 4 это стул,

Который я перевернул. Цифра новая – четыре.

Г. Виеру

Стихи про цифру 5

На что похожа цифра 5?

На серп, конечно,

Как не знать. Г. Виеру

А потом пошла плясать

по бумаге цифра пять.

Руку вправо протянула,

Ножку круто изогнула. С. Маршак

Стихи про цифру 6

Цифра шесть – дверной замочек:

Сверху – крюк, внизу кружочек. С. Маршак

Стихи про цифру 7

Цифра 7 или, как ее еще называют, семерка, похожа на косу, которой косят траву. Цифра 7 состоит из двух палочек. Одна палочка лежит горизонтально сверху, а вторая палочка, как ножка, держит верхнюю. Иногда у цифры 7 посредине рисуют перекладинку.

Семь — точно острая коса.

Коси, коса, пока остра. Г. Виеру

Вот семерка-кочерга.

У нее одна нога. С. Маршак

Стихи про цифру 8

Цифру восемь, цифру восемь

На носу всегда мы носим,

Цифра восемь плюс крючки –

Получаются очки…

То ли нуль с другим нулем

Рядышком уснули,

То ли дедушка очки

Позабыл на стуле. Ф. Дагларджа

К этой цифре ты привык.

Это цифра-снеговик.

Лишь зима сменяет осень,

Дети лепят цифру восемь!

Только к цифре ты, дружок,

Третий не лепи кружок. В. Бакалдин

Цифра восемь или, как ее еще называют, восьмерка, похожа на снеговика или на куклу Неваляшку.

Стихи про цифру 9

Цифра 9 – девятка похожа на толстого кота, который отвернулся от нас и хочет вздремнуть. Цифра 9 – это колечко с хвостиком, она похожа на перевернутую цифру 6.

Девять, как и шесть, вглядись.

Только хвост не вверх, а вниз. Г. Виеру

Цифра девять, иль девятка,

Цирковая акробатка:

Если на голову встанет,

Цифрой шесть девятка станет. С. Маршак

Стихи про число 10

Цифра вроде буквы О —

Это ноль иль ничего.

Круглый ноль такой хорошенький,

Но не значит ничегошеньки!

Если ж слева рядом с ним

Единицу примостим,

Он побольше станет весить,

Потому что это — десять. С. Маршак

Ноль встает за единицей —

Цифра 10 на странице. Г. Виеру

Математическая игра «Найди цифру»

Для этой игры потребуется:

нарисованные (напечатанные) на бумаге цифры от 1 до 9
рисунки, похожих на цифры, предметов.

Малыш смотрит на рисунок и затем угадывает, какая же цифра в нем спряталась. Затем мама показывает цифру 2 и просит малыша найти рисунок, похожий на эту цифру.

Математическая игра «Картонные цифры»

Для этой игры надо будет заранее вырезать цифры из картона. Малыш закрывает глазки, берет одну картонную цифру и на ощупь угадывает, что же это за цифра.

Математическая игра «Потерянные цифры»

На картоне печатаются цифры от 1 до 9. Затем каждая из них разрезается на две части. Малыш должен их восстановить. Если для него это задание слишком легкое, его можно усложнить, разрезав цифры на 3, 4 или 6 частей.

Игра «Что там на спинке»

Малыш ложится на живот, а мама рисует у него на спинке пальчиком цифру. Кроха должен угадать, что же это за цифра.

Консультацию составила:

учитель-дефектолог

Болдовская К.В.

Числа 6, 7. Письмо цифры 6. 1 класс

муниципальное бюджетное общеобразовательное учреждение

средняя школа №10 г.Ярцево

Конспект урока математики по теме:

«Числа 6, 7. Письмо цифры 6».

1 класс

Учитель начальных классов:

Красноперова Л.Н.

г. Ярцево

2016г.

Предмет: математика

Класс: 1

Тема урока: Числа6 и7. Письмо цифры 6

Тип урока: урок «открытия» нового знания

Методы: словесный, практический, наглядный

Цели:в ходе практической работы и наблюдений познакомить с образованием чисел 6 и 7; учить писать цифру 6

Планируемые результаты:

учащиеся научатся воспроизводить числа от 1 до 10 как в прямом, так и в обратном порядке, начиная с любого числа, определять место чисел 6 и 7 в натуральном ряду, соотносить цифру и число; устанавливать аналогии и причинно-следственные связи; слушать учителя и выполнять его требования, оценивать себя, границы своего знания и незнания.

Оборудование:

Математика. 1 класс. Учеб. для общеобразоват. учреждений М.И. Моро, С.И. Волкова, С.В. Степанова, рабочая тетрадь на печатной основе, числовые веера, разрезная касса цифр и математических знаков, математические наборы с геометрическими фигурами, «домики» чисел, рисунок к задаче, карточки с записью примеров, образец написания цифры 6, письмо.

Рисунки: Самоделкина, «Таможни», «Математического леса», «Цифрового пригорка», «Задачного болота», «Замка Ошибок» (Приложение)

Ход урока

I.Организационный момент.

Ну-ка проверь, дружок,

Ты готов начать урок?

Всё ль на месте?

Всё ль в порядке?

Ручка, книжка и тетрадка?

Все ли правильно сидят?

Все ль внимательно глядят?

Начинается урок,

Он пойдёт ребятам впрок.

– Сегодня мы отправимся в некоторое математическое царство, в некоторое геометрическое государство, за логическое море, за математический лес к нашему знакомому. Интересно, кто там живёт?

II.Устный счёт.

– А это вы узнаете «заселив» числа в домики.

– 5 это 4 и …

Дети показывают результат с помощью числового веера, затем один ученик говорит вслух: 5 это 4 и 1. Учитель ставит цифру и букву. Аналогично далее.

– Итак, ребята, это Самоделкин. (На доску прикрепить рисунок с изображением героя). К нему мы сегодня и отправимся.

На доске прикреплено письмо (можно под домик).

– Ребята, посмотрите, нам письмо.

– Давайте скорее его прочитаем. Интересно, что же там написано.

(Читает ученик).

(Текст: Ребята! Я попал в беду! Меня одолела Лень, этим воспользовались Злые Ошибки и утащили меня в подземелье своего замка.

Помогите!!! Самоделкин.)

– Есть у нас такой знакомый?

– Будем помогать?

– На пути встретятся различные препятствия, может не пойдём?

– Путь предстоит не лёгкий. Чтобы попасть в другое государство нужно пройти таможню.

(Вывешивается рисунок «Таможни»)

– Таможня закрыта на замки. Откроим их.

– Из каких геометрических фигур состоят ворота?

– Сколько треугольников?

– Сколько кругов?

– Сколько прямоугольников?

– Сколько квадратов?

– Как назвать одним словом прямоугольники и квадраты?

– Сколько всего четырёхугольников?

– Сколько всего геометрических фигур составляют ворота?

– Молодцы! Замки открыты! Путь свободен.

III. Работа над новым материалом.

– Мы прошли таможню и попали…

(Вывешивается рисунок «Математического леса»)

– Как вы думаете, куда?

В «математический лес».

– Нас встречают жители этого леса – числа и стража, которая охраняет лес.

– Как нужно вести себя в лесу?

Постановка цели урока.

– Что нам нужно сделать, чтобы стража нас пропустила?

(Стража пропустит нас, если мы узнаем, как получаются числа 6 и 7).

Итак, ребята, за работу!

Изучение нового материала.

а) Практическая работа.

– Кого же звать на помощь?

Может нам поможет наш математический набор и касса цифр и знаков

– Пока достаём наборы посчитаем хором от 1 до 10 и обратно.

– Какое самое большое число мы изучили? (5)

– Какое самое маленькое число? (1)

– Положите перед собой столько кругов, сколько груш на доске.

(На доску прикрепляются нарисованные груши)

– Сколько кругов положили? (5)

– Сделайте так, чтобы кругов стало 6. (Дети выполняют на партах.)

– Как получили 6? (к 5 прибавили 1)

– Что нужно сделать, чтобы и груш стало 6? (добавить 1 грушу)

– Сколько стало груш? (6)

– Как получили 6? (к 5 прибавили 1)

– Найдите цифру 6 в кассе цифр и покажите.

– Запишите (на партах) при помощи математических знаков и цифр из кассы, как получили число 6.

На партах появляется запись: 5+1=6

После проверки учитель делает такую же запись на доске.

Вывод: чтобы получить 6, нужно к 5 прибавить 1.

– Ура, ребята, одно задание стражников выполнили. Срочно приступаем к выполнению другого.

б) – Положите перед собой 6 квадратов.

Рядом положите 1 круг.

– Сколько стало всего геометрических фигур? (7)

– Как получили 7? (к 6 прибавили 1)

– Найдите цифру 7 и покажите.

– Запишите при помощи математических знаков и цифр как получили число 7.

На партах появляется запись: 6+1=7

После проверки учитель делает такую же запись на доске.

Вывод: чтобы получить 7, нужно к 6 прибавить 1.

– А как вы думаете, что больше 5или 6? 5 или 7? 6 или 7? (больше то число, которое при счёте встречается позднее).

– Итак, как получить число 6? 7?

IV. Физкультминутка.

Поработали, ребятки,

А теперь все на зарядку!

Мы сейчас все дружно встанем,

Отдохнём мы на привале.

Влево, вправо повернитесь.

Наклонитесь, поднимитесь.

Руки вверх, руки вбок

И на месте прыг да скок!

А теперь бежим вприпрыжку.

Молодцы, вы, ребятишки!

Замедляем дети шаг.

И на месте стой! Вот так!

А теперь мы сядем дружно,

Нам ещё работать нужно.

V. Первичное закрепление.

– Ребята, стражники нас не пропускают. Они не верят, что мы уже хорошо усвоили как получаются числа 6 и 7.

Стража требует, чтобы мы поработали ещё в учебнике на 52 странице.

– Работать нужно быстро, не допуская ошибок.

– Рассмотрите рисунок в верхней части страницы.

– Кого видим на рисунке? (мама и дочка)

– Что делает мама? (вырезает печенье)

– Какой формы мама вырезает печенье? (круглые, треугольные, квадратные)

а) – Сколько круглых печений девочка уже положила на противень? (5)

– Девочка кладёт ещё одно. Сколько всего круглых печений будет на противене? (6)

– Как получили 6? (к 5 прибавили 1)

– Найдите соответствующую запись в учебнике. Которая она по счёту?

б) – Сколько треугольных печений лежит на столе? (6)

– Сколько треугольных печений на противени? (1)

– Сколько всего треугольных печений? (7)

– Как получили 7? (к 6 прибавили 1)

– Найдите нужную запись под рисунком. Которая она по счёту?

в) – Сколько всего квадратных печений на столе и противени? (6)

– Сколько квадратных печений уже лежит на противени? (1)

– Сколько квадратных печений осталось на столе? (5)

– Как получили 5? (из 6 вычли 1)

– Найдите соответствующую запись под рисунком. Которая она по счёту?

г) – Сколько всего треугольных печений вырезала мама? (7)

(Смотреть на столе и на противени)

– Сколько треугольных печений девочка убрала на противень? (1)

– Сколько треугольных печений осталось на столе? (6)

– Как получили 6? (из 7 вычли 1)

– Найдите соответствующую запись под рисунком. Которая она по счёту?

Итак: как получть 6? 7?

– Молодцы! Стражники нами довольны и пропускают нас дальше.

VI. Работа в тетради.

– Ребята, перед нами « Цифровой пригорок».

(Вывешивается рисунок)

– Как нам его преодолеть? (Мы преодолеем его, если научимся писать цифру 6).

На доске образец написания цифры 6.

1) Объяснение написания.

2)А теперь все напишите цифру 6 в своих тетрадях на печатной основе. Откройте тетради.

а) Написание цифры 6 по образцу.

б) Допишите строчку до конца самостоятельно.

в) Поставьте точку под той цифрой, которая больше всего понравилась.

г) Напишите самостоятельно 1 строчку.

Индивидуальная помощь учащимся.

– Молодцы, ребята! Мы преодолели «Цифровой пригорок».

VII. Составление и решение задач.

( Вывешивается рисунок «Задачного болота»)

– Мы попали в «Задачное болото». На его краю сидит Задачник. Он хочет, чтобы мы сами составили и решили задачу.

Нам в помощь он даёт рисунок. (Вывешивается рисунок)

– Сколько бабочек сидит на ромашке? (2)

– Сколько подлетает к цветку? (1)

Составим условие: На ромашке сидели 2бабочки. К ним прилетела ещё 1.

Вопрос: Сколько бабочек стало на ромашке?

– Сколько же бабочек стало на ромашке? (дети показывают результат – 3)

– Как узнали? (к 2 прибавили 1)

– Мы справились с заданием, поэтому Задачник желает нам успехов.

VIII. Повторение пройденного.

– Вот мы и добрались до замка злых Ошибок.

(Вывешивается рисунок замка, а под ним рисунок Самоделкина).

– Они отпустят нашего друга Самоделкина, если мы без ошибок решим примеры, которые для нас приготовили злые Ошибки.

На листочках:

5-1= 5+1=

2+2= 4+1=

4-1= 3+1=

Проверка:

Учитель показывает карточку с записанным примером – дети показывают результат при помощи числовых вееров.

– Молодцы, ребята! Мы всё выполнили верно! А вот и Самоделкин.

(Сдвигаем рисунок замка)

– Мы победили и спасли друга.

IX. Итог урока

– В каком царстве мы сегодня побывали?

-Дружно ли мы работали?

– Смогли ли помочь другу?

-Какие ставили цели на уроке?

(Узнать, как получить числа 6 и 7, научиться писать цифру 6.)

-Всех ли целей мы достигли?

– Как же мы можем получить числа 6 и 7?

X. Рефлексия

Сигнальные карточки.

Понравилось работать – оранжевая карточка, не понравилось – синяя.

Приложение

Числовые «домики» Самоделкин

ТаможняМатематический лес

Цифровой пригорок Задачное болото

З амок Ошибок

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/232030-konspekt-uroka-matematiki-po-teme-chisla-6-7-

Как читать и писать числа до шести цифр: урок для детей – видео и стенограмма урока

Чтение больших чисел

Все числа читаются слева направо. Вы можете использовать разрядное значение , значение цифры, зависящее от ее позиции в числе, чтобы облегчить чтение числа. Посмотрим как.

Однозначные числа

Однозначные числа занимают единицы. Имя однозначного числа – это просто имя цифры.Читаем названия однозначных чисел:

0 читается ноль
1 считывается один
2 читается два
3 читается три
4 читается четыре
5 читается пять
6 читается шесть
7 читается семь
8 читается восемь
9 прочитано девять

Двузначные числа

Двузначные числа расширяются до разряда десятков, который является второй цифрой справа.Чтение двузначного числа требует знания множества названий чисел.

Каждое двузначное число, начинающееся с 1, имеет уникальное имя, поэтому вам просто нужно запомнить каждое из них. Для считайте двузначные числа , начинающиеся с 2 по 9, используйте имя значения разряда десятков плюс имя цифры в разряде единиц. Давайте прочитаем некоторые двузначные числа, начинающиеся с 1, а некоторые с 2 по 9:

10 читается десять
11 читается одиннадцать
12 читается двенадцать
13 прочитано тринадцать
14 читается четырнадцать
15 читается пятнадцать
16 читается шестнадцать
17 читается семнадцать
18 читается восемнадцать
19 прочитано девятнадцать
20 читается двадцать
30 читается тридцать
40 читается сорок
50 читается пятьдесят
60 читается шестьдесят
70 читается семьдесят
80 читается восемьдесят
90 читается девяносто

Теперь давайте попробуем прочитать список предметов, которые Бенджамин нашел в своем саду:

45 прочитано сорок пять слизней
96 тыкв читается девяносто шесть тыкв
27 божьих коровок прочитано двадцать семь божьих коровок

Трехзначные числа

Трехзначные числа доходит до разряда сотен, который является третьей цифрой справа.В прочтите трехзначное число , назовите первую цифру, добавьте слово «сотня», а затем прочтите оставшуюся часть числа:

300 помидоров читается триста помидоров
777 кочанов салата прочитано семьсот семьдесят семь кочанов салата

Четырехзначные числа

Четырехзначные числа доходит до разряда тысяч, что является четвертой цифрой справа. На прочтите четырехзначное число , назовите первую цифру, произнесите слово «тысяча», а затем прочтите оставшуюся часть числа:

4000 редис читается четыре тысячи редис
8,122 перцев прочитано восемь тысяч сто двадцать два перца

Пятизначные числа

Пятизначные числа расширяются до десятичного разряда, который является пятой цифрой справа.Для прочтите пятизначное число , прочтите первые две цифры так, как если бы вы читали двузначное число, добавьте слово «тысяча» и прочтите оставшуюся часть числа:

23000 земляные черви читается двадцать три тысячи дождевых червей
12 212 божьих коровок прочитано двенадцать тысяч двести двенадцать божьих коровок

Шестизначные числа

Шестизначные числа переходят в разряды сотен тысяч, которые являются шестой цифрой справа.Для прочтите шестизначное число , прочтите первые три цифры, как если бы вы читали трехзначное число. Затем добавьте слово «тысяча» и прочтите оставшуюся часть числа:

300000 стручковая фасоль читается триста тысяч стручковая фасоль
8 муравьи прочитаны девятьсот восемнадцать тысяч двести восемь муравьев

Запись чисел

В запишите число , определите значение разряда первой цифры, а затем запишите остальные числа соответственно.Например:

Бенджамин нашел восемь тысяч стручков . Убедитесь, что цифра 8 стоит в разряде тысяч с тремя пустыми точками справа, например: 8 _ _ _. Поскольку других названных цифр нет, используйте нули для обозначения остальных разрядов. Восемь тысяч написано 8000.

Вот другой пример:

Давайте запишем девятьсот девяносто шесть свеклы. Цифра 9 должна идти в разряде сотен с двумя пустыми точками справа, например: 9 _ _.Девяносто шесть должно быть написано с 9 в разряде десятков и 6 в разряде единиц. Итак, девятьсот девяносто шесть написано: 996.

Сводка урока

Когда вы читаете числа , используйте разряд или значение цифры в зависимости от ее позиции в числе, чтобы читать число слева для записи. Когда вы пишете числа , сначала определите значение разряда первой цифры, а затем запишите число.

Расширенная запись – способ расширения чисел

Что означает расширенная запись?

Расширенное представление можно определить как способ выражения чисел путем отображения значения каждой цифры.Запись числа в развернутой форме – это не то же самое, что запись числа в развернутой форме.

В расширенной записи число представлено как сумма каждой цифры, умноженной на ее разрядное значение, тогда как в развернутой форме сложение используется только между числами разрядного значения. Например:

234 в развернутой форме:

= 200 + 30 + 4

в то время как 234 в развернутой форме:

= (2 x 100) + (3 x 10) + (4 x 1)

Исходный Форма числа «234» называется стандартной формой.

Как сделать расширенную нотацию?

Чтобы раскрыть конкретное число (из его стандартной формы), нам нужно расширить его до суммы каждой цифры, умноженной на соответствующее ей разрядное значение (единицы, десятки, сотни и т. Д.).

Эти методы записи числа в расширенной нотации и формах проиллюстрированы в примерах ниже.

Пример 1

Записать 4981 в развернутом виде?

Решение

Число 4981 можно записать в развернутой форме как:

4981 = 4000 + 900 + 80 + 1
В этом методе каждое число, которое идет после цифры, заменяется нулями.Например, 4 и 9 в номере представлены как 4000 и 900 соответственно.

Пример 2

Записать 15 807 в развернутом виде?

Решение

15 807 в развернутой форме представлено как:

15 807 = 10 000 + 5 000 + 800 + 7
В этом примере значение разряда 0 в числе равно нулю; следовательно, значение в разряде десятков не отображается, потому что нет десятков.

Запись числа в расширенной системе счисления влечет за собой указание места числа в экспоненциальной степени десяти.

Пример 3

Запишите расширенное обозначение: 4,981

Решение

4,981 = (4 x 1,000) + (9 x 100) + (8 x 10) + (1 x 1)

= (4 x 10 ³) + (9 x 10 ²) + (8 x 10 ¹) + (1 x 10 ⁰)

Пример 4

Запишите 15,807 в развернутом формате ?

Решение

15,807 = (1 x 10,000) + (5 x 1,000) + (8 x 100) + (7 x 1)

= (1 x 10 ⁴) + (5 x 10 ³) + (8 x 10 ²) + (7 x 10 ⁰)

Пример 5

Запишите тысячи, сотни, десятки и единицы для каждого из следующих чисел:

a.945

945 = 9 сотен + 4 десятков + 7 единиц

= 900 + 40 + 5

б. 458

458 = 4 сотни + 5 десятков + 8 единиц

= 400 + 50 + 8

c. 5973

5973 = 5 тысяч + 9 сотен + 7 десятков + 3 единицы

= 5000 + 900 + 70 + 3

г. 333

333 = 3 сотни + 3 десятки + 3 единицы

= 300 + 30 + 3

д. 789

789 = 7 сотен + 8 десятков + 9 единиц

= 700 + 80 + 9

Расширенная запись с десятичными знаками

Десятичные числа также могут быть записаны в расширенной записи с использованием экспоненциальной степени десяти.

Пример 5

Запишите 96.24 в развернутом виде?

Решение

96,24 = 90 + 6 + 0,2 + 0,04
(9 x 10) + (6 x 1) + (3 x 10 ^-1) + (4 x 10 ^-2)

Пример 6

Запишите десятичное число 536.072 в развернутой записи.

Решение

536,072 = 500 + 30 + 6 + 0,07 + 0,002
(5 x 10 ²) + (3 x 10 ¹) + (6 x 10 ⁰) + (7 x 10 ^-2) + (2 x 10 ^-3)

Практические вопросы

I.Запишите в развернутом виде следующие числа:

6587
1234
29012
49500
4007

II. Ниже представлены развернутые формы разных чисел. Напишите числа в стандартной форме.

50000 + 7000 + 900 + 60 + 1
6000 + 500 + 30 + 7
20000 + 1000 + 200 + 70 + 9
50000 + 7000 +10 + 8
400000 + 80 + 8
70000 + 7000 + 10 + 1

III.Напишите развернутые формы чисел ниже:

(i) 1749, …………., ……………., ……………., …………… .., ……………. .
(ii) 5605, …………., ……………., ……………., …………… .., ……………. .
(iii) 43453, …………., ……………., ……………., …………… .., ……………. .
(iv) 76125, …………., ……………., ……………., …………… .., ……………. .

IV. Заполните пропуски:
(i) 56371 = …… десять тысяч + …… тысяч + …… сотня + …… десятки + …… единицы
(ii)2 = …… сто + …… тысячи + …… единицы
( iii) 59278 = (…… x 10000) + (9 x ……) + (…… x 100) + (2 x ……) + (…… x 8)
(iv) 33602 = 30000 + …… +… … + 2

Предыдущий урок | Главная страница | Следующий урок

Вычитание – | Основы арифметики

Эта страница посвящена основам арифметики – простейшему способу работы с числами посредством вычитания (-).

См. Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Умножение ( × ) и Деление ( ÷ ).

Вычитание

Вычитание – это термин, используемый для описания того, как мы «убираем» одно или несколько чисел у другого.

Вычитание также используется для нахождения разницы между двумя числами. Вычитание противоположно сложению. Если вы еще этого не сделали, мы рекомендуем прочитать нашу дополнительную страницу.

Знак минус «-» используется для обозначения операции вычитания, например 4–2 = 2. Знак «-» можно использовать несколько раз по мере необходимости: например, 8–2–2 = 4.

Этот расчет правильный, но его можно упростить, сложив числа, которые мы вычитаем. В нашем примере 8 – 2 – 2 = 4 можно упростить до 8 – 4 = 4 (две двойки были добавлены вместе, чтобы получить 4, которое затем вычитается из 8).

Предупреждение

Будьте осторожны при использовании знака «-».Числа с отрицательным значением записываются с предшествующим «-», поэтому минус два записывается как -2. Это просто означает, что 2 меньше нуля или 2 меньше нуля.

Для получения дополнительной информации см. Нашу страницу, посвященную положительным числам и отрицательным числам .

Остерегайтесь знаков и порядка при вычитании

Когда мы выполняем вычисление , сложение , порядок, в котором мы складываем числа, не имеет значения.

Например,
8 + 3 + 5 совпадает с 3 + 8 + 5 и дает нам тот же ответ, 16.

Однако, когда мы выполняем вычитание , нам нужно особенно внимательно относиться к порядку чисел.

Обычно при вычитании мы сначала записываем число, которое мы вычитаем из , а числа, которые мы убираем, в любом порядке после этого.

Например,
8-5 = 3
Это НЕ то же самое, что 5-8 = −3

Мы видим, что у нас тот же числовой ответ (3), но его значение другое: 3 в первом вычислении, но минус 3 (−3) во втором.

Аналогично 8-5-3 = 0, но 5-8-3 = −6, что является совершенно другим ответом.

Причина, по которой ответы различаются, не в том, что мы поставили числа в «неправильном» порядке, а в том, что мы не позаботились о том, положительные они или отрицательные.

В нашем примере 8 – положительное число, поэтому мы могли бы записать его как «+ 8», и это было бы правильно, но по соглашению нам не нужно писать символ «+». Однако символ «+» очень важен при изменении порядка, как и символы «-», предшествующие 5 и 3.

Вот последний пример, переписанный для правильного ответа:

8-5-3 = 0, как и раньше, и – 5 + 8-3 = 0, что дает тот же ответ. В этом случае мы написали числа в том же порядке, что и раньше, но учли их положительное или отрицательное значение.

Более подробное объяснение и примеры см. В разделе «Вычитание в особых случаях: ноль и отрицательные числа » ниже.

Выполнение вычитания

Простое вычитание может выполняться так же, как и сложение, путем подсчета или использования числовой строки:

Если у Фиби 9 конфет, а у Люка 5 конфет, какая разница?

Начиная с меньшего числа (5) и считая до большего числа (9).

6 (1), 7 (2), 8 (3), 9 (4).

У Фиби на 4 конфет больше, чем у Люка, разница в конфетах на 4.

Итак: 9-5 = 4 .

Для более сложного вычитания, когда использование подсчета не подходит, полезно записывать наши числа в столбцы один над другим – аналогично вычислению сложения.

Предположим, Майк зарабатывает 755 фунтов стерлингов в неделю и платит 180 фунтов стерлингов за аренду. Сколько денег осталось у Майка после того, как он заплатил за квартиру?

В этом примере мы собираемся убрать 180 фунтов из 755 фунтов стерлингов.Сначала мы записываем начальное число, а снизу – число, которое мы убираем, следя за тем, чтобы числа были в правильных столбцах.

Сот	Десятки	шт.
7	5	5
1	8	0

Шаг 1: Сначала мы выполняем вычитание чисел в столбце «Единицы измерения» справа, затем записываем ответ внизу в том же столбце.В этом случае 5 – 0 = 5.

	Сот	Десятки	шт.
	7	5	5
	1	8	0
Итого			5

Шаг 2: Используя тот же подход, что и при вычислении сложения, мы работаем по столбцам справа налево.Затем нам нужно вычесть числа в столбце десятков. В нашем примере нам нужно вычесть восемь из пяти (5-8), но 8 больше 5, поэтому мы не можем этого сделать, так как в итоге получим отрицательное число. Нам нужно позаимствовать число из столбца сотен. Это может быть сложной концепцией, и мы рассмотрим ее более подробно ниже: у нас есть 7 в столбце сотен, поэтому мы «заимствуем» 1 для столбца десятков, оставляя нас с 6 в сотнях. Перечеркните 7 и напишите 6 в столбце сотен, чтобы избежать ошибок позже.Переместите 1 в столбец десятков и запишите его перед числом 5. Мы не добавляем «1» к десяткам, мы ссужаем «1 лот из 10». Итак, вместо 5 десятков у нас теперь 15 десятков.

15 больше восьми, поэтому мы можем выполнить вычитание в столбце десятков. Возьмите 8 из 15 и напишите ответ (7) внизу столбца десятков.

	Сот	Десятки	шт.
	7 6	15	5
	1	8	0
Итого		7	5

Шаг 3: Наконец, отнимите 1 от 6 в столбце сотен.6 – 1 = 5, поэтому поставьте 5 в столбце ответа сотен, чтобы дать окончательный ответ. У Майка осталось 575 фунтов стерлингов после того, как он заплатил за квартиру.

	Сот	Десятки	шт.
	7 6	15	5
	1	8	0
Итого	5	7	5

Заем в вычет

Заимствование , как в примере выше, может сбивать с толку при вычислениях вычитания.Это похоже на «перенос» в дополнительных вычислениях, но в обратном порядке, потому что вычитание – это обратное (противоположное) сложение.

Повторное заимствование может произойти при вычислении вычитания.
Предположим, у нас есть 10,01 фунта стерлингов, и мы хотим забрать 9,99 фунта стерлингов. Мы можем решить это, не записывая ничего – ответ – 0,02 фунта стерлингов или 2 пенни. Однако если мы выпишем этот расчет формально, то понятие заимствования станет более ясным.

В этом примере мы проигнорировали десятичную точку и записали числа как 1001 и 999.

Начиная с столбца единиц справа, нам нужно отнять 9 от 1. В наших вычислениях вычитания правило (как в приведенном выше примере) состоит в том, что мы никогда не убираем большее число из меньшего числа, потому что это даст нам отрицательный ответ.

Чтобы расчет заработал, нам нужно « позаимствовать » из следующего столбца слева. В столбце десятков стоит 0, поэтому брать нечего, поэтому нам нужно перейти к следующему столбцу слева.В столбце сотен также есть 0, поэтому мы также не можем заимствовать данные из этого столбца, поэтому мы переходим к следующему столбцу слева. Столбец тысяч имеет 1, поэтому мы можем позаимствовать его и переместить в следующий столбец справа, столбец сотен. Мы перечеркнем 1 в столбце тысяч, чтобы избежать ошибок позже.

Одна тысяча равна 10 сотням, поэтому теперь у нас есть 10 в столбце сотен, где раньше было ноль:

Переносной	0	10
	1	0	0	1
		9	9	9

Однако это не помогает с 1–9 (в столбце единиц), потому что у нас все еще есть ноль для заимствования в столбце десятков, но это первый шаг в процессе.

Теперь, когда у нас есть 10 сотен, мы можем позаимствовать одну из них для столбца десятков. Сто равно 10 десяткам, поэтому мы переносим 10 в столбец десятков. Мы не должны забыть настроить столбец сотен, поэтому мы вычеркиваем 10 и вместо этого пишем 9.

Переносной		9	10
Переносной	0	10
	1	0	0	1
		9	9	9

Наконец, мы можем выполнить вычитание в столбце единиц, заимствовав 1 десятку из столбца десятков.Это оставляет 9 десятков в столбце десятков и 10 + 1, которое у нас уже было в столбце единиц, что дает нам 11 единиц.

Переносной			9	10
Переносной		9	10
Переносной	0	10
	1	0	0	1
		9	9	9

Теперь мы можем выполнить полный расчет, начиная со столбца единиц, 10 + 1 = 11 – 9 = 2.Тогда в столбце десятков 9 – 9 = 0. То же самое для столбца сотен 9 – 9 = 0. Наконец, в столбце тысяч 0 – 0 = 0.

Переносной			9	10
Переносной		9	10
Переносной	0	10
	1	0	0	1
		9	9	9
Итого	0	0	0	2

Взяв взаймы несколько раз, мы пришли к нашему ответу 2.Когда мы заменяем десятичную точку, мы получаем 0,02 фунта стерлингов.

Вычитание в особых случаях: ноль и отрицательные числа

Если бы мы выполняли простое сложение, мы могли бы считать в уме или, возможно, на пальцах. Когда мы выполняем вычитание, особенно если оно включает отрицательные числа, помогает представить себя идущим по линии. Каждый шаг – это номер в этой строке. Если мы начнем с нуля, каждый шаг вперед добавляет число, каждый шаг назад убирает единицу.Самое важное, что нужно помнить, – это то, что мы всегда смотрим в позитивном направлении. Возможно, вам будет полезно думать о своей линии как о подъеме и спуске по лестнице, где каждая ступенька имеет номер. Или, возможно, вы более знакомы с перемещением вверх и вниз по многоэтажному блоку на лифте, где ноль – это первый этаж, положительные числа – над землей, а отрицательные – в подвале.

Если бы мы провели эту линию на листе бумаги, она выглядела бы как линейка. Мы можем перемещать ручку вперед и назад по линии так же, как представляем себе наши шаги вперед и назад.Это называется числовой линией и является очень полезным инструментом для сложения и вычитания.

Мы собираемся использовать эту аналогию, чтобы помочь нам понять следующие примеры.

Когда числа равного значения вычитаются друг из друга, результат всегда равен нулю: 19-19 = 0.

Используя нашу аналогию, начав с нуля, если мы пройдем 19 шагов вперед по линии, затем 19 шагов назад, мы вернемся к нулю.

При вычитании нуля из любого числа число остается неизменным: 19-0 = 19.

Используя числовую прямую, мы начинаем с 19 и идем назад нулевых шагов – мы не двигаемся и остаемся на 19.

Когда мы вычитаем из нуля любое положительное число , получаем ответ отрицательное : 0 – 15 = –15

Помните из наших предыдущих примеров, положительное число обычно не нужно записывать с положительным знаком. Когда мы видим число «67», математическое соглашение говорит нам, что оно положительное, т.е.е. «+67».

В этом примере мы вычитаем +15 из нуля: 0 – (+15) = –15. Используя нашу аналогию, мы начинаем с нуля и делаем 15 шагов назад.

Когда мы вычитаем любое положительное число из отрицательного числа , ответ становится « более отрицательный » .

Например, если мы начнем с нашего ответа сверху (–15) и вычтем 6, мы получим: –15 – 6 = –21. Помните, что «6» положительно, поэтому мы можем написать –15 – (+6) = –21, и это означает то же самое.Используя числовую линию, чтобы помочь нам понять, мы начинаем со значения –15. Мы идем назад на шесть шагов, по-прежнему глядя в положительном направлении. В итоге мы делаем 21 шаг назад от нуля, то есть –21.

Но что произойдет, если нам нужно вычесть отрицательное число из любого другого числа?

Начнем с примера: 15 – (–6) = 15 + 6 = 21

Правило: два отрицательных числа дают положительное значение , т.е. вычитание отрицательного числа становится сложением.

Давайте вернемся к нашей числовой прямой, чтобы облегчить понимание: начиная с 15, мы знаем, что нам нужно двигаться назад (в отрицательном направлении), потому что мы делаем вычитание. Но из нам нужно вычесть отрицательное число, поэтому, чтобы проиллюстрировать это, мы должны повернуть вокруг . Затем мы возвращаемся на 6 позиций назад, чтобы прийти к нашему ответу. При повороте и последующем движении назад (два отрицательных момента) наше общее направление движения находится в положительном направлении на , т.е.е. мы выполнили сложение .

Вычитание отрицательного числа – абстрактная концепция, и вы можете подумать, что она не встречается в повседневной жизни. В конце концов, мы не можем удержать отрицательное количество яблок или налить отрицательное количество кофе. Однако это очень важно, когда речь идет о математических понятиях, таких как вектора, . Вектор имеет направление и звездную величину , поэтому, например, важно не только, как далеко проплыла лодка, но и нам нужно знать направление, в котором она плыла.

Дополнительная литература по навыкам, которые вам нужны
Основы счета
Часть необходимых навыков Руководство по счету
Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами. Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Научная запись
Научная нотация (также называемая Стандартной формой в Великобритании) – это особый способ записи чисел:
Как это:
Или это:
Позволяет легко использовать большие и маленькие значения.
Хорошо, как это работает?
Пример: 700
Почему 700 записывается как 7 × 10 ² в научной нотации?
700 = 7 × 100
так 700 = 7 × 10 ²
И 700 , и 7 × 10 ² имеют одинаковое значение, но показаны по-разному.
Пример: 4 900 000 000
1,000,000,000 = 10 ⁹,
, поэтому 4,900,000,000 = 4.9 × 10 ⁹ в научной нотации
Число записывается в виде из двух частей :
Всего цифр с десятичной запятой после первой цифры, за которой следует
× 10 в степень , которая помещает десятичную запятую туда, где она должна быть
(т.е. показывает, на сколько мест нужно переместить десятичную запятую).

В этом примере 5326,6 записывается как 5,3266 × 10 ³ ,
потому что 5326.4 = 3 × 10 × 10 × 10 × 10 = 30,000
Калькуляторы часто используют “E” или “e”, например:
Пример: 6E + 5 совпадает с 6 × 10 ⁵
6E + 5 = 6 × 10 × 10 × 10 × 10 × 10 = 600000
Пример: 3.12E4 совпадает с 3.12 × 10 ⁴
3.12E4 = 3,12 × 10 × 10 × 10 × 10 = 31 200
Как это сделать
Чтобы вычислить степень 10, подумайте: «На сколько раз мне переставить десятичную точку?»
Когда число 10 или больше, десятичная точка должна переместиться на влево , а степень 10 равна положительному .
Когда число меньше 1, десятичная точка должна сместиться на вправо , поэтому степень 10 будет отрицательным .
Пример: записано 0,0055
5,5 × 10 ^-3

Потому что 0,0055 = 5,5 × 0,001 = 5,5 × 10 ^-3
Пример: записано 3.2
3.2 × 10 ⁰

Нам вообще не нужно было перемещать десятичную точку, поэтому степень равна 10 ⁰
Но теперь в научной нотации
Проверить!
После ввода числа в научную нотацию просто проверьте, что:
Цифры от 1 до 10 (может быть 1, но не 10)
«Степенная» часть показывает, на сколько раз нужно переместить десятичную запятую.
Зачем это нужно?
Потому что это облегчает работу с очень большими или очень маленькими числами, которые часто встречаются в научной и инженерной работе.
Пример: проще писать (и читать) 1,3 × 10 ^-9, чем 0,0000000013
Он также может упростить вычисления, как в этом примере:
Пример: крошечное пространство внутри компьютерного чипа было измерено как 0,00000256 м в ширину, 0,00000014 м в длину и 0,000275 м в высоту.
Каков его объем?
Давайте сначала преобразуем три длины в экспоненциальное представление:
ширина: 0.000 002 56m = 2,56 × 10 ^-6
длина: 0,000 000 14м = 1,4 × 10 ^-7
высота: 0,000 275 м = 2,75 × 10 ^-4
Затем умножьте цифры (игнорируя × 10):
2,56 × 1,4 × 2,75 = 9,856
Наконец, умножаем на 10:
10 ^-6 × 10 ^-7 × 10 ^-4 = 10 ^-17 (проще, чем кажется, просто сложите вместе −6, −4 и −7 )
Результат: 9.856 × 10 ^-17 м ³
Много используется в науке:
Пример: Солнца, Луны и планеты
Солнце имеет массу 1,988 × 10 ³⁰ кг.
Легче, чем писать 1 988 000 000 000 000 000 000 000 000 000 кг
(и это число дает ложное представление о точности многих цифр.)
Это также может сэкономить место! Вот что происходит, когда вы удваиваете на каждом поле шахматной доски:

Значения округлены, поэтому 53,6870,912 отображается как 5 × 10 ⁸
Это последнее значение, показанное как 9 × 10 ¹⁸, на самом деле 9 223 372 036 854 775 808
Инженерное обозначение
Engineering Notation похожа на Scientific Notation, за исключением того, что мы используем только те степени десяти, которые кратны 3 (например, 10 ³, 10 ^-3, 10 ¹² и т. Д.).
Примеры:
записано 2700 2,7 × 10 ³
27000 записано 27 × 10 ³
270,000 записано 270 × 10 ³
2,700,000 записано 2,7 × 10 ⁶
Пример: записано 0,00012
120 × 10 ^-6
Обратите внимание, что часть «цифры» теперь может быть от 1 до 1000 (это может быть 1, но никогда не 1000).
Преимущество состоит в том, что мы можем заменить × 10 с метрическими числами. Таким образом, мы можем использовать стандартные слова (например, тысяча или миллион), префиксы (например, кило, мега) или символ (k, M и т. Д.)
Пример: записано 19 300 метров 19,3 × 10 ³ м, или 19,3 км
Пример: записано 0,00012 секунд 120 × 10 ^-6 с или 120 микросекунд
5 способов представления чисел, которые должны знать наши студенты
Важной частью хорошей основы для понимания чисел является знание того, что числа могут быть представлены различными способами.Но студентам также важно знать, что каждое из этих разных представлений означает одно и то же. По мере того, как учащиеся учатся видеть числа по-разному, это помогает им расширить свое понимание числа и его значения. Студентам легко увидеть, что представляет собой число, когда они имеют дело с небольшими числами, такими как 5, 13 или даже 37. Но студенту намного сложнее сосчитать набор из 1359 … и невозможно, когда речь идет о числах, таких как 3,42 x10 ^18. Итак, вместо того, чтобы полагаться на умение считать и видеть, что представляет собой число, мы должны дать нашим ученикам другие инструменты для использования.Вот пять способов представления чисел, которые должны знать наши ученики.
1. Стандартная форма
Это может быть очевидным, но нашим студентам необходимо знать, как писать и читать числа в стандартной форме. Стандартная форма – это запись чисел с помощью цифр, а в математике мы чаще всего пишем числа в стандартной форме. Вот несколько примеров стандартной формы: 138 и 3297. Когда мы учим наших студентов писать числа в стандартной форме, мы также должны научить их читать числа.
Подсказка для учителя: Знаете ли вы, что неправильно говорить «и», когда вы ставите запятую? Многие люди прочитали бы это число (3297) как три тысячи двести девяносто семь.Но это неправильно, и если мы учим этому наших студентов, мы фактически настраиваем их на недопонимание в будущем. Видите ли, слово «и» следует использовать только при чтении числа с десятичной дробью. Это должно звучать так (3 297,5) три тысячи двести девяносто семь и пять десятых.
Стандартная форма может быть базовой, но она важна, поскольку именно так будет записано большинство чисел, с которыми взаимодействуют наши ученики. Они должны уметь правильно писать и читать числа в стандартной форме.Интересный способ попрактиковаться в этом – использовать карточки с цифрами. Раздайте каждому студенту набор карточек с номерами и при необходимости поставьте запятую. Затем произнесите число и попросите учащихся построить его с помощью карточки. После того, как все закончат, попросите их повторить вам номер.
2. Словоформа
Второй наиболее распространенный способ, которым учащиеся будут видеть числа в своей жизни, – это словоформа. Студентам важно знать, что «тридцать пять» и «35» означают одно и то же. Студентам также важно уметь правильно писать числа.Не забывайте важный дефис, начинающийся с числа 21!
Воспроизвести номер «Покажи и расскажи». Раздайте каждому ученику белую доску и маркер для сухого стирания. Назовите число или напишите стандартную форму числа на доске. Студенты напишут число в форме слова. Когда вы скажете «ПОКАЗАТЬ», студенты поднимут свои белые доски, чтобы вы могли их увидеть. Когда вы скажете «СКАЗАТЬ», студенты произнесут номер. Это отличный способ практиковать как словоформу, так и стандартную форму.
3. Таблица значений разряда
Еще один важный способ представления чисел – это таблица значений разряда.Студентам важно понять, что цифра «4» не всегда означает одно и то же. Фактически, очень важно, где эта цифра находится внутри числа. Диаграмма номинальной стоимости – очень полезный инструмент, чтобы увидеть и понять это.
Для учеников младшего возраста или любых учеников, которые добавляют новый столбец в диаграмму разряда, очень полезно попрактиковаться в том, чтобы говорить, что представляет каждая цифра в числе. Вот пример:
Студенты должны научиться определять это число по стандартной форме «двести шестьдесят восемь», а также по разряду: «2 сотни, 6 десятков и 8 единиц».«Учась делать и то, и другое, мы помогаем студентам устанавливать связи между различными числовыми формами.
4. Расширенная форма
После того, как ученики освоятся с таблицей значений разряда и ее значением, можно обучать их работе с числами в развернутой форме. следующий логический шаг. Мне нравится знакомить студентов с расширенной формой, потому что мы встаем и немного активизируемся. Я прошу студентов встать и сказать со мной следующее: «Расширенная форма – это когда я растягиваю число, используя сложение.«Затем мы добавляем несколько движений. Что касается слов« развернутая форма », ученики хлопают в ладоши и держат их вместе перед собой. Затем, как мы говорим «это когда мы вытягиваем число», ученик вытягивает руки прямо в стороны. Наконец, мы поднимаем руки перед собой и скрещиваем их, как знак плюса, как мы говорим «используя сложение». Повторив это пару раз, я прекращаю это делать и просто спрашиваю: «Что такое развернутая форма?» Детям нравится показывать мне, что они знают определение и свои движения.Затем в течение следующих нескольких дней и периодически в течение года меня спрашивали: «Что такое развернутая форма?» и они знают, что делать!

После того, как мы узнаем, что такое развернутая форма, мы научимся записывать ее числами. Я беру таблицу с разметкой и добавляю в ее нижнюю часть несколько знаков «плюс». Затем я добавляю число, и мы начинаем нашу обычную процедуру произнесения числа, записанного в таблице – сначала в стандартной форме, затем в соответствии с его разрядами.
На этот раз, когда мы произносим число с его разрядным значением, я останавливаю класс после каждой цифры.Я мог бы немного мелодраматизировать и сказать что-нибудь вроде: «Что ты сказал?» или “Вы сказали, что в этом номере 4 сотни?” Когда они ответят снова, я моделирую, как мы напишем это в нижней части таблицы в форме.
Это очень конкретный способ для учащихся связать числовую ценность с развернутой формой. По мере того как учащиеся становятся старше и приобретают опыт подсчета пропусков, мне также нравится объединять расширенную форму с некоторой практикой подсчета пропусков. Я мог бы сказать что-то вроде «У этого числа 4 сотни.Давайте посчитаем до 100 четыре раза ».
Мы запишем это в нашу развернутую форму, а затем проделаем то же самое со следующей цифрой.
5. Изображение или представление объекта
Последний способ, которым я учу своих учеников представлять числа, – это с изображением или предметами. В детском саду и в первом классе мы часто используем реальные предметы и подсчитываем их в наборы. Но по мере того, как ученики становятся старше, это становится все труднее. Один из способов помочь с этим – использовать блоки с числовыми значениями. Эти блоки – отличный способ связать свои знания о разрядах с физическим представлением числа.
Проблема в том, что вы часто не получаете достаточно блоков в наборе для представления чисел выше 2 или 3 тысяч. Картинки спешат на помощь! Я люблю учить своих учеников рисовать картинки, изображающие числа. Это не только занимает намного меньше места и не обязательно иметь под рукой блоки и манипуляторы, но и является отличным методом решения проблем.
Я учу своих учеников использовать маленький квадрат как 1, длинный прямоугольник как 10 стержень, большой квадрат как 100 и куб как 1000.Они любят учиться рисовать куб! Они будут использовать эти изображения не только для представления чисел, но и при решении текстовых задач очень высока скорость переноса остатка.
Есть больше способов представления чисел, чем просто рисование блоков значений мест. Учащиеся могут видеть графическое представление чисел через счетные метки, десять рамок или даже рисовать набор объектов. Когда учащиеся могут изобразить число наглядно, тогда вы знаете, что они уже на пути к усвоению того, что означает это число.
Практикуйтесь каждый день
Хотя для ознакомления и обучения каждому из этих представлений чисел требуется урок или два, студентам нужно нечто большее, чтобы практиковаться и овладевать этими представлениями чисел. Вот почему я люблю Числа дня как ежедневное занятие по математике. Всего за несколько минут в день студенты получают много практики – не только с представлениями чисел, но и с различными навыками распознавания ключевых чисел.
Вы можете видеть, что на одной странице задания «Число дня» учащиеся работают с представлениями чисел несколькими способами.В течение недели они будут работать над всеми этими важными представлениями чисел.
Сохраните это на потом
Прикрепите это к своей любимой доске Pinterest в классе, чтобы вы могли быстро вернуться и найти эти советы и идеи по представлению чисел для использования в классе.
Факты сложения сумм с 6
Это полный урок с инструкциями и упражнениями об основных фактах сложения при сумме 6, предназначенных для 1-го класса по математике.Вы можете использовать те же идеи для обучения другим суммам (суммам с 7, 8, 9, 10 и т. Д.).
Видео ниже демонстрирует множество идей и стратегий для изучения основных фактов сложения: группирование сумм, как в этом уроке, трюк с 9-ю, удвоения и многое другое.

1. Шесть бегемотов сгруппированы в две группы по-разному. Напишите дополнительные предложения.
2. Сыграйте «6 Out» и / или «Some Went Hiding» с 6 объектами (см. Введение).
3. Дрель. Не пишите ответы, а решайте их в уме.
4. Сложите числа и напишите сумму в строке.
а. 1 + 5 = ______
г. 2 + 3 = ______ г. 4 + 2 = ______
5. Нарисуйте больше маленьких прямоугольников, чтобы проиллюстрировать пропущенное число.
6.Джек и Джилл по-разному делят 5 огурцов и 6 лимонов. Найдите сколько Джилл получает.
Вы можете накрыть огурцы или лимоны рукой, чтобы помочь.
а. 5
Джек получает: Осталось для Джилл:
2
1
5
3
0
4
г. 6
Джек получает: Осталось для Джилл:
1
4
5
0
2
3
7.Добавлять.
2 + 3 = ______
4 + 1 = ______
3 + 3 = ______
4 + 2 = ______
1 + 3 = ______
1 + 5 = ______
2 + 2 = ______
2 + 4 = ______
Этот урок взят из книги Марии Миллер Math Mammoth Addition 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.

Номера на испанском – испанском 511
Давай Начнем с хороших новостей: нет (почти) разницы между тем, как мы пишем числа на испанском языке и так же, как мы пишем их на английском. Плохие новости в том, что когда мы используем числа в разговоре, они определенно не произносятся так же. Но независимо от того, взяли ли вы его с «Улицы Сезам» или “Исследовательница Дора” вы, наверное, уже знаете по крайней мере несколько Испанские числа.Продолжайте читать, чтобы узнать больше.
Кардинальные числа
“Кардинальное число” – это просто причудливый термин для обозначения чисел. мы используем для подсчета вещей (или для указания времени, даты или возраста). Давайте совершим путешествие по испанским кардинальным числам из cero (0) до un trilión (1,000,000,000,000,000,000) замечая некоторые интересные причуды по пути.
Fun Fact: Cinco – единственный испанский номер с тем же количеством букв, что и число, которое оно представляет.
Первые 10 чисел (а также ноль) все имеют уникальные имена:
серо
ноль
0
uno
одна
1
дос
два
2
трес
три
3
куатро
четыре
4
Синко
пять
5
seis
шесть
6
siete
семь
7
очо
восемь
8
nueve
девять
9
Diez
десять
10
Следующие пять также имеют уникальные имена:
один раз
одиннадцать
11
доче
двенадцать
12
trece
тринадцать
13
catorce
четырнадцать
14
айва
пятнадцать
15
Примечание: Есть два приемлемых варианта записи числа с 16 по 19.”Старая школа” – просто сказать “десять и шесть, “десять и семь” и т. д. Новый метод заключается в объединении эти слова в одно слово. В этот момент «z» в строке diez становится «c», а «y» становится «i». Обе версии произносятся одинаково. В настоящее время отдается предпочтение более коротким, сложным словам.
После этого числа складываются в комбинации. Вы буквально говорите «десять и шесть», «десять и семь», «десять и восемь», др .:
dieciséis / diez y seis
шестнадцать
16
diecisiete / diez y siete
семнадцать
17
dieciocho / diez y ocho
восемнадцать
18
Diecinueve / diez y nueve
девятнадцать
19
Veinte означает «двадцать», и с этого момента узор очень похож на с шестнадцати по девятнадцать; вы буквально говорите «двадцать и один», «двадцать два» и т. д.:
Примечание: Опять же, желательно их конденсировать. числа до одного слова, заменив завершающий “-e” и «y» с «i». Двадцать два, двадцать три и двадцать шесть также потребуется дополнительный знак ударения.
вене
двадцать
20
veintiuno / veinte y uno
двадцать один
21
veintidós / veinte y dos
двадцать два
22
veintitrés / veinte y tres
двадцать три
23
veinticuatro / veinte y cuatro
двадцать четыре
24
veinticinco / veinte y cinco
двадцать пять
25
прожил / выдержан и сейчас
двадцать шесть
26
veintisiete / veinte y siete
двадцать семь
27
veintiocho / veinte y ocho
двадцать восемь
28
veintinueve / veinte y nueve
двадцать девять
29
После veinte следует treinta , и следует тот же образец:
Примечание: После двадцатых годов мы больше не сокращаем наши числа одним словом.
трэйнта
тридцать
30
трэйнта и ун
тридцать один
31
трэйнта и дос
тридцать два
32
трэв и трес
тридцать три
33
и т. Д.
и т. Д.
Все числа сороковых, пятидесятых, шестидесятых, семидесятых, восьмидесятые и девяностые работают так же, как и в тридцатые:
куарента
сорок
40
чинкуента
пятьдесят
50
cincuenta y uno
пятьдесят один
51
сеента
шестьдесят
60
сети
семьдесят
70
очента
восемьдесят
80
очента и синко
восемьдесят пять
85
новента
девяносто
90
Примечание: Множественное число cien – это cientos (не cienes .)
Технически ciento означает «сто» на испанском языке, но его сокращенная форма, cien , предпочтительнее, когда есть ровно 100 чего-то:
cien
сотня
100
ciento uno
сто
101
ciento dos
сто два
102
ciento tres
сто три
103
и т. Д.
и т. Д.
Вы могли заметить, что y больше нет. “Это потому что “y” используется только для отделения десятков от единиц место. Если в разряде 10 нет ничего, мы не используем «y».
ciento diez
сто десять
110
ciento veinte
сто двадцать
120
ciento veintiuno
сто двадцать один
121
ciento treinta y cinco
сто тридцать пять
135
и т. Д.
и т. Д.
Ciento следует:
doscientos
двести
200
doscientos cincuenta
двести пятьдесят
250
trescientos
триста
300
cuatrocientos
четыреста
400
quinientos
пятьсот
500
seiscientos
шестьсот
600
setecientos
семьсот
700
ochocientos
восемьсот
800
novecientos
девятьсот
900
«Одна тысяча» на испанском языке – это мил .И мы не un mil ; это просто мил :
мил
одна тысяча
1.000
мил quinientos
одна тысяча пятьсот
1.500
дос мил
две тысячи
2.000
трес мил
три тысячи
3.000
и т. Д.
и т. Д.
После тысяч идут десятки и сотни тысяч:
Примечание: В составных числах используйте ciento , если следующее число меньше 100. Используйте cien , если следующее число больше 100.
diez mil
десять тысяч
10.000
Сиен Мил
сто тысяч
100,000
ciento treinta mil
сто тридцать тысяч
130.000
doscientos mil
двести тысяч
200.000
trescientos mil
триста тысяч
300.000
и т. Д.
и т. Д.
Далее тысяча тысяча – это миллион или un millón .Когда мы переходим от одного миллиона, миллонов становятся миллионами :
un millón
один миллион
1.000.000
un millón doscientos mil
один миллион двести тысяч
1.200,000
доз миллонов
два миллиона
2.000.000
трем миллонов
три миллиона
3.000.000
и т. Д.
и т. Д.
Примечание: На самом деле разница в языках не так уж велика. поскольку это разница в способах подсчета очень больших чисел. Исторически там есть разногласия даже между англоязычными странами относительно того, что именно «миллиард» представляет.
Бонус: см. Длинная и короткая шкалы
Теперь все становится немного странно.Добавление трех нулей к миллиону в английском языке приводит нас к миллиарду. Но по-испански это mil millón , или тысяча миллионов. Это нарушает синхронизацию остальной части диаграммы с тем, что мы могли бы также ожидать:
млн миллонов
один миллиард
1.000.000.000
дос мил миллонов
два миллиарда
2.000.000.000
un billón
один триллион
10 ¹²
млн биллонов
один квадриллион
10 ¹⁵
un trillón
один квинтиллион
10 ¹⁸
Кардинальные числа как прилагательные
Если вы просто считаете числа (как в «Прятках», пока ваши друзья скрытие) приведенный выше список является точным.Однако в большинстве случаев, когда мы используем число мы добавляем существительное, например «шесть вагонов», «24 стола», «38 домов» и т. Д. Когда мы делаем это, мы фактически используем число как прилагательное и должны произойти некоторые интересные вещи.
Прежде всего uno сокращается до и , когда оно стоит перед существительным мужского рода, и аналогично числа, заканчивающиеся на « -uno », сокращаются до « -ún » (примечание знак ударения). Ciento также сокращается до cien , когда (и только когда) мы имеем дело ровно с сотней чего-то. Например:
un coche
veintiún coches
cien coches
ciento tres coches
Во-вторых, как и в случае с другими прилагательными, нам нужно привести наши числа в соответствие по полу с существительные, которые они модифицируют. Однако это происходит только с номерами, оканчивающимися на « -uno » и слова, оканчивающиеся на « -ientos » (все «сотни» слова от 200 до 900).Например:
мужской род:
женский:
шт. коше
un a casa
veintiún coches
veintiun a casas
cien coches
cien casas
quinientos койки
quinient a s касас
Каждая часть числа, которая может соответствовать пол существительного должен согласовываться.Например, будет выписано 654 321 таблица. как “ seiscient a s cincuenta y cuatro mil trescient a s veintiun a mesas .”
Десятичная точка и запятая
Вы могли заметить странно выглядящие десятичные дроби в правом столбце выше. Это не опечатка. Большинство испаноязычных стран делают противоположность англоязычных. страны, когда дело доходит до десятичных знаков и группировки тысяч: используются запятые для десятичных знаков и точек используются для разделения групп нулей.Номер «21,7» будет написано «21,7» на испанском языке и будет читаться. “ veintiuno punto siete .”
Порядковые номера
В то время как мы используем количественные числа для счета вещей, мы используем “порядковые числа”, чтобы навести порядок. (например, порядок, в котором бегуны заканчивают забег). Вот испанские порядковые номера:
пример
первая
второй
второй
tercero
третья
куарто
четвертый
quinto
пятая
sexto
шестой
séptimo
седьмой
октаво
восьмой
новено
девятый
décimo
десятая
undécimo / decimoprimero
одиннадцатый
duodécimo / decimosegundo
двенадцатая
décimo tercero
тринадцатый
décimo cuarto
четырнадцатый
и т. Д.
и т. Д.
—
—
vigésimo
двадцатая
vigésimo primero
двадцать первая
vigésimo segundo
двадцать второй
и т. Д.
и т. Д.
—
—
тригезимо
тридцатая
cuadragésimo
сороковая
quincuagésimo
пятидесятая
секс
шестидесятые
septuagésimo
семидесятых
восемьдесят девять
восьмидесятые
nonagésimo
девяностые
Centésimo
сотых
миль
тысячная
último
последние
При использовании в качестве прилагательных все порядковые числа совпадают по полу с существительным они модифицируются, поэтому окончания “-o” меняются на “-a” с существительными женского рода.Например: la segunda casa , su tercera novia , миль última tarea .
Порядковые номера primero и tercero сокращаются до primer и tercer при использовании с существительными мужского рода. Например; en primer lugar , en Tercer Grado . Это верно только для primero и tercero .
Когда порядковый префикс, оканчивающийся на «- imo », комбинируется с « octavo », одна из точек опускается, чтобы избежать повторения одного и того же звука, например.грамм. “ decimoctavo .”
Порядковые числа обычно не используются с датами; используйте вместо них количественные числа: «Hoy es el quince de enero».
Мы часто используем что-то вроде сокращенного обозначения порядковых номеров на английском языке – 1-й, 2-й, 3-й и т. Д. Мы можем сделать нечто подобное на испанском языке – 1º, 2º, 3º и т. Д. (Или 1ª, 2ª, 3ª и т. Д., Если женский род)
Дроби
ср выразите испанские дроби следующим образом:
un entero
целое (1/1)
УНА МИТАД
один половина (1/2)
дос терсиос
два трети (2/3)
tres cuartos
три четверти (3/4)
Куатро Квинтос
четыре пятые (4/5)
cinco sextos
пять шестых (5/6)
seis séptimos
шесть седьмых (6/7)
siete octavos
семь восьмых (7/8)
очо новенос
восемь девятых (8/9)
nueve décimos
девять десятых (9/10)
—
—
один разавос
одиннадцатая
doceavos
двенадцатая
treceavos
тринадцатые
catorceavos
четырнадцатые
айвы
пятнадцатая
dieciseisavos
шестнадцатая
diecisieteavos
семнадцатые
dieciochoavos
восемнадцатые
diecinueveavos
девятнадцатые
вейнтеавос
двадцатая
—
—
сентаво
сотых
От «четвертых» до «десятых» мы просто используем порядковые числа.От «одиннадцатого» до «двадцатого» мы используем количественные числа с суффиксом , избегая . Помимо «двадцатых» мы просто используем порядковый номер со словом parte . Например: un trigésimo parte .
Кратное
Примечание: Множественные числа могут также иметь мужские и женские формы: cuádruplo , cuádrupla .
Мы используем “мультипликативы”, чтобы сделать число кратным. Испанские мультипликаторы похожи на английские:
двойных
двойной
тройной
тройной
куб. Группа
четырехместный
пятиместный
пятиместный
шестой
шестиместный
номер
семиместный
двухместная
восьмеричный
нет
без пары
открыто
двойная
и т. Д.
и т. Д.
В процентах
Проценты в испанском написаны так же, как и в английском. Слово «процент» на испанском языке – por ciento .
6 портов
6 процентов (6%)
75 por ciento
75 процентов (75%)
99 por ciento
99 процентов (99%)
Интересные факты о числах
При записи чеки на испанском языке допустимо (и неплохо) написать “ un mil ” вместо грамматически правильного “ mil “, чтобы никто не изменил сумма чека.
Написание «два или три» на испанском языке выглядит как это, «2 o 3», и его, возможно, можно спутать с «203». Из-за этого во избежание путаницы иногда ставится ударение на «или»: «2 – 3.

	Когда число 10 или больше, десятичная точка должна переместиться на влево , а степень 10 равна положительному .

	Когда число меньше 1, десятичная точка должна сместиться на вправо , поэтому степень 10 будет отрицательным .

серо	ноль	0
uno	одна	1
дос	два	2
трес	три	3
куатро	четыре	4
Синко	пять	5
seis	шесть	6
siete	семь	7
очо	восемь	8
nueve	девять	9
Diez	десять	10

один раз	одиннадцать	11
доче	двенадцать	12
trece	тринадцать	13
catorce	четырнадцать	14
айва	пятнадцать	15

dieciséis / diez y seis	шестнадцать	16
diecisiete / diez y siete	семнадцать	17
dieciocho / diez y ocho	восемнадцать	18
Diecinueve / diez y nueve	девятнадцать	19

вене	двадцать	20
veintiuno / veinte y uno	двадцать один	21
veintidós / veinte y dos	двадцать два	22
veintitrés / veinte y tres	двадцать три	23
veinticuatro / veinte y cuatro	двадцать четыре	24
veinticinco / veinte y cinco	двадцать пять	25
прожил / выдержан и сейчас	двадцать шесть	26
veintisiete / veinte y siete	двадцать семь	27
veintiocho / veinte y ocho	двадцать восемь	28
veintinueve / veinte y nueve	двадцать девять	29

трэйнта	тридцать	30
трэйнта и ун	тридцать один	31
трэйнта и дос	тридцать два	32
трэв и трес	тридцать три	33
и т. Д.	и т. Д.

куарента	сорок	40
чинкуента	пятьдесят	50
cincuenta y uno	пятьдесят один	51
сеента	шестьдесят	60
сети	семьдесят	70
очента	восемьдесят	80
очента и синко	восемьдесят пять	85
новента	девяносто	90

cien	сотня	100
ciento uno	сто	101
ciento dos	сто два	102
ciento tres	сто три	103
и т. Д.	и т. Д.

ciento diez	сто десять	110
ciento veinte	сто двадцать	120
ciento veintiuno	сто двадцать один	121
ciento treinta y cinco	сто тридцать пять	135
и т. Д.	и т. Д.

doscientos	двести	200
doscientos cincuenta	двести пятьдесят	250
trescientos	триста	300
cuatrocientos	четыреста	400
quinientos	пятьсот	500
seiscientos	шестьсот	600
setecientos	семьсот	700
ochocientos	восемьсот	800
novecientos	девятьсот	900

мил	одна тысяча	1.000
мил quinientos	одна тысяча пятьсот	1.500
дос мил	две тысячи	2.000
трес мил	три тысячи	3.000
и т. Д.	и т. Д.

diez mil	десять тысяч	10.000
Сиен Мил	сто тысяч	100,000
ciento treinta mil	сто тридцать тысяч	130.000
doscientos mil	двести тысяч	200.000
trescientos mil	триста тысяч	300.000
и т. Д.	и т. Д.

un millón	один миллион	1.000.000
un millón doscientos mil	один миллион двести тысяч	1.200,000
доз миллонов	два миллиона	2.000.000
трем миллонов	три миллиона	3.000.000
и т. Д.	и т. Д.

млн миллонов	один миллиард	1.000.000.000
дос мил миллонов	два миллиарда	2.000.000.000
un billón	один триллион	10 ¹²
млн биллонов	один квадриллион	10 ¹⁵
un trillón	один квинтиллион	10 ¹⁸

мужской род:	женский:
шт. коше	un a casa
veintiún coches	veintiun a casas
cien coches	cien casas
quinientos койки	quinient a s касас

	пример	первая
	второй	второй
	tercero	третья
	куарто	четвертый
	quinto	пятая
	sexto	шестой
	séptimo	седьмой
	октаво	восьмой
	новено	девятый
	décimo	десятая
	undécimo / decimoprimero	одиннадцатый
	duodécimo / decimosegundo	двенадцатая
	décimo tercero	тринадцатый
	décimo cuarto	четырнадцатый
	и т. Д.	и т. Д.
	—	—
	vigésimo	двадцатая
	vigésimo primero	двадцать первая
	vigésimo segundo	двадцать второй
	и т. Д.	и т. Д.
	—	—
	тригезимо	тридцатая
	cuadragésimo	сороковая
	quincuagésimo	пятидесятая
	секс	шестидесятые
	septuagésimo	семидесятых
	восемьдесят девять	восьмидесятые
	nonagésimo	девяностые
	Centésimo	сотых
	миль	тысячная
	último	последние

	un entero	целое (1/1)
	УНА МИТАД	один половина (1/2)
	дос терсиос	два трети (2/3)
	tres cuartos	три четверти (3/4)
	Куатро Квинтос	четыре пятые (4/5)
	cinco sextos	пять шестых (5/6)
	seis séptimos	шесть седьмых (6/7)
	siete octavos	семь восьмых (7/8)
	очо новенос	восемь девятых (8/9)
	nueve décimos	девять десятых (9/10)
	—	—
	один разавос	одиннадцатая
	doceavos	двенадцатая
	treceavos	тринадцатые
	catorceavos	четырнадцатые
	айвы	пятнадцатая
	dieciseisavos	шестнадцатая
	diecisieteavos	семнадцатые
	dieciochoavos	восемнадцатые
	diecinueveavos	девятнадцатые
	вейнтеавос	двадцатая
	—	—
	сентаво	сотых

	двойных	двойной
	тройной	тройной
	куб. Группа	четырехместный
	пятиместный	пятиместный
	шестой	шестиместный
	номер	семиместный
	двухместная	восьмеричный
	нет	без пары
	открыто	двойная
	и т. Д.	и т. Д.

	6 портов	6 процентов (6%)
	75 por ciento	75 процентов (75%)
	99 por ciento	99 процентов (99%)