Образец написания цифры 5: Число и цифра 5. Письмо цифры 5 | Начальная школа

«Число 5. Цифра 5». Конспект открытого занятия по ФЭМП в старшей группе

Цель: дать детям представление о числе 5, его составе, о письменном обозначении числа 5.

Задачи:

• Знакомить с образованием и составом числа 5, с цифрой 5.
• Развивать навык устного счета в пределах 1 до 5.
• Закрепить умение соотносить цифру 5 с количеством.
• Закрепить представление о порядке увеличения и уменьшения размеров.
• Закрепить пространственные отношения: слева, справа, верх, низ, посередине, между. Уточнить представления о формах геометрических фигур – квадрат, треугольник, круг, прямоугольник, овал.
• Развивать внимание, мышление, мелкую и общую моторику.
• Воспитывать любознательность, самостоятельность, умение работать сообща, стремление помогать друг другу.

Тип занятия: комплексное.

Виды деятельности: коммуникативная, игровая, двигательная.

 

Ход НОД

Воспитатель: Ребята, к нам сегодня в гости должен был прийти сказочный герой. Он так сильно к нам торопился, что упал и разлетелся на части.

Как вы думаете, кто этот герой?

Воспитатель: Снеговик пришел к вам не просто так, а посмотреть, как вы занимаетесь. И хотел нас познакомить с чем-то важным. Но с ним произошла вот такая неприятность. Ребята, что делать?

Дети: Давайте его соберем.

Воспитатель: Посмотрите на картинку, она поможет нам его собрать.

Возьмем большой снежный ком. Какую объемную геометрическую форму он имеет? Дети: Форму шара.

Воспитатель: Потом поменьше – это туловище. Еще меньше – это голова. Два самых маленьких – это руки. Сколько всего нам понадобится шаров? Посчитаем.

Воспитатель: Нам понадобится 5шаров. А у нас сколько?

Дети: 4

Воспитатель: Я не нашла еще один, что делать? Нашли.

Давайте построим снеговика.

Воспитатель: Сколько было шаров в начале? Было 4 шара.

А потом еще сколько принесли? Принесли еще 1.

На сколько увеличилось число шаров? На один.

Сколько их стало? 5.

Как это записать? 4 +1= 5.

Ставит цифру 5.

Воспитатель: Собрали мы снеговика. Давайте с ним познакомимся.

Снеговика зовут так же, как называется пятый день недели. Догадались, как зовут снеговика?

Воспитатель: Так как вы думаете, с чем таким важным он нас хотел познакомить? С цифрой 5.

Воспитатель: Ребята, снеговик хочет с вами поиграть. Хотите?

Подвижная игра «Найди свое место»

Дети идут по кругу, в центре которого лежат перевернутые цифры, по сигналу воспитателя каждый берет себе цифру и находит свое место в ряду, расставив числа по порядку.

Игра повторяется 2 раза. Играют девочки, затем мальчики.

Воспитатель: Ребята, посмотрите, у нас получился числовой ряд.

Где располагается число 5 в числовом ряду? (после 4, перед 6, между 4 и 6).

Посчитайте до 5 и обратно.

Воспитатель: Ребята, чем примечательно это число? Чем отличается от других и где встречается? (лучшая отметка в школе, пять лучей у звезды, пять пальцев на руке)

Кто из вас раньше видел цифру 5? Где? (номер дома, монета, страница учебника, на линейке)

Воспитатель: Снеговик просит меня показать вам, как писать цифру пять.

Показ образца написания цифры 5 на доске, сопровождающийся следующими пояснениями:

Воспитатель: Сегодня мы научимся писать цифру 5. Вот так она выглядит.

Ведем палочку наклонно, потом вправо пишем полуовал. Сверху от палочки вправо пишем волнистую линию.

Давайте вместе указательным пальцем в воздухе пропишем цифру 5.

А сейчас давайте изобразим цифру 5 из материала, который лежит перед вами на столах.

Пластилин, фасоль, шнурки, счетные палочки, мозаика.

Молодцы, у всех получились разные цифры, но у всех цифры 5.

Деление на пары. Игра «Найди пару» состав числа.

Воспитатель: Выходите из-за столов. Сейчас вам надо разделиться на пары, но не просто так, а с помощью этих карточек. Сейчас каждый вытянет по одной карточке с цифрой. Вы должны найти свою пару, чтобы сумма чисел равнялась 5.

У детей карточки с цифрами от 1 до 4, дети должны найти свою пару, чтобы сумму чисел равнялась 5.

Давайте проверим, правильно ли вы нашли себе пару.

…, почему ты взяла себе в пару …. Потому что, если к 1 прибавить 4 получиться 5.

На доске воспитатель делает записи, раскрывающие состав числа 5:

1+4

2+3

3 + 2

4+1

Если дети не правильно выбрали пару, нужно предложить детям поискать другие варианты и обосновать их.

Соотнесение числа и цифры. Работа за столами.

Воспитатель: Разделились на пары, теперь парами проходите за любые столы.

Перед вами на столе у каждого лежит лист с заданием и у меня такой же лист с заданием только висит на доске.

Воспитатель вызывает к доске ребенка, для работы возле доски.

Снеговик спешил, сам разлетелся, и все цифры разлетелись.

Задание такое, вы должны посчитать, сколько точек изображено на карточке, и соотнести с нужной цифрой.

Воспитатель: Давайте проверим, все ли выполнили задание правильно.

Молодцы! Справились с заданием.

Игра «Найди лишнюю фигуру». Повторение геометрических фигур.

У вас на столе у каждого лежит тарелочка с фигурами и лист белой бумаги.

Какие фигуры вы видите? Квадрат, прямоугольник, круг, овал, треугольник, звезда.

Для того чтобы выполнить следующее задание, вы должны будете вспомнить понятия: право, лево, верх, низ, между, посередине.

Положите в левый верхний угол – квадрат.

Положите в правый нижний угол – прямоугольник.

Положите в центр альбомного листа – звезду.

Положите в правый верхний угол – круг.

Положите в левый нижний угол – треугольник.

Положите между треугольником и прямоугольником – овал.

Воспитатель: Поменяйтесь листочками, на которых вы выполняли задание со своим соседом. Проверьте, верно ли выполнил задание ваш сосед.

После того, как дети проверили задание друг у друга, демонстрируется образец на доске.

Воспитатель: А теперь давайте посмотрим, как у вас должно было получиться.

Воспитатель: Назовите лишнюю фигуру. Звезда.

Почему? Это не геометрическая фигура.

Правильно! Молодцы!

Сколько концов у звезды? 5.

Сколько углов, вершин? Тоже 5.

Рефлексия: Педагог раздает листочки с заданием, дети выполняют: соединить все точки по порядку, начиная от единицы…до 5.

Должна получиться цифра 5.

Итог занятия: Ребята, с чем сегодня вас познакомил снеговик?

Какое задание было самым интересным?

Какое задание было для вас трудным?

Кто, по вашему мнению, работал сегодня лучше всех?

Что у вас получилось, когда вы соединили все точки?

Да, это цифра 5. Именно этой оценкой мы со снеговиком оценили вашу работу. Молодцы! Всем спасибо.

ЧИСЛО И ЦИФРА 5. ОБРАЗОВАНИЕ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТИЕ «ПЯТЫЙ». КОЛИЧЕСТВЕННАЯ И ПОРЯДКОВАЯ СЧЕТ. «СОСЕДИ» ЧИСЛА. НАПИСАНИЕ ЦИФРЫ 5 – ПРИЗНАКИ И СВОЙСТВА ПРЕДМЕТОВ. МНОЖЕСТВА. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. НАТУРАЛЬНЫЕ ЧИСЛА 1-10 И ЧИСЛО 0 – Математика. 1 класс. Семестр – конспекты уроков – План урока – Конспект урока – Планы уроков

ПРИЗНАКИ И СВОЙСТВА ПРЕДМЕТОВ. МНОЖЕСТВА. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. НАТУРАЛЬНЫЕ ЧИСЛА 1-10 И ЧИСЛО 0

 

Урок 20. ЧИСЛО И ЦИФРА 5. ОБРАЗОВАНИЕ ЧИСЛА ПРИЛІЧУВАННЯМ 1. ПОНЯТИЕ «ПЯТЫЙ». КОЛИЧЕСТВЕННАЯ И ПОРЯДКОВАЯ СЧЕТ. «СОСЕДИ» ЧИСЛА. НАПИСАНИЕ ЦИФРЫ 5

 

Цель: ознакомить учащихся с образованием числа 5 и цифрой 5; учить писать цифру 5, сравнивать числа в пределах 5; упражнять учащихся в порядковій и количественном счете; развивать мышление; воспитывать внимательность.

Ход урока

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

 

II. ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1. Веселый счет

• На лужайке среди лозы,

Спрятались две козы,

А тут стоят еще две

В густой обильной траве.

Посчитаем вместе,

Сколько всех тех коз вместе?

 

• В класс зашел Мишка,

А за ним – Петько,

А за ним – Галинка,

А за ней – Яринка,

А позади – Игнат.

Сколько здесь малышей?

2. Игра «Цепочка»

– Посчитайте от 1 до 10; от 5 до 1; от 1 до 5; от 5 до 10; от 3 до 6.

3. Игра «Закончи предложение»

• Если Антон выше, чем Кирилл, то Кирилл…

• Если Катя сидит справа от Анны, то Анна сидит…

• Если Игорь живет дальше от школы, чем Оля, следовательно, Оля живет…

• Если сестра старше брата, то брат…

• Если буханка хлеба дороже, чем батон, то батон. ..

• Если осенью холоднее, чем летом, тогда летом…

 

III. ОЗНАКОМЛЕНИЕ С НОВЫМ МАТЕРИАЛОМ

1. Вступительное слово учителя

Сколько пальцев на руке

Можно сожмут в кулаке?

Их нетрудно сосчитать:

Раз, два, три, четыре, пять!

– Какое число будем изучать на уроке?

2. Работа по учебнику (с. 27)

Задача 1

1) Беседа по рисунку.

– Скольких животных встретил лошадь?

– Сколько их теперь? Который по порядку лошадь? Каким был бык? А козенятко?

– Как образовалось число 5? Какой цифрой обозначают число 5?

2) Ознакомление с печатной цифрой 5.

Вот и вышла погулять

На бумаге цифра 5.

Руку вправо протянула,

Ножку баранкой согнула.

Задание 2

– Сколько всего скейтов? Каким по порядку желтый скейт? а синий? А если считать справа налево?

Задание 3

– Назовите «соседей» числа 2; 3; 4.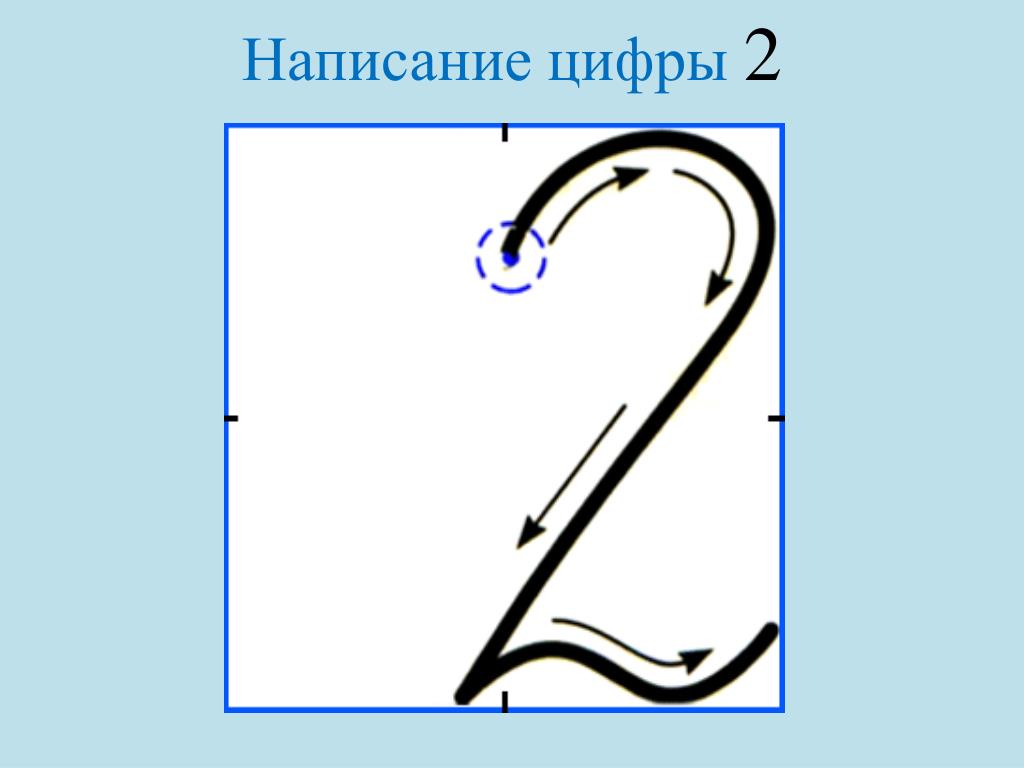

Задание 4

– Заполните пропуски в предложениях.

– Рассмотрите поезд. Кто сел в вагончик с цифрой 4? В какой вагончик слева направо села цифра 5? А справа налево?

Физкультминутка

 

IV. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1. Работа с наборным полотном

– Сколько бабочек слева? справа?

– Как получили число 5?

2. Сравнение чисел в пределах 5 [на основе материала для счета)

– Сравните числа каждой пары, используя слова «больше», «меньше», «равно».

4 5 5 > 3 5 = 5

3. Игра «Найди цифру 5»

 

 

4. Ознакомление с рукописной цифрой 5

1) Объяснение учителя.

– Цифра 5 состоит из маленькой прямой палочки, правого півовала и горизонтальной волнистой линии. Сначала пишется маленькая прямая палочка. Начинают ее писать немного правее середины верхней стороны клетки (как и цифру 4) и ведут наклонно к центру клетки.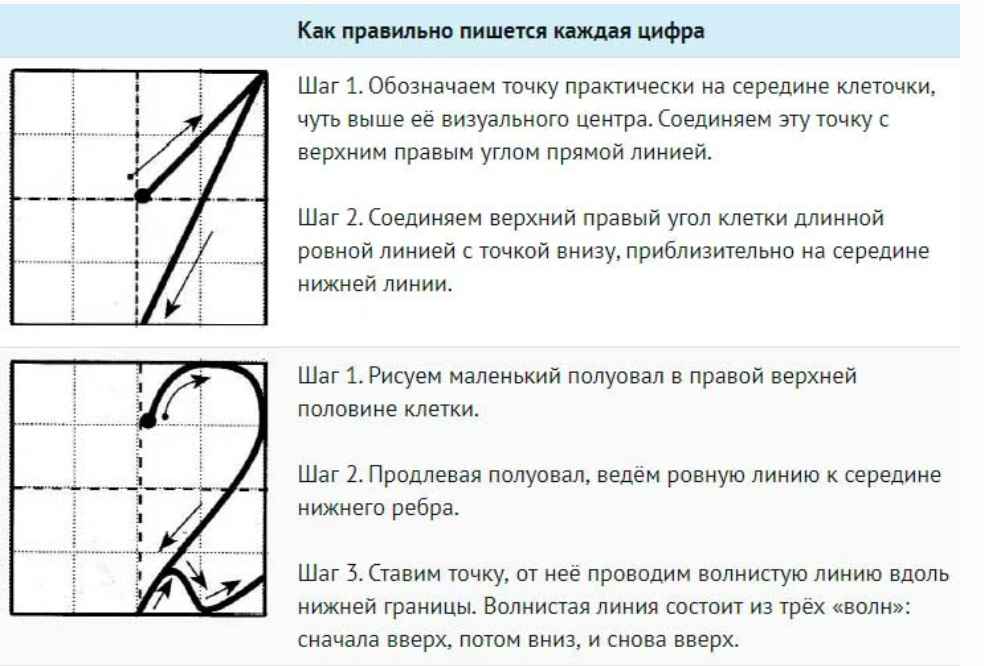 С этой точки пишут малый правый полуовал – такой же, как второй элемент в цифры 3. Затем вверху слева направо пишутся последний элемент (слегка изогнутая палочка вниз). Начало его совпадает с началом первого элемента цифры, а заканчивается элемент в верхнем правом углу клетки.

2) Написание цифры в воздухе под счет «раз-и, два-и».

3) Написание в тетради.

 

V. ИТОГ УРОКА. РЕФЛЕКСИЯ

Загадка

Стоит хлев на четверо овец,

А на пятую – отдельно. (Варежка)

– Какую цифру и число изучали на уроке?

Система счисления – определение, типы, преобразование, примеры, факты

Что такое числа?

Число — это арифметическое значение, используемое для представления количества. Следовательно, число — это математическое понятие, используемое для подсчета, измерения и обозначения. Таким образом, числа составляют основу математики.

Например это 1 бабочка а это 4 бабочки.

История чисел

Надписи, найденные на археологических раскопках, показывают, что ранние люди использовали различные символы для обозначения чисел. Например, древние земледельцы, торговцы и торговцы использовали счетные метки для отображения количества. В подсчетах для каждого счета рисуется стоячая линия, а пятый счет показывается путем вычеркивания четырех линий. Однако это был утомительный способ, и было невозможно показать количество.

С развитием ранних цивилизаций стали использоваться различные способы записи чисел. Они использовали разные символы, чтобы показать большие количества. Но даже с этими системами было непросто показывать большие объемы.

Примерно в седьмом веке в Индии был усовершенствован десятичный (или десятичный) позиционный метод. Этот метод использовал десять уникальных символов для представления любого числа или количества. Это символы 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.

Эта система была распространена по Европе арабскими купцами, учеными и завоевателями.

Эта система называется индийско-арабской системой счисления, и на сегодняшний день она остается наиболее распространенной системой представления чисел.

Числа в повседневной жизни

Числа используются повсюду вокруг нас. Дата вашего рождения имеет числа, обозначающие день, месяц и год вашего рождения.

Числа используются для отслеживания времени. Мы пользуемся часами, которые показывают нам время. Мы планируем наш день и события в соответствии со временем.

Числа тоже участвуют в покупке и продаже. Чтобы считать деньги и единицы товара, мы используем числа.

Для измерения используются числа. Температура, вес, длина, емкость, скорость, расстояние, площадь, объем и т. д. измеряются с помощью чисел.

Числа также играют важную роль в нашем теле. У нас есть 2 глаза, 2 уха, 1 нос, 2 руки, 2 ноги, а в теле взрослого человека 206 костей.

У наших домов есть номера, у банковских счетов есть номера, как и у наших машин, автобусов, поездов и самолетов.

Представление номера

1. Цифры 0-9

Система счисления — это система записи для обозначения чисел с использованием цифр или символов в логическом порядке.

Мы используем цифры от 0 до 9 для формирования всех остальных чисел.

С помощью этих цифр мы можем создавать бесконечные числа.

Например, , 121; 34 987; 2 987 633; 459 227 904; …

Эта система счисления, использующая 10 цифр, называется десятичной системой счисления.

2. Алфавитная форма номера

Числовые слова — это алфавитная форма чисел. Как следует из названия, это числа, написанные словами.

Например:

1 Один

2 Два

15 Пятнадцать

33 Тридцать три 

3. Символически, с использованием цифр
4. 3
5. 3
6. 3

Числовые символы — это цифры, такие как индийско-арабские цифры (например: 112, 415, 999) или римские цифры (I, II, V, VIII).

Количественные и порядковые числительные

Кардинальные числа являются счетными числами. Числа, которые мы используем для счета, называются количественными числами.

Числа говорят нам, сколько есть вещей, предметов или объектов.

Пример: 1, 2, 3, 10, 158

Порядковые числа дают нам точное положение вещи, предмета или объекта в списке. Порядковые номера говорят о положении объекта, а не о его количестве.

Пример: 1-й, 2-й, 3-й, 9-й, 150-й 

Типы чисел

Кроме перечисленных, существуют и другие числа, а именно четные и нечетные числа, простые числа и составные числа. Их можно определить следующим образом:

Дробные и десятичные числа:

Решенные примеры чисел

Пример 1. Классифицируйте данный набор чисел как дроби или десятичные числа.

7/12; 0,0008; 1,52; 100/10; 4 1/2; 7555.0

Решение:

Пример 2. Запишите числитель и знаменатель заданных рациональных чисел.

1. 17/21 (б) 4/5 (в) 25/22

Решение:

Пример 3: Запишите числа словами.

1. 548
2. 1 660

Решение:

1. Пятьсот сорок восемь.
2. Одна тысяча шестьсот шестьдесят.

Практические задачи

1

Сколько нечетных чисел находится между 64 и 90?

11

12

13

14

Правильный ответ: 13
65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89

2

Сумма простых чисел от 10 до 20 и от 30 до 40 равна

5

6

7

8

Правильный ответ: 6
Простые числа от 10 до 20 равны 11 и 119, 17 , есть 4 простых числа от 10 до 20. Простые числа от 30 до 40 – это 31 и 37 Итак, есть 2 простых числа от 30 до 40. Сумма = 4 + 2 = 6

3

Four thousand eight hundred and eight in numeral form is written as:

4,880

4,808

4,800

48,008

Correct answer is: 4,808
4,000 + 800 + 8 = 4,808

4

Что за число -5?

Натуральное число

Целое число

Целое число

Правильный ответ: Целое число
–5 — отрицательное число, поэтому оно целое.

Часто задаваемые вопросы

Как определить, четное число или нечетное?

Если число делится на 2 без остатка, то это четное число. Если число делится на 2 и в остатке остается 1, то это нечетное число.

Является ли ноль четным числом?

При делении нуля на 2 в частном получается 0 и в остатке тоже 0. Итак, ноль — четное число.

Могут ли рациональные числа быть отрицательными?

Да, рациональные числа классифицируются как положительные, нулевые или отрицательные рациональные числа.

Дроби считаются целыми числами?

Целые числа не включают дроби и десятичные дроби.

Числа и статистика — Purdue OWL®

Писателям часто приходится обсуждать числа и статистику в своих рукописях, и может быть непросто определить, как представить их в наиболее удобочитаемом виде. APA 7 содержит подробные инструкции по написанию чисел и статистики, наиболее распространенные из которых перечислены ниже. Эти рекомендации, однако, не являются исчерпывающими, и авторам может потребоваться оценить отдельные экземпляры чисел в своем собственном письме, чтобы определить, применимы ли рекомендации или следует сделать исключение для ясности.

Номера

Как правило, вы можете писать числа меньше 10 словами (семь, три) и использовать цифры для чисел от 10 и выше (10, 42).

• Вы должны использовать арабские цифры (1, 7) вместо римских цифр (II, XI), если только римские цифры не являются частью устоявшейся терминологии в вашей области.
• В числах больше 1000 используйте запятые для разделения групп из трех цифр, за исключением номеров страниц, двоичного кода, серийных номеров, температур, акустических частот и степеней свободы.
• Не добавляйте апострофы при написании множественного числа числа (2000-е, 70-е).

В этих случаях используйте цифру:

• число 10 или выше в любом месте бумаги
• число перед единицей измерения (3 м, 24 г)
• число, обозначающее: математические функции, дроби, десятичные дроби, проценты, соотношения, процентили (соотношение 2:1, 5%)
• число, обозначающее: время, дату, возраст, точку на шкале, точную сумму денег или цифру (клавиша 3 на клавиатуре, 7 лет, 5 на тесте)
• номер, обозначающий место в серии или часть книги/таблицы, если номер стоит после существительного (т. е. пункт 4, но слова используются в случаях типа «четвертый пункт»)

Произнесите число прописью в следующих случаях:

• число от 0 до 9 в любом месте документа, за исключением особых случаев выше
• номер, с которого начинается предложение, заголовок или заголовок (хотя этого следует избегать)
• число, являющееся обыкновенной дробью (половина, две трети)
• число, которое является частью общей фразы (Благородный Восьмеричный Путь)

Когда числа в предложении написаны рядом друг с другом, одна из стратегий, помогающих читателям разобрать предложение, состоит в объединении слов и числительных (3 двухлетних совы, четыре трехэтапных плана), но изменение формулировки для разделения чисел может быть лучшим выбором для ясности в некоторых случаях. Ясность для читателей всегда является самым важным фактором.

Порядковые номера

Обращайтесь с порядковыми номерами (3-й, четвертый) так же, как и с другими номерами, используя приведенные выше рекомендации. Вы можете использовать надстрочный индекс или нет (1 ^st , 1st), но вы должны использовать одно и то же во всей своей статье.

Десятичные дроби

В числах меньше 1 средства записи могут включать или не включать начальный 0 перед десятичной точкой. Этот выбор основан на максимально возможном количестве статистики:

• Если статистика может быть больше 1, используйте начальный 0 (0,24 дюйма)
• Если статистика не может быть больше 1, не используйте начальный 0 (p = 0,042)

Общий принцип APA для округления десятичных знаков в экспериментальных результатах заключается в следующем, цитируемом здесь для точности: «Округляйте как можно больше, учитывая предполагаемое использование и статистическую точность» (7-е издание руководства, стр. 180). Читатели могут легче понимать числа с меньшим количеством знаков после запятой, и обычно APA рекомендует округлять до двух знаков после запятой (и при необходимости масштабировать данные для достижения этого).

Ниже перечислены некоторые более конкретные рекомендации для конкретных значений.

Один десятичный знак:

• означает
• стандартных отклонений

Два десятичных знака:

• корреляции
• пропорции
• выводная статистика
• точные значения p (можно указать два или три места; когда p меньше 0,001, напишите p < 0,001)

Статистическая копия 

Эти правила касаются представления данных, а не точности данных или наилучшего способа проведения анализа.

Данные можно представить в виде текста, таблицы или рисунка. Эмпирическое правило:

• <3 числа → попробуйте предложение
• 4-20 чисел → попробовать таблицу
• >20 цифр → попробуйте цифру

Ясность всегда превыше всего.

При обсуждении общеупотребительной статистики нет необходимости указывать ссылку или формулу.

Если статистика или выражение являются новыми, редкими, неотъемлемой частью статьи или используются нетрадиционным образом, предоставьте ссылку или формулу.

Цель сообщения статистики обычно состоит в том, чтобы помочь читателям подтвердить ваши выводы и анализы; как таковая, степень конкретности результатов отчетности должна соответствовать этой цели.

Если ваши данные являются многоуровневыми, вы должны включить сводную статистику для каждого уровня в зависимости от типа выполненного анализа. Когда ваши данные представлены в виде таблицы или рисунка, вам не нужно повторять каждое число в тексте, но вы должны упомянуть таблицу или рисунок в тексте при обсуждении статистики и подчеркнуть ключевые точки данных в тексте, которые помогают интерпретировать ваши данные. результаты.

Используйте такие слова, как «соответственно» или «для того, чтобы» пояснить каждую статистику, упомянутую в тексте, и их ссылку.

Например:

«Очки за тесты 4-6 составили 42, 36 и 58 соответственно» означает, что результат за тест 4 составил 42, за тест 5 — 36, а за тест 6 — 58.

Доверительные интервалы должны быть указаны: 90% ДИ [ LL, UL ], с LL в качестве нижнего предела и UL в качестве верхнего предела интервала. Вам не нужно повторять доверительные интервалы в том же абзаце или в серии, когда смысл ясен и доверительный интервал не изменился. Когда ЭК следуют за отчетом о точечной оценке, вам не нужно повторять единицу измерения.

В статистике используется большое количество символов и сокращений (когда термин может быть и тем и другим, то сокращение относится к понятию, а символ указывает числовое значение).

Вам не нужно определять их, когда они представляют статистические данные или состоят из греческих букв. Вам do необходимо определить любую другую аббревиатуру (такую ​​как ANOVA, CFA, SEM) в вашей статье. Если в анализе, который вы выполняете, используются несколько стилей обозначений для символов и аббревиатур, последовательно используйте только один из них во всей статье.

Некоторые другие рекомендации по статистическим символам включают:

• использовать в повествовательном тексте слова, а не символы; когда вы сообщаете термин статистики с другими математическими символами, такими как = или +, используйте символ
• параметры населения используют греческие буквы, в то время как оценщики используют латинские буквы курсивом (обычно)
• прописные, курсив N указывает общее членство в выборке; нижний регистр, курсив n указывает на принадлежность к подгруппе выборки, такой как лечебная группа или контрольная группа
• % и символы валюты, такие как $, должны использоваться только с цифрами (15%, $25) или в заголовках таблиц и подписях к рисункам для экономии места
• используйте стандартный шрифт (без курсива или жирного шрифта) для греческих букв, идентификаторов подстрочных и надстрочных индексов и сокращений, которые не являются переменными, такими как log
• использовать жирный шрифт для векторных и матричных символов
• используйте курсив для всех других статистических символов

Математическая копия

Для удобства чтения используйте пробелы между элементами в математическом выражении ( a + b = c ), за исключением случая со знаком минус, указывающим на отрицательное число, в котором используется пробел перед минусом, но не между минусом и цифрой.

Сначала используйте нижние индексы, а затем верхние индексы, за исключением ключевых символов, таких как верхний индекс для простого числа.

Все уравнения должны быть отмечены пунктуацией, чтобы соответствовать синтаксису предложения, даже если они представлены на отдельной строке.

Короткие простые уравнения можно записывать обычной строкой текста с косой чертой (/) для дробей. Скобки, квадратные скобки и фигурные скобки следует использовать (в таком порядке, от самого внутреннего к самому внешнему), чтобы указать порядок операций. Уравнения, которые не помещаются вертикально в строку текста, должны отображаться на отдельной строке.

Все отображаемые уравнения (уравнения в отдельной строке) должны быть пронумерованы, как таблицы и рисунки, чтобы к ним можно было обратиться позже (и простые уравнения могут быть отображены, а не записаны в строке текста, если они будут необходимы далее по номеру).

В тексте уравнения следует называть по имени (уравнение 1 или первое уравнение оба допустимы).