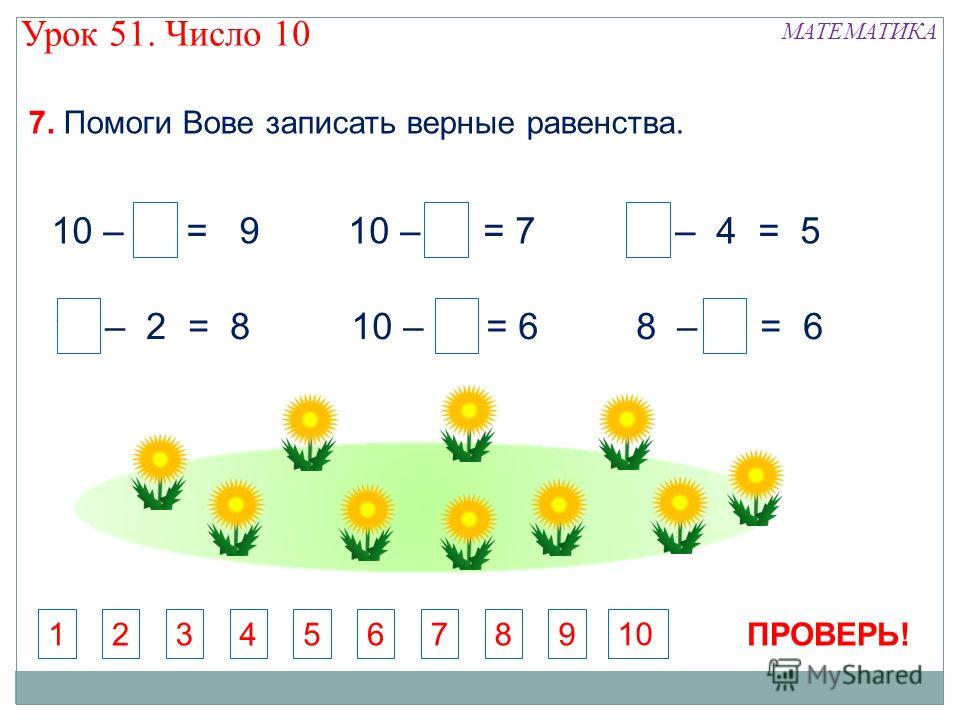
Неравенство 2 класс примеры: “Равенства и неравенства” Уравнения 2 класс – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Линейные неравенства, решение и примеры

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, <, >, ≤, ≥.

Линейные неравенства — это неравенства вида:

ax + b < 0,
ax + b > 0,
ax + b ≥ 0,
ax + b ≤ 0,

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти все значения переменной, при которой неравенство верное.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Типы неравенств

Строгие — используют только больше (>) или меньше (<):

a < b — это значит, что a меньше, чем b.
a > b — это значит, что a больше, чем b.
a > b и b < a означают одно и тоже, то есть равносильны.

Нестрогие — используют сравнения ≥ (больше или равно) или ≤ (меньше или равно):

a ≤ b — это значит, что a меньше либо равно b.
a ≥ b — это значит, что a больше либо равно b.
знаки ⩽ и ⩾ являются противоположными.

Другие типы:

a ≠ b — означает, что a не равно b.
a ≫ b — означает, что a намного больше, чем b.
a ≪ b — означает, что a намного меньше, чем b.
знаки >> и << противоположны.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

Если а > b , то b < а. Также наоборот: а < b, то b > а.

Если а > b и b > c, то а > c. И также если а < b и b < c, то а < c.

Если а > b, то а + c > b+ c (и а – c > b – c).

Если же а < b, то а + c < b + c (и а – c < b – c). К обеим частям можно прибавлять или вычитать одну и ту же величину.

Если а > b и c > d, то а + c > b + d.

Если а < b и c < d, то а + c < b + d.

Два неравенства одинакового смысла можно почленно складывать. Но важно перепроверять из-за возможных исключений. Например, если из 12 > 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а > b и c < d, то а – c > b – d.

Если а < b и c > d, то а – c < b – d.

Из одного неравенства можно почленно вычесть другое противоположного смысла, оставляя знак того, из которого вычиталось.

Если а > b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа < nb и

Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.

Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а < b и c < d, где а, b, c, d > 0, то аc < bd.

Неравенства одного смысла на множестве положительных чисел можно почленно перемножать.

Следствие данного правила или квадратный пример: если а > b, где а, b > 0, то а2 > b2, и если а < b, то а2 < b2. На множестве положительных чисел обе части можно возвести в квадрат.

Если а > b, где а, b > 0, то

Если а < b , то

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Важно знать

Два неравенства можно назвать равносильными, если у них одинаковые решения.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Правила линейных неравенств

Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

Разделим обе части на минус два 2x > 9 ⇒ 2x : (–2) > 9 : (–2) ⇒ x < 4,5.

Решение линейных неравенств

Линейные неравенства с одной переменной x выглядят так:

ax + b < 0,
ax + b > 0,
ax + b ≤ 0,
ax + b ≥ 0,

где a и b — действительные числа. А на месте x может быть обычное число.

Равносильные преобразования

Для решения ax + b < 0 (≤, >, ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

Алгоритм решения ax + b < 0 при a ≠ 0

перенесем число b в правую часть с противоположным знаком,
получим равносильное: ax < −b;
произведем деление обеих частей на число не равное нулю.

Когда a положительное, то знак неравенства остается без изменений, если a — отрицательное, знак меняется на противоположный.

Рассмотрим пример: 4x + 16 ≤ 0.

Как решаем: В данном случае a = 4 и b = 16, то есть коэффициент при x не равен нулю. Применим вышеописанный алгоритм.

Перенесем слагаемое 16 в другую часть с измененным знаком: 4x ≤ −16.
Произведем деление обеих частей на 4. Не меняем знак, так как 4 — положительное число: 4x : 4 ≤ −16 : 4 ⇒ x ≤ −4.
Неравенство x ≤ −4 является равносильным. То есть решением является любое действительное число, которое меньше или равно 4.

Ответ: x ≤ −4 или числовой промежуток (−∞, −4].

При решении ax + b < 0, когда а = 0, получается 0 * x + b < 0. На рассмотрение берется b < 0, после выясняется верное оно или нет.

Вернемся к определению решения неравенства. При любом значении x мы получаем числовое неравенство вида b < 0. При подстановке любого t вместо x, получаем 0 * t + b < 0 , где b < 0. Если оно верно, то для решения подойдет любое значение. Когда b < 0 неверно, тогда данное уравнение не имеет решений, так как нет ни одного значения переменной, которое может привести к верному числовому равенству.

Числовое неравенство вида b < 0 (≤, > , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

Рассмотрим пример: 0 * x + 5 > 0.

Как решаем:

Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

Ответ: промежуток (− ∞ , + ∞).

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов заключается в следующем:

вводим функцию y = ax + b;
ищем нули для разбиения области определения на промежутки;
отмечаем полученные корни на координатной прямой;
определяем знаки и отмечаем их на интервалах.

Алгоритм решения ax + b < 0 (≤, >, ≥) при a ≠ 0 с использованием метода интервалов:

найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если < или ≤ — над отрицательным промежутком.

Рассмотрим пример: −6x + 12 > 0.

Как решаем:

В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
−6x = −12,
x = 2.
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6 < 0 . Знак на промежутке является отрицательным.
Штриховку сделаем над положительным промежутком.

По чертежу делаем вывод, что решение имеет вид (−∞, 2) или x < 2.

Ответ: (−∞, 2) или x < 2.

Графический способ

Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

Алгоритм решения y = ax + b графическим способом

во время решения ax + b < 0 определить промежуток, где график изображен ниже оси Ох;
во время решения ax + b ≤ 0 определить промежуток, где график изображается ниже Ох или совпадает с осью;
во время решения ax + b > 0 определить промежуток, где график изображается выше Ох;
во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

Рассмотрим пример: −5 * x − √3 > 0.

Как решаем

Так как коэффициент при x отрицательный, данная прямая является убывающей.
Координаты точки пересечения с Ох равны (−√3 : 5; 0).
Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

Ответ: (−∞, −√3 : 5) или x < −√3 : 5.

Линейные неравенства в 8 классе — это маленький кирпич, который будет заложен в целый фундамент знаний. Мы верим, что у все получится!

Числовые неравенства и их свойства. Сложение и умножение числовых неравенств 8 класс онлайн-подготовка на Ростелеком

Тема 8: Неравенства

Видео
Тренажер
Теория

Заметили ошибку?

Числовые неравенства и их свойства. Сложение и умножение числовых неравенств.

Мы можем сравнить любые числа а и b и результат сравнения записать в виде равенства или неравенства, используя знаки =, <, >. Для произвольных чисел а и b выполняется одно и только одно из соотношений: a=b, a<b, a>b.

Пример 1. Сравним обыкновенные дроби 58 и 47.

Для этого приведем их к общему знаменателю: 58=3556; 47=3256.

Так как 35>32, то 58>47.

Пример 2. Сравним десятичные дроби 3,6748 и 3,675.

Цифры в разрядах единиц, десятых и сотых совпадают, а в разряде тысячных в первой дроби стоит цифра 4, а во второй – цифра 5. Так как 4<5, то 3,6748<3,675.

Пример 3. Сравним обыкновенную дробь 920 и десятичную дробь 0,45. Обратив дробь 920 в десятичную, получим, что 920=0,45.

Пример 4. Сравним отрицательные числа -15 и -23. Модуль первого числа меньше модуля второго. Значит, первое число больше второго, -15>-23.

В зависимости от вида числа мы использовали тот или иной способ сравнения. Но есть универсальный способ сравнения, который охватывает все случаи.

Число а больше числа b, если разность а-b – положительное число; число а меньше числа b, если разность a-b – отрицательное число. Если разность а-b = 0, то числа а и b равны.

На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.

Рассмотрим некоторые свойства числовых неравенств.

Если a>b, то b<a, если a<b, то b>a.

Действительно, если разность a-b – положительное число, то разность b-a – отрицательное число, и наоборот.
Если a<b и b<c, то а<c.

Докажем, что разность а-с – отрицательное число. Прибавим к этой разности числа b и –b и сгруппируем слагаемые:

а-с = а-с+b-b = (а-b)+(b+c).

По условию а<b и b<c. Поэтому слагаемые а-b и b-c – отрицательные числа. Значит, и их сумма является отрицательным числом. Следовательно, а<c.
Если a<b и c – любое число, то а+с<b+c.

Преобразуем разность (а+с)-(b+c) = а-b

По условию а<b, поэтому a-b – отрицательное число. Значит, и разность (а+с)-(b+c) отрицательна. Следовательно, a+c<b+c.

Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство.
Если a<b и c – положительное число, то aс<bс. Если a<b и c – отрицательное число, то aс>bc.

Представим разность ас-bc в виде произведения: ас-bc = с(а-b).

Так как a<b, то a-b – отрицательное число. Если с>0, то произведение с(а-b) отрицательно, и, следовательно, ас<bc. Если с<0, то произведение с(а-b) положительно, и, следовательно, ас>bc.

Так как деление можно заменить умножением на число, обратное делителю, то аналогичное свойство справедливо и для деления.

Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.

Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство.
s
Если а и b – положительные числа и а<b, то 1a>1b.

Разделим обе части неравенства a<b на положительное число ab: aab<bab. Сократив дроби, получим, что 1b<1a, т.е. 1а>1b.

Приведем пример использования рассмотренных свойств неравенств.

Пример 5. Оценим периметр равностороннего треугольника со стороной а мм, если известно, что 54,2<a и a<54,3, и запишем результат в виде двойного неравенства.

54,2·3 < 3a < 54,3·3,

162,6 < 3a < 162,9.

Значит, периметр Р данного треугольника больше 162,6 мм, но меньше 162,9 мм.

Рассмотрим теперь, как выполняется сложение и умножение числовых неравенств.
Если a<b и c<d, то a+c<b+d.

Прибавив к обеим частям неравенства a<b число с, получим а+с<b+с. Прибавив к обеим частям неравенства с<d число b, получим b+c<b+d.

То есть а+с<b+с<b+d. Из этого следует, что a+c<b+d.

Если почленно сложить верные неравенства одного знака, то получится верное неравенство.
Если a<b и c<d, где а,b,c,d – положительные числа, то ac<bd.

Умножим обе части неравенства a<b на положительное число с, получим ac<bс. Умножив обе части неравенства c<d на положительное число b, получим bc<bd. Получим ac<bс<bd. Следовательно ac<bd.

Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство.

Из этой теоремы следует, что

Если числа а и b положительны и a<b, то aⁿ<bⁿ, где n – натуральное число.

Доказанные свойства используют для оценки суммы, разности, произведения и частного.

Пример 6. Известно, что 15<x<16 и 2<y<3. Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у.

Сложим почленно неравенства 15<x<16 и 2<y<3, получим 17<x+y<19.

Оценим разность. Для этого умножим 2<y<3 почленно на (-1). Получим -3<-y<-2.

Теперь сложим почленно неравенства 15<x<16 и -3<-y<-2. Получим 12<x-y<14.

Оценим произведение ху. Перемножим почленно неравенства 15<x<16 и 2<y<3. Получим 30<xy<48.

Оценим частное. Для этого сначала запишем неравенство для 1у. Получится 13<1y<12. Теперь перемножим почленно 15<x<16 и 13<1y<12. Получим 5<xy<8.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Равенства и неравенства / Сравнение чисел / Справочник по математике для начальной школы

Главная
Справочники
Справочник по математике для начальной школы
Сравнение чисел
Равенства и неравенства

Сначала повтори тему “Больше. Меньше” и вспомни, что такое больше, меньше, поровну, столько же.

Рассмотри рисунок.

Сколько синих кругов? 5.

Сколько красных кругов? 5.

Каких кругов больше? Каких меньше?

Синих кругов столько же, сколько красных. Их поровну.

Красных кругов столько же, сколько синих. Их поровну.

Составим запись к рисунку:

5 = 5.

Прочитаем запись: пять равно пяти.

Это равенство.

Запись, в которой есть знак РАВНО, называется РАВЕНСТВОМ.

Рассмотри рисунок.

Сколько синих кругов? 5.

Сколько красных кругов? 6.

Каких кругов больше? Красных.

Каких кругов меньше? Синих.

Синих кругов меньше, чем красных.

Красных кругов больше, чем синих.

Составим запись к рисунку:

6 > 5

Прочитаем запись: шесть больше пяти.

Это неравенство.

5 < 6

Прочитаем запись: пять меньше шести.

Это неравенство.

Запись, в которой есть знак БОЛЬШЕ или МЕНЬШЕ, называется НЕРАВЕНСТВОМ.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Уменьшить на… Увеличить на…

Сравнение чисел

Правило встречается в следующих упражнениях:

1 класс

Страница 115, Моро, Волкова, Степанова, Учебник, часть 1

Страница 52. Вариант 1. Тест, Волкова, Проверочные работы

Страница 44, Моро, Волкова, Степанова, Учебник, часть 2

Страница 72, Моро, Волкова, Степанова, Учебник, часть 2

Страница 48. Урок 30, Петерсон, Учебник, часть 1

Страница 57. Урок 35, Петерсон, Учебник, часть 1

Страница 59. Урок 36, Петерсон, Учебник, часть 1

Страница 16. Урок 9, Петерсон, Учебник, часть 2

Страница 29. Урок 15, Петерсон, Учебник, часть 2

Страница 32. Урок 17, Петерсон, Учебник, часть 3

2 класс

Страница 22, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 53, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 8. Вариант 1. № 3, Моро, Волкова, Проверочные работы

Страница 68. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы

Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 40, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 53, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 77, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 86. Урок 36, Петерсон, Учебник, часть 2

3 класс

Страница 33, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 17, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 29. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы

Страница 87. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы

Страница 62, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 80, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 103, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 47, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 25. Урок 8, Петерсон, Учебник, часть 1

4 класс

Страница 34, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 42, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 93, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 23. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы

Страница 51. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы

Страница 62. Вариант 1. Проверочная работа 2, Моро, Волкова, Проверочные работы

Страница 63. Вариант 2. Проверочная работа 2, Моро, Волкова, Проверочные работы

Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 106, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

5 класс

Задание 626, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 120, Мерзляк, Полонский, Якир, Учебник

Номер 121, Мерзляк, Полонский, Якир, Учебник

Номер 122, Мерзляк, Полонский, Якир, Учебник

Линейные неравенства — определение, формулы, графики, примеры

В математике неравенство возникает, когда проводится неравное сравнение между двумя математическими выражениями или двумя числами. В общем случае неравенства могут быть либо числовыми, либо алгебраическими, либо их комбинацией. Линейные неравенства – это неравенства, включающие хотя бы одно линейное алгебраическое выражение, то есть многочлен степени 1 сравнивается с другим алгебраическим выражением степени меньше или равной 1. Существует несколько способов представления различных видов линейных неравенств.

В этой статье мы узнаем о линейных неравенствах, решении линейных неравенств, построении графиков линейных неравенств.

1.	Что такое линейные неравенства?
2.	Правила линейных неравенств
3.	Решение системы линейных неравенств
4.	Решение систем линейных неравенств с помощью графика
5.	Графики линейных неравенств
6.	Часто задаваемые вопросы о линейных неравенствах

Что такое линейные неравенства?

Линейные неравенства определяются как выражения, в которых два линейных выражения сравниваются с использованием символов неравенства. Пять символов, которые используются для представления линейных неравенств, перечислены ниже:

Нужно заметить, что если p < q, то p — некоторое число, строго меньшее q. Если p ≤ q, то это означает, что p — некоторое число, которое либо строго меньше q, либо в точности равно q. То же самое относится и к оставшимся двум неравенствам > (больше) и ≥ (больше или равно).

Теперь предположим, что у нас есть линейное неравенство, 3x – 4 < 20. В этом случае LHS < RHS. Мы можем видеть, что выражение в левой части, то есть 3x - 4, на самом деле меньше, чем число в правой части, равное 20. Мы можем графически изобразить это неравенство на весах как:

Правила линейных неравенств

Над линейными неравенствами выполняются 4 типа операций: сложение, вычитание, умножение и деление. Линейные неравенства с одним и тем же решением называются эквивалентными неравенствами. Существуют правила как равенства, так и неравенства. Все упомянутые ниже правила также верны для неравенств, включающих меньше или равно (≤) и больше или равно (≥). Прежде чем научиться решать линейные неравенства, давайте рассмотрим некоторые важные правила неравенства для всех этих операций.

Правило сложения линейных неравенств:

Согласно правилу сложения линейных неравенств, добавление одного и того же числа к каждой стороне неравенства дает эквивалентное неравенство, то есть символ неравенства не меняется.

Если x > y, то x + a > y + a, а если x < y, то x + a < y + a.

Правило вычитания линейных неравенств:

Согласно правилу вычитания линейных неравенств, вычитание одного и того же числа с каждой стороны неравенства дает эквивалентное неравенство, то есть символ неравенства не меняется.

Если x > y, то x − a > y − a, а если x < y, то x − a < y − a.

Правило умножения линейных неравенств:

Согласно правилу умножения линейных неравенств, умножение обеих частей неравенства с положительным числом всегда дает эквивалентное неравенство, то есть символ неравенства не меняется.

Если x > y и a > 0, то x × a > y × a, а если x < y и a > 0, то x × a < y × a. Здесь × используется как символ умножения.

С другой стороны, умножение обеих частей неравенства на отрицательное число не дает эквивалентного неравенства, если мы также не поменяем направление символа неравенства.

Если x > y и a < 0, то x × a < y × a, а если x < y и a < 0, то x × a > y × a.

Правило деления линейных неравенств:

Согласно правилу деления линейных неравенств, деление обеих частей неравенства на положительное число дает эквивалентное неравенство, то есть символ неравенства не меняется.

Если x > y и a > 0, то (x/a) > (y/a), а если x < y и a > 0, то (x/a) < (y/a).

С другой стороны, деление обеих частей неравенства на отрицательное число дает эквивалентное неравенство, если символ неравенства перевернуть.

Если x > y и a < 0, то (x/a) < (y/a), а если x < y и a < 0, то (x/a) > (y/a)

Решение системы линейных неравенств

Решение линейных многошаговых неравенств с одной переменной аналогично решению многошаговых линейных уравнений; начните с выделения переменной из констант. По правилам неравенств, при решении многошаговых линейных неравенств нам важно не забывать менять знак неравенства при умножении или делении с отрицательными числами.

Шаг 1: Упростите неравенство с обеих сторон – как с левой, так и с правой стороны в соответствии с правилами неравенства.
Шаг 2: Когда значение получено, если неравенство является строгим, решение для x меньше или больше значения, полученного в соответствии с вопросом. И, если неравенство не является строгим неравенством, то решение для x меньше или равно или больше или равно значению, полученному в соответствии с вопросом.

Теперь давайте попробуем решить линейные неравенства на примере, чтобы понять концепцию.

2x + 3 > 7

Чтобы решить это линейное неравенство, мы должны выполнить следующие шаги:

2x > 7 – 3 ⇒ 2x > 4 ⇒ x > 2

Решением этого неравенства будет множество всех значений x, для которых выполняется это неравенство x > 2, то есть всех действительных чисел, строго больших 2.

Решение линейных неравенств с переменной с обеих сторон

Попробуем решить линейные неравенства с одной переменной, применяя изученную концепцию. Рассмотрим следующий пример.

3x – 15 > 2x + 11

Действуем следующим образом:

-15 – 11 > 2x – 3x ⇒ – 26 > – x ⇒ x > 26

Решение системы линейных неравенств с помощью графика

Система линейных неравенств с двумя переменными имеет вид ax + by > c или ax + by ≤ c. Знаки неравенств могут меняться в соответствии с заданным набором неравенств. Чтобы решить систему линейных неравенств с двумя переменными, мы должны иметь по крайней мере два неравенства. Теперь, чтобы решить систему линейных неравенств с двумя переменными, рассмотрим пример.

2y – x > 1 и y – 2x < -1

Сначала нанесем данные неравенства на график. Для этого выполните указанные шаги:

Замените знак неравенства на равно =, то есть имеем 2y – x = 1 и y – 2x = -1. Поскольку линейное неравенство строгое, на графике проводим пунктирные линии.
Проверить, удовлетворяет ли начало координат (0, 0) заданным линейным неравенствам. Если это так, то заштрихуйте область на одной стороне линии, которая включает в себя начало координат. Если начало координат не удовлетворяет линейному неравенству, заштрихуйте область по одну сторону от линии, которая не включает начало координат.
Вместо 2y – x > 1 подставьте (0, 0) и мы получим: 2 × 0 – 0 > 1 ⇒ 0 > 1, что неверно. Следовательно, заштрихуйте сторону прямой 2y – x = 1, которая не включает начало координат. Аналогично, для y – 2x < -1, подставляя (0, 0), мы имеем: 0 - 2 × 0 < -1 ⇒ 0 < -1, что неверно. Следовательно, имел сторону прямой y - 2x = -1, которая не включает начало координат.
Общей заштрихованной будет допустимая область, образующая решение системы линейных неравенств. Если нет общей заштрихованной области, то решения не существует. Фиолетовая область на приведенном ниже графике показывает решение данной системы линейных неравенств.

Графики линейных неравенств

Линейные неравенства с одной переменной изображаются на числовой прямой, так как на выходе получается решение с одной переменной. Следовательно, графическое отображение линейных неравенств в одной переменной выполняется с использованием только числовой прямой. Напротив, линейные неравенства с двумя переменными изображаются на двумерном графике с осями x и y, поскольку на выходе получается решение двух переменных. Следовательно, построение графика линейных неравенств с двумя переменными выполняется с помощью графика.

Графики линейных неравенств — одна переменная

Рассмотрим приведенный ниже пример.

4x > -3x + 21

Решение в этом случае простое.

4x + 3x > 21 ⇒ 7x > 21 ⇒ x > 3

Это можно изобразить на числовой прямой следующим образом:

Любая точка, расположенная на синей части числовой прямой, удовлетворяет этому неравенству. Обратите внимание, что в этом случае мы нарисовали пустую точку в точке 3. Это указывает на то, что 3 не является частью множества решений (это потому, что данное неравенство имеет строгое неравенство). Согласно полученному решению синяя часть числовой прямой удовлетворяет неравенству. Возьмем другой пример линейных неравенств:

3x + 1 ≤ 7

Действуем следующим образом:

3x ≤ 7 – 1 ⇒ 3x ≤ 6 ⇒ x ≤ 2

Мы хотим представить это множество решений на числовой прямой. Таким образом, мы выделяем ту часть числовой прямой, которая лежит слева от 2

. Мы видим, что любое число, лежащее в красной части числовой прямой, будет удовлетворять этому неравенству и, следовательно, является частью набора решений для этого неравенство. Обратите внимание, что мы нарисовали сплошную точку точно в точке 2. Это означает, что 2 также является частью набора решений.

☛ Связанные темы:

Ознакомьтесь со следующими страницами, посвященными линейным неравенствам

Линейные неравенства с двумя переменными
Неравенства, включающие абсолютные значения
Умножение многочленов
Особые случаи в линейных уравнениях
Линейные уравнения и неравенства с одной переменной

Важные замечания о линейных неравенствах

Вот несколько моментов, которые следует помнить при изучении линейных неравенств:

В случае линейного неравенства, некоторые другие отношения, такие как меньше или больше, чем существуют между LHS и RHS.
Линейное неравенство называется так из-за того, что наибольшая степень (показатели) переменной равна 1.
«Меньше чем» и «больше чем» являются строгими неравенствами, в то время как «меньше или равно» и «больше или равно» не являются строгими линейными неравенствами.
Для каждого линейного неравенства, в котором используется строгое линейное неравенство, значение, полученное для x, показано пустой точкой. Он показывает, что полученное значение исключено.
Для каждого линейного неравенства, которое не является строгим неравенством, значение, полученное для x, показано сплошной точкой. Это показывает, что полученное значение включено.

Примеры решения линейных неравенств

Пример 1. Найдите решение линейного неравенства -2x – 39 ≥ -15 и нанесите его на числовую прямую.
Решение: Задачу решим следующим образом:
– 2x – 39≥ – 15 ⇒ – 2x ≥ 24
⇒ 2x ≤ – 24 ⇒ x ≤ – 12
Линейное неравенство будет отображено на числовой прямой следующим образом:
Набор решений изображен выше. Можно сказать, что любое число, лежащее в красной части числовой прямой, будет удовлетворять этому линейному неравенству и, следовательно, является частью множества решений этого неравенства. Следовательно, мы нарисовали сплошную точку точно в точке -12. Это указывает на то, что -12 также является частью набора решений.
Ответ: Следовательно, решение x ≤ -12
Пример 2. Решить линейные неравенства в этом линейном неравенстве 2x – 5 > 3 – 7x
Решение: Решим данное линейное неравенство следующим образом:
2x + 7x > 3 + 5 ⇒ 9x > 8 ⇒ x > 8/9
Ответ: x > 8/9 является решением линейного неравенства 2x – 5 > 3 – 7x

перейти к слайдуперейти к слайду

Хотите создать прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Записаться на бесплатный пробный урок

Вопросы о линейном неравенстве

перейти на слайдперейти на слайд

Часто задаваемые вопросы о линейных неравенствах

Что такое линейные неравенства в алгебре?

Линейные неравенства определяются как выражения, в которых два линейных выражения сравниваются с использованием символов неравенства. Эти выражения могут быть числовыми, алгебраическими или их комбинацией.

Что является примером линейного неравенства?

Примером линейного неравенства является x – 5 > 3x – 10. Здесь левое значение строго больше, чем правое, поскольку в этом неравенстве используется символ больше. После решения неравенство выглядит так: 2x < 5 ⇒ x < (5/2).

Каково реальное использование линейных неравенств?

Неравенства чаще используются во многих реальных задачах, чем равенства, для определения наилучшего решения проблемы. Это решение может быть таким же простым, как определение количества продукта, которое должно быть произведено, чтобы максимизировать прибыль, или оно может быть столь же сложным, как поиск правильной комбинации лекарств, которые нужно дать пациенту.

Каково использование линейных неравенств в бизнесе?

Предприятия используют неравенство для создания моделей ценообразования, планирования своих производственных линий и контроля запасов. Они также используются для отгрузки или складирования материалов и товаров.

Какие символы используются в линейных неравенствах?

Символы, используемые в линейных неравенствах:

Не равно (≠)
Меньше чем (<)
Больше, чем (>)
Меньше или равно (≤)
Больше или равно (≥)

Каковы два сходства между линейными неравенствами и уравнениями?

Сходства между линейными неравенствами и уравнениями:

Оба математических утверждения связывают два выражения друг с другом.
Оба решаются одинаково.

Как решать линейные неравенства с двумя переменными?

Чтобы решить систему линейных неравенств с двумя переменными, необходимо иметь хотя бы два неравенства. Мы нанесем данные неравенства на график и проверим наличие общей заштрихованной области, чтобы определить решение.

Как решать системы линейных неравенств графически?

Данные неравенства изобразим на графике аналогично линейным уравнениям, но пунктирными линиями из-за неравенства. Далее мы проверяем общую заштрихованную область, чтобы найти решение. Если нет общей заштрихованной области, то решения не существует. Заштрихованная область может быть ограниченной или неограниченной.

Чем квадратные неравенства отличаются от линейных неравенств?

Квадратные неравенства состоят из алгебраических выражений степени 2, тогда как линейные неравенства состоят из алгебраических выражений степени 1.

Социально-классовое неравенство: Концепция и примеры

Социально-классовое неравенство: Концепция и примеры | StudySmarter

Выберите язык

Предлагаемые языки:

Европа

английский (DE) английский (Великобритания)

StudySmarter — универсальное учебное приложение.

4.8 • Рейтинг +11k

Более 3 миллионов загрузок

Бесплатно

Сохранять

Распечатать

Редактировать

Социальное классовое неравенство

СОДЕРЖАНИЕ :

ОГЛАВЛЕНИЕ

Несмотря на то, что в мире много богатства, оно очень неравномерно распределено. Миллиардеры копят свое богатство и используют его для личной выгоды, в то время как подавляющее большинство населения борется за то, чтобы свести свои повседневные концы с концами. Это «неравенство», имеющее несколько измерений.

Здесь мы рассмотрим социальное классовое неравенство , его распространенность и социологию, которая его объясняет.

Во-первых, мы начнем с определения терминов «социальный класс», «неравенство» и «социальное неравенство».
Далее мы рассмотрим понятие социального неравенства и его отличия от социального классового неравенства. Мы рассмотрим несколько примеров социального неравенства.
Мы рассмотрим статистику социального неравенства и рассмотрим, как социальный класс взаимодействует с образованием, работой, здоровьем и гендерным неравенством.
Наконец, мы рассмотрим влияние социального класса на жизненные шансы.

Нам предстоит многое пройти, так что давайте погрузимся!

Что такое социальный класс?

Рис. 1. «Правильный» способ определения и измерения социального класса является весьма спорной темой в социологии.

В широком смысле социальный класс считается разделением общества по трем параметрам:

экономический аспект фокусируется на материальном неравенстве,
политический аспект фокусируется на роли класса в политической власти , и
культурное измерение фокусируется на образе жизни, престиже и социальном поведении.

Кроме того, социальный класс измеряется экономическими показателями, такими как богатство, доход, образование и/или род занятий. Для изучения неравенства социальных классов используется множество различных шкал социальных классов.

Что такое неравенство?

Рассмотрим неравенство вообще. Исторически сложилось много различных типов систем стратификации , таких как рабская и кастовая системы . Сегодня именно классовая система определяет природу наших современных обществ, таких как британское.

Ознакомьтесь с нашим объяснением S стратификации и дифференциации , чтобы освежить в памяти эту тему!

Стратификация

Важно отметить, что стратификация происходит по многим параметрам. Однако обычно класс считается основной формой стратификации в обществе.

Остальные формы вторичные . Многие люди считают, что различия в экономических рейтингах оказывают большее влияние на формирование жизни людей, чем другие, неэкономические типы рейтингов.

Концепция социального неравенства

Обратите внимание на разницу между социальным неравенством и классовым неравенством. В то время как первое является более конкретным, второе представляет собой многогранный подход, который относится к различным формам неравенства, включая такие аспекты, как пол, возраст и этническая принадлежность.

Примеры социального неравенства

Примеры социального неравенства помимо относятся к классам:

гендерное неравенство,
этническое неравенство,
эйджизм и
эйблизм.

Теперь, когда мы рассмотрели понятия социального класса и неравенства, давайте посмотрим на неравенство социальных классов.

Что такое социально-классовое неравенство?

Проще говоря, термин социально-классовое неравенство сигнализирует о том факте, что в современном обществе богатство распределяется среди населения неравномерно.

Самые известные весы были изобретены Карлом Марксом и Фредерихом Энгелем s (1848), который определил «два великих класса», возникших с капитализмом .

Для Маркса и Энгельса неравенство было непосредственно связано с отношением человека к средствам производства. Они воспринимали неравенство в социальном классе следующим образом:

Социальный класс	Определение
Bourgeoisie		Bourgeoisie	. Также известен как «правящий класс».
ПРОЛЕТАРИАТ	Те, кто не владеет капиталом, а только свой труд продает как средство выживания. Также известен как «рабочий класс».

Марксизм подвергался критике за его дихотомическую двухклассовую модель. Итак, два дополнительных класса являются общими для различных классовых шкал:

Средний класс расположен между правящим классом и высшими классами. Они часто более квалифицированы и занимаются нефизическим трудом (в отличие от рабочего класса).
Низший класс является самым низким по шкале стратификации. Разница между рабочим классом и низшим классом заключается в том, что первые, несмотря на рутинную работу, по-прежнему работают. Обычно считается, что низший класс состоит из тех, кто в еще большей степени борется с трудоустройством и образованием.

Джон Вестергаард и Генриетта Реслер (1976) утверждали, что правящий класс имеет наибольшую власть в обществе; источник этой силы богатство и экономическая собственность . В истинно марксистской манере они считали, что неравенство укоренено в капиталистической системе , поскольку государство постоянно представляет интересы правящего класса .

Взгляды Дэвида Локвуда (1966) на иерархию социальных классов аналогичны взглядам Вестергаарда и Реслера, основанным на понятии силы . Локвуд утверждает, что люди символически относят себя к определенным социальным классам, основываясь на своем опыте власти и престижа.

Социальное классовое неравенство: жизненные шансы

Жизненные шансы — еще один распространенный способ изучения распределения ресурсов и возможностей в обществе. Понятие «жизненные шансы» впервые было введено Максом Вебером в качестве контраргумента марксистскому экономическому детерминизму .

Вебер считал, что экономические факторы не всегда оказывают наибольшее влияние на социальные структуры и изменения — другие важные факторы также способствуют возникновению конфликтов в обществе.

Кембриджский социологический словарь (стр. 338) определяет жизненные шансы как «доступ, который человек имеет к ценным социальным и экономическим благам, таким как образование, здравоохранение или высокий доход». Это включает в себя способность избегать нежелательных аспектов, таких как низкий социальный статус.

Многочисленные исследования доказывают тесную историческую связь между социальным классом, неравенством и жизненными шансами. Как и следовало ожидать, высшие социальные классы, как правило, имеют больше жизненных шансов. Вот несколько важных примеров.

Семья: наследство и доступ к важным социальным сетям.
Здоровье: более высокая продолжительность жизни и снижение распространенности/тяжести заболеваний.
Богатство и доход: дополнительные доходы, сбережения и располагаемый доход.
Образование: повышена вероятность завершения школьного и высшего образования.
Работа: вышестоящих должности с гарантией занятости.
Политика: доступ и влияние на избирательную практику.

Социально-классовое неравенство: статистика и объяснение

Установлено, что представители низших классов, как правило, имеют более низкие образовательные достижения и результаты, более низкие шансы на трудоустройство и худшее общее состояние здоровья. Давайте посмотрим на некоторые статистические данные о социально-классовом неравенстве и их социологические объяснения.

Социальный класс и неравенство в образовании

Рис. 2 – Социальный класс сильно коррелирует с разнообразием жизненных шансов.

Учащиеся из неблагополучных семей отстают в учебе с течением времени. В возрасте 11 лет средний разрыв в баллах между более бедными и более богатыми учащимися составляет около 14 процентов. Этот разрыв увеличивается примерно до 22,5% в возрасте 19 лет.
Учащиеся, которые имели право на бесплатное школьное питание, за пять лет после выпуска зарабатывали на 11,5% меньше, чем их коллеги.
75 процентов 16-19-летних из неблагополучных семей выбирают профессиональное образование, которое создает и закрепляет классовый разрыв в образовании.

Профессиональное образование дает учащимся навыки и компетенции, ориентированные на конкретную профессию, например, сельское хозяйство. Это более практическое, чем традиционное образование.

Ниже приведены распространенные социологические объяснения связи между социальным классом и уровнем образования.

Лица с меньшим доходом, как правило, живут в жилье более низкого качества . Это делает их более склонными к заболеванию. Кроме того, они могут не иметь доступа к высококачественному здравоохранению и/или питанию – общее ухудшение здоровья означает, что академическая успеваемость учащихся из неблагополучных семей также может пострадать.
У учащихся с более низким социально-экономическим статусом, как правило, родители с более низким уровнем образования , которые не могут помочь своим детям в учебе.
Финансовые трудности неблагополучных семей могут подвергнуть школьников стрессу , нестабильности , потенциальной бездомности , неприспособленности , а также снижению способности позволить себе дополнительные учебные материалы (например, учебники или экскурсии).
Помимо материальных ресурсов и богатства, Pierre Bourdieu (1977) утверждал, что люди из неблагополучных семей, вероятно, также имеют меньше культурная столица . Отсутствие культурного образования дома, например, походов в музеи, книг и культурных дискуссий, также негативно влияет на успеваемость.

Существует также тесная связь между образовательными достижениями и жизненными шансами на более поздних этапах, касающихся таких аспектов, как работа и здоровье. Это означает, что учащиеся с неблагополучным социально-экономическим положением также с большей вероятностью будут испытывать трудности в дальнейшей жизни.

Социальный класс и неравенство в сфере труда

Люди из рабочего класса имеют на 80% меньше шансов получить профессиональную работу , чем представители среднего или высшего классов.
Если они находят профессиональную работу, работники рабочего класса зарабатывают в среднем около , что на 17% меньше, чем их коллеги.
Риск безработицы статистически выше для представителей низших классов.

Ниже приведены распространенные социологические объяснения связи между социальным классом, образованием и возможностями трудоустройства.

Существует сильная статистическая связь между уровнем образования и занятостью. Поскольку низшие классы, как правило, имеют более низкие образовательные достижения, это, как правило, приводит к тому, что у них также меньше шансов на работу.
Существует также сильная статистическая связь между ручным трудом специализацией и риском безработицы. Поскольку учащиеся из неблагополучных семей чаще, чем их сверстники, склонны выбирать путь профессионально-технического образования , это объясняет связь между низшими классами и меньшими шансами на трудоустройство.
Люди из более низкого рабочего класса более уязвимы к болезням из-за плохого качества жилья, загрязненных районов и отсутствия медицинской страховки. Более высокий риск заболевания для тех, кто, скорее всего, будет работать с тяжелым физическим трудом, также приводит к более высокому риску безработицы.
Отсутствие культурного и социального капитала у рабочего класса также обуславливает высокий риск безработицы; оказавшись в ситуации, когда им нужно «выглядеть и вести себя определенным образом», чтобы получить или сохранить работу, они могут не знать об этикете, которого требуют эти ситуации.

Хорошо образованный человек с высоким уровнем культурного капитала может знать, как правильно одеваться и вести себя на собеседовании при приеме на работу, что, скорее всего, произведет хорошее впечатление и даст ему работу (в отличие от представителей рабочего класса). сверстники).

Социальный класс и неравенство в отношении здоровья

Фонд здравоохранения сообщает, что в 2018/2019 году более 10 процентов взрослых из беднейшего социально-экономического класса сообщили о своем «плохом» или «очень плохом» здоровье. Эта статистика была всего 1 процент для людей из самого высокого социально-экономического класса.
По данным Всемирной организации здравоохранения и Всемирного банка, вакцинация против COVID-19 примерно в 18 раз в раз выше в странах с высоким уровнем дохода, чем в странах с низким уровнем дохода.
Ожидаемая продолжительность жизни статистически выше среди богатых, чем среди бедных по всем социальным классификациям (таким как пол, возраст и этническая принадлежность).

Ниже приведены распространенные социологические объяснения связи между социальным классом и здоровьем.

Существует связь между социально-экономическим статусом и другими формами неравенства. Например, этнических меньшинств и женщины чаще живут в бедности. По этой причине они также обычно сообщают об ухудшении общего состояния здоровья.
Существует связь между социально-экономическим статусом и другими жизненными шансами, такими как образование и работают как . Например, те, кто беднее, как правило, менее образованы и, как правило, менее осведомлены о признаках здорового/нездорового образа жизни (в отношении таких привычек, как занятия спортом или курение).
Люди с высоким доходом, скорее всего, будут в состоянии позволить себе частную медицинскую помощь и дорогостоящие виды лечения , такие как операции или лекарства.
Как уже упоминалось, люди с более низким социально-экономическим положением, скорее всего, будут жить в более тесном жилье более низкого качества. Это делает их уязвимыми для болезней, например, неспособностью дистанцироваться от больного члена семьи в общем жилище.

Социальный класс и гендерное неравенство

Женщины чаще, чем мужчины, занимают низкооплачиваемую работу.
Фонд здравоохранения установил, что у женщин в беднейших и наиболее неблагополучных районах Англии ожидаемая продолжительность жизни составляет 78,7 лет. Это почти на 8 лет меньше, чем у женщин в самых богатых районах Англии.
Женщины чаще залезают в долги и живут в бедности, чем мужчины.
Женщины, живущие в бедности, чаще работают на низкооплачиваемых работах и имеют меньшие пенсионные фонды.

Ниже приведены распространенные социологические объяснения связи между социальным классом и полом.

Стоимость ухода за детьми не позволяет женщинам из низших социальных классов работать, что приводит к неравенству доходов, поскольку женщины из более высоких социальных классов с большей вероятностью могут позволить себе уход за детьми .
Среди родителей-одиночек больше женщин, что влияет на их способность работать сверхурочно и выполнять тяжелую работу. Работающие матери чаще, чем мужчины, работают неполный рабочий день.
В целом женщины с большей вероятностью, чем мужчины, получают меньшую оплату за эквивалентную работу (гендерный разрыв в оплате труда), что приводит к более высокой вероятности бедности женщин.

Влияет ли социальный класс на жизненные шансы?

Давайте посмотрим, какое влияние на жизненные шансы все еще оказывает социальный класс.

Социальные структуры

Рис. 3. Смена доминирующих способов производства привела к структурным изменениям в иерархии классов.

За прошедшие годы в структуре классов произошло много заметных изменений. Как правило, изменения в структуре классов являются результатом изменений в доминирующие способы производства используемые в обществе. Важным примером этого является сдвиг между индустриальными , постиндустриальными , и знаниями обществами.

Крупнейшей отраслью промышленного общества было производство, которое характеризовалось развитием массового производства, автоматизации и технологий.

Бум сферы услуг был важной чертой постиндустриального общества , особенно в области информационных технологий и финансов.

Наконец, общество знаний (возникшее в конце двадцатого века) ценит нематериальные активы (такие как знания, навыки и инновационный потенциал), которые теперь имеют гораздо более высокую экономическую ценность, чем раньше.

В результате смены доминирующих в обществе способов производства изменились условия труда и требования рынка труда. На это указывают изменения в каждом классе иерархии.

Высший класс в целом уменьшился в размерах, поскольку владение акциями как форма собственности теперь более распространено среди среднего класса.
Средние классы расширились по мере того, как индустрия знаний породила гораздо больше занятий среднего класса (таких как управленческая и интеллектуальная работа).
Упадок обрабатывающей промышленности привел к сокращению низшего класса.

Эти структурные изменения указывают на то, что жизненные шансы в британском обществе, возможно, начали выравниваться в очень небольшой степени за последние несколько десятилетий. Жизненные шансы многих людей улучшились, поскольку неравенство в доходах сократилось с изменением доминирующих способов производства.

Однако до полного равенства еще далеко. Это путешествие должно учитывать другие соответствующие факторы, такие как пол, этническая принадлежность и инвалидность.

Социально-классовое неравенство — основные выводы

Социальный класс считается основной формой стратификации, а вторичные формы (включая пол, этническую принадлежность и возраст) оказывают меньшее влияние на жизненные шансы. Обычно его исследуют с точки зрения экономических, политических и культурных факторов.
Высшие классы обычно характеризуются более тесным отношением к средствам производства и более высоким уровнем владения экономическими благами.
Жизненные шансы — это доступ человека к ресурсам и возможностям, которые его общество или сообщество считает желательными, например к работе, образованию и высокому уровню жизни.
Меньшее количество образовательных возможностей и результатов также приводит к меньшему количеству жизненных шансов, связанных с работой, поскольку группы, находящиеся в неблагоприятном положении, более уязвимы к безработице или низкой заработной плате, если они найдут работу.
Связь между социально-экономическим положением и здоровьем играет ключевую роль в обеспечении жизненных шансов в других аспектах жизни, таких как работа и образование.

Часто задаваемые вопросы о социально-классовом неравенстве

Примеры социального неравенства, помимо классового, включают:

гендерное неравенство,
этническое неравенство,

70
эйджизм
и

«Социально-классовое неравенство» — это неравное распределение возможностей и ресурсов в системе стратификации социально-экономических классов.

Те, кто находится выше по шкале социального класса, обычно имеют лучшее здоровье. Это происходит из-за структурного неравенства, такого как более высокий уровень жизни, доступность передовых методов лечения и более длительная продолжительность жизни из-за более низкой общей вероятности физической инвалидности.

Государство может уменьшить неравенство социальных классов с помощью щедрой политики социального обеспечения, прогрессивных налоговых систем, расширения возможностей трудоустройства и всеобщего доступа к качественному здравоохранению и образованию.

В социологии социальный класс считается одной из многих форм неравенства, существующих в обществе. Как правило, «класс» определяется с точки зрения экономического доступа людей к товарам, ресурсам и возможностям, которые ценятся обществом. Не у всех есть для этого экономический капитал, поэтому неодинаковый доступ к жизненным шансам с помощью экономических средств — это то, что относит людей к разным классам и, в конечном счете, вызывает неравенство между ними.

Финальная викторина о социальном неравенстве

Вопрос

Что имеют в виду социологи, когда говорят, что социальный класс является «основной формой стратификации»?

Показать ответ

Ответ

Когда социологи говорят, что социальный класс является «основной формой стратификации», это означает, что экономические факторы оказывают большее влияние на формирование жизни людей, чем другие параметры, такие как пол, этническая принадлежность и возраст.

Показать вопрос

Вопрос

Каковы три измерения социального класса?

Показать ответ

Ответ

Три измерения социального класса – это экономические измерение, политическое измерение и культурное измерение .

Показать вопрос

Вопрос

Каковы, по Марксу и Энгельсу (1948), «два больших класса»?

Показать ответ

Ответ

Согласно Марксу и Энгельсу (1948), «два великих класса» — это буржуазия и пролетариат .

Показать вопрос

Вопрос

Какие два класса были добавлены к различным шкалам в дополнение к высшему классу и рабочему классу?

Показать ответ

Ответ

Два класса, которые были добавлены к различным шкалам в дополнение к высшему классу и рабочему классу, — это средний класс и низший класс .

Показать вопрос

Вопрос

Каков главный источник власти в обществе, согласно Вестергаарду и Реслеру (19). 76)?

Показать ответ

Ответ

Богатство и экономическая собственность.

Показать вопрос

Вопрос

Согласно Локвуду (1966), как люди относят себя к социальным классам?

Показать ответ

Ответ

Согласно Локвуду (1966), люди символически относят себя к социальным классам, основываясь на своем опыте власти и престижа.

Показать вопрос

Вопрос

Что такое «жизненные шансы»?

Показать ответ

Ответ

Жизненные шансы – это доступ людей к ресурсам и возможностям, которые общество считает желательными.

Показать вопрос

Вопрос

Высшие социальные классы, как правило, имеют _____ жизненные шансы.

Показать ответ

Ответ

Показать вопрос

Вопрос

Почему существует классовый разрыв в типах образования?

Показать ответ

Ответ

Существует классовый разрыв в типах образования, поскольку 75% 16-19-летних из неблагополучных семей выбирают профессиональное образование.

Показать вопрос

Вопрос

Перечислите четыре социологических объяснения различий в жизненных шансах, связанных с образованием, в зависимости от социального класса.

Показать ответ

Ответ

Четыре социологических объяснения различий в жизненных шансах, связанных с образованием, в зависимости от социального класса:

более низкий уровень здоровья,
родители с более низким уровнем образования,
стресс, вызванный финансовыми трудностями, и
отсутствие культурного капитала.

Показать вопрос

Вопрос

Назовите четыре социологических объяснения различий в жизненных шансах, связанных с работой, в зависимости от социального класса.

Показать ответ

Ответ

Четыре социологических объяснения различий в жизненных шансах, связанных с работой, в зависимости от социального класса:

более низкие образовательные достижения, приводящие к более низким шансам на работу,
более высокий риск безработицы среди квалифицированных рабочих (т. имеют профессиональное образование),
низкий общий уровень здоровья и
отсутствие культурного и социального капитала.

Показать вопрос

Вопрос

Какие три стадии общественного развития возникают в результате смены доминирующих способов производства?

Показать ответ

Ответ

Три стадии общественного развития, возникающие в результате смены доминирующих способов производства:

индустриальное общество,
постиндустриальное общество и
общество знаний.

Показать вопрос

Вопрос

Почему численность высшего класса уменьшилась с появлением общества знаний?

Показать ответ

Ответ

Численность высшего класса уменьшилась с появлением общества знаний, поскольку владение акциями стало более распространенной и доступной формой собственности. Благодаря этому вырос и средний класс.

Показать вопрос

Вопрос

Упадок обрабатывающей промышленности привел к…

Показать ответ

Ответ

меньший низший класс.

Показать вопрос

Вопрос

Какая связь между здоровьем и жизненными шансами, такими как образование и работа?

Показать ответ

Ответ

Существует связь между более низким социально-экономическим статусом и более слабым здоровьем. Следовательно, существует также значительная связь между общим уровнем здоровья и другими жизненными шансами, такими как образование и работа.

Показать вопрос

Вопрос

Плохое здоровье характерно для бедных, независимо от других маркеров неравенства, таких как пол и этническая принадлежность. Правда или ложь?

Показать ответ

Ответ

Показать вопрос

Вопрос

По данным Всемирной организации здравоохранения и Всемирного банка, вакцинация против COVID-19 проводится примерно в __x раз чаще в странах с высоким уровнем дохода, чем в странах с низким уровнем дохода.

Показать ответ

Ответ

Показать вопрос

Вопрос

В чем разница между социальным неравенством и социальным неравенством?

Показать ответ

Ответ

Хотя социально-классовое неравенство является более конкретным, социальное неравенство включает в себя многогранный подход, относящийся к различным формам неравенства, включая такие аспекты, как пол, возраст и этническая принадлежность.

Показать вопрос

Вопрос

Чем профессионально-техническое образование отличается от традиционного образования?

Показать ответ

Ответ

Профессиональное образование дает учащимся навыки и компетенции, ориентированные на конкретную профессию, например, сельское хозяйство. Это более практическое, чем традиционное образование.

Показать вопрос

Вопрос

Перечислите четыре социологических объяснения дифференциального неравенства, связанного со здоровьем, в социальном классе.

Показать ответ

Ответ

1. Связь между социально-экономическим статусом и другими формами неравенства

2. Связь между социально-экономическим статусом и шансами на жизнь

3. Возможность позволить себе частную медицинскую помощь и дорогостоящее лечение

4. Связь между социально-экономическим статусом и качеством жизни

Показать вопрос

Подробнее о социально-классовом неравенстве

Откройте для себя подходящий контент для ваших предметов

Не нужно жульничать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!

Учебный план

Будьте идеально подготовлены вовремя с индивидуальным планом.

Тесты

Проверьте свои знания с помощью игровых тестов.

Карточки

Создавайте и находите карточки в рекордно короткие сроки.

Заметки

Создавайте красивые заметки быстрее, чем когда-либо прежде.

Учебные наборы

Все учебные материалы в одном месте.

Документы

Загружайте неограниченное количество документов и сохраняйте их в Интернете.

Study Analytics

Определите сильные и слабые стороны вашего исследования.

Еженедельные цели

Ставьте индивидуальные учебные цели и зарабатывайте баллы за их достижение.

Умные напоминания

Хватит откладывать на потом наши напоминания об учебе.

Награды

Зарабатывайте очки, открывайте значки и повышайте уровень во время учебы.

Волшебный маркер

Создавайте карточки в заметках полностью автоматически.

Умное форматирование

Создавайте самые красивые учебные материалы, используя наши шаблоны.

примеров и как это измеряется

Что такое неравенство доходов?

Неравенство доходов — это неравномерность распределения доходов среди населения. Чем менее равномерно распределение, тем выше неравенство в доходах. Неравенство доходов часто сопровождается имущественным неравенством, то есть неравномерным распределением богатства. Население можно разделить по-разному, чтобы показать разные уровни и формы неравенства доходов, такие как неравенство доходов по признаку пола или расы. Различные меры, такие как коэффициент Джини, могут использоваться для анализа уровня неравенства доходов населения.

Ключевые выводы

Исследования неравенства доходов помогают выявить неравенство доходов среди различных слоев населения.
При анализе неравенства доходов исследователи обычно изучают распределение в зависимости от пола, этнической принадлежности, географического положения и рода занятий.
Тематические исследования и анализ неравенства доходов, неравенства доходов и распределения доходов регулярно предоставляются различными ведущими источниками.
Индекс Джини — популярный способ сравнить неравенство доходов во всем мире.

Неравенство доходов

Понимание неравенства доходов

Неравенство доходов и сегрегация неравенства доходов могут быть проанализированы с помощью различных сегментаций. Сегменты анализа неравенства доходов используются для анализа различных типов распределения доходов. Распределение доходов по демографической сегментации составляет основу для изучения неравенства доходов и неравенства доходов.

Различные типы сегментации доходов, изучаемые при анализе неравенства доходов, могут включать распределения для:

Пол
Этническая принадлежность
Географическое положение
Род занятий
Исторический доход

Примеры неравенства доходов

Существует несколько известных тематических исследований и аналитических отчетов, дающих представление о неравенстве доходов, неравенстве доходов и распределении доходов в США и во всем мире.

Городской институт

Институт городского развития является одним из источников информации о неравенстве доходов. Анализ экономических данных за 50 лет, проведенный Urban Institute, показал, что самые бедные стали еще беднее, а самые богатые стали намного богаче.

С 1963 по 2016 год:

Беднейшие 10% американцев перешли от нулевых активов к долгу в 1000 долларов.
Семьи со средним доходом более чем удвоили свой прежний средний уровень благосостояния.
Семьи из 10% самых богатых людей имели состояние, более чем в пять раз превышающее их прежнее состояние.
Семьи из 1% самых богатых людей имели более чем в семь раз больше своего прежнего состояния.

Urban Institute также исследует расовый и этнический разрыв в благосостоянии в США. Организация сообщила, что белые семьи в 1963 человека накопили в среднем на 45 000 долларов больше, чем цветные семьи. К 2019 году средний уровень благосостояния белых семей увеличился примерно на 153000 долларов больше, чем у латиноамериканских семей, и на 165000 долларов больше, чем у черных семей.

Федеральная резервная система

Федеральная резервная система представляет ежеквартальный отчет о финансовых счетах распределения. В этом отчете показано распределение благосостояния домохозяйств США. По состоянию на первый квартал 2021 года Федеральная резервная система показала следующее распределение богатства в США.

Институт экономической политики

Институт экономической политики опубликовал отчет за 2018 год, показывающий общую тенденцию к увеличению доходов самых высокооплачиваемых работников после рецессии 2008 года. В период с 2009 по 2015 год Институт экономической политики показывает, что доходы тех, кто входит в 1% самых богатых, росли быстрее, чем доходы остальных 99% в 43 штатах и Вашингтоне, округ Колумбия.

С этой тенденцией может быть связано множество факторов, в том числе стагнация заработной платы работающих американцев, снижение налогов для самых богатых американцев, потеря рабочих мест в обрабатывающей промышленности и стремительный рост фондового рынка, который привел к завышению стоимости руководителей корпораций и менеджеров хедж-фондов.

После рецессии компании также вкладывают значительные средства в наем и удержание работников со специальными навыками в таких областях, как машиностроение и здравоохранение. Это привело к сокращениям или новым поглощениям автоматизации в других функциях, что привело к снижению заработной платы работников на менее конкурентоспособных должностях.

Кроме того, данные EPI регулярно отслеживают заработную плату по сегментам. По состоянию на 2020 год он показал следующие средние значения для белых, черных и латиноамериканцев.

Институт исследований политики в отношении женщин

Неравенство доходов — это экономическая концепция, которая, как правило, бьет по некоторым слоям населения сильнее, чем по другим, при этом значительный разрыв в заработной плате часто выявляется у женщин, чернокожих и латиноамериканцев, работающих в США. Согласно исследованию доходов за 2020 год, проведенному Институтом исследований политики в отношении женщин. , женщины всех рас и национальностей получали в среднем 82,3% заработной платы, выплачиваемой мужчинам.

Исторически сложилось так, что это самый узкий разрыв, который когда-либо был. Он улучшается с каждым годом с 1980 лет, когда женщины зарабатывали примерно на 64% меньше, чем мужчины.

Исследовательский центр Пью

Данные исследовательского центра Pew Research Center также определяют неравенство в доходах по признаку пола. Исследовательский центр Pew Research Center показывает, что разрыв в гендерном неравенстве в доходах сокращается для всех работников в возрасте 16+, при этом женщины, по сообщениям, получают 84% средней заработной платы мужчин. Различие в доходах было меньше среди работников в возрасте от 25 до 34 лет. В этой группе женщины получали примерно 93% заработной платы мужчин в 2020 году.

Разрыв в доходах относится к разнице в доходах между демографическими сегментами.

Особые указания

Индекс Джини был разработан итальянским статистиком Коррадо Джини в начале 1900-х годов, чтобы помочь количественно оценить и упростить сравнение уровней неравенства доходов в разных странах мира. Индекс может варьироваться от 0 до 100, при этом более высокий уровень показывает большее неравенство в доходах среди населения страны и наоборот. Данные Всемирного банка показывают, что Южная Африка сообщает об одном из самых высоких показателей дисперсии неравенства доходов с уровнем индекса Джини 63,0. По данным Всемирного банка, Соединенные Штаты сообщают об уровне индекса Джини 41,4. В Словении самое низкое значение индекса Джини Всемирного банка — 24,6.

Рассеивание неравенства доходов является постоянной областью анализа как для местных, так и для глобальных институтов управления. Международный валютный фонд (МВФ) и Всемирный банк поставили перед собой цель помочь повысить доход 10% самых низкооплачиваемых работников во всех странах, стремящихся обеспечить всестороннюю глобальную поддержку. В глобальном масштабе новые инновации в финансовых технологиях и производствах также помогают улучшить банковские услуги для людей с самыми низкими доходами в мире, поскольку всемирная инициатива по расширению доступа к финансовым услугам находится в стадии реализации.