Названия фигур математика 2 класс: Геометрические фигуры, 2 класс
Урок математики 2 класс по теме “Плоские и объемные фигуры”
Учитель: Ребята, я рада видеть вас и наших гостей. Повернитесь и поприветствуйте гостей своими улыбками. – Начинаем урок математики.
Учитель: Чтобы вы сразу включились в мыслительную деятельность, хочу начать урок с загадки. Послушайте. В чёрном небе до зари Тускло светят фонари Фонари – фонарики Меньше чем комарики. Дети: звёзды Учитель: Молодцы, догадались. – Кто из вас любит смотреть на звёзды? Почему? – Я тоже очень люблю разглядывать звёзды, ведь они такие разные, такие непохожие одна на другую. Каждая звезда уникальна. Точно так же и вы, непохожи друг на друга, каждый из вас в чём-то уникален, только надо развивать свои способности, не лениться, заниматься. А ваши помощники вам всегда помогут. Учитель: Что же является вашими первыми помощниками на уроке?
Дети: глаза, уши, язычок
Учитель: Давайте подготовим их к уроку. Выполним 1 задание
* Запишите число, в котором 2 десятка и 8 единиц.
* Замените число 28 суммой разрядных слагаемых
* Запишите предыдущее число для числа 28
* Назовите последующее число для числа 28
* Уменьшите число 28 на 20
* Уменьшите число 28 на 8
Учитель: Я считаю, что ваши помощники уже включились в работу, а как вы сами считаете
– Оцените себя в листе достижения. Если без ошибок – звёздочку закрасьте жёлтым цветом, если – 1 -2 ошибки – синим, если – 3 и более ошибок, не закрашиваем. К концу урока у каждого из вас появится кусочек звёздного неба.
Учитель: Пожалуйста, прокомментируйте свои результаты.
Учитель: А сейчас задание для внимательных, кто заметил, какое число сегодня работало на устном счёте
Дети: Число 28
Учитель: Почему именно это число?
Дети: Сегодня 28 октября.
Учитель: Запишите в тетради число.
Учитель: Следующее задание для ваших глаз. Если вы будете внимательны, то возможно сможете определить тему урока.
Учитель: Посмотрите на экран. Кто же приготовил это задание для вас?
Кто же приготовил это задание для вас?
Дети: инопланетянин.
Учитель: Рассмотрев его внимательно, какие из моих высказываний истинны, а какие ложны. Если предложение истинно, вы записываете в тетради букву И, если ложно – букву Л.
-На чертеже нет ни одного прямоугольника. Л
-Некоторые фигуры на чертеже – квадраты. И
-Все фигуры на чертеже – четырёхугольники. И
-На чертеже есть круг. Л
-На рисунке 6 квадратов. И
Учитель: Как же поработали ваши глазки, оцените в листе достижений.
Учитель: Кто верно. Без ошибок справился с этим заданием? _ Есть ли такие, кто допустил 1 ошибку. Кто допустил больше ошибок, не расстраивайтесь, в следующий раз будьте внимательнее. Учитель: Ребята, скажите, можем ли уже определить, какая тема урока? Дети: пока не можем
Учитель: Инопланетянин приготовил для вас подсказку. Рассмотрите рисунки. Что видите?
– Кто из вас сможет назвать все предметы, одним словом.
Учитель: Трудно? Еще подсказка. Анаграмма – расположите буквы в нужном порядке и прочитайте слово
Анаграмма – расположите буквы в нужном порядке и прочитайте слово
ИФУГЫР
Дети: фигуры
Учитель: Какие здесь изображены фигуры?
Дети: Шахматная фигура, фигура человека, геометрические фигуры.
Учитель: О фигуре человека, о его осанке мы говорим практически на каждом уроке, следим за посадкой при письме.
Учитель: А сейчас сравните оставшиеся фигуры.
учитель: Можно ли их разделить на 2 группы. Какие?
Дети: Квадрат – это плоская фигура, а кубик и пешка – это объёмные фигуры.
Учитель: Совершенно верно, пешка и кубик – это объёмные фигуры, а квадрат – плоская фигура. Какие вы молодцы, что помните из детского сада и с урока труда о плоских и объёмных фигурах
Учитель: О чём будем говорить на уроке.
ПЛОСКИЕ И ОБЪЁМНЫЕ ФИГУРЫ
Учитель: Что бы вы хотели узнать о плоских и объёмных фигурах?
Дети: (задают вопросы)
Учитель: Вам многое хочется узнать, поэтому, кто будет внимательным, сможет найти ответы на эти вопросы
Учитель: Давайте проведём опыт.
Попробуйте приложить квадрат к плоской поверхности парты.
Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
Дети: квадрат целиком поместился на поверхности парты.
Учитель: Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности?
Дети: Плоской фигурой.
Учитель: Что можно измерить у квадрата?
Дети: У квадрата можно измерить длину и ширину. Что знаете о сторонах квадрата
Учитель: Возьмите кубик. Можно ли его полностью (весь) прижать к парте? Проверим.
Учитель: Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
Дети: Кубик полностью не помещается на поверхности, есть пространство между рукой и партой, т. е. кубик возвышается над поверхностью.
Учитель: Значит, что мы можем сказать о кубике?
Дети: Кубик занимает определённое пространство, а значит является объёмной фигурой.
Учитель: Что можно измерить у кубика?
Дети: У кубика есть длина, ширина и…высота.
Учитель: Совершенно верно, у кубика можно измерить длину, ширину и высоту. Такие фигуры называют трёхмерными или объёмными.
Учитель: Давайте сделаем вывод, чем же отличаются плоские и объёмные фигуры?
ПЛОСКИЕ ОБЪЁМНЫЕ
Можно целиком расположить Возвышаются над плоской поверхностью
на одной плоской поверхности. .
Можно измерить ширину и длину Можно измерить длину, ширину и высоту
Учитель: Оценим себя в листе достижений.
Учитель: Молодцы, вы были внимательны. Устали? Надо отдохнуть, т. к. впереди много работы.
Музыкальная физкультминутка
Учитель: Кто повторит тему урока
Учитель: Ребята, объёмные фигуры ещё называют геометрическими телами
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ГЕОМЕТРИЧЕСКИЕ ТЕЛА
Учитель: Поучимся различать геометрические тела и фигуры. Я показываю фигуру, а вы определяете, это геометрическое тело или фигура и называете её. Учитель: Все ли фигуры смогли назвать? Рассмотрите рисунок на стр. 47 учебника. Какие фигуры не назвали?
47 учебника. Какие фигуры не назвали?
Учитель: Ребята, а вы встречали такие фигуры? А знаете как они называются? У них очень сложное название – додекаэдр, тетраэдр, октаэдр и др. Вы можете узнать о них из энциклопедии. – Это будет ещё одна страничка в нашей «Книге удивительных открытий»
Учитель: Прочитайте пословицу.
Дети: Без друга в жизни туго.
Учитель: Как вы её понимаете?
Учитель: Как вы думаете, почему я предлагаю эту пословицу?
Учитель: Да потому что сейчас вы поработайте в группе и поможете тем, кто ещё не запомнил название и признаки геометрических фигур и тел.
Вспомним правила работы в группе.
Дети: * говорим шёпотом; *активно работает каждый; * говорим по делу; *выслушиваем мнения каждого и т. д.
Учитель: Задание для групп следующее: в корзинке у вас лежат геометрические фигуры и тела. Вам надо разложить все фигуры на две группы. (треуг, круг, прямоуг, куб, параллелип, цилиндр)
Учитель: Проверим, как разделили фигуры и объясните свой выбор
Учитель: оцените себя.
Учитель: Кто может сказать, что группа ему помогла. Я очень рада. Что в нашем классе такие дружные ребята.
Учитель: Геометрические тела можно встретить не только в математике, но и в жизни. Значит, не зря мы изучаем эту тему, нам надо их хорошо знать. Так вот сейчас снова помогите друг другу и следующее задание выполните в парах.
– Рассмотрите задание, что видите на листочках
Дети: в 1 столбике изображены предметы, которые встречаются в быту, во 2 столбике – геометрические тела. А в 3 столбике название геометрических тел. Вам надо соединить предмет, тело и название.
шар
пирамида
цилиндр
Учитель: Позовём на помощь глазки, проверим, как справились с заданием. Сравните свои результаты с экраном.
Оцените себя. Прокомментируйте.
Зарядка для глаз
Чтоб глаза наши зоркие были Чтоб в очках нам не ходить, Эти лёгкие движенья Предлагаем повторить.
Вдаль посмотрим и под ноги
Вправо, влево побыстрей.
Удивимся, что такое?
И закроем их скорей.
Учитель: – А как вы считаете, могут ли быть задачи о геометрических фигурах. Найдите в учебнике № 4 (б)
– Прочитайте задачу.
Дети: «На рисунке было 5 плоских фигур и 4 объёмные фигуры. Сколько фигур осталось на рисунке после того, как Саша стёр изображения шара и куба?
Учитель: Что особенного заметили? (О чём говорится в задаче?)
Дети: Эта задача тоже о фигурах.
Учитель: Что известно в задаче о фигурах?
Дети: Было 5 пл. и 4 объёмные фигуры
Учитель: Что обозначают числа 5 и4?
Дети: Целое.
Учитель: Как его запишем?
Дети: (5+4) фигуры
Учитель: Что ещё известно в задаче?
Дети: Саша стёр шар и куб
Учитель: Что узнали об этих фигурах сегодня на уроке?
Дети: Это объёмные фигуры.
Учитель: Так сколько всего фигур стёр Саша?
Дети: Саша стёр 2 фигуры.
Учитель: Что обозначает число 2 в задаче?
Дети: Число 2 в задаче обозначает часть.
Учитель: Что надо узнать в задаче?
Дети: В задаче надо узнать сколько фигур осталось, вторую часть.
Учитель: Составьте схему, проверьте.
Учитель: Можно сразу ответить на вопрос задачи и узнать, сколько всех фигур осталось??
Дети: Нельзя. Потому что мы не знаем, сколько объёмных фигур осталось.
Учитель: Можно узнать, сколько объёмных фигур осталось?
Дети: Можно. Надо из 4 вычесть 2.
Учитель: Можно ответить на вопрос задачи?
Дети: Надо к 5 прибавить результат 1 действия.
Учитель: Запишите решение.
Учитель: Проверьте.
Учитель: Прочитайте 2 вопрос задачи. Надо ли узнавать сколько плоских фигур осталось?
Дети: Не надо, потому что их не стирали.
Прочитайте 3 вопрос задачи. Можем ответить на него?
Дети: Да мы уже узнали. Их осталось 2.
Учитель: Оцените себя. Прокомментируйте.
Учитель: О чём сегодня говорили на уроке. Урок наш был посвящён фигурам, много говорили о плоских и объёмных фигурах.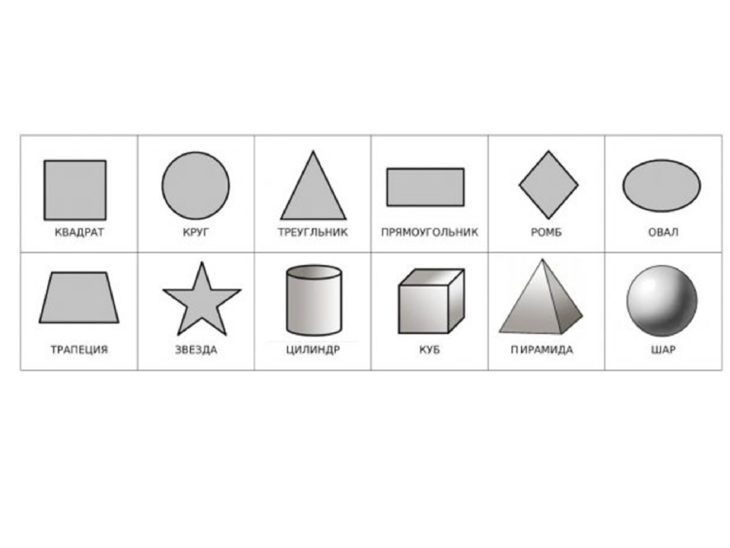 Вы готовы проверить себя как усвоили новую тему?
Вы готовы проверить себя как усвоили новую тему?
Поиграем в игру «Да-нетка». Я читаю высказывания, если вы согласны со мной, то показываете карточку «Да», не согласны – «Нет»
1. – эта фигура куб. (нет)
2) Эта фигура – параллелограмм (да)
3) У куба можно измерить длину, ширину и высоту (да)
– имеет форму шара.(да)
5) Круг – это объёмная фигура (нет)
6) Объёмные фигуры ещё называют геометрическими телами (да)
Учитель: – Оцените себя.
Учитель: Прокомментируйте, как вы поработали на уроке.
Вывод: Молодцы, что очень справедливо уже себя оцениваете.
Соберём звёздное небо из ваших кусочков. Посмотрите, как много жёлтых звёздочек и почти нет белых звёздочек, а значит, вы хорошо поработали на уроке.
Ребята, я хочу поблагодарить за урок. Может быть, у некоторых ещё не всё получилось, но это только первый урок по данной теме. На следующих уроках мы будем учиться различать и называть фигуры.
приветствие гостей. проверка учебных принадлежностей
проверка учебных принадлежностей
(слайд – мерцающие звёзды)
после каждого задания проверка на экране, дети ставят + под числом, если ответ верный или – , если ответ неверный оценивают себя на линеечке знаний, комментируют свои результаты
записывают число в тетради
На экране инопланетянин
Дети записывают ответы в тетрадь. По ходу работы сверяют свои результаты с экраном и ставят знак +, если верно выполнили задание и -, если неверно
оценивают себя, комментируют
ученики рассматривают рисунки на экране
ученики делают предположения
фигуру человека убираю
показываю шахматную фигуру, кубик и квадрат
Тема урока на экране
Дети задают вопросы, на которые бы хотели получить ответы
На экране – термины
У каждого – куб и квадрат. Ребята кладут плоскую фигуру на тетрадь и прижимают ладонью На экране появляется первая отличительная особенность плоских фигур.
На экране появляется вторая отличительная особенность плоских фигур.
Дети пробуют проделать этот же опыт и с объёмной фигурой, но понимают, что это невозможно.
На экране появляется первая отличительная особенность плоских фигур.
На экране появляется вторая отличительная особенность плоских фигур.
На экране появляются новые термины: геометрические фигуры и тела.
Учитель показывает – куб, треугольник, конус, шар, круг, прямоугольник, цилиндр, параллелепипед. Дети дают определение.
На экране фигуры Название проговаривают хором. Показываю энциклопедию и книгу. .
поют песенку и выполняют движения.
Пословица на экране Дети объясняют смысл пословицы
Выполняют задание в группах
Дети называют фигуры, объясняют, показ на экране. Оценивают себя и комментируют.
Выполняют работу в паре
Дети сравнивают свои результаты с экраном.
Оценивают себя.
Дети проговаривают стихотворение и выполняют движения.
Дети читают задачу.
Составляют схему в тетради и проверяют.
Дети записывают решение в тетради и проверяют
.
Дети показывают карточки
Выходят к доске и прикрепляют листы достижений.
.
ГДЗ по математике 2 класс учебник Рудницкая, Юдачева часть 2 Стра
Страница 116
1. Измерь длину каждой стороны прямоугольника.
Сделай вывод.
Ответ:
2. Отрезки АС и BD называют диагоналями прямоугольника. Измерь длину каждой диагонали
прямоугольника. Сделай вывод.
Ответ:
Страница 117
3. Рассмотри фигуры на рисунке.
Дай общее название всем фигурам.
Чем отличаются фигуры 1 и 2 от фигуры 3?
Дай общее название фигурам 1 и 2.
Чем отличается фигура 2 от фигуры 1?
Какое название можно дать фигуре 2?
Что ты знаешь о сторонах фигуры 1?
Что ты знаешь о сторонах фигуры 2?
Ответ:
– Дай общее название всем фигурам.
Все три фигуры – это четырехугольники.
– Чем отличаются фигуры 1 и 2 от фигуры 3?
У фигур 1 и 2 – углы прямые, а у фигуры 3 – нет.
– Дай общее название фигурам 1 и 2.
Прямоугольники.
– Чем отличается фигура 2 от фигуры 1?
В отличие от фигуры 1, у фигуры 2 все стороны равны.
– Какое название можно дать фигуре 2?
Квадрат.
– Что ты знаешь о сторонах фигуры 1?
Поскольку фигура 1 является прямоугольником, то у него противоположные стороны равны.
– Что ты знаешь о сторонах фигуры 2?
Поскольку фигура 2 является квадратом, то у него все стороны равны.
4. Начерти в тетради прямоугольник, не являющийся квадратом, и проведи его диагональ.
Симметричны ли противоположные вершины относительно этой диагонали?
Ответ:
5. Рассмотри рисунок, на котором изображён прямоугольник с вершинами А, В, С и D.
Назови стороны прямоугольника ABCD. Что ты знаешь о сторонах прямоугольника?
Назови диагонали прямоугольника ABCD.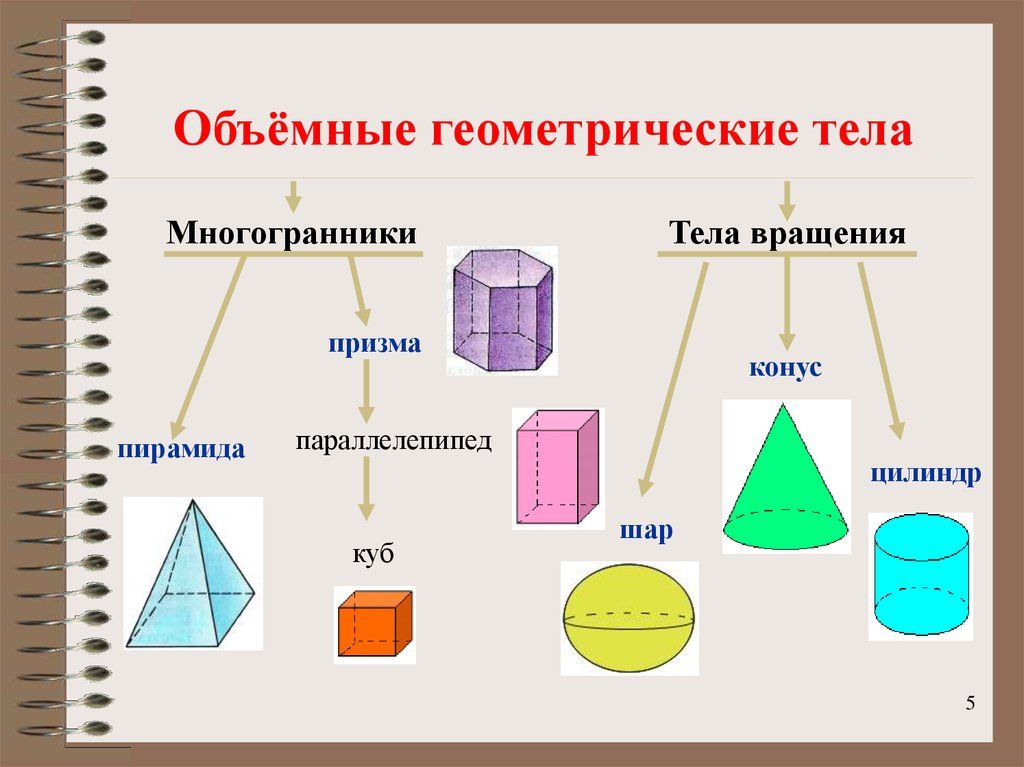 Что ты знаешь о диагоналях прямоугольника?
Что ты знаешь о диагоналях прямоугольника?
Ответ:
Стороны прямоугольника ABCD: AB, BC, CD, DA.
В прямоугольнике противоположные стороны равны.
Диагонали AC и BD.
В прямоугольнике диагонали равны.
Страница 118
6. Симметричны ли противоположные вершины квадрата относительно его диагоналей?
Проверь свой ответ: используй кальку.
Ответ:
7. Длина каждой стороны прямоугольника — 9 дм. Можно ли утверждать, что этот прямоугольник — квадрат? Продумай план ответа. Отвечай на вопрос задания, используя составленный план.
Ответ:
Квадрат – это прямоугольник, у которого все стороны равны.
В данном прямоугольнике длина каждой стороны равна 9 дм, поэтому можно утверждать, что этот прямоугольник является квадратом.
8. Чем похожи выражения и в чём их различие?
50 – (30 + 10) (50 – 30) – 10
Найди значения выражений.
Ответ:
9. Сумма двух чисел равна 17, одно из слагаемых — 6. Назови другое слагаемое.
Сумма двух чисел равна 17, одно из слагаемых — 6. Назови другое слагаемое.
Ответ:
17 – 6 = 11
Проверка 11 + 6 = 17
10. Одно число равно 5, а другое в 3 раза больше. Назови разность этих чисел.
Ответ:
5 • 3 = 15 – другое число
15 – 5 = 10 – разность
11. Запиши любое двузначное число, не используя цифру 0. Поменяй в нём местами цифры единиц и десятков. Запиши получившееся число. Какое число больше и на сколько?
Ответ:
47
74
74 > 47
74 – 47 = 27 – на столько 74 больше, чем 47
Страница 119
12. Уменьшаемое — число 40, вычитаемое — 4. Назови разность.
Разность чисел — 20, уменьшаемое — 80. Чему равно вычитаемое?
Ответ:
40 – 4 = 36 – разность
80 – 20 = 60 – вычитаемое
13. У продавщицы было 20 роз в одной вазе и 15 в другой. Она сделала из них 7 одинаковых букетов. Сколько роз в каждом букете?
Для решения задачи составь числовое выражение по условию задачи и найди его значение.
Ответ:
(20 + 15) : 7 = 35 : 7 = 5 роз – в каждом букете
14. Мама испекла 8 пирожков с капустой и столько же с мясом. Все пирожки она разложила поровну на 4 блюда. Сколько пирожков оказалось на каждом из них?
Ответ:
1) 8 + 8 = 16 пирожков – всего
2) 16 : 4 = 4 пирожка – на каждом блюде
15. Из данных выражений составь несколько верных записей, используя знак равенства.
32 : 4 12 + 6 50 – 8
3 • 9 6 • 7 56 – 48
Ответ:
32 : 4 = 8
3 • 9 = 27
12 + 6 = 18
6 • 7 = 42
50 – 8 = 42
56 – 48 = 8
32 : 4 = 56 – 48
6 • 7 = 50 – 8
16. Между каждыми двумя из пяти посёлков ходят рейсовые автобусы. Сколько всего автобусных маршрутов между посёлками?
Ответ:
Между поселками всего 10 автобусных маршрутов.
Страница 120
17. Начерти два отрезка, каждый из которых длиннее 1 дм, но короче 12 см.
Ответ:
1 дм = 10 см
18. Вырежи такой четырёхугольник. Разрежь его на 4 равные части так, как показано на рисунке.
Сложи из всех частей прямоугольник.
Ответ:
19. Олегу 27 лет. Возраст его младшего Андрея составляет третью часть возраста брата Олега. Сколько лет Андрею?
Ответ:
27 : 3 = 9 лет – Андрею
20. Вырежи 4 таких многоугольника и сложи из них квадрат.
Ответ:
21. Имеется 49 яблок. Сколько яблок не хватает, чтобы раздать шестерым детям по 9 штук?
Ответ:
1) 6 • 9 = 54 яблока – нужно, чтобы раздать шестерым детям по 9 штук
2) 54 – 49 = 5 яблок – не хватает
Страница 121
22. Петя вырезал из бумаги три прямоугольника. На рисунке все размеры этих прямоугольников уменьшены в 2 раза. Построй на листе тетради в клетку прямоугольники, которые вырезал Петя.
Ответ:
На рисунке прямоугольники уменьшены в 2 раза, значит, чтобы построить эти прямоугольники в тетради, нужно все стороны прямоугольников увеличить в 2 раза.
1) На рисунке первый прямоугольник – квадрат со стороной 4 клетки.
Значит, в тетради нужно построить квадрат со стороной: 4 • 2 = 8 клеток.
2) На рисунке второй прямоугольник – квадрат со стороной 3 клетки.
Значит, в тетради нужно построить квадрат со стороной: 3 • 2 = 6 клеток.
3) На рисунке третий прямоугольник имеет длину 6 клеток и ширину 2 клетки.
Значит, в тетради нужно построить прямоугольник, который будет иметь длину: 6 • 2 = 12 клеток и ширину: 2 • 2 = 4 клетки.
23. Уменьши размеры каждой из фигур в 3 раза. Построй фигуры на листе тетради в клетку.
Ответ:
Чтобы уменьшить фигуру в 3 раза, нужно все ее стороны уменьшить в 3 раза.
Урок математики 2 класс УМК “Планета знаний” Тема: “Наглядная геометрия” | План-конспект урока по математике (2 класс) по теме:
Тема: Наглядная геометрия
Цели:
- повторить материал о видах геометрических фигур,
- нахождение длины ломаной,
- познакомить с плоскими и объемными фигурами
- познакомить с определением диагонали
- отрабатывать умение работать в группах,
- способствовать развитию творческих способностей.

Оборудование: раздаточный материал (геометрические фигуры), наглядный раздаточный материал, презентация, конструктор, объемные геометрические фигуры, карточки , линейки, простые карандаши.
ХОД УРОКА
1. Орг. класса. Слайд №1 (звонок)
Прозвенел уже звонок.
Начинается урок
2. Постановка цели. Слайд№ 1 щелчок
– Ребята! мы отправляемся в увлекательное путешествие по стране Геометрии.
3. Актуализация знаний. 1 ученик
Удивительная страна- Геометрия!
Фигуры и линии в ней живут,
Меряют, чертят и узнают:
Периметр, площадь, длину, ширину,
Диаметр, радиус и высоту.
Скорей собирай своих знаний багаж!
Готовь поскорее простой карандаш!
Интересные задания ждут нас, друзья!
Пора отправляться:
В дорогу пора!
4.Вызов. Цели и задачи на урок. -Ребята, чтобы отправиться в эту замечательную страну, нам необходимо выяснить, что мы уже знаем о геометрии , а что хотим узнать нового. Для этого надо заполнить таблицу Слайд 2
У вас на столах лежат фигуры разного цвета, возьмите фигуру зеленого цвета, прочитайте выражения, которые записаны на ней и найдите те понятия, которые вам уже знакомы, то, что вы знаете.
1.Инструменты для построения геометрических фигур
2.Название геометрических фигур
3.Виды линий
4.Находить длину ломаной
5.Что такое геометрия?
6.Что такое объемные фигуры?
7.Чем отличается круг от шара?
8.Что такое пирамида?
(Заполнение таблицы) слайд 3
Слайд 4-задачи на урок
Слайд 5
Таблица «Знаю – Хочу узнать – Узнал»
«Знаю» | «Хочу узнать» | «Узнал» |
1.Название геометрических фигур 2. Инструменты для построения геометрических фигур 3.Находить длину ломаной | 1.Что такое геометрия? 2.Что такое диагональ? 3.Что такое объемные фигуры? 4.Чем отличается круг от шара? 5.Что такое пирамида? |
5. Актуализация знаний.
А)Название геометрических фигур.
-Какие знаете геометрические фигуры? об этом нам расскажут учащиеся
2, 3 ученик с показом фигур
-О фигурах что мы знаем?
-Их по форме различаем
Вот квадрат, а это круг.
Глянь внимательно вокруг-
На фронтоне – треугольник,
Вот цветок- многоугольник.
Дом как прямоугольник,
в небе облако – овал,
от солнца луч нам тепло прислал,
Вот прямая, вот – кривая,
А поверхность –то какая!
Много всякой красоты
составишь с нами ты! слайд 6
-О каких геометрических фигурах говорится в стихотворении? (фронтально)
Б) Составление геометрического словарика.(на доске) Дети выходят по одному и прикрепляют слова к доске
Составим геометрический словарик (на доске появляются слова )
Квадрат, круг, треугольник, многоугольник, овал, луч, прямоугольник, прямая, кривая.
Слайд 7 –назвать геометрические фигуры на экране. На первый вопрос нашей таблицы мы ответили . Второй вопрос.
Второй вопрос.
Слайд 8
В) инструменты для построения фигур
-А какие инструменты нужны для построения геометрических фигур?
Нам подготовили загадки дети:
Палочка волшебная
Есть у меня, друзья.
Палочкою этой
Могу построить я
Башню, дом и самолет,
И большущий пароход.(карандаш) слайд 8 щелчок
Я люблю прямоту, Я сама прямая.
Сделать новую черту
Вам я помогаю.
Что-нибудь без меня
Начертить сумей-ка.
Угадайте-ка, друзья,. Кто же я?-…(линейка) слайд 8 щелчок
Г) Практические работы №1 – построение прямой в тетради (индивидуальная работа)
-Ребята, а теперь нам предстоит практическая работа – построить геометрические фигуры – прямую. Вспомните свойство прямой(у прямой нет конца и края)Прямая может быть горизонтальная, ….
Слайд 9, 10
Практическая работа №2- построить фигуру из загадки
Слайд №11 Чем отличается луч от прямой?(у луча есть начало)
Слайд №12 – проверка .
Д) Практическая работа №3 – найти длину ломаной линии (работа в парах)
-Ребята, у вас на столах лежат карточки розового цвета , какая геометрическая фигура на ней начерчена? Ломаная. Как называются отрезки, из которых состоит ломаная? Звенья. Как найти длину ломаной?
Как называются отрезки, из которых состоит ломаная? Звенья. Как найти длину ломаной?
Вспомним правила работы в парах: (хором)
- при разговоре смотри на собеседника
- тихо говори в паре
- называй товарища по имени
- внимательно слушай ответ товарища
- дополняй
- оценивай
-Перед началом работы построим «домик сотрудничества»
Работаем в парах – выполнение практической работы №3, проверка
Слайд №13 .
Микроитог. Слайд №14
-Итак, мы повторили все вопросы из первой графы нашей таблицы. Отдохнем.
6. Физминутка для глаз -Слайд №15, 16.
7. Работа над новым материалом.
-Ребята, а в какой волшебной стране живут наши геометрические фигуры?
Слайд №17
-Геометрии. Откуда оно к нам пришло?
А) Работа с толковым словарем.
Мои помощники исследовали Толковый словарь и нашли ответ на вопрос Что такое геометрия.
Ученик читает
В переводе с греческого «гео» – земля, «метрио» – измерять. Это слово означает «землемерие».
Это слово означает «землемерие».
Слайд №18
-Слово зародилось еще в древнем Египте. В Египте протекает великая река Нил. По берегам Нила в те времена люди сажали различные растения, собирали богатые урожаи. Слайд №19
Во время разливов великая река выходила из берегов, смывала все изгороди между участками
Слайд №20
и каждый раз надо было заново делить поля на участки и обозначать их границы, а для этого надо было измерять и вычислять площадь земельных участков.
Так появилась наука геометрия. Слайд №21
Мы ответили на первый вопрос таблицы из графы –Хочу узнать.
Слайд №22 Таблица
Слайд №23
-Какой вопрос еще мы хотели узнать? Смотрим в таблицу Вопрос №2
Б)Работа с толковым словарем . Значение слова «диагональ».
– Обратимся к моим помощникам, изучавшим слово по толковому словарю.
Читает ученик
Диагональ многоугольника –
это отрезок, который соединяет вершины двух его углов, не имеющих общей стороны.
Слайд №24
-Выполним практическую работу №4
Слайд №25
В)Практическая работа № 4- начертить прямоугольник со сторонами 5 и 3 см и провести диагонали.
Проверка щелчок слайд 25
-Что же такое диагональ? Внесем в таблицу ответ
Слайд №26 Таблица
3. Физпауза.
Музыкальная пауза Слайд №27
4.Работа над новым материалом .
Знакомство с понятием объемная фигура Слайд №28, 29
Г) Знакомство с понятиями плоская и объемная фигура.
Что такое объемная фигура ? тесто, скалка
– Вы видели, как лепят пельмени? Сначала ставят тесто, из которого получается большой тёплый ком. Его можно обнять руками. А всё что можно обнять руками называется объёмным. Но стоит только раскатать этот ком скалкой обнять его уже невозможно, потому что он стал плоским. (Рассказ учителя сопровождается показом.)
Е) Практическая работа №5
Слайд №30
Найти в наборах фигур указанные на экране объемные фигуры:
куб, цилиндр, шар, конус, параллелепипед.
Таблица Слайд №31
Д) Практическая работа №6
Возьмите круг (розовая фигура) и шар. Чем же отличается круг от шара?
(шар- объемная фигура, круг – плоская).
Таблица Слайд №32
Е) Работа по учебнику. Стр.71. №6
-Чтение задание б) самостоятельно.
– Как вы понимаете слово пирамида?
-Что такое пирамида? Мои помощники исследователи словаря расскажут, что узнали об этом слове.
Ученик читает
-Где мы в жизненных ситуациях встречали пирамиду?
Слайд № 33
Египедские пирамиды Слайд №34
Практическая работа №7 Слайд №35
Собрать из конструктора пирамиду,(индивидуально)
8.Итог урока. Таблица. Слайд №36
Таблица «Знаю – Хочу узнать – Узнал»
«Знаю» | «Хочу узнать» | «Узнал» |
1.Название геометрических фигур 2. Инструменты для построения геометрических фигур 3. | 1.Что такое геометрия? 2.Что такое диагональ? 3.Что такое объемные фигуры? 4.Чем отличается круг от шара? 5.Что такое пирамида? | 1.Геометрия означает «землемерие». 2. Диагональ-отрезки, проведенные из противоположных углов прямоугольника или квадрата 3. Всё , что можно обнять руками называется объёмным 4. Круг плоская фигура, шар – объёмная фигура 5. пирамида- объемная фигура |
9.Рефлексия
. Вот и подошел к концу наш урок. Подведём итоги. Ответьте на вопросы.
– Что нового узнали на уроке?
– Что показалось самым трудным?
-Когда услышите слово « геометрия», какие ассоциации у вас появятся?
Ассоциации Слайд №37
Геометрия
Квадрат, плоская фигура
круг, объемная фигура
треугольник, диагональ
многоугольник, пирамида
прямоугольник,
шар,
цилиндр,
прямая,
кривая.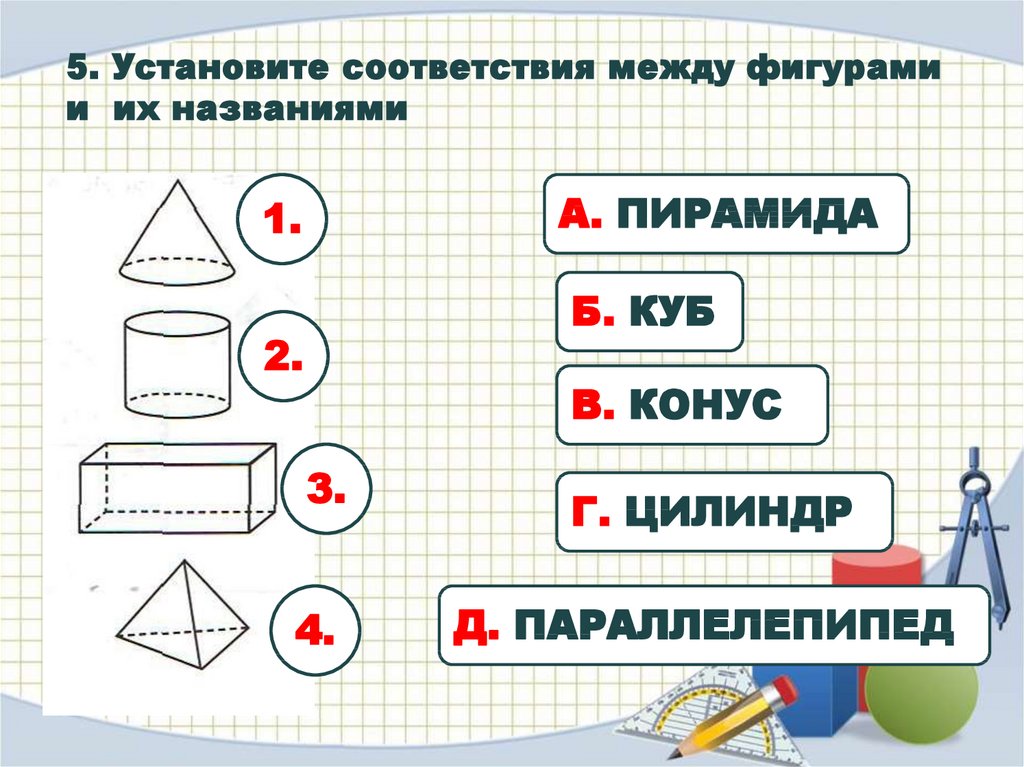
Геометрию учить, значит с пользой в мире жить.
10.Домашнее задание. Слайд №38
Из цветной бумаги вырежи геометрические фигуры и составь из них аппликацию.
Оцените свою работу на уроке: было интересно- зеленая наклейка, непонятно- желтая, скучно – розовая. (на плакате)
2 класс. ПНШ. Методическая разработка урока по математике. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
Урок 2
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
Цели: повторить названия геометрических фигур; учить сравнивать геометрические фигуры, называть их свойства и признаки; совершенствовать навык построения геометрических фигур; развивать наблюдательность, мышление.
Ход урока
I. Организационный момент.
II. Сообщение темы урока.
– Какие фигуры вы видите на рисунке? Назовите их.
– Сегодня на уроке вспомним свойства изученных геометрических фигур.
III. Устный счет.
1. Продолжите закономерность: 1, 5, 9, 13, … (17, 21).
2. Геометрическая сказка.
Жили-были два брата: треугольник с квадратом.
Старший – квадратный, добродушный, приятный.
Младший – треугольный, вечно недовольный.
Стал расспрашивать квадрат: «Почему ты злишься, брат?»
Тот кричит ему: «Смотри, ты полней меня и шире.
У меня углов лишь три, у тебя же их четыре!»
Но квадрат ответил: «Брат! Я же старше, я – квадрат».
И сказал еще нежней: «Неизвестно, что нужней!»
Но настала ночь, и к брату, натыкаясь на столы,
Младший лезет воровать срезать младшему углы.
Уходя, сказал: «Приятных я тебе желаю снов!
Спать ложился – был квадратным, а проснешься без углов!»
Но наутро младший брат страшной мести был не рад.
Поглядел он – нет квадрата. Онемел… Стоял без слов…
Вот так месть! Теперь у брата сколько новеньких углов? (8.)
3. Геометрические фигуры.
– Посмотрите внимательно на фигуры и распределите их на две группы. Укажите признак, по которому вы распределили фигуры по группам.
4. Выполните вычисления:
IV. Работа по теме урока.
1. Задание 6.
– Назовите признаки отрезка.
– Что общего между прямой, отрезком и лучом? Чем эти фигуры отличаются друг от друга?
– Какие предметы в нашей повседневной жизни напоминают нам прямую (линейка, указка и т. д.), луч (гвоздь, молоток, т. п.), отрезок (дверная ручка и т. п.)?
– Прочитайте задачу 6.
– Что известно? Что требуется узнать?
Запись:
Решение: 12 – 8 = 4 (см).
Ответ: на 4 см первый отрезок длиннее второго.
2. Задание 7.
– Какая фигура изображена в учебнике? (Прямоугольник.)
– Назовите признаки прямоугольника.
– Измерьте и запишите длины сторон прямоугольника. Нужно ли измерять все стороны прямоугольника?
Вывод: у прямоугольника противоположные стороны равны.
3. Задание 8.
Решение:
Физкультминутка
4. Задание 9.
– Какие линии называются кривыми?
– Проведите две кривые линии, которые пересекаются в трех точках.
5. Задание 10.
– Какой угол называют прямым?
– С помощью какого инструмента можно построить прямой угол? (Угольника.)
– Начертите две прямые, пересекающиеся под прямым углом.
– Сколько прямых углов на чертеже? (Четыре.)
6. Задание 11.
– Назовите геометрические фигуры, изображенные на чертеже.
– Сколько кругов на чертеже?
– Сколько треугольников?
– Сколько четырехугольников?
– Сколько прямоугольников?
– Сколько квадратов?
V. Работа по карточкам.
1. Распределите линии в три группы.
– Назовите признаки, по которым вы образовали группы.
(1-я группа – 1, 4, 5 – прямые линии; 2-я группа – 2, 3 – кривые линии; 3-я группа – 6, 7 – ломаные линии.)
2. Продолжите закономерность.
3. Разделите квадрат на четыре равные части. Найдите как можно больше решений.
Ответ:
VI. Итог урока.
Итог урока.
– Что нового узнали на уроке?
– Назовите свойство сторон прямоугольника.
Домашнее задание: начертить ломаную линию, состоящую из пяти звеньев.
Урок математики по теме “Геометрические фигуры и их классификация”. 1-й класс
- Хавлюк Марина Васильевна
Разделы: Начальная школа, Мастер-класс
Класс: 1
Ключевые слова: геометрические фигуры
Цель обучения, которая достигается на данном уроке | 1. |
Цели урока | Все учащиеся смогут: распознавать и называть геометрические фигуры: точка, прямая, кривая, ломаная, замкнутая, незамкнутая, отрезок луч, угол. |
Критерии оценки | Различает и называет геометрические фигуры: точка, прямая, кривая, ломаная, замкнутая, незамкнутая, отрезок луч, угол. |
Языковые цели | Все учащиеся смогут: правильно назвать и распознать геометрические фигуры: точка, прямая, кривая, ломаная, замкнутая, незамкнутая, отрезок луч, угол. |
Привитие ценностей | Воспитание уважения, взаимопомощи, к каждому члену команды, умение слушать и слышать, трудолюбие. Воспитание осуществляется через все приемы и методы, используемые на уроке; основанных на Общенациональной идее «Мәнгілік ел». |
Межпредметны связи | математика, трудовое обучение. |
Предыдущие знания по теме | Называют некоторые геометрические фигуры. |
Ход урока
Запланированные этапы урока | Запланированные этапы урока | Ресурсы |
| Начало урока | 1. – Встаньте в круг. Сегодня мы будем желать друг другу успехов, здоровья и много других хороших пожеланий. 2.Актуализация знаний. | |
3. – На какую геометрическую фигуру она похожа?
(точку) |
горошинка | |
Активный метод обучения – К доске вызываются два ученика. Они держат натянутую верёвку.  – Что в руках у наших ребят? (верёвка) – Какую фигуру она напоминает? (прямую линию) К доске вызываются другие ученики. (опустили вниз) – Значит кривая, которая была у нас первой, была… (П) Работа в паре. Активный метод. «Каждый учит каждого» Метод дифференциации через классификацию. Пара №1 – (средний, низкий) Пара №2 – (средний, низкий) Пара №3 – (высокий, высокий) Критерий оценивания. |
веревка | |
| Середина урока | Ресурс: – Посмотрите на фигуры, обведённые жёлтым цветом. Самооценивание, сравнивают с образцом. ФО «Светофор» Правильно выполнили – красный; Допустили ошибки – зеленый. | картинка с геометрическими фигурами
слайд |
(И) Индивидуальная работа. ФО «Словесная похвала» Физминутка |
сюжетная картинка интернет-ресурсы | |
(К) Коллективная работа. |
веревка | |
Завяжите на концах веревки узлы. – Мы получили новую геометрическую фигуру – отрезок. |
проволока | |
– У вас на партах лежит проволока. Согните проволоку в нескольких местах. |
ручки | |
– Возьмите две ручки и соедините их по образцу. (показ) | ||
| ФО «Устная обратная связь Учитель → ченик» Активный метод обучения «Юный исследователь» (Г) Работа в группе.  Метод дифференциация через группирование. Метод дифференциация через группирование.Деление на группы (у детей на стульчиках геометрические фигуры: точка, кривая линия, отрезок) 1 группа – (средний, высокий, низкий) 2 группа – (средний, высокий, низкий) 3 группа – (средний, высокий, низкий) Метод дифференциации через ресурсы. Ресурс для 1 группы: палочки и пластилин. Ресурс для 2 группы: верёвочки и пластилин. Ресурс для 3 группы: проволока и пластилин. Метод дифференциации через задание. Задание в группах: Задание для 1 группы: Придумайте и смоделируйте знакомые вам геометрические фигуры, используя предложенные ресурсы. Задание для 2 группы: Придумайте и смоделируйте знакомые вам геометрические фигуры, используя предложенные ресурсы. Задание для 3 группы: Придумайте и смоделируйте знакомые вам геометрические фигуры, используя предложенные ресурсы.  |
веревочки | |
ФО «Сигнальные кружочки». (И) Индивидуальное задание: Напишите свое имя на листочке. | интернет-ресурсы
лист бумаги | |
Конец урока | 5. |
|
Математика Обозначение геометрических фигур буквами
Материалы к уроку
Конспект урока
5. Обозначение геометрических фигур буквами
|
Организационный этап
Не крутите пестрый глобус,
|
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Ребята, мы отправимся путешествовать по чудесной стране под названием Геометрия. Что такое геометрия? В переводе с греческого это слово означает «землемерие» («гео» – земля, «метрио» – измерять). Появление геометрии было связано с разными измерительными работами при проведении дорог и строительстве зданий. Возникли правила, относящиеся к геометрическим измерениям. В стране Геометрии живут геометрические фигуры и тела. Сегодня на уроке мы будем учиться обозначать геометрические фигуры буквами латинского алфавита. Но чтобы нам попасть в страну Геометрию, нужно решить несколько заданий.
|
|
Устный счёт
Задание Увеличьте числа шестнадцать, тридцать один, сорок три, семьдесят на пять и запишите только ответы. Проверьте себя. 21, 36, 48, 75
9, 36, 63, 80.
Задание Расставьте знаки плюс или минус так, чтобы равенства остались верными. (40 … 25) … 5 = 20 50 … (43 … 10) = 83 (90 … 35) … 25 = 80 (16 … 3) … 7 = 20 Проверьте себя.
50 + (43 – 10) = 83 (90 – 35) + 25 = 80 (16 – 3) + 7 = 20
Задание Продолжите ряды чисел, соблюдая закономерность. 16, 26, 37, 49, …, …, … . 88, 87, 85, 82, 78, …, …, …, … . Проверьте себя.
88, 87, 85, 82, 78, 73, 67, 60, 52.
Молодцы, ребята! Справились с заданиями. Вот мы и попали в Страну Геометрию. А встречает нас королева этой страны Точка. Без нее нельзя построить ни одной фигуры. Кто такая королева Точка? Жила-была королева Точка. Она была очень любопытна и хотела все знать. И решила она обойти свое королевство. Шла Точка, шла и встретила точку точно такую, как она сама, потом еще одну, и еще одну. Раз, два, три, четыре, пять Сегодня на уроке мы будем учиться обозначать геометрические фигуры буквами латинского алфавита.
|
|
Объяснение нового материала
Точку рисуют или изображают легким прикосновением карандаша или ручки к бумаге и обозначают одной буквой. Точки любят выбирать себе имена из букв латинского алфавита. Посмотрите, как называются буквы латинского алфавита и постарайтесь запомнить их. Знакомьтесь: БУКВА а буква бэ, буква дэ, буква эм, буква пэ, буква тэ, буква е, буква ка, буква эн, буква эр, буква икс, буква цэ, буква эф, буква эль, буква о, буква эс, буква игрек. Чтобы назвать отрезок, его концы обозначают буквами латинского алфавита, в данном случае отрезок называется эм эн. Название фигуры читают, начиная с буквы, обозначающей нижний левый угол, одну за другой по часовой стрелке не пропуская. Например, данный прямоугольник называется а бэ цэ дэ. А треугольник о эм ка. Каждый угол многоугольника имеет название. Оно может состоять из одной буквы, вершины угла, или из трех букв, которыми обозначены лучи, при этом в середине должна стоять буква вершины угла. Читается так: угол О или угол эм о ка. |
|
Этап усвоения новых знаний
Задание Отметьте одну за другой четыре точки. Дайте им имена.
Задание Отметьте синим карандашом три точки. Приложите к ним Проверьте себя.
Задание Отметьте две точки на расстоянии 6 см одна от другой. Соедините линией. Назовите отрезок о ка. Проверьте себя.
Задание Срисуйте точки. Не забывайте, что точка рисуется прикосновением.
Задание Назовите фигуры. Прямоугольник ка о эм эн Многоугольник а бэ цэ дэ о эм.
|
|
Задание Начертите отрезок а ка длиной 7 см 4 мм и отрезок бэ цэ длиной 5 см 2 мм. Выразите их длину в миллиметрах. Проверьте себя. 7 см 4 мм = 74 мм 5 см 2 мм = 52 мм
Задание Постройте ломаную линию со звеньями: АВ = 3 см, ВС = 6 см, СМ= 2 см, МК = 4 см. Проверьте себя. Длина ломаной равна 15 см. Задание Начертите отрезок ВС длиной 80 мм. Отметьте на нём точку О так, чтобы длина отрезка ВО была 25 мм. Найдите длину отрезка ОС, не измеряя его. Проверьте себя. Длина отрезка ОС равна 55 мм.
Итог урока
Говорит сова Ребята, сегодня на уроке мы узнали, что геометрические фигуры обозначаются буквами латинского алфавита. Как читают название фигуры? Название фигуры читают с буквы вершины, обозначающей нижний левый угол, одну за другой не пропуская по часовой стрелке. Спасибо, ребята, за урок. До новых встреч! |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
2D-фигуры – названия, определения, свойства, формулы, примеры
2D-форма представляет собой плоскую форму, имеющую только два измерения – длину и ширину, без толщины и глубины, поэтому ее называют двухмерной. -объемная форма. Например, лист бумаги имеет двумерную форму. Он состоит из длины и ширины, но не имеет ни глубины, ни высоты. Некоторыми распространенными 2D-формами являются квадраты, прямоугольники, треугольники, круги и шестиугольники. По сравнению с ними трехмерная (трехмерная) форма имеет три измерения — длину, ширину и высоту. Например, игральная кость трехмерна, потому что состоит из длины, ширины и высоты. Некоторыми распространенными трехмерными формами являются кубоиды, конусы, пирамиды и цилиндры. Давайте узнаем больше о двумерных фигурах в этой статье.
-объемная форма. Например, лист бумаги имеет двумерную форму. Он состоит из длины и ширины, но не имеет ни глубины, ни высоты. Некоторыми распространенными 2D-формами являются квадраты, прямоугольники, треугольники, круги и шестиугольники. По сравнению с ними трехмерная (трехмерная) форма имеет три измерения — длину, ширину и высоту. Например, игральная кость трехмерна, потому что состоит из длины, ширины и высоты. Некоторыми распространенными трехмерными формами являются кубоиды, конусы, пирамиды и цилиндры. Давайте узнаем больше о двумерных фигурах в этой статье.
| 1. | Что такое 2D-фигуры? |
| 2. | Разница между 2D и 3D фигурами |
| 3. | Свойства 2D-фигур |
| 4. | Площадь и периметр 2D-фигур |
| 5. | Часто задаваемые вопросы о 2D-фигурах |
Что такое 2D-фигуры?
В геометрии 2D-формы могут быть определены как плоские фигуры, которые являются абсолютно плоскими и имеют только два измерения — длину и ширину. Они не имеют толщины и могут быть измерены только по двум измерениям.
Они не имеют толщины и могут быть измерены только по двум измерениям.
Определение 2D-фигур
Многоугольник представляет собой 2-мерную форму , состоящую из сегментов прямой линии, которые соединены друг с другом, что придает ему замкнутую форму. Круг, квадрат, прямоугольник и треугольник являются примерами двухмерных фигур, которые можно нарисовать на бумаге. Все двумерные фигуры имеют стороны, вершины (углы) и внутренние углы, за исключением круга, который представляет собой изогнутую фигуру. Двумерные фигуры, имеющие по крайней мере три прямые стороны, называются многоугольниками, и к ним относятся треугольники, квадраты и четырехугольники. На приведенном ниже рисунке показаны 2D-формы, с которыми мы обычно сталкиваемся.
Типы 2D-фигур — правильные и неправильные 2D-фигуры
2D-форма может быть классифицирована как правильная или неправильная в зависимости от длины и внутренних углов:
- Двухмерная форма (2D-форма) называется правильным, если все его стороны равны по длине и все внутренние углы равны между собой.
- Двумерная фигура (2D-форма) является неправильной, если все стороны имеют разную длину и все ее углы имеют разную величину.
Обратите внимание на следующий рисунок, на котором показана разница между правильными и неправильными 2D-формами.
Разница между 2D и 3D фигурами
В следующей таблице показано сравнение двухмерных и трехмерных форм.
| 2D-формы | 3D-фигуры | |
|---|---|---|
| Полная форма | 2D- = двумерный | 3D = трехмерный |
| Определение | 2D-формы являются плоскими и имеют только два измерения длины и ширины без толщины или глубины. | Трехмерная фигура имеет 3 измерения длины, ширины и высоты. |
| Размеры | Только длина и ширина | Длина, ширина и высота |
| Математические оси | ось X и ось Y | ось X, ось Y и ось Z |
| Примеры | Прямоугольник, квадрат, круг, треугольник и т. д. д. | Цилиндр, сфера, куб, призма и т. д. |
Свойства 2D-фигур
Двухмерные фигуры плоские и могут быть нарисованы на листе бумаги. Существуют различные типы правильных и неправильных 2D-форм, таких как круг, треугольник, квадрат, прямоугольник, пятиугольник и шестиугольник. Давайте узнаем о некоторых из них вместе с их свойствами.
Имена 2D-фигур
Вот несколько примеров 2D-фигур вместе с их свойствами.
Круг:Круг — это замкнутая 2D-форма, состоящая из изогнутой линии без углов и краев. Некоторыми реальными примерами круга являются монеты, колеса и пицца. Круг состоит из различных частей, таких как радиус, диаметр, длина окружности и так далее.
Свойства круга
Изучите свойства круга, чтобы идентифицировать его как двумерную форму.
- Круги полностью круглые и состоят из одной изогнутой линии.
- Окружность — это длина границы окружности.

- Радиус — это расстояние от центра круга до границы круга.
- Диаметр — это отрезок, проходящий прямо через окружность через центр. Это самая длинная линия, которую можно провести внутри круга, и ее длина вдвое больше радиуса.
На следующем рисунке показаны различные части круга.
Треугольник:
Треугольник — это двумерная фигура с тремя сторонами и тремя вершинами (углами).
Свойства треугольника
Изучите свойства треугольника, чтобы идентифицировать его как двумерную фигуру.
- Треугольник — это замкнутая фигура с 3 сторонами, 3 вершинами и 3 углами.
- Это многоугольник, внутренние углы которого в сумме составляют 180°.
Примерами треугольников из реальной жизни являются дорожные знаки, пирамиды и начос. На следующем рисунке показаны стороны и вершины треугольника.
Квадрат: Квадрат — это двумерная фигура с четырьмя равными сторонами, каждый из которых равен 90˚. Некоторые из реальных примеров квадрата: буханка хлеба и шахматная доска.
Некоторые из реальных примеров квадрата: буханка хлеба и шахматная доска.
Свойства квадрата
Изучите свойства заданного квадрата PQSR, чтобы идентифицировать его как двумерную форму.
- Все четыре стороны равны, т. е. сторона PQ = QS = RS = PR
- Сторона PQ параллельна RS.
- Сторона PR параллельна QS.
- Все четыре внутренних угла равны 90°.
Прямоугольник — это двумерная фигура с четырьмя сторонами, у которой противоположные стороны равны и параллельны, а все четыре угла равны 90°. Некоторыми реальными примерами прямоугольника являются столешницы, классные доски, картон и т. д.
Свойства прямоугольника
Изучите свойства заданного прямоугольника ABCD, чтобы идентифицировать его как двумерную фигуру.
- Сторона AB = DC
- Сторона AD = BC
- Сторона AB параллельна стороне DC.
- Сторона AD параллельна стороне BC.

- Все четыре угла равны 90°.
Площадь и периметр 2D-фигур
Площадь 2D-фигуры — это заключенное внутри нее пространство. Периметр двумерной фигуры — это общая длина ее границы. В следующей таблице показаны формулы, которые используются для расчета площади и периметра нескольких распространенных 2D-фигур:
| 2D-форма | Формула площади | Формула периметра |
|---|---|---|
| Круг | A = π × r 2 , где r — радиус окружности, а π — константа, значение которой принимается равным 22/7 или 3,14 | Окружность (Периметр) = 2πr |
| Треугольник | Площадь = ½ (основание × высота) | Периметр = сумма трех сторон |
| Квадрат | Площадь = Сторона 2 | Периметр = 4 × сторона |
| Прямоугольник | Площадь = длина × ширина | Периметр = 2 (длина + ширина) |
Важные примечания
Вот несколько важных примечаний, которые следует помнить при изучении 2D-форм.
- Любую 2D-форму можно измерить по ширине и длине.
- Все 2D-формы полностью плоские.
☛ Статьи по теме
- Геометрические фигуры
- Плоские формы
- Твердые формы
- Визуализация твердых фигур
- Рабочие листы 2D и 3D форм
Часто задаваемые вопросы о 2D-фигурах
Что такое 2D-фигуры?
Двухмерная (двумерная) фигура может быть определена как плоская фигура, которую можно нарисовать на плоской поверхности. Он имеет только два измерения – длину и ширину, без толщины и глубины. Некоторые из основных 2D-форм: прямоугольник, пятиугольник, четырехугольник, круг, треугольники, квадрат, восьмиугольник и шестиугольник.
Что такое 2D-фигуры и 3D-фигуры?
Плоская фигура, имеющая два измерения — длину и ширину, — это двумерная фигура, а фигура, имеющая три измерения — длину, ширину и глубину (высоту), — трехмерная фигура.
Каковы свойства 2D-фигур?
Двухмерная фигура — это плоская фигура, которую можно нарисовать на плоской поверхности. Как следует из названия, он имеет только два измерения длины и ширины без какой-либо толщины. В то время как некоторые 2D-фигуры имеют стороны и вершины, другие состоят из изогнутых линий.
Сколько существует двухмерных фигур?
Существует множество различных видов 2D-форм, таких как прямоугольник, пятиугольник, четырехугольник, круг, треугольник, квадрат, восьмиугольник и шестиугольник. Это плоские фигуры, которые можно рисовать на плоской поверхности.
Как найти площадь двумерных фигур?
Площадь 2D-фигуры — это занимаемое ею пространство. Поскольку существуют различные виды 2D-фигур, такие как круги, квадраты, прямоугольники и т. д., для нахождения их площадей используются разные формулы. Например, площадь круга можно рассчитать по формуле Площадь = πr 2 , где ‘r’ — радиус окружности, а (pi) π — константа со значением 22/7. Площадь квадрата рассчитывается по формуле Площадь = сторона × сторона. Площадь двумерных фигур выражается в квадратных единицах.
Площадь квадрата рассчитывается по формуле Площадь = сторона × сторона. Площадь двумерных фигур выражается в квадратных единицах.
Как обучать двухмерным фигурам?
Обучение двухмерным формам легко, если эта концепция представлена в первые годы. Прежде всего, можно заставить выучить названия основных фигур. Затем учащимся предлагается назвать названия фигур. Еще один интересный способ — попросить их определить фигуры вокруг них.
Назовите двухмерные фигуры вокруг дома.
Некоторые часто встречающиеся в доме 2D-формы: прямоугольная поверхность ноутбука (прямоугольник), круглая форма часов (круг), круглая форма пиццы, окно квадратной формы (квадрат )
Является ли круг двумерной фигурой?
Да, круг — это двумерная форма, потому что он существует на плоскости без глубины. Это изогнутая форма, которая не имеет углов или краев.
Какая двумерная фигура имеет 4 стороны?
Четырехугольник — это двумерная фигура, имеющая четыре стороны. Например, четырехугольники, такие как квадраты и прямоугольники, представляют собой двумерные фигуры с 4 сторонами.
Например, четырехугольники, такие как квадраты и прямоугольники, представляют собой двумерные фигуры с 4 сторонами.
Является ли овал 2D или 3D формой?
Овал является двухмерной формой, поскольку он существует на плоскости и не имеет глубины. Это изогнутая фигура без краев и углов.
Как преподавать 2D- и 3D-фигуры
Этот пост посвящен занятиям 2-го класса по 2D- и 3D-фигурам. Эти занятия основаны на общих стандартах базовой геометрии 1-го класса и готовят учащихся к стандартам 3-го класса. Этот пост в блоге будет посвящен тому, как использовать эти упражнения при изучении стандарта 2-го класса 2.G.1. Ваши ученики изучат различные стратегии рассуждений с фигурами и их атрибутами.
Стандарты по геометрии:
2 класс 2.Г.1: Распознавать и рисовать фигуры, имеющие заданные признаки, такие как заданное количество углов или заданное количество равных граней. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.
Знакомство с терминологией
Очень эффективно представить свой модуль геометрии с помощью якорной диаграммы, которая анализирует ключевую терминологию и предоставляет визуальные эффекты. Это служит спиральным обзором предыдущих навыков работы с 2D- и 3D-формами, которые они изучили, а также сильным визуальным представлением для этого модуля. В 1-м классе учащиеся учатся различать определяющие признаки формы. Повторение этих атрибутов является отличной разминкой для учащихся. Эта якорная диаграмма служит наглядной иллюстрацией для учащихся при изучении 2D- и 3D-форм и их атрибутов. Это прочный фундамент, на котором они будут строить знания во 2-м классе.
Это служит спиральным обзором предыдущих навыков работы с 2D- и 3D-формами, которые они изучили, а также сильным визуальным представлением для этого модуля. В 1-м классе учащиеся учатся различать определяющие признаки формы. Повторение этих атрибутов является отличной разминкой для учащихся. Эта якорная диаграмма служит наглядной иллюстрацией для учащихся при изучении 2D- и 3D-форм и их атрибутов. Это прочный фундамент, на котором они будут строить знания во 2-м классе.
Основное используемое действие с 2D-фигурами — эта якорная диаграмма, описывающая атрибуты 2D-фигур. Очень важно, чтобы учащиеся связали определяющие атрибуты с именем и суффиксом слова формы. Это поможет им более конкретно понять количество сторон, вершин и углов. Также важно показать примеры различных способов создания этой формы. Это позволяет учащимся выйти за рамки базовой версии каждой 2D-формы.
Подобно приведенному выше упражнению с 2D-фигурами, эта якорная диаграмма атрибутов 3D-фигур служит той же цели. Эта диаграмма разбивает каждую трехмерную фигуру и показывает количество граней, ребер и вершин. Примеры каждой формы помогают учащимся связать термин «твердый» с определяющими атрибутами. Они также могут видеть различия между 2D-полигонами и 3D-телами.
Эта диаграмма разбивает каждую трехмерную фигуру и показывает количество граней, ребер и вершин. Примеры каждой формы помогают учащимся связать термин «твердый» с определяющими атрибутами. Они также могут видеть различия между 2D-полигонами и 3D-телами.
Эти интерактивные видеоролики от BrainPop Jr – интересный способ для учащихся попрактиковаться в распознавании и определении 2D- и 3D-фигур.
- BrainPop Jr — 2D-фигуры
- BrainPop Jr — 3D-фигуры
Идентификация фигур
Сосредоточив внимание на 2D- и 3D-фигурах, полезно начинать с изучения одного типа фигур за раз. Это дает учащимся время понять каждый тип формы отдельно, прежде чем сравнивать их. Один день модуля будет посвящен исключительно 2D-формам. После всего группового занятия учащиеся будут работать в парах, малых группах и индивидуально, чтобы изучить эти формы и их атрибуты. В этот урок включены практические занятия, интерактивные подсказки в блокноте и двухмерные фигуры.
После того, как учащиеся продемонстрируют мастерство владения двухмерными фигурами, следующим шагом будет изучение трехмерных фигур и их атрибутов. Точно так же у студентов будет целый групповой урок с якорной диаграммой и плакатами. Затем они будут работать с партнерами, небольшими группами и индивидуально, чтобы показать, что они знают о трехмерных формах и их атрибутах. Эта книга о 3D-фигурах — одно из моих любимых занятий в этом разделе, поскольку она служит отличным «путеводителем» для студентов по мере прохождения этого исследования.
Точно так же у студентов будет целый групповой урок с якорной диаграммой и плакатами. Затем они будут работать с партнерами, небольшими группами и индивидуально, чтобы показать, что они знают о трехмерных формах и их атрибутах. Эта книга о 3D-фигурах — одно из моих любимых занятий в этом разделе, поскольку она служит отличным «путеводителем» для студентов по мере прохождения этого исследования.
Описание атрибутов
Теперь, когда учащиеся подробно изучили двухмерные и трехмерные формы, пришло время приступить к их описанию. Эти занятия с 2D- и 3D-фигурами помогут учащимся описать атрибуты различных фигур. Карточки с 2D- и 3D-формами можно смешивать для дополнительной сложности или разделять на 2D- и 3D-формы. Когда учащиеся описывают атрибуты, а затем сортируют их самостоятельно, они развивают навыки критического мышления.
Рисование фигур
По мере того, как учащиеся продолжают выполнять предыдущие упражнения с 2D- и 3D-фигурами, теперь они готовы рисовать фигуры. Используя свои знания о фигурах и их атрибутах, учащиеся могут продемонстрировать свои знания, рисуя 2D- и 3D-фигуры. Мне нравится, как на карточках в этом упражнении учащиеся сначала обводят форму. Это позволяет им подумать обо всех атрибутах и почувствовать, как выглядит эта фигура и как ее рисовать. Это отлично подходит для наших кинестетиков. После этого учащиеся рисуют рядом с ним свою фигуру. Это также помогает нашим визуальным ученикам, позволяя им увидеть, насколько их рисунок близок к оригиналу.
Используя свои знания о фигурах и их атрибутах, учащиеся могут продемонстрировать свои знания, рисуя 2D- и 3D-фигуры. Мне нравится, как на карточках в этом упражнении учащиеся сначала обводят форму. Это позволяет им подумать обо всех атрибутах и почувствовать, как выглядит эта фигура и как ее рисовать. Это отлично подходит для наших кинестетиков. После этого учащиеся рисуют рядом с ним свою фигуру. Это также помогает нашим визуальным ученикам, позволяя им увидеть, насколько их рисунок близок к оригиналу.
Дифференциация занятий в малых группах
Как и в случае с любой концепцией, не все учащиеся будут учиться в одном темпе или одним и тем же способом. В этот блок я включил 3 уровня действий с 2D и 3D фигурами. Учащиеся в группе исправления получат пользу от простого повторения и практики сопоставления. Учащиеся на первом уровне могут больше работать над определением атрибутов фигур, в то время как учащиеся в группе повышения квалификации готовы к занятиям по рисованию фигур и более сложным играм. Как всегда, для учителя крайне важно встретиться со студентами там, где они находятся, и двигаться дальше. Ключевым моментом является формирование этих базовых навыков, прежде чем двигаться дальше.
Как всегда, для учителя крайне важно встретиться со студентами там, где они находятся, и двигаться дальше. Ключевым моментом является формирование этих базовых навыков, прежде чем двигаться дальше.
Уделите много времени смешанным обзорам и практической практике
Как и все остальное, практика делает совершенным! Крайне важно предоставить учащимся несколько возможностей для работы с этими 2D- и 3D-фигурами. Использование различных практических и смешанных обзорных заданий, включенных в этот блок, позволяет учащимся практиковать эти концепции и стать более беглыми. Они начнут определять, рисовать и распознавать различные формы и их атрибуты с большей точностью по мере того, как они работают над достижением мастерства. Этот модуль упрощает дифференциацию, предоставляя вашим учащимся необходимую поддержку.
Предложения по обучению для 2-го класса…
Этот модуль разбивает стандарт 2-го класса, 2.G.1, обучая учащихся тому, как распознавать и рисовать 2D- и 3D-формы, имеющие определенные атрибуты, такие как заданное количество углов или заданное число равных лиц. Студенты также узнают, как идентифицировать треугольники, четырехугольники, пятиугольники, шестиугольники и кубы. Все изображения, которые вы видите в этом сообщении в блоге, взяты из блока атрибутов 2D и 3D Shape.
Студенты также узнают, как идентифицировать треугольники, четырехугольники, пятиугольники, шестиугольники и кубы. Все изображения, которые вы видите в этом сообщении в блоге, взяты из блока атрибутов 2D и 3D Shape.
Нажмите кнопки нужной ссылки.
Купить в TPT
Купить в Elementary Nest
Ищете другие статьи по математике в блогах?
- Поддержание порядка в математическом блоке
- Написание статей о математике
- Как учить числовые строки
6 отличных книг для Дня труда в классе
День труда быстро приближается! Этот праздник часто упускают из виду, потому что начало года очень занято. Но это отличный шанс
Подробнее »
3 способа, как чтение выходных билетов может улучшить ваше преподавание
Как учителя, мы постоянно ищем способы проверки понимания. Мы хотим знать: был ли этот урок эффективным? Они «поняли»? Кто
Подробнее »
5 причин, почему вы должны предлагать мероприятия для раннего финиша
Мы все сталкивались с разрушительной серией событий, когда ученик поднимает руку и говорит: «Я закончил. что делать
что делать
Подробнее »
enVision Math Common Core Grade 2 Ключевой ответ Тема 13 Фигуры и их атрибуты – большие идеи Математические ответы
Практика с помощью enVision Math Common Core Grade 2 Ключ ответа Тема 13 Фигуры и их атрибуты регулярно и повышайте точность решения вопросы.
Основной вопрос:
Как можно описывать, сравнивать и разбивать формы на части?
Проект enVision STEM: все о форме
Узнать Нарисуйте инструменты, используемые для садоводства, приготовления пищи или ремонта. Опишите форму каждого инструмента. Расскажите, как форма каждого инструмента помогает ему работать.
Journal: Make a Book Покажите свою работу в книге. В вашей книге также:
- Выберите инструмент, которым вы пользуетесь в школе. Расскажите, как форма инструмента помогает ему работать.
- Нарисуйте и опишите многоугольники.
Обзор того, что вы знаете
Словарь
Вопрос 1.
Обведите фигуру с 6 сторонами.
Ответ:
Многоугольник с 6 сторонами называется шестиугольником.
У синей фигуры 5 сторон, а у зеленой фигуры 6 сторон.
Итак, ответ – зеленая цифра.
Вопрос 2.
Обведите каждую плоскость. Поместите коробку вокруг каждой твердой фигуры.
Ответ:
Вопрос 3.
Поместите прямоугольник вокруг круга, который показывает четверти.
Ответ:
Первая фигура разделена на четыре части.
Основные факты
Вопрос 4.
Запишите каждую сумму.
Ответ:
Вопрос 5.
Напишите каждое различие.
Ответ:
Math Story
Вопрос 6.
У Эдны есть книжный шкаф с 5 полками. Она ставит по 5 книг в ряд на каждую полку. Напишите уравнение, которое показывает, сколько всего книг у Эдны.
Ответ:
Дано,
У Эдны есть книжный шкаф с 5 полками.
Она ставит по 5 книг в ряд на каждую полку.
5 × 5 = 25
Таким образом, всего 25 книг.
Выберите проект
ПРОЕКТ 13A
Какие формы вы можете найти в дизайне плитки?
Проект: создание дизайна плитки
ПРОЕКТ 13B
Как архитекторы проектируют дом?
Проект: Нарисуй здание своей мечты
ПРОЕКТ 13C
Какие национальные достопримечательности есть в вашем штате?
Project: Build a Landmark
3-ACT MATH PREVIEW
Math Modeling Straw Shaped
Перед просмотром видео подумайте: что можно построить из соломки? Какие фигуры? Как можно сравнивать эти формы?
Урок 13.1 2-мерные фигуры
Решить и поделиться
Посмотрите на картинку. Сколько треугольников вы можете найти? Обведите каждый треугольник. Будьте готовы объяснить, откуда вы знаете, что нашли их все.
Я могу… узнавать формы по тому, как они выглядят.
________ треугольников
Ответ: 10 треугольников
Визуальный обучающий мост
Убедите меня! Как стороны и вершины помогают назвать плоскую форму?
Практика под руководством
Сопоставьте каждую фигуру с ее названием.
Вопрос 1.
Ответ:
Скажите, сколько сторон и вершин. Назовите каждую фигуру.
Вопрос 2.
________ стороны
________ Вершины
Форма: __________
Ответ:
4 Стороны
4 Vertices
ФОРМА: Четырехногенный .
Вопрос 3.
________ стороны
________ Вершины
Форма: __________
Ответ:
5 Стороны
5 Сервицы
Форма: Pentagon 9000
.
Независимая практика
Сопоставьте каждую фигуру с ее названием.
Вопрос 4.
Ответ:
Вопрос 5.
Ответ:
Нарисуйте фигуру. Укажите, сколько сторон и вершин.
Вопрос 6.
Четырехугольник
________ сторон
________ вершин
Ответ:
4 сторон
4 вершин
Четырехугольник является правильным четырехугольником и четырьмя вершинами.
Вопрос 7.
Шестиугольник
________ сторон
________ вершин
Ответ:
6 сторон
6 вершин
Шестиугольник – это многоугольник с 6 сторонами.
Вопрос 8.
Треугольник
________ сторон
________ вершин
Ответ:
3 сторон
3 вершин
Треугольник — это многоугольник с тремя сторонами и тремя вершинами.
Вопрос 9.
Мышление высшего порядка Бьянка нарисовала треугольник и пятиугольник. Сколько всего сторон и вершин она нарисовала? Нарисуйте фигуры.
________ сторон
________ вершин
Ответ:
3 сторон
3 вершин
Треугольник — это многоугольник с тремя сторонами и тремя вершинами.
5 сторон
5 вершин
На рисунке выше изображен пятиугольник с пятью сторонами и пятью вершинами.
Решение проблем
Решите каждую проблему.
Вопрос 10.
Модель Маркос имеет 4 зубочистки. Он размещает их, как показано. Какую фигуру может сделать Маркос, если он добавит еще одну зубочистку?
Ответ:
Если Маркос добавит еще одну зубочистку, получится пятиугольник.
Вопрос 11.
Словарь Соедините все точки, чтобы получились две фигуры с вершинами. Назовите фигуры, которые вы делаете.
Ответ:
Вопрос 12.
Мышление высшего порядка Рэндалл сказал, что квадрат — это четырехугольник. Сьюзан сказала, что квадрат есть квадрат, а значит, это не четырехугольник. Кто прав? Объяснять.
Ответ:
Квадрат есть квадрат и также четырехугольник. Итак, Рэндалл прав.
Вопрос 13.
Практика оценивания Какая форма НЕ является шестиугольником?
Ответ: Вариант C имеет 5 сторон, поэтому это не шестиугольник.
Таким образом, ответ – вариант C.
Урок 13.2 Многоугольники и углы
Решить и поделиться
Посмотрите на три формы плоскости ниже. Чем они похожи? Насколько они разные? Измерьте длину сторон, чтобы описать их. Назовите каждую фигуру.
Чем они похожи? Насколько они разные? Измерьте длину сторон, чтобы описать их. Назовите каждую фигуру.
Я могу… описать плоские формы по тому, как они выглядят.
Мост визуального обучения
Убедите меня! Сколько углов у этой фигуры? Сколько прямых углов? Назовите форму.
Практика под руководством
Напишите количество углов и попрактикуйтесь, затем назовите форму.
Вопрос 1.
________ углов
Форма: _________
Ответ:
5 углов
Форма: пятиугольник
Пояснение:
На приведенном выше рисунке изображен пятиугольник с пятью углами.
Вопрос 2.
________ углов
Форма: _________
Ответ:
5 углов
Форма: Пятиугольник
Пояснение:
На приведенном выше рисунке изображен пятиугольник с пятью углами.
Вопрос 3.
________ углов
Форма: _________
Ответ:
6 углов
Форма: Шестиугольник
Пояснение:
На приведенном выше рисунке изображен шестиугольник с шестью углами.
Вопрос 4.
________ углов
Форма: _________
Ответ:
3 угла
Форма: Треугольник
Пояснение:
На приведенном выше рисунке изображен треугольник с тремя углами.
Независимая практика
Напишите количество углов и назовите фигуру.
Вопрос 5.
________ углов
Форма: _________
Ответ:
5 углов
Форма: пятиугольник
Пояснение:
На приведенном выше рисунке изображен пятиугольник с пятью углами.
Вопрос 6.
________ углов
Форма: _________
Ответ:
6 углов
Форма: Шестиугольник
Пояснение:
На приведенном выше рисунке изображен шестиугольник с шестью углами.
Вопрос 7.
________ углов
Форма: _________
Ответ:
4 угла
Форма: четырехугольник
Пояснение:
На приведенном выше рисунке изображен четырехугольник с четырьмя углами.
Вопрос 8.
________ углов
Форма: _________
Ответ:
6 углов
Форма: Шестиугольник
Пояснение:
На приведенном выше рисунке изображен шестиугольник с шестью углами.
Вопрос 9.
________ углов
Форма: _________
Ответ:
4 угла
Форма: Четырехугольник
Пояснение:
На приведенном выше рисунке изображен четырехугольник с четырьмя углами.
Вопрос 10.
________ углов
Форма: _________
Ответ:
5 углов
Форма: Пятиугольник
Пояснение:
На приведенном выше рисунке изображен пятиугольник с пятью углами.
Вопрос 11.
Мышление высшего порядка Нарисуйте многоугольник с 2 прямыми углами и 2 непрямыми углами. Назовите фигуру, которую вы рисуете.
Ответ:
Решение задач
Решите каждую задачу.
Вопрос 12.
Будьте точны Какие формы плоскостей сшиты вместе в футбольном мяче?
Ответ: Пятиугольник и шестиугольник изображены вместе на футбольном мяче.
Вопрос 13.
enVision® STEM Пчелы делают соты. Сотовая форма использует меньше воска, чем другие формы. Назовите форму. Укажите, сколько углов у фигуры.
Назовите форму. Укажите, сколько углов у фигуры.
Ответ:
Дано,
Пчелы делают соты. Сотовая форма использует меньше воска, чем другие формы.
Форма сот – шестиугольник.
Вопрос 14.
Мышление высшего порядка Нарисуйте многоугольник с 7 углами. Сколько сторон у многоугольника? Сколько у него вершин?
Ответ:
Вопрос 15.
Практика оценивания Назовите форму приведенного ниже знака. Напишите 3 вещи, которые описывают форму.
Ответ:
Вышеуказанный знак имеет форму пятиугольника.
Урок 13.3 Рисование двумерных фигур
Решить и поделиться
Нарисуйте многоугольник с тремя сторонами одинаковой длины. Затем нарисуйте многоугольник с тремя сторонами разной длины. Измерьте длины сторон, которые вы нарисовали. Назовите 4 способа, которыми фигуры похожи.
Я могу… рисовать многоугольники.
Мост визуального обучения
Убедите меня! Начертите четырехугольник с 4 сторонами одинаковой длины и 4 прямыми углами. Напишите 2 названия четырехугольника.
Напишите 2 названия четырехугольника.
Практика под руководством
Нарисуйте каждую фигуру. Закончите предложения.
Вопрос 1.
Нарисуйте многоугольник с 3 вершинами.
Многоугольник также имеет _______ сторон.
Многоугольник представляет собой ________
Ответ:
Многоугольник также имеет три стороны.
Многоугольник представляет собой треугольник.
Вопрос 2.
Нарисуйте многоугольник с 6 сторонами.
Многоугольник также имеет _______ углов.
Многоугольник представляет собой _______
Ответ:
Многоугольник также имеет шесть углов.
Многоугольник представляет собой шестиугольник.
Независимая практика
Нарисуйте каждую фигуру. Закончите предложения.
Вопрос 3.
Нарисуйте многоугольник с 3 вершинами и прямым углом.
Многоугольник также имеет _______ сторон.
Многоугольник представляет собой _______
Ответ:
Многоугольник также имеет три стороны.
Многоугольник является прямым углом.
Вопрос 4.
Нарисуйте четырехугольник с противоположными сторонами одинаковой длины.
Многоугольник также имеет _______ вершин.
Многоугольник представляет собой _______
Ответ:
Многоугольник также имеет четыре вершины.
Многоугольник представляет собой прямоугольник.
Вопрос 5.
Нарисуйте многоугольник с 4 сторонами одинаковой длины.
Многоугольник также имеет _______ углов.
Многоугольник представляет собой _______
Ответ:
Многоугольник также имеет четыре угла.
Многоугольник представляет собой квадрат.
Вопрос 6.
Нарисуйте многоугольник с четырьмя сторонами разной длины.
Многоугольник также имеет _______ углов.
Многоугольник представляет собой _______
Ответ:
Многоугольник также имеет четыре угла.
Многоугольник является четырехугольником
Вопрос 7.
Начертите многоугольник с 5 вершинами и 3 сторонами одинаковой длины.
Многоугольник также имеет _______ сторон.
Многоугольник представляет собой _______
Ответ:
Многоугольник также имеет всего пять сторон.
Многоугольник является пятиугольником
Вопрос 8.
Мышление высшего порядка Можете ли вы нарисовать многоугольник с 3 вершинами и 4 сторонами? Объяснять.
Ответ: Нет
Решение проблем
Решите приведенные ниже проблемы.
Вопрос 9.
Будьте точны Нарисуйте прямоугольник с 4 равными сторонами.
Как еще называется эта фигура?
Ответ:
Многоугольник также имеет четыре угла.
Многоугольник представляет собой квадрат.
Вопрос 10.
Нарисуй 3 фигуры. Первая фигура – четырехугольник. Количество вершин в каждой фигуре увеличивается на одну.
Назовите третью фигуру. __________
Ответ:
Многоугольник имеет пять сторон и пять вершин.
Название фигуры – пятиугольник.
Многоугольник также имеет шесть углов.
Многоугольник представляет собой шестиугольник.
Вопрос 11.
Мышление высшего порядка Владелец рыбного рынка Джо хочет новую вывеску. Он хочет, чтобы у знака были изогнутые стороны. Нарисуйте знак «Рыбный рынок Джо».
Является ли знак многоугольником? Объяснять.
Ответ: Знак рыбного рынка Джо не является многоугольником.
Вопрос 12.
Практика оценивания Дэвид нарисовал два разных многоугольника. Один из многоугольников был квадратом. Если Давид нарисовал всего 9 сторон и 9 вершин, то какой еще многоугольник нарисовал Давид?
Ответ: вариант D
Урок 13.4 Кубики
Решить и разделить
m Опишите две фигуры 4 или более способами. Расскажите, чем они отличаются и чем похожи. Используйте инструмент, чтобы включить измерения в ваше описание.
Я умею… рисовать кубики и описывать, как они выглядят.
Мост визуального обучения
Убедите меня! У какой объемной фигуры 6 равных граней? Какова форма каждого лица?
Практика под руководством
Обведите кубы в группе фигур. Будьте готовы объяснить, откуда вы знаете, что это кубики.
Будьте готовы объяснить, откуда вы знаете, что это кубики.
Вопрос 1.
Ответ:
Вопрос 2.
Используйте точечную бумагу. Нарисуйте куб.
Ответ:
Симметричная трехмерная фигура, твердая или полая, состоящая из шести равных квадратов
Независимая практика
Решите, является ли фигура кубом. Затем проведите линию от каждой формы к кубу или НЕ к кубу.
Вопрос 3.
Ответ:
Вопрос 4.
Нарисуйте куб, показанный ниже.
Сколько лиц вы видите?
________ граней
Ответ: 6 граней
Алгебра Используйте свои знания о кубах, чтобы написать уравнение и решить каждую задачу.
Вопрос 5.
Сколько всего вершин у этих двух кубов?
Ответ: 8 + 8 = 16
Таким образом, в двух кубах 16 вершин.
Вопрос 6.
Сколько всего граней у этих двух кубиков?
Ответ:
6 + 6 = 12
Таким образом, в двух кубах 12 граней.
Решение задач
Используйте свои знания о кубиках для решения каждой задачи.
Вопрос 7.
Объясните, что Скотт держит объемную фигуру с 6 равными гранями, 12 ребрами и 8 вершинами. Скотт говорит, что это куб. Кармен говорит, что это квадрат. Кто прав? Объяснять.
Ответ:
Куб или Кубоид имеет 6 равных граней, 12 ребер и 8 вершин.
Вопрос 8.
Лексика Обведите словарное слово, которое завершает предложение.
вершин
граней
ребер
Куб имеет 6 _________.
Ответ: У куба 6 граней.
Вопрос 9.
Мышление высшего порядка Используйте куб с разрядными единицами или другой сплошной куб. Смотрите на куб, когда вы его поворачиваете. Поверните куб в любом направлении.
Какое наибольшее количество лиц вы можете видеть одновременно? Объяснять.
Ответ: Количество граней равно 4
Вопрос 10.
Практика оценивания Закончите предложения о кубе.
Куб — это твердое тело ________.
Куб имеет ________ равных граней, ________ вершин и _______ ребер.
Ответ:
Куб — это твердая фигура.
У куба 6 равных граней, 8 вершин и 12 ребер.
Урок 13.5 Равные доли
Решить и разделить
Сколько одинаковых квадратов покрывают этот прямоугольник? Как вы могли бы показать это с помощью уравнения сложения?
Я могу … покрыть прямоугольники квадратами одинакового размера и посчитать, чтобы найти их общее количество.
__________ равных квадратов
Уравнение: _________
Ответ:
20 равных квадратов
Уравнение: 4 × 5 = 20
Мост визуального обучения
Убедите меня! Объясните, как можно покрыть прямоугольник квадратами одинакового размера, чтобы найти их общее количество.
Практика под руководством
Решить.
Вопрос 1.
Используйте квадратные плитки, чтобы закрыть прямоугольник. Проследите плитки. Колонка 1 сделана для вас.
Колонка 1 сделана для вас.
Ответ:
Используя приведенную выше диаграмму, квадратные плитки заполнены в строках и столбцах
Количество квадратов в прямоугольнике равно количеству строк в количестве столбцов
3 x 6 = 18
Вопрос 2.
Сосчитай и прибавь. Сколько квадратов покрывают прямоугольник?
Сложить по строкам: ________ + ________ + ______ = _______
Сложить по столбцам:
________ + ________ + ______ + ________ + ________ + ______ = _______
Ответ:
6 квадратов покрывают прямоугольник
Объяснение:
Сложить по строкам: 6+6+6=18
Сложить по столбцам:
3+3+3+3+3+3=18
Независимая практика
Используйте квадратные плитки, чтобы покрыть каждый прямоугольник . Проследите плитки. Сосчитай квадраты.
Вопрос 3.
Сложить по строкам: ________ + ________ + ________ + ______ = _______
Сложить по столбцам:
________ + ________ + ______ + ________ + ________ = _______ строки и столбцы
Количество квадратов в прямоугольнике равно количеству строк в количестве столбцов.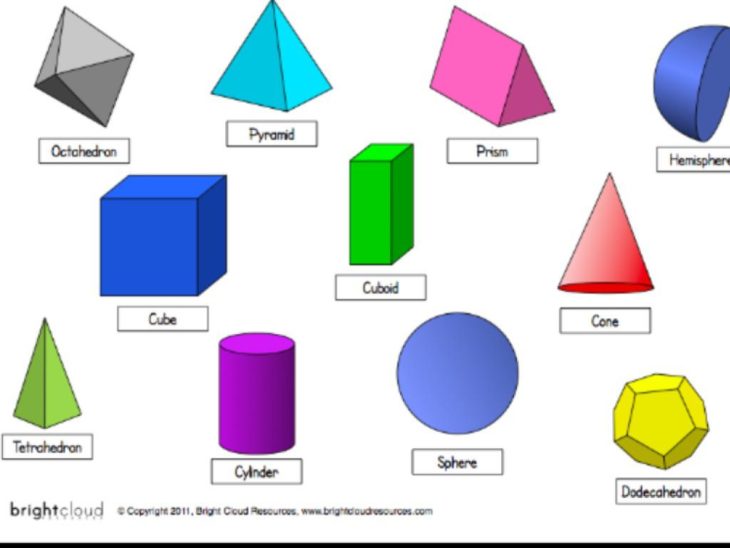
Сложить по строкам: 5+5+5+5=20
Сложить по столбцам: 4+4+4+4+4=20
Вопрос 4.
Сложить по строкам: ________ + ________ + ________ + ______ = _______
Сложить по столбцам:
________ + ________ + ______ + ________ + ________ = _______
Ответ:
Используя приведенную выше диаграмму, квадратные плитки заполняются по строкам и столбцам
Количество квадратов в прямоугольнике равно количеству строк в количество столбцов.
Сложение по строкам: 5+5+5+5=20
Сложение по столбцам: 4+4+4+4+4=20
Вопрос 5.
Чувство чисел Нарисуйте прямоугольник, состоящий из 6 равных квадратов.
Ответ:
Прямоугольник состоит из 6 равных квадратов.
Решение проблем
Решите каждую проблему.
Вопрос 6.
Ищите закономерности Лиза печет кукурузный хлеб. Она разрезает его на равные квадратные кусочки. Сколько равных квадратов вы видите? Напишите два уравнения, чтобы показать общее количество квадратных частей.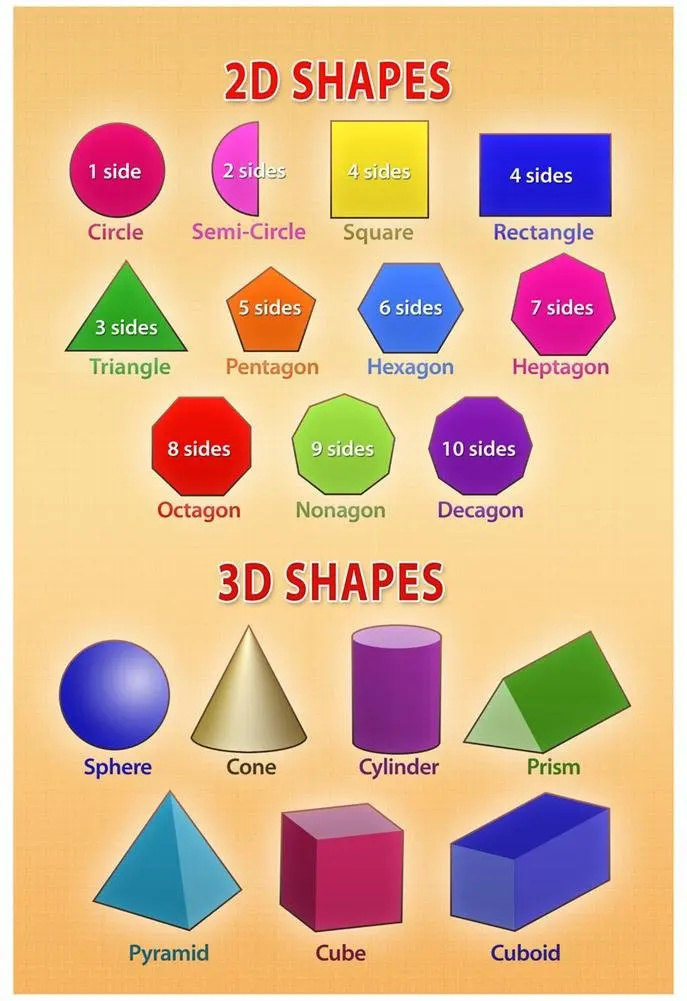
Ряды: _____ + _____ + _____ + _____ + _____ + _____ = _____ шт.
Столбцы: _____ + _____ + _____ + _____ = _____ шт. квадратов в прямоугольнике равно количеству строк на количество столбцов
Объяснение:
Сложить по рядам: 4+4+4+4+4+4=24 шт.
Сложить по столбцам: 6+6+6+6=24 штук
Вопрос 7.
Словарь Обозначьте столбцы и строки для большого квадрата ниже.
Ответ: количество строк на количество столбцов 3×3=9
Вопрос 8.
Мышление высшего порядка Посмотрите на большой квадрат в пункте 7. Что вы заметили в отношении количества строк и количества столбцы? Объяснять.
Ответ:
Если взять квадрат с элементом 7
Число строк равно 7, а количество столбцов равно 7
7 x 7 = 49
Вопрос 9. столбцы прямоугольника. Затем используйте числа на карточках, чтобы вписать недостающие числа в уравнения.
Строка = _____ + ______ = ______
Столбцы = ______ + ______ + ______ + ______ + ______ + ______ + ______ = ______
Ответ:
Используя приведенную выше диаграмму, квадратные плитки заполняются в строках и столбцах
Количество квадратов в прямоугольник равен количеству строк на количество столбцов
Объяснение:
строк =7+7=14
столбцов = 2+2+2+2+2+2+2=14
Урок 13.
 6 Формы разделов
6 Формы разделов Решить & Share
Сложите бумажный квадрат один раз, чтобы получились равные доли. Сколько существует равных долей? Сложите другой квадрат 2 раза, чтобы получились равные доли. Сколько существует равных долей? Нарисуйте линии сгиба на квадратах ниже. Что вы можете сказать о количестве фолдов и количестве равных долей?
Я могу… показывать круги и прямоугольники пополам, втрое и в четверть.
Мост визуального обучения
Убедите меня! Покажите этот прямоугольник с тремя равными долями. Сколько третей составляет одна акция? Сколько третей составляет весь прямоугольник?
Ответ: Например, если взять платок квадратной формы и сложить его, то получится 2 равные доли, а если сложить 2 раза, то получится 4 доли.
Практика под руководством
Решите каждую задачу.
Вопрос 1.
Покажите каждый квадрат пополам. Покажите четыре разных способа.
Ответ:
Первый квадрат разделен по диагонали,
Второй квадрат разделен по вертикали,
Третий квадрат разделен по диагонали,
Четвертый квадрат разделен по горизонтали.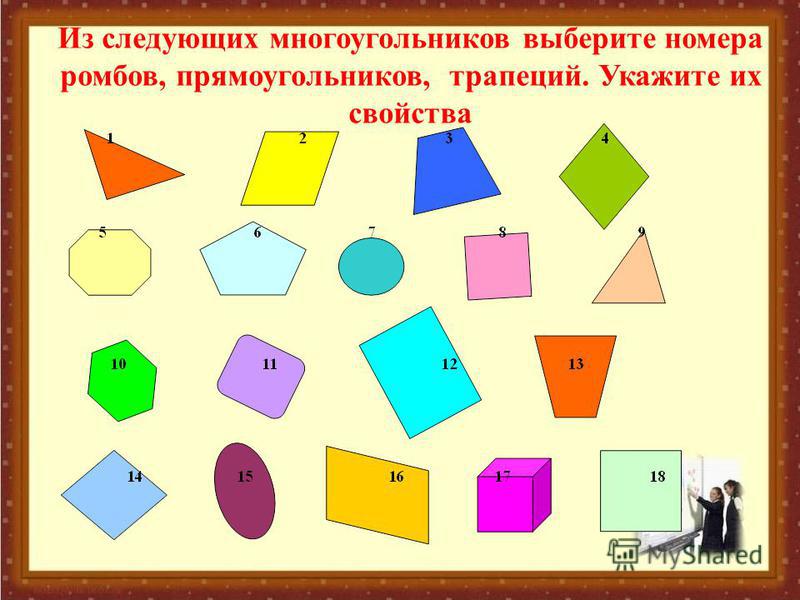
Вопрос 2.
Скажите, какой частью целого является каждая равная доля. Напишите половину, треть или четверть.
Ответ:
Четвертый прямоугольник
Третий круг
Квадрат половинный
Объяснение:
На приведенном выше рисунке прямоугольник равен 1/4 доли,
Круг равен 1/3 части, а квадрат равен 1/2.
Независимая практика
Покажите каждую фигуру с указанным количеством равных долей. Покажите 2 способа. Затем завершите предложения.
Вопрос 3.
3 равные доли
Каждая доля составляет ________ целое.
Каждое целое равно ______________.
Ответ:
Первый прямоугольник разделен по вертикали
Второй прямоугольник разделен по горизонтали.
Объяснение:
Каждая доля составляет одну треть целого
Каждое целое составляет одну треть
Вопрос 4.
4 равные доли
Каждая доля составляет _________ целого.
Каждое целое равно __________.
Ответ:
Первый прямоугольник разделен по вертикали
Второй прямоугольник разделен по горизонтали.
Объяснение:
Каждая доля составляет одну четвертую целого
Каждое целое составляет одну четвертую
Вопрос 5.
2 равные доли
Каждая доля составляет _________ целого.
Каждое целое равно __________.
Ответ:
Первый круг разделен по вертикали
Второй круг разделен по горизонтали.
Объяснение:
Каждая доля составляет половину целого
Каждое целое составляет половину
Вопрос 6.
Мышление высшего порядка Нарисуй, что будет дальше.
Ответ:
Решение задач
Решите каждую задачу.
Вопрос 7.
Модель Леон разрезала вафлю пополам. Нарисуйте линии, чтобы показать 3 разных способа, которыми он мог бы разрезать вафли.
Ответ:
Первый квадрат разделен по вертикали
Второй квадрат разделен по горизонтали
Третий квадрат разделен по диагонали.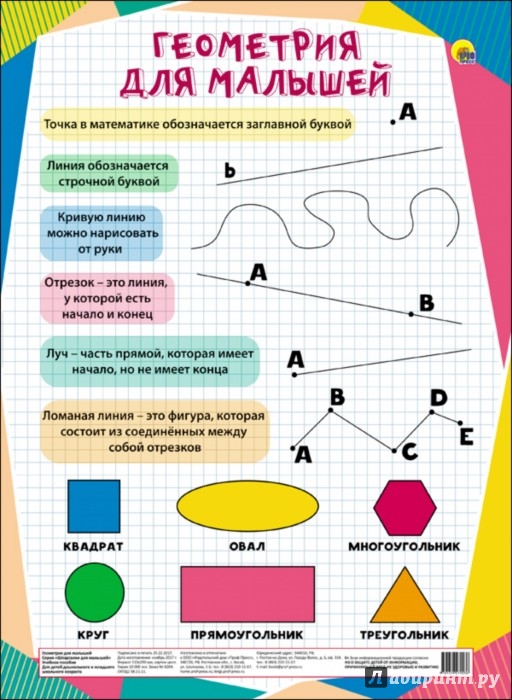
Вопрос 8.
enVision® STEM Тина сажает сад. Она хочет иметь равные части для бобов, помидоров и перца. Нарисуйте, как она могла бы посадить свой сад.
Ответ:
Рассмотрим сад в форме прямоугольника
Одна треть отведена под бобы, вторая часть — под помидоры, а последняя часть — перец.
Вопрос 9.
Мышление высшего порядка Нарисуйте линии на картинке, чтобы решить задачу. 4 друга хотят разделить арбуз. Как они могли разрезать арбуз, чтобы каждый друг получил поровну?
Ответ:
Каждый друг получит __________.
Ответ:
Каждый друг получит одну четверть
Вопрос 10.
Практика оценки Мэтт хочет флаг, показывающий четверти. Какие флаги мог бы использовать Мэтт? Выберите все подходящие.
Ответ:
Первые три мата можно использовать как флажки
Урок 13.7 Равные доли, разные формы
Решить и разделить
Используйте мелок, чтобы показать 4 равные части этой пиццы. Сравните свой ответ с партнером. Вы оба сделали 4 равные доли? Ваши акции выглядят одинаково?
Сравните свой ответ с партнером. Вы оба сделали 4 равные доли? Ваши акции выглядят одинаково?
Я могу… сделать равные доли, которые не имеют одинаковой формы.
Ответ:
В разрезании пиццы Анны она сделала 4 равные части в виде квадратов
В разрезании пиццы Марка он сделал 4 равные части в виде прямоугольников.
Оба варианта верны.
Мост визуального обучения
Убеди меня! Как проверить, что все доли равны?
Практическое руководство
Нарисуйте линии, чтобы показать 2 равные доли. Каждый способ должен быть разным.
Вопрос 1.
Ответ: Первый прямоугольник разделен по горизонтали
Второй прямоугольник разделен по вертикали.
Вопрос 2.
Сколько квадратов приходится на каждую равную долю прямоугольников?
Ответ:
В прямоугольнике, если его разделить пополам, доли будут равными двум.
Вопрос 3.
Охарактеризуйте равные доли и целое.
Каждая доля составляет половину целого.
Каждое целое состоит из двух половинок.
Ответ: Когда вы делите целое пополам, вы получаете равные доли.
Независимая практика
Нарисуйте линии в каждом прямоугольнике, чтобы показать 4 равные доли. Каждый способ должен быть разным. Затем ответьте на вопросы.
Вопрос 4.
Покажите равные доли одинаковой формы.
Показать равные доли разной формы.
Ответ:
В приведенных выше двух прямоугольных коробках одна разделена поровну, а другая разделена на 3 части, но не на равные части.
Вопрос 5.
Сколько квадратов приходится на каждую равную долю в пункте 4?
Ответ:
В квадрате если разделить на 4, то квадратов будет четыре
Вопрос 6.
Опишите равные доли и целое в пункте 4.
Каждая доля ___________ целого.
Каждое целое равно ___________.
Ответ:
Каждая доля равна одной четвертой целого
Каждое целое равно одной четвертой
Нарисуйте линии, чтобы показать 3 равные доли двумя разными способами.
Вопрос 7.
Ответ:
Первый разделен по вертикали, а другой по горизонтали.
Вопрос 8.
Мышление высшего порядка Как равные части прямоугольника могут иметь разную форму?
Ответ:
Первая фигура имеет вертикальный прямоугольник
Вторая фигура имеет квадрат
Третий имеет горизонтальные прямоугольники.
Решение проблем
Решите каждую проблему.
Вопрос 9.
Аллен хочет разделить эту сковороду кукурузного хлеба с 3 друзьями. Аллен и его друзья получат поровну.
Сколько штук будет в каждой доле?
___________ штук
Ответ:
Аллен хочет разделить эту сковороду кукурузного хлеба с 3 друзьями. Если разрезать хлеб горизонтально.
Каждому другу по 4 штуки
Вопрос 10.
Объясните, что Грег говорит, что равные доли могут быть разными по форме и размеру. Грег прав? Объяснять.
Ответ:
Приведенный выше рисунок поясняет, что серый цвет говорит о том, что равные доли могут быть разными по форме и размеру.
Если форма одинаковая.
Вопрос 11.
Мышление высшего порядка Донна провела линию в этом прямоугольнике, чтобы получить 2 равные доли. Равны ли доли? Почему или почему нет?
Ответ:
Приведенная выше цифра делится поровну и имеет равные доли: в первой половине 10 ящиков, во второй тоже 10 ящиков.
Вопрос 12.
Методика оценивания Мэг показывает прямоугольник с 3 равными долями, которые НЕ ОДИНАКОВЫ по форме. Какой может быть прямоугольник Мэг?
Ответ:
Мэг показывает прямоугольник с 3 равными долями, которые НЕ одинаковой формы. 4 прямоугольник Мэг.
Урок 13.8 Решение проблем
Повторные рассуждения
Решить и поделиться
Создайте два разных флага. На каждом флаге нарисуйте 15 квадратов одинакового размера. Используйте строки и столбцы.
Сделайте три равные доли разных цветов в каждом флаге. Затем напишите уравнение для каждого флажка, чтобы показать общее количество квадратов.
Я могу… использовать повторяющиеся рассуждения, чтобы показать прямоугольники со строками и столбцами и создать дизайн с равными долями.
Привычки мышления Что-то повторяется в задаче? Как решение может помочь мне решить другую проблему?
Мост визуального обучения
Убедите меня! Откуда вы знаете, что каждая доля в Плане 2 составляет четвертую часть всего квадрата?
Ответ: Если мы делаем по уравнению, он должен дать 4 квадрата, следовательно, схема 2 верна.
Практика под руководством
Решите проблему. Используйте цветные карандаши для раскрашивания. Практика
Вопрос 1.
Хамаль рисует рисунок. В дизайне должно быть 3 цвета с равной долей каждого цвета. Создайте два возможных дизайна для Хамала.
Ответ:
В дизайне два по подсчету квадратов использовано 3 цвета в дизайне 1 по столбцам мы раскрасили.
Каждая доля состоит из 4 маленьких квадратов, поэтому любая фигура с 4 маленькими квадратами является равной долей.
Я могу делать доли одинаковой формы, все эти четверти квадратные.
В другом дизайне я использовал разные формы для акций
Независимая практика
Решите каждую задачу. Используйте цветные карандаши для раскрашивания. Объясни свою работу.
Вопрос 2.
Мари хочет нанести прямоугольный рисунок на футболку. В дизайне должно быть 4 цвета с равной долей каждого цвета. Создайте два возможных дизайна для Мари.
Ответ:
Каждая доля состоит из 4 маленьких квадратов, поэтому любая фигура с 4 маленькими квадратами является равной долей.
Я могу делать доли одинаковой формы, все эти четверти квадратные.
В других проектах я использовал лемехи другой формы.
Вопрос 3.
Грант хочет нарисовать круг на своей игрушечной машине. В дизайне должно быть 3 цвета с равной долей каждого цвета. Создайте два возможных дизайна для Гранта.
Ответ:
В кругах это невозможно.
Решение проблем
Задание на выполнение
Дизайн плитки Мисс Уолтон создала этот прямоугольный файл. Какая доля дизайна оранжевая? Какая часть дизайна желтая? Сколько акций составляет весь дизайн? Сколько третей составляет целое?
Какая доля дизайна оранжевая? Какая часть дизайна желтая? Сколько акций составляет весь дизайн? Сколько третей составляет целое?
Вопрос 4.
Разумно Как дизайн г-жи Уолтон показывает равные доли? Объяснять.
Ответ:
Каждая доля состоит из 4 маленьких квадратов, поэтому любая фигура с 4 маленькими квадратами является равной долей.
Я могу делать доли одинаковой формы, все эти четверти квадратные.
В другом дизайне я использовал лемехи другой формы.
Вопрос 5.
Рассуждение Какая часть рисунка оранжевая? Какая часть дизайна желтая? Сколько акций составляет весь дизайн? Сколько третей составляет целое?
Ответ:
Мисс Уолтон создала этот дизайн прямоугольной плитки, одна треть рисунка оранжевого цвета, две трети рисунка желтого цвета, а три трети — целого.
Вопрос 6.
Обобщение Скопируйте рисунок плитки выше на эту сетку. Затем раскрасьте его оранжевым и желтым, чтобы он соответствовал рисунку, показанному выше.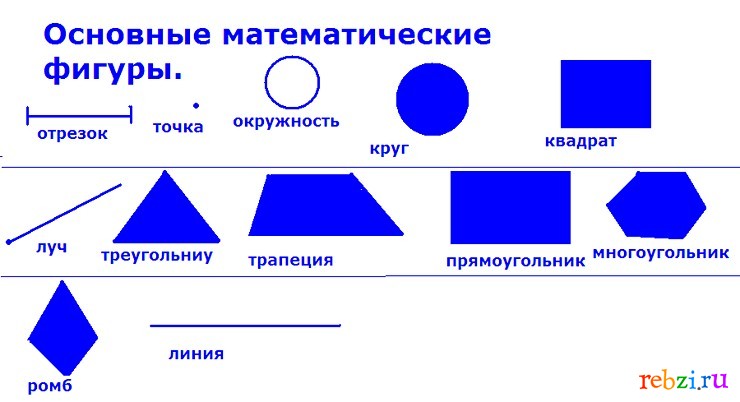
Как вы скопировали дизайн? Опишите один или два ярлыка, которые вы использовали.
Ответ:
Количество квадратов равно 12
Объяснение
Я сделал это, приравняв количество строк к количеству столбцов. По количеству квадратов мы можем сделать это
Тема 13 Практика беглости речи
Следуйте по пути
Найдите каждую сумму или разность. Затем раскрасьте путь от начала до конца. Следите за суммами и разностями, которые являются четными числами. Вы можете двигаться только вверх, вниз, вправо или влево.
Я умею … складывать и вычитать в пределах 100.
Тема 13. Обзор словарного запаса
Понимание словарного запаса
Пишите всегда, иногда или никогда.
Список слов
• угол
• шестиугольник
• куб
• пятиугольник
• ребро
. многоугольник
• равные доли
• четырехугольник
• грань
• прямой угол
• четверти
• трети
• половинки
• вершина
Вопрос 1.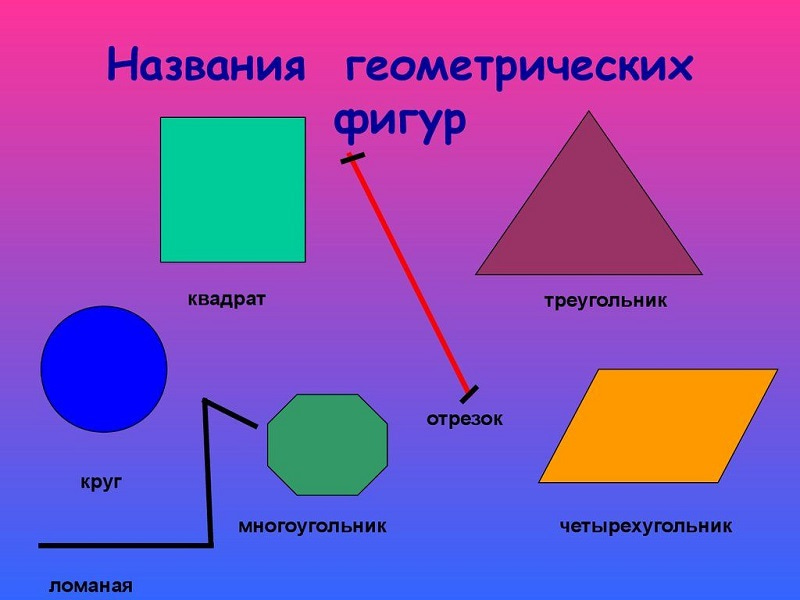
Куб имеет ровно 4 грани. _________
Ответ: Всегда
Вопрос 2.
Прямой угол образует квадратный угол. ___________
Ответ: Всегда
Вопрос 3.
Четырехугольники являются квадратами. ___________
Ответ: Иногда
Вопрос 4.
Объемная фигура с гранями имеет ребра. ___________
Ответ: Иногда
Проведите линию от каждого термина к его примеру.
Вопрос 5.
Hexagon
Ответ:
Вопрос 6.
Пентагон
Ответ:
Вопрос 7.
Vertex
Ответ:
Использование Vocabulary в письменном виде
. на две равные доли. Затем скажите, как можно разделить этот же квадрат на 3 равные доли. Используйте термины из списка слов.
Ответ: Трети
Тема 13 Повторное обучение
Набор A
Вы можете назвать форму плоскости по количеству сторон и вершин.
Напишите количество сторон и вершин. Назовите форму.
Вопрос 1.
_________ стороны
_________ Вершины
Форма: ________
Ответ:
5 Сторон
Пять версий
Пентагон
Вопрос 2.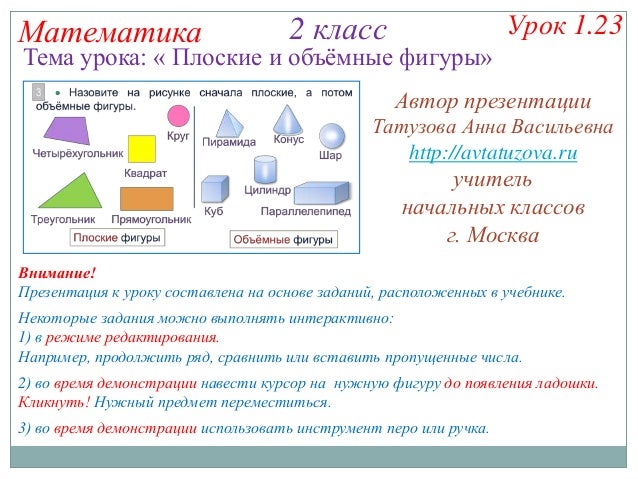
_________ Сайды
№
. вершины
Пентагон
Set B
Вы можете назвать многоугольник по количеству его углов.
Напишите количество углов. Затем назовите форму.
Вопрос 3.
________ углы
Форма: ________
Ответ:
Четыре угла
Прямоугольник и быть четырехсторонним также
4.
________ Angles
. C
Вы можете нарисовать многоугольник с заданным количеством сторон, вершин или углов.
Нарисуйте многоугольник с 4 сторонами. Две стороны имеют разную длину.
Нарисуйте многоугольник с 5 вершинами.
Нарисуйте многоугольник с тремя углами. Один угол прямой.
Нарисуйте каждый описанный многоугольник.
Вопрос 5.
6 сторон
Ответ:
Вопрос 6.
3 вершины
Ответ:
Вопрос 7.
5 сторон и 2 прямых угла
Ответ:
7 An Oct Ответы: 6 6 восьмиугольников 8 углов представляет собой многоугольник, состоящий из 8 сторон. Он имеет восемь углов. Octagon = Octa + gon, где octa означает восемь, а gon означает 9 сторон.0007
Он имеет восемь углов. Octagon = Octa + gon, где octa означает восемь, а gon означает 9 сторон.0007
Набор D
Можно описывать и рисовать кубики.
Вопрос 9.
Вычеркните фигуры, которые НЕ являются кубами.
Ответ:
У куба 6 граней, 12 ребер и 8 вершин
Вопрос 10.
Нарисуйте куб. Используйте точки, чтобы помочь вам.
Ответ:
Считаем по строкам: 3 + 3 = 6
Считаем по столбцам: 2 + 2 + 2 = 6
6 квадратов покрывают прямоугольник.
Набор E
Повторное обучение Продолжение
Вы можете покрыть прямоугольник квадратами.
Счет по строкам: 3 + 3 = 6
Счет по столбцам: 2 + 2 + 2 = 6
6 квадратов покрывают прямоугольник.
Используйте квадратные плитки, чтобы закрыть прямоугольник. Проследите плитки. Затем посчитайте квадраты.
Вопрос 11.
__________ квадратов покрывают прямоугольник.
Ответ: 8 квадратов покрывают прямоугольник
Set F
Можно показывать круги и прямоугольники с равными долями.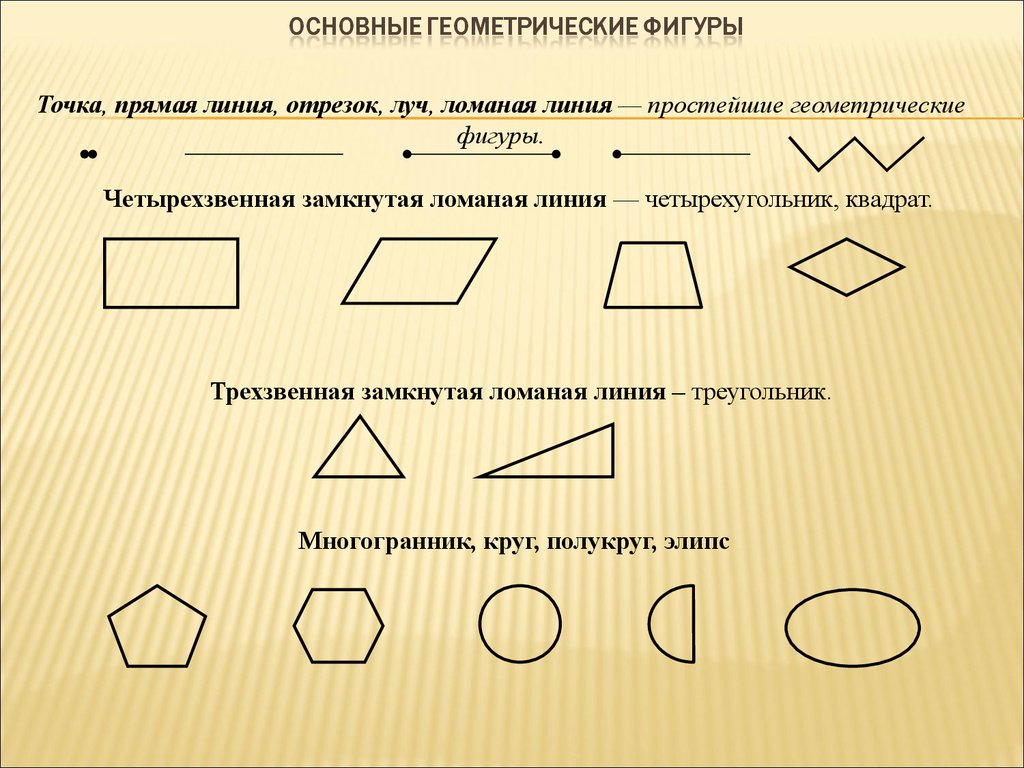
Покажите каждую фигуру с заданным количеством равных долей. Покажите 2 способа.
Вопрос 12.
половинок
Ответ:
Первый круг разделен по горизонтали
Второй круг разделен по вертикали.
Вопрос 13.
третей
Ответ:
Первый прямоугольник делится на трети по горизонтали
Второй прямоугольник делится на трети по вертикали.
Вопрос 14.
четвертей
Ответ:
Первый квадрат разделен на четверти по горизонтали и вертикали
Второй квадрат разделен на четверти по диагонали.
Комплект G
Равные доли могут быть разной формы. Это один из способов показать этот прямоугольник с 3 равными долями.
Каждая равная доля составляет 4 квадрата.
Нарисуйте линии, чтобы показать еще 2 способа, которыми эти прямоугольники могут иметь 3 равные доли.
Вопрос 15.
равные доли, которые НЕ имеют одинаковой формы
Ответ:
Прямоугольник не имеет одинаковых форм.
Вопрос 16.
равных долей одинаковой формы
Ответ: Делим на 4 квадрата
Set H
Привычки мышления Повторяющиеся рассуждения
Что-то повторяется в задаче?
Как это решение может помочь мне решить другую проблему?
Используйте показанный дизайн. Создайте другой дизайн с 3 равными долями.
Вопрос 17.
Ответ:
Каждая доля состоит из 4 маленьких квадратов, поэтому любая фигура с 4 маленькими квадратами является равной долей.
Я могу делать доли одинаковой формы, все эти четверти квадратные.
В других проектах я использовал лемехи другой формы.
Тема 13 Практика оценивания
Вопрос 1.
Какие многоугольники являются пятиугольниками?
Ответ: 2 и 4 – пятиугольники
Вопрос 2.
Рита рисует многоугольник. У него меньше восьми сторон и больше углов, чем у квадрата. Какую фигуру нарисовала Рита?
A. треугольник
B. прямоугольник
C.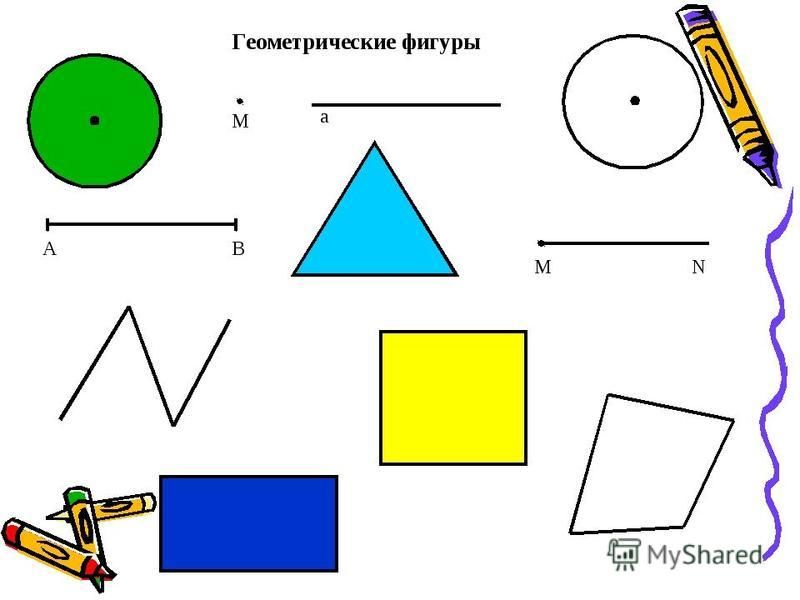 шестиугольник
шестиугольник
D. четырехугольник
Ответ:
шестиугольник
Плоская фигура с шестью прямыми сторонами и углами.
Вопрос 3.
Какие прямоугольники изображены четвертями? Выберите все подходящие.
Ответ: Варианты A, D
Вопрос 4.
Нарисуйте многоугольник с 4 углами. Сделайте один угол прямым. Затем назовите многоугольник.
Имя: ______________
Ответ: Четырехугольник
Вопрос 5.
Является ли многоугольник четырехугольником? Выберите Да или Нет.
Ответ: Четырехугольник будет иметь 4 стороны и 4 угла.
Вопрос 6.
Мэнди рисует многоугольник с 6 сторонами и 6 углами. Какую фигуру она нарисовала?
A. пятиугольник
B. шестиугольник
C. восьмиугольник
D. четырехугольник
Ответ:
Шестиугольник — это замкнутая двумерная фигура, состоящая из прямых линий. Это двумерная фигура с шестью сторонами, шестью вершинами и шестью ребрами. Название делится на гекс, что означает шесть, и гониа, что означает углы.
Вопрос 7.
Назовите фигуру ниже. Напишите 3 вещи, которые описывают форму.
Ответ:
Четырехугольник.
Пояснение:
Четырехугольник имеет 4 стороны, 4 угла и 4 вершины.
Четырехугольник может быть правильным и неправильным.
Сумма всех внутренних углов четырехугольника равна 360°.
Вопрос 8.
Нарисуйте описанный ниже многоугольник.
Тогда закончи предложение.
У меня на 2 стороны меньше, чем у пятиугольника. У меня угол меньше, чем у квадрата. У меня есть один прямой угол.
Форма __________.
Ответ: Прямоугольный треугольник
Объяснение:
Прямоугольный треугольник имеет 3 стороны, 3 угла и 3 вершины,
На один угол меньше, чем у квадрата,
На 2 стороны меньше, чем у пятиугольника
Вопрос 9.
Закончите предложение, чтобы назвать и описать сплошную фигуру ниже.
A _______ имеет _______ граней, _______ вершин, имеет _______ ребер.
Ответ: У куба 6 граней, 8 вершин, 12 ребер.
Вопрос 10.
Покажите этот круг двумя равными долями. Затем завершите предложения.
Каждая акция составляет ________ от целого.
Целое состоит из _________ половин.
Ответ:
Каждая доля составляет половину целого
Отверстие составляет 2 половинки
Вопрос 11.
Брэд говорит, что есть только два способа разделить один и тот же прямоугольник ниже на 3 равные части. Вы согласны? Используйте слова и изображения, чтобы объяснить.
Ответ: Рисунок выше показывает, что Брэд был неправ.
Вопрос 12.
Подсчитайте количество квадратов в строках и столбцах прямоугольника. Используйте числа на карточках, чтобы вписать недостающие числа в уравнения.
Строки: _____ + _____ + _____ = ______ квадратов
Столбцы: _____ + _____ + _____ + _____ + _____ = _____ квадратов
Ответ:15
Объяснение:
В каждом ряду 5 клеток, если сложить строки 5+ 5+5=15
В каждом столбце 3 клетки, если добавить клетки 3 +3+3+3+3=15.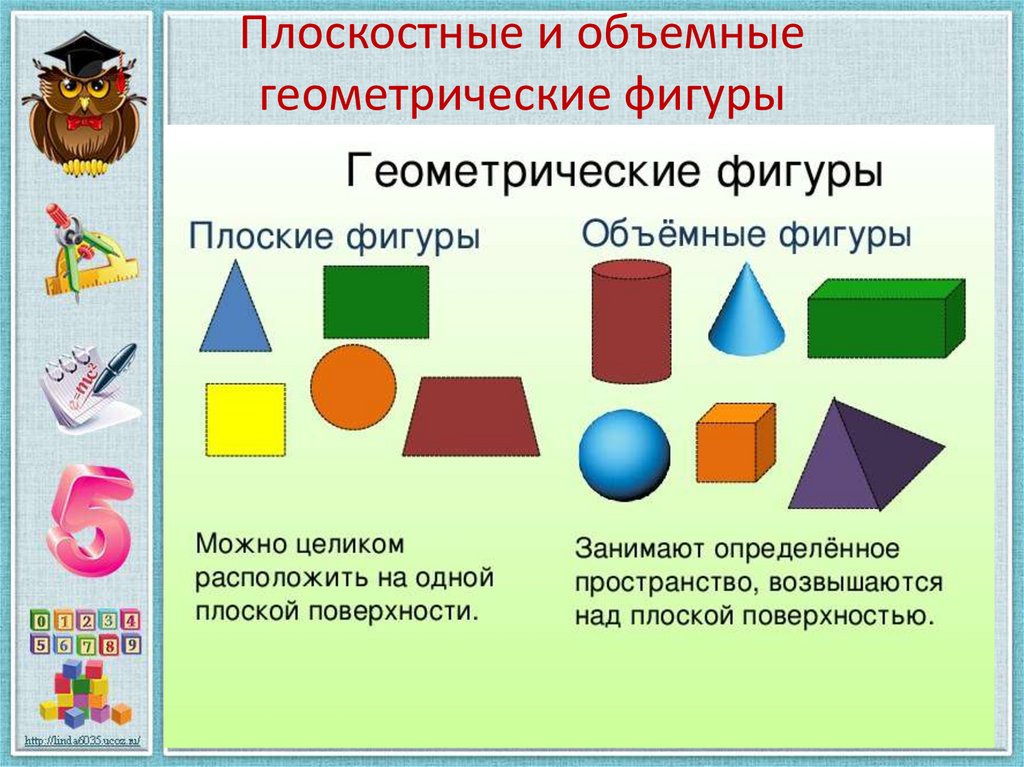
Вопрос 13.
Керри хочет дизайн, показывающий трети. Какой дизайн мог бы использовать Керри? Выберите все подходящие.
Ответ:
Керри хочет схему, показывающую, что трети равны 3, а 4 прямоугольника разделены, а трети
1,2,5 не разделены поровну.
Вопрос 14.
Является ли объемная фигура кубом? Выберите Да или Нет.
Ответ:
Симметричная трехмерная фигура, твердая или полая, состоящая из шести равных квадратов
Вопрос 15.
Используйте точечную бумагу. Нарисуйте куб.
Ответ:
Вопрос 16.
Разделите прямоугольник на строки и столбцы квадратов такого же размера, как зеленый квадрат. Затем посчитайте и запишите количество квадратов.
________ квадратов
Ответ:
В каждом ряду 3 квадрата 3 + 3 = 6.
Тема 13 Реализация задания
Happy Home Тина и ее семья переехали в новый дом. Они купили разные вещи для каждой комнаты.
Вопрос 1.
На стену вешают картины. Назовите форму каждой рамки.
Назовите форму каждой рамки.
Ответ:
1. Треугольник
2. Прямоугольник.
Вопрос 2.
У коврика на кухне 5 сторон и 5 вершин. Нарисуйте форму коврика.
Назовите фигуру. ___________
Ответ: Пятиугольник — это многоугольник с 5 сторонами и 5 углами.
Вопрос 3.
На обоях используется этот рисунок.
Назовите фигуру в узоре.
Запишите количество сторон, вершин и углов фигуры.
_______ сторон _______ вершин ________ углов
Ответ:
5 сторон, 5 вершин и 5 углов.
Вопрос 4.
В гостиной есть 2 столика.
Обведите стол, представляющий собой куб. Объяснять.
Ответ: Симметричная трехмерная фигура, сплошная или полая, состоящая из шести равных квадратов.
Вопрос 5.
У Тины новое одеяло для кровати. Ее одеяло имеет этот дизайн.
Какая доля зеленая? ___________
Какая доля желтая? _________
Ответ:
Зеленое равно 2, желтое равно 2.
Пояснение:
Квадрат разделен на 4 равных части, из которых 2 зеленые и 2 желтые.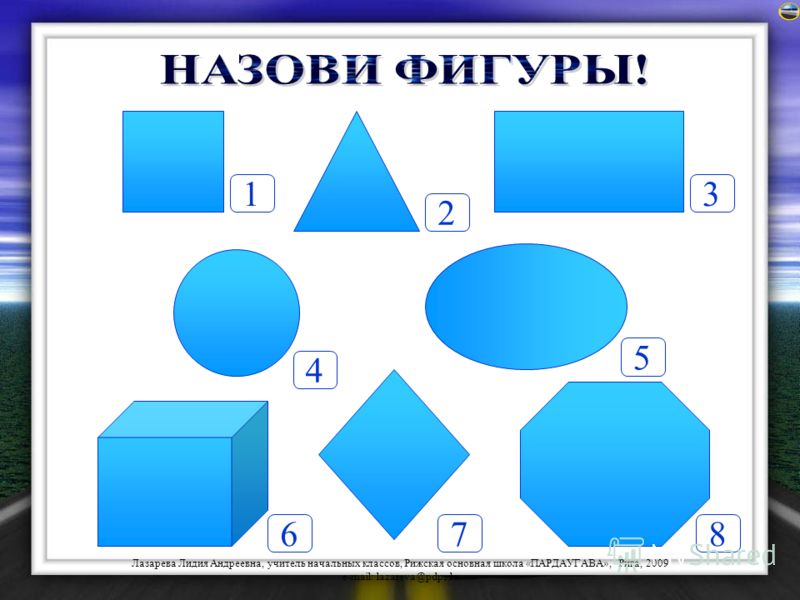
Вопрос 6.
Мама Тины вяжет одеяло из маленьких квадратиков. Она хочет, чтобы одеяло было четырехцветным. Каждый цвет имеет равную долю.
Часть A
Используйте 4 цвета, чтобы сделать дизайн лоскутного одеяла, показанный ниже. Сделайте равные доли одинаковой формы.
Дизайн 1
Ответ:
Каждая доля состоит из 4 маленьких квадратов, поэтому любая фигура с 4 маленькими квадратами является равной долей.
Я могу сделать доли одинаковой формы, все эти четверти квадраты.
В других проектах я использовал лемехи другой формы.
Часть B Используйте 4 цвета, чтобы создать другой дизайн лоскутного одеяла, показанный ниже. Сделайте равные доли, которые не имеют одинаковой формы.
Дизайн 2
Ответ:
Каждая доля состоит из 4 маленьких квадратов, поэтому любая фигура с 4 маленькими квадратами является равной долей.
Я могу делать доли одинаковой формы, все эти четверти квадратные.
В других проектах я использовал лемехи другой формы.
Двумерные фигуры – Математика 3 класса
Можете ли вы назвать формы этих объектов?
Отлично! 😁
Первый треугольник . Монета представляет собой круга , а шахматная доска представляет собой квадрата .
Это примеры двух – размерных форм !
Что такое двумерные фигуры?
Видите, чем квадрат отличается от куба ? 🤔
✅ Квадрат имеет длину и ширину , но не имеет глубины.
Квадрат может лежать плоско на поверхности.
2D Формы плоские . У них только два измерения – длина и ширина. Вот почему они называются двухмерными или 2D!
Другими примерами двумерных фигур являются круги, треугольники и прямоугольники.
Стороны, вершины и углы
😎 Большинство двухмерных фигур состоят из линий и углов. Эти части формы имеют специальные имена.
— Отрезки линий, образующие двумерную фигуру, называются ее сторонами .
— Угол, в котором встречаются две стороны 2D-фигуры, называется вершиной . Два или более угла называются вершинами ( не вершины !) .
Два или более угла называются вершинами ( не вершины !) .
– Мера поворота между двумя сторонами, которые встречаются в вершине, называется углом между сторонами.
Различные 2D-формы имеют разное количество сторон. 🤓
Давайте узнаем о самых распространенных 2D-фигурах.
Треугольник
Треугольник состоит из трех сторон. Эти стороны могут быть, а могут и не быть равными.
Имеет 3 вершины и 3 угла.
Прямоугольник
Прямоугольник имеет 4 стороны, 4 вершины и 4 прямых угла (углы 90°).
Противоположные стороны прямоугольника равны и параллельны друг другу.
🤓 Совет: Слово четырехугольник означает 4-стороннюю форму. Прямоугольники – это четырехугольники.
Квадрат
Квадрат представляет собой особый тип прямоугольника, в котором все 4 стороны равно равно .
Как и прямоугольник, квадрат также имеет 4 вершины, 4 прямых угла и параллельные противоположные стороны.
Ромб
Ромб выглядит как ромб или перекошенный квадрат .
Как и квадрат, ромб также имеет 4 равные стороны и 4 вершины.
Противоположные стороны ромба параллельны друг другу.
Противоположные углы ромба равны равны друг другу.
Совет: Квадрат – это ромб. Но не все ромбы квадраты!
Трапеция
Трапеция также имеет 4 стороны, 4 вершины и 4 угла.
Трапеция четырехгранная, только 1 пара из параллельные стороны .
Значит, квадраты и прямоугольники не трапеции. 👍
👍
Пятиугольник
A Пятиугольник имеет 5 равных сторон, 5 вершин и 5 равных углов.
Шестиугольник
Шестиугольник имеет 6 равных сторон, 6 вершин и 6 равных углов.
Восьмиугольник
Восьмиугольник имеет 8 равных сторон, 8 вершин и 8 равных углов.
Круг
Круг — это круглая форма, не имеющая сторон и вершин.
Расстояние от центра круга до любой точки на его границе всегда остается тем же .
Отличная работа по изучению двухмерных фигур! 👏
Теперь завершите практику, которая поможет вам помнить дольше. 💪
Распознавать и рисовать фигуры с заданными атрибутами, такими как заданное количество углов или заданное количество равных граней. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и кубы.
Экспорт
Распечатать
Связанные точки доступа
Альтернативная версия этого теста для учащихся с серьезными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Формирующие оценки MFAS
Фигуры с пятью сторонами:
Учащихся просят нарисовать пятистороннюю фигуру и назвать ее.
Четырехсторонние фигуры:
Учащимся показывают четырехугольник и просят определить его. Затем учащимся предлагается нарисовать еще один пример четырехугольника, отличный от того, который им показали.
Трехсторонние фигуры:
Учеников просят нарисовать треугольник и обосновать нарисованную фигуру. Затем учащимся показывают фигуру, которая не является треугольником, но имеет три стороны, и просят определить, является ли фигура на листе треугольником.
Какие из них являются кубами?:
Учащимся показывают набор трехмерных фигур и просят определить кубы. Кроме того, их просят объяснить, почему остальные фигуры не являются кубиками.
Оригинальные учебники для учащихся по математике – классы K-5
Фигуры в космосе:
Узнайте, как распознавать и рисовать треугольники, пятиугольники и шестиугольники, используя атрибуты фигур, в этом интерактивном учебном пособии на космическую тематику.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом тесте.
Оригинальный учебник для студентов
Фигуры в космосе:
Узнайте, как распознавать и рисовать треугольники, пятиугольники и шестиугольники, используя атрибуты фигур, в этом интерактивном учебном пособии на космическую тематику.
Тип: оригинальное учебное пособие для учащихся
Образовательная игра
Подбери 2D-форму:
Сыграй в игру на концентрацию. Сопоставьте 2D-форму с правильным названием.
Тип: Обучающая игра
Руководство
Галерея многоугольников:
Это сочетание иллюстраций и повествования определяет выпуклые и вогнутые многоугольники и описывает особенности различных многоугольников. Примеры показанных многоугольников включают треугольники и четырехугольники различных типов, в том числе выпуклые и вогнутые, и даже тот, в котором есть отверстие. Пояснение или текст для чтения описывает формы для пользователя. Copyright 2005 Национальный информационный центр Эйзенхауэра
Примеры показанных многоугольников включают треугольники и четырехугольники различных типов, в том числе выпуклые и вогнутые, и даже тот, в котором есть отверстие. Пояснение или текст для чтения описывает формы для пользователя. Copyright 2005 Национальный информационный центр Эйзенхауэра
Тип: Учебник
Виртуальные манипуляторы
Сортировка многоугольником:
Это интерактивное действие Flash предлагает пользователю отсортировать фигуры в диаграмму 2 на 2, известную как диаграмма Кэрролла, на основе их свойств. Свойства, используемые для сортировки, включают «четырехугольник» или «не четырехугольник» и «правильный многоугольник» или «неправильный многоугольник».
Тип: Virtual Manipulative
Инструмент Shape:
Этот виртуальный инструмент позволяет создавать, раскрашивать, увеличивать, уменьшать, вращать, отражать, нарезать и склеивать геометрические фигуры, такие как: квадраты, треугольники, ромбы, трапеции и шестиугольники. .
.
Тип: виртуальный манипулятор
Shape Cutter:
Этот виртуальный манипулятор позволяет учащимся рисовать геометрические фигуры, а затем разлагать и перекомпоновывать их в другие формы, используя слайды, повороты и перевороты для вырезания и перемещения частей.
Тип: Virtual Manipulative
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом тесте.
Виртуальные манипуляторы
Сортировка многоугольником:
Это интерактивное действие Flash предлагает пользователю отсортировать фигуры в диаграмму 2 на 2, известную как диаграмма Кэрролла, на основе их свойств. Свойства, используемые для сортировки, включают «четырехугольник» или «не четырехугольник» и «правильный многоугольник» или «неправильный многоугольник».
Тип: Virtual Manipulative
Инструмент Shape:
Этот виртуальный инструмент позволяет создавать, раскрашивать, увеличивать, уменьшать, вращать, отражать, нарезать и склеивать геометрические фигуры, такие как: квадраты, треугольники, ромбы, трапеции и шестиугольники. .
Тип: Виртуальный манипулятивный
Учение о классификации полигонов | Houghton Mifflin Harcourt
Вернуться к формеМатематика
Посох в форме
8 минут чтения
Оглянитесь вокруг. Как бы вы описали формы, из которых состоит место, где вы живете и где ходите в школу? Это один из способов, которым математическое мышление не совсем то же самое, что числовое мышление. (Хотя числа иногда являются идеальным способом описания различных качеств формы!)
В этой статье мы даем определение многоугольникам и описываем некоторые основные способы классификации треугольников и четырехугольников. Затем мы проводим два урока для учащихся 2-х классов и старше: на одном учащиеся знакомятся с названиями различных многоугольников ( Идентификация многоугольников ) и один, где они практикуют классификацию треугольников и четырехугольников ( Классификация многоугольников ).
Затем мы проводим два урока для учащихся 2-х классов и старше: на одном учащиеся знакомятся с названиями различных многоугольников ( Идентификация многоугольников ) и один, где они практикуют классификацию треугольников и четырехугольников ( Классификация многоугольников ).
Что такое многоугольник
?Когда люди слышат слово «геометрия», они обычно думают о формах. Многие из этих фигур или многоугольников можно описать как плоские замкнутые фигуры с тремя или более сторонами. Многоугольники — это двумерные объекты, а не трехмерные тела. Предложите учащимся изучить различные способы классифицируют полигонов. Направьте их на такие идеи, как подсчет сторон, измерение углов и сравнение длин сторон (например, поиск конгруэнтных сторон). Многие полигоны имеют специальные названия, которые могут быть знакомы вашим ученикам.
На этом рисунке показаны некоторые из наиболее распространенных многоугольников. Обратите внимание, что мы идентифицировали четырехугольник как четырехугольник. Чаще всего вы бы назвали эту форму многоугольника прямоугольником , но прямоугольник — это только один вид четырехугольника. Прямоугольник — это особый четырехугольник, у которого противоположные стороны конгруэнтны, то есть имеют одинаковую длину, и каждый угол равен 9.0003 прямой угол . Квадрат также является особым четырехугольником, потому что все четыре стороны конгруэнтны, а все четыре угла прямые.
Обратите внимание, что мы идентифицировали четырехугольник как четырехугольник. Чаще всего вы бы назвали эту форму многоугольника прямоугольником , но прямоугольник — это только один вид четырехугольника. Прямоугольник — это особый четырехугольник, у которого противоположные стороны конгруэнтны, то есть имеют одинаковую длину, и каждый угол равен 9.0003 прямой угол . Квадрат также является особым четырехугольником, потому что все четыре стороны конгруэнтны, а все четыре угла прямые.
В чем разница между квадратами и прямоугольниками?
Прямоугольники и квадраты во многом похожи:
- Оба являются четырехугольниками (четырехсторонними многоугольниками).
- Оба имеют конгруэнтные противоположные стороны.
- Оба имеют четыре угла, все прямые.
Однако у квадрата равны все четырех сторон. Можно сказать так: все квадраты — прямоугольники, но не все прямоугольники — квадраты. Готовых учеников можно познакомить с нашей игрой на нахождение площади прямоугольников.
Как классифицировать треугольники
Треугольники также имеют свои особые случаи. Равносторонний треугольник можно считать двоюродным братом квадрата, поскольку все три стороны равны. Еще один особый треугольник — 9.0003 равнобедренный треугольник, у которого равны только две стороны. Треугольник не имеет конгруэнтных сторон.
Урок 1: Идентификация многоугольников
Поскольку большая часть лексики для многоугольников будет новой для ваших учеников, рекомендуется начать с установления связей между объектами в вашем классе и новой лексикой. Это позволит вам связать то, что изучают учащиеся, с реальными примерами полигонов, а также с уроками ELA.
Стандартный ключ: Распознавать фигуры, имеющие заданные атрибуты, такие как заданное количество углов. Определите треугольники, четырехугольники, пятиугольники, шестиугольники и восьмиугольники. (Common Core 2.G.A.1, Florida B.E.S.T. MA.2.GR.1.1)
MA.2.GR.1.1)
Материалы :
- Цветная бумага (идеальная плакатная бумага)
- Прямой край
- Scissors
PREREQUISIT : Учащиеся должны уметь распознавать треугольники и четырехугольники по количеству сторон.
Подготовка : Создайте большие версии следующих многоугольников, осторожно используя линейку и ножницы, а затем опубликуйте их для всех. Убедитесь, что они достаточно большие, чтобы их мог видеть весь класс. При дистанционном обучении используйте цифровые изображения или слайды, которые могут видеть все учащиеся, а вы можете свободно перемещаться. Используйте цветную бумагу и напишите название каждого многоугольника в центре.
- (Укажите на треугольник.) Спросите : Что это за фигура? (треугольник) Может ли кто-нибудь сказать мне, чем треугольник отличается от других фигур? Поощряйте все идеи, не заявляя, что ответы неверны. Предложите учащимся определить треугольник как фигуру с тремя сторонами.
 Некоторые могут также сказать, что у него три угла. Запишите эти свойства под формой многоугольника.
Некоторые могут также сказать, что у него три угла. Запишите эти свойства под формой многоугольника. - (Публично напишите слово трехколесный велосипед.) Спросите : Кто из вас знает, что такое трехколесный велосипед? Сколько колес у трехколесного велосипеда? Что общего у трехколесного велосипеда и треугольника? Когда учащиеся определят, что у трехколесного велосипеда три колеса, а у треугольника три стороны, проведите связь между приставкой три- и числом три. Посмотрите, слышали ли учащиеся другие английские слова, которые начинаются с tri- и состоят из трех слов, например триатлон, трио, трилогия, штатив или трехъязычный.
- Под свойствами треугольника напишите «Три означает 3».
- (Укажите на четырехугольник.) Спросите : Эта фигура называется четырехугольником. Что вы можете мне сказать об этом? =Поощряйте все идеи, не называя ответы неправильными. Предложите учащимся определить четырехугольник как фигуру с четырьмя сторонами.
 Некоторые могут также сказать, что у него четыре угла. Запишите эти свойства под формой многоугольника.
Некоторые могут также сказать, что у него четыре угла. Запишите эти свойства под формой многоугольника. - Продолжайте объяснять, что счетверенный означает четыре . Студенты вряд ли знают много слов, которые начинаются с quad- и состоят из четырех слов, но вы можете показать примеры, например, quadruple, quadrant или quadriceps (что относится к мышце человека, состоящей из четырех частей). Напишите «квадрат означает 4» под четырехугольником.
- (Указывая на пятиугольник.) Произнеси : Это пятиугольник. Что вы можете мне сказать об этом? Учащиеся должны определить количество сторон и, возможно, углов пятиугольника.
- Спросите : Кто знает, что означает приставка пять в слове пятиугольник? Объясните, что в данном случае пента- означает пять. Студенты могут быть знакомы с пятиборьем или зданием Пентагона.
- Продолжайте, вводя шестиугольник и восьмиугольник.
 Некоторые учащиеся задумаются и увидят, что префиксы шести и восьми равны 9.2397 гекса- и окта-. Хотя в этом уроке префиксы даны с конечными гласными (например, окта-, а не окта-), обратите внимание, что иногда префикс встречается с другой гласной (например, осьминог) или вообще без гласной (например, октет ).
Некоторые учащиеся задумаются и увидят, что префиксы шести и восьми равны 9.2397 гекса- и окта-. Хотя в этом уроке префиксы даны с конечными гласными (например, окта-, а не окта-), обратите внимание, что иногда префикс встречается с другой гласной (например, осьминог) или вообще без гласной (например, октет ).
Урок 2: Классификация многоугольников
Когда ваши ученики смогут идентифицировать различные многоугольники, переходите к определению свойств конкретных многоугольников. Это также время, чтобы убедиться, что ваши студенты знают и используют правильный математический словарь при описании свойств многоугольников.
Ключевой стандарт: Поймите, что фигуры в разных категориях могут иметь общие атрибуты и что общие атрибуты могут определять более крупную категорию (например, четырехугольники). (Common Core 3.G.A.1, Florida B.E.S.T. MA.2.GR.1.3)
Материалы :
- Рабочий лист 1: Треугольники и Рабочий лист 2: Четырехугольники (по одному на ученика и один на вас)
- Проектор или средства публичного показа рабочих листов
- Линейка для каждого учащегося или пары учащихся
- Линейка для использования с рабочими листами перед классом
Подготовка : Подготовьте диапозитивы рабочих листов 1 и 2. В качестве альтернативы отобразите рабочие листы на мониторе или интерактивной доске, чтобы все учащиеся могли их видеть. Раздайте студенческие рабочие листы каждому ребенку в виде распечаток или цифровых файлов.
В качестве альтернативы отобразите рабочие листы на мониторе или интерактивной доске, чтобы все учащиеся могли их видеть. Раздайте студенческие рабочие листы каждому ребенку в виде распечаток или цифровых файлов.
- Скажем : Мы говорили о различных типах полигонов. Как мы описали треугольник? Перечислите свойства треугольника, которые видны всем учащимся: трехсторонний многоугольник, содержит три угла или угла.
- Скажем : Посмотрите на рабочий лист 1. Все эти фигуры треугольники, но некоторые из них имеют специальные названия. Посмотрите на рисунок в. С помощью линейки измерьте три стороны этого треугольника. Продемонстрируйте, используя собственную линейку.
- Спросите : Все ли три стороны одинаковой длины? (да) Обратите внимание, что люди не могут точно измерить , поэтому учащиеся могут обнаружить, что некоторые стороны имеют немного разную длину. Объясните, что изображение было разработано таким образом, что все стороны имеют одинаковую длину.

- Скажем : Треугольник, у которого все стороны имеют одинаковую длину, называется равносторонним треугольником. Посмотрите на рабочий лист. Являются ли остальные треугольники равносторонними? Используйте линейку для проверки. Предоставьте учащимся достаточно времени для измерения, а затем попросите добровольцев. Предложите учащимся сравнить свои рассуждения, не называя никого правым или неправым. Фигура д тоже равносторонняя.
- Спросите : Кто-нибудь думал, что Фигура а была равносторонней? Посмотрите, могут ли учащиеся объяснить, почему это не так. Если необходимо, покажите, что на рисунке а две стороны имеют одинаковую длину, а третья сторона имеет другую длину.
- Скажем : Треугольник с двумя равными сторонами называется равнобедренным треугольником . Есть ли на листе другие равнобедренные треугольники? Используйте линейку для проверки.
- Скажем : Фигура f равнобедренная.
 Убедитесь, что учащиеся понимают разницу между равнобедренными и равносторонними треугольниками. Обычно равносторонний треугольник считается частным случаем равностороннего треугольника.
Убедитесь, что учащиеся понимают разницу между равнобедренными и равносторонними треугольниками. Обычно равносторонний треугольник считается частным случаем равностороннего треугольника. - Произнесите : Посмотрите на другие треугольники на рабочем листе. Эти треугольники имеют стороны разной длины. Они называются разносторонних треугольников.
- Вы можете провести аналогичный урок с четырехугольниками, используя рабочий лист 2. Попросите учащихся идентифицировать прямоугольники и квадраты. Позвольте учащимся сравнить свои рассуждения, не называя никого правым или неправым. Направьте учащихся на определение того, что квадраты и прямоугольники имеют четыре прямых угла, но только квадраты имеют четыре конгруэнтные стороны. Квадрат считается частным случаем прямоугольника.
Учащимся необходимо попрактиковаться в определении различных многоугольников. Предложите учащимся отсортировать группы многоугольников, ориентированных по-разному, чтобы убедиться, что они могут идентифицировать многоугольники, как бы они ни были повернуты. Вы также можете попросить учащихся нарисовать различные многоугольники с помощью линейки. Также рекомендуется, чтобы дети рисовали более одного многоугольника каждой формы, используя разные положения. Это позволит вам получить более качественную оценку своего истинного понимания свойств каждого полигона.
Предложите учащимся отсортировать группы многоугольников, ориентированных по-разному, чтобы убедиться, что они могут идентифицировать многоугольники, как бы они ни были повернуты. Вы также можете попросить учащихся нарисовать различные многоугольники с помощью линейки. Также рекомендуется, чтобы дети рисовали более одного многоугольника каждой формы, используя разные положения. Это позволит вам получить более качественную оценку своего истинного понимания свойств каждого полигона.
***
Ищете учебную программу для повышения уверенности учащихся в геометрии, формах и многоугольниках? Исследуйте HMH Into Math , наше основное математическое решение для классов K–8 , которое подчеркивает «почему», стоящее за «как».
Математика Мероприятия и уроки 1-2 классы 3–5 классы
Дополнительная литератураРичард Бланкман
Фасонный Редактор
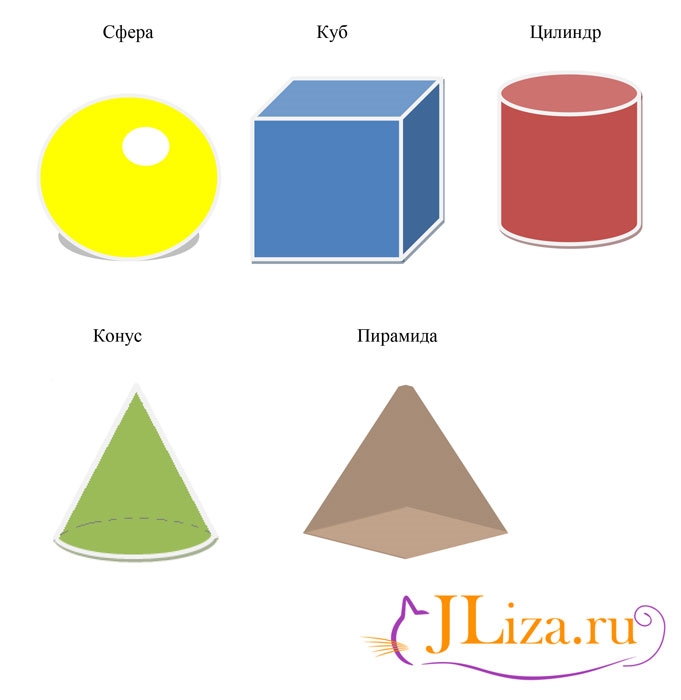

 Психологический настрой. «Здравствуйте!».
Психологический настрой. «Здравствуйте!».
 Обучающийся находит и обводит прямые и кривые линии.
Обучающийся находит и обводит прямые и кривые линии.
 Рефлексия.
Рефлексия. 

 И все они были одинаковыми. Стала королева думать, как же сделать так, чтобы их можно было различить. И придумала.
И все они были одинаковыми. Стала королева думать, как же сделать так, чтобы их можно было различить. И придумала.
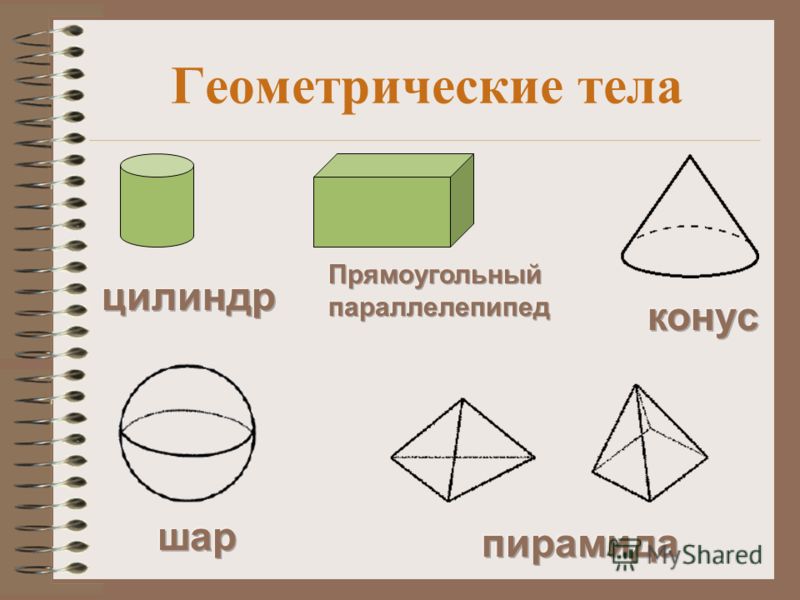 Отметьте красным карандашом две точки, расположив их между синими точками.
Отметьте красным карандашом две точки, расположив их между синими точками.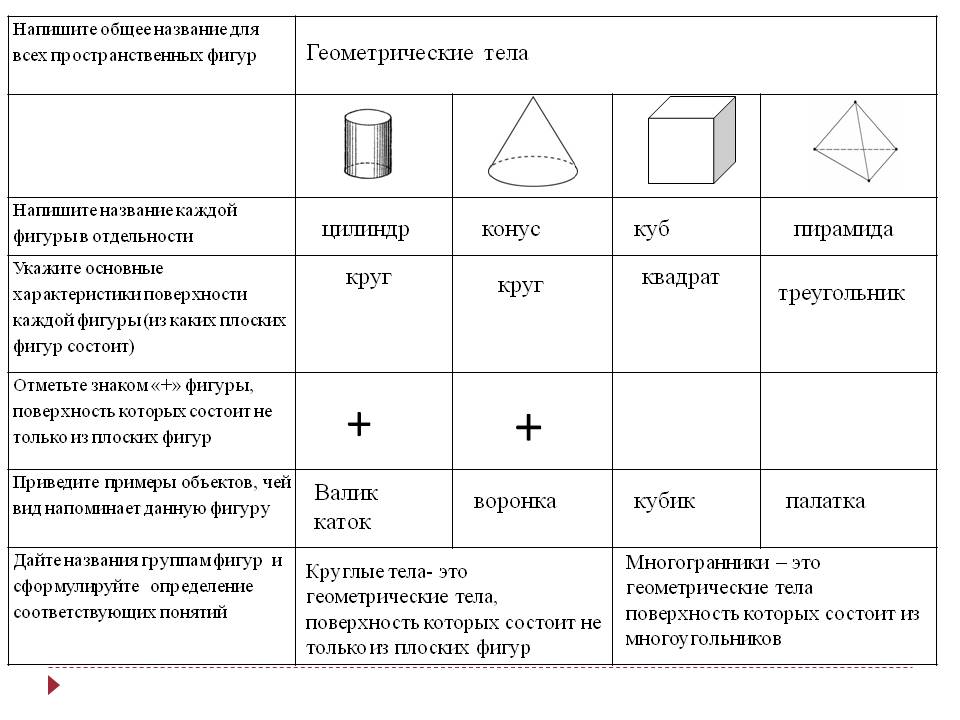 Найдите длину ломаной.
Найдите длину ломаной.