Название геометрических фигур в математике: Основные геометрические фигуры 🟢🟨🔺 и их названия

«Как произошли названия геометрических фигур» | Творческая работа учащихся:

Муниципальное бюджетное общеобразовательное учреждение

начальная общеобразовательная школа № 2 г. Охи

Город Оха

Школа №2

Класс 3 б

Направление естественнонаучное

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

«Как произошли названия геометрических фигур»

Руководитель Васильченко Нина Владимировна,

Первая  квалификационная категория

Учащийся Хетик Полина Юрьевна

2018

Оглавление

Введение        3

Теоретическая часть        5

1.1 Понятие «геометрические фигуры » в математике        5

1.2 Виды геометрических фигур        6

1.3 Кто же и когда придумал названия  геометрических фигур?        7

Практическая работа.        9

Заключение.        10

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ        11

Приложение 1        12

Приложение 2        13

Приложение 3        14

Приложение 4        15

Мы с первого класса на уроках математики стали знакомиться с различными геометрическими фигурами. Это меня очень увлекло. Геометрические фигуры окружают каждого человека в повседневной жизни, но мы их не замечаем. У меня зародился вопрос: кто же дал название геометрическим фигурам?

Актуальность моего исследования заключается в том, что уже с рождения все мы видим вокруг геометрической фигуры. Каждая фигура имеет свое название и форму. Но кто и когда дал им названия?

Цель исследовательской работы: узнать, как геометрические фигуры получили свои названия.

Объект исследования: геометрические фигуры.

 Для достижения поставленной цели в работе решаются следующие задачи:

 1. Узнать, что такое геометрические фигуры;

2. Какие виды геометрических фигур существуют;

3. Собрать информацию о названиях геометрических фигур, используя словари и энциклопедии.

Гипотеза: исследование названий геометрических фигур позволяет развивать не только математические и логические навыки, но оттачивает ассоциативное, пространственное и образное мышление.

Методы исследования: анкетирование, обзор литературы, сравнение, обобщение.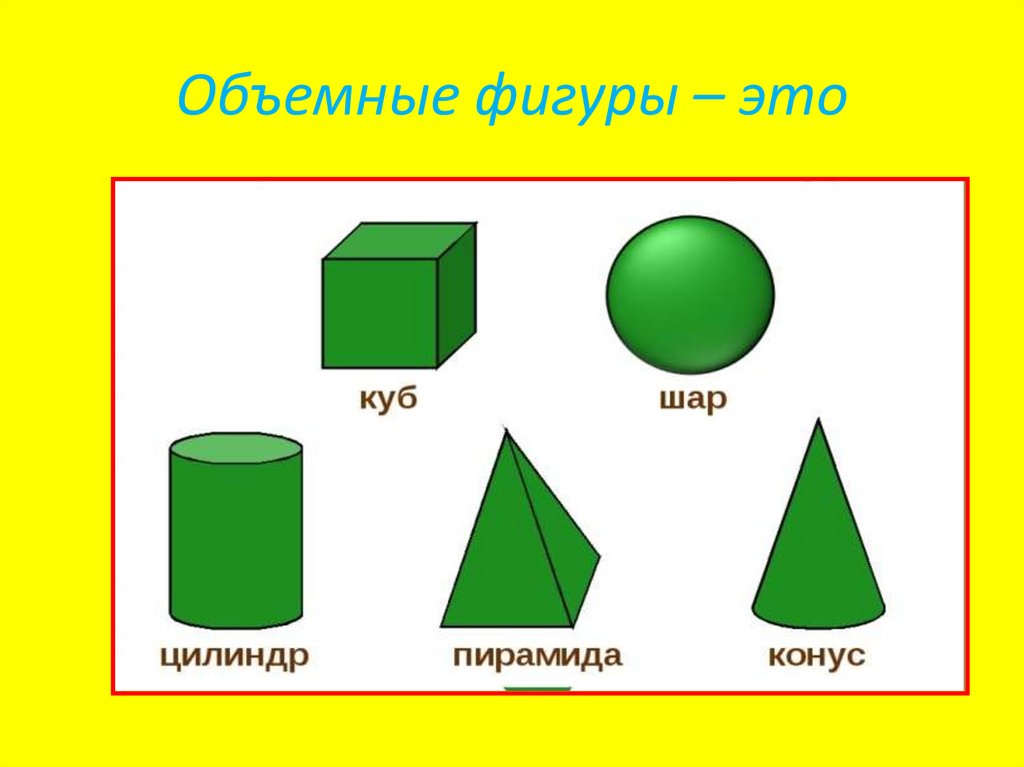

Исследовательская работа состоит из введения,  теоретической части, практической  части, заключения, списка используемой литературы и приложений.

Во введении определены актуальность темы, объект, цель и задачи исследования.

В теоретической части исследовательской  работы рассматриваются теоретические аспекты, понятия геометрической фигуры и виды геометрических фигур.

В практической части исследовательской  работы анализируются и оцениваются знания учащихся о геометрических фигурах, о происхождение названий геометрических фигур.

В заключении представлены основные выводы по результатам исследования.

Теоретической базой исследования послужили научные и учебные издания по математике, материалы периодических изданий по вопросам геометрических фигур.

Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учеными-археологами  был найден папирусный свиток с геометрическими задачами, в которых упоминались геометрические фигуры.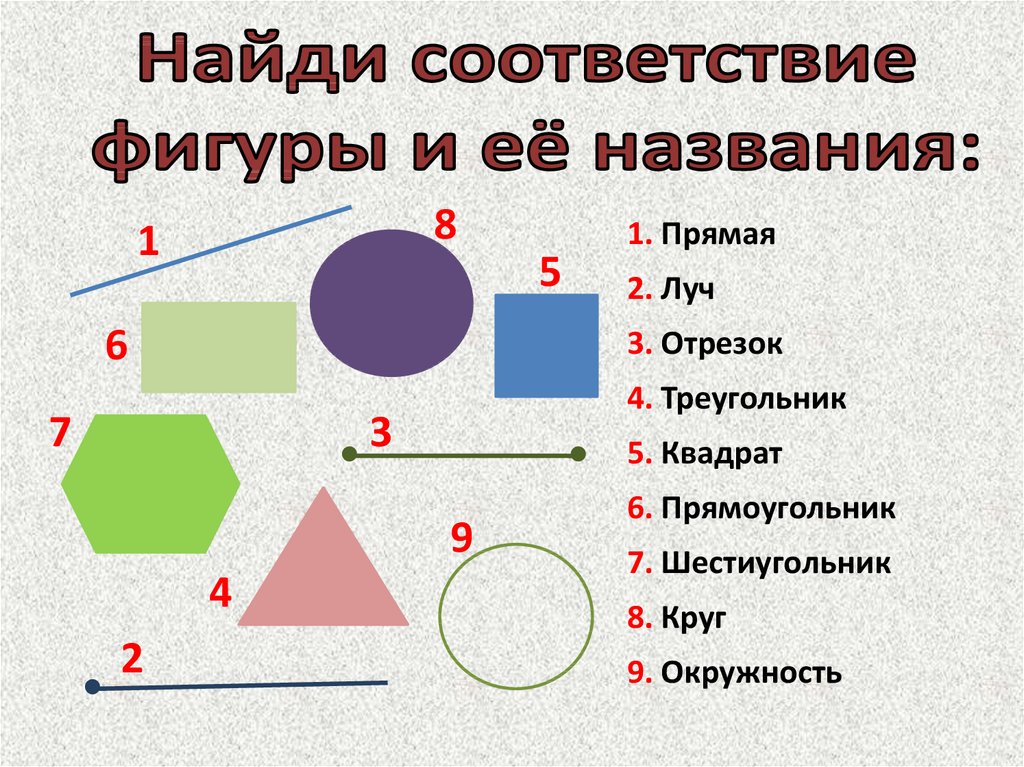 И каждая из них называлась каким-то определенным словом.

Само слово «ФИГУРА» – латинское слово, означает “образ”, “вид”, “начертание”. Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — “форма”, также означающее ”наружный вид”, “внешнее очертание предмета”.

         По определению Ожегова «геометрическая фигура» – это часть плоскости, ограниченная замкнутой линией, а также совокупность определенным образом расположенных точек, линий на поверхностей или тел.        

В советской энциклопедии геометрической фигуре даётся следующее определение – термин, применяемый к разнообразным множествам точек; обычно фигурой называют такие множества, которые можно представить состоящими из конечного числа точек, линий или поверхностей, в частности сами точки, линии и поверхности.

В современном словаре иностранных слов геометрическая фигура – это совокупность точек на плоскости; совокупность точек в пространстве.

В словаре Р. Якубова геометрической фигуре даётся следующее определение – часть плоскости, ограниченная замкнутой линией, а также совокупность точек, линий, поверхностей или тел.

Вывод: геометрическая фигура – множество точек на поверхности (зачастую на плоскости), которое образует конечное количество линий.

Какие же бывают геометрические фигуры? Фигуры бывают плоские (двухмерные) фигуры и объёмные фигуры (трёхмерные).

К плоским относят: круг, полукруг, окружность, луч, прямоугольник, треугольник и другие. Их изучает планиметрия. Точка тоже плоская фигура.

К объёмным относят: шар, конус, сфера, куб, цилиндр, пирамида и другие. Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек. Их изучает стереометрия.

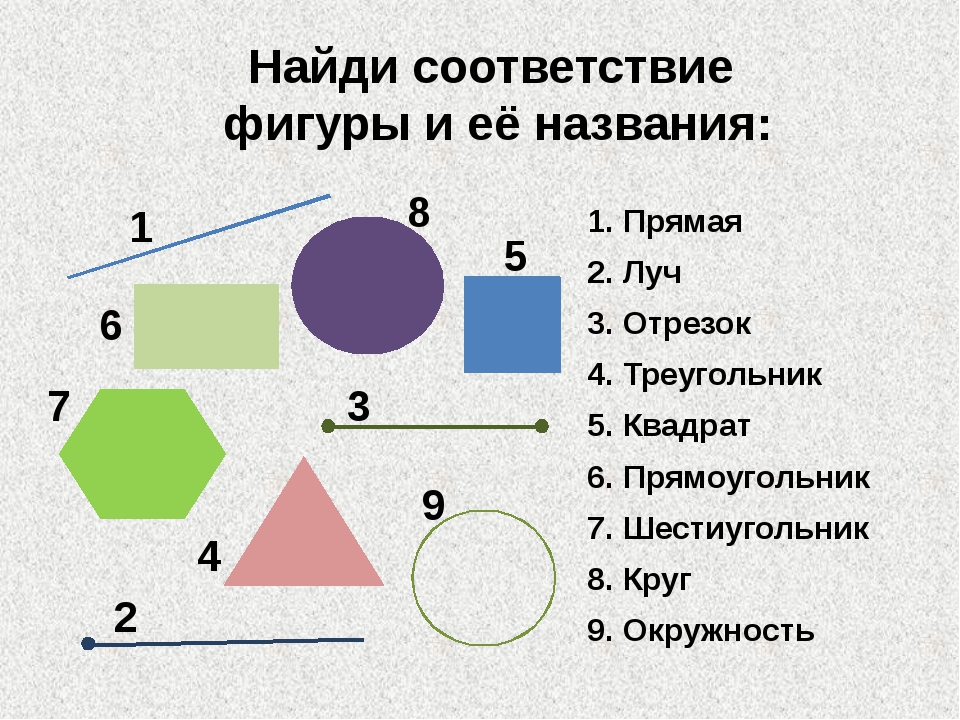
Основными геометрическими фигурами на плоскости являются точка и прямая линия. Отрезок, луч, ломаная линия — самые простые геометрические фигуры на плоскости. 

Точка — мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.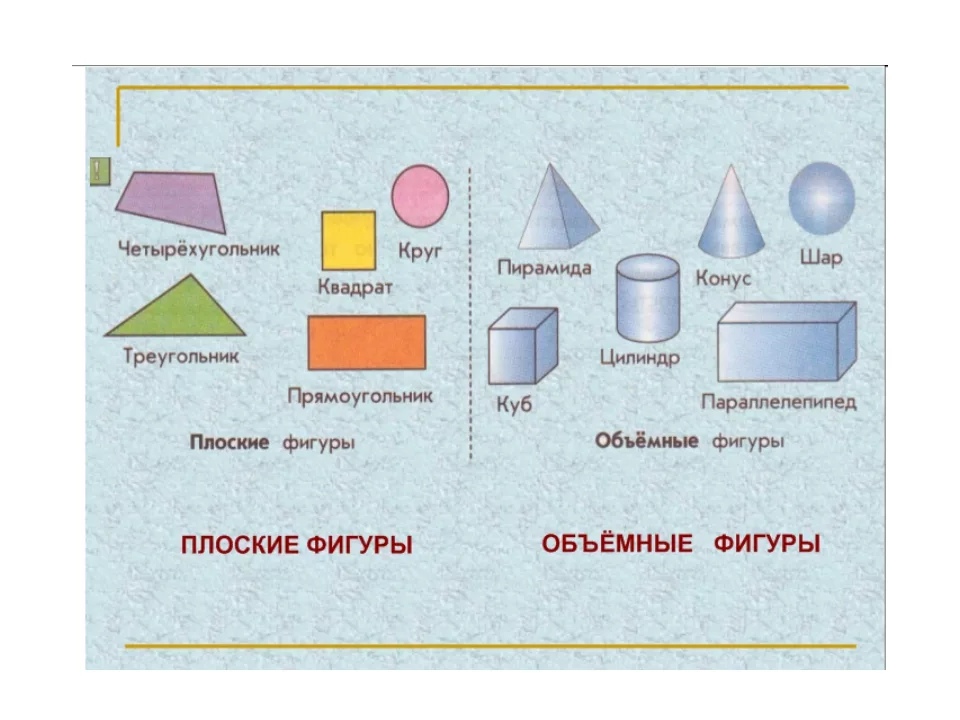

Каждая более сложная геометрическая фигура есть множество точек, которые обладают определенным свойством, характерное только для этой фигуры.

Прямая линия, либо прямая – это бесконечное множество точек, расположенных на одной линии, которая не имеет начала и конца. На листе бумаги можно увидеть лишь часть прямой линии, так как она не имеет предела.

Часть прямой линии, которая ограничена с двух сторон точками, называют отрезком прямой, либо отрезком.

Луч — это направленная полупрямая, имеющая точку начала и у которой нет конца. Если на прямой поставить точку, то эта точка будет разбивать прямую на два противоположно направленных луча. Эти лучи называют дополнительными.

Ломаная линия — несколько отрезков, которые соединены друг с другом таким образом, что конец первого отрезка оказывается началом второго отрезка, а конец второго отрезка — началом третьего отрезка и так далее, причем соседние (которые имеют одну общую точку) отрезки располагаются на разных прямых.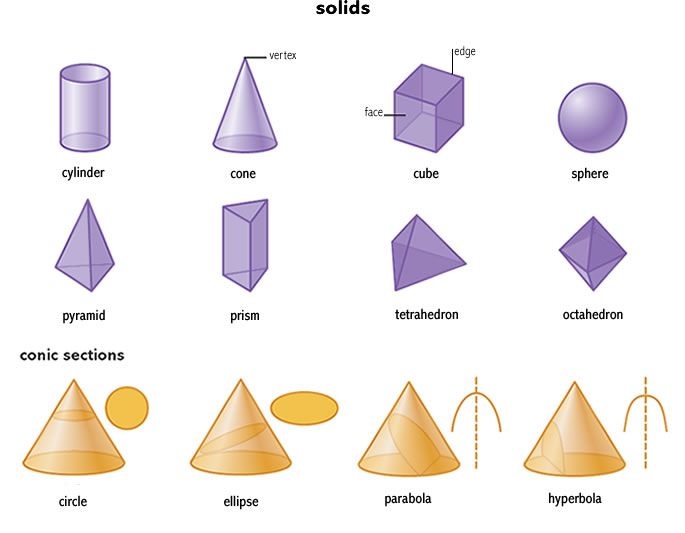 Когда конец последнего отрезка не совпадает с началом первого, значит, эта ломаная линия будет называться незамкнутой. Когда конец последнего отрезка ломаной совпадает с началом первого, значит, эта ломаная линия будет замкнутой.      Четырехзвенная замкнутая ломаная линия — четырехугольник. Трехзвенная замкнутая ломаная линия — треугольник.

 На самом деле фигур в математике достаточно. Мы рассмотрели основные и наиболее часто встречающие на уроках математике в начальной школе.

Термин “геометрическая фигура” придумали древние греки. До греков фигуры никто не изучал и никаких названий у них не было. Греки нашли гениальный выход: они стали называть геометрические фигуры словами, обозначавшими предметы похожей формы.

Слово “точка” происходит от латинского глагола “ткнуть”, а равнозначное слово “пункт” – от латинского глагола punktum (“укол”), то есть первоначально под точкой понимали укол. Точка – в русском языке означало конец заточенного гусиного пера. 

«ЛИНИЯ» происходит от латинского слова «линеа» – льняная (имеется в виду льняная нить).

КВАДРАТ произошел от латинского слова «кваттуор» (четыре) – фигура с четырьмя сторонами. 

КРУГ – общеславянское слово, имеющее соответствия в германских языках: в древнегерманском “кригер” — “кольцо”, “круг”, в греческом – “колесо”, “круг”).

ОКРУЖНОСТЬ в переводе с греческого это слово означает “периферия”.

ОТРЕЗОК – это общеславянское слово, производное от “резать”.

ПРЯМАЯ – общеславянское слово, в греческом “промос” — “передовой”, “прямой”.

Термин ПРЯМОУГОЛЬНИК образован путем соединения двух слов: “прямой” и “угол”.

Одни считают, что греческое слово ”пирамида” происходит от египетского “пирамус” — “боковое ребро сооружения”. Существует другое предположение: термин берет своё начало от формы хлебцев в Древней Греции, то есть является производным от греческого слова “пирос” — “рожь”. Некоторые ученые считают, что термин произошел от греческого слона “пир” — “огонь”, так как пламя иногда напоминает по форме пирамиду.

Одни считают, что термин РОМБ произошел от греческого слова “ромбос”, означающего ”бубен”, т. к. ромб похож на четырехугольный бубен, другие — что от греческого слова “‘ромб”, которое означает «вращающееся тело», «веретено», так как сечение в обмотанном веретене имеет форму ромба.

УГОЛ – общеславянское слово индоевропейского характера (сравним в латинском ”ангулус” — “угол”, “кривой”).

ЦИЛИНДР – происходит от греческого «кылиндрос» — «валик».

Я поняла, что названия геометрических фигур совсем не странные, а очень даже разумные и понятные. Названия геометрических фигур первоначально были названиями предметов, имеющих форму близкую к форме фигур. Названия некоторых геометрических фигур отражают их свойства.  Просто почти все они пришли к нам из греческого или латинского языков.

Изучив теорию я преступила к исследованию. Исследование я проводила на базе МБОУ НОШ №2 г.Охи, среди учащихся 3б класса. В классе обучается 22 человека: 11 мальчиков и 11 девочек.

 На начальном этапе своей исследовательской работы я решила выяснить, какие знают геометрические фигуры учащиеся моего класса.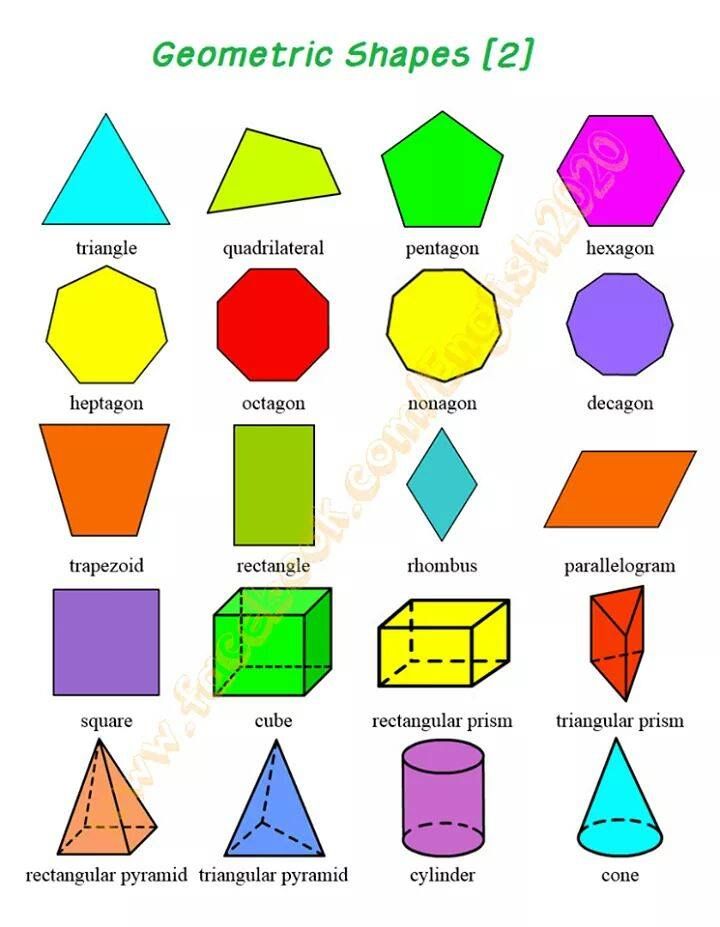 Учащимся было предложено назвать геометрические фигуры которые они знают.  Обработанные данные показали, что геометрические фигуры знают многие учащиеся. Поученный материал  я составила в виде диаграммы. (Приложение 1).

Дальше я решила узнать, а что ребята моего класса знают о происхождении названий геометрических фигур. Для этого я предложила учащимся 3 б класса ответить на вопрос: Кто  и когда придумал названия  геометрических фигур?

 Обработанные данные показали, что мои одноклассник ничего не знают о происхождении названий геометрических фигур, полученный материал я составила в виде диаграммы. (Приложение 2).

Исходя из данных полученных на начальном этапе моей исследовательской работы, я провела работу, задача которой состояла в том, чтобы раскрыть и умножить знания учащихся о происхождении названий геометрических фигур.

Моя работа заключалась в следующем: я на уроках математике в течение нескольких уроков рассказывала своим одноклассникам о происхождении названий геометрических фигур.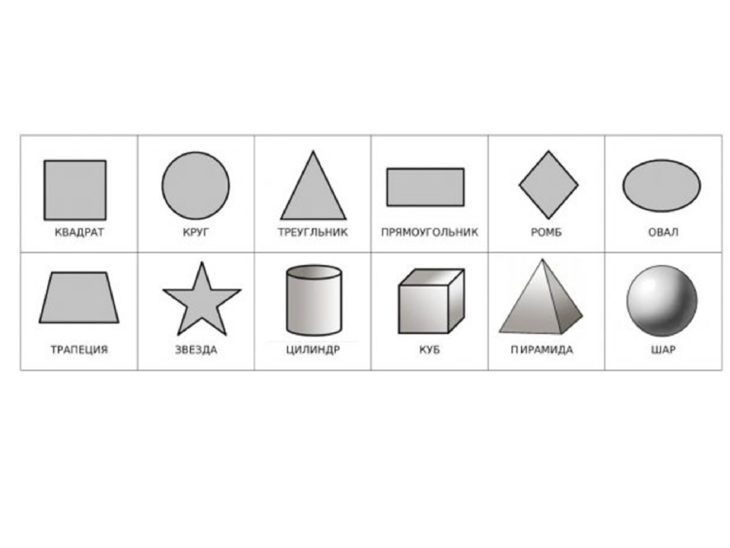 Также изготовила информационные листы, где учащиеся моего класса могли познакомиться самостоятельно и познакомить других  с  происхождением названий геометрических фигур.

После проведённой мною работы, я провела повторное анкетирование учащихся моего класса. Результаты анкетирования представила в виде диаграммы. (Приложение 3).

По результатам исследовательской работы я могу сделать вывод, что проведя в классе целенаправленную работу по ознакомлению учащихся с происхождением названий геометрических фигур, уровень знаний у учащихся повысился, а также повысился интерес к изучаемому предмету.

Я проделала большую работу и ответила на все вопросы, которые возникли у меня в самом начале моей исследовательской работы. Отвечая на вопросы, я узнала для себя очень много интересного и полезного.

Математика очень важная и интересная наука. Я отметила, что в нашей жизни мы часто встречаем геометрические фигуры. Геометрические фигуры – это множество точек на поверхности.

 В ходе исследовательской работы я узнала, что существуют разные виды геометрических фигур, узнала что названия геометрических фигур пришли к нам из греческого или латинского языков.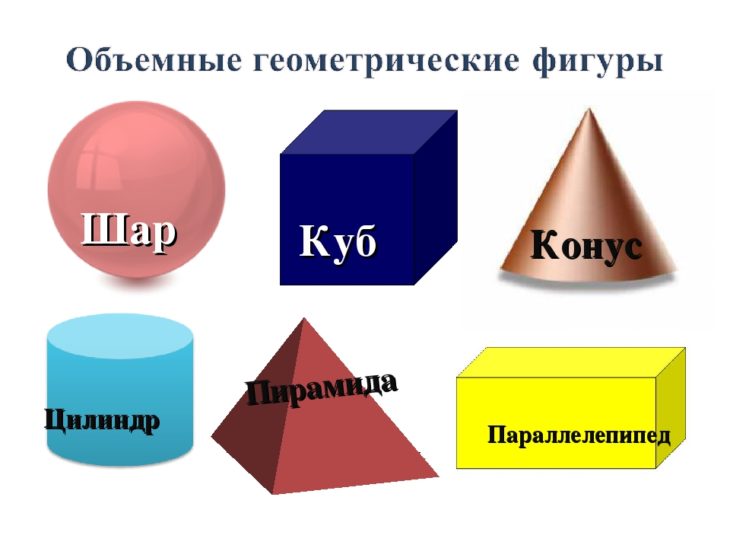

 Значимость моей работы заключается в том, что  материал моего исследования можно использовать как на уроках математике, так во внеурочной деятельности. Многие ученики, познакомившись с данным материалом, на вопрос о необходимости изучать геометрические фигуры – ответят положительно! И, конечно же, будут с интересом изучать их  в дальнейшем.

1. Детская энциклопедия. 3-е издание. Том 02. Мир небесных тел. Числа и фигуры 3-е изд. – М.: Педагогика, 1972. – 480 с.
2. Крысин, Л.П. Современный словарь иностранных слов: Свыше 7000 слов и выражений, толкование значений, происхождение, употребление / Л.П. Крысин. – М.: АСТ-Пресс, 2012. – 416 c.
3. Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров . – М. : Советская энциклопедия, 1988 . – 847 с. 
4. Ожегов, Сергей Иванович. Толковый словарь русского языка : около 100 000 слов, терминов и фразеологических выражений / С. И. Ожегов ; под ред. Л. И. Скворцова. – 26-е изд., испр. и доп. – М. : Оникс [и др. ], 2009. – 1359 c.
5. Словарь “3 в 1” для начальной школы: орфографический, толковый, этимологический / Р. Б. Якубова, Н. Б. Якубова. – Ростов-на-Дону : Феникс, 2016. – 410 с.

Рисунок 1 – «Какие знаете геометрические фигуры?»

Рисунок 2 –  Уровень знаний учащихся на начальном этапе

Рисунок 3 – Уровень знаний учащихся на заключительном этапе

Информационный лист «Происхождение названий геометрических фигур»

Точка                ●	происходит от латинского глагола “ткнуть”
Линия	происходит от латинского слова «линеа» – льняная
Квадрат	произошел от латинского слова «кваттуор» (четыре) – фигура с четырьмя сторонами.
Круг	общеславянское слово, в греческом – “колесо”, “круг”
Окружность	в переводе с греческого это слово означает “периферия”
Отрезок	общеславянское слово, производное от “резать”
Прямая	общеславянское слово, в греческом “промос” — “передовой”, “прямой”
Прямоугольник	образован путем соединения двух слов: “прямой” и “угол”
Ромб	от греческого слова “ромбос”, означающего ”бубен”
Цилиндр	происходит от греческого «кылиндрос» — «валик»

Статья «Изучаем названия геометрических фигур в игре «Танграм».

| Статья по математике (средняя группа) по теме:

Статья

 «Изучаем названия геометрических

фигур в игре «Танграм».

                                                                                                                                                                                              

Группа детей среднего дошкольного возраста с 4 до 5 лет, с которыми я работаю первый год, показала свою контрастность и неоднородность      общего развития. Некоторые дети значительно опережают своих сверстников. Они любопытны, пытливы, проявляют большой интерес к новому, неизвестному, при этом обладая неплохим запасом знаний. Это дети, которым дома уделяют большое внимание со стороны взрослых. Такие ребята, придя в детский сад, поднимаются на более высокую ступень, тренируя свой интеллект в игровой деятельности.

В работе с детьми большую пользу приносят занимательные игры и упражнения геометрического содержания: они развивают интерес к математическим представлениям, способствуют формированию умственных способностей детей.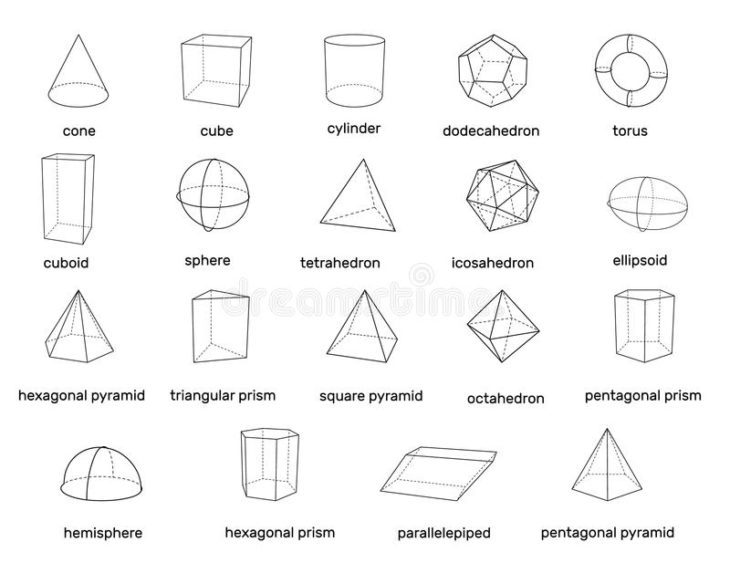

Дошкольники с удовольствием решают задачи на смекалку, головоломки, задачи на построение, например: перекладывают 1, 2, 3 палочек из одной фигуры, получают другую (из фигуры домика делают флажок и др.).

Для закрепления и уточнения знаний даю разного рода задания. Дети вырезают плоские фигуры из бумаги, лепят объемные из пластилина, преобразуют фигуры, получают из них другие.

Одной из составных частей методического сопровождения по разделу «Элементарные математические представления в детском саду» является игра «Танграм». Игра интересна детям, их увлекает результат, они включаются в активную практическую деятельность по подбору способа расположения фигур с целью создания силуэта.

Для увлечения детей предложенной мною игрой «Танграм» я использовала брошюру Тарабариной Т.И. «И учеба и игра: математика и свои знания по разделу «Математика в детском саду», полученные в педагогическом Колледже, студенткой которого я являюсь и сегодня.

Игра «Танграм» – одна из несложных математических игр.  Игра проста в изготовлении. Квадрат 10 на 10 см. из картона или пластика, одинаково окрашенный с обеих сторон, разрезаю на 7 частей, которые называются танами. В результате получаются 2 больших, 2 маленьких и 1 средний треугольники, квадрат.

Каждому ребенку дается конверт с 7 танами и лист картона, на котором они выкладывают картинку с образца. Используя все 7 танов, плотно присоединяя их один к другому, дети составляют очень много разных изображений по образцам и по собственному замыслу.

Играя, дети запоминают названия геометрических фигур, их свойства, отличительные признаки, свободно перемещают их с целью получения новой фигуры. У детей развивается умение анализировать простые изображения, выделять в них и окружающих предметах геометрические формы.

На первом этапе освоения игры «Танграм» провожу ряд упражнений, направленных на  развитие у детей пространственных представлений, элементов геометрического воображения, на выработку практических умений в составлении новых фигур путем присоединения одной из них к другой.

Для успешного воссоздания фигур необходимо умение зрительно анализировать форму плоскостей фигуры и ее частей. Дети часто допускают ошибки в  соединении фигур по сторонам и в пропорциональном соотношении.

Затем следуют упражнения в составлении фигур. В случае затруднений дети обращаются к образцу. Он изготовляется в виде таблицы на листе бумаги такой же по размеру фигуры-силуэта, как и наборы фигур, имеющихся у детей. Это облегчает на первых занятиях анализ и проверку воссозданного изображения с образцом.

                           

 Сначала игра «Танграм» проводилась как часть занятия по математике в течение 5-7 минут. Наблюдая за детьми во время игры подтвердили факт,  что игра детям понравилась. После этого был введен элемент соревнования, и тот, кто быстрее других выкладывал картинку, получал награду – фишку. Детей это еще больше заинтересовало. Они стали просить оставлять побольше времени для игры «Танграм».

Во время игры в «Танграм» у детей закрепляются навыки количественного счета.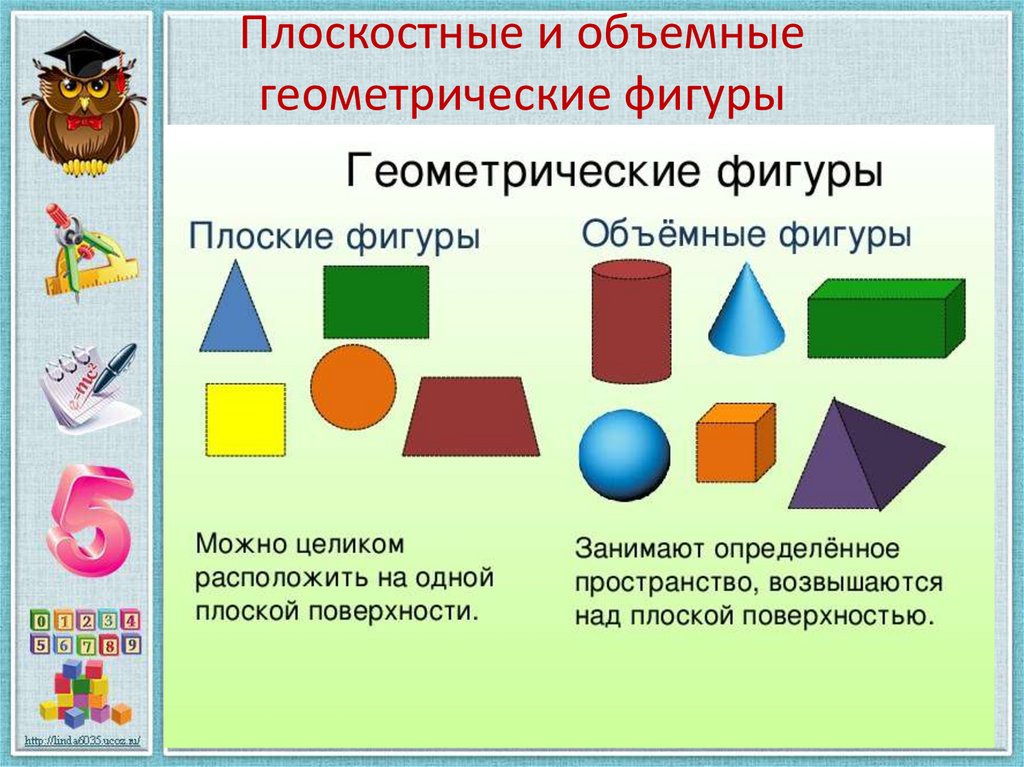 Они практически овладевают порядковым счетом. Так, если считать таны картинки «Ракета» сверху вниз, то квадрат стоит на пятом месте, маленькие треугольники стоят на первом и четвертом месте, средний треугольник – на третьем, большие треугольники – на шестом и седьмом месте. Считая таны сверху вниз, слева направо, дети упражняются в ориентировке на листе бумаги.

Составляя ту или иную картинку, дети сравнивают по величине треугольники, определяют место для маленьких, больших и средних треугольников в картинках игры «Танграм». Постоянно закрепляются знания детьми геометрических фигур в данной игре (треугольника, квадрата). Играя, переставляя маленькие картонные фигурки – таны, дети тренируют мелкие мышцы рук и пальцев.

Полезно в процессе практической деятельности вести с ребенком разговоры о способе составления фигуры. Дети называют вновь полученную фигуру, сосчитывают стороны, углы, показывают составляющие ее геометрические фигуры, отмечают количество, видоизменяют. Такая деятельность развивает сенсорные способности, воображение, приобщает к творчеству.

Последовательные этапы освоения игры «Танграм» в группе детей 5 лет.

Первый этап – ознакомление с набором фигур к игре, преобразование их с целью составления из 2-3 имеющихся новой.

Цель: упражнять детей в сравнении треугольников по размеру, составлением из них новых геометрических фигур: квадратов, четырехугольников, треугольников.

Материал: у детей наборы фигур к игре «Танграм», у воспитателя – фланелеграф и набор фигур к нему.

Ход игры: Я предлагаю детям рассмотреть фигуры, назвать их, сосчитать количество общее.

Предлагаю поиграть с геометрическими фигурами:

1. Отобрать все треугольники, сосчитать. Сравнить по размеру, накладывая один на другой.

Вопросы для анализа: Сколько больших, одинаковых по размеру треугольников? Сколько маленьких?  Сравните этот треугольник (среднего размера) с большим и маленьким. (Он больше самого маленького и меньше самого большого из имеющихся). Сколько всего треугольников и какого они размера? (Два больших,                                            

2 маленьких и 1 средний).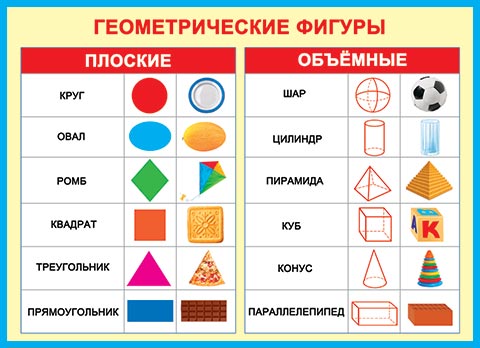

2. Взять 2 больших треугольника и составить из них последовательно: квадрат, треугольник, четырехугольник. Один из детей составляет фигуры на фланелеграфе. Я прошу назвать вновь полученную фигуру и сказать, из каких фигур она составлена.

3. Из 2 маленьких треугольников составить те же фигуры, располагая их по-разному в пространстве.

4. Из большого и среднего по размеру треугольников составить четырехугольник.

Вопросы для анализа: Какую фигуру составили? Как? (Присоединили к большому треугольнику средний и наоборот). Покажите стороны и углы четырехугольника каждой отдельной фигуры.

В итоге я обобщаю: «Из треугольников можно составлять новые различные фигуры – квадраты, четырехугольники, треугольники. Фигуры присоединяются одна к другой по сторонам». (Показываю на фланелеграфе).

Цель: упражнять детей в умении составлять новые геометрические фигуры из имеющихся по образцу и замыслу.

Материал: у детей – наборы к игре «Танграм». У воспитателя – фланелеграф и таблицы с изображениями на них геометрическими фигурами.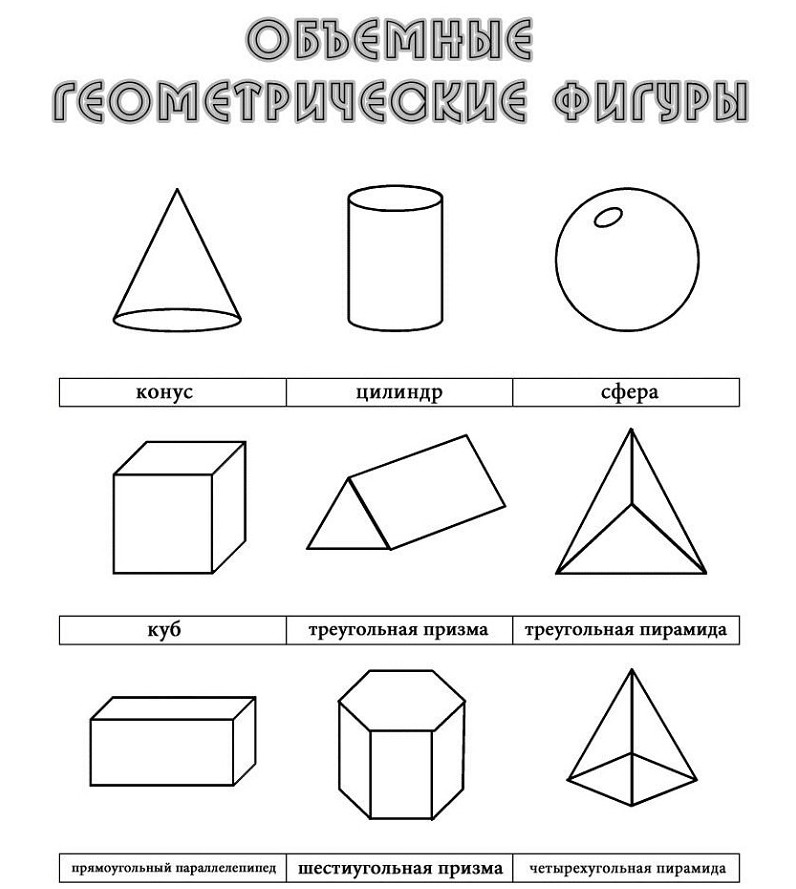

Ход игры: дети рассматривают фигуры, делят их по моему заданию на 2 группы: треугольники и четырехугольники. Я поясняю, что этот набор фигур к игре, называется «Танграм». Так ее назвали по имени ученого, придумавшего игру. Можем составить много интересных изображений.

1. Составить четырехугольник из большого и среднего треугольников.

2. Составить новую фигуру из квадрата и 2 маленьких треугольников. (Сначала – квадрат, затем – четырехугольник).

3. Составить новую фигуру из 2 больших  и среднего треугольника (пятиугольник и четырехугольник).

4. Я показываю таблицу и прошу детей составить такие же фигуры. Дети последовательно составляют фигуры, рассказывают, как они делали, называют их, а я составляю их на фланелеграфе.

Итак, на первом этапе освоения игры «Танграм» проводится ряд упражнений, направленных на развитие у детей пространственных представлений, элементов геометрического воображения, на выработку практических умений в составлении новых фигур путем присоединения одной из них к другой.

Второй этап освоения игры – составление фигур-силуэтов по расчлененным образцам.

Второй этап работы с детьми является наиболее важным для усвоения ими в дальнейшем более сложных способов составления фигур. Для успешного воссоздания фигур-силуэтов необходимо анализировать форму и ее частей. Кроме этого, при воссоздании фигуры (на плоскости очень важно умение мысленно представлять изменения в расположении фигур, которые  происходят в результате их трансфигурации. Наиболее простым видом анализа образца является зрительный,  но он невозможен без развитого умения  видеть пропорциональное соотношение частей фигуры.

Игры на составление фигур-силуэтов по расчлененным образцам должны быть использованы воспитателем с целью упражнения не только в расположении частей составляемой фигуры, но и в приобщении детей к зрительному и мысленному анализу образца.

Детям показываю расчлененный образец (силуэт зайца) и объясняю цель: создать такой же. Составляя силуэт зайца дети допускают ошибки в соединении фигур по сторонам в пропорциональном соотношении. Ошибки объясняются тем, что в этом возрасте недоступен самостоятельный анализ расположения частей. Дети затрудняются, могут вместо большого треугольника поместить средний по размеру и заметить ошибку  только после указания.

Таким образом, исходя из особенностей анализа и практических действий детей, можно определить содержание работы на втором этапе развертывания игры: это обучение детей анализу предъявляемого образца и словесному выражению способа соединения и пространственного расположения частей.

Составление фигуры-силуэта зайца.

Цель: учить детей анализировать способ расположения частей, составлять фигуру-силуэт, ориентируясь на образец.

Материал: у детей набор фигур к игре «Танграм», образец.

Ход работы: Я показываю детям образец фигуры-силуэта зайца и говорю:

– Посмотрите внимательно на зайца и расскажите, как он составлен. Из каких геометрических фигур сделаны туловище, голова, ноги зайца? Надо назвать фигуру и ее величину, т.к. треугольники, из которых составлен заяц (показываю), разных размеров.

Предлагаю нескольким детям выложить фигуры.

Стёпа: Голова зайца составлена из квадрата, ухо – их четырехугольника, туловище – из 2-х треугольников, а лапы тоже из треугольников.

Я спрашиваю: Правильно ли рассказал Стёпа? Если заметили ошибки, исправьте их.

Настя: Туловище надо составить из 2 больших треугольников, лапу (вот эту) – из среднего треугольника и маленького, а другую – из маленького треугольника.

Я говорю: Теперь смотрите, какую геометрическую фигуру образуют 2 больших треугольника. Покажите стороны, углы этой фигуры.

Маша: Это четырехугольник (показываю его контур, считаю углы, стороны).

Я спрашиваю: А какую фигуру образуют вместе средний и маленьких треугольник?

Алена: Прямоугольник.

Саша: Нет, это четырехугольник, вот здесь (показывает) не как у прямоугольника.

Я говорю: Вот мы и рассмотрели, как составлен заяц, из каких фигур составлены туловище, голова, лапы. А теперь возьмите свои наборы и составьте. Кто выполнит задание, проверьте, правильно ли сделал.

После того, как фигура готова, я прошу двоих детей рассказать, как они составляли ее, т.е. назвать расположение частей по порядку.

Маша Маз.: Я составила так: голову и ухо из квадрата и четырехугольника, туловище из 2 больших треугольников, лапы из среднего и маленького и 1 лапку из маленького треугольника.

Сережа: У меня ухо сделано из четырехугольника, голова из квадрата, туловище – из больших треугольников, лапы – из 2 треугольников.

Анализ образца проводится под моим руководством. В дальнейшем предлагаю детям самостоятельно рассмотреть фигуру и составить ее. Дети 5-ти лет составляют наиболее простые фигуры-силуэты: зайца, журавля, лисы.

В течение 5 занятий дети учатся анализировать расчлененный образец, создавать плоскостное изображение, правильно располагая в пространстве геометрические фигуры.

                       

Учебный проект “История названий геометрических фигур”

МКОУ «Торбеевская основная общеобразовательная школа имени А. И.Данилова»

Районная научно практическая конференция – 2013

математика

История названий

геометрических фигур

учебный проект

ученицы 5 класса

Соколовой Татьяны

Руководитель: Жарикова Л.С., учитель математики

Кто хочет ограничиться настоящим,

без знания прошлого, тот никогда его не поймет .

Вильгельм Лейбниц

Цель: узнать, как геометрические фигуры получили

свои названия.

Задачи:

• собрать информацию о названиях геометрических

фигур, используя словари и энциклопедии;

• найти стихотворения и загадки о геометрических

фигурах;

• сделать на математическом кружке сообщение;
• выпустить листки для стендов в кабинете

математики.

Как возникла геометрия

В глубокой древности, когда люди делали примитивные орудия: каменный нож, лук, стрелы,… появилась потребность в измерениях. Земледелие, ремёсла и торговля привели к необходимости вести сложные расчёты, определять площади земельных участков…

4000 лет назад

Египет

В жарком, засушливом Египте выращивать зерно можно было только в долине реки. Весной, после дождей Нил широко разливался и покрывал поля своим плодородным илом. Эта земля давала богатые урожаи и очень высоко ценилась, она была распределена между крестьянами.

Но вот в чём была незадача: поля друг от друга отделялись межами, а разлившийся Нил их смывал и часто менял русло. Приходилось после схода воды границы участков восстанавливать. А участки были и прямоугольные, и треугольные, и квадратные, и другой сложной формы .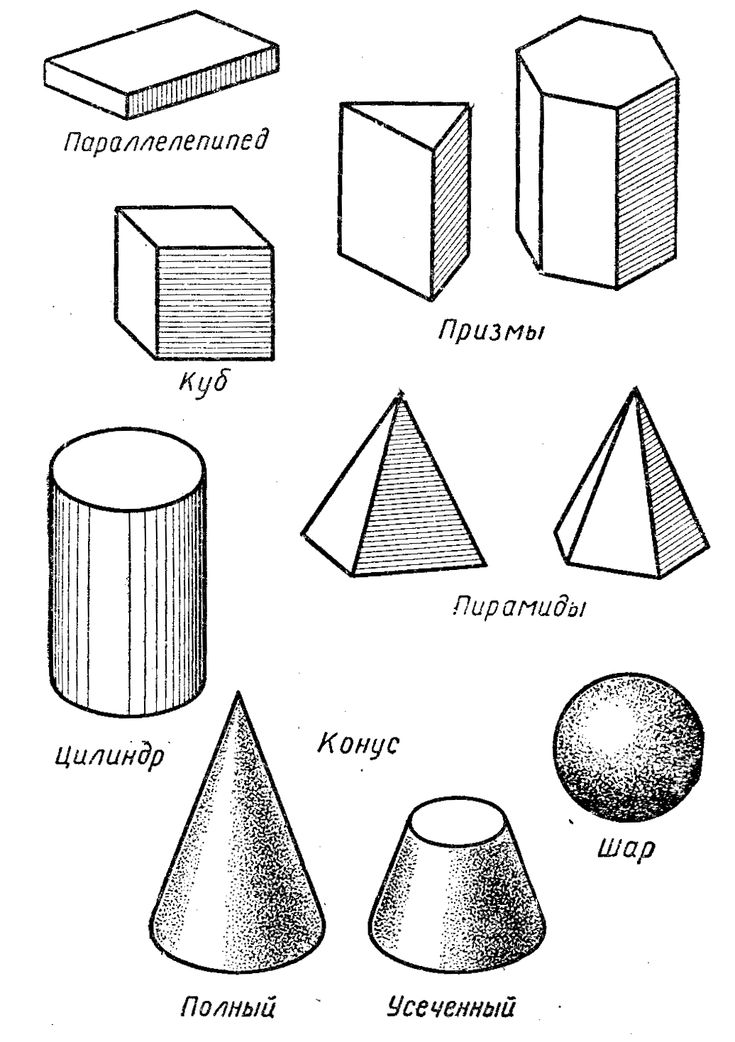

Восстанавливали границы участков особые чиновники – гарпедонапты (натягиватели верёвок), которые занимались межеванием земель .

Так из практических задач о межевании полей и возникла наука ГЕОМЕТРИЯ

ГЕО geо –

ГЕОМЕТРИЯ ( греч.) geometria

МЕТРИЯ

metreo

Земля

Измеряю

Древняя Греция

Древние греки были первооткрывателями геометрии. Это был удивительный и очень умный народ.

Греки были отличными моряками, во всех направлениях они бороздили Средиземное море. Везли посуду и украшения из Вавилона, бронзовое оружие из Египта, шкуры зверей и хлеб с берегов Черного моря.

И вместе с товарами они привозили в Грецию знания.

О названиях геометрических фигур

Различных геометрических фигур очень много. Прежде чем изучать их свойства, нужно было придумать им названия. До греков никто фигуры не изучал и никаких имён у них не было. Греки нашли гениальный выход: они стали называть фигуры словами, обозначавшими предметы похожей формы.

Эта дама очень упряма.

Она всегда идёт прямо

И от точки и до точки,

Несмотря на мох и кочки,

Остановки и отсрочки,

Как ни думай, ни крути –

По кратчайшему пути .

Линия. Прямая линия

linea (лат.) – льняная нить

Биссектриса

Биссектриса – это крыса, которая

бегает по углам и делит угол пополам.

Биссектриса – это луч, который выходит из вершины угла и делит угол пополам.

«bis» (лат.) – дважды

«sektio» (лат.)- рассчение

рассекающая

надвое

Перпендикуляр

Но если в раздумье застынет школяр,

Примером пусть служит перпендикуляр.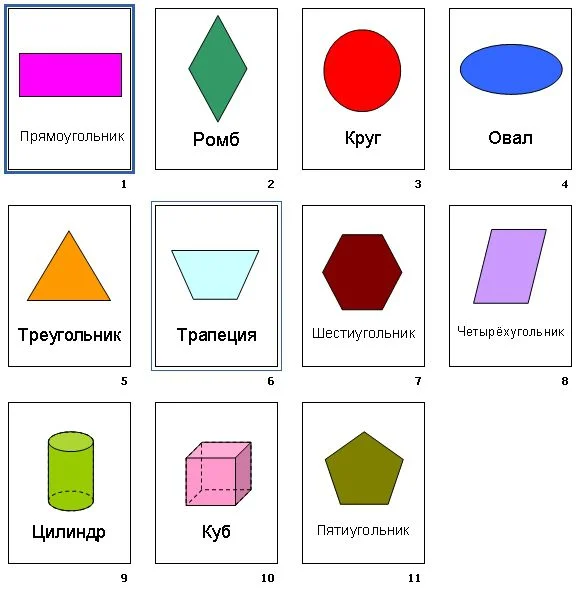

Ведь к цели идёт он не как-нибудь,

А выбирает кратчайший путь.

«pendula» (лат.) – маятник, отвес

Когда-то перпендикуляром назвали просто вертикальное направление, направление отвеса. Оно образует прямой угол с земной поверхностью.

Радиус

«radius» (греч. лат.) – спица в колесе

Обод колеса соединялся с осью планками, которые греки называли радиусами. Поэтому когда древние геометры начертили окружность и соединили её центр с точкой на окружности, то они увидели рисунок колеса и стали проведенный отрезок называть спицей, т.е. радиусом.

Параллелограмм

Ты не знаешь, сколько грамм

Весит параллелограмм?

Не могу понять, в чём дело?

Сколько это «параллело»?

– Где, дружок, твоя культура?

Параллелограмм – фигура!

Знает каждый школьник в мире

У него сторон – четыре.

Их рисуют не бесцельно,

А попарно параллельно.

«parallelos» (греч.)- идущие рядом

Ромб

«rhombos» (греч. лат.) – бубен

Мы привыкли к тому, что бубен имеет круглую форму, но раньше, во времена древних греков бубны имели четырёхугольную форму – форму ромба .

Трапеция

«trapezion» (греч. лат.) -столик

Цилиндр

«kylindros» (греч.) – каталка

Название цилиндру, наверное, дали прачки или кухарки. Потому что для стирки и прокатки белья женщины применяли скалку, которая по-гречески до сих пор называется «каландер» .

Конус

«conos» (греч.) – сосновая шишка

• Геометрических фигур очень много. Те фигуры, которые известны людям с древних времён, носят греческие (или латинские имена), потому что именно греки создали геометрию и дали фигурам имена.
• Названия геометрических фигур первоначально были названиями предметов, имеющих форму близкую к форме фигур. Это показывает, что геометрия возникла для решения практических задач и тесно связана с человеческим трудом.
• Названия некоторых геометрических фигур отражают их свойства.

Выводы:

… я поняла, что названия геометрических фигур совсем не странные, а очень даже разумные и понятные. Просто почти все они пришли к нам из греческого или латинского языков.

Источники

• Словарь иностранных слов. М. «Наука» 1954.

• http :// ru . wikipedia .

• И.Ф.Шарыгин Уроки дедушки Гаврилы или Развивающие каникулы. М. «Дрофа», 2003

Как называть простые геометрические фигуры, такие как линии и углы — Криста Кинг Математика

Называние простых геометрических фигур

В этом уроке мы рассмотрим основные геометрические фигуры, такие как точки, линии, отрезки, лучи и углы, и поговорим о том, как их называть.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Точки

Точка — это представление местоположения в пространстве. Его символ — одна буква, и он представлен в виде точки. Точка ???А??? может выглядеть так:

Линии

Линия простирается до бесконечности в двух противоположных направлениях, поэтому ее можно рассматривать как прямой путь, соединяющий две точки (и проходящий мимо них). Символом линии являются две буквы, обозначающие две точки на линии, с линией с двойной стрелкой над ними. Рисунок линии должен быть прямым и иметь стрелки на обоих концах. Линия ???АВ??? (также называемая линией ???BA???), может выглядеть так:

Строка также может быть названа строчной буквой. Строка ???p??? может выглядеть так:

Отрезки

Отрезок — это часть линии, соединяющая две точки.

Точки в конце отрезка линии называются конечными точками. Вы называете сегмент линии, используя его конечные точки.

Символ сегмента линии представляет собой буквенное обозначение каждой из конечных точек с линией поверху. На чертеже отрезка есть две точки на концах.

Лучи

Другая часть линии называется лучом. Луч — это часть прямой, которая имеет одну конечную точку и одну сторону, уходящую в бесконечность. Вы называете луч с конечной точкой и любой другой точкой на луче.

Символ луча должен включать конечную точку, которая обычно пишется первой, и еще одну точку луча. Две точки будут иметь одностороннюю стрелку сверху, которая указывает на букву точки на «линейной» части луча. Рэй ???\vec{AB}??? может выглядеть так:

Иногда вы также можете назвать луч строчной буквой. Рэй ???l??? может выглядеть так:

Углы

Когда два луча имеют общий конец, они образуют угол.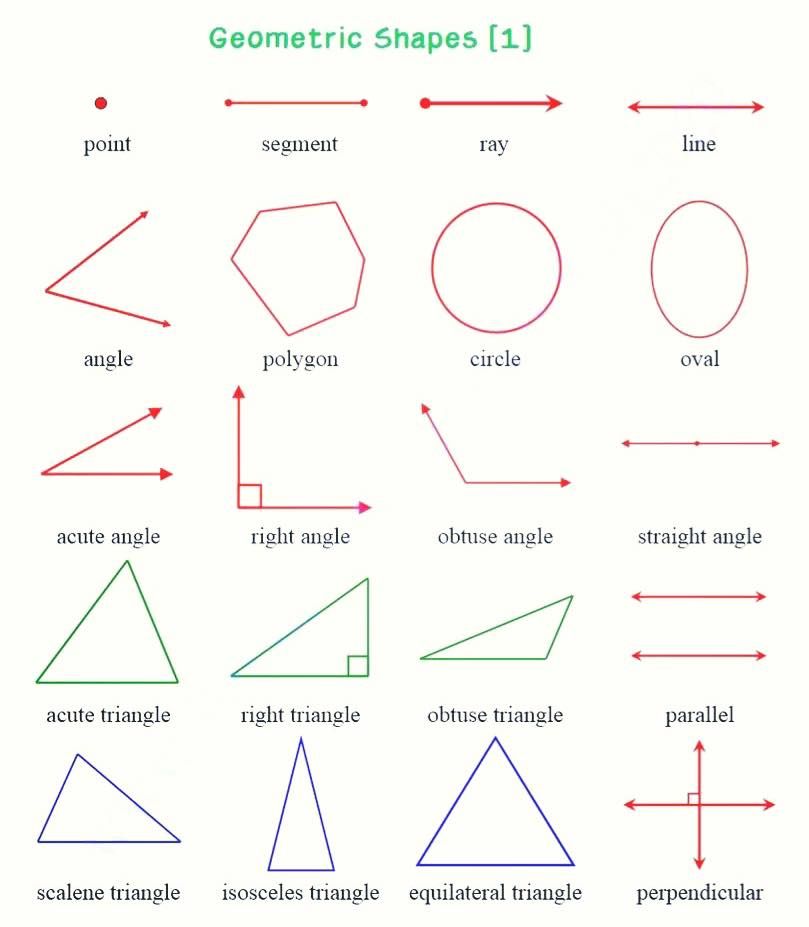 Общий конец угла называется вершиной. Вот способы обозначения углов:

1. Написание формы угла, а затем буквы, соответствующей вершине.

2. Написание формы угла, а затем трех букв: точка от первого луча, точка от вершины и точка от последнего луча.

3. Запись формы угла, точка от последнего луча, точка от конечной точки, точка от первого луча.

4. Вы также можете назвать угол строчной буквой или цифрой. Если строчная буква или цифра написаны внутри угла, то вы пишете символ угла и любое имя внутри угла.

Если вы выберете метод 2 или 3, обязательно поместите вершину в середине имени! Вот угол, названный четырьмя разными способами: Угол ???\угол B??? или ???\угол ABE??? или ???\угол EBA??? или ???\угол 1???.

Как писать названия точек, отрезков, прямых, лучей и углов

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.

🙂

Учить больше

Какая часть диаграммы представлена ​​буквой?

Пример

Что означает буква ???f??? изобразить на схеме?

Буква ???f??? представляет собой линию. Эту же линию можно также назвать линией ???AB??? или строка ???BA???.

Давайте посмотрим на углы именования.

Пример

Какие три других названия для ???\угол 4???? Являются ли какие-либо имена плохим выбором? Почему или почему нет?

???Е??? является вершиной ???\угла 4???, поэтому его можно назвать ???\угол E???, ???\угол CEB??? или ???\угол BEC???. В этом случае ???\угол E??? было бы плохим выбором для имени, потому что углы ???1???, ???2??? и ???3??? также имеют общую вершину ???E???.

Давайте рассмотрим пример, в котором мы идентифицируем геометрические фигуры по их письменным названиям.

Когда два луча имеют общий конец, они образуют угол. Общий конец угла называется вершиной.

Пример

Сопоставьте символ слева с названием рисунка справа.

Запоминание того, что обозначает каждый символ, может значительно помочь вам решать и интерпретировать вопросы по геометрии. Мы перестроим столбец справа, чтобы каждое описание соответствовало правильному символу.

Получить доступ к полному курсу геометрии

Начать

Учимся математикеКриста Кинг 26 ноября 2020 математика, учимся онлайн, онлайн курс, онлайн математика, геометрия, геометрические фигуры, простые геометрические фигуры, линии, углы, лучи, точки, отрезки, называя углы, называя линии, разные способы именные углы

0 лайков

20011 – Геометрические фигуры и нахождение площадей

Введение: соединение вашего обучения

Большинство студентов, изучающих математику в старших классах и колледжах, задают вопрос: «Когда я когда-нибудь буду использовать это понятие в реальной жизни?» На самом деле геометрия имеет множество практических применений как в повседневном, так и в компьютерном мире.

Геометрия может быть интересна, когда вы думаете о том, как она связана с дизайном компьютерных приложений, включая реальные и виртуальные объекты, или если вы пытаетесь определить информацию и свойства геопространственного местоположения или области. В этом модуле вы обсудите области геометрических фигур и объектов. К концу модуля вы должны знать значение и обозначения площади и формулы площади для некоторых распространенных геометрических фигур, а также уметь вычислять площади некоторых распространенных геометрических фигур.

Сосредоточение вашего обучения

Цели урока

К концу этого урока вы должны уметь:

1. Вычислять площади обычных геометрических фигур.

Представление

Площадь

Площадь поверхности – это количество квадратных единиц длины, содержащихся на поверхности.

Вы начнете с изучения формул вычисления площади различных геометрических фигур. У каждой фигуры есть определенная формула, по которой нужно вычислить площадь, то есть количество квадратных единиц длины, содержащихся на поверхности.

Например, 3 кв. дюйма означает, что 3 квадрата со стороной 1 дюйм можно точно разместить на поверхности. (Возможно, квадраты придется вырезать и переставить, чтобы они соответствовали форме поверхности.)

Выберите следующую ссылку, чтобы увидеть представление площади на листе бумаги. Вы сможете увидеть, как измеряется площадь, разделив бумагу на маленькие квадратные единицы.

Площадь

Теперь, когда вы лучше понимаете, что такое площадь, посмотрите на квадрат. У него четыре равные стороны и четыре равных угла: Каждый угол равен 90°. Чтобы определить площадь квадрата, используйте следующую формулу.

Площадь квадрата

Площадь = сторона ⋅ сторона = сторона ²

Пример

Вычислите площадь квадрата со стороной 6 дюймов.

Площадь = сторона ⋅ сторона = сторона ²

Площадь = 6 дюймов ⋅ 6 дюймов = 36 кв. ² .

6 ⋅ 6 или 6 ² = 36 кв. дюймов

Пример

Вычислите площадь квадрата со стороной 9 см.

Площадь = сторона ⋅ сторона = сторона ²

Площадь = 9 см ⋅ 9 см = 81 кв. см

Поскольку сторона равна 9 см, вам нужно умножить 9 на 9, что также означает 9 ² .

9 ⋅ 9 или 9 ² = 81 кв. см

Теперь вы изучите формулы площади, чтобы ознакомиться с тем, как найти площадь следующих геометрических фигур.

 

Формулы площади

Площадь этих геометрических фигур можно определить с помощью следующих формул.

Заявление

	Рисунок	Формула площади
	Треугольник	А = б ⋅ ч	Площадь треугольника равна половине произведения основания на высота.
	Прямоугольник	А = л ⋅ ш	Площадь прямоугольника равна произведению длины на ширина.
	Параллелограмм	А = б ⋅ ч	Площадь параллелограмма равна произведению основания на высоту.
	Трапеция	А = ⋅( б 1 + б 2 )⋅ ч	Площадь трапеции равна половине суммы два основания умножить на высоту.
	Круг	А = π r 2	Площадь круга в π раз больше квадрата радиус.
На основе диаграмме выше, геометрические фигуры имеют разные формулы для площади в зависимости от их формы. Взгляните на некоторые примеры.

 

Примеры: Нахождение площадей обычных геометрических фигур

Найдите площадь треугольника.

A = ⋅ b ⋅ h = ⋅ 20 ⋅ 6 кв. футов = 10 ⋅ 6 кв. футов = 60 кв. футов = 60 футов ²

Площадь этого треугольника составляет 60 квадратных футов, что часто записывается как 60 футов ² .

 

Найдите площадь прямоугольника.

Прежде чем вы сможете вычислить площадь, вам нужно, чтобы длины сторон были в одних и тех же единицах.

1) Сначала переведите 4 фута 2 дюйма в дюймы.

Преобразуйте 4 дюйма в футы, умножив 4 на 12; в 1 футе 12 дюймов. В 4 футах 48 дюймов. Таким образом, 4 фута 2 дюйма составляют 48 дюймов + 2 дюйма, что составляет 50 дюймов

2) Формула площади (прямоугольник): A = L ∙ W

A = L ⋅ W

A W

6. Вт 9000

6. Вт 9000 9000 37 A W 9000

37 A W 9000

.. . A = 400 кв. дюймов

Ответ: Площадь этого прямоугольника равна 400 кв. дюймов

Найдите площадь параллелограмма.

A = b ⋅ h = 10,3 см ⋅ 6,2 см = 63,86 кв. см

Площадь этого параллелограмма равна 63,86 кв.см.

Найдите площадь трапеции.

a = ⋅ ( B ₁ + B ₂ ) ⋅ H

A = ⋅ (14.5 мс + 20 ММ + 20,4 млн. М). ) ⋅ (4,1 мм) = ⋅ (143,09 кв. мм)

A = 71,545 кв. мм

Площадь этой трапеции равна 71,545 кв. мм.

Найдите приблизительную площадь круга.

A = πt R ² ≈ (3,14) ⋅ (16,8 фута) ² ≈ (3,14). Площадь этого круга составляет приблизительно 886,23 кв. фута.

Посетите следующий веб-сайт для получения дополнительной информации о том, как найти площадь обычных геометрических фигур.

Область геометрических фигур: плоские формы

Теперь, когда вы ознакомились с формулами и примерами, пришло время посмотреть несколько видеороликов Академии Хана. Эти видеоролики предоставят вам дополнительные пояснения и демонстрации вычисления площади, чтобы помочь вам глубже понять концепции.

Математический видео-инструментарий: Основы области Площадь прямоугольников и треугольников Площадь круга

Упражнение: нахождение площади

Теперь у вас есть шанс решить некоторые проблемы. Вам нужно будет взять лист бумаги и карандаш, чтобы выполнить практическое задание. Вы можете использовать калькулятор, если хотите. Внимательно изучите каждую из этих проблем; вы увидите похожие проблемы на проверке знаний урока. Выберите следующую ссылку, чтобы завершить практическое задание. Решение практических задач После завершения практического задания проверьте, насколько хорошо вы справились, выбрав следующую ссылку: Решения: Решение проблем для местной практики

Подведение итогов

На этом уроке вы познакомились с различными геометрическими фигурами и формулами для вычисления их площадей. Эта информация может быть использована для расчета площадей экранов телевизоров, мониторов компьютеров, объективов фотоаппаратов и многого другого.

Большинство курсов, которые вы будете изучать в колледже или техникуме, не всегда могут включать конкретные примеры, применимые к вашей программе обучения. Вместо этого они, как правило, дают широкий обзор ключевых понятий, оставляя вас желать большего. Как и в предыдущих уроках, вам предлагается исследовать, как каждая концепция связана с выбранной вами областью обучения. Этот процесс исследования является бесценной частью вашего образования; не упустите эту возможность продвинуть свои знания.

Оценка вашего обучения

Теперь, когда вы внимательно прочитали урок и попытались решить практические задачи, пришло время для проверки знаний. Обратите внимание, что этот является оцениваемой частью этого урока, поэтому убедитесь, что вы подготовились перед началом.

1. Заполните геометрические фигуры: нахождение площади.

 

Ресурс:

«Измерение и геометрия: площадь и объем геометрических фигур и объектов», Ellis, W. & Burzynski, D. © 2010, получено с http://cnx.org/content/m35023/1.2/. под лицензией Creative Commons Attribution http://creativecommons.org/licenses/by/3.0/. Это адаптация урока под названием «Геометрические фигуры и решение для площади», подготовленного Национальным консорциумом по информационной безопасности и геопространственным технологиям (NISGTC) под лицензией Creative Commons Attribution 3. 0 Unported License. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by/3.0

 

Дополнительные атрибуты

Геометрические фигуры: типы, свойства и примеры

• Автор Шротасвини Мохапатра
• Последнее изменение 18-10-2022

Геометрические фигуры: В программе по математике геометрические фигуры играют жизненно важную роль. Учащиеся должны быть особенно осторожны и решительно готовить темы и концепции, потому что эти темы важны для будущих экзаменов. Студенты должны иметь лучшее понимание для лучшего плана подготовки и отлично сдать экзамен.

Учащиеся находят геометрические формы непосильными и сложными. По этой причине в этой статье есть ряд понятий, таких как геометрические узоры, которые обсуждаются для учащихся. В статье представлены подробные объяснения форм треугольников и геометрических фигур, которые помогут учащимся успешно сдать экзамен, а также хорошо подготовиться к будущим конкурсным экзаменам. Чтобы узнать больше, продолжайте читать статью.

Геометрические формы/узоры Определение

Определение геометрических фигур относится к двумерным формам, которые являются формами и замкнутыми фигурами, такими как круги, квадраты, прямоугольники, ромбы и т. д. В объемной геометрии трехмерными формами являются куб, прямоугольный параллелепипед, конус, сфера и цилиндр. . Все эти формы мы наблюдаем повсюду в различных формах.

Изучение концепций 12-го экзамена CBSE

Давайте посмотрим на некоторые использованные нами объекты из реальной жизни, которые напоминают некоторые основные формы.

Геометрические фигуры — это фигуры, представляющие формы различных объектов. Некоторые фигуры двумерные \(2\,{\rm{D}}\), а некоторые – трехмерные \(3\,{\rm{D}}\) формы.\(2\,{\rm {D}}\) фигуры лежат только на оси \(x- \) и \(y – \) оси, а фигуры \(3\,{\rm{D}}\) лежат на \(x, y – \) и \(z – \)оси. Ось \(z – \) представляет высоту объекта. В геометрии определены различные формы, такие как круг, квадрат, прямоугольник, треугольник и т. д.

Чтобы создать любую из этих фигур, начните с линии, сегмента линии или кривой. В зависимости от количества линий и их расположения мы получаем различные типы фигур и фигур, такие как треугольник (фигура, в которой соединены сегменты из трех линий), пятиугольник (сегменты из пяти линий) и т. д.

Формы в геометрии могут быть открытыми или закрытыми.

Изучите концепцию базовой геометрии

Открытая форма: Фигура, которая начинается и заканчивается в разных точках, образуя границу с помощью отрезков линии или кривых, называется открытой формой.

Замкнутая форма: Фигура, которая начинается и заканчивается в одной и той же точке, образуя границу отрезками или кривыми, называется замкнутой формой .

Загрузить математические формулы для классов от \(6\) до \(12:\)

Изучение концепций экзамена на Embibe

Список геометрических фигур

или единообразие. Правильная форма симметрична, например квадрат, круг и т. д. Неправильные формы асимметричны. Их также называют формами произвольной формы или органическими формами. Например, форма дерева неправильная или органичная. Список некоторых геометрических форм \(2\,{\rm{D}}\) и \(3\,{\rm{D}}\) фигур приведен ниже:

\(2\,{\rm{D}}\) Shapes:

1. Triangle
2. Circle
3. Semi-circle
4. Square
5. Rectangle
6. Parallelogram
7. Rhombus
8. Trapezium
9. Воздушный змей
10. Многоугольники (пятиугольник, шестиугольник, восьмиугольник, нонагон, десятиугольник и т. д.)

\(3\,{\rm{D}}\) Формы :

9 2 Сфера
1. 2 Сфера
2. Прямоугольный
3. Конический
9\circ }\) называется квадратом.

Прямоугольник : Тип четырехугольника, в котором противоположные стороны имеют одинаковую длину, а каждый угол прямой, называется прямоугольником.

Параллелограмм : Четырехугольник называется параллелограммом, если обе пары его противоположных сторон параллельны.

Ромб: Тип четырехугольника, у которого все стороны равны, называется ромбом.

Трапеция: Тип четырехугольника, имеющего ровно одну пару параллельных сторон, называется трапецией.

Воздушный змей: Четырехугольник называется воздушным змеем, если у него есть две пары равных смежных сторон, но неравные противоположные стороны.

Многоугольники (пятиугольник, шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник и т. д.): Многоугольники состоят из сегментов прямых и не содержат кривых. Это закрытые конструкции, основанные на разной длине сторон и разных углах.

Практические экзаменационные вопросы

Трехмерные формы

Сфера: Сфера представляет собой \(3\,{\rm{D}}\) круглую форму, радиус которой расширен до трех измерений.
Пример: Глобус

Куб: Куб — это фигура \(3\,{\rm{D}}\), которая имеет \(6\) граней, \(8\) вершин и \(12\) края. Все грани куба квадратные.
Пример: Кубик Рубика

Прямоугольник: Прямоугольник — это трехмерная объемная фигура, имеющая \(6\) граней,\(8\) вершин и  \(12\) ребер, но все грани прямоугольного параллелепипеда в прямоугольной форме.
Пример: Коробка для завтрака

Конус: Конус представляет собой твердое тело, имеющее круглое основание и плавно сужающееся от поверхности к вершине в точке, называемой вершиной или вершиной.
Пример: кепка на день рождения

Цилиндр: Цилиндр представляет собой \(3\,{\rm{D}}\) твердое тело, имеющее два параллельных круглых основания, соединенных криволинейной поверхностью. У него нет вершины.
Пример: Газовый баллон

Примеры геометрических фигур

Здесь мы обсудили некоторые геометрические фигуры:

Плоскость Примеры геометрических фигур

Круг : Колесо является примером круга в реальной жизни.

Квадрат: Карамбольная доска — пример квадрата в реальной жизни.

Треугольник: Один кусок пиццы является примером треугольника в реальной жизни.

Прямоугольник: Классная доска — пример прямоугольника в реальной жизни.

Овал: Яйцо — пример овала в реальной жизни.

Твердые геометрические фигуры Пример

Сфера: Футбол, сферические шарики, глобусы и т. д. являются примерами сферы.

Куб: Кубик льда, кубики сахара, кости и т. д. являются примерами кубика.

Прямоугольный параллелепипед: Спичечный коробок, книги, коробки для обеда и т. д. являются примерами прямоугольного параллелепипеда.

Вафельный рожок: Вафельный рожок для мороженого, праздничные шапки и т. д. являются примерами рожков.

Баллон: Банка, труба, газовый баллон и т. д. являются примерами баллона.

Важные замечания по геометрическим фигурам

1. Точка не имеет размеров, а линия представляет собой одномерную форму. Оба являются основой геометрии. Когда две прямые пересекаются в одной точке, они образуют угол, где говорят, что точка является вершиной, а прямые — плечами.
2. Двухмерные и трехмерные формы формируются с помощью точек, линий и углов.
3. Двумерные фигуры, имеющие \(4\) стороны, такие как прямоугольники, квадраты, параллелограммы, воздушные змеи, трапеции и т. д., называются четырехугольниками.
4. Четырехугольники представляют собой четырехсторонние замкнутые фигуры, состоящие из прямых линий.
5. Многоугольники представляют собой замкнутые формы, состоящие из прямых линий. Они названы в соответствии с количеством сторон, которые у них есть.
6. Трехмерная форма имеет длину, ширину и высоту.

Геометрические узоры

Геометрические узоры — это набор фигур, повторяющихся или изменяемых для создания определенного дизайна.
Примеры геометрических узоров приведены ниже,

Давайте посмотрим на узор, используя некоторые основные плоские формы. Некоторыми основными формами плоскостей являются круги, квадраты, треугольники, прямоугольники и т. д.

Попытка 12-го экзамена CBSE Пробные тесты

Решенные примеры

Ниже приведены некоторые решенные примеры геометрических фигур для вашего понимания:

Q.1.Цифра, приведенная ниже, является открытой или закрытой фигурой?

А.1. Фигура, которая начинается и заканчивается в разных точках, образуя границу отрезками или кривыми, называется незамкнутой фигурой. Так как данная фигура имеет как начальную, так и конечную точки, различна и не является непрерывной, то это открытая фигура.

Q.2. Фигура, приведенная ниже, является открытой или закрытой фигурой?

А.2. Фигура, которая начинается и заканчивается в одной и той же точке, образуя границу отрезками или кривыми, называется замкнутой фигурой. Поскольку у данной фигуры начальная и конечная точки одинаковы, это замкнутая фигура.

Q.3. Приведите три реальных примера прямоугольника.
А.3. Прямоугольник — плоская геометрическая замкнутая фигура, имеющая всего четыре стороны (две противоположные стороны равны и параллельны), четыре угла.
Реальными примерами прямоугольника являются банкноты, сотовые телефоны, обложки книг и т. д.

Попытка пробных тестов

Q.4. Напишите два примера конуса.
А.4. Конус представляет собой объемную \(3\,{\rm{D}}\) форму. Два примера конуса – это кепки на день рождения и конусное мороженое.

Q.5.Сосчитайте и запишите количество кругов, овалов, треугольников, прямоугольников и квадратов на рисунке ниже.

А.5.
Количество кругов равно \(7\).
Количество овалов равно \(6\).
Количество треугольников равно \(8\).
Количество прямоугольников равно \(4\).
Количество квадратов равно \(3\).

Сводка

Геометрические формы повсюду. Почти все состоит из двухмерных \(2\,{\rm{D}}\) и трехмерных \(3\,{\rm{D}}\) геометрических фигур. В этой статье мы рассмотрели определение геометрических фигур, геометрические фигуры, используемые в реальных объектах, типы геометрических фигур и их свойства, открытые формы, закрытые формы, список геометрических фигур, некоторые примечания о геометрических фигурах, примеры геометрических фигур, узор геометрических фигур и т. д.

Это поможет учащимся понять геометрические узоры и поможет понять геометрические фигуры, их свойства и т. д.

Изучите важные математические понятия

Часто задаваемые вопросы о геометрических фигурах

Ниже перечислены некоторые часто задаваемые вопросы о геометрических фигурах:

Q1: Какие основные формы \(10\) ?
Ответ: \(10\) основных форм: круг, овал, треугольник, ромб, квадрат, прямоугольник, трапеция, пятиугольник, шестиугольник и восьмиугольник.

Q2: Какие \(3\) примеры геометрической формы?
Ответ: Тремя примерами геометрической формы являются круг, треугольник и квадрат

Q3: Какие \(4\) основные формы?
Ответ: \(4\) основных геометрических плоских форм – это круг, треугольник, прямоугольник и квадрат.

Q4: Какая геометрическая форма является наиболее распространенной?
Ответ: Круг — самая распространенная геометрическая фигура.

Q5: Определить уравнение Эйлера на примере?
Ответ: Уравнение Эйлера для любого многогранника имеет вид \(F + V – E = 2\), где \(F\) – количество граней, \(V\) – количество вершин, а \( E\) количество ребер.
Пример:
Теперь \(F + V – E = 2\)
\(F = 2 – V + E\)
\(F = 2 – 6 + 12\)
\(F = 8\)
Следовательно, число граней равно \(8.