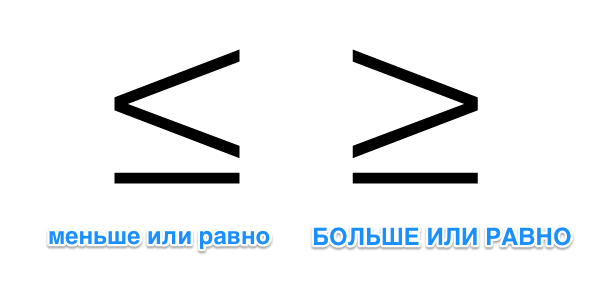
Математика знак меньше и больше: Больше, меньше, равно — урок. Математика, 1 класс.

Равенство и неравенство. Знаки: больше, меньше, равно. Что значат в математике

Автор Historian Просмотров 83 Опубликовано 22.07.2022

В каждое «блюдо» можно положить что-то вроде еды. Например, вы можете сделать пластилин, или соль, или солевой раствор и договориться с ребенком, что горох означает крокодила. Символов в этой игре достаточно. Это можно сделать с помощью небольших карточек. Символы «>» и «

Содержание

1. Знаки больше меньше в какую сторону. Знаки больше и меньше на клавиатуре
2. Как и в какую сторону пишется знак больше
3. Как и в какую сторону пишется знак меньше
4. Математические знаки
5. Равенство и неравенство
6. Типы неравенств
7. Основные математические понятия и обозначения
8. Множества чисел и их обозначения
9. Основные операции над множествами
10. Логические символы
11. Специальные математические символы
12. Таблица математических символов
13. Как легко понять знаки Σ и П с помощью программирования
14. Знак Σ — сумма
15. Произведение П
16. Переменные

Знаки больше меньше в какую сторону.

Знаки больше и меньше на клавиатуре

Уже с первого занятия ребенка отличают от колосьев, которые визуально выглядят как 10 ягод с 3 и более. Чтобы ввести новые символы, посмотрите на символы «больше», «меньше» и «равно» на картинке.

Самый (>) символ — это когда острый нос галочки виден справа. Если первое число больше второго, следует использовать его.

Символ равенства (=) используется, когда два небольших отрезка пишутся горизонтально и одновременно. Используется при сравнении двух одинаковых чисел.

Чтобы помочь детям запомнить похожие знаки, можно использовать игровые методы. Для этого необходимо сравнить числа и указать их порядок. Затем поставьте точку рядом с наименьшим числом, сделав две точки больше. Соедините точки и найдите правильный знак. Это просто:.

Ниже приведена схема расположения математических знаков с цветовой кодировкой. Вы можете использовать их непосредственно с экрана при обучении или при печати на цветном принтере.

Как и в какую сторону пишется знак больше

Символ «больше» отмечен знаком «. ». Символ обозначается стрелкой с острым углом, указывающей правильное направление. Немного теории: решающим фактором является левая сторона символа. Если стрелка начинается с двух линий, сходящихся в одной точке с правой стороны, то это символ ‘>’.

В общем, логика понимания довольно проста — с какой стороны от точки (большей или меньшей) смотреть влево по направлению написания. Соответственно, самый большой знак слева смотрит в более широкую сторону, т.е. самый большой знак.

Это пример использования максимальных баллов.

• 50>10 – число 50 больше числа 10;
• посещаемость студента в этом семестре составила >90% занятий.

Как и в какую сторону пишется знак меньше

Вероятно, нет необходимости повторно объяснять, как пишется самый маленький символ. Это полностью пропорционально максимальному символу. Если знак находится на узкой стороне (наименьшей) и обращен влево, то денежный знак меньше.

Пример использования меньшего количества:.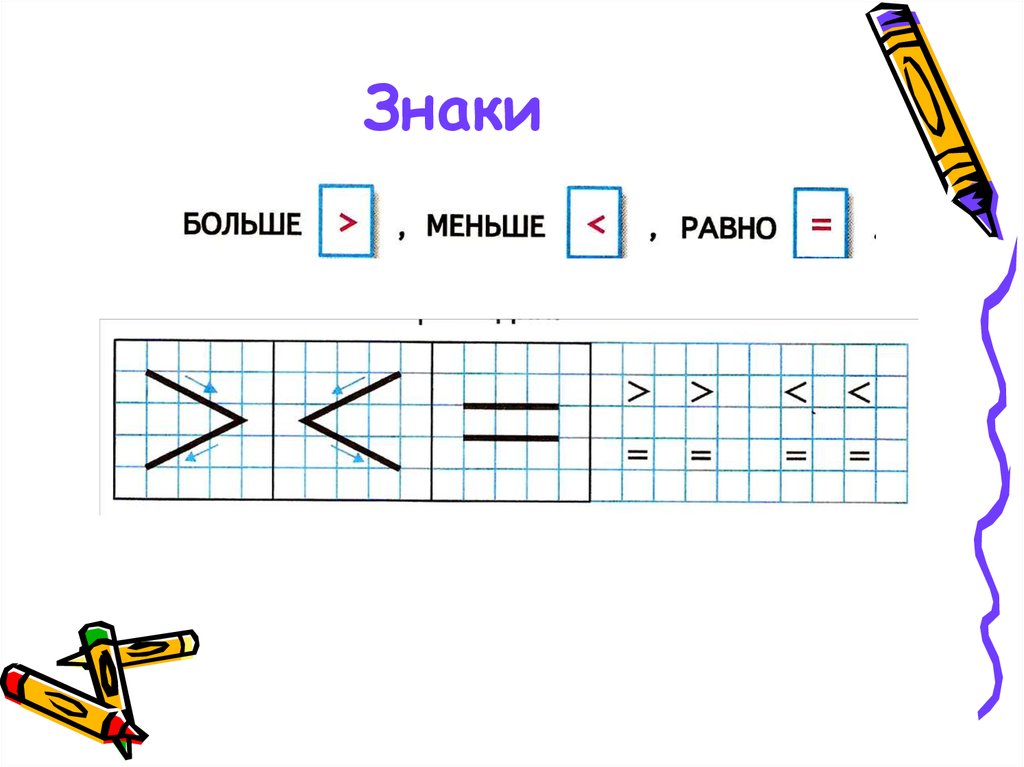

100 = » часто в принципе нормально, но могло бы быть красивее и правильнее.

На самом деле, существуют специальные символы, которые можно вставить в клавиатуру, чтобы сделать эти точки. Согласен, ‘≤’ и ‘≥’ выглядят гораздо лучше.

Как видите, все настолько упорядочено и просто, что нет необходимости задавать вопросы, кроме того, как создать syn или в будущем.

Человеческий мозг легко усваивает знаки, буквы и сокращения – математические обозначения запоминаются сами при изучении предмета. Понимание смысла каждого конкретного действия создает настолько прочные ассоциативные связи, что знаки, обозначающие термины, а зачастую и формулы, связанные с ними, остаются в памяти на многие годы и даже десятилетия.

Математические знаки

Уже с первого занятия ребенка отличают от колосьев, которые визуально выглядят как 10 ягод с 3 и более. Чтобы ввести новые символы, посмотрите на символы «больше», «меньше» и «равно» на картинке.

Самый (>) символ — это когда острый нос галочки виден справа. Если первое число больше второго, следует использовать его.

Символ равенства (=) используется, когда два небольших отрезка пишутся горизонтально и одновременно. Используется при сравнении двух одинаковых чисел.

Чтобы помочь детям запомнить похожие знаки, можно использовать игровые методы. Для этого необходимо сравнить числа и указать их порядок. Затем поставьте точку рядом с наименьшим числом, сделав две точки больше. Соедините точки и найдите правильный знак. Очень легко:.

Равенство и неравенство

Математическое равенство — это когда одно число похоже на другое и между ними можно поставить символ.

Например, посмотрите на изображение геометрической фигуры. Числа справа и слева одинаковы, поэтому можно поставить символ «равно».

Неравенство — это алгебраическое выражение, содержащее знаки ≠, ≤, ≥.

Пример неравенства показан на рисунке ниже. На левой стороне изображены три числа, а на правой — четыре. Мы знаем, что три не равно четырем. В противном случае мы знаем, что три меньше четырех.

Уроки в школе часто проходят перед книгами, тетрадями и столами. Однако дома вы можете использовать свой компьютер для занятий в Интернете. Как найти знаки клавиатуры? Ответ находится на картинке:.

Типы неравенств

Строгое неравенство — используйте только символы больше (>) или меньше (>)

Нестрогое неравенство — используйте символ сравнения ≥ (больше равно) или ≤ (меньше или равно).

• a ≤ b — это значит, что a меньше либо равно b.
• a ≥ b — это значит, что a больше либо равно b.
• знаки ⩽ и ⩾ являются противоположными.

Другие виды неравенства.

• a ≠ b — означает, что a не равно b.
• a ≫ b — означает, что a намного больше, чем b.
• a ≪ b — означает, что a намного меньше, чем b.
• знаки >> и

Онлайн-курсы математики для детей помогают им быстрее выучить математические символы и отработать их с опытными преподавателями.

Рогатость. Современная символика экспоненции была введена Декартом в его «Геометрии» (1637), но только с натуральными силами, превышающими 2.

Ньютон распространил эту форму символики на отрицательные и дробные экспоненты (1676).

Основные математические понятия и обозначения

Одним из основных математических понятий является понятие целого.

Определение: множество — это совокупность объектов, объединенных в соответствии с правилом или функцией.

Примеры множеств: — числа, целые числа, действительные числа.

Определение: объекты, составляющие часть целого, называются элементами целого.

Наборы обычно символизируются прописными латинскими буквами (a, b, c) и их элементами в нижнем регистре (a, b, c).

ОПРЕДЕЛЕНИЕ: Множество с конечным числом элементов называется конечным множеством. Бесконечное множество называется бесконечным множеством.

Обычно каждое множество задается некоторыми свойствами, т.е. свойствами только некоторых элементов целого, например, M = a, b, c, d-.

Наборы натуральных чисел: n₂= n

Определение: множество, не содержащее элементов, называется пустым множеством и обозначается 0.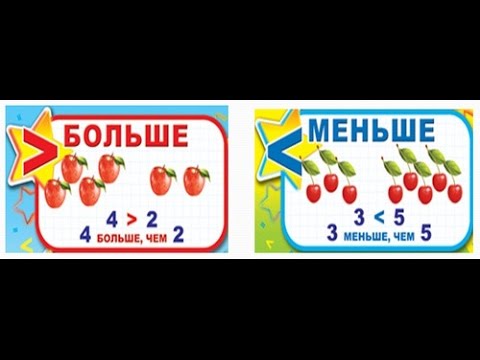

Множества чисел и их обозначения

n — множество положительных положительных чисел -.

Z — сумма интегральных чисел

Q — множество рациональных чисел — это число, которое может быть выражено как часть m/n где m — множество целых чисел, а n — множество натуральных чисел.

Отрицательные числа: j =

Множество вещественных чисел: r = q u j

Комплексные множества чисел:.

Каждый набор можно представить графически в виде круга (Эйлер — диаграмма событий):.

Определение: множество b называется подмножеством множества A (b a), если каждый элемент целого b является элементом множества a.

Основные операции над множествами

1. сумма (комбинация) двух множеств A и B — это такое множество, которое состоит только из элементов, принадлежащих хотя бы одному множеству A или B.

В виде характеристического свойства — A u b =.

2. произведение (пересечение) двух множеств a и b состоит из элементов, одновременно принадлежащих a и b

3. разность двух множеств a и b (обозначается a/b) — это множество, состоящее из элементов, принадлежащих a и не принадлежащих b.

Логические символы

Вместо слов для сокращения обозначений: ложь, используются символы, используются символы.

Вместо слов: все, все, все.

Специальные математические символы

Для сокращения записи приводится произведение первых n натуральных чисел.

Для сокращения записи сумм и произведений используются символы.

Таблица математических символов

В математике символы используются повсеместно для упрощения и сокращения текста. Здесь перечислены наиболее распространенные математические символы, соответствующие им команды TEX, описания и примеры их использования.

В дополнение к вышеперечисленным значкам можно использовать зеркальные изображения символов, например.

Символы актов или математические символы — это символы, которые символизируют конкретный математический акт в аргументе.

Математическая таблица символов, таблица символов, таблица символов ASCII, таблица символов HTML, таблица кодов HTML, таблица символов WordPress, таблица символов ников, таблица символов на клавиатуре, таблица символов клавиатуры WK

Таблица математических символов что, таблица математических символов кто, таблица математических символов

Символ равенства (=) используется, когда два небольших отрезка пишутся горизонтально и одновременно. Используется при сравнении двух одинаковых чисел.

Как легко понять знаки Σ и П с помощью программирования

Говорят, что если ты не закончил физтех, математическую школу или Бауманку, то тебе нечего делать в программировании. Почему они так говорят? Потому что, мол, вы не изучали сложную математику, а без нее в программировании не обойтись.

Все это, конечно, чепуха. Если вы не сильны в математике, вы можете стать отличным программистом. Вы вряд ли будете писать драйверы для видеокарт, но вы легко сможете создавать мобильные приложения и онлайн-сервисы. А это основные деньги в данной среде.

Но опять же, для умственной пользы, я приведу несколько примеров из ужасающего мира математики. Покажите им, что не все дело в математическом аде, но в конце концов это не так. Вот два нестрашных квадрата

Знак Σ — сумма

Когда математикам нужно сложить много чисел подряд, они иногда пишут их: s

s (читается как «сигма») — символ алгебраической суммы.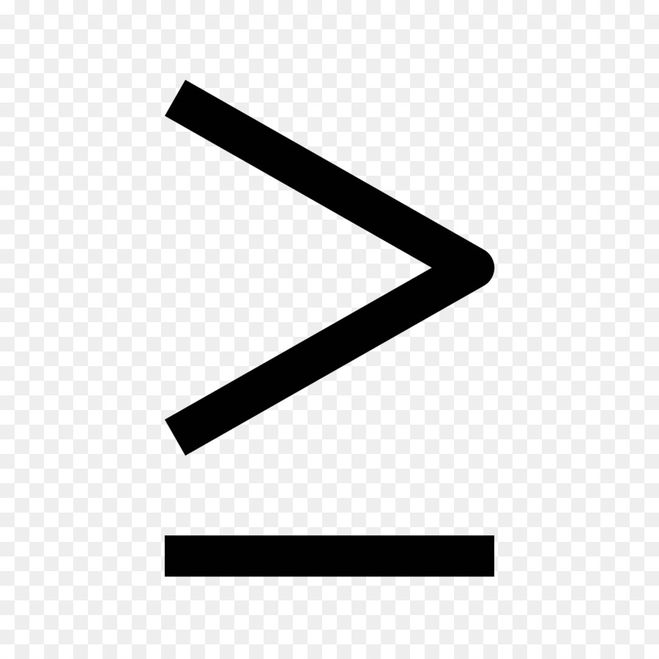 Это означает, что все числа должны складываться снизу вверх.

На рисунке выше написано: «сумма всех чисел от 5 до 15, умноженная на два». Вот этот:.

1. Взять все числа от 5 до 15 (снизу и сверху знака Σ).
2. С каждым из этих чисел сделать то, что написано справа от Σ, — то есть умножить на два.
3. Сложить результаты этих операций.

Давайте рассмотрим еще один пример, чтобы подкрепить это. На рисунке ниже написано: «Найдите сумму квадратов чисел 5-10». Другими словами, «сложите результат, сделав все числа 5-10, каждое из которых является квадратом».

Но мы с вами, как разработчики, можем видеть, что здесь есть повторяющиеся действия. Добавьте изменяющиеся числа снова и снова по тому же правилу. А поскольку мы знаем это правило и количество раз, которое его нужно применить, его легко превратить в цикл. Для наглядности мы показали, что параметр s указывает на ответственность в цикле.

Произведение П

То же правило применяется и к математическому произведению, только складываются все элементы, но умножаются на

Если это перевести в круг, то алгоритм практически идентичен дополнительному алгоритму.

Символы из области теории множеств были придуманы в 1888-1889 гг. А перечеркнутый круг, который сегодня известен любому учащемуся средней школы как знак пустого множества, появился в 1939 году.

Переменные

Буквы в символьном выражении называются переменными. Например, в выражении c + x + 2 переменными являются буквы c и x. Если эти переменные заменить на числа, то выражение с буквами c + x + 2 переводится в числовое выражение, значение которого можно найти.

Число, которое заменяет переменную, называется значением переменной. Например, переменные c и x меняют свои значения. Символ равенства используется для изменения цены

Измените значения переменных c и x. Переменной c присваивается значение 2, переменной x присваивается значение 3, и тогда c + x + 2 выглядит следующим образом

Символы «угол» и «вертикаль» были изобретены французским математиком Пьером Эригоном в 1634 году. Вертикальный символ был перевернут, подобно букве Т. Символ угла похож на символ и принял свою современную форму от Уильяма О’Толедо (1657).

Математические знаки и символы на английском

Основные математические знаки и символы на английском языке (плюс, минус, деление, умножение и другие, менее распространённые знаки и символы).

* – для самостоятельно изучающих английский язык также могут быть интересными разделы «Фильмы на английском» и «Аудиокниги на английском».

 

В данной статье мы рассмотрим наиболее распространенные математические знаки и символы на английском языке. Графическое изображение математических знаков и символов универсально во всех языках, но их звучание и произношение значительно отличаются друг от друга. Если вы работаете за границей или даже просто общаетесь на английском с друзьями, вам необходимо знать произношение основных символов на английском языке.

 

Математические знаки, использующиеся для основных арифметических действий:

«+» – plus – плюс

«-» – subtraction sign – знак вычисления

«x» – multiplication sign – знак умножения

«/»  slash . .. divided by – косая линия. Этот математический символ в английском языке также употребляется в качестве знака деления.

«÷» division sign  – знак деления

«:» – сolon – двоеточие; или ratio sign – знак отношения или деления в английском языке

«=» еqual sign – знак равенства

Эти математические знаки известны всем и употребляются повсеместно, поэтому нужно знать, как они звучат на английском языке.

 

Следующие математические символы не так распространены, но всё же не помешает их знание на английском:

«%» Percent symbol – математический символ в английском языке, который употребляется для обозначения процентов

«[ ]» square brackets – квадратные скобки

«±» рlus/minus sign  – знак плюс/минус

«≈» аpproximate equal sign – приближенное равенство

«<» inequality sign (less than – меньше чем) – знак неравенства

«>» inequality sign (greater than – больше чем) – знак неравенства

« ≤ » inequality sign (less than or equal to . .. – меньше чем или соответствует …)

«{ }» сurly brackets (the quantity …… the set …- общее количество) – фигурные скобки

«√» surd (… root of … – корень из) – иррациональное число

«√» square root – квадратный корень

 

Математические знаки и символы очень разнообразны и отличаются сферой употребления. Ниже перечисленные математические знаки и символы менее распространены и употребляются в основном в специализированных областях. Вот написание ещё нескольких математических символов на английском:

«∫» – integral – интегральный

«i» – imaginary unit – мнимая единица

«z*» – complex conjugate – комплексно сопряжённая величина

«∇» – nabla/del – набла

«δ» – delta function – дельта-функция

«∞» – infinity symbol – символ бесконечности

«∅» null symbol – нуль или  недействительный; несущественный

 

Вот еще несколько математических символов, которые используют в геометрии, которые на английском выглядят следующим образом:

«|» – perpendicular – перпендикулярный

«||» – parallel – параллельный

«≅» – congruent to – соответствующий (эквивалентность геометрических форм и размеров)

«∠» angle symbol – знак, который используют в геометрии для обозначения угла

 

Это лишь небольшой список наиболее употребляемых математических знаков и символов на английском, но, если углубиться в специализированную тематику, можно увидеть еще много знаков и символов, характеризующих различные понятия в данной сфере.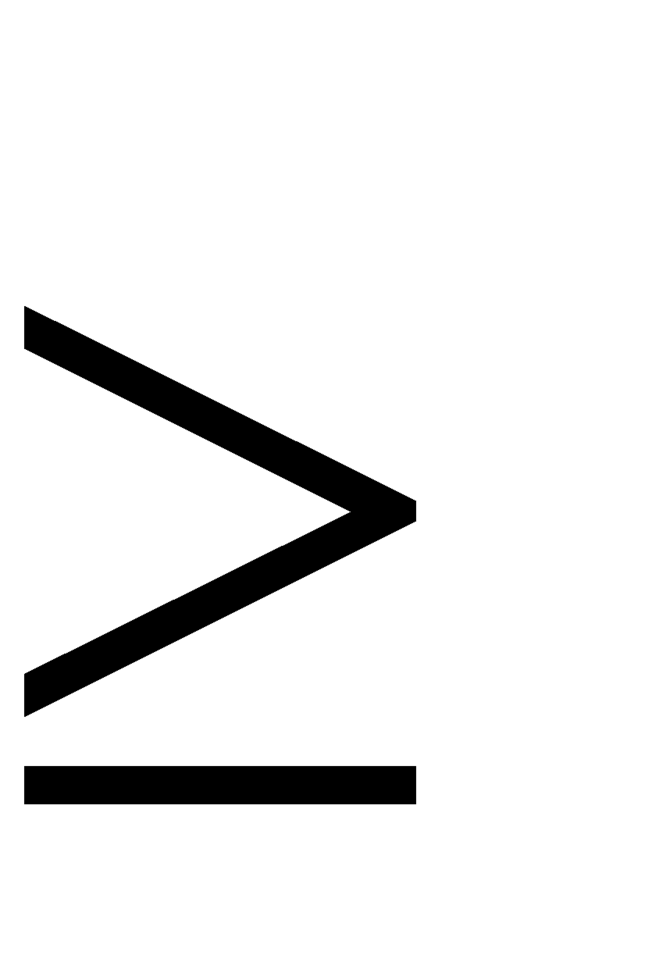

Гораздо меньше, Гораздо больше

Символы ≪ и ≫ ​​могут сбивать с толку при первом знакомстве, но они очень удобны.

Символ ≪ означает «намного меньше», а его аналог ≫ означает «намного больше». Вот небольшая таблица, показывающая, как создавать символы.

 |-------------------+---------+-------+------|
    | | Юникод | латекс | HTML |
    |-------------------+---------+--------+------|
    | Гораздо меньше, чем | U+226А | \ll | ≪ |
    | Гораздо больше, чем | U+226B | \гг | > |
    |-------------------+---------+--------+------|
 

Конечно, «многое» зависит от контекста. 5 намного меньше 7? Это если вы описываете рост людей в футах, но, возможно, не в контексте цен на гамбургеры в долларах.

Иногда вы увидите ≫ или, что более вероятно, >> (два символа больше чем), как сленговое выражение «намного лучше, чем». Например, кто-то может сказать «прототип >> PowerPoint», чтобы показать, что работающий прототип намного лучше, чем презентация PowerPoint.

Символы ≪ и ≫ ​​могут вызвать у людей дискомфорт, потому что это жаргон инсайдеров. Вы должны знать контекст, чтобы понять, как их интерпретировать, но они очень удобны, если вы инсайдер. Весь жаргон такой.

Ниже приведены некоторые примеры ≪ и ≫ ​​на практике.

Приближение квадратного корня

Возможно, вы где-то видели, что для | б | ≪ a , выполняется следующее приближение:

Итак, когда | б | намного меньше, чем ? Это зависит от вас. Если в вашем контексте вы решите, что b / a мало, ошибка аппроксимации будет на порядок меньше.

Предположим, вам нужно знать √103 с точностью до пары знаков после запятой. Здесь a = 100 и b = 3. Отношение b/a = 0,03, и ваша ошибка должна быть небольшой по сравнению с 0,03, поэтому вышеприведенное приближение должно быть достаточно хорошим. Посмотрим, так ли это.

Приведенное выше приближение дает

√103 ≈ √100 + 3/2√100 = 10 + 3/20 = 10,15

, а точное значение √103 равно 10,14889…, и поэтому мы получили два правильных знака после запятой, и мы почти получили три.

Синусоидальная аппроксимация

Вместо того, чтобы говорить, что переменная «маленькая», мы могли бы сказать, что она намного меньше 1. Например, вы можете увидеть

sin θ ≈ θ

для |θ| ≪ 1. Если θ мало, ошибка в приведенном выше приближении очень мала.

Через несколько лет я написал сообщение в блоге из 700 слов, подробно раскрыв значение предыдущего предложения. Многие люди запоминают фразу «Вы можете заменить sin θ на θ для малых углов», не понимая до конца, что это значит. Насколько мал достаточно мал? В посте объясняется, как узнать.

Формула Стирлинга

Иногда вы видите что-то вроде n ≫ 1, чтобы указать, что n должны быть большими. Например, формула Стирлинга для факториалов говорит:

для n ≫ 1. Например, если n = 10, приведенная выше аппроксимация имеет ошибку менее 1%.

Обратите внимание, что приведенная выше ошибка аппроксимации мала по сравнению с точным значением . Относительная ошибка мала, а не абсолютная ошибка. Ошибка в примере больше 30 000, но это значение мало по сравнению с 10! = 3 628 800.

Асимметрия между малым и большим

Из контекста часто труднее сказать, когда что-то большое, чем когда оно маленькое.

Если для | х | ≪ 1 часто присутствует неявный степенной ряд в фоновом режиме, а ошибка составляет порядка x ². Это имеет место в нашем приближении квадратного корня выше. Аппроксимация синуса еще лучше, с ошибкой порядка x ³.

Но если верно приближение для x ≫ 1, часто имеется неявное асимптотический ряд на заднем плане, и они более тонкие. Вероятно, вам нужно больше информации о том, насколько большим должно быть x для конкретного приложения.

Связанные сообщения

• Unicode <-> LaTeX
• Не имеет большого значения, если рулетка прямая
• Прикладная математика

Символы больше и меньше

Написано администратором в математических операторах, математических символах

В математике знаки меньше и больше обозначают неравенство между двумя значениями. Эти знаки легко набираются в LaTeX с помощью имеющихся на клавиатуре клавиш < и > , которые производят вывод \(<\) и \(>\) в математическом режиме (их также можно использовать вне математического режима, но вывод выглядит немного иначе).

В следующей таблице приведены различные команды для сравнения величин:

901le01010101010101010134 01010134 0101010101010134

Описание	Команда	Выход
Менее9	\(A
Больше	>	\(A>B\)
Меньше или равно	\le
больше или равна, чем	\ GE	\ (A \ ge B \)
намного меньше	\ LL	\ (A \ ll B \)
\.	\(A \gg B\)

• Когда мы хотим обозначить это какая-то величина меньше или равна какой-то другой, мы должны использовать символ ≤ , который создается в математическом режиме с кодом $\le$. Точно так же мы можем создать символ больше или равно ≥ с кодом $\ge$ .

• Мы также можем более качественно обозначить, что количество намного больше другого, используя символ \( \gg \), который можно получить с помощью $\gg$ . Опять же, мы можем также обозначить, что количество намного меньше, чем другое, используя \( \gg \), которое получается с $\ll$ .

Мы подошли к концу этого руководства. Если у вас есть какие-либо замечания или предложения, не стесняйтесь обращаться к нам по электронной почте [email protected]

Пожалуйста, включите JavaScript

Как написать минималистичное резюме в LaTeX: пошаговое руководство

Последние сообщения

ссылка на набор вопросов с несколькими вариантами ответов в LaTeX

Набор вопросов с несколькими вариантами ответов в LaTeX

В этом руководстве мы увидим, как написать экзамен с несколькими вариантами ответов в LaTeX, используя класс документа экзамена.