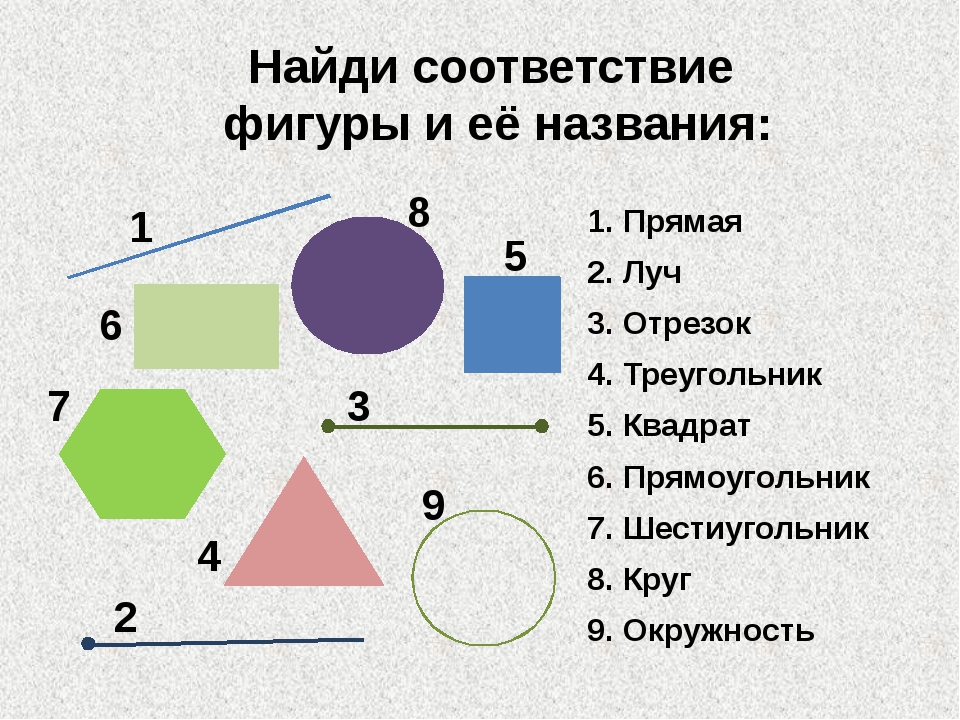
Математика фигуры геометрические: Основные геометрические фигуры 🟢🟨🔺 и их названия
геометрические фигуры. Математика средняя группа | План-конспект занятия по математике (средняя группа):
КОНСПЕКТ НОД
«Геометрические фигуры»
Цель: Знакомство с геометрическими фигурами
Педагогический замысел:
1. Закрепить с детьми названия геометрических фигур.
2. Расширять представления детей о геометрических фигурах (призма, пирамида)
3. повысить или удержать умственную работоспособность детей на занятиях, обеспечить кратковременный отдых для дошкольников во время проведения
4. Продолжать знакомить детей с образование числа 2 и цифрой 2.
5. Развивать пространственное мышление.
6. Повысить и удержать умственную работоспособность детей на занятиях, обеспечить кратковременный отдых для дошкольников во время проведения физкультминутки.
Предварительная работа. Показ сказки «В лесу» с использованием динамических картинок, знакомство с образование числа 2 и цифрой 2
Материалы.
Демонстрационный материал: Игрушки зайчонок и котёнок, шар, куб, кирпичик, призма, пирамида (много), квадрат, круг, прямоугольник, треугольник, 4 коробки.
Для физкультминутки: бубен, игрушка зайчик, 2 картинки уточки, 1 ёлочка, 2 круга, 1 цветок, 2 мячика.
Раздаточный материал: 2 квадрата и 2 треугольника на каждого ребёнка.
Примерный ход совместной деятельности.
Вводная часть (2 минуты)
Дети сидят на стульчиках. Воспитатель:
– Ребята посмотрите, кто это? (Воспитатель показывает детям игрушку котёнка) Котёнок собирается в гости к зайчонку, как вы думаете, во что они могут поиграть вместе? (Варианты ответов детей) Правильно. Они решили поиграть с деревянным конструктором, но не знают, как называются фигуры. Давайте мы напомним им названия разных фигур.
Основная часть. (15 минут)
Воспитатель достаёт коробку, в ней лежит шар, куб, кирпичик, призма, пирамида. Спрашивает детей:
– Ребята, кто помнит, как называются эти фигуры (показывает шар, куб, кирпич). Молодцы, я хочу познакомить вас с фигурами, которые называют призма и пирамида (показывает эти фигуры). Для чего в постройке нам нужны эти фигуры, что могут зайчонок и котёнок построить из них? (ответы детей)
Воспитатель берёт 2 куба, призму и пирамиду и строит 2 домика.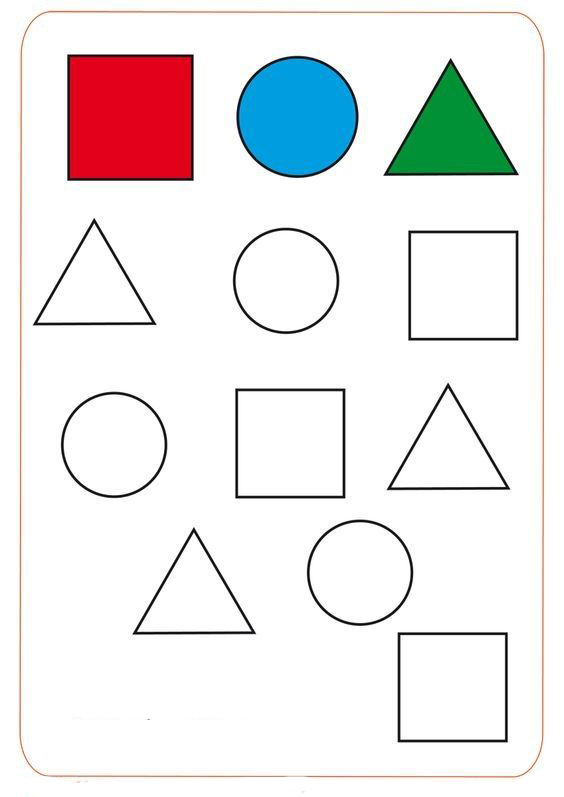
Наши зверюшки отлично поиграли, но они перемешали все фигуры и теперь не могут разобраться, где какие фигуры. Давайте мы разберём все фигуры по разным коробкам.
Воспитатель высыпает на ковёр из коробки много фигур: кубы, кирпичики, призмы и пирамиды. Показывает коробочки, на которых изображены фигуры, детям даётся задание разложить всё по коробкам.
Воспитатель:
– Молодцы ребята, вы справились с заданием. Посмотрите на доску, там тоже есть фигуры. Но они отличаются от фигур, которые мы только что раскладывали.
Воспитатель показывает на доску. На доске круг, квадрат, прямоугольник, треугольник.
Воспитатель:
– Чем же они отличаются? (воспитатель берёт в руку круг и шар, дети пытаются ответить) Ребята, посмотрите это круг, а это шар. Если повернуть шар другой стороной, то мы опять увидим такой же шар, а если мы повернём круг, то круг превратится в полоску или овал. Вот этим и отличаются эти фигуры, круг плоский, а шар объёмный. Тоже можно сказать про квадрат и куб, треугольник и пирамиду, прямоугольник и кирпичик.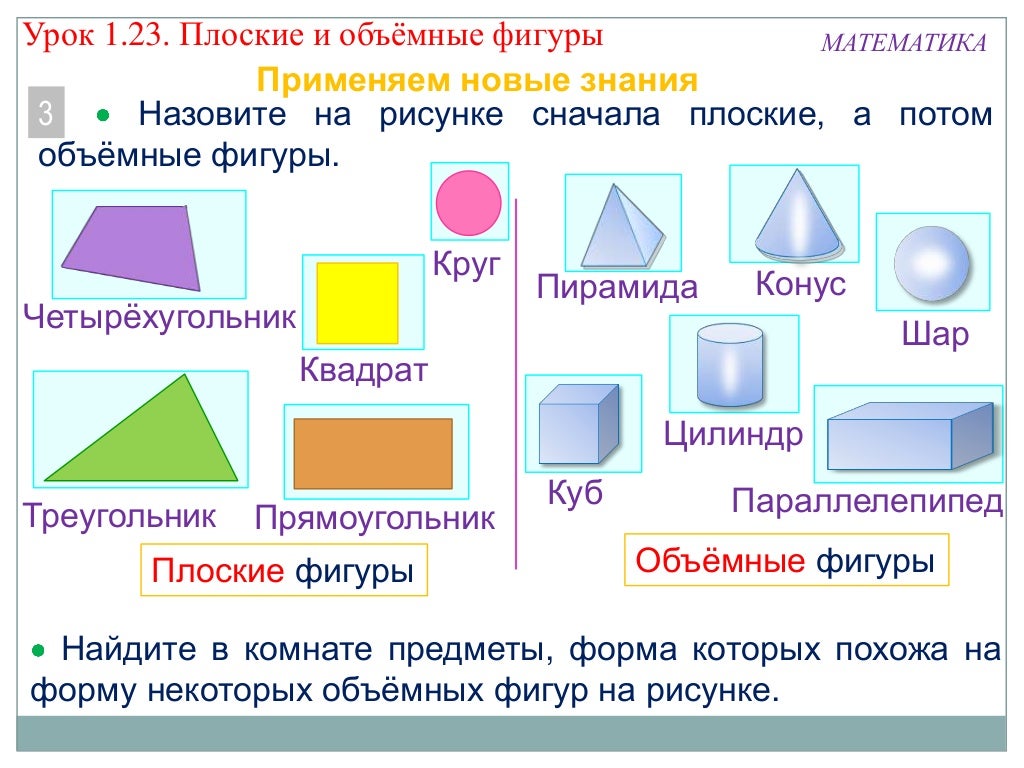
Давайте мы сейчас встанем и немного подвигаемся. Воспитатель проводит физкульт.минутку:
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем два квадрата,
А на них огромный круг,
А потом еще кружочек,
Треугольный колпачок.
Вот и вышел очень, очень
Развеселый чудачок. (Дети рисуют в воздухе геометрические фигуры.)
Воспитатель:
-Молодцы, а теперь садитесь за столы. Котёнок и зайчонок очень любят выкладывать на столе картинки. Вот и вы сейчас этим займётесь. Посмотрите, на тарелочках у вас лежат квадраты, возьмите себе 2 квадрата, а ещё возьмите 1 треугольник. Чего больше квадратов или треугольников? Что надо сделать, чтобы у вас получилось поровну квадратов и треугольников? Молодцы, я вам сейчас раздам ещё по одному треугольнику, а вы подумайте, что можно сложить из этих фигур (на доске воспитатель через некоторое время выкладывает подсказку «домик»).
Воспитатель задаёт вопросы:
– Сколько у вас было треугольников (1), сколько треугольников вы добавили (1) , а сколько треугольников стало? (2) .
Что получилось у вас из квадратов и треугольников? Сколько домиков у вас получилось? (2) Вот молодцы, давайте с вами поиграем.
Заключительная часть. (3 минуты)
Проводится игра «Сколько, столько»
Сколько раз ударю в бубен,
Столько раз дрова нарубим.(2 раза).
Сколько зайчиков у нас,
Столько мы подпрыгнем раз.(1 раз)
Мы присядем столько раз
Сколько уточек у нас (2 раза)
Сколько елочек зеленых,
Столько выполним наклонов.(1 раз)
Сколько покажу кружков,
Столько сделаем прыжков.(2 раза)
Столько сделали хлопков,
Сколько на лугу цветков.(1 раз)
Приседаем столько раз
сколько мячиков у нас (2 раза)
Потолок достанем и тихонько сядем.
(Воспитатель произнося строчку, показывает предметы, которые в ней упомянуты)
Предполагаемый результат: Закрепление с детьми названия геометрических фигур. Закрепление знаний детей об образовании числа 2 и цифрой 2.
Дальнейшая работа: Продолжать развивать знания о геометрических фигурах.
Знакомить детей с количественным счётом и цифрой 3.
Тест: Геометрические фигуры – Математика 5 класс
Тест: Геометрические фигуры – Математика 5 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP – доступ
- Предметы »
- Математика »
- 5 класс »
- Геометрические фигуры
Геометрические фигуры
Этот тест для любознательных пятиклассников. В помощь учителю, работающему по любому УМК.
Математика 5 класс | Автор: Овчинникова Любовь Викторовна | ID: 5696 | Дата: 4.10.2015
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Прямоугольник, у которого стороны равны, называется
ромб
квадрат
треугольник
куб
Вопрос №
2
Стороны прямоугольника равны 4 см и 6 см, его разрезали на 4 равных фигуры.
Площадь каждой получившейся фигуры равна
6 квадратных сантиметров
4 квадратных сантиметров
6 сантиметров
невозможно ответить
Вопрос №
3
Длины сторон прямоугольника – натуральные однозначные числа, а P = S. Чему же равна площадь этого прямоугольника, если он не квадрат?
18 сантиметров
18 квадратных сантиметров
такого прямоугольника не существует
Вопрос №
4
Какое наименьшее количество распилов надо сделать, чтобы куб с ребром 3 см распилить на кубики с ребром 1 см?
6
12
16
4
Вопрос №
5
Равнобедренный треугольник – это треугольник, у которого две стороны равны, а прямоугольный треугольник – это треугольник, у которого один из углов прямой.
Какое наименьшее количество равных прямоугольных равнобедренных треугольников необходимо взять, чтобы составить из них прямоугольник с разными сторонами?
6
2
8
4
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.ru 2013-2022
E-mail администратора: [email protected]
Геометрические фигуры и прямые линии
Прямые линии являются ключом к распознаванию форм, которые мы часто видим в реальном мире: геометрические фигуры .
В сегодняшнем посте мы будем классифицировать геометрические фигуры, образованные прямыми линиями, и подумаем, где их можно найти.
Начнем с самого простого:
Две прямые Можно ли составить фигуру из двух прямых?
Ну конечно можно! Однако мы не называем эту фигуру геометрической фигурой. Чтобы быть геометрической фигурой, она должна быть «замкнутой».
То есть, если мы поместим шарик внутрь фигуры, он не сможет вырваться. На сделанном нами рисунке мяч мог улететь!
Если вы попытаетесь сдвинуть две линии, то увидите, что никоим образом ее нельзя замкнуть. Можно взять два прямых предмета, например, две палочки для еды, и попробовать.
Базовые геометрические фигуры
А теперь попробуем с тремя прямыми…
Готово! Теперь вы можете сделать фигуру, от которой мяч не сможет убежать.
Каждая из прямых линий, которые мы использовали, теперь действует как часть фигуры.
Будем называть каждую прямую стороной фигуры . Итак, эта фигура имеет три стороны и называется треугольником. Когда мы говорим «треугольник», мы имеем в виду либо расположение трех линий, либо окружающее их пространство.
Можете ли вы представить, где мы можем найти треугольники вокруг нас? Я нашел несколько в Smartick , посмотрим, узнаете ли вы их!
4-сторонние геометрические фигуры
Давайте посмотрим, что мы можем сделать с 4 прямыми линиями…
Мы могли бы сделать, например,
Мы называем эти фигуры четырехугольниками.
Есть несколько особых четырехугольников, у которых есть пары параллельных сторон. То есть есть две стороны, которые параллельны друг другу, и две другие тоже. Кроме того, параллельные стороны равны. Как мы могли сделать это? Получаем две равные стороны и ставим их параллельно друг другу:
Как расположить две другие стороны так, чтобы они тоже были параллельны? Вот и все! Просто объединив их вместе.
На данный момент у нас есть три возможности:
- Все стороны равны, образуя ромб.
Где найти алмазы?
Я нашел два!
- Если четыре угла фигуры прямые, то мы создали прямоугольник.
Мы можем найти много прямоугольников вокруг себя… Я уверен, что вы можете придумать множество!
- Если мы создадим геометрическую фигуру, которая удовлетворяет обоим вышеуказанным условиям, а также имеет все равные стороны и четыре прямых угла, то это квадрат.
Геометрические фигуры с более чем 4 сторонами
Мы можем продолжать добавлять все линии, которые мы хотим, чтобы создать разные фигуры с разным количеством сторон. Они особенно важны, когда у них равные стороны. Например, следующим будет пятиугольник (5-сторонний).
Мы можем найти их, например, в рисунке футбольных мячей.
И затем у нас есть шестигранник (6-гранный).
Мы можем найти их… в ульях! Откуда пчелы умеют делать такие идеальные геометрические фигуры?
А потом семиугольники, восьмиугольники, эннагоны, нонагоны… чего-то не хватает? Конечно! Что мы можем сделать с изогнутыми линиями? Кривые линии не имеет смысла классифицировать, потому что они различаются гораздо больше… но я могу сказать вам, что есть очень, очень важная изогнутая фигура, о которой, я уверен, вы уже знаете… круг !
Мы получаем круг, когда сохраняем расстояние от точки. Например, с помощью компаса мы устанавливаем точку с помощью стрелки.
Затем, сохраняя отверстие, рисуем карандашом окружность. Вы можете найти множество кругов вокруг себя, на колесах вашего автомобиля или на теннисном мяче.
Если вы хотите, вы можете продолжить изучение элементарной математики с помощью Smartick!
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения Smartick (посмотреть все)
Mathwords: Geometric Figure
Mathwords: Geometric Figure
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
