Математика 4 класс примеры столбиком: сложение, вычитание, умножение, деление Номер 38
ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 10. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник – страница 10Готовое домашнее задание
Пишу единицы по единицами, десятки по десятками, сотни под сотнями.
Номер 37.
Объясни, как вычислены произведения 192 ∙ 2 и 72 ∙ 4.
Ответ:
Пишу: 194 ∙ 2
Умножаю единицы: 4 ∙ 2 = 8. Пишу 8 единиц под единицами.
Умножаю десятки: 9 ∙ 2 = 18. 18 десятков – это 1 сотня и 8 десятков. 8 десятков пишу под десятками, а 1 сотню запоминаю и прибавлю её к сотням, после умножения сотен.
Умножаю сотни: 1 ∙ 2 = 2.
К 2 сотням прибавлю 1 сотню. 2 + 1 = 3. Число 3 пишу под сотнями.
Ответ: 388.
Номер 38.
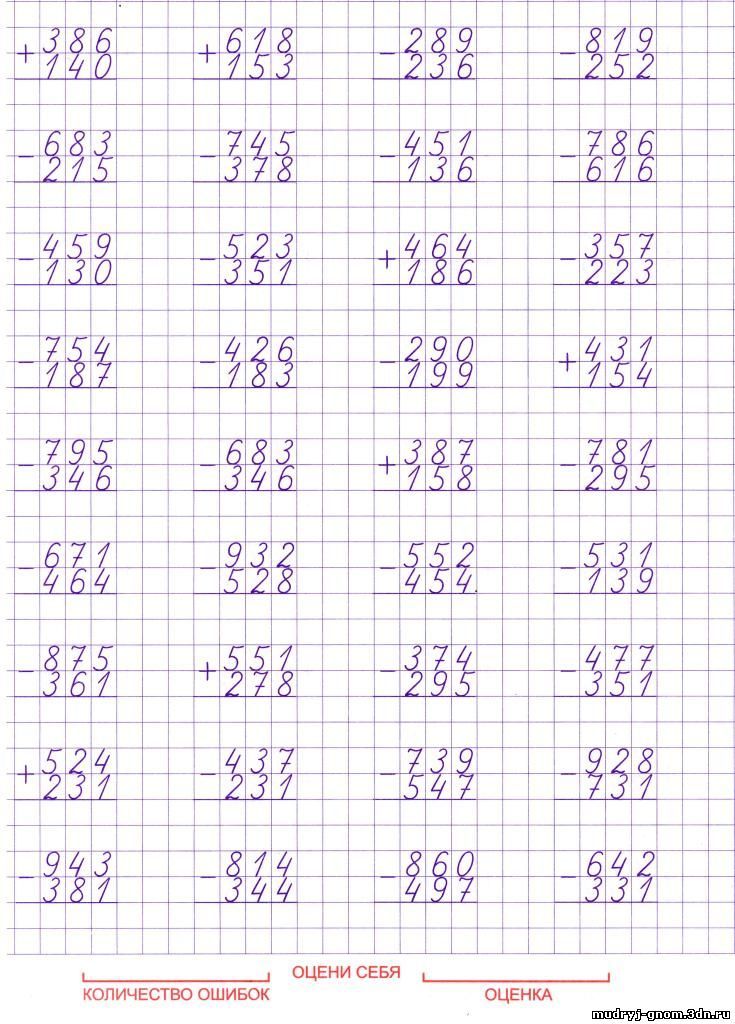
Запиши примеры столбиком и выполни вычисления.
Ответ:
Номер 39.
1) Реши задачу, составив выражение: В саду посадили 4 ряда яблонь, по 12 яблонь в каждом ряду, и 2 ряда слив, по 18 слив в каждом ряду. Сколько всего деревьев посадили?
2) Измени вопрос задачи, чтобы она решалась так: 12 ∙ 4 − 18 ∙ 2.
Ответ:
Задача 1: Яблони – 4 ряда по 12 д. Сливы – 2 ряда по 18 д. Всего – ? д.
Ответ: 84 дерева всего.
Задача 2:
На сколько яблонь посадили больше, чем слив?
12 ∙ 4 − 18 ∙ 2 = 12 (д.
Номер 40.
Сестра нашла 27 грибов, а брат – ☐. Среди этих грибов было 3 несъедобных. Сколько всего съедобных грибов нашли дети? Заполни пропуск. Реши задачу разными способами.
Ответ:
Допустим, что брат нашел 20 грибов. Нашли – 27 гр. и 20 гр. Несъедобные – 3 гр. Съедобные – ? гр. 1 способ: (27 + 20) − 3 = 44 (гр.) 2 способ: (27 − 3) + 20 = 44 (гр.) 3 способ: (20 − 3) + 27 = 44 (гр.) Ответ: 44 съедобных грибов.
Номер 41.
Используя слово «больше» или «меньше» в условии или в вопросе, составь задачи по выражениям: 64 : 16 и 64 − 16.
Ответ:
Задача 1:
В корзине было 64 яблока, а слив в 16 раз меньше. Сколько слив было в корзине?
64 : 16 = 4 (сл.)
Ответ: 4 сливы было.
Сколько слив в корзине?
64 − 16 = 48 (сл.)
Ответ:48 слив было.
Номер 42.
Вычисли и выполни проверку.
Ответ:
Номер 43.
Ответ:
Оформить можно иначе:
Задание внизу страницы
Вычисли.
Ответ:
Задание на полях страницы
Цепочка:
Ответ:
84 : 3 = 28 28 ∙ 2 = 56 56 + 4 = 60 60 ∙ 3 = 180 180 − 80 = 100
Рейтинг
Выберите другую страницу
1 часть| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Ваше сообщение отправлено!
+
Страница 10 – ГДЗ Математика 4 класс.
Моро, Бантова. Учебник часть 1- Главная
- ГДЗ
- 4 класс
- Математика
- Моро, Бантова. Учебник
- Числа от 1 до 1000
- Страница 10. Часть 1
Вернуться к содержанию учебника
Числа от 1 до 1000
Вопрос
37. Объясни, как вычислены произведения: 194 • 2, 72 • 4.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
38. Запиши примеры столбиком и выполни вычисления.
| 127 • 3 | 236 • 2 | 192 • 3 | 68 • 4 | 79 • 2 | 82 • 4 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
39.
1) Реши задачу, составив выражение:
В саду посадили 4 ряда яблонь, по 12 яблонь в каждом ряду, и 2 ряда слив, по 18 слив в каждом ряду. Сколько всего деревьев посадили?
2) Измени вопрос задачи, чтобы она решалась так:
12 • 4 – 18 • 2
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
40. Сестра нашла 27 грибов, а брат – . Среди этих грибов было 3 несъедобных. Сколько всего съедобных грибов нашли дети?
Заполни пропуск. Реши задачу разными способами.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
41. Используя слово “больше” или “меньше” в условии или в вопросе, составь задачи по выражениям:
64 : 16 и 64 – 16
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
42.
Вычисли и выполни проверку.
| 248 + 407 | 420 – 176 | 302 – 254 | 703 + 94 + 128 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
43.
| 760 – (120 + 80) + 60 | 120 : (60 : 6) : 2 |
| 500 – (270 + 130) – 1 | 90 : (45 : 9) • 2 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Вычисли.
| 374 • 2 | 186 • 3 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Цепочка:
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
KS2 Математика 4–5 классы Методы работы со столбцами
Как складывать и вычитать?
Когда нам нужно складывать большие числа, наиболее полезно учитывать разрядное значение каждой цифры.
Это означает, что мы можем затем сложить вместе все единицы, десятки, сотни и тысячи и убедиться, что мы сгруппировали вместе все одинаковые значения.
Использование столбцов для сложения
Чтобы убедиться, что мы складываем правильные цифры, мы можем расположить наши числа так, чтобы они были в столбцах. Мы должны всегда выстраивать единицы, десятки, сотни и тысячи друг с другом, чтобы сложить их вместе.
Когда числа расположены в правых столбцах, мы складываем цифры и помещаем ответ ниже, начиная с единиц и двигаясь влево. Если мы получаем больше десяти в качестве ответа на сумму, мы добавляем лишнее в следующий столбец слева. Например, 5 единиц плюс 7 единиц дают 12 единиц. Это 1 десяток и 2 единицы, поэтому 1 десяток будет добавлен к столбцу десятков.
Использование столбцов для вычитания
поэтому они в столбцах. Мы всегда должны выстраивать единицы, десятки, сотни и тысячи друг с другом, чтобы убедиться, что мы вычитаем правильные вещи.
Большее общее число должно идти выше меньшего общего числа.
Когда числа расположены в правильных столбцах, мы вычитаем число ниже из числа выше и записываем ответ ниже. Если число, которое мы вычитаем, больше, чем число, которое у нас есть, мы должны «позаимствовать» значение из следующего столбца. Например, 5 единиц минус 7 единиц сделать невозможно, поэтому мы должны взять 10 из следующего столбца слева и сделать 15 минус 7.
Сложение и вычитание: методы столбцов мы делаем сейчас?
Теперь, когда вы можете складывать и вычитать числа до 4 цифр, вы можете отвечать на такие вопросы:
1) Что такое 1234 + 4321?
2) В городе Литтсвоппинг проживает 4351 человек. После наводнения 234 человека переезжают из Литлсвопинга в Биддлстон, где раньше проживало 653 человека. Сколько человек сейчас живет в каждом городе?
3) Миссис Смит открывает прилавок для школьной благотворительной ярмарки.
Она берет 2145 фунтов во второй половине дня на ярмарке. Она потратила 9 фунтов4 на материалы для киоска, а затем на следующий день получил пожертвование в размере 652 фунтов стерлингов. Сколько она в итоге отдала на благотворительность?
HYPERLINKS
- Adding
- Maths is Fun
- BBC Bitesize
Click here for Year 4 Maths Home Page
Click here for KS2 Curriculum Dashboard (All Subjects)
Национальная учебная программа
Учащиеся должны научиться:
- складывать и вычитать числа, содержащие до 4 цифр, используя формальные письменные методы столбцового сложения и вычитания, где это применимо
- оценивать и использовать обратные операции для проверки ответов на вычисления решение, какие операции и методы использовать и почему.
Матрица столбцов — определение, формула, свойства, примеры.
Матрица-столбец — это матрица, все элементы которой находятся в одном столбце.
Элементы расположены вертикально, а порядок матрицы-столбца равен n x 1. A матрица столбцов имеет только один столбец и может иметь множество строк, количество которых равно количеству элементов в столбце.
Давайте узнаем больше о свойствах матрицы-столбца, матричных операциях над матрицей-столбцом, на примерах, в часто задаваемых вопросах.
| 1. | Что такое матрица-столбец? |
| 2. | Свойства матрицы столбца |
| 3. | Операции над матрицей столбцов |
| 4. | Примеры на матрице столбцов |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о матрице столбцов |
Что такое матрица столбцов?
Матрица-столбец — это матрица, в которой все элементы находятся в одном столбце. Матрица столбцов имеет только один столбец и несколько строк.
Порядок матрицы-столбца равен n × 1, и она состоит из n элементов. Элементы расположены вертикально, при этом количество элементов равно количеству строк в матрице-столбце. Общая форма матрицы-столбца выглядит следующим образом.
Примеры матриц столбцов
Давайте рассмотрим три примера матриц столбцов ниже.
B = \(\begin{bmatrix}4\\5\end{bmatrix}_{2×1}\)
C = \(\begin{bmatrix}a\\b\\c\end{bmatrix }_{3×1}\)
D = \(\begin{bmatrix}8\\-2\\4\\1\end{bmatrix}_{4×1}\)
Свойства матрицы столбцов
Следующие свойства матрицы-столбца помогают глубже понять матрицу-столбец.
- Матрица столбцов имеет только один столбец.
- Матрица-столбец имеет множество строк.
- Количество элементов в матрице-столбце равно количеству строк в матрице.
- Матрица-столбец также является прямоугольной матрицей.
- Транспонирование матрицы-столбца является матрицей-строкой.
- Матрица-столбец может быть добавлена или вычтена только из матрицы-столбца того же порядка.
- Матрица-столбец может быть умножена только на матрицу-строку
- Произведение матрицы-столбца на матрицу-строку дает одноэлементную матрицу.
Операции над матрицей столбцов
Над матрицами-столбцами можно выполнять следующие алгебраические операции сложения, вычитания, умножения и деления. Операции сложения и вычитания над матрицами-столбцами можно выполнять так же, как и над любыми другими матрицами. Матрица-столбец может быть добавлена или вычтена только из любой другой матрицы-столбца. Здесь порядок двух матриц должен быть одинаковым.
A = \(\begin{bmatrix}7\\-3\\4\\5\end{bmatrix}\), B = \(\begin{bmatrix}3\\8\\2\\-7 \end{bmatrix}\)
A + B = \(\begin{bmatrix}7+3\\(-3)+8\\4+2\\5+(-7)\end{bmatrix}\ ) = \(\begin{bmatrix}10\\5\\6\\-2\end{bmatrix}\)
Умножение матрицы-столбца возможно на матрицу-строку. При выполнении условия умножения матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
То есть количество столбцов в матрице столбцов для умножения равно количеству строк в столбце строки.
A = \(\begin{bmatrix}4\\2\\3\\1\end{bmatrix}\), B = \(\begin{bmatrix}7&4&6&5\end{bmatrix}\)
A × B = \(\begin{bmatrix}4\\2\\3\\1\end{bmatrix}\), × \(\begin{bmatrix}7&4&6&5\end{bmatrix}\)
= \(\begin {bmatrix}4×7&4×4&4×6&4×5\\2×7&2×4&2×6&2×5\\3×7&3×4&3×6&3×5\\1×7&1×4&1×6&1×5\end{bmatrix} \)
= \(\begin{bmatrix}28&16&24&20\\14&8&12&10\\21&12&18&15\\7&4&6&5\end{bmatrix}\)
Умножение матрицы-столбца на матрицу-строку дает квадратную матрицу. Кроме того, матрицу-столбец нельзя использовать для деления, поскольку обратной матрицы-столбца не существует.
Связанные темы
Следующие темы помогают лучше понять матрицу столбцов.
- Операции с матрицами
- Матрица трансформации
- Несингулярная матрица
- Эрмитова матрица
- Нильпотентная Матрица
Примеры на матрице столбцов
Пример 1: Найти транспонирование матрицы-столбца \(\begin{bmatrix}5\\11\\4\\3\end{bmatrix}\).
Решение:
Дана матрица A = \(\begin{bmatrix}5\\11\\4\\3\end{bmatrix}\)
Чтобы найти транспонирование этой матрицы-столбца, элементы столбца записываются как элементы строки.
A T = \(\begin{bmatrix}5&11&4&3\end{bmatrix}\)
Следовательно, транспонированная матрица-столбец является матрицей-строкой.
Пример 2: Найдите произведение матрицы-столбца \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) и матрицы-строки \(\begin{bmatrix}2&6&9\end{ bматрица}\).
Решение:
Даны матрицы A = \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) и B = \(\begin{bmatrix}2&6&9\end{ bматрица}\).
A × B = \(\begin{bmatrix}4 \\5\\3\end{bmatrix}\) × \(\begin{bmatrix}2&6&9\end{bmatrix}\)
= \(\begin{bmatrix}4×2&4×6&4×9\\5×2&5×6&5×9\\3×2&3×6&3×9\\\end{bmatrix}\ )
= \(\begin{bmatrix}8&24&36\\10&30&45\\6&18&27\\\end{bmatrix}\)
Следовательно, произведение матрицы-столбца и матрицы-строки является одноэлементной матрицей.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по матрице столбцов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о матрице столбцов
Что такое матрица столбцов?
Матрица-столбец — это матрица только с одним столбцом, все элементы которой расположены друг под другом по вертикальной линии. В матрице столбцов A = \(\begin{bmatrix}a\\b\\c\\d\end{bmatrix}\) четыре элемента размещены в одном столбце. Матрица столбцов имеет только один столбец и множество строк. Порядок матрицы-столбца равен n × 1,9.0005
Каков порядок матрицы столбцов?
Порядок матрицы-столбца равен n × 1.
Матрица-столбец состоит из одного столбца и n строк. Количество строк в матрице-столбце равно количеству элементов.
Какой тип матрицы является матрицей-столбцом?
Матрица-столбец представляет собой прямоугольную матрицу. Он имеет неравное количество строк и столбцов. Матрица столбцов имеет один столбец и множество строк в зависимости от количества элементов в матрице.
Что такое транспонирование матрицы столбцов?
Транспонирование матрицы-столбца дает матрицу-строку. Матрица-столбец порядка n × 1 имеет транспонированную матрицу, которая представляет собой матрицу-строку порядка 1 × n. В матрице столбцов элементы расположены вертикально, а в матрице строк элементы расположены вертикально.
Какие операции выполняются над матрицей столбцов?
Матричные операции сложения, вычитания и умножения можно выполнять с помощью матрицы-столбца. Обратная матрица-столбец невозможна, так как это не квадратная матрица. Сложение или вычитание матриц возможно между двумя матрицами-столбцами одного порядка.