Математика 2 класс примеры со скобками: Выражения со скобками – 2 класс, примеры, порядок действия

Порядок действий. Правила и примеры — Kid-mama

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Мы видим, что порядок действий  в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.

Запомните правило: Если в примере нет скобок, мы выполняем все действия по порядку, слева направо. Если  в примере есть скобки, то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.

*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи. 

Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем  все действия по порядку, слева направо:

В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.

 

Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Запомните правило: Если в примере нет скобок, сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо. Если  в примере есть скобки, то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий  полученные результаты.  Затем выполняем сложение и вычитание по порядку:

Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:

Примеры, в которых много действий

Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно.  Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).

Эти знаки и будут делить наш пример на блоки:

 Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.

Порядок действий в примерах со скобками: попробуйте решить простой пример

Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу. Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?

Twitter: 1RealMir

Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.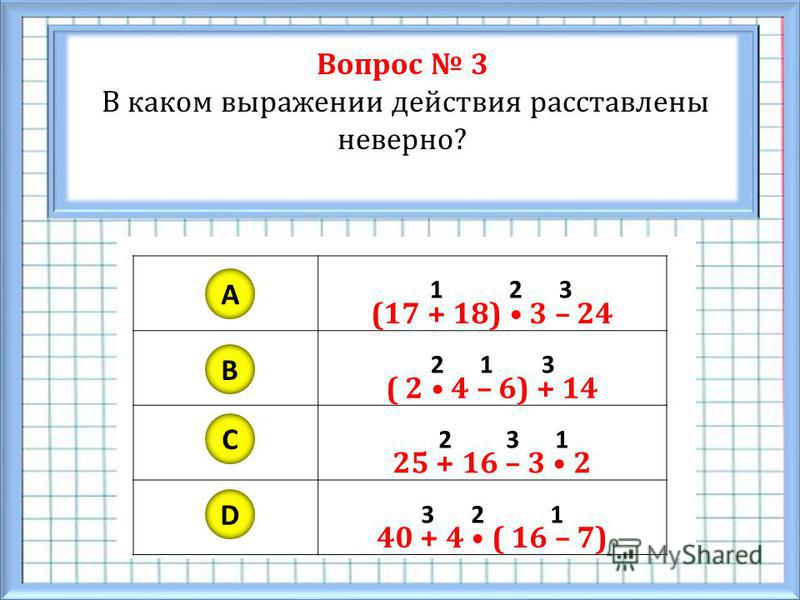

Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.

Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:

Не торопитесь давать ответ: правила хотя бы вспомните!

ВОПРОС 1 ИЗ 1

3

17

21

Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

• Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
• Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
• Последними выполняются сложение и вычитание. Это действия второй ступени.

Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.

Для закрепления рассмотрим следующий пример действия со скобками:

5+(7−2⋅3)⋅(6−4):2

В этом сложном примере со скобками порядок действий будет точно таким же.

Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2

Давайте подставим решение примеров в скобках в первоначальное выражение:

5+(1)⋅(2):2 .  

Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.

Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания. Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:

5+1⋅2:2=6

Таким образом первоначальный пример со скобками также будет равняться 6

5+(7−2⋅3)⋅(6−4):2=6.

Что такое скобки в математике? Определение, типы, примеры и использование

Что такое скобки?

Вы, должно быть, видели в учебниках по математике различные символы, подобные этим: (, ), [ ], { и }. Эти символы называются скобками. Скобки в математике служат очень важной цели; эти символы помогают нам сгруппировать различные выражения или числа вместе. Скобки подразумевают, что вещь или выражение, заключенное в них, должно иметь более высокий приоритет по сравнению с другими вещами.

Родственные игры

Различные виды скобок

В математике вам часто придется использовать скобки при создании или решении уравнений. Они помогают группировать числа и определять порядок операций. Как правило, в математике используются три вида скобок:

• Скобки или круглые скобки, ( )
• Фигурные скобки или фигурные скобки { }
• Квадратные или коробчатые скобы [ ]

Скобки всегда идут парами, и если есть открывающая скобка, должна быть и закрывающая скобка. Открывающие скобки: (, [  и {. Соответствующие им закрывающие скобки: ), ] и }.

Скобки Скобки

Они также известны как круглые скобки и записываются как ( ). Это самые распространенные виды брекетов. Они используются для группировки различных значений и уравнений вместе. Скобки или «круглые скобки» используются для группировки терминов или указания порядка операций в уравнении.

Как использовать скобки в математике?

1. В математике вы можете использовать скобки для разделения чисел. Например, вы можете использовать их для упоминания отрицательных чисел при написании уравнения сложения.

Вот пример, чтобы лучше понять это:

$3 + (−5) = −2$

2. Второе использование скобок в математике — умножение чисел. Если в уравнении нет арифметической операции, наличие скобок означает, что вы должны применить умножение.

Разберем это на примере:

$6 (4 + 2)$

можно записать как $6 \times (4 + 2)$

Следовательно, ответ: $6 \times 6 = 36$.

3. Третье и последнее применение скобок в математике — это группировка чисел и определение порядка операций.
4. При использовании просто вокруг чисел круглые скобки обозначают умножение.

Например: $(3)(4) = 12$

5. Их также можно использовать для записи отрицательных целых чисел в математических выражениях.

Например, $5 + (−4) = 1$

6. Скобки также можно использовать для отделения чисел от их показателей. {-3}$

Примеры: $(2 + 4), 5(111), 25 − (12 + 8)$ и т. д.

Фигурные скобки

Скобки в математике — это символы, которые используются дважды: один раз, чтобы закрыть «}» аргумент, выражение или уравнение. Их обычно называют фигурными скобками и записывают как {}.

В общем, мы используем фигурные скобки в математике для двух целей:

• Для группировки больших уравнений, в которых предпоследняя скобка является фигурными или фигурными скобками. Например, $7[2 + \влево\{3(1 + 1) + 1\вправо\}]$
• Для обозначения набора, например {x, y, z,…}

Как и круглые скобки, фигурные скобки также используются для группировки различных математических компонентов; однако фигурные скобки также используются для обозначения множеств или для написания вложенных выражений. Примеры: 

$[\left\{4+[3 \times ( −2)\right\}] − [\left\{(4 \times 6)+(14 \div 7)\right\} − ( −3)]$,

 $[\left\{12 − (12 − ​​2)\right\} + (5 − 7)] + 9$ и т. д.

Как мы используем фигурные скобки в математике?

Фигурные скобки в математике часто используются в математических выражениях, когда у нас есть две или более вложенных групп для вычислений.

Итак, в первой вложенной группе мы используем круглые скобки. Во второй вложенной группе мы используем фигурные скобки, а в третьей вложенной группе мы используем прямоугольные скобки, которые содержат как скобки, так и фигурные скобки.

Например: $3[2 − \left\{4(2 + 2) + 2\right\}]$

Здесь у нас есть три вложенные группы с соответствующими скобками.

Итак, порядок решения будет :

Забавный факт: Некоторые соглашения различают порядок решения скобок, а именно:

В этой статье мы будем использовать первое соглашение с фигурными скобками во второй позиции.

Вам необходимо знать БОДМАС или порядок операций, чтобы упростить и решить проблему.

Квадратные скобки

Квадратные скобки обычно используются для различения подвыражений сложного математического выражения.

Примеры: $[100 − (3 − 1) + (7 \times 8)], 10 \times [(4 − 2) \times ( 4 \times 2)]$ и т. д.

Порядок операций Кронштейны

Когда мы вычисляем математическое выражение, состоящее из разных скобок, мы должны следовать определенным правилам. Это называется правилами работы или порядком работы скобок.

Когда у нас есть длинное уравнение для умножения, деления, сложения и вычитания, мы решаем каждую функцию, чтобы найти правильный ответ. Если задача решается без этого порядка, то шансы получить неверный ответ высоки!

• Общий порядок работы скобки можно проиллюстрировать как $[ \left\{ ( ) \right\} ]$; это означает, что в данной задаче вам придется сначала упростить значения в самой внутренней скобке. Это означает, что сначала будут решены скобки $( )$, затем будут решены скобки $\left\{ \right\}$ и, наконец, скобки $[ ]$.
• Вторым шагом в решении этих задач является поиск показателя степени; если есть, решите сначала.
• На третьем шаге ищем выражения с операторами умножения или деления. Если оба оператора присутствуют, мы проверяем выражение слева направо. Какой бы оператор ни пришел первым, мы сначала решим этот оператор.

Например, в выражении $10 \times 6 \div 5$ мы проверяем слева направо, поскольку сначала идет умножение, поэтому мы сначала решаем умножение, а затем деление.

$10 \times 6 \div 5$ 

$=60 \div 5$

$= 12$

• На четвертом и последнем шаге мы ищем числа, которые нужно сложить или вычесть. Мы следуем той же инструкции, если присутствуют оба оператора, мы смотрим слева направо в выражении, и какой бы оператор ни был первым, мы решаем это выражение первым. Но если операции в скобках, мы всегда сначала решаем скобки, так как скобки имеют наивысший приоритет.

Чтобы запомнить упомянутые выше шаги, мы можем использовать аббревиатуру PEMDAS,

P – Круглые скобки (или квадратные скобки)

E – Показатель степени (или порядок)

M – Умножение

D – Деление

A – Сложение

S – Вычитание.

Пример 1. Воспользуемся pemdas для вычисления выражения Соблюдайте порядок решения сначала круглых скобок $( )$, затем фигурных скобок $\left\{ \right\}$, а затем квадратных скобок $[ ]$.

$ = 100 − [(2) + (56)] $

$= 100 − 58$

Шаг 2: В данном выражении нет показателя степени.

Шаг 3: В данном выражении нет ни умножения, ни деления.

Шаг 4: Решите вычитание.

$= 100 − 58$

$= 42$

Пример 2: Пока мы записываем порядок в приведенной выше форме, деление или умножение и сложение или вычитание имеют одинаковое значение. Это означает, что вы можете либо сначала заняться умножением, либо сначала делением.

Точно так же вы можете сначала выполнить либо сложение, либо сначала вычитание. Ответ будет таким же. Итак, мы обычно пытаемся решить эти две задачи слева направо.

Давайте решим приведенный выше пример:

$4[2 + \left\{3(1 + 1) + 2\right\}]$

Сначала мы начнем с самой внутренней скобки (скобки).

$= 4[2 + \left\{3(2) + 2\right\}]$

Теперь решим фигурные скобки.

$= 4[2 + \left\{6 + 2\right\}]$

$= 4[2 + 8]$

Затем мы раскрываем квадратные скобки.

$= 4[10]$

$= 40$

Итого:

Вот порядок, которому вы можете следовать, когда в уравнении присутствует несколько символов:

Если вы столкнетесь со скобками в уравнении, вы сначала посмотрите на содержащиеся в них термины.

Давайте лучше разберемся на примере.

Возьмем задачу: $9 − 10 \div 5 – 3 \times 2 + 7$

Давайте решим ее, используя порядок операций, который вы узнали.

$= 9 − 10 \div 5 – 3 \times 2 + 7$

$= 9 − 2 − 3 \times 2 + 7$ (Сначала вы делите)

$= 9 − 2 − 6 + 7 $ (Затем умножить)

$= 7 − 6 + 7$ (Затем вычесть)

$= 1 + 7$ (Затем вычитаете)

$= 8$ (И, наконец, складываете)

Теперь давайте рассмотрим ту же задачу со скобками: 

$9 − 10 \div (5 − 3) \times 2 + 7$

Сначала нужно вычислить числа в скобках.

$= 9 − 10 \div 2 \times 2 + 7$ (Решите выражение в скобках)

$= 9 − 5 \times 2 + 7$ (Разделение)

$= 9 − 10 + 7$ (Умножить)

$= −1 + 7$ (Добавить)

$= 6$

Вы заметили? Ответ на то же уравнение изменился, потому что в уравнении присутствовали круглые скобки!

Помните: если внутри других скобок есть скобки, сначала нужно решить внутреннее выражение.

Давайте разберем это на примере:

Упростим выражение $(2 + (3 х 4))$

Здесь мы сначала решим внутреннюю скобку.

Таким образом, выражение примет вид $(2 + 12) = 14$

Обратите внимание, что настоятельно рекомендуется записывать любое математическое уравнение или выражение с правильным использованием круглых скобок, не оставляя места для двусмысленности. Важно передать намерение написания математических операций и указать, какие операции следует выполнять в первую очередь.

Решенные примеры

Вопрос 1: Найдите значение выражения: $(5 + 4) − (3 − 2)$ .

Ответ: Данное выражение:

$(5 + 4) − (3 − 2)$,

Шаг 1: Решение значений в скобках,

$(9) − (1) $,

Таким образом, ответ: $(9) − (1) = 8$.

Вопрос 2: Найдите значение выражения: $\left\{(7 − 2) \times 3\right\}  \div 5$

Ответ: Данное уравнение равно

$\left\{(7 − 2) \times 3\right\}  \div 5$

Шаг 1: Решение скобок 

$\left\{(7 − 2) \times 3\right\} \div 5$

$= \left\{5 \times 3\right\} \div 5$

Решение фигурной скобки

$= \left\{15\right\} \div 5$

$ = 15 \div 5$

$= 3$

Вопрос 3: Найдите значение выражения: $(12 \div 6) \times (4 − 2)$

Решение:

Заданное уравнение г.,

$(12 \div 6) \times (4 − 2)$ 

Решение значений в скобках,

$(2) \times (2)$

Таким образом, ответ $(2) \times (2) = 4$

Вопрос 4: Найдите значение выражения: $[120 + \left\{ (3 \times 4) + (4 − 2) − 1 \right\} + 20 ]$

Ответ: Сначала по правилу PEMDAS, 1 \справа\} + 20 ]$

$= [ 120 + \left\{ (12 ) + ( 2 ) − 1 \right\} + 20 ]$,

Теперь вычисляем значения в скобках { },

$= [ 120 + \ left\{ 13 \right\} + 20 ]$,

Наконец, добавьте все значения в скобках [ ],

Ответ: 153.

Пример 5: Упростите выражение: $(2 + 4 \times 6) − 4 + (2 \times 3)$

Решение . Начните с решения выражений в скобках.

$= (2 + 24) − 4 + 6$ (умножить в скобках)

$= 26 − 4 + 6$ (Решите условия в скобках)

$= 22 + 6$ (Сложение)

$= 28$

Пример 6: Упростите выражение: $( 2 \ умножить на (7 − 5)) − ((6 \div 3) + 4)$

Начать с решения самых внутренних скобок

$= (2 \times 2) − (2 + 4)$

$= 4 − 6$

$= − 2$

Пример 7: Упростите выражение: $2 (3 + 5) + 8 (4 − 1)$

Сначала решите выражения в скобках.

Здесь скобки также обозначают знак умножения.

$= 2 х 8 + 8 х 3$

$= 16 + 24$

$= 40$

Пример 8: Если вам нужно решить следующее уравнение, как вы будете действовать?

$2[1 − \left\{2(2 + 2) + 2\right\}]$

Решение: Сначала раскроем скобки:

$= 2[1 − \left\{2 (4) + 2\right\}]$

$= 2[1 − \left\{8 + 2\right\}]$

Теперь решим фигурные скобки:

$= 2[1 − \left\{10\right\}]$

Наконец, разгадаем квадратные скобки:

$= 2[ −9]$

$= −18$

Пример 9: Как бы вы решили следующее уравнение?

$4\left\{5(4 + 2) + 1\right\}$

Решение: Сначала раскроем скобки:

$= 4\left\{5(6) + 1\ right\}$

Теперь нам нужно решить фигурные скобки. Но в этих скобках мы должны решить умножение и сложение.

Итак, сначала умножаем, а затем складываем:

$= 4 \left\{30 + 1\right\}$

$= 4 \left\{31\right\}$

Наконец, умножаем 4 со значением в фигурных скобках:

$= 124$

Пример 10. Как вы будете решать уравнение с более чем одной скобкой?

$20 \div \left\{1(2 + 2) + (3 + 3)\right\}$

Решение: Начнем с решения уравнений в скобках: 9{3}) \times 42\right\} − (20 \div 5)]$
$= [\left\{(4 + 27) \times 16\right\} − (4)]$
$= [ \left\{(31) \times 16\right\} − (4)]$
$= [{31 \times 16} − 4]$
$= [496 − 4]$
$= 492$

2

Какое правильное представление порядка работы в скобках?

$( \left\{ [ ] \right\} )$

$[ ( \left\{ \right\} ) ]$

$\left\{ [ ( ) ] \right\}$

$[ \left\{ ( ) \right\} ]$

Правильный ответ: $[ \left\{ ( ) \right\} ]$ 9{2} = 4096$

4

Решите это выражение, $12 + (5 + 3)$,

18

20

16

8

16

8

3 правильный ответ ) = 12 + 8 = 20$

5

Упростим выражение: $(3 + 2 х 8) – 4 + (5 х 7)$

45

50

20 5

4

5 400005 Правильный ответ: 50

Мы знаем, что сначала решается уравнение в скобках.
Итак, 19$ – 4 + 35 = 50$

6

Упростите выражение: $( 4 \times (6 – 2)) – ((8 \div 2) + 5 )$

7

2

17

10

90 Правильный ответ: 7
Мы знаем, что сначала решается уравнение в скобках.
Итак, $(4 х 4) – (4 + 5)$
$16 – 9 = 7$

7

Упростим выражение: $4 (3 + 2) + 4 (7 – 2)$

10

50

20

40

Правильный ответ: 40
Мы знаем, что скобки также обозначают умножение.
Таким образом, $4 \times 5 + 4 \times 5$
$20 + 20 = 40$

8

Решите уравнение, содержащее фигурные скобки, по математике.

$57 \div \left\{5 + (4 \times 2) + (3 + 3)\right\}$

3

4

13

4

Правильный ответ: 3
После решения задачи $( )$, выполняем сложение внутри $\left\{ \right\}$, а затем делим. $57 \div {5 + (4 2) + (3 + 3)} = 57 {5 + 8 + 6} = 57 19 = 3$

9

В каких из следующих примеров скобки, скобки и круглые скобки используются правильно ?

60 $\div$ [(2 $\times$ 2) + (3 + 3)}

60 $\div$ {(2 ​​$\times$ 2) + (3 + 3)}

60 $ \div$ {[2 $\times$ 2] + (3 + 3)}

(60 $\div$ {[2 $\times$ 2] + (3 + 3})

Правильный ответ: 60 $\div$ {(2 ​​$\times$ 2) + (3 + 3)}
Он правильно использует фигурные скобки, скобки и круглые скобки, потому что в самых внутренних скобках есть скобки, а затем фигурные скобки

10

Если у нас есть следующие выражения в фигурных скобках, какое из выражений вы бы решили в первую очередь?

$10\left\{(\frac{4}{2}) + (6 \times 2) – (3 + 3) + (7 – 2)\right\}$

$(\frac{4}{ 2})$

$(\frac{4}{2}) \text{or} (6 \times 2)$

Любые скобки внутри $\left\{ \right\}, (\frac{4 {2}), (6 \times 2), (3 + 3), (7 – 2)$}

Ничего из вышеперечисленного

Правильный ответ: Любые скобки внутри $\left\{ \right\ }, (\frac{4}{2}), (6 \times 2), (3 + 3), (7 – 2)$}
Сначала мы можем решить любую скобку внутри фигурных скобок. Как только эти скобки раскрыты, нам нужно просто складывать и вычитать, что можно делать в любом порядке.

Часто задаваемые вопросы

Почему скобки важны в математике?

Скобки являются очень важными частями математического уравнения; они отделяют разные математические выражения друг от друга и помогают установить приоритет для выражений, которые необходимо решить в первую очередь.

Является ли PEMDAS единственным методом решения проблем с брекетами?

BODMAS — это другой аббревиатура от PEMDAS, где B означает скобки, O — числа или степени, D — деление, M — умножение, A — сложение и S — вычитание. Любое выражение считается правильно решенным, если оно соответствует правилу PEMDAS или BODMAS.

Есть ли еще виды скоб?

Угловые скобки также используются в различных математических выражениях; они представлены с〈 〉. Угловые скобки используются для представления списка чисел или последовательности чисел.

В каких еще случаях используются скобки?

Скобки также используются для определения координат точки на карте или для описания переменной функции.

Круглые скобки — это то же самое, что фигурные скобки?

Нет. Скобки, обозначенные ( ), отличаются от фигурных скобок { }. Они имеют различные применения в математике. Они используются во вложенных выражениях. Вы узнаете о них больше позже.

Есть ли другое название для скобок?

Да. Иногда скобки также называют круглыми скобками.

Как называются { }?

Это фигурные скобки, также известные как фигурные скобки в математике. Скобки используются в математических уравнениях, когда мы делаем как минимум две вложенные группы для вычислений.

Какими еще способами мы можем использовать фигурные скобки, кроме как в математических уравнениях?

Фигурные скобки также используются для определения набора.

Например, $\left\{3, 5, 7, 9, 10\right\}$ означает набор, содержащий числа 3, 5, 7, 9, 10.

Фигурные скобки означают умножение?

Да, фигурные скобки также могут означать умножение. Вам нужно умножить значение вне фигурных скобок на значение внутри фигурных скобок.

Возьмем это уравнение в качестве примера: $2\left\{2(4 + 2) + 1\right\}$

Здесь 2 будет умножено на ответ в фигурных скобках или фигурных скобках.

Ассоциативное свойство сложения — примеры, определение, формула

LearnPracticeDownload

Ассоциативное свойство сложения — это свойство чисел, которое утверждает, что способ группировки трех или более чисел не меняет суммы этих чисел . Это означает, что сумма трех или более чисел остается неизменной независимо от того, как они сгруппированы. Давайте узнаем больше об ассоциативном свойстве сложения в этой статье.

1.	Что такое ассоциативное свойство сложения?
2.	Ассоциативное свойство формулы сложения
3.	Ассоциативное свойство сложения и умножения
4.	Часто задаваемые вопросы об ассоциативном свойстве добавления

Что такое ассоциативное свойство сложения?

Ассоциативное свойство сложения — это правило, которое гласит, что при сложении трех и более чисел мы можем сгруппировать их в любую комбинацию, и полученная сумма останется неизменной независимо от того, как они сгруппированы. В этом случае группировка относится к размещению скобок. Например, на приведенном ниже рисунке видно, что сумма чисел не меняется независимо от того, как сгруппированы слагаемые.

Ассоциативное свойство формулы сложения

Формула ассоциативности сложения показывает, что группировка чисел другим способом не влияет на сумму. Скобки, которые группируют числа, помогают упростить процесс сложения. Обратите внимание на следующую формулу для ассоциативного свойства сложения.

Давайте рассмотрим пример, чтобы понять и доказать формулу. Сгруппируем 13 + 7 + 3 тремя способами.

• Шаг 1: Мы можем сгруппировать набор чисел как (13 + 7) + 3, 13 + (7 + 3) и (13 + 3) + 7.
• Шаг 2: Сложите первый набор чисел, то есть (13 + 7) + 3. Далее это можно решить как 20 + 3 = 23.
• Шаг 3: Добавьте второй набор, т. е. 13 + (7 + 3) = 13 + 10 = 23.
• Шаг 4: Теперь решите третий набор, то есть (13 + 3) + 7 = 16 + 7 = 23.
• Шаг 5: Сумма всех трех выражений равна 23. Это показывает, что как бы мы ни группировали числа с помощью скобок, сумма остается неизменной.

Ассоциативное свойство сложения и умножения

Ассоциативное свойство применимо к сложению и умножению, но не существует к вычитанию и делению. Мы знаем, что ассоциативное свойство сложения говорит о том, что группировка чисел не меняет суммы данного набора чисел. Это означает, что (7 + 4) + 2 = 7 + (4 + 2) = 13. Точно так же ассоциативное свойство умножения говорит о том, что группировка чисел не меняет произведения данного набора чисел. Эта формула выражается как (a × b) × c = a × (b × c). Например, (2 × 3) × 4 = 2 × (3 × 4) = 24,9.0005

Важные примечания:

• Ассоциативность применима только к сложению и умножению.
• Ассоциативные свойства соответствуют возможности связывать или группировать числа, что невозможно в случае вычитания и деления.
• Ассоциативное свойство входит в список математических свойств, полезных при работе с математическими уравнениями и их решениями.

☛ Похожие темы

• Свойства дополнения
• Коммутативное свойство сложения
• Нулевое свойство умножения
• Свойство мультипликативной идентичности
• Распределительная собственность
• Коммутативное свойство
• Аддитивная идентичность против мультипликативной идентичности
• Распределительная собственность
• Ассоциативное свойство дополнительных рабочих листов

 

Ассоциативное свойство примеров сложения

1. Пример 1: Следует ли данное уравнение ассоциативному свойству сложения?
   (25 + 2) + 8 = 25 + (2 + 8)

   Решение: Следующие шаги помогут выяснить, следует ли данное уравнение ассоциативному свойству сложения или нет:

   • Шаг 1: Складываем набор чисел, указанный в левой части, то есть (25 + 2) + 8 = 27 + 8 = 35,
   • Шаг 2: Теперь сложите набор чисел, указанный в правой части, то есть 25 + (2 + 8) = 25 + 10 = 35.
   • Мы видим, что сумма, полученная из левой части уравнения, равна сумме, полученной из правой части. Итак, уравнение следует ассоциативному свойству сложения.

2. Пример 2: Вставьте пропущенное число и напишите сумму:

   7 + (10 + 6) = (7 + 10) + ___ = ___

   Решение: Согласно ассоциативному свойству формулы сложения, a + (b + c) = (a + b) + c. Если мы подставим значения в эту формулу, мы получим 6 как пропущенное число, то есть 7 + (10 + 6) = (7 + 10) + 6 , а сумма равна 23.

3. Пример 3: Выберите правильный вариант для отсутствующего номера.

   8 + (4 + 2) = (8 + ___) + 2

   а) 4

   б) 7

   в) 6

   Решение:

   По ассоциативному свойству сложения: а + (b + c) = (a + b) + c. Подставляя значения в формулу: 8 + (4 + 2) = (8 + 4 ) + 2,

   Следовательно, пропущенное число равно 4, потому что сумма обоих выражений равна 14,

   Следовательно, правильный вариант (а).

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы по ассоциативному свойству сложения

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по ассоциативному свойству дополнения

Что такое ассоциативное свойство сложения?

Ассоциативное свойство сложения гласит, что независимо от того, как набор из трех или более чисел сгруппирован вместе, сумма остается неизменной. Группировка чисел осуществляется с помощью скобок. Формула для этого свойства выражается как, a + (b + c) = (a + b) + c = (a + c) + b. Например, если мы сгруппируем числа 3 + 4 + 5 как 3 + (4 + 5) или (3 + 4) + 5, сумма, которую мы получим из обоих наборов, равна 12.

Что является примером ассоциативного свойства сложения?

Ассоциативное свойство сложения гласит, что группировка чисел не меняет их суммы. Например, (75 + 81) + 34 = 156 + 34 = 190; и 75 + (81 + 34) = 75 + 115 = 190. Сумма обеих сторон равна 190.

В чем преимущество использования ассоциативного свойства сложения?

Преимущество ассоциативного свойства сложения заключается в том, что оно помогает формировать более мелкие компоненты, что упрощает вычисление сложения. Группировка чисел с помощью скобок облегчает процесс упрощения выражения.

Как проверить ассоциативность сложения?

Ассоциативность сложения легко проверить, сложив заданный набор чисел. Например, сгруппируем 6 + 7 + 8 двумя способами.

• Шаг 1: Мы можем сгруппировать данный набор чисел как (6 + 7) + 8 и 6 + (7 + 8).
• Шаг 2: Теперь давайте сложим первый набор чисел, то есть (6 + 7) + 8. В результате получится 13 + 8 = 21.
• Шаг 3: Теперь добавим второй набор, то есть 6 + (7 + 8) = 6 + 15 = 21,
• Шаг 4: Сумма обоих выражений равна 21. Это доказывает ассоциативное свойство сложения, которое показывает, что независимо от того, как мы группируем числа с помощью скобок, сумма остается неизменной.

Всегда ли ассоциативное свойство сложения включает 3 или более чисел?

Да, ассоциативное свойство сложения всегда включает 3 или более чисел, потому что правило свойства гласит, что изменение группировки слагаемых не меняет суммы, а в случае только двух чисел мы не можем создавать группы.

Какова формула ассоциативного свойства сложения?

Формула ассоциативного свойства сложения утверждает, что сумма трех или более чисел остается неизменной независимо от того, как эти числа сгруппированы. Это выражается как, a + (b + c) = (a + b) + c = (a + c) + b.

В чем разница между коммутативным и ассоциативным свойством сложения?

Следующие пункты показывают разницу между коммутативным и ассоциативным свойством сложения:

• Переместительное свойство сложения утверждает, что изменение порядка слагаемых не меняет сумму. Например, 4 + 6 = 6 + 4 = 10. Ассоциативное свойство сложения утверждает, что группировка чисел не меняет сумму. Например, 8 + (2 + 3) = (8 + 2) + 3 = 13.
• Переместительное свойство сложения можно применять к двум числам, а ассоциативное свойство применимо к трем и более числам.
• В коммутативном свойстве сложения порядок слагаемых не имеет значения, а в ассоциативном свойстве сложения не имеет значения группировка слагаемых.

Как ассоциативное свойство сложения используется в повседневной жизни?

Есть много мест, где можно применить ассоциативное свойство сложения. Например, если мы тратим 3 доллара на кекс, 6 долларов на мороженое и 2 доллара на конфеты, мы можем сложить стоимость предметов в любом порядке как 3 + (6 + 2) или (3 + 6). + 2. Оба выражения дают одну и ту же сумму, то есть 11. Это показывает ассоциативное свойство сложения, которое гласит, что независимо от того, как мы группируем 3 или более чисел, сумма остается неизменной.