Математик геометрический мальчик: Юный математик покорил Максима Галкина – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Как понять, что у ребенка есть способности к математике?

Как распознать будущего математика еще в детском саду, рассказывает Лидия Бычкова, доцент факультета математики Высшей школы экономики.

Вопрос. Что такое способности к математике, существуют ли они и в каком возрасте вообще их можно увидеть? В каком классе можно сказать: ребенок точно гуманитарий, математика — это не про него?

Ответ. Есть дети, которые очень любят считать в маленьком возрасте — это основной критерий. Однозначно можно говорить о способностях к математике ребенка, который желает заниматься чем-то связанным с этим — считать, что-то решать, разгадывать какие-то головоломки, ручные или геометрические — тогда, когда его к этому никто никак не побуждает.

Если ребенка привели на кружок и предложили там что-то делать, он не сопротивляется и делает, возможно даже успешно, выигрывает олимпиаду, то можно говорить о том, что ребенок обучаем. Его смогли обучить, он научился. Но с математикой это не связано никак — может быть, он с таким же удовольствием научился бы чему-то другому и тоже бы показал результат.

Если школьника привели к очень хорошему учителю, который взял хорошие учебники и это дало отличные результаты, то это говорит о том, что ученику повезло с учителем, учебником и что ребенок, опять же, обучаем. Он способен взять и использовать то, что ему предлагали автор учебника и учитель. Но к математике это имеет косвенное отношение.

Верная примета — когда ребенок согласен сам, когда ему вообще никто ничего не предлагает, в свободное время, где-нибудь на даче летом вечерком заниматься тем, о чем узнал случайно от старшего брата или друзей.

Расскажу про самый большой в моей жизни педагогический успех. Это было в гуманитарной школе. После урока я не стираю с доски и следующий класс видит, что делал предыдущий. Пришли дети 7-го класса после 11-го и увидели на доске арксинус. Два мальчика-семиклассника попросили рассказать про арксинус. Я говорю: «Знаете, за перемену не получится». — «Мы можем когда-нибудь встретиться? Сегодня после уроков?» Я говорю: «Нет, после уроков не получится, у меня факультатив с 11-м классом до пяти». Я уже забыла этот разговор, когда в пять часов вечера открыла дверь в коридор и обнаружила в полумраке две скрюченные фигурки. Они сидели на полу и ждали, когда узнают, что такое арксинус.

Это был мой лучший момент. Я рассказала, что такое арксинус, до полного понимания. Мальчики поменяли профиль школы, сейчас это два прекрасных программиста. Их вообще никто никак не побуждал — это точно способности. Это не значит, что семикласснику нужно знать про арксинус. Но у него есть абсолютно бескорыстный интерес и готовность жертвовать — вот она, способность в чистом виде.

Мама одного замечательного современного математика рассказывала, как на прогулке в парке захотела показать двухлетнему сынишке белочку. Она стучала по дереву, чтобы белочка спустилась, и та действительно спустилась. Ребенок с горящими глазами говорит ей: «Три, три». Мама поднимает глаза и видит, что за этой белочкой спускаются еще две. Она говорит: «Тут я поняла, что с белочками мы закончили, математик уже родился». Он их уже посчитал. Он и белочке рад, и количеству — дело серьезное. Такие люди — в седьмом классе или в два года — имеют интерес ко всему, что связано с математикой.

Или Софья Васильевна Ковалевская — классический вариант прирожденного математика. В девять лет она читала листочки, приклеенные вместо обоев за кроватью, хотела понять, что это за значки, и поняла. Она поняла, что такое синус — не искала, кто ей расскажет, а сама догадалась. Когда она рассказала, призналась своему дяде, брату матери, он ошалел, пошел к отцу и заявил, что девочку учить надо. Семья пошла навстречу, взяла ей частного учителя из мужской гимназии. Вот они, способности. Если ребенок жаждет знать — это точно способности, его ничто не собьет.

Интервью с Лидией Бычковой на «Правмире»

Ваш вопрос лучшим специалистам об образовании и воспитании детей

Поскольку вы здесь. ..

У нас есть небольшая просьба. Эту историю удалось рассказать благодаря поддержке читателей. Даже самое небольшое ежемесячное пожертвование помогает работать редакции и создавать важные материалы для людей.

Сейчас ваша помощь нужна как никогда.

Подпишитесь на Правмир в

Выбор читателей «Правмира»

Подпишитесь на самые интересные материалы недели.

Сокровище геометрии | Наука и жизнь

Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI—XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.

Теорема Пифагора для случая равнобедренного прямоугольного треугольника.

Наука и жизнь // Иллюстрации

Иллюстрация к теореме Пифагора из «Трактата об измерительном шесте» (Китай, III век до н. э.) и реконструированное на его основе доказательство.

Наука и жизнь // Иллюстрации

С. Перкинс. Пифагор.

Чертёж к возможному доказательству Пифагора.

«Мозаика Пифагора» и разбиение ан-Найризи трёх квадратов в доказательстве теоремы Пифагора.

П. де Хох. Хозяйка и служанка во внутреннем дворике. Около 1660 года.

Я. Охтервелт. Бродячие музыканты в дверях богатого дома. 1665 год.

‹

›

Открыть в полном размере

Пифагоровы штаны

Теорема Пифагора едва ли не самая узнаваемая и, несомненно, самая знаменитая в истории математики. В геометрии она применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами a < b < c, усмотреть соотношение a

2 + b² = c² невозможно.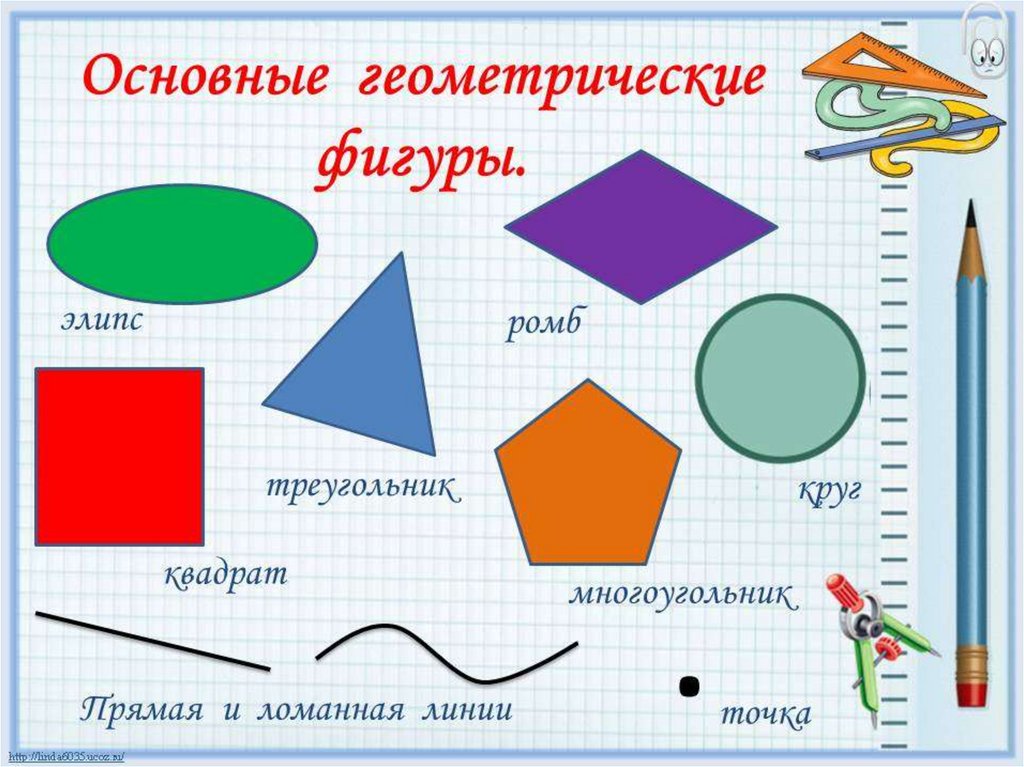

Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.

Фигуры, изображённые на рис. 1 и 2, напоминают простейший орнамент из квадратов и их равных частей — геометрический рисунок, известный с незапамятных времён. Им можно сплошь покрыть плоскость. Математик назвал бы такое покрытие плоскости многоугольниками паркетом, или замощением*. При чём тут Пифагор? Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.

4000 лет спустя

История теоремы Пифагора уходит в глубокую древность. Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора. Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне. Не исключено, что соотношение a² + b² = c² для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a² + a² = c². Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.

Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!

Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV—III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.

Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.

Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его… самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!

Первый математик

Пифагора Самосского (570—495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII—VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.

Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции. С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.

Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.

Такое простое доказательство

Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c. Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a² = c · m и b² = c · n. Тогда a² + b² = = c · (m + n) = c² (рис. 4).

Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять… Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.

Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны. Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.

Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.

Мозаика Пифагора

Если покрыть плоскость квадратами двух разных размеров, окружив каждый малый квадрат четырьмя большими, получится паркет «мозаика Пифагора». Такой рисунок издавна украшает каменные полы, напоминая о древних доказательствах теоремы Пифагора (отсюда его название). По-разному накладывая на паркет квадратную сетку, можно получить разбиения квадратов, построенных на сторонах прямоугольного треугольника, которые предлагались разными математиками. Например, если расположить сетку так, чтобы все её узлы совпали с правыми верхними вершинами малых квадратов, проявятся фрагменты чертежа к доказательству средневекового персидского математика ан-Найризи, которое он поместил в комментариях к «Началам» Евклида. Легко видеть, что сумма площадей большого и малого квадратов, исходных элементов паркета, равна площади одного квадрата наложенной на него сетки. А это означает, что указанное разбиение действительно пригодно для укладки паркета: соединяя в квадраты полученные многоугольники, как показано на рисунке, можно заполнить ими без пробелов и перекрытий всю плоскость.

Комментарии к статье

* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.

Карл Фридрих Гаусс | Биография, открытия и факты

Карл Фридрих Гаусс

Смотреть все СМИ

Дата рождения:: 30 апреля 1777 г. Брауншвейг

Умер:: 23 февраля 1855 г. (77 лет) Геттинген Ганновер

Награды и награды:: Медаль Копли (1838 г.)

Изобретения:: гелиотроп магнитометр

Известные работы:: «Арифметические исследования»

Просмотреть весь связанный контент →

Прочтите краткий обзор этой темы

Карл Фридрих Гаусс , настоящее имя Иоганн Фридрих Карл Гаусс , (родился 30 апреля 1777, Брауншвейг [Германия] — умер 23 февраля 1855, Геттинген, Ганновер), немецкий математик, обычно считается одним из величайших математиков всех времен за его вклад в теорию чисел, геометрию, теорию вероятностей, геодезию, планетарную астрономию, теорию функций и теорию потенциала (включая электромагнетизм).

Гаусс был единственным ребенком бедных родителей. Он был редкостью среди математиков тем, что был вундеркиндом и сохранял способность производить сложные вычисления в уме большую часть своей жизни. Впечатленные этой способностью и его даром к языкам, учителя и преданная мать рекомендовали его герцогу Брауншвейгскому в 179 г.1, который предоставил ему финансовую помощь для продолжения образования на месте, а затем для изучения математики в Геттингенском университете с 1795 по 1798 год. Новаторская работа Гаусса постепенно сделала его выдающимся математиком той эпохи сначала в немецкоязычном мире, а затем и за его пределами. , хотя он оставался далекой и отчужденной фигурой.

Викторина “Британника”

Викторина по астрономии и космосу

Первое значительное открытие Гаусса в 179 г.2, заключалась в том, что правильный многоугольник с 17 сторонами можно построить только с помощью линейки и циркуля. Его значение заключается не в результате, а в доказательстве, которое основывалось на глубоком анализе факторизации полиномиальных уравнений и открыло дверь более поздним идеям теории Галуа. Его докторская диссертация 1797 г. дала доказательство основной теоремы алгебры: всякое полиномиальное уравнение с действительными или комплексными коэффициентами имеет столько корней (решений), сколько его степени (наибольшей степени переменной). Доказательство Гаусса, хотя и не вполне убедительное, отличалось критикой более ранних попыток. Позже Гаусс дал еще три доказательства этого важного результата, последнее к 50-летию первого, что показывает важность, которую он придавал этой теме.

Узнайте о жизни и карьере математического гения Карла Фридриха Гаусса.

Просмотреть все видео к этой статье. по алгебраической теории чисел, Disquisitiones Arithmeticae . Эта книга начинается с первого описания модульной арифметики, дает подробное описание решений квадратных многочленов от двух переменных в целых числах и заканчивается упомянутой выше теорией факторизации. Этот выбор тем и их естественные обобщения определили повестку дня в теории чисел на протяжении большей части XIX века.

веке, и постоянный интерес Гаусса к этому предмету стимулировал множество исследований, особенно в немецких университетах.

Второй публикацией было его повторное открытие астероида Церера. Его первоначальное открытие, сделанное итальянским астрономом Джузеппе Пиацци в 1800 году, произвело сенсацию, но он исчез за Солнцем до того, как удалось провести достаточно наблюдений, чтобы рассчитать его орбиту с достаточной точностью, чтобы узнать, где он снова появится. Многие астрономы соревновались за честь найти его снова, но Гаусс победил. Его успех основывался на новом методе обработки ошибок в наблюдениях, который сегодня называется методом наименьших квадратов. После этого Гаусс много лет работал астрономом и опубликовал крупную работу по вычислению орбит — числовая сторона такой работы была для него гораздо менее обременительна, чем для большинства людей. Как чрезвычайно преданный подданный герцога Брауншвейгского и, после 1807 года, когда он вернулся в Геттинген в качестве астронома, герцога Ганноверского, Гаусс чувствовал, что его работа имеет общественную ценность.

Подобные мотивы побудили Гаусса принять вызов по обследованию территории Ганновера, и он часто отсутствовал в полевых условиях, отвечая за наблюдения. Проект, который длился с 1818 по 1832 год, столкнулся с многочисленными трудностями, но привел к ряду достижений. Одним из них было изобретение Гауссом гелиотропа (прибора, отражающего солнечные лучи в виде сфокусированного луча, который можно наблюдать на расстоянии нескольких миль), что повысило точность наблюдений. Другим было его открытие способа сформулировать понятие кривизны поверхности. Гаусс показал, что существует внутренняя мера кривизны, которая не меняется, если поверхность изгибается, но не растягивается. Например, круглый цилиндр и плоский лист бумаги имеют одинаковую внутреннюю кривизну, поэтому на бумаге можно делать точные копии фигур на цилиндре (как, например, в полиграфии). Но сфера и плоскость имеют разную кривизну, из-за чего невозможно составить абсолютно точную плоскую карту Земли.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

Гаусс опубликовал работы по теории чисел, математической теории построения карт и многим другим предметам. В 1830-х годах он заинтересовался земным магнетизмом и участвовал в первом в мире исследовании магнитного поля Земли (для его измерения он изобрел магнитометр). Вместе со своим геттингенским коллегой, физиком Вильгельмом Вебером, он сделал первый электрический телеграф, но некоторая ограниченность помешала ему энергично заняться изобретением. Вместо этого он извлек важные математические следствия из этой работы для того, что сегодня называется теорией потенциала, важной ветви математической физики, возникающей при изучении электромагнетизма и гравитации.

Гаусс также писал о картографии, теории картографических проекций. За свое исследование карт, сохраняющих угол, он был удостоен премии Датской академии наук в 1823 году. Эта работа была близка к предположению, что комплексные функции комплексной переменной обычно сохраняют угол, но Гаусс не сделал этого фундаментального утверждения. ясное понимание, оставив его Бернхарду Риману, который глубоко ценил работу Гаусса. У Гаусса были и другие неопубликованные идеи о природе сложных функций и их интегралов, некоторые из которых он поделился с друзьями.

На самом деле Гаусс часто отказывался публиковать свои открытия. Будучи студентом в Геттингене, он начал сомневаться в априорной истинности евклидовой геометрии и подозревал, что ее истинность может быть эмпирической. Для этого должно существовать альтернативное геометрическое описание пространства. Вместо того чтобы опубликовать такое описание, Гаусс ограничился критикой различных априорных защит евклидовой геометрии. Казалось, он постепенно убедился, что существует логическая альтернатива евклидовой геометрии. Однако, когда венгр Янош Бойяи и русский Николай Лобачевский опубликовали свои отчеты о новой неевклидовой геометрии около 1830 года, Гаусс не смог последовательно изложить свои собственные идеи. Можно объединить эти идеи в впечатляющее целое, в котором его концепция внутренней кривизны играет центральную роль, но Гаусс так и не сделал этого. Одни приписывали эту неудачу его врожденному консерватизму, другие — его непрекращающейся изобретательности, которая всегда влекла его к следующей новой идее, третьи — его неспособности найти центральную идею, которая управляла бы геометрией после того, как евклидова геометрия перестала быть уникальной. Все эти объяснения имеют некоторые достоинства, хотя ни одно из них не может быть исчерпывающим объяснением.

Другой темой, по которой Гаусс в значительной степени скрывал свои идеи от современников, были эллиптические функции. В 1812 году он опубликовал отчет об интересном бесконечном ряду и написал, но не опубликовал отчет о дифференциальном уравнении, которому удовлетворяет бесконечный ряд. Он показал, что ряды, называемые гипергеометрическими рядами, могут использоваться для определения многих знакомых и многих новых функций. Но к тому времени он знал, как использовать дифференциальное уравнение для создания очень общей теории эллиптических функций и полностью освободить теорию от ее истоков в теории эллиптических интегралов. Это был крупный прорыв, потому что, как обнаружил Гаусс в 179 г.0s теория эллиптических функций, естественно, трактует их как комплекснозначные функции комплексного переменного, но современная теория комплексных интегралов была совершенно неадекватна для этой задачи. Когда часть этой теории была опубликована норвежцем Нильсом Абелем и немцем Карлом Якоби примерно в 1830 году, Гаусс заметил своему другу, что Абель прошел одну треть пути. Это было точно, но это печальная мера личности Гаусса, поскольку он все еще воздерживался от публикации.

Гаусс сделал меньше, чем мог бы, и в других отношениях. Геттингенский университет был небольшим, и он не стремился расширить его или набрать дополнительных студентов. К концу его жизни через Геттинген прошли математики калибра Рихарда Дедекинда и Римана, и он был полезен, но современники сравнивали его стиль письма с жидкой кашицей: он ясен и устанавливает высокие стандарты строгости, но ему недостает мотивации и может быть медленным и утомительным, чтобы следовать. Он переписывался со многими, но не со всеми, людьми, достаточно опрометчивыми, чтобы написать ему, но мало что делал, чтобы поддерживать их публично. Редким исключением были случаи, когда Лобачевский подвергался нападкам со стороны других русских за его идеи о неевклидовой геометрии. Гаусс достаточно выучил русский язык, чтобы следить за полемикой, и предложил Лобачевского в Геттингенскую академию наук. Напротив, Гаусс написал Бойяи письмо, в котором сообщил ему, что он уже обнаружил все, что Бойяи только что опубликовал.

После смерти Гаусса в 1855 году открытие стольких новых идей среди его неопубликованных работ расширило его влияние на оставшуюся часть века. Принятие неевклидовой геометрии произошло не с оригинальными работами Бойяи и Лобачевского, а с почти одновременной публикацией общих идей Римана о геометрии, подробного и строгого изложения ее итальянцем Эудженио Бельтрами, а также частных заметок Гаусса и переписка.

Джереми Джон Грей

IBM100 – Фрактальная геометрия

Геометрия. Его принципам учат молодых студентов по всему миру. Теорема Пифагора. Площадь поверхности и объем. Пи. Эта классическая, или евклидова, геометрия идеально подходит для мира, созданного людьми. Но если рассмотреть структуры, существующие в природе, то, что находится за пределами гладкой человеческой конструкции, многие из этих правил исчезают. Облака — не идеальные сферы, горы — несимметричные конусы, а молния не движется по прямой. Природа груба, и до недавнего времени эту грубость невозможно было измерить. Открытие фрактальной геометрии сделало возможным математически исследовать виды грубых неровностей, существующих в природе.

В 1961 году Бенуа Мандельброт работал научным сотрудником в Исследовательском центре Томаса Дж. Уотсона в Йорктаун-Хайтс, штат Нью-Йорк. Талантливый молодой ученый, которому еще предстояло найти свою профессиональную нишу, Мандельброт был именно таким интеллектуальным индивидуалистом, благодаря которому IBM стала известна тем, что приняла на работу. Задача была достаточно простой: IBM участвовала в передаче компьютерных данных по телефонным линиям, но что-то вроде белого шума продолжало нарушать поток информации, прерывая сигнал, и IBM обратилась к Мандельброту за новым взглядом на проблему.

С детства Мандельброт всегда мыслил визуально, поэтому вместо использования устоявшихся аналитических методов он инстинктивно смотрел на белый шум с точки зрения форм, которые он генерировал, — ранняя форма широко известной сегодня практики IBM по визуализации данных. График турбулентности быстро выявил своеобразную характеристику. Независимо от масштаба графика, представляли ли он данные в течение одного дня, одного часа или одной секунды, картина возмущения была на удивление одинаковой. Работала более крупная структура.

Эта проблема была знакома Мандельброту, и он вспомнил совет, который много лет назад дал ему его дядя-математик Золем Мандельбройт во Франции: попытаться сделать что-то из малоизвестных теорий итераций, созданных французскими математиками Пьером Фату и Гастоном Жюли. Их работа заинтриговала математиков всего мира и вращалась вокруг простейших уравнений: z = z² + c . С переменной z и параметром c это уравнение отображает значения на комплексной плоскости, где ось x измеряет действительную часть комплексного числа, а ось y измеряет действительную часть комплексного числа. мнимая часть ( i ) комплексного числа.

Во время совета Мандельброт не мог найти прорыва, но интеллектуальная свобода, которую он нашел в IBM, позволила ему полностью включиться в этот новый проект. В 1980 году, опираясь на технологии и талант IBM, Мандельброт использовал мощные компьютеры для итерации уравнения или использования первого результата уравнения в качестве следующего ввода. С помощью этих компьютеров Мандельброт обрабатывал и манипулировал числами тысячу раз, миллион раз и выводил результаты в виде графиков.

В результате получилась неуклюжая форма, похожая на жука, и это, мягко говоря, озадачивало. Но когда Мандельброт пригляделся, он увидел детализированные края этого образования, содержащие меньшие, повторяющиеся версии более крупного жукоподобного образования. Более того, каждая уменьшенная версия содержала более сложные детали, чем предыдущая версия. Эти структуры не были совершенно одинаковыми, но общая форма была поразительно похожа, отличались лишь детали. Как оказалось, специфика этих деталей ограничивалась только мощностью машины, вычисляющей уравнение, и подобные формы могли существовать вечно, раскрывая все больше и больше деталей в бесконечном масштабе. Это была определенная геометрия, у этой шероховатости были свои правила и параметры, но это была форма геометрии, ранее не идентифицированная научным сообществом.

Мгновенно Мандельброт понял, что он что-то понял. Он увидел несомненно органические структуры в деталях этой формы и быстро опубликовал свои выводы. Эта форма и структура, позже известная как множество Мандельброта, была необычайно сложным и красивым примером «фрактального» объекта, фрактал — это название, придуманное Мандельбротом в 1975 году для описания таких повторяющихся или самоподобных математических паттернов. Но так было до его книги 1982 года, Фрактальная геометрия природы , что Мандельброт получит общественное внимание и широкую легитимность. В этой книге Мандельброт осветил многочисленные проявления фрактальных объектов в природе. Самым простым примером, который он привел, было дерево. Он отметил, что каждое расщепление дерева — от ствола к ветви и так далее — было удивительно похоже, но с небольшими различиями, которые обеспечивали увеличение деталей, сложности и понимания внутренней работы дерева в целом. Верный своим академическим корням, Мандельброт вышел за рамки идентификации этих естественных примеров и представил надежные математические теории и принципы, на которых основывалась его недавно придуманная «фрактальная геометрия».

Возникла геометрия космоса, которая нарушила все евклидовы законы рукотворного мира и подчинялась свойствам природного мира. Мандельброт утверждал, что если бы кто-то идентифицировал существенную структуру в природе, концепции фрактальной геометрии можно было бы применить, чтобы понять ее составные части и сделать предположения о том, чем она станет в будущем. Этот новый взгляд на окружающее, это новое восприятие реальности привели с тех пор к ряду замечательных открытий в отношении мира природы и человека и показали, что они не так разъединены, как считалось раньше.

Возьмем, к примеру, биологию. Фрактальные паттерны появились почти во всех физиологических процессах в нашем организме. Веками считалось, что человеческое сердце бьется регулярным, линейным образом, но недавние исследования показали, что истинный ритм здорового сердца радикально колеблется в отчетливой фрактальной схеме. Кровь также распределяется по всему телу фрактальным образом. Исследователи из Торонто используют ультразвуковую визуализацию для определения фрактальных характеристик кровотока как в здоровых, так и в больных почках. Надежда состоит в том, чтобы измерить фрактальные размеры этих потоков крови и использовать математические модели для обнаружения раковых клеточных образований раньше, чем когда-либо прежде. При фрактальном подходе врачам не нужны более четкие медицинские изображения или более мощные машины, чтобы увидеть эти крошечные предраковые структуры. Математика, а не микроскопы, обеспечит самое раннее обнаружение.

Биология и здравоохранение — это лишь некоторые из последних приложений фрактальной геометрии. Развитие, вытекающее из множества Мандельброта, столь же разнообразно, как и привлекательные формы, которые оно порождает. Антенны на основе фракталов, улавливающие широчайший диапазон известных частот, в настоящее время используются во многих беспроводных устройствах. Программы графического дизайна и редактирования изображений используют фракталы для создания красивых сложных ландшафтов и реалистичных спецэффектов. А фрактальный статистический анализ лесов может измерить и количественно определить, сколько углекислого газа мир может безопасно переработать.

Сегодня мы только поверхностно коснулись того, чему нас может научить фрактальная геометрия. Погодные паттерны, колебания цен на фондовом рынке и скопления галактик оказались фрактальными по своей природе, но что мы будем делать с этим открытием? Куда приведет нас кроличья нора? Возможности, как и множество Мандельброта, безграничны.

Бенуа Мандельброт был интеллектуальным мастером на все руки. Хотя он всегда будет известен своим открытием фрактальной геометрии, Мандельброт также заслуживает признания за преодоление разрыва между искусством и математикой и демонстрацию того, что эти два мира не исключают друг друга.