Логічні задачі: Логические задачи для 3 класса с ответами и решениями, задания на логику для детей 9-10 лет

Логические задачи для 3 класса с ответами и решениями, задания на логику для детей 9-10 лет

Занимательная математика / 3 класс / Задачи на логику

Задания на логику для 3 класса от ЛогикЛайк — это более 300 видов занимательных задач и упражнений. Подсказки, решения и пояснения помогут научиться решать любые задачи.

Попробуйте развивающий курс ЛогикЛайк!

Выберите возраст для старта

3 класс

4+ класс

Рекомендуем тематические курсы

онлайн для 3 класса

Курс логики и мышления Начать

Подготовка к олимпиаде Начать

Почему дети и родители выбирают ЛогикЛайк?

2 варианта занятий, выбор сложности

• Пройдите 3 стартовые главы курса логики – и откройте доступ к разным категориям. Попробуйте «Логические задачи», «Закономерности», «Истина и ложь», «Умный счёт».
• Попробуйте задания разного уровня сложности: «Новичок», «Опытный», «Эксперт».

На LogicLike.com дети учатся рассуждать, развивают логику, способности к математике и познавательный интерес.

У нас есть всё, что вы искали!

Попробуйте задания от ЛогикЛайк

Логические задачи

Вопросы и загадки на логику

Задания на 2D- и 3D‑мышление

Простые высказывания

Математические ребусы

Графические и числовые закономерности

Начать курс! Начать курс!

Решение логических задач по математике — один из самых полезных способов тренировки ума, развития мышления и сообразительности у младших школьников. Смотрите подробный материал о развитии логики у детей.

Задачи на логику 2-3 уровня сложности

Подборка из обучающего курса ЛогикЛайк

Для ознакомления предлагаем несколько задач из раздела «Классические логические задачи». У нас ещё очень много (более 3500) интересных задач: логические, математические, пространственные головоломки от простых к сложным.

Задача 1. На разделение предметов

Условие: Для проведения очередного опыта Профессор купил 9 металлических стержней.
Некоторые из них он распилил на 5 частей. Всего стало 33 стержня.

Вопрос: Сколько стержней распилил Профессор?

Cмотреть решение

Ответ:

6 стержней.

Решение
Если распилить один стержень на 5 частей, то количественно добавляется 4 куска.

Всего добавилось 33 – 9 = 24 куска.
Значит, ученый распилил 24 : 4 = 6 стержней.

Решать задачи онлайн!

ВСЯ ЛОГИКА В ИГРОВОЙ ФОРМЕ!

• Гибкий ум и уверенность Когда дети решают задачи и головоломки на LogicLike, они тренируют «извилины» и развивают смекалку.
• Фундамент для IT Учим работать с информацией, тренируем память и развиваем логико-математический интеллект.
• Свобода родителю Потратьте 20-30 минут на себя, пока ребёнок занят полезным делом.

Начать занятия!

Задача 2. Разрезание на части

Условие: Юра разрезал огромную пиццу на 10 кусков. Затем он взял один из кусков и разрезал его еще на 10.

После этого из имеющихся кусков он выбрал два и разрезал каждый из них на 10.

Вопрос: Сколько в результате кусков пиццы у него получилось?

Показать решение

Ответ:

37 кусков.

Решение

После того, как Юра разрезает один кусок пиццы на 10 кусков, общее количество кусков увеличивается на 9
(1 кусок исчезает — разрезается, но вместо него появляется 10 новых).
Изначально был один кусок (целая пицца), а всего, по условию задачи, указанную операцию Юра проделал 4 раза. Следовательно, общее количество кусков увеличилось на 9 ∙ 4 = 36.
Всего стало 1 + 36 = 37 кусков.

Научиться решать задачи!

Задача 3. Сосчитай количество попаданий в цель

Условие: В компьютерной игре нужно победить монстра.
Изначально у Юры было только 9 выстрелов. Но за каждое попадание он получал дополнительно еще 3 выстрела.

Вопрос: Сколько раз Юра попал в цель, если всего он выстрелил 30 раз, израсходовав все выстрелы?

Узнать ответ

Ответ:

7.

Комментарий:
30 – 9 = 21 – столько дополнительных выстрелов Юра заработал за попадания.
За каждое попадание давалось 3 выстрела:
21 ÷ 3 = 7 попаданий.

Начать интерактивные занятия!

Взять подсказку

Подсказка

Решить эту задачу можно методом последовательных рассуждений, а можно еще быстрее и проще.

Занятия на ЛогикЛайк помогут научиться с легкостью решать любые задачи на логику и сообразительность.

Решайте 10-15 разных задач в день: математические ребусы, текстовые логические, пространственные, закономерности, алгоритмы и другие.

Понравился материал? Поделитесь с друзьями!

Научим решать любые логические задачи

Более 150 000 детей и родителей со всего мира уже занимаются на сайте ЛогикЛайк. Подключайтесь и развивайте логику и мышление.

Начать обучение! Начать обучение

Другие категории заданий

по возрасту и по темам

5-6 лет

6-7 лет

1 класс

2 класс

4 класс

Логические задачи

45 интересных загадок на логику с ответами

Логика для детей | Загадки

Увлекательные загадки на логику и сообразительность для детей и взрослых – на сайте и в приложении ЛогикЛайк.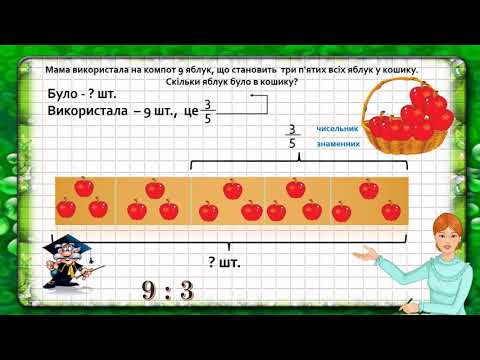 Вопросы с подвохом, смешные и серьёзные, простые и сложные – более 3500 заданий.

Выберите возраст ученика, чтобы начать

4-6 лет

1 класс

2 класс

3 класс

4-5 класс

старше

ЛогикЛайк — онлайн-платформа для развития мышления у детей и их родителей. Разгадывайте загадки, решайте головоломки и развивайте логику в игровом формате!

Содержание

• Зачем решать логические загадки?
• Логические загадки для детей
• Загадки на логику с подвохом
• Смешные логические загадки
• Загадки-обманки на внимательность
• Логические загадки для взрослых
• Сложные загадки на логику

Зачем детям и взрослым решать логические загадки?

• Многие дети и взрослые любят загадки просто потому, что это интересно и занимательно.
• Процесс отгадывания, поиска ключа к недоговоренному, зашифрованному улучшает настроение и тренирует ум.
• Хорошие загадки расширяют кругозор и развивают наблюдательность.
• Кто отгадывает загадки регулярно – развивают логику, скорость мышления, сообразительность и находчивость.
• Когда дети решают логические задачи, они учатся анализировать информацию, мыслить логически правильно, рассуждать и принимать решения.

ЛогикЛайк — увлекательный обучающий комплекс для развития логики, мышления и кругозора. Начните курс мышления на сайте или в приложении прямо сейчас!

Хотите просто посмотреть логические задачи? Вам сюда — задачи на логику и смекалку.

Простые загадки на логику для детей

• Загадки для детей 4-5 лет
• Загадки для 6 лет
• Загадки для детей 7 лет
• Загадки для 8 лет
• Загадки для 9 лет
• Загадки для детей 10 лет

Это кто то тут, то там
тускло светит по ночам?
Словно горстка звезд с небес,
опустилась ночью в лес.

Узнать ответ

Светлячок.

Бывает маленьким, большим.
Железо очень дружит с ним.
С ним и незрячий непременно
найдет иголку в стоге сена.

Узнать ответ

Магнит.

Hа суку сидит ворона. Что надо сделать, чтобы отпилить сук, не потревожив ворону?

Узнать ответ

Дождаться пока она улетит.

Решать интерактивные загадки и задачи!

Странный дождь порой идет:
сотней струй он кверху бьет.

Узнать ответ

Фонтан.

Вот так чудо! Вот так диво!
Как сорвался он с обрыва,
так уже который год
все никак не упадет.

Узнать ответ

Водопад.

Можно выполнять задания онлайн. Собирайте звёзды, соревнуйтесь и развивайте интеллект!

Как каплю превратить в цаплю?

Узнать ответ

Заменить букву «к» на «ц».

Чем больше из неё берёшь, тем больше она становится.

Узнать ответ

В клетке находились 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?

Узнать ответ

Одной девочке дали кролика вместе с клеткой.

У отца Мэри есть 5 дочерей: Чача, Чичи, Чече, Чочо. Как зовут 5 дочь?

Узнать ответ

Кто может поднять и передвинуть и коня, и слона?

Узнать ответ

Шахматист.

Нужны ещё похожие детские загадки? Перейти к загадкам на логику для детей: простые и сложные, загадки на внимательность и с подвохом.

Отгадывайте загадки онлайн, решайте логические задачи и головоломки ЛогикЛайк!

Простые загадки

Логические задачи

Математические загадки

Загадки дошкольнику

Загадки школьнику

Загадки взрослому

Начните заниматься логикой сегодня — игровая форма, пошаговая методика, удовольствие от процесса.

Логические загадки и вопросы с подвохом

Висит груша — нельзя скушать. Не лампочка.

Узнать ответ

Это чужая груша.

Любят, с искренностью всей, в дом пускать они гостей,
Но в гостях, скажу вам сразу, сами не были ни разу.

Узнать ответ

Двери.

Растет в саду берёза.
У нее 5 больших веток.
На каждой большой ветке по 10 маленьких веточек,
на каждой маленькой веточке — по 1 яблоку.
Сколько всего яблок растет на этом дереве?

Узнать ответ

А разве яблоки на берёзах растут?

Электричка едет на восток со скоростью 80 км/час. В какую сторону летит дым?

Узнать ответ

Электрички не дымят (если нет пожара).

Алиса написала на листке бумаги число 86 и спросила у своей подружки Иришки:
«Можешь увеличить это число на 12 и показать мне ответ, ничего не зачеркивая, и не дописывая?»
Иришка справилась. А вы сможете?

Узнать ответ

Переверни листок на полоборота и увидишь 98.

Бывает лёгкой и тяжёлой, но ничего не весит.
Бывает быстрой и медленной, но не ходит, не бегает, не летает.
Что же это?

Узнать ответ

Музыка.

Быстро топчешься на месте,
Он летит с тобою вместе.

Узнать ответ

Велосипед.

Хотите ещё загадки с подковыркой? Смотрите другие загадки и вопросы с подвохом – отгадывайте и развивайте нестандартное мышление.

Хотите развить логику? Начать занятия!

Смешные и шуточные загадки на логику

Какой рукой нужно размешивать чай?

Узнать ответ

Чай нужно размешивать ложкой, а не рукой.

Что делает сторож, когда у него на голове сидит воробей?

Узнать ответ

На уроках будешь спать —
За ответ получишь …

Узнать ответ

Два, скорее, а не пять.

Две стройные колонны
Держат замок огромный:
С двумя окошками,
Уступами, подножками.
Колонны не стоят на месте,
Всегда гуляют с замком вместе.

Узнать ответ

На самом перекрёстке
Висит колдун трёхглазый,
Но никогда не смотрит
Тремя глазами сразу.

Узнать ответ

Светофор.

Вот короткая загадка:
У кого за носом пятка?

Узнать ответ

Обувь / туфли / ботинки.

Есть ли где такое поле,
Где конь через коня прыгает?

Узнать ответ

Шахматное поле.

Нужны ещё весёлые загадки? Смотрите подборку смешных и шуточных загадок на логику.

День за днём более 250 000 детей и взрослых

решают и разгадывают по 10-20 задач и загадок на сайте ЛогикЛайк. А сколько сможете вы?

Логические задачи

Загадки и вопросы

Занимайтесь в удобное для вас время, с любого устройства! Всего 15 минут в день – и мозг в тонусе.

Рифмованные загадки-обманки

Во дворе трещит мороз,
шапку ты надень на …

Узнать ответ

голову (не нос).

Моим сестричкам маленьким
купили к лету …

Узнать ответ

босоножки (не валенки).

Смотреть больше загадок про времена года.

На прививки и уколы
мамы деток водят в …

Узнать ответ

поликлинику (не школу).

Подобрать себе я смог
пару варежек для …

Узнать ответ

рук (не ног).

Хоккеистов слышен плач
пропустил вратарь их …

Узнать ответ

шайбу (не мяч).

Вышел зайчик погулять,
лап у зайца ровно …

Узнать ответ

четыре (не пять).

У Иринки и Оксанки
трехколесные есть …

Узнать ответ

велосипеды (не санки).

Хотите ещё загадки-обманки? Переходите к подборке загадок-обманок, тренируйте внимание и развивайте чувство юмора.

Готовы начать приключение? Вперёд к знаниям!

Загадки и вопросы на логику для взрослых

Что принадлежит вам, однако другие этим пользуются чаще, чем вы сами?

Узнать ответ

Ваше имя.

Не ружьё, а стреляет, не змея, а шипит. Не водка, а …

Узнать ответ

Шампанское.

В небе одна, в земле нету, а у бабы их целых две.

Узнать ответ

Буква «Б».

Кто ходит сидя?

Узнать ответ

Шахматист.

На столе 70 листов бумаги.
За каждые 10 секунд можно посчитать 10 листов.
Сколько секунд понадобится, чтобы отсчитать 50 листов?

Узнать ответ

20 секунд (70 – 10 – 10 – остается 50).

Что делать, если вы сели в машину и собрались ехать, а ноги не достают до педалей?

Узнать ответ

Пересесть на водительское сиденье.

«Завязать» можно,
А развязать не получится.

Узнать ответ

Разговор.

Нужны ещё хорошие загадки для взрослой компании? Смотрите нашу подборку загадок для взрослых: на логику и с подвохом, смешные и серьезные.

Хотите занять ребёнка? Начните занятия для детей с 5 лет.

Сложные логические загадки и задачки

Что не является вопросом, но требует ответа?

Узнать ответ

Звонок в двери или по телефону.

Из половины коробки с деталями у робота Клапана получается 3 фигурки роботов.
Сколько фигурок он сможет сделать из 2 таких коробок?

Узнать ответ

Когда всё видишь, то её не видишь,
А когда ничего не видишь, то её видишь.

Узнать ответ

Темнота.

Зайка очень любит шутить. Он задал маме такую загадку:
«Если бы я был тяжелее медведя, но легче божьей коровки, кто был бы самым лёгким?»

Узнать ответ

Медведь.

Перейти к подборке загадки о животных с ответами.

Что вчера было «завтра», а завтра будет «вчера»?

Узнать ответ

«Сегодня».

Профессор решил угостить друзей своим фирменным овощным салатом.
Для этого ему понадобилось: перца – 3 штуки и столько же помидоров; огурцов меньше, чем помидоров, но больше, чем редисок.
Сколько всего штук разных овощей использовал Профессор в салате?

Узнать ответ

Посмотрите все загадки про фрукты и овощи от команды ЛогикЛайк.

Дед Вруниш (всегда лжёт) и дед Правдиш (говорит только правду) решили взять домой одного бездомного кота.
Правдиш: Рыжего кота брать не будем.
Вруниш: Возьмём белого.
Какого кота возьмут в дом?

Узнать ответ

Чёрного.

Что тяжелее: рюкзак или чемодан?

Подсказка

Сперва сравни массу Клапана с массой чемодана и рюкзака.

Нужны только сложные вопросы? У нас есть и другие трудные загадки.

Вернуться в раздел Загадки для детей.

Подключайтесь к ЛогикЛайк!

Учим работать с информацией и развиваем мышление. Более 2000 логических загадок и задач с пояснениями

Начать занятия! Начать занятия!

Логические задачи на собеседовании тестировщика |

Собеседование на должность тестировщика ПО включает несколько этапов: интервью с HR-специалистом, с техническим экспертом, а также проверка навыков логического мышления.

Сначала вас попросят рассказать общую информацию о себе, о мотивации работы в QA и зададут базовые вопросы на понимание предметной области. Это нужно, чтобы понять уровень ваших знаний, умение применять их на практике и оценить готовность обучаться и развиваться в новой сфере.

Затем технический эксперт проверит ваши аналитические способности, задав несколько вопросов на логику. Такие задания обычно нестандартные и требуют размышления. В этот момент не нужно паниковать и молчать. Не знаете ответ наверняка? Рассуждайте вслух, даже если задача кажется очень трудной.

В этой статье мы собрали примеры головоломок, нередко встречающихся на собеседованиях в ИТ-компаниях и их решения. Перед тем как узнать ответ, попробуйте найти разгадку самостоятельно.

С какими задачами я могу столкнуться на интервью при трудоустройстве в QA?

На собеседовании встречаются различные задачи, которые помогают специалистам компании сформировать представление о вас, как о кандидате. Такие задания не всегда имеют однозначное решение. Здесь важно показать умение мыслить логически и нестандартно.

#1 Фишки

Предположим, вы выиграли в казино стопку фишек высотой с Empire State Building. Каждая фишка равнозначна пяти долларам США. Поместятся ли все фишки в телефонной будке?

Решение. Прежде всего стоит оценить высоту Empire State Building. Она составляет примерно 100 этажей, а значит больше высоты обычной комнаты в 100 раз. Представим, что мы разделили фишки на 100 равных по высоте стопок высотой в один этаж. Таким образом получилась матрица 10 на 10. Возможно ли разместить её в телефонной будке? Вполне.

#2 Задача от Microsoft

Есть три стакана: с черникой, земляникой и смесью ягод. Каждый стакан помечен неверно. Вы можете достать один плод из одного стакана, при этом заглядывать внутрь нельзя. Как узнать содержимое всех стаканов и правильно расставить метки?

Решение. Так как стаканы подписаны неверно, ни в одном из них не лежит то, что указано на пометках. Стоит начать с надписи смесь (С). Достанем ягоду — черника? Значит этот стакан с черникой. Остаётся два стакана с пометкой черника (Ч) и земляника (З). В стакане (З) может быть черника или смесь. Но так как чернику мы уже нашли, то в стакане с пометкой (З) может быть только смесь. И в последнем стакане с пометкой (Ч) останется земляника.

#3 Сосуды с водой

У вас в запасе бесконечный источник воды, а также два сосуда — на 5 литров и 3 литра. Как отмерить 4 литра, используя только данный инвентарь?

Решение. Для начала необходимо наполнить ёмкость в 5 литров и вылить часть воды в трёхлитровый сосуд. Сейчас в меньшем сосуде находится 3 литра, в большом — 2. Затем нужно полностью опустошить маленькую ёмкость и перелить в него оставшуюся воду из большого. После этого, заново наполнить пятилитровый сосуд и перелить из него воду в трёхлитровую ёмкость. За счёт уже имеющихся 2 литров, доливать придётся всего литр, а в большей ёмкости останется 4 литра.

#4 Задача от Apple

На Землю напали инопланетяне и планируют её уничтожить. Однако они решили дать человечеству шанс. Выбрали десять самых умных людей, посадили их в ряд в абсолютно тёмной комнате и надели на них шляпы. Шляпы были либо жёлтые, либо синие.

После включения света инопланетянин начинает спрашивать последнего человека в ряду, какого цвета шляпа у него на голове. Люди должны соблюдать следующие условия при ответе: говорить только цвет головного убора и не молчать. Если ответ правильный, человек выживает, если нет — умирает.

Людям запрещено смотреть цвет своих шляп, но можно договориться между собой о некотором принципе ответов. Цветные шляпы располагаются в случайном порядке. Отвечающий видит все шляпы, кроме своей.

Вопрос: что нужно отвечать, чтобы осталось в живых как можно больше людей?

Решение. Первый отвечающий подсчитывает количество синих шляп. Если в итоге получилось нечётное число, он называет «синий», если чётное — «жёлтый». Так, заранее оговорив шифр, следующий человек может понять какого цвета шляпа у него на голове, имея в обзоре оставшихся людей. Например, если синих всё ещё нечётное количество, то на нём — жёлтая. Таким образом, со стопроцентной вероятностью выживут 9 из 10, а у первого шансы 50 на 50.

#5 Загадочная смерть

В поле был найден мёртвый человек. В его руке обнаружили спичку. При каких обстоятельствах погиб человек?

Решение. Это одна из тех задачек, о которых мы говорили в начале статьи. Суть не в правильном ответе, а в том, чтобы увидеть, как кандидат будет использовать воображение.

Например, этот человек умер при крушении самолёта. В момент аварии на борту не оказалось парашютов, и пассажирам пришлось тянуть жребий. Найденному человеку не повезло.

#6 Дождь и солнце (напоследок самое лёгкое задание)

Сейчас два часа ночи. За окном моросит дождь. Насколько велика вероятность того, что через 71 час будет солнечная погода?

Решение. Так как через 71 час также будет ночь, вероятность составит 0%.

Как можно подготовиться к этапу собеседования с логическими задачами?

Практика, практика и ещё раз практика. Есть большое количество сборников с заданиями на логику, которые помогут развить аналитические способности. К тому же, зачастую на интервью при трудоустройстве встречаются однотипные задачи, а значит, чем больше задач вы уже решили, тем выше шанс справиться с ним быстрее.

Также тренировать свои навыки в логике можно через настольные игры или мобильные приложения. Например, чтобы в долгой поездке провести время с пользой, загрузите несколько приложений и порешайте логические задачи.

Слушайте условия внимательно. Например, задача про дождь и солнце строилась на одних обстоятельствах, которые многие пропускают из-за невнимательности. Всегда можно переспросить: так вы получите дополнительное время, чтобы тщательнее обдумать детали.

Читайте форумы. В интернете вы сможете получить уникальную информацию от кандидатов, которые уже проходили собеседования, и задать интересующие вопросы.

В завершение

Каждый специалист ― как начинающий, так и продвинутый тестировщик ― сталкивается с логическими задачами на собеседовании. Важно помнить, что ваша цель ― это не ответ на скорость или бездумное заучивание ответов. Важно показать, что вы действительно умеете размышлять и мыслить логически.

Рассуждайте, ищите новые идеи, и должность QA-специалиста точно станет вашей!

Логические задачи, которые задают на собеседованиях: топ-10

Иногда на собеседованиях предлагают решить логические задачи, чтобы посмотреть, как быстро кандидат на должность примет решение.

Видео дня

Даже если ваш ответ окажется неправильным, все равно стоит объяснить, как вы пришли к полученному выводу, пишет Tproger. Разобраться в подобных головоломках может помочь подборка таких задач (ответы на них размещены внизу страницы).

Задача № 1

На склад привезли три автомата для напитков. Один выдает чай, второй – кофе, третий – чай или кофе (определяется случайно). За стакан напитка требуется заплатить одну монету. На каждом из них приклеена этикетка с соответствующим напитком. Однако на заводе в результате ошибки на всех автоматах оказались не те этикетки, которые следовало наклеить. Вопрос: сколько нужно денег, чтобы узнать, где какой автомат?

Задача № 2

На Землю напали инопланетяне, чтобы уничтожить человеческую цивилизацию. Однако перед этим они решили дать людям шанс проявить свой интеллект. В полностью темной комнате они собрали десять самых умных людей планеты и построили их в ряд, надев каждому черную или белую шляпу.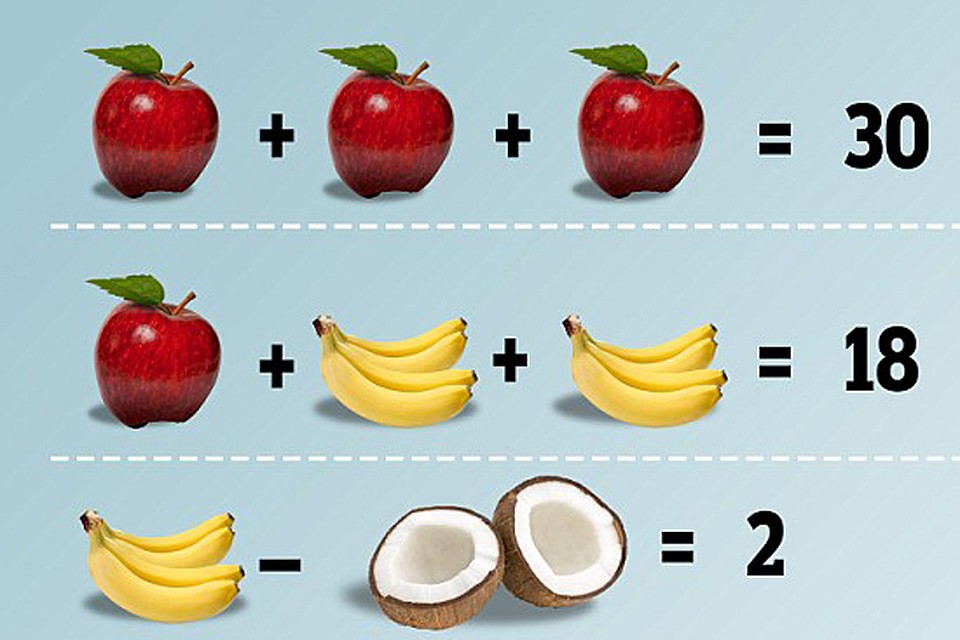 Затем свет включили.

Пришелец просит человека, который стоит в конце ряда, назвать цвет своей шляпы. Если то отвечает правильно – остается жить, если нет – умирает. Увидеть свою шляпу нельзя, но можно с другими обсудить определенный принцип ответа, которого будут придерживаться все. Выбор шляп случайный, но каждый видит цвет шляп остальных. Вопрос: каким должен быть ответ, чтобы выжило как можно больше людей?

Задача № 3

У человека есть 50 мотоциклов с заправленным баком, которого хватает на 100 километров езды. Вопрос: какое расстояние можно проехать, используя все мотоциклы, если все они в начале пути находятся в одной точке?

Задача № 4

Есть две комнаты. Первая закрыта дверью, в ней низкие потолки и висят три лампы накаливания. Во второй – три выключателя, отвечающих за каждую из ламп. Можно по-разному переключать выключатели, но перейти из второй комнаты в первую можно только один раз. Вопрос: как узнать, к какой лампе подключен каждый из выключателей?

Задача № 5

Эта логическая задача популярна на собеседованиях в Apple. Участник квеста дошел до финального задания. Перед ним – две двери. Первая ведет к богатству и победе, другая – к поражению. У каждой стоит по стражнику, которые знают, что за ними, однако один из них, неизвестно, какой именно, скажет неправду. При этом можно спросить одного стражника один раз. Какой вопрос нужно задать стражу, чтобы выйти к богатству и выиграть квест?

Задача № 6

Один из наследников решил убить короля, чтобы скорей получить власть. У короля была 1 тысяча бутылок его любимого вина. Наследник подослал убийцу, чтобы тот отравил его. Однако убийцу поймали, когда он успел отравить лишь одну бутылку. Умный правитель решил использовать десяток кроликов, чтобы узнать, куда подсыпали отраву. От нее погибали спустя один день. Вопрос: сколько минимум потребуется времени, чтобы найти отравленную бутылку и как это сделать?

Задача № 7

1,5 белки за 1,5 минуты поедают 1,5 желудя. Вопрос: сколько желудей за 9 минут съедят 9 белок?

Задача № 8

Есть треугольник с равными углами, на каждом из которых стоят по одному муравью. В определенный момент насекомые начинают идти в другой, выбранный случайно, угол вдоль стороны треугольника. Вопрос: какова вероятность того, что ни один муравей не столкнется с другим?

Задача № 9

У вас есть две сковородки и три котлеты. На приготовление одной котлеты с одной стороны уходит одна минута. На одной сковороде помещается только одна котлета. Вопрос: за какой минимум времени вы сможете полностью пожарить все три котлеты?

Задача № 10

В поместье пришел странник. В кармане – ни гроша, только одна золотая цепь из шести звеньев. Хозяин в качестве оплаты за один день проживания предложил брать одно кольцо с цепочки, при условии, что только одно звено будет распилено. Но плату нужно вносить каждый день: хозяин не хочет принимать предоплату или давать в долг. Вопрос: как путнику нужно распилить цепочку, чтобы платить за жилье ежедневно в течение пяти дней?

Ответы

Задача № 1. Нужна одна монета, которую следует бросить в автомат с наклейкой “случайный напиток”. Известно, что это неправильная наклейка, потому это автомат с чаем или кофе. Затем методом исключения определяются другие два автомата.

Задача № 2. Людям нужно договориться о таком принципе ответов: тот, кто отвечает, считает количество черных шляп у остальных. Если это нечетное число, он говорит “черный”, если четное – “белый”. Следующий человек в ряду, видя шляпы других и зная четность черных, может определить цвет своей шляпы. Например, если черных все еще нечетное число, то на нем – белая шляпа. Таким образом выживут 9 из 10 человек. Один из них погибнет, спасая остальных.

Задача № 3. Простейшее решение, которое может прийти в голову – завести все мотоциклы и проехать на них одновременно 100 километров. Однако можно проехать больше. Так, проедьте сначала 50 километров – у всех мотоциклов будут наполовину заполненные баки. Перелейте топливо из одной половины баков в другую. Тогда у вас будет 25 мотоциклов с полным баком. Через еще 50 километров повторите операцию. Так вы сможете проехать 350 километров.

Задача № 4. Благодаря низким потолкам можно дотронуться до лампы. Известно, что лампы накаливания очень сильно нагреваются. Поэтому, находясь во второй комнате, следует включить одну любую лампу на несколько минут, затем выключить ее и включить любую другую. После этого можно переходить в комнату с лампами. Первый выключатель, который вы включали, будет присоединен к еще теплой лампе. 10) уникальных комбинаций состояний животных. Следует пронумеровать все бутылки в двоичной системе в 10 разрядах (в задаче нумерация регистров начинается с 1):

Первая бутылка = 0000000001

Вторая бутылка = 0000000010

Третья бутылка = 0000000011

…

999-я бутылка = 1111100111

1000-я бутылка = 1111101000

Кроликов нужно пронумеровать от 1 до 10. Каждый из них будет соответствовать одному из 10 разрядов числа. Каждого кролика нужно поить из тех бутылок, где в соответствующем ему разряде есть единица. Например, из первой бутылки пьет только первый кролик; из третьей – первый и второй. Напоив кроликов из всех бутылок, следует подождать один день. Номера погибших кроликов помогут определить разряды числа, в которых должны быть единицы. Таким образом, если погибли только третий и первый кролики, то отравлена пятая бутылка (0000000101 = 5).

Задача № 7. Если 1,5 белки съедают 1,5 желудя за 1,5 минуты, то 1 белка за 1,5 минуты съедает один желудь. Тогда 9 белок за 1,5 минуты съедают 9 желудей. Но по условию нужно узнать количество желудей, съедаемых за 9 минут:

9 / 1,5 = 6 – во столько больше раз нам дается времени;

9 * 6 = 54 – столько желудей съедят 9 белок за 9 минут.

Задача № 8. Можно подумать, что вероятность – 33%, но это не так. Есть два варианта движения муравьев: по часовой стрелке и против. Сконцентрируемся на одном муравье. Выбрав направление, ему нужно, чтоб и другие двигались в ту же сторону. Вероятность того, что второй муравей пойдет в его направлении – 50%. Так же обстоит дело и с третьим. Таким образом, общая вероятность того, что муравьи не столкнутся, составляет 25%.

Задача № 9. Все три котлеты можно обжарить за три минуты. Вот как можно это сделать: 1) положите жариться по одной котлете на каждую сковородку; 2) через минуту переверните первую, а вторую уберите. На ее место положите третью; 3) еще через одну минуту первая котлета будет готова. Уберите ее и положите на ее место дожариваться вторую котлету, а третью переверните. Через минуту все три котлеты будут готовы.

Задача № 10. В задаче ничего не говорится о запрете на обмен звеньями. Поэтому можно распилить третье звено цепи и получить три части из одного, двух и трех звеньев. За первый день путник отдает одно звено. За второй – кусок из двух звеньев и получает одно ранее отданное им звено сдачи. За третий – кусок из трех звеньев и забирает кусок из двух. По такому принципу он может расплатиться за все оставшиеся дни.

Как сообщал OBOZREVATEL, ранее задача для третьего класса сбила с толку пользователей. Согласно ее условиям, ученикам нужно определить, как поровну распределить вилки между спичечными коробками.

Логічні задачі в Україні. Ціни на Логічні задачі на Prom.ua

Працює

Математичний тренажер. Задачі + завдання з логічним навантаженням 1 клас, Решетняк В.В, робочий зошит, Торсінг, укр

На складі в м. Лубни

Доставка по Україні

90 грн

45 грн

Купити

Творчість. Україна

Працює

Математичний тренажер. Задачі + завдання з логічним навантаженням 3 клас, Васютенко В. В., робочий зошит, Торсінг, укр

На складі в м. Лубни

Доставка по Україні

90 грн

45 грн

Купити

Творчість.Україна

Працює

Математичний тренажер. Задачі + завдання з логічним навантаженням 4 клас, Васютенко В. В., робочий зошит, Торсінг, укр

На складі в м. Лубни

Доставка по Україні

90 грн

45 грн

Купити

Творчість.Україна

Працює

Математична кмітливість. Кращі логічні задачі, головоломки та вправи Борис Кордемский

Доставка по Україні

678 грн

Купити

Книжковий бульвар

Працює

1 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Працює

2 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Працює

3 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Працює

4 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Працює

2 клас. Математичний тренажер.Задачі+завдання з логічним навантаженням. Торсінг.

На складі в м. Київ

Доставка по Україні

40 грн

Купити

Моя Книга

Працює

3 клас. Математичний тренажер.Задачі+завдання з логічним навантаженням. Торсінг.

На складі в м. Київ

Доставка по Україні

40 грн

Купити

Моя Книга

Працює

4 клас. Математичний тренажер.Задачі+завдання з логічним навантаженням. Торсінг.

На складі в м. Київ

Доставка по Україні

40 грн

Купити

Моя Книга

Працює

1 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Gugabook. com.ua

Працює

2 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Gugabook.com.ua

Працює

3 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Gugabook.com.ua

Працює

4 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

27 грн

Купити

Gugabook.com.ua

Дивіться також

Працює

Математический тренажер Задачі + завдання з логічним навантаженням 4 класс Берестова Е. В.

Доставка по Україні

32 грн

Купити

Portfel4ik “З нами навчатись легко!”

Працює

Математичний тренажер. Завдання + завдання з логічним навантаженням 1 клас Решетняк Ст. Ст.

Доставка з м. Дніпро

32 грн

Купити

Portfel4ik “З нами навчатись легко!”

Працює

Математичний тренажер. Завдання + завдання з логічним навантаженням 2 клас Решетняк Ст. Ст.

Доставка з м. Дніпро

32 грн

Купити

Portfel4ik “З нами навчатись легко!”

Працює

Математичний тренажер. Завдання + завдання з логічним навантаженням 3 клас Васютенко Ст. Ст.

Доставка по Україні

32 грн

Купити

Portfel4ik “З нами навчатись легко!”

Працює

Математический тренажер. Задачи + задачи с логическим нагрузкой 4 класс Васютенко В. В.

Доставка по Україні

32 грн

Купити

Portfel4ik “З нами навчатись легко!”

Працює

Логічні задачі для дошкільнят. Зошит: Старша група

Доставка з м. Київ

33 грн

Купити

MegaBook

Працює

Велика книга логічних ігор і завдань

Доставка по Україні

640 грн

Купити

Шалтай-Болтай – книги и винил

Працює

Математичний тренажер Задачі + завдання з логічним навантаженням 1 клас Решетняк Ст. Ст.

Доставка по Україні

32 грн

Купити

Навчалка

Працює

Математичний тренажер Задачі +завдання з логічним навантаженням 2 клас. Решетняк Ст. Ст.

Доставка з м. Київ

32 грн

Купити

Навчалка

Працює

Математичний тренажер Васютенко Ст.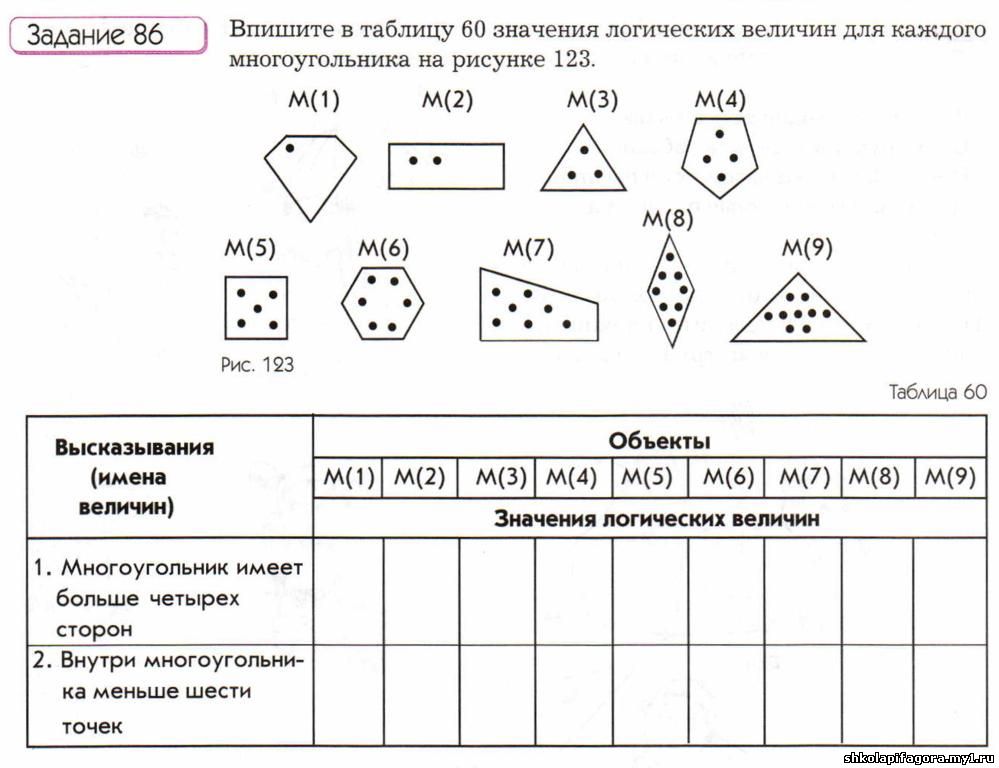 Ст. 3 клас. Задачі +завдання з логічним навантаженням

Доставка по Україні

32 грн

Купити

Навчалка

Працює

Математичний тренажер Васютенко Ст. У,. 4 клас. Задачі +завдання з логічним навантаженням

Доставка з м. Київ

32 грн

Купити

Навчалка

Працює

Л. Буданков Сто логічних завдань

Доставка по Україні

110 грн

Купити

БУКІНІСТ +

Працює

Багатобарвна логіка. 175 Логічні завдання. D. Bizam. І. Герце. 1978

Доставка по Україні

520 грн

Купити

БУКІНІСТ +

Працює

Бітно Л., книга Шахмати. Арифметичні та логічні завдання

Доставка по Україні

112 грн

Купити

Интернет – магазин “BookSide”

72 ЛОГІЧНІ ЗАДАЧІ ДЛЯ РОЗВИТКУ МИСЛЕННЯ ДОШКІЛЬНЯТ

2020-04-30

Пропонуємо величезну добірку логічних задач для дітей дошкільного віку. Такі завдання розвивають не тільки логічне мислення, а й увагу, пам’ять, кмітливість. Вирішуйте з діточками такі завдання! Дітям вони дуже подобаються!

1. Стоїть клен. На клені дві гілки, на кожній гілці по дві вишні. Скільки всього вишень
2. Якщо гусак стоїть на двох ногах, то він важить 4 кг. Скільки буде важити гусак, якщо він стоїть на одній нозі?
3. У двох сестер по одному брату. Скільки дітей в сім’ї?
4. Жираф, крокодил і бегемот жили в різних будиночках. Жираф жив не в червоному і не в синьому будиночку. Крокодил жив не в червоному і не в помаранчевому будиночку. Як ти гадаєш, в яких будиночках жили звірі?
5. Три рибки плавали в різних акваріумах. Червона рибка плавала не в круглому і не в прямокутному акваріумі. Золота рибка – не в квадратному і не в круглому. В якому акваріумі плавала зелена рибка?
6. Жили-були три дівчинки: Таня, Оленка і Даша. Таня була вища за Оленку, Оленка вища за Дашу. Хто з дівчаток найвищий, а хто найнижчий? Кого з них як звуть?
7. У Михайлика три візки різного кольору: червоний, жовтий і синій. Ще у нього три іграшки: ванька встанька, пірамідка і дзига. У червоному візку він повезе НЕ дзигу і не пірамідку. У жовтому – НЕ дзигу і не ваньку встаньку. Що повезе Михайлик в кожному візку?
8. Мишка їде не в першому і не в останньому вагоні. Курча не в середньому і не в останньому вагоні. У яких вагонах їдуть мишка і курча?
9. Бабка сидить не на квітці і не на листку. Коник сидить не на грибку і не на квітці. Сонечко сидить не на листку і не на грибку. Хто на чому сидить? (Краще все намалювати.)
10. Альоша, Саша і Міша живуть на різних поверхах. Альоша живе не на найвищому поверсі і не на найнижчому. Саша живе не на середньому поверсі і не на нижньому. На якому поверсі живе кожен з хлопчиків?
11. Ані, Юлі та Олі мама купила тканину на плаття. Ані не зелену і не червону. Юлі – не зелену і не жовту. Олі – не жовту і не червону. Яка тканина для якої з дівчаток?
12. У трьох тарілках лежать різні фрукти. Банани лежать не в синій і не в помаранчевій тарілці. Апельсини не в синій і не в рожевій тарілці. В якій тарілці лежать сливи? А банани і апельсини?
13. Під ялинкою квітка не росте, під березою не росте грибок. Що росте під ялинкою, а що під березою?
14. Антон і Денис вирішили погратися. Один з кубиками, а інший з машинками. Антон машинку не взяв. Чим гралися Антон і Денис?
15. Віка і Катя вирішили малювати. Одна дівчинка малювала фарбами, а інша олівцями. Чим стала малювати Катя?
16. Рудий і Чорний клоуни виступали з м’ячем і кулею. Рудий клоун виступав не з м’ячиком, А чорний клоун виступав не з кулькою. З якими предметами виступали Рудий і Чорний клоуни?
17. Ліза і Петро пішли в ліс збирати гриби і ягоди. Ліза гриби не збирала. Що збирав Петро?
18. Дві машини їхали по широкій і по вузькій дорогах. Вантажна машина їхала не по вузькій дорозі. По якій дорозі їхала легкова машина? А вантажна?
19. Скільки вух у трьох мишей?
20. Скільки лап у двох ведмежат?
21. У семи братів по одній сестрі. Скільки всього сестер?
22. У бабусі Дарини внучка Маша, кіт Пушок і собака Дружок. Скільки всього онуків у бабусі?
23. Над річкою летіли птиці: голуб, щука, 2 синиці, 2 стрижа і 5 вугрів. Скільки всього летіло птахів? Відповідай швидше!
24. Горіло 7 свічок. 2 свічки погасили. Скільки свічок залишилося?
25. В кошику три яблука. Як поділити їх між трьома дітьми так, щоб одне яблуко залишилося в кошику?
26. На березі три товсті гілки, на кожній товстій гілці по три тоненькі гілочки. На кожній тоненькій гілочці по одному яблучку. Скільки всього яблук?
27. Саша їв яблуко велике і кисле. Оля їла яблуко велике і солодке. Що в цих яблуках однакове? Різне?
28. Маша і Ніна розглядали картинки. Одна дівчинка розглядала картинки в журналі, а інша дівчинка – в книжці. Де розглядала малюнки Ніна, якщо Маша не розглядала картинки в журналі?
29. Толя і Ігор малювали. Один хлопчик малював будинок, а інший – гілку з листям. Що малював Толя, якщо Ігор не малював будинок?
30. Алік, Боря і Вова жили в різних будинках. Два будинки були в три поверхи, один будинок був в два поверхи. Алік і Боря жили в різних будинках, Боря і Вова жили теж у різних будинках. Де жив кожен хлопчик?
31. Коля, Ваня і Сергій читали книжки. Один хлопчик читав про подорожі, інший – про війну, третій – про спорт. Хто про що читав, якщо Коля не читав про війну і про спорт, а Ваня не читав про спорт?
32. Зіна, Ліза і Лариса вишивали. Одна дівчинка вишивала листочки, інша – пташок, третя – квіточки. Хто що вишивав, якщо Ліза не вишивала листочки і пташок, а Зіна НЕ вишивала листочки?
33. Хлопчики Слава, Діма, Петро і Женя садили плодові дерева. Хтось із них садив яблуні, хтось – груші, хтось – сливи, хтось – вишні. Що садив кожен хлопчик, якщо Діма не садив сливи, яблуні та груші, Петро не садив груші та яблуні, а Слава не садив яблуні?
34. Дівчатка Ася, Таня, Іра і Лариса займалися спортом. Хтось із них грав у волейбол, хтось плавав, хтось бігав, хтось грав у шахи. Яким спортом захоплювалася кожна дівчинка, якщо Ася не грала у волейбол, в шахи і не бігала, Іра не бігала і не грала в шахи, а Таня не бігала?
35. Саша сумніша, ніж Толик. Толик сумніший, ніж Алік. Хто веселіший за всіх?
36. Іра акуратніша, ніж Ліза. Ліза акуратніша, ніж Наташа. Хто найакуратніший?
37. Мишко сильніший, ніж Олег, але слабший, ніж Вова. Хто найсильніший?
38. Катя старша за Сергія, але молодша за Таню. Хто наймолодший?
39. Саша на 10 років молодший за Ігора. Ігор на 2 роки старший, ніж Олексій. Хто наймолодший?
40. Іра на 3 см нижча, ніж Клава. Клава на 12 см вища, ніж Люба. Хто найвищий?
41. Толик набагато легший, ніж Сергій, але трохи важчий, ніж Валера. Хто найлегший?
42. Віра трохи темніша, ніж Люда. Віра набагато світліша, ніж Катя. Хто найсвітліший?
43. Льоша слабший, ніж Саша. Андрій сильніший, ніж Олексій. Хто найсильніший?
44. Наташа веселіша, ніж Лариса. Надя сумніша, ніж Наташа. Хто найсумніший?
45. Світлана старша за Іру, і нижча, ніж Марина. Світлана молодша за Марину і вища Іру. Хто наймолодший і хто найнижчий?
46. Костя сильніший, ніж Едик, і повільніший, ніж Алік. Костя слабший, ніж Алік, і швидший, ніж Едик. Хто найсильніший і хто найповільніший?
47. Оля темніша, ніж Тоня. Тоня нижча, ніж Ася. Ася старша, ніж Оля. Оля вища, ніж Ася. Ася світліша, ніж Тоня. Тоня молодша, ніж Оля. Хто найтемніший, найнижчий і найстарший?
48. Коля важчий, ніж Петро. Петро сумніший, ніж Паша. Паша слабший, ніж Коля. Коля веселіший, ніж Паша. Паша легший, ніж Петя. Петя сильніший, ніж Коля. Хто найлегший, хто найвеселіший, хто найсильніший?
49. На груші виросло п’ять яблук, а на ялинці – лише два. Скільки всього яблук виросло?
50. Що станеться з білою хусткою, якщо її опустити в Червоне море?
51. Скільки горіхів в порожній склянці?
52. З якого посуду неможливо нічого з’їсти?
53. Качка важить два кілограми. Скільки буде важити качка, якщо вона стане на одну ногу?
54. Скільки кінців у одній палиці? А у половини палиці?
55. У мого батька є дочка, але вона мені не сестра. Хто це?
56. Що важче – кілограм вати або кілограм цвяхів?
57. Банан розрізали на чотири частини. Скільки зробили розрізів?
58. Два сина і два батька з’їли три яблука. Скільки яблук з’їв кожен?
59. Йшла Маша в місто, а назустріч їй три бабусі, у кожної по два мішки, в кожному мішку по кішці. Скільки всього людей йшло в місто?
60. Михайлику 2 роки, а Люді 1 рік. Яка різниця у віці у них буде через 2 роки?
61. Бублик розрізали на три частини. Скільки зробили розрізів?
62. Сергій гостював у бабусі тиждень і три дні. Скільки днів гостював Сергій?
63. У Насті цілий апельсин, 2 половинки і 4 четвертинки. Скільки у неї апельсинів?
64. У бабусі Марії внучка Даша, кіт Димок, собака Пушок. Скільки у бабусі онуків?
65. Яйце вариться 3 хвилини. Скільки часу знадобиться, щоб зварити 5 яєць одночасно в одній каструлі?
66. Два автомобіля проїхали 40 кілометрів. Скільки кілометрів проїхав кожен?
67. На мотузці зав’язали п’ять вузлів. На скільки частин ці вузли розділили мотузку?
68. З-під паркану виднілися 10 пташиних лапок. Скільки птахів за парканом?
69. Драбина має 9 сходинок. Яка сходинка буде середня?
70. Хлопчик висипав разом 3 купки піску, а потім висипав туди ще дві. Скільки стало купок піску?
71. Міла і Наташа під каменем знайшли дві монети. Скільки монет знайшла б одна дівчинка?
72. Мама купила дітям три шарфики і шість рукавиць. Скільки дітей у мами?

Інформацію подано за матеріалами сайту ДИТЯЧИЙ ПСИХОЛОГ

72 логічні задачі для розвитку мислення дошкільнят

Кiлькiсть переглядiв: 277

Версія для друку

20+ логических загадок и хороших вопросов-загадок с ответами

Головоломки / Загадки / Логические Вопросы

В LogicLike есть еще 2500 логических загадок, логических викторин, загадок на мышление и хитрые головоломки. Простые и сложные загадки для детей и их родителей, чтобы улучшить их мыслительные способности!

Зачем решать логические загадки?

Отвечая на логические вопросы, отгадывая каверзные загадки активизирует многие мыслительные процессы. И это отличный способ развлечь детей или себя и улучшает психическое здоровье. Загадки «Кто я» и вопросы «Кто я» для детей также расширяют их словарный запас.

Просто хорошие загадки и головоломки вопросы стимулируют мозговая деятельность и латеральное мышление. Такая умственная тренировка улучшает способность решать любые проблема творчески и более эффективно. Вас ждут тридцать три потрясающие рождественские загадки!

Выберите уровень сложности, чтобы начать

5-8 лет

9-14 лет

Взрослый

Решайте простые и сложные логические загадки

Выберите список загадок, чтобы начать с!

Легко | Математика | Жесткий

Простые логические вопросы и короткие загадки для детей

Летом и зимой родились брат и сестра.
Сестра родилась не зимой.
Кто родился летом?

Показать ответ

Сестра.

Алекс – отец Чарли.
Кто из них родился позже?

Показать ответ

Чарли.

Я делаю двух людей из одного.
Что я?

Показать ответ

Зеркало.

Что утром теряет голову, а ночью возвращается?

Показать ответ

Подушка.

Жираф выше кенгуру, но ниже ладони.
Какое животное самое высокое?

Показать ответ

Жираф.

Летает, но не птица. Выберите все ответы, которые подходят.

Показать ответ

Пчела, Самолет.

Попробуйте и получите эти отличные мини-курсы

чтобы развлечь вашего ребенка

Число Загадки Попробуй это сейчас!

шахматы Попробуй это сейчас!

Математика и логика Навыки и умения Попробуй это сейчас!

Вам также может понравиться наша коллекция простых загадок для детей, чтобы расширить свой словарный запас и улучшить концентрацию.

Ребенок отца, ребенок матери, но ничей сын.
Кто я?

Показать ответ

Дочь.

Я белый и я черный.
Я быстрый и не толстый.
Я смущаю многих людей своим стилем.
Кто я?

Показать ответ

Зебра.

Хотите более сложные и каверзные вопросы? Вы должны попробовать наши логические головоломки.

Тренируйте свою логику и мышление и наслаждайтесь хорошим досугом с LogicLike!

Попробуйте прямо сейчас!

Все курсы LogicLike

Математические загадки для детей

Сегодня Тиму исполнился 1 год, а Марте исполнился 1 месяц.
Насколько Тим старше Марты?

Показать ответ

12 раз ИЛИ 11 месяцев старше.

Все фрукты одного типа имеют одинаковую цену. Какова цена апельсин?

Показать ответ

Добавьте правильные символы.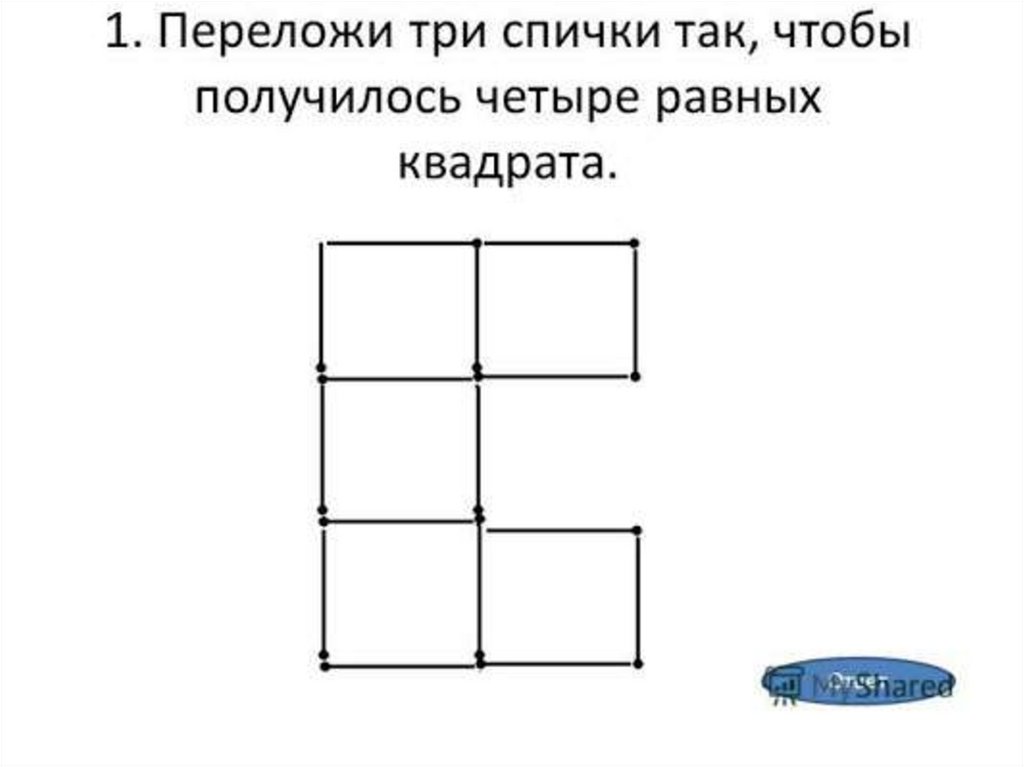

Показать ответ

5+2-1=6.

Ищите похожие логические задачи здесь: номер ребусы, математические ребусы.

Из журнала было вырвано несколько листов: со страницы 3 по страницу 8. Сколько листы вырваны?

Показать ответ

На снимке Чарли, Кейт и Фиби. девочки не стоя рядом друг с другом.
Какая маска на Чарли?

Показать ответ

Вам также могут понравиться онлайн-загадки и ребусы для дошкольников.

Повысьте свою умственную силу! С Logiclike вы научитесь решать логические головоломки и думать нестандартно.

Играть в игру

Сложные логические вопросы и загадки для взрослых и умных детей

Кира, Кларисса и Олив не родственники. У Киры и Клариссы есть братья, и у Олив есть сестра. Кларисса и Олив — самые младшие в семье. а Кира самая старшая в ней.
У кого из них есть старший брат?

Показать ответ

Кларисса.

Сегодня не воскресенье и не среда.
Завтра не воскресенье и не среда.
Вчера не было пятницы.
Понедельник не был позавчера, как и воскресенье.

Какой день недели сегодня (вторник, среда, суббота или воскресенье), если один из утверждений является ложным?

Показать ответ

Воскресенье.

Профессор ехал в свою загородную лабораторию с постоянной скоростью. (не быстрее 90 км/ч).
В один момент счетчик показывал 16961 км пробега. Ровно через 2 часа число на счетчике снова показало число, которое читается одинаково в обоих направления.
С какой скоростью (км/ч) ехал профессор?

Показать ответ

55 (км/ч).

В здании четыре этажа.
Чем выше этаж, тем больше людей там живет.
На какой этаж чаще всего поднимается лифт?

Показать ответ

К 1-му (нулю) пол.

Найдите наименьшее четное четырехзначное число, записанное четырьмя разными цифры.

Показать ответ

Лифт может перевозить не более 6 взрослых или не более 9 детей.
Какое максимальное количество детей может войти в лифт с двумя взрослые люди?

Показать ответ

Запишите разницу между наименьшим четырехзначным числом и самое большое однозначное число.

Показать ответ

1000−9=991.

Решайте загадки и логические головоломки онлайн!

Более 550 000 родителей со всего мире уже улучшают навыки мышления со своими детьми.

Играть в игру Играть в игру

Больше загадок и головоломок для вас

Сложные загадки для любого возраста

Загадки для подростков

Логика и искусственный интеллект (Стэнфордская философская энциклопедия)

1.1 Роль логики в искусственном интеллекте

Теоретическая информатика развилась из логики, теории вычисления (если это следует рассматривать как предмет, отличный от логика) и некоторые смежные области математика. ^[4] Так теоретически мыслящий ученые-компьютерщики хорошо осведомлены о логике, даже если они не логики. Компьютерщики в целом знакомы с идеей эта логика предоставляет методы для анализа выводных свойств языков, и с различием между высокоуровневым логическим анализ проблемы рассуждения и ее реализации. Логика, для Например, может предоставить спецификацию для языка программирования, характеризующее отображение программ на вычисления, которые они лицензия. Компилятор, реализующий язык, может быть неполным или даже несостоятельным, лишь бы оно в каком-то смысле приближалось к логическому Технические характеристики. Это делает возможным участие логики в Приложения ИИ могут варьироваться от относительно слабых применений, в которых логика информирует процесс внедрения с помощью аналитических идей, чтобы применения, в которых можно показать, что алгоритм реализации надежен и полный. В некоторых случаях рабочая система вдохновлена ​​идеями из логика, а затем приобретает черты, которые на первый взгляд кажутся логически проблематичными но позже может быть объяснено развитием новых идей в логической теории. Такого рода вещи произошли, например, в логике программирование.

В частности, логические теории в ИИ не зависят от реализации. Их можно использовать для получения информации о проблема рассуждений без прямого информирования реализации. Прямой реализации идей из логики – доказательство теорем и методы построения моделей — используются в ИИ, но теоретики ИИ, которые полагаются на логику для моделирования своих проблемных областей, могут свободно использовать другие Техники выполнения тоже. Таким образом, в Мур 1995b (Глава 1), Роберт С. Мур различает три применения логики в ИИ; как инструмент анализа, как основу для представления знаний и как средство программирования язык.

Большая часть усилий по развитию ограниченно-объективного мышления системы переходит в управление большими, сложными органами декларативная информация. В ИИ общепризнано, что важно относиться к представлению этой информации, и рассуждение, которое идет вместе с ним, как отдельная задача, со своей исследовательские проблемы.

Эволюция экспертных систем иллюстрирует это. Раннее экспертные системы, такие как M YCIN (программа, о бактериальных инфекциях см. Бьюкенен и Шортлифф 1984), были полностью основаны на больших системах процессуальных правил, без отдельное представление фоновых знаний, например, таксономия инфекционных организмов, о которых рассуждала система не был представлен.

Экспертные системы более поздних поколений демонстрируют большую модульность в своих решениях. дизайн. Отдельный компонент представления знаний полезен для для целей разработки программного обеспечения — гораздо лучше иметь единую представление общего факта, который может иметь множество различных применений, поскольку это упрощает разработку и модификацию системы. И это дизайн оказывается важным для того, чтобы эти системы могли обеспечивать объяснения, а также просто выводы. ^[5]

1.2 Представление знаний

В ответ на необходимость разработки этого декларативного компонента появилось подполе ИИ, известное как представление знаний . в течение 1980-х годов. Представление знаний имеет дело прежде всего с репрезентативные и логические задачи этого отдельного компонента. Лучшее место, чтобы проникнуться этой темой, — это материалы встречи, которые теперь проводятся раз в два года: см. Брахман и др. . 1989 г., Аллен и др. . 1991 г., Небель и др. . 1992 г., Дойл и др. . 1994 г., Айелло и др. . 1996 г., Кон и др. . 1998 г., Кон и др. . 2000 г., Фенсел и др. . 2002 г., Дюбуа и др. . 2004 г., Доэрти и др. . 2006 г., Брюка и Ланг, 2008 г., Лин и др. . 2010 г., Эйтер и др. . 2012 г., Барал и др. . 2012 г., а также Барал и др. . 2016.

Типовые статьи в материалах КР и Аргументация конференции посвящены следующим темам.

1. Темы логической теории и теории вычислений, включая
   1. Немонотонная логика
   2. Теория сложности
2. Исследования в прикладных областях, включая
   1. Темпоральные рассуждения
   2. Формализмы для рассуждений о планировании, действии и изменении, а также о причинно-следственных связях
   3. Метарассуждения
   4. Рассуждение о контексте
   5. Рассуждения о ценностях и желаниях
   6. Рассуждения о психических состояниях других агентов, и особенно о знании и вере
   7. Пространственное мышление
   8. Рассуждение о неясности
3. Аргументация и теория аргументации
4. Проблемы агрегации многих видов, такие как интеграция противоречивые источники знаний
5. Исследования в области прикладных технологий, включая
   1. Логическое программирование
   2. Описание логики
   3. Доказательство теоремы
   4. Модельная конструкция
6. Исследования крупномасштабных приложений, включая
   1. Когнитивная робототехника
   2. Объединение, обновление и исправление баз знаний

Эти темы практически не пересекаются с содержанием журнала .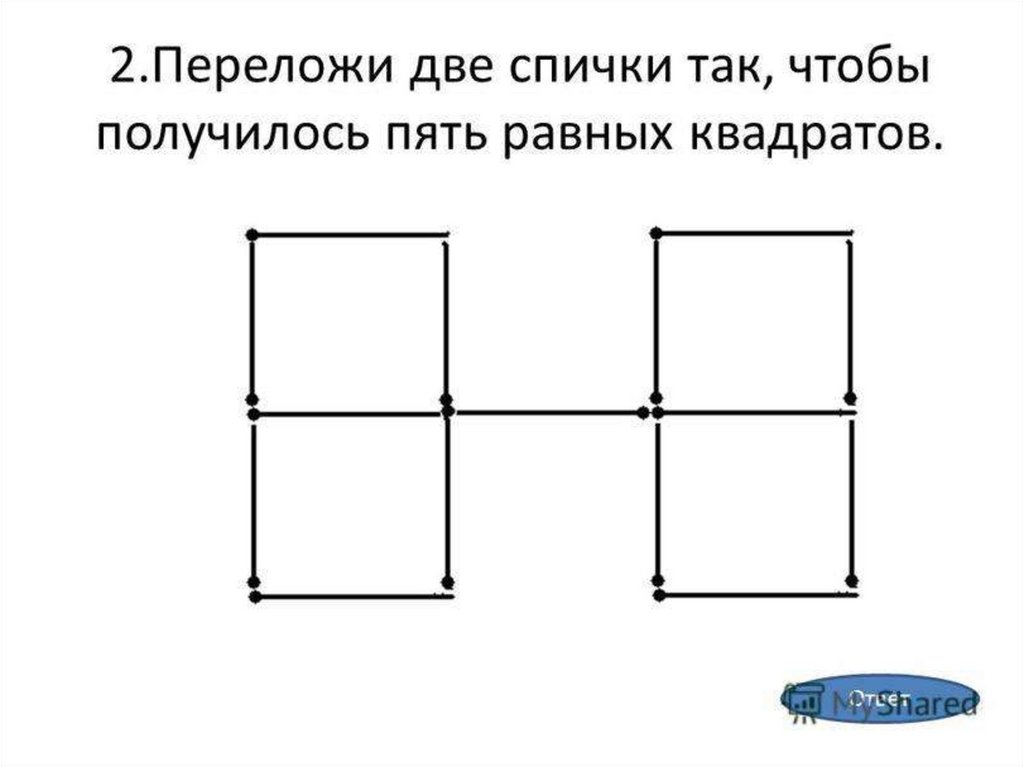 of Symbolic Logic , главный исследовательский архив математических логика. Но есть существенное совпадение в теоретическом акценте с The Journal of Philosophical Logic , где такие темы, как напряжённость логика, эпистемическая логика, логические подходы к практическим рассуждениям, изменение убеждений и неопределенность составляют большой процент взносы. Очень мало 9Однако публикации 0235 JPL касаются теории сложности или с потенциальными приложениями к автоматизированным рассуждения.

1.3 Философская логика

История философской логики еще не написана. Хотя философская логика традиционно отличалась от математической логике, различие вполне может быть случайным по отношению к к общим целям предмета, поскольку техническая строгость и использование математических методов, по-видимому, необходимы во всех областях логического исследовательская работа. Однако различие между двумя подполями было усугубляется различиями в видах профессиональной подготовки, доступны логикам, а взгляды отдельных людей на то, что важно для поля.

Заявление о политике, представленное в Журнал символической логики (1936, том 1, № 1) списки объединение математиков и философов, работающих в области логики среди целей нового журнала. Вероятно, в это время оба математики и философы разделяли чувство, что их предмет считался несколько маргинальным их коллегами, и может почувствовали первостепенную лояльность к логике как к предмету, а не к какому-либо Академическая дисциплина. Статьи в первом томе JSL были разделены примерно поровну между профессиональными математиками и философов, а ранние тома JSL не показывают любые сильные различия между двумя группами по теме.

Ситуация изменилась в 1960-х годах. Том 1969 г. JSL содержал 39 статей математиков и только девять философы. К началу 1970-х годов многие философы считали, что философские работы по логике вряд ли были приняты JSL , и что, если они будут приняты, они вряд ли будут читают философы. На данный момент цели двух групп были значительно расходились.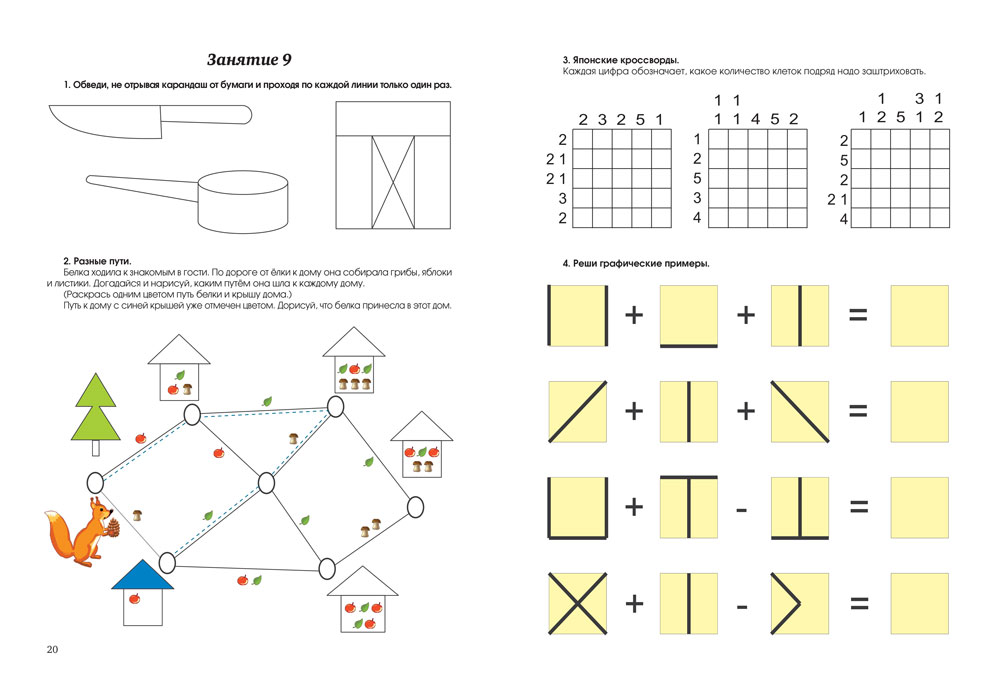 Математики занимались разработкой все более технический и сложный корпус методов и теорем. Многие философы считали, что это стремление становится все более неуместным для целью освещения философских проблем. Эти разделения привели к основание Journal of Philosophical Logic в 1972 году. Список примерных тем в первом выпуске включал:

1. Вклады в разделы логической теории, непосредственно связанные с философские проблемы, такие как индуктивная логика, модальная логика, деонтическая логика, квантовая логика, временная логика, свободная логика, логика вопросов, логика команд, логика предпочтения, логика условностей, многозначная логика, логика релевантности;
2. Участие в философских дискуссиях, использующих аппарат формальной логики…;
3. Обсуждение философских вопросов, касающихся логики и логическая структура языка, …;
4. Философский труд, относящийся к специальным наукам, ….

Большинство статей за последующие 28 лет JPL относятся к первой из этих четырех категорий. Но описание с с чего начинается этот список, не особенно показательно: зачем эти конкретные темы представляют интерес для философов? Их самые важной общей чертой является ощущение, что, несмотря на успехи в формализовав области математической логики, область логики осталась сильно ограничено. Имеются нерешенные проблемы формализации нематематических наук, которые, кажется, требуют осмысления новых и различные логические вопросы (квантовая логика и логика индукции, например). Остальные темы охватывают, по крайней мере, часть еще более насущные проблемы, связанные с распространением логической теории на ненаучные рассуждения. Таким образом, главная цель философского логика – это расширение логических методов до нематематических рассуждений домены. Эта цель имеет теоретическое измерение, если (как много философские логики как будто чувствуют) она требует переработки и расширение логических формализмов.

Разработка и тестирование приложений, таких как проблема формализация рассуждений, связанных с тем, чтобы добраться до аэропорта, выдаваемого за вызов в Маккарти 1959 г. (видеть Раздел 2.2, ниже), даже не отображается как категории в списке тем JPL , и на самом деле большинство литература по философской логике носит теоретический характер и проверяется с помощью философских приемов. По существу, это означает, что теории мотивируются и проверяются с помощью мелкомасштабных, искусственных примеры, отобранные теоретиками. Эти примеры обычно служат больше как демонстрации или иллюстрации, чем как тесты.

1.4 Логика в ИИ и философская логика

Грубое сравнение в Раздел 1.2 принадлежащий содержание основных публикаций по исследованиям в области логического ИИ и философская логика подсказывает следующую картину. Теоретическая работа в логический ИИ и философская логика во многом пересекаются. Оба заинтересованы в разработке неметаматематических приложений логики, и основные темы очень похожи. Это совпадение обусловлено не только общность интересов, но прямое влияние философской логики по логическому ИИ; есть достаточно доказательств, как мы увидим, что первый По крайней мере поколение логиков ИИ читало и находилось под влиянием литературы по философской логике.

С этого момента специальности разошлись. Новый логический теории появились в логическом ИИ (немонотонная логика — самая важный пример), которые мало известны в философской логике. Другие различия связаны с интересом сообщества ИИ к теоретический анализ алгоритмов и, конечно же, с их смыслом. важность реализаций. Некоторые из них связаны с появлением развитие в информатике амбициозных приложений с использованием беспрецедентно большие корпуса логических аксиом. Огромный размер этих приложения порождают новые проблемы и новые методологии. И другие различия возникают из-за интереса философов-логиков к некоторые темы (например, метафизические темы), которые в первую очередь руководствуясь чисто философскими соображениями.

Забота о приложениях может оказать большое влияние на то, как проводятся исследования. выполнено и представлено. Традиция в философской логике предшествует приложениям в автоматизированном мышлении и по сей день остается относительно незаинтересованы в таких приложениях. Методология зависит на интуиции, но без какой-либо общепринятой методологии формулирование и развертывание этих интуитивных представлений. И идеи проиллюстрировано и информировано искусственными, мелкомасштабными Примеры. ^[6] В целом, философская литература не имеет дела с реализуемостью или эффективности рассуждений, да и вообще с какими-либо особенностями процесс рассуждения. И трудно найти случаи, когда философские теории иллюстрируются или проверяются реалистичными, масштабные проблемы с рассуждениями.

Эти различия, однако, являются в большей степени вопросом стиля, чем сути или стратегических целей исследования. Трудно думать через детали процесса рассуждения без вычислительного инструменты, чтобы сделать процесс конкретным и трудным для разработки крупномасштабные формализации задач рассуждения без вычислительных инструменты для ввода, тестирования и поддержки формализации. Поскольку основные теоретические темы (модальные, условные и темпоральные логика, пересмотр убеждений и логика контекста) так похожи, и поскольку конечная цель (формализация нематематических рассуждения) одинаковы, можно рассматривать логику в ИИ как непрерывную продолжение традиции философской логики.

Раннее влияние философской логики на логику ИИ было глубокий. Библиография Маккарти и Хейс, 1969 г., один из самых влиятельных ранних работ по логическому ИИ, иллюстрирует хорошо указать. В библиографии 58 ссылок. Из них 35 обратитесь к литературе по философской логике. (Есть 17 компьютеров научные цитаты, одна цитата по математической логике, одна цитата по экономике цитата и одна цитата по психологии.) Эта статья была написана в время, когда практически не было упоминаний о логическом ИИ в литература по информатике. Естественно, по мере того, как логический ИИ развивался и развивалась как отрасль информатики, доля междисциплинарное цитирование уменьшилось. Подборка статей из первая конференция по представлению знаний, Брахман и др. . 1989 г., удерживается в 1989, показывает только 12 цитат из философской логики из 522. выборочные цитаты; подборка статей из Кон и др. . 1998 г., состоявшийся в 1998 году, показывает 23 цитаты по философской логике из 468. выборка. ^[7]

Несмотря на резкое снижение количества явных ссылок, современная литература по логическому ИИ отражает косвенное знакомство с более ранней литературой по философской логике, поскольку многие вычислительные работы, которые явно цитируются в современных работах, были под влиянием этой литературы. Конечно, влияние становится с течением времени становится все более отдаленным, и эта тенденция ускоряется тот факт, что в логическом ИИ были изобретены новые теоретические темы которые были в лучшем случае лишь смутно предвосхищены в философском литература.

Хотя философская логика в настоящее время представляет собой относительно небольшую область в по сравнению с логическим ИИ, он остается жизнеспособной областью исследований с новыми работы появляются регулярно. Но ссылки на современные исследования в философская логика редко встречается в литературе по ИИ. Точно так же статей, опубликованных в настоящее время в The Journal of Philosophical Логика , по крайней мере, не показывает большого влияния от ИИ. ^[8] В Европе, границы труднее провести между профессиональными подразделениями среди логики: некоторые европейские журналы, особенно Журнал логики, Язык и информация успешно поддерживают фокус в логике, привлекая авторов из всех дисциплин, в которых представлена ​​логика.

1.5 Роль искусственного интеллекта в логике

Важность приложений в логическом ИИ и их масштаб приложений, представляет собой новую методологию логики, которая были невозможны без механизированного мышления. Эта методология заставляет теоретиков продумывать проблемы в новом масштабе и с новый уровень детализации, и это, в свою очередь, оказывает глубокое влияние на результирующие теории. Эффекты этой методологии будут проиллюстрированы в разделах ниже, посвященных различным темам логического ИИ. Но этот момент хорошо иллюстрируется рассуждениями о действии и изменении. Эта тема исследовалась в философской литературе. Рассуждение об изменении, по крайней мере, является частью напряженной логики, и последствия действия исследуются в литературе по «присмотру за тем»; видеть, например, Белнап 1996. Последний теория не имеет очень надежного объяснения действия. Центральная конструкция представляет собой вариация модальности времени ветвления наподобие той, что была знаком с тех пор До 1967 года. Хотя это представляет собой интересное развитие философской логики, шкала достижения сильно отличается от исследовательской традиции в логический ИИ сообщил в Раздел 4, ниже. формализмы в этой традиции не только поддерживают формализацию сложные, реалистичные проблемы планирования, но дают совершенно новое понимание в рассуждения о причинных следствиях действий, постоянстве состояний, а также взаимодействия между действиями и непрерывными физическими процессы. Подобные разработки были бы невозможны без взаимодействия между логическими теориями и крупномасштабными, практические приложения в автоматизированном планировании.

В Карнап 1955 г., Рудольф Карнап пытался прояснить интенсиональный анализ языкового значения и обосновать с методологической точки зрения, представляя, как анализ может быть применен к лингвистическому использованию гипотетического робота. Карнап надеялся, что тот факт, что мы можем представить себя знающими внутренняя структура робота поможет обосновать эмпирическая наука о семантике более правдоподобна. Эта надежда оказалась необоснованный; философский вопрос, который волновал Карнапа, остается вызывает споры и по сей день, а мысленные эксперименты с роботами не оказался особенно полезным в решении этой проблемы. Настоящие роботы, хотя и с настоящим приложения, ^[9] совсем другое дело. Хотя это трудно сказать, окажутся ли они полезными в прояснении фундаментальные философские проблемы, они представляют собой лабораторию логики это революционно в своем потенциальном воздействии на предмет. Они мотивировать разработку совершенно новых логических теорий, которые должны оказываются столь же важными для философии, как и фундаментальные развитие логики конца XIX в.

Появление отдельных математических и философских узкой специализации в логике было не совсем здоровой вещью для поле. Процесс придания математической логике строгости и демонстрация полезности методов в достижении математических цели, которая столь успешно преследовалась в первой половине XX века представляет собой последовательное усовершенствование логического методология. Все логики должны радоваться и гордиться тем, что логика теперь область с совокупностью результатов и проблем, столь же существенных и сложные, как те, которые связаны с большинством областей математики.

Но эти методологические достижения были получены за счет покрытие. В конечном счете, логика имеет дело с рассуждениями — и относительно небольшая часть наших рассуждений является математической, в то время как почти все математические рассуждения, которыми занимаются нематематики, — это просто расчет. Чтобы иметь и строгость, и охват, логика должна сохранять свою математическая и ее философская стороны объединились в единую дисциплину. В последние годы ни математический, ни философский профессий, и это особенно верно в Соединенных Государства — сделали очень много для укрепления этого единства. Но потребности информатики обеспечивают сильные объединяющие мотивы. профессиональные стандарты для логических исследований в области компьютерных наук безусловно, требует строгости, но эта область также ставит своих практиков в контакт с областями рассуждений, которые не являются строго математическими, и создает потребность в инновационном логическом теоретизировании.

Самая инновационная и амбициозная область компьютерных наук, с точки зрения своего охвата рассуждений, и тот, который наиболее близок по духу к философская логика, это ИИ. В этой статье будет предпринята попытка предоставить введение, для посторонних, знакомых с логикой, к аспектам ИИ, которые наиболее близки к традиции философской логики. Эта зона логики заслуживает и срочно нуждается в изучении историками. Но такого исследования здесь не найти.

2.1 Логический AI

Самой влиятельной фигурой в области логического ИИ является Джон Маккарти. Маккарти был одним из основателей ИИ и последовательно выступал за исследования методология, использующая логические приемы для формализации рассуждений проблемы, которые должен решить ИИ. Все, кроме самой последней работы в Исследовательскую программу Маккарти можно найти в Лифшиц 1990а, который также содержит знакомство с творчеством Маккарти Лифшиц 1990b; дополнительную историческую справку см. Израиль 1991.

Методологическая позиция Маккарти существенно не изменилась.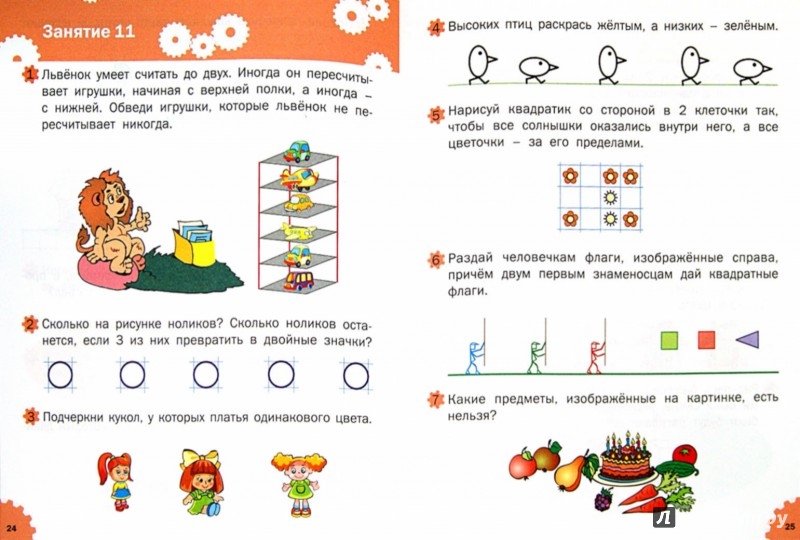 поскольку оно было впервые сформулировано в Маккарти 1959 и доработаны и дополнены в Маккарти и Хейс, 1969. Мотивация использования логики заключается в том, что даже если возможные реализации не используют напрямую и просто логические методы рассуждения, такие как доказательство теорем — логическая формализация помогает нам понять саму проблему рассуждения. Претензия в том, что без понимания того, в чем заключаются проблемы с рассуждениями, невозможно реализовать их решения. Правдоподобно, как это Может показаться платоническим аргументом, но на самом деле он спорен в контексте ИИ; альтернативная методология будет направлена ​​на изучение или развитие желаемое поведение. Представления и рассуждения о том, что это методология может оказаться слишком сложной для характеристики или понимать на концептуальном уровне.

Из Маккарти и Хейс, 1969 г., ясно, что Маккарти рассматривал свою методологию ИИ как в значительной степени пересекается с традиционной философией, но добавляет к ней необходимость сообщать дизайну программ, способных манифестировать общий интеллект. Эта идея не чужда некоторым философам. (см., например, Карнап 1956 г. (стр. 244–247) и Поллок 1995). В практике, фактические теории, возникшие из на методологию наиболее сильно повлияла работа в области философской логика, а исследовательская традиция логического ИИ представляет собой более или менее менее прямое развитие этой работы, с некоторыми изменениями в акцентах. Этот обзор будет посвящен логическому ИИ по отношению к философскому логике, без дальнейших комментариев об отношении к философии вообще или к возможности разработки интеллектуальных систем человеческого уровня.

2.2 Формализация здравого смысла

Долгосрочная цель Маккарти состояла в том, чтобы формализовать здравый смысл. рассуждение , донаучное рассуждение, которое используется в с бытовыми проблемами. Ранний пример такой проблемы, упомянутый в Маккарти 1959, получает от домой в аэропорт. Другие примеры включают:

1. Нарративное понимание. Рассуждения, связанные с восстановление неявной информации из нарративов, например, последовательность случайностей и предполагаемых причинно-следственных связей.
2. Диагностика. Например, обнаружение ошибок в физическом устройства.
3. Пространственное мышление. Например, рассуждая о частях твердых тел и их формы, а также их связи с формой целый.
4. Рассуждения об отношении других агентов. Для Например, делая обоснованные предположения об убеждениях и желаниях других агентов, не из «замочной скважины», а из разговорного подсказки, которые можно было бы получить в кратком интерактивном интервью.

Говоря прямо, цель формализации здравого смысла, вероятно, кажутся возмутительными большинству философов, привыкших думать о здравый смысл как нечто неуловимое. Но независимо от того, является ли конечной целью уместно и достижимо, конкретные проекты формализации которые появились в результате этой программы, были успешными в нескольких способы. Им удалось открыть новую территорию для логики путем расширение круга задач рассуждения, до которых логически техники могут быть успешно применены.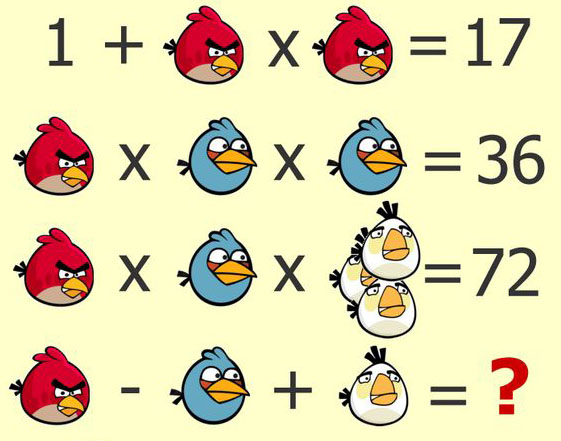 Они продемонстрировали, что логические приемы могут внести полезный вклад в решение конкретных Проблемы с ИИ — планирование — самая успешная из них, но некоторые успехи были достигнуты и в других областях, Что ж. ^[11] Они составляют основу единого подхода к разработке полных, автономных агенты. ^[12] А они осветили многие специфические формы ненаучных рассуждения — например, качественные рассуждения о поведении физических устройств. ^[13]

Хотя Маккарти выступал за эту программу формализации с 1959 года — почти доисторической даты для ИИ — программа не был принят на борт и преследовался преданным сообществом до тех пор, пока совсем недавно. Исследования в этой области получили большой импульс с 1990. Для дальнейшего обсуждения и подробностей см. Раздел 8.

3.1 Немонотонность

Аристотель считал, что большинство рассуждений, в том числе рассуждений о что делать и о подлунных явлениях природы, разобрался с вещами которые выполняются «всегда или по большей части». Но аристотелевская логика имеет дело только с шаблонами вывода, которые верны без исключения. Мы находим в самом начале логики несоответствие между рамками логического теории и здравого смысла. Немонотонная логика является первой устойчивая попытка в рамках логической теории исправить это несоответствие. В качестве таким образом, он представляет собой потенциал для быстрого расширения сферы применения логики, а также значительный объем технических результатов.

Отношения следствия классической логики монотонны. Что состоит в том, что если множество формул Γ влечет за собой следствие C , то больший набор Γ ∪ A будет также подразумевать C . А логика немонотонна , если в ее отношении следствий отсутствует это имущество. Предпочтительные модели обеспечивают общий способ вызвать немонотонное отношение следствия. Вызвать функцию, которая для каждого Γ производит подмножество M _Γ моделей Γ; в целом, мы будем ожидать М _Г до быть правильным подмножеством этих моделей. Тогда мы говорим, что Γ влечет C , если C удовлетворяет каждая модель в М _Г . Пока мы не Предположим, что М _{Γ∪{ А }} ⊆ M _Γ , мы можем легко получить отношение следствия между Γ и C без наложения это отношение на супермножествах Г. ^[14]

Эта теоретико-модельная модель поведения соответствует управляемому ожиданиями рассуждение, где ожидания позволяют пренебречь некоторыми случаями. Вот важное различие между здравым смыслом и математикой. Математики обучены отвергать доказательство по случаям, если только случаи не исчерпать все возможности; но типичные примеры здравого смысла аргументация пренебрегает некоторыми альтернативами. В самом деле, разумно обычно игнорируют маловероятные возможности. Стою на кухне в Калифорния, интересно, есть ли время помыть посуду перед отъездом для работы можно не принимать во внимание возможность землетрясения. учетная запись.

По-видимому, существует множество законных причин для пренебрежения определенными случаи в рассуждениях здравого смысла. Качественное суждение о том, что вероятность случая незначительна является одной из причин. Но, например, в контексте планирования может быть разумно игнорировать даже незначительные вероятности, пока нет практического смысла в планировании эти случаи.

Мотивы немонотонности, по-видимому, включают ряд сложные факторы; вероятность (возможно, в каком-то качественном смысле), нормальность, ожидания, разумные в том смысле, что нельзя быть обоснованно обвиненным в их наличии, взаимном признании и факторах имеет отношение к ограниченной рациональности. Вполне может быть, что ни у кого нет удалось распутать и прояснить эти мотивирующие соображения. На ранних этапах своего появления в логическом ИИ многие исследователи, по-видимому, рассматривали немонотонное рассуждение как общий метод рассуждений о неопределенности; но к концу года 1980-е, реализации полностью количественных вероятностных рассуждений были не только возможны в принципе, но и явно предпочтительнее много видов приложений к методам, включающим немонотонную логику. А правдоподобное и реалистичное обоснование немонотонной логики должно ей соответствовать. в более широкую картину рассуждений о неопределенности, которая также включает вероятностный рассуждения. ^[15]

3.2 Исторические мотивы

Три влиятельные статьи по немонотонной логике появились в 1980: Макдермотт и Дойл 1980, Райтер 1980 г., а также Маккарти 1980. В каждом случае формализмы, представленные в этих работах, были результатом вынашивания период в несколько лет и более. Изложить исторические влияния точно, надо бы взять интервью у авторов, а это не сделано. Тем не менее, похоже, было два мотивирующих фактора: стратегические соображения, связанные с долгосрочными целями ИИ, и гораздо более конкретные тактические соображения, вытекающие из анализ систем рассуждений, которые были развернуты в 1970-е годы.

Раздел 2.2 обратил внимание на Маккарти предложенная цель формализации рассуждений здравого смысла. Бриф обсуждение выше в Раздел 3.1 предполагает, что монотонность может быть препятствием для достижения этой цели. Дополнительный мотив был найден в Минский 1974 г., который был широко читался в то время. В данной статье представлен ассортимент задачи для ИИ, сосредоточив внимание с самого начала на проблеме естественного язык понимание. ^[16] Минский выступает за фрейм-ориентирование представление знаний техника ^[17] и (думая об использовании этих представления как альтернатива логике), он выбрасывает ряд слабо связанные проблемы для логического подхода, в том числе проблема построения крупномасштабных представлений, рассуждений эффективно представлять контрольные знания и обеспечивать гибкий пересмотр опровержимых убеждений. Ретроспективно, большинство исследователей ИИ склонны согласиться с тем, что эти проблемы носят общий характер. бросает вызов любой исследовательской программе в области ИИ (включая программу Минского сам защищал в то время) и что логические методы являются важный элемент в решении некоторых, а может быть, и всех вопросов. (За Например, хорошо структурированный логический план может быть большим подспорьем в масштабирование представления знаний. )

Минский, по-видимому, намеревался привести общие аргументы против логические методы в ИИ, но Макдермотт и Дойл, 1980 г. а также Маккарти 1980 интерпретировать Минский 1974 г. как вызов, который может быть решен разработка логик, не обладающих свойством монотонности. Возможно непреднамеренно, бумага, кажется, послужила некоторым стимулом немонотонным логикам, подчеркивая монотонность как источник предполагаемые недостатки логики. Фактически, термин «монотонность», по-видимому, впервые появляется в печать в Мински 1974 бумага.

Развитие немонотонной логики также во многом обязано прикладная сторона ИИ. В самом деле, необходимость немонотонного анализа число приложений ИИ было столь же убедительным, как и стратегическое соображения, выдвинутые Маккарти, и во многом более влиятельные форму формализмов, которые возникли. Здесь мы упомянем три такие приложения, которые, по-видимому, были важны для некоторых ранние немонотонные логики: пересмотр убеждений, рассуждения о замкнутом мире, и планирование.

3.2.1 Пересмотр убеждений

Дойл 1979 предоставляет анализ и алгоритм для «поддержания достоверности система”. TMS отвечает общей потребности, предоставляя механизм для обновления «верований» баз знаний. Идея TMS должна отслеживать поддержку убеждений и использовать запись этих вспомогательных зависимостей, когда необходимо пересмотреть убеждения.

В TMS часть поддержки убеждения может заключаться в отсутствие какой-либо другой веры. Это вводит немонотонность. Например, он предусматривает значения по умолчанию; что среда по умолчанию день для назначения встречи означает уверенность в том, что встреча будет в среду зависит от отсутствие убеждений особого случая в связи с чем это не будет в среду.

Алгоритм TMS и его усовершенствования оказали значительное влияние на ИИ. приложений, и это создало потребность в логическом анализе. (В даже в довольно простых случаях может быть сложно при отсутствии аналитического инструменты, чтобы увидеть, какие последствия должна дать TMS.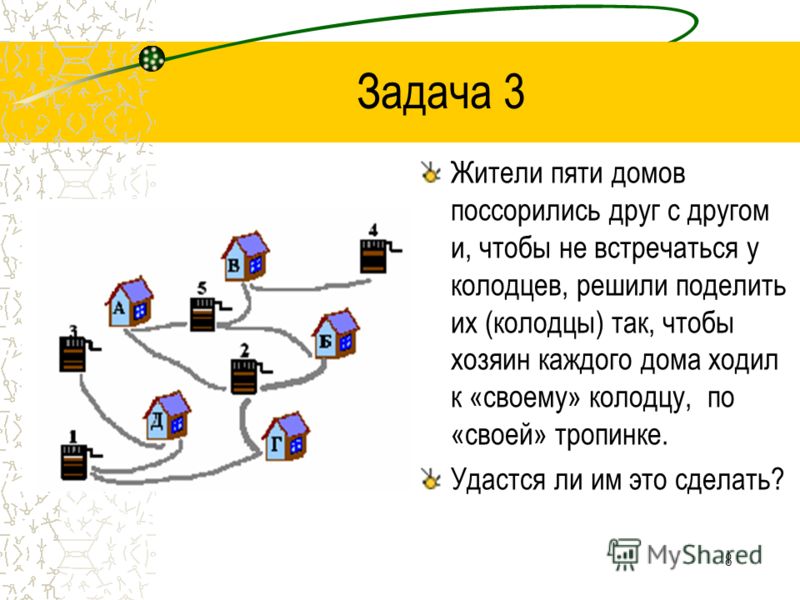 ) Это обеспечило естественная и очень специфическая задача для тех, кто стремится развивать немонотонная логика. TMS также предоставил определенные интуитивные идеи: идея что ключом к немонотонности являются выводы, основанные на недоказуемость была важна для модальных подходов к немонотонным логика и логика по умолчанию. И акцент TMS на взаимодействиях между аргументами началась тема в немонотонной логике, которая остается важно по сей день. (См. обсуждение основанного на аргументах подходы, в Раздел 3.4, ниже.)

3.2.2 Рассуждения о замкнутом мире

Изучение баз данных относится к компьютерным наукам, а не конкретно к ИИ. Но одна из исследовательских парадигм в научном анализе базы данных использует логические модели представлений и рассуждений (видеть Минкер 1997 для недавнего опроса поле), и эта область взаимодействовала с логическим ИИ. дедуктивный парадигма баз данных формировалась примерно в то же время, когда многие исследователи размышляли над проблемами немонотонной логики, и предоставил несколько конкретных примеров немонотонных рассуждений, которые вызвали на анализы. Из них, пожалуй, самым важным является предположение о закрытом мире , согласно которому — по крайней мере, как что касается простых фактов, представленных в базе данных как положительные или отрицательные литералы — система предполагает, что она знает все, что нужно знать. Это предположение закрытого мира, что оправдывает отрицательный ответ на вопрос «Есть ли прямой рейс из Детройта в Болонью?» когда система не находит такого рейса в его данные. Это еще один случай вывода из отсутствия доказательство; отрицательный факт фактически доказывается провалом систематического попытаться доказать положительное. Эта идея, исследованная в бумаги, такие как Райтер 1978 а также Кларк 1978 также поставил задачу немонотонные логики, а также специфические интуиции — обратите внимание, что опять же, идея правил вывода в зависимости от отсутствия доказательства присутствует здесь.

3.2.3 Планирование

Рациональное планирование невозможно без умения рассуждать о результаты ряда предполагаемых действий. Прогнозирующее рассуждение такого рода является местным; в сложном мире со многими особенностями мы предположить, что большинство вещей не изменится после выполнения действие. Но эта местность оказалась трудно формализуемой. проблема, как формализовать эту «каузальную инерция» ^[18] известен как рама . Проблема .

Очень естественно предположить, что инерция имеет место по умолчанию; переменные не меняются при выполнении действия, если только особая причина думать, что они изменятся. Это говорит о том, что немонотонные темпоральные формализмы должны обеспечивать основание для рассуждений о действиях и изменениях. Таким образом, попытки формализация рассуждений, необходимых при планировании, также создала потребность в немонотонные логики. Одна из первых попыток формализовать немонотонное рассуждение, Сандеволл 1972, решает проблему кадра. Инерционные значения по умолчанию являются особенно важный и поучительный пример; о них больше не будет сказано здесь, так как они подробно обсуждаются в Раздел 4. 4, ниже.

3.3 Древнейшие формализмы

Три статьи 1980 года, упомянутые в начале Раздел 3.2 представляют собой три подхода к немонотонная логика, которые и по сей день остаются важными подполями: контур (Маккарти), модальные подходы (Дойл и Макдермотт) и логика по умолчанию (Reiter).

В Маккарти 1993а, Маккарти призывает нам, рассматривая раннюю историю ограничения, принять во внимание счет группы из трех статей: Маккарти 1986 г., 1980 г., а также 1987. Первая статья связывает стратегические идеи Маккарти и Хейс, 1969 г. с потребностью в немонотонной логике, и обрисовывает логические идеи ограничения домена , которое теперь классифицируется как простейший случай ограничения. Секунда статья обеспечивает более тщательное логическое обоснование и вводит более общий и мощный ограничение предиката подход. Третий документ посвящен разработке методов формализации сложные примеры здравого смысла.

Все формы ограничения предполагают ограничение внимания моделями. в которых минимизируются определенные множества; по этой причине ограничение можно сгруппировать с предпочтительными моделями подходов к немонотонности: видеть Раздел 3.4, ниже. Маккарти формализм довольно консервативен; хотя это вызывает интересные логические проблемы в логике высшего порядка и сложности, он использует знакомую логическую рамки. И большое внимание уделяется развитию приемы формализации. Другие разновидности немонотонной логики, включая логику по умолчанию и модальную немонотонную логику, вызывают вопросы того рода, которые знакомы философским логикам, вынужденным делать с разработкой новой логики, систематического исследования вопросы, касающиеся валидности, и управления распространением альтернативная логика.

Как указывалось выше в обсуждении поддержания истины, это очень естественно думать о немонотонных выводах как об огражденных . То есть для немонотонного вывода может потребоваться не только наличие набора доказанных выводов, но отсутствие определенных другие выводы. Общая форма такого правила:

DR :
В присутствии { A ₁ ,…, A _n } и в отсутствие { Б ₁ ,…, Б _н }, заключить C .

Важным частным случаем DR является нормальный . default , простое правило о том, что C выполняется по умолчанию, условно на предположениях А ₁ ,…, А _n . Это может быть формализуется принятием условия, которое должно отсутствовать, чтобы просто быть отрицание заключения.

Отчет о недоставке :
В присутствии { А ₁ ,…, А _n } и в отсутствие ¬ C , заключение C .

На первый взгляд, вызывает некоторое недоумение, как это формализовать. понятие немонотонного вывода, поскольку оно, по-видимому, требует циклического определение доказуемости, которое нельзя заменить индуктивным определение, как и в немонотонном случае. Трудность с ранним теория Сандеволл 1972 это то, что он делает не справиться с этой трудностью успешно. Макдермотт и Дойл 1980 а также Райтер 1980 использовать определения фиксированных точек для решать проблему. В обоих случаях логическая задача состоит в том, чтобы (1) разработать формализм, в котором могут быть выражены такие правила, как DR , и (2) определить связь между теорией DT (которая может включать такие правила) и теории E , которые могли рассчитывать как разумные последствия ДТ . В терминологии, которая позже стали стандартными, нам нужно определить связь между теорией ДТ и его расширения .

Оглядываясь назад, мы можем выделить два вида подходов к немонотонная логика: основанные на предпочтениях и основанные на на конфликт . Теории первого рода (например, ограничение) включают в себя относительно простую модификацию обычного теоретико-модельное определение логического следствия, которое учитывает учитывать отношение предпочтения над моделями. Теории второго рода (например, логика по умолчанию) предполагают более радикальное переосмысление логических идеи. Возможность нескольких расширений — разные возможные последовательные, логически полные наборы выводов, которые можно сделать из единый набор предпосылок — означает, что мы должны думать о логических следствие не как функция, принимающая набор аксиом в свою логическую закрытие, но как отношение между набором аксиом и альтернативные логические замыкания. Поскольку логическое следствие таково фундаментально, это представляет собой серьезный теоретический отход. С несколько расширений, мы все еще можем получить отношение следствия между теорией и формулой различными способами, самый простой из которых говорят, что DT немонотонно влечет C , если C является членом каждого расширения DT . Тем не менее, объяснение последствий, основанное на конфликте, обеспечивает гораздо более богатую основу структура, чем преференциальная.

Райтер подходит к проблеме формализации консервативно. Немонотонность не выражается на языке дефолтной логики, который совпадает с языком логики первого порядка. Но теория может включать набор из правил по умолчанию — правил вида ДР . Райтер 1980 дает определение фиксированной точки расширений такой теории, и развивает теоретические основы подхода, доказывая ряд основных теорем.

Из этих теорем мы особо упомянем одну, которая будет использоваться в Раздел 4.5, в связи с Йельским университетом Стреляющая аномалия. Идея состоит в том, чтобы взять предполагаемое расширение (которое будет набор T *) и использовать этот набор для проверки согласованности в процессе, похожем на доказательство, который последовательно применяет правила по умолчанию в < W , D > до этапов, начинающихся с Вт .

Мы определяем процесс доказательства по умолчанию т ₀ , т ₁ ,… для Вт , D относительно T * следующим образом.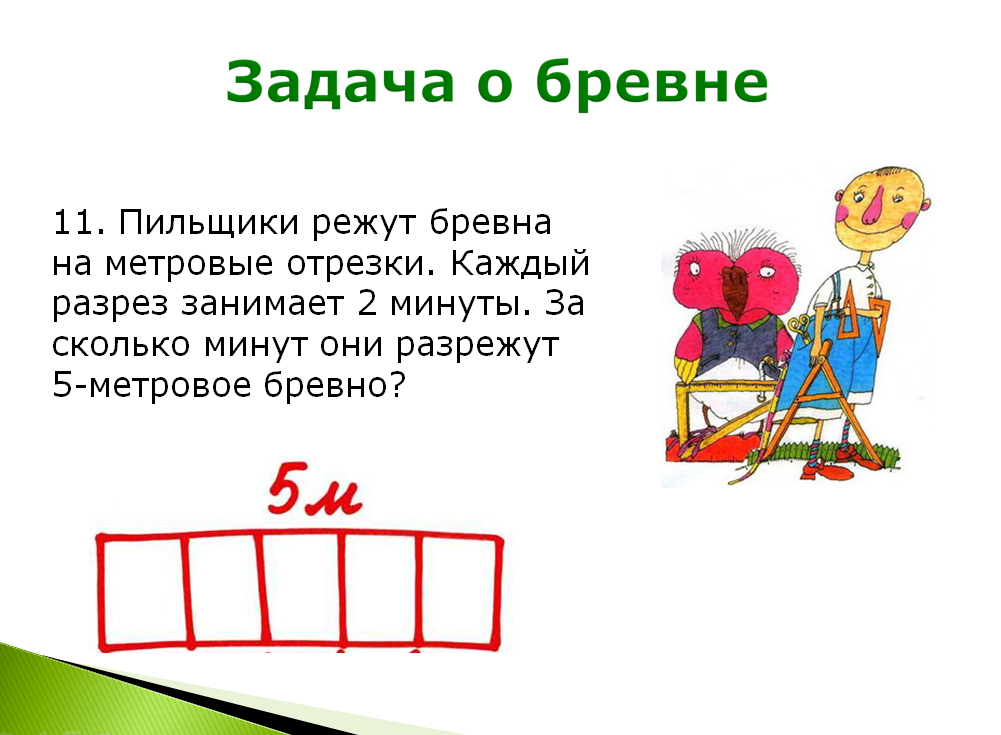

Другими словами, пока мы можем ненадуманно закрыть сцену, мы работая в соответствии с применимым значением по умолчанию, мы делаем это; в противном случае мы делаем ничего такого. Теорема Рейтера говорит, что при этих обстоятельствах:

T является расширением < W , D > тогда и только тогда, когда существует процесс доказательства T ₀ , T ₁ ,… для W , D относительно T , так что

Т =

∪ 0≤ я

Т я .

Таким образом, мы можем показать, что T является расширением (1) с использованием T для проверки непротиворечивости в процессе рассуждений по умолчанию из < W , D >, (2) взятие предела T ′ этого процесса и (3) проверка того, что на самом деле T ′ = Т .

Модальный подход представляет собой «более высокий уровень немонотонного вовлеченность», чем логика по умолчанию. Конструкция недоказуемости явно представленный в языке с помощью модального оператора L неофициально интерпретируется как «доказуемый» (или, как в Макдермотт и Дойл 1980, по двойственный этому оператору). ^[19] Хотя Макдермотт и Дойл терминология отличается от рейтеровской, логические идеи очень похожи — суть их подхода, как и у Райтера, определение неподвижной точки расширений немонотонной логики. Включение немонотичности в объектный язык создает некоторые дополнительные сложности, которые проявляются в раннем модальном подходе главным образом в умножении логики и затруднениях в оценке достоинства альтернатив. Как лучшая основа для модального подход, стало возможным доказать ожидаемые теоремы относительно эквивалентности модальных формализмов по умолчанию логика. ^[20]

Бумага Райтера Райтер 1980 кажется развивались в первую очередь из тактических соображений. Чем раньше бумага Райтер 1978 в значительной степени обеспокоен с предоставлением учета запросов к базе данных. В отличие от других основополагающих работы по немонотонной логике, Рейтер показывает особое влияние более ранняя и независимая работа о немонотонности в логике программирование — работа, кажется, была в значительной степени вдохновлена необходимо предоставить логические основания для немонотонных рассуждений найдены в дедуктивных базах данных. В статье Дойла и Макдермотта показаны оба стратегическая и тактическая мотивация – со ссылкой на более раннюю литературу в логическом ИИ он мотивирует немонотонную логику как часть программы моделирование рациональности здравого смысла. Но теория также очевидна. под влиянием необходимости предоставить формальную отчетность об истине техническое обслуживание.

3.4 Подходы к немонотонной логике

Немонотонная логика — сложная и надежная область исследований. Предоставление изучение предмета затруднено тем, что существует множество различные основополагающие парадигмы для формализации немонотонных рассуждения, и отношения между этими парадигмами непросты. Ан адекватный учет даже значительной части поля требует что-то вроде лечения длиной в книгу. Ряд книг есть в наличии, в том числе Лукашевич 1990, Брёвка 1991 г., Бенар 1992 г., Марек и Трушчински, 1994 г., Антониу 1997, Брюка и др. . 1997 г., Шлехта 1997 г., Антонелли 2005, Макинсон 2005b, а также Хорти 2012. Два коллекции особенно полезны: Гинзберг 1987 а также Габбай и др. . 1994. Первый является полезным источником для читателей, интересующихся ранняя история предмета, и имеет превосходное введение. главы справочника в Габбай и др. . 1994 г. предоставить обзоры важных тем и подходов. Моя текущая рекомендация для читателей, заинтересованных в быстром, читаемом введение в тему будет Брёвка и др. . 1997 г. и самостоятельно выбранные главы Габбай и др. . 1994. Некоторые другие источники включают Бочман 2004, Макинсон 2005, Антониу и Ван 2007 г., Бочман 2007, а также Шлехта 2007. Мы полагаемся на этих ссылках для технического фона, и сосредоточимся на интеллектуальная мотивация, основные идеи и потенциальные долгосрочные значение для логики.

3.4.1 Семантика предпочтений

В самом начале в Раздел 3.1, было упомянуто, как предпочтительные модели могут быть использованы для характеристики немонотонного отношение последствия. Эта общая модель теории немонотонности появился в Шохам 1988, пять лет спустя работа обсуждалась в Раздел 3.2, а также представляет гораздо более общий и абстрактный подход.

Предпочтительная семантика опирается на функцию S , принимающую набор K моделей в подмножество S ( K ) моделей К . Ключевое определение преференциального следствия оговаривает, что A является (немонотонным) следствием Γ если каждая модель M из S (Модели (Γ)) подразумевает А . Теория Шохэма основана на частичном порядке ≼ по моделям: S ( K ) затем можно охарактеризовать как множество моделей в K , которые являются ≼-минимальными в К . Чтобы гарантировать, что ни один набор не может предпочтительно повлечь за собой противоречие, если оно классически не влечет за собой противоречие, бесконечное нисходящие ≼ цепочки должны быть запрещены.

Эта трактовка немонотонности похожа на более раннюю модальную семантические теории условных предложений – сходство особенно очевидно при использовании более общих теорий условного семантика, такая как та, что представлена ​​в Челлас 1975. Конечно, следствие отношение классической условной логики монотонно, и условная семантика использует возможные миры, а не модели. Но лево-немонотонность кондиционалов (тот факт, что A C не подразумевает [ А ∧ Б ] C ) создает проблемы, которые аналогичны немонотонной логике. Ранние работы по немонотонной логике кажется, не знает об аналогии с условной логикой. Но взаимоотношения между ними стали важной темой более совсем недавно; см., например, Гарденфорс и Макинсон 1994, Бутилье 1992 г., Жемчуг 1994 г., Габбай 1995 г., Бенферат и др. . 1997 г., Дельгранде 1998, Арло-Коста и Шапиро 1992, Алькуррон 1995, Ашер 1995, а также Томасон 2007.

Семантика предпочтений дает возможность сформулировать и доказательство теорем о представлении, связывающих условия предпочтения отношения к свойствам абстрактного отношения следствия. Эта линия расследование началось с Lehmann & Magidor 1992.

3.4.2 Модальные и эпистемологические теории

Ни Дойл, ни Макдермотт не преследовали модальный подход намного дальше. начальные этапы Макдермотт 1982, а также Макдермотт и Дойл, 1980. Благодаря полезному совету Роберта Сталнакера (см. Сталнакер 1993), однако Роберт С. Мур создал модальную теорию, которая во многих отношениях улучшает более раннюю идеи. Мур дает модальному оператору своей системы эпистемологическую интерпретация, основанная на представлении правила по умолчанию как правила, которое лицензирует вывод для рассудительного агента, если только что-то, что агент знает блокирует заключение. В доме Мура автоэпистемический логика , расширение E теории T является надмножество T , которое является стабильным , т.е. дедуктивно замкнуто и удовлетворяет следующим двум правилам:

1. Если A ∈ E , то □ A ∈ E .
2. Если А ∉ Е тогда ¬□ A ∈ E .

Также обычно накладывают условие заземленности на аутоэпистемические расширения T , гарантируя, что каждый член расширение почему-то восходит к T . Различные такие условия учтены; самый простой ограничивает расширения к тем, которые удовлетворяют

3. E — множество немодальных последствий Т ∪{ А : □ A ∈ E } ∪ {¬□ А : А ∉ Е }.

Автоэпистемическая логика остается популярным подходом к немонотонной логике. отчасти из-за его полезности в обеспечении теоретических основ для логического программирования. Более свежие ссылки см. Марек и Трушчински 1991, Мур 1995b, Марек и Трушчински 1989, Конолиге 1994 г., Антониу 1997, Мур 1993, а также Денекер и др. . 2003.

Эпистемическая логика вдохновила другие подходы к немонотонной логике. Подобно другим модальным теориям немонотонности, они используют модальность для отражать согласованность в объектном языке и, таким образом, разрешать правила по умолчанию в соответствии с DR , подлежащим выражению. Но вместо последовательность, эти используют невежество . Видеть Халперн и Моисей 1985 а также Левеск 1987 для вариаций этой идеи. Эти теории объясняются и сравниваются с другими немонотонными логика, в Мейер и ван дер Хук, 1995. В более поздних работах идеи Левеска систематически излагаются. представлены и применены к теории баз знаний в Levesque & Lakemeyer 2000.

3.5 Дополнительные темы

Это краткое историческое введение в немонотонную логику оставляет не затронули ряд общих тем, которые могли бы иметь интерес для неспециалиста. К ним относятся графические и теоретико-доказательные подходы к немонотонной логике, результаты, которые связывать различные формализмы, сложность результатов, поддающиеся обработке частные случаи немонотонных рассуждений, отношения между немонотонными и абдуктивное рассуждение, отношения к вероятностной логике, логическое интуиция и кажущиеся закономерности достоверности, лежащие в основе немонотонности логика и методы, используемые для формализации доменов с использованием немонотонных логика. По этим и другим темам читатель может обратиться к литература. Для начала главы в Габбай и др. . 1994 г. очень рекомендуемые.

4.1 Априорная временная логика

Рассуждения о времени и времени были связаны с логикой с тех пор, как Истоки научной логики у Аристотеля. Идея логики время в современном смысле было знакомо, по крайней мере, с работ Ян Лукасевич (см., например, Лукасевич 1970), но форма того, что обычно называют временной логикой, было стандартизировано Артуром Работы Прайора в 1950-х и 1960-х годах: см. Прайор. 1956 г., 1967, 1968. ^[22] По мере развития темы в философская логика, временная логика оказалась разновидностью модальной логики; На творчество Прайора сильно повлияли как Хинтикка, так и Крипке, а также идея о том, что истинность временных логических формул относительна мировых состояний или временных стадий мира; эти теоретико-временные аналоги вневременных возможных миров обыденного модальная логика. Таким образом, центральные логические проблемы и приемы временного логика была заимствована из модальной логики. Например, он стал тема исследования для выработки отношений между аксиоматическими системами и соответствующие теоретико-модельные ограничения на временные порядки. См., например, Берджесс 1984 а также Ван Бентем 1983.

Логика априорного времени разделяет с модальной логикой техническое сосредоточение внимания на вопросах, возникающих при использовании теории первого порядка отношения для объяснения логических явлений, ожидание того, что важные временные операторы будут квантификаторами мировых состояний, и довольно отдаленный и фундаментальный подход к реальным образцам временные рассуждения. Конечно, эта темпоральная логика дает допустимости, такие как

A → PFA

(если A , то A должно было быть случай), которые, безусловно, интуитивно верны. Но в лучшем случае эти могут играть лишь широко основополагающую роль в учете реалистичных рассуждения о времени. Трудно придумать реалистичные примеры в котором они играют ведущую роль.

Эта характеристика, конечно же, характерна для модальной логики. самые традиционные и современные логические теории; связь с повседневное мышление довольно слабое. Хотя современные логические методы объяснить с некоторым успехом рассуждения, связанные с проверкой математические доказательства и логические головоломки, они не объясняют другие случаи технических рассуждений или рассуждений здравого смысла с большим количеством деталей или правдоподобие. Даже в таких случаях, как юридические рассуждения, когда логики и логически мыслящие теоретики права приложили немало усилий для формализации рассуждения, полезность результатов является спорным.

4.2 Проблемы планирования и ситуационный расчет

Проблемы планирования представляют собой одну из самых плодотворных демонстраций для сочетая логический анализ с приложениями ИИ. С одной стороны там много практически важных приложений автоматизированного планирования, и другие логические формализации планирования действительно полезны в понимании проблем и в разработке алгоритмов.

Классическое представление проблемы планирования ИИ, как описано в Амарел 1968, очевидно, происходит в ранняя работа Герберта Саймона, опубликованная в 1966 году в техническом журнале CMU. отчет, Саймон 1966. В такой задаче агент в начальном мировом состоянии оснащен набором действий , которые рассматриваются как частичные функции превращение мировых государств в мировые государства. Действия возможны только в мировых состояниях, отвечающих определенным ограничениям. (Эти ограничения теперь называется «предпосылками» действия.) Планирование проблема становится поиском ряда возможных действий, которые последовательно трансформировать исходное мировое состояние в желаемое мировое государство.

Ситуационное исчисление , разработанное Джоном Маккарти, является происхождение большей части более поздних работ по формализации рассуждений о действии и изменить. Впервые он был описан в 1969 г. Маккарти 1983; самый ранний вообще доступная публикация по теме есть Маккарти и Хейс, 1969.

По-видимому, априорная временная логика не оказала влияния на Амарель 1968 года. Но нет важного разница между мировыми состояниями Амареля и состояниями приорианского времени логика. «Ситуации» ситуационного исчисления такие же. мировые государства под новым имя. ^[23] Они напоминают возможные миры в модальная логика в предоставлении абстрактных местоположений, которые поддерживают последовательную и полное собрание истин. Как и в напряженной логике, эти места упорядочены, и изменение представлено изменением истин от одного места в другое. Принципиальная разница между ситуацией Расчет и напряженная логика заключаются в том, что изменение ситуации динамический — изменения не просто происходят, а происходят причина.

Это различие, конечно, вызвано предполагаемым использованием Ситуационное исчисление: оно предназначено для того, чтобы формализовать представление Саймона о задача планирования, в которой один агент рассуждает о сценарии, в которых ряд действий выполненный.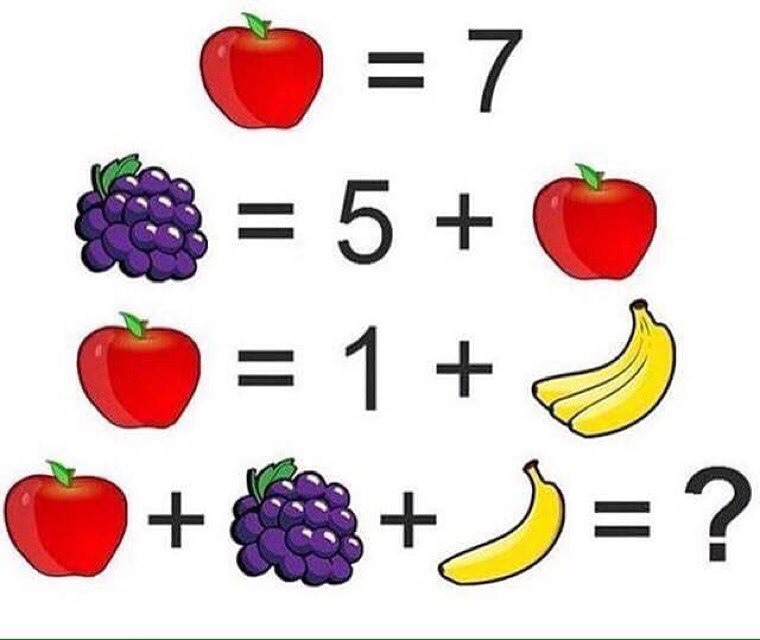 ^[24] В этом модели, то, что движет изменениями, — это выполнение действий, поэтому фундаментальная модель теоретическое отношение есть отношение

R РЕЗУЛЬТАТ (a,s,s′)

между действием а, начальной ситуацией s, в которой выполняется а, и результирующая ситуация s’, непосредственно следующая за выполнение действия. Обычно (хотя это не совсем необходимо) делается детерминированное предположение, что s′ является уникальный. В общем, действия могут быть успешно выполнены только при определенные ограниченные обстоятельства. Это может быть смоделировано с учетом случаи, когда не существует s′ такого, что р РЕЗУЛЬТАТ (а, с, с’). Но обычно предполагается, что R ESULT на самом деле является общей функцией, но в случаях которое s не удовлетворяет «условиям» a, нет ограничения на s′, удовлетворяющие R РЕЗУЛЬТАТ (a,s,s′), так что причинные эффекты в таких случаях будет совершенно неограничен.

Проблема планирования начинается с ограниченного репертуара действий (где наборы предпосылок и эффектов связаны с каждым действие), исходная ситуация и цель (которую можно трактовать как формула). Задача планирования состоит в том, чтобы найти последовательность действия, которые позволят достичь цели, учитывая исходную ситуацию. Что есть, учитывая цель G и исходной ситуации s проблема будет состоит из нахождения последовательности s ₁ ,…,s _n из действия, которые превратят s в конечную ситуацию, удовлетворяющую Г . Это означает (при условии, что R ESULT является функция), что G будет удовлетворен ситуацией s _n , где s ₀ = s и s _{i +1} есть s′ такое, что R РЕЗУЛЬТАТ (a _{i +1} ,s _i ,с’). Проблема планирования, по сути, заключается в поиске последовательности действий. выполнение этих условий. Условия успеха поиска могут быть характеризуется формализмом, подобным ситуационному исчислению, который позволяет информация о результатах действий, подлежащих выражению.

До сих пор ничего не было сказано о подлинном языке Ситуационный расчет. Решающее значение имеет то, как изменения должны быть выражены. Имея в виду напряжённую логику, было бы естественно использовать такую ​​модальность, как [ А ] А , с условием истинности

⊨ _s [ a ] A тогда и только тогда ⊨ _{с ′} А , где R РЕЗУЛЬТАТ (а, с, с’).

Эта формализация в стиле динамической логики фактически является ведущей кандидат; видеть Раздел 4.7, ниже.

Но Маккарти и Хейс, 1969 г. использует язык, который намного ближе к логике первого порядка. (Этот стиль формализации характерен для работ Маккарти; см. Маккарти 1979.) Действия рассматриваются как лица. И некоторые предложения, значения истинности которых могут меняться с течением времени (предполагаемые беглых ) также рассматриваются как лица. Где s — ситуация, а f — беглое выражение, Содержит (f,s) говорит, что f истинно в s.

4.3 Формализация микромиров

Начиная с новаторской работы девятнадцатого и начала двадцатого логики века, процесс формализации математических областей во многом стали рутиной. Хотя (как и в теории множеств) могут возникнуть споры о том, какие аксиомы и логическая инфраструктура лучше всего служат для формализации области математики, методы формализации и критерии их оценки относительно беспроблемны. Этот методологическая ясность не была успешно распространена на другие домены; даже формализация эмпирических наук представляет сложные проблемы, которых еще не было решено. ^[25]

Формализация темпоральных рассуждений и, в частности, рассуждения о действиях и планах, является наиболее развитым успешным распространение современных методов формализации на области, отличные от математические теории. Этот отход потребовал создания новые методики. Одно методологическое нововведение появится в Раздел 4.5: разработка библиотеки сценариев для проверка адекватности различных формализмов и создание специализированные домены, такие как домен блоков мира (упомянутый выше, в разделе 4.2), которые служат лабораториями для проверки идей. Подробнее о мире блоков см. Генесерет и Нильссон 1987; Дэвис 1991. представления Маккарти о допуск обработки Маккарти 1999 представить одну интересную попытку предоставить критерий для адекватность формализации. Еще одна идея, возникшая в ходе формализация областей здравого смысла заключается в важности явного онтология; см., например, Фикес 1996 и Ленат и Гуха 1989. Другим является потенциальная полезность явного представления контекста; видеть Гуха, 1991 год. Другим является использование методов моделирования: см., например, Джонстон и Уильямсон, 2007 г.

4.4 Прогнозирование и проблема фрейма

Чтобы сказать, достигает ли план своей цели, вам нужно цель сохраняется в конечном состоянии плана. Для этого требуется предиктивное рассуждение, тип рассуждения, которым пренебрегали в напряженно-логической литературе. Как и в механике, предсказание включает в себя вывод более поздних состояний из более ранних. Но (в случае хотя бы простые задачи планирования) динамика определяется действий, а не дифференциальными уравнениями. Расследование эта качественная форма временного рассуждения и связанных с ним видов рассуждения (например, распознавание плана, которое стремится вывести цели из наблюдаемые действия и повествовательное объяснение, которое стремится заполнить имплицитная информация в темпоральном нарративе) является одним из наиболее впечатляющие главы в краткой истории логицизма здравого смысла.

Суть предсказания заключается в том, чтобы сделать вывод о том, что имеет место в ситуация, возникающая в результате выполнения действия при наличии информации о исходной ситуации. Часто предполагается, что агент полностью знание исходной ситуации — это допущение обычно классические формализации планирование. ^[26]

Большая часть качественной динамики, которая необходима для планирования состоит в выводе о том, что изменяет , а не . Возьмите простой план чтобы ввести слово «кошка» с помощью программного обеспечения для обработки текстов: естественный план состоит в том, чтобы сначала ввести «с», затем ввести «а», затем введите «т». Частью уверенности в этом плане является то, что действия независимы: например, ввод «a» также не стирает букву «с». Требуемый вывод может быть считается формой инерция . Проблема фрейма проблема формализации необходимых инерционных рассуждений.

Проблема фреймов была названа и введена в Маккарти и Хейс, 1969. В отличие от большинства интересных с философской точки зрения технических проблем, появление в ИИ привлекло внимание философов; большинство соответствующие документы и справочную информацию можно найти в Форд и Пилишин 1996; Пилишин 1987г. Оба этих тома задокументировать взаимодействие между ИИ и философией.

Качество этих взаимодействий обескураживает. Как и любой реалистичный проблема рассуждений на основе здравого смысла, проблема фреймов является открытой, и может зависеть от самых разных обстоятельств. Если вы положите 20 долларов в кошелек, положите кошелек в карман и идите в магазин, вы можете смело предположим, что 20 долларов все еще в кошельке. Но если оставить 20$ на прилавке в магазине во время шоппинга нельзя смело предположим, что он будет там позже. Это может объяснить искушение, которое заставляет некоторых философы ^[27] хотите понять проблему фрейма очень широко, так что очень скоро становится неразличимым от проблема формализации общего здравого смысла в произвольных областях. Такой широкая интерпретация может служить для введения спекулятивных дискуссий относительно природы ИИ, но теряет всякую связь с подлинные, новые логические проблемы во временных рассуждениях, которые обнаружено сообществом ИИ. Он предоставляет форум для повторения некоторых знакомые философские темы, но не привносит ничего нового в философия. Такой способ интерпретации проблемы фреймов разочаровывает, потому что философия может использовать всю возможную помощь; сообщество ИИ удалось расширить и обогатить применение логики к рассуждать здравым смыслом драматическими способами, которые очень важны для философия. Наиболее четкое описание этих событий можно найти в тома под редакцией Пилишина Моргенштерн 1996. Продленное лечение можно найти в Шанахан 1997; также см Сандеволл 1994 и Шанахан 2009.

Чисто логическая проблема фреймов может быть решена с помощью монотонной логики. просто написав явные аксиомы, утверждающие, что не изменяться при выполнении действия. Эта техника может быть успешно применительно к достаточно сложной формализации проблемы. ^[28] Но немонотонных решений каркаса были тщательно исследованы и развернуты; они приводят к новым и интересные линии логического развития.

Некоторые философы (Фодор 1987, Лорманд 1996) почувствовали, что надумано предложения вызовут особые трудности в связи с Проблема с кадром. Как отмечает Шанахан Шанахан 1997 [п. 24]) Фодора Пример «фриджена» легко формализуется в ситуационном исчислении и особых проблем не представляет. Однако, как предполагает Лорман, Гудман Примеры Гудман, 1946 год. создавайте проблемы, если они будут признаны свободно владеющими языком; будет аномально расширения, в которых объекты меняются с зеленого на синий, чтобы сохранить свою суровость.

Это один из немногих моментов, касающихся проблемы фреймов, сделанных философом. что создает настоящую трудность для формальные решения. Но трудность второстепенная, поскольку пример не реальный. Напомним, что потоки представлены как личности первого порядка. Хотя беглые языки зависят от ситуации функций, аксиома понимания, конечно, не предполагается для свободно На самом деле, обычно предполагается, что область текучих будет весьма ограниченным набором всей совокупности ситуационно-зависимых функции; как правило, это будет относительно небольшой конечный набор переменные, представляющие особенности предметной области, которые считаются важный. В конкретных случаях они будут выбираться почти так же, как способ выбора набора переменных в статистическом моделировании.

Похоже, что в литературе по ИИ нет систематического описания как выбрать подходящий набор флюсов, но это, безусловно, было бы часть такой учетной записи, которой должны соответствовать все беглые проектируемые предикаты в смысле Гудмена.

4.5 Немонотонные обработки инерции и Пакет задач

Идея немонотонных решений проблемы фреймов состоит в том, чтобы рассматривать инерцию по умолчанию; предполагается, что изменения происходят только в том случае, если есть какая-то особая причина их возникновения. В аккаунте, ориентированном на действия изменения, это означает, что отсутствие изменения предполагается, когда действие выполняется, если причина изменения не может быть найдена в аксиомах для Действие.

Для наглядности давайте воспользуемся логикой Райтера по умолчанию, чтобы проиллюстрировать это. формализация. Напомним, что в теории Рейтера значения по умолчанию представлены в виде правил, а не формул, так что они не подлежат количественная оценка. Чтобы формализовать инерцию, нам нужно использовать правило по умолчанию схемы. Для каждого беглого f, действия a и ситуации s множество эти схемы будут включать экземпляр следующей схемы:

ИК(ж, а, с)	Т: Удерживает (f,s) ↔ Удерживает (f,R РЕЗУЛЬТАТ (a,s))
	Удерживает (f,s) ↔ Удерживает (f,R РЕЗУЛЬТАТ (a,s))

Такой способ ведения дел делает любой случай, когда fluent изменяется истинное значение аномалии prima facie . Но следует из Счет Райтера о расширениях, что такие значения по умолчанию переопределяются, когда они противоречат монотонной теории динамики ситуации. Так что если, например, существует монотонная причинная аксиома для действия зачернить, гарантируя, что зачернение блока сделает его черным в результирующая ситуация, то соответствующий экземпляр IR будет неэффективен, и не будет расширение, в котором белый блок остается белым, когда он почерневший.

Проблема фреймов каким-то образом привлекла внимание широкой сообщества, но если кто-то заинтересован в понимании сложного проблемы, возникающие при обобщении формализмов, подобных ситуации Расчет, в то же время гарантируя, что они дают правдоподобные решения для самых разных сценариев, полезнее рассмотреть больший круг проблем. Для сообщества ИИ большие проблемы включают саму проблему фрейма, проблему квалификации, Проблема ветвления, обобщаемость по ряду важных параметры, включая неполную информацию, параллелизм (несколько агентов), и постоянные изменения, и, наконец, большой ассортимент конкретные проблемы, такие как сценарии, упомянутые ниже в этом раздел.

Проблема квалификации обычно возникает в связи с с формализацией обобщений здравого смысла. Как правило, они включают исключения, и эти исключения, особенно если человек готов принять надуманные обстоятельства — может повторять бесконечно. То же явление, под ярлыком вроде проблема при прочих равных условиях обобщений», знакома из аналитической философии. Это также проявляется в семантике общих конструкций, встречающихся в естественных языках. ^[29] В некотором смысле это проблема решается на общем уровне с помощью немонотонной логики, которые, хотя и не дают возможности перечислить исключения — допускайте, чтобы обобщения здравого смысла сформулированы как значения по умолчанию, а также позволяют проводить дальнейшие квалификации для добавляться неразрушающим образом. В идеале первоначальное обобщение можно сформулировать как аксиому и добавить оговорки постепенно в виде дальнейших аксиом.

Проблема квалификации была поднята в Маккарти 1986, где это было мотивировано главным образом обобщениями относительно последствий действий; Маккарти довольно подробно рассматривает обобщение о том, что превращение ключ зажигания в автомобиле заведет машину. Почти тот же момент, на самом деле можно совершать практически любые действия, в том числе и складывать одно блокировать на другом — стандартное действие, используемое для иллюстрации Ситуационный расчет. Ограниченный подход к квалификации Проблема представлена ​​в Лифшиц 1987; это явно вводит отношение предусловия между действием и его предпосылки в формализм, а ограничительно минимизирует предварительные условия, исключая из предпочтительных моделей любые «неизвестные предварительные условия», которые могут сделать действие неэффективным.

Некоторые аспекты проблемы квалификации остаются такими же широкими, сложные исследовательские задачи. Во-первых, не всякий немонотонный логика предоставляет изящные механизмы для квалификации. Логика по умолчанию, например, не дает интуитивно желаемых выводов. Предположим, кто-то формализует обобщение здравого смысла: если вы нажмете клавиша «а» на компьютере будет набирать «а» как обычное значение по умолчанию:

T : V ALUE (текст, R ESULT (Нажмите-a,s)) = V ALUE (текст,с) + ‘а’

V ALUE (текст, R ESULT (нажмите-a,s)) = V ALUE (текст,s) + ‘a’

Если мы затем формализуем исключение из этого обобщения, что если вы нажмите клавишу «a», пока клавиша Alt нажата курсор перемещается в начало текущего предложения как обычно по умолчанию по той же схеме получаем два расширения : одно в который нажатием «a» при нажатой клавише Alt перемещает курсор и другой, в котором он добавляет «а» к текст.

Проблема в том, что логика по умолчанию не предусматривает более конкретных значения по умолчанию переопределяют более общие. Этот принцип Специфика подробно обсуждалась в литературе. Включение его в немонотонную логику может усложнить теорию. значительно; см., например, Ашер и Морро, 1991 г. а также Хорти 1994. А также, в качестве Элькан 1995 г. указывает, квалификация Проблема поднимает вычислительные проблемы.

Относительно мало внимания уделяется квалификации. Задача характеристики действий в сравнении с другими задачами во временных рассуждениях. В частности, стандартные счета неудачные действия несколько неинтуитивны. в формализация Лифшиц 1987, например, действия с некоторыми невыполненными предварительными условиями являются только отличается от действий, все предпосылки которых приводят к тому, что условные эффекты действия будут обеспечены только тогда, когда предварительные условия соблюдены. Это как если бы действие по трате 1 000 000 долларов можно выполнить в любой момент, хотя если у вас нет деньги, никаких эффектов, в частности, не будет гарантировано.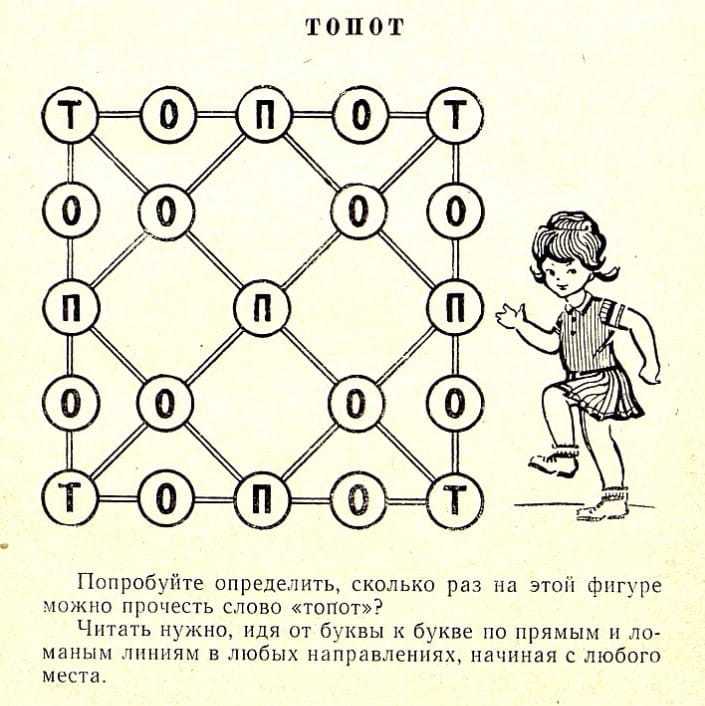 ^[30] А там нет различия между действиями, которые даже не могут быть предприняты (например, при посадке в самолет в Лондоне, когда вы находитесь в Сиднее), действия, которые могут быть предпринята попытка, но в которой можно ожидать, что попытка пойдет не так, как надо (например, снятие средств, когда у вас недостаточно средств), действия которые можно предпринять с разумной надеждой на успех, и действия которые можно попробовать с гарантированным успехом. Как сделал Дж. Л. Остин ясно в Остин 1961, способы, которыми действия могут быть попытки, и в которых попытки действий могут потерпеть неудачу, хорошо развитая часть рассуждений здравого смысла. Очевидно, при рассмотрении план, содержащий действия, которые могут потерпеть неудачу, может потребоваться обдумать последствия отказа. Формализуя патологию действий, предоставление систематической теории способов, которыми действия и планы которые содержат их, могут пойти не так, было бы полезным дополнением к планированию формализмов, и тот, который освещал бы важные темы в философия.

Проблема, связанная с проблемой разветвления (первая характеристика Палец 1987) является формализовать косвенные последствия действий, где «косвенные» эффекты не с задержкой, ^[31] но являются непосредственными во времени, но причинно производными. Если человек зайдет в комнате, прямой эффект состоит в том, что человек сейчас находится в комнате. Это также много косвенных эффектов: например, рубашка того тоже теперь в номер.

Отсюда видно, что формулировка задачи предполагает различение непосредственных последствий действий (следствий непосредственно связаны с действием и обеспечиваются успешное выполнение действия) и другие последствия. Этот предположение, как правило, безоговорочно принимается в литературе по ИИ на формализмах действия. Вы можете хорошо обосновать его здравый смысл правдоподобие — например, многие наши слова вместо действий («согреть», «удлинить», «удлинить». обеспечить’) выводятся из эффектов, которые обычно связанные с ними.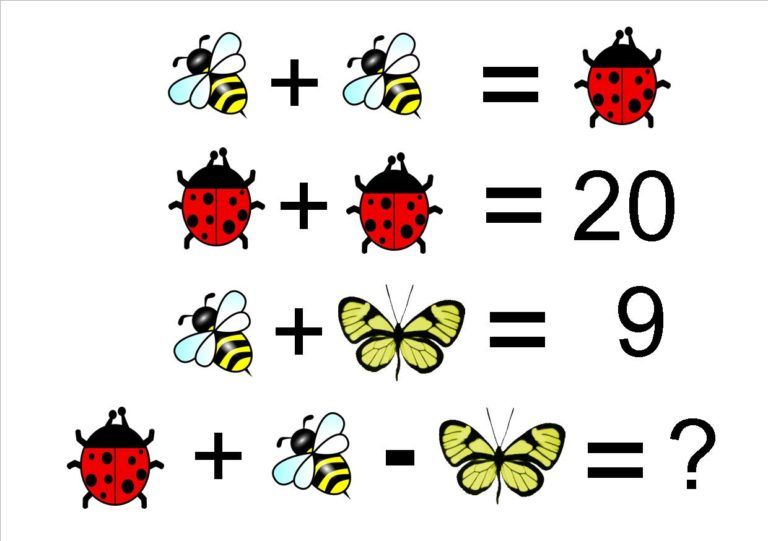 И в этих случаях влечет за собой успех: если кто-то что-то нагрел, это влечет за собой то, что стало тепло. ^[32] А типичный пример обсуждается в Лин 1995: некоторый чемодан имеет два замка и открыт тогда и только тогда, когда оба замка открыты. Затем (при условии, что действия не выполняются одновременно) открытие одного замка откроет чемодан тогда и только тогда, когда другой замок открыт. Здесь открытие замка — это действие с прямыми последствиями; открытие чемодана – это не действие, это косвенный эффект.

Очевидно, что проблема ветвления тесно связана с Проблема с кадром. В подходах, которые принимают немонотонные решения Проблема с рамой, инерциальные значения по умолчанию должны быть переопределены выводы о разветвлениях для получения правильных результатов. В случае, например, левый замок чемодана открыт, и действие открытия правого замка выполняется, то вывод по умолчанию то, что чемодан остается закрытым, нужно как-то подавить. Немного подходы к проблеме ветвления зависят от развития теории причинно-следственной связи здравого смысла и, следовательно, тесно связаны к каузальным подходам к рассуждениям о времени и действии, обсуждаемым ниже в Раздел 4. 6. Смотрите, для пример, Джунчилья и др. . 1997 г., Тильшер 1989, Лин 1995.

Философские логики довольствовались иллюстрацией своих идей. с относительно небольшими примерами. Формализация даже крупномасштабные математические теории относительно беспроблемны. Логист ИИ — первая ветвь логики, взявшая на себя задачу формализации большие примеры, включающие нетривиальные рассуждения здравого смысла. В процессе так что в этой области пришлось изобретать новые методы. Важная часть методология, возникшая при формализации действий и изменений, является особое внимание уделяется вызовам, поставленным в форме сценарии . Эти сценарии представляют проблемы формализации которые обычно включают относительно простые, реалистичные примеры, предназначенные для бросать вызов логическим теориям определенным образом. Как правило, будет иметь ясные интуитивные представления здравого смысла о выводах, которые должны рисуется в этих случаях. Задача состоит в том, чтобы разработать логический формализм которые предоставят общие, хорошо мотивированные решения для этих эталонных проблемы.

Среди многих сценариев, которые обсуждались в литературе Сценарий ребенка, Сценарий поездки на автобусе, Сценарий шахматной доски, Сценарий паромной переправы, Сценарий сборки мебели, Сценарий «Прячущаяся индейка», «Сценарий с кухонной раковиной», «Русская индейка» Сценарий, Загадочное убийство в Стэнфорде, Сценарий доставки в Стокгольм, Сценарий с угнанной машиной, Сценарий с душной комнатой, Автомобиль с билетами Сценарий, сценарий «Ходячая индейка» и аномалия стрельбы в Йельском университете. Отчеты о них можно найти в Шанахан 1997 а также Сандеволл 1994; видеть особенно Сандеволл 1994 [Главы 2 и 7].

Многие из этих сценариев предназначены для тестирования сложных проблем, которые здесь обсуждаться не будет — например, проблемы, связанные с нескольких агентов или с непрерывными изменениями. Здесь мы концентрируемся на одном из самых ранних и, вероятно, самых тонких из этих сценарии: аномалия стрельбы в Йельском университете, о которой впервые сообщается в Хэнкс и Макдермотт, 1985 г.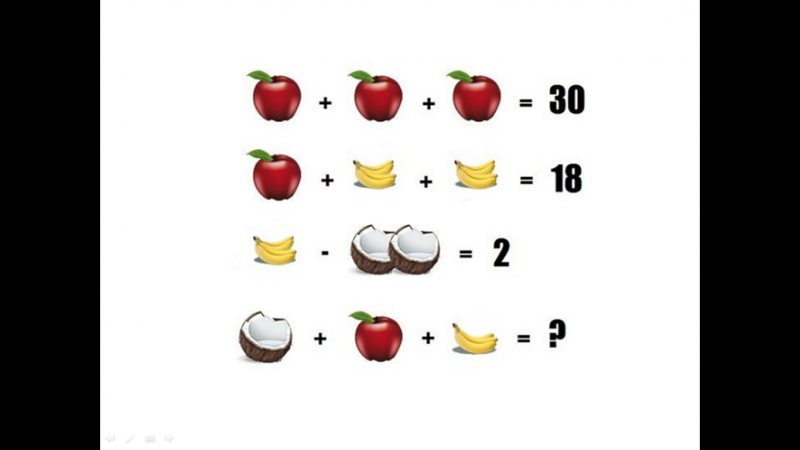 а также опубликовано в Хэнкс и Макдермотт, 1986; Хэнкс и Макдермотт 1987.

Йельская стреляющая аномалия включает в себя три действия: зарядка, стреляй и жди. Пропозициональный беглый Loaded отслеживает, заряжен ли определенный пистолет; еще один бегло, Живой, отслеживает, является ли определенный человек, Фред, в живых. нагрузка не имеет предварительных условий; его единственный эффект Загружено. Свободная съемка загружена как ее только предварительное условие и Живой как отрицательный эффект; ожидание не имеет предварительных условий и не имеет последствий.

Причинная информация относительно аксиом формализуется как следует.

Нагрузка	∀s Вмещает (загружено, R РЕЗУЛЬТАТ (нагрузка,с))
Выстрел 1	∀s[ Содержит (Загружено,s) → Вмещает (¬Живой, R РЕЗУЛЬТАТ (выстрел,с))]
Стрельба 2	∀s[ Содержит (Загружено,s) → Вмещает (¬Загружено, R РЕЗУЛЬТАТ (выстрел,с))]

Аксиомы ожидания не существует, то есть ожидание не имеет предварительные условия и отсутствие последствий.

Мы формализуем инерционное рассуждение в этом сценарии, используя немонотонная логика — если быть точным, мы используем логику Райтера по умолчанию. Набор D значений по умолчанию для этой теории состоит из всех экземпляры инерциальной схемы IR . В начальном ситуация, Фред жив и пистолет разряжен.

IC1	Вмещает (Живой, с 0 )
IC2	¬ Вмещает (Загружен, с 0 )

Монотонная теория W сценария состоит из: (1) аксиомы действия Нагрузить , Стрелять 1 и Выстрел 2 и (2) начальные условия IC1 и IC2 . Пусть с ₁ = R РЕЗУЛЬТАТ (нагрузка, с ₀ ), с ₂ = R РЕЗУЛЬТАТ (ожидание, с ₁ ) и с ₃ = R РЕЗУЛЬТАТ (выстрел, с ₂ ).

Аномалия стрельбы в Йельском университете возникает из-за того, что эта теория позволяет расширение, в котором действия загружаются; стрелять; ждать, и в конечной ситуации s ₃ , пистолет разряжен и Фред жив. исходная ситуация в Аномалии и три действия с их возникающие ситуации можно представить следующим образом.

с 0

нагрузка →

с 1

ждать →

с 2

стрелять →

с 3

Естественный ожидаемый результат этих аксиом состоит в том, что пистолет загружен, а Фред жив после ожидания, так что стрельба дает окончательный исход, в котором Фреда нет в живых, а пистолет разряжен. Есть не проблема показать, что это соответствует расширению; в проблема в наличии другого, аномального расширения, которое выглядит как это.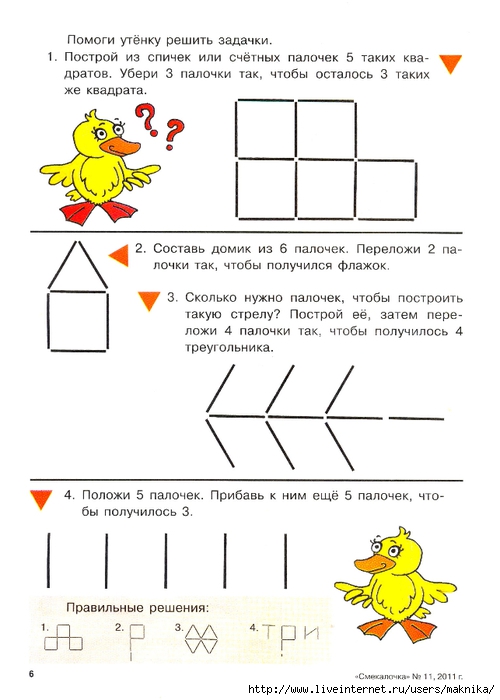

Жив ¬Загружен с 0

нагрузка →

Жив Загружено с 1

ждать →

Жив ¬Загружено с 2

стрелять →

Жив ¬Загружено с 3

Вот описательная версия этого расширения. Сначала Фред жив и пистолет разряжен. После заряжания пистолет заряжается и Фред остается жив. После ожидания пистолет разряжается и Фред остается жив. Тогда стрельба бесполезна, так как пистолет разряжен, поэтому, наконец, после выстрела Фред остается жив, а пистолет остается незагруженным.

Лучший способ ясно увидеть, что это расширение, это работать через доказательство. Менее формально, однако, вы можете видеть, что ожидаемое расширение нарушает только одно значение по умолчанию: значение по умолчанию фрейма для Alive нарушается, когда Фред меняет состояние на последнем шаге.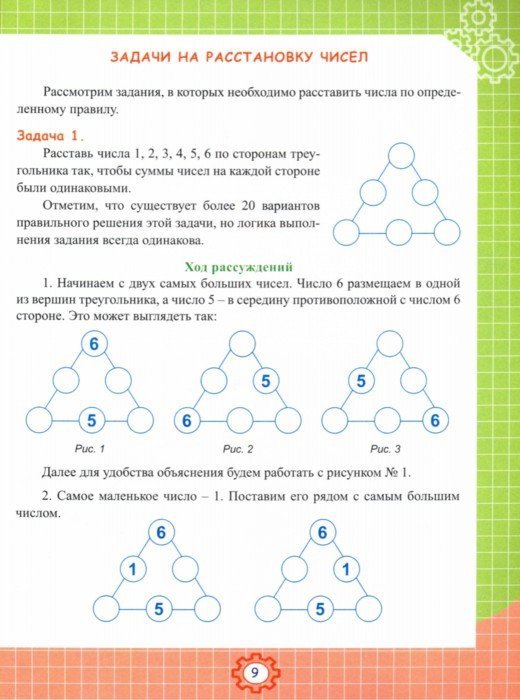 Но аномальное расширение также нарушает только одно значение по умолчанию: фрейм дефолт для Loaded нарушается при самопроизвольном срабатывании пистолета становится выгруженным во время ожидания. Итак, если вы просто идете по количеству значения по умолчанию, которые нарушены, оба расширения одинаково хороши.

Аномалия стрельбы в Йельском университете представляет собой серьезное препятствие в развитии теория предиктивного мышления. Правдоподобный, хорошо мотивированный логический Решение проблемы фрейма противоречит простому и четкому примеру в что он явно дает неправильные результаты. Естественно, литература относительно проблемы стрельбы в Йельском университете обширна. Опросы некоторых из эту работу с библиографическими ссылками можно найти в Шанахан 1997; Morgenstern 1996.

4.6 Некоторые новые концепции

Было предложено много формализмов для решения проблем рассмотрено в предыдущем разделе. Некоторыми более или менее пренебрегают Cегодня. Некоторые из них до сих пор поддерживаются и защищаются ведущими экспертами; некоторые из них связаны с исследовательскими группами, которые не только интересовался развитием логической теории, но и приложениями в планирование и когнитивная робототехника.

Ведущие подходы обеспечивают решение основных проблем упоминается в Раздел 4.5, и ко многим из сценарии, предназначенные для проверки и иллюстрации теорий рассуждений о действие и изменение. Принято считать, что хорошие решения должны быть обобщается на более сложные случаи, чем формализмы раннего планирования, и что, в частности, решения, которые они предлагают, должны быть развертываемыми даже когда непрерывное время, одновременные действия и различные виды невежество допускается. Кроме того, общепризнано, что формализмы должны поддерживать несколько видов рассуждений, и, в частности, не только предсказание и проверка плана, но ретродикт , т.е. построение последовательности состояний и действий из частичных информация, представленная в повествовательной форме.

Здесь мы описываем четыре подхода: (1) Особенности и потоки (Сандеволл), (2) Теория мотивированного действия (Моргенштерн и Штейн), (3) Минимизация состояния в исчислении событий (Шанахан) и (4) причинность Теории (Лифшиц и др. ). Счета первых трех в то, что последует, будет довольно кратким; к счастью, каждый подход хорош задокументировано в одной ссылке. Четвертый подход наиболее вероятен. быть интересным для философов и содержать элементы, которые будут непреходящей важности, независимо от будущих событий в этой область.

4.6.1 Характеристики и потоки

Этот подход, описанный в Сандеволл 1994, использует семантику предпочтений как способ организации немонотонных решения проблем рассуждений о действии и изменении. Скорее чем введение единой логической структуры, Сандеволл считает количество темпоральных логик, в том числе использующих дискретные, непрерывное и время ветвления. Свойства логики систематически тестируется на большом наборе тестовых сценариев.

4.6.2 Теория мотивированного действия

Эта теория выросла из непосредственного рассмотрения проблем в временное рассуждение, описанное выше в Раздел 4.5, и особенно сценарий стрельбы в Йельском университете. В Моргенштерн и Штейн 1994, Моргенштерн и Штейн стремятся найти общее, интуитивно мотивированное логическая структура, решающая трудности. Они останавливаются на идее что немотивированные действия должны быть сведены к минимуму, когда действие («действия», толкуемые достаточно широко, чтобы включать любые изменения) могут быть мотивированы напрямую, т.е. аксиомой или косвенно, через цепочки мотивы. Ключевой технической идеей статьи является (скорее сложно) определение мотивации в интервальной временной логика. В Моргенштерн 1996, Моргенштерн представляет краткое изложение теории вместе с причинами отвергая своих каузальных соперников. Важнейшей из этих причин является что эти теории, основанные на ситуационном исчислении, не кажутся обобщить на случаи, допускающие параллелизм и игнорирование. Она также ссылается на неспособность ранних каузальных теорий справиться с ретродиктией.

4.6.3 Минимизация на основе состояний в исчислении событий

В Бейкер 1989, Эндрю Бейкер представил решение версии проблемы стрельбы из Йельского университета в ситуации Исчисление с использованием ограничивающей аксиомы инерции. очень кратко счет ограничения выше в Раздел 3 указано, что для ограничения используются предпочтительные модели, в которых расширения некоторых предикатов сведены к минимуму. В ходе этого минимизация, набор параметров (включая, разумеется, предикаты быть сведена к минимуму) допускается варьировать; остальные остаются постоянными. Который параметры изменяются, а которые остаются постоянными, определяется заявление.

В самых ранних ограничительных решениях проблемы фреймов правило инерции CIR сформулировано с использованием аномалии предикат.

CIR
∀f∀s∀a[¬ Ab (f,a,s) → [ Содержит (f,s) ↔ Удерживает (f,R ESULT (a,s))]]

Эта аксиома использует бикондиционал, поэтому ее можно использовать для ретродиктия; это типично для более поздних формулировок общих чувство инерции. В описании предикат аномалии сведен к минимуму, а Hold Предикат может меняться и все остальные параметры фиксированы. Эта формализация уступает Йельскому университету. Стрельба по аномалии во многом аналогична логике по умолчанию. (Окружность не предполагает множественных расширений, поэтому проблема возникает как невыводимость вывода о том, что Фред жив после возникновения стрельбы.)

В переформулировке проблемы Бейкером отдельные аксиомы обеспечивают существование ситуации, соответствующей каждой булевой комбинации флюиды, а R РЕЗУЛЬТАТ функция может изменяться, в то время как предикат Holds остается постоянным. В этой настройке необходимо указать функцию R ESULT для «контрфактические» действия — в частности, для стрельбы, а также за ожидание в Йельской стреляющей аномалии. Именно эта особенность устраняет неправильную модель для этого сценария; подробности см. Бейкер 1989 а также Шанахан 1997, Глава 6.

Эта идея, которую Шэнахан называет «минимизацией на основе состояния», разработан и распространен в Шанахан 1997, в контексте темпоральной логики, вытекающей из исчисления событий Ковальски и Серго; видеть Ковальски и Серго 1986. Формализм Шанахана имеет то преимущество, что тесно связаны с реализациями с использованием логического программирования.

4.6.4 Причинно-следственные теории

Напомним, что в аномальной модели Йельского сценария стрельбы оружие становится разряженным после выполнения действия ожидания, действие, которое не имеет обычных последствий — разгрузка, следовательно, беспричинно. В контексте немонотонной логики — и без такой логике, аномалия стрельбы в Йельском университете не возникла бы — она очень естественно формализовать это, рассматривая беспричинные возможности как аномалии должны быть сведены к минимуму.

Эту стратегию преследовал Гектор Геффнер в Геффнер 1992 г. 1990 г., где он формализует эту простую причинную решение аномалии Йельской стрельбы. Но решение представлено в контекст амбициозного общего проекта в немонотонной логике, который не только развивает свойства предпочтительного модельного подхода и показывает как применить его к ряду проблем рассуждения, но это относится немонотонная логика вероятностей, используя идеи, вытекающие из Адамс 1975. В Геффнер 1992, обрисована причинная теория; он не разработан, чтобы показать свою адекватность в борьбе с батареей проблемы, представленные выше, и, в частности, проблема ветвления оставили нетронутым.

Работа, начинающаяся с Лифшиц 1987 внес свой вклад в устойчивую линию исследований причинно-следственных связей подход — не только Лифшица и его учеников, таких как Энрико Giunchiglia и Hudson Turner, но исследователями из других мест. За работу в этой области и дальнейшие ссылки см. Тильшер 1989, Густаффсон и Доэрти, 1996 г., Барал 1995 г., Накашима и др. . 1997 г., Лифшиц 1997, Джунчилья и Лифшиц, 1998 г., Лин 1995 г., Хо 1987 г., Лифшиц 1998, Тернер 1999, Маккейн и Тернер, 1995 г., Элькан 1991 г., Маккейн и Тернер, 1997 г., Тильшер 1996, а также Гельфонд и Лифшиц, 1998.

Здесь мы кратко опишем некоторые из теорий, разработанных Техасская группа действий, приведшая к причинно-следственному решению, представленному в Тернер 1999. Тернер возвращается к идеям из Геффнер 1992, но помещает их в более простое логические установки и применяет их к формализации более сложных сценарии, иллюстрирующие взаимодействие каузальной инерции с другими соображения, особенно проблема ветвления.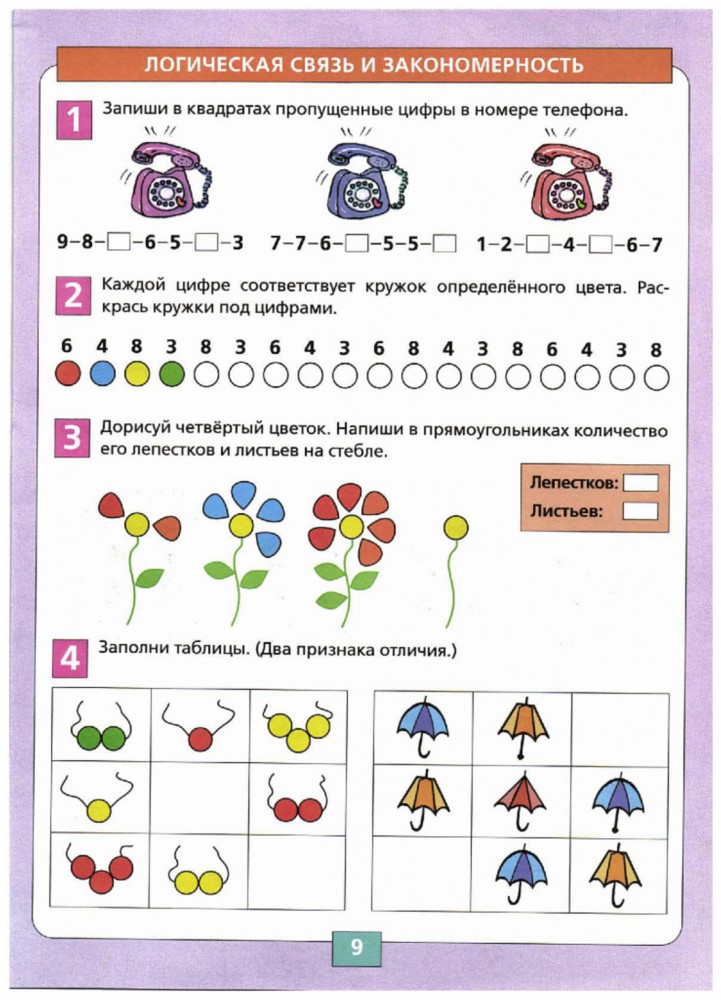

Ветвление вызвано наличием статических законов которые связывают прямые последствия действий с другими изменениями. Давайте воспользуемся сценарием запуска автомобиля, чтобы проиллюстрировать трудности. Там одно действие, включение , которое включает зажигание; Давайте предположим, что это действие не имеет предпосылок. Есть свободный Ig отслеживание включения зажигания, беглый Мертвый отслеживание того, разряжена ли батарея, и беглый Run отслеживание того, работает ли двигатель. Статический закон гласит, что если зажигание включено, аккумулятор не разряжен, двигатель работает. (Давайте предположим, что все остальные источники отказов уже устранены. исключено в этом сценарии; единственная возможная причина не запуска батарея.) Мы хотим рассмотреть переход, в котором включение выполняется в ситуации, при которой зажигание выключено. не горит, аккумулятор не разряжен, машина не заводится.

Конечно, мы хотим, чтобы планирующий агент мог делать выводы в таком случай, когда производительность включение приведет к ситуации в котором зажигание включено, аккумулятор не разряжен, а двигатель Бег. Но противопоставление законов затрудняет разработку принципиальное решение. Неформально эта трудность такова: мы можем заключить, противопоставив наш единственный статический закон, что если зажигание включено а двигатель не работает, значит аккумулятор сдох. Этот закон не верно только в нашем сценарии, но может быть использовано для объяснения неудачного попытка завести машину. Но если мы позволим использовать его для предсказания, тогда трудно понять, как исключить исход включение в котором зажигание включено, аккумулятор разряжен, а двигатель не Бег. Батарея разряжена в этом исходе из-за причинно-следственной инерции. Двигатель не работает из-за противоположного причинного закона.

Читатели, желающие более подробно изучить проблемы вложения немонотонного решения проблемы каркаса в относительно выразительные языки действия могут ориентироваться на Гельфонд и Лифшиц, 1998. В этой статье представлен все более мощные и сложные серии языков действия. Их язык включает в себя ad hoc или хотя бы чисто синтаксическое решение проблемы ветвления.

Теория в языке Б состоит из два набора аксиом:

1. Статические законы вида F → L , где L — литерал, а F — соединение литералов или это Т .
2. Динамические законы вида А Причины L если F , где A срок действия и F — логическая формула.

Гельфонд и Лифшиц налагают слабое условие замыкания на статические законы: где s — набор литералов, s — это ограниченно-закрытое по отношению к теория Б Т , R B Cl _T ( с ) если и только если каждый литерал, который будет добавлен, начиная с s и прямая цепочка через статические законы Б уже есть в s . Другими словами:

R B Cl _T ( с ) если для всех законы статики F → L из T , если s влечет за собой F , затем L ∈ s .

Операция замыкания, вызванная этим условием, используется при определении R ESULT (a,s) для языка Б. Конечно, это решение рассматривает логически эквивалентные статические законы иначе; например, теория, единственный статический закон которой [ P  ∧ ¬ Q ] → R будет вообще определить совершенно другую функцию R ESULT , чем одна единственный статический закон которого [ P ∧ ¬ R ] → Q .

Это имеет некоторые несколько противоречащие здравому смыслу эффекты. В машине-запуске сценарий, язык Гельфонда и Лифшица Б действительно дает желаемый вывод, что автомобиль будет начать, когда есть один динамический закон,

включение   Причины   Ig   если  Т,

когда единственным статическим законом является

[ Ig ∧ ¬ Dead ] → Run ,

когда начальное состояние s = {¬ Ig , ¬ Dead , ¬ Run }, и когда действие включение выполняется.

Однако, если мы добавим истинный закон статики, говорящий, что если зажигание включен, а двигатель не работает, батарея разряжена, мы получаем аномалию. С добавлением этого закона возникает модель, в которой сохраняется тот факт, что автомобиль не работает, приводит к разрядке аккумулятора, когда зажигание включено.

Если два статических закона, [ Ig  ∧ ¬ Мертвый ] → Выполнить и [ Ig ∧ ¬ Run ] → Dead , переформулированы с использованием причинно-следственного языка, первое звучит правильно, а второе явно проблематично: сравните

Если аккумулятор не разряжен, при включенном зажигании заставить двигатель работать.

с

Если двигатель не работает, включенное зажигание привести к разрядке аккумулятора.

Это позволяет с большой долей вероятности предположить, что источником проблема – это представление лежащей в основе причинной информации в действии язык Б это как-то неадекватный.

Гельфонд и Лифшиц продолжают описывать еще одно действие. язык, C, который вызывает явное понятие причинно-следственная связь, мотивированная, по всей вероятности, отчасти необходимостью обеспечить более принципиальное решение проблемы. Вместо описания этого языке, мы сейчас обсуждаем аналогичную теорию Тернер 1999.

Идея Тернера состоит в том, чтобы рассматривать Caused как модальный оператор. [   c   ] , что делает его основе модальной немонотонной логики. В предпочтительных моделях этого логике причинные суждения совпадают с суждениями, которые верно, и это должно быть единственной возможностью, согласующейся с объемная часть модели. Чтобы сделать это более явным, вспомним, что в интерпретации возможных миров S5 это можно идентифицировать возможные миры с описания состояний , которые мы можем представить в виде наборов I литералов (атомарных формул и их отрицания). Таким образом, проводя это отождествление, мы можем думать о модель в виде пары < I , S >, где S — набор интерпретаций (полные, согласованные наборы литералов) в том числе I .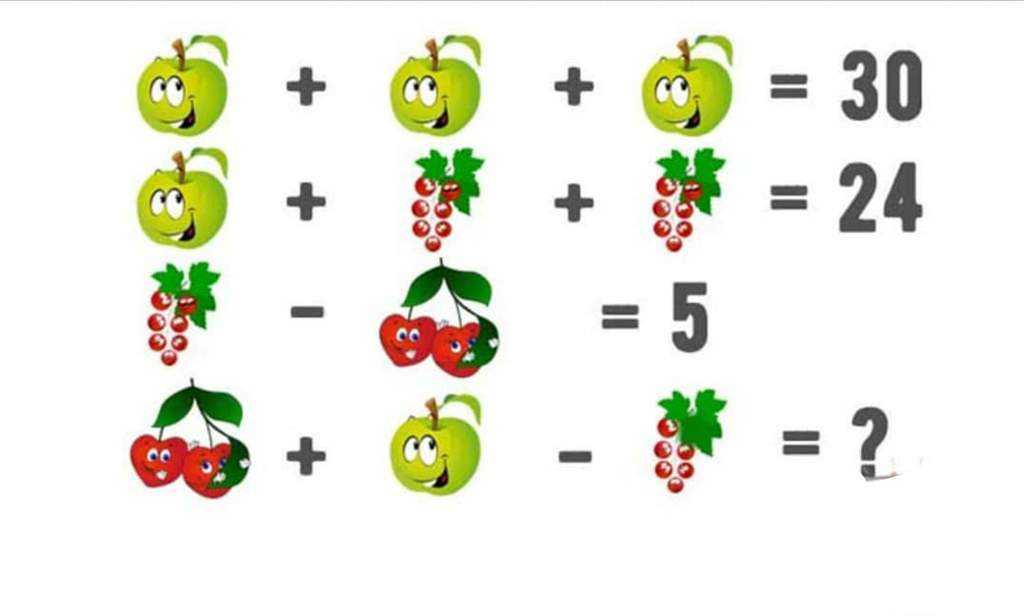 Модальный оператор [   c   ] дается стандартная семантика: где S — набор интерпретаций и где I  ∈  S , S ⊨ _I   [   c   ]   A тогда и только тогда, когда S ⊨ _I′   A для всех I′  ∈ S . < я , с > удовлетворяет набору формул T тогда и только тогда, когда S ⊨ _I   A для всех A  ∈  T .

Предпочтительные модели Тернера из T пары < I , S > такие, что: (1) < I , S > удовлетворяет T , (2) S = { I }, и (3) < I , S > — единственная интерпретация < I′ , S′ > выполнение условий (1) и (2) с I′ = I . Условие (2) гарантирует «универсальность причинности»; это подтверждает A ↔ [   с   ] А . Условие (3) «обосновывает» причинность некаузальной информацией (в интересующие нас модели, это будет информация о возникновение событий), в самом сильном смысле: это однозначно определяется этой информацией.

Хотя это и не следует из формулировки, отчет Тернера о предпочтительные модели связаны с конструкциями более общих немонотонные логики, такие как логика по умолчанию. Проконсультируйтесь Тернер 1999 для деталей.

Аксиомы, определяющие последствия действий, рассматривают эти последствия. как причина; например, схема аксиомы для загрузки будет читаться как следует:

Причинная нагрузка

[   c   ] Крепления (нагрузка, R ESULT (нагрузка, с)) [33]

Ответвления непосредственных последствий действий также рассматриваются как вызванный. И схемы немонотонных аксиом инерции принимают вид

[[ [   c   ] Содержит (f,s)] ∧ Вмещает (f,R ESULT ( a ,s))] → [   c   ] Вмещает (f,R РЕЗУЛЬТАТ ( a ,s))

и

[[ [   c   ] ¬ Содержит (f,s)] ∧ ¬ Содержит (f,R ESULT ( a ,s))] →
[   в   ] ¬ Содержит (f,R ESULT ( a ,s)).

Таким образом, истинное суждение может быть обусловлено либо тем, что оно является прямым или косвенный эффект действия, или потому, что он предполагает постоянство обусловленного предложения. Начальные условия также считаются вызвано, по оговорке.

Чтобы проиллюстрировать работу этого подхода, давайте рассмотрим простейший случай инерции: у нас есть язык только с одной константой обозначающий плавный, f и одну константу, обозначающую действие, подождите. Как и в Йельской задаче о стрельбе, для ожидания нет аксиом; это действие всегда может быть выполнено и не имеет связанных эффектов. Позволять с ₁ be R РЕЗУЛЬТАТ (подождите, с ₀ ). Теория T содержит начальное условие для f, Содержит (f,s ₀ ) и утверждение, что начальный состояние вызвано, [   c   ]   Держит (ф, с ₀ ), а также инерциальные схемы.

Две модели T удовлетворяют условиям (1) и (2):

М ₁ = < я ₁ ,{ I ₁ }> и М ₂ = < I ₂ ,{ I ₂ }>,

где I ₁ = { Содержит (f,s ₀ ), Вмещает (f,s ₁ )} и I ₂ = { Содержит (f,s ₀ ), ¬ Содержит (f,s ₁ )}.

M ₁ – предполагаемая модель, в которой ничего изменения. Удовлетворяет условию (3), так как если < I ₁ , S > удовлетворяет T это удовлетворяет [   c   ] Вмещает (f,s ₁ ) по аксиоме инерции

[[ [   c   ] Содержит (f,s)] ∧ Содержит (f,s ₁ )] → [   c   ] Вмещает (f,s ₁ ).

Следовательно, S = { I ₁ }.

M ₂ — аномальная модель, в которой бегло самопроизвольно прекращается. Эта модель не удовлетворяет условию (3), так как М ₃ = < I ₂ ,{ I ₁ , I ₂ }> также удовлетворяет T ; особенно, он удовлетворяет аксиоме инерции для f, потому что не удовлетворяет Вмещает (f,s ₁ ).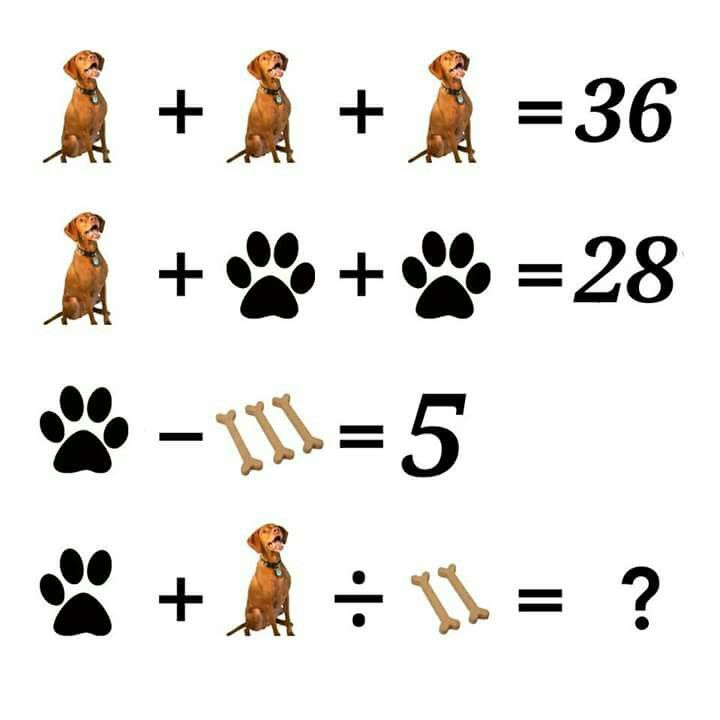 Таким образом, в то время как M ₁ является предпочтительная модель, М ₂ нет.

Подход Тернера позволяет избежать проблемы противопоставления, давая причинно-следственные связи форма

[B ПРЕДПОСЫЛКИ- C УСЛОВИЯ ∧ C AUSE ] → [   c   ] E FFECT .

В противопоставлении это становится

[C AUSE ∧ ¬ [   с   ] E FFECT ] → ¬B ПОДТВЕРЖДЕНИЕ- C УСЛОВИЯ ,

которое не имеет формы причинного закона. Это решение менее чем полностью удовлетворительно при решении интуитивных трудностей, потому что Кажется, что семантика Тернера интуитивно подтверждает такие формулы, как

. [   c   ] [[¬ Мертвые ∧ Ig ] → Прогон ],

и в этой форме было бы восстановлено противопоставление. Задача прояснение основ каузальных теорий действия и изменения может еще не быть полным.

Но кажущаяся полезность «принципа универсальной причинности» в учете ряда проблем качественного здравого смысла рассуждения будут дразнить философов. И причинно-следственная теория, по инициативе Геффнера и разработанной Тернером, имеет много интересных подробные характеристики. Например, в то время как философская работа о причинности сосредоточился на причинно-следственной связи, эта работа в области логического ИИ показывает что многое можно сделать, используя только нереляционную каузальную связь. предикат.

Отношения между причинностью и условностями можно исследовать и эксплуатируются различными способами. Льюис 1977 обязуется объяснить причинность с точки зрения условных выражений. в обратное направление, Великий пост и Томасон, 2015 г. использует каузальный подход Тернера для построения моделей условной логики, в ограниченном случае, когда антецедент является соединением выражение действия и простые ситуационные условия. Мотивация для эта идея заключается в явном решении проблемы фрейма автоматически предоставляет семантику для таких условий.

Две основные критические замечания Моргенштерна в отношении каузального подхода к рассуждения о действиях заключаются в том, что они не дают адекватного отчета объяснения ^[34] и что логический контекст в которой он работает (Ситуационное исчисление) ограничен. По мере работы над подход продолжается, в этих областях наблюдается прогресс. Но ограничения, которым должна соответствовать успешная логика действий и изменений, настолько сложна, что представляется разумной методологией исследования сначала сконцентрируйтесь на ограниченной логической установке.

Для другого подхода к немонотонному каузальному мышлению, основанному на логика ввода-вывода (Makinson & van der Torre 2000), см. Bochman 2004.

4.7 Формализмы действий и естественный язык

Хотя для многих логиков ИИ цель формализмов действия состоит в том, чтобы освещают важный аспект рассуждений здравого смысла, большую часть их исследование не информировано важным источником информации о взгляд здравого смысла на время, а именно, естественный язык. Лингвисты занимается семантикой темпоральных конструкций в естественных язык, как и сообщество ИИ, начали с идей философской логике, но обнаружили, что эти идеи должны быть изменены для того, чтобы иметь дело с явлениями. Главное открытие Логики ИИ считали важность действий и их связь с сдача. Точно так же важное открытие «естественного языка логики» была важность различных видов событий (включая структурированные составные события) в интерпретации природных язык. Из работ, подобных этой, идея «естественного языка метафизика» (см., например, Баха 1989) появился.

Цель сформулировать логическую структуру, адаптированную к репрезентативная система, мотивированная систематическими свидетельствами о значений в естественных языках признается не всеми лингвистическими семантики. Тем не менее, это важная тема в лингвистике. литература. Эта цель удивительно похожа на цели обычного смысл логиков, но методология исследования полностью другой.

Можно ли примирить взгляды этих отдельных традиций и единый? Можно ли ограничить теории темпорального представления и рассуждения с идеями и исследованиями методологии обеих традиций? В Стидман 1995 (а также 2000 г.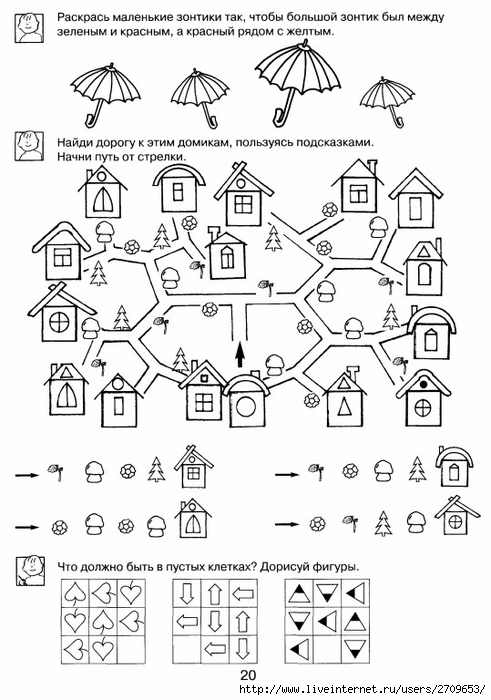 , указан в разделе “Другие” Интернет-ресурсы), эти важные вопросы рассматриваются, и разработана теория, которая расширяет формализмы действия, такие как Ситуационное исчисление, которое включает в себя многие идеи из лингвистическая семантика. О проекте сообщается в Стидман 2000 еще неполный, но сообщаемые там результаты убедительно доказывают, что события, основанные на идеи лингвистики могут быть плодотворно объединены с формализмы, ориентированные на действие, в литературе по ИИ. Возможность это объединение является одним из самых захватывающих логических событий в этой области, объединяющей двух независимых потомков более ранняя работа в логике времени.

В Раздел 4.6, мы проследили причины за развитие теорий, включающих причинность в работу над рассуждения о действии и изменении. Это не единственная область ИИ в какая причинность возникла. Показатели причинности в качественных рассуждениях об устройствах; за важную работу Герберта Саймона в этой области, которая восходит к 1950-м годам, см. Саймон 1952; 1977 год; Ивасаки и Саймон 1986. Оба эти традиции важны. Но самый крепкий и высокоразвитый Программа в области ИИ, связанная с причинностью, принадлежит Джудее Перлу и его студенты и партнеры, основанные на статистических методах известный как модели структурных уравнений . Представлены Халперн и Перл 2001 г. идея о том, что причинно-следственные связи между событиями могут быть выведены из эти модели: байесовские сети доверия можно интерпретировать как причинные сети.

Программа Перла превратилась в далеко идущую кампанию по реабилитировать причинность в статистическом мышлении. Мы не будем это обсуждать тема здесь. Во-первых, в этом обзоре отсутствуют вероятностные рассуждения. ИИ. Во-вторых, взгляды Перла на причинность систематизированы и всесторонне представлено в недавнем исследовании длиной в книгу, Жемчуг 2000.

Но важно отметить, что работа над причинно-следственными связями, обсуждавшаяся в Раздел 4.6 и идеи Перл разделяют некоторые общие темы. При обоих подходах: действие является центральным для причинность. Также внимание уделяется причинно-следственной связи как инструменту рассуждений. это частично обусловлено ограниченными ресурсами. Еще один важный темой является развертывание и систематическое изучение формализмов, в которых причинность связана с другими конструктами (в частности, с вероятностью и к качественным изменениям) и разнообразные реалистические рассуждения проблемы решаются.

Эти общие черты дают основания надеяться, что мы увидим наука о причинно-следственных связях, возникающая в результате исследований ИИ, объединяющая вклад вероятностной, качественной физики и немонотонных традиций и освещения различных фаз причинно-следственной связи. рассуждения.

Недавней вехой в этом направлении является Halpern 2016, который разрабатывает и применяет общую теорию причинно-следственной связи событий, вытекающую из каузально-сетевой подход. Хотя Халперн — ученый-компьютерщик, большая часть этой книги посвящена философии, исследующей такие понятия, как в качестве обвинения и объяснения.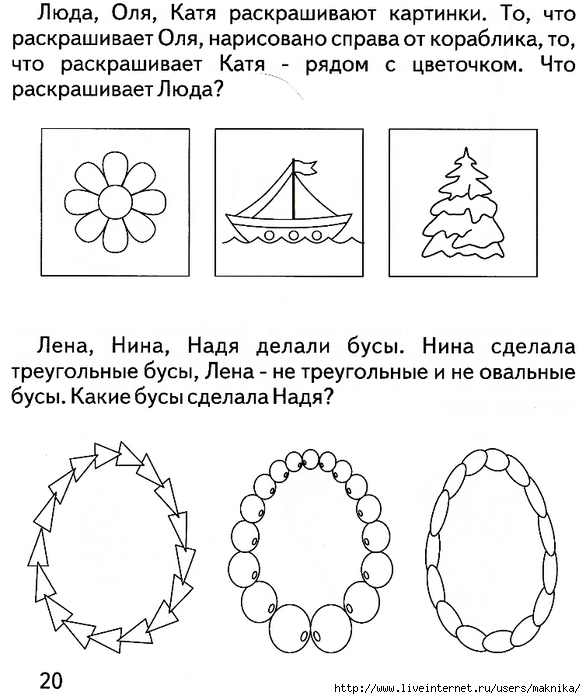 Но книга также исследует практические применения подхода, которые не пришли бы в голову философам, в таких областях, как диагностика ошибок программного обеспечения.

Считаете ли вы причинность фундаментальной конструкцией в естественном наука, или фундаментальное явление здравого смысла, зависит от того, вы имеете в виду идеализированную природу, описываемую дифференциальным уравнений или вы имеете в виду взгляд на природу, который мы должны принять чтобы действовать либо в повседневных ситуациях, либо, если уж на то пошло, в планирование опытов в лаборатории. Тот факт, что Бертран Рассел отметил (см. Рассел 1957), причинность нельзя найти в качестве теоретического примитива в современной физические теории расходятся с его кажущейся важностью во многих знакомые области рассуждений. Строгие теории, возникающие в области ИИ, которые начинают освещать работу причинно-следственной связи, важны не только в самих себе, а в их способности освещать шире философские вопросы.

Довычислительная литература по философской логике, касающаяся пространственные рассуждения очень редки по отношению, например, к временная литература. Необходимость поддерживать вычислительные рассуждения о пространство, однако, в областях применения, таких как планирование движения и манипуляции в физическом пространстве, индексация и поиск изображений, географические информационные системы, диаграммные рассуждения и проектирование графических программ высокого уровня привело к новому интересу к пространственным представления и пространственное мышление. Конечно, геометрическое традиция обеспечивает исключительно сильный математический ресурс для это предприятие. Но, как и во многих других областях, связанных с ИИ, неясно что доступные математические теории подходят для информирования эти приложения, и многие ученые-компьютерщики почувствовали это целесообразно разработать новые основы. Некоторые из этих работ тесно связанных с исследованиями качественных рассуждений, упомянутых выше в Раздел 2.2, и в некоторых случаях переносился исходят от одних и тех же лиц.

Литература по пространственному мышлению обширна; для ссылок на некоторые области, не обсуждаемые здесь, см. Сток 1997 г., Капур и Манди, 1988 г., Молоток 1995 г., Уилсон 1998 г., Ошерсон и Ласник 1990, Ренц и Небель, 1999 г., Йеп и Джеффрис, 1999 г., Форбус и др. . 1991 г., Чен 1990 г., Бургер и Бхану 1992, Олвейн и Барвайз, 1996 г., Глазго и др. . 1995 г., а также Кослин 1990. Здесь мы обсуждаем только один направление, тесно связанное с параллельной работой в философской логика.

Качественные подходы к пространству были введены в логический литература начала двадцатого века Лесневского; видеть Лесневский 1916 г., который представляет идею мереологии , или качественной теории части-целого отношения между физическими лицами. Эта идея логической теории отношения между регионами или занимающими их объектами, что не зависит от построения регионов как наборов точек, остается активной областью философской логики, хотя она и привлекала сравнительно мало исследователи. Более поздняя работа в философской литературе, особенно Казати и Варци 1999, Саймонс 1987, Казати и Варци 1996, Кларк 1981, Кларк 1985 г. , как непосредственное влияние на текущую вычислительную работу.

Расчет региональных связей (RCC), разработанный компьютером ученых из Университета Лидса, основан на примитивном C связанные области пространства: предполагаемая интерпретация C ( x , y ) заключается в том, что пересечение замыкания значений x и y не пусты. (Видеть Кон и др. . 1997 г., Кон 1996) для получения подробной информации и ссылок.) Один область исследований касается определяемости форм в RCC. Степень того, что можно определить с помощью этого простого примитива, удивительно, но технические детали быстро усложняются; см., например, Готц 1994 г., Готтс 1996). Работа, цитируемая в Кон и др. . 1997 г. описывает методы распространения ограничений и кодировки в интуиционистской пропозициональной логике как способы поддержки реализованы рассуждения на основе RCC и некоторых его расширений. Более недавняя работа, основанная на RCC, касается представления и рассуждений о движение, которое, конечно же, сочетает в себе пространственные и временные аспекты; видеть Уолтер и Захарьящев 2000). Для получения дополнительной информации о качественных теориях движения см. со ссылками на другие подходы см. Гальтон 1997.

Эпистемическая логика – еще одна область, в которой логика в информатике под влиянием философской логики. Классический источник для эпистемологическая логика Хинтикка 1962 г., в котором Яакко Хинтикка показали, что модальный подход к одноагентным эпистемическим установкам может быть информативным и полезным. В этой работе подробно обсуждается вопрос о том, какие именно ограничения подходят для знания и убеждение, когда эти установки рассматриваются как эксплицированные моделью теоретическое отношение к возможным мирам; в обоих случаях, утверждает Хинтикка, на S4 операторы типа.

В ряде работ (в том числе Маккарти 1979), Джон Маккарти рекомендовал подход к формализации знание, использующее логику первого порядка, но явно количественно определяющее над такими вещами, как отдельные понятия. В этом разделе мы обсуждаем подход, принятый большинством ученых-компьютерщиков, которые, в отличие от Маккарти, использовать модальный язык для формализации пропозициональных установок.

Логические аспекты модальной эпистемологической логики не имели существенного значения. разработан после 19-летия Хинтикки.62 презентации; вместо этого философской литературы (которая не так обширна, по сравнению со многими другие темы в этой области) концентрируется на проблеме гиперинтенсивность , или закрытие эпистемических установок под логическое следствие. Эта тема особенно актуальна, оказывается тесно связаны с семантическими парадоксами и философскими литература неоднозначна. Интуиция, кажется, конфликтует, и это трудно найти способы моделирования важных явлений, используя логические методы. ^[35]

Феджин и др. . 1984 г. начинается традиции в вычислительной логике, которая возрождает модальный подход к эпистемологической логики, разрабатывая обобщенные логические основания и приложений, которые не пришли в голову философам. технический идея состоит в том, чтобы упростить модальность, используя S5 (или деонтический S5 для убеждения), но ввести несколько агентов и сосредоточиться на рассуждениях, связанных с отношением агентов к отношения друг к другу. Такие логики имеют прямое применение в анализ распределенные системы динамические системы, в которых изменение осуществляется действиями сообщения, которые изменяют знание агенты в соответствии с правилами, установленными сообщениями протокол .

Таким образом, эта работа относится к отдельной области информатики, но тот, который в некоторой степени пересекается с ИИ. Позже эта работа была взаимодействует с исследовательской традицией в экономике, которая касается с ролью знаний в играх и торгах; см., для пример, Геанакополос 1994; Осборн и Рубинштейн, 1994 г. [Глава 5].

Почему-то мультиагентный случай не пришел в голову философам. логики. ^[36] Это еще один пример того, как в котором потребность в приложении (в данном случае потребность в теории распределенных систем) послужили источником вдохновения для важного логическое развитие. Логические детали широко и систематически записано в Феджин и др. . 1995 год; Это обязательное чтение для всех, кто серьезно интересуется этой темой.

Большая часть междисциплинарной работы по приложениям логики знания представлены в материалах серии конференций инициировано в 1986 году с Халперн 1986. Эти конференции зафиксировали одно из самых успешных совместных философов с логиками в компьютерных науках, хотя группа вовлеченных философов было относительно немного. В центре внимания конференции постепенно перешли от компьютерных наук к Экономика.

Приложения ИИ имеют дело со знаниями в виде сохраненных репрезентации и традиции ИИ, которые нас интересуют здесь думает о рассуждении как о манипулировании символическими представления. Кроме того, в основном из-за ИИ проблема ограниченная рациональность стала предметом серьезного интереса, предоставив противовес идеализации философии и экономика. ^[37] Таким образом, вы могли бы подумать, что логично модель пропозициональных установок, которая стремится к закрытию под Логическое следствие было бы крайне непопулярным в ИИ. Но это не так; подход возможных миров к отношениям не только ведущий теории в областях, обсуждаемых в Феджин и др. . 1995 г., но даже пропагандируется в робототехнике Приложения; видеть Розеншайн и Кельблинг, 1995; Розеншайн 1989. Тем не менее, проблема гиперинтенсивности была исследовано в литературе по ИИ; видеть Перлис 1985; Конолиге 1986; Лейкмейер 1997; Левеск, 1984). Хотя есть новинки положительные результаты здесь, работа ИИ в этой области имеет, по большей части часть, была столь же неубедительной, как и в философии.

Философская литература по смежной теме, логике восприятие не было обширным; основная ссылка это Хинтикка 1970. ^[38] Но сенсация рассматривается в недавней работе в литературе по ИИ, которая касается разработка логических структур для приложений общего назначения в робототехника. Основная идея в этой области состоит в том, чтобы добавить сенсорные действия к репертуар формализма планирования, обсуждавшегося в Раздел 4. Первые работы в этой области проводились в 1980-е Роберта Мура; видеть Мур 1995b; Мур 1985. Для некоторых современные работы в области когнитивной робототехники, см. Барал и др. . 2000 г., Бахус и др. . 1999 г., Золотой и сварной, 1996, Пирри и Финзи, 1999 г., а также Тильшер 2000.

Явная долгосрочная цель Джона Маккарти — формализация знаний здравого смысла – принята и преследуется относительно небольшим, но активным подсообществом ИИ исследователи. Большая группа (те, кто занимается знанием представление, когнитивная робототехника и качественная физика) могут быть считается работающим над специализированными проектами, которые поддерживают более крупные Цель. Что-либо похожее на формализацию здравого смысла так далеко от достигнуто, что – если это вообще достижимо – это даже невозможно оценить, когда мы можем ожидать, что задача будет завершенный. Однако с 2001 г. (дата проведения симпозиума по общим смысловые рассуждения, проводимые в Институте Куранта — см. Домашняя страница Common Sense 2001) что-то вроде совместные, устойчивые усилия в этом направлении начали появляться. Эти усилия дают лучшее представление о том, как развивать действенную методологию формализации здравого смысла и того, как разделить большую проблему на более управляемые части.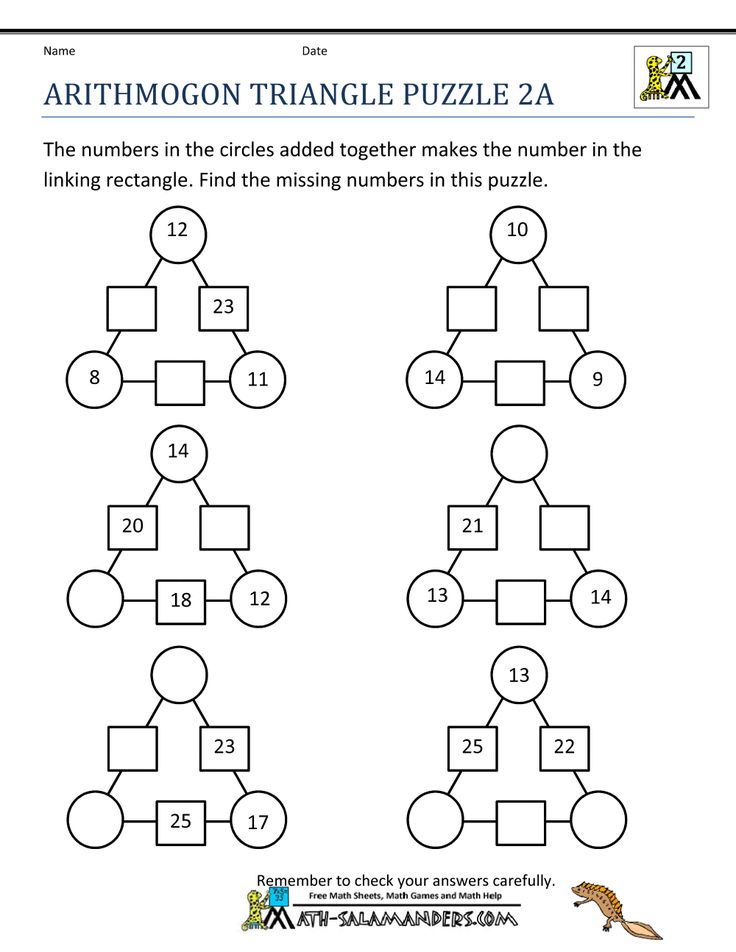 Многие из доклады, представленные на данной конференции, были представлены в развернутом виде в 2004 году в выпуске Искусственный интеллект . введение в этот вопрос, Davis & Morgenstern 2004, представляет собой полезный обзор и оценка общей области исследования.

Эти совместные усилия по формализации (1) направлены на учет многих областях знания, и в то же время (2) попытки увидеть, как это формализованное знание может быть применено к умеренно сложные задачи на здравый смысл. Первая книга рассмотрение этой темы, Davis 1991, делит общую проблему на следующие подтемы.

1. Количество и измерения
2. Время
3. Космос
4. Физика
5. Разум
6. Планы и цели
7. Общество

Некоторые из этих тем пересекаются с проблемами качественная физика и сообщество качественных рассуждений. Хотя это трудно сказать, где кончается здравый смысл и начинается физика, формализация рассуждений здравого смысла может рассматриваться как более общая проект формализации, который может опираться на традицию качественного физика, прошедшая многолетнее развитие и к настоящему времени весьма зрелый. ^[39]

И некоторые из них пересекаются с работа по формализации планирования, описанная выше в Раздел 4. Умы и общество, однако, новы и разные темы; первое имеет отношение к психологии здравого смысла и его применение в интроспективных и межличностных рассуждениях, а также последнее, конечно, должно иметь отношение к социально-политическим знания и рассуждения, но это наименее развитая область формализованное знание здравого смысла: глава по этой теме в Davis 1991 очень краток и обсуждает взаимные отношения и общение. Совсем недавно Эндрю С. Гордон и Джерри Хоббс предприняли крупномасштабную амбициозную формализация психологии здравого смысла. См., например, Хоббс и Гордон 2005.

Более поздняя книга, посвященная формализации здравый смысл, Mueller, 2006, следует аналогичному шаблон. Более половины книги посвящено рассуждениям о действия и изменения. Имеются короткие главы о пространстве и ментальном состояний и более длительное рассмотрение рассуждений по умолчанию. Несмотря на то что логические приемы и методы формализации занимают центральное место в этой книги, она также содержит материалы по нелогическим методам и о реализациях, связанных с формализацией.

Даже при попытке в умеренных масштабах формализация Знание здравого смысла оказывает значительное давление на ресурсы даже самые мощные логические системы, которые были разработаны для формализация математики. Как мы пытались показать при обсуждении особый случай действий и планирования в Разделе 4, это давление может привести нас к поиску логики, которая может облегчить проекты формализации: например, немонотомные логики и логики которые явно представляют контекст.

Когда предпринимаются попытки более масштабной формализации, другие возникают проблемы, аналогичные тем, которые возникают при разработке программного обеспечения. пытается обратиться. Даже достаточно небольшие программы и системы аксиом трудны для понимания и могут быть крайне непредсказуемыми, приводя к неожиданные последствия и непредвиденные взаимодействия. Создание и использование более крупных программ и формализаций поднимает вопросы о том, как чтобы команды разработчиков могли получать согласованные результаты, когда модули интегрированы, как обслуживать и тестировать большие системы, и как использовать источники знаний, такие как словари и базы знаний автоматически генерировать аксиомы.

Вы можете подумать о философской методологии предоставления анализы как совокупность попыток формализовать или частично формализовать различные понятия здравого смысла. Эти попытки далеки меньше по масштабу, менее систематизирована и более разнородна, чем параллельное усилие, которое появляется в ИИ. Философы никогда выбрали конкретную область, сравнимую с областью планирования, и предпринял настойчивую попытку формализовать его вместе с компаньоном усилия по развитию соответствующей логики. И какой бы сложной ни была понятия, которыми они занимаются, философы никогда не позволяли своему анализу вырасти до такой сложности, когда возникают методологические вопросы, аналогичные тем, которые относятся к разработка и сопровождение крупных программных комплексов.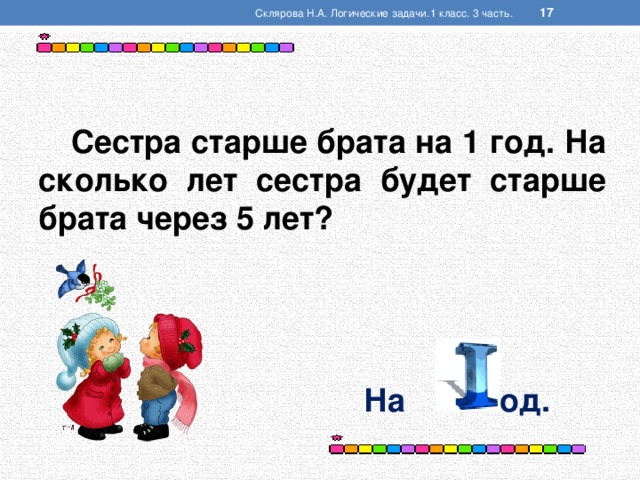

Методы, возникающие в области ИИ, имеют большой потенциал значение для философии, потому что легко заподозрить, что многие философски важные явления имеют такую ​​сложность, которая можно решить, только приняв проблемы, которые сопровождают разработка сложных формализаций. Ограничения философского Методы, которые использовались на протяжении всего ХХ века и до сих пор в использовании может сделать невозможным создание теорий, которые справедливо предмет.

Поэтому было бы большой ошибкой со стороны философов пренебрегать и игнорировать широкомасштабные формализации, которые начинают проявляться в ИИ, потому что эти усилия начинают поднимать инженерные вопросы. Вполне может быть, что хотя философия требует от нас строгого подхода к сложным явлениям, т. традиционные философские методы способны воздать должное к сложности. Методы, которые обещают сделать это, стоят того, чтобы их использовать серьезно.

Среди других методов, заимствованных из информатики, сообщество здравого смысла стремилось развить наборы «эталонных задач».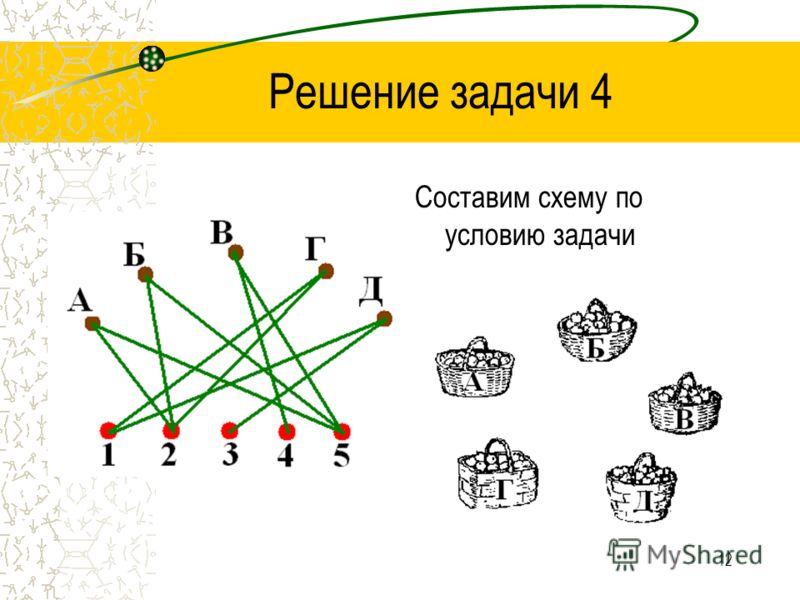 Идея состоит в том, чтобы сделать рекламу проблемы, которые трудны, но не невозможно трудны, чтобы поощрять сообщество создавать решения и сравнивать решения.

Вероятно, наиболее изученной проблемой на сегодняшний день является задача Эрнеста Дэвиса. «проблема с растрескиванием яиц». Это формулируется следующим образом на Веб-страница проблемы здравого смысла.

Повар разбивает сырое яйцо о стеклянную миску. Правильно выполнено, удар яйца о край чаши будет разбить яичную скорлупу пополам. Держа яйцо над миской, повар разделит две половинки скорлупы пальцами, увеличивая трещина, и содержимое яйца мягко упадет в миску. Конечным результатом является то, что все содержимое яйца будет в миске с неразбитым яйцом и что две половинки скорлупы в пальцах повара.

Варианты: Что произойдет, если: Повар поднесет яйцо к удару очень быстро? Очень медленно? Повар кладет яйцо в миску и оказывает постоянное давление рукой? Повар, расколов яйцо, попытки очистить его от содержимого, как яйцо, сваренное вкрутую? Чаша сделана из листовой бумаги? Из мягкой глины? Чаша меньше чем яйцо? Чаша перевернута? Повар пробует это процедура с яйцом вкрутую? С кокосом? С М&М? ^[40]

Вместе с самой проблемой размещены три решения: Шанахан 2004, Лифшиц 1998b, и версия Моргенштерн 2001. Сравнение решения поучительны: сходства перевешивают различия. Все авторы думают об этом как о проблеме планирования и используют версии исчисление ситуаций или исчисление событий в формализации. Каждая аксиоматизация является модульной, например, с отдельными модулями. посвящена соответствующим геометрическим и материальным свойствам. Каждый автор предоставляет «доказательство концепции» для формализации, показывая что аксиомы поддерживают доказательство правильности плана взлома яйцо в простом случае. Ни один из авторов не рассматривает все Дэвиса, но аксиомы сформулированы разработка в виду и некоторые разработки рассматриваются. это не ясно, реализовал ли кто-либо из авторов формализация (например, с помощью средства доказательства теорем).

Дело о разбивании яиц поднимает вопрос о том, как оценивать умеренно большие формализации задач здравого смысла. Моргенштерн и Шанахан прямо выражают эту проблему. Моргенштерн предполагает, что важными критериями являются (1) эпистемологическая адекватность (соответствие интуитивным рассуждениям, переживаемым людьми, которые заниматься этим), (2) верность реальному миру, (3) повторное использование, и (4) допуск на проработку. Неясно, первые два эти критерии слишком субъективны, чтобы быть полезными. К ним, Шанахан добавляет (5) удобство использования, что, вероятно, предполагается Третий критерий Моргенштерна.

Имеются неофициальные свидетельства того, что более широкое сообщество ИИ несколько скептически относятся к таким исследовательским проектам, а если и не скептически, по крайней мере, недоумевают, как их оценивать. В Учитывая эти сомнения, необходимо оценить сложности этих проблем формализации, а также предварительных и предварительный статус исследовательской программы. Тем не менее, это критика имеет некоторую легитимность, сообщество рассуждающих на основе здравого смысла чувствителен к этой критике и работает над развитием и уточнить методы и критерии оценки этой работы.

Пока проблемы формализации остаются относительно простыми, мы можем относиться к формализации как к искусству, а не как к дисциплине с хорошо сформулированная методика. Но тенденции, которые мы были обсуждения показывают, что формализация даже небольших реалистических Проблемы рассуждения здравого смысла – это не просто искусство. Как только системы программирования, экспертные системы и базы знаний создали соответствующие дисциплины разработки программного обеспечения, крупномасштабные проекты формализации требуют тщательно продуманного и проверенного методология.

За последние двадцать пять лет или около того произошло много глубоких отношений. возникла между логикой и грамматикой. Компьютерная лингвистика (или обработка естественного языка) — это ветвь ИИ, и она довольно Естественно отнести некоторые из этих разработок к категории логики и ИИ. Но многие из них также принадлежат к независимой традиции логического основы языкознания; и во многих случаях это трудно (и бессмысленно) пытаться классифицировать. Этот эскиз будет посвящен разработки, связанные с рассуждениями о лингвистике; Другой приложения логики к лингвистике описаны в ван Бентем и тер Меулен 1996.

9.1 Разбор и дедукция

Грамматические формализмы – системы специального назначения для описания лингвистических систем и подсистем — можно рассматривать как логики предназначен для аксиоматизации ассоциации языковых структур с цепочки символов. Вы могли бы сделать вывод из такой системы, для например, что «задания» — это форма множественного числа номинализация глагола «назначать». Таким образом, вы можете посмотреть на процесс разбора строки слов — нахождения лингвистические структуры, если таковые имеются, которые связаны с ним — как искать доказательство в определенной логической системе.

Этот подход оказался очень успешным в качестве аналитического инструмента. Это делает методы теории моделей применимыми к лингвистическим рассуждениям, Это делает лежащие в основе проблемы рассуждения намного более прозрачными, и позволяет применять многие хорошо развитые области логики к грамматические формализмы. Для получения дополнительной информации по этим темам см. Бушковский 1996; Шибер, 1992.

9.2 Логика структуры признаков

Полезность и возможности логических методов по отношению к лингвистика значительно расширилась за счет развития методов анализ того, как информация связана с языковыми единицами.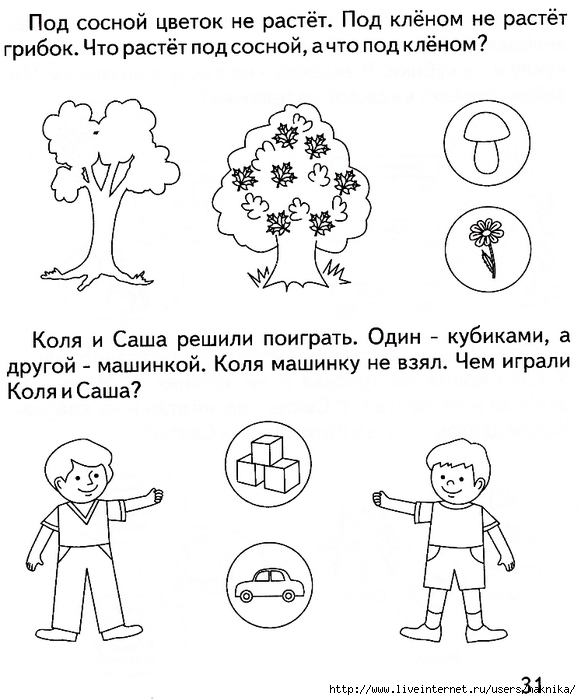 Это очень естественным для представления информации, связанной, скажем, с лексической единицей в виде набора функций (или атрибутов), которые производят значения в какой-либо языковой области. Местоимение x может иметь номер, a человек и падеж: если х = «мы», то

• число(х) = множественное число,
• человек(х) = первый,
• падеж(х) = именительный падеж.

В более общих случаях сами значения этих функций могут быть языковые единицы, которые принимают значения для определенных атрибутов.

Разрешение этим функциям быть частичными обеспечивает полезную информационное представление этапов лингвистического разбора; много работы по синтаксическому анализу включает в себя завершение этой частичной информации, с учетом ограничений, налагаемых условиями лингвистического соглашения. Структуры признаков — наборы идентичностей, которые служат для оценки лингвистические особенности — имеют естественную алгебраическую интерпретацию и есть элегантная трактовка их логики. Для получения дополнительной информации и ссылки см. Раунды 1996.

9.3 Логика и дискурс

Рассуждение, связанное с дискурсом, вероятно, наименее хорошо изученная область компьютерной лингвистики. Хотя логично приемы еще не играют большой роли в дискурсе, они как бы предлагают один из наиболее многообещающих способов обеспечения единообразного учета многие формы рассуждений, которые участвуют в создании и перевод языка в интерактивном разговоре.

Кратко упомянем три вклада в эту область. Основываясь на тот факт, что правила, регулирующие разговор, полны исключений, Алекс Ласкаридес и Николас Ашер разработали методы для формализация дискурсивных явлений на основе немонотонной логики; видеть Ашер и Ласкаридес 1994, Ашер и Ласкаридес, 1997. Джерри Хоббс и его коллеги рассматривают процессы логического вывода, используемые в дискурс как похищение , и предлагают формализовать похищение как поиск доказательства, в котором некоторые «недорогие» допущения могут быть оправданы.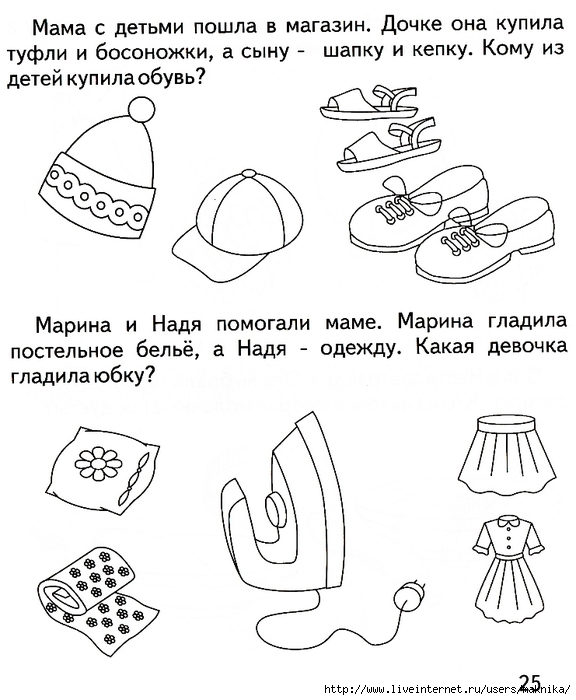 которые служат данными или дополнительными аксиомами для доказательства. Хоббс и др. . 1993 г. показывает, как впечатляющий спектр дискурсивных явлений может быть формализован с помощью этого идея. На практике эта абдуктивная версия выглядит довольно похожей на ту, что Ласкаридиса и Ашера, потому что он включает развертывание аксиом о дискурс (в виде правил оговорки Хорна, дополненных весами с учетом предполагаемой стоимости помещений), которые на самом деле являются немонотонный.

В более поздней работе Мэтью Стоун показывает в Камень 1998 как модальная логика может информировать сложные рассуждения, связанные с генерацией естественного языка. Создание связный, соответствующим образом сформулированный текст, который полезно выполняет задача-ориентированная коммуникативная задача трудно формализуется, поскольку она требует интеграции сложных и сложных доменов информация с планированием дискурса, пользовательским моделированием и лингвистическим ограничения. Стоун показывает, что модальная логика может быть использована для модуляризации формализация информации, необходимой в данной задаче; он также показывает как модальное доказательство теорем может быть использовано для реализации рассуждений.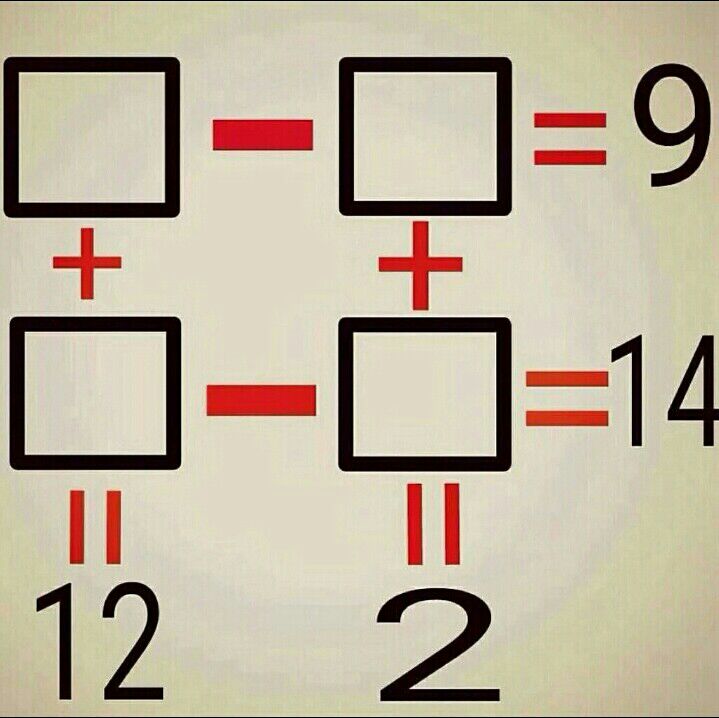

10.1 Классификация на основе концепций

Традиционно задача представления больших объемов домена информация для рассуждений общего назначения была одной из самых важные области представления знаний. Системы, использующие интуитивная таксономическая организация доменов полезна для этого цель; таксономические иерархии не только помогают организовать процесс приобретение знаний, но обеспечивают полезную связь с рассуждения. ^[41]

Для областей, в которых сложные определения являются естественным способом организовывать информационные, инженерные службы знаний на основе определения понятий были чрезвычайно успешными. Нравиться версии логики первого порядка без переменных (см., например, Куайн 1960 г., эти системы ориентированы на концепты или предикаты первого порядка, а также предоставляют ряд механизмов для их определения. Основной алгоритм, связанный с этим таксономическая логика — это классификатор, который вводит систему определения и выводит отношения следствия между определенными и примитивные понятия.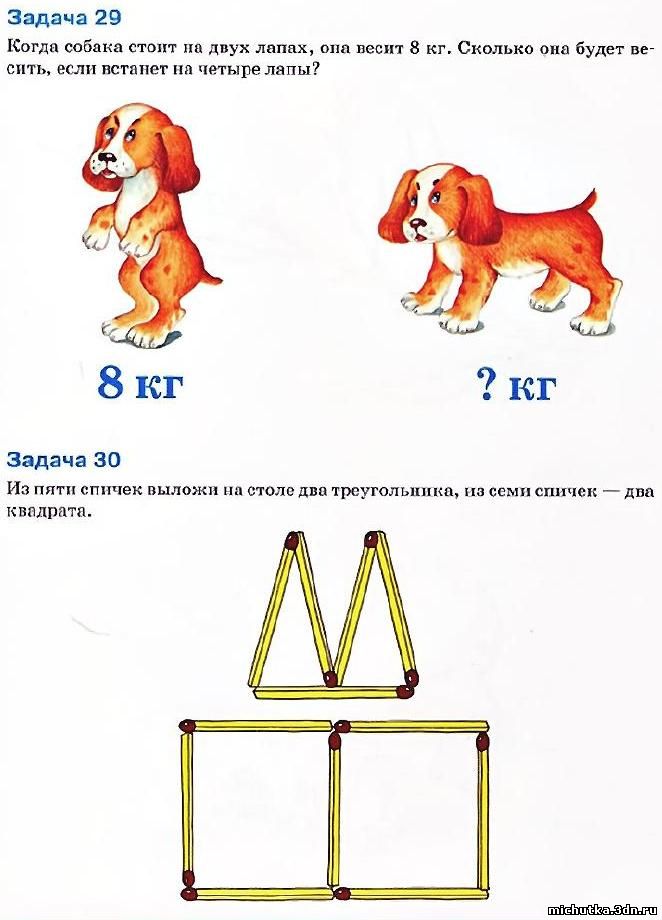 Справочную информацию об этих системах см. Вудс и Шмолце 1992 а также Брахман и др. . 1991.

Простейшие таксономические логики можно рассматривать как подсистемы логика первого порядка со сложными предикатами; но они были расширены во многих отношениях, и проблемы, поднятые многими из этих расширений, пересекаются во многих случаях с темами философской логики.

10.2 Немонотонное наследование

Гораздо более сложные логические вопросы возникают при организации домен в иерархии может иметь исключения. Один из способов Подход к этой теме заключается в том, чтобы изучить, как сделать таксономическую логику немонотонный; но немонотонное наследование является темой в своем владеть правом. Хотя есть сильное сходство с немонотонной логикой, немонотонная логика больше полагается на представления на основе графов чем на традиционных логических идеях, и, кажется, дает много более детальный подход к немонотонным рассуждениям, который полностью новые проблемы, которые быстро становятся проблематичными.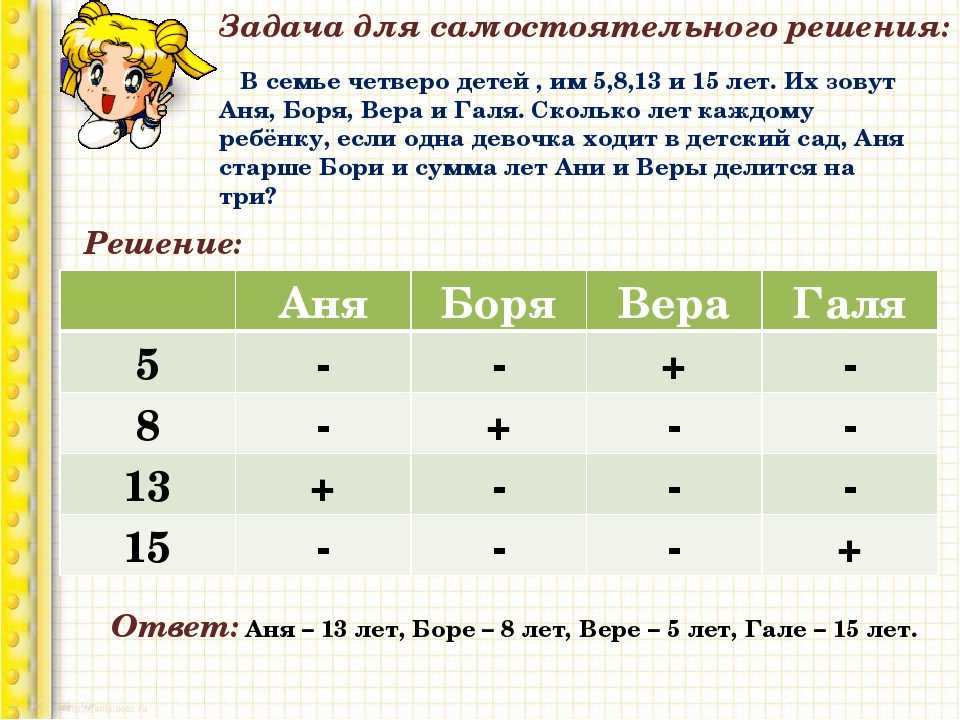 По этой причине, системы немонотонного наследования имеют тенденцию к выраженной слабости, а их отношение к более мощной немонотонной логике никогда не было полностью выяснено. Справочную информацию по этой теме см. Томасон 1992, Хорти 1994.

В традиции философской логики, имеющей дело с контекстуальными влияние на интерпретацию выражений, а также на более недавняя традиция в динамической логике, контекст в первую очередь формализуется как присвоение значений переменным, а язык предназначен для делать явные рассуждения о контексте либо очень ограниченно, либо прямо невозможно.

Обеспокоенность ИИ представлением больших и явно разнородных предметных областей и об интеграции разрозненных знаний источников, а также заинтересованность в формализации здравого смысла обсуждалось в Раздел 2.2, выше, привели к заинтересованность сообщества ИИ в формализации языков, учитывающих контекст учитывать более явно.

В Маккарти 1993b, Маккарти рекомендует изучать языки, содержащие конструкцию

ist ( c,φ ),

где ist читается как «верно». Это по аналогии с Содержит конструкцию ситуационного исчисления, но теперь c означает контекст, а φ — возможно сложный пропозициональная репрезентация, которую многие (включая Маккарти) принимают за обратитесь к предложению.

Здесь есть аналогии как с модальной логикой, так и с языками с явный предикат истинности. Но приложения, которые предусмотрены для логика контекста создает возможности и проблемы, которые во многих способы новые. Работа над логикой контекста после Маккарти оригинальное предложение, включает Маккарти и Бувац 1998, Гуха 1991 и некоторые из доклады в томах конференции Акман и др. . 2001 г., Букет и др. . 1999. Для расширений интенсиональной логики Ричарда Монтегю, мотивированных Предложения Маккарти, см. Thomason 2003. и 2005.

Почему-то работа над явной формализацией контекста не ведется. активно преследовалась вычислительным сообществом за пределами этой точки. Философский интерес к контексту и особенно к взаимодействию контекста с пропозициональными установками и модальными сильный; но очень общие логические рамки для контекста, которые Предвидения Маккарти еще не были восприняты философами.

Есть основания надеяться, что сочетание логических методы с приложениями планирования в ИИ могут позволить разработать гораздо более всеобъемлющая и адекватная теория практического мышления чем это было возможно до сих пор. Как и со многими проблемами, которые нужно делать со здравым смыслом, масштаб и сложность необходимые формализации выходят за рамки традиционных методов философской логики. Однако с помощью вычислительных методов внедрение и тестирование формализации и с такими областями, как когнитивная робототехника в качестве лабораторий для разработки и тестирования идеи, мы можем надеяться радикально продвинуть проблему, которая мало видела прогресс с тех пор, как он был впервые предложен Аристотелем: проблема разработка формализации практических рассуждений, которая действительно применимы к задачам рассуждения здравого смысла.

Классическая работа по деонтической логике, начатая фон Райтом. (видеть фон Райт 1983) является одним из источников идеи; видеть (Хорти 2001, ван дер Торре, 1997). Фактически, как более поздние работы по деонтической логике показывают, что немонотонная логика обеспечивает естественным и полезным дополнением к классической деонтической логике. Один недавняя работа (Horty 2012) стремится основывать деонтическую логику на приоритетной версии стандартной логики Райтера.

Начинает появляться еще более надежное объяснение практического мышления. когда эти идеи дополняются работой над основами планирование и обдумывание действий, которые обсуждались в Раздел 4, выше. Но это развитие можно продолжить даже дальше, расширив формализм, включив в него предпочтения и намерения. ^[42]

В конечном счете, необходима модель разумного рассуждения. и исполняющий обязанности агента. Разработка такой модели не должна быть полностью вопросом логики, но согласно одной школе мысли, логика имеет центральную роль в нем; см., например, Барал и Гельфонд 2000, Вобке и др. . 1998 г., Рао и Джорджефф, 1991 г., Буркхард и др. . 1998).

Логические головоломки

Лампочки

Это один из моих любимых логических головоломок с реальным решением.
Внизу есть три выключателя. Каждая соответствует одной из трех лампочек на чердаке. Вы можете включать и выключать переключатели и оставлять их в любом положении.
Как бы вы определили, какой выключатель соответствует какой лампочке, если вам разрешено только один раз подняться наверх?

 

Шарик для пинг-понга в лунке

Ваш последний хороший шарик для пинг-понга упал в узкую металлическую трубу, замурованную в бетон глубиной в один фут.
Как вытащить его невредимым, если все, что у вас есть, это теннисная ракетка, шнурки и пластиковая бутылка с водой, которая не влезает в трубу?

Мужчина в лифте

Мужчина, живущий на десятом этаже, каждое утро спускается на лифте на первый этаж и идет на работу. Вечером, когда он вернется; в дождливый день или если в лифте есть другие люди, он идет прямо на свой этаж. В противном случае он поднимается на седьмой этаж и поднимается на три лестничных пролета в свою квартиру.
Можете ли вы объяснить, почему?
(Это одна из самых популярных и самых знаменитых головоломок на логику латерального мышления. Это настоящая классика. Хотя существует множество возможных решений, соответствующих условиям, только канонический ответ является действительно удовлетворительным.)

Мяч

Как вы можете бросить мяч так сильно, как только можете, чтобы он вернулся к вам, даже если он ни от чего не отскакивает? К нему ничего не привязано, и никто другой не поймает и не бросит его вам обратно.

Магнит

Эта логическая головоломка была опубликована в колонке Мартина Гарднера в журнале Scientific American. Вы находитесь в комнате без металлических предметов, кроме двух железных стержней. Только один из них является магнитом.
Как определить, какой из них является магнитом?

Мужественные микробы

В чашке Петри находится здоровая колония бактерий. Раз в минуту каждая бактерия делится на две части. Колония была основана одиночной клеткой в ​​полдень. Ровно в 12:43 (через 43 минуты) чашка Петри была наполовину заполнена.
В какое время блюдо будет полным?

Наследие шейха

Арабский шейх велит двум своим сыновьям мчаться на верблюдах в далекий город, чтобы посмотреть, кто унаследует его состояние. Выигрывает тот, чей верблюд медленнее. После бесцельных скитаний в течение нескольких дней братья просят совета у мудреца. Получив совет, они запрыгивают на верблюдов и мчатся в город так быстро, как только могут.
Что сказал им мудрец?

Философские часы

Один рассеянный древний философ забыл завести свои большие часы, висевшие на стене в доме. У него не было ни радио, ни телевидения, ни телефона, ни Интернета, ни каких-либо других средств определения времени. Поэтому он отправился пешком к своему другу на несколько миль вниз по прямой дороге в пустыне. Он остался в доме своего друга на ночь, и когда он вернулся домой, он знал, как настроить свои часы.
Как он узнал?

Мастера логических головоломок (точки)

Три мастера логики хотели выяснить, кто из них самый мудрый. Поэтому они обратились к своему Великому Мастеру с просьбой разрешить их спор.
— Легко, — сказал старый мудрец. «Я завяжу вам глаза и нарисую каждому красную или синюю точку на лбу. Когда я сниму с вас повязку, если вы увидите хотя бы одну красную точку, поднимите руку. Тот, кто угадает цвет точки на своем лоб вперед, побеждает».
И так было сказано, и так было сделано. Великий Магистр завязал глаза трем участникам и нарисовал на каждом красные точки. Когда он снял с них повязку, все трое подняли руки, как того требовали правила, и сидели в молчании, размышляя. Наконец один из них сказал: «У меня на лбу красная точка».
Как он догадался?

Мастера логических головоломок (шапки)

После поражения в конкурсе «Пятно на лбу» два побежденных мастера головоломок пожаловались, что победитель сделал небольшую паузу, прежде чем поднять руку, тем самым сорвав ход их дедуктивных рассуждений. И поэтому Великий Магистр поклялся устроить действительно честное испытание, чтобы выявить среди них лучшего логика.
Он показал троим мужчинам 5 шляп – две белые и три черные. Затем он выключил свет в комнате и надел каждому Мастеру головоломок по шляпе. После этого старый мудрец спрятал оставшиеся две шляпы, но не успел он включить свет, как по воле случая один из Мастеров, победитель предыдущего конкурса, объявил цвет своей шляпы. И он снова оказался прав.
Какого цвета была его шляпа? Какие могли быть его рассуждения?

Мастера логических головоломок (марки)

Попробуй это. Великий Магистр берет набор из 8 марок, 4 красных и 4 зеленых, известных логикам, и свободно прикрепляет по две ко лбу каждого логика так, чтобы каждый логик мог видеть все остальные марки, кроме тех 2, которые находятся в кармане Великого Магистра и два на ее собственном лбу. Он, в свою очередь, спрашивает их, знают ли они цвета своих марок:
А: «Нет».
Б: «Нет».
К: «Нет».
А: «Нет».
Б: «Да».
Марки какого цвета у Б?

Головные повязки

Трое Бледнолицых были взяты в плен враждебным индейским племенем.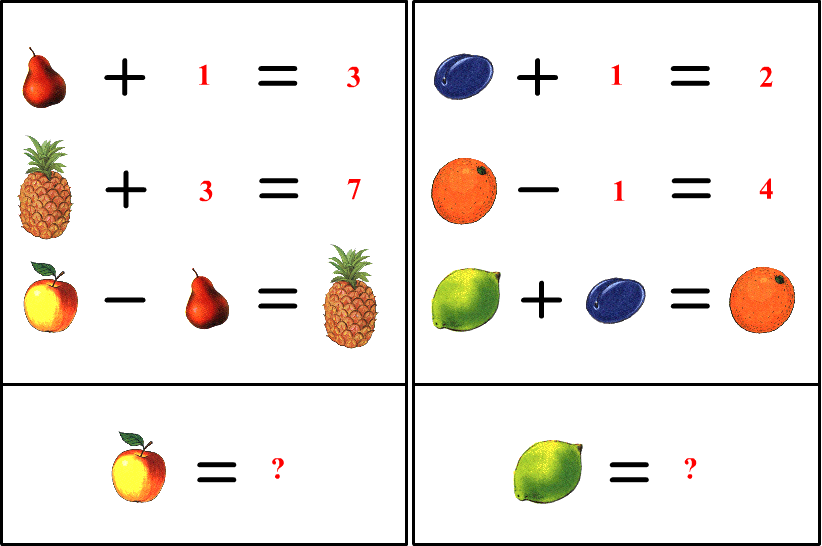 По обычаю племени они должны были пройти тест на интеллект или умереть.
Вождь показал 5 повязок – 2 красных и 3 белых. Трем мужчинам завязали глаза и расположили друг за другом лицом к спине. Вождь надел каждому повязку на голову, две оставшиеся повязки спрятал и снял повязку с глаз. Таким образом, третий человек мог видеть повязки на двух мужчинах перед ним, второй человек мог видеть повязку на голове у первого, а первый вообще не мог видеть никаких повязок.
По правилам любой из троих мог заговорить первым и попытаться угадать цвет своей повязки на голове. И если он угадал правильно — они прошли испытание и могли выйти на свободу, если нет — провалили. Так получилось, что все трое Бледнолицых были выдающимися логиками из ближайшей академии. Итак, после нескольких минут молчания первый мужчина в очереди сказал: «Моя повязка на голову…».
Какого цвета была его повязка на голове? Почему?

Рождественская головоломка

Четыре ангела сидели на елке среди других украшений.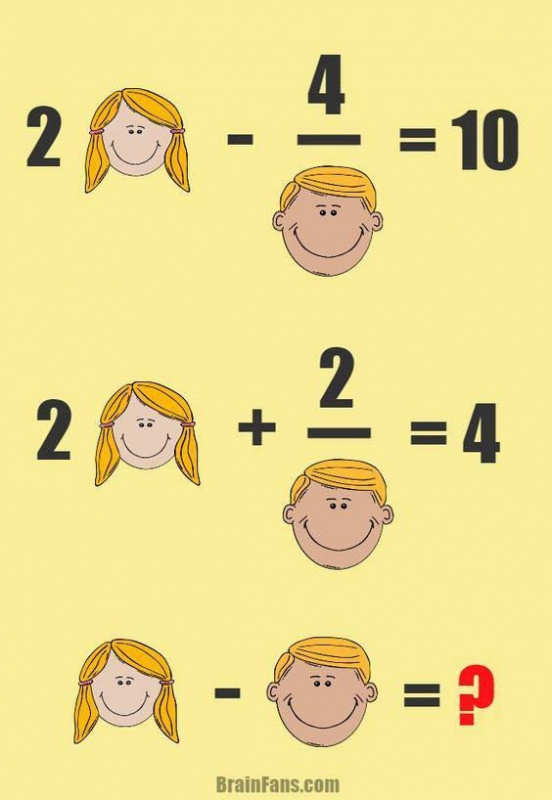 У двух были голубые ореолы и у двух — желтые. Однако никто из них не мог видеть выше своей головы. Ангел А сидел на верхней ветке и мог видеть ангелов В и С, которые сидели под ним. Ангел Б мог видеть ангела С, который сидел на нижней ветке. А ангел D стоял у подножия дерева, скрытый от глаз густыми ветвями, так что его никто не видел, и он тоже никого не видел.
Кто из них сможет первым угадать цвет его нимба и произнести его вслух, чтобы его услышали все остальные ангелы?

Головоломка дня

 

Поделитесь этой страницей с друзьями

Посмотреть другие логические загадки >>

Плакаты с треугольными цифрами и логические головоломки

1 Бесплатная загрузка плакатов с треугольными числами

2 Еще больше бесплатных математических плакатов для печати

Этот пост в блоге содержит партнерские ссылки Amazon. Как партнер Amazon, я получаю небольшую комиссию от соответствующих покупок. Это бесплатно для вас. Спасибо за вашу поддержку Math = Love!

Сегодня я поделюсь с вами несколькими плакатами с треугольными числами. Сейчас январь, а я все еще нахожу новые вещи, которые нужно разместить на стенах моего класса. Это немного одержимость. Не верите мне? Вы только посмотрите на мой класс!

Мой класс математических концепций работал над головоломками «Это логично» с тех пор, как мы вернулись в школу после рождественских каникул в январе. Это распроданный набор книг-головоломок от Creative Publications. Это то же самое издательство, которое принесло нам «Алгебру с пиццей» и все другие книги на тему пиццы. Из моего исследования следует, что компания была куплена McGraw Hill и больше не издает никаких книг…

Изображение предоставлено Amazon

В течение первых нескольких недель семестра мы работали над учебником для 1–4 классов. Я НЕ говорил своим ученикам, что они работают над головоломками, предназначенными для учащихся 1-4 классов. Студентам дается 9буквы (3 X, 3 O и 3 V), которые нужно поместить в сетку 3 x 3, чтобы удовлетворить ряд предоставленных «подсказок».

Головоломки бывают трех разных уровней в зависимости от количества заданных подсказок.

Вот пример головоломки 1-го уровня.

Сложность головоломок на протяжении всей книги увеличивается до тех пор, пока не исчезнут фиксированные подсказки. Вот пример головоломки уровня 3.

Я напечатал шаблон сетки решения, и каждый ученик использует карман для сухого стирания, чтобы решить свою головоломку в качестве ежедневной разминки.

Первые несколько дней мои дети сомневались в этих головоломках, но когда они начали понимать, как они работают, они действительно увлеклись ими. Я обнаружил, что три из этих головоломок идеально подходят для разминки моих студентов, изучающих математические концепции. Имейте в виду, что это учащиеся 9-го класса, но не готовые к математике на уровне 9-го класса. В моей школе это означает, что они не готовы к алгебре 1. Итак, я счастлив давать им задания, которые улучшают их навыки рассуждения, поскольку я считаю, что рассуждение является важнейшей предпосылкой для занятий по математике на уровне средней школы (и всех остальных). уроки математики, если на то пошло).

Первые две недели эти головоломки давались моим ученикам невероятно легко, как только они освоились. Они должны были быть легкими, так как согласно книге это были головоломки элементарного уровня. В последнюю неделю или около того головоломки становились все более сложными, поскольку требовали более высокого уровня рассуждений. Но они не были невозможными, поэтому мои ученики все еще чувствовали огромное чувство выполненного долга.

На этой неделе мы закончили учебник для 1-4 классов и начали второй том, предназначенный для учащихся 4-8 классов. Эти головоломки определенно делают скачок по уровню сложности между первым томом и вторым томом.

Взгляните на первую головоломку в учебнике для 4-8 классов.

Внезапно мы используем цифры 1-9 вместо букв алфавита. И есть все эти странные символы, значение которых нам нужно знать. Квадраты обозначают идеальные квадраты. Кубы обозначают идеальные кубы.

К счастью, у меня на стене висят плакаты с идеальными квадратами и идеальными кубами!

E означает четный. Если есть буква E с косой чертой, это означает не четное. Их нет на моей стене. Я как бы предполагаю, что мои старшеклассники уже знают, какие числа четные. Но это не всегда так…

P означает простое число. У меня также есть список простых чисел на моей стене.

Последний символ — треугольник, обозначающий треугольные числа. Мои ученики быстро поняли, что у меня на стене нигде нет треугольных чисел. Что ж, так было до вчерашнего дня, когда я планировал распечатать и заламинировать набор плакатов с треугольными цифрами.

Я напечатал плакаты с треугольными числами на желтой бумаге и решил, что они мне немного напоминают знаки доходности…

Мне нравится, что я стал учителем с репутацией, что каждое новое понятие, которое мы изучаем на моем уроке математики, должно быть найдено где-то на стене.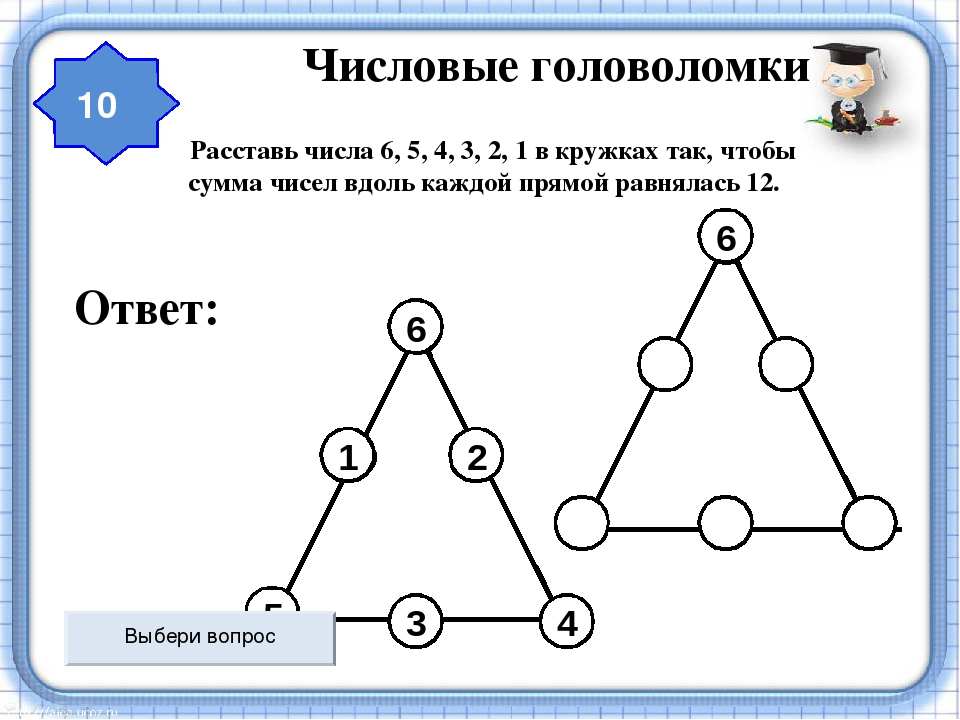

Моим ученикам потребовалась большая помощь и моделирование, чтобы решить эти новые головоломки «Это логично», но я думаю, что через несколько дней мои ученики начинают это понимать. Несколько студентов отказываются пытаться, но я не знаю, что с этим делать. Я уверен, что наши впечатления от этих головоломок будут улучшаться, поскольку мы продолжаем решать их в качестве ежедневной разминки. Эти головоломки занимают гораздо больше времени, чем другие головоломки, поэтому я выделяю время только на две из этих головоломок каждый день.

Хотите получить эти головоломки «Это логично»? Вы можете забрать использованные экземпляры книг-головоломок на Amazon. Вот ссылки для 1-4 классов и 4-8 классов. Раньше в Интернете были сканы обеих книг в формате PDF сомнительной законности, но, похоже, они были удалены.

Существует цифровая версия некоторых из этих головоломок, которыми поделился читатель, которую я разместил в своем посте «Репозиторий цифровых действий». Проверьте это!

Скачать бесплатно плакаты с треугольными числами

Плакаты с треугольными числами (PDF) (194 загрузки)

Плакаты с треугольными числами (редактируемый файл Publisher ZIP) (93 загрузки) – Последнее обновление: 5 сентября 2022 г.

Стратегии от участника с рейтингом 180 — Shemmassian Academic Consulting

Высокоэффективные советы, которые помогут вам улучшить результат LSAT по логическому мышлению, а также практические вопросы

СОДЕРЖАНИЕ

ЧАСТЬ 1: Введение в раздел LSAT Logical Assuling Раздел

Часть 2: LSAT LOGICAL SECTION Структура Раздела

Часть 3: Логический разум. для сдачи LSAT Logical Reasoning Section

Часть 5: Советы по изучению LSAT Logical Reasoning Section

Часть 6: Практическая практика раздел логической рассуждения. юристов и студентов юридических факультетов. Секция логического мышления LSAT проверяет навыки критического мышления, необходимые для анализа аргументов. Такой анализ может включать в себя понимание, оценку, сравнение, построение, подрыв и укрепление аргументов. Вопросы в разделе логического рассуждения LSAT просят вас завершить различные аспекты этого анализа в условиях времени.

Используя примеры аргументов, взятых из различных тем, вопросы раздела логического мышления LSAT оценивают вашу способность анализировать аргументы. Немногие вопросы связаны с юридическими темами, но каждый вопрос предназначен для соответствия образцам юридических аргументов, как по структуре, так и по сложности. Независимо от того, учитесь ли вы на адвоката или работаете таковым, аргументы, которые вам предстоит анализировать на протяжении всей вашей карьеры, будут громоздкими и длинными, что потребует от вас фильтрации информации на предмет актуальности. Вопросы в разделе логического мышления LSAT влекут за собой аналогичные оценки релевантной и нерелевантной информации.

Секция логического мышления LSAT проверяет ряд навыков критического мышления, необходимых для юридического рассуждения. По данным LSAC, Приемного совета юридических факультетов и администратора теста, эти навыки включают:

• Распознавание частей аргумента и их взаимосвязей

• Распознавание сходств и различий между моделями рассуждений

• Хорошо рисовать -поддерживаемые выводы

• Рассуждения по аналогии

• Признание недоразумения или точки разногласий

• Определение того, как дополнительные доказательства влияют на аргумент

• Обнаружение предположений, сделанных по конкретным аргументам

• Идентификации и применения.

• Идентификация объяснений

Это звучит как много, и для некоторых людей раздел логического рассуждения LSAT является пугающим препятствием, но с подготовкой и пониманием раздела, который мы предоставляем, вы можете чувствовать себя более уверенно в своей готовности для и производительности в разделе логического мышления LSAT. Это руководство содержит полезную справочную информацию, объясняющую структуру и состав теста, а также советы по сдаче и подготовке к разделу. Наконец, мы включили несколько дополнительных примеров вопросов и пояснений к ответам, чтобы вы могли увидеть, как вам будут задавать эти вопросы в день экзамена.

Щелкните по следующим ссылкам, чтобы узнать о высокоэффективных стратегиях, которые можно использовать в каждом из разделов LSAT:

Часть 2: Структура раздела логического рассуждения LSAT

Каждый раздел логического рассуждения LSAT состоит из 24–26 вопросов и длится 35 минут. Вопросы предполагают множественный выбор с пятью вариантами ответов, обозначенными буквами A-E. В каждом вопросе есть только один правильный вариант ответа. В некоторых вопросах есть слово «кроме». Для этих вопросов слово «кроме» будет написано заглавными буквами, и каждый из вариантов ответа будет иметь рассматриваемую черту «кроме» для одного.

Каждый вопрос раздела логического мышления LSAT состоит из трех частей: короткого абзаца (часто называемого стимулом), вопроса и ответов. В редких случаях один стимул применим к двум вопросам. Когда это произойдет, это будет четко отмечено на тесте.

 Стимул будет состоять из нескольких предложений, обычно в диапазоне от 50 до 70 слов. Иногда стимулы будут заметно длиннее. Стимулы включают аргументы, и некоторые из этих аргументов взяты из академических тем и истории, в то время как другие описывают гипотетические сценарии. Для ответа на эти вопросы не требуется никаких посторонних знаний. Кроме того, описанные сценарии следует воспринимать как факт, несмотря на любые имеющиеся у вас знания извне.

За стимулами следует основа вопроса. Основа вопроса — это вопрос из одного предложения, касающийся аргумента, который ему предшествовал. Эти основы вопросов, как правило, следуют определенным шаблонам, поэтому можно ознакомиться с различными типами вопросов, и мы дадим некоторое представление об этих шаблонах в этом руководстве.

Варианты ответов перечислены после основы вопроса. Хотя ответ может быть верным, это не значит, что он правильный. Кроме того, некоторые варианты ответов могут быть точными цитатами или близким перефразированием частей стимула. Будьте осторожны с перефразированием с тонкими изменениями, которые меняют смысл.

Ниже приведен пример того, как вы видите вопрос в тесте. Каждый компонент помечен для ясности, но не будет помечен на самом тесте:

Стимул	1. Политический корреспондент: По мнению Мэдисона, новый закон не следует принимать, потому что он будет противоречить существующему закону. Но Мэдисон только что обвинили в растрате.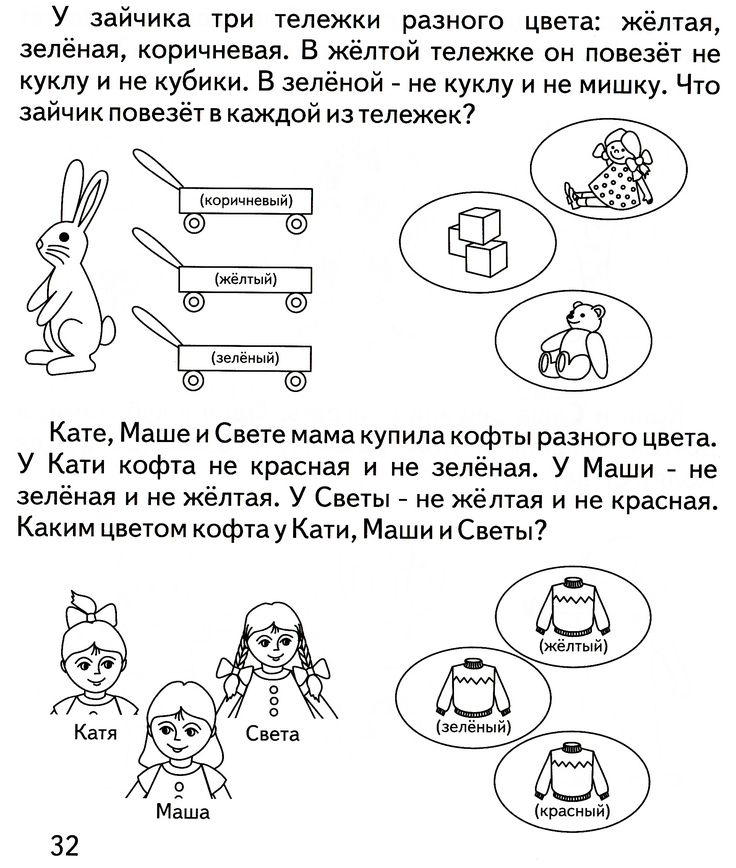 Следовательно, Мэдисон не прав, и нужно принять новый закон.
Основная часть вопроса	Аргумент корреспондента ошибочен в том смысле, что аргумент
Варианты ответов	A) путает корреляцию и причинно-следственную связь B) использует двусмысленные рассуждения C) упускает из виду возможность невиновности Мэдисон D) не учитывает аргумент Мэдисон E) делает вывод о Мэдисон в целом, основываясь только на одном факте о Мэдисон

Часть 3. Типы вопросов на логическое мышление

Хотя LSAT со временем развивался, в типах вопросов есть определенные повторяющиеся шаблоны. LSAT проверяет конкретные навыки, упомянутые выше, и создает вопросы для оценки этих навыков. Наиболее распространенные типы вопросов: вопросы-предположения, усиливающие/ослабляющие вопросы, вопросы о недостатках и вопросы на вывод. Менее распространенные типы вопросов включают вопросы о методе аргументации, вопросы о парадоксах, вопросы о параллельных рассуждениях, вопросы о проблеме, принципиальные вопросы и ролевые вопросы.

Наиболее распространенные типы вопросов: предположение, усиление/ослабление, недостаток и вывод углубимся в каждый тип вопроса.

Тип вопроса 1: Вопросы на предположения

Вопросы на предположения касаются невысказанных предположений в аргументе и могут быть разбиты на две категории: необходимое предположение и достаточное предположение. Вопросы о необходимых предположениях будут задаваться вопросом: «Какие из следующих предположений требуются для аргумента?» В необходимых вопросах предположения аргумент сделал по крайней мере одно невысказанное предположение, чтобы оправдать вывод. Этот вопрос просит вас определить это предположение.

Поскольку это «необходимое» допущение, вы можете считать его существенным для аргумента. Если бы это было неправдой, спор был бы недействителен. Чтобы ответить на этот вопрос, отрицайте варианты ответа и смотрите, какой отрицательный вариант ответа разрушает аргумент. Правильный выбор ответа разрушит аргумент, когда он будет отвергнут, потому что это необходимое допущение, а без него аргумент больше не имеет силы.

Некоторые формулировки необходимых предположений включают:

«Какое из следующих утверждений предполагается в данном аргументе?»

«Какое из следующих предположений требуется аргументом?»

«Что из следующего является предположением, от которого зависит аргумент?»

Вопросы о достаточном предположении касаются предположения, которое позволяет сделать логический вывод. В этих вопросах отсутствует предпосылка, добавление которой сделает общий аргумент обоснованным. Ответы на эти вопросы потребуют от вас понимания предпосылки и вывода вопроса-стимула. Иногда сопоставление аргумента может помочь в вопросах с недостаточным предположением, но это не обязательно.

Правильный ответ свяжет предпосылки с заключением, поэтому может быть полезно найти ответ, в котором есть компоненты каждой из них. Неправильные ответы не будут служить основанием для заключения. Они часто не имеют отношения к аргументу в целом или оправдывают вывод, отличный от того, который сформулирован в стимуле.

Помните, что раздел логического рассуждения LSAT не всегда представляет информацию в хронологическом порядке. Следовательно, заключение может быть помещено между поддерживающими его посылками.

Некоторые формулировки для вопросов о достаточных предположениях включают:

«Вышеприведенный вывод следует логически, если предполагается одно из следующего?»

«Вышеприведенный вывод сделан правильно, если предполагается, что из следующего?»

«Что из следующего, если оно верно, позволяет сделать правильный вывод?»

Тип вопроса 2: усиление/ослабление

Еще один распространенный тип вопросов – усиливающие и ослабляющие вопросы. Эти вопросы просят вас либо усилить, либо ослабить аргумент стимула. По этим вопросам вы пытаетесь сделать вывод более или менее верным. Вам не нужно полностью аннулировать или гарантировать его. Будьте осторожны, чтобы оставаться в рамках вопроса, и не полагайтесь на внешние знания и предположения .

Правильный ответ подтвердит или опровергнет предпосылку или допущение в стимуле, очевидно, в зависимости от того, смотрите ли вы на усиливающий или ослабляющий вопрос. К счастью, эти вопросы очень распространены и следуют определенным шаблонам. Часто аргумент представляет предполагаемую причинно-следственную связь. Вы можете укрепить или подтвердить отношения, поддерживая или оспаривая причинно-следственные связи.

Вопросы требуют выбора ответа, который «наиболее» ослабляет или усиливает аргумент. Вы можете увидеть более одного ответа, который влияет на аргумент, но выберите только тот вариант ответа, который влияет на него больше всего и в направлении, заданном вопросом.

Некоторые основы укрепляющих вопросов включают:

Какой из следующих вопросов, если он верен, в наибольшей степени поддерживает приведенный выше вывод?

Что из следующего, если оно верно, больше всего усиливает аргумент?

Что из следующего, если оно верно, больше всего усиливает вышеприведенное рассуждение?

Какое из следующих утверждений, если оно верно, больше всего укрепило бы приведенные выше рассуждения?

Некоторые ослабляющие основы вопросов включают:

Какой из следующих, если он верен, является логически самым сильным противоречием приведенному выше аргументу?

Какое из следующих утверждений, если оно верно, больше всего ослабляет аргумент?

Что из следующего, если оно верно, наиболее серьезно подрывает вывод, сделанный в рассуждении выше?

Помните, что в усиливающих вопросах вы добавляете поддержку , а в ослабляющих вопросах вы убираете поддержку .

Тип вопроса 3: Вопросы о недостатках

Вопросы о недостатках касаются логических ошибок, допущенных в аргументе. Хотя они могут быть трудными, эти вопросы довольно просты при правильном подходе. Поняв аргумент в стимуле, вы часто можете предсказать ответ. Если вы не сразу заметили изъян в рассуждении или заметили более одного, оцените варианты ответов. Правильный выбор ответа будет фактическим логическим недостатком (в отличие от слабости) и будет недостатком, который действительно имел место в аргументе. Неправильные варианты ответа не будут логическими ошибками или будут логическими ошибками, которых не было в конкретном стимуле, о котором вас спрашивают.

Недостаточные основы вопроса включают:

Какая из следующих ошибок рассуждения совершается в аргументе?

Обоснование аргумента сомнительно, поскольку аргумент…?

Аргументация выше ошибочна в том, что аргумент…?

Аргументация ошибочна, поскольку аргумент упускает из виду возможность того, что…?

Аргументация наиболее уязвима для критики на том основании, что аргумент…?

Что из следующего наиболее точно описывает недостаток аргументации?

Тип вопроса 4: вопросы на вывод

Вопросы на вывод также просты, хотя на них не всегда легко ответить. Вопросы на вывод задают вопрос о том, что можно сделать вывод ТОЛЬКО на основании приведенной выше информации. Для вопросов на вывод, как и для всех вопросов по LSAT, критически важно не опираться на внешние знания. Для вопросов на вывод может быть полезно составить карту аргумента, чтобы убедиться, что вы не втягиваете в свой мозг информацию извне. Обычно проверяемые выводы включают транзитивные, контрапозитивные и контрапозитивные транзитивные. Нет необходимости изучать символические рассуждения, чтобы пройти раздел «Логические рассуждения» LSAT, но базовое понимание карт и этих типов вывода может быть полезным.

Исходная выписка:	Выводы:
А → В В → С	А → В В → С
Переходный:	А → С
Противоположный:	~B → ~A и ~C → ~B
Противоположный переходному:	~С → ~А

Правильные ответы на логические вопросы будут верными и подтверждены информацией в стимуле. Неправильные ответы будут либо противоречить стимулу, не поддерживаться стимулом, либо быть только возможностью, основанной на стимуле, то есть это также может быть неправдой. Основываясь на информации, содержащейся в стимуле, правильный выбор ответа должен быть верным.

Некоторые основы вопросов на вывод включают:

Основываясь на приведенном выше аргументе, что из следующего должно быть правдой?
Что из нижеследующего можно логически вывести из приведенного выше рассуждения?

Какое из следующих утверждений больше всего подтверждается приведенными выше утверждениями?

Тип вопроса 5: метод аргументации

Вопросы метода аргументации касаются того, как проходит аргументация. Эти вопросы просят вас обобщить аргумент в стимуле, понять и назвать отношения между предпосылкой (посылками) и заключением. Эти вопросы встречаются реже, чем первые четыре типа вопросов, но время от времени появляются. Правильный ответ будет точно описывать аргумент стимула.

Если правильный вариант ответа сразу не ясен, сравните каждый вариант ответа со стимулом, оценив его соответствие аргументу. Обратите особое внимание на глаголы в каждом варианте ответа, так как они могут быть четкими сигналами того, что постулирует вариант ответа. Делает ли аргумент то, что предполагает выбор ответа? Если нет, то выбор ответа неверный. Этот тип вопросов оценивает вашу способность анализировать аргументы и понимать, как формируются аргументы.

Некоторые основы вопросов метода аргументации включают:

Что из следующего наиболее точно описывает метод рассуждения?

Каким из следующих способов работает аргумент?

Аргумент продолжается…?

Тип вопроса 6: Paradox

Вопросы Paradox также реже встречаются в тесте, но, тем не менее, к ним важно подготовиться. К счастью, они не слишком сложны, и на них можно ответить с некоторым простым пониманием. Парадоксальные вопросы представляют информацию, которая кажется противоречивой. Когда вы читаете стимул, обратите внимание на любые противоречия, парадоксы или несоответствия. Правильный выбор ответа устранит эту проблему.

Вместо того, чтобы предвосхищать ответ, потому что часто существует множество способов разрешения гипотетического парадокса, отфильтруйте варианты ответа, ища вариант ответа, который допускает, что оба компонента парадокса верны, а также объясняет, как они сосуществуют. Неправильный выбор ответа не разрешит парадокс или будет противоречить одному или обоим компонентам парадокса.

Некоторые основы парадоксальных вопросов включают:

Что из следующего, если оно верно, помогло бы разрешить очевидный парадокс, представленный выше?

Что из следующего, если оно верно, в наибольшей степени способствует объяснению очевидного несоответствия, описанного выше?

Что из следующего помогает объяснить несоответствие?

Тип вопроса 7: Параллельное рассуждение

Вопросы на параллельное рассуждение — еще один менее распространенный тип вопросов. Они могут показаться сложными, но часто очень просты. По сути, вопросы параллельного рассуждения касаются сопоставления. Вы должны сопоставить стимул с выбором ответа. Трудность, однако, возникает в том, чтобы быстро понять структуру аргумента в стимуле, а затем понять структуру аргумента выбора ответа.

Ответить на этот вопрос без полного понимания стимула может быть очень сложно, поэтому постарайтесь понять стимул, прежде чем оценивать вариант ответа. Для этого типа вопроса сопоставление может быть полезным, но не обязательным. Другим полезным инструментом может быть перефразирование: перефразируйте аргумент и сосредоточьтесь на том, как продвигается аргумент. Правильный выбор ответа будет иметь аргумент, который постулирует аналогичную связь между посылками и заключением.

Некоторые основы вопросов на параллельные рассуждения включают: 

Что из следующего больше всего похоже на приведенный выше аргумент?

Что из следующего содержит рассуждения, параллельные приведенному выше аргументу?

Что из следующего наиболее точно соответствует приведенному выше аргументу?

Что из следующего больше всего похоже на приведенный выше аргумент?

Помните, что определенные компоненты в правильном ответе могут быть представлены не в том же порядке, что и стимул, но они будут связаны так же, как отношения в стимуле.

Тип вопроса 8: Спорные вопросы

Спорные вопросы нечасто появляются в разделе логического мышления LSAT, но вы все равно должны быть с ними знакомы. Эти вопросы включают в себя понимание и обозначение разногласий и несоответствий между двумя точками зрения. Часто эти вопросы представляют аргументы двух людей посредством двух-трех коротких ответов. Вопрос поставит перед вами задачу обнаружить несоответствие между их утверждениями. Реже вас могут попросить отметить, в чем они согласны.

Чтобы ответить на этот вопрос, поймите, что говорит каждый из говорящих, а затем обратитесь к вариантам ответа. Что касается вопросов о разногласиях, у каждого выступающего будет свое мнение по этому вопросу, и их мнения будут противоположными. Если один или оба говорящих не имеют мнения по данному вопросу или их мнения не противоположны, то выбор ответа неверен. В вопросах на согласие оба говорящих будут иметь мнение по этому вопросу в правильном выборе ответа, и их мнения будут согласовываться.

Некоторые спорные вопросы включают:

____ и ____ не согласны?

____ и ____ не согласны с истинностью следующих утверждений

Приведенные выше утверждения в наибольшей степени подтверждают мнение о том, что авторы не согласятся с каким из следующих утверждений?

Что из следующего лучше всего описывает спорный вопрос между ____ и ____?

Тип вопроса 9: принцип

Принципиальные вопросы, как и все вопросы в разделе логического рассуждения LSAT, требуют от вас понимания аргумента стимула. Для этих вопросов вы сводите аргумент к простому руководящему принципу. Правильный выбор ответа будет соответствовать рассуждениям, представленным в аргументе. Неправильный выбор ответа не будет точно отражать аргумент.

Иногда принципиальные вопросы представляют принцип в стимуле, и вас попросят определить ситуацию, которая соответствует этому принципу. Применяется та же концепция дистилляции и сопоставления. Правильный ответ будет соответствовать обстоятельству/принципу в стимуле принципу/обстоятельству в выборе ответа.

Некоторые основы вопросов включают:

Какое из следующих обобщений наиболее ярко иллюстрируется отрывком?

Какой из следующих принципов, если он действителен, больше всего помогает обосновать рассуждения в редакционной статье?

Какое из следующих утверждений лучше всего иллюстрирует описанная выше ситуация?

Какое из следующих суждений наиболее точно соответствует принципу, указанному обозревателем?

Что из нижеследующего лучше всего иллюстрирует изложенный выше принцип?

Вопрос 10: Роль 

Ролевые вопросы фокусируются на определенных частях стимула и просят вас определить их функцию. Иногда вы разделяете части аргумента на предпосылки или выводы. В других случаях вы определяете, как используется эта предпосылка или вывод. В эту категорию также входят основные вопросы, в которых вас просто просят описать основную мысль (заключение) стимула. Сопоставление может быть полезным для этого типа вопросов, но не обязательно.

Очень важно понимать, что некоторые слова, такие как «поэтому», имеют тенденцию вводить выводы, в то время как другие слова, такие как «потому что», имеют тенденцию вводить предпосылки. Кроме того, некоторые выводы могут быть промежуточными выводами, которые, хотя и выводятся из набора предпосылок, становятся поддержкой для другого вывода. Вы также должны помнить, что порядок, в котором излагаются рассуждения, не всегда объясняет, какой частью аргумента они являются.

Некоторые основы ролевых вопросов включают:

Что из следующего лучше всего описывает роль утверждения ____ в аргументе выше?

Что из следующего лучше всего описывает функцию оператора ____ в приведенном выше аргументе?

Какой из вариантов лучше всего описывает суть приведенного выше аргумента?

Ниже приведен список типов вопросов, рассматриваемых в этом разделе. Он охватывает большинство вопросов, которые вы увидите в разделе логического мышления LSAT. Однако иногда вы можете столкнуться с вопросом, который не вписывается ни в одну из этих категорий. Если это произойдет, сохраняйте спокойствие и обязательно найдите время, чтобы понять как основу вопроса, так и стимул, прежде чем оценивать варианты ответов и выбирать наиболее точный ответ.

Тип вопроса 1: Вопросы-предположения

Тип вопроса 2: Усиление/ослабление

Тип вопроса 3: Вопросы о недостатках

Тип вопроса 4: Вопросы на вывод

Тип вопроса 5: Метод аргументации

Тип вопроса 6: Парадокс Тип вопроса 7: Параллельное рассуждение

Тип вопроса 8: Суть проблемы

Тип вопроса 9: Принцип

Вопрос 10: Роль 

Часть 4: Советы по сдаче LSAT Логическое мышление Раздел

Совет 1. Сначала прочтите основу вопроса

По мере заполнения раздела LSAT «Логическое рассуждение» рекомендуется начинать сначала со основы вопроса. Понимание того, какой тип вопроса задается, может значительно ускорить процесс понимания стимула и ответа на вопрос. Чтение сначала основы вопроса поможет вам более целенаправленно прочитать стимул, выискивая конкретную информацию.

Совет 2: Шаг

Когда вы закончите раздел логического мышления LSAT, важно следить за собой. Для 35-минутного раздела и максимум 26 вопросов у вас есть около одной минуты и двадцати секунд, чтобы ответить на каждый вопрос. Чтобы не отставать, важно понимать, когда вы тратите слишком много времени на вопрос. Иногда полезно отойти от вопроса и вернуться к нему со свежим взглядом.

Некоторые тестируемые также считают полезным разбить 35 минут на группы вопросов, стремясь выполнить первые десять вопросов за десять минут, следующие десять вопросов за пятнадцать минут и оставшиеся вопросы за последние десять минут. Этот подход рассматривает вопросы LSAT как возрастающие по сложности на протяжении всего раздела.

Совет 3: Сопоставление

Сопоставление рассуждений не является обязательным для секции логического рассуждения LSAT, но может быть очень полезно иметь базовое понимание сопоставления условных операторов. Для начала вы можете поискать инструменты по символическим рассуждениям и отображению условных операторов. Эта система представления может оказаться полезной при прохождении теста, поскольку она позволяет быстро синтезировать и сохранять информацию.

Совет 4. Аннотирование

Во время прохождения теста вам может быть полезно делать заметки. Это может быть полезно, если вам трудно следить за стимулом или вы склонны упускать определенные детали. Если вы решите комментировать, делайте это аккуратно и быстро. Легко чрезмерно аннотировать и тратить драгоценное время, которое можно было бы использовать для понимания вопроса и ответа на него. Аннотации также могут быть полезны, когда вы застряли на вопросе. Вы можете использовать аннотацию, чтобы напомнить себе, к каким вопросам вам нужно вернуться, а также отметить ответы, между которыми вы выбирали. При прохождении теста обязательно разработайте систему аннотирования, чтобы вы могли быть преднамеренными и эффективными.

Часть 5. Советы по изучению раздела логического мышления LSAT

Совет 1. Практика на время

При подготовке к разделу логического мышления LSAT важно приспособиться к временным условиям раздела. Когда вы только начинаете, у вас могут возникнуть проблемы с завершением раздела, но с практикой вы улучшите свою скорость. Одним из ключевых компонентов повышения скорости является практика определения типа вопроса и практики выделения аргументов. Можете ли вы быстро определить вывод аргумента? Если нет, попробуйте подчеркнуть вывод в каждом стимуле в разделе.

Совет 2: Практика без учета времени

Еще один полезный подход — пройти разделы логического мышления LSAT без учета времени. Позвольте себе завершить раздел, не заботясь о времени. Отметьте, какие вопросы занимают у вас больше всего времени. Есть ли какие-то закономерности в вопросах, которые замедляют вас? Вам требуется много времени, чтобы определить тип задаваемого вопроса? Ответив на несвоевременные вопросы, вы сможете лучше познакомиться с разделом, а также выявить некоторые трудности, с которыми вам приходится сталкиваться.

Совет 3. Просмотрите

При подготовке к секции логического мышления LSAT обязательно тщательно проверьте свою работу. После завершения теста, не глядя на правильные ответы, вернитесь и просмотрите тест. Есть ли ответы, которые вы бы изменили? Если это так, запишите их и повторите тест с этими измененными ответами.

Часто вы будете видеть, что ваши баллы выше, когда вы просматриваете материал еще раз. Это позволит диагностировать области теста, в которых вы понимаете, как правильно ответить на вопрос, но не можете этого сделать из-за нехватки времени. Может быть полезно усилить эти области, а также любые области, которые остаются неверными даже после повторного просмотра.

Совет 4. Определенные типы вопросов

При просмотре заполненных разделов логического рассуждения LSAT отметьте, какие типы вопросов беспокоят вас больше всего. Потратьте дополнительное время на рассмотрение этих вопросов. Также может быть полезно пройти тесты и специально попрактиковаться в этом типе вопросов.

Часть 6: Практика LSAT Вопросы логического мышления

Вопрос 1: В некоторых школах есть спортзалы. Во всех спортзалах есть баскетбольные кольца. Некоторые баскетбольные кольца имеют стеклянные щиты.

Исходя из приведенной выше информации, что из следующего должно быть правдой?

А) Во всех школах есть спортивные залы.

B) В некоторых школах есть баскетбольные кольца с пластиковыми щитами.

C) В некоторых школах есть баскетбольные кольца со стеклянными щитами.

D) Во всех школах есть баскетбольные кольца.

E) В некоторых школах есть баскетбольные кольца

Вопрос 2: Энни любит шоколад. Все, кто любит шоколад, любят и арахисовое масло. Поэтому Энни любит арахисовое масло.

Какие из следующих рассуждений аналогичны предыдущему аргументу?

A) Студенты, которые читают книги, любят театр. Пятиклассник любит театр. Поэтому пятиклассник любит читать книги.

B) Студенты, которые читают книги, любят театр. Пятиклассник читает книги. Поэтому пятиклассник любит театр.

C) Студенты, которые читают книги, любят театр. Ученик – пятиклассник. Поэтому пятиклассник любит читать книги.

D) Пятиклассник любит театр. Студенты, которые любят книги, любят театр. Поэтому пятиклассник любит читать книги.

E) Пятиклассник читает книги. Студенты, которые любят театр, читают книги. Поэтому пятиклассник любит театр.

Вопрос 3: Из-за того, что на улице очень холодно, библиотека будет открыта как согревающий центр. Библиотека обычно открывается как согревающий центр, когда очень холодно или когда есть вероятность другого опасного погодного явления. Чрезвычайно низкие температуры считаются опасным погодным явлением.

Что из следующего лучше всего выражает заключение вышеприведенного отрывка?

A) На улице очень холодно.

B) Чрезвычайно низкие температуры считаются опасным погодным явлением.

C) Библиотека обычно открывается как согревающий центр, когда очень холодно.

D) Библиотека будет работать как согревающий центр.

E) Библиотека обычно открывается как согревающий центр, когда есть вероятность другого опасного погодного явления.

Вопрос 4: Исторический спад в экономике был вызван высокими процентными ставками, которые были введены непосредственно перед достижением спада.

Что из следующего больше всего ослабляет вышеприведенное утверждение?

A) Состояние экономики ухудшалось задолго до повышения процентных ставок.

B) Высокие процентные ставки раньше улучшали экономику.

C) Высокие процентные ставки всегда влияют на экономический рост.

D) Процентные ставки влияют и на другие части общества за пределами экономики.

E) Эксперты сходятся во мнении, что низкие процентные ставки — лучший способ улучшить экономику.

Вопрос 5: Маркхэм говорит, что цена на новую разработку завышена. Но Маркхэм также был осужден за растрату. Следовательно, Маркхэм должен быть неверным, потому что ему нельзя доверять.

Приведенное выше рассуждение ошибочно, потому что оно

A) ошибочно принимает необходимый вывод за достаточный вывод.

B) Полагается на двусмысленные формулировки для продвижения своей точки зрения.

C) Нападает на человека вместо аргумента, который он выдвигает.

D) Предполагает причинно-следственную связь на основе взаимосвязанных событий.

E) Предполагается, что одно обстоятельство является репрезентативным для всех обстоятельств.

Ключ к ответу на практические вопросы

1. Вариант ответа E правильный.   Основа вопроса указывает на то, что это вопрос на вывод. Таким образом, правильный выбор ответа должен быть точно выведен из текста. Правильный вариант ответа — E, потому что это единственный ответ, поддерживаемый текстом. Другие варианты ответа либо противоречат тексту, либо не поддерживаются текстом явно. Вариант ответа E правильный, потому что если в некоторых школах есть спортзалы и во всех спортзалах есть баскетбольные площадки, то должна быть какая-то школа с баскетбольной площадкой.

2. Вариант ответа B правильный. Как следует из основы вопроса, это вопрос параллельного рассуждения. Правильный вариант ответа — B, потому что он моделирует транзитивную логику стимула. Стимул предполагает, что Энни любит шоколад, и все, кто любит шоколад, также наслаждаются арахисовым маслом, и, следовательно, Энни нравится арахисовое масло (потому что она любит шоколад и, следовательно, соответствует правилу о любви к шоколаду и наслаждении арахисовым маслом). Это переходный аргумент, который объединяет две связанные посылки, чтобы прийти к заключению. Вариант ответа Б демонстрирует схожую логику, объясняя, что ученики, которые читают книги, любят театр, а пятиклассник читает книги и, следовательно, пятиклассник любит театр. Элементы не представлены в том же порядке, но структура аргументов остается прежней.

3. Вариант ответа D правильный. Это ролевой вопрос, который специально фокусируется на определении вывода аргумента. Выводы – это утверждения, подкрепленные посылками. Правильный вариант ответа — D, потому что он выражает заключение предложения. Это единственная часть аргумента, поддерживаемая предпосылкой. Посылки часто вводятся словом «потому что».

4. Вариант ответа A правильный. Как отмечено в основе вопроса, это ослабляющий вопрос. Аргумент постулирует причинно-следственную связь, основанную на последовательных событиях. Правильный вариант ответа — А, потому что он лишает предпосылку поддержки, предполагая, что экономика уже падала еще до того, как процентные ставки были повышены, так что должна быть другая причина. Такой вариант ответа делает недействительной предполагаемую причинно-следственную связь, предложенную последовательностью событий, на которые ссылается аргумент.

5. Вариант ответа C правильный. Основа вопроса указывает на то, что это вопрос с ошибкой. Правильный вариант ответа — C, потому что он правильно указывает на ошибку, допущенную в аргументе. Хотя каждый из ответов предполагает фактическую ошибку, только ошибка, отмеченная в варианте ответа C, является ошибкой, фактически демонстрируемой аргументом.

Вы можете найти больше примеров вопросов LSAT на логическое мышление здесь.

Часть 7: Часто задаваемые вопросы

Как быстрее пройти секцию логического мышления LSAT? Практика раздела логического мышления LSAT станет отличным инструментом, поскольку вы стремитесь улучшить свою скорость. Во время практики сосредоточьтесь на темпе, следя за тем, чтобы не тратить слишком много времени на один вопрос.

Возможно, будет полезно заранее составить план того, сколько времени вы потратите на каждый вопрос. Вы можете захотеть ответить на определенное количество вопросов за определенное время или потратить определенное количество времени на каждый вопрос. Кроме того, по мере того, как вы будете больше практиковаться, ваше знакомство с основами вопросов будет улучшаться, и вы сможете быстрее понять поставленный вопрос.

Как узнать, какой тип вопроса задается в разделе логического рассуждения LSAT? Готовясь к разделу логического мышления LSAT, ознакомьтесь с основами вопросов, перечисленными в этом руководстве. По мере того, как вы будете практиковаться, вы можете увидеть другие вариации этих вопросов с небольшими изменениями. Если вы столкнулись с совершенно незнакомой вам основой вопроса, постарайтесь понять, о чем спрашивают, а затем подумайте, относится ли это к какой-либо из основ и типов вопросов, которые вы видели раньше. Если вы все еще застряли, вы можете найти некоторое представление о предлагаемых вариантах ответа.

Сколько разделов логического мышления есть в LSAT? Из-за COVID-19 LSAT предлагает сокращенную версию под названием LSAT Flex, которая включает только один оцениваемый раздел логического мышления. При нормальных обстоятельствах LSAT состоит из двух разделов логического мышления с оценкой. Пожалуйста, проверьте веб-сайт LSAT для получения самой последней информации.

Логические задачи | Codecademy

Почему логические проблемы?

Логическая задача — это общий термин для типа головоломки, которая решается путем дедукции. Учитывая ограниченный набор истин и вопрос, мы шагаем по разным сценариям, пока не найдем ответ. Хотя эти проблемы редко связаны с кодированием, они требуют решения проблем и способности сформулировать правдоподобные результаты.

Вы можете столкнуться с логическими проблемами во время технических собеседований на должность программиста, поэтому стоит разработать стратегию того, как подходить к этим вопросам. Это также интересный способ укрепить свои навыки алгоритмического мышления!

Наш вопрос: яблоки, апельсины или и то, и другое?

Начнем со следующей задачи. Перед вами три банки с надписями «Яблоки», «Апельсины» и «Оба». Вы не можете видеть содержимое этих банок, но вам сообщают, что каждая имеет неправильную маркировку . Содержимое банки не соответствует описанию на этикетке.

Сколько раз вам нужно рисовать из банки, чтобы точно пометить каждую банку?

Наше решение: использование информации

Давайте сведем нашу проблему к фактическим утверждениям, которые мы можем использовать, чтобы делать выводы.

1. Банки неправильно маркированы
2. Есть три баночки
3. Одна банка представляет собой комбинацию содержимого двух других банок.

Мы можем использовать эти факты для получения дополнительной информации, которая поможет решить проблему.

Во-первых, мы можем перефразировать «банки неправильно маркированы» как «банка с надписью «Яблоки» не содержит яблок ». Это та же информация, но представленная таким образом, чтобы было легче найти решение.

Мы также должны обратить внимание на пункт 3: в банке «Оба» доступно больше информации, что делает его более «плодотворным» источником запросов. В общем, будьте в курсе любых исключений или отклонений в формулировке вопроса.

Наше решение: заполнение сценариев

Теперь приступим к рассмотрению гипотетических ситуаций. Способность осмыслить проблему и сформулировать свой мыслительный процесс имеет важное значение для успешного прохождения технического собеседования.

Давайте представим, что мы достаем фрукт из банки с надписью «Яблоки». Мы знаем, что в этой банке не только яблоки, но у нас есть две возможности. Мы могли бы нарисовать яблоко или мы могли бы нарисовать апельсин. Если бы мы нарисовали яблоко, мы бы узнали, что это банка «Оба», но что, если бы мы нарисовали апельсин? Тогда эта баночка остается загадкой, то ли «Оба» и мы просто случайно нарисовали апельсин, то ли это чисто «Апельсины». Мы все еще в темноте!

Мыслительный процесс тот же, что и при рисовании из банки «Апельсины», так что теперь представьте рисование из банки «И то, и другое». Опять же, мы можем нарисовать любой тип фруктов, но мы узнали нечто более существенное. Если мы нарисуем апельсин, мы узнаем, что это «Апельсины». Если мы нарисуем яблоко, мы узнаем, что это «Яблоки». Нет никакой двусмысленности, потому что на банке ошибочно написано «Оба».

Наше решение: подведение итогов

Мы определили одну банку, нужно ли делать дополнительные запросы? Мы должны вернуться к нашему Используйте шаг Информация . Допустим, мы идентифицировали «Апельсины».

У нас есть старая банка «Оба», теперь правильно маркированная «Апельсины», и две банки с неправильными этикетками: «Апельсины» и «Яблоки». Можем ли мы сделать дальнейшие выводы? Мы можем!

«Яблоки» и «Апельсины» имеют неправильную маркировку, но у нас есть новая информация. Мы знаем, где находятся настоящие «Апельсины». Это не помогает нам с неправильной маркировкой «Апельсины», это может быть либо «Оба», либо «Яблоки».

Это помогает с «Яблоками». Мы знаем, что «яблоки» — это не «апельсины», потому что мы уже определили «апельсины». Мы также знаем, что «яблоки» не на самом деле «Яблоки», потому что он неправильно маркирован. Это оставляет только один вариант, эта банка «Оба».

При наличии двух правильно помеченных банок третья легко идентифицируется как «Яблоки»

В завершение: «Оба» -> «Апельсины», что приводит нас к «Яблокам» -> «Оба» и «Апельсины» — > «Яблоки»

Практика ведет к совершенству!

Мы закончим эту статью несколькими практическими задачами, которые вы можете попробовать самостоятельно. У каждой проблемы есть ссылка, которая приведет вас к объяснению решения.

Рыцари и лжецы

«Рыцари и лжецы» — популярный тип логической головоломки, в которой участвует остров, населенный двумя типами людей: рыцарями и лжецами.

• Рыцари всегда говорят правду
• Мошенники всегда лгут

На острове вы встречаете трех человек: Теда, Бена и Лил.

Тед говорит: «По крайней мере одно из следующих утверждений верно, что Лил — лжец, а я — рыцарь».