Логические задачи круги эйлера: Круги Эйлера — примеры и методы решения логических задач » Kupuk.net
Развитие детей. Как решать логические задачи с помощью кругов Эйлера? | Обучение
Круги Эйлера — это геометрическая схема. С ее помощью можно изобразить отношения между подмножествами (понятиями), для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения.
Леонард Эйлер был гениальным математиком, который умел применять математические приемы на практике. Он успешно использовал для решения различных задач идею изображения понятий и классов предметов в виде кругов. Впервые Эйлер их применил в письмах к немецкой принцессе. Он писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления». И действительно, с помощью этих диаграмм можно легко и наглядно решить задачи, для решения которых обычным способом понадобилось бы составление системы из нескольких уравнений, например, с тремя неизвестными.
Способ изображения понятий в виде кругов позволяет развивать воображение и логическое мышление не только детям, но и взрослым (конечно, для взрослых подойдут более сложные логические задачи). Начиная с 4−5 лет детям доступно решение простейших задач с кругами Эйлера, сначала с разъяснениями взрослых, а потом и самостоятельно. Овладение методом решения задач с помощью кругов Эйлера формирует у ребенка способность анализировать, сопоставлять, обобщать и группировать свои знания для более широкого применения.
Вот несколько задач для маленьких детей на логическое мышление:
Определить круги, которые подходят к описанию предмета. При этом желательно обратить внимание на те качества, которыми предмет обладает постоянно и которыми временно.
Определение круга, который не подходит к описанию предмета. Например, баранка — она круглая и вкусная, а определение зеленая к ней не подходит. Можно также придумать, какой предмет подойдет для пересечения другой пары кругов. Пример — круглая и зеленая может быть пуговица.
Определить предмет, который подходит под описание всех кругов. Для каждого круга выбирается какое-либо качество (например — сладкое, оранжевое, круглое). Ребенок должен назвать предмет, который одновременно соответствует всем этим описаниям (в данном примере подойдет апельсин), также можно спросить ребенка, какие предметы могут соответствовать двум описаниям из трех, то есть будут находиться на пересечении каждой пары кругов (например, сладкое и оранжевое — карамелька, оранжевое и круглое — мяч, круглое и сладкое — арбуз).
Ребенок должен назвать предмет, который одновременно соответствует всем этим описаниям (в данном примере подойдет апельсин), также можно спросить ребенка, какие предметы могут соответствовать двум описаниям из трех, то есть будут находиться на пересечении каждой пары кругов (например, сладкое и оранжевое — карамелька, оранжевое и круглое — мяч, круглое и сладкое — арбуз).
Для детей постарше можно предлагать варианты задач с вычислениями — от достаточно простых до совсем сложных. Причем самостоятельное придумывание этих задач для детей обеспечит родителям очень хорошую разминку для ума. Приведем два простых примера с диаграммами.
1. Из 27 пятиклассников все изучают иностранные языки — английский и немецкий. 12 изучают немецкий язык, а 19 — английский. Необходимо определить, сколько пятиклассников заняты изучением двух иностранных языков; сколько не изучают немецкий; сколько не изучают английский; сколько изучают только немецкий и только английский?
Необходимо определить, сколько пятиклассников заняты изучением двух иностранных языков; сколько не изучают немецкий; сколько не изучают английский; сколько изучают только немецкий и только английский?
При этом первый вопрос задачи намекает в целом на путь к решению этой задачи, сообщая, что некоторые школьники изучают оба языка, и в этом случае использование схемы также упрощает понимание задачи детьми.
2. В одном доме в 45 квартирах есть домашние животные. При этом в 22 квартирах хозяева держат только кошек, а еще в 7 квартирах есть и кошка, и собака. Нужно узнать, в скольких квартирах находятся собаки, в скольких кошки, а в скольких нет кошки, но есть собака.
Задача, по сути, такая же, однако изменены исходные данные, сектор пересечения кругов известен, но нужно узнать информацию о каждом полном круге. Собаки находятся в числе квартир, оставшемся после вычитания из количества всех квартир с животными количества квартир только с кошками. Круг с общим числом кошек состоит из известных данных секторов «только кошек» и «кошек и собак», поэтому общее число кошек находится объединением сумм этих секторов. Последнее неизвестное находится соответственно. Определенно, значительно проще объяснить решение этой задачи с помощью кругов Эйлера.
Собаки находятся в числе квартир, оставшемся после вычитания из количества всех квартир с животными количества квартир только с кошками. Круг с общим числом кошек состоит из известных данных секторов «только кошек» и «кошек и собак», поэтому общее число кошек находится объединением сумм этих секторов. Последнее неизвестное находится соответственно. Определенно, значительно проще объяснить решение этой задачи с помощью кругов Эйлера.
Задачи, связанные с множествами, могут быть гораздо более сложными, причем чем более запутанными будут условия задачи, тем более очевидна рациональность применения диаграмм для ее решения. Конечно, иногда встречаются задачи, которые проще решить с помощью арифметических действий, поэтому, прежде чем приступить к решению, желательно проанализировать условия задачи.
Круги Эйлера имеют прикладное значение не только в решении школьных задач, ими также пользуются для усвоения и структуризации изучаемых материалов, конспектирования и добавления наглядности в некоторых обучающих курсах.
Так что обязательно научите ребенка рисовать такие кружочки, это, несомненно, обернется пользой в развитии логического мышления, поможет решать задачи интересно и с пониманием происходящего.
Теги: развитие способностей, логическое мышление, задачи, решение, интеллект, обучение, логические задачи
6 класс Математика. Решение задач с помощью кругов Эйлера | Презентация к уроку по математике (6 класс):
Конспект урока
6 класс
Предмет: Математика
Тема: Решение задач с помощью кругов Эйлера
Здравствуйте, ребята! Сегодня на занятии мы с вами познакомимся с новым для вас методом решения логических задач – кругами Эйлера.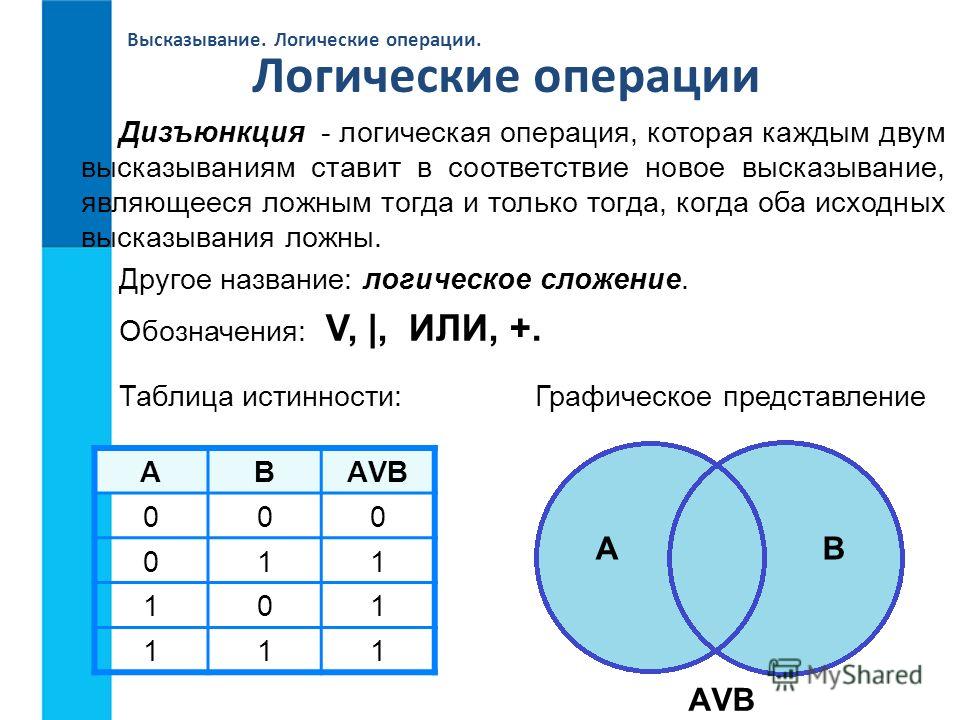 Мы научимся решать некоторые из тех задач, которые входят в группу конкурсных и олимпиадных. Целью нашего урока: является познакомиться с решением простейших логических задач методом кругов.
Мы научимся решать некоторые из тех задач, которые входят в группу конкурсных и олимпиадных. Целью нашего урока: является познакомиться с решением простейших логических задач методом кругов.
Разминка
Устно:
- Кирпич весит 3кги ещё полкирпича. Сколько весит кирпич?
- Два спортсмена на соревновании пробежали по стадиону 8 кругов. Сколько кругов пробежал каждый?
- Назовите два числа, разность которых равна их сумме.
- Сколько будет: два плюс пять умножить на три?
Изучение нового материала
В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук.
Для наглядной геометрической иллюстрации понятий и соотношений между ними используется диаграммы Эйлера-Венна (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) – в виде пересекающихся кругов.
Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) – в виде пересекающихся кругов.
Перед решением задачи ответьте сначала на следующие вопросы:
- О скольких множествах идет речь в данной задаче?
- Какие из перечисленных в задаче данных относятся к разным множествам одновременно?
Задачи разобрать и записать в тетрадь с правильным оформлением: дано, рисунок (круги Эйлера), решение, ответ.
Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро – собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?
Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом – собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части “кошачьего” круга ставим цифру 4 (6 – 2 = 4). В свободной части “собачьего” круга ставим цифру 3 (5 – 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
В оставшейся части “кошачьего” круга ставим цифру 4 (6 – 2 = 4). В свободной части “собачьего” круга ставим цифру 3 (5 – 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
Ответ. 9 подруг.
Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 – в районной. Сколько учеников не являются читателями школьной библиотеки?
Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р – только районной. Тогда ШР – изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:
(не Шк.биб) = Р – ШР.
Всего 30 учеников,
Ш = 20 человек,
Р = 15 человек.
Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) – 30 = (20 + 15) – 30 = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно.
Тогда (не Шк.биб) = Р – ШР= 15 – 5= 10.
Ответ: 10 учеников не являются читателями школьной библиотеки.
Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: “Белоснежка и семь гномов”, “Винни Пух”, “Микки Маус”. Всего в классе 28 человек. “Белоснежку и семь гномов” выбрали 16 учеников, среди которых трое назвали еще “Микки Маус”, шестеро – “Винни Пух”, а один написал все три мультфильма. Мультфильм “Микки Маус” назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм “Винни Пух”?
Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только “Белоснежку” выбрали 16-6-3-1=6 человек. Только “Микки-Маус” выбрали 9-3-2-1=3 человека.
Только “Винни-Пух” выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что “Винни-Пух” выбрали 7+6+1+2=16 человек.
Задачи на оценку:
Задача 1. Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 – в волейбол, 12 – в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 – в футбол и баскетбол, а 5 – в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?
Задача 2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
Задача 3. 12 моих одноклассников любят читать детективы , 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
Домашнее задание:
Задача 1. Хобби. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу – 8 человек, спортивную школу – 12 человек, музыкальную и художественную школу- 3, художественную и спортивную школу – 2, музыкальную и спортивную школу – 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?
Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?
Круги Эйлера в решении задач
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Решение задач с помощью кругов Эйлера
Круги Эйлера
Смысл логических связок становится более понятным, если
проиллюстрировать их с помощью кругов Эйлера
Круги Эйлера – это геометрическая схема, которая помогает
находить и/или делать более наглядными логические связи
 А также помогает
А также помогаетизобразить отношения между каким-либо множеством и его
частью.
9-ые классы
5-ые классы
Школа
9 «А» класс
Круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга
в том, что наглядность упрощает рассуждения и помогает
быстрее и проще получить ответ.
Метод Эйлера является незаменимым при решении
некоторых задач.
Пример.
Конструктор
Игрушка
Заводная
игрушка
Заводной
автомобиль
На рисунке представлено множество – все возможные игрушки.
Некоторые из игрушек являются конструкторами – они
выделены в голубой овал. Это часть большого множества
«игрушки» и одновременно отдельное множество (ведь
конструктором может быть и «Лего», и примитивные
конструкторы из кубиков для малышей). Какая-то часть
большого множества «игрушки» может быть заводными
игрушками. Они не конструкторы, поэтому мы рисуем для них
отдельный овал.
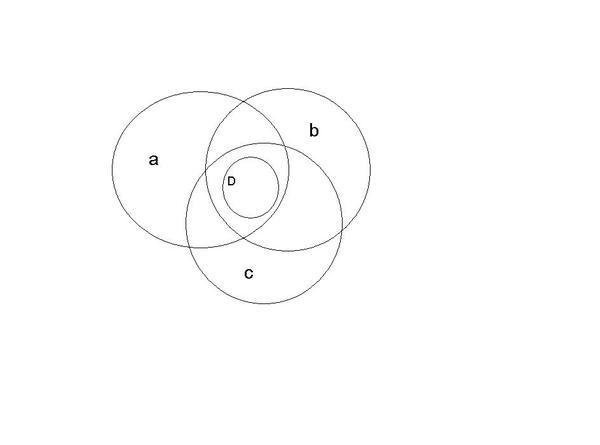 Желтый овал «заводной автомобиль»
Желтый овал «заводной автомобиль»относится одновременно к множеству «игрушки» и является
частью меньшего множества «заводная игрушка». Поэтому и
изображается внутри обоих овалов сразу.
Задача 1.
“Обитаемый остров” и “Стиляги”
Некоторые ребята из нашего класса любят ходить в
кино. Известно, что 15 ребят смотрели фильм
«Обитаемый остров»
11 человек смотрели фильм «Стиляги», из них 6
смотрели и «Обитаемый остров», и «Стиляги».
Сколько человек смотрели
только фильм «Стиляги»?
Решение:
Решение:
Чертим два множества таким образом:
«Обитаемый
остров»
«Стиляги»
6
6 человек, которые смотрели фильмы «Обитаемый остров» и
«Стиляги», помещаем в пересечение множеств.
остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
«Обитаемый
остров»
9
6
5
«Стиляги»
Ответ: 5 человек смотрели только «Стиляги».

Задача 3.
«Экстрим»
Из 100 ребят, отправляющихся в детский оздоровительный
лагерь, кататься на сноуборде умеют 30 ребят, на
скейтборде – 28, на роликах – 42.
На скейтборде и на сноуборде умеют кататься 8 ребят, на
скейтборде и на роликах – 10, на сноуборде и на роликах
– 5, а на всех трех – 3.
Сколько ребят не умеют кататься ни на
сноуборде, ни на скейтборде, ни на роликах?
Решение:
Решение:
Скейтборд
Ролики
30
Всеми тремя спортивными снарядами
владеют три человека, значит, в общей
части кругов вписываем число 3. На
скейтборде и на роликах умеют кататься 10
человек, а 3 из них катаются еще и на
сноуборде. Следовательно, кататься только
на скейтборде и на роликах умеют 10-3=7
ребят.
7
2
13
3 5
Сноуборд
20
Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься
8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти
данные в соответствующие части.
 Определим теперь, сколько человек умеют
Определим теперь, сколько человек умеюткататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30
человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только
на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на
скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию
задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на
одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на
одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.
Задача 4.
В таблице приведены запросы и количество найденных
по ним страниц некоторого сегмента сети интернет.
Запрос
Найдено страниц (в тыс.)
Крейсер | Линкор
Крейсер
7000
4800
Линкор
4500
Какое количество страниц (в тысячах) будет найдено по
запросу Крейсер &
Линкор?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые
слова, не изменялся за время выполнения запросов.
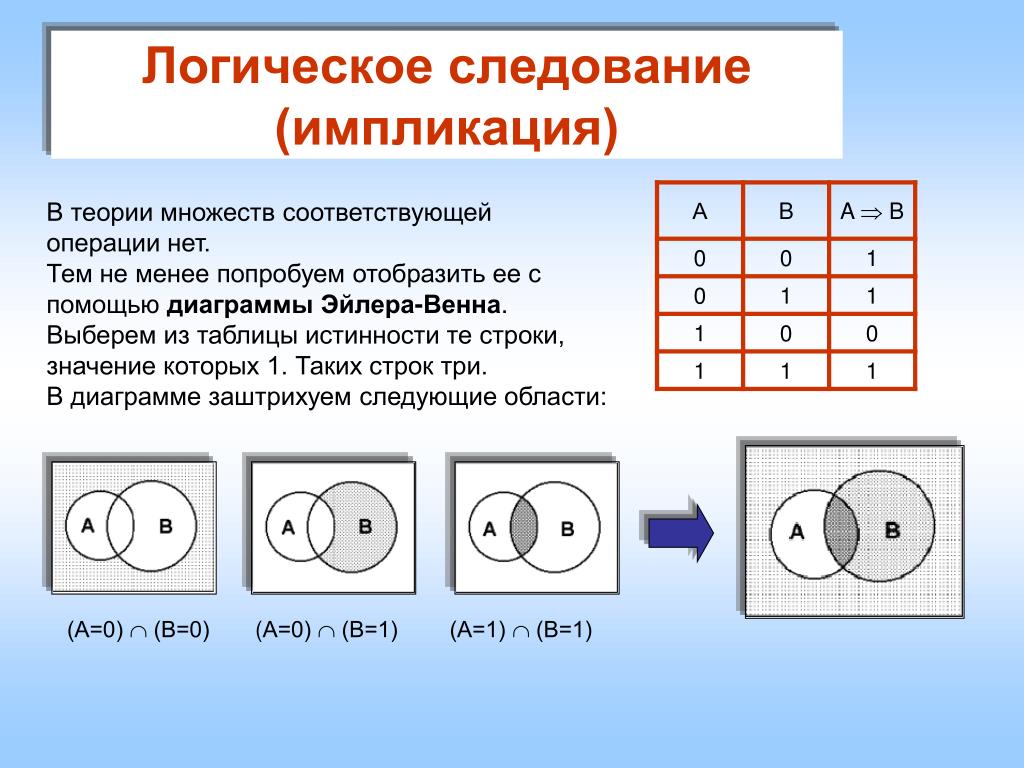
Решение:
Решение:
При помощи кругов Эйлера изобразим условия задачи. При
этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
линкор
крейсер
1
2
3
Опираясь на условия задачи, составим уравнения:
Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2),
подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 – количество страниц, найденных по запросу Крейсер & Линкор
English Русский Правила
Решение задач с помощью кругов Эйлера.
Задачи занятия:
Образовательные:
рассмотреть решение логических задач с помощью кругов Эйлера.
Развивающие:
развитие логического мышления;
развитие поисковой, творческой, познавательной деятельности;
развитие познавательного интереса к предмету;
Воспитывающие:
формирование эстетического наслаждения от выполненной работы;
формирование навыков само- и взаимоконтроля.
Оборудование:
набор задач каждому ученику;
компьютер, проектор;
презентация.
Ход занятия:
Организационный момент.
Всё то что мы изучили раннее используем при решении задач. ( слайд 2—5)
Зачем нужны круги Эйлера? (слайд 6)
Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.
Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение
А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера
Изучение нового материала.
Задача 1. (слайд 7,8)
(слайд 7,8)
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.
Сколько шестиклассников:
1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?
Заметим, что первый вопрос является ключевым для понимания и решения данной задачи. Ведь не сразу сообразишь, как получается 20 + 25 = 45 из 35. В первом вопросе звучит подсказка к пониманию условия: есть ученики, которые посещают обе библиотеки. А если условие задачи изобразить на схеме, то ответ на первый вопрос становится очевидным.
Решение.
1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2. 35 – 20 = 15 (человек) – не являются читателями районной библиотеки. (На схеме левая часть левого круга)
3. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки. (На схеме правая часть правого круга)
4. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки. (На схеме правая часть правого круга)
5. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки. (На схеме левая часть левого круга).
Очевидно, что 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают
Задача №2: (слайд 9,10)
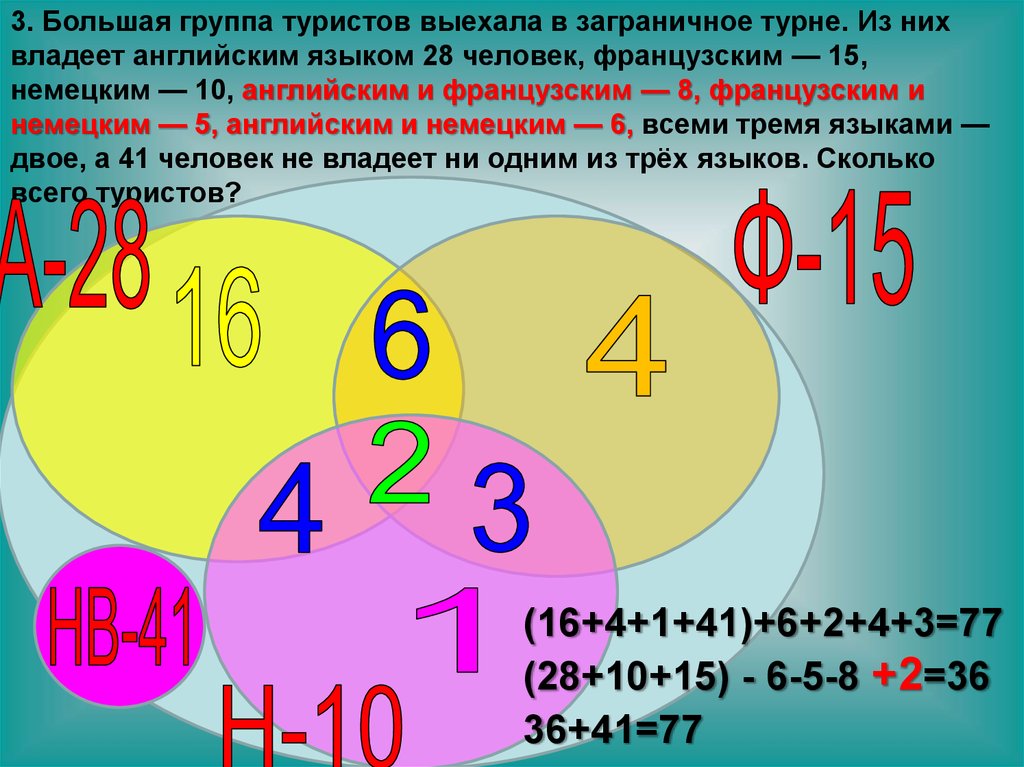
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.
Сколько туристов не владеют ни одним языком?
Решение:
Выразим условие задачи графически. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знают немецкий.
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3.
Английским и французским языками владеют 10 человек, а 3 из них владеют ещё и немецким. Значит, английским и французским владеют 10-3=7 человек.
В общую часть английского и французского кругов вписываем цифру 7.
Английским и немецким языками владеют 8 человек, а 3 из них владеют ещё и французским. Значит, английским и немецким владеют 8-3=5 человек
В общую часть английского и немецкого кругов вписываем число 5
Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека.
В общую часть немецкого и французского кругов вписываем цифру 2.
Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них владеют и другими языками, значит, только немецкий знают 20 человек.
Английский язык знают 28 человек, но 5+3+7=15 человек владеют и другими языками, значит, только английский знают 13 человек.
Французский язык знают 42 человека, но 2+3+7=12 человек владеют и другими языками, значит, только французский знают 30 человек
По условию задачи всего 100 туристов. 20+30+13 +5+2+3+7=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним языком
французский
немецкий
2
30
20
3
5
7
13
английский
Задача 3.( слайд 11,12) ( самостоятельно парами)
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение.
Пусть
Д – драмкружок,
Х – хор,
С – спорт.
Тогда
в круге Д – 27 ребят,
в круге Х – 32 человека,
в круге С – 22 ученика.
Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8 – 3 = 5 спортсменов, не поющих в хоре и 6 – 3 = 3, не посещающих драмкружок.
Легко видеть, что 5 + 3 + 3 = 11 спортсменов посещают хор или драмкружок,
22 – (5 + 3 + 3) = 11 занимаются только спортом;
70 – (11 + 12 + 19 + 7 + 3 + 3 + 5) = 10 – не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.
Ответ: 10 человек и 11 человек
Задача 4°
Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка?
10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка?
83
х
75
Получим уравнение: 75+83-х=90
158-х=90
х=68
Задача 4. (слайд 16,17,18)
В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение.
1 способ. Для решения опять воспользуемся кругами Эйлера. Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются
только метро и троллейбусом – (10 – х) человек,
только автобусом и троллейбусом – (9 – х) человек,
только метро и автобусом – (12 – х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.
Аналогично получаем: х – 6 – только автобусом и х + 4 – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
2 способ. А можно эту задачу решить задачу другим способом: 20 + 15 + 23 – 10 – 12 – 9 + х = 30, 27 + х = 30, х = 3. Здесь сложили количество учеников, которые пользуются хотя бы одним видом транспорта и из полученной суммы вычли количество тех, кто пользуется двумя или тремя видами и, поэтому, вошли в сумму 2-3 раза. Таким образом, получили количество всех учеников в классе.
Ответ. 3 человека ежедневно пользуются всеми тремя видами транспорта.
Отрабатывание навыков решения задач.
Решение примеров
Урок 1: №
Урок 2: №
Д/З: Урок 1: п. 9.3, №
Урок 2: №
Проект Решение логических задач с помощью кругов Эйлера доклад, проект
ИСПОЛЬЗОВАНИЕ КРУГОВ ЭЙЛЕРА ПРИ РЕШЕНИИ ЛОГИЧЕСКИХ ЗАДАЧ
Исследовательский проект по математике
Задача «Детки из детского садика»
В одной из групп детского садика 11 деток любят манную кашу, 13 – гречневую, 7 – перловую; 4 – манную и гречневую, 3 – манную и перловую, 2 – уплетают все три вида .
Сколько деток в этой группе, если в ней нет ни одного ребёнка, кто не любит кашу?
Проблема
Не знаем, как решить логическую задачу.
Актуальность
Решение логических задач способствует повышению интеллектуального развития, помогает вырабатывать умение наблюдать, анализировать и делать выводы. Эти качества нам пригодятся как в учебной деятельности, так и в различных жизненных ситуациях.
Гипотеза
Существует способ решения задачи с громоздким условием и со многими данными. Этот способ должен быть простым и не требовать особых умозаключений.
Цель
Выяснить, как с помощью «кругов Эйлера» можно решать логические задачи.
Задачи
Изучить теоретический материал: биографию Леонарда Эйлера, «круги Эйлера».
Научиться применять круги в решении логических задач.
Провести исследование по классификации задач.
Сформулировать алгоритм решения задач.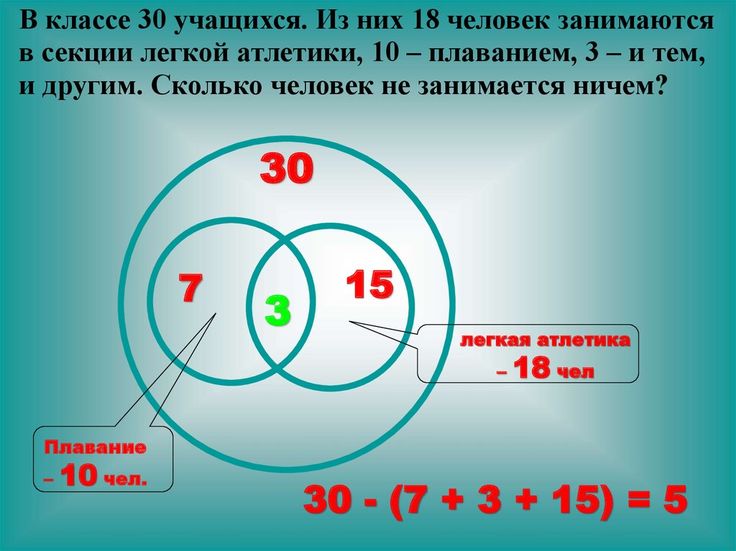
Создать пособие для учащихся «Круги Эйлера в логических задачах».
Объекты исследования
Множество.
Пересечение множеств.
Объединение множеств.
Разность множеств.
Предмет исследования
«Круги Эйлера».
Метод исследования
Сравнительный анализ.
ЛЕОНАРД ЭЙЛЕР
(1707 – 1783)
«Учиться всему надо легко, доступно и наглядно».
Леонард Эйлер
ЛЕОНАРД ЭЙЛЕР
(1707 – 1783)
«…Нет ученого, имя которого упоминалось бы в учебной литературе по математике столь же часто, как имя Эйлера.
В энциклопедии можно найти сведения о шестнадцати формулах, уравнениях, теоремах и т. д., носящих имя Эйлера…».
Из книги
“Замечательные ученые”
под ред. С.П. Капицы.
ЛЕОНАРД ЭЙЛЕР
(1707 – 1783)
Родился 15 апреля 1707 года в семье пастора, жившей в швейцарском городке Базеле.
ЛЕОНАРД ЭЙЛЕР
(1707 – 1783)
20 октября 1720 года 13-летний Леонард Эйлер стал студентом факультета искусств Базельского университета, где преподавались и математика и астрономия.
ЛЕОНАРД ЭЙЛЕР
(1707 – 1783)
В 1726 году был приглашён в Петербургскую Академию наук и в 26 лет получает кафедру высшей математики в должности академика.
«Круги Эйлера»
С 1761 по 1768 годы Эйлером были написаны знаменитые «Письма к немецкой принцессе», где он рассказывает об изображении множеств в виде кругов и отмечает, что при решении логических задач такое изображение «очень подходит для того, чтобы облегчить наши рассуждения».
«Круги Эйлера»
Немного о множествах…
Множество – это совокупность элементов, обладающих некоторым общим свойством.
«Круги Эйлера»
Пересечение множеств
Пересечение множеств – это новое множество, состоящее из элементов, принадлежащих одновременно нескольким множествам.
яблоки
апельсины
«Круги Эйлера»
Объединение множеств
Объединение множеств – это новое множество, состоящее из элементов, принадлежащих хотя бы оному из множеств
«Круги Эйлера»
Разность множеств
Разность множеств – это множество всех элементов из первого множества, не являющихся элементами из второго множества.
Классификация задач
Простые задачи
Сложные задачи
Алгоритм решения логических задач определённого вида
с помощью кругов Эйлера
Записать краткое условие задачи.
Выполнить рисунок.
Записать данные в круги.
Анализировать, рассуждать и записывать результаты в части кругов.
Записать решение и ответ.
Простые задачи
Задача «Друзья»
(объединение множеств)
Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Сколько у меня друзей?
Записываем краткое условие задачи:
Занимаются футболом – 16 друзей.
Занимаются баскетболом – 12 друзей.
Занимаются футболом и баскетболом – 2 друга.
Вопрос: сколько всего друзей?
Простые задачи
Задача «Друзья»
Все мои друзья занимаются каким-нибудь видом спорта. 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Сколько у меня друзей?
Б = 12
Ф = 16
2
Только Ф
14
Только Б
10
Простые задачи
Задача «Друзья»
Все мои друзья занимаются каким-нибудь видом спорта.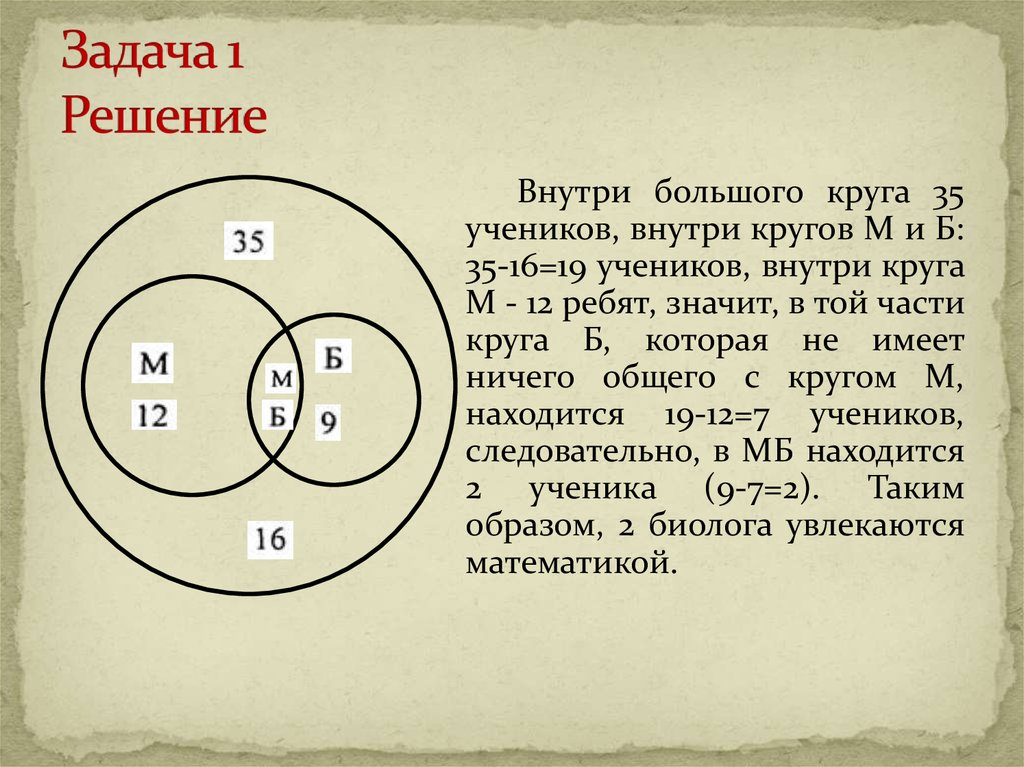 16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Сколько у меня друзей?
16 из них увлекаются футболом, а 12 — баскетболом. И только двое увлекаются и тем и другим видом спорта. Сколько у меня друзей?
Решение.
Занимаются только футболом: 16 – 2 =14 друзей
Занимаются только баскетболом: 12 – 2 = 10 друзей.
Всего друзей 14 + 2 + 10 = 26.
Ответ: 26.
Простые задачи
Задача «Читатели»
(пересечение множеств)
В классе 30 учеников. Все они являются читателями школьной или городской библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 – в городской. Сколько учеников не являются читателями школьной библиотеки?
Записываем краткое условие задачи:
Всего учеников – 30.
Читатели школьной библиотеки – 20 учеников.
Читатели городской библиотеки – 15
Вопрос: сколько учеников не являются читателями школьной библиотеки?
Простые задачи
Задача «Читатели»
(пересечение множеств)
В классе 30 учеников.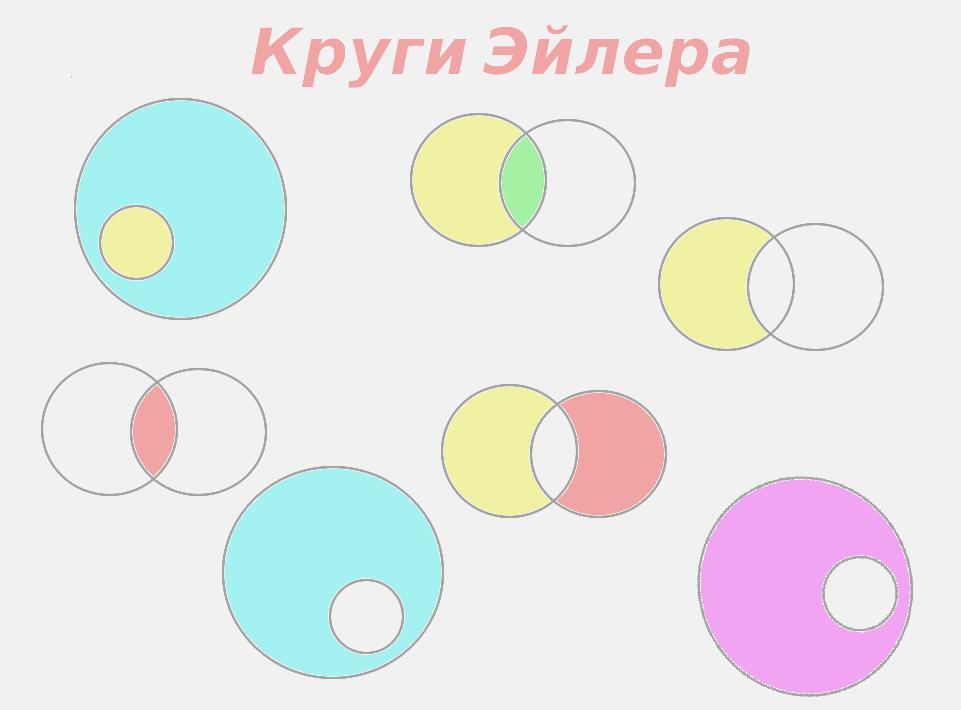 Все они являются читателями школьной или городской библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 – в городской. Сколько учеников не являются читателями школьной библиотеки?
Все они являются читателями школьной или городской библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 – в городской. Сколько учеников не являются читателями школьной библиотеки?
Всего = 30
Ш = 20
Г = 15
Только
город. – ?
5
10
Простые задачи
Задача «Читатели»
(пересечение множеств)
В классе 30 учеников. Все они являются читателями школьной или городской библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 – в городской. Сколько учеников не являются читателями школьной библиотеки?
Решение.
20 + 15 = 35 учеников – читатели школьной или городской библиотек.
35 – 30 = 5 учеников – читатели школьной и городской библиотек.
15 – 5 = 10 учеников – читатели только городской библиотеки, то есть 10 учеников не являются читателями школьной библиотеки.
Ответ. 10.
Простые задачи
Задача «Лакомки»
(разность множеств)
В детском саду 52 ребенка.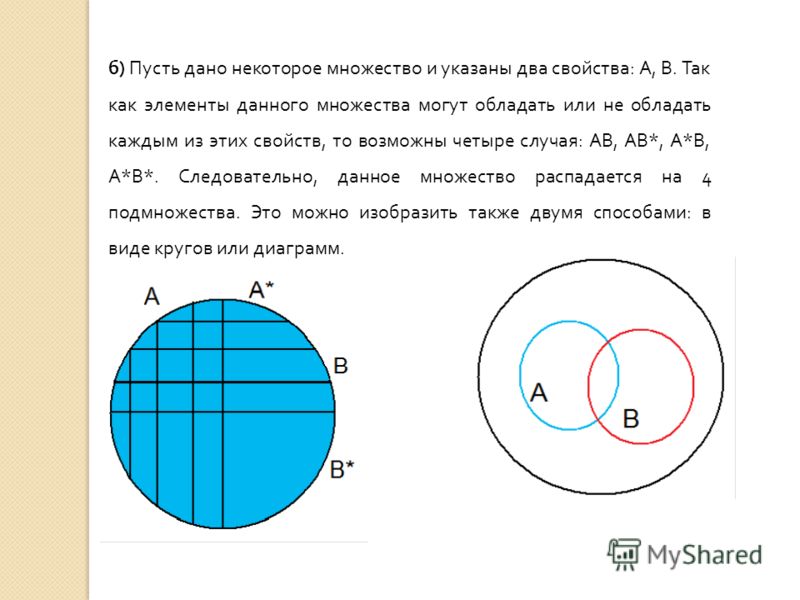 Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит только мороженое?
Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит только мороженое?
Записываем краткое условие задачи:
Всего детей – 52.
Любят пирожное – 26 детей.
Любят пирожное и мороженое – 20 детей.
Вопрос: сколько детей любит только мороженое?
Простые задачи
Задача «Лакомки»
(разность множеств)
В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит только мороженое?
П = 26
М = 46
20
Только П
6
Только М
26
Простые задачи
Задача «Лакомки»
(разность множеств)
В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое.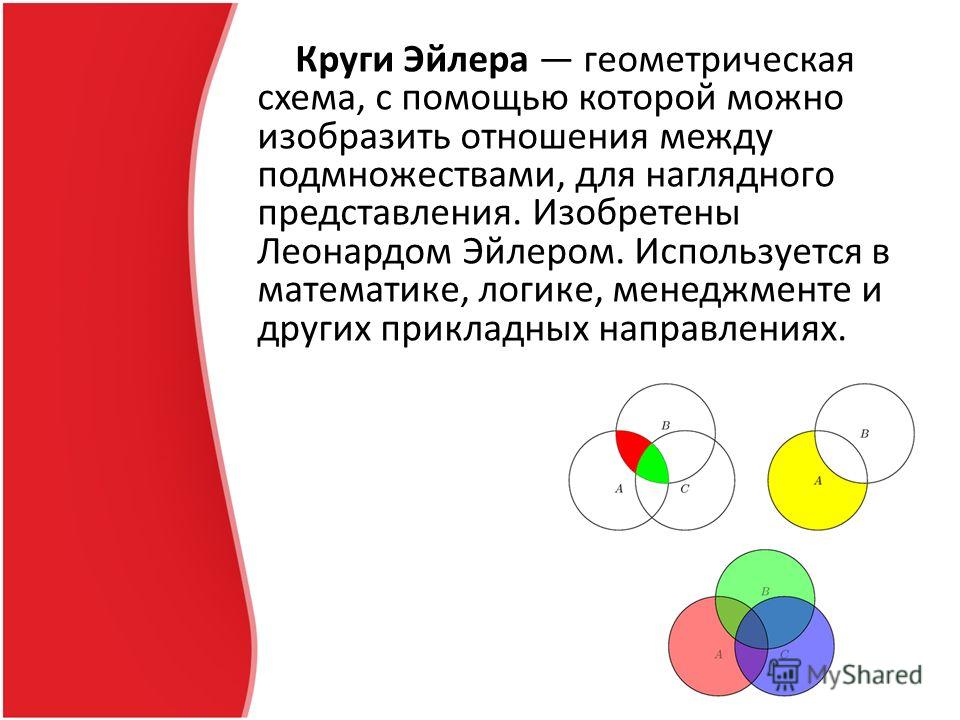 Сколько детей любит только мороженое?
Сколько детей любит только мороженое?
Решение.
Пирожное любят 52:2=26 человек.
Только пирожное любят 26 – 20 = 6 человек.
Любят мороженое 52 – 6 = 46 человек.
Любят только мороженое 46 – 20 = 26 человек.
Ответ: 26.
Сложные задачи
Задача из нашего пробного действия
«Детки из детского садика»
В одной из групп детского садика 11 деток любят манную кашу, 13 – гречневую, 7 – перловую; 4 – манную и гречневую, 3 – манную и перловую, 2 – уплетают все три вида .
Сколько деток в этой группе, если в ней нет ни одного ребёнка, кто не любит кашу?
Записываем краткое условие задачи:
Любят манную кашу – 11 детей.
Любят гречневую кашу – 13 детей.
Любят перловую – 7 детей.
Любят манную и гречневую – 4 детей.
Любят манную и перловую – 3 деток.
Любят все каши – 2.
Вопрос: сколько детей в группе, если нет ни одного, кто не любит кашу?
Сложные задачи
Задача из нашего пробного действия
«Детки из детского садика»
В одной из групп детского садика 11 деток любят манную кашу, 13 – гречневую, 7 – перловую; 4 – манную и гречневую, 3 – манную и перловую, 2 – уплетают все три вида .
Сколько деток в этой группе, если в ней нет ни одного ребёнка, кто не любит кашу?
М = 11
Г = 13
П = 7
6
5
2
2
1
4
Решение.
МПГ = 2.
Только МГ: 4 – 2 = 2.
Только МП: 3 – 2 = 1.
Только М: 11 – 5 = 6.
Только ПГ: 7 – 3 = 4.
Только гречневую : 13 – 2 – 2 – 4 = 5.
Только перловую :
7 – 1 – 2 – 4 = 0.
8. Всего: 6 + 2 + 5 + 1 + 2 + + 4 = 20 деток.
0
Сложные задачи
Задача «Спортивный класс»
В классе 32 ученика. Из них 10 катаются на сноуборде, 15 – играют в хоккей, 20 – увлекаются фигурным катанием. Увлекаются двумя видами спорта – сноубордом и хоккеем – четверо, сноубордом и фигурным катанием – трое, фигурным катанием и хоккеем – пятеро. Трое не увлекаются ни сноубордом, ни хоккеем, ни фигурным катанием. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?
Сложные задачи
Задача «Спортивный класс»
.
Всего 32
х
10-7-х
15-9-х
4
3
5
20-8-х
3
Ф=20
Х=15
С=10
Условие:
Всего учеников в классе – 32.
Сноуборд – 10.
Хоккей – 15.
Фигурное катание – 20.
Только сноуборд и хоккей – 4.
Только сноуборд и фигурное катание – 3.
Только фигурное катание и хоккей – 5.
Сколько ребят увлекаются тремя видами спорта?
Решение.
Не занимаются ничем 3 ученика.
Только сноубордом 10 – (3+х+4) =
=10 –7–х .
3. Только хоккеем 15-(4+х+5) =15-9-х.
4. Только фигурным катанием
20-(3+х+5)= 20-8-х.
(3-х)+ (6-х)+(12-х)+4+3+5+х+3=32; х=2. Ответ:2; 15.
Математический эксперимент
Время решения задач
Заключение
В процессе нашей работы, мы научились грамотно оперировать такими понятиями, как «множество», «объединение множеств», «пересечение множеств», «разность множеств» и использовать их при решении задач.
Наша гипотеза подтвердилась. Применение кругов Эйлера позволяет без затруднений и с маленькими затратами времени решать логические задачи с громоздким условием и со многими данными.
Практическая значимость нашей работы заключается в расширении возможностей решения логических задач.
Теоретическая значимость заключается в разработке способа действий при решении логических задач с помощью кругов Эйлера в общем виде (разработка алгоритма).
Задачи, решаемые с помощью кругов Эйлера предлагаются на олимпиадах по математике и информатике. Теперь мы сможем узнавать такие задачи и быстро их решать.
Наше пособие можно использовать на уроках и факультативах по математике как учащимся, так и учителю.
Над проектом работали
учащиеся 5 «Б» класса
Засульская Анастасия и Пучка Ольга.
Руководитель: Козлова Е. А.
Леонард Эйлер родился 15 апреля 1707 года в семье пастора, жившей в Швейцарском городке Базеле.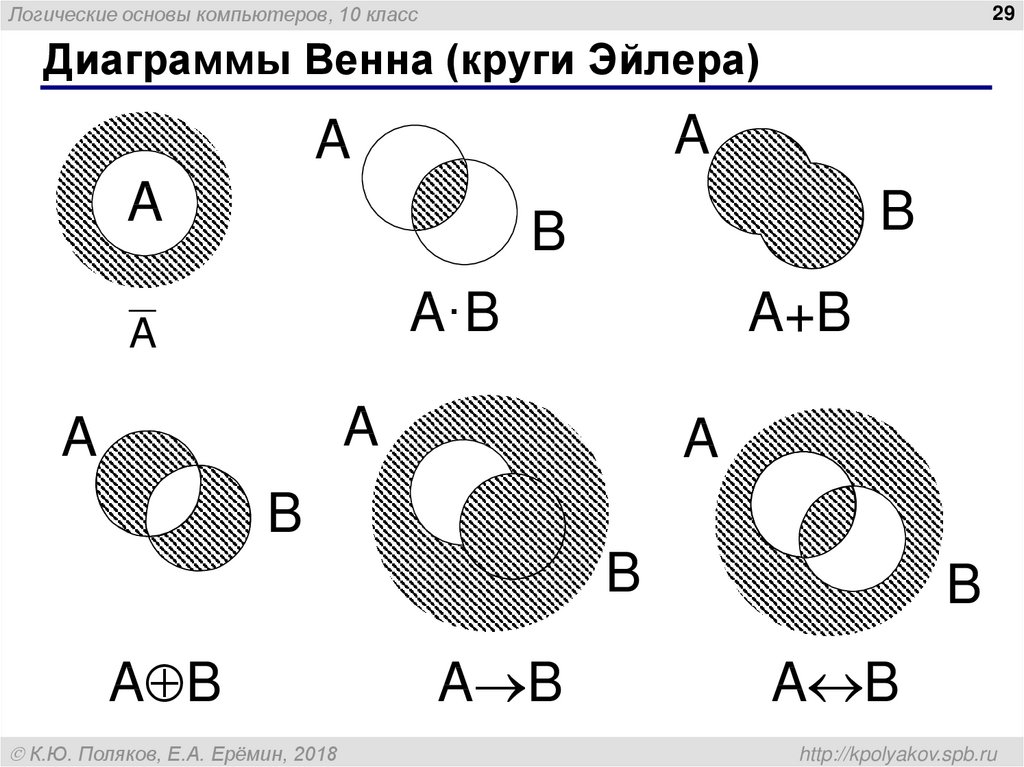 Его отец Пауль Эйлер был хорошо образован и с ранних лет привил сыну увлечение математикой.
Его отец Пауль Эйлер был хорошо образован и с ранних лет привил сыну увлечение математикой.
Уже в 13 лет Леонард Эйлер стал студентом Базельского университета. Его проницательный и острый ум поражали преподавателей.
В 17 лет был удостоен ученой степени магистра.
В 19 лет приглашён в Петербургскую Академию наук, где успешно трудился 15 лет.
Затем он переезжает в Берлин и только в 1766 году по приглашению Екатерины II снова возвращается в Россию.
Вскоре Эйлер полностью ослеп (сказалась его грандиозная работоспособность).
Слепой Эйлер стал диктовать свои открытия мальчику-портному, который записывал их на немецком языке.
С 1761 по 1768 годы Эйлером были написаны знаменитые «Письма к немецкой принцессе», где он рассказывает об изображении множеств в виде кругов и отмечает, что при решении логических задач такое изображение «очень подходит для того, чтобы облегчить наши рассуждения».
Эйлер активно трудился до конца своих дней. Похоронен в 1783 году на Смоленском лютеранском кладбище в Петербурге.
виды, примеры задач и решение, для дошкольников, для школьников
Пожаловаться
Содержание:
Виды кругов Эйлера
Где применяются круги Эйлера
Для дошкольников
Пример
Для школьников
Применение на уроках математики
Применение на уроках русского языка
Видео
Круги Эйлера – это простая диаграмма, с помощью которой можно показать отношения между общим и его частями. Она также помогает увидеть логические цепочки между явлениями и понятиями.
Метод Эйлера применяют для упрощения решения задач во многих областях: от математики до менеджмента. Он помогает находить ответы с помощью наглядных логических цепочек.
Леонард Эйлер (1707-1783) – швейцарский математик, физик, механик и философ. Долгое время (более 30 лет) проработал в Петербургской Академии Наук. Внес большой вклад в становление российской науки.
Расскажем, что собой представляют круги Эйлера и как их применяют в разных сферах.
Виды кругов Эйлера
Круги Эйлера помогают увидеть логические цепочки между явлениями и понятиями и используются во множестве сфер.Эйлер выделил шесть типов соотношений между понятиями, которые выразил в соответствующих схемах.
- Равнозначные. Два одинаковых круга. Например, А.С.Пушкин = автор повести «Капитанская дочка».
- Пересекающиеся. Часть одного круга частично совпадает с частью другого (человек может быть одновременно и футболистом, и поэтом).
- Подчиненные. Один маленький круг внутри большого (корова относится к классу млекопитающих).
- Соподчиненные. Несколько одинаковых по размеру маленьких кругов внутри большого (яблоко, груша, персик – фрукты).
- Противоречащие. Разделенный пополам круг, каждая часть которого не имеет ничего общего с другой. Например, две конкурирующие между собой компании, производящие автомобили.

- Противоположные. Две части круга, между которыми есть свободное пространство. В отличие от предыдущей группы, между ними нет конфликта (холодное и горячее).
В сложной логической задаче иногда может встречаться сразу несколько видов таких схем.
Где применяются круги Эйлера
Круги Эйлера широко используются во многих упражнениях на развитие мышления и логики. Сам ученый применял этот метод для решения сложных математических задач, поскольку схематичное изображение простых фигур позволяет упрощать рассуждения и наглядно демонстрировать возможные пути решения.
Сегодня круги Эйлера широко используют в своей работе:
- математики;
- экономисты;
- маркетологи;
- менеджеры и др.
Основное преимущество данного метода – его универсальность. Он подойдет и для развития мышления у детей, и для решения сложных математических (и не только!) задач.
Для дошкольников
Соподчиненные круги Эйлера отлично подойдут для обучения в детском саду, так как с их помощью можно наглядно объяснить расположение множеств относительно друг другаКруги Эйлера применяют для обучения детей уже в старшей группе детского сада. С их помощью легко наглядно объяснить малышам все варианты расположения множеств относительно друг друга.
Пример
Воспитатель просит детей разложить карточки по двум категориям:
- предметы красного цвета;
- транспорт.
На пересечении этих двух «кругов» окажется красная машинка, так как она подходит под оба требования.
Результат: в игровой форме дошкольники учатся находить изображения, обладающие одним или несколькими отличительными признаками.
Подобные занятия способствуют развитию у детей нестандартного мышления и помогают концентрировать внимание.
С их помощью малыши учатся логически рассуждать, сравнивать и делать выводы.
Для школьников
Задачи с использованием кругов Эйлера встречаются и в школьной программе. Некоторые из них включены в ОГЭ и ЕГЭ.
Применение на уроках математики
Задача. В школьной и городской библиотеке зарегистрировано 35 учеников. Из них 25 ребят постоянно посещают школьную, а 20 – городскую библиотеку. Требуется найти количество тех детей, которые являются читателями:
- обеих библиотек;
- только городской или только школьной библиотеки.
Решение
Круги Эйлера используют во время уроков математики. Фото: https://4brain.ru/1. Определим, сколько школьников посещает обе библиотеки:
(25 + 20) – 35 = 10 (человек).
2. Из них только в городскую библиотеку ходят:
35 – 25 = 10 (человек).
3. А только в школьную библиотеку предпочитают ходить:
35 – 20 = 15 (человек).
Применение на уроках русского языка
Круги Эйлера используют при разных видах разбора предложения, чтобы найти общие и схожие черты в их строении.
Например, при морфологическом разборе ученики сравнивают слова одной и той же части речи (или разных частей), которые имеют общие морфологические признаки. В этом случае графическая схема быстрее помогает детям научиться различать похожие лингвистические обороты.
Круги Эйлера способствуют развитию и тренировке зрительной памяти. С их помощью ученики лучше запоминают, а также усваивают прочитанный и увиденный материал.
Круги Эйлера широко применяются во многих сферах, помогают справляться с нестандартными задачами. Например, определиться с будущей профессией или планами на выходные. Попробуйте и вы применить этот метод к решению своих повседневных вопросов!
Видео
Список литературы
- Круги Эйлера, сайт.
- Использование кругов Эйлера на занятиях по развитию логического мышления у дошкольников, сайт.
- Круги Эйлера: почему один раз увидеть лучше, чем сто раз услышать, сайт.
- Использование Кругов Эйлера в русском языке, сайт
Фото: © Depositphotos
РубрикаОбучение
Новая эра: ученые создали искусственный интеллект, который заменяет учителей при проверке ЕГЭ
Игры на английском языке для детей: 12 идей, как изучать его весело
Ваша семья ценит и любит вас, даже если забывает об этом сказать
Комментарии
Узнавай и участвуй
Клубы на Бэби.ру — это кладезь полезной информации
Как не провести осень на больничном?Покупать ли лекарства на маркетплейсах?Как выбрать продукты для ребенка?Первая аптечка для малышаГалерея пятен вашего малыша
17.
 9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера
9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 41408
- Дэвид Липпман
- Колледж Пирса через OpenTextBookStore
Мы можем визуально интерпретировать дедуктивный аргумент с помощью диаграммы Эйлера, которая, по сути, является тем же самым, что и диаграмма Венна. Это может облегчить определение того, является ли аргумент действительным или недействительным.
Пример 31
Рассмотрим дедуктивный аргумент «Все кошки — млекопитающие, а тигр — кошка, поэтому тигр — млекопитающее». Является ли этот аргумент действительным?
Решение
Помещения:
Все кошки млекопитающие.
Тигр – это кошка.
Вывод:
Тигр – млекопитающее.
Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, мы можем использовать диаграмму Венна. Исходя из первой посылки, мы рисуем множество кошек как подмножество множества млекопитающих. Из второй посылки нам говорят, что тигр содержится в множестве кошек. Из этого мы видим на диаграмме Венна, что тигр также должен быть внутри множества млекопитающих, так что вывод верен.
Анализ аргументов с помощью диаграмм Эйлера
Чтобы проанализировать аргумент с помощью диаграммы Эйлера:
1) Нарисуйте диаграмму Эйлера на основе предпосылок аргумента
2) Аргумент недействителен, если есть способ нарисовать диаграмму, которая делает вывод ложным
3) Аргумент действителен, если нельзя построить диаграмму, чтобы сделать вывод ложным
4) Если посылок недостаточно для определения местоположения элемента или множества, упомянутых в заключении, то аргумент недействителен.
Попробуйте сейчас 9
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Все кошки боятся пылесосов.} \\ \text{ Предпосылка:} & \text{Макс – кошка.} \\ \text{Вывод:} & \text{Макс боится пылесосов.} \end{array}\)
- Ответ
Действителен. Кошки — это подмножество существ, которых пугают пылесосы. Макс входит в набор котов, значит, он тоже должен быть в наборе существ, которых пугают пылесосы.
Пример 32
\(\begin{array} {ll} \text{Предпосылка:} & \text{Все пожарные знают СЛР.} \\ \text{Предпосылка:} & \text{Джилл знает СЛР.} \ \ \text{Вывод:} & \text{Джилл – пожарный.} \end{array}\)
Решение
Из первой посылки мы знаем, что все пожарные находятся внутри набора тех, кто знает СЛР. (Пожарные — это подмножество людей, знающих СЛР.) Из второй посылки мы знаем, что Джилл является членом этой большей группы, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшей подгруппы, т. е. пожарные.
е. пожарные.
Поскольку вывод не обязательно следует из посылок, это неверный аргумент. Возможно, что Джилл — пожарный, но структура аргумента не позволяет сделать вывод, что это определенно так.
Важно отметить, что действительно ли Джилл пожарный или нет, не имеет значения для оценки обоснованности аргумента; нас интересует, достаточно ли посылок для доказательства вывода.
Попробуйте сейчас 10
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Все велосипеды имеют два колеса.} \\ \text{Предпосылка:} & \text{Это У Harley-Davidson два колеса.} \\ \text{Вывод:} & \text{Этот Harley-Davidson — велосипед.} \end{array}\)
- Ответ
Недействительно. Множество велосипедов является подмножеством множества транспортных средств с двумя колесами; Harley-Davidson входит в число двухколесных транспортных средств, но не обязательно в меньший круг.
Попробуйте сейчас 11
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Нет фиолетовых коров.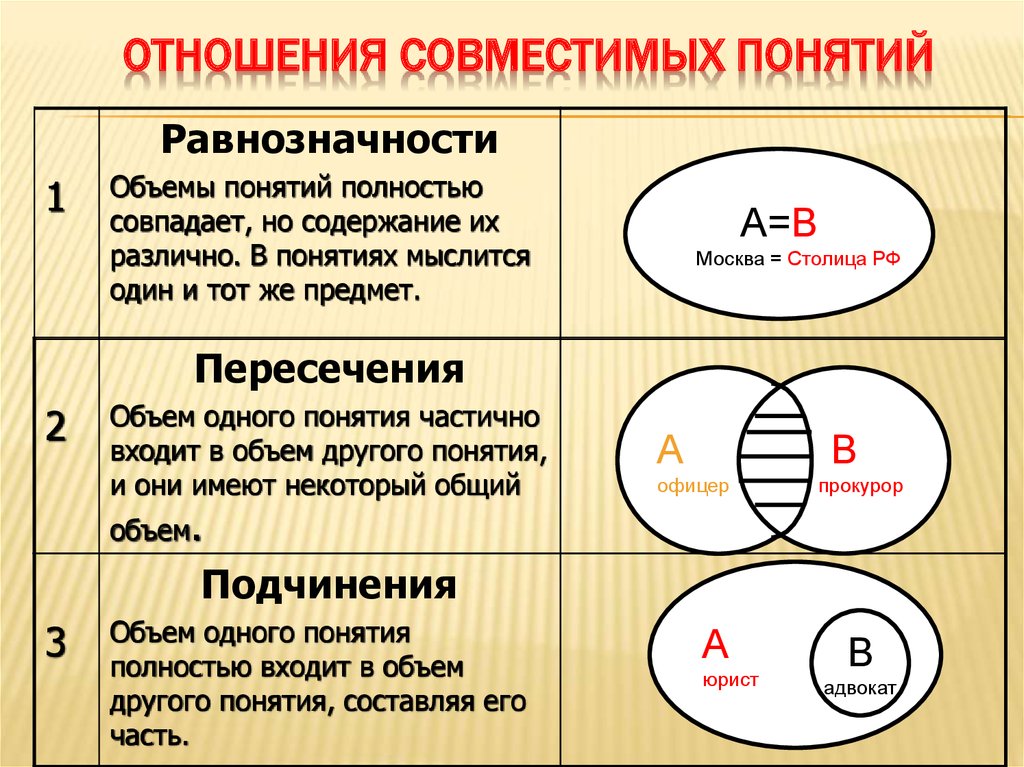 } \\ \text{Предпосылка: } & \text{Фидо не корова.} \\ \text{Вывод:} & \text{Фидо фиолетовый.} \end{массив}\)
} \\ \text{Предпосылка: } & \text{Фидо не корова.} \\ \text{Вывод:} & \text{Фидо фиолетовый.} \end{массив}\)
- Ответ
Недействительно. Поскольку фиолетовых коров нет, мы знаем, что набор коров и набор фиолетовых вещей не пересекаются. Мы знаем, что Фидо не находится в наборе коров, но этого недостаточно, чтобы сделать вывод, что Фидо находится в наборе фиолетовых вещей.
Кроме этих категориальных стилевых посылок вида «все ___», «некоторые ____» и «нет ____», также часто встречаются условные посылки.
Пример 33
\(\begin{array} {ll} \text{Предпосылка:} & \text{Если вы живете в Сиэтле, вы живете в Вашингтоне.} \\ \text{Предпосылка:} & \text{Маркус не живет в Сиэтле.} \\ \text{Вывод:} & \text{Маркус не живет в Вашингтоне.} \end{array}\)
Решение
Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет. Это неверный аргумент.
Это неверный аргумент.
Попробуйте сейчас 12
Определите справедливость этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Если у вас на воротнике помада, то вы изменяешь мне.} \\ \text{Предпосылка:} & \text{Если ты мне изменяешь, я разведусь с тобой.} \\ \text{Предпосылка:} & \text{ У тебя нет помады на губах воротник.} \\ \text{Вывод:} & \text{Я с вами не разведусь.} \end{array}\)
- Ответить
Недействительно. Помада на твоем воротнике — это подмножество сценариев, в которых ты изменяешь, а обман — это подмножество сценариев, в которых я разведусь с тобой. Хотя прекрасно, что у тебя на воротнике нет помады, ты все равно можешь мне изменять, и я разведусь с тобой. На самом деле, даже если ты мне не изменяешь, я могу развестись с тобой по другой причине. Тебе лучше привести себя в форму.
Эта страница называется 17.9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера распространяется под лицензией CC BY-SA 3.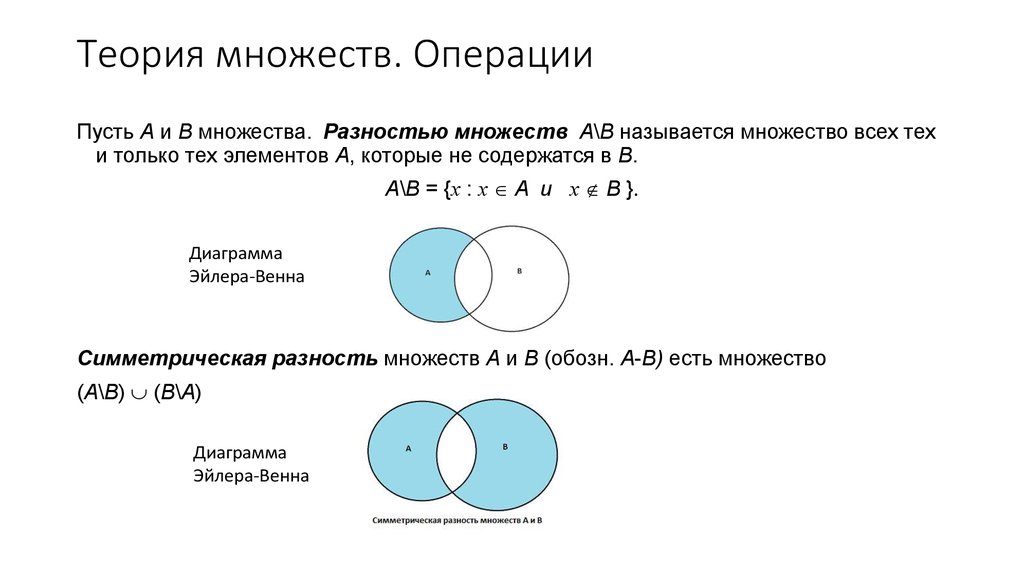 0 и была создана, изменена и/или курирована Дэвидом Липпманом (OpenTextBookStore) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Дэвидом Липпманом (OpenTextBookStore) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Липпман
- Лицензия
- CC BY-SA
- Версия лицензии
- 3,0
- Теги
- источник@http://www.
 opentextbookstore.com/mathinsociety
opentextbookstore.com/mathinsociety
- источник@http://www.
Как строить круги Эйлера в презентации. Презентация – решение задач с использованием кругов Эйлера. Презентация
Эйлеровы круги (круги Эйлера).
Цель урока: Познакомить учащихся с решением простейших логических задач методом круга Цели урока Образовательная: дать учащимся представление о методе круга Эйлера; Развивающие: развитие логического и аналитического мышления; Воспитательная: воспитание умения прислушиваться к мнению других учащихся и отстаивать свою точку зрения.
Окружности Эйлера (круги Эйлера) – принятый в логике метод моделирования, наглядного представления отношений между объемами понятий с помощью окружностей, предложенный известным математиком Л. Эйлером (1707–1783). Обозначение отношений между объемами понятий с помощью окружностей использовал представитель афинской неоплатонической школы Филопон (VI век), написавший комментарии к «Первой аналитике» Аристотеля.
1. Условно принято, что кружок четко изображает объем одного из некоторых понятий. Объем же понятия отражает совокупность объектов определенного класса объектов. Следовательно, каждый объект класса объектов может быть представлен точкой, помещенной внутри круга:
2. Группу предметов, составляющих вид данного класса предметов, изображают в виде меньшего круга, проведенного внутри большего круга. Такая связь существует между объемами понятий «небесное тело» (А) и «комета» (Б). Объем понятия “небесное тело” соответствует большему кругу, а объем понятия “комета” – меньшему кругу. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
3 . Когда ни один объект, отображаемый в объеме понятия А, не может быть одновременно отображен в объеме понятия Б, то в этом случае отношение между объемами понятий изображается посредством двух окружностей, проведенных одна вне другой. Никакая точка, лежащая на поверхности одной окружности, не может лежать на поверхности другой окружности. Такая связь существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». Ни один остроугольный треугольник не отображается в объеме понятия «тупоугольный треугольник», и ни один тупоугольный треугольник не отображается в объеме понятия «остроугольный треугольник».
Такая связь существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». Ни один остроугольный треугольник не отображается в объеме понятия «тупоугольный треугольник», и ни один тупоугольный треугольник не отображается в объеме понятия «остроугольный треугольник».
4 . По-иному выглядит схема соотношения объемов подлежащего и сказуемого в общем утвердительном суждении, не являющемся определением понятия. В таком суждении объем сказуемого больше объема подлежащего, объем подлежащего целиком входит в объем сказуемого. Поэтому отношения между ними изображаются с помощью больших и малых кружков, как показано на рисунке:
5. Отношения между равнозначными понятиями, объемы которых совпадают, отображаются визуально с помощью одного круга, на поверхности которой пишутся две буквы, обозначающие два понятия, имеющие одинаковый объем: Такая связь существует, например, между понятиями «основатель английского материализма» и «автор «Нового Органона». Объемы этих понятий одинаковы, в них отражено одно и то же историческое лицо — английский философ Ф. Бэкон.
Объемы этих понятий одинаковы, в них отражено одно и то же историческое лицо — английский философ Ф. Бэкон.
6. Часто бывает так: одному понятию (родовому) подчинены сразу несколько частных понятий, которые в данном случае называются подчиненными. Связь между такими понятиями визуализируется с помощью одного большого круга и нескольких меньших кругов, которые нарисованы на поверхности большего круга: Такая связь существует между понятиями «скрипка», «флейта», «фортепиано», «фортепиано». “, “барабан”. Эти понятия в равной степени подчинены одному общему родовому понятию «музыкальные инструменты».
7. В тех случаях, когда между понятиями имеется связь противоположностей, связь между объемами таких понятий отображается посредством одного кружка, обозначающего родовое понятие, общее для обоих противоположных понятий, и указывается связь между противоположными понятиями следующим образом: А — родовое понятие, В и С — противоположные понятия. Противоположные понятия исключают друг друга, но входят в один и тот же род, что может быть выражено следующей схемой: Вместе с тем ясно, что между противоположными понятиями возможен третий, средний, так как они не исчерпывают полностью Объем родового понятия. Таково соотношение понятий «легкий» и «тяжелый». Они исключают друг друга. Один и тот же предмет, взятый в одно и то же время и в одном и том же отношении, нельзя назвать одновременно легким и тяжелым. Но между этими понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но и среднего веса.
Таково соотношение понятий «легкий» и «тяжелый». Они исключают друг друга. Один и тот же предмет, взятый в одно и то же время и в одном и том же отношении, нельзя назвать одновременно легким и тяжелым. Но между этими понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но и среднего веса.
8. Когда между понятиями имеется противоречивое отношение, то соотношение между объемами понятий изображается иначе: круг делится на две части следующим образом: А – родовое понятие, Б и не-В (обозначается Б ) — противоречивые понятия. Противоречивые понятия исключают друг друга и входят в один и тот же род, что может быть выражено такой схемой: Ясно, что третье, среднее, между противоречащими понятиями невозможно, так как они полностью исчерпывают объем родового понятия. Такая связь существует, например, между понятиями «белый» и «небелый». Они исключают друг друга. Об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, нельзя сказать, что он одновременно и белый, и небелый.
9. С помощью кругов Эйлера изображаются также отношения между объемами подлежащего и сказуемого в суждениях. Так, в общем утвердительном суждении, выражающем определение понятия, объемы подлежащего и сказуемого, как известно, равны. Наглядно такое отношение между объемами подлежащего и сказуемого изображается посредством одного круга, аналогично изображению отношений между объемами равнозначных понятий. Разница лишь в том, что в этом случае на поверхность круга всегда вписаны две определенные буквы: S (подлежащее) и P (сказуемое), как показано на рисунке:
Задание 1. Домашние животные. У всех моих друзей есть домашние животные. Шестеро из них любят и держат кошек, а пятеро – собак. И только у двоих есть оба. Угадай, сколько у меня девушек? Решение: Нарисуйте два круга, так как у нас есть два типа питомцев. В одном зафиксируем владельцев кошек, в другом – собак. Так как у некоторых друзей есть и те, и другие животные, будем рисовать кружочки так, чтобы у них была общая часть. В этой общей части мы ставим цифру 2, так как у двух есть кошки и собаки. В оставшейся части «кошачьего» круга поставьте цифру 4 (6 – 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь сам рисунок подсказывает, что всего у меня 4+2+3=9подруги.
В этой общей части мы ставим цифру 2, так как у двух есть кошки и собаки. В оставшейся части «кошачьего» круга поставьте цифру 4 (6 – 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь сам рисунок подсказывает, что всего у меня 4+2+3=9подруги.
Ответ. 9 подружек.
Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 детей берут книги из школьной библиотеки, 15 из районной. Сколько учащихся не являются читателями школьной библиотеки? Решение: Пусть кружок W представляет читателей только школьной библиотеки, кружок P – только районной библиотеки. Тогда ШР – это образ читателей и районной, и школьной библиотеки одновременно. Из рисунка следует, что количество учащихся, не являющихся читателями школьной библиотеки, равно: (не W) = P – SHR. Всего 30 студентов, W = 20 человек, R = 15 человек. Тогда значение СР можно найти следующим образом (см. рисунок): СР = (W + P) – 30 = (20 + 15) – 30 = = 5, т. е. 5 учащихся одновременно являются читателями школьной и районной библиотек. время. Тогда (не W) = P – WR = 15 – 5 = 10.
е. 5 учащихся одновременно являются читателями школьной и районной библиотек. время. Тогда (не W) = P – WR = 15 – 5 = 10.
Ответ: 10 учащихся не являются читателями школьной библиотеки.
Задание 3. Любимые мультики. Среди школьников пятого класса был проведен опрос об их любимых мультфильмах. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Винни-Пух», «Микки Маус». В классе 28 человек. «Белоснежку и семь гномов» выбрали 16 учеников, среди которых трое также назвали «Микки Мауса», шестеро — «Винни-Пуха», а один написал все три мультфильма. Мультфильм «Микки Маус» получил 9 названий.ребята, среди которых пятеро выбрали по два мультфильма. Сколько людей выбрали мультфильм «Винни-Пух»? Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются друг с другом. Только «Белоснежку» выбрали 16-6-3-1=6 человек. Только «Микки Мауса» выбрали 9-3-2-1=3 человека. Только «Винни-Пуха» выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые из них выбрали несколько мультфильмов, получаем, что «Винни-Пуха» выбрали 7+6+1+2=16 человек.
Задание 7. Спорт для всех. В классе 38 человек. Из них 16 занимаются баскетболом, 17 – хоккеем, 18 – футболом. Увлекаются двумя видами спорта – баскетболом и хоккеем – по четыре, баскетболом и футболом – по три, футболом и хоккеем – по пять. Трое не увлекаются баскетболом, хоккеем или футболом. Сколько детей увлекаются тремя видами спорта одновременно? Сколько детей занимаются только одним из этих видов спорта? Решение. Воспользуемся кругами Эйлера. Пусть большой круг представляет всех учеников класса, а три меньших круга B, X и F представляют баскетболистов, хоккеистов и футболистов соответственно. Затем на фигуре Z, общей части кругов B, X и F, изображены ребята, увлекающиеся тремя видами спорта. Из рассмотрения окружностей Эйлера видно, что 16 – (4 + z + 3) = 9- z занимаются только одним видом спорта – баскетболом; только хоккей 17 – (4 + z + 5) = 8 – z ; только футбол
18 – (3 + з + 5) = 10 – з. Составляем уравнение, пользуясь тем, что класс разбит на отдельные группы детей; число парней в каждой группе обведено на рисунке рамками: 3 + (9 – z) + (8 – z) + (10 – z) + 4 + 3 + 5 + z = 38,z = 2. Таким образом , два парня увлекаются всеми тремя видами спорта. Складывая числа 9 – z , 8 – z и 10 – z , где z = 2, находим количество ребят, увлекающихся только одним видом спорта: 21 человек. Ответ: Два парня увлекаются всеми тремя видами человеческого спорта. Увлекается только одним видом спорта: 21 человек.
Таким образом , два парня увлекаются всеми тремя видами спорта. Складывая числа 9 – z , 8 – z и 10 – z , где z = 2, находим количество ребят, увлекающихся только одним видом спорта: 21 человек. Ответ: Два парня увлекаются всеми тремя видами человеческого спорта. Увлекается только одним видом спорта: 21 человек.
Задача Спортивный класс. В классе 35 учеников. Из них 24 занимаются футболом, 18 — волейболом, 12 — баскетболом. 10 учеников одновременно занимаются футболом и волейболом, 8 – футболом и баскетболом, 5 – волейболом и баскетболом. Сколько учеников одновременно занимаются футболом, волейболом и баскетболом? Домашнее задание
1 слайд
2 слайд
3 слайд
Один из крупнейших математиков, петербургский академик, за свою долгую жизнь написал более 850 научных работ. В одном из них появились эти круги. Эйлер писал, что «они очень подходят для облегчения наших размышлений». Леонардо Эйлер 1707-1783
4 слайд
Задание №1 В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 в биологическом, 10 детей эти кружки не посещают. Сколько биологов увлекаются математикой?
Из них 20 занимаются в математическом кружке, 11 в биологическом, 10 детей эти кружки не посещают. Сколько биологов увлекаются математикой?
5 слайд
Решение (По рисунку) в левом кружке (М) размещены все математики, а в правом – все биологи, те ребята, которые не ходят в кружки и они размещены в самых больших круг. А теперь посчитаем: Внутри большого круга 35 парней. Внутри 2 меньших 35-10=25 парней. Внутри М 20 парней. Внутри Б 25-20=5 биологов (не посещающих математический кружок) Внутри МБ 11-5=6 биологов, увлекающихся математикой. М Б МБ
6 слайд
Задание №2 В пионерском лагере 70 детей. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 10 спортсменов; И драмкружок, и хор посещают по 3 спортсмена. Сколько парней не поют в хоре, не занимаются спортом и не играют в драмкружке? Сколько детей занимаются только спортом?
7 слайд 92. A B C 5-1-0,5-1=2,5 4-1-0,5-1=1,5 3-1-0,5-1=0,5 1 1 ABC 0,5
10 слайд
Задание № 4 В группе 38 человек. класс. Из них 16 занимаются баскетболом, 17 – хоккеем, 18 – волейболом. Увлекаются двумя видами спорта – баскетболом и хоккеем – по четыре, баскетболом и волейболом – по три, волейболом и хоккеем – по пять. Трое не увлекаются баскетболом, волейболом или хоккеем. Сколько детей увлекаются тремя видами спорта одновременно? Сколько детей занимаются только одним из этих видов спорта?
класс. Из них 16 занимаются баскетболом, 17 – хоккеем, 18 – волейболом. Увлекаются двумя видами спорта – баскетболом и хоккеем – по четыре, баскетболом и волейболом – по три, волейболом и хоккеем – по пять. Трое не увлекаются баскетболом, волейболом или хоккеем. Сколько детей увлекаются тремя видами спорта одновременно? Сколько детей занимаются только одним из этих видов спорта?
слайд 2
Окружности Эйлера
слайд 3
Один из крупнейших математиков, петербургский академик, за свою долгую жизнь написал более 850 научных работ. В одном из них появились эти круги. Эйлер писал, что «они очень подходят для облегчения наших размышлений». Леонардо Эйлер 1707-1783
слайд 4
Задание №1
В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 в биологическом, 10 детей эти кружки не посещают. Сколько биологов увлекаются математикой?
слайд 5
Решение
(По рисунку) в левый кружок (М) помещаются все математики, а в правый – все биологи, те ребята, которые не ходят в кружки и они помещаются в самый большой круг. А теперь посчитаем: Внутри большого круга 35 парней. Внутри 2 меньших 35-10=25 парней. Внутри М 20 ребят. Внутри В 25-20=5 биологов (не посещающих математический кружок). Внутри МБ 11-5=6 биологов, увлекающихся математикой. М Б МБ
А теперь посчитаем: Внутри большого круга 35 парней. Внутри 2 меньших 35-10=25 парней. Внутри М 20 ребят. Внутри В 25-20=5 биологов (не посещающих математический кружок). Внутри МБ 11-5=6 биологов, увлекающихся математикой. М Б МБ
слайд 6
Задание №2
В пионерском лагере 70 детей. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 10 спортсменов; И драмкружок, и хор посещают по 3 спортсмена. Сколько парней не поют в хоре, не занимаются спортом и не играют в драмкружке? Сколько детей занимаются только спортом?
Слайд 7
Решение 92. A B C 5-1-0,5-1=2,5 4-1-0,5-1=1,5 3-1-0,5-1=0,5 1 1 ABC 0,5
Слайд 10
Задание №4
В классе 38 человек. Из них 16 занимаются баскетболом, 17 – хоккеем, 18 – волейболом. Увлекаются двумя видами спорта – баскетболом и хоккеем – по четыре, баскетболом и волейболом – по три, волейболом и хоккеем – по пять. Трое не увлекаются баскетболом, волейболом или хоккеем. Сколько детей увлекаются тремя видами спорта одновременно? Сколько детей занимаются только одним из этих видов спорта?
Сколько детей увлекаются тремя видами спорта одновременно? Сколько детей занимаются только одним из этих видов спорта?
слайд 11
Решение
Большой круг представляет всех учеников класса, а три меньших круга B, X и C представляют соответственно баскетболистов, хоккеистов и волейболистов. Цифра БХВ обозначает ребят, увлекающихся всеми тремя видами спорта – з. В один баскетбол играют 16-(4+z+3)=9-z, в хоккей – 8-z, в волейбол – 10-z. Составляем уравнение: 38 = 3 + (9-z) + (8-z) + (10-z) + 4 + 3 + 5 + z, откуда z = 2 3 B X B 9-Z 8-Z 4 З 3 5 10-З
слайд 12
П.А. Вакульчик «Нестандартные и олимпиадные задачи по математике» В.А. Гусев. А.Н. Орлов. А П. Розенталь “Внеклассная работа по математике” И.Л. Бабинская “Задачи математических олимпиад” А.В. Фарков «Подготовка к олимпиадам по математике» И.С. Петраков “Математические кружки” Литература: http://poznayko.at.ua/photo/16-2-0-0-2 http://www.math-on-line.com.forum-tur http://images .yandex. ru/yandsearch?текст
ru/yandsearch?текст
Посмотреть все слайды
Вычислить значение выражения. Рыба ничего не сказала, только шлепнула хвостом по воде и ушла в морскую пучину. Сказка о мертвой царевне и семи богатырях. Из какого рассказа этот отрывок? Сказка о золотом петушке. Сказка о царе Салтане. К 213-летию со дня рождения А.С. Пушкин. Следуйте шагам, найдите результаты в таблице и угадайте зашифрованные слова. Найдите значение выражения. устная работа. Ответы уравнений в конкурсе “Рыбалка”.
“Координаты точек на координатной плоскости” – Карл Гаусс. Тренажеры. Выберите нужную ячейку таблицы. Абсцисса точки. Учебники. Координатная плоскость. Координаты точки. Николай Иванович Лобачевский. Объяснение нового материала. Цвет. Леонард Эйлер. Исаак Ньютон. Четверть. Готфрид Лейбниц. Координат. Курсор. координатный квартал. Точка лежит на оси x. Великие математики. Тест. Технические консультации. Отметьте точку. Рене Декарт. Блез Паскаль.
«Приемы устного умножения» – Умножение и деление на 25 и 75. Значение приемов устного умножения. Умножение чисел, оканчивающихся на 1. Устные способы умножения двузначных натуральных чисел. Умножение чисел, близких к 100. Умножение двузначных чисел, в которых десятки цифр совпадают. Умножение на 11. Умножение двузначных чисел, в которых сумма десятков цифр равна. Умножение чисел, оканчивающихся на 5. Умножение на числа, оканчивающиеся на 5.
Значение приемов устного умножения. Умножение чисел, оканчивающихся на 1. Устные способы умножения двузначных натуральных чисел. Умножение чисел, близких к 100. Умножение двузначных чисел, в которых десятки цифр совпадают. Умножение на 11. Умножение двузначных чисел, в которых сумма десятков цифр равна. Умножение чисел, оканчивающихся на 5. Умножение на числа, оканчивающиеся на 5.
“Дни недели” – Воскресенье – день Солнца (старое название – неделя). Понедельник. Воскресенье – день солнца. Славяне называли неделю неделей. Суббота – день Сатурна. Гипотеза. Среда. Названия дней недели на русском и английском языках. Тайна. Библия говорит, что семидневная неделя была создана Богом. Как появились 7 дней недели? Среда — день Меркурия (среда — середина). Неделя красная для дней. Конек-Горбунок. Четверг — день Юпитера (четвертый).
«Путешествие в мир математики» – остров Умейка. Решите с помощью координатной линии. Давайте измерим температуру снаружи корабля. Прибавить число B к числу A означает заменить число A на число B. Сумма двух противоположных чисел равна нулю. Остров повторов. Найдем сумму чисел. Результаты двух последовательных изменений находятся с помощью сложения. Найдем сумму чисел. Показания приборов на корабле. Любое число от сложения положительного числа увеличивается.
Сумма двух противоположных чисел равна нулю. Остров повторов. Найдем сумму чисел. Результаты двух последовательных изменений находятся с помощью сложения. Найдем сумму чисел. Показания приборов на корабле. Любое число от сложения положительного числа увеличивается.
“Десятичная система счисления и двоичная” – Преобразование целых десятичных чисел в двоичную систему счисления. Преобразование целых чисел из двоичного в десятичное. Ей было 1100 лет, она пошла в 101 класс. Калькулятор. Какую цель мы поставили перед собой в начале первого занятия. Преобразование чисел из двоичных в десятичные. «Рождение» цветка. Необычное стихотворение. Цвет в ячейках. Разделить целое десятичное число на 2.
«Письма по различным физическим и философским вопросам, написанные некой немецкой принцессе…», где впервые появились «круги Эйлера» «Письма по различным физическим и философским вопросам, написанные некой немецкой принцессе…» , где “круги Эйлера”
Решение задач с использованием окружностей Эйлера. Кто-то из жителей нашего города говорит только на русском, кто-то только на башкирском, а кто-то на обоих языках. На башкирском говорят 85%, на русском 75%. Какой процент жителей говорит на обоих языках?
Кто-то из жителей нашего города говорит только на русском, кто-то только на башкирском, а кто-то на обоих языках. На башкирском говорят 85%, на русском 75%. Какой процент жителей говорит на обоих языках?
Спортивное задание В футбольной команде «Баймак» 30 игроков: 18 нападающих. 11 полузащитников, 17 защитников, 3 вратаря могут быть нападающими и защитниками, 10 защитников и полузащитников, 6 нападающих и 1 защитник и нападающий, защитник и полузащитник. Вратари незаменимы. Сколько вратарей в команде Баймак?
Решение = 28 (игроков) на этой диаграмме. Но в команде всего 30 игроков. Значит будет 30-28=2 вратаря. Ответ: 2 вратаря.
“Озеро Графское” Из 100 отдыхающих на турбазе “Графское” 30 детей – отличники, 28 – участники олимпиад, 42 – спортсмены. 8 учащихся являются и участниками олимпиад, и спортсменами, 10 – участниками олимпиад и отличниками, 5 – спортсменами и отличниками, 3 – и отличниками, и участниками олимпиад, и спортсменами.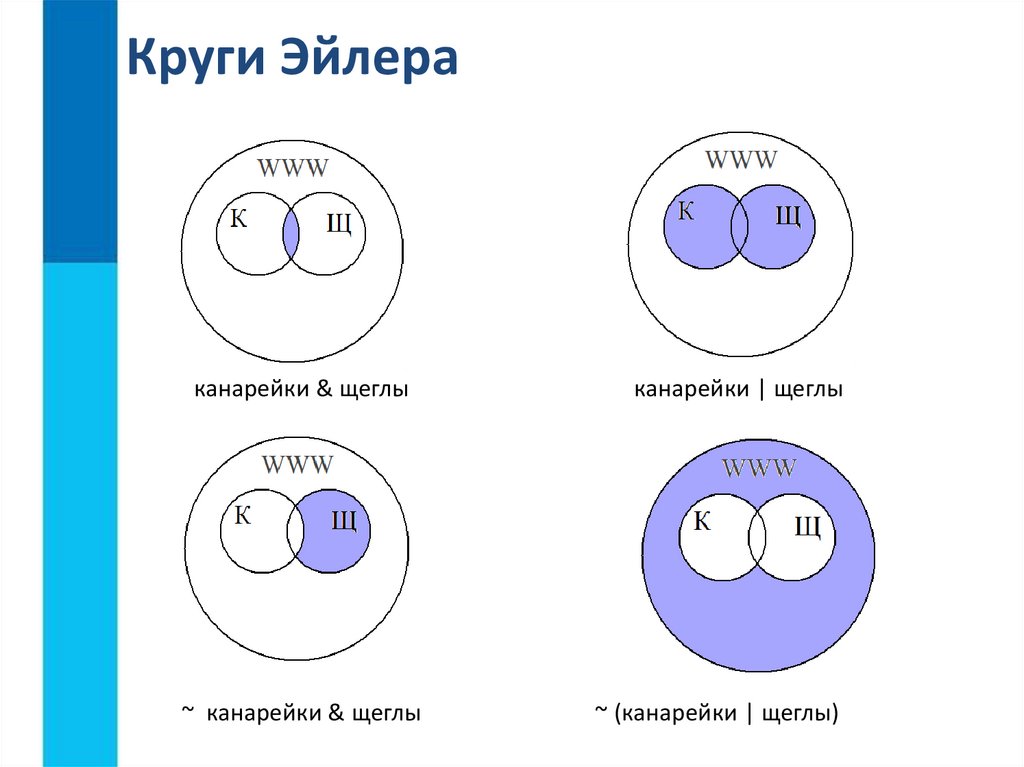 Сколько отдыхающих не принадлежит ни к одной из групп?
Сколько отдыхающих не принадлежит ни к одной из групп?
Выводы Использование окружностей Эйлера (диаграмм Эйлера-Венна) позволяет легко решать задачи, которые можно решить обычным способом только при составлении системы из трех уравнений с тремя неизвестными. Использование окружностей Эйлера (диаграмм Эйлера-Венна) позволяет легко решать задачи, которые можно решить обычным способом только при составлении системы из трех уравнений с тремя неизвестными.
Что такое диаграмма Венна
Что вам нужно для диаграммы Венна?
Я новичок в диаграммах Венна и хочу узнать больше.Я хочу создать свою собственную диаграмму Венна в Lucidchart.
Я хочу сделать диаграмму Венна из шаблона Lucidchart.
Создавать диаграммы Венна очень просто и легко с помощью нашего конструктора диаграмм Венна. Изучите основы диаграмм Венна, а также их долгую историю, универсальные цели и способы использования, примеры и символы, а также шаги по их рисованию.
7 минут чтения
Хотите построить собственную диаграмму Венна? Попробуйте Люсидчарт. Это быстро, просто и совершенно бесплатно.
Составьте диаграмму Венна
Что такое диаграмма Венна?
На диаграмме Венна используются перекрывающиеся круги или другие формы для иллюстрации логических отношений между двумя или более наборами элементов. Часто они служат для графической организации вещей, подчеркивая, чем они похожи и чем отличаются друг от друга.
Диаграммы Венна, также называемые диаграммами множества или логическими диаграммами, широко используются в математике, статистике, логике, обучении, лингвистике, информатике и бизнесе. Многие люди впервые сталкиваются с ними в школе, когда изучают математику или логику, поскольку диаграммы Венна стали частью учебных программ «новой математики» в XIX веке. 60-е годы. Это могут быть простые диаграммы, включающие два или три набора из нескольких элементов, или они могут стать довольно сложными, включая трехмерные презентации, по мере того, как они будут увеличиваться до шести или семи наборов и выше. Они используются для продумывания и изображения того, как элементы относятся к каждому из них в рамках определенной «вселенной» или сегмента. Диаграммы Венна позволяют пользователям визуализировать данные четкими и эффективными способами и поэтому обычно используются в презентациях и отчетах. Они тесно связаны с диаграммами Эйлера, которые отличаются отсутствием наборов, если в них нет элементов. Диаграммы Венна показывают отношения, даже если множество пусто.
60-е годы. Это могут быть простые диаграммы, включающие два или три набора из нескольких элементов, или они могут стать довольно сложными, включая трехмерные презентации, по мере того, как они будут увеличиваться до шести или семи наборов и выше. Они используются для продумывания и изображения того, как элементы относятся к каждому из них в рамках определенной «вселенной» или сегмента. Диаграммы Венна позволяют пользователям визуализировать данные четкими и эффективными способами и поэтому обычно используются в презентациях и отчетах. Они тесно связаны с диаграммами Эйлера, которые отличаются отсутствием наборов, если в них нет элементов. Диаграммы Венна показывают отношения, даже если множество пусто.
История диаграмм Венна
Диаграммы Венна названы в честь британского логика Джона Венна. Он написал о них в статье 1880 года, озаглавленной «О диаграммном и механическом представлении утверждений и рассуждений» в «Философском журнале» и «Журнале науки».
Но корни этого типа диаграмм уходят гораздо дальше, по крайней мере, на 600 лет. В 1200-х годах философ и логик Рамон Луллий (иногда пишется Луллий) с Майорки использовал аналогичный тип диаграммы, как писал автор М. Э. Барон в 1919 году.69 статей, прослеживающих их историю. Она также приписала немецкому математику и философу Готфриду Вильгельму фон Лейбницу создание подобных диаграмм в конце 1600-х годов.
В 1700-х годах швейцарский математик Леонард Эйлер (произносится как Ой-лер) изобрел то, что стало известно как диаграмма Эйлера, самый непосредственный предшественник диаграммы Венна. Фактически, Джон Венн называл свои собственные диаграммы Эйлеровыми кругами, а не диаграммами Венна. Термин «Диаграммы Венна» впервые был опубликован американским философом Кларенсом Ирвингом (К.И.) Льюисом в его 1918 книга, Обзор символической логики.
Диаграммы Венна продолжали развиваться в течение последних 60 лет благодаря достижениям экспертов Дэвида В. Хендерсона, Питера Гамбургера, Джерролда Григгса, Чарльза Э.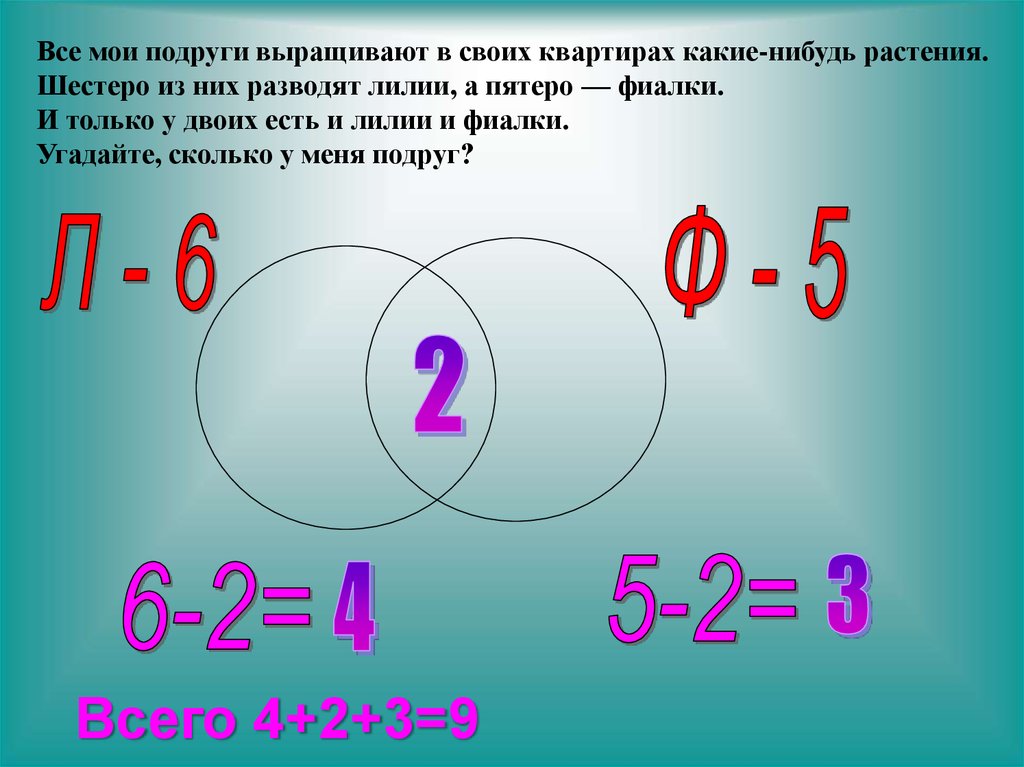 «Чипа» Киллиана и Карлы Д. Сэвидж. Их работа касалась симметричных диаграмм Венна и их связи с простыми числами или числами, неделимыми другими числами, кроме 1 и самого числа. Одна такая симметричная диаграмма, основанная на простом числе 7, широко известна в математических кругах как Виктория.
«Чипа» Киллиана и Карлы Д. Сэвидж. Их работа касалась симметричных диаграмм Венна и их связи с простыми числами или числами, неделимыми другими числами, кроме 1 и самого числа. Одна такая симметричная диаграмма, основанная на простом числе 7, широко известна в математических кругах как Виктория.
Другими известными именами в разработке диаграмм Венна являются A.W.F. Эдвардс, Бранко Грюнбаум и Генри Джон Стивен Смит. Среди прочего, они изменили формы диаграмм, чтобы упростить отображение диаграмм Венна при увеличении количества наборов.
Пример Диаграмма Венна
Допустим, наша вселенная — это домашние животные, и мы хотим сравнить, с каким типом домашних животных согласится наша семья.
Набор А содержит мои предпочтения: собака, птица, хомяк.
Набор B содержит предпочтения члена семьи B: собака, кошка, рыба.
Набор C содержит предпочтения члена семьи C: собака, кошка, черепаха, змея.
Перекрытие или пересечение трех наборов содержит только собаку. Похоже, у нас появится собака.
Конечно, диаграммы Венна могут быть гораздо более сложными, поскольку они широко используются в различных областях.
Диаграмма Венна назначение и преимущества
- Для визуальной организации информации для просмотра взаимосвязей между наборами элементов, таких как общие черты и различия. Студенты и профессионалы могут использовать их, чтобы продумать логику концепции и изобразить отношения для визуальной коммуникации. Эта цель может варьироваться от элементарной до очень продвинутой.
- Чтобы сравнить два или более варианта и четко увидеть, что у них общего, а что может их различать. Это может быть сделано для выбора важного продукта или услуги для покупки.
- Для решения сложных математических задач. Если вы математик, конечно.

- Чтобы сравнить наборы данных, найдите корреляции и предскажите вероятность определенных событий.
- Разбирать логику , стоящую за утверждениями или уравнениями, например, булеву логику поиска слов, включающую операторы «или» и «и», и то, как они сгруппированы.
С Lucidchart можно легко и быстро создавать диаграммы. Начните бесплатную пробную версию сегодня, чтобы начать создавать и сотрудничать.
Создание диаграммы Венна
Варианты использования диаграммы Венна
- Математика: Диаграммы Венна обычно используются в школе для обучения основным математическим понятиям, таким как множества, объединения и пересечения. Они также используются в высшей математике для решения сложных задач, и о них много пишут в научных журналах.
 Теория множеств — это целая отрасль математики.
Теория множеств — это целая отрасль математики. - Статистика и вероятность: Специалисты по статистике используют диаграммы Венна для прогнозирования вероятности определенных событий. Это связано с областью предиктивной аналитики. Различные наборы данных можно сравнивать, чтобы найти степени общности и различий.
- Логика: Диаграммы Венна используются для определения достоверности конкретных аргументов и выводов. В дедуктивных рассуждениях, если посылки верны и форма аргумента верна, то вывод должен быть верным. Например, если все собаки — животные, а наш питомец Моджо — собака, то Моджо должен быть животным. Если мы назначаем переменные, то, скажем, собаки — это C, животные — это A, а Mojo — это B. В форме аргумента мы говорим: все C — это A. B — это C. Следовательно, B — это A. Связанная диаграмма в логике называется Таблица истинности, которая помещает переменные в столбцы, чтобы определить, что является логически правильным. Другая родственная диаграмма называется диаграммой Рэндольфа или R-диаграммой в честь математика Джона Ф.
 Рэндольфа. Он использует линии для определения наборов.
Рэндольфа. Он использует линии для определения наборов. - Лингвистика: Диаграммы Венна использовались для изучения сходств и различий между языками.
- Обучение пониманию прочитанного: Учителя могут использовать диаграммы Венна, чтобы улучшить понимание прочитанного своими учениками. Учащиеся могут рисовать диаграммы, чтобы сравнивать и сопоставлять идеи, о которых они читают.
- Информатика: Программисты могут использовать диаграммы Венна для визуализации компьютерных языков и иерархий.
- Бизнес: Диаграммы Венна можно использовать для сравнения и сопоставления продуктов, услуг, процессов и почти всего, что может быть изображено в наборах. И они являются эффективным инструментом коммуникации, чтобы проиллюстрировать это сравнение.
Глоссарий диаграмм Венна
| Набор | Коллекция вещей.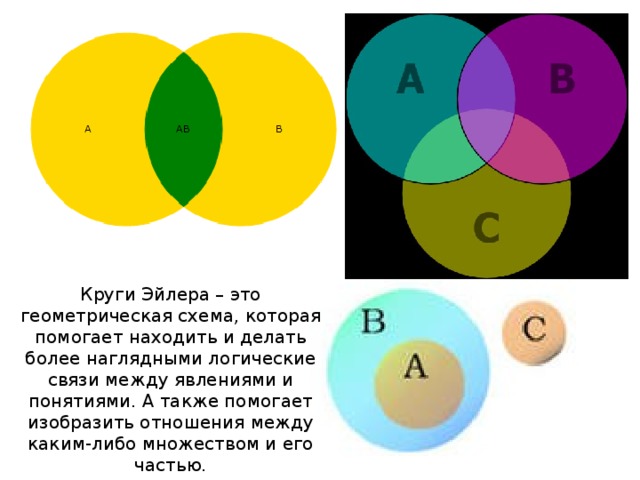 Учитывая универсальность диаграмм Венна, на самом деле все может быть что угодно. Вещи могут называться элементами, объектами, членами или подобными терминами. Учитывая универсальность диаграмм Венна, на самом деле все может быть что угодно. Вещи могут называться элементами, объектами, членами или подобными терминами. | |
| Союз | Все элементы в наборах. | |
| Пересечение | Перекрывающиеся элементы в наборах. Иногда называется подмножеством. | |
| Симметричная разность двух множеств | Все, кроме пересечения. | |
| Полный комплект | Все, чего нет в наборе. | |
| Соответствующее дополнение | В одном наборе, в другом нет. | |
| Диаграмма Венна в масштабе | Также называется пропорциональной площади. Круги (или другие формы) имеют размер в соответствии с их пропорциональным представлением целого. | |
| Треугольник Рело | Форма, образованная пересечением трех кругов или фигур, например, на диаграмме Венна.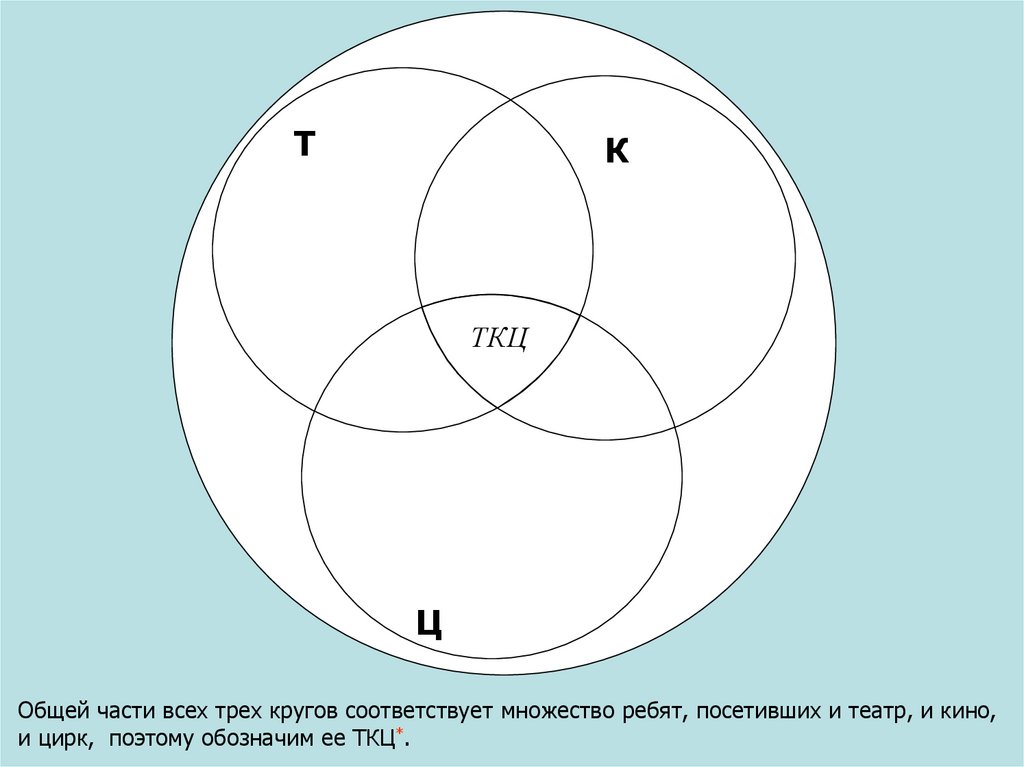 | |
| Набор обозначений | Понятия, проиллюстрированные на диаграммах Венна, выражены с помощью математических обозначений, таких как представления множеств и подмножеств (в скобках), объединений (с помощью U-образного символа) и пересечений (с перевернутым U-символом). | |
| Теория множеств | Давний раздел математики, занимающийся множествами. |
На заметку полегче: диаграммы Венна появились на маленьком экране
Немногие диаграммы перешли в популярную культуру, но уважаемая диаграмма Венна сделала это.
- Драма: В телешоу CBS NUMB3RS, выходившем с 2005 по 2010 год, математический гений Чарльз Эппс использует диаграмму Венна, чтобы определить, какие подозреваемые соответствуют описанию и имеют историю насилия.
- Комедия: В программе NBC «Поздняя ночь с Сетом Мейерсом» у комика есть повторяющаяся процедура под названием «Диаграммы Венна», в которой он сравнивает два, казалось бы, не связанных между собой предмета, чтобы найти их забавную общность (он надеется).
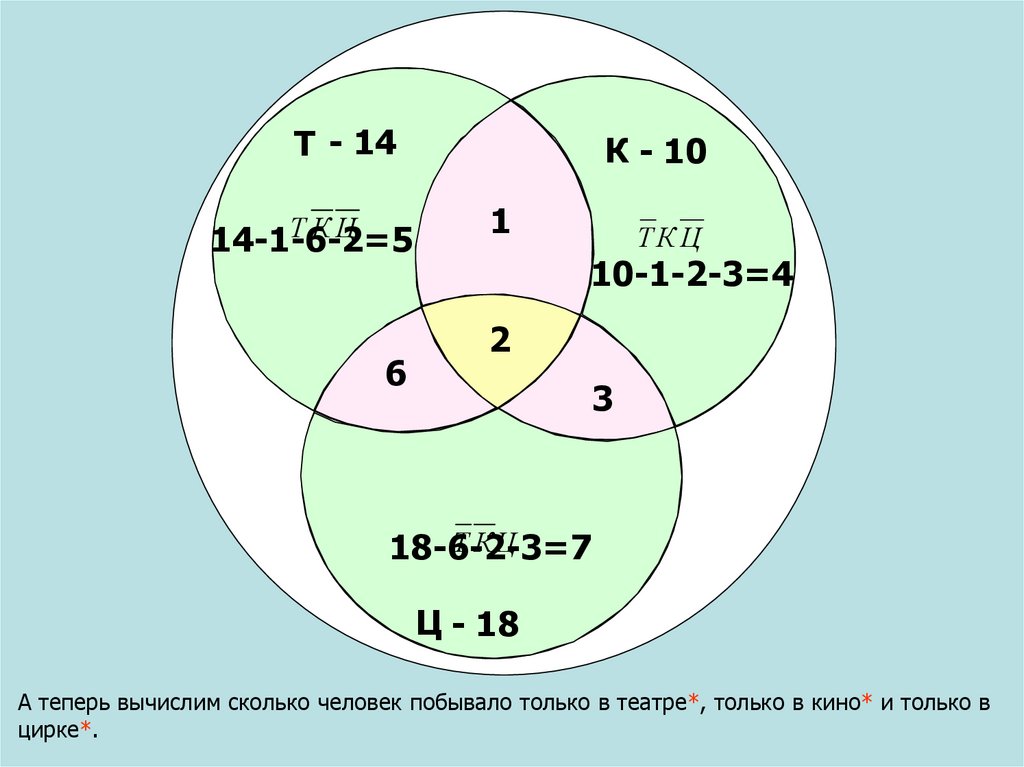
Шаги по рисованию и использованию базовой диаграммы Венна
- Определите свою цель. Что вы сравниваете и почему? Это поможет вам определить наборы.
- Проведите мозговой штурм и перечислите предметы в своих наборах либо на бумаге, либо с помощью такой платформы, как Lucidchart.
- Теперь используйте свою диаграмму, чтобы сравнить наборы. Вы можете смотреть на вещи по-новому и быть в состоянии делать наблюдения, делать выбор, аргументировать или принимать решения.
Дополнительные ресурсы
- Шаблоны диаграмм Венна
- Как создать диаграмму Венна в Excel
- Как создать диаграмму Венна в PowerPoint
Lucidchart позволяет создавать профессионально выглядящие диаграммы Венна с помощью простого в использовании программного обеспечения . Поскольку все редактирование происходит в облаке, с коллегами легко работать над диаграммой Венна. Вы даже можете импортировать изображения и делиться своей схемой в цифровом виде или через печать.
Вы даже можете импортировать изображения и делиться своей схемой в цифровом виде или через печать.
Хотите построить собственную диаграмму Венна? Попробуйте Люсидчарт. Это быстро, просто и совершенно бесплатно.
Построить диаграмму Венна
сек. 3.6 – Математика колледжей для начального образования
Глава 3, Раздел 6
Математические темы – Диаграммы Эйлера и логические аргументы, «Если… то» (условные) утверждения
Тема обучения – Какие типы представлений подходят?
Логические аргументы
В предыдущем разделе у нас был пример
Все кошки – животные. Флаффи — кот.
Флаффи — кот.
Если вы посмотрите на диаграмму (не внося свои собственные знания), диаграмма также показывает, что Пушистик должен быть животным.
Мы можем записать это как заключение логического аргумента:
Первые две строки аргумента — это предпосылки, то, что мы принимаем за истину.
Последняя строка – заключение.
Чтобы быть действительным аргументом, заключение должно следовать из двух посылок. То есть, если мы за исключением того, что посылки верны, заключение должно быть истинным на базе помещения . Приведенный выше аргумент действителен.
Что сделало бы аргумент не действительным? Попробуем несколько изменить набор предпосылок и выводов:
Все кошки — животные.
Дэн — животное.
Значит Дэн - кот.
Чтобы проверить, верный ли это аргумент, нарисуйте только помещения.
Даже не смотрите на вывод, когда рисуете картинку!
Глядя на нашу картинку, мы видим, что вывод о том, что Дэн является котом , неверен. Дэн может быть котом, или Дэн может быть другим видом животных. На диаграмме показано, что D может находиться в двух возможных местах.
Дэн может быть котом, или Дэн может быть другим видом животных. На диаграмме показано, что D может находиться в двух возможных местах.
Это означает, что аргумент недействителен (недействителен).
Чтобы аргумент был действительным, мы должны быть на 100% уверены в том, что вывод верен на основе предпосылок.
Пример 1 Какой вывод правильный?
Чтобы решить, постройте диаграмму Эйлера, используя каждый набор предпосылок.
Помните, что для построения диаграммы используйте только предпосылки, а не заключение.
Помещения:
Обратите внимание, что М может стоять в двух возможных местах. М должно быть в четырехстороннем круге вещей, потому что это первая предпосылка. M также может быть в круге квадратов, потому что это еще одно возможное место внутри четырехстороннего круга вещей.
Для X есть только одно возможное место внутри квадратного круга, так как это первая предпосылка этого аргумента. X не может быть вне этого круга, так как это означало бы, что X не был квадратом. Помните, мы берем каждый из помещения абсолютно правда.
X не может быть вне этого круга, так как это означало бы, что X не был квадратом. Помните, мы берем каждый из помещения абсолютно правда.
Теперь посмотрим на выводы, чтобы увидеть, следуют ли они из посылок.
Верен ли вывод Следовательно, M является квадратом ?
№
Глядя на нашу диаграмму, мы видим, что M может быть квадратом, а может и не быть. M может быть за пределами круга квадратов и иметь только 4 стороны. Например, M может выглядеть так:
M — 4-сторонний.
Вывод, Следовательно, X четырехсторонний , верно?
Да, потому что X находится внутри четырехстороннего круга вещей. Все квадраты четырехсторонние.
Но когда вы излагаете причину, по которой аргумент действителен, используйте первую часть причины, приведенную выше: «Да, потому что X находится внутри четырехстороннего круга вещей». Вторая часть, « Все квадраты четырехсторонние», просто повторяет предпосылку.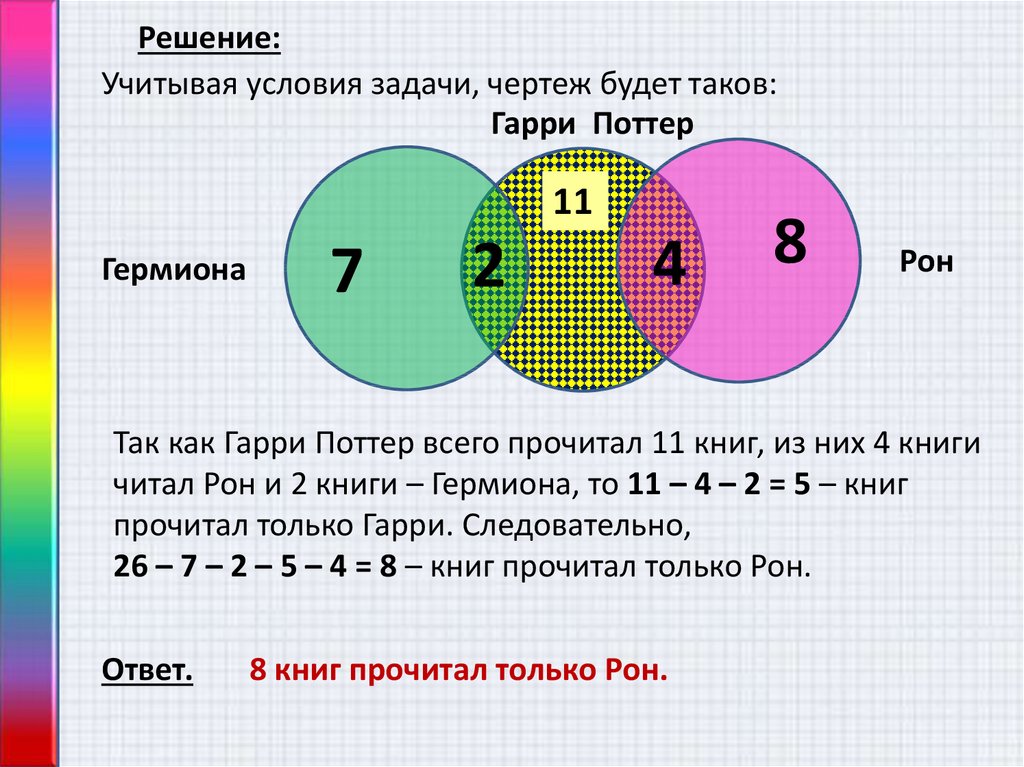 Переформулирование посылки (даже курсивом или подтекстом!) не является достаточным основанием для поддержки вашего аргумента. Вместо этого обратитесь к своей диаграмме и объясните, используя диаграмму.
Переформулирование посылки (даже курсивом или подтекстом!) не является достаточным основанием для поддержки вашего аргумента. Вместо этого обратитесь к своей диаграмме и объясните, используя диаграмму.
Итог
НЕВЕРНЫЙ Аргумент и причина
Все квадраты четырехсторонние.
М четырехсторонний.
Следовательно, M — квадрат.
Недействительно, так как M может находиться в части круга вне квадратов
(см. схему).
ДЕЙСТВИТЕЛЬНО Аргумент и причина
Все квадраты четырехсторонние.
X — квадрат.
Следовательно, X четырехсторонний.
Действителен, потому что X должен быть в круге квадратных вещей,
, который находится внутри четырехсторонних вещей, так что это автоматически делает X
также четырехсторонним (см. схему).
Условное
Другой способ показать логический аргумент — использовать символы вместо диаграмм Эйлера или в дополнение к ним.
Все кошки — животные — это то же самое, что сказать: Если — это кошка, , то — это животное.
Утверждение «если…тогда» известно как условное .
Мы используем стрелку для обозначения условного выражения: c → a, где c означает «это кошка, а a — это животное». Мы используем три точки, ∴, чтобы представить слово поэтому.
Действительный аргумент
Обратите внимание, что когда мы используем условную стрелку, мы больше не называем кота Пушистиком. Это делается для того, чтобы вторая посылка могла точно соответствовать первой части условного предложения.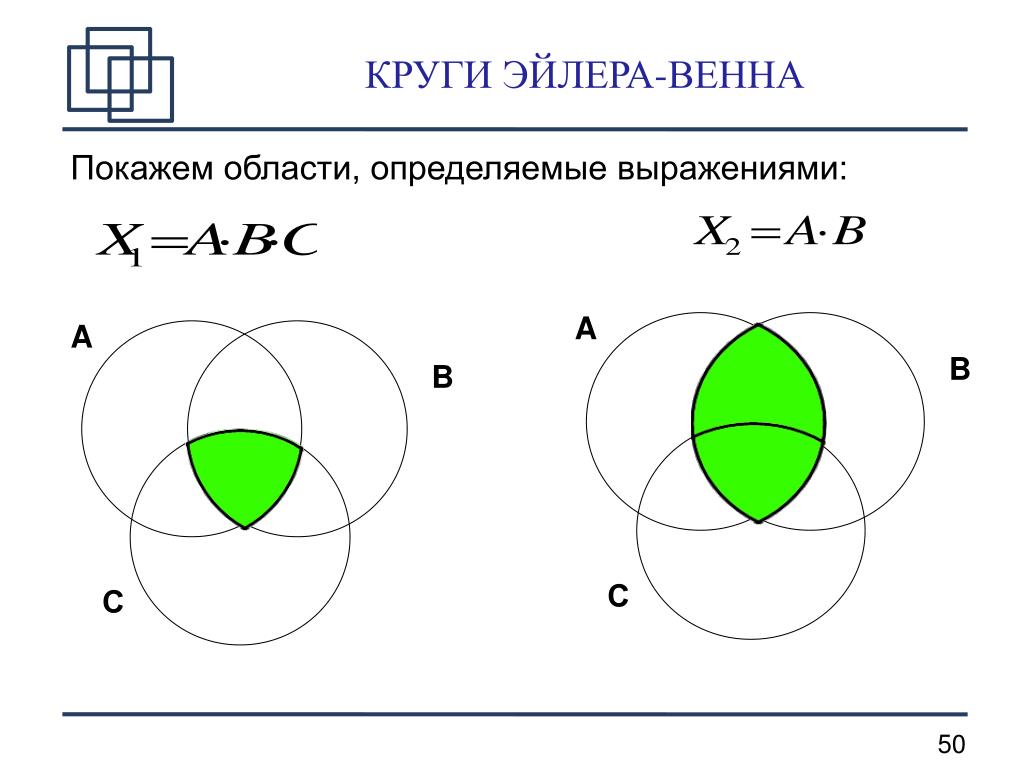
В действительный ( не действительно) аргумент
Посмотрите внимательно на порядок двух аргументов выше. Следуя этому шаблону, для оператора if-then типа A → B, какая вторая строка и вывод будут давать действительный аргумент?
Официальное название действительной формы аргумента — modus ponens , но можно просто сказать «правильный порядок». В правильном аргументе вторая посылка и вывод следуют в том же порядке, что и в условном выражении. Ученик в моем классе указал, что это происходит потому, что условная стрелка не является коммутативной. То есть сказать A → B — это не то же самое, что сказать B → A. Или, вернувшись к нашему предыдущему примеру, , если это кошка, значит, это животное, — это не то же самое, что сказать , если это животное, то это животное. кот .
Мы можем использовать как диаграмму Эйлера , так и символическую логику , чтобы решить, является ли аргумент допустимым.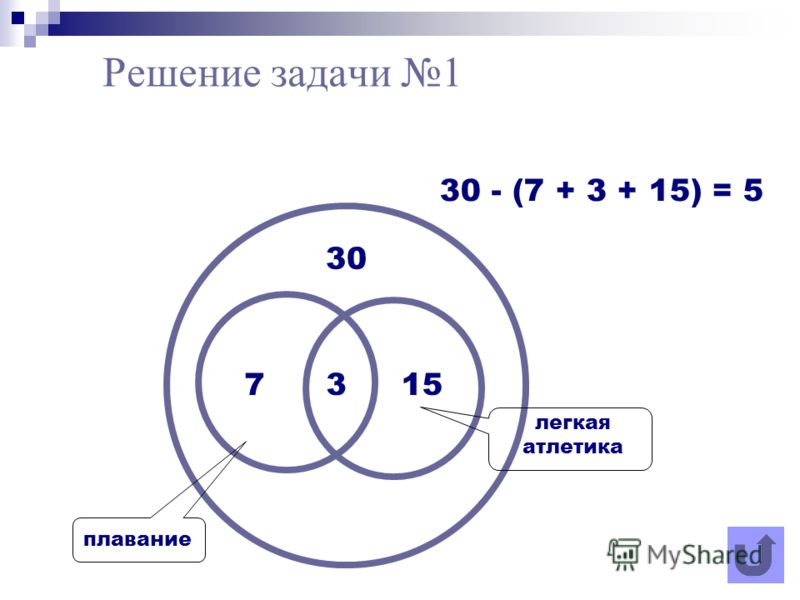 Некоторым учащимся визуальное представление проще всего; для других студентов символическое представление является самым простым. Вот почему мы хотим всегда стараться дать нашим ученикам множество способов представления математики!
Некоторым учащимся визуальное представление проще всего; для других студентов символическое представление является самым простым. Вот почему мы хотим всегда стараться дать нашим ученикам множество способов представления математики!
Пример 2 Верен или неверен следующий аргумент? Для принятия решения используйте диаграмму Эйлера и символическую логику с условным символом.
Все собаки дружелюбны.
Бонзо — собака.
Значит, Бонзо дружелюбен.
Чтобы принять решение, сначала перепишите аргумент в виде условного оператора («Если… то»). Посмотрите, к какому из приведенных выше шаблонов он подходит. Наконец, проверьте, нарисовав диаграмму Эйлера, чтобы визуально увидеть, действительна ли она.
Этот аргумент действителен – думайте о собаке как об А и дружелюбной как Б; вы можете видеть, что порядок аргумента правильный. У вас есть
A → B
A
∴ B
Диаграмма Эйлера приводит нас к тому же выводу. вещи», а это значит, что Бонзо находится внутри круга «дружеских вещей».
вещи», а это значит, что Бонзо находится внутри круга «дружеских вещей».
Пример 3 Верен или недействителен следующий аргумент?
Все собаки дружелюбны.
Рекс дружелюбный.
Значит, Рекс — собака.
Чтобы решить, мы перепишем аргумент как условное, чтобы увидеть шаблон. Затем мы рисуем диаграмму Эйлера, чтобы визуально увидеть, верна ли она.
Этот аргумент недействителен – думайте о собаке как A и дружелюбной как B; вы можете видеть, что порядок аргумента неверен. У вас есть
A → B
B
∴ A
Если у нас есть A → B , правильный порядок будет иметь A в качестве первой посылки, за которой следует B. Но в этом аргументе сначала B, а затем A.
Диаграмма Эйлера приводит нас к тот же вывод – аргумент недействителен , потому что Рекс может быть в любом месте. Не факт, что Рекс находится внутри круга «Собаки». Чтобы быть действительным аргументом, вывод должен быть уверен на 100%.
Символ «не» в логических аргументах
В логических рассуждениях, если мы хотим сказать: «Это , а не собака», мы должны использовать букву d, чтобы обозначить «это собака», и поставить символ «не», ~, перед ним: ~d означает «не собака». Этот символ подобен символу дополнения в наборах.
Пример 4 Верен или неверен следующий аргумент?
Если зеленый, то это не собака.
Зеленый.
Следовательно, это не собака.
Чтобы решить, пишем аргумент символами, чтобы увидеть закономерность. Мы также переписываем утверждение, чтобы мы могли нарисовать диаграмму Эйлера, чтобы визуально увидеть, верно ли оно.
Этот аргумент действителен: вторая посылка и вывод следуют в том же порядке, что и в условном (если… то). То есть в первой строке g → ~d, g стоит первой, а ~d — второй. Следующая посылка g и заключение ~d следуют в том же порядке.
С диаграммой Эйлера, Если это зеленый, значит это не собака переводил бы на два отдельных кружочка. Это то же самое, что и , без зеленых собак .
Используя диаграмму Эйлера, мы видим, что аргумент действителен , так как Гарри находится в круге зеленых вещей, поэтому он не может быть в круге собак, так как они не пересекаются.
Логические аргументы с использованием «Некоторые» и «Нет»
Пример 5 Является ли следующий аргумент допустимым или недействительным?
Некоторые кошки являются домашними животными.
Пушистый кот.
Следовательно, Пушистик — домашнее животное.
Из предыдущего раздела мы знаем, что букву F можно поставить в двух местах: Пушистик может быть котом, который является домашним животным (посередине), или котом, который не является домашним животным (слева). Поскольку мы не знаем наверняка, что Пушистик находится в кошачьем круге, аргумент недействителен. Помните, что для того, чтобы аргумент был недействительным, заключение должно следовать без сомнения из посылок.
В этом примере мы делаем , а не , изменяем аргумент на символы, потому что оператор some преобразует , а не в условное выражение.
Некоторые кошки являются домашними животными не эквивалентны c → p, это будет все кошки являются домашними животными.
Важно уметь выбирать, какой тип представления — визуальный или символический — лучше всего использовать в данной ситуации.
Пример 6 Верен или неверен следующий аргумент? Используйте диаграмму Эйлера или символы, в зависимости от того, что лучше, чтобы решить.
Некоторые телешоу смешные.
Вебстер не смешной.
Следовательно, Вебстер — это не телешоу.
Для любого аргумента с «some» мы не можем использовать условное выражение , поэтому рисуем диаграмму Эйлера. Здесь у нас есть «Некоторые телешоу смешные».
Поскольку Вебстер не смешной, есть два возможных места, чтобы поместить Вебстера, кроме «Забавных вещей». Одно из этих возможных мест находится внутри телешоу, поэтому вывод «Вебстер — это не телешоу» будет 9.0071 неверный .
Все отношения и Транзитивность
Какой вывод правильный, чтобы сообщить нам о том, как связаны квадраты и четырехугольники?
Все квадрата являются прямоугольниками.
Все прямоугольники являются четырехугольниками (имеют четыре стороны).
Следовательно, все ____ являются _______.
Правильный вывод создаст действительный аргумент.
Используйте схему, чтобы увидеть, какой набор будет подмножеством другого.
действительный вывод равен Следовательно, все квадраты четырехугольники (имеют четыре стороны).
Мы знаем, что это правда, потому что на нашей диаграмме множество квадратов внутри множества четырехугольников.
Мы также можем использовать условные операторы и символы, чтобы понять, почему.
Условный Символы
Если это квадрат, то это прямоугольник. с → р
Если это прямоугольник, то это четырехугольник r → q
Следовательно, если это квадрат, то это четырехугольник. ∴ s → q
Символы по порядку: s → r, r → q. То есть s → r → q
То есть s → r → q
Это образует непрерывную цепочку от s, хотя и r, до q. Таким образом, вывод s → q верен.
Этот тип аргумента,
A → B
B → C
∴ A → C
, называется действительным аргументом на транзитивность .
Он показывает цепочку, идущую от А к В, затем от В к С, поэтому А идет к С. Если одно число на меньше другого на , мы пишем a < b . Например, 3 < 4.
Теперь предположим, что мы знаем, что a < b и мы знаем, что b < c. Мы можем записать это как одно неравенство: a < b < c ( a меньше b меньше c ).
Мы можем заключить, что a должно быть на меньше, чем c , то есть a < c.
Написанное числами, это все равно, что сказать, что если 3 < 4 и 4 < 5, мы знаем, что 3 < 5. .
A → B
C → B
∴ A → C
– это , а не , допустимый аргумент по транзитивности.
, а не показывает цепочку, идущую от A к B, а затем от B к C. Вместо этого и A, и C ведут к B, так что ничего не связывает A с C.
Пример 7 Используйте ваше знание наборов чисел для создания действительного аргумента по транзитивности.
Все натуральные числа являются целыми числами. N → W
Все целые числа являются целыми числами W → I
Следовательно, все натуральные числа ____? ∴ N → ____?
Можно было бы правильно заключить, что N → I. Это следует из построения цепочки из посылок: N → W, W → I, значит имеем N → W → I
Пример 8 аргумент в силе?
Все целые числа являются целыми числами. W → I
Все натуральные числа целыеN → I
Следовательно, все целые числа являются натуральными числами ∴ W → N
Мы можем видеть, что этот аргумент недействителен , глядя на ту же диаграмму – множество целых чисел не входит в множество натуральных чисел числа,
Мы также можем видеть, что этот аргумент неверен , взглянув на символы:
W → I, N → I
Цепочки от W до N нет, каждая стрелка указывает на I, ничто не указывает от до №
Пример 9 Какие из следующих аргументов, показанных только символами, верны транзитивностью? Что недействительно? Совет: посмотрите, сможете ли вы найти цепочку, ведущую от одной буквы в заключении к другой.
Аргумент 1 Аргумент 2 Аргумент 3 Аргумент 4
P → Q M → Z x → ~ y a → B
A → B M → R ~ Y → Q C → B
Q → R A → T Q → M ∴ A → C
∴ P → R ∴ M → T ∴ x → Q
Первый аргумент может быть указан в одной длинной строке, чтобы увидеть, что соединяется с тем, что. Имеем p → q, a → b, q → r. Мы можем избавиться от a → b, так как эта посылка не имеет ничего общего с остальными. Теперь у нас есть p → q, q → r, что дает нам цепочку: p → q → r, что означает, что p действительно ведет к r , p → r. Аргумент равен действительный .
Можно удалить из посылок аргумент, который не влияет на ваш вывод! Предположим, кто-то сказал вам: «Все свиньи быстрые» (p → q), все аллигаторы большие (a → b) и все быстрые существа быстрые (q → r). Вы определенно можете проигнорировать эту часть об аллигаторах и сделать вывод, что все свиньи быстрые (p → r).
Для аргумента 2 имеем m → z, m → r, a → t. Поскольку в заключении m → t, мы ищем в посылках цепочку, связывающую m с t, например: m → ___ → ___ …→ t. Нет цепи, ведущей от m к t. Вместо этого у нас есть m, идущий к z и к r, но ни z, ни r не ведут ни к чему другому. Аргумент неверный .
Поскольку в заключении m → t, мы ищем в посылках цепочку, связывающую m с t, например: m → ___ → ___ …→ t. Нет цепи, ведущей от m к t. Вместо этого у нас есть m, идущий к z и к r, но ни z, ни r не ведут ни к чему другому. Аргумент неверный .
Для аргумента 3 имеем x → ~ y, ~ y → q и q → m в посылках. Поскольку вывод x → q, мы ищем в посылках цепочку, которая связывает x с q. У нас есть эта цепочка: у нас есть x → ~ y, ~ y → q, что становится x → ~ y → q, так что мы имеем x → q. Аргумент допустим .
Наконец, аргумент 4 равен недействителен , так как у нас нет цепочки, идущей от а к с в помещении. У нас есть a, идущий к b, и у нас также есть c, идущий к b. Нет ничего, что привело бы к c. Проблема в том, что вторая посылка — это наоборот . Если бы мы вместо этого имели a → b и b → c, то мы могли бы заключить, что ∴ a → c.
сек-3.6-домашнее заданиеСкачать
сек-3. 6-домашнее задание-ответыСкачать
6-домашнее задание-ответыСкачать
Нравится:
Нравится Загрузка…
Льюис Кэрролл: Логика | Интернет-энциклопедия философии
Чарльз Л. Доджсон (также известный как Льюис Кэрролл), 1832–1898, был британским математиком, логиком и автором книг «Алиса», «Приключения Алисы в стране чудес» и «Зазеркалье» и . Что там нашла Алиса . Его слава проистекает в основном из его литературных произведений, но в двадцатом веке некоторые из его математических и логических идей нашли важное применение. Его подход к ним побудил его изобрести различные методы, которые поддаются механическим рассуждениям. Он не был традиционным математиком. Скорее, он применял математические и логические решения проблем, которые его интересовали. Как прирожденный логик в то время, когда логика не считалась частью математики, он успешно работал в обеих областях. Все, что он публиковал по математике, отражало логический образ мышления, особенно его работы по геометрии. Доджсон проявлял неизменный интерес к геометрии Евклида. Из десяти книг по математике, которые он написал, включая две его книги по логике, пять были посвящены геометрии. Изучая геометрию, он развил сильную склонность к определению достоверности аргументов не только в математике, но и в повседневной жизни. Доджсон твердо относился к логике как к основе убедительного мышления во всех сферах жизни, но он не осознавал, что разработал концепции, которые будут исследованы или расширены в двадцатом веке. Подход Доджсона к решению логических задач привел его к изобретению различных методов, в частности метода диаграмм и метода деревьев. В качестве метода для большого количества наборов диаграммы Кэрролла рисовать легче, чем диаграммы Венна, потому что они самоподобны. Его необычное изложение элементарной логики позабавило современных авторов, которые продолжают цитировать его книги по логике. На взгляды математика и логика Хью Макколла на логику повлияло чтение книги Доджсона 9.0680 Символика Логика, часть I .
Доджсон проявлял неизменный интерес к геометрии Евклида. Из десяти книг по математике, которые он написал, включая две его книги по логике, пять были посвящены геометрии. Изучая геометрию, он развил сильную склонность к определению достоверности аргументов не только в математике, но и в повседневной жизни. Доджсон твердо относился к логике как к основе убедительного мышления во всех сферах жизни, но он не осознавал, что разработал концепции, которые будут исследованы или расширены в двадцатом веке. Подход Доджсона к решению логических задач привел его к изобретению различных методов, в частности метода диаграмм и метода деревьев. В качестве метода для большого количества наборов диаграммы Кэрролла рисовать легче, чем диаграммы Венна, потому что они самоподобны. Его необычное изложение элементарной логики позабавило современных авторов, которые продолжают цитировать его книги по логике. На взгляды математика и логика Хью Макколла на логику повлияло чтение книги Доджсона 9.0680 Символика Логика, часть I . Их обмен мнениями показывает, что оба были глубоко заинтересованы в точном использовании слов. И оба не видели никакого вреда в приписывании произвольных значений словам, пока это значение является точным и присвоение согласовано. Репутация Доджсона как автора книг об Алисе делала его прежде всего автором детских книг и мешала серьезному отношению к его книгам по логике. Барьер, созданный славой, которую Кэрролл заслуженно заработал благодаря своим книгам «Алиса», в сочетании с стилем письма, более литературным, чем математическим, мешал сообществу британских логиков должным образом признать его значительным логиком при жизни.
Их обмен мнениями показывает, что оба были глубоко заинтересованы в точном использовании слов. И оба не видели никакого вреда в приписывании произвольных значений словам, пока это значение является точным и присвоение согласовано. Репутация Доджсона как автора книг об Алисе делала его прежде всего автором детских книг и мешала серьезному отношению к его книгам по логике. Барьер, созданный славой, которую Кэрролл заслуженно заработал благодаря своим книгам «Алиса», в сочетании с стилем письма, более литературным, чем математическим, мешал сообществу британских логиков должным образом признать его значительным логиком при жизни.
Содержание
- Жизнь Доджсона
- Логическая установка в его время
- Логика и геометрия
- Силлогизмы, соритесы и задачи-головоломки
- Диаграммы Венна и Кэрролла
- «Методы» Доджсона
- Автоматизация дедукции
- Логический круг Доджсона
- Эффект «Алисы»
- Логические парадоксы
- Парадокс парикмахерской
- Ахиллес и черепаха
- Доджсон и современная математика
- Кэрролл как популяризатор
- Заключение
- Ссылки и дополнительная литература
- Первичный
- Среднее
1.
 Жизнь Доджсона
Жизнь ДоджсонаЧарльз Лютвидж Доджсон (1832–1898), более известный под псевдонимом Льюис Кэрролл, который он принял в 1856 году, в 1852 году поступил в Крайст-Черч, Оксфордский университет в Англии. три обязательных экзамена и получение первого класса по математике и второго класса по классике в модерации, второго обязательного экзамена, он получил степень бакалавра в 1854 году, заняв первое место в списке с отличием первого класса по математике и получив с отличием третьего класса в нужной Классике. Он получил степень магистра искусств в 1857 году. Он оставался в Крайст-Черч-колледже до конца своей жизни.
Он начал в частном порядке обучать отдельных студентов дифференциальному исчислению, коникам, евклидовой геометрии, алгебре и тригонометрии. В 1856 году настоятель церкви Христа, преподобный Генри Лидделл, назначил его лектором по математике. Он занимал эту должность в течение 25 лет, прежде чем уйти в отставку в 1881 году. видные деятели правительства, науки, искусства и театра. Его подданными были премьер-министр Солсбери, Майкл Фарадей и Джон Раскин. Он стал одним из самых выдающихся фотографов своего времени. Он также был плодовитым писателем, ведя реестр писем, которые он получал и отправлял, 98721 из них за последние тридцать пять лет его жизни.
Его подданными были премьер-министр Солсбери, Майкл Фарадей и Джон Раскин. Он стал одним из самых выдающихся фотографов своего времени. Он также был плодовитым писателем, ведя реестр писем, которые он получал и отправлял, 98721 из них за последние тридцать пять лет его жизни.
Принятие духовного сана было требованием для всех преподавателей. Он решил стать дьяконом, а не священником, чтобы посвятить свое время преподаванию и продолжать ходить в театр в Лондоне, что было его любимым занятием. Он был рукоположен в диаконы в 1861 году. Доджсон развил в своей жизни глубоко религиозные взгляды. Его отец, архидиакон Чарльз Доджсон, до женитьбы считался сильным кандидатом на пост архиепископа Кентерберийского.
Его первые публикации (брошюры и книги с 1860 по 1864 год) были разработаны, чтобы помочь студентам: A Syllabus of Plane Algebraic Geometry , Систематически организованная с формальными определениями, постулатами и аксиомами ; Заметки о первых двух книгах Евклида ; Заметки по первой части алгебры ; Формулы плоской тригонометрии ; Изречения Евклида I, II ; Общий список [математических] предметов и цикл рабочих примеров; Руководство для студентов-математиков .
В середине 1860-х годов Доджсон стал активным участником студенческой жизни, сочиняя юмористические математические «стяжки» для обсуждения различных вопросов в Крайст-Черч, голосуя на выборах студентов (стипендиатов) и о физических изменениях в зданиях и территории колледжа. Эта деятельность пробудила его интерес к методам ранжирования и голосования. Он стал членом Правления в 1867 году и оставался в нем на всю жизнь. В 1868 году он приобрел квартиру в северо-западном углу Том-Куад, части Крайст-Черч, где построил на крыше студию для своих фотографий. Его квартира была самой изысканной и самой дорогой в колледже.
Став активным участником политических дел за пределами колледжа в 1880-х годах, он отправил много писем в редакцию The St. James’s Gazette, Pall Mall Gazette и других газет, излагая свою позицию по различным вопросам государственной важности. Благодаря своей фотографии он подружился с лордом Солсбери, который стал премьер-министром в 1881 году. Их социальные отношения, начавшиеся в 1870 году, продолжались на протяжении всей жизни Доджсона и побудили его задуматься о проблеме справедливости как в представительстве, так и в распределении, достигнув кульминации в его брошюре о 1884, Принципы парламентского представительства .
Их социальные отношения, начавшиеся в 1870 году, продолжались на протяжении всей жизни Доджсона и побудили его задуматься о проблеме справедливости как в представительстве, так и в распределении, достигнув кульминации в его брошюре о 1884, Принципы парламентского представительства .
Его публикации, брошюры и две книги за оставшуюся часть 1860-х годов отражают эти интересы, а также интересы математики и те, которые свидетельствуют о его значительных литературных способностях: Динамика частицы с экскурсом по новому методу оценки применительно к Π; Алиса в Стране Чудес; Элементарный трактат об определителях с их приложениями к одновременным линейным уравнениям и алгебраической геометрии; Пятая книга Евклида, трактуемая алгебраически, поскольку она относится к соизмеримым величинам, с примечаниями; Алгебраические формулы для использования кандидатов на ответы; Фантасмагория и другие стихи.
Его публикации 1870-х годов продолжались в том же духе: Алгебраические формулы и правила использования кандидатов на ответы; Арифметические формулы и правила использования кандидатов в ответы; Зазеркалье и что там нашла Алиса; Изречения Евклида, книги I – VI; Примеры по арифметике; Обсуждение различных процедур проведения выборов; Предложения по наилучшему методу голосования; Книга V Евклида, доказанная алгебраически в отношении соизмеримых величин, с примечаниями; Охота на Снарка; метод голосования по более чем двум вопросам; Евклид и его современные соперники .
После ухода с поста преподавателя математики у Доджсона появилось больше времени для писательства. В первой половине 1880-х годов Доджсон опубликовал « турниров по лаун-теннису», «Принципы парламентского представительства», «Запутанная история», «Приключения Алисы под землей» (факсимильное издание).
Но во второй половине 1880-х годов произошел тектонический сдвиг с его первой книгой по логике: Игра логики , а также с его шифром Memoria Technica, еще двумя книгами, Curiosa Mathematica, Часть I: Новая теория параллелей, и Сильвия и Бруно . В 1887 году он опубликовал первую из трех статей в Nature «Найти день недели для любой заданной даты».
За последнее десятилетие его жизни было издано больше книг . The Nursery Alice появилась в 1890 году. Curiosa Mathematica, Part II: Pillow Problems и Sylvie и Bruno Concluded появились в 1893 году. Его единственные другие публикации по логике вышли между 1894 и 1896. Это были две статьи в Mind , «Логический парадокс», «Что черепаха сказала Ахиллесу», и книга Symbolic Logic, Part I: Elementary . С 1892 по 1897 год он работал над главой запланированной книги об играх и головоломках, которая так и не была опубликована. Он включал его «Правило нахождения дня Пасхи для любой даты до 2499 года нашей эры». Его последними публикациями были: « Краткий метод деления заданного числа на 9 или 11 », (1897) и «Сокращенное длинное деление» (1898). Оба появились в журнале Nature .
Это были две статьи в Mind , «Логический парадокс», «Что черепаха сказала Ахиллесу», и книга Symbolic Logic, Part I: Elementary . С 1892 по 1897 год он работал над главой запланированной книги об играх и головоломках, которая так и не была опубликована. Он включал его «Правило нахождения дня Пасхи для любой даты до 2499 года нашей эры». Его последними публикациями были: « Краткий метод деления заданного числа на 9 или 11 », (1897) и «Сокращенное длинное деление» (1898). Оба появились в журнале Nature .
2. Логика в его время
Отношение к логике в Англии начало коренным образом меняться, когда в 1847 году Джордж Буль опубликовал короткую книгу под названием Математический анализ логики . В нем он развил представление о том, что логические отношения могут быть выражены алгебраическими формулами. Буль, используя свои законы вычисления, смог алгебраически представить все методы рассуждений в традиционной классической логике. А в книге, которую он опубликовал в 1854 г., Исследование законов мышления , Буль поставил перед собой цель создать совершенно общий метод в логике.
А в книге, которую он опубликовал в 1854 г., Исследование законов мышления , Буль поставил перед собой цель создать совершенно общий метод в логике.
Параллельно с работой Буля была работа Де Моргана, чья книга « Формальная логика » появилась примерно в то же время, что и книга Буля в 1847 году. Де Морган заинтересовался развитием логики отношений в дополнение к логике классов Буля. Его целью было показать наиболее общую форму силлогизма. Его вера в то, что законы алгебры можно сформулировать формально, не давая конкретной интерпретации, такой как система счисления, повлияла на Буля.
Хотя Буль и его последователи понимали, что они просто алгебраизируют логику, то есть переписывают силлогизмы в новой системе обозначений, а не изобретают новое логическое исчисление, они справедливо утверждали, что все действительные аргументы не могут быть сведены к этим формам. Венн понял это; он опубликовал статью в Mind в 1876 году, которая включала следующую проблему как иллюстрацию неадекватности аристотелевских форм рассуждения и превосходства булевых методов. Венн поставил задачу, вывод из которой таков: ни один акционер не является держателем облигаций, в качестве контрольного вопроса для студентов Кембриджского университета. Он заметил, что из примерно 150 студентов только пятеро или шестеро смогли решить следующую простую задачу:
Венн поставил задачу, вывод из которой таков: ни один акционер не является держателем облигаций, в качестве контрольного вопроса для студентов Кембриджского университета. Он заметил, что из примерно 150 студентов только пятеро или шестеро смогли решить следующую простую задачу:
В одной компании был совет директоров. Каждый директор владел либо облигациями, либо акциями; но ни один директор не держал оба. Каждый держатель облигаций был в Совете директоров. Выведите все, что может быть выведено логически, в как можно меньшем количестве предложений.
Для Доджсона и его современников центральной проблемой логики классов, известной как проблема исключения, было определение максимального количества информации, получаемой из заданного набора предложений. В своей книге 1854 года Буль значительно усложнил решение этой проблемы, предоставив механизм чисто символической обработки, который позволял высказываниям иметь любое количество терминов, тем самым вводя возможность огромного количества вычислений.
Логические аргументы, использующие правила вывода, являются основным компонентом как геометрии, так и логики. Для Доджсона логика и геометрия имели общие характеристики истины и определенности, качества, которые держали его в рабстве. С середины 1880-х годов он переключил свое внимание с истины, данной геометрическими теоремами (истинными утверждениями), на обоснованность логических аргументов, правил, гарантирующих, что только истинные выводы могут быть сделаны из истинных предпосылок, и он раздвинул границы возможного. стандартные формы господствовавшей в его время логики, которая была аристотелевской.
Доджсон начал подробно писать о логике в 1870-х годах, когда он начал свой magnus opus «Символическая логика», первая часть которого вышла в 1896 году. 1870-е годы. В математике вообще и в геометрии в частности начинают с набора аксиом и определенных правил вывода, чтобы сделать вывод, что если одно утверждение истинно, то верно и другое предложение. Для Доджсона геометрия и логика имели общую характеристику определенности, качество, которое всегда интересовало его. Но к началу 189С тех пор он сместил свое внимание с истины, выдаваемой геометрическими теоремами, на обоснованность логических аргументов.
Но к началу 189С тех пор он сместил свое внимание с истины, выдаваемой геометрическими теоремами, на обоснованность логических аргументов.
Доджсон работал один, но он вовсе не был изолирован от сообщества логиков своего времени. Он переписывался с рядом британских логиков. Среди них: Джеймс Велтон, автор двухтомного «Руководства по логике »; Джон Кук Уилсон, профессор логики в Оксфорде с 1889 г. до своей смерти в 1915 г.; Томас Фаулер , профессор логики Уайкхэма в Оксфорде (1873–1889 гг.).) и автор книги Элементы дедуктивной логики ; Уильям Эрнест Джонсон, сотрудник Джона Невилла Кейнса в Кембридже и автор «Логического исчисления», серии из трех статей, опубликованных в Mind в 1892 году; Герберт Уильям Блант; Генри Сиджвик, профессор моральной философии в Кембридже; Джон Венн, автор влиятельной книги « Symbolic Logic»; , а также Ф. Х. Брэдли, автор книги «Принципы логики» ; и Стюарт. Он также процитировал книгу 9.0680 Studies in Logic под редакцией Пирса и включает произведения учеников Пирса: Марканда, Лэдда-Франклина, Оскара Ховарда Митчелла и Б. И. Гилмана. Из рецензии Венна на « Studies in Logic », появившейся в октябрьском издании « Mind » за октябрь 1883 г., вскоре после публикации книги Пирса, мы знаем, что Пирс был хорошо известен британским символистам и что они знали о публикациях Пирса.
И. Гилмана. Из рецензии Венна на « Studies in Logic », появившейся в октябрьском издании « Mind » за октябрь 1883 г., вскоре после публикации книги Пирса, мы знаем, что Пирс был хорошо известен британским символистам и что они знали о публикациях Пирса.
Вклады Марканда, короткая статья «Машина для производства силлогистических вариаций» и его «Заметки о восьмичленной логической машине», содержат идеи, которые Доджсон зафиксировал в своем Реестре атрибутов, инструменте, который он создал для организации предпосылок. когда он применил свой древовидный метод к соритесам (соритезис – это аргумент, имеющий много предпосылок и один вывод. Его можно представить в виде списка силлогизмов, вывод каждого из которых становится предпосылкой следующего силлогизма). Доджсон использовал идеи, связанные с логической машиной еще раньше в Логическая игра .
Продажа библиотеки Доджсона после его смерти включала работы по логике Буля, Венна, Аллана Маркванда, Митчелла, Лэдд-Франклина, Бенджамина Айвса Гилмана, Пирса, Джона Невилла Кейнса, Рудольфа Германа Лотце (в английском переводе Бернара Бозанке) Джеймса Уильям Гилбарт, Де Морган, Бернар Бозанке, Фрэнсис Х. Брэдли, Джон Стюарт Милль, Уильям Стирлинг Гамильтон, Уильям Уэвелл и Джевонс, среди прочих. Некоторые из этих работ повлияли на его собственное творчество, а также предоставили материал, необходимый ему в отношениях с противниками из Оксфорда.0071
Брэдли, Джон Стюарт Милль, Уильям Стирлинг Гамильтон, Уильям Уэвелл и Джевонс, среди прочих. Некоторые из этих работ повлияли на его собственное творчество, а также предоставили материал, необходимый ему в отношениях с противниками из Оксфорда.0071
3. Логика и геометрия
На имплицитном уровне Доджсон писал о логике на протяжении всей своей профессиональной карьеры. Все, что он публиковал по математике, отражало логический образ мышления, особенно его работы по геометрии. Повышенное внимание Доджсона к логике последовало за его публикациями по евклидовой геометрии 1860-х и 1870-х годов.
С середины 1880-х годов он переключил свое внимание с истины, данной геометрическими теоремами (истинными утверждениями), на достоверность логических аргументов, правил, гарантирующих, что только истинные выводы могут быть получены из истинных предпосылок. На стр. xi предисловия к третьему изданию (1890) своей книги о геометрии Curiosa Mathematica Part I: A New Theory of Parallels , он указал, что достоверность силлогизма не зависит от истинности его предпосылок. Он привел такой пример:
Он привел такой пример:
Я послала за вами, мои дорогие Утки, сказала достопочтенная миссис Бонд, «чтобы узнать, с каким соусом вы хотели бы, чтобы вас съели?» «Но мы не хотим быть убитыми — закричали Утки. « Вы блуждаете от точки », — совершенно логично ответила миссис Бонд.
Доджсон всегда интересовался геометрией Евклида. Из десяти книг по математике, которые он написал, включая две его книги по логике, пять были посвящены геометрии. Изучая геометрию, он развил сильную склонность к определению достоверности аргументов не только в математике, но и в повседневной жизни. Возможно, Доджсон сформулировал формальную логику в конце своей жизни и стал кульминацией его публикаций по геометрии Евклида в 1860-х и 1870-х годах. Ровно за месяц до своей смерти в неопубликованном письме, которое Доджсон написал Дугалду Стюарту, критикуя рукопись, которую Стюарт дал ему для ознакомления, он прокомментировал:0032
С этой точки зрения логика стала бы для меня наукой такой неопределенности, что я не должен [должен] больше интересоваться ею. Именно его абсолютная определенность меня в настоящее время восхищает. ( Dodgson , Berol Collection, New York University, 14 декабря 1897 г.)
Именно его абсолютная определенность меня в настоящее время восхищает. ( Dodgson , Berol Collection, New York University, 14 декабря 1897 г.)
Мы также знаем, что Доджсон умел доказывать теоремы методом от противного в своих многочисленных публикациях по геометрии. Точно так же, как логика наполняла его геометрические работы, геометрия наполняла его логические сочинения. В своей книге по логике он использовал геометрические обозначения и термины, например, символ обратного абзаца для основной связки, силлогизм, отношение импликации и соответствующий символ 9.0071 ∴ для «поэтому».
а. Силлогизмы, сориты и задачи-головоломки
В классической аристотелевской логике есть четыре формы предложений:
A : Все x есть y
E : Нет x есть y
I : Некоторые x есть 1y O : некоторый x не является y.
Эти Буль записали как:
x(1 – y) = 0
xy = 0
xy ≠ 0
x(1 – y) ≠ 0.
Символы x, y, z обозначают классы; а Буль использовал обычные алгебраические законы, управляющие вычислениями с числами, для интерпретации своей системы классов и допустимых операций над ними. Он предположил, что каждый из этих законов, таких как xy = yx, выражает утверждение, которое является истинным. Буль также разработал правила для решения проблем исключения. Если уравнение f(x) = 0 обозначает информацию, доступную о классе x, и мы хотим найти отношения, которые выполняются между x и другими классами (y, z и т. д.), с которыми x связан, что символизируется с помощью выражения f (x) Буль, используя свои законы вычисления, смог алгебраически представить все методы рассуждений в традиционной классической логике. Например, силлогистическое рассуждение включает в себя сведение двух уравнений класса (посылок) к одному уравнению (заключение), удаление среднего термина и последующее решение уравнения вывода для предметного термина. Механический характер этих шагов очевиден.
Доджсон, как и большинство его сверстников, использовал классические формы, такие как силлогизм и сориты, для решения логических задач. Эти формы традиционной аристотелевской логики были основой системы логических рассуждений, господствовавшей в Англии до первой четверти ХХ века. Но Доджсон пошел намного дальше, создавая логические задачи-головоломки, некоторые из которых содержали аргументы, призванные сбить с толку читателя, а другие можно было назвать парадоксальными, поскольку они, казалось, доказывали то, что считалось ложным. Имея в виду эти цели, он хотел показать, что классическая силлогистическая форма, преобладающая логическая система его времени, допускает гораздо более общие рассуждения, чем это обычно считалось.
Эти формы традиционной аристотелевской логики были основой системы логических рассуждений, господствовавшей в Англии до первой четверти ХХ века. Но Доджсон пошел намного дальше, создавая логические задачи-головоломки, некоторые из которых содержали аргументы, призванные сбить с толку читателя, а другие можно было назвать парадоксальными, поскольку они, казалось, доказывали то, что считалось ложным. Имея в виду эти цели, он хотел показать, что классическая силлогистическая форма, преобладающая логическая система его времени, допускает гораздо более общие рассуждения, чем это обычно считалось.
Средневековые логики-аристотелики сформулировали классификации пятнадцати, девятнадцати или двадцати четырех верных силлогизмов, в зависимости от ряда допущений. А в часть II книги «Символическая логика » Бартли включает еще три валидные силлогистические формулы, которые Доджсон сконструировал главным образом для обработки силлогизмов, содержащих утверждения «не все».
Силлогистическое рассуждение со времен Аристотеля и до работ Джорджа Буля по логике в середине девятнадцатого века было основным методом всех логических рассуждений. В силлогизме есть три термина (класса) в его трех утверждениях: подлежащее, сказуемое (выражение, приписывающее свойства) и средний термин, который встречается один раз в каждой посылке. Существует несколько систем классификации силлогизмов, включающих относительное положение повторяющегося среднего термина (которое определяет его значение).0680 фигура , или падеж — всего четыре падежа) и способ построения силлогизма внутри фигуры (что определяет его наклонение ).
В силлогизме есть три термина (класса) в его трех утверждениях: подлежащее, сказуемое (выражение, приписывающее свойства) и средний термин, который встречается один раз в каждой посылке. Существует несколько систем классификации силлогизмов, включающих относительное положение повторяющегося среднего термина (которое определяет его значение).0680 фигура , или падеж — всего четыре падежа) и способ построения силлогизма внутри фигуры (что определяет его наклонение ).
Доджсон создал первую часть своей системы визуального доказательства, диаграммную систему, начиная с 1887 года в небольшой книге под названием Логическая игра . Его диаграммная система могла обнаруживать ошибки, и эта тема его очень интересовала. Он определил заблуждение как «аргумент, который обманывает нас , кажущимся доказывающим то, чего на самом деле не доказывает…». (Бартли 1977, с. 129)
В «игре» используются только двух- и трехсеточные диаграммы. Его диаграммы могут представлять как универсальные, так и экзистенциальные утверждения. В этом учебнике, предназначенном для молодежи, много примеров и их решений.
В этом учебнике, предназначенном для молодежи, много примеров и их решений.
С целью расширения своего метода доказательства Доджсон расширил свой набор диаграмм, в конечном итоге создав диаграммы для восьми множеств (классов) и описав построение диаграмм девяти множеств и десяти множеств.
Он считал, что умственная деятельность и умственные развлечения, такие как игры и особенно головоломки, доставляют удовольствие и придают чувство силы тем, кто прилагает усилия для их решения. В рекламе четвертого выпуска Символическая логика, часть I . Elementary адресовано учителям он писал:
Я утверждаю, что символическая логика занимает очень высокое место среди развлечений, имеющих характер игр или головоломок… Символическая логика обладает одной уникальной особенностью по сравнению с играми и головоломками, что, я считаю, дает ему право стоять выше их всех… Он может применить свое мастерство к любому предмету человеческой мысли; в каждом из них это поможет ему получить ясных идей, сделать упорядоченных упорядочивания своих знаний и, что более важно, чтобы обнаружить и разгадать заблуждений, с которыми он столкнется в каждом предмете, который может его интересовать. (Бартли 1977, стр. 46)
(Бартли 1977, стр. 46)
основа для обоснованного мышления во всех сферах жизни, но он не осознавал, что разработал концепции, которые будут исследованы или расширены в двадцатом веке. Хотя он признавал свои нововведения значительными, тот факт, что он представлял их прежде всего в дидактическом, а не исследовательском контексте, повлиял на то, как они воспринимались и оценивались в его время и даже после публикации Бартли.
Представление Кэрролла о силлогистической конструкции отличалось как от классического и средневекового, так и от его современников. Некоторые причины, которые он привел для объединения девятнадцати различных форм, появляющихся в современных учебниках, включали следующее: правила силлогистики были слишком специализированными; многие выводы были неполными; и многие законные силлогистические формы игнорировались. Хотя Буль считал, что решения, которые были найдены при использовании его методов, были полными, было показано, что это не всегда так.
Кэрролл внес несколько изменений в силлогистические конструкции по сравнению с тем, что было принято в его время. Результатом являются пятнадцать действительных силлогизмов, хотя он на самом деле их не перечислял, которые Кэрролл признал. Силлогизм — это рассуждение, имеющее две посылки и одно заключение, причем каждое предложение относится к одному из четырех видов: A : «все… есть…»; E : ‘нет… есть…’; I : ‘некоторые… есть…’; O : «некоторые… не…». В трех утверждениях есть три термина (класса): субъект, предикат (выражение, приписывающее свойства) и средний термин, который встречается один раз в каждой посылке. Число его действительных силлогизмов колеблется от восемнадцати до двадцати четырех.
Результатом являются пятнадцать действительных силлогизмов, хотя он на самом деле их не перечислял, которые Кэрролл признал. Силлогизм — это рассуждение, имеющее две посылки и одно заключение, причем каждое предложение относится к одному из четырех видов: A : «все… есть…»; E : ‘нет… есть…’; I : ‘некоторые… есть…’; O : «некоторые… не…». В трех утверждениях есть три термина (класса): субъект, предикат (выражение, приписывающее свойства) и средний термин, который встречается один раз в каждой посылке. Число его действительных силлогизмов колеблется от восемнадцати до двадцати четырех.
В своей более ранней книге Логическая игра Кэрролл создал диаграммную систему для решения силлогизмов. Десять лет спустя, в Symbolic Logic , Part I , он расширил метод диаграмм, чтобы обрабатывать до десяти классов (множеств), изображающих их отношения и соответствующие предложения. Этот визуальный логический метод, в котором используются трехбуквенные и двубуквенные диаграммы, представляет собой систему доказательства категорических силлогизмов, предложения которых относятся к А , Е , I тип. Он подвел тип O под тип I , то есть «некоторые х не являются у» эквивалентно «некоторые х являются у, а некоторые х не являются у». система за пределами силлогизмов. Для более сложных соритесов он остановился на «методах закрытых помещений и закрытых групп» и своем последнем визуальном методе, методе деревьев, который оставался неопубликованным до 1977 года, когда он появился в книге У. В. Бартли III, Символическая логика Льюиса Кэрролла. . В построении Бартли части II Symbolic Logic с использованием сохранившихся документов, писем и рукописей Доджсона основными темами восьми книг являются: заблуждения, логические схемы, два метода закрытых помещений и деревьев, а также задачи-головоломки.
Этот визуальный логический метод, в котором используются трехбуквенные и двубуквенные диаграммы, представляет собой систему доказательства категорических силлогизмов, предложения которых относятся к А , Е , I тип. Он подвел тип O под тип I , то есть «некоторые х не являются у» эквивалентно «некоторые х являются у, а некоторые х не являются у». система за пределами силлогизмов. Для более сложных соритесов он остановился на «методах закрытых помещений и закрытых групп» и своем последнем визуальном методе, методе деревьев, который оставался неопубликованным до 1977 года, когда он появился в книге У. В. Бартли III, Символическая логика Льюиса Кэрролла. . В построении Бартли части II Symbolic Logic с использованием сохранившихся документов, писем и рукописей Доджсона основными темами восьми книг являются: заблуждения, логические схемы, два метода закрытых помещений и деревьев, а также задачи-головоломки. . В части I « Symbolic Logic » Доджсон использовал всего три формулы, которые он назвал фигурами или формами для обозначения классических силлогизмов. В четвертом издании Symbolic Logic, Part I . Elementary , Доджсон указал на это в Приложении, адресованном учителям, где он написал:
. В части I « Symbolic Logic » Доджсон использовал всего три формулы, которые он назвал фигурами или формами для обозначения классических силлогизмов. В четвертом издании Symbolic Logic, Part I . Elementary , Доджсон указал на это в Приложении, адресованном учителям, где он написал:
Что касается силлогизмов , то я нахожу их [в учебниках] девятнадцать форм вместе с десятком других, которые они проигнорировали, и все они могут быть организованы в три формы, каждая из которых имеет свое очень простое правило. (Bartley 1977, p. 250)
В Symbolic Logic, Part I , вышедшем в четырех изданиях в 1896 г., Доджсон представил силлогизмы, как в этом примере:
No x are mʹ;
Все м есть у.
∴ No x are yʹ
в форме условных операторов с использованием формы нижнего индекса, которая символически записывается как: xmʹ 0 † m 1 yʹ 0 (обратное ¶) xyʹ 0 (Bartley 1977, стр. 122) с обратным знаком абзаца, обозначающим связующее отношение импликации, которое он определил как: предложения на левой стороне «было бы, если бы оно было истинным, доказывало бы» предложение в правой части. (Bartley 1977, стр. 119) Алгебраическая нотация Доджсона — это модификация Булевой, которую он считал громоздкой.
122) с обратным знаком абзаца, обозначающим связующее отношение импликации, которое он определил как: предложения на левой стороне «было бы, если бы оно было истинным, доказывало бы» предложение в правой части. (Bartley 1977, стр. 119) Алгебраическая нотация Доджсона — это модификация Булевой, которую он считал громоздкой.
Почему Доджсон решил писать свои книги по логике под своим псевдонимом? Бартли предлагает сочетание мотивов: он хотел, чтобы материал понравился широкой аудитории, особенно молодежи, и эту задачу облегчило широкое признание, полученное им как писателем Льюисом Кэрроллом. Кроме того, был финансовый мотив; книги, написанные Льюисом Кэрроллом, могли принести больший доход, чем книги математика Чарльза Доджсона. К 1896 Доджсон был очень обеспокоен своей смертностью и ответственностью, которую он нес за будущую заботу о своей семье, особенно о своих незамужних сестрах. Но были и другие причины, по которым он хотел разоблачения, которое предлагал его псевдоним. Глубоко религиозный человек, Доджсон считал свои математические способности даром, который он должен использовать в служении Богу. В письме к своей математически одаренной сестре Луизе от 28 сентября 1896 г. он писал: 2 nd Часть Логики. Также у меня в голове есть книга по логике… Поэтому я решил сначала закончить вторую часть ….Книга станет отличной новинкой и поможет, я полностью уверен, в изучении логики намного легче, чем сейчас: и я также верю, что это поможет религиозным мыслям, придав ясность концепции и выражения, что может позволить многим людям столкнуться и преодолеть многие религиозные трудности для себя. . Так что я действительно считаю это работой для Бог . (Бартли 1977, стр. 366-371)
В письме к своей математически одаренной сестре Луизе от 28 сентября 1896 г. он писал: 2 nd Часть Логики. Также у меня в голове есть книга по логике… Поэтому я решил сначала закончить вторую часть ….Книга станет отличной новинкой и поможет, я полностью уверен, в изучении логики намного легче, чем сейчас: и я также верю, что это поможет религиозным мыслям, придав ясность концепции и выражения, что может позволить многим людям столкнуться и преодолеть многие религиозные трудности для себя. . Так что я действительно считаю это работой для Бог . (Бартли 1977, стр. 366-371)
б. Диаграммы Венна и Кэрролла
В своих диаграммных методах и Венн, и Кэрролл использовали простые симметричные фигуры и ценили визуальную ясность и простоту рисования как наиболее важные атрибуты. Подобно Булю и Джевонсу, оба придерживались традиции исчисления-рационализатора , то есть механической дедукции. Каждый из них использовал систему символических форм, изоморфную их диаграммным формам.
И диаграммы Венна, и диаграммы Кэрролла равны максимальное , в том смысле, что никакая дополнительная логическая информация, такая как инклюзивные дизъюнкции, ими не может быть представлена. Но диаграммы Кэрролла легче рисовать для большого количества наборов из-за их самоподобия и алгоритмической конструкции. Эта закономерность упрощает обнаружение и, таким образом, стирание ячеек, соответствующих классам, уничтоженным предпосылками аргумента. Хотя и диаграммы Венна, и диаграммы Кэрролла могут представлять экзистенциальные утверждения, диаграммы Кэрролла способны легко решать более сложные задачи, чем система Венна, без ущерба для визуальной ясности диаграммы. Кэрролл только намекнул на превосходство своего метода, когда сравнил собственное решение силлогизма с тем, что дал Венн. (Кэрролл 1958, pp. 182-183)
И в системе Доджсона, и в системе Венна могут быть представлены экзистенциальные предложения. Использование маленького знака плюс «+» в области для обозначения того, что она не пуста, не появлялось до 1894 года, и Доджсон сообщил об этом в своей книге по символической логике. Однако Доджсон, возможно, был первым, кто использовал его. Рабочий лист MS по логическим задачам, вероятно, 1885 года, содержит вариант трехбуквенной диаграммы со знаком «+», представляющим непустую область. Но в своей опубликованной работе Доджсон предпочел символ «1» для обозначения непустой области и символ «0» для обозначения пустой области.
Однако Доджсон, возможно, был первым, кто использовал его. Рабочий лист MS по логическим задачам, вероятно, 1885 года, содержит вариант трехбуквенной диаграммы со знаком «+», представляющим непустую область. Но в своей опубликованной работе Доджсон предпочел символ «1» для обозначения непустой области и символ «0» для обозначения пустой области.
Диаграммы Венна и Кэрролла могут представлять исключительные дизъюнкции; ни один из них не может представлять инклюзивные дизъюнктивные утверждения, такие как x + y, когда x и y имеют что-то общее. Эксклюзивные дизъюнкции важны в силлогистической логике, потому что экзистенциальные утверждения, такие как «некоторые x есть y», могут быть записаны как дизъюнкция xyz или xyz¢; а утверждение «некоторые y есть z¢» можно записать в виде дизъюнкции xyz¢ или x¢yz¢. На самом деле невозможно представить общую дизъюнктивную информацию на диаграмме без добавления произвольного дополнительного синтаксического устройства, а такое добавление привело бы к потере наглядности диаграммы. Кэрролл также представил универсальное множество, включив диаграмму, особенность, которую Венн не считал достаточно важной, чтобы беспокоиться о ней, но которая необходима для изображения вселенной дискурса, ключевого понятия современной логики, обсуждаемого Булем и развитого им дальше.
Кэрролл также представил универсальное множество, включив диаграмму, особенность, которую Венн не считал достаточно важной, чтобы беспокоиться о ней, но которая необходима для изображения вселенной дискурса, ключевого понятия современной логики, обсуждаемого Булем и развитого им дальше.
Пятнадцать силлогизмов Кэрролла могут быть представлены диаграммами Венна и даже диаграммами Эйлера, но не с визуальной ясностью диаграмм Кэрролла. Сам Кэрролл показал это, когда представил решение силлогизма по методу Эйлера, состоящее из восемнадцати диаграмм, и решение, которое Венн дал для того же силлогизма, где, возможно, впервые, поскольку он не появляется во втором издании В своей книге по символической логике Венн использовал маленький «+» для обозначения непустой области. (Кэрролл 1958, pp. 180-182)
Энтони Макула разработал итерационный метод для получения новых диаграмм Кэрролла, которые он назвал (k+n)-граммами, где k > 4 и кратно четырем, а n = 1, 2, 3, 4, поместив 2 k разделов k-граммы в каждый из разделов n-граммы соответственно. Алгоритм строит (k + n)-грамму для любого такого k путем итерации. Теперь легко видеть, что описание Доджсоном в части I Symbolic Logic диаграммы 9-множества, составленной из двух диаграмм 8-множества, одной для внутренней и одной для внешней части восьмого множества, является результатом размещения разделы 8-грамм в каждом из двух разделов 1-грамм. А 10-множественная диаграмма, которую он описал как расположение четырех восьмибуквенных диаграмм в квадрате, является результатом помещения частей 8-граммы в каждую из четырех частей 2-граммы. Заметим, что при k > 4 построение новой (k+n)-граммы меняет порядок вставки разбиений, поскольку вставки кратны 4-граммам в n-граммы. (Кэрролл 1958, стр. 178-9; Macula 1995, pp. 269-274)
Алгоритм строит (k + n)-грамму для любого такого k путем итерации. Теперь легко видеть, что описание Доджсоном в части I Symbolic Logic диаграммы 9-множества, составленной из двух диаграмм 8-множества, одной для внутренней и одной для внешней части восьмого множества, является результатом размещения разделы 8-грамм в каждом из двух разделов 1-грамм. А 10-множественная диаграмма, которую он описал как расположение четырех восьмибуквенных диаграмм в квадрате, является результатом помещения частей 8-граммы в каждую из четырех частей 2-граммы. Заметим, что при k > 4 построение новой (k+n)-граммы меняет порядок вставки разбиений, поскольку вставки кратны 4-граммам в n-граммы. (Кэрролл 1958, стр. 178-9; Macula 1995, pp. 269-274)
Хотя система Венна изоморфна булевой логике классов, она не изоморфна булевой алгебре, потому что нет способа проиллюстрировать инклюзивные дизъюнктивные утверждения, то есть утверждения, отличные от тех, которые могут выражаться в терминах удаления классов, как в предыдущем примере, и в других исключительных дизъюнктивных выражениях, таких как: x’w(yz’ + y’z), то есть то, что не является x, но есть w, и либо y, но не z, либо z, но не y. (Венн 1881, стр. 102) Экзистенциальные утверждения могут быть представлены в диаграммах Венна, и он представил механизм во втором издании Символическая логика (на самом деле два разных представления: штриховка горизонтальной линии, целые числа) . Выбор маленького знака плюса в области «+» для обозначения того, что она не пуста, по-видимому, был сделан после 1894 года и описан Кэрроллом в его книге по символической логике . (Venn 1971, стр. 131-132; Carroll 1958, стр. 174)
(Венн 1881, стр. 102) Экзистенциальные утверждения могут быть представлены в диаграммах Венна, и он представил механизм во втором издании Символическая логика (на самом деле два разных представления: штриховка горизонтальной линии, целые числа) . Выбор маленького знака плюса в области «+» для обозначения того, что она не пуста, по-видимому, был сделан после 1894 года и описан Кэрроллом в его книге по символической логике . (Venn 1971, стр. 131-132; Carroll 1958, стр. 174)
В 1959 году Тренчард Мор-младший доказал то, что Венн знал как истину, что диаграммы Венна могут быть построены для любого числа односвязных регионы. Его конструкция сохраняет свойство, которое Венн считал существенным, а именно то, что каждая подобласть односвязна и представляет собой различную комбинацию перекрытия всех односвязных областей, ограниченных кривыми Жордана. Но диаграммы, полученные в результате построения Мора, довольно сложны и содержат то, что Мор назвал «кривой плетения». (Еще 1959, стр. 303-304)
(Еще 1959, стр. 303-304)
Для большого числа множеств диаграммы Кэрролла легче рисовать, поскольку они самоподобны, т. е. каждая диаграмма остается инвариантной при изменении масштаба, разрывной и допускающей построение алгоритмически. Их регулярность упрощает обнаружение и стирание ячеек, которые должны быть уничтожены посылками силлогистического аргумента, задача, которую трудно выполнить в диаграммах Венна для пяти или более классов. Например, диаграмма с пятью наборами получается путем помещения вертикального отрезка в каждую из шестнадцати частей диаграммы с четырьмя наборами, а диаграмма с шестью наборами получается путем размещения 2 2 разделов подходящим образом уменьшенной диаграммы из двух множеств на каждый из шестнадцати разделов диаграммы из четырех множеств. Аналогичным образом строятся семи- и восьмимножественные диаграммы. Мы видим, что каждая k-грамма (диаграмма k-наборов) имеет 2 k разделов, например, диаграмма с пятью наборами имеет тридцать два раздела, а диаграмма с 8 наборами — двести пятьдесят шесть.
г. «Методы» Доджсона
Подход Доджсона к решению логических задач привел его к изобретению различных методов. В Символическая логика, часть I это метод подчеркивания, метод нижних индексов и метод диаграмм. В части II это методы зарешеченных помещений и зарешеченных групп, хотя он не называл их «методами», и, главное, метод деревьев. В Книге (главе) XII второй части Символическая логика вместо того, чтобы просто демонстрировать дерево решений по частям для конкретной проблемы, он дает «монолог» по мере его работы, сопровождаемый «постановочными указаниями», показывающими, что он делает. чтобы дать читателю возможность построить дерево в забавной форме. Бартли приводит множество примеров проблем соритов, решаемых методом дерева, в Книге xii части II символической логики. И несколько сложных задач-головоломок, решенных методом дерева, появляются в Книге xiii части II из 9.0680 Символическая логика .
В то время как его известность как логика основывается на этих визуальных нововведениях, методы Доджсона существенно зависят от его идиосинкразической алгебраической нотации, которую он назвал методом нижних индексов. Он использовал буквы для терминов, которые могут представлять классы или атрибуты. (В части II Symbolic Logic буквы также используются для представления утверждений.) Нижний индекс 0 на букве обозначает отрицание существования объекта; индекс 1 означает существование объекта. Когда в выражении две буквы, не имеет значения, какая из них первая или какая из них подстрочная, потому что каждая подстрочная буква действует обратно к началу выражения, то есть справа налево.
Он использовал буквы для терминов, которые могут представлять классы или атрибуты. (В части II Symbolic Logic буквы также используются для представления утверждений.) Нижний индекс 0 на букве обозначает отрицание существования объекта; индекс 1 означает существование объекта. Когда в выражении две буквы, не имеет значения, какая из них первая или какая из них подстрочная, потому что каждая подстрочная буква действует обратно к началу выражения, то есть справа налево.
Бартли заметил, что экзистенциальный импорт подразумевается в методе индексов Доджсона. Используя это обозначение, у Доджсона не было другого способа отделить подлежащее от сказуемого, например, xy 1 z’ 0 , которое выражает, что все xy являются z, подразумевает, что существует некоторых xy. Но мы можем интерпретировать это как то, что либо xy не являются z, либо все xy являются z, что эквивалентно в современной логике. Однако Доджсон, возможно, не придерживался этой идеи как философского убеждения.
Как отмечает Джордж Энглбретсен, «хорошее обозначение делает скрытые вещи очевидными… Кэрролл считал, что его собственное обозначение по крайней мере проще, чем у Буля». (Englebretsen 2007, стр. 145)
Когда Доджсон впервые применил свой метод дерева? Конечно, раньше, чем 16 июля 1894 г., когда он записал в своем дневнике, что решал задачу о сорока посылках. Это дата, когда он разработал свой последний формальный метод, который он назвал методом деревьев. Существенной характеристикой этого метода является то, что он использует reductio ad absurdum подход, стандартный метод доказательства в геометрии, когда для того, чтобы доказать, что множество ретинендов (терминов в заключении) является ничтожным (пустым), мы начинаем с предположения вместо этого, что это сущность, затем посредством процесса дедукции, приходящего к противоречию с этим предположением, которое доказывает, что множество ретинендов действительно ничтожно. Ему нужен был новый формальный метод для решения этих более сложных задач, потому что он понимал, что его диаграммный метод уже не годится. Существенная особенность метода дерева состоит в том, что если вывод, следующий из набора посылок, предполагается ложным, то если рассуждение из него вместе со всеми посылками приводит к противоречию, то исходное рассуждение оказывается верным. Это самое раннее современное использование дерева истинности, используемое для эффективного рассуждения в логике классов.
Существенная особенность метода дерева состоит в том, что если вывод, следующий из набора посылок, предполагается ложным, то если рассуждение из него вместе со всеми посылками приводит к противоречию, то исходное рассуждение оказывается верным. Это самое раннее современное использование дерева истинности, используемое для эффективного рассуждения в логике классов.
4 августа 1894 года он соединил свой метод дерева с методом подчеркивания, записав в своем дневнике: «Я только что обнаружил, как превратить генеалогию в размеченные сориты». (Abeles 1990, стр. 30) Похоже, он планировал продолжить работу с этим методом и его естественными расширениями, закрытыми помещениями и закрытыми группами.
Три месяца спустя он записал:
Сделал открытие в Логике,… преобразование «генеалогического» доказательства в регулярный ряд соритов… Сегодня я придумал план работы с каждой колонкой вверх по до развязки – потом начинать заново с Прем. только выше, и внесите в него результаты столбцов, в любом порядке, который работает лучше всего . … Это единственный известный мне способ упорядочить, как Сориты, количество премий, намного превышающее количество исключений, где каждый атрибут появляется 2 или 3 раза в в каждом столбце таблицы. Мой пример был последним в новой редакции Кейнса. (Wakeling 2005, p.155)
… Это единственный известный мне способ упорядочить, как Сориты, количество премий, намного превышающее количество исключений, где каждый атрибут появляется 2 или 3 раза в в каждом столбце таблицы. Мой пример был последним в новой редакции Кейнса. (Wakeling 2005, p.155)
В другом письме Луизе Доджсон от 13 ноября 1896 г., в котором он ответил на заданные ею вопросы об одной из его проблем, которую она пыталась решить, мы снова видим, что использование Доджсоном своего визуальные методы перешли от его метода диаграмм к его методу деревьев. Он написал:
Что касается ваших 4 вопросов… Лучший способ взглянуть на это – предположить, что Ретиненды являются Атрибутами Унив. Затем представьте Диаграмму, назначенную этому Университету и разделенную повторяющейся Дихотомией для всех Атрибутов, чтобы иметь 2 n Ячеек для n Атрибутов. (Веселая диаграмма для рисования, скажем, с 50 атрибутами!
(Там должно быть около 1000 000 000 000 ячеек.) Если Дерево исчезает, это показывает, что каждая ячейка: пустая . 2005, стр. 40)
2005, стр. 40)
Доджсон считал, что метод дерева превосходит «метод» закрытых помещений. Он написал:
Мы обнаружим, что метод деревьев избавляет нас от многих проблем, связанных с предыдущим процессом. В этом более раннем процессе мы были обязаны внимательно следить за всеми запрещенными предпосылками, чтобы быть уверенными в том, что не будем использовать какую-либо такую посылку до тех пор, пока все ее «бары» не появятся в этом сорите. В этом новом Методе Закрытые Помещения сами о себе заботятся. (Бартли 1977, стр. 287)
Перед созданием своего древовидного метода Додсон использовал свой «метод» закрытых предпосылок для создания наиболее перспективных (упорядоченных) списков предпосылок и частичных выводов для получения полного заключения сорита. Он понял, что слишком много таких списков не приведет к правильному заключению, поэтому отказался от этого подхода в пользу своего метода дерева. Но современные автоматизированные программы рассуждений могут использовать прямой подход, управляемый соответствующим образом, чтобы предотвратить доказательство ложных частичных результатов, которые не имеют отношения к получению полного результата.
Когда Доджсон использовал свой «метод» закрытых предпосылок для проверки дерева, он руководил созданием упорядоченных списков, применяя стратегию упорядочения, известную сейчас как единиц предпочтения , которая выбирает сначала предложения с наименьшим количеством терминов. По его собственным словам:
«[W]когда есть два филиала, из которых один возглавляется одиночным письмом , а другой парой , сначала нужно взять одиночное письмо. , превратите его в сорит и запишите его частичный вывод: затем возьмите двойное -Письменное отделение: превратите его также в сориты. (Бартли, 1977, стр. 295)
При проверке дерева он также использовал правило исключения лишних посылок (тех посылок, которые ничего не исключают). Его правилом было игнорировать такую предпосылку, даже если она вызывала разветвление дерева. Но в отсутствие более мощных правил вывода и дополнительных стратегий, впервые разработанных в двадцатом веке, у него не было возможности более эффективно подойти к решению этих многобуквенных задач.
Метод дерева является расширением таблиц истинности, переход к деревьям из таблиц выполняется легко. (Полное обсуждение этой темы см. в Anellis 2004.) Использование таблиц истинности для проверки несоответствия прямолинейно, но очень неэффективно, как знает любой, кто работал с таблицами истинности, включающими восемь или более случаев. Вместо этого метод дерева истинности одновременно исследует наборы случаев, что делает его эффективным для проверки достоверности аргументов, включающих очень большое количество предложений, вручную или с помощью компьютера. Чтобы проверить обоснованность аргумента, состоящего из двух посылок и вывода, равнозначно определив, является ли набор из двух предпосылок и отрицание заключительного предложения противоречивым, с помощью метода таблиц истинности, включающего, скажем, три условия, требуется вычислить значения истинности в восьми случаях, чтобы определить, есть ли случай, когда значения всех трех терминов истинны. Но готовое закрытое дерево устанавливает эту обоснованность аргумента, показывая, что нет случаев, в которых три предложения верны. Однако, если какой-либо путь в готовом дереве не может быть закрыт, аргумент недействителен, поскольку открытый путь представляет собой набор контрпримеров.
Однако, если какой-либо путь в готовом дереве не может быть закрыт, аргумент недействителен, поскольку открытый путь представляет собой набор контрпримеров.
Современный метод дерева как процедура принятия решений в классической логике высказываний и логике первого порядка берет свое начало в работе Генцена по естественной дедукции, в частности, в его формулировке исчисления секвенций, известной как LK. Но путь не прямой; главными участниками являются Эверт В. Бет, Яакко Хинтикка, Рэймонд Смаллян и Ричард Джеффри.
16 июля 1894 года Доджсон соединил свой метод дерева со своей более ранней работой «Метод диаграмм». Он писал: «Мне пришло в голову попробовать сложные сориты с помощью метода, который я использовал для выяснения того, какие клетки, если таковые имеются, выживают для возможного занятия, когда заданы определенные нулевые значения» (Бартли 19).77, с. 279)
Редактор журнала в примечании к статье Метод деревьев Льюиса Кэрролла: его истоки в «Исследованиях логики», отметил:
Бет в его разработке дедуктивных и семантических картин, уходят своими корнями в работы Чарльза Пирса, учеников и коллег Пирса, и, в частности, в собственные экзистенциальные графики Пирса». (Anellis 1990, стр. 22)
(Anellis 1990, стр. 22)
В своей обширной статье он предположил, что «Возможно, этот ценный вклад в теорию доказательств [метод дерева Доджсона] следует назвать методом дерева Хинтикка-Смалляна или даже методом дерева Доджсона- Дерево Хинтикка-Смаллян…». (Анеллис 1990, с. 62).
В восьми книгах или главах Символическая логика, часть I . Элементарно Кэрролл вводит понятия вещей и их атрибутов, предложений и их типов, диаграмм и диаграммного метода, силлогизмов и их типов, более сложных соритесов, а также двух методов нижних индексов и подчеркивания.
Когда Доджсон использовал «метод запретных предпосылок» для проверки дерева, он руководил созданием упорядоченных списков, применяя стратегию упорядочения, известную сейчас как предпочтение единиц , которое сначала выбирает предложения с наименьшим количеством терминов. Он также использовал правило исключения лишних посылок (тех посылок, которые ничего не исключают) при проверке дерева. Его правилом было игнорировать такую предпосылку, даже если она вызывала разветвление дерева. Но из-за отсутствия более мощных правил вывода и дополнительных стратегий у него не было возможности более эффективно подойти к решению этих многобуквенных задач.
Его правилом было игнорировать такую предпосылку, даже если она вызывала разветвление дерева. Но из-за отсутствия более мощных правил вывода и дополнительных стратегий у него не было возможности более эффективно подойти к решению этих многобуквенных задач.
В то время как современники, такие как Венн, использовали диаграммы для представления логических задач в логике, Доджсон поднял визуальный подход к этому на новый уровень в своем методе деревьев. Это был один из двух дополнительных методов формальной логики, которые он представил во второй части 9.0680 Символическая логика . Первый, прямой подход к решению многобуквенных соритесов, который он назвал запретными посылками, является расширением его метода подчеркивания. Посылка с перемычкой — это такая, в которой термин t встречается в одной посылке, а его отрицательный t N встречается в двух или более посылках, и наоборот. Например, если посылка содержит термин a и два исключенных термина bc , то abc является ничтожным, подразумевая, что a has the pair of attributes: bc N or b N c or b N c N , that is, a is barred by the nullity от наличия атрибутов до .
Доджсон распространил эту идею на то, что он назвал группой с перемычкой : когда термин t встречается в двух или более посылках, а t N также встречается в двух или более посылках. Его правило работы с зарешеченными помещениями требует, чтобы все помещения, запирающие данное помещение, использовались в первую очередь. Доджсон явно не определял этот метод, поэтому мы будем называть эти определения и правило работы с ними его методом закрытых предпосылок. Это ранний формальный метод определения порядка использования посылок соритов для получения заключения.
Похоже, он планировал продолжить работу со своим методом дерева и методом перечеркнутых групп. В неопубликованном письме, первая страница которого отсутствует, вероятно, датированном концом 1896 или началом 1897 года, он написал, скорее всего, своей сестре Луизе:
Я думал об этом вопросе о «запрещенных группах»…. Она принадлежит к самой увлекательной области предмета, которую я хочу назвать «теорией вывода»:… Вот одна теорема. Я полагаю, что если вы построите Сориты, которые будут устранять все время и дадут совокупность Ретинендов как Недействительность, и если вы введете в него ту же букву, 2 или 3 раза, как Исключение, и его Противоречие такое же количество раз, и исключая его каждый раз, когда он встречается, вы обнаружите, что если вы решите его как Дерево , что вы не Не используйте все помещения! (Коллекция Weaver, без даты; воспроизведено Abeles 2005, стр. 40)
Я полагаю, что если вы построите Сориты, которые будут устранять все время и дадут совокупность Ретинендов как Недействительность, и если вы введете в него ту же букву, 2 или 3 раза, как Исключение, и его Противоречие такое же количество раз, и исключая его каждый раз, когда он встречается, вы обнаружите, что если вы решите его как Дерево , что вы не Не используйте все помещения! (Коллекция Weaver, без даты; воспроизведено Abeles 2005, стр. 40)
Пример, названный «Проблема свиней и воздушных шаров», находится у Бартли на стр. 378-80. Там Доджсон создал Реестр Атрибутов , показывающий элиминанды (термин, который появляется в обеих строках Реестра, то есть в положительной и отрицательной форме в двух посылках). Когда термин появляется в обеих строках и в одной строке более чем в двух посылках, мы имеем случай закрытых посылок. Все остальные термины являются ретинендами.
Его почти навязчивая забота о точности привнесла определенную жесткость во многие его серьезные математические работы, но юмор, который он использует, заразителен и придает этим работам, особенно по логике, привлекательную легкость. То, что его использование юмора отличало его работу, видно из обзоров Symbolic Logic, Part I. Elementary , которые появились при его жизни.
То, что его использование юмора отличало его работу, видно из обзоров Symbolic Logic, Part I. Elementary , которые появились при его жизни.
Анонимный рецензент книги написал в номере The Educational Times , что «его очень необычное изложение элементарной логики, кажется, пощекотало воображение людей». (1 июля 189 г.6, 316) Цитаты, которые продолжают цитироваться современными авторами, особенно из его книг по логике, подкрепляют эту точку зрения. Однако реакция математика Хью Макколла, анонимного рецензента Symbolic Logic, Part I. Elementary в The Athenaeum, , была неоднозначной. Он описал диаграммный метод Кэрролла для решения логических задач как элегантный, но он критически относился к нотации Кэрролла (метод индекса) и использованию экзистенциального значения, которое утверждает существование субъекта в А предложения. Например, предложение «Все философы логичны» предполагает существование по крайней мере одного философа. Макколл добавил: «[Мы] не можем сказать, какие важные сюрпризы в частях ii. и iii. его системы, возможно, приготовили для нас, когда они появятся» (17 октября 1896 г., стр. 520–521). И Макколл, и Доджсон были активными участниками раздела «Математические вопросы и решения» книги 9.0680 Educational Times . И по крайней мере один раз их интересовал один и тот же вопрос вероятности. Макколл представил решение логической проблемы Доджсона, вопрос 14122, версию парадокса парикмахерской, опубликованную посмертно.
Макколл добавил: «[Мы] не можем сказать, какие важные сюрпризы в частях ii. и iii. его системы, возможно, приготовили для нас, когда они появятся» (17 октября 1896 г., стр. 520–521). И Макколл, и Доджсон были активными участниками раздела «Математические вопросы и решения» книги 9.0680 Educational Times . И по крайней мере один раз их интересовал один и тот же вопрос вероятности. Макколл представил решение логической проблемы Доджсона, вопрос 14122, версию парадокса парикмахерской, опубликованную посмертно.
Вдобавок к четкому изложению и необычному стилю, которые характеризуют его книги, кажется, есть еще одна существенная близость, которая поддерживала интерес Макколла к работам Кэрролла. Их обмен мнениями показывает, что оба были глубоко заинтересованы в точном использовании слов. И оба не видели ничего плохого в том, чтобы приписывать словам произвольное значение, если значение является точным, а присвоение согласовано.
Кажется очевидным, что между августом и декабрем 1894 года Доджсон, возможно, рассматривал направление, которое было более формально развито позже Хью Макколлом, еще в 1896-97 годах, и расширено в его книге 1906 года, Символическая логика и ее приложения , где он определил строгую импликацию , в которой содержание антецедента и консеквента имеют отношение к действительности условного, за двадцать лет до того, как модальная логика начала ставиться на современную основу, начиная с работ американского философа и логик Кларенс Ирвинг Льюис.
4. Автоматизация дедукции
Начало автоматизации дедукции восходит к 1920-м годам с работы Торальфа Скулема, который изучал проблему существования модели, удовлетворяющей заданной формуле, и который ввел функции для обработки универсальных и кванторы существования. Другие логики, такие как Давид Гильберт, Вильгельм Аккерманн, Леопольд Лёвенгейм, Жак Эрбранд, Эмиль Пост и чуть позже Алонзо Черч, Курт Гёдель и Алан Тьюринг, внесли дополнительные важные идеи. Одним из наиболее важных, вытекающих из метаматематической основы Гильберта, было представление о том, что формализованные логические системы могут быть предметом математического исследования. Но только в 19В 50-х годах компьютерные программы, использующие дерево в качестве основной структуры данных, использовались для доказательства математических теорем.
Основное внимание в этих ранних программах уделялось доказательству теорем логики высказываний и логики предикатов. Описывая «логическую машину» Ньюэлла, Шоу и Саймона 1957 года, Мартин Дэвис отметил, что направленный путь в дереве дает доказательство действительного аргумента, где его предпосылки и заключение представлены в виде узлов, а ребро, соединяющее два узла предпосылок, представлено действительный вывод в соответствии с заданным набором правил для вывода доказательств.
Современный древовидный метод как решающая процедура для классической логики высказываний и логики первого порядка возник в работах Герхарда Генцена по естественной дедукции, в частности, в его формулировке исчисления секвенций, известной как LK. Но маршрут не был прямым, основными участниками были Эверт Бет, Ричард Джеффри, Яакко Хинтикка и Рэймонд Смаллиан. В 1955 году Бет представил разработанный им табличный метод, состоящий из двух деревьев, которые позволили бы систематически искать опровержение данной (истинной) последовательности. Дерево — это левосторонняя таблица Бет, в которой верны все формулы. Правила разложения дерева, то есть правила вывода, эквивалентны правилам Генцена в его секвенциальном исчислении.
Бартли сказал следующее о методе дерева Доджсона для получения достоверных выводов из соритов и головоломок:
Процедура Кэрролла имеет поразительное сходство с используемыми деревьями . . .согласно методу «Семантических таблиц», опубликованному в 1955 г. голландским логиком Э. У. Бетом. Основные идеи идентичны. (Bartley 1977, p. 32)
голландским логиком Э. У. Бетом. Основные идеи идентичны. (Bartley 1977, p. 32)
Доджсон был первым человеком в наше время, который применил механическую процедуру, свой древовидный метод, чтобы продемонстрировать правильность решения некоторых сложных задач. Метод дерева является прямым расширением таблиц истинности, и Доджсон работал с неполной таблицей истинности в одном из решений, которые он дал своей проблеме парикмахерской в сентябре 189 г.4. Бартли пишет: «Матрица используется… для компонентов; но анализ и присвоение значений истинности соединениям проводятся в прозаическом комментарии к таблице». (Bartley 1977, p. 465n.)
4 августа он соединил метод дерева с рифлеными соритами:
Я только что обнаружил, как превратить генеалогию в рифленые сориты: трудность заключается в том, чтобы иметь дело с разветвлениями. Скажем, «все a есть b или c» = «все A есть b» и «все α есть c», где два множества A, α составляют a. Затем докажите каждый столбец отдельно. (Уэйклинг, 2005, стр. 158)
158)
30 октября, используя задачу из нового издания книги Кейнса « Исследования и упражнения по формальной логике », он обнаружил, как перемещаться по дереву, представляющему сориты с 21 посылкой, имеющей 10 атрибутов, из которых 8 исключены. (Wakeling 2005, стр. 181)
Когда открытая ветвь делится на две ветви и термин, здесь б́, появляется в одной из ветвей, а его отрицание добавляется к другой ветви, мы имеем пример использования правило разреза. Доджсон предвидел метод, который не был полностью разработан до 19 века.30 с. Он писал:
Стоит отметить, что в в каждом случае мы прибавляем к одно одиночных букв, Противоречащее из другое : этот факт следует помнить как правило … .У нас теперь есть Правило процедуры, которое следует соблюдать всякий раз, когда мы обязаны разделить наше Древо на две Ветви. (Бартли 1977, стр. 287)
Он продолжал открывать новые способы улучшения своего обращения с деревьями, записывая это в своем дневнике 12/13 ноября 1896, «Открыл [a] метод объединения 2 Деревьев, доказывающих abcʹ 0 † abdʹ 0 , в одно доказывающее ab(cd)ʹ 0 , с помощью Аксиомы cd(cd)ʹ 0 . ” (Wakeling 2005, p. 279)
” (Wakeling 2005, p. 279)
В обмене письмами в октябре и ноябре 1896 года с Джоном Куком Уилсоном, профессором логики Уайкхема в Оксфорде, Доджсон изменил версию задачи с восемнадцатью посылками, содержащую лишние посылки, на одну с пятнадцатью посылками. помещение. Бартли включает обе версии, а также их решения методом дерева.
В неопубликованном письме Куку Уилсону от 25 сентября 1896 г. в связи с проблемой соритов Доджсон писал:
То, что вы говорите о «лишних предпосылках», меня очень интересует. Дело в том, что у меня бьет , на данный момент. . . И, если вы сможете сформулировать какое-либо доказательство, позволяющее вам сказать: «все посылки равны 90 680, безусловно, 90 681 необходимы для доказательства Заключения», я буду очень рад его увидеть. ( Доджсон , Коллекция Воробья, 25 сентября 189 г.6. Courtesy Morton N. Cohen)
Трудность установления теоремы для определения лишних предпосылок беспокоила его. Это была проблема, которую он не смог решить.
5. Логический круг Доджсона
Джон Венн был еще одним английским логиком, с работами которого Доджсон был знаком и с которым он контактировал. Венн, сторонник подхода Буля к логике, опубликовал первое издание своей книги Symbolic Logic в 1881 году. Оно включало уже знакомые ему диаграммы, изображающие отношения между классами, чтобы можно было установить истинность или ложность предложений, использующих их.
В 1892 году Уильям Э. Джонсон опубликовал первую из трех статей в Mind под названием «Логическое исчисление», в которой он различал термин условный от термина гипотетический . Доджсон, как и большинство логиков его времени, не делал этого различия, используя термин гипотетических для обеих ситуаций. Точка зрения Джонсона заключалась в том, что условное предложение выражает отношение между двумя явлениями, тогда как гипотетическое выражает отношение между двумя предложениями, имеющими независимое значение. Итак, условное связывает два термина, а гипотетическое связывает два суждения. Джон Невилл Кейнс, с работами которого Доджсон был хорошо знаком, согласился с точкой зрения Джонсона. Однако Венн, хотя он тоже был знаком с работами Джонсона, придерживался совершенно иного взгляда на гипотетики, утверждая, что, поскольку они носят неформальный характер, их действительно не следует рассматривать как часть символической логики.
Итак, условное связывает два термина, а гипотетическое связывает два суждения. Джон Невилл Кейнс, с работами которого Доджсон был хорошо знаком, согласился с точкой зрения Джонсона. Однако Венн, хотя он тоже был знаком с работами Джонсона, придерживался совершенно иного взгляда на гипотетики, утверждая, что, поскольку они носят неформальный характер, их действительно не следует рассматривать как часть символической логики.
Уильям Стэнли Джевонс был еще одним сторонником Буля, чьи книги, Pure Logic; или «Логика качества отдельно от количества» (1864 г.) и «Принципы науки: трактат о логике и научном методе» (1874 г.), принадлежащие Доджсону. Джевонс представил логический алфавит для классовой логики в 1869 году, а в следующем году он представил Королевскому обществу в Лондоне машину, которая использовала его для механического решения логических задач, которую он назвал логическим пианино.0031 Доджсон был хорошо знаком с Кейнсом « Исследования и упражнения по формальной логике » во втором издании 1887 года, цитируя непосредственно из него в главе II Книги X в части II « Символическая логика ». Кейнс включил парадокс парикмахерской Доджсона в качестве упражнения в главу IX издания 1906 года своей книги. (Кейнс 1906, стр. 273 – 274)
Кейнс включил парадокс парикмахерской Доджсона в качестве упражнения в главу IX издания 1906 года своей книги. (Кейнс 1906, стр. 273 – 274)
а. Эффект «Алисы»
В переписке между Венном и Доджсоном в 1894 г. и из обзоров, появившихся вскоре после публикации обоих Логическая игра и Символическая логика, часть I , мы видим, что репутация Доджсона как автора книг «Алиса» делала его прежде всего автором детских книг и мешала серьезно относиться к его книгам по логике. Барьер, созданный славой, которую Кэрролл заслуженно заработал благодаря своим книгам об Алисе, в сочетании со стилем письма, более литературным, чем математическим, помешал сообществу британских логиков должным образом признать его значительным логиком.
Этому впечатлению способствовал его собственный, более литературный стиль письма. То, что такой была его репутация, видно из обзоров Symbolic Logic, Part I при его жизни. Конечно, большинство его современников не знали о важности его диаграммного метода решения силлогизмов, который он впервые представил в «Логической игре» . В неопубликованном письме Венну от 11 августа 1894 года он писал:
В неопубликованном письме Венну от 11 августа 1894 года он писал:
«Вы можете использовать задачу, которую я вам послал, как вам угодно, и (конечно) ссылаться на статью в «Разуме» — [ A Logical Paradox, N. S. v. 3, 1894, pp. 436-438 относительно примера гипотетических предложений] Ваше письмо, как я вижу, перечеркнуло одно от меня, в котором я послал вам «алгебраическую иллюстрацию Немо». Надеюсь, вы сможете найти для него место в своей следующей книге. Возможно, вы могли бы добавить его в качестве примечания в конце книги и дать на стр. 442, ссылка на него? Буду признателен, если Вы никому не будете упоминать мое настоящее имя, в связи с моим псевдонимом. С удовольствием изучу новое издание вашей книги». (Документы Венна, библиотеки Гонвилля и Кая, Кембриджский университет)
И на с. 442 второго исправленного издания его Symbolic Logic Венн писал:
[T] что фраза «x подразумевает y» не подразумевает, что рассматриваемые факты известны как связанные или что одно суждение формально выводится из другой. Этот конкретный аспект вопроса, весьма вероятно, будет знаком некоторым из моих читателей по проблеме, недавно распространенной среди логиков для сравнения мнений. Поскольку автор предложения для широкого читателя более известен в совсем другой области литературы, я назову его 9.0680 Задача Алисы .
Этот конкретный аспект вопроса, весьма вероятно, будет знаком некоторым из моих читателей по проблеме, недавно распространенной среди логиков для сравнения мнений. Поскольку автор предложения для широкого читателя более известен в совсем другой области литературы, я назову его 9.0680 Задача Алисы .
6. Логические парадоксы
а. Парадокс парикмахерской
Приложение к Книге XXI содержит восемь версий парадокса парикмахерской Доджсона, одна из которых была опубликована в Mind как «Логический парадокс». В другом приложении к этой книге Бартли обсуждает другой вклад Кэрролла в Mind : «Что черепаха сказала Ахиллесу». Эти два приложения делают вопросы, затронутые Кэрроллом в этих опубликованных статьях, — наряду с комментариями, которые они порождали у современных логиков и философов, — гораздо более доступными.
Задача о парикмахерской была первой публикацией Доджсона в журнале Mind . Это транскрипция спора, который противопоставил его Джону Куку Уилсону. Бертран Рассел использовал проблему парикмахерской в своей книге «Принципы математики », чтобы проиллюстрировать свой принцип, согласно которому ложное суждение подразумевает все остальные. Венн был одним из первых, кто обсудил это в печати, во втором издании своего « Symbolic Logic ». Бартли включает восемь версий «Парадокс парикмахерской» Доджсона, одна из которых была опубликована в Mind вместе с подробным комментарием.
Бертран Рассел использовал проблему парикмахерской в своей книге «Принципы математики », чтобы проиллюстрировать свой принцип, согласно которому ложное суждение подразумевает все остальные. Венн был одним из первых, кто обсудил это в печати, во втором издании своего « Symbolic Logic ». Бартли включает восемь версий «Парадокс парикмахерской» Доджсона, одна из которых была опубликована в Mind вместе с подробным комментарием.
В парадоксе парикмахерской есть два правила, регулирующие движения трех парикмахеров Аллена, Брауна и Карра. Первое правило заключается в том, что когда уходит Карр, то если уходит Аллен, Браун остается дома. Второе правило заключается в том, что когда уходит Карр, уходит Браун. Задача состоит в том, чтобы использовать эти правила для определения возможных движений Карра. В ходе оживленной двухлетней переписки конца 1892 года, хранящейся в Бодлианской библиотеке, Доджсон и Кук Уилсон отточили свои различные взгляды на парадокс парикмахерской. Уилсон считал, что все суждения категоричны и поэтому гипотетические не могут быть суждениями.
Уилсон считал, что все суждения категоричны и поэтому гипотетические не могут быть суждениями.
Неурегулированный характер темы гипотез при жизни Доджсона становится очевидным в начале примечания , которое Кэрролл написал в конце своей статьи: в теории гипотез. Спорный вопрос некоторое время обсуждался несколькими практикующими логиками, которым я его представил; и различные и противоречивые мнения, которые выявила моя переписка с ними, убеждают меня в том, что этот предмет нуждается в дальнейшем рассмотрении, чтобы преподаватели логики и писатели могли прийти к какому-то согласию относительно того, что такое гипотезы.0680 — это , и как с ними следует обращаться. (Carroll 1894, p. 438)
Бартли отмечает в своей книге, что парадокс парикмахерской не является подлинным логическим парадоксом, как парадокс лжеца. Как правило, парадокс — это утверждение, которое кажется либо противоречивым, либо противоречащим ожиданиям.
Многие версии парадокса парикмахерской, разработанные Доджсоном, демонстрируют эволюцию его мыслей о гипотетических и материальных импликациях, в которых связь между антецедентом и консеквентом условного (если (антецедент), то (консеквент)) равна формальное, то есть не зависит от их истинностных значений. Это результат логики Буля. Шесть версий парадокса парикмахерской дают представление о том, как Доджсон думал о проблеме по мере ее развития. Бартли опубликовал пять из этих шести, а также три других, два из которых являются примерами; один почти такой же, как один из других, опубликованных Бартли. Кроме того, есть три более ранние версии, которые Бартли не публиковал; все датированы мартом 1894 года.
Это результат логики Буля. Шесть версий парадокса парикмахерской дают представление о том, как Доджсон думал о проблеме по мере ее развития. Бартли опубликовал пять из этих шести, а также три других, два из которых являются примерами; один почти такой же, как один из других, опубликованных Бартли. Кроме того, есть три более ранние версии, которые Бартли не публиковал; все датированы мартом 1894 года.
Ранние версии «Парадокса парикмахерской» показывают изменение способа представления условных выражений Доджсоном. В более ранних версиях он выражал гипотетическое суждение в терминах классов, т. е. если А есть В, то С есть D. Только позже он обозначил А, В, С и D как предложения.
Вариант парадокса парикмахерской, вопрос 14122, который Бартли не признал таковым, был опубликован в феврале 1899 года в The Educational Times после смерти Доджсона и перепечатан в Mathematical Questions and Solutions в следующем году. В том же году появилось два разных решения: одно принадлежит Гарольду Уортингтону Керджелу, члену Лондонского математического общества, а другое — Хью Макколлу. (Более подробное обсуждение парадокса парикмахерской см. в публикациях А. Моктефи.)
(Более подробное обсуждение парадокса парикмахерской см. в публикациях А. Моктефи.)
Статья под названием «Логический парадокс», опубликованная в 1894 году в Mind , вызвала отклики в виде последующих статей, опубликованных в Mind многими выдающимися логиками времен Доджсона, включая Хью МакКолла, Э. Э. Констанс Джонс. , преподаватель логики в Гертоне, одном из женских колледжей в Кембридже, Альфред Сиджвик, автор книги « заблуждений». Взгляд на логику с практической стороны , а также Джонсон, Кейнс, Кук Уилсон и Рассел.
Письмо Доджсона от 11 августа 1894 года Джону Венну привело к тому, что Венн включил версию парадокса парикмахерской во второе издание (1884 г.) своей книги Symbolic Logic . Кейнс включил версию парадокса парикмахерской в свою книгу, а Брэдли обсудил ее в книге Selected Correspondence .
Бертран Рассел дал то, что сейчас является общепринятым выводом по этой проблеме в своей книге 1903 года Принципы математики . Если p представляет «Карр отсутствует»; q означает «Аллен выбыл»; r означает «Браун отсутствует», тогда парадокс парикмахерской можно записать так: (1) q подразумевает r; (2) из p следует, что q подразумевает не-r. Рассел утверждал, что единственный правильный вывод из (1) и (2) таков: если p истинно, q ложно, то есть если Карр выбыл, Аллен в игре (Рассел 19).03, с. 18)
Если p представляет «Карр отсутствует»; q означает «Аллен выбыл»; r означает «Браун отсутствует», тогда парадокс парикмахерской можно записать так: (1) q подразумевает r; (2) из p следует, что q подразумевает не-r. Рассел утверждал, что единственный правильный вывод из (1) и (2) таков: если p истинно, q ложно, то есть если Карр выбыл, Аллен в игре (Рассел 19).03, с. 18)
б. Ахиллес и черепаха
В следующем году Доджсон опубликовал в Mind более важный парадокс: «Что черепаха сказала Ахиллесу». Хотя при жизни Доджсона она не вызвала никаких откликов, много откликов было получено после его смерти, и проблема остается нерешенной по сей день. (См. Moktefi and Abeles 2016.)
Это парадокс:
- Вещи, равные одной и той же вещи, равны друг другу,
- Две стороны этого треугольника равны.
- Две стороны этого треугольника равны друг другу.
Доджсон первым осознал, что при логическом выводе правило, позволяющее сделать вывод из посылок, не может рассматриваться как дополнительная посылка без порождения бесконечного регресса.
И парадоксы парикмахерской, и парадоксы Ахилла включают условные выражения, и Доджсон использовал материальный смысл возразить им, но ему было неудобно с этим. Он боролся с несколькими дополнительными проблемами, связанными с гипотезами. В примечании к опубликованной версии «Парадокса парикмахерской» в июле 1894 года Доджсон задал несколько вопросов, первый из которых заключался в том, может ли гипотеза быть законной, если ее предпосылка ложна; второй — могут ли быть совместимы две гипотезы, формы которых — «если А, то В» и «если А, то не-В».
Бартли опубликовал второе издание Symbolic Logic, Part II в 1986 году, в которую он включил решения некоторых из наиболее важных проблем и головоломок Кэрролла, дополнительные открытия доказательства гранки и новую интерпретацию Марком Р. Ричардсом логических схем Кэрролла.
К 1897 году Доджсон, возможно, переосмыслил свое использование экзистенциального импорта. Бартли цитирует дневниковую запись 1896 года и недатированное письмо Куку Уилсону в качестве доказательства (Bartley 1977, стр. 34–35). импорт. Книга (глава) XXII содержит решения Доджсона проблем, поставленных другими логиками. Одно из этих решений проблемы, поставленной Августом де Морганом относительно существования их подданных, содержится в безадресном письме от 15 марта 189 г.7. (Bartley 1977, стр. 480–481) Из ответа Доджсона на это письмо шесть дней спустя мы теперь знаем, что оно было отправлено его сестре Луизе в ответ на ее решение проблемы. В этом неопубликованном письме Доджсон предложил:
34–35). импорт. Книга (глава) XXII содержит решения Доджсона проблем, поставленных другими логиками. Одно из этих решений проблемы, поставленной Августом де Морганом относительно существования их подданных, содержится в безадресном письме от 15 марта 189 г.7. (Bartley 1977, стр. 480–481) Из ответа Доджсона на это письмо шесть дней спустя мы теперь знаем, что оно было отправлено его сестре Луизе в ответ на ее решение проблемы. В этом неопубликованном письме Доджсон предложил:
[I]если вы примете во внимание вопрос существования и предположите, что каждое Предложение подразумевает существование его Субъекта и, следовательно, его Предиката, тогда вы, безусловно, делаете получить различия между ними: каждый подразумевает определенные существования не подразумеваются другими. Но это усложняет дело: & я думаю, будет более аккуратной проблемой согласиться (как я предложу сделать в своем решении), что Предложения следует понимать как подразумевающие существование этих отношений, а только следует понимать как утверждение, что если бы существовали такие-то и такие-то отношения , то следуют определенные результаты. (Доджсон, коллекция Берола, Нью-Йоркский университет, 21 марта 1897 г.)
(Доджсон, коллекция Берола, Нью-Йоркский университет, 21 марта 1897 г.)
7. Доджсон и современная математика
В части II книги «Символическая логика » подход Доджсона привел его к изобретению различных методов, которые поддаются механическим рассуждениям. Это «методы» зарешеченных помещений и зарешеченных групп и, главное, метод деревьев. Хотя Доджсон работал с ограниченной формой логики классов и использовал довольно неудобные обозначения и странные имена, методы, которые он представил, предвосхитили современные концепции и методы автоматизированных рассуждений, такие как деревья истинности, двоичное разрешение, предпочтение единиц и набор стратегий поддержки, а также опровержение. полнота.
Его система логических диаграмм является надежной и полной системой доказательства силлогизмов. Надежность системы доказательств гарантирует, что могут быть сделаны только верные выводы. (Система доказательств верна тогда и только тогда, когда выводы, которые мы можем вывести из посылок, являются их логическими следствиями. ) И наоборот, ее полнота гарантирует, что могут быть выведены все истинных выводов. (Система доказательств является полной тогда и только тогда, когда всякий раз, когда набор посылок логически подразумевает вывод, мы можем вывести этот вывод из этих посылок.)
) И наоборот, ее полнота гарантирует, что могут быть выведены все истинных выводов. (Система доказательств является полной тогда и только тогда, когда всякий раз, когда набор посылок логически подразумевает вывод, мы можем вывести этот вывод из этих посылок.)
Несколько методов, использованных Доджсоном в его Symbolic Logic , содержат ядра концепций и методов, которые использовались в автоматическом доказательстве теорем, начиная с двадцатого века. Эти ранние программы были сосредоточены на доказательствах теорем логики высказываний и логики предикатов.
Его единственное правило вывода, подчеркивание, которое берет два предложения, выбирает термин в каждом из одного и того же подлежащего или сказуемого, имеющих противоположные знаки, и дает другое предложение, является примером двоичное разрешение , самый важный из этих ранних методов доказательства в автоматизированной дедукции.
Хотя Доджсон не сделал следующего шага, присоединив идею несоответствия к набору предпосылок и выводов, этот метод обработки многобуквенных силлогизмов на первом рисунке является формальным тестом на несоответствие , который квалифицируется как конечное опровержение множества исключений и повторений. Его построение дерева использует одно правило вывода (алгоритм), двоичное разрешение , и он направляет развитие дерева с помощью стратегии ограничения, теперь известной как набор поддержки , которая применяет двоичное разрешение на каждом последующем шаге вывода, только если предыдущий шаг был выведен из подмножества вывода. предпосылки и отрицание вывода, то есть из множества ретиноидов. Эта стратегия повышает эффективность рассуждений, предотвращая создание бесплодных путей. И этот древовидный тест — это и , и звук , и 9.0680 завершить , то есть, если начальный набор посылок и заключения непротиворечив, будет открытый путь через дерево, делающий его обоснованным; если в готовом дереве есть открытый путь, начальный набор предпосылок и вывод согласован, что делает его завершенным.
Его построение дерева использует одно правило вывода (алгоритм), двоичное разрешение , и он направляет развитие дерева с помощью стратегии ограничения, теперь известной как набор поддержки , которая применяет двоичное разрешение на каждом последующем шаге вывода, только если предыдущий шаг был выведен из подмножества вывода. предпосылки и отрицание вывода, то есть из множества ретиноидов. Эта стратегия повышает эффективность рассуждений, предотвращая создание бесплодных путей. И этот древовидный тест — это и , и звук , и 9.0680 завершить , то есть, если начальный набор посылок и заключения непротиворечив, будет открытый путь через дерево, делающий его обоснованным; если в готовом дереве есть открытый путь, начальный набор предпосылок и вывод согласован, что делает его завершенным.
Сравнение двух частей Символическая логика показывает прогресс, достигнутый Доджсоном в автоматизированном подходе к решению многосвязных силлогистических задач (соритесов) и головоломок с интригующими названиями, такими как «Задача бакалейщиков на велосипедах». и «Проблема свиней и воздушных шаров».
и «Проблема свиней и воздушных шаров».
Многие современные автоматические программы рассуждений используют аргумент доведение до абсурда , в то время как другие программы рассуждений, которые используются для поиска дополнительной информации, не пытаются установить противоречие. В 1985 году Юинг Ласк и Росс Овербик модифицировали одну из головоломок Доджсона, «Задачу школьников», чтобы сделать ее совместимой с прямой генерацией утверждений (в клаузальной форме) с помощью автоматизированной программы рассуждений. Их программа сначала дала более слабый вывод, а затем — такой же более сильный вывод, как и Доджсон, используя свой метод дерева. Решение Ласка и Овербика в 1985 к «Проблеме соли и горчицы» Доджсона и А. Г. Кону в 1989 г. к той же проблеме пятью годами позже использовалась многосортная логика, чтобы проиллюстрировать мощь двух из этих программ.
В информатике база данных имеет состояние , которое является значением для каждого из ее элементов. Триггер может проверять условие, которое может быть указано в предложении when , то есть определенное действие будет выполняться только в том случае, если правило срабатывает и условие сохраняется, когда происходит событие запуска.
Триггер может проверять условие, которое может быть указано в предложении when , то есть определенное действие будет выполняться только в том случае, если правило срабатывает и условие сохраняется, когда происходит событие запуска.
Доджсон определил термин Космофаза как «состояние Вселенной в какой-то конкретный момент: и я рассматриваю любое Утверждение, истинное в этот момент, как Атрибут этой Космофазы». (Бартли, 1977, стр. 481). Любопытно, что данное Доджсоном определение космофазы прекрасно вписывается в эту современную структуру.
8. Кэрролл как популяризатор
Доджсон был популяризатором и преподавателем математики и логики. Он начал преподавать математику в школе Св. Олдата напротив Крайст-Черч в 1856 году.0680 Логическая игра и, в большей степени, Символическая логика, часть I. Элементарная , чтобы значительно превосходить те, которые используются в настоящее время, и быть полезными при обучении учащихся в возрасте от двенадцати до четырнадцати лет. Цель игры, в которую играли с доской и фишками, состояла в том, чтобы решить силлогизмы. Он считал, что вся его книга Symbolic Logic , включая запланированные части II и III, понравится учащимся в возрасте до двадцати лет и, следовательно, будет полезна на университетском уровне.
Цель игры, в которую играли с доской и фишками, состояла в том, чтобы решить силлогизмы. Он считал, что вся его книга Symbolic Logic , включая запланированные части II и III, понравится учащимся в возрасте до двадцати лет и, следовательно, будет полезна на университетском уровне.
В то время как он был лектором по математике в Крайст-Черч, он часто давал бесплатные частные уроки семейным группам родителей, их детей и друзей их детей в их частных домах по таким математическим темам, как шифры, особенно его Memoria Technica шифр, арифметический и алгебраические головоломки, а также алгоритмический метод определения дня недели для любой заданной даты. Первоначально он создал шифр Memoria Technica в 1875 году для вычисления логарифмов, но нашел для него множество других применений в качестве общего средства для запоминания, написав упрощенную версию для учебных целей в 1888 году.0032
Темы, которые он выбрал для преподавания в частном порядке, были сосредоточены на вспомогательных средствах памяти, математических трюках, вычислительных упрощениях и задачах, подходящих для быстрых вычислений в уме, и развил эту последнюю тему в книгу, Curiosa Mathematica, Часть 2 : Проблемы с подушкой, обдумываемые во время бодрствования Часы (1894 г. ), опубликованный в 1893 г. Таким образом, он продолжал давать инструкции по темам логики. Он также давал уроки логики в своих комнатах в Крайст-Черч. В июне 1886 года он читал лекции в Леди Маргарет Холл в Оксфорде, а в мае 1887 года — в Оксфордской средней школе для девочек. Там он читал лекции как студентам, так и отдельно их учителям. Он читал лекции в Сент-Хьюз-холле, еще одном женском колледже Оксфорда, в мае и июне 189 г.4. В январе 1897 г. он начал курс лекций по символической логике в больнице Эббота в Гилфорде.
), опубликованный в 1893 г. Таким образом, он продолжал давать инструкции по темам логики. Он также давал уроки логики в своих комнатах в Крайст-Черч. В июне 1886 года он читал лекции в Леди Маргарет Холл в Оксфорде, а в мае 1887 года — в Оксфордской средней школе для девочек. Там он читал лекции как студентам, так и отдельно их учителям. Он читал лекции в Сент-Хьюз-холле, еще одном женском колледже Оксфорда, в мае и июне 189 г.4. В январе 1897 г. он начал курс лекций по символической логике в больнице Эббота в Гилфорде.
Он использовал материал, который в конечном итоге включил в свою книгу Игра логики , работу, которую он по существу завершил в июле 1886 года, но которая не появлялась до ноября в издании, которое Доджсон отверг как некачественное. Второе (опубликованное) издание вышло в феврале следующего года. Доджсон надеялся, что книга понравится молодежи как забавное развлечение для ума. Он нашел эту книгу, а тем более свою Символическая логика, часть I. Элементарная необходимая при обучении студентов. Он считал, что его собственная книга по символической логике намного превосходит те, что используются в настоящее время.
Элементарная необходимая при обучении студентов. Он считал, что его собственная книга по символической логике намного превосходит те, что используются в настоящее время.
21 августа 1894 года, отвечая на письмо бывшей подруги детства Мэри Браун, которой сейчас тридцать два года, он написал:
Вы спрашиваете, какие книги я написал…. В настоящее время я усердно работаю (и работаю уже несколько месяцев) над своей книгой по логике. (Это действительно было наготове уже дюжину лет: «месяцы» относятся к подготовке к Прессе.) Сейчас Symbolic Logic , в 3 частях — и часть I должна быть достаточно легкой для мальчиков и девочек (скажем) 12 или 14 лет. Я очень надеюсь, что она попадет в средние школы и т. д. Я преподавал ее в Оксфорде класс девушек в средней школе, еще один класс любовниц (!), и еще один класс девушек в одном из женских колледжей. (Cohen 1979, p. 1031)
В письме своей сестре Элизабет от 25 ноября 1894 г. он писал: чтобы помочь людям, у которых есть религиозные трудности, чтобы они увидели абсолютную необходимость иметь четкие определения , чтобы, прежде чем приступить к обсуждению любого из этих головоломных вопросов, они могли иметь ясное представление о чем они говорят о . (Cohen 1979, p. 1041)
(Cohen 1979, p. 1041)
Формулировки почти всех задач в обеих частях его книг по символической логике забавно читать. Этот атрибут вытекает из объявленной цели книг – популяризировать предмет. Но Доджсон, естественно, включил юмор в большую часть своих серьезных математических работ, придав этой работе печать своего литературного гения.
Эдвард Уэйклинг отмечает, что его обучение логике принимало три формы: серия уроков в школе, уроки для небольшой группы друзей или семей, которых он знал, или обучение одного уверенного в себе, умного и внимательного друга-ребенка. Последний метод был его любимым. Эдит Рикс, которой он посвятил Запутанная история (1885) в виде восьмистрочного акростиха, в котором вторая буква каждой строки составляет ее имя, была его первой ученицей по логике. Доджсон написал ей много писем по поводу проблем логики. По его словам, она была самой умной женщиной, которую он когда-либо знал.
В Приложении, адресованном учителям, к части I книги Symbolic Logic , четвертое издание, Кэрролл указал некоторые из тем, которые он запланировал для части II. К ним относятся «очень загадочные темы гипотез, дилемм и парадоксов». (Bartley 1977, стр. 229) Доджсона обычно интересовало качество аргументов, особенно тех, которые могли сбить с толку. Парадоксы попадают в эту категорию, потому что они, кажется, доказывают то, что заведомо ложно. И парадоксы, безусловно, побудили его создать оригинальные методы для их решения, такие как его метод дерева.
К ним относятся «очень загадочные темы гипотез, дилемм и парадоксов». (Bartley 1977, стр. 229) Доджсона обычно интересовало качество аргументов, особенно тех, которые могли сбить с толку. Парадоксы попадают в эту категорию, потому что они, кажется, доказывают то, что заведомо ложно. И парадоксы, безусловно, побудили его создать оригинальные методы для их решения, такие как его метод дерева.
Доджсон выразил свои мысли о том, как лучше всего обучать логике молодых людей в «Увлекательном умственном развлечении для молодежи», когда он написал: и специально для детей, я могу только сказать, что я обучил методу символической логики многих детей с полным успехом … Школьницы охотно берутся за это. У меня были занятия с такими девушками, а также с любовницами, ….Что касается Symbolic Logic, являющегося сухим , и неинтересным , я могу только сказать, попробуйте это! Я развлекался различными научными занятиями в течение примерно сорока лет и не нашел ничего, что могло бы соперничать с ним в устойчивой и чарующей привлекательности. (Carroll 1896, воспроизведено в Abeles 2010, стр. 96-97)
(Carroll 1896, воспроизведено в Abeles 2010, стр. 96-97)
9. Заключение
Вдохновение для большей части того, что Доджсон написал о логике, пришло из его контактов с преподавателями других колледжей в Оксфорде, Кембридже и других местах. Он рассказывал о своей работе в кругу коллег и спрашивал их мнения. В отличие от большинства из них, он не добивался членства в профессиональных математических и философских обществах, не посещал их собрания и не читал лекций, за немногими исключениями. Он не был традиционным математиком. Скорее, он применял математические и логические решения проблем, которые его интересовали. Как прирожденный логик в то время, когда логика не считалась частью математики, он успешно работал в обеих областях.
Хотя изобретательность головоломок и примеров, созданных Доджсоном, в целом приветствовалась, утверждения Бартли о значении работы Доджсона были подвергнуты сомнению, так что ее значение для развития логики не было полностью оценено, когда книга была впервые опубликована. Но впоследствии другие ученые, работавшие над логическими и математическими работами Кэрролла, такие как Дункан Блэк, Джордж Энглбретсен, Амируш Моктефи, Адриан Райс, Марк Ричардс, Юджин Сенета, Эдвард Уэйклинг и Робин Уилсон, сделали важные открытия, которые значительно укрепили репутацию Кэрролла.
Но впоследствии другие ученые, работавшие над логическими и математическими работами Кэрролла, такие как Дункан Блэк, Джордж Энглбретсен, Амируш Моктефи, Адриан Райс, Марк Ричардс, Юджин Сенета, Эдвард Уэйклинг и Робин Уилсон, сделали важные открытия, которые значительно укрепили репутацию Кэрролла.
Почему ученые заинтересовались серьезной работой Доджсона только во второй половине ХХ века? Помимо публикации Бартли книги Кэрролла «Символическая логика», есть еще несколько причин. Одной из наиболее важных является роль некоторых издателей в том, чтобы сделать его работу доступной. К ним относятся: Clarkson N. Potter и Dover Press в США и Kluwer в Нидерландах, чьи книги распространялись как в США, так и в Великобритании. Статьи в популярном разделе «Математические игры» Мартина Гарднера из Журнал Scientific American также включал несколько математических идей Доджсона и был бесценным источником информации для ученых. Другая важная причина заключается в том, что только в двадцатом веке некоторые из его математических и логических идей нашли применение в том смысле, что его работа предвосхитила их использование. Математические и логические работы Доджсона имели широкую основу, но его влияние на важные события двадцатого века произошло в основном после его смерти.
Математические и логические работы Доджсона имели широкую основу, но его влияние на важные события двадцатого века произошло в основном после его смерти.
10. Ссылки и дополнительная литература
a. Начальная школа
- Буль Г. Исследование законов мышления . Лондон, Макмиллан, 1854 г.
- Буль, Г. Математический анализ логики . Лондон, Макмиллан, 1847 г.
- Брэдли, Ф. Х. Принципы логики , Лондон, Oxford University Press, 1883.
- Кэрролл, К.Л. Логическая игра . Макмиллан, Лондон, 1887 г. .
- Кэрролл, К.Л. Символическая логика: Часть I . Лондон, Макмиллан, 1896 г.
- Кэрролл, К.Л. Логическая игра . Опубликовано вместе с Symbolic Logic, Part I , как The Mathematical Recreations of Lewis Carroll , New York, Dover, 1958.
- Кэрролл, Л. «Логический парадокс». Разум т.3, н.11, 1894, стр. 436-438.
- Кэрролл, Л.
 Что Черепаха сказала Ахиллесу». Разум , т.4, н.14, 1895, стр. 278-280.
Что Черепаха сказала Ахиллесу». Разум , т.4, н.14, 1895, стр. 278-280. - Коэн, М. Н. Письма Льюиса Кэрролла . 2 тт. Нью-Йорк, издательство Оксфордского университета, 1979. .
- Де Морган, А. Формальная логика . Лондон, Тейлор и Уолтон, 1847 г.
- Де Морган, А. О силлогизмах и других логических сочинениях . Лондон, Рутледж и Кеган Пол, 1966 год. .
- Доджсон, К.Л. Евклид и его современные соперники . Лондон, Макмиллан, 1879 г.
- Dodgson, CL Curiosa Mathematica. Часть I: Новая теория параллелей . Лондон, Макмиллан, 1888 г. .
- Dodgson, CL Curiosa Mathematica. Часть II: Проблемы с подушками . Лондон, Макмиллан, 1893 г. .
- Джевонс, В. С. Чистая логика, или логика качества помимо количества , Лондон, Э. Стэнфорд, 1864.
- Джонсон, У. Э. «Логическое исчисление I, II, III», Mind 1, стр. 3-30; II, стр. 235-250; III, стр.
 340-357, 1892.
340-357, 1892. - Кейнс, Дж. Н. Исследования и упражнения по формальной логике , 3 , изд. . Лондон, Macmillan, 1894.
- Рассел Б. Основы математики . Кембридж, издательство Кембриджского университета, 1903. .
- Сиджвик, А. Заблуждения: взгляд на логику с практической стороны . Лондон, Кеган, Пол, Тренч, 1883.
- Венн, Дж. Символическая логика . Лондон, Макмиллан, 1881.
- Venn, J. Symbolic Logic , 2 nd исправленное изд. Лондон, Макмиллан, 1894 г. .
- Уэйклинг, Э., изд. Дневники Льюиса Кэрролла . т. 6. Клиффорд, Херефордшир, Общество Льюиса Кэрролла, 2001 г.
- Уэйклинг, Э., изд. Дневники Льюиса Кэрролла . т. 8. Клиффорд, Херефордшир, Общество Льюиса Кэрролла, 2004.
- Уэйклинг, Э., изд. Дневники Льюиса Кэрролла . т. 9. Клиффорд, Херефордшир, Общество Льюиса Кэрролла, 2005.
б. Среднее
- Абелес, Ф.
 Ф. «Метод деревьев Льюиса Кэрролла: его истоки в исследованиях логики». Современная логика , т. 1, н. 1, 1990, стр. 25-35.
Ф. «Метод деревьев Льюиса Кэрролла: его истоки в исследованиях логики». Современная логика , т. 1, н. 1, 1990, стр. 25-35. - Абелес, Ф.Ф., изд. Математические брошюры Чарльза Лютвиджа Доджсона и связанные с ними статьи . Нью-Йорк, Североамериканское общество Льюиса Кэрролла, 1994.
- Абелес, Ф. Ф. «Формальная логика Льюиса Кэрролла». История и философия логики т. 26, 2005 г., стр. 33-46.
- Абелес, Ф. Ф. «От метода дерева в современной логике к началу автоматизированного доказательства теорем». В: Шелл-Геллаш, А. и Джардин, Д., ред. От исчисления к компьютерам . Вашингтон, округ Колумбия, Математическая ассоциация Америки, 2005 г., стр. 149–160.
- Абелес, Ф. Ф. «Визуальная логика Льюиса Кэрролла». История и философия логики т. 28, 2007 г., стр. 1-17.
- Абелес, Ф.Ф., изд. Логические брошюры Чарльза Лютвиджа Доджсона и связанные с ними произведения . Нью-Йорк, Североамериканское общество Льюиса Кэрролла, 2010.
 .
. - Абелес, Ф. Ф. «На пути к системе визуального доказательства: метод деревьев Льюиса Кэрролла». Logica Universalis , т. 6, н. 3/4, 2012, стр. 521-534.
- Абелес, Ф. Ф. «Математическое наследие». В: Уилсон, Р. и Моктефи, А. ред. Математический мир Чарльза Л. Доджсона (Льюис Кэрролл) . Оксфорд, издательство Оксфордского университета, 2019, стр. 177–215.
- Анеллис, Ирвинг. «От семантических таблиц к деревьям Смаллиан: история метода дерева фальсифицируемости». Современная логика , т. 1, н. 1, 1990, стр. 36-69.
- Коркорон, Дж. «Информационно-теоретическая логика». В Martinez, C. et al . ред. Правда в перспективе , Олдершот, Ашгейт, 1998, стр. 113-135.
- Энглебрецен, Г. «Черепаха, черепаха и дедуктивная логика». Бармаглот , т. 3, 1974, стр. 11-13.
- Энглбретсен, Г. «Правильно викторианская черепаха». Бармаглот , т. 23, 1993/1994, стр. 12-13.
- Энглбретсен, Г.
 , «Додо и ДО: Льюис Кэрролл и Изречение Омни». Труды Канадского общества истории и философии математики, , т. 20, 2008 г., стр. 142–148.
, «Додо и ДО: Льюис Кэрролл и Изречение Омни». Труды Канадского общества истории и философии математики, , т. 20, 2008 г., стр. 142–148. - Макула, А. «Льюис Кэрролл и перечисление минимальных покрытий». Mathematics Magazine , т. 69, 1995, стр. 269-274.
- МакКолл, Х. «Обзор символической логики , часть I , Льюиса Кэрролла». The Athenaeum , 17 октября 1896 г., стр. 520–521.
- Марион, М. и Моктефи, А. «Символическая логика в Себате в Оксфорде а-ля Fin du XIXe Siècle: Les Disputes Logiques de Lewis Carroll et John Cook Wilson». Revue d’Histoire des Sciences , т. 67, с. 2, 2014, стр. 185-205.
- Моктефи, А. «Помимо силлогизмов: (отмеченная) четырехбуквенная диаграмма Кэрролла». В: Моктефи, А., Шин, С.-Дж., ред. Visual Reasoning with Diagrams , Basel, Birkhäuser, 2013, стр. 55-72.
- Моктефи, А. «О социальной пользе символической логики: Льюис Кэрролл против «логиков». Studia Metodologiczne 35, 2015, стр.
 133-150.
133-150. - Моктефи А. Трудно ли читать чужие книги? Книги по логике в частной библиотеке Льюиса Кэрролла». Acta Baltica Historiae et Philosophiae Scientiarum , т. 5, н. 1, 2017, стр. 28-49.
- Моктефи, А. «Логика». В: Уилсон, Р.Дж., Моктефи, А., ред. Математический мир Чарльза Л. Доджсона (Льюиса Кэрролла) , Оксфорд, Oxford University Press, 2019, стр. 87–119.
- Моктефи, А. и Абелес, Ф.Ф. «Создание «То, что черепаха сказала Ахиллесу»: логические исследования Льюиса Кэрролла на пути к работоспособной теории гипотез». Кэрроллиан , т. 28, 2016 г., стр. 14–47.
- Моктефи, А. «Зачем упрощать, если можно усложнить? Оценка символической логики Льюиса Кэрролла», Logica Universalis , том 15 (2021), страницы 359–379.
- Мор, Т., младший «О построении диаграмм Венна». J. of Symbolic Logic v. 24, n.4, 1959, стр. 303-304.
- Райс, Адриан. “Алгебра.” В: Уилсон, Р.Дж., Моктефи, А., ред. Математический мир Чарльза Л.
 Доджсона (Льюиса Кэрролла) , Оксфорд, Oxford University Press, 2019, стр. 57–85.
Доджсона (Льюиса Кэрролла) , Оксфорд, Oxford University Press, 2019, стр. 57–85. - Ричардс М. Логическая игра . https://lewiscarrollresources.net/gameoflogic/.
- Сенета, Э. «Льюис Кэрролл как вероятностный и математик». Mathematical Scientist, т. 9, 1984, стр. 79-84.
- Сенета, Э. «Викторианская вероятность и Льюис Кэрролл». Журнал Королевского статистического общества, серия А-Статистика в обществе , т. 175, н. 2, 2012, стр. 435-451.
- Ван Эвра, Дж. «Развитие логики, отраженное в судьбе силлогизма 1600–1900». История и философия логики , т. 21, 2000 г., стр. 115-134.
- Уилсон, Р. «Геометрия». В: Уилсон, Р. и Моктефи, А. ред. Математический мир Чарльза Л. Доджсона (Льюис Кэрролл) . Оксфорд, Oxford University Press, 2019, стр. 31–55 .
- Уилсон, Р. и Моктефи, А. ред. Математический мир Чарльза Л. Доджсона (Льюис Кэрролл) . Оксфорд, издательство Оксфордского университета, 2019.
 .
.
Информация об авторе
Francine F. Abeles
Email: [email protected]
Kean University
U. S. A.
Диаграмма Венна
Узнайте все об определении и увлекательной истории диаграммы Венна!
Чтение за 9 минут
Диаграмма Венна Определение
Диаграмма Венна (также известная как набор или логическая диаграмма) может показать различия, сходства и перекрывающиеся отношения между наборами, то есть группами данных. Чаще всего его используют для описания общих черт между противоборствующими фракциями — например, в приведенном ниже примере диаграммы Венна мы можем видеть общие характеристики клеток растений и животных.
Исходные клетки растений и клетки животных — https://owlcation.com/stem/Plant-Cells-vs-Animal-Cells-With-Diagrams
Набор данных визуализируется как совокупность фиксированных точек внутри замкнутой окружности (обычно это круги, но иногда эллипсы, сферы или даже треугольники): визуальное описание одной категории, общей для всех включенных данных. В приведенном выше примере окружность, содержащая характеристики клеток животных, имеет точки данных: неправильная/круглая, центросомы, центриоли, лизосомы, ядро, клеточная мембрана, цитоплазма, митохондрии, аппарат Гольджи и рибосомы. Только около из этих точек данных/характеристик являются общими для растительных клеток, визуализированных в синем пересечении.
В приведенном выше примере окружность, содержащая характеристики клеток животных, имеет точки данных: неправильная/круглая, центросомы, центриоли, лизосомы, ядро, клеточная мембрана, цитоплазма, митохондрии, аппарат Гольджи и рибосомы. Только около из этих точек данных/характеристик являются общими для растительных клеток, визуализированных в синем пересечении.
Нравится внешний вид этого примера диаграммы Венна? Начните создавать свои собственные!
Главной достопримечательностью диаграмм Венна является это пересечение — данные, которые попадают более чем в одну категорию (в приведенном выше примере это поясняется меткой «оба», хотя следует помнить, что пересечение — это ). не свой собственный, отдельный набор данных). Диаграммы Венна могут состоять из нескольких пересечений и наборов окружностей, но чаще всего используется 3-круговая или тройная диаграмма Венна.
Одним из конкретных факторов популярности тройки Венна является то, что она создает в центре криволинейный треугольник идеальной и постоянной ширины, известный как «треугольник Рело». Эта форма очаровала инженеров, математиков, архитекторов и графических дизайнеров как своими математическими возможностями, так и визуальной красотой, и использовалась эрудитами от немецкого инженера Франца Рело (в честь которого они теперь названы) для создания кинетических машин до Леонардо Да. Винчи для картографической проекции.
Эта форма очаровала инженеров, математиков, архитекторов и графических дизайнеров как своими математическими возможностями, так и визуальной красотой, и использовалась эрудитами от немецкого инженера Франца Рело (в честь которого они теперь названы) для создания кинетических машин до Леонардо Да. Винчи для картографической проекции.
Начните создавать собственные диаграммы и бизнес-графику.
Попробуйте Vizzlo бесплатно
Развитие и история диаграммы Венна
В той или иной форме диаграммы Венна существуют со времен Средневековья. Абстрактное визуальное представление соединений и пересечений различных наборов — невероятно старая концепция, поскольку существует глубокое человеческое стремление показать, что связано, а что нет. Как и в случае с большинством логических сред, с годами он органично рос и менялся, совершенствуясь, переориентируясь и перепрофилируясь в круговую диаграмму, с которой мы так знакомы сегодня.
Первым математиком, непосредственно связанным с этим стилем диаграмм, был немецкий эрудит и философ Готфрид Вильгельм Лейбниц, живший примерно в конце 1600-х годов. По сути, Лейбниц был одним из первых, кто применил многие концепции визуализации данных: он верил в символическое представление сложных мыслей, чтобы не только лучше передавать эти идеи, но и оставлять меньше места для человеческих ошибок, неправильного толкования и вытекающих из этого споров. По мнению Лейбница, этого добились расчеты и визуализация различий во мнениях в формализованных логических диаграммах.
По сути, Лейбниц был одним из первых, кто применил многие концепции визуализации данных: он верил в символическое представление сложных мыслей, чтобы не только лучше передавать эти идеи, но и оставлять меньше места для человеческих ошибок, неправильного толкования и вытекающих из этого споров. По мнению Лейбница, этого добились расчеты и визуализация различий во мнениях в формализованных логических диаграммах.
Диаграмма Эйлера
Примерно сто лет спустя известный швейцарский математик Леонард Эйлер стал широко известен тем, что использовал перекрывающиеся круги для представления логических выводов (или силлогистических рассуждений). Эти круги используются для изображения четырех категориальных утверждений силлогизма:
- Универсальное утверждение «Все графики Виззло выглядят красиво»
- Универсальное отрицание «Ни один из графиков Виззло не представляет сложности»
- Частное утвердительное «Некоторые из Виззардов Виззарда включают диаграммы Венна»
- Особый негатив «Некоторые из Виззардов Виззарда не являются диаграммами Венна»
Примечание: Знаете ли вы, что в соответствии с логической семантикой в английском языке до конца 16 века было четыре слова для «да» и «нет»?! Универсальное утвердительное было бы произнесено как «да», универсальное отрицательное — как «нет», частное утвердительное — как «да», а частное отрицательное — как «нет».
Чтобы было ясно, стало обычным делом группировать диаграммы Эйлера и Венна под более известным названием «диаграмма Венна», чтобы избежать путаницы — только в очень технических математических ситуациях было бы необходимо провести разграничение между два.
Современная диаграмма Венна
Известная нам сегодня диаграмма Венна была разработана английским математиком Джоном Венном. В 1880 г. он опубликовал статью под названием «О диаграммном и механическом изображении предложений и рассуждений». В нем Венн предложил изменить диаграмму Эйлера, чтобы она стала более полной визуализацией вероятности, требуя изображения всех возможностей. Однако название «диаграмма Венна» было придумано американским философом Кларенсом Ирвингом лишь несколько лет спустя, в 1918.
С тех пор диаграмма Венна была центром обширных исследований многих других известных ученых, в том числе А.В.Ф. Эдвардс, Бранко Грюнбаум и Генри Джон Стивен Смит. Они стали важной визуализацией для математических исследований, будь то традиционная диаграмма с тремя кругами или более сложные версии, включающие сферы и эллипсы, для таких областей, как теория множеств, теория логики, вращательная симметрия и изучение сложных форм и чисел, таких как тессеракт.
Что НЕ является диаграммой Венна?
Из-за такой простой диаграммы Venn неправильно маркировали на протяжении многих лет. На самом деле, чаще всего мы теперь ссылаемся почти исключительно на диаграммы Эйлера, когда обсуждаем «Венна».
Диаграммы Венна, по существу, представляют собой более конкретный тип диаграмм Эйлера. Вот удобная диаграмма Эйлера, наглядно описывающая, что все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна:
Золотое правило диаграммы Венна заключается в том, что она всегда визуализирует все возможности, даже если ни одна из данных не вписывается в эти пересечения, тогда как диаграмма Эйлера визуализирует только те категории, для которых есть данные. Если бы мы заставили приведенную выше диаграмму соответствовать параметрам диаграммы Венна, нам пришлось бы представить, что существуют некоторые диаграммы Венна, которые не являются диаграммами Эйлера. Если поместить это в контекст, это все равно, что заявить, что некоторые животные не являются пингвинами, и, следовательно, некоторые пингвины не являются животными.
Чтобы показать эту разницу на практике, давайте представим, что трое друзей сравнивают свою домашнюю работу. Люси подготовила два домашних задания: одно по «Прокариотам и эукариотам» по естественным наукам и одно по «Вероятности и статистике» по математике. Анвар также написал домашнюю работу по математике «Вероятность и статистика», но выбрал для науки тему «Клетки животных и клетки растений». вообще
Если оранжевый набор данных представляет Янса, розовый набор данных представляет Анвара, а синий набор данных представляет Люси, мы можем организовать эту информацию двумя различными способами.
Диаграмма Эйлера показывает только возможности, для которых у нас уже есть фактические данные. Мы знаем, что Анвар и Люси сделали домашнюю работу по математике по теме «Вероятность и статистика», и пересечение показывает это. Мы знаем, что Янс не создавал домашних заданий по математике, как Анвар и Люси, и что они не выбирали ту же тему, что и он, для естественных наук, поэтому набор данных Янса не пересекается ни с каким другим.
На диаграмме Венна показана одна и та же информация — темы, которые трое друзей изучили индивидуально, и тема по математике, которую выбрали Анвар и Люси. Однако у нас также есть пересечения, которые лишены данных, но представляют все другие возможности.
Оранжевый перекресток слева представляет собой случай, когда Янс вместе с Анваром помнит свою домашнюю работу по математике, а также по естественным наукам, но в этом гипотетическом результате Люси забывает выполнить работу по математике. Зеленый перекресток справа предполагает ту же судьбу для Анвара. Центральный перекресток показывает возможность того, что все трое друзей не забудут поработать над «Вероятностью и статистикой» по математике, а также над различными темами по естественным наукам, и никто не будет наказан…
Готовы создать собственную диаграмму Венна? Вот небольшой ярлык на страницу Vizzard специально для вас.
Для создания диаграммы Венна между двумя наборами данных должны быть как общие черты, так и различия. Если вся классифицированная информация идентична, ваша диаграмма будет выглядеть так:
Если вся классифицированная информация идентична, ваша диаграмма будет выглядеть так:
Даже с двумя наборами данных, если содержащаяся информация не имеет различий, две кривые будут полностью перекрываться, образуя только один круг.
Противоположная проблема, два набора данных без общих черт, также не создадут диаграмму Венна (но вполне приемлемую диаграмму Эйлера, показывающую непересекающихся наборов ).
Удивительно, но то, что выглядит так же знакомо, как приведенный ниже пример, математически не считается диаграммой Венна.
Как объяснялось ранее, одно из ключевых требований к диаграмме Венна состоит в том, что она должна отображать все возможные логические результаты. Поскольку в приведенном выше примере нет пересечения, в котором встречаются только желтый и красный или только синий и оранжевый, его нельзя считать полным изображением универсальной логики.
Резюме
Подводя итог, диаграмма Венна:
- Тип диаграммы Эйлера
- Диаграмма с двумя или более наборами данных, изображенная внутри окружностей
- Используется для визуализации различий и общих черт между этими наборами данных
- Используется для выработки всех логических выводов
- Невероятно быстрое производство с использованием диаграммы Венна от Vizzlo Vizzard
Vizzlo очень прост, и вы можете попробовать его бесплатно.