Линейка для счета по математике: Линейка счетная для работы со счетным материалом, 1 метр (Серия “От 1 до 100”)
К школе готов! (основы счета для детей 6-7 лет)
11+11=22 и серая пятница 12.11.22 Самостоятельный доступ к курсу 5 ев. или 390р
Для оплаты в рубля при оформлении заказа выбирайте “российские кредитные карты”
Чтобы попасть в хорошую школу, ребенку нужно выдержать испытание!
Математика – часть этого испытания!
Вы хотите зараннее приготовиться, заходите в магазин пособий для дошкольников и застываете.
Сотни рабочих тетрадей, всевозможные методички. Что делать? Какие выбрать?
Надежнее, прийти к специалисту, который много лет готовит детей в школу.
В 1995 году я стала работать в дошкольной гимназии “Эрудит” . Именно в этот год школы решили отбирать себе учеников. И возникла необходимость подготовки детей к школе.
Мы с коллегами создали развивающее пространство для наших детей. Они играли, конструировали, пели, танцевали. Мы много говорили о том, о чем взрослые обычно не говорят с детьми. О понятиях и смыслах.
Если ребенок будет ПОНИМАТЬ МАТЕМАТИКУ, ОН ВЫДЕРЖИТ ВСТУПИТЕЛЬНЫЙ ЭКЗАМЕН,
11 лет я шлифовала курс “Занимательной математики”. С трехлетними говорили об одном, с пятилетними о другом. Шестилетние уже могли очень многое. Занятия были выстроены в логичную систему. Я применяла яркие образы и игры, которые делали математику живой, увлекательной и любимой.
Когда я переехала в Германию и стала преподавать дошкольную математику он-лайн, родители и преподаватели развивающих центров из 10 стран стали заниматься с дошкольниками по моим курсам.
Когда я вас спрашиваю, какой должна быть математика для дошкольников, вы отвечаете:
- не скучной
- занятия должны быть выстроены последовательно, чтобы я понимал, откуда мы вышли и куда должны прийти
- игровой
- интересной и для родителя
- с практической деятельностью
Здесь вы найдете множество практических упражнений, которые помогут разобраться с сутью процесса.
Математика для дошкольника должна быть предметна.
Когда он видит не только карточки с цифрами, но и разнообразне предметы, которые можно считать, он гораздо быстрее сможет привязать количество к числу.
Понять, как устроен счет, его логику помогают приспособления для счета.
Если подвести ребенка к собственному изобретению десятичных счётов, приборов для измерения времени, шкалы для измерения расстояния, дело пойдет быстрее. Именно этим мы и будем заниматься в курсе “К школе готов!”
Начнем мы с изобретения АБАКА, первого прибора, который облегчает процесс вычисления. Он может быть таким:
Или вот таким:
Но скорее всего ваш ребенок изобретет совершенно другой прибор! Когда мы понимаем процесс, его суть, то можем выразить в понятной нам форме.
Тема сделал АБАК из своих коллекционных мышей Glocke кошек и собак. Показал нам, какой зверь что значит. И мы легко стали узнавать число, равное 4 мыши, 3 кошки и целых 7 собак!
Магия превращения множества мышей в одну кошку, а множество кошек в собаку – присутствовала!
И на счетах, и в часах, на линейки мы видим числа, запоминаем их взаимное расположение.
И именно эти приборы становятся нашими тренажерами для счета.
Этот семинар для родителей я читала в Москве и Санкт-Петербурге, Бад Наухауме, Мюнхене, Лейдене, Париже, Ганновере, Берлине, Хайфе и Тель-Авиве.
На каждом семинаре родители видели, что игры делаются за несколько минут, а упражения могут быть такими увлекательными, что занятия пролетают мгновенно и азартно!
И почти все говорят: спасибо, вы научили меня считать на счётах. Я не умел.
Доступ к этому курсу бессрочный. Нажав кнопку ОТВЕТИТЬ В ДНЕВНИКЕ вы можете задать мне любой вопрос и получить ответ (в июле я в отпуске, без интернета)
Акционная цена – 11 ев или 847р
Курс расчитан на 9 месячный учебный год в детском развивающем центре, если заниматься 2 раза в неделю.
Этот курс мы сейчас переносим с форума на сайт.
ОТЗЫВЫ.
Как купить курс:
- Зарегистрируйтесь на сайте.
2. На телефоне – в шапке курса, на компьютере – справа есть кнопка КУПИТЬ.
Нажмите ее и курс окажется в корзине.
3. Оформите заказ. (дом и улицу писать не нужно. Страна, любой индекс вашего города и город покупателя нужен нашей налоговой)
4. Выбирайте удобную систему оплаты:
- Российские кредитные карты (оплата в рублях)
- Кредитные карты других стран. (любая валюта переводится в евро)
- Или пейпейл ( конвертируется в евро)
5. Курс окажется в вашем профиле(раздел курсы)
В курсе можно задавать вопросы и просить совета в вашей конкретной ситуации. Кнопка – ответить в дневнике.
Если сайт не принимает вашу карту – пишите на [email protected] Найдем выход!
Линейка “Открытие предметной недели по математике в начальных классах”
Линейка, посвящённая открытию недели математики
1.
Вступительное слово ведущего.
– Ребята, сегодня мы все собрались на линейку, посвященную открытию «Недели математики». В течение всей этой недели на уроках вы будете выполнять разные интересные задания, связанные с математикой. Сегодня, в понедельник, после линейки, ваши учителя расскажут вам занимательный материал, связанный с историей математики (расписание недели).
– Ребята, поднимите руку, кто из вас хорошо считает?
– Знает таблицу умножения?
– Умеет правильно решать задачи?
– Кто из вас любит математику?
– Раз вы так любите математику, сегодня она пришла к нам в гости.
2. Входит Математика.
– Здравствуйте ребята. Как вас много. А сколько здесь классов собралось, чтобы встретиться со мной?
Ведущий:
– Ребята, давайте, быстро сосчитайте? Сколько 1 классов? 2 классов? 3 классов? 4 классов? Всего – 7.
– 7 классов пришли, чтобы поприветствовать тебя царица математика.
Математика:
– Молодцы, ребята, вы хорошо считаете.
Математика – основа и царица всех наук,
И тебе с ней подружиться я советую, мой друг.
Ее мудрые законы, если будешь выполнять,
Свои знанья приумножишь,
Станешь ты их применять.
Сможешь по морю ты плавать,
Сможешь в космосе летать.
Дом построить людям сможешь:
Будет он сто лет стоять.
3. Выступление детей.
– Уважаемая Математика, наши ребята тоже хотят прочитать тебе стихи.
Почему торжественность вокруг?
Слышите, как быстро смолкла речь?
Это о царице всех наук
Поведем сегодня с вами речь.
Не случайно ей такой почет.
Это ей дано давать ответы,
Как хороший выполнить расчет
Для постройки здания, ракеты.
Есть о математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даёшь
Для победы трудностей закалку,
Учится с тобой молодёжь
Развивать и волю и смекалку.
И за то, что в творческом труде
Выручаешь в трудные моменты,
Мы сегодня искренне тебе
Посылаем гром аплодисментов.
Математика-наука
хороша и всем нужна,
без нее прожить нам трудно,
без нее нам жизнь сложна.
Но порой настанет так вот,
что не знаешь, как и быть
математику насильно
я пытаюсь зазубрить.
Но зубрежка вся напрасна,
не доходит до меня
это вовсе не игрушка
ничего, не сдамся я.
Не ленись, трудись, старайся,
Познавая соль наук.
Все доказывать пытайся,
Но не покладая рук.
Математика.
– Вы правы, ребята, чтобы знать математику, нужно очень стараться, быть внимательным и любознательным.
Давайте, ребята, учиться считать,
Делить, умножать, прибавлять, вычитать.
Запомните все, что без точного счета,
Не сдвинется с места любая работа.
Без счета не будет на улице света.
Без счета не сможет подняться ракета.
Без счета письмо не найдет адресата,
И в прятки сыграть не сумеют ребята.
Летит выше звезд арифметика наша,
Уходит в моря, строит здания, пашет,
Сажает деревья, турбины кует,
До самого неба рукой достает.
Считайте, ребята, точнее считайте:
Хорошее дело смелей прибавляйте,
Плохие дела поскорей вычитайте.
Учебник научит вас точному счету,
Скорей за работу, скорей за работу!
4. Окончание линейки.
Ведущий:
– Спасибо тебе, Математика, за твои мудрые слова.
– Царица – Математика, мы приглашаем тебя на неделю математики. А ещё мы приглашаем на все мероприятия, которые будут проходить у нас на этой неделе администрацию нашей школы.
Слово администрации.
Counting Ruler – Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.
(
61 соответствующий результат,
с рекламой
Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров.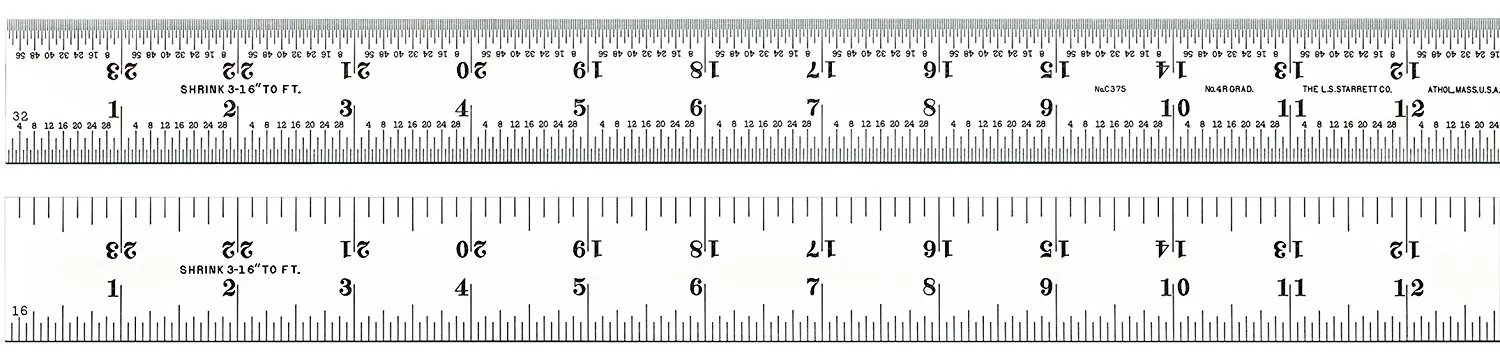
Вы увидите результаты объявлений, основанные на таких факторах, как релевантность и сумма, которую продавцы платят за клик. Узнать больше.
)
Числовая линия – вычитание и измерение – Элементарная математика
Числовая линия в математике
Числовая линия – это не просто школьный предмет.
Это такая же математическая идея, как и функции. В отличие от отеля «Числовая линия», таблиц сотен, палочек Кюизенера и блоков с основанием 10, числовая линия — это не просто педагогическое пособие, используемое только для того, чтобы помочь детям учиться; на это ссылаются и математики.
Числовая линия представляет собой геометрическую «модель» всех действительных чисел, включая 0 1, 2, 25, 374 триллиона и -5, а также 1/2, -17,359., 0,0000000000000001 и . В отличие от счетчиков, которые моделируют только счет, числовая линия моделирует измерение, поэтому она должна начинаться с нуля. (Когда мы считаем, первый объект, к которому мы прикасаемся, называется «единицей». Когда мы измеряем с помощью линейки, мы кладем один конец измеряемого объекта на нулевую отметку на линейке.
Часть мощности сложение и вычитание заключается в том, что эти операции работают как со счетом, так и с измерением, поэтому, чтобы понять основные операции, такие как сложение и вычитание, нам нужна модель числовой линии, а также счетчики.
Числовая линия в обучении математике
Одна из причин использования этого математического объекта для учащихся заключается в том, что им необходимо видеть арифметику в обоих контекстах: счет и измерение. В начале дети могут иногда использовать числовую линейку, чтобы найти ответы на арифметические задачи (например, выяснить, что такое 3 + 10, прежде чем это станет для них автоматическим), но это никогда не является ее целью. Мы не полагаемся на числовую линейку для получения ответов — для этого мы хотим, чтобы дети знали основные факты и методы и использовали свои мысли, — но мы используем числовую линейку, чтобы понимать операции (сложение и вычитание) и понять, что означают ответы.
Например, ответом на задачу на вычитание 92–49 является расстояние между этими двумя числами на числовой прямой. Этот образ может очень помочь в умственных вычислениях: от 49 до 50 — это один шаг, от 50 до 90 — еще сорок шагов, а от 90 до 92 — еще два шага, так что всего 43 шага. (См.
«Сложение и вычитание числовой строки» ниже.) Это также упрощает арифметику с отрицательными числами, когда учащиеся позже узнают об этих числах. А числовая линия необходима для полного понимания дробей и десятичных знаков. На самом деле, линейка (числовая линия!) — одно из важных мест, с которыми сталкиваются учащиеся и которым необходимо использовать дроби.
При счете
Числовые строки сначала используются только для того, чтобы показать последовательность — числа, стоящие в строке по порядку! На данном этапе ни прямолинейность линии, ни расстояние между числами не имеют математического значения, хотя наши изображения и так всегда стандартны. Часть стратегии, которую мы использовали, была взята из работы Фредерика Папи, чьи учащиеся дошкольного и школьного классов даже рисовали их по спирали и зигзагам. Дети будут смотреть на куски строки, не всегда начиная с 1, и будут двигаться вперед или назад от некоторого числа, помещенного в строку. Они узнают о последовательности и порядке, и это развивается независимо от счета.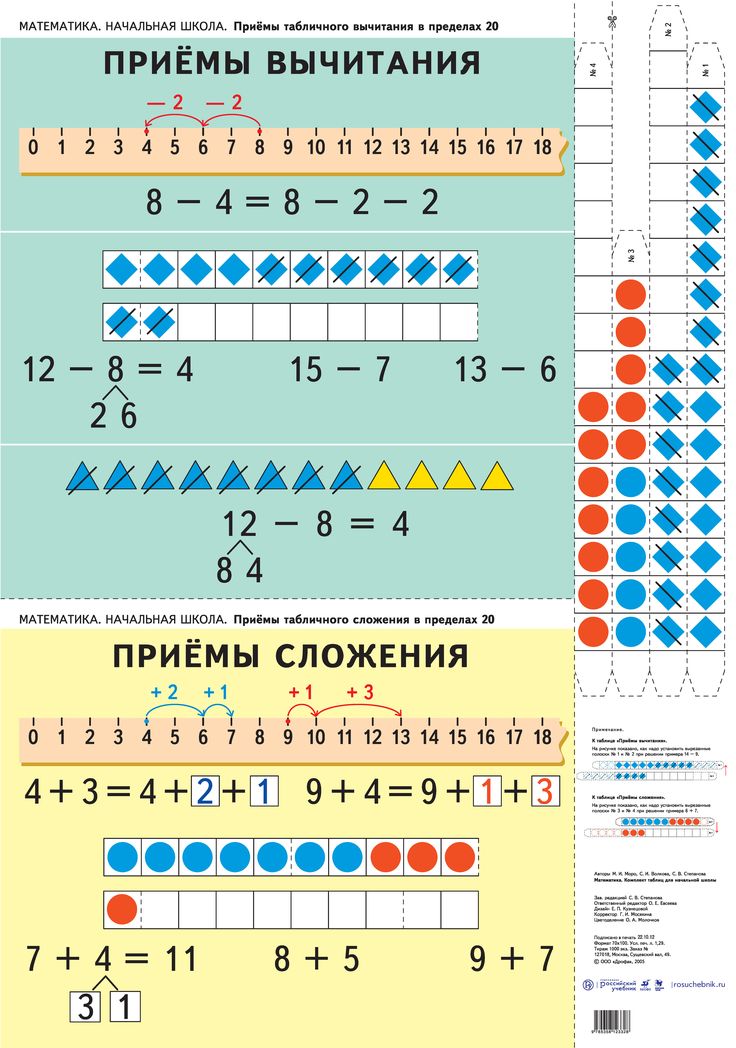
Как вы знаете (и я упомянул по телефону, чтобы заверить вас, что я тоже знал), дети часто могут повторять числа — «считать», как могли бы сказать их родители, — прежде чем они действительно смогут правильно считать предметы, один к одному. один.
В измерении
Тысяча учеников также узнают об интервалах на числовой прямой, но только начинают этот процесс. (У меня с собой только 1-5 классы, поэтому я не могу сказать, где в К.) Это требует времени, и его труднее развивать, чем сорок (или около того) лет назад. Раньше дети получали представление об интервале (в несколько иной форме) из своего опыта игры в настольные игры. Они знали, что когда они выбрасывают 5, они должны считать свои пять клеток, начиная со следующей клетки. То есть считали ходы, а не позиции. У сегодняшних детей — на всех уровнях СЭ, лишь немного отличающихся друг от друга — гораздо меньше опыта в настольных играх, поэтому они должны получить это представление в школе. Измерение зависит от этого. Сложение и вычитание со счетчиками от него не зависят, но от него зависят те операции на числовой прямой.
Сложение и вычитание
Если мы можем складывать и вычитать с помощью счетчиков, зачем использовать числовую прямую? Чтобы связать эти операции с измерением, а также потому, что счетчиков уже недостаточно, когда мы переходим к дробям, десятичным числам и отрицательным числам. Со временем дети будут соединять изображения числовых линий с термометрами, часами, линейками (с дробными дюймами)… Графики координат основаны на перпендикулярных числовых линиях; даже гистограммы требуют идеи измерения больше, чем идеи счета, хотя они могут начинаться со счета.
Сложение и вычитание или сравнение расстояний также является причиной того, что мы используем стержни Кюизенера вместо кубов Unifix. (Кубики Unifix делают акцент на счете — нельзя узнать взаимосвязь между стержнями Unifix без счета, потому что нет фиксированной длины.) Часть-часть-целое в красном стержне + зеленый стержень = желтый стержень легко увидеть, не заботясь о том, какие числа они представляют. А если R + G = Y, то Y – R = G.
(См., например, Гр. 2, гл. 8, урок 1, но дети видят это и в Гр. 1.) Добавление расстояния получает дальнейшее развитие на открытых числовых рядах. Учащиеся осваивают множество способов вычитания (во втором классе они учатся вычитать 8 из чего угодно, вычитая 10 и затем компенсируя, а затем распространяя эту идею на другие сложения и вычитания). Во 2 классе, гл 2, уроке 8 развивают представление о числовой прямой
, а в третьем классе они развивают его дальше и используют для вычитания гораздо больших чисел.
Его ценность как модели заключается в том, что он продолжает работать и для отрицательных чисел.
А также в десятичных дробях и дробях
Несколько математиков и исследователей отметили, что расположение дробей на числовой прямой необходимо для понимания их как чисел, а не только частей пиццы.
Студенты должны научиться найти дробь на числовой прямой.
Многие неверные представления о значении слова «половина» становятся очевидными, когда учащихся просят найти его на числовой прямой.
Как и число , число меньше 1 и больше 0, на самом деле «половина» между ними, но это довольно обычно для студентов, когда их в первый раз просят поместить это число на числовую прямую, расположить его между 1 и 2, возможно, потому, что эти две цифры используются в , записывающем символ ”, или, возможно, из-за общепринятой стратегии думать о значении «один из двух». Учащиеся, которые знают об отрицательных числах до того, как впервые столкнутся с вопросом «где на числовой прямой поместится 1/2», иногда помещают ее точно над 0, потому что они видят ноль как знак, который делит числовую прямую «пополам». Это, соответственно, стратегии, основанные на том, как записывается число, и на том, как дробь представляет «часть» геометрического объекта, обе из которых, как правило, изучаются раньше и интенсивнее, чем сообщения о дробях, являющихся числами, сами по себе. , и имеющие величину и порядок (как и все другие действительные числа).
Сложение и вычитание дробей также могут быть полезны при использовании изображения числовой строки.
Вычисление 10 – 2 можно представить, как и любую другую задачу на вычитание, в виде расстояния на числовой прямой.
Четкое понимание того, что означает вычисление , облегчает интерпретацию и решение в уме задач, подобных приведенным ниже, без багажа преобразования смешанных чисел в неправильные дроби и обратного преобразования.
Цель состоит не только в том, чтобы упростить вычисления, и не в том, чтобы сделать устаревшим (чего нет) метод преобразования смешанных чисел в неправильные дроби, но и в том, чтобы прояснить, что такое вычисление означает , чтобы можно было лучше понять алгоритм в тех случаях, когда необходимо , потому что числа без преобразования слишком сложны для обработки.
Вопросы развития
В 1 классе (глава 2, урок 1) учащиеся «записывают прыжки» на числовой прямой. Изображение
представляет собой сложную когнитивную задачу для детей. Визуально выделяются точки, а не промежутки между ними.