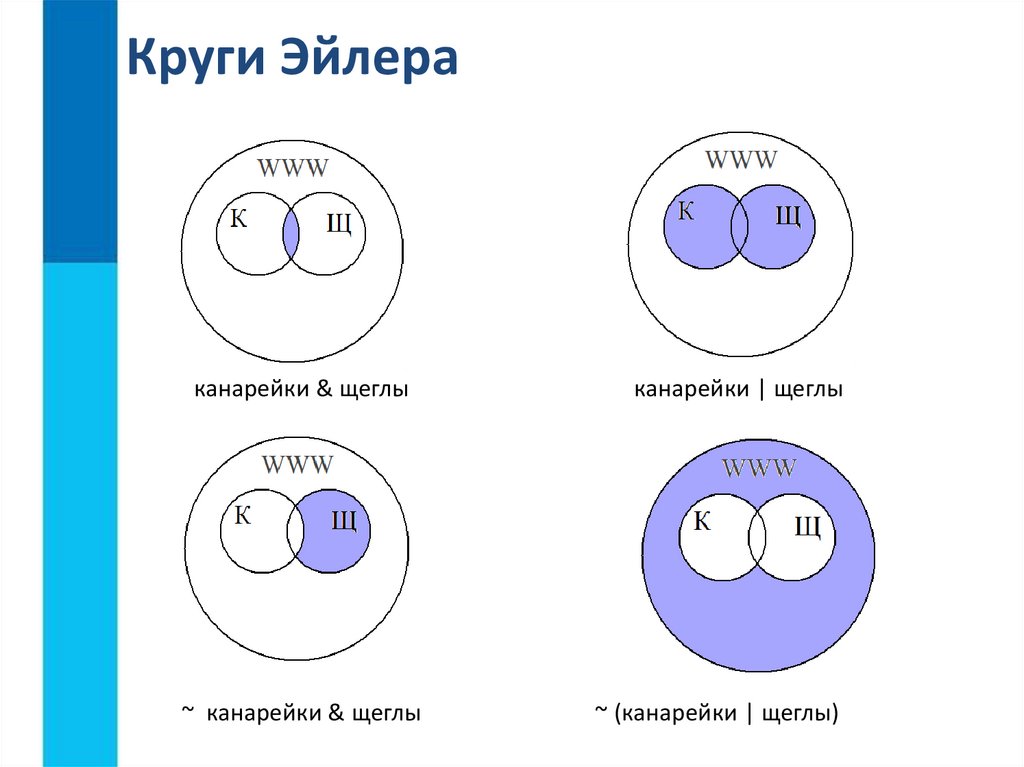
Круги эйлера примеры: описание, примеры, для дошкольников, для школьников
Множества. Решение задач с помощью кругов Эйлера. 5, 6, 7 класс
Братунова Вера Дмитриевкна,
преподаватель математики и информатики,
Гимназия-детсад им. С. Демиреля, мун. Комрат, АТО Гагауз Ери, Республика Молдова
Множества. Решение задач с помощью кругов Эйлера
Классы: 5, 6, 7
Ключевые слова: круги Эйлера
Пояснительная записка
Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.
В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
С
данным способом решения задач учащихся можно познакомить как на уроках, так и
на кружковых занятиях.
Главной целью этой работы является помощь учителям математики для подготовки учащихся к олимпиадам, а также к экзаменам.
Основные понятия
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.
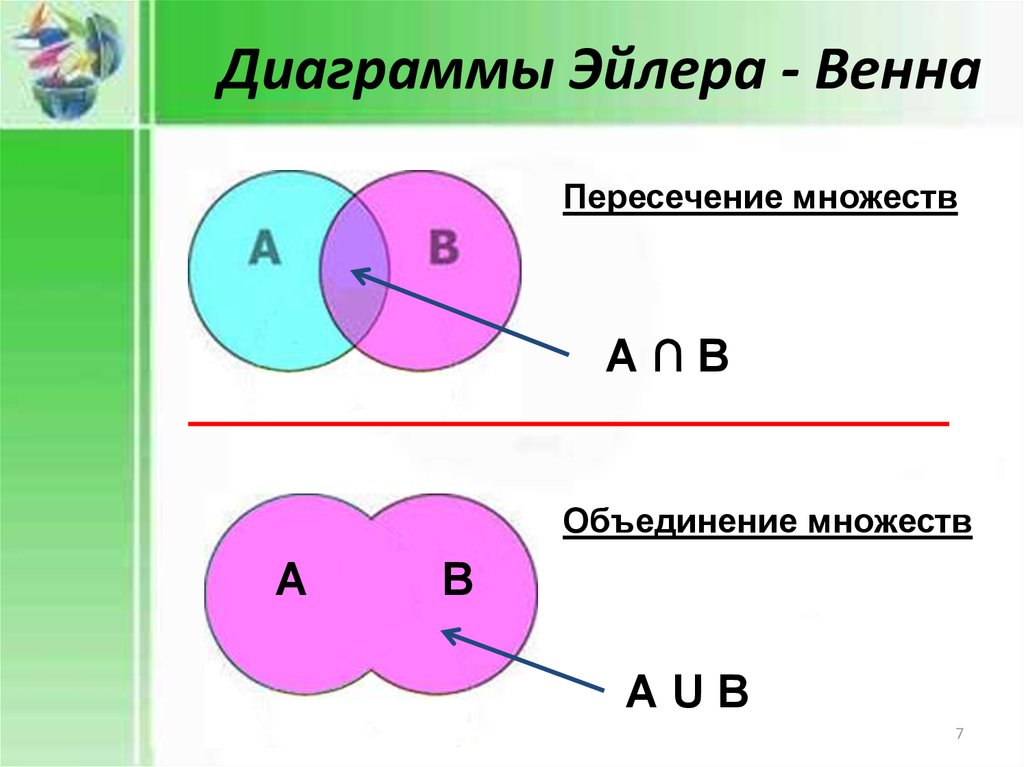
Пересечение множеств в теории множеств – это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Круги
Эйлера – геометрическая схема, с помощью
которой можно изобразить отношения между подмножествами, для наглядного
представления. Изобретены Леонардом Эйлером. Используется в математике, логике,
менеджменте и других прикладных направлениях.
2. Решение задач с помощью кругов Эйлера
2.1. “Обитаемый остров” и “Стиляги”
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
1. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров»,
2. 11- 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
Ответ: 5 человек.
2.2. Задача про библиотеки
Каждый из 35 шестиклассников
является читателем, по крайней мере, одной из двух библиотек: школьной и
районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.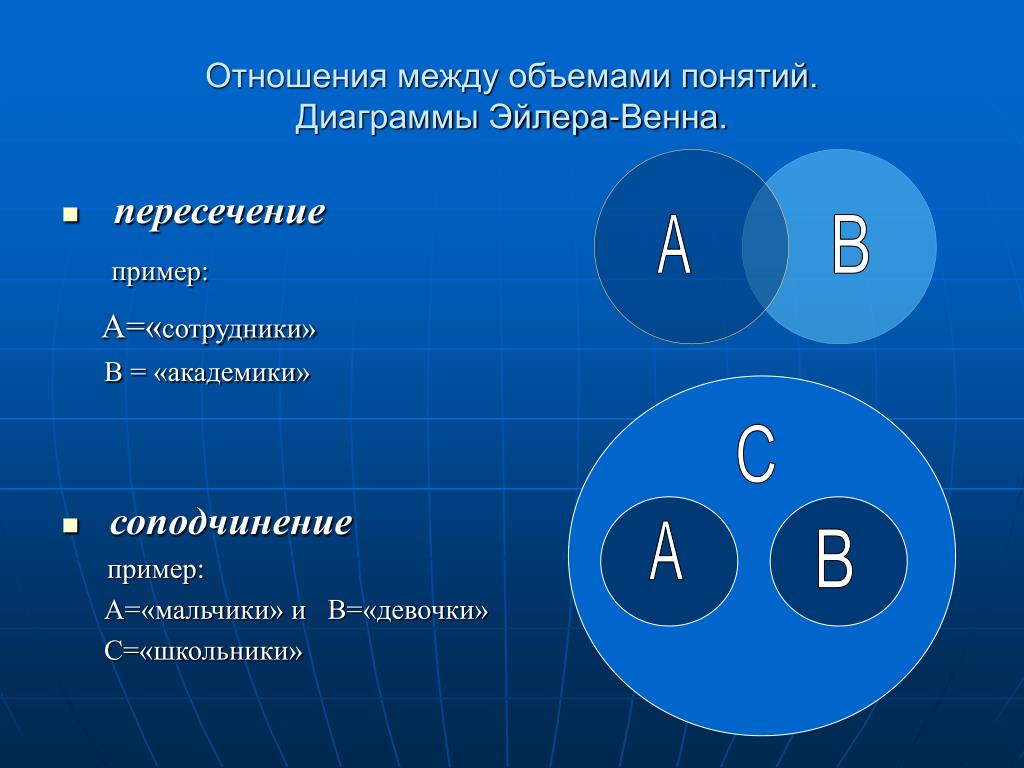
Сколько шестиклассников:
1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?
Решение:
Чертим два множества таким образом:
1) 20+ 25 – 35 = 10 (человек) – являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2) 35 – 20 = 15 (человек) – не являются читателями районной библиотеки,
3) 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки,
4) 35- 20 = 10 (человек) – являются читателями только районной библиотеки,
5) 35- 20 = 15 (человек) –
являются читателями только школьной библиотеки.
Очевидно, что вопросы 2 и 5, а также 3 и 4 – равнозначны и ответы на них совпадают.
Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.
2.3. Гарри Поттер, Рон и Гермиона
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Учитывая условия задачи, сделаем чертеж:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.
Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.
Ответ: 8 книг.
2.4. Задача про любимые мультфильмы
Шестиклассники
заполняли анкету с вопросами об их любимых мультфильмах.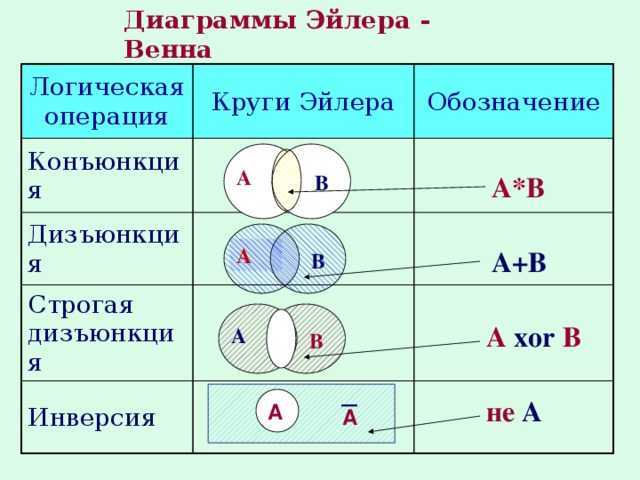 Оказалось, что
большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные
Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов»
нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок»,
шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три
мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете
два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка
Боб Квадратные Штаны».
Оказалось, что
большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные
Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов»
нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок»,
шестерым – «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три
мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете
два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка
Боб Квадратные Штаны».
Решение:
Чертим три круга, таким образом:
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым – «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.
Мы помним, что по условиям задачи
среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма
сразу, т.е. 5 – 3 = 2 – ученика выбрали «Волк и теленок» и «Губка Боб
Квадратные Штаны».
1) 21 – 3 – 1 – 6 = 11 – учеников выбрали только «Белоснежка и семь гномов»,
2) 13 – 3 – 1 – 2 = 7 – учеников выбрали – «Волк и теленок»,
3) 38 – (11 + 3 + 1 + 2 + 6 + 7) = 8 – ребят выбрали «Губка Боб Квадратные Штаны».
4) 8 + 2 + 1 + 6 = 17 – человек выбрали мультик «Губка Боб Квадратные Штаны».
Ответ: 17 учеников.
2.5. Задача про Крейсер и Линкор
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
Запрос | Найдено страниц, тыс. |
Крейсер и Линкор | 7000 |
Крейсер | 4800 |
Линкор | 4500 |
Какое
количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор?
(Считается, что все вопросы выполняются практически одновременно, так что набор
страниц, содержащих все искомые слова, не изменялся за время выполнения
запросов.
Решение:
При помощи кругов Эйлера изобразим условия задачи.
1) 4800 + 4500 – 7000 = 2300 (тыс. страниц) – найдено по запросу Крейсер и Линкор,
2) 4800 – 2300 = 2500 (тыс. страниц) – найдено по запросу Крейсер,
3) 4500 – 2300 = 2200 (тыс. страниц) – найдено по запросу Линкор.
Ответ: 2300 тыс. страниц.
2.6. Задача про блондинок
Каждый ученик класса – либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика – блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
Решение:
Изобразим с помощью кругов Эйлера данные из задачи:
1) 12 – 1 = 11 (учеников) – девочек блондинок,
2) 12 – 1 = 11 (учеников) – блондины и любят математику,
3) 6 – 1 = 5 (учеников) – девочек, которые любят математику,
4) 20 – 11 – 1 – 5 = 3 (ученика) – девочки,
5) 24 – 11 – 1 – 11 = 1 (ученик) – блондин,
6) 17- 5 – 1 – 11 = 0 (учеников) – любят математику,
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 =
32 (ученика) – всего в классе.
Ответ: 32 ученика.
2.7. Задача про кружки
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение:
Учитывая условия задачи, сделаем чертеж:
1) 10 – 3 = 7 (ребят) – посещают драмкружок и хор,
2) 6 – 3 = 3 (ребят) – поют в хоре и занимаются спортом,
3) 8 – 3 = 5 (ребят) – занимаются спортом и посещают драмкружок,
4) 27 – 7 – 3 – 5 = 12 (ребят) – посещают драмкружок,
5) 32 – 7 3 – 3 = 19 (ребят) – поют в хоре,
6) 22 – 5 – 3 – 3 = 11 (ребят) – увлекаются спортом,
7) 70 – (12 + 19 + 11 + 5+ 7 + 3 +
3) = 10 (ребят) – не поют в хоре, не увлекаются спортом и не занимаются в
драмкружке.
Ответ: 10 человек и 11 человек.
Задачи для самостоятельного решения
1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 – немецкий язык, а 23 – оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
2. Из 40 учащихся нашего класса 32 любят молоко, 21 – лимонад, а 15 – и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
3. 12 моих одноклассников любят читать детективы, 18 – фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
5. Из 29 мальчишек нашего двора
только двое не занимаются спортом, а остальные посещают футбольную или
теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом –
19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
Из 29 мальчишек нашего двора
только двое не занимаются спортом, а остальные посещают футбольную или
теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом –
19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
6. В одном классе 25 учеников. Из них 7 любят груши, 11 – черешню. Двое любят груши и черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 – умных и 9 – добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
8. В нашем классе 35 учеников. За
первую четверть пятерки по русскому языку имели 14 учеников; по математике –
12; по истории – 23. По русскому и математике – 4; по математике и истории – 9;
по русскому языку и истории – 5. Сколько учеников имеют пятерки по всем трем
предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по
одному из этих предметов?
По русскому и математике – 4; по математике и истории – 9;
по русскому языку и истории – 5. Сколько учеников имеют пятерки по всем трем
предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по
одному из этих предметов?
9. Из 100 человек 85 знают английский язык, 80 – испанский, 75 – немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
10. Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии; в Англии и Италии – 5; в Англии и Франции – 6; во всех трех странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Список использованных источников
1. Баженов И.И, Порошкин А.Г.,
Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб. пособие / Сыктывкар: Сыктывкарский университет, 2006.
пособие / Сыктывкар: Сыктывкарский университет, 2006.
2. Марков И.С. Новые олимпиады по математике – Ростов н/Д: Феникс, 2005.
3. https://ru.wikipedia.org/wiki/
4. http://logika.vobrazovanie.ru
5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22
6. http://urok.1sept.ru/articles/550092/
7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera
Множества на кругах Эйлера-Венна – презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике.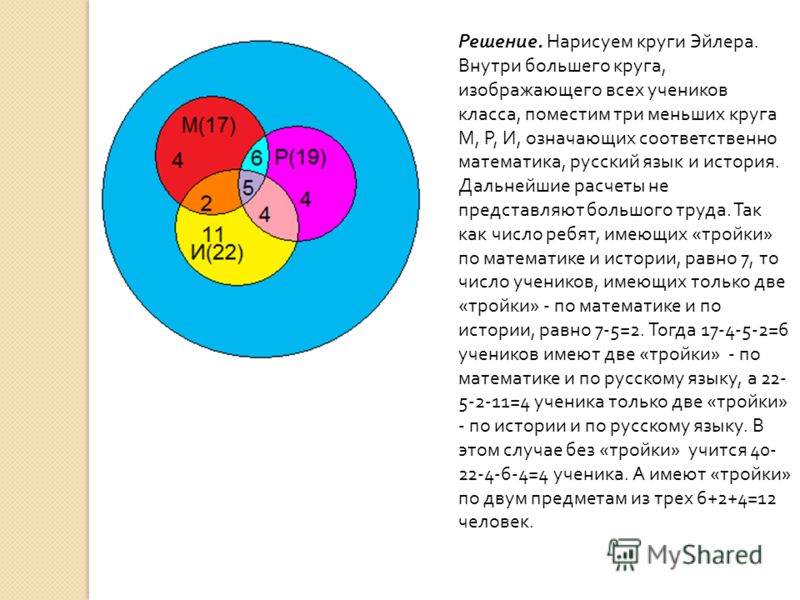 Базовый уровень Сложные задачи
Базовый уровень Сложные задачи
Множество
геометрических фигур
Множество
четных однозначных чисел
– элемент множества геометрических фигур
– элемент множества четных однозначных чисел
знак называется включением (можно сравнить со знаком )
A
A
B
Например:
• Множество цифр:
0;1;2;3;4;5;6;7;8;9
• Множество букв русского алфавита
Предметы, из которых состоит
множество, называются его
ЭЛЕМЕНТАМИ
Например:
1). Цифра 6 – элемент множества цифр.
2). Буква Л – элемент множества букв
русского алфавита
Для обозначения множеств используют большие
буквы латинского алфавита или фигурные скобки,
внутри которых записывают элементы
множества(при этом порядок элементов не имеет
значения).
Например:
1). А— множество цифр: А={0;1;2;3;4;5;6;7;8;9}.
2). W— множество букв русского алфавита:
W={А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;
Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я }
Для обозначения элементов множества
используют малые буквы латинского алфавита
Например:
1). f = 6 – элемент множества цифр
f = 6 – элемент множества цифр
2). а = Р – элемент множества букв русского
алфавита
Принадлежность предмета данному множеству
обозначается
Непринадлежность – символом
Например:
1). f = 6 ; 6 є А, где А— множество цифр.
2). К є W, где W— множество букв русского
алфавита
Множество может быть:
• 1). Конечное :
Например: А— множество цифр
• 2). Бесконечное:
Например: N – множество натуральных чисел
3). Пустое:
ø- множество, в котором нет ни одного элемента
Например: X – множество решений уравнения
õ 25
2
Первый способ: перечислительный
A={1; 2; 3; 4; 5}
Второй способ: описательный – множество
выделяется из всевозможных других тем или
иным свойством
A={Х/ – первые пять натуральных чисел}
Объединение множеств
Объединением (суммой) множеств А и В называется
множество тех элементов, каждый из которых принадлежит
хотя бы одному из множеств А или В .
A B x x A x B
A, B
А U В=А
A
A
АUВ
АUВ
B
А
В
1. Объединение A B = х / х А или х В
Объединение A B = х / х А или х В
множества
пересекаются
множества не
пересекаются
одно множество является
подмножеством другого
множества A B
A
A
A
B
B
А В
А В
B
А В=А
Пересечение множеств
A B x x A x B
A, B
А В= А
A
A
А В= Ø
B
А
В
2. Пересечение A B = х / х А и х В
множества
пересекаются
В
А В
множества не
пересекаются
одно множество является
подмножеством другого
множества A B
А
В
А В=
А
В
А В=В
Разность множеств
• Разностью множеств А и В называется
множество, которое содержит все элементы
А, не входящие в В. A \ B x x A x B
Если А=В, то A\B = ø
A
A
A
В
А \ В
А \ В
А \ В= А
B
А
В
3. Разность A \ B = х / х А и х В
множества
пересекаются
А
множества не
пересекаются
одно множество является
подмножеством другого
множества A B
А
В
А\В
А
В
В
А \ В=А
А\В
Разбиение множества
• Разбиением множества А называется
семейство Аi , i I непустых и различных
подмножеств А, таких, что объединение Аi
равно А и Аi∩Aj=ø.
Множества Аi называются классами
разбиения.
Разбиением А={1, 2, 3, 4} является множество
B={{1}, {2, 3}, {4}} или С={{1}, {2, 3, 4}}
Универсальное множество
• Если все рассматриваемые в ходе какого –
либо рассуждения множества являются
подмножествами некоторого множества U,
то множество называется универсальным
множеством (универсум).
Например множество действительных чисел
для арифметики является универсумом.
Мощность множества
• Число элементов конечного множества А
называется мощностью множества и обозначается
|А|.
• Если между элементами двух различных множеств
А и В можно установить взаимно однозначное
соотношение по любому закону, то эти множества
называются эквивалентными или равномощными.
Записывается А≈В.
Например множество натуральных чисел и четных
чисел равномощные
• Множество называется счетным,
элементы которого можно поставить во
взаимно-однозначное соответствие со
всеми числами натурального ряда.
Пример Множество целых чисел,
множество нечетных чисел.
О множествах, эквивалентных множеству
всех действительных чисел,
принадлежащих интервалу [0,1],
говорят, что они имеют мощность
континуума. (continuumнепрерывное).
Леонард Эйлер, крупнейший математик
XVIII века, родился в Швейцарии. Эйлер
принадлежит к числу гениев, чьё творчество
стало достоянием всего человечества. До сих
пор во всех странах изучают тригонометрию
и логарифмы в том виде, какой придал им
Эйлер.
Он оставил важнейшие труды по самым
различным отраслям математики, механики,
физики, астрономии и по ряду прикладных
наук.
Трудно
даже
перечислить
все
отрасли, в которых
трудился
великий
учёный.
Леонард Эйлер написал более 850 научных работ. В
одной из них и появились круги. А впервые он их
использовал в письмах к немецкой принцессе. Эйлер
писал тогда, что «круги очень подходят для того, чтобы
облегчить наши размышления».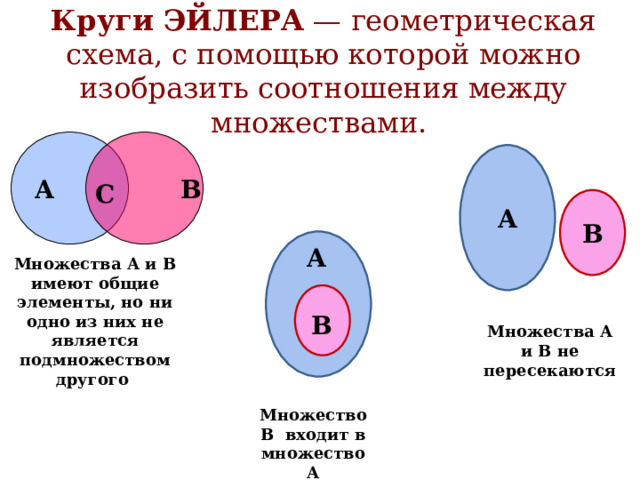
Позднее
аналогичный
прием
использовал ученый Джон Венн —
британский логик и философ; основные
труды в области логики классов; и этот
приём назвали «диаграммы Венна»,
который используется во многих областях:
теория множеств, теория вероятностей,
логика, статистика, компьютерные науки.
При решении целого ряда задач Леонард Эйлер
использовал идею изображения множеств с помощью кругов,
и они получили название «круги Эйлера».
Этот метод даёт более наглядное представление о
возможном способе изображения условий, зависимости,
отношений в логических задачах.
Множество всех действительных чисел
Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.
R
Q
5/6
-0,25
Z
-36
0
-7
N
5
1
9
Круги ЭЙЛЕРА —
геометрические схемы, с
помощью которых можно
изобразить отношения между
подмножествами, для
наглядного представления.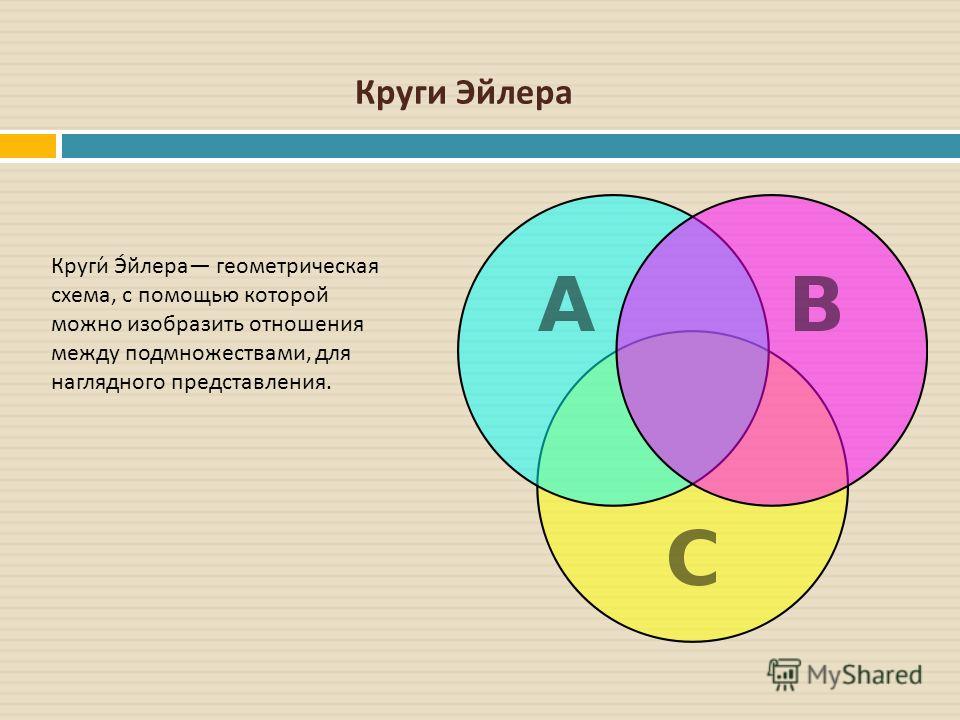
Наряду с кругами в подобных
задачах применяют
прямоугольники и другие фигуры.
А∪В-?
Натуральные числа
Простые
числа
2
А
Четные
числа
В
А∩В-?
D
C
естественные
социальные
технические
гуманитарные
философия
Примеры кругов Эйлера-Венна
Игрушка
Кукла
Заводная
игрушка
Заводной
автомобиль
Пистолет
Даны множества A={1; 3; 6; 8}, В={2; 4; 6; 8}.
Найти объединение, пересечение и разность
множеств А и В: A∪B, A∩B, A∖B, B∖A – ?
Очевидно, что объединение двух данных
множеств A∪B={1; 2; 3; 4; 6; 8}, их пересечение
A∩B={6; 8}, а разности A∖B={1; 3} и В∖А={2; 4}
А
1
3
6
8
В
2
4
Так эти
множества
можно
представить на
кругах.
В магазин «Мир музыки» пришло 35 покупателей.
Из них 20 человек купили новый диск певицы
Максим, 11 – диск Земфиры, 10 человек не купили ни
одного диска. Сколько человек купили диски и
Максим, и Земфиры?
Изобразим эти множества
на кругах Эйлера.
11
20
диски
Максим
35
диски
Земфиры
Теперь посчитаем: Всего внутри большого круга 35
покупателей, внутри двух меньших 35–10=25 покупателей.
По условию задачи 20 покупателей купили новый диск
певицы Максим, следовательно, 25 – 20 = 5 покупателей
купили только диск Земфиры. А в задаче сказано, что 11
покупателей купили диск Земфиры, значит 11 – 5 = 6
покупателей купили диски и Максим, и Земфиры:
не купили
диски
6
диски
Максим
10
5
диски
Земфиры
Ответ: 6 покупателей купили диски и Максим, и Земфиры
Использованные Интернет-ресурсы:
1. http://mat.1september.ru Газета «Математика» Издательского дома
«Первое сентября»
2. http://www.math.ru Math.ru: Математика и образование
3. http://festival.1september.ru/articles/635933/
4. https://znanija.com/task/3231925
5. https://yandex.ru/images/search?textstype=image&lr=43&noreask=1&p
arent-reqid=1483952074037160-1110803268472871449321762-sas13418&source=wiz
English Русский Правила
Как анализировать аргументы с помощью диаграмм Эйлера
На экзамене по конечной математике вас могут попросить проанализировать аргумент с помощью визуального подхода с использованием диаграммы Эйлера. Эта изобразительная техника используется для проверки правильности аргумента.
Эта изобразительная техника используется для проверки правильности аргумента.Аргумент может быть классифицирован как допустимый или недопустимый. Действительный аргумент возникает в ситуациях, когда, если посылки верны, то и заключение должно быть верным. И аргумент может быть верным, даже если вывод ложный.
Следующий аргумент имеет две предпосылки: (1) «У всех собак есть блохи». (2) «Хэнк — собака». Вывод таков, что, следовательно, у Хэнка блохи.Эти аргументы обычно имеют следующий формат с предпосылками, перечисленными первыми, и выводом, подчеркнутым горизонтальной линией:
Используя диаграмму Эйлера для анализа этого аргумента, нарисуйте круг, содержащий все объекты, на которых есть блохи. Внутри круга поместите еще один круг, чтобы содержать всех собак. А внутри круга собак посади Хэнка. Рисунок иллюстрирует этот подход.
У бедного Хэнка блохи.
Этот аргумент не обязательно верен, потому что вы знаете, что не у всех собак есть блохи.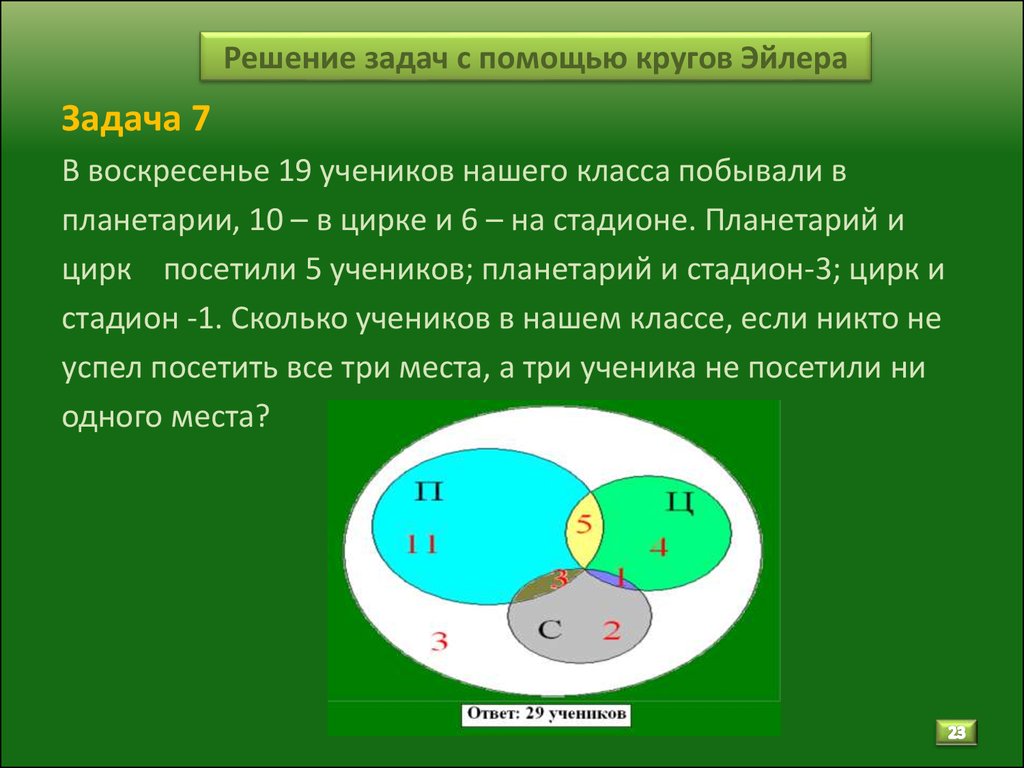 Все это показывает, что аргумент равен действительный . Если обе посылки верны, то и заключение должно быть верным.
Все это показывает, что аргумент равен действительный . Если обе посылки верны, то и заключение должно быть верным.
Теперь рассмотрим аргумент, включающий прямоугольники и треугольники. Многоугольник — это фигура, состоящая из отрезков, соединенных концами.
При анализе правильности этого аргумента диаграмма Эйлера начинается с круга, содержащего все многоугольники, как показано здесь.
Два типа полигонов.
Два круга нарисованы внутри большего круга — один содержит прямоугольники, а другой — треугольники. Два круга не пересекаются, потому что у прямоугольников четыре стороны, а у треугольников три стороны.
Аргумент недействителен . Прямоугольники — это не треугольники, даже иногда.
Аргументы могут иметь более двух посылок. Например:
Одна диаграмма Эйлера, которая может представить эту ситуацию, имеет три пересекающихся круга, как показано здесь.
Президент Авраам Линкольн и другие юристы штата Иллинойс.
Как видно из диаграммы, могут быть президенты, родившиеся в Кентукки, которые не были юристами в Иллинойсе, и могут быть президенты, которые были юристами в Иллинойсе, но не родились в Кентукки. Аргумент равен неверный . Чтобы быть действительным, оно всегда должно быть истинным.
Эта статья из книги:
- Конечная математика для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором Алгебра I для чайников, Алгебра для чайников, и многих других Для чайников книг. Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.
Эту статью можно найти в категории:
- Расчет и анализ,
Диаграмма Эйлера – значение, примеры, диаграмма Венна, как создать?
Диаграммы Эйлера — это общепринятое обозначение для отображения информации о множествах и их отношениях друг с другом.
Их часто изображают в виде групп (потенциально связанных) замкнутых кривых. Эти диаграммы допускают некоторое упущение множественных взаимодействий, позволяя им использовать в своих интересах пространственные качества удержания и непересекающихся кривых.
Эти диаграммы полезны в различных приложениях для представления теоретико-множественных данных, включая визуализацию статистических данных, построение основ диаграммной логики, разработку программного обеспечения и отображение результатов поисковых запросов в базе данных. Однако эти методы могут генерировать диаграммы только для ограниченной части всех мыслимых абстрактных описаний.
Содержание
- Что такое диаграмма Эйлера?
- Объяснение диаграммы Эйлера
- Steps to Create Euler Diagram
- Example
- Euler vs Venn Diagram
- Frequently Asked Questions (FAQs)
- Recommended Articles
- An Euler Diagram is a visual or diagrammatic representation of sets and their interactions with друг друга.
 Они состоят из простых замкнутых кривых на плоскости (обычно кругов), которые представляют наборы.
Они состоят из простых замкнутых кривых на плоскости (обычно кругов), которые представляют наборы. - Леонард Эйлер, швейцарский математик, создал концепцию.
- У них много общего с диаграммами Венна, но есть и небольшие различия.
- Это естественный способ представления данных в теории множеств. Визуализация статистических данных, создание основы для диаграммных рассуждений, разработка программного обеспечения и отображение результатов поисковых запросов в базе данных — все это примеры полезности диаграмм Эйлера.
Объяснение диаграммы Эйлера
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Диаграмма Эйлера (wallstreetmojo.com)
Диаграмма Эйлера — это представление замкнутых кругов или кривых, которые делят плоскость на отдельные, но соединенные подмножества. Их называют областями, каждая из которых окружена набором кривых. Общие примеры диаграмм Эйлера показывают теоретико-множественные отношения, где каждая кривая представляет набор, а каждая область представляет собой пересечение нескольких наборов. Представления, созданные с помощью онлайн-конструктора диаграмм Эйлера, могут иметь кривые любой геометрической формы. Ценность диаграммы заключается в том, как кривые перекрываются, а не в их размерах или формах. Следовательно, теоретико-множественные взаимодействия (пересечение, подмножество и непересекаемость) относятся к пространственным отношениям между областями, заключенными в каждой форме.
Их называют областями, каждая из которых окружена набором кривых. Общие примеры диаграмм Эйлера показывают теоретико-множественные отношения, где каждая кривая представляет набор, а каждая область представляет собой пересечение нескольких наборов. Представления, созданные с помощью онлайн-конструктора диаграмм Эйлера, могут иметь кривые любой геометрической формы. Ценность диаграммы заключается в том, как кривые перекрываются, а не в их размерах или формах. Следовательно, теоретико-множественные взаимодействия (пересечение, подмножество и непересекаемость) относятся к пространственным отношениям между областями, заключенными в каждой форме.
Швейцарский математик Леонард Эйлер (1707–1783) дал миру представление о диаграммах Эйлера, эйлеровых кругах и постоянной Эйлера. Здесь каждая кривая делит плоскость на две зоны или области. Внутренние части изображения представляют собой элементы множества, а внешние – элементы, не входящие в их состав. Кривые, не имеющие общих элементов, не пересекаются и являются непересекающимися множествами.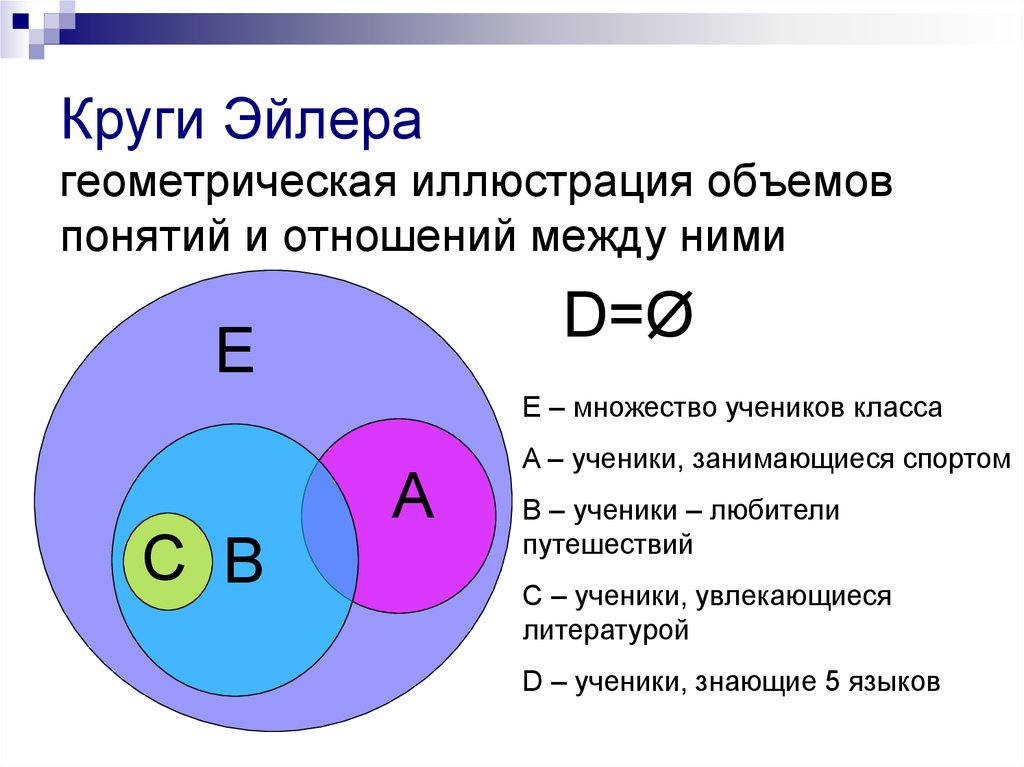 Те множества, которые пересекаются, имеют общие черты. В то же время кривая, полностью находящаяся внутри другой, является ее подмножеством. Люди могут использовать генератор диаграмм Эйлера, чтобы получить общее представление о том, как выглядят диаграммы.
Те множества, которые пересекаются, имеют общие черты. В то же время кривая, полностью находящаяся внутри другой, является ее подмножеством. Люди могут использовать генератор диаграмм Эйлера, чтобы получить общее представление о том, как выглядят диаграммы.
Шаги по созданию диаграммы Эйлера
Эти диаграммы полезны для убедительных логических рассуждений. В этих посылках метод определения правильности рассуждений, в которых фигурируют термины «все, некоторые и нет». Здесь первым шагом должно быть создание диаграммы для первой предпосылки. Затем над первой посылкой рисуется вторая посылка. Создатель диаграмм Эйлера помогает легко создавать эти диаграммы благодаря развитию технологий. А теперь можно делать выводы. Однако аргумент действителен тогда и только тогда, когда каждая мыслимая диаграмма изображает вывод аргумента и соответствует ему. Если хотя бы одна мыслимая диаграмма противоречит концовке, вывод не во всех случаях верен, а значит, утверждение неверно.
Пример
Ниже приведены некоторые аргументы, которые необходимо определить, являются ли они действительными или недействительными.
- Все гении, которые поют, не умеют читать.
- Все гении, не умеющие читать, не могут учиться.
- Следовательно, Все гении, которые поют, не годятся для учебы.
Первым шагом будет создание диаграммы Эйлера для предпосылки первого аргумента.
Это будет:
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Диаграмма Эйлера (wallstreetmojo.com)
Следующим шагом является создание диаграммы посылки для второго аргумента, и единственный логический вывод:
Вы можете использовать это изображение на Ваш веб-сайт, шаблоны и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Диаграмма Эйлера (wallstreetmojo. com)
com)
Следовательно, аргумент «Все гении, которые поют, непригодным для учебы».
Диаграмма Эйлера и Венна
Понятия «диаграмма Эйлера» и «диаграмма Венна» Диаграмма Венна Диаграммы Венна относятся к схематическому представлению множеств с помощью окружностей. Этот метод был введен английским логиком Джоном Венном в 1880 году. Он также известен как диаграммы множеств или логические диаграммы и используется в таких дисциплинах, как математика, статистика и бизнес-исследования. Однако на самом деле последняя является своего рода подклассом диаграмм Эйлера. В отличие от диаграмм Венна, которые должны отображать все потенциальные пересечения множества, другая должна представлять только их подмножество.
В рамках нового математического движения 1960-х годов диаграммы Венна и Эйлера использовались для обучения теории множеств. Последние изображают установленные отношения между кругами относительно отношений включения и исключения. Кроме того, он представляет пустоту либо затенением, либо устранением этой области из-за ее отсутствия.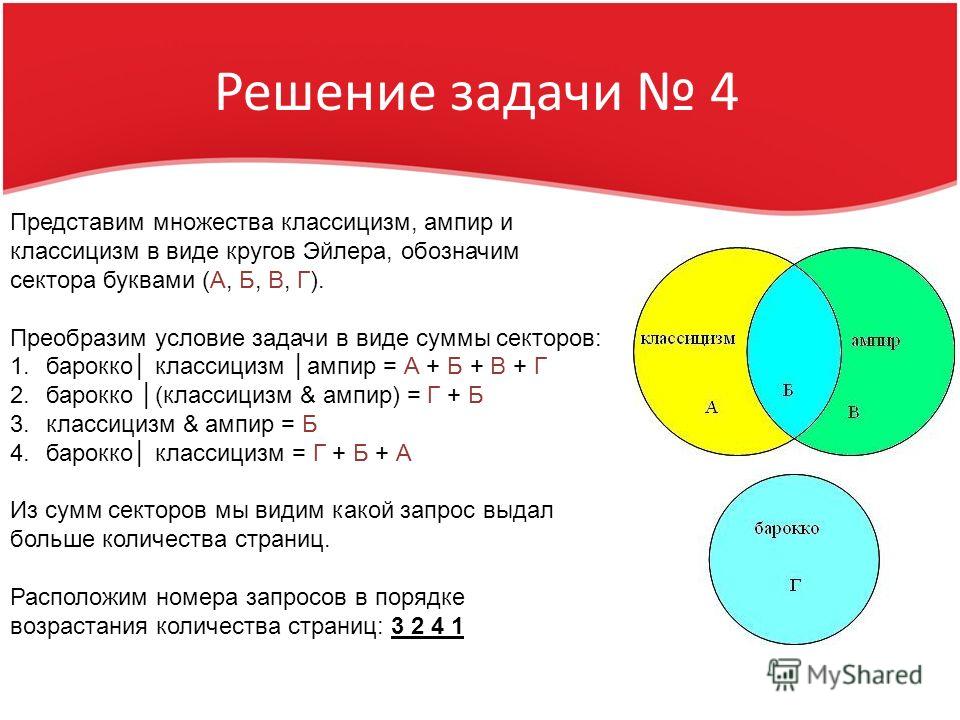 С другой стороны, диаграммы Венна содержат фиксированную конфигурацию круга и изображают отношения множества, указывая, что темные части символизируют пустое множество.
С другой стороны, диаграммы Венна содержат фиксированную конфигурацию круга и изображают отношения множества, указывая, что темные части символизируют пустое множество.
Если их метки не находятся в пересекающемся круге, перекрывающиеся круги на диаграммах Венна не обязательно показывают общность между наборами, а скорее вероятную логическую связь. То есть они содержат все возможные зоны перекрытия между элементами, представляющими кривые. Немногие различия, такие как эти, различают две темы; однако нельзя отрицать, что у них гораздо больше общего.
Часто задаваемые вопросы (FAQ)
Как узнать, верна ли диаграмма Эйлера?
Аргумент диаграммы Эйлера верен тогда и только тогда, когда каждая мыслимая диаграмма изображает заключение этого аргумента. Если хотя бы одна мыслимая диаграмма противоречит заключению, вывод не во всех случаях верен, а рассуждение неверно.
Кто изобрел диаграмму Эйлера?
Эти диаграммы были построены Леонардом Эйлером, швейцарским математиком. Он является пионером различных открытий в различных математических дисциплинах и внес значительный вклад в науку, физику и астрономию. Диаграмма Эйлера — это схематическое представление множеств и отношений.
Он является пионером различных открытий в различных математических дисциплинах и внес значительный вклад в науку, физику и астрономию. Диаграмма Эйлера — это схематическое представление множеств и отношений.
Почему вы используете диаграмму Эйлера?
Они особенно удобны для объяснения сложных иерархий и перекрывающихся определений. Визуализация статистических данных, создание основы для диаграммных рассуждений, разработка программного обеспечения и отображение результатов поисковых запросов в базе данных — все это было выполнено с помощью этих диаграмм. Они также помогают в логических рассуждениях
Рекомендуемые статьи
Это руководство по диаграммам Эйлера. Мы объясняем шаги по созданию диаграммы Эйлера вместе с примером и ее отличиями от диаграммы Венна. Вы можете узнать больше из следующих статей —
- Диаграмма Fishbone Диаграмма Fishbone Диаграмма Fishbone или диаграмма Исикавы — это современный инструмент управления качеством, который объясняет причинно-следственную связь для любой проблемы с качеством, которая возникла или может возникнуть.