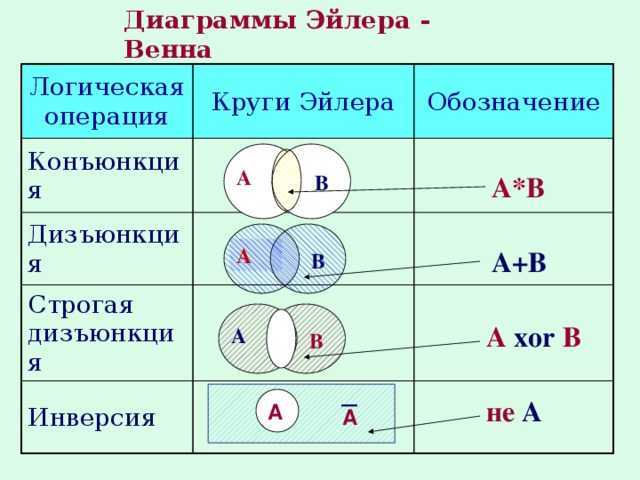
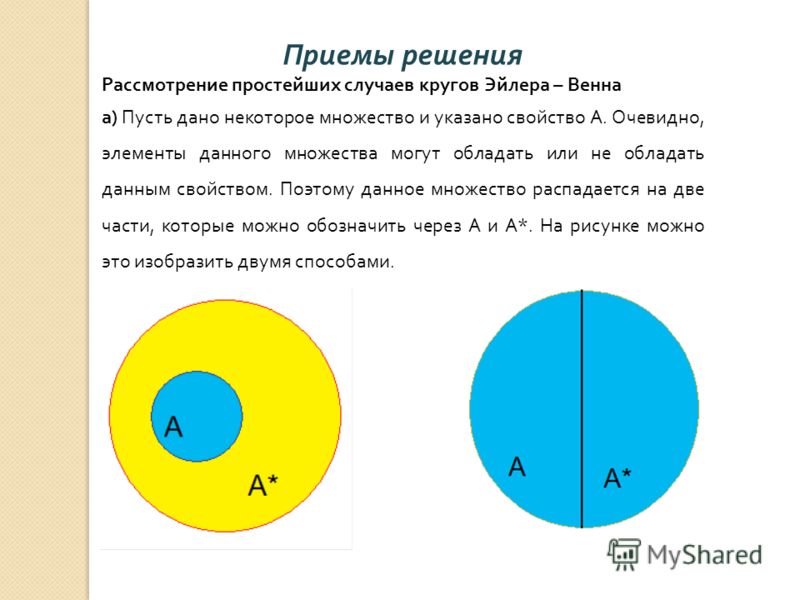
Круги эйлера калькулятор: Диаграммы Эйлера-Венна онлайн
| Алгоритм Луна Вычисляет контрольную сумму последовательности цифр при помощи алгоритма Луна, вычисляет проверочную цифру (цифру, которую можно добавить к исходной последовательности, чтобы получить последовательность с контрольной суммой оканчивающейся на 0). |
| Антилогарифм Калькулятор для вычисления антилогарифма. |
| Аппроксимация функции одной переменной Калькулятор использует методы регрессии для аппроксимации функции одной переменной. |
| Арифметика римских чисел Калькулятор поддерживающий основные математические действия (сложение, вычитание, умножение и деление) над целыми числами, представленными римскими цифрами. |
| Быстрое возведение в степень по модулю Калькулятор возводит большие числа в степень по модулю |
| Вероятность возникновения некоторого числа событий при проведении нескольких испытаний. Испытания Бернулли. Используя формулу Бернулли, вычисляет вероятность возникновения нескольких событий. |
| Взаимно простые числа и попарно взаимно простые числа Этот калькулятор проверяет, являются ли введенные числа взаимно простыми и попарно взаимно простыми. Правило проверки описано под калькулятором. |
| Выражение длины разными единицами Калькулятор выражает заданную длину через разные единицы. |
| Вычисление выражений с несколькими переменными Калькулятор вычисляет значение математического выражения с несколькими переменными. |
| Вычисление производной по ее определению Этот онлайн калькулятор выполняет численное дифференцирование – приближенное вычисление производной функции в заданной точке. Используется метод перехода к пределу последовательными приближениями до достижения заданной точности. |
| Вычисление частной производной по ее определению Этот онлайн калькулятор выполняет численное дифференцирование функции нескольких переменных – приближенное вычисление всех частных производных функции в заданной точке – по всем переменным. |
| Генератор нормально распределенных случайных чисел Калькулятор генерирует заданное количество нормально распределенных случайных чисел, используя преобразование Бокса-Мюллера над равномерно распределенными случайными числами, полученными из встроенного в Javascript генератора случайных чисел. |
| Генератор последовательности выпадания чисел Калькулятор генерирует последовательность выпадания чисел из заданного диапазона. Например, порядок вытаскивания бочонков в лото — числа от 1 до 90 будут перечислены в случайном порядке, или лотерея «5 из 36». |
| Генератор случайной матрицы Этот онлайн калькулятор генерирует случайную матрицу с заданными параметрами. |
| Двоично-десятичное кодирование Калькулятор преобразует число из десятичное в двоичное, но записанное упакованным двоично-десятичным кодом, и наоборот. |
| Дополнение числа Этот онлайн калькулятор вычисляет дополнение числа и дополнение числа с уменьшенным основанием для заданной системы счисления |
| Дроби с факториалом Этот онлайн калькулятор вычисляет результат деления, когда и в числителе и в знаменателе находится факториал числа |
| Египетские дроби Калькулятор преобразует дробь в Египетскую дробь. |
| Египетские числа Калькулятор отображает числа в виде набора древнеегипетских иероглифов. |
| Задача про бочку и ведра Как набрать из бочки определенный объем воды, используя ведра разного размера? |
| Запись математических выражений Содержит калькулятор с примерами записи математических выражений. |
| Золотое сечение Расчет длин отрезков в золотом сечении. |
| Из египетской дроби в рациональное число Калькулятор преобразует египетскую дробь в простую дробь |
| Интерполяционный многочлен Лагранжа (полином Лагранжа) Этот онлайн калькулятор строит интерполяционный многочлен Лагранжа для заданного набора точек. Калькулятор также строит график, на который выводит как полином Лагранжа, так и базисные полиномы, интерполирует заданные точки и показывает пошаговое решение. |
| Интерполяционный многочлен Ньютона (полином Ньютона) Этот онлайн калькулятор строит интерполяционный многочлен Ньютона для заданного набора точек. |
| Ковариация Этот онлайн калькулятор рассчитывает значение ковариации, или корреляционного момента для двух дискретных случайных величин |
| Корень и степень Возведение в произвольную степень, извлечение корня произвольной степени. |
| Линейная рекуррентная последовательность Этот онлайн калькулятор выполняет расчет заданного числа членов линейной рекуррентной последовательности (возвратной последовательности), а также выводит их сумму нарастающим итогом. |
| Линейные диофантовы уравнения с двумя переменными Калькулятор решает линейные диофантовы уравнения с двумя переменными. |
| Мальтузианская модель роста Этот онлайн калькулятор по заданным начальным параметрам строит график мальтузианской модели роста также известной как экспоненциальный закон. |
| Метод Крамера с подробным решением Калькулятор для решения систем линейных уравнений методом Крамера. |
| Метод Рунге – Кутты Этот онлайн калькулятор реализует классический метод Рунге – Кутты (встречается также название метод Рунге – Кутта) четвертого порядка точности. Метод используется для решения дифференциальных уравнений первой степени с заданным начальным значением |
| Метод Эйлера Этот онлайн калькулятор реализует метод Эйлера, числовой метод решения дифференциальных уравнений первой степени первого порядка точности. |
| Метод итераций (метод последовательных приближений) Отыскание корней функциональных уравнений методом итераций (последовательных приближений). |
| Модель Ферхюльста Этот онлайн калькулятор по заданным начальным параметрам строит график уравнения Ферхюльста – Пирла, или логистическую кривую. |
| Наибольший общий делитель (НОД) двух целых чисел Этот калькулятор находит наибольший общий делитель (НОД) двух целых чисел алгоритмом Евклида. |
| Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) нескольких чисел Этот калькулятор находит наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) двух и более целых чисел, выполняя разложение чисел на простые множители. Описание алгоритма можно найти под калькулятором. |
| Наименьшее общее кратное и наибольший общий делитель двух целых чисел Нахождение наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) двух целых чисел. |
| Наименьший общий знаменатель для двух или нескольких дробей Нахождение наименьшего общего знаменателя для двух или нескольких дробей. |
| Непрерывная дробь Калькулятор представляет обычную дробь в виде непрерывной (цепной) дроби. |
| Нормальное распределение Строит график плотности вероятности и функции плотности распределения для нормального распределения. |
| Обратная матрица Нахождение обратной матрицы с помощью союзной матрицы. |
| Обратная матрица по модулю Нахождение обратной матрицы по модулю с помощью союзной матрицы и обратного элемента в кольце по модулю. |
| Олимпиадные задания Калькуляторы, решающие несколько олимпиадных задач по математике. |
| Определение ранга матрицы Калькулятор, определяющий ранг матрицы |
| Определитель (детерминант) матрицы Расчет определителя (детерминанта) матрицы по определению. |
| Определитель матрицы методом Гаусса Нахождение определителя матрицы путем преобразования матрицы к треугольному виду. Работает в рациональных и комплексных числах |
| Остаток от деления Калькулятор выдает остаток от деления двух целых (или дробных) чисел. |
| Перевод меры угла из часовой системы в градусную и из градусной системы в часовую Статья содержит два калькулятора, первый предназначен для перевода угла из часовой меры в градусную, второй – из градусной меры в часовую |
| Подсчет суммы и произведения чисел, соответствующих буквам в слове Нумерологический калькулятор по запросу пользователя. |
| Поиск пропущенных номеров При помощи этого калькулятора можно искать пропуски в последовательности номеров. |
| Поиск простых чисел. Решето Эратосфена. Калькулятор находит простые числа используя алгоритм, известный как “Решето Эратосфена” |
| Приведение матрицы к треугольному виду Приведение матрицы к треугольному виду методом Гаусса и методом Барейса. |
| Производная показательно-степенной функции Функция возводится в степень самой себя заданное количество раз и затем берется производная. |
| Пропорция Расчет неизвестного члена пропорции. Создано по запросу пользователя. |
| Разложение квадратной матрицы на симметричную и кососимметричную матрицы Этот онлайн калькулятор представляет квадратную матрицу как сумму симметричной и кососимметричной матрицы |
| Распределение Стьюдента Вычисляет значение функции распределения и плотности вероятности для распределения Стьюдента. |
| Расстояние Левенштейна Калькулятор для расчета расстояния Левенштейна между двумя словами. |
| Расчет спирали Расчет неизвестных размеров спирали по известным размерам. Параметры спирали: внешний диаметр, внутренний диаметр, толщина (шаг спирали), длина спирали, число витков. |
| Расширенный алгоритм Евклида Калькулятор, реализующий расширенный алгоритм Евклида. |
| Результант Калькулятор вычисляет результант для двух многочленов. Также отображается матрица Сильвестра. |
| Решение задач Калькулятор выводит и вычисляет значения недостающих переменных из заданных формул и входных параметров. |
| Решение задач на арифметическую прогрессию Этот онлайн калькулятор помогает решить некоторые типы задач на арифметическую прогрессию |
| Решение задач на геометрическую прогрессию Этотонлайн калькулятор помогает решить некоторые типы задач на геометрическую прогрессию |
| Решение канонической задачи линейного программирования симплекс-методом Решение канонической задачи линейного программирования однофазным симплекс-методом. |
| Решение квадратных уравнений Квадратные уравнения — это уравнения вида axx+bx+c=0. Например, 4xx+2x+1=0. Такие уравнения решаются через дискриминант. Данный калькулятор поможет вам быстрее высчитать значение квадратного уравнения. Только прежде его приведите к вышеуказанному виду. Например, из 5xx-2x-0=0 в 5xx+(-2x)+0=0, из 3xx=0 в 3xx+0x+0=0. |
| Решение неоднородной системы линейных алгебраических уравнений матричным методом Решение неоднородной системы линейных алгебраических уравнений (СЛАУ) матричным методом (методом решения через обратную матрицу). |
| Решение системы линейных алгебраических уравнений методом Гаусса Калькулятор решает систему линейных алгебраических уравнений, заданных в виде матрицы методом Гаусса. Выдается пошаговое решение. |
| Решение системы линейных алгебраических уравнений методом Гаусса с сохранением дробей Калькулятор решает систему линейных алгебраических уравнений, заданных в виде матрицы, методом Гаусса, сохраняя дроби на всем протяжении процесса. |
| Решение системы линейных уравнений методом Гаусса с нахождением общего решения Решает систему линейных алгебраических уравнений методом Гаусса. Умеет выводить решение для совместных неопределенных систем линейных уравнений. Кроме того, выводит результат в формате с плавающей точкой и в формате дроби. |
| Решение системы нелинейных уравнений Этот онлайн калькулятор пытается найти решение системы нелинейных уравнений методом покоординатного поиска. |
| Решение сравнений по модулю Этот калькулятор находит решения линейных сравнений, или сравнений первой степени по модулю m |
| Сложение / вычитание многочленов Калькулятор вычисляет сумму или разность двух многочленов |
| Соотношения между двумя числами Всевозможные соотношения между двумя числами. Создано по запросу пользователя. |
| Стандартный вид числа Преобразует число в стандартный вид – произведение мантиссы от 1 до 10 и порядка числа 10. |
| Сумма сумм арифметической прогрессии Калькулятор вычисляет ряд сумм арифметической прогрессии до указанного номера, а также ряд, представляющий суммы сумм прогрессии. |
| Сумма чисел Этот онлайн калькулятор поможет вычислить сумму чисел записанных друг за другом. |
| Таблица независимых испытаний по формуле Бернулли Этот онлайн калькулятор рассчитывает вероятность k успехов при выполнении n повторных независимых испытаний с заданной вероятностью успеха p (схема Бернулли), для k меняющегося от нуля до n. |
| Теорема Байеса Этот онлайн калькулятор рассчитывает апостериорные вероятности событий в соответствии с теоремой Байеса |
| Тест простоты Миллера-Рабина Калькулятор проверяет является ли число составным, используя тест Миллера-Рабина. |
| Тест простоты Ферма Выполняет тест простоты числа, основанный на малой теореме Ферма по заданным основаниям. |
| Транспонирование матрицы Транспонирование матрицы, что тут еще сказать. |
| Умножение матриц Калькулятор умножает две матрицы. |
| Уравнение Мальтуса Этот онлайн калькулятор рассчитывает неизвестный параметр мальтузианского уравнения по известным параметрам. |
| Уравнение прямой по двум точкам Данный онлайн калькулятор находит формулы параметрического уравнения прямой и уравнения прямой с угловым коэффициентом по координатам двух точек, принадлежащих прямой. |
| Факториал Этот онлайн калькулятор рассчитывает факториал положительного целого числа. Практически любого положительного целого числа – он ограничен только временем, которое вы готовы потратить, чтобы дождаться окончания расчета. Я, например, дождался результата расчета факториала 100000! |
| Факторизация целых чисел. Перебор делителей Факторизация целых чисел методом перебора делителей. |
| Функция распределения дискретной случайной величины Функция распределения случайной величины используется для описания систем, представления опытных данных в аналитической форме для статистического анализа. |
| Центрированное скользящее среднее Этот калькулятор рассчитывает центрированное скользящее среднее для заданного периода усреднения |
| Числа Ацтеков Калькулятор преобразует целые положительные числа в форму записи числа Ацтеков. |
| Числительные Майя Калькулятор переводит число в систему счисления Майя |
| Числовые ребусы – замена цифр буквами Решатель числовых ребусов. Числовые или математические ребусы — математические выражения, в котором все или часть цифр заменены на некоторые символы, например, буквы. Требуется вместо каждого символа подставить нужную цифру, чтобы выражение было верным. |
Онлайн калькулятор: Метод Эйлера
УчебаМатематика
Этот онлайн калькулятор реализует метод Эйлера, числовой метод решения дифференциальных уравнений первой степени первого порядка точности.
Этот онлайн калькулятор можно использовать для решения дифференциальных уравнений первой степени с заданным начальным значением методом Эйлера.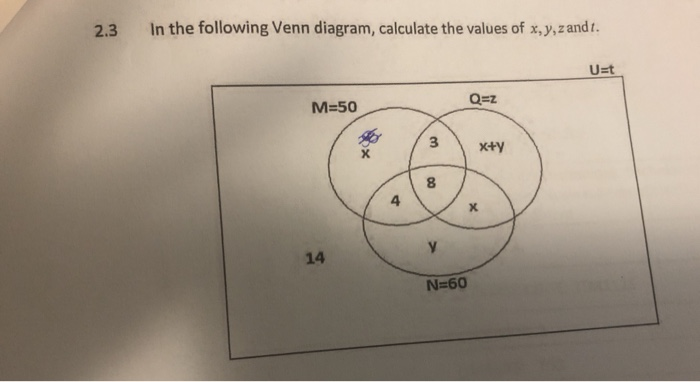
Для использования метода дифференциальное уравнение должно быть записано в форме:
Правую часть выражения f(x,y) надо записать в поле y’ .
Кроме этого потребуется начальное значение:
и точка x для которого требуется аппроксимировать значение y.
Последний параметр метода – размер шага – это приращение вдоль касательной для вычисления следующего приближения кривой функции.
Если Вам известно точное решение дифференциального уравнения в виде y=f(x), вы можете также задать его. В этом случае калькулятор построит график этого решения вместе с приближением, а также вычислит абсолютную ошибку для каждого шага приближения.
Описание метода можно найти сразу за калькулятором.
Метод Эйлера
Начальное значение x
Начальное значение y
Точка вычисления приближенного значения
Размер шага
Точное решение (не обязятельно)
Точность вычисления
Знаков после запятой: 2
Дифференциальное уравнение
Приближенное значение y
Приближение
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Метод Эйлера
Предположим мы имеем следующее:
Если мы вычислим:
мы найдем производную y’ в начальной точке.
Для достаточно малой , мы можем предположить значение y как
Или кратко
И в общем случае
Мы продолжаем вычислять следующие значения y используя это выражения до тех пор пока мы не достигнем точки x .
В этом заключается сущность метода Эйлера. – размер шага (приращение). Погрешность на каждом шаге (локальная погрешность) приблизительно пропорциональна квадрату приращения, таким образом, чем меньше приращение, тем точнее будет работать метод Эйлера. Однако общая погрешность (погрешность в конечной точке) накапливается за счет локальных погрешностей с каждым шагом. Общая погрешность пропорциональна приращению, поэтому метод Эйлера называют методом первого порядка точности.
Более сложные методы имеют более высокий порядок точности. Одна из возможностей – использовать большее число вычислений функции. Это проиллюстрировано тут: Midpoint method
Это проиллюстрировано тут: Midpoint method
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Метод Рунге – Кутты
- • Решение квадратного уравнения
- • Решение неоднородной системы линейных алгебраических уравнений матричным методом
- • Решение системы двух уравнений первой степени с двумя неизвестными
- • Решение системы линейных уравнений методом Гаусса с нахождением общего решения
- • Раздел: Математика ( 269 калькуляторов )
дифференциальные уравнения дифференцирование Математика числовое решения дифференциальных уравнений Эйлер
PLANETCALC, Метод Эйлера
Timur2022-06-30 08:45:40
Генератор диаграмм Эйлера| Онлайн-инструмент для построения диаграмм Эйлера
Creately уже используют более 10 миллионов человек и тысячи команд.
ВИЗУАЛИЗИРУЙТЕ
Создавайте диаграммы Эйлера без усилий
Шаблоны диаграмм Эйлера для различных сценариев.
Используя пользовательские цветовые темы и шрифты, выделяйте и маркируйте контуры и зоны.
Нарисуйте диаграммы Эйлера с невыпуклыми контурами, используя рисунок от руки.
Импортируйте или перетаскивайте изображения, графику и т. д. для создания визуально динамичных диаграмм Эйлера.
ПОДКЛЮЧАЙТЕ И ОРГАНИЗУЙТЕ
Добавьте больше контекста к вашей диаграмме Эйлера
Добавьте больше информации о различных зонах с интегрированными примечаниями.
библиотек форм для более чем 50 типов диаграмм для дальнейшего расширения диаграмм Эйлера.
Создавайте интерактивные презентации с помощью встроенных инструментов, таких как рамки, режим просмотра и т. д.
СОТРУДНИЧАТЬ
Сотрудничайте с другими в любое время и в любом месте
Совместная работа в режиме реального времени для работы со студентами или коллегами на общем холсте.
Комментарий с контекстом, чтобы обсуждения и последующие действия были на одном холсте. Асинхронно!
Автономная синхронизация для постоянной синхронизации вашей работы.
Экспортируйте свои диаграммы в несколько форматов изображений для встраивания, печати или совместного использования.
Что такое диаграмма Эйлера?
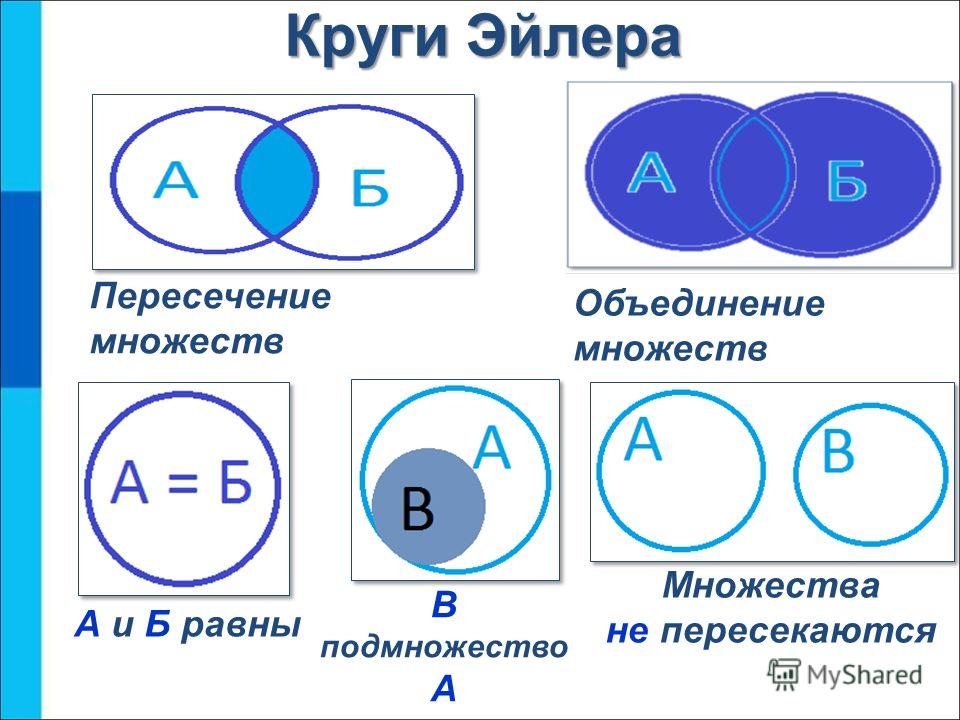
Диаграмма Эйлера — это графическое изображение, обычно используемое для иллюстрации отношений между наборами или группами; диаграммы обычно рисуются в виде кругов или овалов, хотя их можно рисовать и в других формах. Диаграммы Эйлера могут быть полезны в ситуациях, когда диаграммы Венна могут быть слишком сложными или неясными, и они предлагают более гибкий и адаптируемый способ представления множеств и отношений.
Что такое генератор диаграмм Эйлера?
Генератор диаграмм Эйлера — это онлайн-инструмент, который позволяет легко создавать диаграммы Эйлера и делиться ими. Они предоставляют формы, цветовые темы, параметры импорта и экспорта изображений, а также готовые шаблоны для настройки и быстрого старта.
Они предоставляют формы, цветовые темы, параметры импорта и экспорта изображений, а также готовые шаблоны для настройки и быстрого старта.
Как пользоваться генератором диаграмм Эйлера от Creately?
Создатель диаграмм Эйлера от Creately прост в использовании и интуитивно понятен. Он поставляется с множеством шаблонов диаграмм Эйлера, разработанных для нескольких сценариев, и возможностями настройки диаграмм для создания динамических диаграмм Эйлера. Вы можете сразу начать с одного из готовых шаблонов диаграммы Эйлера или начать с нуля, перетащив круги на холст. Затем приступайте к дальнейшей настройке, добавляя цвета, изображения или значки. Вы также можете сотрудничать с другими в режиме реального времени с помощью возможностей совместной работы, доступных в инструменте диаграммы Эйлера Creately.
Как я могу поделиться своей диаграммой Эйлера?
Генератор диаграмм Эйлера от Creately предоставляет несколько вариантов обмена диаграммами Эйлера. Вы можете экспортировать свою диаграмму Эйлера в формате PNG, SVG, JPEG или PDF для встраивания в документы или презентации, или вы можете поделиться ссылкой с правами редактирования или просмотра с человеком, с которым вы хотите поделиться диаграммой.
Оптимизируйте свои рабочие процессы за счет интеграции с любимыми инструментами
Creately интегрируется с инструментами, которые ваши команды используют каждый день, и беспрепятственно поддерживает рабочий процесс вашей команды.
Начать пробную версию
Почему Creately является лучшим генератором диаграмм Эйлера
Creately — это интеллектуальная визуальная платформа, обеспечивающая визуальную совместную работу, управление знаниями и выполнение проектов.
Более 100 фирменных функций обеспечивают гибкую, не требующую кода визуальную платформу, профессионально настроенную для простоты использования.
Бесконечный визуальный холст
Визуально создавайте и организуйте любую структуру, которую вы себе представляете. Перетаскивайте фигуры или наборы данных, встраивайте внешний контент.
Перетаскивайте фигуры или наборы данных, встраивайте внешний контент.
Совместная работа в режиме реального времени
Работайте удаленно или гибридно с отслеживанием курсора в реальном времени, синхронизированным предварительным просмотром и правильными контекстными комментариями и задачами.
Пользовательские базы данных
Создавайте пользовательские базы данных для любого вида информации, от задач, кадровых записей до вопросов для юридических фирм.
Документы, управляемые данными
Создавайте документы и заметки, чтобы углубиться в визуальные представления высокого уровня. Двусторонняя ссылка на другие документы, фигуры или данные с помощью @mentions.
Профессиональное построение диаграмм
Более 50 типов стандартных схем с более чем 1000 специально разработанных форм и соединителей обеспечивают молниеносное построение диаграмм.
Управление проектами и задачами
Используйте встроенные инструменты гибкого управления проектами или интегрируйте их с вашими любимыми инструментами управления проектами, чтобы обеспечить бесперебойную работу.
Масштабируемость предприятия
От SSO, SCIM до четко определенных рабочих процессов адаптации и увольнения сотрудников Creately может масштабироваться для удовлетворения различных потребностей предприятия.
Мощное визуальное моделирование
Визуальные элементы, поддерживаемые базами данных, обновляются один раз, отражают рабочие процессы в нескольких представлениях.
Безопасность и соответствие требованиям корпоративного уровня
Мы обеспечиваем конфиденциальность и информационную безопасность как клиентов, так и пользователей с помощью усиленных мер безопасности данных, соответствующих отраслевым стандартам безопасности. Creately соответствует требованиям GDPR и предназначен для обеспечения конфиденциальности, безопасности и сохранности ваших данных. Создать безопасность
Просто подключи и работай
Простой в использовании интерфейс с минимальными затратами на обучение. Просто войдите в систему, используя свой рабочий адрес электронной почты, чтобы автоматически добавить членов команды в корпоративный план. Установка не требуется.
Установка не требуется.
Зарегистрируйте бесплатную учетную запись сегодня.
Формула Эйлера и калькулятор тождеств Эйлера
Ниже приведен калькулятор и интерактивный график, который позволяет вам исследовать концепции, лежащие в основе знаменитой и необычной формулы Эйлера:
e iθ = cos( θ ) + i sin( θ )
Когда мы устанавливаем θ = π, мы получаем классический Тождество Эйлера:
e iπ + 1 = 0
Формула Эйлера используется во многих областях науки и техники. Это очень удобное тождество в математике, так как оно может значительно упростить выполнение многих вычислений, особенно связанных с тригонометрией. Мы видели часть этой концепции в произведениях и частных комплексных чисел ранее. 9п
И формулу, и тождество можно использовать для выполнения вычислений, а также для графических функций. Калькулятор можно использовать для ввода комплексного числа и вычисления различных степеней этого числа, а также для построения графика функции. График можно увеличить или уменьшить, а комплексное число можно изменить, чтобы увидеть, как оно влияет на график.
Калькулятор можно использовать для ввода комплексного числа и вычисления различных степеней этого числа, а также для построения графика функции. График можно увеличить или уменьшить, а комплексное число можно изменить, чтобы увидеть, как оно влияет на график.
Формула Эйлера и тождество очень полезны в математике и технике, поскольку они могут значительно упростить выполнение многих расчетов. Попробуйте поиграть с калькулятором и графиком, чтобы увидеть, что вы можете обнаружить!
Формула Эйлера, калькулятор тождества и график
На следующем графике реальная ось (обозначенная «Re») горизонтальна, а воображаемая ось (`j=sqrt(-1)`, обозначенная «Im») вертикальна, как обычно. У нас есть единичная окружность , и мы можем варьировать угол, образованный отрезком OP.
Точка P представляет комплексное число. Угол θ , разумеется, в радианах.
Чем заняться
- Выберите, будут ли ваши углы выражаться десятичными знаками или числами, кратными π.

- Выберите i или j в качестве символа мнимого числа. (Во многих учебниках используется и для символа мнимого числа, но IntMath, как и многие инженерные тексты, использует j , чтобы попытаться уменьшить путаницу с символом тока в электронике.)
- Вы можете перетащить точку P , чтобы изменить угол θ.
- Когда вы установите θ = π, вы увидите (эквивалент) Тождество Эйлера: e iπ = − 1
Углы: кратные π
Мнимый символ: i j
Формула Эйлера
Прямоугольный и полярный эквиваленты
Некоторая справочная информация о том, что происходит, и дополнительные пояснения см. на предыдущих страницах,
Комплексные числа и полярная форма комплексного числа
См. также калькулятор полярного преобразования в прямоугольное и прямоугольного в полярное, на котором основано приведенное выше:
Онлайн-калькулятор преобразования полярных координат в прямоугольные
Комплексная экспоненциальная форма
В математике комплексная экспоненциальная функция — это функция вида f(z) = ea(z), где z — комплексное число, а a — произвольная комплексная константа. Функция целая, что означает, что она определена и дифференцируема для всех комплексных чисел z. В отличие от вещественно-показательных функций сложные показательные функции не являются взаимно однозначными; то есть два разных комплексных числа могут иметь одинаковый образ под функцией. 9{-би}.
Функция целая, что означает, что она определена и дифференцируема для всех комплексных чисел z. В отличие от вещественно-показательных функций сложные показательные функции не являются взаимно однозначными; то есть два разных комплексных числа могут иметь одинаковый образ под функцией. 9{-би}.
Сложные функции
Комплексная функция — это функция вида f(z) = u(x, y) + iv(x, y), где z = x + iy — комплексная переменная, u и v — вещественнозначные функции две действительные переменные x и y, а i — мнимая единица измерения. В этой статье будут рассмотрены некоторые свойства сложных функций с упором на формулу Эйлера и тождество Эйлера.
Сложные функции имеют множество приложений в физике и технике, а также в чистой математике. В физике они используются для моделирования волновых явлений, а в технике — для проектирования электрических цепей. В чистой математике они изучаются сами по себе как красивые и интригующие объекты. 9(i*pi) + 1 = 0. Это уравнение важно, потому что оно связывает вместе пять наиболее важных чисел в математике: e, pi, i, 1 и 0.
 Таблица и график функции биноминального распределения показывает вероятность всех возможных случаев.
Таблица и график функции биноминального распределения показывает вероятность всех возможных случаев.
 Калькулятор показывает пошаговое решение, интерполирует заданные точки, а также строит график.
Калькулятор показывает пошаговое решение, интерполирует заданные точки, а также строит график.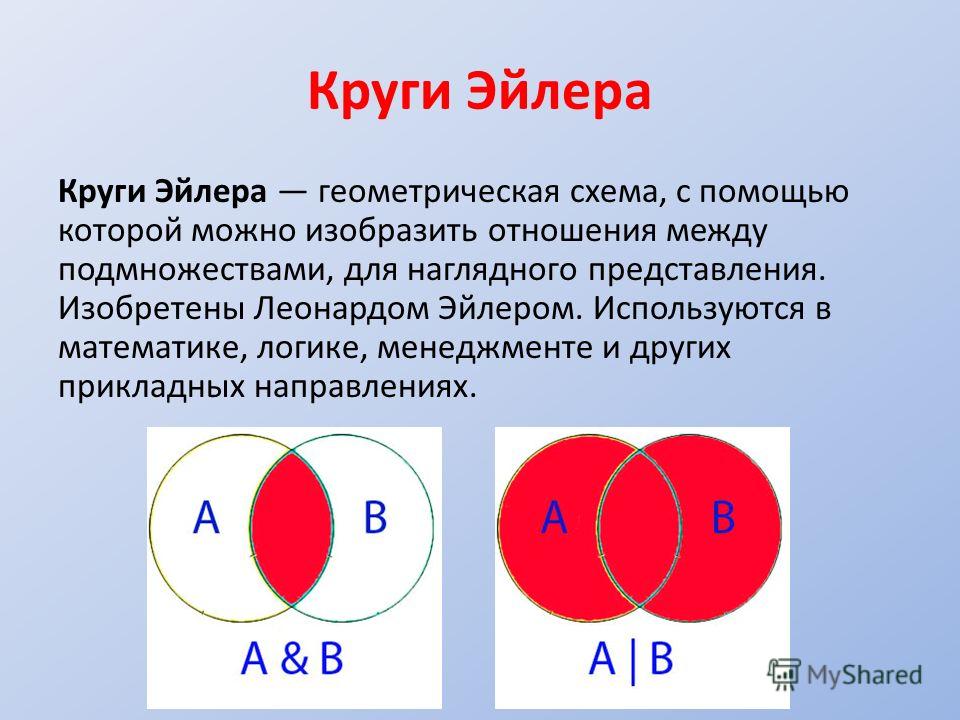 Приведено подробное решение — калькулятор выводит все промежуточные матрицы и значения определителей.
Приведено подробное решение — калькулятор выводит все промежуточные матрицы и значения определителей.
 Вычисляет квантили Стьюдента для заданного количества степеней свободы и заданной вероятности.
Вычисляет квантили Стьюдента для заданного количества степеней свободы и заданной вероятности.
 В конце результат выдается как в виде действительного числа, так и в виде дроби с числителем и знаменателем.
В конце результат выдается как в виде действительного числа, так и в виде дроби с числителем и знаменателем.