Карточка деление на трехзначного числа на однозначное: Деление трехзначного числа на однозначное (карточки) 3 класс скачать
Предметы |
| Начальная школа | |||||||||||||||||||||||||||||||||||||||||
Сколько килограммов меда налили в каждый бидон ?Карточки Деление столбиком – Стоматология в Химках
Математика 3 класс деление в столбик
С письменным приемом деления на однозначное число или, как его обычно называют, «в столбик», учащиеся начальной школы знакомятся в 3 классе и углубляют свои знания в 4 классе.
Прием письменного деления многозначного числа на однозначное получил еще одно название «деление уголком»
Деление в столбик нельзя начинать без подготовки. Для успешной работы необходимо знать:
- разряды натуральных чисел (десятки, сотни, тысячи) и легко ориентироваться в многозначном числе; таблицу умножения. Нужно блестящее знание таблицы умножения и деления; сложение и вычитание многозначных чисел; .
С помощью Карточек «Деление многозначного числа на однозначное» учитель осуществит проверку знаний, а учащимся тренировка поможет развить и систематизировать вычислительные навыки.
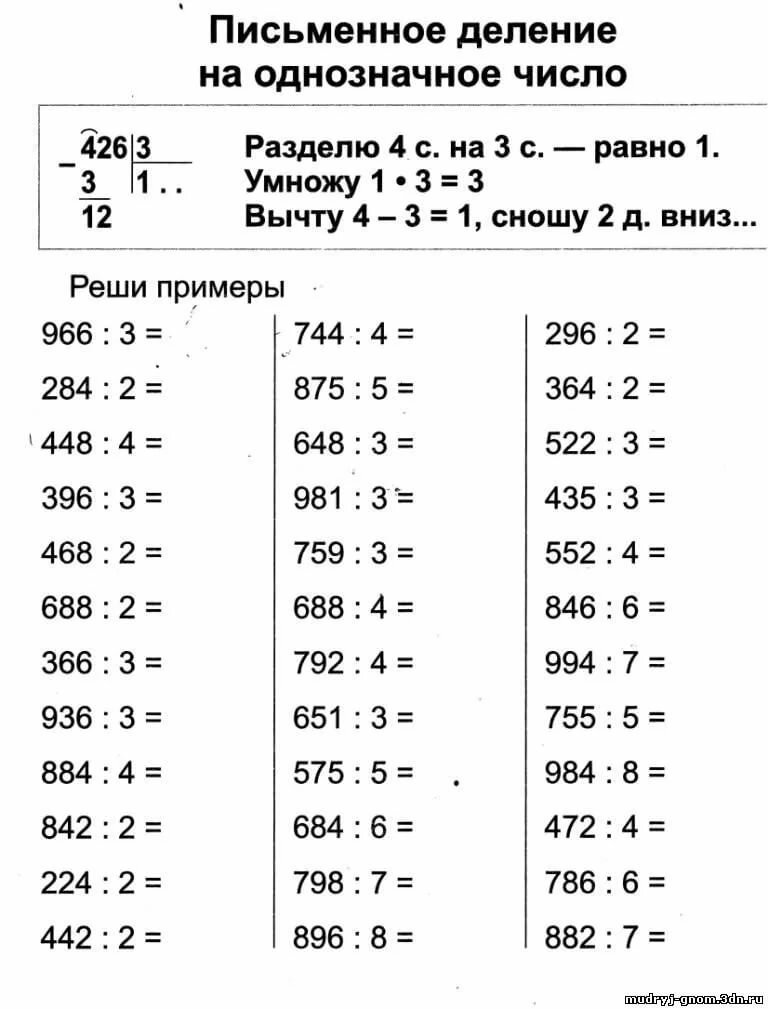
Готовые карточки «Деление на однозначное число в столбик» можно легко скачать и распечатать.
Готовые карточки деление столбиком
Карточка «Деление столбиком на однозначное число»
Скачать набор готовых карточек (10 шт) «Деление на однозначное число в столбик» вы можете по ссылке ниже
Карточка «Деление столбиком на однозначное число»
Готовые карточки деление столбиком
Карточка Деление столбиком на однозначное число.
Koncpekt. ru
13.11.2020 1:31:12
2020-11-13 01:31:12
Источники:
Https://koncpekt. ru/nachalnye-klassy/konspekty-urokov/matematika-3klass/4486-kartochka-delenie-stolbikom. html
Урок 66. приём письменного деления на однозначное число — Математика — 3 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Математика 3 класс деление в столбик
Как выполняется письменное деление на однозначное число?
Как применяется алгоритм деления трёхзначного числа на однозначное?
Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют Разрядом.
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют Разрядными единицами:
— единицы называют единицами 1-го разряда;
— сотни называют единицами 3-го разряда и т. д.
Деление (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению.
Деление — это такая операция, в результате которой получается число (частное), которое приумножении на делитель даёт делимое.
Основная и дополнительная литература:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 92-94.
2. Волкова С. И. Математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018. С. 84-85.
3. Рудницкая В. Н. Математика. Дидактические материалы. Ч.1 3 кл. – М. «Вентана — Граф», 2016, с. 23-24.
Теоретический материал для самостоятельного изучения
Сегодня мы займёмся делением.
Вам предстоит научиться выполнять деление трёхзначных чисел в столбик.
Вы справитесь с этим без проблем, если хорошо знаете таблицу умножения.
Три математических действия — сложение, вычитание и умножение в столбик вы уже умеете выполнять. Осталось одно, но самое сложное. Помните, чем сложнее – тем интереснее!
Деленье нам служит на деле,
Оно нам поможет всегда.
Кто поровну трудности делит,
Разделит успехи труда.
Мы уже выяснили, что невозможно быстро и точно делить без знания таблицы умножения.
Надо ещё хорошо знать компоненты деления и взаимосвязь между ними, быстро и точно выполнять вычитание и конечно уметь работать с разрядами.
Вспомним компоненты деления: число, которое делим – делимое, число на которое делим – делитель, результат деления – значение частного.
В тех случаях, когда деление выполнить устно сложно, выручает умение делить в столбик, или уголком.
Это название придумали не случайно. Привычный знак деления заменён на уголок.Записываем делимое, рядом чертим уголок. В верхнем углу записываем делитель, а в нижний угол вписываем цифры частного.
Обратите внимание, цифры делимого и частного имеют названия в зависимости от разряда, который обозначают.
Кроме этого, делимое придётся раскладывать на неполные делимые – первое, второе, третье. Это те числа, которые делим на делитель, пока не разделим всё число.
Рассмотрим пример 938 : 7
Записываем числа, разделив их «уголком».
Сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Умножаем делитель 7 ∙ 1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2. Записываем результат.
Число, которое мы видим, меньше делителя, поэтому его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7 ∙ 3) записываем внизу под числом 23 в столбик.
Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23 — 21) получаем разницу.
Она равняется 2.
Из делимого у нас осталось неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное = 134.
Рассмотрим ещё деление в столбик на примере 512 : 8.
1 шаг. Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева направо. Сначала берем цифру 5
3 шаг. Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг. Ставим точку под делителем.
5 шаг. После 51 стоит еще цифра 2, а значит, в ответе будет ещё одно число, то есть, частное – двузначное число.
Ставим вторую точку:
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг. Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг. Затем из 51 вычитаем 48 и получаем ответ 3.
9 шаг. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Как и в остальных случаях выполнения письменных приёмов вычислений, при делении очень важно не отступать от алгоритма.
Когда число цифр разряда меньше делителя, надо добавить к нему число цифр следующего разряда.
Если при делении неполного делимого остался остаток, спускаем его под черту и к нему приписываем цифру следующего разряда.
Остаток не может быть больше делителя!
Если цифра неполного делимого меньше делителя, то в частном пишем 0.
Вы сегодня получили ключ к успеху в математике. Смело открывайте им замки любой сложности.
Помните, чем сложнее тем интереснее.
Resh. edu. ru
17.06.2018 23:25:37
2018-06-17 23:25:37
Источники:
Https://resh. edu. ru/subject/lesson/5714/conspect/
Деление в столбик ➗ примеры и правила, как научиться » /> » /> .keyword { color: red; }
Математика 3 класс деление в столбик
Деление — это разбиение целого на равные части. Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно. Для этого разберем примеры для 3 и 4 классов, где покажем деление двузначных и трехзначных чисел.
О чем эта статья:
3 класс, 4 класс
Деление с остатком
Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5.
Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.
Деление трехзначного числа на однозначное
Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить; 7 — делитель или то, на что нужно поделить: частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2.
Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.
Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Деление трехзначного числа на двузначное с примерами
Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса.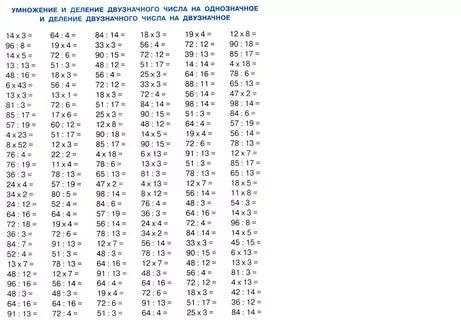
Будьте внимательны: мы перешли к самому сложному.
Пример №1.
Разделим трехзначное число 324 на двузначное 81.
Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.
Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!
Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.
Пример №2.
Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.
Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.
Как делить однозначные и многозначные числа в столбик с остатком
Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.
Пример №1
Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.
Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.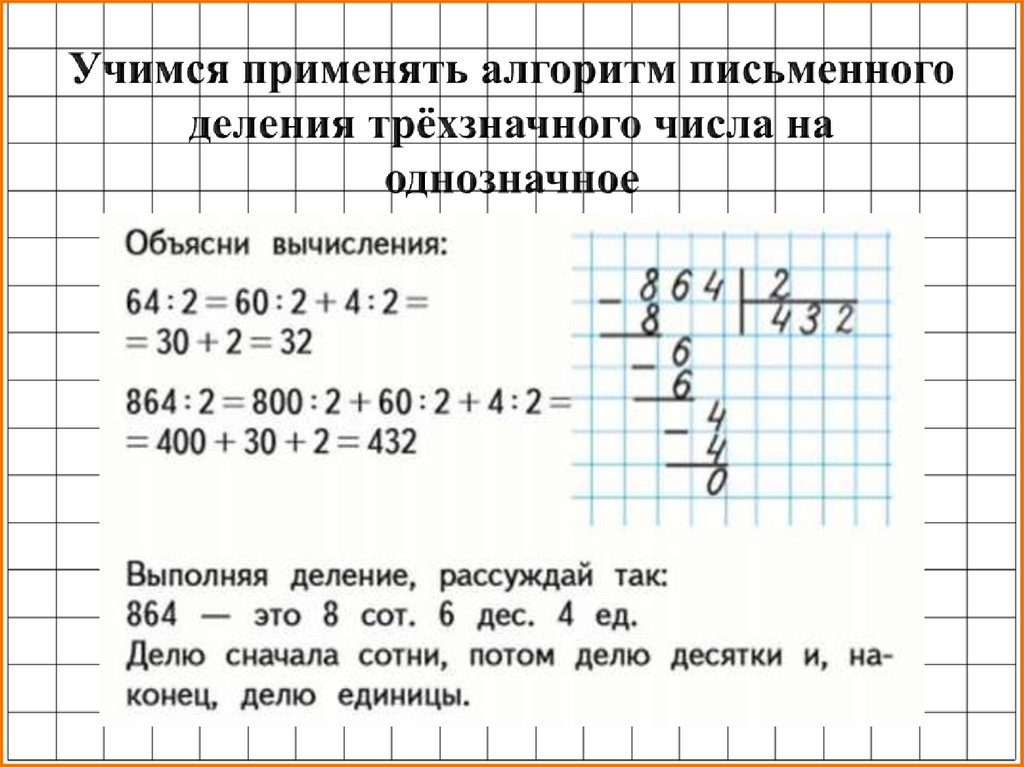
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.
Пример №2.
Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.
Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.
Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.
Примеры на деление в столбик для 3 класса
Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье.
Это задание со звездочкой.
Теперь 29 будет делимым, а 6 делителем.
Skysmart. ru
20.11.2018 16:22:58
2018-11-20 16:22:58
Источники:
Https://skysmart. ru/articles/mathematic/delenie-v-stolbik
Умножение однозначных чисел на трехзначные числа
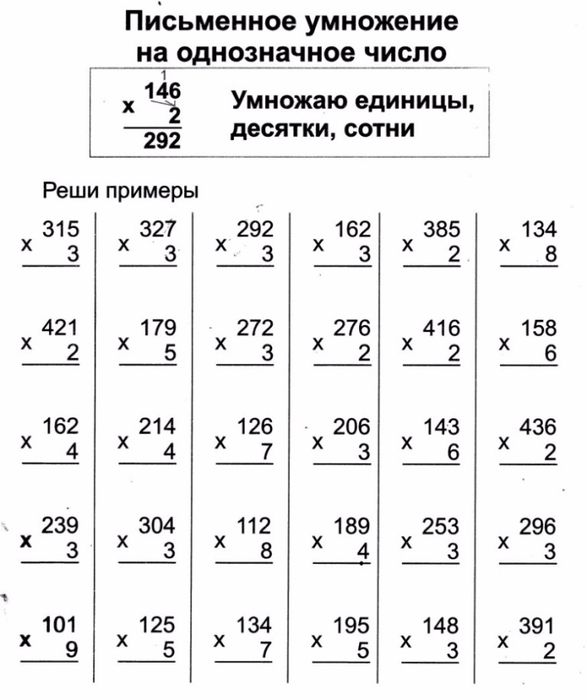
Изучив основные таблицы умножения (см. предыдущие сообщения в блоге — 1,2,3) для однозначных чисел, то есть от 2 до 9, теперь пришло время обобщить умножение на многозначные числа, начиная с умножения однозначных чисел на трехзначные числа.
Прежде чем перейти к стандартному алгоритму, лучше заложить некоторые важные основы. Здесь важно четкое понимание значения места.
Во-первых, давайте начнем с умножения на 10. Вместо использования таких правил, как «добавьте ноль позади», лучше использовать таблицы разрядных значений, чтобы учащиеся могли визуализировать процесс для каждого из разрядных значений. Например:
Разобравшись с умножением на 10, мы готовы приступить к основным задачам умножения.
Во-первых, мы начнем с случаев без перегруппировки. Опять же, мы начинаем с диаграмм стоимости места, например. для 3 x 212:
Далее мы введем частичное произведение, которое является просто абстрактным представлением примера разряда (вспомните C-P-A). Мы можем помочь учащимся, добавив метки разрядов вверху (например, HTO):
Теперь мы готовы представить стандартный алгоритм умножения:
Это было не так уж сложно, не так ли? А как насчет случаев с перегруппировкой? Теперь все становится интереснее. Мы начнем с умножения, включающего сначала 2 цифры.
Прежде чем мы приступим к работе со стандартным алгоритмом, дайте учащимся самостоятельно понять умножение, включающее перегруппировку. Используйте пример, скажем, 3 x 35, и пусть учащиеся придумают разные способы найти продукт. Вот несколько примеров.
- Разрядное значение
- Используя числовую связь
- Частичные произведения
Наконец, вводим стандартный алгоритм, поясняем концепцию перегруппировки с помощью таблицы разрядных значений:
Теперь что имеем хорошее понимание умножения с перегруппировкой, умножение однозначных чисел на трехзначные числа является простым.
Например. 3 x 145 с использованием стандартного алгоритма:
Теперь мы готовы представить простые одношаговые текстовые задачи.
Вопрос: Эбби зарабатывает 890 долларов за неделю. Сколько она заработает за 3 недели?
Даже несмотря на то, что учащиеся могут видеть числовое уравнение, которое вопрос уже задает в голове, полезно визуализировать то, что мы хотим найти, используя линейчатое моделирование. Это закладывает основу для более сложных задач на умножение и деление позже.
Видео объяснение и план урока (ресурс участника)
- https://teachablemath.com/lesson-plans/grade-3-lesson-plans/grade-3-semester-1-week-12-13/
Общие базовые стандарты
- 3NBT.A3 Умножайте одноразрядные целые числа на кратные 10 в диапазоне от 10 до 90 (например, 9 x 80, 5 x 60), используя стратегии, основанные на позиционном значении и свойствах операций.
- 4NBT.B5 Умножение целого числа, состоящего максимум из четырех цифр, на целое однозначное число.
Рекомендуемая серия рабочих тетрадей
- Рабочая тетрадь Math in Focus (3A) Глава 7. Умножение (страницы 119–146)
- Рабочая тетрадь по основной математике (Common Core Edition) (3A) Глава 3. Умножение и деление (страницы 9)от 7 до 124)
Сколько трехзначных чисел можно составить из цифр 1, 2 и 3?
Система счисления — это математическое значение, используемое для счета и измерения объектов, а также для выполнения арифметических вычислений. Это система письма для выражения чисел. Он дает особое представление каждому числу и представляет арифметическую и алгебраическую форму числа. Это позволяет нам выполнять арифметические операции, такие как сложение, вычитание, умножение и деление.
Уравнение — это оператор, который соединяет два алгебраических выражения с одинаковыми значениями со знаком «=». Например: В уравнении 9x + 4 = 7, 9x + 4 — это выражение в левой части, а 7 — это выражение в правой части, связанное со знаком «=».
Что такое число?
Слово или символ, обозначающий количество, называется числом. Числа 2, 4, 6 и т. д. — четные числа, а 1, 3, 5 и т. д. — нечетные числа. Число — это значение, созданное слиянием целых чисел. Эти числа используются для представления алгебраических величин. Целое число — это знак из набора из 10 символов в диапазоне от 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Любая комбинация целых чисел представляет число. Размер числа зависит от количества цифр, которые используются для его формирования. Например: 126, 128, 0,356, -12, 78, 94 и т. д.
Типы чиселЧисла бывают разных типов в зависимости от шаблонов цифр, которые используются для их создания. Различные символы и правила также применяются к числам, которые классифицируют их по различным типам:
- Целые числа : Целые числа представляют собой набор целых чисел плюс отрицательные значения натуральных чисел. Целые числа не включают дробные числа, т. е. их нельзя записать в форме a/b. Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом З . Целые числа — это числа, дробная часть которых равна 0, например -3, -2, 1, 0, 10, 100.
- Натуральные числа: Натуральные числа — это числа в диапазоне от 1 до бесконечности. Эти числа также известны как положительные числа или счетные числа. Мы также можем представить Натуральные числа символом N . Все целые числа, которые больше 0, являются натуральными числами. Счетные числа, такие как 1, 2, 3, 4, 5, 6.
- Целые числа: Целые числа такие же, как натуральные числа, но они также включают «ноль». . Целые числа также могут быть представлены символом Вт . Целые числа — это все натуральные числа и 0 (ноль).
- Простые числа и составные числа: Все те числа, которые имеют только два различных делителя, само число и 1, называются простыми числами. Все числа, которые не являются простыми числами, называются составными числами, кроме 0. Ноль не является ни простым, ни составным числом. Некоторые простые числа: 2, 3, 5, 53, 59, 97 и 191. Все числа больше 1 являются составными числами. Некоторые составные числа 4, 6, 9, 15, 16 и 100.
- Дроби: Дроби — это числа, записанные в виде a/b , где a принадлежит целым числам, а b принадлежит натуральным числам, т. е. b никогда не может быть 0. Верхняя часть дроби, т. е. a, называется числителем, тогда как нижняя часть, т. е. b, называется знаменателем. Пример: -1/5, 0,25, 2/5, 18/4,…
- Рациональные числа: Рациональные числа — это числа, которые могут быть представлены в форме дроби, т. е. a/b. Здесь a и b оба являются целыми числами и b ≠ 0. Все дроби — рациональные числа, но не все рациональные числа — дроби. Пример: -2/5, 0,54, 1/5, 13/4,…
- Иррациональные числа: Иррациональные числа — это числа, которые нельзя представить в виде дробей, т. е. их нельзя записать в виде a/b. Пример: √2, √3, √.434343, π,…
- Действительные и мнимые числа: Действительные числа — это числа, которые могут быть представлены в десятичной форме. Эти числа включают целые числа, целые числа, дроби и т. д. Все целые числа принадлежат к действительным числам, но не все действительные числа принадлежат к целым числам. Воображаемые числа — это все те числа, которые не являются реальными числами. Эти числа при возведении в квадрат дадут отрицательное число. √-1 представлен как i. Эти числа также называются комплексными числами. Пример: √-2, √-5,…
е. их нельзя записать в форме a/b. Диапазон целых чисел — от бесконечности на отрицательном конце до бесконечности на положительном конце, включая ноль. Целые числа представлены символом З . Целые числа — это числа, дробная часть которых равна 0, например -3, -2, 1, 0, 10, 100.
Все числа, которые не являются простыми числами, называются составными числами, кроме 0. Ноль не является ни простым, ни составным числом. Некоторые простые числа: 2, 3, 5, 53, 59, 97 и 191. Все числа больше 1 являются составными числами. Некоторые составные числа 4, 6, 9, 15, 16 и 100.
е. их нельзя записать в виде a/b. Пример: √2, √3, √.434343, π,…Перестановки и комбинации
Перестановка – это различное расположение определенного количества компонентов, взятых по одному, по частям или по всем одновременно. Например, если у нас есть два компонента X и Y, то есть два возможных расположения: XY и YX.
Количество перестановок, когда элементы «r» расположены из общего числа «n» элементов, составляет
n P r = n!/(n – r)!
Например, пусть n = 4 (A, B, C и D) и r = 2 (все перестановки размера 2).
Ответ 4!/(4-2)! = 12. Итак, двенадцать перестановок — это AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB и DC.
Комбинация – это различные наборы определенного количества компонентов, взятые по одному, по частям или все вместе. Например, если у нас есть два компонента A и B, то есть только один способ выбрать два элемента, мы выбираем их оба.
Количество комбинаций при выборе ‘r’ элементов из ‘n’ элементов равно
n C r = n!/[(r!) × (n – r)!]
Например, пусть n = 4 (A, B, C и D) и r = 2 (все комбинации размера 2). Ответ: 4!/((4-2)! × 2!) = 6. Итак, шесть комбинаций: AB, AC, AD, BC, BD, CD.
n C r = n C (n –r)
Примечание: В том же примере у нас есть разные случаи перестановки и комбинации. Если говорить о перестановке, то АВ и ВА — разные вещи, но для отбора АВ и ВА — одно и то же.
Сколько трехзначных чисел можно составить из цифр 1, 2 и 3?
(i) разрешено ли повторение цифр?
Решение:
Ответ: 27
Метод:
Здесь общее количество цифр = 3
Предположим, что трехзначное число равно ABC.
Теперь количество цифр, доступных для A=3
Поскольку повторение разрешено,
Таким образом, количество цифр, доступных для B и C, также будет 3 (каждая).
Таким образом, общее количество трехзначных чисел, которые можно составить = 3 × 3 × 3 = 27
(ii) повторение цифр не допускается?
Решение:
Похожие вопросыОтвет: 6
Метод:
Здесь общее количество цифр = 3
число ABC.
Теперь количество цифр, доступных для A = 3,
Поскольку повторение не разрешено,
Таким образом, количество цифр, доступных для B = 2 (поскольку одна цифра уже была выбрана в A),
Аналогично, количество цифр, доступных для C = 1,
Таким образом, общее количество трехзначных чисел, которые можно составить = 3 × 2 × 1 = 6,
Вопрос 1: Сколько трехзначных чисел можно составить из четырех цифр 1, 2, 3, 4?
(i) разрешено ли повторение цифр?
Решение:
Ответ: 64
Метод:
Здесь общее количество цифр = 4 цифра.
Теперь количество цифр, доступных для A=4
Поскольку повторение разрешено,
Таким образом, количество цифр, доступных для B и C, также будет 4 (каждая).
Таким образом, общее количество трехзначных чисел, которые можно составить = 4 × 4 × 4 = 64
(ii) повторение цифр не допускается?
Решение:
Ответ: 24
Метод:
Здесь общее количество цифр = 4
Предположим, что трехзначное число равно ABC.
Теперь количество цифр, доступных для A = 4,
Поскольку повторение запрещено,
Таким образом, количество цифр, доступных для B = 3 (поскольку одна цифра уже была выбрана в A),
Аналогично, количество цифр, доступных для C = 2.
Таким образом, Общее количество трехзначных чисел, которые можно составить = 4 × 3 × 2 = 24
Вопрос 2: Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4 , и 5 при условии, что –
(i) повторение цифр разрешено?
Решение:
Ответ: 125
Метод:
Здесь общее количество цифр = 5
Пусть трехзначное число будет ABC.
Теперь количество цифр, доступных для A = 5,
Поскольку повторение разрешено,
Таким образом, количество цифр, доступных для B и C, также будет 5 (каждая).
Таким образом, общее количество трехзначных чисел, которые можно составить = 5 × 5 × 5 = 125.
(ii) повторение цифр не допускается?
Решение:
Ответ: 60
Метод:
Здесь общее количество цифр = 5
Пусть трехзначное число будет ABC.
Теперь количество цифр, доступных для A = 5,
Поскольку повторение не разрешено,
Таким образом, количество цифр, доступных для B = 4 (поскольку одна цифра уже была выбрана в A),
Аналогично, количество цифр, доступных для C = 3,
Таким образом, общее количество трехзначных чисел, которые можно составить = 5 × 4 × 3 = 60,
Вопрос 3: Сколько трехзначных четных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение:
Ответ: 108
Метод:
Здесь общее количество цифр = 6
3 900 цифр.
Теперь, поскольку число должно быть четным, цифры в разряде единиц должны быть четными, поэтому число
цифр, доступных для C = 3 (поскольку 2, 4, 6 здесь четные цифры),
Поскольку повторение разрешено,
Таким образом, количество цифр, доступных для A = 6,
Аналогично, количество доступных цифр для B = 6.
Таким образом, общее количество трехзначных четных чисел, которые могут быть сформированным = 6 × 6 × 3 = 108
Вопрос 4: Сколько четырехбуквенных кодов можно составить из первых 10 букв английского алфавита, если ни одна буква не повторяется?
Решение:
Ответ: 5040
Метод:
Здесь общее количество букв = 10
Пусть 4-буквенный код будет 1234.
Теперь количество букв, доступных для 1-го места = 10,
Поскольку повторение запрещено ,
Таким образом, возможное количество букв на 2-м месте = 9 (Поскольку одна буква уже была выбрана на 1-м месте
),
Аналогично, количество букв, доступных для 3-го места = 8,
и количество буквы доступны для 4-го места = 7.
