Картинка квадрат круг треугольник: ᐈ Круглый квадрат фото, рисунки круг квадрат треугольник
Презентация “Геометрические фигуры” | Презентация к уроку по математике (средняя группа) на тему:
Слайд 1
Геометрические фигуры ( для средней группы) Воспитатель: Андрусенко О.Н Муниципальное дошкольное образовательное учреждение детский сад № 8Слайд 2
Задачи: 1.Учить детей выделять особые признаки фигур (наличие или отсутствие углов и др.) 2.Познакомить детей с прямоугольником, сравнивая его с кругом, квадратом, треугольником. 3.Формировать представление о том, что фигуры могут быть разных размеров: большой, маленький. 4.Учить соотносить форму предметов с известными геометрическими фигурами: тарелка-круг, платок-квадрат, мяч-шар, дверь-прямоугольник и др. 5.Развивать умения различать пространственные направления: вверху-внизу, справа-слева. Цель: развивать представления детей о геометрических фигурах: круге, квадрате, треугольнике.
Слайд 3
Он давно знакомый мой, Каждый угол в нём прямой, Все четыре стороны Одинаковой длины. Вам его представить рад Как зовут его? Квадрат
Слайд 5
Словно стол стоит квадрат.
Он гостям обычно рад. Он квадратное печенье Положил для угощенья. Он – квадратная корзина И квадратная картина. Все четыре стороны У квадратика равны. Квадрат
Слайд 7
На фигуру посмотри И в альбоме начерти Три угла. Три стороны Меж собой соедини. Получился не угольник, А красивый… Треугольник
Слайд 9
Треугольник Треугольный треугольник Угловатый своевольник. Он похож на крышу дома И на шапочку у гнома. И на острый кончик стрелки, И на ушки рыжей белки. Угловатый очень с виду Он похож на пирамиду!
Слайд 11
Круг Прикатилось колесо, Ведь похожее оно, Как наглядная натура Лишь на круглую фигуру. Догадался, милый друг? Ну, конечно, это …
Слайд 13
Круг Круглый круг похож на мячик, Он по небу солнцем скачет. Круглый словно диск луны, Как бабулины блины, Как тарелка, как венок, Как веселый колобок, Как колеса, как колечки, Как пирог из теплой печки!
Слайд 15
Растянули мы квадрат И представили на взгляд, На кого он стал похожим Или с чем-то очень схожим? Не кирпич, не треугольник – Стал квадрат… Прямоугольник
Слайд 17
Прямоугольник Как окно прямоугольник, Аккуратный, словно школьник.
Он похож на дверь , на книжки, И на ранец у мальчишки. На автобус, на тетрадку, На большую шоколадку. На корыто поросенка И на фантик у ребенка.
Слайд 19
Если взял бы я окружность, С двух сторон немного сжал, Отвечайте дети дружно – Получился бы … Овал
Слайд 21
Овал С высоты кружок упал. Он теперь не круг – овал! Он овальный, как жучок, Он похож на кабачок, На глаза и на картошку, А еще похож на ложку, На орех и на яйцо, На овальное лицо!
Слайд 23
Взял треугольник и квадрат, Из них построил домик. И этому я очень рад: Теперь живет там гномик. Поиграем
Слайд 25
Мы встречаем их везде: На земле и на воде В небесах и под землей, Нам они нужны с тобой! Будем их мы называть, В окружении искать. Треугольник, круг, квадрат, Тем фигурам каждый рад! Различить их с вами сможем, Мы без них никак не можем!
Слайд 26
Физкультминутка «Все умеем мы считать» Раз, два, три, четыре, пять — Все умеем мы считать. Раз! Подняться потянуться. ( Под счет воспитателя дети выполняют потягивани я.
) Два! Согнуться, разогнуться . (Наклоны. Повороты туловища.) Три! В ладоши три хлопка, Головою три кивка. ( Движения головой.) На четыре – руки шире. ( Хлопки в ладоши.) Пять — руками помахать . ( Движения руками.) Шесть — на стульчик тихо сесть. ( Прыжки. Ходьба на месте.)
Слайд 27
СОБЕРИ КРУГИ
Слайд 28
СОБЕРИ КВАДРАТЫ
Слайд 29
СОБЕРИ ТРЕУГОЛЬНИКИ
Слайд 30
ИЗ КАКИХ ФИГУР СОСТОИТ КАРТИНКА
Слайд 31
ИЗ КАКИХ ФИГУР СОСТОИТ КАРТИНКА
Аппликации из геометрических фигур для детей с шаблонами
Прежде, чем знакомить малыша с миром аппликации, ему нужно показать основные геометрические фигуры: круг, квадрат, треугольник, ведь, именно на их основе и строится весь творческий процесс. Со временем малыш научится самостоятельно вырезать сложные фигуры из бумаги, ну а пока все картинки должны состоять лишь из основных фигур.
Аппликация из геометрических фигур довольно просты, да с вырезанием трудных фигур у ребенка не возникнет никаких трудностей.
Все шаблоны, представленные ниже, содержат картинку-пример, общий фон, на который нужно приклеивать цветные фигуры. Вам остается лишь распечатать на цветном принтере все шаблоны и приклеить.
Возраст, для которого предназначена такая работа – от 1,5 до 3 лет, но самые простые работы можно делать с малышом даже тогда, когда он не умеет вырезать – вырезает пусть мама, а малыш приклеивает деталь на основу-фон. Если нет возможности использовать готовые шаблоны, то по примеру можно все фигуры вырезать из цветной бумаги. Для более старших деток для аппликации можно использовать не только цветную бумагу, но и другие материалы: картон, бархатную или гофрированную бумагу, фетр.
Чтобы распечатать шаблоны аппликаций с сайта – нажмите на картинке для увеличения
Аппликация из геометрических фигур “Цыпленок”
Картинка, черно-белый фон и шаблоны для работы:
Скачать архив (размер: 420 Кб)
Аппликация из геометрических фигур “Рыбка”
Картинка, черно-белый фон и шаблоны для работы:
Скачать архив (размер: 160 Кб)
Принцип работы у всех аппликаций одинаковый: вырезаем цветные шаблоны-детали и приклеиваем на черно-белую заготовку.
Для работы вам понадобятся такие инструменты, как:
- ножницы;
- клей ПВА.
Для детей важно подобрать удобные ножницы, чтобы в процессе вырезания у них не возникло трудностей. Ножницы должны быть безопасными, с закругленными концами.
Аппликация из геометрических фигур “Домик”
Картинка для примера, фон и шаблоны для работы:
Скачать архив (Размер: 249 Кб)
Аппликация для детей “Замок” из цветной бумаги
Скачать архив (размер 493 Кб)
Все материалы являются собственностью портала Вкусняша.ру и защищены авторским правом. Данный материал не предназначен для коммерческого использования, только для работы в детских коллективах и в домашних условиях.
Цель подобных работ – познакомить малыша с такими простыми геометрическими фигурами, как круг, квадрат, прямоугольник, полукруг, треугольник. В некоторых шаблонах используются более сложные фигуры – трапеция, тор, ромб, овал. Размеры и цвет у фигур тоже разные, что знакомит малыша с понятием формы и цвета.
Аппликация для детей “Паровоз”
Скачать архив (размер 163 Кб)
Распечатывать все шаблоны можно как на обычной белой бумаге (для ксерокса) формата А4, либо использовать альбомные листы, чтобы детали не помялись.
Аппликация из фигур “Аквариум”
Скачать архив (303 Кб)
Шаблоны для работы “Тракторист”
Скачать архив (433 Кб)
“Мельница”
Скачать архив (294 Кб)
Шаблоны для аппликации из геометрических кругов “Мальчик”
Скачать архив (1,07 Мб)
Аппликации из геометрических фигур “Животные”
Как же сделать маленького петушка или слоника из цветной бумаги? Покажите малышу, что даже самая обычная геометрическая фигура, например, круг или овал, может превратиться в забавную обезьянку или веселого слоника-циркача! Животные из цветной бумаги также очень просты в изготовлении, предназначены для детей 2-3 лет.
Аппликация для малышей из фигур “Петушок”
Картинка для примера, фон и шаблоны для работы:
Скачать архив (Размер: 549 Кб)
Аппликация из геометрических фигур “Обезьянка”
Скачать архив (размер 186 Кб)
Шаблоны для аппликации “Слон-циркач”
Скачать архив (209 Кб)
Шаблоны для аппликации из фигур “Динозавр”
Скачать архив (487 Кб)
Шаблоны для работы “Попугай”
Скачать архив (856 Кб)
Шаблоны для работы “Бабочка”
Скачать архив (размер 1,81 Мб)
Все представленные аппликации лучше выполнять вместе с ребенком.
Подобный творческий процесс развивает не только фантазию, воображение и знакомит малыша с окружающим миром. Такие простейшие действия, как вырезание мелких деталей и наклеивание их точно на предназначенное место развивает мелкую моторику малыша.
Аппликация – это основа, на которой строится такой увлекательный процесс, как скрапбукинг, а также изготовление открыток к праздникам своими руками. Со временем ребенок научится сам придумывать сюжеты и оформлять свои работы, ну а пока задача родителей состоит в том, чтобы познакомить его с волшебным миром аппликации.
Психогеометрия: психотипы людей в геометрических фигурах
Пять психотипов созданы Сьюзен Деллингер, американским психологом. Она назвала свою теорию – психогеометрия, так как все ее психотипы ассоциируются с одной из основных геометрических фигур. По мнению психологов, люди редко бывают ярко выраженным одним психотипом, чаще всего, это смешанные типы, с преобладанием одного основного типа.
У психологов есть шутка, которая наглядно показывает, как ведут себя представители пяти психотипов по психогеометрии: подошло пять автобусов, в которые надо рассесться представителям всех 5 фигур.
Круги – полезли в автобус весело, балагуря, подшучивая друг над другом, расселись по трое на сидениях, в результате, их влезло больше, чем надо.
Треугольники – каждый пытался отодвинуть другого, и сели они по одному, стараясь занять лучшие места в начале автобуса и четко по одному на два сидения, в результате, их поместилось в два раза меньше, чем было мест в автобусе.
Квадраты – дисциплинированно вошли, аккуратно расселись, четко выполняли указания, доставили меньше всего хлопот.
Прямоугольники – их пришлось загонять в автобус, кто-то боялся войти, кто-то потерялся на станции, кто-то не знал, как входить и просил разъяснить ему, на их рассадку ушло больше всего времени.
Зигзаги – полезли в автобус всеми способами, кто-то через окно, кто-то через люк в крыше, расселись тоже, кто во что горазд, стали давать советы водителю, как лучше вести автобус, начался обмен идеями, что можно в этом автобусе усовершенствовать.
Эта шутка наглядно и быстро показывает все пять психотипов, которые созданы Сьюзен Деллингер, американским психологом. Она назвала свою теорию – психогеометрия, так как все ее психотипы ассоциируются с одной из основных геометрических фигур.
Небольшой тест
Как можно определить, к какому типу по психогеометрии принадлежит тот или иной человек? Дайте ему лист бумаги и ручку и попросите нарисовать три геометрические фигуры из пяти основных (квадрат, треугольник, круг, зигзаг, прямоугольник). Первая нарисованная фигура – это и будет основной психотип человека, две остальных – дополнительные. По мнению психологов, люди редко бывают ярко выраженным одним психотипом, чаще всего, это смешанные типы, с преобладанием одного основного типа. Например, лидер – треугольник, а внутри – консервативный квадрат. Или мягкий круг, а вторая фигура этого человека – креативный зигзаг.
Подобный тест можно провести с близкими или друзьями, да и коллег по работе можно протестировать.
Подходит он и для собеседования при приеме на работу. Но как быть, если нужно быстро определить психотип собеседника, например, клиента или покупателя, чтобы знать, как с ним общаться, взаимодействовать, предлагать те или иные услуги или товары? В таком случае просить нарисовать фигуры на бумаге не получится. Тогда необходимо знать основные черты пяти психотипов, каждому из которых соответствует своя геометрическая фигура.
Треугольник
Это – лидеры во всех сферах жизни, бизнеса, политики. Как правило, у многих руководителей основная фигура по психогеометрии именно треугольник. Как их определить? Они дорого и со вкусом одеты, любят пафосные и статусные вещи, престижные автомобили. У них – новейшая компьютерная техника и мобильные телефоны. Им нравится элитный алкоголь, сигары. Рабочее место – дорого обставленное, со статусными аксессуарами. Ценят качество во всем. Их речь – властная, с элементами приказов, быстрая и четкая. Они не любят, когда им возражают.
Считают, что они лучше других по многим показателям и лучше других во многом разбираются. Быстро принимают решения, способны взять на себя ответственность за эти решения. Для них важно быть очень информированными. Ловят информацию на лету, умеют в ней разбираться. Часто занимаются сразу несколькими делами. Их слабость – в излишнем деспотизме и тщеславии.
Квадрат
Консервативные и аккуратные педанты. Их можно часто встретить среди бухгалтеров, чиновников, администраторов, хозяйственников компаний. Они всегда аккуратно и чисто одеты, выбриты, причесаны, обувь начищена. Одежда не всегда модная и стильная, но практичная и удобная. Рабочее место – чистое, прибранное, все лежит на своем месте. При выборе автомобиля руководствуются максимальной практичностью и экономичностью. Послушные, уважительно относятся к представителям власти, четко следуют правилам, стандартам, приказам, инструкциям. Умеют работать с различными документами и цифрами.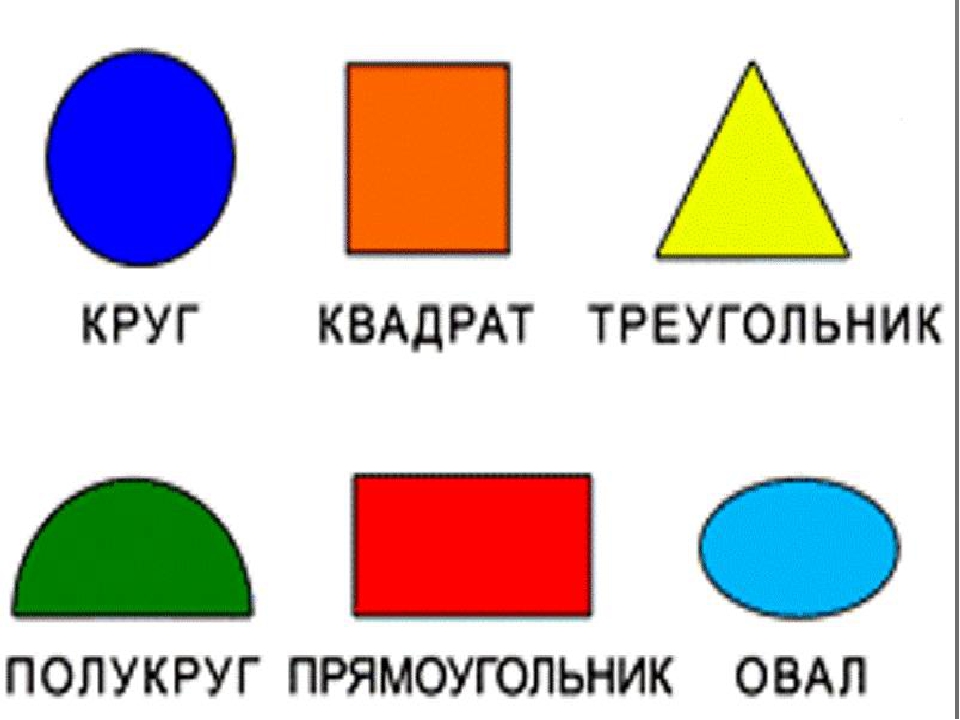
Круг
Коммуникабельные, жизнерадостные, общительные. Если у вас есть на работе «душа компании», то это точно круг по психогеометрии. Общение для них – высшая жизненная ценность. Они любят заниматься общественной работой, собирают деньги на дни рождения и другие мероприятия, организовывают различные мероприятия, корпоративы, тусовки. Им можно «поплакаться в жилетку», они всегда поймут и выслушают, а также дадут совет. Круги – врожденные психологи, которые хорошо разбираются в тонкостях человеческих взаимоотношений. Оптимистичны и эмоционально устойчивы. Они – самые активные посетители социальных сетей. Рабочее место – часто бывает беспорядок, в котором они что-то подолгу ищут, потому что материальный мир для них не так важен.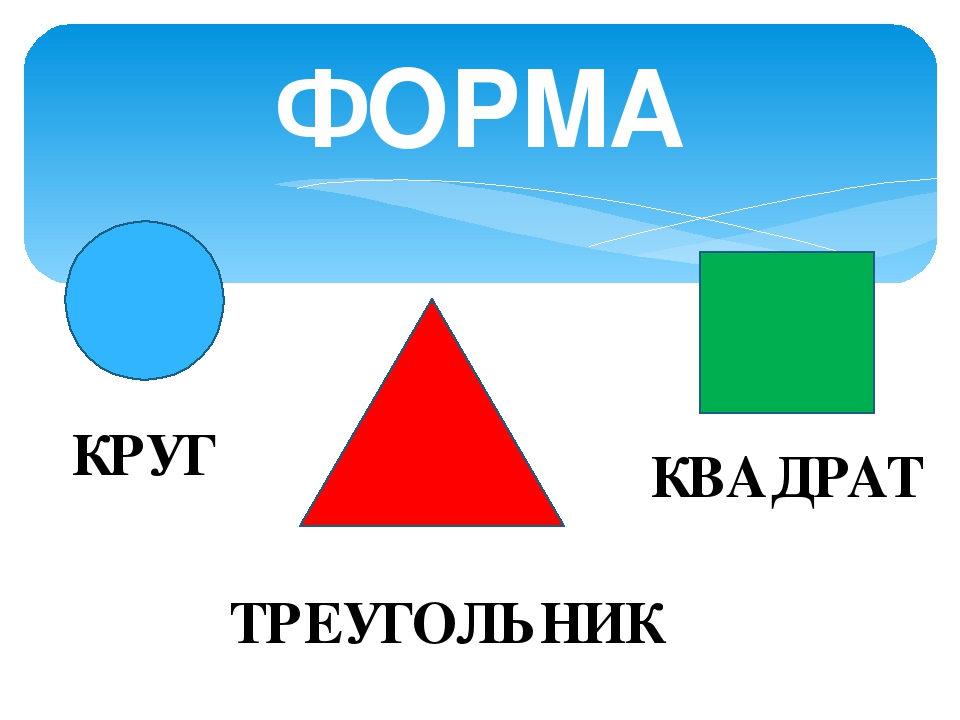
На столе – фотографии семьи или друзей, много сувениров. Одежду предпочитают мягкую и удобную, например, теплые вязаные свитера, нежные кофточки и т. п. Именно у кругов чаще всего бывают домашние животные, с которыми они охотно возятся. Автомобили – небольшие, ярких цветов, внутри украшены различными зверюшками, подушками. Речь – эмоциональная, с множеством оттенков и нюансов, обожают юмор, шутки, прибаутки. Их слабость в том, что они могут быстро попасть под чужое влияние и порой зависимы от мнения других.
Зигзаг
Это самый творческий психотип. Оригинальные и креативные, буквально фонтанирующие новыми и интересными идеями. Это – изобретатели и творческие личности, для которых самая важная жизненная ценность – творческая самореализация. Они нестандартны во всем, начиная от манеры одеваться и заканчивая рабочим местом. На рабочем столе – у них еще тот кавардак, но при этом, они умудряются отлично в нем разбираться, всегда быстро выискивая нужную бумагу или деталь.
Прямоугольник
Самая неустойчивая фигура психогеометрии. Ими бывают почти все дети, а также другие фигуры, когда они в стрессе. Хотя некоторые люди настолько инфантильны и зависимы от чужого мнения, что так и остаются прямоугольниками на долгие годы. Это фигура роста, определенной стадии в жизни человека. Прямоугольники многое еще не знают или не понимают, они чаще остальных задают вопросы, они любопытны и им многое интересно.
Они охотно слушают различные объяснения, ходят на экскурсии, читают мнения и комментарии других людей. У них зачастую не сформировано еще собственное мнение, пэтому они охотно перенимают мнения других людей. В одежде – меняют стили в одежде, постоянно копируя кого-то. Рабочее место – может меняться, утром – порядок, к вечеру – бардак на столе. Автомобили – они покупают, четко следуя принципу «на чем ездят остальные». Зачастую они переоценивают или недооценивают собственные силы. Когда остальные фигуры по психогеометрии впадают в стрессовое состояние, они становятся неустойчивыми прямоугольниками: неопределенными, колеблющимися. Например, сильные и властные треугольники начинают пить, квадраты становятся хаотичными и неаккуратными, круги замыкаются в себе и молчат, а зигзаги сидят на кресле и смотрят в потолок или в окно, и ничего не хотят делать.
источник
квадратный треугольник круга, Стоковые Фотографии и Роялти-Фри Изображения квадратный треугольник круга квадратный треугольник | Depositphotos® Фото деревянной игрушкиЗатемненный вид человека в нижнем белье, держащего в руках серые бумажные фигуры, изолированные на сером Установите нарисованные вручную фигуры, круг, квадрат, треугольник, числа, линию, четыре акварельные фигуры (квадрат, круг, прямоугольник; треугольник) на четырех акварельных фигурах на белом.
в качестве фона Четыре акварельные фигуры (квадрат, круг, прямоугольник; треугольник) на Фото деревянного грузовика, загруженного маленькими красочными деревянными геометрическими фигурами: круг, треугольник, прямоугольник, квадрат из бука на белом изолированном фоне. грузовик, загруженный небольшими красочными деревянными геометрическими фигурами: круг, треугольник, прямоугольник, квадрат из бука на белом изолированном фоне. Рисование руки света и тени в сферу, круг, треугольник, шестиугольник, цилиндр и квадрат.Basic Shapes3D Red ShapesDoodle, Набор рисованной формы, круг, квадрат, треугольникТри геометрические формыФормы блоковКрасочные деревянные игрушечные блоки в геометрических формах. Красочная текстура с копией пространства. Оранжевый прямоугольник, зеленый квадрат, красный круг, желтый треугольник и синий пятиугольник на белом фоне. Блоки форм, мода девушка, желтый фон абстрактная акварель. круги, пятна, пятна и брызги. Ребенок держит в руках ножницы и картонный квадрат. Цветные картонные листы и различные геометрические фигуры на деревянном столе.
Площадь (многоугольник, треугольник, круг, квадрат)
Площадь – это пространство внутри двухмерной фигуры.
Если вы подумаете о полу в своей спальне, то это будет максимальная площадь пола, на которую вы можете бросить свои вещи, прежде чем вы не увидите ни одного оставшегося пола.
Площадь всегда выражается в квадратных единицах ( единиц 2 ). Это потому, что он двумерный (длина и высота).
Вы можете определить площадь фигур, посчитав квадраты внутри фигур. На этих трех рисунках каждая ячейка представляет.
- Рисунок A занимает 25 маленьких коробок, поэтому его площадь составляет
- Рисунок B занимает 36 маленьких коробок, поэтому его площадь составляет
- Рисунок C занимает 21 полную коробку и 7 половинных коробок, поэтому его площадь составляет
Площадь прямоугольника = основание x высота
Вот.
Если мы разделим его на секцию шириной 1 см, это будет выглядеть так:
Каждая строка содержит 10 квадратов и 6 рядов, что в сумме дает 10 × 6 квадратных см.
Это то же самое, что умножение основания на высоту:.
Площадь треугольника = ½ (основание × высота)
Вот треугольник с основанием 5 см и высотой 6 см.
Если мы поместим еще один треугольник с такой же высотой и основанием поверх этого, мы получим.
Теперь мы уже знаем, как вычислить площадь прямоугольника (основание × высота). Итак, площадь прямоугольника
. Однако нам нужен только треугольник, который составляет половину прямоугольника. По сути, мы взяли ½ площади всего прямоугольника или ½ (основание × высота).
Площадь параллелограмма = основание × высота
Теперь давайте посмотрим на параллелограмм с основанием 6 см и высотой 3 см.
Если переместить маленький треугольник слева до упора вправо, эта форма станет прямоугольником с основанием 6 и высотой 3 см.
Поскольку вы уже знаете, как найти площадь прямоугольника (основание × высота), у вас есть все инструменты, необходимые для определения площади этого параллелограмма.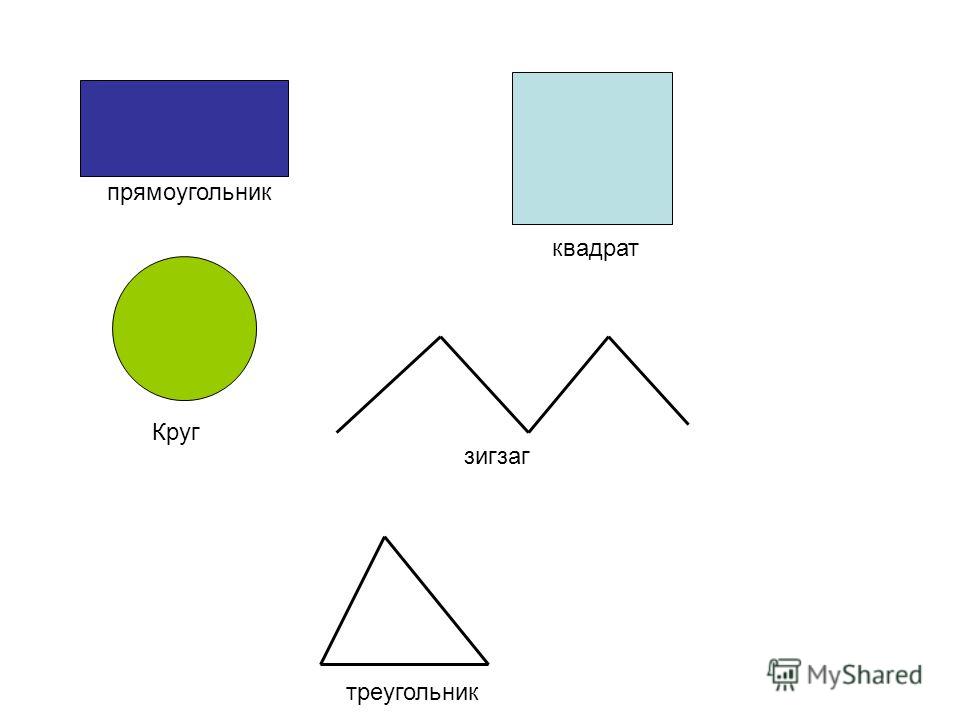
Площадь трапеции = ½ (основание 1 + основание 2 ) x высота
Представьте, что вы отрезаете треугольный нижний левый угол и вставляете его в верхний правый угол следующим образом:
Теперь у нас есть еще один прямоугольник, но с новой основой.База этой новой цифры – это среднее значение исходной базы. Площадь этой новой фигуры равна .Просто будьте осторожны, потому что основание, которое мы используем, является средним из двух исходных оснований!
Площадь круга = πr 2
Наконец, мы рассмотрим красивый круг. Вот такой, радиусом 6 см.
Вот тот же круг, но с линиями, проведенными через каждые сантиметры.
Сначала мы объединили части квадрата, чтобы получился полный квадрат, затем мы очень тщательно и усердно сосчитали каждый из этих квадратов и обнаружили, что там примерно 113 квадратов.Это почти равно.
Калькулятор треугольников
Укажите 3 значения, включая как минимум одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать».
Когда радианы выбраны в качестве единицы измерения угла, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.
Треугольник – это многоугольник с тремя вершинами. Вершина – это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами.Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Отметки на краю треугольника – это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину.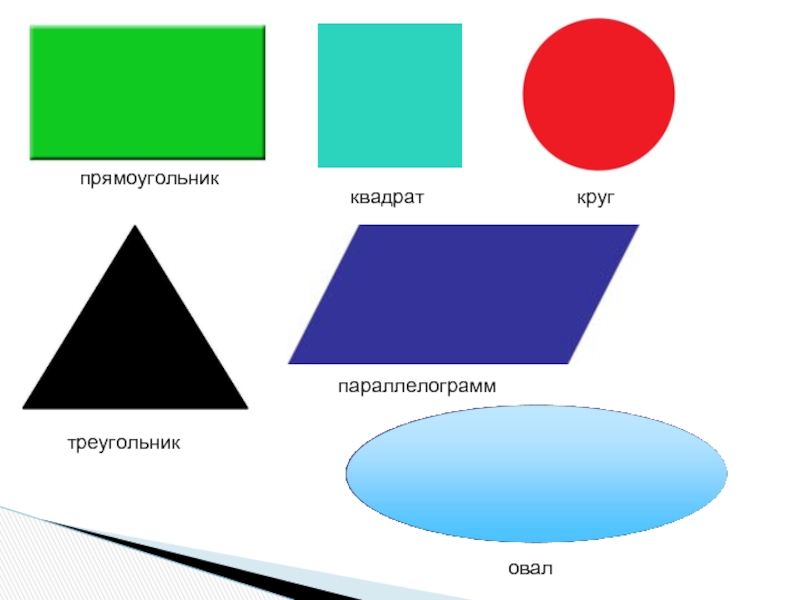
Аналогичные обозначения существуют для внутренних углов треугольника, которые обозначаются разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из треугольников выше, длина и внутренние углы треугольника напрямую связаны, поэтому логично, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины.Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто треугольник. Когда введены фактические значения, выходные данные калькулятора будут отражать то, как должна выглядеть форма входного треугольника.
Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник – это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол.
Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.
Факты, теоремы и законы о треугольнике
- Учитывая длины всех трех сторон любого треугольника, каждый угол можно рассчитать с помощью следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c – известные значения.
Площадь треугольника
Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.
Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:
Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и радиус окружности
Медиана
Медиана треугольника определяется как длина отрезка прямой, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.
См. Рисунок ниже для пояснения.
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m a может быть рассчитана следующим образом:
Inradius
Inradius – это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус – это перпендикулярное расстояние между центром вращения и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
В данном калькуляторе внутренний радиус рассчитывается с использованием площади (площади) и полупериметра (ов) треугольника по следующим формулам:
где a, b и c – стороны треугольника
Круговой радиус
Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину), и, следовательно, радиус описанной окружности.
В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:
Где a – сторона треугольника, а A – угол, противоположный стороне a
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
Площадь треугольника
Площадь треугольника , формулы для расчета площади различных типов треугольников в зависимости от известных исходных данных, калькулятор для нахождения площади онлайн и таблица с формулами площадей треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
– Вычисление (показано) (скрыта)
– примечания (показаны) (скрыта)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона а
Высота h
Основание треугольника может быть выбрано с любой стороны треугольника.
2
Площадь двухстороннего треугольника и угол между ними
Сторона а
Сторона b
Угол α ° между сторонами а и б
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трех сторонам
Сторона а
Сторона b
Сторона c
Радиус r вписанный круг
4
Площадь треугольника по радиусу описанной окружности и трех сторонам
Сторона а
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
Полупериметр:
Сторона а
Сторона b
Сторона c
6
Площадь произвольного треугольника сбоку и двух смежных углов
Сторона а
Угол β °
Угол α °
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по сторонам и основанию
Сторона а (а = б)
Сторона c
8
Площадь равнобедренного треугольника по сторонам и угол между ними
Сторона а (а = б)
Угол α ° между сторонами
9
Площадь равнобедренного треугольника со сторонами, основанием и углом между ними
Сторона а (а = б)
Основание треугольника c
Угол β ° между основанием и стороной
10
Площадь равнобедренного треугольника в основании и угол между сторонами
Основание треугольника c
Угол α ° между сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника на стороне
Сторона a (a = b = c)
13
Площадь равностороннего треугольника высотой
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
Радиус r вписанный круг
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Квадрат прямоугольного треугольника с двумя катетами
Катет а
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
Сторона c
Угол α
18
Площадь прямоугольного треугольника, проходящего через катет и угол
Сторона b
Угол α
19
Площадь прямоугольного треугольника вдоль отрезков, делящих гипотенузу на вписанную окружность
Отрезок d
Сегмент линии e
20
Площадь прямоугольного треугольника, проходящего через гипотенузу и вписанную окружность
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
Полупериметр:
Сторона а
Сторона b
Сторона c
Наш калькулятор расчета площади поможет вам рассчитать площади треугольников разного типа или проверить уже выполненные расчеты.
В зависимости от известных входных данных для вычисления площади треугольника используются различные формулы. Выше формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные расчеты. Общие формулы даны для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
В зависимости от типа треугольника и известных исходных данных площадь треугольника может быть вычислена с использованием различных формул.
Таблица с формулами площади треугольника
Определения
Площадь треугольника – это числовая характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя сегментами (сторонами), соединяющими три точки (вершины), не лежащие на одной прямой.
Треугольник – это геометрическая фигура, образованная тремя сегментами, соединяющими три точки, не лежащие на одной прямой.
Отрезки называются сторонами треугольника, а точки – вершинами треугольника.
Площадь – числовая характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в квадрате единиц измерения: км 2 , м 2 , см 2 , мм 2 и т. Д.
Скачать формулы площади треугольника как картинку
Как построить круг через 3 вершины треугольника с помощью циркуля и линейки или линейки
В
описанный круг
треугольника – это круг, проходящий через все три вершины треугольника.Конструкция сначала устанавливает центр описанной окружности, а затем рисует круг. центр окружности
треугольника – это точка, в которой
перпендикулярные биссектрисы
сторон пересекаются. На этой странице показано, как построить (нарисовать) описанную окружность треугольника с помощью циркуля и линейки или линейки. Эта конструкция предполагает, что вы уже знакомы с Построением серединного перпендикуляра отрезка линии.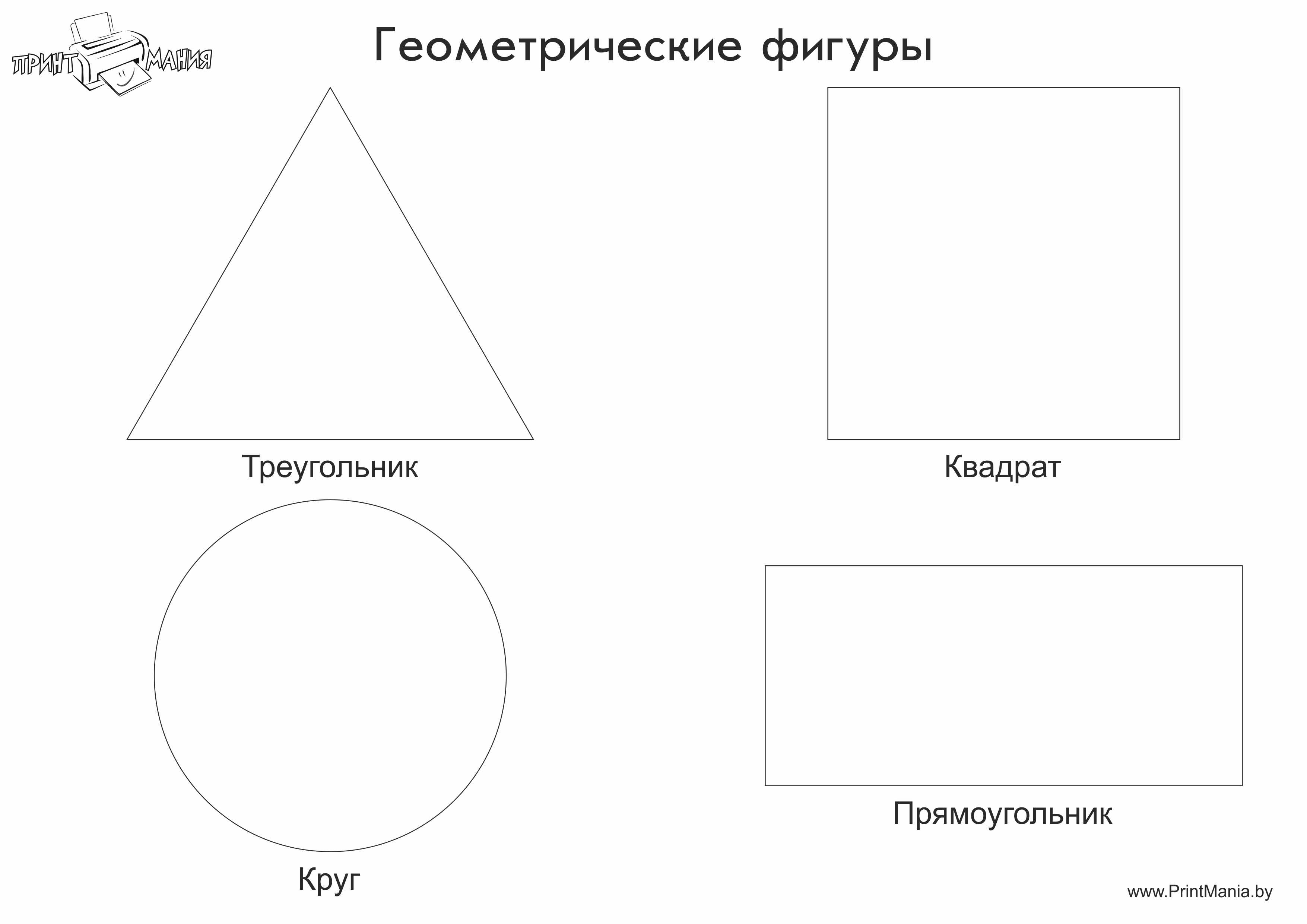
Пошаговые инструкции для печати
Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Проба
Изображение ниже – это последний рисунок выше с добавленными красными метками.
Примечание: это доказательство почти идентично доказательству в Построение центра описанной окружности треугольника.
| Аргумент | Причина | |
|---|---|---|
| 1 | JK – это серединный перпендикуляр AB. | По конструкции. Для доказательства см. Построение серединного перпендикуляра отрезка |
| 2 | Существуют круги, центр которых лежит на прямой JK, а AB является аккорд.(* см. примечание ниже) | Серединный перпендикуляр к
аккорд
всегда проходит через центр круга. |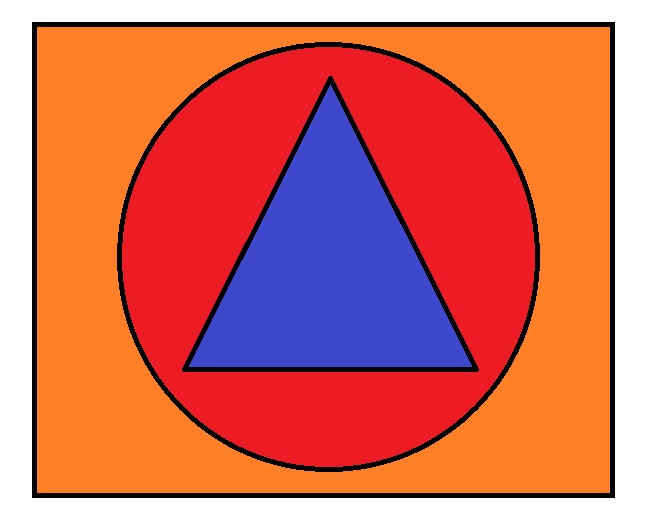
| 3 | LM – это серединный перпендикуляр BC. | По конструкции. Для доказательства см. Построение серединного перпендикуляра отрезка |
| 4 | Существуют круги, центр которых лежит на прямой LM, а BC является хордой. (* см. примечание ниже) | Серединный перпендикуляр к аккорд всегда проходит через центр круга. |
| 5 | Точка O – это центр описанной окружности треугольника ABC, центр единственной окружности, проходящей через A, B, C. | O – единственная точка, которая лежит как на JK, так и на LM, и поэтому удовлетворяет как 2, так и 4 выше. |
| 5 | Окружность O является описанной окружностью треугольника ABC. | Окружность проходит через все три вершины A, B, C |
– Q.E.D
* Примечание
В зависимости от того, где находится центральная точка на биссектрисе, существует бесконечное количество окружностей, которые могут удовлетворить это требование.
Два из них показаны ниже.
Шаги 2 и 4 работают вместе, чтобы уменьшить возможное количество до одного.
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист, содержащий две задачи с описанной окружностью треугольника. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.Другие конструкции, страницы на сайте
Строки
Уголки
Треугольники
Правые треугольники
Центры треугольника
Окружности, дуги и эллипсы
Полигоны
Неевклидовы конструкции
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Круглый квадратный треугольник Головоломка
Можете ли вы представить себе единый твердый объект, который одновременно является Кругом, Квадратом и Треугольником, никоим образом не меняя своей формы?
Всем известно, что квадратный колышек нельзя вставить в круглое отверстие.
Если добавить в смесь треугольник, это просто смешно.
Очевидно, что этот круг не проходит через треугольник, треугольник не проходит сквозь круг, а квадрат не проходит ни через круг, ни через треугольник.Что, если бы я сказал вам, что у меня есть один-единственный объект – круглый квадратный треугольник. Это круг. Он идеально вписывается в круг, проходя через него, и это треугольник, который проходит через все три стороны, и он квадратный, касается всех четырех сторон на всем протяжении.
Вот он круглый квадратный треугольник
Эту головоломку можно легко носить с собой в кармане. Вы получаете круглый квадратный треугольник диаметром 3/4 дюйма и деревянную визитку, вырезанную лазером, чтобы вы могли повторить эту демонстрацию для друзей и семьи.Такое видение форм приводит к интересным беседам, как и должна быть головоломка. Обсуждения этого странного, но простого дизайна, заставляющего задуматься, могут заставить вас переосмыслить предыдущие представления о физике, математике и других идеях, которые, по вашему мнению, были правдой.
Очевидно, мы не собираемся разрывать ваш мир на части или заставлять вас проводить недели в одержимости смыслом жизни, но эй, немного критического мышления никому не повредило. Кто знает, может быть, вы действительно сможете победить гравитацию, чтобы нанести данк в следующей игре по соседству, или закончить эту машину времени, которая стояла в вашем гараже, позволяя вам путешествовать во времени …Продвигать обучение STEM
Часть выручки направляется на усовершенствование обучения STEM в Jackson Makerspace посредством выполнения программы.Когда вы можете видеть, трогать и делать это самостоятельно, наука, технологии, инженерия и математика становятся более увлекательными и легкими для понимания.
Следите за обновлениями, мы только начали делать невозможное реальностью!Получите круглый квадратный треугольник
Отлично подходит для подарков
Обзоры
Дэвид Инглэнд «Блестящий»Частично предоставлено вам Solvtech, Inc.
