Калькулятор онлайн на умножение и деление в столбик: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.

Калькулятор дробей онлайн

Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:

Просто заполните необходимые поля и получите ответ и подробное решение.

Данный калькулятор может работать как с положительными, так и с отрицательными дробями.

При этом нужно помнить, что:

− ac = a− c = − ac

Всегда нужно использовать только последний вариант.

Сложение дробей

С одинаковыми знаменателями

При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.

Формула

ac + bc = a + bc

Пример

Для примера сложим следующие дроби с равными знаменателями:

27 + 47 = 2 + 47 = 67

С разными знаменателями

При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.

Формула (универсальная)

ac + bd = a⋅d + b⋅cc⋅d

Пример №1

Для примера сложим следующие дроби с разными знаменателями:

12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56

Пример №2

Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:

12+14=1⋅22⋅2+14=24+14=2+14=34

Этот же пример можно решить и применяя вышеуказанную универсальную формулу:

12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34

Обратите внимание, что мы сократили дробь:

68=3 ⋅ 24 ⋅ 2=34

Сложение смешанных чисел

Смешанные числа – это такие числа, у которых есть как дробная часть, так и целая.

Преобразуя в неправильную дробь

Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.

Формула

a bc + d ef = b + a ⋅ cc + e + d ⋅ ff

Пример

Для примера сложим два смешанных числа:

312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅66 + 16=516

Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:

316=5⋅6+16=5⋅66 + 16=516

Складывая целую и дробную части отдельно

Целую и дробную части смешанных чисел можно складывать по отдельности.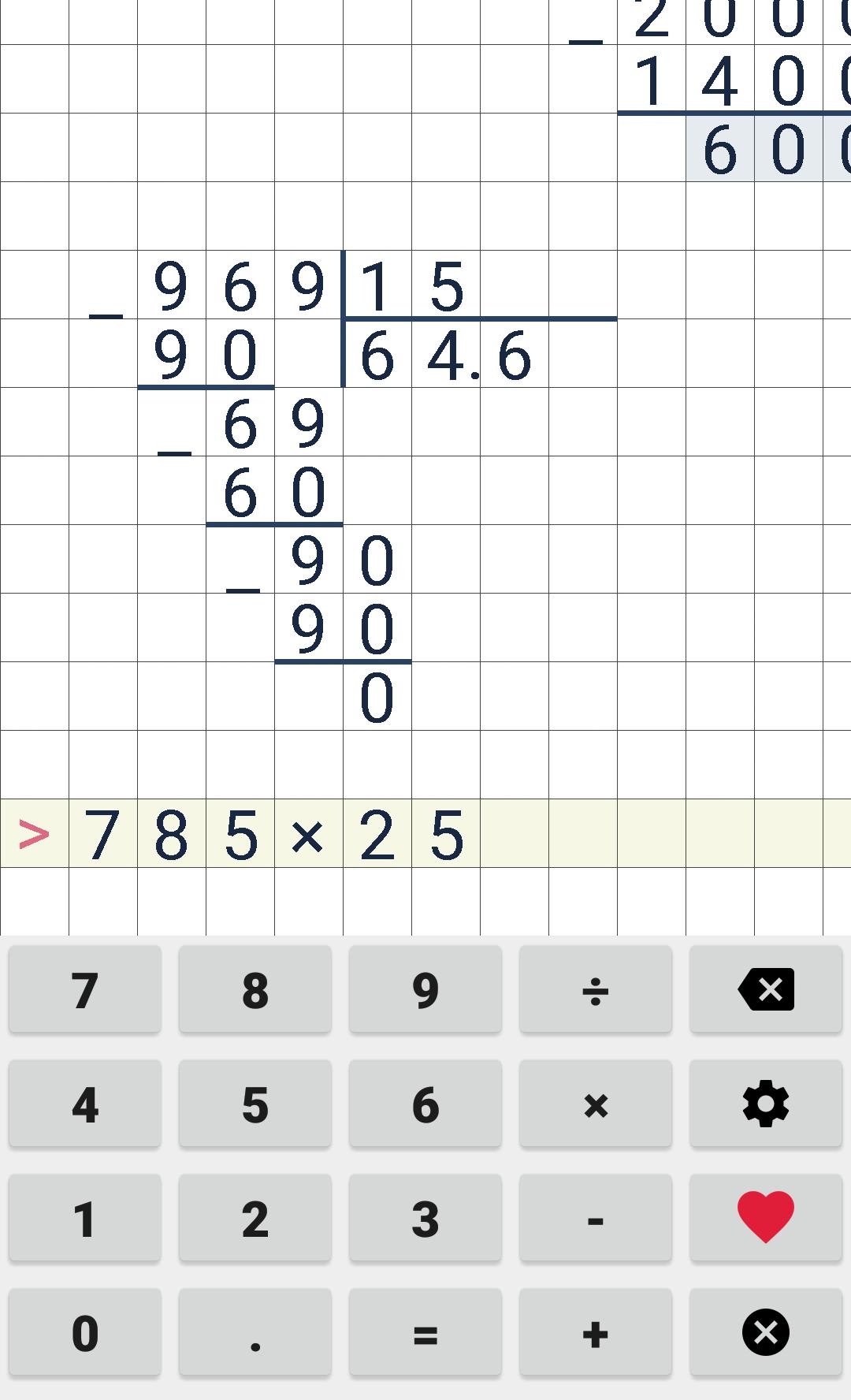

Формула

a bc + d ef = (a + d) + (bc + ef)

Пример

Решим предыдущий пример этим способом:

3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516

Вычитание дробей

Вычитание дробей происходит по тем же принципам, что и сложение.

С одинаковыми знаменателями

Формула

ac − bc = a − bc

Пример

Для примера вычтем одну дробь из другой с равными знаменателями:

35−25=3−25=15

С разными знаменателями

Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.

Формула

ac − bd = a⋅d − b⋅cc⋅d

Пример

Для примера вычтем одну дробь из другой, с разными знаменателями:

34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512

Вычитание смешанных чисел

Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.

Формула

a bc − d ef = b + a ⋅ cc − e + d ⋅ ff

Пример

312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅66 + 56=156

Умножение дробей

При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.

Формула

ac ⋅ be = a ⋅ bc ⋅ e

Давайте рассмотрим несколько примеров:

Пример №1

Умножим дроби с одинаковыми знаменателями:

13⋅23=1⋅23⋅3=29

Пример №2

Умножим дроби с разными знаменателями:

13⋅24=1⋅23⋅4=212=1⋅26⋅2=16

Пример №3

Умножим смешанные числа:

112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4

Деление дробей

При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.

Формула

ac : be = a ⋅ ec ⋅ b

Давайте рассмотрим несколько примеров:

Пример №1

Разделим одну дробь на другую с таким же знаменателем:

23:13=23⋅31=2⋅33⋅1=63=2

Пример №2

Делим дроби с разными знаменателями:

12:23=12⋅32=1⋅32⋅2=34

Пример №3

Деление смешанных чисел:

412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅1616 + 1116=11116

См. также

Онлайн-калькулятор для деления в столбик десятичных дробей

Делить десятичные дроби в столбик немного сложнее, чем целые числа из-за плавающей точки, еще задачу усложняет надобность деления остатка. Поэтому если вы хотите упростить этот процесс или проверить свой результат, можно воспользоваться онлайн-калькулятором, который не только выведет ответ, но и покажет всю процедуру решения.

Читайте также: Конвертеры величин онлайн

Делим в столбик десятичные дроби с помощью онлайн-калькулятора

Подходящих под эту цель онлайн-сервисов существует большое количество, однако практически все они мало чем отличаются друг от друга.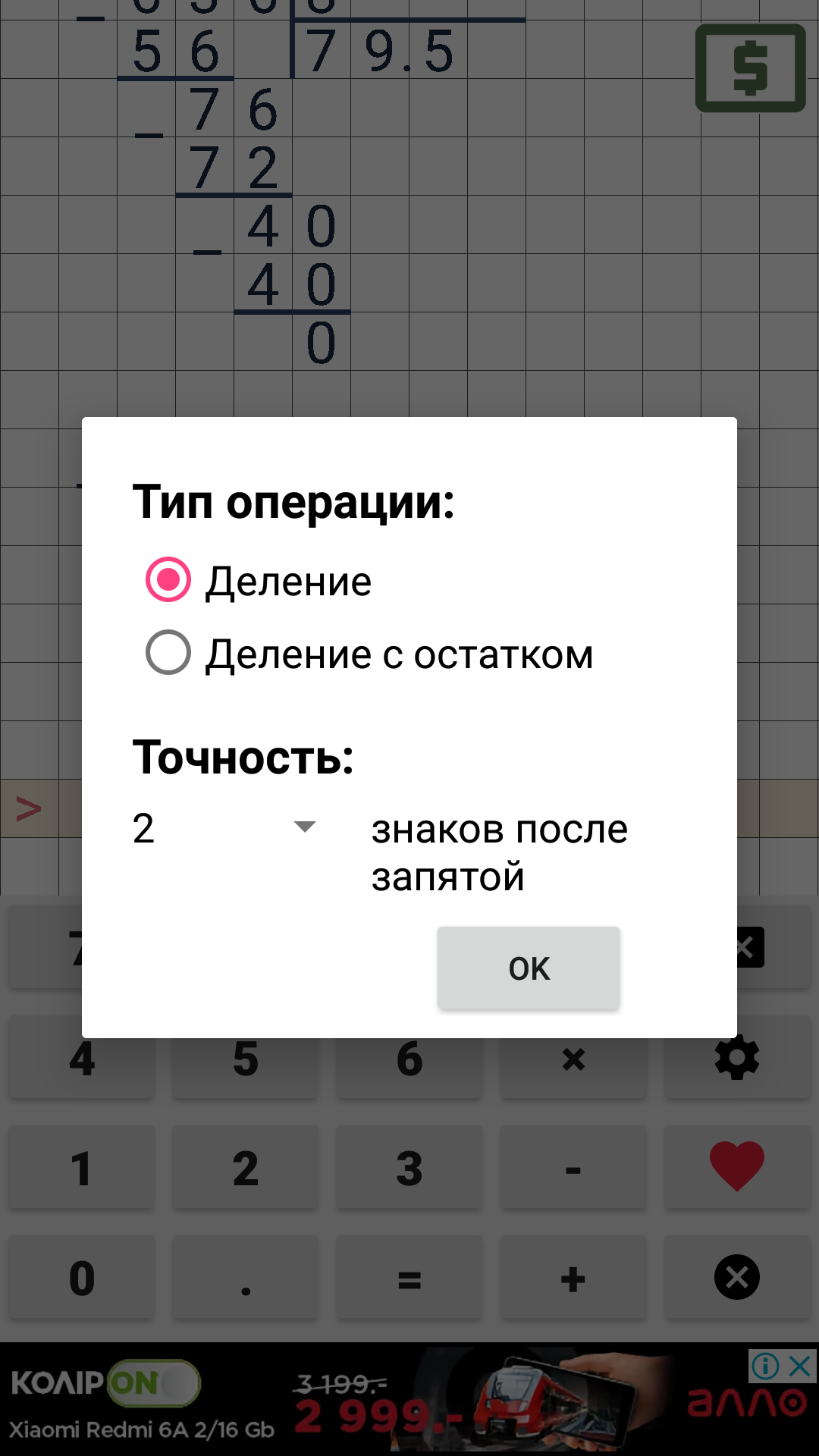 Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.

Способ 1: OnlineMSchool

Сайт OnlineMSchool был разработан для изучения математики. Сейчас на нем присутствует не только множество полезной информации, уроков и задач, но и встроенные калькуляторы, один из которых мы сегодня задействуем. Деление в столбик десятичных дробей в нем происходит так:

Перейти на сайт OnlineMSchool

1. Откройте главную страницу сайта OnlineMSchool и перейдите в раздел «Калькуляторы».
2. Внизу вы найдете сервисы для теории чисел. Выберите там «Деление в столбик» или «Деление в столбик с остатком».
3. В первую очередь обратите внимание на инструкцию по использованию, представленную в соответствующей вкладке. Рекомендуем с ней ознакомиться.
4. Теперь вернитесь в «Калькулятор». Здесь вам следует еще раз убедиться, что выбрана правильная операция. 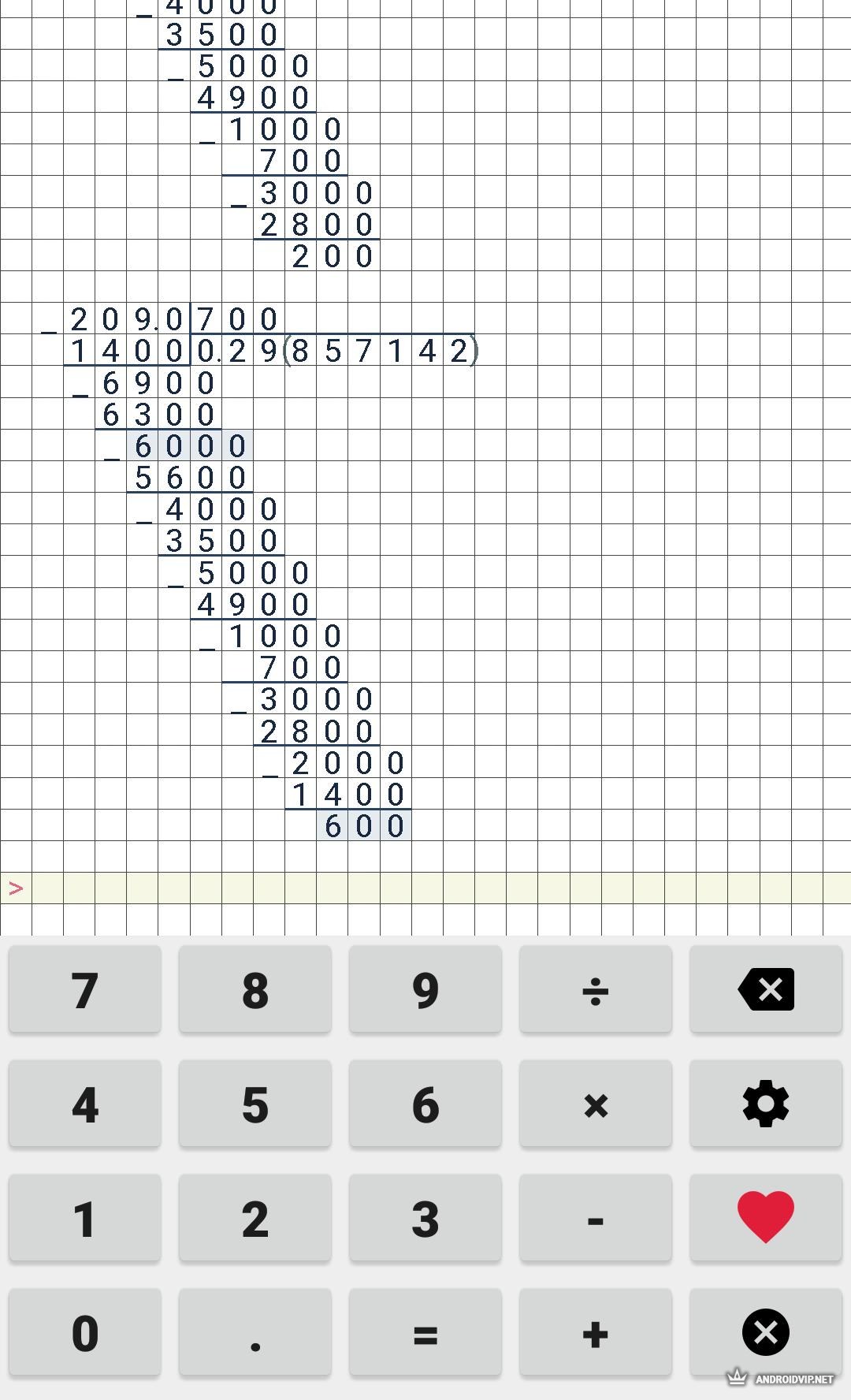Если нет, измените ее, воспользовавшись всплывающим меню.
5. Введите два числа, используя точку для обозначения целой части дроби, а также отметьте галочкой пункт, если необходимо делить остаток.
6. Для получения решения щелкните левой кнопкой мыши на знаке равно.
7. Вам будет предоставлен ответ, где подробно расписан каждый шаг получения конечного числа. Ознакомьтесь с ним и можете переходить к следующим вычислениям.

Перед тем как делить остаток, внимательно изучите условие задачи. Часто этого делать не нужно, иначе ответ могут засчитать неправильным.

Всего за семь простых шагов мы смогли поделить десятичные дроби в столбик с помощью небольшого инструмента на сайте OnlineMSchool.

Способ 2: Rytex

Онлайн-сервис Rytex также помогает в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует присутствующий в нем калькулятор, переход к работе с которым осуществляется следующим образом:

Перейти на сайт Rytex

1. Воспользуйтесь ссылкой выше, чтобы перейти на главную страницу Rytex. На ней кликните по надписи
   «Онлайн калькуляторы».
2. Опуститесь в самый низ вкладки и на панели слева отыщите «Деление столбиком».
3. Перед началом выполнения основного процесса прочтите правила использования инструмента.
4. Теперь в соответствующие поля введите первое и второе число, а затем укажите, нужно ли делить остаток, отметив галочкой необходимый пункт.
5. Для получения решения нажмите на кнопку «Вывести результат».
6. Теперь вы можете узнать, как было получено итоговое число. Поднимитесь выше по вкладке, чтобы перейти к вводу новых значений для дальнейшей работы с примерами.

Как видите, рассмотренные нами сервисы практически не отличаются между собой, разве что только внешним видом. Поэтому можно сделать вывод – нет разницы, какой веб-ресурс использовать, все калькуляторы считают правильно и предоставляют развернутый ответ по вашему примеру.

Читайте также:
Сложение систем счисления онлайн

Перевод из восьмеричной в десятичную онлайн
Перевод из десятичной в шестнадцатеричную систему онлайн

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

Очень продвинутый онлайн калькулятор

Как Вы, наши уважаемые читатели и читательницы, уже могли догадаться, речь пойдет об онлайн калькуляторах, если быть точнее — об одном из самых полезных и, частенько, незаменимых изобретений человека, которое не так давно перекочевало в интернет.

Мы долго выбирали роль самого классного, удобного и полезного онлайн калькулятора и выбор пал на молодой вебдванольный сервис — Web20calc.

Вы, наверное, уже успели возмутиться относительно важности этой темы? Честно говоря, это Вы зря — калькулятор Windows ему совсем не ровня, а ближайшие соперники — типа eCalc, может и превосходят его в функционале, но стоят от 45 евро за копию и при этом устанавливаются на ПК или нетбук или Iphone, что нам не так и нужно.

Данный онлайн калькулятор может:

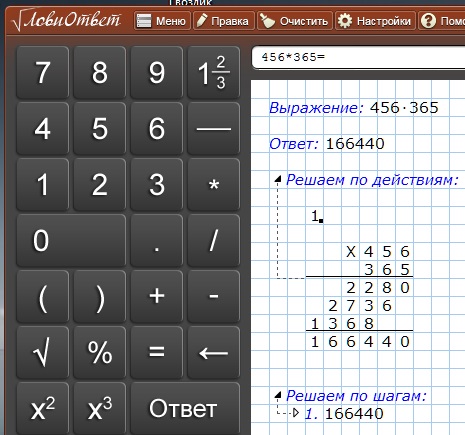
• Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел). Выводится, к сожалению такое число в файл изображения (защита от автоматического использования скорее всего).
• Кроме тангенса, косинуса, синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса, арккотангенса и прочих.
• Доступны в арсенале логарифмы, факториалы и другие интересные функции

Но самое главное — данный онлайн калькулятор умеет строить графики!!!

Если не верите, смотрим на скриншот:

Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или  буквенное представление этой функции (Plot).

Чтобы построить график в онлайн калькуляторе, достаточно записать функцию, например такую как у нас в скриншоте:

plot(tan(x)),x=-360..360

Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.

Построить можно абсолютно любую функцию, с любым количеством переменных, например такую:

plot(cos(x)/3z, x=-180. .360,z=4) или ещё более сложную, какую сможете придумать.

Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.

Для сравнения с калькулятором Майкрософта, приводим наглядный скриншот

Думаем игра «Найдите N отличий» Вам знакома. Теперь пора подвести некоторые итоги:

С помощью онлайн калькулятора мы можем:

• Серьезно облегчить себе жизнь в школе или институте.
• Получить профессиональный онлайн калькулятор в бесплатное пользование.
• Считать огромные числа на любом компьютере в любой точке планеты.
• Строить графики по сложным функциям прямо онлайн.
• Не захламлять свой ноутбук приложениями  и, тем более, не тратить на них деньги.

Вполне добротный список преимуществ.
Update 21.10.2011: Мы оформили более удобную страницу с примерами для эффективного использования калькулятором — посмотреть. Её можно открыть с любой точки нашего сайта.
Update 02.12.2010: Теперь можно опробовать этот калькулятор  в действии прямо у нас в журнале:

UPDATE 09.04.2011: Функции арктангенса, арксинуса и т.д. запускаются кнопками:
tan^-1, sin^-1 и т.д.
Включить продвинутые функции для решения матриц, построения графиков, дифференциалов и другого можно с помощью специальных клавиш:

Для полной функциональности нужно использовать оригинал, но этот тоже сойдет для быстрых рассчетов.

Технический калькулятор | Онлайн калькулятор (⇒)

 

Сейчас другие читают

Калькулятор длинного умножения

Использование калькулятора

Умножение положительных или отрицательных целых или десятичных чисел в качестве множимого и множителя для вычисления произведения с использованием длинного умножения.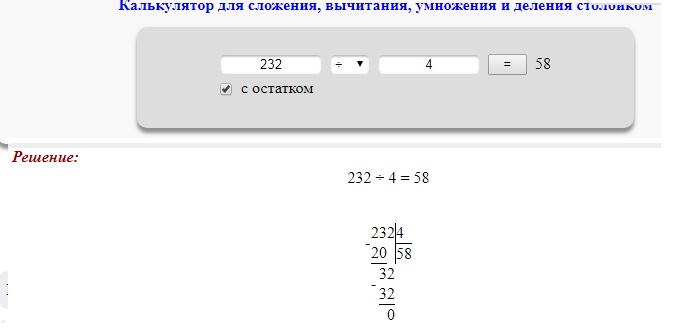 Решение показывает работу стандартного алгоритма.

Части длинного умножения

2

5

6

Множаемое

×

3

2

Множитель

+

5

1

2

Частичный продукт

+

7

6

8

Частичный продукт

Как сделать длинное умножение

Длинное умножение означает, что вы выполняете умножение вручную. Традиционный метод, или стандартный алгоритм, включает в себя умножение чисел и выстраивание результатов в соответствии с разрядами. Вот шаги, чтобы выполнить длинное умножение вручную:

1. Расположите числа одно над другим и выровняйте значения разряда в столбцы. Число с наибольшим количеством цифр обычно ставится сверху как множимое.
2. Начиная с разряда единиц нижнего числа, множителя, умножьте его на последнюю цифру верхнего числа
3. Напишите ответ под строкой равно
4. Если этот ответ больше девяти, запишите единицы в качестве ответа и перенесите цифру десятков
5. Продолжайте движение справа налево.Умножьте единицы нижнего числа на следующую цифру слева в верхнем числе. Если у вас есть цифра, добавьте ее к результату и напишите ответ под линией равенства. Если вам нужно снова нести, сделайте это.
6. Когда вы умножили цифру единиц на каждую цифру верхнего числа, перейдите к разряду десятков в нижнем числе.
7. Умножьте, как указано выше, но на этот раз запишите ответы в новой строке со сдвигом на одну цифру влево.
8. Когда вы закончите умножение, нарисуйте еще одну линию ответов под последним рядом номеров ответов.
9. Используйте длинное сложение для добавления столбцов чисел справа налево, как обычно при длинном сложении.

Длинное умножение с десятичными знаками

Для умножения длинных чисел с десятичными знаками с использованием стандартного алгоритма необходимо следовать нескольким простым дополнительным правилам.

1. Подсчитайте общее количество десятичных знаков, содержащихся как в множимом, так и в множителе.
2. Игнорировать десятичные дроби и выравнивать числа одно над другим по правому краю, как если бы они были целыми числами
3. Умножайте числа, используя длинное умножение.
4. Вставьте десятичную запятую в продукт, чтобы оно имело такое же количество десятичных знаков, как сумма из шага 1.

Пример длинного умножения с десятичными знаками

Умножить 45,2 на 0,21

Всего в обоих числах 3 десятичных знаков.

Игнорируйте десятичные разряды и завершите умножение, как если бы работали с двумя целыми числами.

Перепишите произведение, используя 3 десятичных знаков.

Ответ = 9,492

Следовательно: 45,2 × 0,21 = 9,492

Длинное умножение на отрицательные числа

При выполнении длинного умножения вы можете игнорировать знаки, пока не завершите стандартный алгоритм умножения.После завершения умножения следуйте этим двум правилам:

1. Если одно число положительное, а одно отрицательное, сделайте произведение отрицательным.
2. Если оба числа отрицательны или оба числа положительны, сделайте произведение положительным.

Пример длинного умножения: умножить 234 на 56

Длинные шаги умножения:
Сложите числа с большим числом наверху.Выровняйте числа по столбцам с разрядными значениями.

---

Умножьте цифру из единиц нижнего числа на каждую цифру верхнего числа
6 × 4 = 24
Поместите 4 на место
Отнести 2 к десяткам

---

6 × 3 = 18
Добавьте 2, что у вас есть, = 20
Поставьте 0 на место десятков
Отнеси 2 к сотням место

---

6 × 2 = 12
Добавьте 2, что у вас есть = 14
Это последнее число, которое нужно умножать, поэтому напишите ответ целым числом. Не нужно носить с собой 1.

---

Переместитесь на одну позицию влево. Умножьте цифру десятков в нижнем числе на каждую цифру в верхнем числе.
5 × 4 = 20
Добавьте строку в свой ответ на умножение
Когда вы пишете свой ответ, сдвиньте один столбец влево
Поставьте 0 на место
Отнести 2 к десяткам

---

5 × 3 = 15
Добавьте 2, что у вас есть = 17
Поставьте 7 на место десятков
Отнести 1 к сотням место

---

5 × 2 = 10
Добавьте 1, что у вас есть = 11
Это последнее число, которое нужно умножать, поэтому напишите ответ целым числом. Не нужно носить с собой 1.

---

Сложите числа в столбцах, используя длинное сложение
4 + 0 = 4
0 + 0 = 0
4 + 7 = 11
написать 1 и перенести 1
1 + 1 + 1 = 3

Сложив столбцы, вы увидите результат длинного умножения: 234 × 56 = 13104.

---

Связанные калькуляторы

Если вам нужна помощь с длинным сложением, см. Наш

Калькулятор длинного деления

с пошаговой работой

Запишите частное и остаток для 9452, разделенное на 11, используя метод длинного деления.

Приведенный ниже решенный пример длинного деления 4 на 2 цифры с остатком может быть полезен для понимания того, как выполнять длинное деление вручную для заданий, классных и домашних заданий.

1. Расположите 4-значное делимое и 2-значное делительное число для метода длинного деления и сравните, больше ли первые две цифры делимого 9452, чем делитель 11.
2. Проверьте, сколько раз делитель может быть помещен в число 94, и запишите значение как часть частного. Делитель 11 может быть 8 раз помещен в 94. Запишите 8 как наиболее значимую цифру частного.
3. Найдите разницу между 94 и произведением 8 и 11, если есть. 6 – разница между 94 и 88.
4. Опустите третью цифру начального дивиденда и добавьте (не прибавляя) ее к правой части остатка 6, чтобы сформировать новый дивиденд. Следовательно, новый дивиденд составляет 65
5. Сравните, больше ли новый дивиденд 65, чем делитель 11, и проверьте, сколько раз делитель может быть помещен в новый дивиденд, образованный понижением 3-й цифры. Делитель 11 может быть 5 раз помещен в 65. Добавьте значение 5 (количество раз) прямо к предыдущему частному 8. Следовательно, остаток теперь равен 85.
6. Найдите разницу между 65 и произведением 5 и 11, если таковая имеется. 10 – разница между 65 и 55.
7. Опустите вниз и добавьте 4-ю цифру 2 к правой части более ранней разницы 10. Следовательно, новый дивиденд станет 102.
8. Проверьте, сколько раз делитель 11 может быть включен в новый дивиденд, образованный понижением 4-й цифры. Делитель 11 можно разместить 9 раз в 102. Добавьте значение 9 (количество раз) прямо к предыдущему частному 85.Следовательно, остаток теперь составляет 859.
9. Проверьте разницу между 102 и произведением 11 и 9. Из-за того, что больше нет цифр для уменьшения, окончательная разница 3 представляет собой десятичный остаток от дивиденда 9452, деленный на 11.

Этот калькулятор деления в столбик поддерживает деление больших чисел. Используйте этот калькулятор деления в столбик, который поддерживает деление больших чисел. Пользователи могут указать до 9-значного делителя и до 7-значного делителя для выполнения или проверки задач с длинным делением. Вы можете использовать длинный рабочий лист с делениями, чтобы выполнять бесчисленные практические задания, чтобы отточить свои математические навыки.

Двоичные, обратные и дополнительные коды

Наш пользователь попросил создать онлайн-калькулятор для преобразования введенного целого числа в его двоичную форму, а также отображать его обратные и дополнительные коды / 743/

Ниже представлен калькулятор, который выполняет эту задачу. Он принимает положительные или отрицательные целые числа и выводит вышеупомянутые двоичные коды.

Под калькулятором, как обычно, объясняется, что все это значит.

Обновление : Из комментариев я вижу, что люди неправильно интерпретируют результаты калькулятора. Моя ошибка. Калькулятор просто применял описанный алгоритм к любому введенному числу. Сейчас меняю, чтобы не было путаницы. То есть для положительных чисел он показывает двоичное представление числа (потому что нет обратного или комплиментарного для положительного), а для отрицательного числа он показывает его представление из положительного в обратном и дополнительном кодах.

Двоичные, обратные и дополнительные коды

Обратный код (дополнение до единицы)

Дополнительный код (дополнение до двух)

content_copy Ссылка сохранить Сохранить расширение Виджет

Итак, немного теории

Двоичный код – это двоичное представление целого числа без знака.Если мы говорим о компьютерах, для представления числа используется определенное количество битов. Итак, общий диапазон, который может быть представлен n-битами, составляет

Обратный код или дополнение до единицы – это просто инвертированный двоичный код числа. То есть все нули становятся единицами, а все единицы становятся нулями.

Дополнительный код или Дополнение до двух является обратным кодом плюс один

Итак, о чем все?

Эти коды были придуманы, чтобы сделать работу со знаками более удобной (для машин). Поскольку я из тех людей, которые любят учиться на примерах, я объясню это утверждение на примерах.

Предположим, у нас есть компьютер с 4-битными двоичными числами. Общий диапазон, который может быть представлен 4-мя битами, составляет 16 – 0,1, … 15
00 – 0000
…
15 – 1111

Но это беззнаковые числа и от них мало толку. Нам нужно ввести знак. Итак, половина диапазона берется за положительные числа (восемь, включая ноль), а половина диапазона – за отрицательные (также восемь). Обратите внимание, что машина считает ноль положительным числом, в отличие от обычной математики.

Итак, наши положительные значения – 0, …, 7, а отрицательные – -1, …, – 8.

Чтобы различать положительные и отрицательные числа, мы назначаем самый левый бит как знаковый бит . Нулевой знаковый бит говорит о том, что это положительное число, а единица – отрицательное.

Положительные числа представлены в виде простого двоичного кода
0 – 0000
1 – 0001
. ..
7 – 0111

Но как можно представить отрицательные числа? А вот и дополнительный код.

То есть дополнение -7 – это
двоичное 7 = 0111
обратное 7 = 1000
дополнение 7 = 1001

Обратите внимание, что двоичный код 1001 равен 9, что отличается от -7 на 16, или.Или, что то же самое, дополнительный код “дополняет” двоичный код до, например, 7 + 9 = 16

Это оказалось очень полезным для машинных вычислений – использование дополнительного кода для представления отрицаний позволяет инженерам использовать схему сложения как для сложения, так и для вычитания, что упрощает конструкцию ALU (арифметическая и логическая единица – часть процессора). Кроме того, это представление легко обнаруживает переполнение, когда не хватает битов для представления данного числа.

Несколько примеров

7-3 = 4
0111 двоичное 7
1101 двойное дополнение 3
0100 результат сложения 4

-1 + 7 = 6
1111 дополнение до двух 1
0111 двоичное 7
0110 результат сложения 6

Переполнение обнаруживается при просмотре двух последних переносов, включая перенос за крайний правый бит. Если биты переноса 11 или 00, переполнения нет, если биты переноса 01 или 10, переполнение происходит. И, если нет переполнения, перенос за крайний правый бит можно безопасно игнорировать.

Некоторые примеры с переносами и пятым битом (бит за крайним правым битом)

7 + 1 = 8

00111 двоичный 7
00001 двоичный 1
01110 несет
01000 результат сложения 8 – переполнение

Два последних переноса – 01. Это дает сигнал о переполнении

-7 + 7 = 0
00111 двоичный 7
01001 два дополнения до 7
11110 несет
10000 результат сложения 16 – но пятый бит можно игнорировать, реальный результат 0

Два последних переноса – 11.Переполнения нет, поэтому правильный результат равен нулю.

Проверка переполнения может быть выполнена простой операцией XOR над двумя последними битами переноса.

Из-за этих удобных свойств дополнение до двух является наиболее распространенным методом представления отрицательных чисел на компьютерах.

П.С. Инверсный код или дополнение до единицы «дополняет» двоичный код до (всех). Его также можно использовать для представления отрицательных значений, но схема сложения должна использовать циклический перенос и является более сложной. Кроме того, диапазон, который может быть представлен n-битами, уменьшается на 1, поскольку 1111 занято как инвертированное 0000 – отрицательный ноль.Так что это менее удобно.

Музыка для обучения таблицам умножения, счету пропусков и делению

полных альбомов для умножения
умножение – Intelli-мелодии
умножение – учитель и рок-боты
умножение Джамз – Джойс Паултре
умножение горы – Хэп Палмер
умножение ходов – музыка с мар.
умножение рэп-DVD – рок-н-учись
умножение – Kidzup
Умножение отключено – Сара Джордан Публикация
Каникулы умножения – Googol Power
Умножьте на музыку – Джек Хартманн
Умножьте это – Земной тон
Musical Recal, Vol.2 – Музыкальный отзыв
Подсчет пропусков – Музыкальная математика

полных альбомов для Division
Divide and Conquer – Музыка с март
Правила делимости – Intelli-Tunes
Division Songs – Kidzup
Division Rap DVD – Rock n ‘Learn
Division Unplugged – Sara Jordan Publishing

Эти песни умножения и деления доступны во множестве альбомов:

Таблицы умножения Песни
Однократные таблицы
Таблица одного раза – Джек Хартманн

Таблицы двукратного умножения
Счет по двойкам – Джойс Паултр
Комбинации 2, двойки, я получил бит для вас (умножение рэпа) – земной тон
Таблица 2 раз – Джек Хартманн
Двойки – Музыкальная математика
Умножение и марш на два – Музыка с мар.

Трехкратный стол
Умножение рэпа – 3X – Музыка с мартом
Трехкратная настольная песня – Тим Пасифик
Threes – Кэтлин Уайли
Threes – Музыкальная математика
Вальс и умножение на три – Музыка с марком

Four Times Tables
The Four Times Table Song – Tim Pacific
Fours – Kathleen Wiley
Fours – Musical Mathematics

Five Times Tables
Fives – Kathleen Wiley
Fives – Musical Mathematics
The Five Times Table Song – Tim Pacific

Таблицы умножения на шесть
Счет на 6 – Джойс Паултр
Умножение магии на 6, 7, 8 и 9 – Учение по песне
Шестерки – Кэтлин Уайли
Шестерки – Музыкальная математика
Песня на 6 таблиц – Тим Пасифик

Таблицы умножения на семь
Таблицы умножения на семь – Кэтлин Уайли
Выучите семерки прямо сейчас (умножение рэпа) – земной тон
Mu ltiplying Magic for 6, 7, 8 и 9 – Learning by Song
The Seven Times Table Song – Tim Pacific
Sevens – Kathleen Wiley
Sevens – Musical Mathematics
Surf and Multiply By Seven – Music with Mar.

Eight Times Tables
The Eight Times Table Song – Tim Pacific
Eights – Kathleen Wiley
Eights – Musical Mathematics
Умножение магии на 6, 7, 8 и 9 – обучение по песне

Девять умножений
Счет на 9 – Джойс Паултре
Умножение магии на 6, 7, 8 и 9 – Учение по песне
Песня по девяти временам – Тим Пасифик
Девятки – Музыкальная математика
Девятки – Кэтлин Уайли

Десять таблиц умножения
Счет по десяткам – Джойс Полтр
Группировка по десяткам – Музыка с мар.
Умножить на десять – Джек Хартманн

Eleven Times Tables
Cha Cha Multiply! By 11 – Музыка с мар.
Elevens – Кэтлин Уайли
Eleven Times Table Song – Tim Pacific

Twelve Times Tables
The Умножение на 12 Salsa – Музыка с Mar.
The Twelve Times Table Song – Tim Pacific

Песни умножения: Skip-Counting
Skip-Counting Reggae Man (2s, 5s и 10s) – Music, Movement & Magination
Twos: Countin ‘Fishes – Skip-Counting Pattern Songs
Counting by Fives – Skip-Counting Pattern Songs
Counting by Fives – Музыка с Мар.
Counting Aliens (6s) – Песни по шаблону с пропуском подсчета
Счет по семеркам – Песни по шаблону с пропуском счета
Музыкальная математика Программа счета с пропуском – Musical Mathematics
Zero the Hero празднует 100 дней в школе – Джек Хартманн

Общие таблицы умножения для различных чисел
Блюзовое умножение – Музыка с мартом
Хип-хоп Классная викторина на умножение – Джек Хартманн
Умножение – MindMuzic
Умножение десятичных знаков – Джим Томпсон
Some Times Tables Song – Tim Pacific
The Times Tables Blues – Арнольд Розенталь

Концепции умножения
Семейство фактов (семейства фактов) – Карл М.Sherrill
The Switch (Коммутативное свойство умножения) – Джек Хартманн
Turn It ‘Round (Коммутативное свойство умножения) – Carl M. Sherrill
Word Clues for Multiplication and Division – Tim Pacific

песни с разделением
Digital Root – Intelli-Tunes
Divide By a Dixie Beat (5) – музыка с мар.
с разделением на четыре песни с разделением
с разделением на пять песен с разделением
с разделением с десятичными знаками – Кэтлин Вили
с разделением песни – обучение Математика по песне
Делимость – Джим Томпсон
Правила делимости – Intelli-Tunes
Правило делимости 2-12 – Intelli-Tunes
Division – MindMuzic
Long Division – Intelli-Tunes
Surf and Divide (7) – Музыка с Mar.
Turn It ‘Round: Коммутативное свойство умножения – Карл М. Шерилл
Вы просто возьмете половину: деление на 2 – Карл М. Шерилл
Disco Divide (10) – Музыка с марта

Математические книги
математических фактов до максимума! – Карл Шерилл
MatheMagical Showtime! – Carl Sherrill
Учебное пособие по музыкальной математике для преподавателей – Музыкальная математика
Учебное пособие по музыкальной математике для родителей – Музыкальная математика
RiddleMath – Carl Sherrill

См. Также: Песни на сложение и вычитание-
Песни, обучающие элементарным числам уровня
Песни по математике, алгебре и геометрии
Песни по элементарной математике

Онлайн-калькулятор | Базовый калькулятор

Калькулятор Операции

Этот базовый онлайн-калькулятор похож на небольшой портативный калькулятор и имеет четыре стандартные функции для сложения, вычитания, деления и умножения. Как и большинство калькуляторов с 4 функциями, он также включает в себя клавиши для вычисления процентов, вычисления квадрата, квадратного корня и числа Пи. Этот базовый калькулятор имеет десятичную точность до 10 цифр и предлагает следующие функции:

• mc = Очистить память: очистить память калькулятора
• m + = Memory Plus: добавить отображаемое значение в память
• m- = Память Минус: вычесть отображаемое значение из памяти
• mr = вызов из памяти: отобразить значение памяти
• CE = Clear Entry: очистить текущее отображаемое значение, изменится на AC
• AC = All Clear: очистить все и начать новую операцию
• √x = Квадратный корень: извлечь квадратный корень из отображаемого значения и отобразить его
• +/- = Плюс / Минус : изменить знак отображаемого значения с положительного на отрицательный или наоборот
• π = pi: отобразить значение π как 3. 141592654 для использования в расчетах
• x² = Квадрат: возвести отображаемое значение в квадрат и отобразить его
• R2 = Округлить до 2 десятичных знаков: округлить текущее отображаемое значение до 2 десятичных знаков, например, в денежный или денежный формат
• R0 = Округлить до 0 десятичных знаков: округлить текущее отображаемое значение до 0 десятичных знаков
• % = Процент: использовать отображаемое значение для вычисления процента

Специальные возможности калькулятора

Масштаб : Увеличьте размер калькулятора в браузере с помощью функции масштабирования браузера.Размер калькулятора, текста и кнопок изменяется пропорционально.

Масштаб сенсорного экрана : Увеличьте размер калькулятора на сенсорном экране, увеличивая масштаб пальцы. Размер калькулятора, текста и кнопок изменяется пропорционально.

Размер текста : в некоторых браузерах, например на рабочем столе Chrome, вы можете изменить размер текста в браузере. настройки и размер калькулятора, текста и кнопок будут пропорционально увеличиваться или уменьшаться.

Управление с клавиатуры : Вы можете использовать калькулятор без мыши, перемещаясь по нему с помощью табуляции. ключи. Когда клавиша сфокусирована, нажмите «Enter». Однако этот метод может быть трудным, поскольку вы должны последовательно перебирать все клавиши табуляцией.

Управление цифровой клавиатурой : Вы можете использовать калькулятор с большинством цифровых клавиш и клавиатур в самых популярных браузерах для числа, очистка и основные функции сложения, вычитания, умножения и деления, а также удаления / возврата.

Свяжитесь со мной, если у вас есть предложения.

Расчет процентов

• Умножение и деление преобразует отображаемое значение в проценты в десятичной форме и завершит операция при нажатии [=]
  • Пример: найти 20% от 25
  • Введите 25 x 20%, и дисплей изменится с 20% на 0,2
  • Введите = для завершения расчета 25 x 0,2 = 5.