Какой ученый впервые разделил числа на четные и нечетные: Простые числа. Решето Эратосфена.
Простые числа. Решето Эратосфена.
Простые числа. Решето Эратосфена.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Шадрин А.И. 1
1МБОУ “Киясовская СОШ”
Козырева Л.Л. 1
1МБОУ “Киясовская СОШ”
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
«Простые числа не так просты,
как это кажется с первого взгляда!»
Фома Евграфович Топорищев,
писатель-философ
ВВЕДЕНИЕ
Актуальность.
В арифметике Эратосфен стал вторым гроссмейстером (после Евклида). Он составил первую таблицу простых чисел («Решето Эратосфена») и заметил, что многие простые числа группируются в пары близнецов: таковы 11 и 13, 29 и 31, 41 и 43… А Евклид доказал, что множество всех простых чисел бесконечно. Верно ли то же самое для чисел-близнецов? Эта задача не покорилась Эратосфену. Знать бы ему и его насмешливым питомцам, что она не будет решена даже через 22 столетия! В наши дни “проблема близнецов” остается единственной не решенной задачей, которая досталась нам от Античности. Справятся ли с нею математики 21 века?
Сейчас простые числа используются в разных областях: шифрование, нанотехнологии, программирование и во многих других. Простые числа помогают людям быть точнее в этих областях, а сейчас точность очень важна. В нанотехнологиях, например: в эти проекты вложены большие деньги, одно неверное действие – и эти вложения не принесут пользы.
Программирование: набрал не ту цифру – и придётся программировать заново. Одна ошибка может запросто поломать многодневную работу.
Данная работа посвящена простым числам и их вычислению, а также изучению трудов Эратосфена.
Цель исследования: Изучить алгоритм построения «Решета Эратосфена» и решить систему задач на простые числа.
Задачи исследования:Изучить историю возникновения простых чисел и способы их нахождения.
Познакомиться со способом нахождения простых чисел «Решетом Эратосфена» и научиться находить простые числа с его помощью.
Найти ответы на вопросы, самостоятельно решив «Системы задач на простые числа».
Гипотеза: если простые числа так просты, как это кажется, то математики давно их изучили, и тогда про них должно быть все известно.
Методы исследования:
1.Работа с учебной и научно-популярной литературой, ресурсами сети
Интернет.
2. Решение задач на простые числа.
Объект исследования: Простые числа.
Предмет исследования: Решето Эратосфена.
Глава I. Теоретические основы простых чисел.
I.1. Понятие простого числа.
Слово «простой» в толковом словаре русского языка С.И.Ожегова обозначает «однородный по составу, не составной, не сложный, не трудный, легкодоступный пониманию, осуществлению».
Так неужели эти числа так просты, понятны и доступны? Соответствуют ли они своему названию? Из чего составлены целые числа? Конечно же, из единиц. Число 12 есть сумма двенадцати единиц.
Но в то же время 12 – это произведение 3 и 4, 2 и 6. В свою очередь число 4 равно произведению 2 и 2, а 6 – произведению 2 и 3. Числа 2 и 3, так же как и числа 5, 7, 11, 13 и т. д. дальше не раскладываются. Их назвали простыми. Эти числа раскладываются на два различных множителя – единицу и себя самого. Число 1 не считают простым, поскольку оно раскладывается на два одинаковых множителя: 1 = 1 • 1.
Самое маленькое простое число – 2. Самое большое простое число, 391 581·2216193 – 1, было открыто 6 августа 1989 г. группой Aмдал-6. Число, содержащее 65 087 знаков, было получено на суперкомпьютере «Амдал-1200» в Санта-Кларе, штат Калифорния, США. Группа также открыла самые большие парные простые числа: (1 706 595·2
I.2. Историческая справка
Эратосфен – древнегреческий математик, живший в 276-194 г. г. до нашей эры.Один из самых разносторонних ученых античности.
Он заложил основы математической географии, вычислив с большой точностью величину земного шара, изобрел Широту и Долготу, а так же придумал високосный год. Большую часть своей жизни провел в Александрии (Египет), где был вторым главой Великой библиотеки.
Особенно прославили Эратосфена труды по астрономии, географии и математике, однако он успешно трудился и в области филологии, поэзии, музыки и философии, за что современники дали ему прозвище Пентатл, т.е. Многоборец. Другое его прозвище, Бета, т.е. “второй”, по-видимому, также не содержит ничего унизительного: им желали показать, что во всех науках Эратосфен достигает не высшего, но превосходного результата.
Труды Эратосфена
Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда «О шаре и цилиндре». В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.
С ведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего Собрания называет сочинение Эратосфена О средних величинах, замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.
О сочинении Эратосфена «Платоник», посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Геразским
Самым знаменитым математическим открытием Эратосфена стало так называемое “решето Эратосфена”, с помощью которого находятся простые числа. Предложил свой способ великий греческий учёный Эратосфен около 200г. до н. э.
Впервые доказал, что простых чисел бесконечно много, великий учёный Евклид. К наиболее достоверным сведениям о жизни Евклида принято относить то немногое, что приводится в Комментариях Прокла к первой книге Начал Евклида.
Дополнительные штрихи к портрету Евклида можно почерпнуть у Паппа и Стобея. Папп сообщает, что Евклид был мягок и любезен со всеми, кто мог хотя в малейшей степени способствовать развитию математических наук, а Стобей передаёт ещё один анекдот о Евклиде. Приступив к изучению геометрии и разобрав первую теорему, один юноша спросил у Евклида: «А какая мне будет выгода от этой науки?» Евклид подозвал раба и сказал: «Дай ему три обола, раз он хочет извлекать прибыль из учёбы».
Некоторые современные авторы трактуют утверждение Прокла — Евклид жил во времена Птолемея I Сотера — в том смысле, что Евклид жил при дворе Птолемея и был основателем Александрийского Мусейона.
Следует, однако, отметить, что это представление утвердилось в Европе в XVII веке, средневековые же авторы отождествляли Евклида с учеником Сократа философом Евклидом из Мегар. Анонимная арабская рукопись XII века сообщает:
Евклид, сын Наукрата, известный под именем «Геометра», ученый старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира…
I.3. Способ нахождения простых чисел: Решето Эратосфена.
Теория чисел до сих пор имеет множество нерешенных задач, трудность которых связана, в том числе, и с чрезвычайной трудоемкостью проверки свойств числа, с ростом его значения. Большое число таких задач связано с понятием простого числа.
С древних времен известно, что во множестве натуральных чисел встречаются числа, которые делятся только на 1 и на само число. Такие числа назвали простыми.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27,…
Еще Эвклид доказал, что простых чисел бесконечно много, но до сих пор не найдена формула, позволяющая вычислять следующее простое число, если известны все предыдущие простые числа.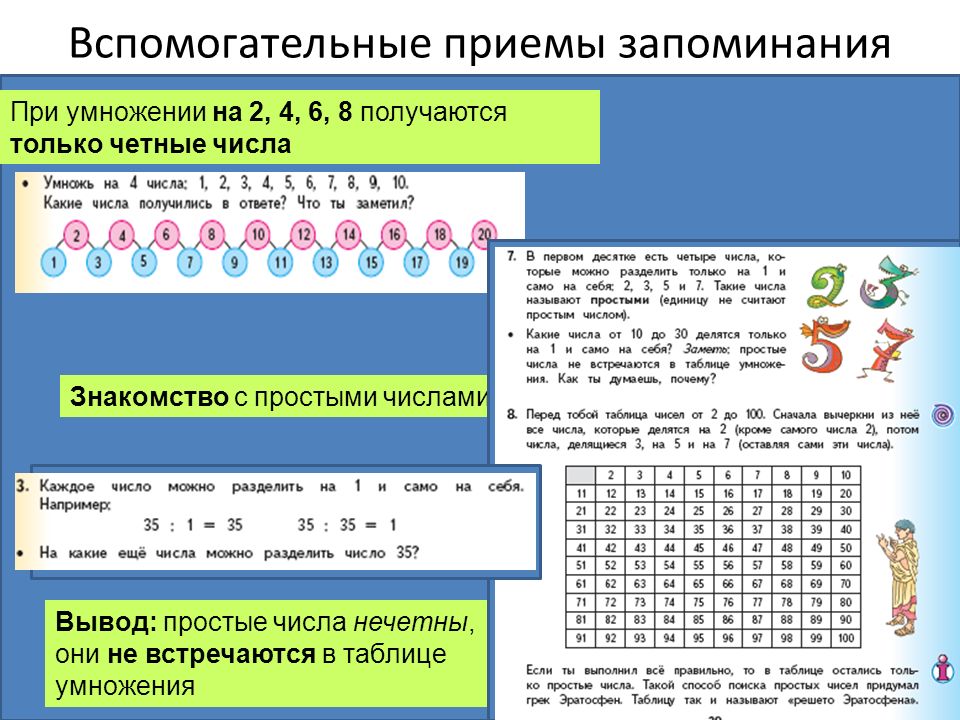
Знаменитый греческий учёный-математик Эратосфен Киренский разработал метод нахождения простых чисел – Решето Эратосфена.
А почему решето? Объясняют так: мы зачеркиваем числа, потом зачеркиваем еще числа, то, что остается, как бы напоминает то, что ОСТАЕТСЯ В РЕШЕТЕ. На самом деле все, что мы делаем, еще больше напоминает решето. Дело в том, что вычеркиваемые числа находятся на прямых линиях, а настоящее решето состоит из нитей, которые в натянутом виде тоже прямые. И эта мысль толкает нас к тому, чтобы построить решето весьма своеобразным способом: не вычисляя, а только лишь ПРОВОДЯ ЛИНИИ по линейке.
Получается что-то вроде… решета…
Те немногие числа, которые остались незачеркнутыми, – простые (а также 2, 3, 5 и 7): 11, 13,17 и т.д. Итак, Решето Эратосфена работает как своего рода аналоговая вычислительная машина. И, значит, вот что изобрел великий грек: он изобрел СЧЕТНУЮ МАШИНУ. А ведь для простых чисел не существует даже формулы, по которой их можно вычислить все. Нет такой формулы, а Решето есть. Простые числа располагаются на числовом ряду весьма причудливым образом, но, создав Решето Эратосфена достаточно большого размера, мы отсеем (построим) их ВСЕ без исключения. Все они окажутся в дырках совершенно правильного геометрически Решета! Так «правильно» ли их расположение или «неправильно»? Никто не может сказать.
Решето Эратосфена для чисел от 1 до 100.
Подобным образом, в Научно-исследовательской лаборатории Лос-Аламоса1 были получены все простые числа до 100 000 000.
Другим очень простым методом является применение таблиц простых чисел, т. е. использование простых чисел уже найденных другими. За последние 200 лет было составлено и издано много таблиц простых чисел. Наиболее обширной из них является таблица Д. X. Лемера, содержащая все простые числа до 10 000 000. Но, по-видимому, не имеет большого смысла идти на значительные затраты и усилия, чтобы опубликовать эти таблицы. Лишь в очень редких случаях математику, даже специалисту в теории чисел, приходится решать вопрос о том, является ли какое-то большое число простым. Кроме того, большие числа, о которых математик хочет узнать, являются они составными или простыми, не берутся им произвольно. Числа, которые он хочет исследовать, обычно появляются в специальных математических задачах, и, таким образом, эти числа имеют очень специфическую форму.
Глава II. Практическое применение простых чисел
II.
1. Задачи на простые числа.
1. Какие из следующих чисел являются простыми:
а) год Вашего рождения
б) текущий год
в) номер Вашего дома.
Решение:
а) Год моего рождения – 2005. 2005 – составное число, так как делится на 5.
б) Текущий год – 2018. 2018 – составное число, так как делится на 2.
в) Номер моего дома – 13. 13 является простым числом, так как делится только на само себя и на 1.
2. Найдите простое число, следующее за простым числом 1973.
Решение:
Нужно отсчитывать по числу:
1974 – делится на 2.
1975 – делится на 5.
1976 – делится на 2.
1977 – делится на 3.
1978 – делится на 2.
1979 – ни на что не делится. Значит, 1979 будет следующим простым числом после 1973.
3. Попытайтесь определить количество простых чисел в диапазоне 10001 – 10100.
Решение:
10007, 10009, 10037, 1039, 1061, 10067, 10069, 10079, 10091, 10093, 10099;
Т. е. 11 простых чисел
4. а) Кто и когда впервые разделил числа на чётные и нечётные, простые и составные?
б) Как Вы думаете, как учёный пришёл к этому открытию?
в) Могло ли случиться так, что простые числа так и не были открыты?
а) Впервые разделил числа на чётные и нечётные, простые и составные великий учёный Пифагор.
б) Как мне кажется, Пифагор пришёл к этому открытию, когда решал очередные задачи. И заметил, что числа, оканчивающиеся на 0, 2, 4, 6, и 8, делятся на 2 без остатка, а те, что оканчиваются на 1, 3, 5, 7 или 9, делятся на 2 с остатком, и разделил их на чётные и нечётные. После этого он заметил очередной факт – некоторые нечётные числа делятся только на 1 и сами на себя.
Он назвал их простыми, а те, у кого больше двух делителей определил в группу составных чисел. Т.е. Пифагор пришёл к этому открытию методом наблюдения.
в) Я считаю, что такого случиться не могло, в связи с развитием мыслительной деятельности человека.
5. Какие числа называются чётными, а какие – нечётными? Какие числа называются простыми, а какие – составными? Приведите пример чётных и нечётных чисел, простых и составных.
Чётные – числа, которые делятся на 2 без остатка, а нечётные – с остатком.
Примеры: нечётные – 1, 57, 83… чётные – 2, 52, 98…
Простые числа – числа, которые имеют только два делителя (1 и само число), а составные – больше двух делителей.
Примеры: простые – 2, 1999, 10007… составные – 6, 198, 153…
6. а) Назовите два простых нечётных числа.
б) Сможете ли Вы привести пример двух простых чётных чисел?
в) Назовите все простые чётные числа.
а) Два простых нечётных числа – 3, 2011.
б)Нет, потому что простое чётное число только одно.
в)2.
7. С помощью решета Эратосфена найдите все простые числа от 1 до 50.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
8. В разные времена математики пытались найти формулу, которая позволяла бы вычислять простые числа. Так, Леонард Эйлер указал формулу: p = x * x – x + 41, позволяющую вычислять сорок одно простое число, если х = 0, 1, 2… 40. С помощью этой формулы найдите пять простых чисел.
p = простое число
х = целое число от нуля до сорока.
0 х 0 – 0 + 41 = 41.
5 х 5 – 5 + 41 = 61.
20 х 20 – 20 + 41 = 421.
3 х 3 – 3 + 41 = 47.
40 х 40 – 40 = 1601
9 . Леонард Эйлер (1707г.
– 1793г.), швейцарец по национальности, большую часть своей жизни проработавший в Петербургской академии наук, много сил отдавал изучению натуральных чисел. Одним из первых он высказал догадку, что всякое натуральное чётное число, большее 2, можно представить в виде суммы двух простых чисел. Проверьте это на примере нескольких чисел.
4 = 2 + 2; 8 = 5 + 3; 4010 = 2011 + 1999; 30 = 17 + 3.
10. Знаменитый учёный Христиан Гольдбах (1690г. – 1764г.), работавший в Петербургской академии наук, высказал догадку (в 1742г.), что любое нечётное число, большее 5, может быть представлено в виде суммы трёх простых чисел. Русский учёный академик Иван Матвеевич Виноградов (1891г. – 1983г.) сумел доказать это. Проверьте это на примере нескольких чисел.
7 = 2 + 2 + 3; 21 = 17 + 2 + 2; 55 = 19 + 19 + 17.
11. Несколько столетий ждёт решения «проблема близнецов». Какие числа называются числами-близнецами? Пользуясь таблицей простых чисел, назовите несколько пар чисел-близнецов.
Числа-близнецы – это простые числа, находящиеся на расстоянии друг от друга в одно составное число.
Примеры: 17 и 19, 1997 и 1999, 1301 и 1303…
12. Изучением простых чисел занимался русский математик Пафнутий Львович Чебышев (1821г. – 1894г.). Он доказал предположение француза Ж. Бертрана, что между любым натуральным числом, большим единицы, и числом, вдвое большим данного, всегда имеется не менее одного простого числа. Проверьте это на примере нескольких простых чисел.
2 х 2 = 4. Между 2 и 4 простое число – 3.
4 х 2 = 8. Между 4 и 8 простое число – 7.
20 х 2 = 40. Между 20 и 40 – 23, 29, 31, 37.
ЗАКЛЮЧЕНИЕ
Подводя итог проделанной работы, мы выяснили, чтопроблема простых чисел всё ещё существует, так как человечество ещё не знает, бесконечно ли много чисел-близнецов, или нет.
С одной стороны – дело любопытное, интересно же, так оно или не так, но с другой – зачем заморачиваться по такой ерунде… Так считают некоторые. Как хорошо, что я к ним не отношусь, иначе не писал бы эту работу…
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
http://ru.wikipedia.org/wiki/Решето_Эратосфена
Олехник С.Н., Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи. – М.:”Вита-Пресс”, 1994.
Энциклопедия «Занимательная математика»
http://www.natalimak1.narod.ru/prost.htm
http://intoclassics.net/news/2010-11-22-19805
Учебник «Математика 6 класс», Н.Я.Виленкин, В.И. Жохова и др.изд. «Мнемозина», Москва 2013
1 Справка: Лос-А́ламос (исп. Los Álamos — «хлопковое дерево») — населённый пункт и округ в штате Нью-Мексико
Просмотров работы: 667
Математическая викторина«Что?, Где, Когда?» – презентация, доклад, проект
Вы можете изучить и скачать доклад-презентацию на
тему Математическая викторина«Что?, Где, Когда?».
Презентация на заданную тему содержит 15 слайдов. Для просмотра воспользуйтесь
проигрывателем,
если материал оказался полезным для Вас – поделитесь им с друзьями с
помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Образование» Математическая викторина«Что?, Где, Когда?»
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Математическая викторина «Что?, Где, Когда?» С тех пор, как существует мирозданье, Такого нет, кто б не нуждался в знанье. Какой мы не возьмем язык и век,- Всегда стремился к знанью человек…
Слайд 2
Описание слайда:
Древнегреческий ученый – философ, живший в VI в.
до н.э., которому приписывается высказывание «Все есть число». Согласно мнению этого ученого и его последователей, числа управляют не только мерой и весом, но так же всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса. Первые числа 1,2,3 и 4 означают огонь, землю, воду и воздух. Сумма этих чисел – число 10 – изображает весь мир. Этот ученый впервые разделил числа на четные и нечетные, простые и составные. Кто он?
Древнегреческий ученый – философ, живший в VI в. до н.э., которому приписывается высказывание «Все есть число». Согласно мнению этого ученого и его последователей, числа управляют не только мерой и весом, но так же всеми явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире, душой космоса. Первые числа 1,2,3 и 4 означают огонь, землю, воду и воздух. Сумма этих чисел – число 10 – изображает весь мир.
Этот ученый впервые разделил числа на четные и нечетные, простые и составные. Кто он?
Слайд 3
Описание слайда:
ПИФАГОР Самосский Древнегреческий философ, религиозный и политический деятель, основатель пифагореизма, математик. Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др.
Слайд 4
Описание слайда:
Недалеко от берега стоит корабль со спущенной на воду веревочной лестницей вдоль борта.
Недалеко от берега стоит корабль со спущенной на воду веревочной лестницей вдоль борта.
У лестницы 10 ступеней, расстояние между ступеньками 30см. Первая ступенька касается воды.
Океан очень спокоен, но начинается прилив, который поднимает воду на 15см в час.
Внимание: Вопрос!
Через сколько времени вода достигнет
3-ей ступеньки?
Слайд 5
Описание слайда:
Внимание! Правильный ответ! Ступенька не покроется водой, так как вместе с водой поднимается и корабль
Слайд 6
Описание слайда:
Что за предмет, который незаменим в архитектуре и строительстве, и о котором известный писатель Ю. Олеша, автора «Трех толстяков», писал: «В бархате лежит, сжав ноги, холодный и сверкающий. У него тяжелая голова. Я намериваюсь поднять его, он неожиданно раскрывается и производит укол в руку». Это, согласно римскому поэту Овидию (Iв.), было изобретено в Древней Греции.
Что за предмет, который незаменим в архитектуре и строительстве, и о котором известный писатель Ю. Олеша, автора «Трех толстяков», писал: «В бархате лежит, сжав ноги, холодный и сверкающий.
У него тяжелая голова. Я намериваюсь поднять его, он неожиданно раскрывается и производит укол в руку». Это, согласно римскому поэту Овидию (Iв.), было изобретено в Древней Греции.
Слайд 7
Описание слайда:
Внимание! Правильный ответ!
Слайд 8
Описание слайда:
История их изобретения насчитывает тысячи лет. Вряд ли кто-нибудь возьмет на себя смелость назвать имя изобретателя. В древности их называли «клепсидрами». Эта вещь не имеет единственного числа.
Слайд 9
Описание слайда:
Внимание! Правильный ответ!
Слайд 10
Описание слайда:
В египетской пирамиде на гробнице начертано число, которое делится без остатка на все числа от 1 до 10 включительно.
В египетской пирамиде на гробнице начертано число, которое делится без остатка на все числа от 1 до 10 включительно.
Внимание: Вопрос!
Назовите это число.
Слайд 11
Описание слайда:
Внимание! Правильный ответ! 2520
Слайд 12
Описание слайда:
Назовите самую красивую, Назовите самую красивую, самую известную, самую величественную царицу-долгожительницу, царицу из цариц.
Слайд 13
Описание слайда:
Внимание! Правильный ответ! Арифметика
Слайд 14
Описание слайда:
7 сектор
Математик, оказавшись случайно в городе и желая как-то убить время, решил подстричься.
В городе имелось лишь два мастера. Заглянув к одному мастеру, математик увидел, что в салоне грязно, сам мастер неряшливо одет и небрежно пострижен. В салоне другого мастера было идеально чисто, а владелец был безупречно одет и пострижен.
Поразмыслив, математик отправился стричься к первому мастеру. Не могли бы вы объяснить причину столь странного на первый взгляд, поведения математика?
[Так как в городе лишь два парикмахера, каждый мастер вынужден стричься у другого. Математик выбрал того мастера, который лучше постриг своего конкурента]
Слайд 15
Описание слайда:
Чтоб врачом, моряком Чтоб врачом, моряком Или летчиком стать, Надо прежде всего Математику знать.
Tags Математическая викторина«Что?, Где, Когда?»
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Сложная математическая загадка | Гипотеза Коллатца 3n+1 решена?
На этой неделе мы отпраздновали долгожданный ответ на математическую задачу, стоящую десятилетиями, и теперь мы на шаг ближе к еще более старой головоломке с числами, которая поставила в тупик самые яркие умы мира.
Но многие математики, в том числе тот, кто сделал это новейшее открытие, считают, что полный ответ на загадку 82-летней давности еще далеко.
Теренс Тао — один из величайших математиков нашего времени. В 21 год он получил докторскую степень. в Принстоне. В 24 года он стал самым молодым профессором математики в Калифорнийском университете в Лос-Анджелесе. А в 2006 году в возрасте 31 года он получил Филдсовскую медаль, известную как Нобелевская премия по математике.0003
Одно из лучших качеств Тао — это то, что он действительно поставляет контент и открыто делится им со всем миром. Его блог похож на современный блокнот да Винчи. Назовите предмет высшей математики, и он напишет об этом.
Итак, на этой неделе Тао подводит нас к гипотезе Коллатца. Гипотезу Коллатца, предложенную в 1937 году немецким математиком Лотаром Коллатцем, довольно легко описать, так что приступим.
Возьмем любое натуральное число.
Существует правило или функция, которую мы применяем к этому числу, чтобы получить следующее число. Затем мы применяем это правило снова и снова и смотрим, куда оно нас приведет. Правило такое: если число четное, то делим его на 2, а если число нечетное, то умножаем на 3 и прибавляем 1.
В закрытой форме это выглядит так:
Дэйв Линклеттер
Например, давайте возьмем 10. Это четное число, поэтому правило говорит делить на 2, что дает нам 5. Теперь это нечетное число, поэтому мы умножаем 5 на 3. а затем прибавляем 1, получая 16. Теперь 16 четно, поэтому мы разрезаем его пополам, чтобы получить 8. Еще раз четно, так что делим пополам, получаем 4. Теперь 4 четно, поэтому мы берем половину, получая 2, что четно , и сокращается пополам до 1.
Начните с цифр, отличных от 10, и вы все равно неизбежно закончите на 1… мы думаем. Это гипотеза Коллатца.
Это определенно верно для всех чисел, содержащих менее 19 цифр, так что это охватывает все, что вы, вероятно, имели в виду.
Но даже если компьютеры проверят до 100 или 1000 цифр, это далеко не доказательство для всех натуральных чисел.
Прорывной пост Тао называется «Почти все орбиты Коллатца достигают почти ограниченных значений». Давайте немного сломаем это. Орбиты Коллатца — это всего лишь небольшие последовательности, которые вы получаете в процессе, который мы только что сделали. Таким образом, орбита Коллатца числа 10 равна (10, 5, 16, 8, 4, 2, 1, 4, 2, 1, …). Поскольку половина от 4 равна 2, половина от 2 равна 1, а 3*1+1 равно 4, орбиты Коллатца циклически повторяются через 4, 2 и 1 навсегда.
Самая важная деталь в заявлении Тао — это первое «Почти». Это слово — последний барьер на пути к полному решению, и оно принимает разные значения в разных математических контекстах. Так что же здесь имеется в виду?
Технический термин в данном случае логарифмическая плотность . Он описывает, насколько редки контрпримеры к гипотезе Коллатца, если они вообще существуют.
Они могут существовать, но их частота приближается к 0 по мере продвижения вниз по числовой прямой. Целью остается доказать, что их вообще не существует.
По сути, результаты Тао говорят о том, что любые контрпримеры к гипотезе Коллатца будут невероятно редки. В том, как редко мы здесь говорим, есть глубокий смысл, но он все же сильно отличается от несуществующего.
Больше математики!
- Как решить вызывающую бешенство вирусную математическую задачу
- Как подстричь газон с помощью математики
- College Board неправильно решает сложную математическую задачу SAT
Итак, теперь, когда мы знаем, что ее контрпримеры встречаются реже, чем когда-либо, что же остается? проблема? Мы в одном шаге от полного решения? Ну, даже Тао говорит нет.
В комментариях к сообщению в блоге он говорит: «Обычно невозможно строго преобразовать положительные результаты среднего случая в положительные результаты худшего случая, и когда результат худшего случая в конечном итоге доказан, это часто происходит с помощью совершенно другого набора методов.
” Другими словами, этот классный новый метод может дать нам почти решение, но полное решение может потребовать совершенно другого подхода.
Таким образом, математики будут использовать новейшие инновации Тао для решения (или почти решения) других важных проблем, но похоже, что сама гипотеза Коллатца все еще остается незавершенной. Насколько нам известно, потребуются десятилетия и совершенно новые области математики, чтобы наконец положить конец. Но по крайней мере в итоге было решено около невозможных математических задач.
Дэйв Линклеттер
Дэйв Линклеттер — доктор философии. кандидат чистой математики в Университете Невады, Лас-Вегас. Его исследования относятся к теории больших кардинальных множеств. Он также преподает в старших классах и любит разбирать популярные математические темы для широкой аудитории.
Суммирование по Гауссу | Давайте поговорим о науке
Суммарная сумма Гаусса названа в честь Иоганна Карла Фридриха Гаусса.
Он был немецким математиком. Гаусс — один из самых влиятельных математических мыслителей в истории. Легенда гласит, что Гаусс придумал новый метод суммирования последовательностей в очень молодом возрасте. Легенда гласит, что его учитель математики попросил класс сложить числа от 1 до 100. Другими словами, учитель хотел, чтобы они сложили 1 + 2 + 3 + 4 + 5… вплоть до 100!
Учитель предполагал, что это займет у учеников очень много времени. Подумайте, сколько времени вам понадобится, чтобы сложить все числа от 1 до 100 одно за другим. Однако Гаусс ответил 5050 почти сразу.
Эта история может быть не совсем правдой. Но это напоминает нам, что самые младшие ученики иногда открывают новые математические закономерности. Теперь давайте подумаем о шаблоне, который Гаусс использовал для быстрого решения этой проблемы.
Уловка, которую использовал Гаусс для решения этой задачи, заключается в том, что не имеет значения, в каком порядке мы складываем числа.
В каком бы порядке мы ни следовали, мы получим один и тот же результат.
Например:
2 + 3 имеет тот же ответ, что и 3 + 2.
Мы можем хитрым образом изменить порядок чисел от 1 до 100. Это может помочь нам добавить их быстрее. Вот простой пример, который покажет вам, как работает эта стратегия группировки.
Допустим, вы хотите сложить числа от 1 до 10.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?
Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).
Возможно, вы заметили кое-что странное. Каждая из этих пар в сумме дает 11. Итак, мы можем думать о нашей задаче так:
(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) знак равно
(11) + (11) + (11) + (11) + (11) = ?
Поскольку у нас 5 пар, наш ответ:
11 + 11 + 11 + 11 + 11 = 11 x 5 = 55
Ну, это куда-то идет!
Давайте посмотрим на это по-другому.
Вместо того, чтобы выстраивать числа в один ряд. Расставь цифры в два ряда. В первом ряду числа увеличиваются. Во втором ряду числа уменьшаются. От 1 до 10 это будет выглядеть так.
Числа от 1 до 10 выстроены в порядке возрастания в верхнем ряду. Числа от 10 до 1 выстраиваются в порядке убывания в нижнем ряду.
Теперь просуммируйте каждый столбец.
Изображение – Версия текстаСумма каждого столбца равна 11.
Сумма всех приведенных выше чисел равна количеству пар , умноженному на сумму каждой пары . Но нам нужна сумма только одной строки, а не обеих строк. Итак, нам нужно разделить наш ответ на 2.
Мы можем записать это как:
Изображение – Текстовая версия Сумма – это количество пар, умноженное на сумму каждой пары, и эта сумма делится на 2. В нашем случае десять умножается на одиннадцать, а затем делится на два. . Это дает окончательную сумму 55.
Мы можем использовать алгебру , чтобы представить этот шаблон. Алгебра использует буквы и другие символы для представления чисел в уравнениях. Мы можем использовать букву n , чтобы представить, сколько чисел в нашем списке. Это самое большое число. В нашем примере n будет равно 10. Количество пар будет равно этому числу, деленному на 2. Вы заметите, что размер пары равен количеству пар плюс 1. Таким образом, мы могли бы написать использовать n для записи
(количество пар) x (сумма каждой пары) = n/2 x (n +1)
Но помните, как и раньше, нам нужна сумма только одной строки, а не обеих. Таким образом, мы делим приведенную выше формулу на 2 и получаем:
Изображение – Версия текстаn вне скобки, за которой следует n плюс один внутри скобки. Это делится на 2.
Можем ли мы сделать то же самое для суммы, которая является нечетным числом, скажем, 67? Попробуйте сами, прежде чем смотреть ответ ниже.
Вопрос:
1 + 2 + 3 + 4 ….. 66 + 67 =?
(Ответ внизу страницы)
Шаблон, показывающий сложение пар от одного до десяти (© Let’s Talk Science, 2021).Реальные приложения
Эта задача является примером нахождения суммы арифметической последовательности . Последовательность – это набор упорядоченных чисел. В арифметической последовательности расстояние между любыми двумя последовательными числами одинаково. Мы можем использовать метод Гаусса, чтобы найти сумму любой арифметической прогрессии.
Последовательность извлечения кусочков пиццы (Источник: Lebazele через iStockphoto).
Нахождение суммы последовательности может помочь людям решить множество реальных задач. Компании находят сумму последовательностей, чтобы оценить затраты или доход. Даже расчет стоимости проезда на такси представляет собой сумму арифметической последовательности. Вы начинаете с базового тарифа. Ваша общая стоимость увеличивается на ту же сумму каждую минуту.