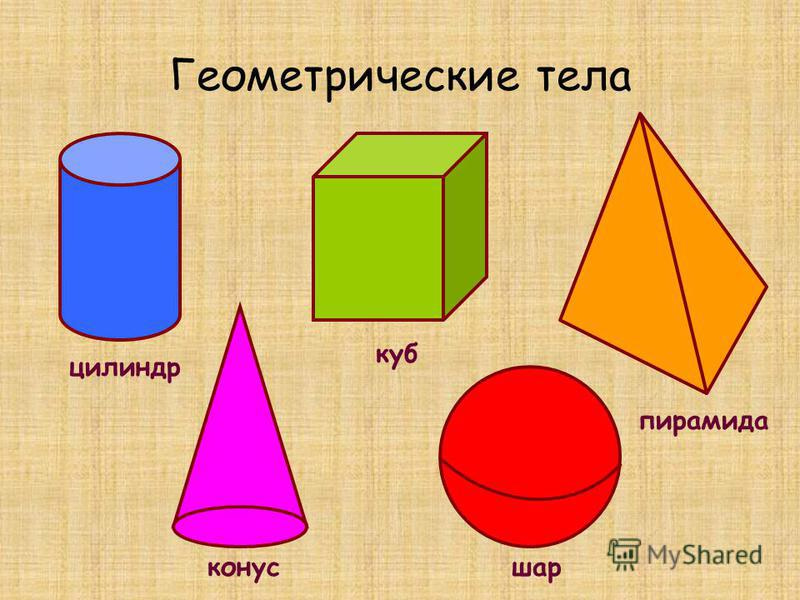
Какие фигуры есть в математике: Основные геометрические фигуры 🟢🟨🔺 и их названия

Простейшие геометрические фигуры

Простейшие геометрические фигуры – это фигуры, из которых состоят сложные геометрические фигуры. Чтобы построить дом нам необходимы кирпичи. Также и для сложных фигур нам необходимы простейшие фигуры. К простейшим геометрическим фигурам относятся: точка, линия, луч, отрезок и ломаная линия.

Необходимо заметить, что мы изучаем геометрические фигуры, которые лежат на плоскости. Плоскость – это бесконечная поверхность. Представь, что на столе лежит лист бумаги. Плоскость – это бесконечный лист бумаги, на котором мы будем рисовать различные геометрические фигуры. Начнем изучать и рисовать.

Точка

Точка это самая простая фигура. Точка очень важная фигура, так как она используется для построения всех фигур. На рисунке мы нарисовали точки. Точки очень легко рисовать на бумаге. Возьми чистый лист бумаги и карандашом прикоснись к бумаге. Нарисуй несколько точек, например, как сделали мы на рисунке ниже. Точки обозначаются заглавными латинскими буквами. На своем рисунке обозначь точки заглавными буквами, например A, B, C, D, F.

Линия

Линия, также как и точка, является одним из фундаментальных понятий в математике. Существуют прямые и кривые линии. Прямая линия (или просто прямая) не имеет начала и конца – она бесконечна. Изобразить всю прямую и измерить ее невозможно. Кривая линия отличается от прямой тем, что она кривая по форме. Ее можно назвать границей более сложных геометрических фигур. Давай на рисунке, где ты нарисовал точки, проведем прямую красную линию через точки А и В, а кривую линию зеленым через точки D и F. Линии обозначаются маленькими латинскими буквам – на рисунке обозначим латинскими буквами a и b.

Луч или полупрямая

Луч – это часть линии, которая имеет начал, но не имеет конца. Луч направлен из точки в бесконечность. Луч также называют полупрямой. В начале луча находится точка – начало луча или начальная точка полупрямой.  Давай на рисунке нарисуем синий луч от точки C, который пройдет через точку B, и светло синий луч от точки C к точке D. Луч обозначается двумя большими латинскими символами, где первый символ – это точка начало луча, а вторая точка – это произвольная точка на линии.  У луча есть направление. Если мы на прямой линии поставим точку, то у нас получится два луча, направленных в разные стороны. На рисунке мы нарисовали 2 луча CB и CD и указали направление в виде маленьких стрелок. 

Отрезок

Отрезок – это часть прямой линии, ограниченная двумя точками. Эти точки называются концами отрезка. Точки на линии, между концами отрезка, называются внутренними точками. Отрезок мы можем измерить, так как он ограничен двумя точками. Отрезок, концами которого являются точки G и H, обозначается GH или HG. У отрезка есть направление как у луча. Например на рисунке отрезки GH и HG одинаковые, но имеют разное направление. GH направлен в вправо, а HG направлен в противоположную сторону, влево.

Найди на рисунке все отрезки, кроме GH и HG

• AB и BA;
• DB и BD;
• DC и CD;
• CB и BC.

Ломаная

Ломаная линия – это несколько отрезков, которые последовательно соединены друг другом и точки соседних отрезков не лежат на одной прямой. Точка конца отрезка, является точкой начала нового отрезка. Все точки в ломаной линии называются вершинами. Если начальная точка первого отрезка совпадает с конечной точкой последнего отрезка, то такая ломаная называется замкнутой. Ломаная линия обозначается заглавными латинскими буквами: перечень всех точек-вершин в ломаной по порядку, например, ABCDFG. На рисунке мы нарисовали две ломаные красным и синим цветом. Синяя ломаная – замкнутая, так как первая и последняя вершины совпадают.

Тебе нравится этот урок?

thumb_upthumb_down

66

35

Поделись с Друзьями:

Основные Геометрические Фигуры

• 1.Простейшие геометрические фигуры
• 2.Геометрическая фигура угол
• 3.Все о треугольниках
• 4.Четырехугольники

Геометрические фигуры. | Методическая разработка по математике (2 класс) по теме:

  Геометрия — важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.

  Название фигуры «трапеция» происходит от греческого слова «трапезион» (столик), от которого произошли также слово «трапеза» и другие родственные слова.

  От греческого слова «конос» (сосновая шишка) произошло название «конус».

  А простейшими в геометрии являются три фигуры: – точка, прямая, плоскость. Конечно, самая главная – это точка.  Древнегреческий  геометр Евклид говорил, что «точка – это то, что не имеет частей». Слово точка по латыни означает результат мгновенного касания, укол. Так, точкой является отверстие, оставленное иглой в листе бумаги.

Линия – льняная нить.

Луч света также представляет собой модель прямой линии. Натянутая линия – также модель прямой.

СКАЗКА О ПРЯМОУГОЛЬНИКЕ

Жили-были в чудесной стране Геометрии Карандаш и Линейка. Как-то раз задумали они начертить четырехугольник, у которого все углы – по 90о. Чертили-чертили целый день. Особенно старалась Линейка. Она ложилась ровно, не наклоняясь. Карандаш отчетливо проводил и соединял линии. В конце концов у них получилась такая фигура. На радостях отправились они к своему другу Транспортиру. Он жил неподалеку от наших героев. Это был удивительно трудолюбивый и внимательный инструмент. Он напоминал половину круга, и поэтому его еще иногда ласково называли Пирожок. Пришли наши герои и попросили у него помощи:

– Послушай, Пирожок, помоги нам. Мы целый день чертили фигуру, у которой все углы должны быть по 90 градусов. А так ли у нас получилось, мы не знаем. Проверь, пожалуйста.

А у Транспортира на спинке было много делений от 0 до 180. Проверка величины углов – его самое любимое занятие. Поэтому он, конечно, согласился. Все углы у четырехугольника действительно были равны 90о. А потом он улыбнулся и сказал:

– Угол, равный 90о, – это прямой угол, а четырехугольник, у которого все углы – по 90о, называется прямоугольником. В следующий раз, когда соберетесь что-нибудь чертить, – сказал Транспортир, – не забудьте про меня. Я обязательно приду к вам на помощь, и дело быстрее сладится.

И еще он добавил:

Раз, два, не ленись,

Дружно за дело вместе берись!

 

СКАЗКА О КВАДРАТЕ

Жил-был в стране Геометрии Лист. Его края были неровными, с множеством загибов, потому что его вырвал из тетради мальчик по имени Вовка, и уже долгое время Лист находился в пути. А нашему герою очень хотелось, чтобы все его стороны стали вновь ровными.

Собравшись с силами, Лист отправился на поиск Линейки, Карандаша и Ножниц. Только они могли ему помочь. Лист целых пять дней провел в пути, потому что двигаться он мог только с помощью ветра, а ветреная погода была не каждый день. На шестой день своего пути Лист встретил Карандаша. Карандаш в это время чертил углы на песке. Его углы были разной величины, и он упорно повторял вслух: “Острый, тупой, прямой, развернутый!” Лист тихонько подлетел к Карандашу и рассказал свою историю. Карандаш его пожалел и согласился помочь, но, к сожалению, без Линейки и Ножниц он ничего сделать не мог. Теперь они отправились в путешествие уже вдвоем. Но Линейку им не пришлось долго искать, потому что она вместо мостика лежала на двух противоположных берегах ручья. Карандаш и Лист аккуратно перетащили Линейку на свой берег и попросили ее помощи.

– Да! Да! Да! – воскликнула Линейка (так соскучилась она по своей работе), – Конечно, помогу!

Началась работа. Карандаш чертил ровно. Линейка замеряла стороны так, чтобы все они были одинаковой длины. Когда работа была сделана, Линейка объявила Листу:

– Ну, теперь ты будешь квадратом!

– Квадратом? – удивился Лист.

– Да! Да! Квадратом! – убедительно ответила Линейка.

– А что это такое? – спросил Лист.

– Это прямоугольник, у которой все стороны не только ровные, но и равные, – сказала Линейка.

Лист обрадовался. Он поблагодарил Карандаша и Линейку и отправился на поиски Ножниц.

Идя по дорожке, Лист увидел красивый домик с очень необычной акацией вместо забора. Он поднялся по ступенькам и постучался. Дверь тихонько заскрипела, и к нему навстречу вышли Ножницы. Радость Листа невозможно было описать. Он прыгал от счастья. А Ножницы в это время смотрели на него и не понимали, в чем дело. Наконец Лист успокоился и рассказал Ножницам свою историю. Ножницы повели себя необычно, они вдруг стали резать воздух. Это оказалось, они так выражали свое удовольствие. Ножницы действительно очень любили работать, то есть резать. Через пять минут наш Лист превратился в настоящий Квадрат. Ножницы принесли ему зеркало. Он долго смотрелся в него, а потом закричал:

– Квадрат! Квадрат!

А Ножницы опять стояли в недоумении и смотрели на Лист. Они не понимали, что это за слово повторял наш герой. Но мы-то с вами знаем, что это за фигура.

Стихи о геометрических фигурах.

ШАР

Удар! Удар! Ещё удар!

Летит в ворота мячик – ШАР!

А это – шар арбузный

Зелёный, круглый, вкусный.

Вглядитесь лучше – шар каков!

Он сделан из одних кругов.

Разрежьте на круги арбуз

И их попробуйте на вкус.

ТРАПЕЦИЯ

ТРАПЕЦИЯ, ТРАПЕЦИЯ

Фигура есть такая,

А я её не знаю.

Ты где живёшь, трапеция,

В Америке, в Китае?

Может, за трапецией

Поехать надо в Грецию?

Мама говорит: “Не надо,

Трапеция с тобою рядом.

Развею я твою тоску,

Ты подожди минутку”, –

И на гладильную доску

Укладывает юбку,

По ней проводит утюжком,

Чтоб не топорщилась мешком:

– Вот тебе ТРАПЕЦИЯ,

  Не стоит ехать в Грецию.

ОВАЛ

А как нарисовать овал?

На помощь брата я позвал.

Брат взял фломастер и искусно

Мне овал нарисовал:

Ты слегка окружность сплюсни,

Получается ОВАЛ.

Сколько раз его видал,

В ванной зеркало – овал!

Овал и блюдо, и яйцо.

Мама говорит:Лицо

У тебя овальное.

Пусть будет овальное,

Лишь бы не печальное.

Мы рассмеялись и в овале

Рожицу нарисовали.

Овал – окружность удлинённая

И рожица в ней удивлённая.

КУБ

Принёс нам ящик почтальон –

Посылка мне и брату.

Ящик – КУБ, в нём шесть сторон,

Все стороны – квадраты.

А что лежит в посылке?

Там стружки и опилки,

Конфеты и баранки,

Ещё с вареньем банки.

ЦИЛИНДР

“Цилиндр – что такое?” – спросил я у папы.

Отец рассмеялся: Цилиндр – это шляпа.

Чтобы иметь представление верное,

Цилиндр, скажем так, это банка консервная.

Труба парохода – цилиндр,

Труба на нашей крыше – тоже,

Все трубы на цилиндр похожи.

А я привёл пример такой –

Калейдоскоп любимый мой,

Глаз от него не оторвёшь,

И тоже на цилиндр похож.

КОНУС

Сказала мама: А сейчас

Про конус будет мой рассказ.

В высокой шапке звездочёт

Считает звёзды круглый год.

КОНУС – шляпа звездочёта.

Вот какой он. Понял? То-то.

Мама у стола стояла,

В бутылки масло разливала.

– Где воронка? Нет воронки.

Поищи. Не стой в сторонке.

– Мама, с места я не тронусь,

Расскажи ещё про конус.

– Воронка и есть в виде конуса лейка.

Ну-ка, найди мне её поскорей-ка.

Воронку я найти не смог,

Но мама сделала кулёк,

Картон вкруг пальца обкрутила

И ловко скрепкой закрепила.

Масло льётся, мама рада,

Конус вышел то, что надо.

ПИРАМИДА

Я видел картину. На этой картине

Стоит ПИРАМИДА в песчаной пустыне.

Всё в пирамиде необычайно,

Какая-то есть в ней загадка и тайна.

А Спасская башня на площади Красной

И детям, и взрослым знакома прекрасно.

Посмотришь на башню – обычная с виду,

А что на вершине у ней? Пирамида!

Форма

Math Strands

AllPrecursor Concepts (13) Sets (25) Pattern (19) Number Sense (52) Count (50) Number Operations (42) Измерение (33) Data Analysis (20) Пространственные отношения (28) Shape (34)

Types

AllActivities (71) Видео (187) Статьи (36) Книги (56) Игры (21) Загрузки (10) за

Аудитория

AllAdult Учащиеся (61) Младенцы (35) Малыши (35) Pre-K (304) Детский сад (29)2) 1 класс (165) 2 класс (122) 3 класс (116)

Специальные темы

AllRacial Justice (5) Семейная математика (33) Изучающие английский язык (36)

Все в материальном мире имеет форму.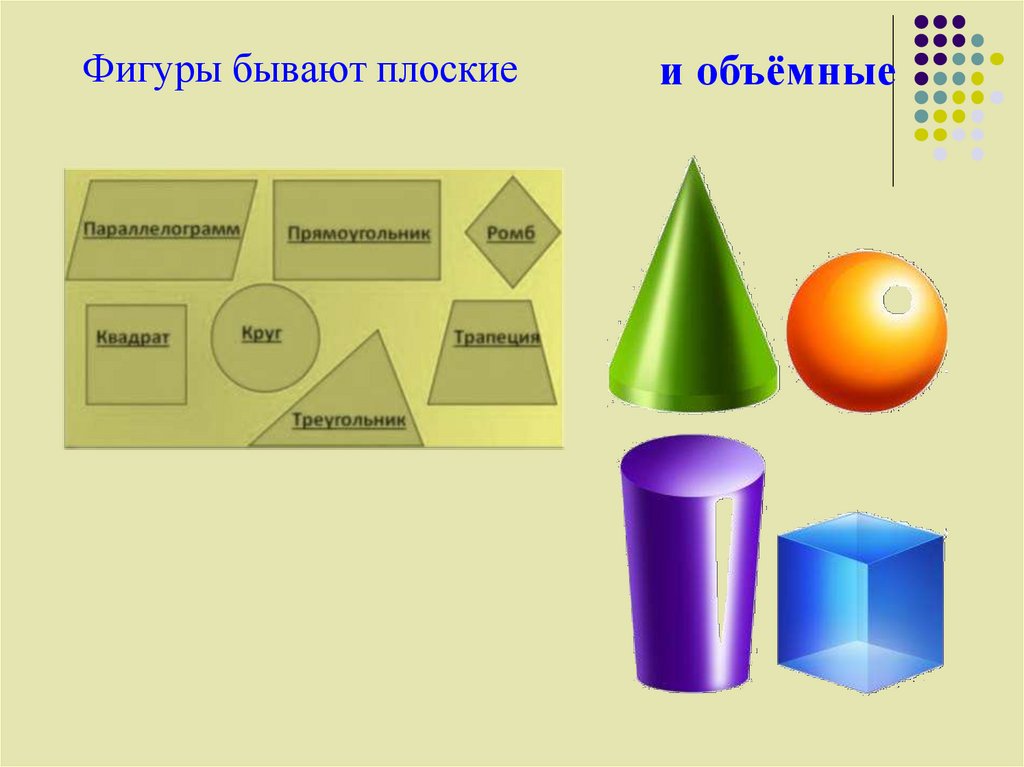 В математике большое внимание уделяется правильным формам, таким как двумерный круг, треугольник и прямоугольник, а также трехмерным телам, известным как сферы и многогранники. В нашем повседневном мире эти твердые тела обычно появляются в объектах, которые мы описываем как коробки, пирамиды, блоки, цилиндры и шары. Более глубокие знания о том, как двух- и трехмерные формы определяются и соотносятся друг с другом, помогут преподавателям осознать тонкие различия и правила. Такое понимание позволяет педагогам замечать и выделять ключевые открытия детей и направлять их опыт, чтобы сделать эти знания понятными для них.

Авторские права: Коллаборатив ранней математики Эриксоновского института. Перепечатано из книги «Большие идеи ранней математики: что нужно знать учителям маленьких детей» (2014 г.), Pearson Education.

Серия

: Идеи на работе

11 сентября 2020 г.

Штамповка или тиснение по рецепту домашнего пластилина с использованием повседневных предметов домашнего обихода — это активный способ для детей исследовать большие идеи формы.

• Тема: Концепции предшественников, форма
• Уровень возраста/класса: Младенцы, малыши, Pre-K, детский сад, 1-й класс
• Теги Семейная математика

9Серия 0022: Идеи на работе 26 апреля 2020 г.

Мы идем на прогулку по математике, собираемся поговорить о математике

En Español También.

Прогулки — отличное время, чтобы поговорить с ребенком о математике. Вы будете удивлены, как много можно говорить о математике, когда вы ищете математику в своем…

• Тема: Чувство числа, подсчет, пространственные отношения, форма
• Уровень возраста/класса: Pre-K, детский сад, 1-й класс, 2-й класс, 3-й класс
• Теги En Español, семейная математика

9Серия 0022: Книжные идеи

23 марта 2020 г.

Карточки для занятий дома: формы

Книги могут иллюстрировать концепции формы детского сада и дошкольного образования, а также знакомить с основополагающими большими идеями математики. Эти карточки с заданиями могут помочь перенести обучение в домашнюю среду, где родители и опекуны могут начать обсуждение.

• Тема: Форма
• Уровень возраста/класса: Pre-K, Детский сад
• Теги Color Farm, Color Zoo, Cubes Cones Cylinders & Spheres, скачать, Lois Ehlert, Tana Hoban, Roseanne Thong, Shapes Shapes Shapes, Round as a Tortilla

Серия

: Книжные идеи

29 июля 2019 г.

Различные типы фигур и не-примеры для обучения геометрии

В наших силах находить, делиться и обсуждать с детьми различные формы таким образом, чтобы расширить их понимание и построить связи между фигурами, нарисованными на бумаге, и конкретными объектами…

• Тема: Концепции предшественников, форма
• Уровень возраста/класса: Младенцы, малыши, Pre-K, детский сад, 1-й класс
• Теги Что теперь? Математическая сказка, Роби Х.
  Харрис, Тана Хобан, Атрибут, Формы Формы Формы

Серия

: Идеи на работе

8 июня 2019 г.

Сборка фигур Танграма с помощью головоломок «Сделай сам»

Головоломка танграм состоит из семи частей — пяти треугольников и двух четырехугольников, составленных из одного квадрата. Танграм зародился в Китае сотни лет назад. Они путешествовали по Европе в 1800-х годах, где приобрели…

• Тема: Пространственные отношения, форма
• Уровень возраста/класса: Pre-K, детский сад, 1-й класс, 2-й класс
• Теги Игра, Семейная математика, История дедушки Танга, Энн Томперт

9Серия 0022: Обучение взрослых 25 февраля 2019 г.

Изучение взаимосвязей блоков

Изучение наборов блоков блоков заставляет педагогов задуматься о взаимосвязях блоков. Более глубокое понимание особенностей модульных блоков дает учителям возможность поддерживать детей способами, способствующими радостному обучению математике.

• Тема: Операции с числами, форма
• Уровень возраста/класса: Взрослые учащиеся, Pre-K, детский сад
• Теги Блоки

9Серия 0022: Послушайте мнение экспертов 26 марта 2017 г.

Пазлы Tangram: сделай для своих детей

Инструктор Лиза Гинет объясняет, как собирать танграм — древнюю китайскую игру, состоящую из семи фигур, вырезанных из квадрата. Из этих семи простых форм можно составить более 6500 различных композиций!

• Тема: Пространственные отношения, форма
• Уровень возраста/класса: Взрослые учащиеся, Pre-K, детский сад, 1-й класс, 2-й класс, 3-й класс
• Теги Игры

9Серия 0022: Книжные идеи 22 февраля 2017 г.

Обсуждение культур и форм в треугольнике для Адаоры

Эта восхитительная книга подчеркивает несколько больших идей в геометрии, а также дает возможность исследовать различные культуры и людей.

• Тема: Форма
• Уровень возраста/класса: Pre-K, Детский сад
• Теги Природа, Книги, Треугольник для Адаоры, Ифеома Оньефулу, Культура

 

Бесплатные видео.

Бесплатный информационный бюллетень, полный идей.

Бесплатные модули профессионального обучения.

 

---

Создание фигур – начальные математические расчеты

Шаг 1. Соберите материалы.

• Цветные палочки из пенопласта (продаются в магазинах для рукоделия)

Если вы не можете их найти, вы можете разрезать листы пенопласта на полоски или купить цветные деревянные палочки для рукоделия. Разделите палочки для поделок по цветам и обозначьте правильное количество палочек названием фигуры, количеством сторон и небольшим рисунком фигуры. Для треугольника используйте три желтых палочки и напишите на каждой из них цифру 3, а также слово “треугольник” и изображение треугольника. Сделайте достаточно групп для треугольника, квадрата, прямоугольника (помните, что две из четырех палочек нужно обрезать короче и одинакового размера для прямоугольника), пятиугольника, шестиугольника и восьмиугольника. Как только палочки будут готовы, поместите их в корзину с водой.

Влажная пена прилипает к окнам, доскам, противням или мольбертам. Если вы используете деревянные палочки для рукоделия, поместите все палочки в корзину или корзину и предоставьте им поверхность, которую дети могут использовать для создания своих фигур.

Примечание : Мелкие детали представляют опасность удушья и не подходят для детей в возрасте до пяти лет. Обязательно выбирайте материалы урока, отвечающие требованиям безопасности.

Шаг 2. Введите действие.

1. Объясните детям , что сегодня они будут собирать фигуры. Они будут использовать палочки для рукоделия/палочки от эскимо, чтобы сделать квадраты, треугольники, прямоугольники, шестиугольники, пятиугольники и восьмиугольники.
2. Опишите и объяснить детям шестиугольников, пятиугольников и восьмиугольников. Point out сколько сторон у каждой фигуры.
3. Попросите детей указать на различные предметы в комнате, имеющие форму квадратов, треугольников, прямоугольников, шестиугольников, пятиугольников и восьмиугольников.

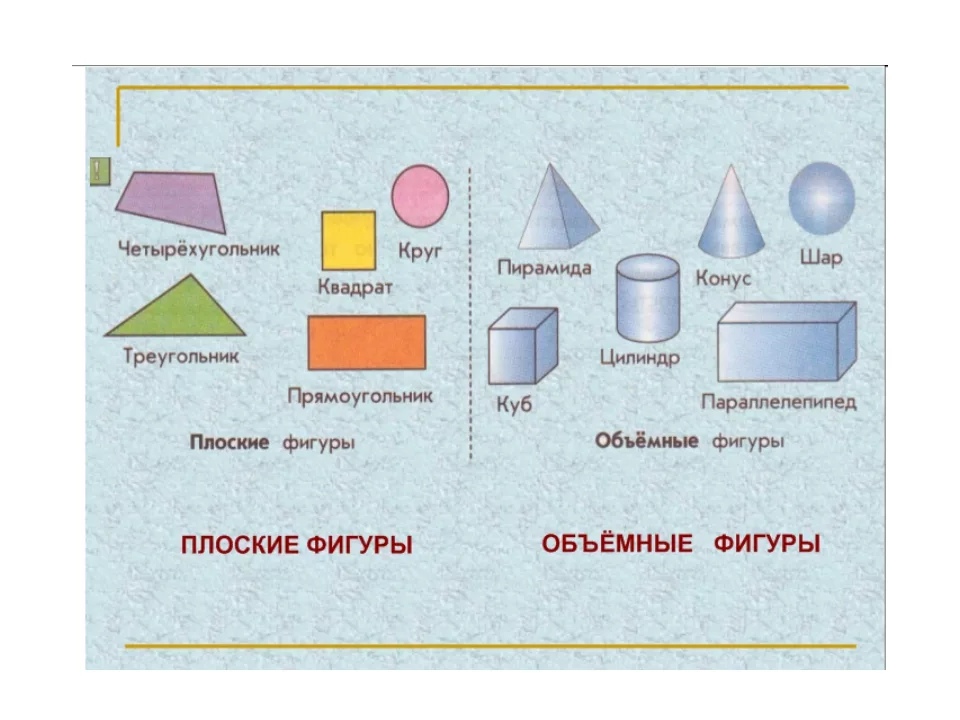
Шаг 3. Вовлеките детей в занятия на уроке.

1. Дети по очереди достают из воды одну палочку и читают на ней номер. Число подскажет ребенку, сколько еще палочек этого цвета ему нужно найти, чтобы построить свою фигуру. Дети будут искать свои палочки и прикреплять их к своим поверхностям. (Мокрая пена прилипает к поверхности, как съемная наклейка.)
2. Когда у детей будут все палочки, необходимые для создания фигур, они смогут посмотреть на изображения фигур на своих палочках и определить, какие фигуры они собираются строить. Им может понадобиться помощь в чтении названия фигуры, написанной на палочке. Затем каждый ребенок должен построить фигуру и подсчитать количество сторон.
3. Повторите действие для всех фигур. Закончив построение всех фигур, дети могут выполнить задание самостоятельно.
4. Вы также можете сыграть в небольшую игру, называя фигуру и предлагая детям спешить, чтобы первыми указать на нее.

Дополнительные удлинители

• Используя палочки для обводки или рисуя от руки, дети могут рисовать свои фигуры на листе бумаги и обозначать атрибуты каждой фигуры. Например, если ребенок строит треугольник, он нарисует изображение треугольника, а затем напишет слово «треугольник» под фигурой. Ребенок также напишет, что у треугольника три стороны. Дети могут сделать книгу «фигуры» из всех фигур, которые они строят.

Шаг 4: Словарь.

• Многоугольник : Плоская форма с тремя или более прямыми сторонами
• Четырехугольник : Многоугольник с четырьмя сторонами
• Квадрат : Четырехугольник с четырьмя равными сторонами и четырьмя прямыми углами
• Треугольник : Многоугольник с тремя углами и тремя сторонами
• Прямоугольник : Четырехугольник с двумя парами противоположных равных параллельных сторон
• Шестиугольник : Многоугольник с шестью сторонами
• Пентагон : Многоугольник с пятью сторонами
• Восьмиугольник : Многоугольник с восемью сторонами

Соедините примеры обычных объектов с их формами.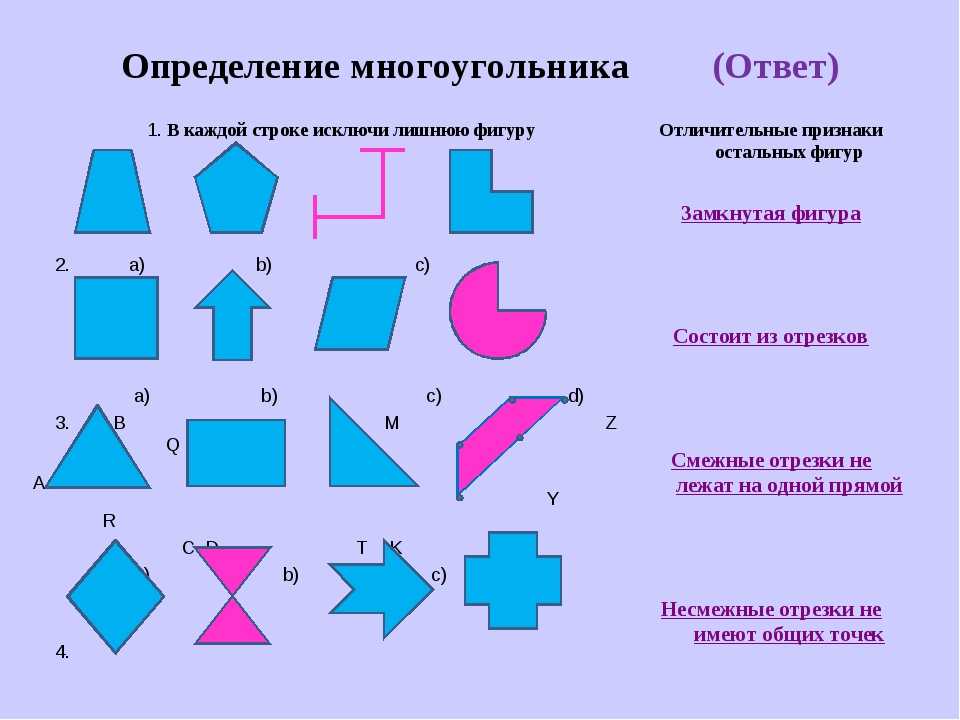

Глоссарий ранней математики

Шаг 5: Адаптируйте урок для малышей или дошкольников.

Урок адаптации для малышей

Малыши могут:

• Трудно распознавать формы
• Невозможно построить фигуры
• Не распознавать название каждой формы
• Не уметь рисовать фигуры

Воспитатели могут:

• Помочь ребенку выбрать все палочки одного цвета, а затем оказать поддержку, пока ребенок читает свою палочку
• Используйте подсказки на палочке (необходимое количество палочек, изображение фигуры и слово фигуры), чтобы помочь детям определить, сколько еще палочек им понадобится, чтобы собрать и построить свои фигуры
• После того, как фигура будет построена, вместе с малышом сосчитайте количество сторон на фигуре

Урок адаптации для дошкольников

Дошкольники могут:

• Уметь различать различные формы
• Уметь рисовать и говорить об атрибутах нескольких различных фигур
• Не уметь рисовать сложные фигуры

Поставщики услуг по уходу за детьми могут:

• Предоставить бумагу и цветные карандаши, чтобы дети могли перенести свои сконструированные фигуры на бумагу и нарисовать рисунок, используя эти фигуры
• Предоставьте чистую книгу (несколько листов чистой бумаги, скрепленных вместе), которую дети могут использовать для записи своих фигур и их атрибутов (например, ребенок, строящий восьмиугольник, нарисует фигуру, напишет слово “восьмиугольник, отметьте количество сторон, а затем нарисуйте изображение знака остановки)

Предлагаемые книги

• Форма за формой Сьюз Макдональд (Нью-Йорк: Маленький Саймон, 2009)
• Mouse Shapes Эллен Столл Уолш (Нью-Йорк: HMH Books for Young Readers, 2007)
• Формы, формы, формы Таны Хобан (Нью-Йорк: Greenwillow Books, 1996)

Музыка и движение

• Спойте «Основные фигуры».