Как выучить состав чисел: Как быстро выучить состав числа до 20. Как научить ребенка считать примеры в пределах 20

Изучаем с ребенком состав числа

Как объяснить ребёнку состав числа и зачем его вообще нужно знать? Состав чисел от 2 до 10 знать просто необходимо, ведь на этом строится весь дальнейший счёт:

• сложение и вычитание в пределах десятка;
• сложение и вычитание с переходом через десяток;
• сложение и вычитание многозначных чисел;
• умножение и деление.

С чего же начать? Объясните ребёнку, что любое число можно разделить на 2 части, каждая из которых будет меньше исходного числа. Каждой части этого «большого» числа соответствует число «поменьше». И если сложить эти два «маленьких» числа, то получим первое «большое».

У детей 5-7 лет основной источник получения знаний – игровая (наглядная) деятельность. Поэтому настраиваемся на приятное времяпрепровождение и берём те предметы, которые:
а) нравятся и интересны ребёнку;

б) вызывают яркие положительные эмоции.

А теперь предлагаю вам несколько вариантов игр, в процессе которых достаточно легко будет объяснить нашему непоседе, из чего же состоят числа от 2 до 10. В любом из перечисленных занятий вам потребуется 10 небольших однотипных предметов (макаронины, кубики – что угодно).
⠀

1. Ребёнок больше настроен на подвижные игры

Берём две машинки, отсчитываем 2 предмета и предлагаем ребёнку их перевезти: либо оба на одной машине, либо по одному на каждой. В следующий раз транспортируем уже 3 груза. В этом случае мы можем положить в первую машину один груз, а во вторую 2 либо наоборот. И так постепенно увеличиваем количество грузов. Юный исследователь наверняка заметит: чем большее количество предметов нужно перевезти, тем больше получается различных вариантов, как распределить грузы между машинами.

Однако я не рекомендую изучать за один раз состав всех 10 чисел сразу. Ребёнку необходимо время для усвоения новой информации.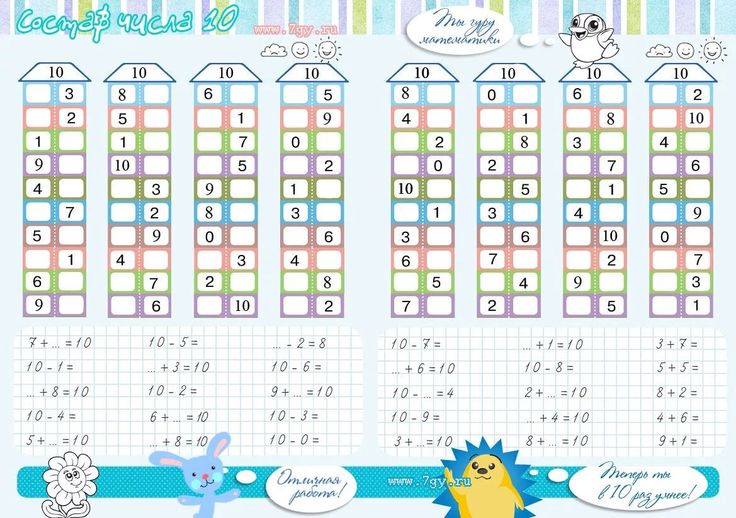 В следующий раз начните с повторения состава пройденных чисел и добавьте несколько новых.

2. Ребёнок хочет поиграть спокойно

В этом случае транспортировку грузов можно заменить распределением игрушечных или настоящих фруктов между вами двоими. Здесь на время забудьте, что «делиться нужно поровну».
⠀

3. Ребёнок обожает рисовать

Предложите ему изобразить какой-нибудь объект несложной формы. Например, для исследования состава числа 7 нарисуйте 6 одинаковых цветков с семью лепестками. И карандашами двух цветов закрашивайте соответствующие лепестки. Например, на первом цветке раскрасьте жёлтым один лепесток, а оставшиеся 6 красным. На втором – 2 и 5 соответственно и т. д.

Экспериментируйте с разными предметами и играми, визуализируйте состав числа. Увлекательных вам занятий!

Другие статьи блога “Настольная математика” на Уфамаме:

Математические фокусы для младших школьников
Как заинтересовать ребенка математикой
Геометрия для малышей 1-3 лет
Занятия математикой с малышом до двух лет. Личный опыт мамы

Теги: игры для развития детей , игры для развития мышления детей , математика для детей 5 лет , математика для детей 6 лет , математика для детей 7 лет , математика для детей 8 лет

Игра “Числиус” – как выучить состав числа, смешивая волшебное зелье: janemouse — LiveJournal

Игра “Числиус” – как выучить состав числа, смешивая волшебное зелье: janemouse — LiveJournal ?

Category:

• Игры
• Cancel

У нас на семинаре был сюрприз для участников от компании “Простые правила”.
Мы сложили в шапку имена участников, а потом разыграли три экземпляра новой арифметической игры “Числиус”

Игра простая, красивая, на отработку такой скучной штуки как сосиав числа.
Есть карточки с заданием – зелья. Они бывают разного цвета, скажем, у нас есть карточка “7” зелёная, это зелье можно собрать из жёлтых и синих ингредиентов.
А оранжевое зелье можно сделать, если смешать нужное количество красных и жёлтых. Можно собирать зелье из трёх карт или из двух, или из четырёх.
Очень наглядно и красиво!
@prostyepravila, спасибо за сюрприз!

Tags: #мышематика, @prostyepravila, арифметические игры, мышематика, настольные игры

Subscribe

• Удивительные наблюдения про арифметику и детей с нумиконом

  У нас есть один ребёнок в группе пятилеток, который плохо помнит цифры и числа, и при этом хорошо соотносит количество предметов и пальцев. Один,…

• Математика 1 класс. Что остаётся от сказки потом, после того, как её рассказали?

  Иногда к концу дня даже жалко стирать с доски то, что там накопилось за несколько уроков. Вот, например, какая красота. У нас по-прежнему есть…

• Мышематика Беляево сент 22. Играем в нумикон: арифметические и геометрические игры

  Помните ли вы, в каком возрасте ваши дети начинали уверенно пересчитывать предметы и хорошо ориентировались в числовом ряду? Я вот вижу очень разных…

• Арифметические игры для школьников

  С третьим классом недавно очень азартно играли в код фараона. Это такая арифметическая настолка, к сожалению, снятая с производства. Там поле в…

• Чем отличается Мышематика и Подготовка к школе?

  Ходили ли ваши дети на Подготовку, и если да, то зачем ходили, и чему полезному там научились? И если ходили к нам на Мышематику, то тоже – что было…

• Арифметические игры и головоломки

  Арифметические игры бывают самые разные. У нас есть целая серия игр с игральными кубиками – для первоклашек и шестилеток. А ещё у нас гора…

• Арифметические и логические игры – семинар и видео-обзоры

  В ближайшую пятницу 4 февраля с 18 до 21 у нас будет зум-семинар про логику и логические игры для дошкольников. Будем показывать и подвижные игры,…

• Настольные игры как способ учить рассуждать и считать

  У нас дома огромная коллекция настольных игр, и для дошкольников (их мы таскаем на очные занятия), и для школьников, и для всей семьи. Мы тут…

• Какие у вас новые настольные игры в этом году?

  У нас весной появилась конфетная игра ” чупер”, немного похожая на упрощённый “СЕТ”, и эта игра нас так увлекла, что мы по мотивам сделали целую…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

0 comments

• 0 comments

Состав | NCETM

Знание того, что числа состоят из двух или более других меньших чисел, предполагает понимание «часть-целое». Научиться «видеть» целое число и его части одновременно — ключевой момент в понимании детьми чисел. Разделение чисел на другие числа и их повторное сложение лежит в основе понимания сложения и вычитания как обратных операций.

Типичное развитие ключевых идей в этой концепции

Детям нужна возможность увидеть маленькие числа в большой коллекции. «Числовые беседы» позволяют детям обсуждать то, что они видят. Например, с гигантскими божьими коровками: «Всего пятен 5. Я вижу 4 и 1, я вижу 3 и 2, и я вижу 1 и 1, 1, 1 и 1». Детям предлагается внимательно смотреть на числа, чтобы увидеть, что еще они могут увидеть. Это усиливает концепцию сохранения.

Деятельность и возможности:

• поощрение заключения договоренностей с (например) десятью. Убедитесь, что дети рассказывают о различных механизмах, которые они могут видеть в целом
.

Детям нужна возможность разделить некоторые вещи на две группы и понять, что эти группы можно рекомбинировать, чтобы получить одинаковую сумму. Предложите детям назвать целое число, которое составляют «части» вместе.

Деятельность и возможности:

• изучение песен; например, «Пять булочек со смородиной» — покажите, что всего осталось пять, но часть есть в магазине, а часть увезли; проверьте, что осталось еще пять булочек со смородиной
• играет в кегли и смотрит сколько стоит. Сколько упало? Сколько их всего?

Детям нужна возможность изучить различные способы разделения целого числа. Акцент здесь делается на выявлении пар чисел, составляющих сумму. Дети могут сделать это двумя способами — физически разделив группу или сконструировав группу из двух видов вещей.

Действия и возможности:

• Башни Нумикон: наслоение частей Нумикона из одной и той же суммы
• положить вещи в два контейнера разными способами
• делает номер из двух разных вещей. Например, сделать фруктовую шпажку из пяти кусочков фруктов, используя на выбор тарелки с бананами/клубникой; затем попросите детей описать, как они сделали свои. Они должны сравнить его с партнером: «Что такого же в ваших шашлыках? Чем отличается?»
• Кроличьи ушки: используйте пальцы как кроличьи ушки. «Двумя руками покажи мне пять пальцев. Вы можете сделать это по-другому? Или «Покажи вместе с другом пять пальцев»
• Рассыпать бобы: используя двухсторонние жетоны или бобы, одна сторона которых окрашена, бросьте коллекцию и отметьте, сколько каждого типа можно увидеть и сколько всего
• , используя шесть кресел-мешков с разной тканью с каждой стороны, бросьте коллекцию и отметьте, сколько можно увидеть каждого типа.

Детям нужна возможность изучить различные способы разделения чисел, т. е. более чем на две группы. Ситуации, способствующие этому, включают увеличение количества горшков, в которые можно положить определенную сумму, например. посадка десяти семян в три или более горшков.

Деятельность и возможности:

• ролевая игра, напр. в магазине игрушек нужно расставить десять игрушек на трех полках. Как вы их организуете?
• иметь более двух мест для сортировки в любом данном контексте, например. расстановка персонажей игры в маленьком мире по разным локациям
• игр, таких как «Шикарные утки» (Гриффитс, Р., Бэк, Дж. и Гиффорд, С. (2016) три разных места (гнездо, вода, настил), бросьте кубики и сделайте так, чтобы одна группа соответствовала указанной сумме, не добавляя и не убавляя.

Детям нужна возможность сказать, сколько скрыто в известном количестве вещей. Например: «Пять игрушек входят в палатку, потом выходят две. Сколько осталось в палатке?» Ребенок должен ответить, что в палатке еще три игрушки.

Занятия и возможности:

• игры в прятки с несколькими предметами в ящике, под тканью, в палатке, в пещере и т. д.
• , используя классные процедуры, такие как время уборки, чтобы определить, сколько еще не хватает в горшке с этикеткой с номером.

• детей, предполагающих, что спрятано большее число, чем общее количество.

Может ли ребенок:

• разделить малые группы на большее число?
• угадать скрытое число?
• в контексте укажите две группы, которые составляют большую сумму? Например, как могут приземлиться (шесть) мешков с фасолью? У вас может быть три с полосками вверх и три с пятнами вверх.

Загрузки

Загрузите диаграмму прогрессии для этой концепции

Составление и разложение чисел для сложения и вычитания

Трудно ли вашим ученикам составлять и разлагать числа при сложении и вычитании ? Моим ученикам трудно разбить число на части и использовать его части для вычислений.

Этот тип чувства числа требует тонны практики, и это тяжелая работа!

Старые крылатые фразы, такие как заимствование и перенос, больше не используются в Common Core. Они не имеют никакого отношения к математическому мышлению, поэтому я думаю, что хорошо, что мы их не используем. Точно так же интересно запоминать запоминающиеся фразы и стихи, но мне интересно, насколько студенты понимают и могут объяснить, что происходит в процессе.

Моя цель состоит в том, чтобы мои ученики поняли, как работают числа , как числа можно разбивать на части и складывать вместе разными способами . Я хочу, чтобы они гибко думали о числах и применяли эту гибкость к сложению и вычитанию.

В начале года мы начали с разложения и составления меньших чисел, чтобы получить 10. Используя факты +8 и +9, мы рассмотрели, как составление 10 может помочь нам решить проблемы.

Хотя я дал студентам стратегию, им потребовалось много практики, чтобы помочь им понять преимущества ее использования, а не считать на пальцах.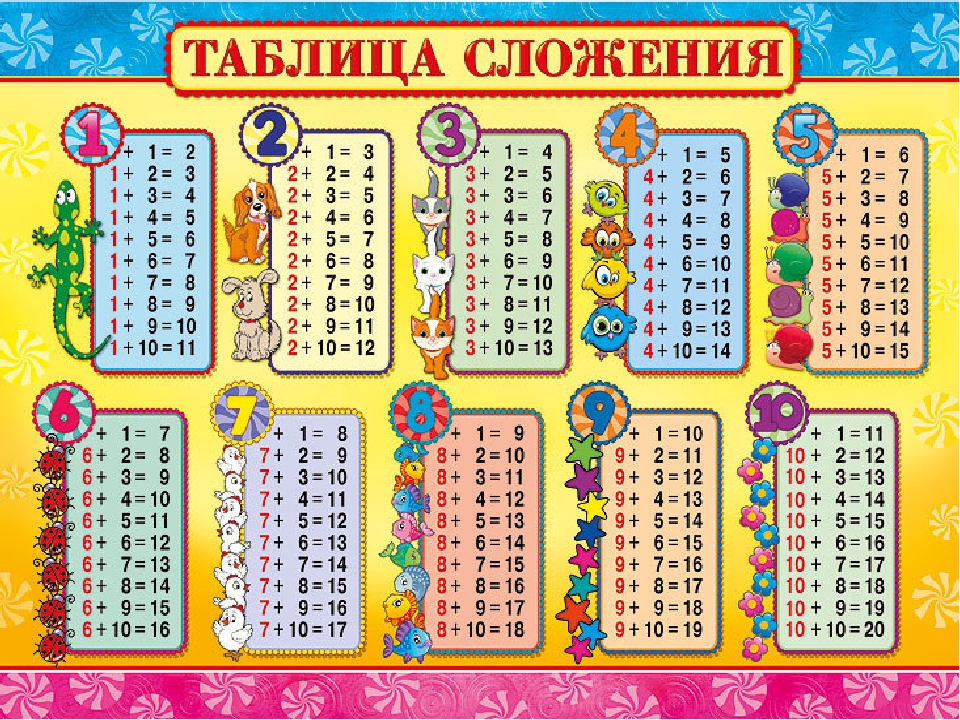 Я создал пакет математических станций, посвященных использованию 10 для сложения (+9).& +8). С этого началось наше путешествие по разложению чисел.

Позже в том же году, когда мы перешли к сложению больших чисел, мы снова пересмотрели стратегию составления 10 для сложения чисел, но работали над сложением десятков и сложением 100.

Одна из стратегий, которая хорошо сработала для учащихся, заключалась в том, чтобы они рисовали палочки, обозначающие количество десятков в каждом числе, а затем считали и вычеркивали каждую палочку по мере подсчета. Когда ученик доходил до 100, он останавливался и писал 100, затем начинал заново и считал оставшиеся палочки.

Благодаря этому упражнению учащиеся начали понимать «понятные числа» и научились использовать 100 при сложении.

Другим ресурсом, который мы использовали в этом году, были «Разложение числовых головоломок». Это помогло учащимся понять, что 44 равно 40 + 4, что также равно 30 + 14 и 30 + 10 + 4. Не все мои детишки смогли понять, как все эти числа связаны между собой и как разложить числа. У нас еще осталось совсем немного работы!

Мы использовали числовые головоломки в ноябре, и зимой я снова вытащил их, чтобы обсудить с несколькими моими учениками, которым нужно немного укрепить их.

Последнее, что я недавно сделал, это давал ученикам рамки предложений при вычитании. Пару недель назад я перешел от написания горизонтальной задачи к задаче на вычитание по вертикали. Они не знали, что делать! Это было так тяжело для них!

Мое решение состояло в том, чтобы дать студентам рамки предложений. Я начал с простых, например: «Есть/недостаточно единиц, чтобы вычесть _____ единиц. Вы не должны / должны разлагать десятку. Теперь есть ___ десятков и ___ единиц».

Честно говоря, я бы не дал ученику разложить десятку, чтобы вычесть 4, но нам нужно было попрактиковаться в этой концепции с меньшими числами, прежде чем переходить к большим числам.

«Разложи десятку» — это набор рамок предложений и заданий типа беготни, в которых учащиеся смотрят, нужно ли им разложить десятку, прежде чем решать задачи.