Как выучить быстро таблицу степеней: Таблица степеней | Таблица умножения
Таблица степеней | Таблица умножения
Для облегчения задачи возведения в степень чисел, результаты были систематизированы и занесены в единую таблицу. Таблица может быть представлена в виде равенств. Столбцы с показателем степени 1, 2 ,3 часто заучивают наизусть. Для всех остальных степеней удобно пользоваться именно табличными значениями.
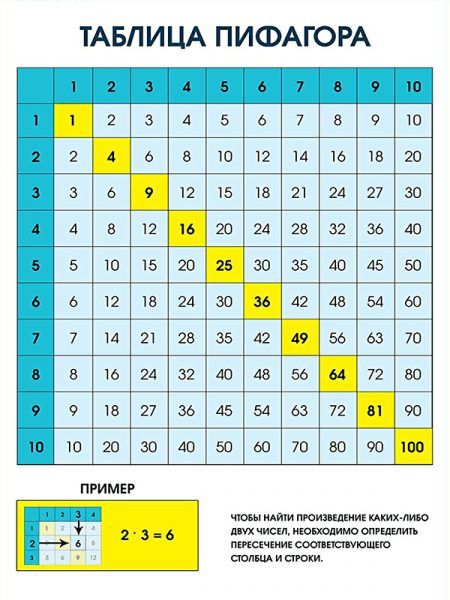
Существует также прямоугольное представление данной таблицы, в которой в первой колонке указано основание степени, в первой строке – показатель степени. Для того, чтобы найти нужное значение, достаточно выбрать нужные для примера значения и провести мысленно линии до их пересечения. На пересечении будет искомое значение.
К примеру, нужно возвести пять в четвертую степень. По вертикали (в первом столбце) ищем число 5, по горизонтали (в первой строке) – 4, видим, что на пересечении линий находится число 625.
Более сложные вычисления с помощью таблиц встречаются достаточно редко. В таких случаях прибегают к использованию калькуляторов и прочих аналогичных устройств или к специальным методам быстрого устного счета.
Файлы:
Что такое степень числа? Это в общем смысле некое число, умноженное само на себя несколько раз.
Вместо записи а ∙ а ∙ а ∙ а ∙ а можно использовать равнозначную запись a5.
Почему рядом с “a” именно пятая степень? Потому, что число “а” мы умножаем пять раз на него же.
Теперь рассмотрим на конкретном примере возведение в четвертую степень. Запись 5х5х5х5 удобно было бы представить покороче, на сегодняшний день в большинстве книг коротко она будет записана как 54. Исторически предлагались и другие способы записи, но наиболее распространенным на сегодня является вышеприведенный, где для 54 результатом вычислений будет число 625, но нужно понимать, что это условное обозначение, за которым на самом деле имеется ввиду вполне конкретный смысл, и на сегодняшний день эти вполне определнные действия именно так обозначают на бумаге. Озвучивают такую запись обычно как «пять в четвертой степени». Если бы не было такой короткой записи, а также не использовали бы короткую запись для обозначения многократного сложения одинаковых слагаемых (т.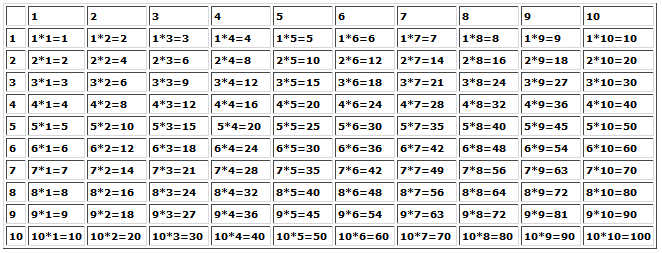
Вместо 53 или 5*5*5 пришлось бы писать (5+5+5+5+5) + (5+5+5+5+5)+ (5+5+5+5+5) + (5+5+5+5+5) + ( 5+5+5+5+5),
вместо 54 или 5*5*5*5* пришлось бы писать
(5+5+5+5+5) + (5+5+5+5+5)+ (5+5+5+5+5) + (5+5+5+5+5) + ( 5+5+5+5+5) +
(5+5+5+5+5) + (5+5+5+5+5)+ (5+5+5+5+5) + (5+5+5+5+5) + ( 5+5+5+5+5) +
(5+5+5+5+5) + (5+5+5+5+5)+ (5+5+5+5+5) + (5+5+5+5+5) + ( 5+5+5+5+5) +
(5+5+5+5+5) + (5+5+5+5+5)+ (5+5+5+5+5) + (5+5+5+5+5) + ( 5+5+5+5+5) +
(5+5+5+5+5) + (5+5+5+5+5)+ (5+5+5+5+5) + (5+5+5+5+5) + ( 5+5+5+5+5).
Все это вышеприведенное выражение можно заменить короткой записью с помощью обозначения возведения в степень. На сегодняшний день чаще всего применяют такую запись 54 при письме. Если Вы встретите литературу с другими обозначениями, то главное не путать между собой разные способы и вне зависимости от способа записи помнить, что на самом деле имеется ввиду.
7;
2) с помощью специальных кнопок в редакторах;
3) при создании страниц сайтов и использовании языка программирования HTML с помощью помещения показателя степени между специальными тегами.
Таблица степеней 🆕
Бесплатный вводный урок по математике
Записаться
После изучения арифметических основ в виде сложения, вычитания, деления и умножения, открывается математика и ее большой мир. В этом материале рассмотрим такое понятие, как степень.
Основные понятия
Степень числа с натуральным показателем — это результат многократного умножения числа на себя. Само число называют основанием степени, а количество операций умножения — показателем степени.
- an = a × a × … × a, где a — основание степени,
- n — натуральный показатель степени.
Запись читается, как «a» в степени «n».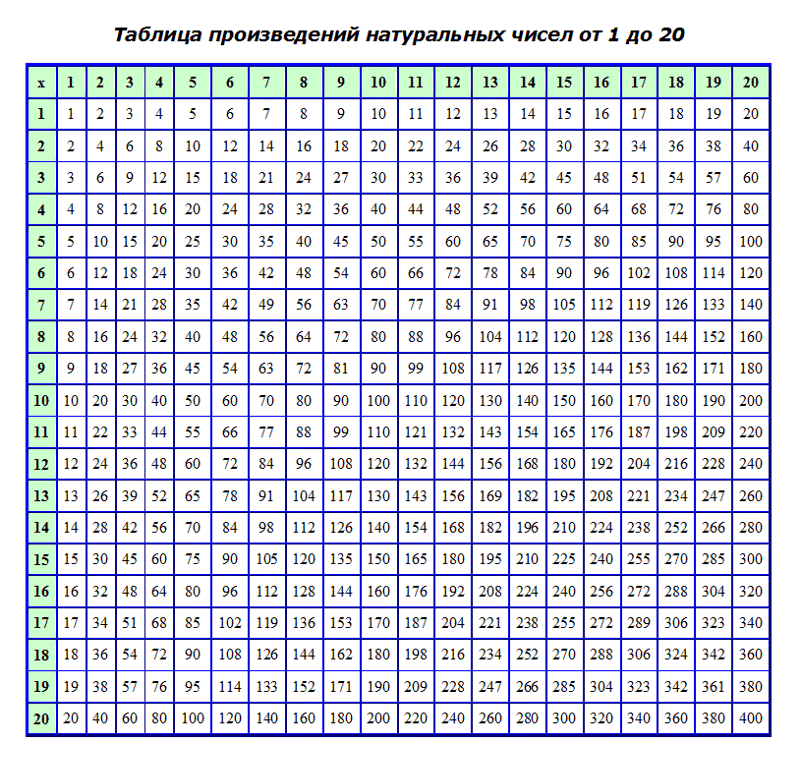
Вот пример для наглядности:
- 35 = 3 × 3 × 3 × 3 × 3 = 243
Эту запись можно прочитать тремя способами:
- 3 в 5 степени;
- пятая степень числа три;
- возвести число три в пятую степень.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Свойства степеней
Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.
a1 = а a0 = 1 (a ≠ 0) a−n = 1 : an am × an = am+n am : an = am-n (a × b)n = an × bn (am)n = am×n (a : b)n = an : bn |
Подготовка к ЕГЭ по математике онлайн поможет снять стресс перед экзаменом и повысит шансы на высокий балл.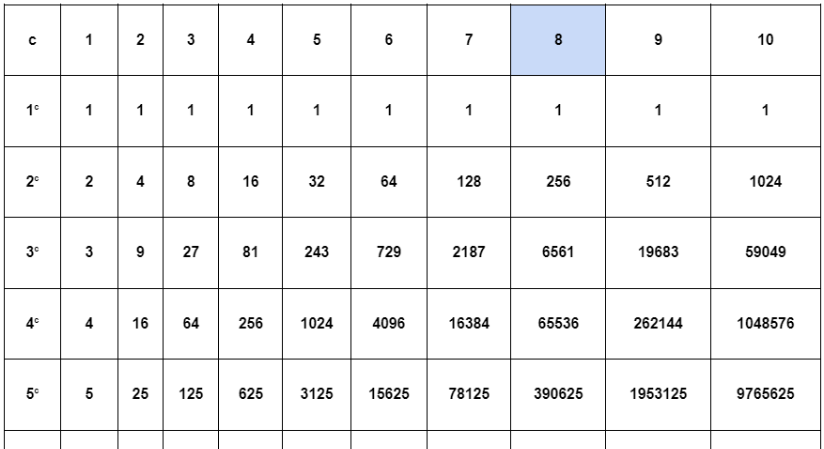
Таблица степеней от 1 до 10
Таблица степеней — это перечень чисел от 1 до 10, возведенных в степень от 1 до 10. Ниже приведены два вида таблиц: выберите ту, которая удобнее для вас, скачайте на телефон или распечатайте и положите в учебник.
Как найти необходимые значения в этой таблице:
- В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
- В первой строке находим показатель степени. Запомним найденный столбец.
- На пересечении строки и столбца находится ответ.
В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.
А если ответ нужно получить как можно быстрее, можно использовать онлайн-калькулятор степеней.
Решение задач
Задание 1. Упростить и решить выражение 5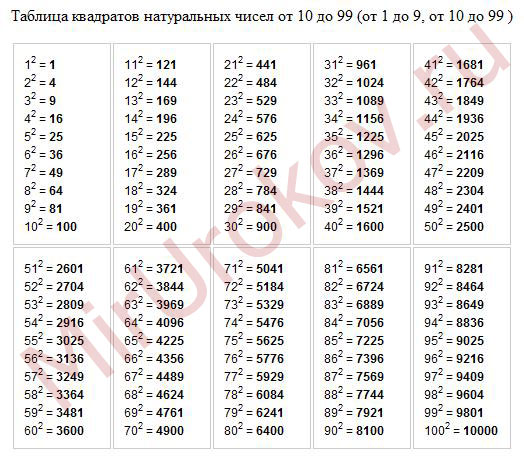
Как решаем:
52 × 53 = 52+3 = 55 = 3125
Задание 2. Упростить и решить выражение 24 × 33 × 25.
Как решаем:
24 × 33 × 25 = 24+5 × 33 = 29 × 33 = 512 × 27 = 13 824
Задание 3. Найти 364.
Как решаем:
При условии, что у нас есть только таблица до 10, разложим основание степени на множители:
364 = 64 × 64 = 1296 × 1296 = 1 679 616
364 = 64 × 64 = 6 8 = 1 679 616
Шпаргалки по математике родителей
Все формулы по математике под рукой
Как запоминать таблицы умножения [с подсказками зрительной памяти]
Математика
По Джен Уинтерс
Когда дело доходит до изучения таблицы умножения, стандартный способ преподавания этого предмета состоит в том, чтобы использовать механическое заучивание для быстрого запоминания математических фактов.
Хотя этот утомительный процесс запоминания таблицы умножения может работать для многих детей, многие другие пытаются вспомнить ответ с помощью этого повторяющегося метода обучения. Для этих детей факты попадают в категорию кратковременной памяти — они усваивают таблицу умножения за один день, а на следующий день совершенно забывают. Выход из этой бесконечной повторяющейся петли с карточками (которая, кажется, никогда не застревает!) состоит в том, чтобы превратить верхние, самые сложные факты умножения в визуальные картинки, которые включают модальности обучения правого полушария. Эта система запоминания работает
Раскрытие информации: этот пост был написан членом команды Trigger Memory — основателями Times Tales, Pet Math и Kids Chore Chart.
Как изображения, эмоции и воображение могут помочь ребенку освоить таблицу умножения
Когда мы обычно думаем об умножении, мы представляем себе набор чисел на сетке.
Благодаря механическому запоминанию (в сочетании со временем… много времени!) дети в конечном итоге могут заполнить сетку таблицы умножения, поскольку числа волшебным образом появляются в их памяти. Но что, если память не выдаст число? Если учащийся не сможет вернуться к сложению (попробуйте это с 7×8!), он не сможет быстро вспомнить ответ. Вот что делает запоминание ключа t o освоение таблицы умножения.
Сила мнемотехники!
Существует новый способ запоминания фактов старшего умножения с помощью системы, использующей мнемонику для запоминания. Для тех, кто не знаком с мнемоникой, в самых простых терминах это «привязка» памяти, которая заставляет мозг что-то вспомнить. Например, когда вы встречаете кого-то нового, вы связываете его имя с кем-то, чье имя вы уже знаете, например, с вашим соседом Джо. Когда ты увидишь новый Джо, вы изобразили старого соседа Джо вместе с ним.
Это, в свою очередь, вызывает название. Вуаля! Джо и Джо теперь вместе, и их не так-то просто забыть.
Так какое отношение старый сосед Джо имеет к таблицам умножения?
Оба Джо могут быть сохранены в банке памяти, который не настроен на удаление сразу после сохранения информации. Как только вы объединяете математические факты с правым полушарием мозга, визуальными эффектами и привязываете историю к числам (с небольшим количеством эмоций по поводу этой истории), этот математический факт сохраняется в памяти на неопределенное время. Это как магия умножения!
Умножение с помощью механического запоминания и умножение с помощью мнемонического запоминания
Times Tales® — это один из новых способов, с помощью которых школы обучают таблице умножения с помощью системы мнемонического запоминания. Многие учителя, которые перешли от механического заучивания к мнемоническому заучиванию , обнаружили, что время в классе, традиционно затрачиваемое учащимися на изучение таблицы умножения, сокращается до дроби .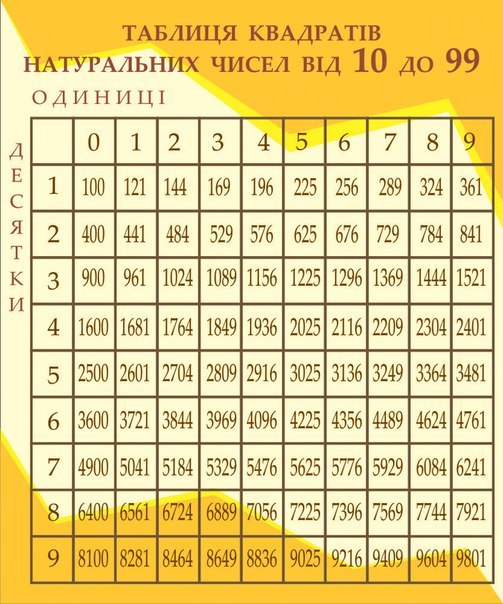
Еще одно замечательное преимущество обучения детей тому, как использовать эту мощную технику запоминания, заключается в том, что это инструмент, который они могут использовать всю жизнь. Многие дети, которые научились использовать этот инструмент памяти в раннем возрасте (например, запоминать таблицу умножения), сообщили, что использовали его во время учебы в средней школе и колледже. Мнемотехника работает для всех типов учащихся и доказала свою эффективность для детей с нарушениями обучаемости, такими как дислексия и дискалькулия. (см. статистический отчет об эффективности Times Tales для людей с ограниченными возможностями обучения)
Изучение таблиц умножения в течение многих лет было тем, что мы бы назвали обучением левого полушария, таким как: обработка чисел, аналитическое мышление и язык.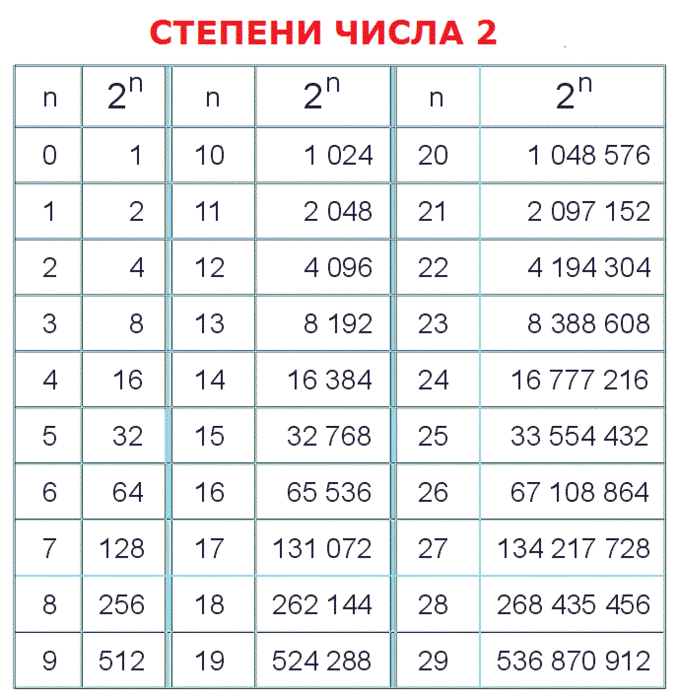
Однако, как только учащийся усвоит концепцию умножения, самым быстрым и эффективным способом запоминания математических фактов станет вовлечение правого полушария через визуальные эффекты, воображение и эмоции… да, умножение и эмоции — это очень хорошо!
5 причин, по которым дети должны использовать сказки о временах, чтобы освоить таблицы умножения
- БЫСТРО. Общее время обучения составляет всего час, а большинство детей осваивают верхнюю таблицу умножения всего за две недели!
- EASY. После завершения программы Times Tales дети в возрасте 5 лет могут повторять свои таблицы умножения, даже не понимая, что такое умножение!
- УДОВОЛЬСТВИЕ – Детям нравится этот метод обучения, и они просят еще!
- СООТВЕТСТВУЮЩИЙ – Охватывает самые сложные для запоминания таблицы умножения- 3×6, 3×7, 3×8, 3×9, 4×6, 4×7, 4×8, 4×9, 6×6, 6×7, 6×8, 6×9, 7×7, 7×8, 7×9, 8×8, 8×9, 9×9
- ЭФФЕКТИВНЫЙ – отлично подходит для детей с ограниченными возможностями обучения.
Работает для многих детей, когда другие программы потерпели неудачу.
Работает для многих детей, когда другие программы потерпели неудачу.Times Tales работает в школах
Этот мнемонический метод изучения таблицы умножения оказался настолько эффективным, что многие школы в США переходят на этот способ обучения своему классу таблице умножения. Узнайте больше о школьных изданиях Times Tales.
Multiplication_Chart_Drills_Printables
Закрепить!
Таблицы экспонент и шаблоны
Горячая математикаВ таблицах степеней целых чисел можно найти много интересных закономерностей.
Полномочия 2 | Полномочия 3 | Полномочия 4 |
| 2 1 знак равно 2 | 3 1 знак равно 3 | 4 1 знак равно 4 |
| 2 2 знак равно 4 | 3 2 знак равно 9 | 4 2 знак равно 16 |
| 2 3 знак равно 8 | 3 3 знак равно 27 | 4 3 знак равно 64 |
| 2 4 знак равно 16 | 3 4 знак равно 81 | 4 4 знак равно 256 |
| 2 5 знак равно 32 | 3 5 знак равно 243 | 4 5 знак равно 1024 |
| 2 6 знак равно 64 | 3 6 знак равно 729 | 4 6 знак равно 4096 |
| 2 7 знак равно 128 | 3 7 знак равно 2187 | 4 7 знак равно 16384 |
| 2 8 знак равно 256 | 3 8 знак равно 6561 | 4 8 знак равно 65536 |
| 2 9 знак равно 512 | 3 9 знак равно 19683 | 4 9 знак равно 262144 |
| 2 10 знак равно 1024 | 3 10 знак равно 59049 | 4 10 знак равно 1048576 |
Одна вещь, которую вы можете заметить, это закономерности в цифрах.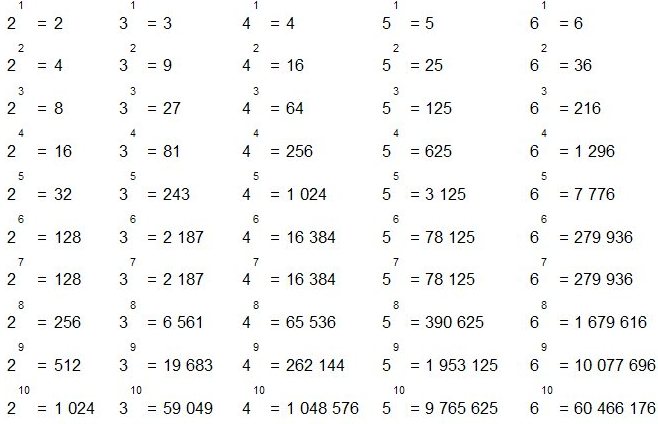
В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9,
7
,
1
,
3
,
9
,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях 4 таблица, чередуются единичные цифры: 4 , 6 , 4 , 6 . На самом деле, вы можете видеть, что силы 4 совпадают с четными степенями 2 :
4
1
знак равно
2
2
4
2
знак равно
2
4
4
3
знак равно
2
6
и т.
п.
Такие же отношения существуют между силы 3 и силы 9 :
Полномочия 3 | Полномочия 9 |
| 3 1 знак равно 3 | 9 1 знак равно 9 |
| 3 2 знак равно 9 | 9 2 знак равно 81 |
| 3 3 знак равно 27 | 9 3 знак равно 729 |
| 3 4 знак равно 81 | 9 4 знак равно 6561 |
| 3 5 знак равно 243 | 9 5 знак равно 59 049 |
| 3 6 знак равно 729 | 9 6 знак равно 531 441 |
| 3 7 знак равно 2187 | 9 7 знак равно 4 782 969 |
| 3 8 знак равно 6561 | 9 8 знак равно 43 046 721 |
| 3 9 знак равно 19 683 | 9 9 знак равно 387 420 489 |
| 3 10 знак равно 59 049 | 9 10 знак равно 3 486 784 401 |
силы
10 легко, потому что мы используем
база
10
: за
10
н
просто напишите ”
1
” с
н
нули после него.
За
отрицательные силы
10
−
н
, записывать ”
0.
” с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
Полномочия 10 | |
| 10 1 знак равно 10 | 10 0 знак равно 1 |
| 10 2 знак равно 100 | 10 − 1 знак равно 0,1 |
| 10 3 знак равно 1000 | 10 − 2 знак равно 0,01 |
| 10 4 знак равно 10 000 | 10 − 3 знак равно 0,001 |
10 5 знак равно 100 000 (сто тысяч) | 10 − 4 знак равно 0,0001 (одна десятитысячная) |
10 6 знак равно 1 000 000 (один миллион) | 10 − 5 знак равно 0,00001 (стотысячный) |
10 7 знак равно 10 000 000 (десять миллионов) | 10 − 6 знак равно 0,000001 (одна миллионная) |
10 8 знак равно 100 000 000 (сто миллионов) | 10 − 7 знак равно 0,0000001 (одна десятимиллионная) |
10 9 знак равно 1 000 000 000 (один миллиард) | 10 − 8 знак равно 0,00000001 (стомиллионный) |
10 10 знак равно 10 000 000 000 (десять миллиардов) | 10 − 9 знак равно 0,000000001 (одна миллиардная) |
Нажмите
здесь
для большего количества имен для
очень большие и очень маленькие числа
.