Как учить состав числа: Как быстро выучить состав числа до 20. Как научить ребенка считать примеры в пределах 20

Консультация для родителей «Учим с дошкольником состав числа на домашних занятиях» | Консультация по математике (подготовительная группа):

Консультация для родителей

«Учим с дошкольником состав числа на домашних занятиях»

В подготовительной к школе группе воспитанники изучают состав числа до 10. Не всем ребятам эти знания даются легко, поэтому родителям приходится помогать чаду во время домашних занятий. Невозможно оставить без внимания этот пробел, так как знания о составе числа помогают быстро осваивать математику, ее основные азы.

Учим состав числа на домашних занятиях. Домочадцы могут помочь ребенку, если будут в ненавязчивой и увлекательной форме повторять темы, изученные на занятиях в детском саду. Не надо браться за какие-то сложные задания, достаточно заняться основным, например, четко знать, как объяснить ребенку состав числа.

Важно! Современное образование упирается именно в освоение состава числа. Это помогает запомнить основные понятия математики. Арифметические операции и сравнение чисел будут проходить легко для ребенка.

Как учить быстрому счету

Еще до поступления ребенка в школу, родители могут быстро научить его считать до 10. Главное, сделать этот процесс максимально доступным, чтобы затем приступить к более сложным знаниям – ознакомлению детей с составом числа. Даже младшего дошкольника можно учить считать деревья, шаги, ступеньки и все окружающие предметы. При закреплении следует делать акцент на единице, правильно называть цифру “один”, а не “раз”, объяснить, что такое пустота, математический “0”. После этого полезно показать графическое изображение цифр. Лучше делать это в игровой форме. Следует применять наглядные примеры, пользоваться магнитными досками, цифрами, игрушками.

К сведению родителей! Нужно рассказать маленькому ученику, что цифра – это символ для записи чисел, а число – это математическое понятие. Цифр только девять, от 0 до 9, а чисел множество.

После того, как все цифры усвоены, можно приступать к счету.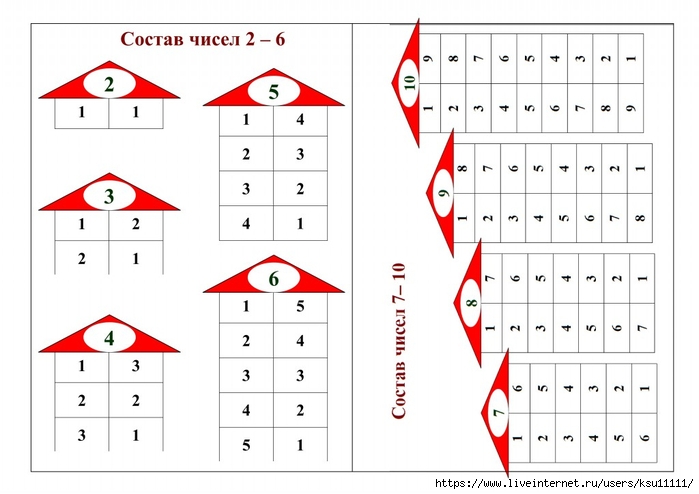 Следует показать, как необходимо считать на пальцах, счетных палочках, других приспособлениях. Рекомендуется сравнивать цифры, объяснять, какое число больше или меньше, насколько. Также необходимо выучить математические знаки для наглядного предоставления информации. Важно правильно объяснить, что два меньших числа могут превратиться в большее и, наоборот, большее число разделиться на два меньших.

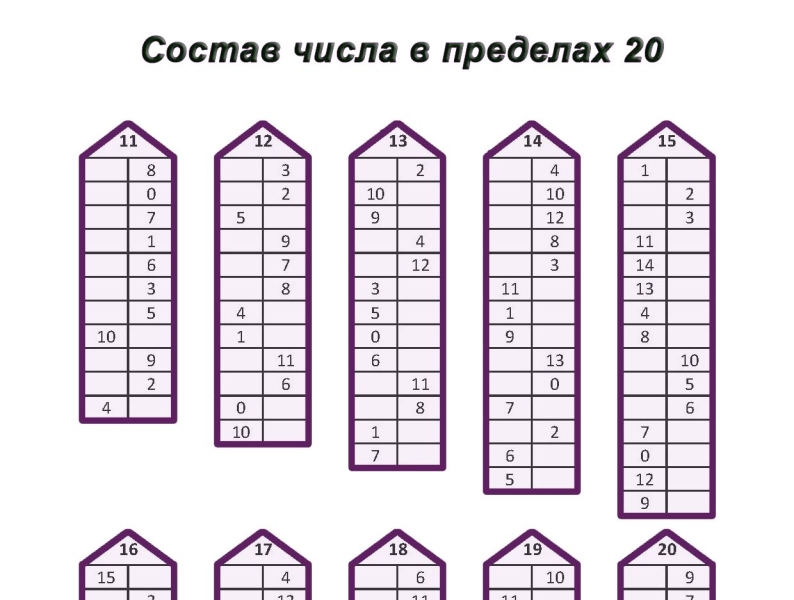
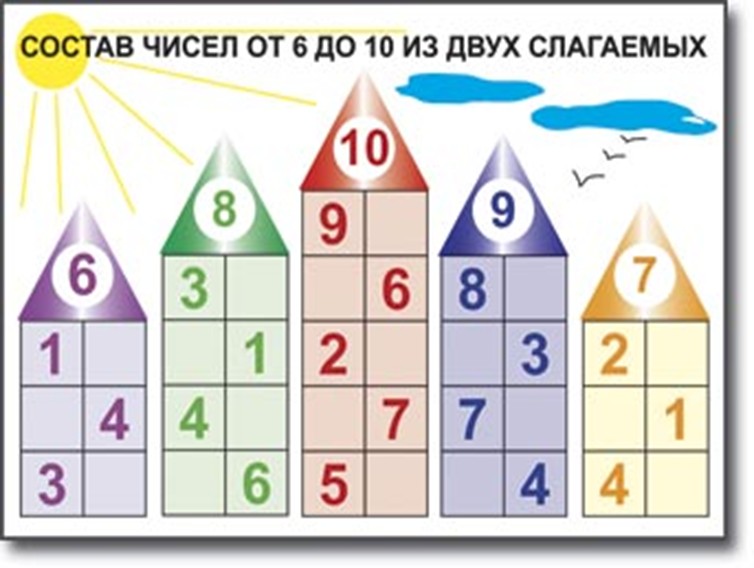
Чтобы запомнить состав чисел, можно поиграть с ребенком в числовые домики. Это классическое игровое упражнение. Взрослый вместе с малышом рисует несколько домиков, которые отличаются друг от друга количеством этажей. Начинать с одноэтажного, последним будет девятиэтажный. На крыше изображается определенное число. На каждом этаже по две квартиры, в которых проживают жильцы. Их количество зависит от этажности дома. Например, в трехэтажном на первом этаже живут 0 и 4, на втором – 1 и 3, на третьем – 2 и 2. Так ребенок узнает о составе числа 4.

Можно задать число и предложить малышу назвать “соседей”, какое число стоит перед ним и после него, задать два числа, спросить, что стоит между ними. Обсудить, чем отличаются числа (предыдущее – меньше на 1, последующее – больше на 1).

На листе бумаги написать цифру и попросить найти указанное количество карандашей, горошин или стаканчиков. Поменять задание, предложить составить записанное число из разных предметов. Показать, как по-разному можно составить заданное число.

Когда выучены цифры до 10, можно вводить понятие “единицы и десяток”. Цифры могут превращаться в домики, где десятки являются этажами, а единицы квартирами. Хорошо помогают одинаковые мелкие игрушки, когда надо их выстроить по десять в два ряда. Таким образом заучивается второй десяток.

Устный счет помогает выполнять задания с максимальной скоростью. Для легкого счета нужно обязательно объяснить ребенку состав чисел, выучить в игровой форме расклад чисел до 10, причем, чем больше цифра, тем большее внимание ей уделяется. Вначале на своем примере показать, как в уме следует перебирать состав определенного числа. К примеру, нужно спросить ученика, сколько нужно еще добавить к числу 2, чтобы получить 5. Естественно, сначала возникнут сложности с усвоением, но в скором времени ребенок будет легко считать устно.

Важно! Обучая устному счету, желательно ограничить ученика в применении различных предметов, палочек и пальцев, так как это замедляет навык считать в уме.

Подходящий возраст для занятий

Оптимальный возраст для обучения счету является понятием относительным. Некоторые дети уже в 4 года пытаются считать и делают это весьма успешно, другие даже в 6 лет не готовы к этому. Однако в 5 – 6 лет следует обязательно готовить малыша к школе. Именно в этот период мозг легко воспринимает новую информацию, чадо тянется к знаниям. Воспитатели подготовительной группы основной упор делают на действия с числами в пределах 10. Дети в состоянии в этом возрасте выполнять сложение и вычитание, запомнить состав числа. Школьная программа не стоит на месте, новая тема осваивается ежедневно, поэтому без определенных навыков у ребенка могут возникнуть проблемы с математикой.

Устный счет.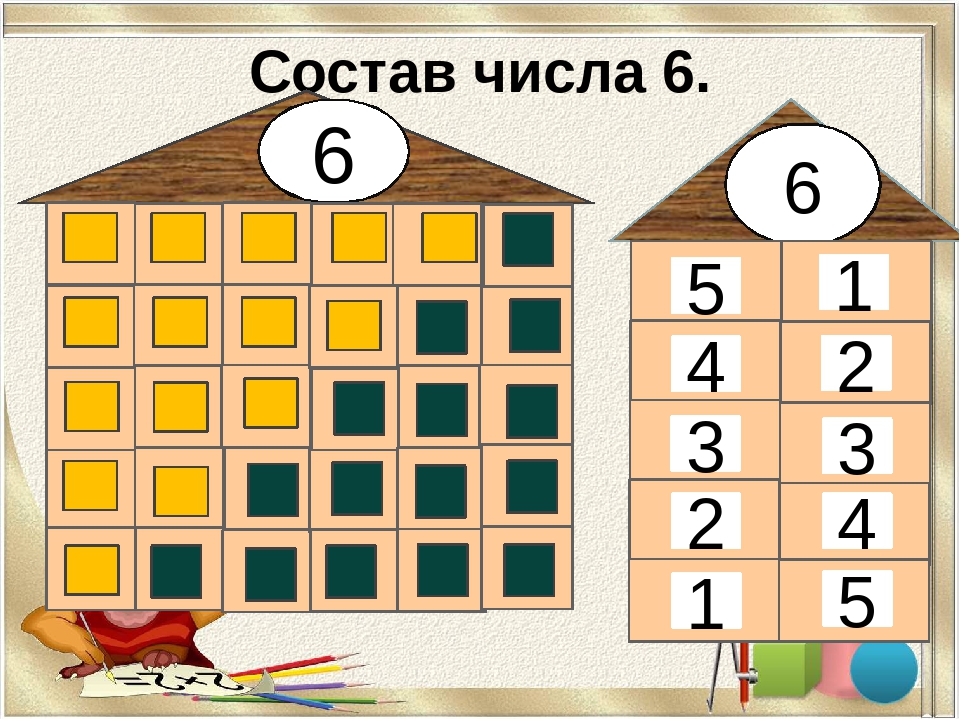 Сложение и вычитание

Существенное повышение интеллектуального потенциала

Беспроблемное обучение точным дисциплинам

Повышает скорость и качество восприятия информации

Умение быстро считать в уме прибавляет уверенности в себе

Навыки устного счета – на всю жизнь

Процент людей, отлично считающих в уме, среди руководителей выше, чем среди их подчиненных

Начать курс 

Что пригодится для домашних занятий

Сегодня для домашних занятий можно выбрать любые счетные материалы. Наиболее популярными среди них являются палочки для счета. Однако немногие задумываются над тем, что они недостаточно эффективны. Дошкольник при использовании палочек не в состоянии научиться быстро считать устно. Для ознакомления детей с составом числа предлагается использовать следующие счетные приспособления:

Быстро выучить состав числа помогут карточки с различными предметами (домиками, цветочной полянкой, угощением для зверей), домино. Они входят в наборы для счета, как игровая форма. Когда малыши учатся находить составляющие чисел, к ним приходит понимание истин и основных математических понятий.

Наборы из дерева и пластика с цифрами и математическими знаками тоже помогают ускорить учебный процесс и сделать его максимально эффективным. Различные игры с озвучиванием позволяют освоить запоминание цифр и чисел.

Наиболее интересными материалами для счета станут созданные своими руками пособия. Можно вместе рисовать, клеить коробочки с цифрами, считать карандаши, лепить цифры из пластилина и теста. Все это помогает легко и прочно запомнить цифры.

Простые и доступные методики обучения

Существует множество эффективных методов, помогающих родителям понять, как научить ребенка составу числа до 10. Есть возможность выбрать для домашних занятий наиболее подходящую.

 

Для облегчения подготовки к домашним занятиям можно приобрести материалы для дидактических игр, книги, обучающие предметы, мультики. Все они способствуют легкому обучению числам, составу числа, запоминанию и правильному применению. Все задания представлены в этих пособиях, родителям не надо ничего придумывать.

Чтобы повторять школьные темы, можно воспользоваться наглядными примерами. Рекомендуется остаться с учеником в комнате вдвоем и спросить, сколько находится человек в помещении. Когда он скажет, что два, можно попросить других домочадцев по очереди входить в комнату. Пусть ребенок посчитает два плюс один и научится понимать, из чего состоит число три. Таким образом действовать дальше. Малыш должен видеть, как все происходит, почему меняются числа и как их можно складывать или вычитать.

Для дошколят хорошо использовать игру со счетом шагов. К примеру, мама и дети отправились на прогулку. Нужно отмерять шагами расстояние и считать их по порядку. А затем возвращаться и считать шаги в обратной последовательности. Ребята быстро освоят это задание, а оно и является составом числа.

Даже бытовые ситуации помогут выучить с ребенком состав числа. Например, попросить малыша накрыть стол к обеду, поставить 5 тарелок, столько же ложек, разложить по два куска хлеба. Если ребенок испытывает затруднения со счетом, нужно обязательно помочь ему сориентироваться, объяснить, почему нужно именно столько предметов.

Счетные палочки помогут даже самым маленьким членам семьи научиться счету в пределах 10. Для этого следует положить на стол одну палочку, а затем попросить добавить определенное количество палочек, чтобы получилось пять. Примеры нужно постоянно усложнять, тренироваться не только увеличивать числа, но и уменьшать их.

Советы педагогов для правильного домашнего обучения

Педагоги категорически не рекомендуют применять запись состава числа для дошкольников. Пока для них это трудно. Следует устно научить считать до 10. Желательно использовать для этого игрушки, окружающие вещи, столовые предметы, книги.

На первом плане должны производиться действия с предметами, к примеру, был один кубик, к нему добавили еще один, стало их два, и так дальше.

Рекомендуется как можно чаще спрашивать малыша о количестве предметов. Посчитать можно все, что находится рядом, даже ступеньки на лестнице при выходе из подъезда.

Важно! Ребенок должен четко уяснить, что каждое число меньше следующего на единицу и больше предыдущего на столько же.

Преподаватели в первом классе нередко используют классический прием для изучения цифр и чисел:

сначала выходит один ученик и сообщает, что он первый вагон поезда;

за ним выходит еще один и говорит, что он второй вагон;

каждый раз проговаривается, что на один больше будет последующая цифра;

и так дальше;

затем вагоны называются в обратном порядке.

Основные рекомендации

Родители должны осознать важность изучения состава чисел, в процессе домашних занятий соблюдать некоторые рекомендации специалистов, чтобы дошкольник мог спокойно освоить информацию и правильно применить ее. Естественно, не исключены кризисы в процессе, недопонимания, но все это проходит, а остаются знания, которые необходимы при школьном обучении.

Нужно обязательно давать ребенку свободу. Родители часто предъявляют требования к чаду, которые не соответствуют его возможностям. Следует задуматься о запретах и наказаниях за незнание, выяснить, обоснованы ли они в действительности.

Необходимо учитывать мнение ребенка. Нужно понимать, что у малыша существует собственная позиция по всем вопросам. Если учить ребенка насильно, то это не принесет желаемого эффекта. Приказной тон на занятиях попросту неуместен.

Если малыш категорически отказывается учить цифры, то нужно поинтересоваться причинами этого. Вполне возможно, что он попросту боится расстроить родителей своим незнанием. Тогда хорошим выходом будет организация творческого процесса с привлечением всех домочадцев. Совместное изготовление пособий, рисунков из цифр, соревнования, кто быстрее назовет числа, напишет цифры, посчитает игрушки – сделает обучение легким и увлекательным.

Необходимо всегда позитивно оценивать достижения малыша, демонстрировать доброжелательность, показывать поддержку в сложных ситуациях, совместно устранять ошибки, обсуждать варианты возможных решений. Главное дать понять ребенку, что у него все получится, по-другому и быть не может.

Родителям важно помнить, что домашние занятия не должны вызывать неприязнь у чада. Ребятишки воспринимают подачу информации лучше всего в игре. В начале школьного учения педагоги продолжают вести занятия именно в игровой форме. Это способствует легкому и быстрому восприятию математических знаний.

Математика 1 класс. Тема: Состав числа 6. | Уроки по Математике

Цель: Ознакомление с составом числа6.

Задачи: 1. Формировать у учащихся знания о составе числа 6. Учить писать цифру 6.

2. Развивать математическое мышление, память, внимание, развитие речи, правильно читать соответствующие равенства.

3. Воспитывать  дружбу, коллективизм, интерес к предмету.

Ожидаемые результаты. :1. у учащихся  сформируются знания о составе числа 6. Научатся писать цифру 6.

2. Развивают математическое мышление, память, внимание, речь, правильно читать соответствующие равенства.

3. Вырабатывают   дружбу, коллективизм, интерес к предмету.

 Оборудование: счетный ряд, демонстрационные цифры, фигурки для оценивания, домики для заполнения по составу чисел.

 

Ход урока.

 

1.Орг момент. Эмоциональный настрой. Музыкальная разминка.

2.Основная часть. Деление на группы. На столе учителя лежат стикеры с числами 1.2.3.4.

 Дети разбирают их и рассаживаются по группам.

 – Ребята, сегодня  у цифр   в числовом ряду случилась беда. Волшебник нечаянно совершил ошибку и заколдовал цифру,  и я не могу понять какую.

 – Посмотрите на числовой ряд, и скажите, какая это цифра. (Цифра 6).

 – Чтобы ее расколдовать, нам необходимо выполнить  задания волшебника. За каждое правильно выполненное задание волшебник будет дарить вам волшебную звездочку.

 3 .И так мы приступаем.

 «Мозговая атака» Устный счет.

 – назовите число , которое следует за числом 2.4,5,1,0

– какое число получится, если из 5 – 1.

– назовите число, которое стоит между 2 и 3, 8 и10, 1 и3, 4 и6

– к задуманному числу  прибавили 1, получили 3. Какое число задумали?

 Молодцы, Оценивание.

4.  Повторение состава чисел 4,5 работа в группах.

 Две группы заполняют домики по составу чисел. Защищают свои работы , сравнивают и оценивают друг у друга.

5. Работа над изучение состава числа 6.

 У ребят на партах счетные палочки.

– разложите палочки на две кучки  разными способами так, чтобы в результате получилось число шесть, а результаты запишите на листах.

 Ребята выполняют работу, демонстрируют результаты, взаимооценивают, получают звездочки.

 Сравнение результатов работы с наглядным пособием по составу числа.

6. Работа по учебнику. Стр. 44.

– №1 работа в парах. Заполнить клеточки. Проверка, оценивание.

№2 Составление и чтение равенств.

№3. Назвать пропущенные числа.

7. Работа в тетради.  Повторное письмо цифры 6. Взаимороценивание. Дети рисуют друг другу на полях  звездочку.

 Выполнение задания на  сравнение. Двое у доски.

7. Обобщение.

 -Ну вот мы и справились с заданиями.

Посмотрите на числовой ряд. Что произошло?

 А что мы сегодня узнали?  (состав числа 6).

8 Рефлексия. Мы сегодня с вами хорошо потрудились. Вы получили от волшебника звездочки. А где живут  звездочки?

 Давайте поместим звездочки на небо. ( Дети наклеивают звездочки на звездное небо)

9. Итог урока.

 

 

3.4: Композиция функций — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

32512

• OpenStax
• OpenStax

Цели обучения

• Комбинирование функций с помощью алгебраических операций.
• Создать новую функцию по композиции функций.
• Оценить составные функции.
• Найдите область определения составной функции.
• Разложить составную функцию на составные функции.

Предположим, мы хотим рассчитать, сколько стоит обогреть дом в определенный день года. Стоимость отопления дома будет зависеть от среднесуточной температуры, а среднесуточная температура, в свою очередь, зависит от конкретного дня в году. Обратите внимание, что мы только что определили два отношения: стоимость зависит от температуры, а температура зависит от дня.

Используя описательные переменные, мы можем обозначить эти две функции. Функция \(C(T)\) дает стоимость \(C\) отопления дома при заданной среднесуточной температуре в \(T\) градусах Цельсия. Функция \(T(d)\) дает среднесуточную температуру в день d года. Для любого заданного дня \(Стоимость=C(T(d))\) означает, что стоимость зависит от температуры, которая, в свою очередь, зависит от дня года. Таким образом, мы можем оценить функцию стоимости при температуре \(T(d)\).

Например, мы могли бы вычислить \(T(5)\) для определения средней дневной температуры на 5-й день года. Затем мы можем оценить стоимостная функция при этой температуре. Мы бы написали \(C(T(5))\).

Рисунок \(\PageIndex{1}\): Объяснение \(C(T(5))\), которое представляет собой стоимость температуры и \(T(5)\) является температурой в день 5.

Объединив эти два отношения в одну функцию, мы выполнили композицию функций, которой посвящен этот раздел.

Объединение функций с использованием алгебраических операций

Композиция функций — это только один из способов объединения существующих функций. Другой способ — выполнять обычные алгебраические операции над функциями, такие как сложение, вычитание, умножение и деление. Мы делаем это, выполняя операции с выходами функции, определяя результат как результат нашей новой функции.

Предположим, нам нужно сложить два столбца чисел, представляющих отдельные годовые доходы мужа и жены за определенный период, и в результате получить их общий доход домохозяйства. Мы хотим сделать это для каждого года, добавив только доходы за этот год, а затем собрав все данные в новый столбец. Если \(w(y)\) — доход жены, а \(h(y)\) — доход мужа в году \(y\), и мы хотим, чтобы \(T\) представляло общий доход, то мы можно определить новую функцию.

\[T(y)=h(y)+w(y) \nonnumber\]

Если это верно для каждого года, то мы можем сосредоточиться на отношении между функциями без привязки к году и написать

\[T=h+w \nonnumber\]

Так же, как для этой суммы двух функций , мы можем определить функции разности, произведения и отношения для любой пары функций, которые имеют одни и те же входные данные (не обязательно числа), а также одинаковые виды выходных данных (которые должны быть числами, чтобы можно было выполнять обычные алгебраические операции). применяются к ним, и которые также должны иметь одинаковые единицы или не иметь единиц, когда мы складываем и вычитаем). Таким образом, мы можем думать о сложении, вычитании, умножении и делении функций.

2−1 \nonumber\] 92\)

Нет, функции не те.

Создание функции путем составления функций

Выполнение алгебраических операций над функциями объединяет их в новую функцию, но мы также можем создавать функции путем составления функций. Когда мы хотели рассчитать стоимость отопления по дням в году, мы создали новую функцию, которая принимает день в качестве входных данных и дает стоимость в качестве выходных данных. Процесс объединения функций таким образом, что выходные данные одной функции становятся входными данными другой, известен как

Состав функций . Полученная функция известна как составная функция . Мы представляем эту комбинацию следующими обозначениями:

\[f{\circ}g(x)=f(g(x))\]

Левую часть читаем как «\(f\), составленную из \(g\) в \(x\)», а правая часть как «\(f\) от \(g\) от \(x\)». Две части уравнения имеют одинаковые математические смысл и равны. Символ открытого круга \(\circ\) называется оператором композиции. Мы используем этот оператор главным образом, когда хотим подчеркнуть отношения между самими функциями, не обращаясь к какому-либо конкретному входному значению. Композиция — это бинарная операция, которая берет две функции и формирует новую функцию, подобно тому, как сложение или умножение берет два числа и дает новое число. Однако важно не путать композицию функций с умножением, потому что, как мы узнали выше, в большинстве случаев \(f(g(x)){\neq}f(x)g(x)\).

Также важно понимать порядок операций при вычислении составной функции. Мы следуем обычному соглашению со скобками, начиная с самых внутренних скобок, а затем переходя к внешним. В приведенном выше уравнении функция \(g\) сначала принимает входные данные \(x\) и дает выходные данные \(g(x)\). Тогда функция \(f\) принимает \(g(x)\) в качестве входных данных и дает результат \(f(g(x))\).

Рисунок \(\PageIndex{2}\): Объяснение составной функции.

В общем случае \(f{\circ}g\) и \(g{\circ}f\) – разные функции. Другими словами, во многих случаях \(f(g(x)){\neq}g(f(x))\) для всех \(x\). Мы также увидим, что иногда две функции могут быть составлены только в одном определенном порядке. 92+2 \end{align*}\]

Эти выражения не равны для всех значений x, поэтому две функции не равны. Неважно, что выражения совпадают для единственного входного значения \(x=−\frac{1}{2}\).

Обратите внимание, что диапазон внутренней функции (первой оцениваемой функции) должен находиться в пределах домена внешней функции. Менее формально, композиция должна иметь смысл с точки зрения входов и выходов.

Композиция функций

Когда выход одной функции используется как вход другой, мы называем всю операцию композицией функций. Для любого входа \(x\) и функций \(f\) и \(g\) это действие определяет составная функция , которую мы записываем в виде \(f{\circ}g\) так, что

\[(f{\circ}g)(x)=f(g(x))\]

Область составной функции \(f{\circ}g\) – это все \(x\) такие, что \(x\) находится в области определения \(g\) и \(g(x)\) находится в домен \(f\).

Важно понимать, что произведение функций \(fg\) не совпадает с композицией функций \(f(g(x))\), потому что, вообще говоря, \(f(x)g( х) {\ neq} е (г (х)) \).

Пример \(\PageIndex{2}\): Определение коммутативности композиции функций

Используя предоставленные функции, найдите \(f(g(x))\) и \(g(f(x))\). Определить, является ли композиция функций коммутативной .

\[f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber\]

Решение

Начнем с подстановки \(g(x)\) в \(f(x)\).

\[\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \ end{align*}\]

Теперь мы можем заменить \(f(x)\) на \(g(x)\).

\[\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end {выравнивание*}\]

Получаем, что \(g(f(x)){\neq}f(g(x))\), поэтому операция композиции функций некоммутативна.

Пример \(\PageIndex{3}\): интерпретация составных функций )\) дает количество приседаний, которое человек может выполнить за \(t\) минут. Интерпретировать \(c(s(3))\).

Решение

Внутреннее выражение в композиции равно \(s(3)\). Поскольку входом для \(s\)-функции является время, \(t=3\) представляет 3 минуты, а \(s(3)\) – это количество приседаний, выполненных за 3 минуты.

Использование \(s(3)\) в качестве входных данных для функции \(c(s)\) дает нам количество калорий, сожженных во время количества приседаний, которые можно выполнить за 3 минуты, или просто количество сожженных калорий за 3 минуты (при выполнении приседаний).

Пример \(\PageIndex{4}\): исследование порядка композиции функций

Предположим, что \(f(x)\) дает количество миль, которые можно проехать за \(x\) часов, а \(g(y) \) дает количество галлонов бензина, израсходованное на \(y\) миль. Какое из этих выражений имеет смысл: \(f(g(y))\) или \(g(f(x))\)?

Решение

Функция \(y=f(x)\) — это функция, выходом которой является количество пройденных миль, соответствующее количеству часов езды.

\[\text{количество миль } =f (\text{количество часов}) \nonumber\]

Функция \(g(y)\) — это функция, выходом которой является количество использованных галлонов, соответствующих к количеству пройденных миль. Это означает:

\[\text{количество галлонов } =g(\text{количество миль}) \nonumber\]

Выражение \(g(y)\) принимает мили в качестве входных данных и число галлонов на выходе. Функция \(f(x)\) требует на входе количество часов. Попытка ввести количество галлонов не имеет смысла. Выражение \(f(g(y))\) бессмысленно.

Выражение \(f(x)\) принимает часы в качестве входных данных и количество пройденных миль в качестве выходных данных. Функция \(g(y)\) требует количества миль в качестве входных данных. Использование \(f(x)\) (пройденных миль) в качестве входного значения для \(g(y)\), где галлоны бензина зависят от пройденных миль, имеет смысл. Выражение \(g(f(x))\) имеет смысл и даст количество использованных галлонов газа, \(g\), проехав определенное количество миль, \(f(x)\), в \(х\) часов.

Вопрос/Ответ

Существуют ли ситуации, когда выражения \(f(g(y))\) и \(g(f(x))\) могут быть осмысленными или полезными выражениями?

Да. Для многих чисто математических функций обе композиции имеют смысл, хотя обычно они производят разные новые функции. В реальных задачах функции, входы и выходы которых имеют одинаковые единицы измерения, также могут давать композиции, которые имеют смысл в любом порядке

Упражнение \(\PageIndex{2}\)

Гравитационная сила на планете \) от солнца задается функцией \(G(r)\). Ускорение планеты под действием любой силы \(F\) определяется функцией \(a(F)\). Составьте осмысленную композицию из этих двух функций и объясните, что она означает.

Ответить

Гравитационная сила остается силой, поэтому \(a(G(r))\) имеет смысл как ускорение планеты на расстоянии \(r\) от Солнца (из-за силы тяжести), но \(G (a(F))\) не имеет смысла.

Вычисление составных функций

После того, как мы составим новую функцию из двух существующих функций, нам нужно иметь возможность оценивать ее для любых входных данных в ее области.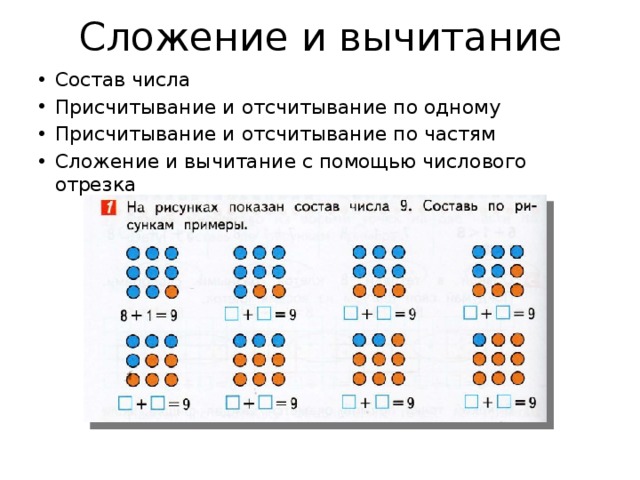 Мы сделаем это с конкретными числовыми входными данными для функций, выраженных в виде таблиц, графиков и формул, и с переменными в качестве входных данных для функций, выраженных в виде формул. В каждом случае мы оцениваем внутреннюю функцию, используя начальный ввод, а затем используем вывод внутренней функции в качестве ввода для внешней функции.

Вычисление составных функций с использованием таблиц

При работе с функциями, представленными в виде таблиц, мы считываем входные и выходные значения из записей таблицы и всегда работаем изнутри наружу. Сначала мы оцениваем внутреннюю функцию, а затем используем выходные данные внутренней функции в качестве входных данных для внешней функции.

Пример \(\PageIndex{5}\): использование таблицы для вычисления составной функции

Использование таблицы \(\PageIndex{1}\), оценка \(f(g(3))\) и \( г(f(3))\).

Таблица \(\PageIndex{1}\)

\(х\)	\(ф(х)\)	\(г(х)\)
1	6	3
2	8	5
3	3	2
4	1	7

Решение

Чтобы вычислить \(f(g(3))\), мы начинаем изнутри с входного значения 3. Затем мы оцениваем внутреннее выражение \(g(3)\), используя таблица, определяющая функцию \(g: g(3)=2\). Затем мы можем использовать этот результат в качестве входных данных для функции \(f\), так что \(g(3)\) заменяется на 2, и мы получаем \(f(2)\). Затем, используя таблицу, определяющую функцию \(f\), находим, что \(f(2)=8\).

\[g(3)=2 \не число\]

\[f(g(3))=f(2)=8 \nonumber\]

Чтобы вычислить \(g(f(3))\), мы сначала вычислим внутреннее выражение \(f(3) \), используя первую таблицу: \(f(3)=3\). Затем, используя таблицу для \(g\), мы можем оценить

\[g(f(3))=g(3)=2 \nonumber\]

Таблица \(\PageIndex{2}\) показывает составные функции \(f{\circ}g\) и \(g{\circ}f\) в виде таблиц.

Таблица \(\PageIndex{2}\)

\(х\)	\(г(х)\)	\(ф(г(х))\)	\(ф(х)\)	\(г(е(х))\)
3	2	8	3	2

Упражнение \(\PageIndex{3}\)

Используя таблицу \(\PageIndex{1}\), оцените \(f(g(1))\) и \(g(f(4)) \).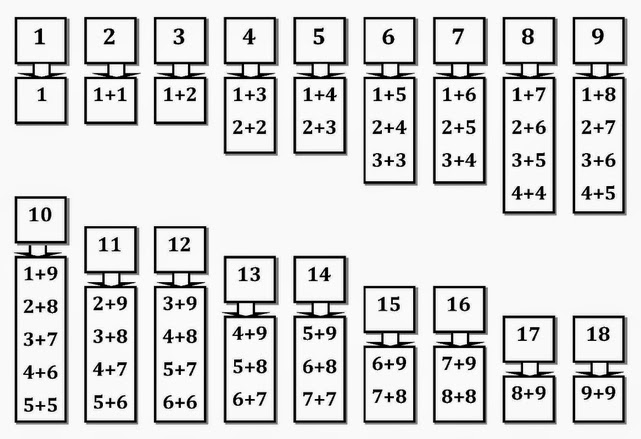

Ответить

\(f(g(1))=f(3)=3\) и \(g(f(4))=g(1)=3\)

Вычисление составных функций с помощью графиков

Когда отдельные функции представлены в виде графиков, процедура вычисления составных функций аналогична процессу, который мы используем для вычисления таблиц. Мы считываем входные и выходные значения, но на этот раз из осей x и y графиков.

Как …

Дана составная функция и графики ее отдельных функций, оцените ее, используя информацию, представленную на графиках.

1. Найдите заданный вход во внутреннюю функцию на оси x ее графика.
2. Считать вывод внутренней функции с оси Y ее графика.
3. Найдите выход внутренней функции на оси X графика внешней функции.
4. Считайте выходные данные внешней функции по оси Y ее графика. Это результат составной функции.

Пример \(\PageIndex{6}\): использование графика для вычисления составной функции

Используя рисунок \(\PageIndex{3}\), оцените \(f(g(1))\).

Рисунок \(\PageIndex{3}\): Два графика положительной и отрицательной параболы.

Решение

Чтобы оценить \(f(g(1))\), мы начнем с внутренней оценки. См. рисунок \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Два графика положительной параболы \(g(x)\) и отрицательной параболы \(f(x)\). Наносятся следующие точки: \(g(1)=3\) и \(f(3)=6\).

Мы оцениваем \(g(1)\), используя график \(g(x)\), находя вход 1 на оси x и находя выходное значение графика на этом входе. Здесь \(g(1)=3\). Мы используем это значение в качестве входных данных для функции \(f\).

\[f(g(1))=f(3) \nonumber\]

Затем мы можем оценить составную функцию, взглянув на график \(f(x)\), найдя вход 3 на по оси x и чтение выходного значения графика на этом входе. Здесь \(f(3)=6\), поэтому \(f(g(1))=6\).

Анализ

На рисунке \(\PageIndex{5}\) показано, как мы можем отметить графики стрелками, чтобы проследить путь от входного значения до выходного значения.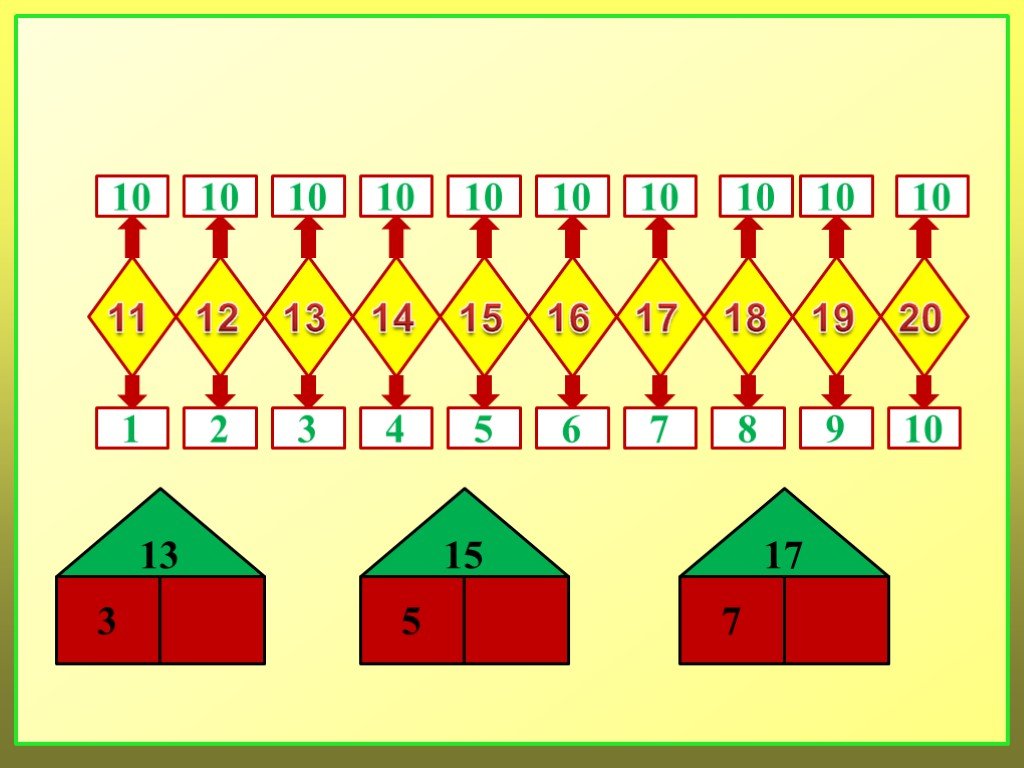

Рисунок \(\PageIndex{5}\): Два графика положительной и отрицательной параболы.

Упражнение \(\PageIndex{4}\)

Используя рисунок \(\PageIndex{3}\), оцените \(g(f(2))\).

Ответить

\(г(е(2))=г(5)=3\)

Вычисление составных функций с использованием формул

При вычислении составных функций, для которых мы либо создали, либо получили формулы, правило работы изнутри наружу остается тем же. Входное значение для внешней функции будет выходом внутренней функции, которое может быть числовым значением, именем переменной или более сложным выражением. 92−t\), мы подставляем значение в скобках в формулу везде, где мы видим входную переменную.

Как…

Дана формула сложной функции, вычислить функцию.

1. Оцените внутреннюю функцию, используя предоставленное входное значение или переменную.
2. Использовать полученный результат в качестве входных данных для внешней функции.

Пример \(\PageIndex{7}\): оценка композиции функций, выраженных в виде формул, с числовым вводом 92−t\) и \(h(x)=3x+2\), вычислить

a. \(h(f(2))\)
б. \(h(f(−2))\)

Ответить на

8

Ответ б

20

Нахождение области определения составной функции

Как мы обсуждали ранее, область определения составной функции , такой как \(f{\circ}g\), зависит от области определения \(g\) и области определения выключенный\). Важно знать, когда мы можем применять составную функцию, а когда нет, то есть знать область определения такой функции, как \(f{\circ}g\). Предположим, что мы знаем области определения функций \(f\) и \(g\) по отдельности. Если мы запишем составную функцию для входа \(x\) как \(f(g(x))\), мы сразу увидим, что \(x\) должен быть членом области определения g, чтобы выражение должно быть осмысленным, потому что иначе мы не сможем завершить вычисление внутренней функции. Однако мы также видим, что \(g(x)\) должен быть членом области определения \(f\), иначе второе вычисление функции в \(f(g(x))\) не может быть завершено, и выражение по-прежнему не определено. Таким образом, домен \(f{\circ}g\) состоит только из тех входов в домен \(g\), которые производят выходы из \(g\), принадлежащие домену \(f\). Обратите внимание, что домен \(f\), составленный из \(g\), представляет собой множество всех \(x\), таких что \(x\) находится в домене \(g\) и g(x)\ ) находится в области определения \(f\).

Определение: область определения составной функции

Область составной функции \(f(g(x))\) – это набор входных данных \(x\) в области определения \(g\) для которого \(g(x)\) находится в области определения \(f\).

Как…

Для данной композиции функции \(f(g(x))\) определите ее область определения.

1. Найдите домен \(g\).
2. Найдите домен \(f\).
3. Найдите те входные данные \(x\) в домене \(g\), для которых \(g(x)\) находится в домене \(f\). То есть исключите те входы \(x\) из домена \(g\), для которых \(g(x)\) не находится в домене \(f\). Полученный набор является доменом \ (f {\ circ} g \).

Пример \(\PageIndex{8A}\): поиск домена составной функции

поиск домена

\[(f∘g)(x) \text{ где } f(x)=\ dfrac{5}{x−1} \text{ и } g(x)=\dfrac{4}{3x−2} \nonumber\]

Решение

Область определения \(g(x)\ ) состоит из всех действительных чисел, кроме \(x=\frac{2}{3}\), так как это входное значение заставит нас делить на 0. Точно так же область определения \(f\) состоит из всех действительных чисел, кроме 1. Итак, нам нужно исключить из области определения \(g(x)\) то значение \(x\), для которого \(g(x)=1\).

\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]

Таким образом, областью определения \(f{\circ}g\) является множество всех действительных чисел, кроме \(\frac{2}{3}\) и \(2\) . Это означает, что

\[x{\neq} \dfrac{2}{3} \text{ или } x\neq2 \nonumber\]

Мы можем записать это в интервальной записи как

\[\left(− \infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]

Пример \(\PageIndex{8B}\): нахождение области определения составной функции, включающей радикалы

Найдите область определения

\[(f{\circ}g)(x) \text{ где } f(x )=\sqrt{x+2} \text{ и } g(x)=\sqrt{3−x} \nonumber\]

Решение

Поскольку мы не можем извлечь квадратный корень из отрицательного числа, область определения \(g\) равна \(\left(−\infty,3\right]\). Теперь проверим область определения составной функции

\[(f{\circ}g)(x)=\ sqrt {\ sqrt {3−x} + 2} \ не число \]

Для \((f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,\), поскольку подкоренное число квадратного корня должно будь позитивным. Поскольку квадратные корни положительны, \(\sqrt{3−x}≥0\) или \(3−x≥0,\), что дает область определения \((-∞,3]\).

Анализ

Этот пример показывает, что знание диапазона функций (в частности, внутренней функции) также может быть полезным при нахождении области определения сложной функции. ) могут содержать значения, не входящие в домен \(f\), хотя они должны быть в домене \(g\).

Упражнение \(\PageIndex{6}\)

Найдите домен

\[(f{\circ}g)(x) \text{где } f(x)=\dfrac{1}{x −2} \text{ и } g(x)=\sqrt{x+4} \nonumber\]

Ответ

\([−4,0)∪(0,∞)\)

Разложение составной функции на составные функции

В некоторых случаях необходимо разложить сложную функцию. Другими словами, мы можем записать его как композицию двух более простых функций. Может быть более одного способа 92}\)

\(ч(х)=\dfrac{4}{3−x}\)

\(f=h{\circ}g\)

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с составными функциями.

• Составные функции (http://openstaxcollege.org/l/compfunction)
• Приложение для записи составных функций (http://openstaxcollege.org/l/compfuncnot)
• Составные функции с использованием графиков (http://openstaxcollege.org/l/compfuncgraph)
• Функции декомпозиции (http://openstaxcollege.org/l/decompfunction)
• Значения составных функций (http://openstaxcollege.org/l/compfuncvalue)

Ключевое уравнение

• Составная функция \((f{\circ}g)(x)=f(g(x))\)

Ключевые понятия

• Мы можем выполнять алгебраические операции над функциями. См. Пример.
• При объединении функций выход первой (внутренней) функции становится входом второй (внешней) функции.
• Функция, полученная путем объединения двух функций, является составной функцией. См. пример и пример.
• При интерпретации значения составных функций необходимо учитывать порядок композиции функций. См. Пример.
• Составную функцию можно вычислить, вычислив внутреннюю функцию, используя заданное входное значение, а затем вычислив внешнюю функцию, взяв в качестве входных данных выходные данные внутренней функции.
• Составную функцию можно вычислить из таблицы. См. Пример.
• Составную функцию можно вычислить по графику. См. Пример.
• Составную функцию можно вычислить по формуле. См. Пример.
• Область определения составной функции состоит из тех входных данных в области определения внутренней функции, которые соответствуют выходам внутренней функции, находящимся в области определения внешней функции. См. пример и пример.
• Точно так же, как функции могут быть объединены в составную функцию, составные функции могут быть разложены на более простые функции.
• Функции часто можно разложить более чем одним способом. См. Пример.

Глоссарий

составная функция

новая функция, образованная композицией функций, когда выход одной функции используется как вход другой

---

Эта страница под заголовком 3.4: Состав функций распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

   Включено

   да

2. Теги

   1. составная функция
   2. источник@https://openstax. org/details/books/precalculus
   3. источник[1]-math-15056

Композиция функций — определение, предметная область, составная функция

Композиция функций — это процесс объединения двух или более функций в одну функцию. Функция представляет некоторую работу. Возьмем приготовление хлеба. Пусть x — мука, кухонный комбайн выполняет функцию приготовления теста с использованием муки (и пусть эта функция равна g(x)) и пусть печь выполняет функцию приготовления хлеба (и пусть эта функция равна f (Икс)). Для приготовления хлеба выход g(x) нужно поместить в функцию f(x) (т. е. приготовленное тесто нужно поставить в печь). Результат обозначается f(g(x)) и представляет собой композицию функций f(x) и g(x).

Давайте посмотрим, что такое композиция функций в математике вместе с ее вычислением. Давайте также посмотрим, как найти его домен и диапазон.

1.	Что такое композиция функций?
2.	Символ композиции функций
3.	Как решать составные функции?
4.	Нахождение составной функции на графике
5.	Поиск составной функции из таблицы
6.	Область составных функций
7.	Диапазон составных функций
8.	Часто задаваемые вопросы о составе функций

Что такое композиция функций?

Состав функций f(x) и g(x), где g(x) действует первым, представляется как f(g(x)) или (f ∘ g)(x). Он объединяет две или более функций, чтобы получить другую функцию. В составе функций выход одной функции, находящейся внутри скобок, становится входом внешней функции. т. е.

• В f(g(x)), g(x) является входом f(x).
• В g(f(x)), f(x) является входом g(x).

Мы можем понять это, используя следующую цифру:

т. е. чтобы найти f(g(x)) (что читается как «f от g от x»), мы должны сначала найти g(x), а затем подставить результат в f(x).

Символ композиции функций

Символ композиции функций ∘. Его также можно показать без использования этого символа, но с помощью скобок. т. е.

• (f ∘ g)(x) = f(g(x)) и читается как «f of g of x». Здесь g — внутренняя функция, а f — внешняя функция.
• (g ∘ f)(x) = g(f(x)) и читается как «g of f of x». Здесь f — внутренняя функция, а g — внешняя функция.

Как решать составные функции?

Используя BODMAS, мы всегда сначала упрощаем то, что находится в скобках. Таким образом, чтобы найти f (g (x)), сначала необходимо вычислить g (x) и подставить его в f (x). Точно так же, чтобы найти g (f (x)), сначала нужно вычислить f (x) и подставить его в g (x). т. е. при нахождении составных функций порядок имеет значение. Это означает, что f(g(x)) НЕ может быть равно g(f(x)). Для любых двух функций f(x) и g(x) составную функцию f(g(a)) находим, используя следующие шаги:

1. Найдите g(a), подставив x = a в g(x).
2. Найдите f(g(a)) подставив x = g(a) в f(x).

Мы можем понять эти шаги, используя пример ниже. Здесь мы находим f(g(-1)) при f(x) = x ² – 2x и g(x) = x – 5.

Мы можем обобщить этот процесс с помощью простых математических вычислений, как показано ниже. :

f(g(-1)) = f(-1-5)
= f(-6)
= (-6) ² – 2 (-6)
= 36 + 12
= 48

Поиск составной функции по графику

Чтобы найти составную функцию двух функций (которые не определены алгебраически), показанную графически, мы должны вспомнить, что если (x, y) — точка на функции f(x), то f(x) = y. Используя это, найти f(g(a)) (т.е. f(g(x)) при x = a):

• Сначала найти g(a) (т.е. координату y на графике g (x), что соответствует x = a)
• Найти f(g(a)) (т. е. координату y на графике f(x), которая соответствует g(a))

Пример: Найдите f(g(5)) по следующему графику.

Решение:

f(g(5)) = f(3) (Поскольку g(5) = 3, поскольку (5, 3) находится на g(x))
= 2 (Поскольку f(3) = 2, так как (3, 2) принадлежит f(x))

Следовательно, f(g(5)) = 2.

Поиск составной функции из таблицы

Мы уже видели, как найти составную функцию, когда задан график функций. Иногда точки на графике функций изображают таблицами. Таким образом, мы применяем ту же процедуру, что описана в предыдущем разделе.

Пример: Найдите g(f(-3)) с помощью следующих таблиц.

х	ф(х)
-1	-4
-2	-3
-3	-2
-4	-1

 

x	г(х)
-4	1
-3	0
-2	-1
-1	-2

Решение:

Из таблицы f(x), f(-3) = -2.

Итак, g(f(-3))= g(-2).

Из таблицы g(x), g(-2) = -1.

Таким образом, g(f(-3)) = -1.

Область составных функций

В общем случае, если g : X → Y и f : Y → Z, то f ∘ g : X → Z, т. е. областью определения f ∘ g является X, а область значений — Z. Но когда функции определены алгебраически, вот шаги, чтобы найти область определения составной функции f (g (x)).

• Найти область определения внутренней функции g(x) (пусть это будет A)
• Найдите область определения функции, полученной путем нахождения f(g(x)) (пусть это будет B)
• Найдите пересечение A и B и A ∩ B дает область определения f(g(x))

Пример: Найдите область определения f(g(x)) при f(x) = 1/(x+2) и g(x) = 1/(x+3).

Решение:

В f(g(x)) внутренней функцией является g(x), а ее областью определения является A = {x | х ≠ -3}.

Теперь вычислим f(g(x)).

\(\begin{выровнено}
f(g(x)) &=f\left(\frac{1}{x+3}\right) \\
&=\frac{1}{\frac{1}{x+3}+2} \\
&=\frac{1}{\frac{1+2 x+6}{x+3}} \\
&=\фракция{х+3}{2х+7}
\end{aligned}\)

Его домен B = {x : x ≠ -7/2}

Таким образом, домен f(g(x)) равен A ∩ B = {x : x ≠ – 3 и х ≠ -7/2}.

В интервальной записи это (-∞, -7/2) U (-7/2, -3) U (-3, ∞).

Диапазон составных функций

Диапазон составной функции вычисляется так же, как диапазон любой другой функции. Это не зависит от внутренних или внешних функций. Вычислим диапазон f(g(x)), показанный в последнем примере. Мы получили f(g(x)) = \(\frac{x+3}{2 x+7}\). Предположим, что y = \(\frac{x+3}{2 x+7}\). Это рациональная функция. Следовательно, мы решаем это для x и устанавливаем знаменатель не равным нулю, чтобы найти диапазон.

(2x + 7) y = x + 3

2xy + 7y = x + 3

2xy – x = 3 – 7y

x (2y – 1) = 3 – 7y

x = (3 – 7y ) / (2y – 1)

Для диапазона 2y – 1 ≠ 0, что дает y ≠ 1/2.

Следовательно, диапазон = {y : y ≠ 1/2}.

☛ Связанные темы:

• Производные сложных функций
• Алгебра функций
• Алгебраическая функция

Часто задаваемые вопросы о составе функций

Что такое определение составной функции?

Составная функция из двух функций объединяет данные две функции в заданном порядке. т. е. для любых заданных двух функций f(x) и g(x) может быть 4 составные функции:

• f(g(x)) которая заменяет g(x) в f(x)
• g(f(x)) который заменяет f(x) на g(x)
• f(f(x)), которая заменяет f(x) на себя
• g(g(x)), которая заменяет g(x) на себя

Как найти состав функций?

Чтобы вычислить составную функцию f(g(x)) при некотором x = a, сначала вычислите g(a), подставив x = a в функцию g(x). Затем подставьте g(a) в функцию f(x), подставив x = g(a). Точно так же мы можем вычислить и g(f(a)).

Важен ли порядок в составных функциях?

Да, в составных функциях порядок действительно важен. т. е. f (g (x)) ≠ g (f (x)) (т. е. они могут не быть равными все время). Но иногда они могут быть равны.

Как найти область определения составной функции?

Чтобы найти область определения составной функции, найдите область определения внутренней функции и область определения результирующей функции. Возьмите пересечение обоих доменов.