Как решать задачи в 2 действия 2 класс: Решение задач в два действия. Математика, 2 класс: уроки, тесты, задания.
Дистанционный урок по математике “Решение задач. Задачи в два действия” 2 класс
Маршрутный лист для учащегося 2 «В» класса
Предмет | Математика (интегрированный урок) |
Ф.И.О. учителя | Стрельцова Ирина Александровна |
№ урока, тема | 1. «Решение задач. Казахские народные ремесла» 2. «Задачи в два действия. Юрта – традиционное жилище казахов.» |
Цели обучения | 1. Моделировать и решать задачи в 2 действия (разные комбинации простых задач на увеличение / уменьшение в несколько раз; кратное сравнение). 2. Составлять,
знать и применять таблицу умножения и деления на 2; 3; 4; 5. |
Ф.И. учащегося |
|
1. Открой тетрадь, запиши число: 6 апреля
2. Пропиши минутку чистописания: 37, 82 до конца строки
Повторяем |
Будь внимателен, считай в уме. В тетрадь, через запятую запиши только ответ. 4 × 4 20 : 5 3 × 3 28 : 7 9 × 4 24 : 4 5 × 3 18 : 6 |
Изучаем |
Сегодня, твоя цель: научиться анализировать и решать задачи в 2 действия. Первые
задачи мы разберем вместе.
№1 Прочитай задачи, рассуждая над тем, что тебе необходимо найти. Подумай как бы ты записал краткую запись. Выполни решение задач в тетради. А) Мастер – ювелир изготовил 4 браслета, а колец – в 2 раза больше. Сколько всего изделий изготовил ювелир? Б) Один ювелир изготовил 24 украшения, что в 4 раза больше, чем другой. Сколько украшений изготовили оба мастера? В) Мастер изготовил 18 колец. Он уложил по 4 кольца в 3 шкатулки. Сколько колец осталось? |
Отвечаем / объясняем |
Задание № 2 Составляем задачу устно. Рассуждаем вместе.
а) Масса одной юрты – примерно 3 центнера. Сколько весит 4 юрты? Давай начнем рассуждать! – Сколько весит одна юрта? – Что нам необходимо узнать? – Как ты вычислишь? Какое действие выполнишь? Проверь:
3 * 4 = 12 (ц. – Что надо сделать, чтобы составить обратную задачу? Правильно, то что было известным – станет неизвестным. Например: масса одной юрты – ?, а 4 юрты весят примерно 12 центнеров или масса одной юрты – 3 центнера, сколько юрт будут весить 12 центнеров? Решение: 12 : 4 = 3 (ц) и 12 : 3 = 4 (ю)
|
Выполни / Решаем самостоятельно |
| А теперь попробуй выполнить самостоятельно подобное задание. Письменно. № 2 б) На одного верблюда можно погрузить 3 центнера груза. Сколько верблюдов потребуется, чтобы перевезти 15 центнеров груза?
в) Грузоподъёмность одного верблюда – 3 центнера. Сколько груза могут перевезти 6 верблюдов?
|
Рефлексия |
–
Сегодня я повторил (повторила)…. – Сегодня я научился (научилась)…… – Теперь я знаю …… – Теперь я умею ….. – Мне надо повторить….! |
Оцени свою работу |
Нарисуй себе на полях тетради смайлик, который ты выбираешь!
|
А теперь давай проверим! Все ли задания ты
выполнил (а)?
У тебя в тетради должно быть записано:
– число
– минутка чистописания
– ответы на устный счет
– задачи № 1 (а,б,в)
– задачи № 2 (б, в)
Если всё сделано! Ты большой (большая) МОЛОДЕЦ!!!
Теперь попроси маму: ровно и четко сфотографировать и прикрепи фото своей работы в кунделик!
Помни! Каждую страницу фотографируем отдельно!
Урок по математике 2 класс Путешествие в Алматы – Балабақша әлемі
Школа: О. С.Ш. №5 им.М.Ауэзова
С.Ш. №5 им.М.Ауэзова
Дата: «____»____________20___г. ФИО учителя: Абдрахманова Р,А.
Класс: 2 «____» класс. Количество присутствующих:
отсутствующих:
Лексическая тема: Путешествие в Алматы
Тема урока: Составные задачи.
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
2.5.1.4. Анализировать и решать задачи на увеличение/ уменьшение числа в несколько раз; кратное сравнение, составлять и решать обратные задачи.
2.5.1.5**. Различать задачи с прямыми и косвенными вопросами (связанные с отношениями «больше/меньше на», «больше/меньше в раз»).
2.5.1.8. Моделировать решение простых задач на все действия в виде числового выражения; составных – в виде числового выражения и отдельных действий.
Критерии успеха (Предполагаемый результат): Все учащиеся будут:
решать задачи в 2 действия.
Многие учащиеся будут:
моделировать и решать задачи в 2 действия.
Некоторые учащиеся будут:
составлять и решать задачи в 2 действия.
Языковая
цель Учащиеся могут:
пояснять, почему конкретная задача решается в одно или два действия.
Предметная лексика и терминология:
Задача, условие, вопрос, анализ, план решения, ответ, выражение.
Серия полезных фраз для диалога/письма
Обсуждение:
Можно ли сразу ответить на вопрос задачи? Обоснуйте.
Что можно узнать, выполнив действие…?
Объясните последовательность выполнения действий (что узнали
сначала, что потом…).
Письмо:
Запись условия, решения, ответа, выражения по задаче.
Привитие
ценностей Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.
Навыки
использования ИКТ ИКТ – просмотр видеоролика, презентация урока.
Предварительные
знания Умение анализировать и решать задачи.
Ход урока
Этапы урока, t Запланированная деятельность на уроке
Ресурсы
Начало урока
0-3 Мотивация.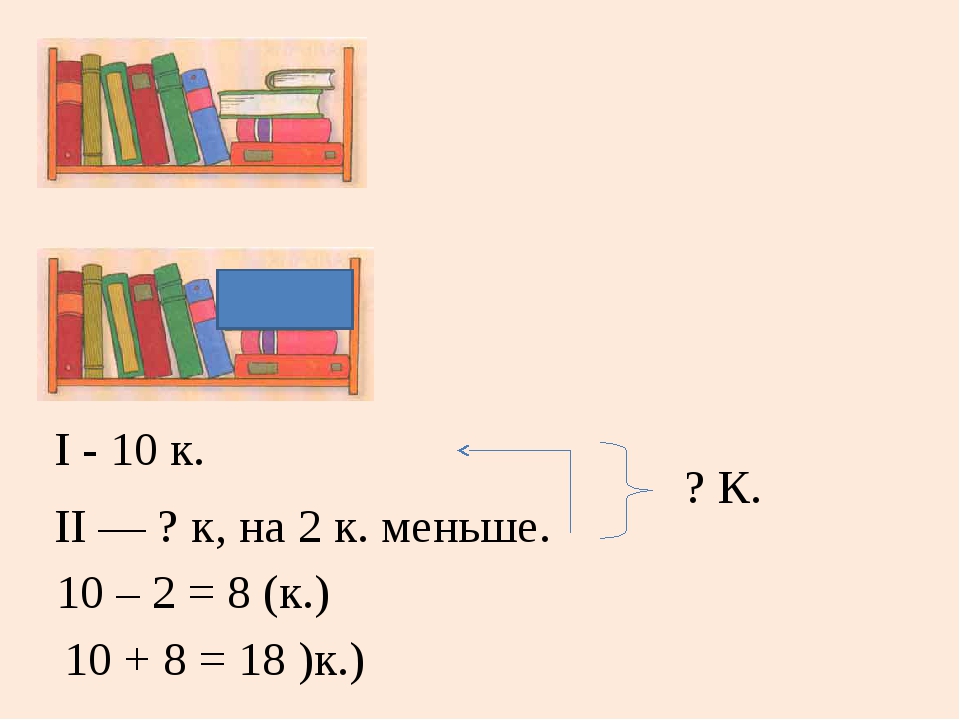
На этом уроке мы продолжим наше математическое
путешествие. Сегодня мы отправимся в крупнейший город
нашей страны – Алматы, будем выполнять новые задания,
узнаем некоторые достопримечательности этого города.
4-6 Актуализация.
Устный счет. Напиши только ответы.
1) — Уменьшите 27 в 3 раза.
— Первый множитель 5, второй — 4. Запиши произведение этих чисел.
— Запиши число, в котором 7 десятков.
— Запиши число, в котором 9 единиц.
— Запиши число, в котором 9 десятков и 4 единицы.
— Запиши число, в котором 5 десятков и 6 единиц.
2) Посмотри на числа: 45, 27, 18, 54, 9, 10, 90, 36, 50, 70:
— На какие две группы можно разделить данные числа?
Попробуйте найти разные варианты. (Дети замечают, что можно разделить на однозначные и двузначные или числа, в записи которых есть пятерка, или числа, в записи которых пятерки нет, или числа, сумма цифр которых равна 9 и не равна 9, или круглые числа и некруглые числа и т. д.) 3).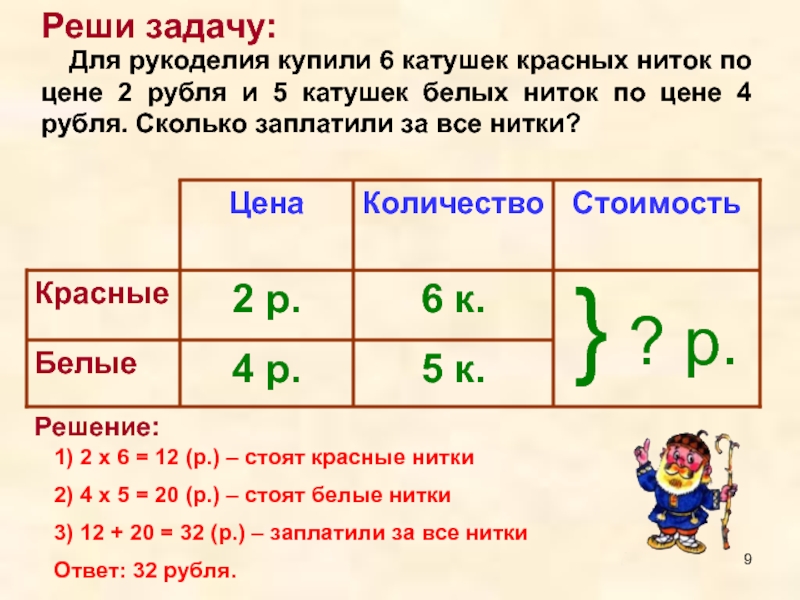 Реши задачу.
Реши задачу.
На остановке из автобуса вышли 4 пассажира, а вошло в автобус в 2 раза больше людей, чем вышло. Сколько пассажиров вошли в автобус на остановке?
Измени условие так, чтобы задача решалась сложением, реши новую задачу. Учебник.
Середина урока
7-11 Постановка цели.
Учитель предлагает прочитать задачу и рассмотреть
выражения.
– Какова цель нашего урока? Учебник.
Критерии успеха Учащиеся формулируют цель урока.
12-29 №1 стр.30
Предлагает выполнить задание №1 в учебнике.
Учитель предлагает детям выполнить вычисления и узнать
название горнолыжного курорта в Алматы .
15 – 3 5 + 7 2 = 14 7 4 + 20 : 2 – 6 5 = 8
24 : 4 5 + 50 = 80 47 + (12 + 6) : 3 = 53
4 9 – 3 2 1 = 30 45 : 9 5 + 18 : 2 = 34
27 : (12 : 4) + 32 : 4 = 17 24 : (2 + 6) – 14 : 7 = 1
14 80 8 53 17 30 34 1
М К Ы А Б У Л Ш
№2 стр.31
Прочитай условие задачи. Что ты узнаешь, выполнив вычисления? Поставь вопрос и реши задачу.
В одну кабинку на канатной дороге помещается 8 человек. На экскурсию приехали 24 ребёнка, а взрослых – в 3 раза меньше. Вопрос: сколько потребуется кабинок, чтобы все посетили экскурсию?
24 : 3 = 8 взрослых поехали на экскурсию
24 +( 24 : 3) = 32 человека всего
(24 + 24 : 3) : 8 = 4 кабинки надо чтобы перевезти всех
Детей – 14ч.
Взрослых – ?, в 3 раза меньше
Разместились- по 8 ч в ? к.
1)
2)
3)
Ответ: _______________________
Физминутка
Мы считали и устали,
Дружно все мы тихо встали,
Ручками похлопали,
Раз, два, три. (Хлопки в ладоши под счет учителя.)
Ножками потопали,
Раз, два, три. (Шаги ногами на месте.)
Сели, встали, встали, сели,
И друг друга не задели. (Приседания.)
Мы немножко отдохнем и опять считать начнем. (Повороты туловища. Ходьба на месте.)
№3 стр.31
Составь выражения к задачам.
а) На каток приехали 9 детей, что в 3 раза больше, чем взрослых. Сколько взрослых приехало на каток?
9 : 3
б) На каток приехали 9 детей, а взрослых – в 3 раза больше. Сколько всего человек приехало на каток?
Сколько всего человек приехало на каток?
9 3
в) В автобусе разместились 24 ребёнка, учителей – в 3 раза мень¬ше, а родителей – в 2 раза меньше, чем учителей. Сколько родителей разместилось в автобусе?
24 : 3 : 2
Учитель предлагает в парах обсудить план решения задачи
и записать его в тетрадях с комментированием.
Самостоятельная работа
Предлагает выполнить задачи в тетради с критериями оценивания.
Критерии оценивания:
Я составляю задачу по условию и схеме.
Определяю способ решения задачи.
Составляю и записываю выражение.
Нахожу значение выражения.
Записываю ответ.
Коррекция затруднений
Проверяем. У кого возникли затруднения?
– В каком месте вы допустили ошибку?
– В чем причина допущенной ошибки?
Коррекция выявленных затруднений.
– Те, у кого не возникло затруднений в самостоятельной
работе, сформулируйте цель вашей деятельности.
(Выполнить дополнительные задания).
– Какова дальнейшая цель работы у тех, кто выявил
затруднения?
(Исправить решение, используя эталон для самопроверки).
– Используем алгоритм исправления ошибок.
– Каждый проговаривает свою учебную задачу. Тетрадь,
учебник.
30-40 Физминутка для глаз
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами
Ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!
Работа над ранее изученным
Задания на отработку вычислительных навыков учитель
предлагает дифференцировано. Дети выполняют само или
взаимопроверку.
Тетрадь, учебник.
№5 – по рядам (по вариантам)
1 ряд 2 ряд 3 ряд
х + 7 ∙ 4 = 40
6 ∙ 3 + х = 72 80 – х = 9 ∙ 5
12 + х = 5 ∙ 8 х – 32 : 4 = 50
х + 2 ∙ 6 = 94
х + 7 • 4 = 40
х + 28 = 40
х = 40 – 28
х = 12
6 • 3 + х = 72
18 + х = 72
х = 72 – 18
х = 54 80 – х = 9 • 5
80 – х = 45
х = 80 – 45
х = 35
12 + х = 5 • 8
12 + х = 40
х = 40 – 12
х = 28 х – 32 : 4 = 50
х – 8 = 50
х = 50 + 8
х = 58
х + 2 • 6 = 94
х + 12 = 94
х = 94 – 12
х = 82
№3 в тетради
2 5 1 3 6 4
24 : 6 + (19 + 6) : 5 + 6 • 2 = 21
1 2 4 3
(27 – 19) • 4 + 18 : 3 = 38
1 2 3
(18 + 27) : 5 – 7 = 2
2 4 1 3
8 • 5 – (60 – 42 ) : 3 = 34
3 6 1 4 7 2 5
5 • 7 + (18 +14) : 4 – (26 – 8) : 3 = 37
1 2 4 5 3
(58 – 31) : 3 – 2 + 12 : 6 = 9
41-40 Рефлексия.
я выполнял задания…
я понял… что… теперь я могу…
я почувствовал, что… я приобрел умение …
Карточки с
незаконченными
фразами..
Критерии успеха – все решают задачи в 2 действия;
– многие моделировать и решать задачи в 2 действия;
-некоторые составлять и решать задачи в 2 действия
Дифференциация Оценивание Здоровье и соблюдение ТБ
Способные учащиеся строят свои высказывания самостоятельно, а менее способным учитель оказывает поддержку, задавая наводящие вопросы.
Учитель раздает ученикам карточки с незаконченными
фразами.
Ученики записывают продолжение:
я выполнял задания…
я понял… что… теперь я могу…
я почувствовал, что… я приобрел умение … Физминутка
Мы считали и устали, Дружно все мы тихо встали, Ручками похлопали, Раз, два, три. (Хлопки в ладоши под счет учителя.) Ножками потопали, Раз, два, три. (Шаги ногами на месте.) Сели, встали, встали, сели, И друг друга не задели. (Приседания.) Мы немножко отдохнем и опять считать начнем. (Повороты туловища. Ходьба на месте.) Физминутка для глаз
(Шаги ногами на месте.) Сели, встали, встали, сели, И друг друга не задели. (Приседания.) Мы немножко отдохнем и опять считать начнем. (Повороты туловища. Ходьба на месте.) Физминутка для глаз
Рисуй глазами треугольник
Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами
Ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!
конспект урока по математике (4 класс)
Учитель начальных классов, МОУ С(к) ОШ №5 VIII вида, г. Кыштым
Ссылка на статью, при указании в списке литературы (по ГОСТ Р 7.0.5–2008):
Нейфельд Т.В. Решение простых и составных задач на увеличение и уменьшение числа в несколько раз. Закрепление: конспект урока по математике (4 класс) // Совушка. 2019. N2 (16). URL: https://kssovushka.ru/zhurnal/16/ (дата обращения: 30.04.2021).
Закрепление: конспект урока по математике (4 класс) // Совушка. 2019. N2 (16). URL: https://kssovushka.ru/zhurnal/16/ (дата обращения: 30.04.2021).
Заказ № 376893
Тема: Решение простых и составных задач на увеличение и уменьшение числа в несколько раз. Закрепление.
Цель: формирование умения решать простые и составные задачи на уменьшение и увеличение числа в несколько раз. Закрепление знаний о единицах длины.
Задачи:
Предметные: способствовать формированию умений решать задачи на увеличение и уменьшение числа в несколько раз, выбирать и обосновывать выбор действия для решения задач содержащих отношения « больше в…», «меньше в…», выполнять краткую запись к задаче, решать простые и составные задачи в 2 действия.
Закрепить знания о единицах длины.
Метапредметные: развивать умение анализировать, сравнивать через решение задач и проблемных ситуаций, активный словарный запас учащихся, коммуникативные учебные действия через формирование умения работать в паре.
Личностные: формировать целеустремлённость при решении учебной задачи; представление о значении математики в жизни человека; взаимное уважение друг к другу, умение адекватно оценить себя и товарищей.
Технологии: проблемное обучение, ИКТ, игровая
Методы: словесные, наглядные, практические.
Формы: фронтальная, индивидуальная, парная.
Ход урока
I. Организационный момент
Улыбнитесь друг другу, у вас прекрасное настроение.
Садитесь.
Руки? На месте!
Ноги? На месте!
Локти? У края!
Спинка? Прямая
– Не забывайте, пожалуйста о том, что правильная осанка, залог хорошего здоровья
– Готовы ли вы к уроку?
– Сегодня вам ещё понадобятся: внимание, память, математическая смекалка.
– Слушаем внимательно, работаем старательно!
Ручейки бегут быстрее,
Солнце светит всё сильнее.
Воробей погоде рад –
Он встречает месяц …
(март)
– О каком месяце говорится в этой загадке? (март)
– А какое это время года? (весна)
– Теперь откройте тетради, запишите дату.
– Сегодня 19 марта.
II. УСТНЫЙ СЧЕТ. «Мозговой штурм.»
1) «Найди лишний»
– Уберите лишнюю единицу измерения: км, м, мин., см, дм, мм.
– Запишите единицы длины в порядке возрастания
– Назовите самую маленькую и самую большую единицу длины
– Какие единицы длины используют для измерения небольших отрезков?
– Увеличьте 1 см в 10 раз. Каким действием нашли? Сколько получилось? Значит, чтобы увеличить число в несколько раз, что мы делаем (умножаем)
– Уменьшите 100 см в 10 раз. Каким действием нашли? Сколько получилось? Значит, чтобы уменьшить число в несколько раз, что мы делаем (делим)
(Задачи фронтально, 1 на индивидуальной доске)
– Весной перелетные птицы возвращаются в родные края. Ласточка за 1 минуту пролетает 1 км, а стриж в 2 раза больше. Сколько км пролетает стриж за 1 минуту?
Ласточка за 1 минуту пролетает 1 км, а стриж в 2 раза больше. Сколько км пролетает стриж за 1 минуту?
– Как решили? (Х 2 или увеличили в 2 раза). Значит, чтобы увеличить число в несколько раз, что мы делаем (умножаем)
Во время перелета птицы отдыхают 8 дней, а летят в 4 раза меньше. Сколько дней летят птицы?
– Как решили? (: на 4 или уменьшили в 4 раза). Значит, чтобы уменьшить число в несколько раз, что мы делаем (делим)
– Для чего же необходимо уметь считать, выполнять действия сложения и вычитания, умножения и деления? (Решать задачи)
– Где мы встречаемся с задачами? (в учебнике, в жизни)
– Как вы думаете, что будем делать сегодня на уроке? Определите тему урока? (записываю тему урока)
Определение цели урока.
– Давайте вместе подумаем, что нам нужно повторить и чему учиться на уроке.
Закрепить умение решать задачи на увеличение и уменьшение в несколько раз с использованием действий умножения и деления.
Закрепить умение пользоваться таблицей умножения
Повторить единицы длины
III Работа по теме урока
1) задача
– Прочитайте задачу
Осенью в тёплые края гуси летели 20 дней, а весной в родные края в 2 раза быстрее. Сколько дней гуси летели весной?
Сколько дней гуси летели весной?
– Прочитайте условие задачи.
(Разбор задачи и составление краткой записи)
– Прочитайте вопрос задачи.
– Каким действием решаем задачу?
(Решение задачи) (1 у доски остальные на местах)
Физминутка
Лебеди летят, крыльями машут,
Прогнулись над водой,
Качают головой.
Прямо и гордо умеют держаться
Очень бесшумно на воду садятся.
2) задача
– Составьте задачу по краткой записи
Утка-3кг
Лебедь- ? кг, в 5 раз больше
Утка весит 3кг, а лебедь в 5 раз больше.
– Задайте вопрос так, чтобы задача решалась в 2 действия
(Самостоятельное решение задачи, взаимопроверка)
Проверка на слайде.
Объяснение решения.
– Как вы думаете расстояние, которое преодолевает птица без остановки, зависит от веса птицы? (Более крупные птицы способны преодолевать большие расстояния в отличии от мелких. Так лебедь без остановки преодолевает 400 км, а утка-200 км.)
Так лебедь без остановки преодолевает 400 км, а утка-200 км.)
IV Геометрическое задание
При перелётах птицы преодолевают многие тысячи километров. Путь птиц не похож на прямой путь.
Сегодня мы проследим путь ласточки с места зимовки в родные края, хотя много веков назад предполагали, что ласточки зимуют на дне водоемов, зарывшись в ил, а с наступлением весны выбираются на поверхность.
(Работа в парах)
– Возьмите карты. На карте найдите *1- это бассейн Конго в Африке; найдите *2-это Индия; найдите*3- это Тайланд; найдите*4- это Урал, родной край.
(учащиеся соединяют цифры)
– Посмотрите на чертеж, что мы начертили?
– Из скольких отрезков состоит ломанная?
– Измерьте длину каждого отрезка и вычислите длину ломаной. Как вычислить длину ломанной?
Проверка
Это расстояние ласточки преодолевают за 2-3 мес.
Как высчитывать точное расстояние с помощью линейки и карты вы научитесь в старших классах на уроках географии и математики.
V Итог.
– Давайте подведем итоги урока
– Вспомним что мы должны были повторить и закрепить на уроке.
– Какие задания выполняли?
– Мы сегодня хорошо работали на уроке.
Закрепили умение решать задачи на увеличение и уменьшение в несколько раз с использованием действий умножения и деления.
Закрепили умение пользоваться таблицей умножения
Повторили единицы длины
VI Рефлексия
– У вас на партах скворцы разного цвета. Прикрепите на скворечник:
– Зеленого скворца, если считаете, что урок прошел удачно: я активно участвовал в работе класса, с заданиями справлялся успешно. Я доволен очень собой!
– Желтого скворца, если сегодня на уроке не все задания оказались такими уж легкими. Мне было трудно, но я справился. Я вполне доволен собой
– Красного скворца, если задания на уроке оказались слишком трудными. Мне нужна помощь!
Математика.
 Составные выражения. Скобки | Сайт Леонида Некина
Составные выражения. Скобки | Сайт Леонида НекинаГлавная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Допустим, у Дениса было 5 конфет, мама дала ему еще 3 конфеты, а папа — еще одну конфету. Сколько конфет стало у Дениса? Такая задача решается в два действия.
Первое: 5 + 3 = 8 . Столько конфет стало у Дениса после того, как он получил конфеты от мамы.
Второе: 8 + 1 = 9. Столько конфет стало у Дениса в конечном итоге.
Это же самое решение можно представить в виде одной-единственной строчки. Поскольку « 8 » было получено как « 5 + 3 », то во втором равенстве « 8 » можно заменить на « 5 + 3 »:
До замены: | 8 | + 1 = 9. |
После замены: | ( 5 + 3 ) | + 1 = 9. |
Новую вставку принято заключать в скобки. Таким образом, если в каком-нибудь длинном выражении встречаются скобки, это говорит о том, что в первую очередь следует выполнять действия внутри скобок. В нашем примере порядок выполнения действий таков:
[1] | [2] |
|
( 5 + 3 ) | + | 1 = 8 + 1 = 9. |
На этот раз оказалось, что действия выполняются в самом привычном порядке — слева направо. В этом особом случае скобки можно вообще не писать. Смысл выражения остается тем же самым:
[1] | [2] |
|
5 + 3 | + | 1 = 8 + 1 = 9. |
Однако ту же самую задачу можно решить и по-другому.
Первое действие: 3 + 1 = 4 . Столько конфет получил Денис от мамы и папы.
Второе действие: 5 + 4 = 9. Столько конфет оказалось у Дениса.
В одну строку это записывается так:
| [2] | [1] |
|
5 | + | ( 3 + 1 ) | = 5 + 4 = 9. |
Итак, у нас есть два разных решения одной и той же задачи, и им соответствуют два разных выражения, но значения этих выражений одинаковы, поэтому
5 + (3 + 1) = 5 + 3 + 1.
Это равенство показывает, каким образом можно избавиться от скобок, или, выражаясь более грамотно, как можно раскрыть скобки. В данном примере скобки можно просто стереть, а все остальное оставить без изменений. Но так просто дело обстоит далеко не всегда.
В данном примере скобки можно просто стереть, а все остальное оставить без изменений. Но так просто дело обстоит далеко не всегда.
Задача 2.2.1. У Дениса было 5 конфет. 3 конфеты он дал маме, и еще одну конфету — папе. Сколько конфет осталось у Дениса? Эту задачу требуется решить двумя способами, причем каждое решение записать в виде одного-единственного выражения.
Решение. Первый способ.
5 − 3 = 2 . Столько конфет осталось у Дениса, после того как он поделился конфетами с мамой.
2 − 1 = 1. Столько конфет осталось у Дениса в конце.
Записываем решение в виде одного выражения:
5 − 3 − 1 = 2 − 1 = 1.
Второй способ.
3 + 1 = 4 . Столько конфет Денис отдал маме и папе.
5 − 4 = 1. Столько конфет осталось у Дениса.
Объединяем решение в одно выражение:
5 − ( 3 + 1 ) = 5 − 4 = 1.
Сравнивая два решения, мы убеждаемся, что
5 − (3 + 1) = 5 − 3 − 1.
На этот раз, для того чтобы раскрыть скобки, недостаточно их просто стереть. Требуется еще и поменять знак «+» на знак «−».
Требуется еще и поменять знак «+» на знак «−».
Задача 2.2.2. У Дениса было 7 конфет. Он решил поделиться конфетами с Матвеем. Он протянул Матвею 3 конфеты, однако в последний момент передумал и одну конфету забрал обратно. Сколько конфет стало у Дениса?
Решение. Первый способ.
7 − 3 = 4 . Столько конфет оставалось у Дениса, когда он протянул конфеты Матвею.
4 + 1 = 5. Столько конфет стало у Дениса в конечном итоге.
Единое выражение:
7 − 3 + 1 = 4 + 1 = 5.
Второй способ.
3 − 1 = 2 . Столько конфет досталось Матвею.
7 − 2 = 5. Столько конфет стало у Дениса.
Единое выражение:
7 − ( 3 − 1 ) = 7 − 2 = 3.
Сравнивая два решения, получаем:
7 − (3 − 1) = 7 − 3 + 1.
И на этот раз одного только стирания скобок недостаточно. Нужно еще поменять тот знак «−», который стоял в скобках, на знак «+».
Задача 2.2.3. У Дениса было 5 конфет. Мама подарила ему еще 3 конфеты, из которых одну Денис дал папе. Сколько конфет стало у Дениса?
Сколько конфет стало у Дениса?
Рассуждая, как обычно, получаем:
5 + (3 − 1) = 5 + 3 − 1.
Здесь, как и в самый первый раз, нужно просто стереть скобки. Почему же иногда этого оказывается достаточно, а иногда нет? Выпишем все наши наблюдения еще раз:
5 + (3 + 1) = 5 + 3 + 1;
5 + (3 − 1) = 5 + 3 − 1;
5 − (3 + 1) = 5 − 3 − 1;
5 − (3 − 1) = 5 − 3 + 1.
Ага! Теперь всё ясно. Если перед скобкой стоит «+», то скобки можно просто стереть, и больше ничего делать не требуется. Но если перед скобкой стоит «−», то нужно еще поменять тот знак, который стоял внутри скобки.
Дополнение: выражения, содержащие умножение или деление
Разумеется, в составных выражениях могут встречаться не только сложение и вычитание, но также и умножение и деление. Если, решая какую-нибудь задачу, мы составили выражение из двух действий и в этом выражении в первую очередь надо выполнить умножение или деление, а во вторую очередь — сложение или вычитание, то скобки можно не ставить:
10 + (2 ∙ 3) = 10 + 2 ∙ 3;
10 + (6 / 2) = 10 + 6 / 2;
10 − (2 ∙ 3) = 10 − 2 ∙ 3;
10 − (6 / 2) = 10 − 6 / 2.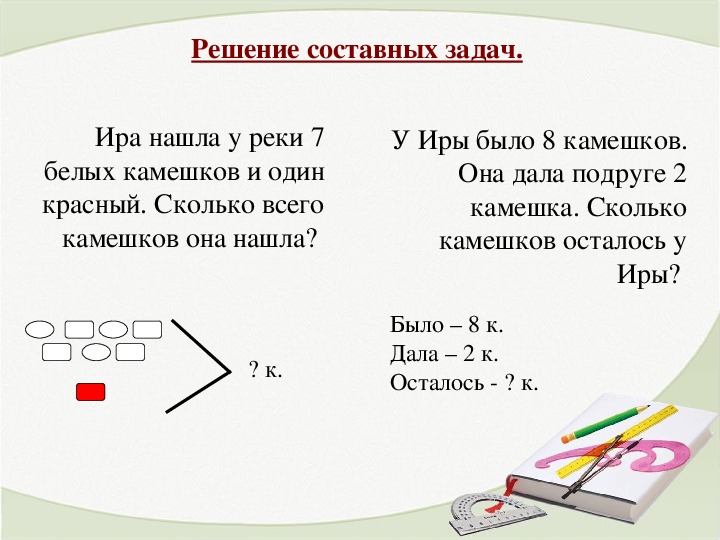
Точно так же: (2 ∙ 3) + 10 = 2 ∙ 3 + 10
и т.п.
Это означает, что в выражениях без скобок вначале нужно выполнять умножение и деление, а затем — сложение и вычитание:
10 + 2 ∙ 3 = 10 + 6 ≠ (10 + 2) ∙ 3 = 12 ∙ 3.
В выражениях, которые содержат только умножение и деление, скобки можно не ставить в таких случаях:
(3 ∙ 4) ∙ 6 = 3 ∙ 4 ∙ 6;
(3 ∙ 4) / 6 = 3 ∙ 4 / 6.
Примеры из «бесконечного» сборника типовых упражнений
Примеры на сложение и вычитание в два действия без скобок
Примеры на сложение и вычитание в два действия со скобками
Примеры в два действия, которые легко можно упростить изменением порядка действий
Примеры в два действия на сложение, вычитание, умножение и деление
2.АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ(УМЕНИЙ) (повторение, самостоятельная работа, самопроверка) 2. 2.2. Обобщение затруднений во внешней речи (учащиеся, не допустившие ошибок в самостоятельной работе, решают задания творческого уровня или выступают в качестве консультантов) Физкультминутка 3.4. самостоятельная работа 2.4. Повторение 4.Рефлексия учебной деятельности | Проверка владения материалом прошлых уроков. -Ребята, давайте попробуем устно решить примеры. УСТНЫЙ СЧЕТ 72-10 88-4 60+32 96-6 82-12 24+60 43-20 Организует работу с текстовыми задачами устно. 1)У Оли было 5 ирисок, 8 карамелей, а шоколадных конфет столько, сколько ирисок и карамелей вместе. Сколько шоколадных конфет у Оли? 2)Буратино сделал в диктанте 8 ошибок, а Незнайка – 14. На сколько ошибок Незнайка сделал больше, чем Буратино? 3)Пьеро сочинил 5 веселых стихов, а грустных – на 20 больше. Сколько грустных сочинил Пьеро? 4)У Карабаса-Барабаса было 6 деревянных кукол и 9 тряпочных. Сбежали из театра 9 кукол. Сколько кукол осталось в театре Карабаса-Барабаса? Создание проблемной ситуации. Предлагает решить устно задачу. Пассажир ехал в село на такси. По пути ему встретились 5 грузовых машин и 3 легковых автомобиля. Сколько машин ехало в село? -Ребята как вы думаете, что мы сегодня будем делать на уроке? – Да ребята совершенно верно, мы будем закреплять наши знания и будем решать задачи. -Откройте тетради, запишите число, классная работа. Предлагает выполнить задания по учебнику на с.64, № 1 Организует работу над содержанием задачи. Прочитайте задачу. Беседа по содержанию задачи – О ком говорится в задаче? -Какое действие они выполняют? Выполнение краткого условия задачи в виде чертежа. -Давайте решим эту задачу, начертив отрезок в тетрадь. Отступите от полей две клетки и поставьте точку. От конца отступите две клетки и поставьте вторую точку, соедините точки. Это у нас будет длина аллеи. -Нам известно длина аллеи? Отметим это дугой на отрезке. -Сколько метров прошел один мальчик? Отметим на этом чертеже 5 клеток это путь, который прошел один мальчик. -Сколько метров прошел второй? Отметим это на чертеже. Поиск решения задачи: Если длина всей аллеи 70 м а первый прошел 22 м. Каким действием узнать сколько прошел второй? Какое решение мы запишем? -Запишите решение в тетрадь Предлагает выполнить задание по учебнику на с64, № 2 (ученик у доски) -Чтение задачи. Беседа о задаче. -О чем говорится в задаче -Что надо найти в задаче? -Подумайте, как выполнить схематический чертеж -Что сказано о длине дорожки? Выполнение чертежа -Что в задаче известно? Отметьте это на чертеже. -Что еще известно? -Как обозначим на схеме? -Что значит «найти длину дорожки»? -Какое выражение мы можем записать? Как решить? Запишите решение. Видеоролик Выявление качества усвоения материала. Предлагает выполнить самостоятельно задание на карточках. Две девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна прошла до встречи 50 м, а другая 35 м. Найдите длину дорожки. 100-8-40 100-4-70 Включение изученного материала в выполнение заданий. Предлагает выполнить задание на стр. 64 № 3 -Что нам надо сделать в этом номере? Предлагает выполнить задание на стр.64 № 6 -Что нам надо сделать? -Как мы можем сделать? Запишите в тетрадь (ученик у доски) Прочитайте второе задание. -Что надо сделать? Сколько будет равна длина каждого звена ломаной? -Начертите ломаную Оценка работы класса. Подведение итогов урока. Самооценка. – Что мы повторяли сегодня на уроке? -Какие задачи решали? -Ребята, поднимите руки, кто бы себе поставил 5, 4, 3. Я вижу, что многие честно себя оценили. Запишите д/з, стр. 64 №4 -Спасибо вам за урок. До свидания! | Считают примеры. 72-10=62 88-4=84 60+32=92 96-6=90 82-12=70 24+60=84 43-20=23 Выполняют задание 5+8=13 14-8=6 5+20=25 6+9-10=5 Слушают и анализируют задачу. -Одна машина Определяют тему -Закрепление материала. Решение задач. Открывают тетради записывают число Выполняют задания учебника -о двух мальчиках –двигаются по дорожке навстречу друг другу Чертят отрезок в тетрадь. -70 м. Указывают величины. -22м -не известно -Вычитанием -70-22=48 Читают задачу -Митя бежал по дорожке… -Длину дорожки -она не известна ее нужно найти. -Митя пробежал 50 м -Что ему осталось пробежать еще 25 м. -Добавим к 50 м отрезок длиной 25м. -к 50 м прибавить 25 м и это будет длина дорожки 1)50+25=75(м) Выполняют физминутку Решают самостоятельно на карточках. 50+35=85 (м) длина дорожки 100-8-40=52 100-4-70=26 -Поставить знак + или – (Выполняют задание у доски) 7+5+8=20 16-9-5=2 4+9-7=6 6-4+9=11 -Узнать длину ломаной -Сложить длину каждого отрезка. 4+2+6=12 (см) Читают задание Начертить ломанную из двух звеньев. -6 см Чертят ломаную из двух звеньев. Подводят итоги. Отвечают на вопросы. -Решение задач -На движение | РУУД -умения принимать и сохранять цели и задачи деятельности ПУУД -умение сравнивать, анализировать, обобщать ПУУД: -умение устанавливать причинноследственные связи в изучаемом свойства сложения РУУД -умения принимать и сохранять цели и задачи деятельности РУУД – планировать, оценивать учебные действия в соответствии с поставленной задачей ПУУД: Владеть навыками смыслового чтения текстов математического содержания в соответствии с поставленными целями и задачами РУУД -умение планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей ПУУД: -умение устанавливать причинноследственные связи в изучаемом свойстве сложения КУУД -умение формулировать собственное мнение и позицию КУУД – умение слушать речевое высказывание в устной форме, использовать математическую терминологию ПУУД: -умение устанавливать причинноследственные связи в изучаемом свойства сложения ЛУУД Формировать умение использовать освоенные математические способы познания для решения учебных задач. ЛУУД понимание причин успеха в учебной деятельности. КУУД умение формулировать собственное мнение и позицию ЛУУД Формировать понимание причин успеха в учебной деятельности | Анализ, синтез, обобщение Обсуждение Беседа Создание проблемной ситуации Практическая работа Объяснение Беседа Практическая работа Объяснение Практическая работа Практическое задание Обсуждение самооценка |
Урок по математике во 2 классе «В гости к осени. Решение задач в два действия
Урок по математике во 2 классе
«В гости к осени. Решение задач в два действия
Тип урока: освоение новых знаний.
Цель:
- Научить вычитанию однозначного числа из двузначного с переходом через разряд.
- Развивать устную речь учащихся; логические приемы мышления: анализ, синтез, сравнение; умение добывать знания, опираясь на ранее полученные умения.
- Воспитывать интерес к предмету; уважительное и доброжелательное отношение друг к другу. Формировать коммуникативную культуру, самостоятельность.
Задачи:
- Актуализировать знания состава чисел десятка.
- Познакомить с приемом вычитания однозначного числа из двузначного с переходом через разряд.
- Закрепить изученные вычислительные приемы.
- Совершенствовать умение решать текстовые задачи с новым приемом вычитания.
Методы:
- частично-поисковый,
- групповой
Используемое программное обеспечение:
презентация урока по теме: «Решение задач в два действия. Периметр многоугольника.
компьютер, интерактивная доска, карточки, учебник под редакцией Богдановича 2 класс.
Ход урока
I.Организационный момент.
Прозвенел звонок весёлый.
Все готовы? (да)
Всё готово? (да)
Мы сейчас не отдыхаем,
Мы работать начинаем.
Учитель:
-Природа и математика связаны друг с другом. В природе есть солнце. Оно светит и всех нас любит и греет. Так пусть же каждый его лучик заглянет к нам в класс и не только обогреет, но и придаст уверенности.
-Давайте прочитаем хором девиз нашего урока: «Лучший способ изучить что-либо – это открыть самому» – девиз написан на доске.
-Значит, чему будет посвящён урок?
Дети: Открытию нового знания.
Учитель:
-Я загадаю вам загадку, а вы отгадайте, и скажите, какое время года пришло к нам на урок.
«Несу я урожаи,
Поля вновь засеваю,
Птиц к югу отправляю
Деревья раздеваю,
Но не касаюсь сосен
И елочек. Я … (Осень). (СЛАЙД 2 – КАРТИНКА ОСЕНИ)
Учитель читает стихотворение А.С. Пушкина
Уж небо осенью дышало,
Уж реже солнышко блистало,
Короче становился день,
Лесов таинственная сень
С печальным шумом обнажалась.
Ложился на поля туман,
Гусей крикливый караван тянулся к югу:
Приближалась довольно поздняя пора;
Стоял ноябрь уж у двора.
Учитель:
-Сегодня мы с вами отправимся в гости к осени.
Учитель:
– Дайте характеристику числу 23
Дети:
– Оно двузначное.
– В нём 2 десятка, 3 единицы.
– Записывается при помощи цифр 2 и 3
– Соседи числа 23, числа 22 и 24
– Число некруглое, нечётное.
– Сумма разрядных слагаемых 20 и 3 равна 23
– Число 23 записывается при помощи цифр 2 и 3
Учитель:
Используя эти цифры запишем число, классная работа, строка чистописания.
II.Актуализация опорных знаний.
Определение темы, постановка цели.
Учитель:
– Посмотрите на экран. Найдите лишнюю картинку. (СЛАЙД 3)
(солнце, дождь, птицы, туман, листья, бабочки).
– Какая картинка лишняя? (бабочки)
-Почему? (они летают только летом)
– К какому времени года относятся остальные картинки? (к осени)
– Какие сезонные изменения происходят осенью в неживой природе? (наступает похолодание, появляется иней, бывают первые заморозки, последняя гроза, мелкие затяжные дожди, первый снег )
-Как меняется осенью жизнь растений? (они желтеют, увядают)
– Осень принесла вам интересные задания, выполнив которые мы научимся новым вычислительным приёмам и закрепим изученный материал.
1.Устный счёт.
Раз, два, три, четыре, пять –
Вот и в клеточку тетрадь!
6,7,8,9,10 –
Устный счёт всегда чудесен!
МАТЕМАТИЧЕСКИЙ ДИКТАНТ (1 УЧЕНИК У ДОСКИ, остальные в тетрадях).
- 30 уменьши на 10.
- 50 увеличь на 8.
- На сколько 75 больше, чем 5?
- Уменьшаемое 30, вычитаемое 3. Чему равна разность?
- Найдите сумму чисел 23 и 7.
- Из 48 вычесть 20.
ПРОВЕРИМ
(ОТВЕТЫ к математическому диктанту) (СЛАЙД 4)
20 (Я) 58(К) 70(А) 27(Г) 30(Д) 28(О)
-Какое число самое маленькое?
-Какое число самое большое?
Учитель:
*Каждому числу соответствует определённая буква.
– Запишите числа в порядке увеличения и вы прочитаете зашифрованное слово.
-Какое слово получилось? Прочитайте.
Дети: ЯГОДА. (СЛАЙД 5)
Учитель:
-Какая лечебная ягода созревает осенью? (плоды шиповника)
Учитель:
И плоды его. Ребята,
Витаминами богаты,
Кто настой из них попьёт –
Очень долго проживёт!!!
Учитель:
-Чтобы набрать в лукошки много ягод, необходимо выполнить следующее задание.
РЕШИТЕ ЦЕПОЧКУ ПРИМЕРОВ (на ягодках числа и арифметические знаки)
(дети при решении используют слова: увеличить, уменьшить, прибавить, вычесть, сумма, разность)
81 + 5 – 30 – 6 + 24 + 6 – 5 = ….. (75) (СЛАЙД 6)
Учитель:
-Молодцы ребята, полные лукошки ягод собрали.
2. Работа с геометрическим материалом.
Учитель:
(демонстрирует фартук)
-Вот какой яркий фартук есть у нашей Осени.
Сейчас об этом Амалия расскажет стихотворение.
(Ученица читает стихотворение).
Повязала осень пёстрый фартук
И ведёрки с красками взяла
Ранним утром, проходя по лесу
Листья позолотой обвела.
Учитель:
– Объясните, как понимаете выражение «Позолотой обвела».
Дети: Значит листья стали жёлтого цвета, как золото.
(учитель показывает фартук выполненный из геометрических фигур)
Учитель:
-Какие геометрические фигуры составляют фартук Осени.
Дети: Часть круга, треугольник, четырёхугольник, круги
Учитель:
-Сколько четырёхугольников?
Дети:1
Учитель:
-Что знаете о четырёхугольнике?
Дети: Четырёхугольник это геометрическая фигура, которая состоит из четырёх вершин (точек), четырёх сторон, четырёх углов
Учитель:
-Фигуры, какого цвета не являются четырёхугольниками?
– Чему будет равен периметр четырёхугольника, если одна сторона 7см, а другая 5см? Дети: 24см
Учитель:
-Что значит найти периметр фигуры?
Дети: Необходимо найти сумму длин её сторон
Учитель:
-А если у четырёхугольника все стороны равны. Как будет называться эта фигура? Дети: Квадрат
Учитель:
-Осень довольна вашими ответами.
-Ребята, листья каких деревьев не изменяют осенью свою окраску?
Дети:
-Хвойных: сосны, ели, туи, кедра.
Учитель:
-Посмотрите, какое задание приготовили для вас ЁЛОЧКИ (СЛАЙД 7 – ПРИМЕТЫ)
III.Работа над темой урока.
2.Выход к учебной проблеме.
–
IV. Физминутка-музыкальная –проводит ученик (СЛАЙД 10)
Немного отдохнём под красивую осеннюю мелодию.
Листья
Листья осенние тихо кружатся,
Листья нам под ноги тихо ложатся.
И под ногами шуршат, шелестят,
Будто опять закружиться хотят.
Н.Нищева
Дети кружатся, расставив руки в стороны.
Приседают.
Движение руками влево, вправо.
Снова кружатся на носочка.
3.Решение учебной проблемы.
V.Работа по учебнику (
Учитель:
-Но к сожалению, в осеннем лесу не услышишь весёлого, беззаботного пения птиц. Многие птицы собираются в стаи и улетают на юг.
– Как называются такие птицы?
Дети: Перелётные
Учитель:
-Почему они улетают на юг?
Дети: Им недостаточно корма, т.к. насекомые исчезают. А эти птицы насекомоядные.
Учитель:
-Каких перелётных птиц вы знаете?
Дети: Ласточка, стриж, кукушка, иволга, соловей, журавль (СЛАЙД 12 – ПТИЦЫ)
Учитель:
-Все ли птицы улетают в тёплые края?
Дети: Нет
Учитель:
-Какие остаются у нас и как они себя ведут?
Дети: Мы видим синиц, ворон, воробьёв, прилетают снегири, свиристели. Это зимующие птицы, они питаются плодами и семенами растений
Учитель:
-Птицы хотят посмотреть, как вы справитесь со следующим заданием.
Учитель: Учебник стр.67 №2 ,
Учитель:
-Птицы остались довольны вашей работой, но вы также не забывайте подкармливать их зимой.
Пальчиковая гимнастика (проводит ученик)
Без пальто гулял глупышка
И замёрз он, как ледышка
Чтобы пальчик отогреть,
Будем мы его тереть.
VI.Закрепление ранее изученного материала. Работа по учебнику.
Учитель:
– Какие изменения происходят в жизни животных? Как они готовятся к зиме?
Дети: Многие животные линяют (смена шерсти), осенью делают запасы на зиму: крот, хомяк, мышь, бобр, барсук, белка, запасают семена хвойных деревьев, грибы, орешки, жёлуди, веточки, зёрнышки; не делают запасов на зиму ёж, медведь, они до весны ложатся в спячку.
Учитель:
Хожу в пушистой шубке,
Живу в густом лесу.
В дупле на старом дубе
Орешки я грызу.
-О ком идёт речь в загадке?
Дети: О белке. (СЛАЙД 13)
Учитель:
– И белка принесла нам своё задание, постарайтесь его выполнить без ошибок.
а) ЗАДАЧА
Дети: Белочка делала запасы на зиму. Она собрала 30 орехов, а грибов на 7 больше. Сколько орехов и грибов всего собрала белочка? (СЛАЙД 15)
Учитель:
-Прочитаем задачу.
-Что известно в задаче?
-Что нужно узнать?
(Запишем краткую запись)
-Можем ли сразу ответить на вопрос задачи? (нет)
-Почему? (мы не знаем, сколько грибов собрала белочка)
-Каким действием? (сложением)
-Почему будем складывать? (грибов больше на 7)
-А теперь, сможем ответить на вопрос задачи? (да)
-Каким действием? (сложением)
-Почему будем складывать? (находим сколько всего)
-Во сколько действий задача? (2)
-Какое первое действие? (30 + 7 = 37)
-Какое второе? (30 + 37 = 67)
-Запишем задачу выражением (1 ученик у доски):
30 + (30 + 7) = 67 (шт.)
Ответ: 67 орехов и грибов собрала белочка.
– Что обозначает сумма? (сколько грибов)
-А всё выражение? (сколько грибов и орехов)
Учитель:
-Вот мы и выполнили задание, которое дала нам белочка.
ДОПОЛНИТЕЛЬНО
-А как называется вот это явление природы? (демонстрирую рисунок «Туман»)
-Что вы можете о нём сказать?
Дети:
-Туманы бывают во все времена, обычно они стелются над рекой, в низине, где много воды. Гуще всего туманы бывают по утрам, когда земля сильно остывает.
-Ой, и нас накрывает туман, нужно скорее его разогнать.
– Выполнить следующее задание.
б) задания в рабочей тетради или тестирование
VII.Подведение итогов урока. Выставление оценок.
-Вы ребята молодцы
Математики – бойцы
Наш закончился урок
Подведём ему итог.
– С какой проблемой мы столкнулись сегодня на уроке? (необходимо было научиться вычитать из двузначного числа однозначное с переходом через разряд)
– Какой приём вычислений нам в этом помог? (нужно сначала число двузначное уменьшить до круглого числа, а затем из круглого числа вычесть необходимое количество единиц)
– Что больше всего понравилось и запомнилось на уроке?
– Кто доволен своей работой на уроке?
*** Оценки за урок
VIII.Домашнее задание
стр67 №4
IX.Рефлексия
– У вас у каждого на партах разноцветные осенние листья. Оцените свою работу на уроке:
– если вы активно участвовали в работе на уроке, делились с ребятами своими суждениями и овладели всей информацией, возьмите зелёный листочек;
– если вы участвовали в уроке, но не всегда могли ответить на вопросы, возьмите жёлтый листочек;
– если вы не разобрались с вычислительными приёмами, вам было очень трудно, возьмите красный листочек.
– Я очень рада, что наш листопад состоит из зелёных и жёлтых листьев. Сегодня хорошо поработали, молодцы. Спасибо за работу!
как сдать часть 2 ЕГЭ по математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Татьяна Петрова,
аспирантка механико-математического факультета МГУ им. Ломоносова,
преподаватель математики учебного центра Challenge
Задание № 9
Что требуетсяВыполнить вычисления и преобразования.
ОсобенностиЭто задача на вычисление значения числового или буквенного выражения. Здесь достаточно уметь выполнять действия с числами и знать определение и простейшие свойства степеней с рациональным показателем, тригонометрических функций, корней n-степени и логарифмов.
СоветыНужно знать базовые формулы и уметь их применять.
Задание № 10
Что требуетсяРешить задачу с прикладным содержанием.
ОсобенностиЗдесь предлагаются задачи прикладного характера, связанные с такими областями науки, как физика, химия, биология. В этом задании можно встретить все типы уравнений и неравенств: линейные, квадратные, степенные, рациональные, иррациональные, показательные, логарифмические и тригонометрические. Ваша задача — выразить требуемую величину из заданной формулы.
СоветыВнимательно читайте условие и старайтесь его понять. Следите, чтобы единицы измерения были приведены к одному виду. Выражайте ту или иную переменную в общем виде и только потом подставляйте числовые значения. Не спешите считать в лоб, пробуйте сокращать.
Задание № 11
Что требуетсяРешить текстовую задачу.
ОсобенностиВсего существует шесть типов текстовых задач. Они могут быть на движение, на совместную работу, на проценты, на смеси, растворы и сплавы, на прогрессии, на оптимальный выбор и целые числа. Соответственно, нужно знать основные законы и формулы для каждого типа. Традиционная текстовая задача сводится к составлению уравнения и его решению.
| Задачи на движение | \(S = V \cdot t\) |
| Задачи на совместную работу | \(A = p \cdot t\) |
| Задачи на смеси, растворы и сплавы | \(C = \frac{V_{1}}{ V} \cdot 100\%\) |
Обратите внимание, что формулы в задачах на движение и на работу очень похожи. Производительность — это аналог скорости. Для задач на смеси и растворы не забывайте формулу концентрации. В качестве неизвестной выбирайте искомую величину. Составленное уравнение будет рациональным и в основном сводится к линейному или квадратному.
Задание № 12
Что требуетсяНайти наибольшее или наименьшее значение функции.
ОсобенностиЗдесь требуется уметь находить производную функции, а также исследовать функцию с помощью производной. Вопрос может быть двух типов: найти точку минимума/максимума функции или найти наибольшее/наименьшее значение функции. Многие школьники не различают этих понятий, а ведь ответ будет совершенно разный. Еще в этом задании мы сталкиваемся с задачей нахождения минимума/максимума на отрезке или на всей действительной прямой. Если вас ограничивают отрезком, то не забывайте находить значения на его концах и сравнивать их с локальными минимумами/максимумами функции на отрезке.
СоветыВыучите базовую таблицу производных, а также формулы производной произведения, частного и композиции функций. Помните, что если производная положительна, то функция растет, если производная отрицательна — функция убывает. Когда производная меняет свой знак с плюса на минус, это значит, что мы попали в точку максимума. Если производная поменяла свой знак с минуса на плюс, значит, мы попали в точку минимума.
Задание № 13
Что требуетсяРешить тригонометрическое, рациональное, показательное, логарифмическое уравнение, уравнение с радикалом или смешанное уравнение, содержащее одновременно логарифмы, модули, радикалы.
ОсобенностиДля решения любого уравнения существует два основных правила. Во-первых, решение всегда должно начинаться с нахождения ОДЗ — области допустимых значений, то есть всех значений переменной, при которых это уравнение имеет смысл. Во-вторых, нужно помнить основные методы решения уравнений и уметь применять их. Как правило, решение данной задачи требует замены, позволяющей свести уравнение к квадратному.
СоветыДля решения тригонометрических уравнений важно знать формулы приведения и знаки тригонометрических функций на четвертях окружности. Формулы приведения позволяют упростить вычисления, привести сложные аргументы тригонометрических функций к аргументам первой четверти. Помните про мнемоническое правило («правило лошади»), которое позволит вам не заучивать все многообразие формул приведения: если вы откладываете угол от вертикальной оси, то «лошадь говорит вам „да“», то есть кивает головой вдоль оси ординат, тем самым вы меняете функцию. Если вы откладываете угол от горизонтальной оси, то «лошадь говорит вам „нет“», то есть кивает головой вдоль оси абсцисс, следовательно, приводимая функция не меняет своего названия (не забудьте про знак, он совпадает со знаком исходной функции!).
Задание № 14
Что требуетсяРешить стереометрическую задачу.
ОсобенностиЭто задача на построение сечения многогранника и нахождение его площади, а также на нахождение расстояний и углов в пространстве, нахождение объемов различных многогранников и круглых тел (цилиндр, конус, шар). Здесь нужно хорошо владеть формулировками аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства, знать формулы площадей и объемов. Также в этом задании нужно понимать, что такое угол между прямыми, угол между скрещивающимися прямыми, угол между прямой и плоскостью и угол между плоскостями (вспомните, что такое линейный угол двугранного угла).
СоветыВ этой задаче, как правило, два пункта. В первом пункте нужно либо что-то построить, либо доказать. Для доказательства очень часто используются признаки подобия треугольников и теорема Фалеса. Во втором пункте нужно найти угол, расстояние или площадь. Вспомните основные формулы расстояний: расстояние от точки до прямой, от точки до плоскости, между двумя плоскостями. Вы должны знать основные тригонометрические функции, теорему синусов и косинусов, теорему Пифагора и теорему о трех перпендикулярах. Нужно уметь проводить дополнительные построения и владеть координатным и векторным методами.
Задание № 15
Что требуетсяРешить тригонометрическое, рациональное, показательное, логарифмическое (в том числе с переменным основанием) неравенство, неравенство с радикалом, смешанное неравенство, содержащее одновременно логарифмы, модули, радикалы.
ОсобенностиЗдесь необходимо свести сложное неравенство к простейшему. Часто для этого используются замены показательных и тригонометрических функций (не забывайте про ограничения!). Также нужно знать метод интервалов и метод рационализации для логарифмических, показательных неравенств и неравенств, содержащих модуль.
СоветыМетод решения логарифмических неравенств опирается на монотонность логарифмической функции. Помните, что если у логарифма переменное основание, то нужно рассматривать два случая: а) основание лежит в диапазоне от 0 до 1 (функция убывает), б) основание больше единицы (функция возрастает). Если основание переменное, то можно избавиться от перебора случаев, перейдя к новому, постоянному основанию.
В логарифмических неравенствах внимательно следите за областью допустимых значений, применяя формулы действий с логарифмами, она может как расширяться, так и сужаться. И если первую ситуацию легко исправить, то вторая приведет к потере решений, что недопустимо.
Задание № 16
Что требуетсяРешить планиметрическую задачу.
ОсобенностиПод этим номером может быть два варианта задания. Первый вариант: в задаче два пункта — а и b. В пункте a требуется что-то доказать, в пункте b — что-то найти. Могу сказать, что чаще всего надо начинать решать эту задачу именно с пункта b, а уже решение этого пункта поможет доказать пункт а. Как правило, абитуриентам проще что-то найти, чем доказать.
Второй вариант: задача без подпунктов. Здесь чаще всего скрыт подводный камень: задача требует рассмотрения двух случаев и приводит к двум разным ответам. Например, в условии задачи сказано, что окружности касаются в точке A, но не сказано каким образом, внешним или внутренним. Часто бывает так, что выпускник рисует один рисунок и возможно даже находит правильный ответ. А второй случай он не рассматривает, в результате чего получает ровно половину баллов за это задание.
СоветыНеобходимое условие для решения этой задачи — хорошее владение теоретическим материалом, например, из классического учебника по геометрии для 7-9 классов (Л.С. Атанасян). Необходимо знать формулировки аксиом и определений, уметь формулировать и доказывать теоремы, признаки, свойства и формулы. Изучите дополнительные методы: метод дополнительного построения, метод подобия, метод замены, метод введения вспомогательного неизвестного, метод удвоения медианы, метод вспомогательной окружности, метод площадей.
Также здесь важен рисунок. 80% успеха геометрической задачи — это правильно нарисованный рисунок. Сделайте большой, хороший, наглядный рисунок, не экономьте на нем место.
И последнее, лайфхак для абитуриента — для решения задач по планиметрии выучите пять формул площади треугольника: через высоту и основание, через две стороны и угол между ними, через радиус вписанной окружности, через радиус описанной окружности и формулу Герона.
| Площадь треугольника через высоту и основание | \(S = \frac{1}{2}a \cdot h_{a}\) |
| Площадь треугольника через две стороны и угол между ними | \(S = \frac{1}{2}a \cdot b \cdot \sin \alpha\) |
| Площадь треугольника через радиус вписанной окружности | \(S = p \cdot r\), где \(p = \frac{a+b+c}{2}\), \(r\) – радиус вписанной окружности |
| Площадь треугольника через радиус описанной окружности | \(S = \frac{a \cdot b \cdot c}{4R}\), где \(R\) – радиус описанной окружности |
| Формула Герона | \(S = {\sqrt{p(p-a)(p-b)(p-c)}}\), где \(p = \frac{a+b+c}{2}\) |
Задание № 17
Что требуетсяРешить текстовую задачу преимущественно экономического содержания на кредиты, вклады и оптимальный выбор.
ОсобенностиЗадача на злобу дня, которая появилась на ЕГЭ только в последние годы. Задания на банковские проценты могут быть двух типов: задачи на проценты по вкладам (депозитам) и задачи на проценты по кредитам. Помимо них под этим номером на ЕГЭ могут дать задачу на оптимизацию производства товаров и услуг, в которой необходимо будет либо использовать графическую интерпретацию, либо решать аналитически с помощью производной, чтобы понять, как минимизировать расходы или максимизировать прибыль.
СоветыВнимательно читайте условие задачи, вникайте в процедуры выдачи кредита или открытия вклада, которые там описываются. Каждый пункт условия сразу переводите в уравнение. Таким образом вы получите уравнение или систему уравнений, которые вам останется только решить. Чтоб подготовиться, изучите основные схемы кредитования с дифференцированными и аннуитетными платежами. В задачах оптимизации нужно уметь работать с линейными/нелинейными целевыми функциями с целочисленными/нецелочисленными точками экстремумов.
Задание № 18
Что требуетсяРешить уравнение или неравенство с параметрами, систему уравнений или неравенств с параметрами.
ОсобенностиЭти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения. Самое главное в этом задании — логика.
СоветыЧтобы подготовиться к заданиям с параметрами, я рекомендую решать задачи из учебников С.А. Шестакова «Задачи с параметрами», А.И. Козко и В.Г. Чирского «Задачи с параметрами для абитуриентов». Также хочется дать лайфхак для уравнений с двумя неизвестными: как правило, там спрятана геометрическая фигура, построй ее и получишь честное графическое решение.
Задание № 19
Что требуетсяРешить задачу на числа и их свойства.
ОсобенностиЭто самая сложная задача экзамена, олимпиадного уровня, она оценивается в четыре первичных балла. Тем не менее материал для ее решения школьники проходят еще в 6-8 классе. Задание требует хорошего логического мышления и математической культуры.
СоветыПовторите основные признаки делимости целых чисел, вспомните понятия «НОК/НОД», выучите формулы арифметической и геометрической прогрессии. «Прорешайте» типовые задания из сборника Г.И. Вольфсона и М.Я. Пратусевича «Арифметика и алгебра». Последние два задания (№ 18 и № 19) — это прямая заявка на 100 баллов.
Задачи по обучению словарю во 2-м классе
Если вы ищете лучший способ научить словесным задачам и, что более важно, хотите, чтобы ваши ученики были более успешными в решении словесных задач, я здесь, чтобы помочь. Учить словесные задачи во 2-м классе не должно быть проблемой.
Почему во 2-м классе так сложно учить словесные задачи?
Когда я только начал преподавать, я учил своих учеников использовать ключевые слова, подчеркивать и обводить, выделять и вставлять рамку… и, тем не менее, это не помогло.Они все еще не знали, когда складывать, а когда убирать.
И мои ученики не понимали и не успевали лучше.
Не помогало то, что я постоянно не учил и не позволял своим ученикам практиковаться в решении словесных задач.
Задачи со словом всегда были источником разногласий для моих учеников, независимо от того, в каком классе я преподавал (1-й, 2-й и 4-й), и всегда были тем, что я преподавал наугад в рамках принятой математической программы.
Большинство учебных программ по математике предлагают следующее:
- Задачи на 1 или 2 слова в конце каждого урока, но на самом деле не предлагают способ научить студентов решать задачи со словами
- 1 глава о «решении задач»
И серьезно, ни один из них полезно.
Я хотел, чтобы мои ученики ежедневно практиковались в стратегических задачах по решению словесных задач.
И знаете что? Когда я начал последовательно и стратегически преподавать задачи со словами во 2-м классе, мои ученики были менее разочарованы и гораздо более искусно решали задачи со словами.
Итак, какое решение?
Сейчас я следую 4-дневному плану обучения и оцениваю его на 5-й день.
Я больше не учу ключевые слова или подчеркивание, обводку, выделение и / или бокс… вместо этого я учу своих учеников искать закономерности в том, как структурированы проблемы со словами… ситуации со словами.
Кроме того, я посвящаю 5-10 минут каждый день обучению и практике словесных задач.
Как я узнаю, чему учить?
Начну со стандарта.
Честно говоря, что бы я ни преподаю, именно здесь я начинаю. Мне нужно точно знать, чего я ожидаю, чтобы потом я мог помочь своим ученикам справиться с этим.
Стандарт Common Core для 2-го класса гласит:
CCSS.MATH.CONTENT.2.OA.A.1
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Хотя многие штаты больше не используют термин «Common Core», многие принятые ими стандарты совпадают или, по крайней мере, схожи.
MAFS.2.OA.1.1 (стандарты Флориды)
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Итак, второклассники должны уметь решать:
- Сложение / вычитание в пределах 100
- Одно- и двухступенчатое
- Добавить к
- Взять из
- Соединить
- Разобрать
- Сравнить
Когда вы посмотрите на то, что должны делать второклассники, неудивительно, что учить словесные задачи так сложно, не говоря уже о том, что студенты действительно их осваивают.
Как я учу задачи по словам во 2-м классе:
В начале года ученики знакомятся с нашей рутинной задачей со словом после первых двух недель в школе.
Я объясняю, что словесные задачи подобны историям, которые мы должны читать и понимать, что происходит в рассказе. Мы называем эти слова «проблемными ситуациями».
Затем я учу студентов, что есть 4 вещи, которые они всегда должны делать, решая задачу со словами:
- Запишите числовое предложение
- Используйте стратегию для решения
- Я объясняю студентам, что не могу залезть в их мозг, чтобы увидеть, что они думают, и если я не знаю, о чем они думают, я не может помочь им лучше решать проблемы со словами.
- Учащиеся могут рисовать картинки, использовать семейство фактов, базовые 10 блоков и / или стандартный алгоритм.
- Вычисление
- Я хочу убедиться, что ученик дал правильный ответ.
- Ответ в предложении
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки». Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Запуск рутинной задачи со словом – это все о моделировании и рутине. Студентам не нужно много времени, чтобы научиться этому.
Я проделал для вас тяжелую работу – у меня на весь год есть задачи по словам во 2-м классе, готовые для вас!
Что такое рутинная задача для 2-х классов?
По понедельникам я использую слово «проблемная ситуация». Я считаю полезным, чтобы ученики «разыгрывали» ситуацию. Используйте пример на ситуационном плакате / диаграмме привязки, чтобы показать учащимся образец.(Я учу студентов, что подчеркнутые части числового предложения – это известные нам части, а квадрат представляет неизвестное.)
Смоделируйте и решите практическую задачу со словами и поделитесь своими отзывами со студентами.
В течение следующих 3 дней мы моделируем и решаем задачу со словом, которая имеет ту же ситуацию, что и понедельник. Так что мы не скучаем. Это очень систематично.
Наконец, по пятницам ученики самостоятельно решают 2 задачи со словами, следуя той же ситуации, которую мы использовали всю неделю.
Для дифференциации или расширения учащиеся могут написать задачу на обратной стороне своего экзамена, которая соответствует той же ситуации, которую они изучали на этой неделе. Это отличный способ узнать, действительно ли студенты понимают ситуацию, которую мы узнали на той неделе.
Возможно вам понравится:
Давайте подключимся!Instagram // Pinterest // Facebook // Учителя платят учителям
Решение проблем в действии | Scholastic
Возраст от 0 до 2 лет: Пул
Младенцы рождаются со встроенными инструментами решения проблем, называемыми рефлексами.Менее чем через час после рождения ребенок будет использовать свои рефлексы укоренения и сосания для кормления. По мере роста многие из ее автоматических реакций будут заменены более произвольными действиями.
В 2 месяца младенцы становятся более внимательными и стремятся исследовать окружающий мир. К 4 месяцам ребенок развил мышечный контроль и координацию рук и глаз, чтобы подносить игрушки и другие предметы ко рту. Начались радостные исследования и эксперименты, ведущие к решению проблем.
В поисках результатов
К 8 месяцам младенцам нравится играть с игрушками, которые вызывают интересную реакцию на их действия.Особой популярностью пользуются игрушки, которые издают необычные звуки и двигаются, хватают, трясут и стучат. Эти забавные события помогают заложить основу для дальнейшего понимания детьми причинно-следственных связей.
Намеренное подражание
К своему первому дню рождения дети переходят на более целенаправленный уровень решения проблем. Больше не ограничиваясь тем, что находится прямо перед ними, теперь они могут отодвинуть игрушку, чтобы добраться до другой, более интересной.
Годовалые дети тоже начинают решать проблемы через наблюдение и подражание. Четырнадцатимесячная Дейзи, например, озадачена складывающейся игрушкой своего нового детского сада. Она внимательно наблюдает, как ее опекун снимает верхнее кольцо с игрушки. Затем Дейзи снимает следующее кольцо. Когда ее опекун заменяет первое кольцо, Дейзи снова следует за ней и заменяет кольцо, которое она держала. Ее воспитатель улыбается и хлопает в ладоши, а Дейзи с удовольствием смеется, узнав, как пользоваться этой новой игрушкой.
Все изо всех сил
Достигнув раннего возраста, дети используют цитату: «Что бы случилось, если …» подход к решению проблем. Они экспериментируют со всем понемногу в своем настойчивом поиске решения.
Например, восемнадцатимесячная Эмма пытается заставить механическую собаку двигаться. Она встряхивает его, переворачивает вверх дном, нажимает на ключ и гладит щенка по голове. Наконец, она поворачивает ключ – и щенок движется!
Вспоминая решения
К 2 годам дети начинают использовать новый важный инструмент решения проблем: память.Теперь малыш может наблюдать, думать о проблеме, а затем вспоминать то, что он видел, и подражать этому.
Когда двухлетняя Сьюзи хочет открыть ящик в предмете мебели кукольного домика, например, она больше не трясет и не стучит им, как несколько месяцев назад. Вместо этого она вспоминает, как смотрит, как ее опекун открывает ящик, и использует ту же технику.
Что вы можете сделать
Маленьким детям нужно решить так много проблем и так мало времени! Вы можете помочь, предоставив возможности для открытых исследований и предложив помощь до того, как дети станут слишком разочарованы.
Предложите малышам множество интересных предметов, которые они могут схватить и сосать. Изучение новых материалов создает основу для последующих навыков решения проблем.
Дайте детям игрушки, которые вызывают реакцию на их действия. Игрушки, которые издают забавные звуки, когда их берут, трясут или хлопают, очень популярны.
Размещайте интересные игрушки, недоступные для годовалых детей. Это заставит ее работать, чтобы получить игрушку . Однако, если она потеряет интерес, подбросьте игрушку и подтолкните ее немного ближе.
Помогите детям найти решения реальных проблем. Например, когда мяч катится за полкой, спросите малыша, как, по его мнению, он сможет получить мяч. Попробуйте его предложения, а затем поделитесь своими идеями.
Обеспечьте разнообразие материалов на уровне грунтовых вод. Изучение того, какие предметы тонут или плавают, сколько контейнеров с водой может вместить и какие предметы поглощают воду, – все это отличное решение проблем.
Краткий обзор
- Страстное познание мира ребенком закладывает основу для навыков решения проблем.
- Годовалые дети решают проблемы, наблюдая за людьми вокруг себя, а затем подражая им.
- Для малышей лучшее решение – пробовать все подходы, пока они не выберут тот, который работает.
- Обладая улучшенной памятью, двухлетние дети могут вспомнить, как другие люди решали проблемы, подобные тем, с которыми они сталкиваются.
Возраст от 3 до 4: Миллер
Трехлетняя Сара пытается показать собранные ею листья на листе бумаги, но они продолжают падать. Она вспоминает, как ее учитель использовал клей в пластиковой бутылке, чтобы наклеить картинку на бумагу. Увлеченная исследованием новых материалов, Сара решает попробовать решить свою проблему с помощью клея.
Сара выдавливает струйки клея на бумагу, а затем прижимает листья сверху. Как и большинство троек, она решает проблему методом проб и ошибок, в первую очередь полагаясь на свои чувства, а не на рассуждения.Так что может пройти несколько экспериментов, прежде чем она поймет, что листья не прилипнут быстро к большой куче клея.
Сосредоточенность, но разочарование
Тройкам нравится использовать свое воображение для решения возникающих проблем. Желая получить каску строителя для его драматической пьесы, Макс с энтузиазмом решает использовать перевернутую пластиковую миску. Обрадованный, он затем неоднократно демонстрирует, как использовать рацию воображаемого руководителя, которую он творчески сделал из коробки сока.
Тройки иногда разочаровываются в своих попытках решить проблему, потому что они видят только одно возможное решение, которое может оказаться неприменимым. Например, когда у Томми застряла молния на куртке, он все время ее подтягивает, убежденный, что это единственный доступный способ.
Если сначала …
Отважные 4-летние дети часто бросаются вперед в своих поисках решения проблем. Хотя им может потребоваться помощь, чтобы сосредоточиться на реальной проблеме, они более терпеливы, чем трое, и могут пробовать разные решения.
Например, несколько четверок изо всех сил пытаются вытащить свою повозку из грязи на детской площадке. Сначала они пытаются его подтолкнуть. Затем они пытаются его вытащить. Когда эти методы не позволяют сдвинуть повозку с места, они решают вытащить тяжелые камни и попробовать снова. Дети, типичные для четверых, хвастаются тем, какие они сильные и хорошие мыслители!
Командные усилия
Четверки, используя свой большой словарный запас, готовы вести переговоры друг с другом. Их развивающиеся языковые навыки помогают им работать вместе и участвовать в групповом процессе принятия решений.С практикой они учатся выбирать из различных решений.
Например, несколько детей решают построить дом. Они собирают различные материалы – цветную фольгу, гофрированный картон, одуванчики, кору деревьев – а затем вместе решают, какие из них использовать. Они делятся своими предположениями о том, какие материалы могут работать и как их лучше всего использовать.
Что вы можете сделать
Дошкольники лучше всего учатся на частом опыте решения важных для них проблем, возникающих в их повседневной жизни.
Предоставьте возможности для практических исследований. Предложите детям интересные предметы для изучения, такие как магниты, найденные предметы и сломанные (но безопасные) приборы. Меняйте материалы, чтобы они оставались свежими и заставляли задуматься.
Развивайте навыки творческого и критического мышления, предлагая детям использовать предметы по-новому и разнообразно. Цветные бусины, например, могут стать поводьями для скаковых лошадей, волосами для кукол, измерительными звеньями или могут быть отпечатаны в глине для создания рисунков.
Поощряйте предложения и решения детей. Поощряйте мозговой штурм, задавая открытые вопросы: «Что вы можете сделать с …?» “Сколько способов вы можете …?” Внимательно слушайте их идеи.
Позвольте детям найти свои собственные решения. Предложите помощь, когда они расстроены, но не решайте их проблемы за них.
Используйте литературу как трамплин. Поделитесь книгами, в которых показано, как персонажи решают проблемы, например King of the Playground Филлис Нейлор (Antheneum) и Caps for Sale Esphyr Slobodkina (Scholastic Inc.).
Краткий обзор
- Threes решают проблемы методом проб и ошибок, основывая свои идеи на том, что они видят и чувствуют.
- Трехлетние дети могут сосредоточиться на одном решении. Если это не сработает, они могут разочароваться.
- Четверки более терпеливы и способны пробовать несколько решений проблемы.
- Развитие языковых навыков позволяет четверым делиться своими идеями и совместно решать проблемы.
Возраст от 5 до 6: Церковь
“Как я могу заставить эту башню не подниматься?” “Почему краска не прилипает к этой коробке?” “Как я могу взвесить эти камни?” “Они не дадут мне по очереди!” Каждый день вы можете слышать голоса детей, которые сталкиваются с проблемами и решают их в вашем классе. Когда дети сталкиваются с этими, казалось бы, небольшими проблемами, они развивают и применяют важные мыслительные, социальные и эмоциональные навыки.
Сохранение спокойствия: позитивное мышление
Навыки решения проблем пяти- и шестилетних детей во многом отличаются от навыков детей младшего возраста.Одно из самых важных изменений – это их развивающаяся способность терпеть разочарование. Воспитанники детского сада с большей вероятностью смогут выдержать период разочарования, поскольку они сталкиваются с трудной проблемой и работают над ней. В то время как младшие дети могут отказаться от кусочка головоломки, который не подходит, или попытаться разбить его на место! – Детским садовникам потребуется время, чтобы понаблюдать и определить проблему, опробовать несколько решений и сделать вывод.
Их вновь обретенная способность справляться с разочарованием проистекает из повышенной концентрации внимания и чувства собственного достоинства.А к 5-6 годам эмоциональная зрелость детей дает им больше уверенности в том, что они могут рисковать – и даже совершать ошибки.
За пределами конкретного: мышление в абстракциях
Обучение абстрактному мышлению является неотъемлемой частью развития навыков решения проблем. К детскому саду дети становятся более искусными в размышлениях о решении проблемы, фактически не пробуя ее. Когнитивно они способны представить и обдумать проблему и ее решение с меньшим практическим опытом.
Хорошие языковые навыки необходимы для абстрактного мышления, а воспитанники детского сада часто очень вербальны. Они могут объяснить свое мышление и очень подробно изложить свои идеи.
Например, рассказывая истории, дети теперь могут предлагать возможные решения проблем персонажей. Им также нравится творческое мышление, например, мозговой штурм всех способов использования знакомого объекта.
Нет проблем слишком больших: мыслить глобально
Глобальное мышление – интересная характеристика развития детсадовцев, способных решать проблемы.Возможно, из-за перехода от эгоцентрического мышления и поведения дети в возрасте 5-6-6 лет лучше осознают проблемы других людей.
Детсадовцы начинают понимать масштабные проблемы, влияющие на планету, и могут стать революционерами в своем мнении о таких мировых проблемах, как исчезающие животные, загрязнение окружающей среды и войны. Конечно, они еще достаточно молоды, чтобы думать, что их решения сработают!
Что вы можете сделать
Благоприятная среда, в которой дети регулярно изучают материалы и обсуждают идеи, является идеальным местом для молодых людей, решающих проблемы.Поощряя детей пробовать новые подходы – и поздравляя всех их усилий – помогает им развить уверенность в том, чтобы экспериментировать, не опасаясь неудач.
Дайте детям пространство и время, чтобы преодолеть свои разочарования . Поддерживайте их попытки решить проблемы, задавая открытые вопросы, которые помогут им сосредоточиться на возможных решениях.
Помогите детям создать абстрактные представления их конкретных проблем. Есть ли у детей эксперимент? Поговорите об этом, нарисуйте, напишите об этом! Это помогает им развивать абстрактное мышление более высокого уровня при записи своих идей и достижений.
Предоставляйте возможности для обсуждения социальных проблем – от школьных вопросов до глобальных тем . Групповые собрания могут быть форумом для изучения множества проблем, а затем обмена идеями и предложения решений. Интересные темы можно найти во многих детских книгах, образовательных видео, а также в школьных и местных журналах и газетах.
Краткий обзор
- Детсадовцы могут справиться с разочарованием из-за трудной для решения проблемы, и им потребуется время, чтобы обдумать ее.
- Пятерка и шестерка начинают понимать абстрактное мышление и могут размышлять о проблеме, с которой у них не было практического опыта.
- По мере того как детсадовцы становятся менее эгоцентричными, они начинают осознавать проблемы, затрагивающие других людей.
Как научить детей (в возрасте от 3 до 14 лет) решать проблемы – Big Life Journal
ЭТА СТАТЬЯ ВКЛЮЧАЕТ БЕСПЛАТНУЮ ПЕЧАТЬ
Будь то конфликт из-за игрушек, сложное математическое уравнение или отрицательное давление со стороны сверстников, дети ВСЕХ возрастов ежедневно сталкиваются с проблемами и проблемами.
Как родители или учителя, мы не всегда можем решить каждую проблему для наших детей. На самом деле это не наша работа. Наша работа – УЧИТЬ наших детей, как решать проблемы самими . Таким образом они могут стать уверенными, независимыми и успешными людьми.
Вместо того, чтобы сдаваться или разочаровываться, когда они сталкиваются с проблемой, дети с навыками решения проблем управляют своими эмоциями, творчески думают и упорствуют, пока не найдут решение.Естественно, эти способности идут рука об руку с установкой на рост.
Прежде чем двигаться дальше, не забудьте подписаться на наши БЕСПЛАТНЫЕ еженедельные распечатки , тщательно разработанные, чтобы научить ваших детей менталитету роста, устойчивости и многому другому. Зарегистрируйтесь ниже, чтобы убедиться, что вы в списке!
После регистрации вы сразу же получите наше популярное руководство для родителей по методу роста .
Итак, КАК вы учите детей навыкам решения проблем?
Ну это зависит от возраста .По мере того, как когнитивные способности и размер проблем ребенка со временем растут / развиваются, ваш подход к обучению навыкам решения проблем должен измениться.
Прочтите, чтобы узнать об основных стратегиях обучения детей решению проблем, а также о некоторых идеях и упражнениях для разных возрастов.
3 общие стратегии обучения решению проблем в любом возрасте
1. Модель эффективного решения проблем
Когда ВЫ сталкиваетесь с проблемой, сделайте «подумай вслух» на благо своего ребенка.МОДЕЛИРУЙТЕ, как применить те же навыки решения проблем, над которыми вы работали вместе, приводя реальные примеры, которые она может применить в своей жизни.
В то же время покажите своему ребенку готовность совершать ошибки. Каждый сталкивается с проблемами, и это нормально. Иногда первое решение, которое вы попробуете, не сработает, и это тоже нормально!
Когда вы моделируете решение проблем, объясните, что есть некоторые вещи, которые находятся вне нашего контроля. Решая проблему, мы должны сосредоточиться на том, что мы МОЖЕМ реально контролировать.
Вы можете показать печатную форму Circle of Control , входящую в комплект для печати Growth Mindset Printables Kit.
2. Спросите совета
Спросите совета у детей, когда у вас возникнет проблема. Это учит их тому, что ошибаться и сталкиваться с проблемами – обычное дело. Это также дает им возможность практиковать навыки решения проблем.
Плюс, когда вы укажете, что их идеи оценены в и оценены в , они обретут уверенность и попытаются решить проблемы самостоятельно.
3. Не давай «ответ»
Как бы трудно это ни было, позвольте вашему ребенку бороться, иногда терпеть неудачу, и, в конечном итоге, УЧИТЕСЬ на своих последствиях.
А теперь давайте взглянем на стратегий и занятий с учетом возраста, . Указанные ниже возрасты являются общими рекомендациями, не стесняйтесь выбирать любые стратегии или занятия, которые, по вашему мнению, будут работать для ВАШЕГО ребенка.
3-5 летИспользуйте коучинг эмоций
Чтобы сформировать образ мышления, направленный на решение проблем, маленькие дети должны сначала научиться управлять своими эмоциями .В конце концов, маленькому ребенку трудно логически обдумывать решения проблемы, если он в гуще истерики.
Один из способов добиться этого – использовать процесс тренировки эмоций, описанный Джоном Готтманом.
Во-первых, научите своих детей, что ВСЕ эмоции допустимы. НЕТ «плохих» эмоций. Даже такие, казалось бы, отрицательные эмоции, как гнев, грусть и разочарование, могут преподать нам ценные уроки. Важно то, как мы, , реагируем на эти эмоции .
Во-вторых, выполните этот процесс:
- Шаг первый: наименование и подтверждение эмоций. Когда ваш ребенок расстроен, помогите ему понять, как он себя чувствует. Скажите, например, : «Я понимаю, что вы расстроены, потому что Джессика играет с игрушкой, которую вы хотели».
- Шаг второй: Обработка эмоций. Поместите ребенка в его успокаивающее пространство. Если у нее его нет, неплохо создать его. Позвольте ей успокоить свое тело и обработать свои эмоции, чтобы она могла решать проблемы, учиться и расти.
- Шаг третий: решение проблемы. Обсудите с ребенком решения, делая больше СЛУШАТЬ , чем говорить во время разговора. Это позволяет вашему ребенку практиковать свои навыки решения проблем, и он с большей вероятностью действительно реализует решения, которые придумал сам.
Скажи: «Покажи мне самое сложное»
Когда ваш ребенок борется или чувствует разочарование, попробуйте методику, предложенную мамой и блоггером по воспитанию детей Лорен Тамм.Просто скажите «Покажи мне самое сложное».
Это поможет вашему ребенку определить КОРНИ проблемы, что сделает ее менее пугающей и более простой для решения.
Повторите то, что говорит ваш ребенок, «Итак, вы говорите…»
Когда вы оба поймете настоящую проблему, предложите ребенку решений . «Должен быть способ исправить это…» или «Должно быть что-то, что вы можете сделать…»
Теперь, когда ваш ребенок определил «сложную часть», он, вероятно, сможет придумать решение.Если нет, помогите ей придумать несколько идей. Вы можете попробовать задать вопрос: «Если бы вы знали DID , что бы вы подумали?» и посмотрим, что она придумывает.
Ваш ребенок может попрактиковаться в поиске решений препятствий, с которыми он сталкивается, с помощью печатной формы My Mighty Treasure Coins из набора Self-Esteem & Confidence Kit.
Решение проблем с помощью Creative Play
Позвольте вашему ребенку выбирать занятия и игры в соответствии с его интересами .Бесплатная игра предоставляет множество возможностей для поиска и решения проблем.
Дети часто лучше всего учатся через ИГРУ. Игра с такими предметами, как блоки, простые головоломки и наряды, может научить вашего ребенка решать проблемы.
Даже во время игры ваш ребенок думает критически: Куда подходит этот кусочек пазла? Что это значит? Я хочу нарядиться королевой. Что мне надеть? Куда я положил диадему? Это под диваном?
Поощряйте творческие игры, творческое мышление и решение проблем с помощью нашего замечательного набора для занятий мышлением Growth Mindset Activity Kit для детей!
Решение проблем с помощью сборников рассказов
Прочтите соответствующие возрасту рассказы с участием персонажей, которые испытывают проблемы, например:
- Ladybug Girl и Bumblebee Boy Джеки Дэвис: история двух друзей, которые хотят играть вместе, но не могут найти игру, о которой можно было бы договориться.По очереди внося предложения, они приходят к игре, в которую оба хотят играть: Ladybug Girl и Bumblebee Boy.
- Серия «Любопытный Джордж» Маргарет и Х. Рей: Любопытная обезьянка попадает в дилемму и выходит из нее, обучая детей находить собственные решения проблем.
- Ира спит более чем Бернарда Вабера: Ира очень рад ночевать в доме своего друга Реджи. Но есть одна проблема: брать с собой плюшевого мишку или нет? Это может показаться незначительным, но это тип ранней социальной проблемы, с которой может иметь отношение ваш ребенок.
Соедините эти переживания с аналогичными событиями в жизни вашего ребенка и СПРОСИТЕ своего ребенка, КАК герои этих историй могут решить свои проблемы. Поощряйте различные решения и обсуждайте возможные результаты каждого из них.
Это форма диалога, читающего , или активного ВОВЛЕЧЕНИЯ вашего ребенка в процесс чтения. Взаимодействие с текстом вместо пассивного слушания может «ускорить» развитие у детей дошкольного возраста таких навыков грамотности, как понимание.
Задавая вопросы о проблемах персонажей, вы также можете повысить способность вашего ребенка решать проблемы.
Вы можете даже попросить вашего ребенка разыграть проблему и возможные решения, чтобы закрепить урок.
Рекомендации по книгам можно найти в печатной версии «Топ 85 книг о мышлении роста для детей и взрослых» в нашем наборе для печати «Образ мышления роста».
5-7 лет
Обучайте этапам решения проблем
Придумайте для вашего ребенка простой процесс решения проблем, который вы можете последовательно реализовать.Например, вы можете попробовать следующие пять шагов:
- Шаг 1: Что я чувствую? Помогите своему ребенку понять, что он чувствует в данный момент (разочарование, гнев, любопытство, разочарование, волнение и т. Д.). Обращение к эмоциям и наименование эмоций рассеивают их заряд и дадут вашему ребенку шанс сделать шаг назад.
- Шаг 2: В чем проблема? Помогите своему ребенку определить проблему , характерную для .В большинстве случаев помогите ей взять на себя ответственность за случившееся, а не указывать пальцем. Например, вместо «Джоуи доставил мне неприятности на перемене» ваш ребенок может сказать: «У меня проблемы на перемене из-за того, что я поспорил с Джоуи».
- Шаг 3: Какие есть решения? Поощряйте ребенка придумать как можно больше решений. На данный момент они даже не должны быть «хорошими» решениями. Здесь они просто проводят мозговой штурм, еще не оценивая идеи, которые они сгенерировали.
- Шаг 4: Что произойдет, если…? Что произойдет, если ваш ребенок попробует каждое из этих решений? Является ли решение безопасным и справедливым? Как это заставит других себя чувствовать? На этом этапе вы также можете попробовать ролевую игру. Вашему ребенку важно учитывать как положительные, так и отрицательные последствия своих действий.
- Шаг 5: Какой мне попробовать? Попросите ребенка выбрать одно или несколько решений, чтобы попробовать.Если решение не сработало, обсудите ПОЧЕМУ и переходите к другому. Поощряйте ребенка продолжать попытки, пока проблема не будет решена.
Последовательно выполняйте эти шаги, чтобы они стали вашей второй натурой, и моделируйте решение собственных проблем таким же образом. Хорошая идея – отразить : Что сработало? Что не сделали? Что вы можете сделать по-другому в следующий раз?
Помогите ребенку визуализировать и попрактиковаться в этом процессе с помощью красочной печатной формы «Мое решение проблем » из набора « Самоуважение и уверенность» .
Решение проблем с помощью материалов для творчества
Ремесло – это еще одна форма игры, которая может научить детей творчески решать проблемы.
Дайте ребенку маркеры, пластилин для лепки, картонные коробки, скотч, бумагу и т. Д. Из этих простых материалов они придумают всевозможные интересные творения и изобретательные игры.
В этих «открытых игрушках» нет «правильного способа игры», позволяющего вашему ребенку проявить творческий подход и самостоятельно генерировать идеи .
Задавайте открытые вопросы
Задание открытого вопроса улучшает способность ребенка мыслить критически и творчески, что в конечном итоге делает его лучше решать проблемы. Примеры открытых вопросов:
- Как мы могли бы работать вместе, чтобы решить эту проблему?
- Как у вас это получилось? или как вы это знаете?
- Расскажите мне о том, что вы построили, сделали или создали.
- Как вы думаете, что будет дальше?
- Как вы думаете, что произойдет, если…?
- Что вы узнали?
- Что было легко? Что было сложно?
- Что бы вы сделали по-другому в следующий раз?
Открытые вопросы не имеют правильного ответа, и на них нельзя ответить простым «да» или «нет».”
Вы можете задавать открытые вопросы, даже если ваш ребенок в настоящее время не решает проблему, чтобы помочь ему практиковать свои мыслительные навыки, что пригодится, когда столкнется с проблемой, которую нужно решить.
Чтобы получить больше идей, используйте «10 вопросов о мышлении роста, которые нужно задать своим детям за обеденным столом» в нашем наборе для распечаток с установкой на рост .
7-9 летРазбивать проблемы на части
Эта стратегия является более продвинутой версией «Покажи мне сложную часть».”
Чем больше становится ваш ребенок, тем больше становятся его проблемы. Когда ваш ребенок сталкивается с проблемой, которая кажется непреодолимой или непреодолимой, предложите ему разбить ее на более мелкие, более управляемых частей.
Например, у вашего ребенка плохая оценка на уроке истории. Почему оценка такая низкая? Каковы причины этой проблемы?
Как обычно, СЛУШАЙТЕ, как ваш ребенок проводит мозговой штурм, задавая открытых вопросов , чтобы помочь, если он застрял.
Если низкая оценка является результатом пропущенных заданий, возможно, ваш ребенок сможет составить список этих заданий и выполнять по одному. Или, если проблема заключается в тестах, что заставляет вашего ребенка с трудом сдавать экзамены?
Возможно, ее отвлекают друзья в классе, она не может попросить о помощи и не проводит достаточно времени за учебой дома. Как только вы определили эти «кусочки», помогите ребенку решать их по одному, пока проблема не будет решена.
Обязательно используйте наши распечатанные карточки «Шаги по решению проблем для детей» (доступны в наборе действий для установки мышления роста). Это забавный и интерактивный способ, которым ваш ребенок может научиться решать проблемы и быть уверенным в процессе.
Шоу «Видео о сломанном эскалаторе»
Обсудите важность решения проблем и самостоятельного решения проблем с помощью «видео о сломанном эскалаторе».
На видео неожиданно ломается эскалатор. Люди на эскалаторе «застряли» и кричат о помощи. В этом возрасте, вероятно, ваш ребенок найдет видео забавным и сразу предложит решение: «Просто гуляй! Сойдите с эскалатора! »
Скажите ребенку, что это простой пример того, как люди иногда действуют в трудных ситуациях.Спросите: «Как вы думаете, почему они не сошли с эскалатора?» (не умели, помощи ждали и т. д.)
Иногда ваш ребенок может чувствовать «застрявшим» , когда сталкивается с проблемами. Они могут остановиться и попросить о помощи еще до того, как попытаются найти решение. Поощряйте ребенка принимать вызовы и вместо этого работать над их решением.
9-11 летРешение проблем с помощью подсказок
Обеспечьте вашего ребенка или группу детей такими материалами, как соломка, ватные шарики, пряжа, прищепки, скотч, скрепки, липкие заметки, палочки для мороженого и т. Д.
С помощью этих материалов предложите своим детям решить необычные задачи, например:
- Сделать ловушку для лепреконов
- Создать трамплин для машин
- Создайте свою игру с правилами
- Сделайте устройство для общения двух человек
Это интересный способ попрактиковаться в критическом мышлении и творческом решении проблем. Скорее всего, потребуется несколько попыток, чтобы найти работающее решение, применимое практически к любому аспекту жизни.
Заставьте их работать на это
Когда ваш ребенок просит новую игрушку, технологию или одежду, попросите его составить план, как получить желаемый предмет самостоятельно. Вашему ребенку придется не только провести мозговой штурм и оценить решения, но и обрести уверенность.
Спросите своего ребенка, КАК он может заработать деньги на предмет, который он хочет, и подбодрите его, когда он будет добиваться своей цели.
Положи это на бумагу
Например, используйте этот графический органайзер, разработанный The New York Times Learning Network.Ваш ребенок может определить свою проблему и найти решения.
Но теперь она продвигает этот процесс еще дальше: после попытки каждого решения, которое было успешным? Какие были неудачными? Почему ?
Это помогает вашему ребенку задуматься о различных результатах, узнавая, что работает, а что нет. Уроки, которые она усвоит здесь, будут полезны, когда она столкнется с подобными проблемами в будущем.
Возраст 12+Играем в шахматы вместе
Обучение игре в шахматы – отличный способ для детей научиться решать проблемы И строит свои мозги одновременно.Он требует от игроков критического мышления, творчества, анализа доски, распознавания закономерностей и многого другого. Есть онлайн-версии игры, книги о том, как играть, видео и другие ресурсы. Не умеете играть? Научитесь вместе со своим подростком, чтобы соединить и проблемы решать вместе!
Пусть они научатся кодировать
Наши подростки и подростки уже технически подкованы и могут использовать свои навыки для решения проблем, обучаясь программированию. Кодирование способствует творчеству, логике, планированию и настойчивости .Существует множество отличных инструментов, онлайн-программ или программ для личного общения, которые могут улучшить навыки программирования у вашего ребенка.
Поощрение к началу значимого проекта
Этот проект должен быть значимым для вашего подростка, например, создание канала на YouTube. Ваш подросток будет практиковать навыки решения проблем, когда он будет выяснять, как расширить свою аудиторию, как сделать так, чтобы их видео были обнаружены, и многое другое.
В журнале Big Life Journal – Teen Edition есть раздел, который поможет им спланировать свой канал на YouTube и начать процесс решения проблем.
Примените метод SODAS
Ищете план игры, который ваш подросток может использовать, столкнувшись с проблемой? Метод SODAS можно использовать как для больших, так и для мелких проблем. Просто запомните этот простой акроним и следуйте этим идеям:
- S ituation
- O части
- D – преимущества
- A Преимущества
- S olution
Поощряйте вступление в группы по решению проблем
Любит ли ваш подросток решать задачи в команде? Предложите им присоединиться к группе или клубу , который помогает им отточить свои навыки в различных условиях – от науки и робототехники до дебатов и международных отношений.Некоторые примеры групп включают:
- Одиссея разума
- Модель U.N.
- Дебатная группа
- Научная олимпиада
Процесс решения проблем
Обзор
Вопрос дня: Какие общие шаги мы можем использовать для решения множества различных типов проблем?
Этот урок знакомит с формальным процессом решения проблем, который студенты будут использовать в течение года: «Определить – Подготовить – Попробовать – Обдумать».Урок начинается с того, что учащихся просят провести мозговой штурм по всем типам проблем, с которыми они сталкиваются в повседневной жизни. Затем студентам показывают четыре шага процесса решения проблем, и они работают вместе, чтобы связать эти абстрактные шаги с их реальным опытом решения проблем. Сначала ученики связывают эти шаги с проблемными действиями из предыдущего урока, затем с проблемой, которую они умеют решать, а затем с проблемой, которую они хотят улучшить при решении. В конце урока класс собирает список общепринятых стратегий для каждого шага процесса, чтобы наклеить плакаты, которые будут использоваться на протяжении всего модуля и года.
Назначение
Этот урок направлен на то, чтобы закрепить формальный процесс решения проблем, который студенты будут использовать на протяжении всего курса, в практическом опыте решения проблем, который у них уже есть. Будущие единицы в CS Discoveries будут представлять проблемы в контекстах, которые могут быть знакомы, а могут и не быть. Структурированный процесс решения проблем станет важным инструментом, который поможет учащимся двигаться вперед перед лицом новых и сложных проблем.
Возможности оценки
Для данной проблемы определите отдельные действия, которые будут выполняться на каждом этапе процесса решения проблемы
На странице 2 руководства убедитесь, что учащиеся записали разумные действия для каждого из четырех этапов задачи, которую они пытаются решить.
Определите полезные стратегии на каждом этапе процесса решения проблемы
В заключение убедитесь, что учащиеся придумывают эффективные стратегии для каждого шага процесса.
Повестка дня
Изменения уроков
Разминка (5 мин)
Активность (30 мин)
Заключение (15 мин)
Расширенное обучение
Посмотреть на Code Studio
Цели
Студенты смогут:
- Для данной проблемы определите отдельные действия, которые будут выполняться на каждом этапе процесса решения проблемы
- Определите полезные стратегии на каждом этапе процесса решения проблемы
Препарат
На каждого студента
- Распечатайте копию руководства по деятельности
Для класса
- Бумага для плакатов
- Маркеры / цветные карандаши
Ссылки
Внимание! Сделайте копии всех документов, которыми вы планируете поделиться со студентами.
Учителям
Студентам
Изменения уроков
Внимание, учителя! Если вы преподаете виртуально или в социально удаленном классе, прочтите полный план урока ниже, а затем щелкните здесь, чтобы получить доступ к изменениям.
Разминка (5 мин)
Цель обсуждения
Цель: Этот разговор призван продемонстрировать, что проблемы и их решение являются частью повседневной жизни. Используйте этот мозговой штурм, чтобы перечислить на доске как можно больше различных проблем. Это будет полезно, когда вы позже попросите учащихся выбрать один тип проблемы, который, по вашему мнению, они особенно хорошо решают.
Проблемы, мозговой штурм
Подсказка: Мы используем термин «проблема» для обозначения множества различных ситуаций. Я мог бы сказать, что у меня проблема с домашним заданием, проблема с моим братом и проблема с моей машиной, и все три означают очень разные вещи. На листе бумаги я хочу, чтобы вы обдумали как можно больше различных проблем и были готовы поделиться с классом.
Учебный совет
Сделайте категории: Во время этого разговора вы можете сгруппировать проблемы в более крупные категории и пригласить учащихся помочь вам в этом.Например, если два предложения – «найти ключи» и «найти домашнее задание», предложите более широкую категорию «поиск потерянных вещей».
Реальные проблемы: Постарайтесь отвести учащихся от слишком большого количества домашних заданий или задач по предметной области (например, математических задач, задач со словами, научных задач и т. Д.), Сказав, что вас больше интересуют реальные проблемы, такие как решение разногласия, принятие важных решений, исправление или поиск вещей, перемещение из одного места в другое и т. д.
Обсудить: Студенты должны молча записывать свои идеи в течение нескольких минут.После этого предложите им поделиться написанным с соседом, а затем, наконец, соберите весь класс, чтобы составить список для всего класса. Запишите на доске или где-нибудь в другом месте, о чем думают учащиеся, все различные виды задач, которые они будут четко видеть.
Примечания
Очевидно, что мы сталкиваемся с проблемами в самых разных сферах нашей жизни. В зависимости от контекста это слово может иметь много разных значений. Сегодня мы рассмотрим несколько шагов, которые можно использовать для решения всех видов проблем.
Вопрос дня: Какие общие шаги мы можем использовать для решения множества различных типов проблем?
Активность (30 мин)
Примечания
Мы все время решаем проблемы, но не часто задумываемся о том, как мы их решаем. Наличие стратегии или процесса для решения множества различных проблем может сделать вас более вдумчивым, творческим и успешным в решении проблем.
Раздайте : Раздайте копии руководств по занятиям.
Процесс решения проблем
Видео: Посмотрите видео о процессе решения проблем в Code Studio
Цель обсуждения
Цель: В частности, для этого первого разговора вы должны убедиться, что учащиеся понимают значение четырех различных шагов. Хотя некоторые шаги иногда можно разделить на две категории, используйте этот шанс, чтобы обсудить эту двусмысленность.Ваша цель – использовать общий контекст проблемы алюминиевых лодок, чтобы понять этот процесс. Вот возможный набор шагов, которые могут придумать студенты.
Определите: Понимание проблемы, когда она была назначена, изучение доступных ресурсов, поиск проблем с их первоначальной конструкцией, прежде чем решать, как их исправить, изучение проблем с лодками других групп
Подготовить: Обсуждение с членами команды дальнейших действий, мозговой штурм подходов, прогнозирование возможных недостатков.
Попробуйте: Собственно постройку лодки, запустил тест
Reflect: Изучение результатов своего теста, сравнение их результатов с их прогнозами, обсуждение с членами группы причин, по которым лодка в конце концов затонула.
Представьте и вместе с классом просмотрите описания четырех этапов процесса, прочитав их вслух. Ответьте или обсудите любые вопросы учащихся о процессе, но в противном случае перейдите к заполнению первого раздела руководства.
Как это выглядит
Попросите учащихся заполнить первый раздел руководства по занятиям, заполнив шаги предыдущего дня, которые, по их мнению, относятся к каждому этапу процесса решения проблемы.
Обсудить: После того, как учащиеся завершат первый раздел руководства, попросите их поделиться с соседями, а затем со всем классом.
Проблема, которую вы умеете решать
Попросите учащихся выбрать один тип задач, который, по их мнению, они действительно хорошо решают.Используйте список задач, который уже есть на доске, чтобы помочь учащимся подумать о своем типе проблемы. Снова дайте им пару минут, чтобы спокойно записать шаги своего процесса, прежде чем поделиться с соседом.
Цель обсуждения
Цель: Все три обсуждения направлены на усиление значения четырех шагов в процессе решения проблемы. В этом обсуждении вы можете больше полагаться на других студентов, чтобы убедиться, что стратегии и шаги, предлагаемые студентами, соответствуют определениям 4 шагов, приведенным в руководстве по занятиям.
Обсудить: Предложите учащимся поделиться написанным с соседом, а затем снова провести обсуждение разговоров, которые у них были. Попросите учащихся рассказать об отдельных шагах, которые они используют для решения выбранной ими проблемы, но также укажите случаи, когда одни и те же типы стратегий используются несколько раз.
Проблема, которую вы и ваш одноклассник хотите улучшить в решении
Разделите учащихся на пары и попросите их заполнить последний раздел руководства.Им нужно будет выбрать тип проблемы, которую оба члена группы хотят лучше решать, а затем написать шаги, которые они будут использовать в процессе решения проблемы для решения этой проблемы.
Обсудить: Проведите последнее выступление, в котором учащиеся представят, как они будут использовать процесс решения проблемы, чтобы подойти к менее знакомой проблеме.
Создание плакатов ступеней
Учебный совет
Вы также можете выполнить это действие в цифровом виде.Посетите форум, чтобы узнать, как другие учителя изменили это задание для своих классов, или поделиться своими изменениями.
Раздайте: Раздайте каждой группе лист плаката.
Подсказка: За своими столами выберите одну из задач, над которой вы работали сегодня, и создайте плакат, показывающий, как можно использовать процесс решения проблемы для ее решения.
Обращайтесь: По мере того, как учащиеся работают над своими плакатами, задавайте им вопросы о различных проблемах и о том, как шаги по их решению соотносятся с общими этапами процесса решения проблемы.
Поделиться: Разрешите учащимся поделиться своими плакатами с остальным классом.
Заключение (15 мин)
Вопрос дня: Какие общие шаги мы можем использовать для решения множества различных типов проблем?
Возможность оценки
Убедитесь, что учащиеся придумывают эффективные стратегии для каждого этапа процесса. Это должны быть общие стратегии, а не конкретные проблемы, которые они решили решать.
Подсказка: Сегодня вы видели много разных типов проблем, но все они использовали наш процесс решения проблем. Для каждого шага процесса придумайте один общий совет, который может быть полезен независимо от того, какую проблему кто-то пытается решить.
Примечания
Я начал с того, что формальный процесс решения проблемы может помочь нам решить все виды проблем. Сегодня мы начали понимать, как выглядит этот процесс в самых разных жизненных ситуациях.Завтра мы начнем претворять этот процесс в жизнь, чтобы увидеть, как он работает на самом деле.
Расширенное обучение
Обсуждение статьи
Прочтите статью, Вы решаете не ту проблему
- Чем была интересна эта статья?
- Какие текущие события, по вашему мнению, нам нужно рассмотреть в процессе решения проблем? Почему?
Решение проблем: Найдите шаблон (2–8 классы)
Решение проблем: Найдите шаблон
Что это?
«Поиск закономерностей» – это стратегия, при которой учащиеся ищут закономерности в данных, чтобы решить задачу.Учащиеся ищут повторяющиеся элементы или числа или серию повторяющихся событий. Следующая проблема может быть решена путем поиска шаблона:
В средней школе 1000 шкафчиков, где учится 1000 учеников. Первый ученик открывает все 1000 шкафчиков; затем второй ученик закрывает шкафчики 2, 4, 6, 8, 10 и так далее до шкафчика 1000; третий ученик меняет состояние (открывает закрытые шкафчики, закрывает открытые шкафчики) шкафчиков 3, 6, 9, 12, 15 и т. д .; четвертый ученик меняет состояние шкафчиков 4, 8, 12, 16 и так далее.Это продолжается до тех пор, пока у каждого ученика не будет очереди. Сколько шкафчиков будет открыто в конце?
Чтобы получить ответ, перейдите к: Задача шкафчика от докторов математики
Почему это важно?
Шаблоны часто представляются учащимся без контекста задачи со словом, как в следующем примере: «Найдите шаблон в этой последовательности, объясните, как он работает, и используйте этот шаблон для предсказания следующих четырех чисел. 7, 10, 13 , 16, 19, __, __, __, __. ”
Младшие ученики часто открывают для себя и продолжают использовать узоры, в которых используются геометрические формы.Например, желтый круг, красный квадрат, зеленый треугольник, желтый круг, красный квадрат, зеленый треугольник и т. Д.
Обнаружение закономерностей может помочь учащимся усвоить факты умножения, когда они замечают, что 4 x 7 – это то же самое, что 7 x 4, и что все числа в столбце 10 заканчиваются нулем.
Стратегия «Найти шаблон» может использоваться для решения многих математических задач и может использоваться в сочетании со многими другими стратегиями, включая создание таблицы, составление списка или упрощение задачи.
Как это сделать?
Предложите учащимся задачу, которая требует от них найти образец для решения проблемы.Например:
Если вы построите четырехгранную пирамиду из баскетбольных мячей и не учитываете дно как сторону, сколько мячей будет в пирамиде, состоящей из шести слоев?
Использование совместных учебных групп для поиска решений проблем помогает учащимся выразить свои мысли, провести мозговой штурм, обсудить варианты и обосновать свою позицию. Найдя решение, каждая группа может представить его классу, объясняя, как они пришли к своему решению и почему они считают его правильным.Или студенты могут объяснять свои решения в письменной форме, а учитель может отображать решения. Затем студенты могут перемещаться по комнате, чтобы прочитать решение каждой группы.
Понимание проблемы
Продемонстрируйте, что первым шагом к решению проблемы является ее понимание. Это включает в себя определение ключевой информации, необходимой для поиска ответа. Это может потребовать от студентов прочитать задачу несколько раз или изложить ее своими словами.
Иногда вы можете решить проблему, просто распознав шаблон, но чаще вы должны расширить шаблон, чтобы найти решение. Составление числовой таблицы поможет вам более четко увидеть закономерности.
В этой задаче учащиеся понимают:
На верхнем уровне будет один баскетбольный мяч. Мне нужно найти, сколько шаров будет в каждом слое пирамиды, с первого по шестой. Мне нужно найти, сколько мячей будет во всей пирамиде.
Выберите стратегию
Чтобы успешно использовать эту стратегию, вы должны быть уверены, что модель действительно будет продолжаться.Попросите учащихся назвать причины, по которым они думают, что эта закономерность предсказуема, а не основана на вероятности. Проблемы, которые легче всего решить, найдя шаблон, включают те, которые просят учащихся расширить последовательность чисел или сделать прогноз на основе данных. В этой задаче учащиеся также могут составить таблицу или нарисовать картинку, чтобы организовать и представить свое мышление.
«Поиск шаблона» – подходящая стратегия для решения проблемы. Это предсказуемая модель, которая будет продолжаться.
Решите проблему
Начните с верхнего слоя или одного баскетбольного мяча. Определите, сколько шаров должно быть под этим шаром, чтобы образовался следующий слой пирамиды. При необходимости используйте манипуляторы. Студенты могут использовать любые манипуляторы, от монет до кубиков и мячей для гольфа. Студенты также могут рисовать картинки, чтобы помочь им решить проблему.
Вы можете попросить группы использовать разные манипуляторы, а затем сравнить их решения, чтобы определить, повлиял ли тип манипулятивного действия на решение.Если учащиеся моложе, начните с трех уровней и обсудите их ответы на эту более простую задачу. Затем переходите к другим уровням, по мере того как учащиеся понимают, как решить проблему.
Слой Шары добавлены Шары в этом слое 1 (вверху) 1 1 31258 31258 31258 2 = 4) 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 25 (16 + 9 = 25) 6 11 36 (25 + 11 = 36) Если это помогает визуализировать пирамиду, используйте манипуляторы для создания третьего слоя.Запишите номер и ищите выкройку. Второй слой добавляет 3 баскетбольных мяча, а следующий – 5 баскетбольных мячей. Каждый раз, когда вы добавляете новый слой, количество баскетбольных мячей, необходимых для создания этого слоя, увеличивается на 2.
- 1
- 1 + 3 = 4
- 4 + 5 = 9
- 9 + 7 = 16
- 16 + 9 = 25
- 25 + 11 = 36
Продолжайте, пока не будут записаны шесть слоев. Как только шаблон будет найден, учащимся может не понадобиться использовать манипуляторы.
Затем добавьте баскетбольные мячи, использованные для создания всех шести слоев.Ответ – 91 мяч. Посмотрите на список, чтобы увидеть, есть ли другой узор. Количество шаров, используемых на каждом уровне, равно квадрату номера слоя. Итак, 10-й слой будет иметь 10 x 10 = 100 шаров.
Проверить
Прочтите проблему еще раз, чтобы убедиться, что на вопрос дан ответ.
Да, я нашел общее количество баскетбольных мячей в шестиуровневой пирамиде.
Проверьте математику, чтобы убедиться, что она верна.
1 + 4 + 9 + 16 + 25 + 36 = 91
Определите, была ли выбрана наилучшая стратегия для этой проблемы или существовал другой способ решения проблемы.
Поиск шаблона был хорошим способом решить эту проблему, потому что шаблон был предсказуем.
Объясните
Учащиеся должны объяснить свой ответ и процесс, через который они прошли, чтобы его найти. Студентам важно говорить или писать о своем мышлении. Продемонстрируйте, как написать абзац с описанием шагов, которые предприняли учащиеся, и того, как они принимали решения на протяжении всего процесса.
Сначала я начал с первого слоя.Я использовал блоки, чтобы построить пирамиду, и составил список из количества блоков, которые я использовал. Затем я создал таблицу для записи количества шаров в каждом слое.
Слой Шары добавлены Шары в этом слое 1 (вверху) 1 1 31258 31258 31258 2 = 4) 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 25 (16 + 9 = 25) 6 11 36 (25 + 11 = 36) Я сделал четыре слоя, а затем увидел узор.Я видел, что для каждого слоя количество использованных шаров было числом слоя, умноженным на самого себя. Я закончил узор без блоков, умножив количество шаров, которые будут в слоях 5 и 6.
Затем я сложил все шары в каждом слое.
1 + 4 + 9 + 16 + 25 + 36 = 91Всего у меня 91 мяч.
Практика с инструкциями
Попросите учащихся решить следующую задачу, используя стратегию «Найти шаблон».
Женщина пытается сократить количество банок газировки, которое она пьет каждую неделю. Она составляет план, чтобы через несколько недель выпить только одну банку газировки. Если она начнет с 25 банок в первую неделю, 21 банку во вторую неделю, 17 банок в третью неделю, 13 банок в четвертую неделю и продолжит эту схему, сколько недель ей потребуется, чтобы достичь своей цели?
Попросите учащихся поработать в парах, группах или индивидуально, чтобы решить эту задачу. Они должны уметь рассказать или написать о том, как они нашли ответ, и обосновать свои рассуждения.
Как можно расширить эту стратегию?
Математические задачи могут быть простыми, с несколькими критериями, необходимыми для их решения, или они могут быть многомерными, требуя диаграмм или таблиц для организации мышления учащихся и записи шаблонов. При использовании шаблонов ученикам важно выяснить, будет ли шаблон предсказуемо сохраняться. Попросите учащихся определить, есть ли причина для продолжения шаблона, и убедитесь, что учащиеся используют логику при поиске шаблонов для решения проблем.
Например, если идет дождь в воскресенье, снег в понедельник, дождь во вторник и снег в среду, будет ли дождь в четверг?
Другой пример: если Лорен выиграла первую и третью партию в шахматы, а Уолтер выиграл вторую и четвертую партию, кто выиграет пятую партию?
Другой пример: если растение выросло на 13 сантиметров за первую неделю и 10 сантиметров за вторую неделю, на сколько сантиметров оно вырастет за третью неделю?
Поскольку это вопросы вероятности или природы, убедитесь, что учащиеся понимают, почему нельзя использовать шаблоны для поиска ответов.
5-этапное решение проблем для детей младшего возраста
Даже маленьких детей можно научить решать свои проблемы мирным путем с помощью следующих 5 шагов:
Шаг первый: Как вы себя чувствуете? Успокойся. – Часто, когда мы сталкиваемся с проблемой, мы чувствуем разочарование или злость. Прежде чем мы сможем решить нашу проблему, нам нужно узнать, как мы себя чувствуем, и успокоиться. Есть разные способы успокоиться; мы могли бы сделать перерыв, сделать три глубоких вдоха, использовать “”.
Шаг второй: в чем проблема? – Нам нужно знать, в чем проблема, прежде чем мы сможем ее решить.Почему вы злитесь или расстроены? Помните, что эта проблема принадлежит вам, а не другим людям.
Шаг третий: Найдите решения – Полезно подумать о как можно большем количестве различных решений проблемы. Не все решения подойдут. Решение может сработать один раз, но не в другой раз. Чем больше проблем вы решите, тем легче придумать решения.
Шаг четвертый: что произойдет? – Подумайте, что произойдет, если вы выберете каждое из предложенных вами решений.Решение безопасно? Безопасное решение означает, что никто не пострадает и не расстроится. Справедливо ли решение? Как все будут себя чувствовать?
Шаг пятый: попробуйте решение – выберите решение. Попробуйте свое решение. Это решило проблему? Если решение не решает проблему, вы можете попробовать одно из других решений, которые вы придумали.
План урока: мирное решение проблем
Предпосылки и результаты обучения:
Номерпредназначен для детей в возрасте от 4 до 6 лет для работы в детских учреждениях, дошкольных учреждениях, детских садах или на дому.Однако его можно адаптировать для других возрастов. Обучая детей основным шагам решения проблем и предоставляя им возможность практиковать этот навык, дети могут стать компетентными в решении проблем.
Материалы:
- Большая бумага и маркер для написания идей
Учебная и обучающая деятельность:
Представьте тему «Проблемы». Попросите детей рассказать о недавних проблемах. Вы можете добавить свои собственные примеры проблем, которые у вас были, или проблем, которые вы наблюдали в классе.
Объясните детям, что они могут стать экспертами в решении проблем, используя пять шагов для решения проблем.
Представьте и кратко объясните каждый этап решения проблемы.
Выберите пример проблемы, которую поделили дети. Решите проблему с детьми, используя пять шагов для решения проблемы.
Шаг 1. Как вы себя чувствуете? Успойкойся. Попросите детей определить, что они чувствовали или как бы они себя чувствовали, если бы эта проблема случилась с ними.Попросите их посоветовать успокоиться. Практикуйте способы успокоиться, например трижды глубоко вдохните.
Шаг 2: В чем проблема? Попросите детей описать, в чем проблема. Помогите детям переосмыслить проблему, чтобы она была определена как их проблема, а не проблема кого-то другого. Например: «Я хочу использовать красный карандаш» вместо «они не поделятся красным карандашом».
Шаг 3. Придумайте решения. Поощряйте детей придумать как можно больше решений.Вначале вам может потребоваться помочь им с решениями. Запишите возможные решения. На этом этапе основное внимание уделяется созданию как можно большего числа решений, а не их оценке.
Шаг 4: Что произойдет? Попросите детей подумать, что было бы дальше, если бы они выбрали решение. Решение безопасно? Безопасное решение означает, что никто не пострадает. Справедливо ли решение? Как все будут себя чувствовать? Предложите детям обсудить найденные ими решения и подумать о том, что будет дальше.Разыгрывание решений по ролям может помочь детям понять возможные последствия.
Шаг 5. Попробуйте решение. Попросите детей выбрать решение проблемы. Будет ли проблема решена? Выбранное решение тоже может быть ролевым.
Адаптации:
- Сопровождение каждого шага визуальной подсказкой полезно, особенно для детей с ограниченными словесными навыками.
- В зависимости от возраста и степени внимания детей выполнение шагов по решению проблем на примере задачи можно разделить на разные уроки.Начните с введения пяти шагов в первом уроке, а затем на каждом последующем уроке практикуйте по одному шагу.
- Ролевая игра «Различные решения проблем с детьми», чтобы помочь им понять последствия решений.
Дополнительная деятельность:
Когда детей научат этим пяти шагам решения проблем, им понадобится возможность попрактиковаться в их использовании. Эти последующие действия усиливают шаги по решению проблем и предоставляют возможности для практики:
Разместите наглядные изображения шагов по решению проблем в комнате, где они будут видны детям, чтобы они могли постоянно к ним обращаться.
Регулярно возвращайтесь к этапам решения проблем. Попросите детей привести другие примеры проблем, с которыми они столкнулись, или создать гипотетические проблемы, имеющие отношение к их жизни. Поработайте над этими проблемами в классе, используя шаги по их решению.
Когда в классе возникают проблемы, напомните детям использовать их шаги по решению проблем и проведите их через процесс. По мере того, как они становятся более компетентными в решении проблем, им потребуется меньше помощи для проработки шагов.
Ролевая модель эффективного решения проблем для вашего ребенка.
Выберите детские книги, в которых персонажи сталкиваются с проблемой. Спросите детей, как герой рассказа мог бы решить их проблему. Поощряйте разнообразные решения. Попросите детей разыграть проблему и возможные решения. Примеры книг:
Хороший день (2007) Кевина Хенкеса. Птица, Лисица, Собака и Белка не очень хорошо начинают свой выходной день.Однако, проявив немного терпения, они обнаруживают, что могут преодолеть незначительные неудачи, чтобы в конце концов провести очень хороший день. Возраст 0-6 лет.
Бобби против девочек (случайно) (2009) Лиза Йи. Бобби и Холли были лучшими друзьями в течение многих лет, пока разногласия не грозили разлучить их навсегда. Однако, когда их аргумент случайно вызывает настоящую войну между мальчиками и девочками в их четвертом классе, они должны найти способ вернуть все в норму.Возраст от 6 до 12 лет.
9 советов и приемов по обучению задачам со словами
Привет! Меня зовут Джо-Эллен из Love Believe Teach с Джо-Эллен Фуди, и я рада быть приглашенным блогером для Рэйчел Линетт.
Давайте поговорим о… проблемах со словами. Я могу начать с того, что мне нравится учить детей решать словесные задачи, но я не буду этого делать. Проблемы со словом сложны. Двухэтапные задачи со словами еще сложнее, и научить их решать, возможно, будет самым сложным навыком, которому вы обучаете в течение всего года.Хуже всего то, что вы ничего не можете с этим поделать. Неа! Нада! Задачи со словами есть в каждой математической программе, в каждом классе, в каждом стандартизированном математическом тесте, и они являются важным навыком, которым ученики должны овладеть, чтобы выжить в нашем мире. И это наша главная цель, верно?
Итак, вот что я нашел наиболее полезным и наименее болезненным для учащихся способом научиться решать сложные словесные задачи.
Не ожидайте 100% мастерства после одного урока.Этого просто не произойдет. Я знаю, что это может быть трудно понять, но этот навык требует ВРЕМЕНИ и очень много. К сожалению, от этого никуда не деться.
Признайте, что задачи со словом сложны и вашим ученикам потребуется много практики с ними. Почему-то произнесение этого вслух делает весь процесс немного менее пугающим.
Используйте много, много, много форм практики. Я не могу этого достаточно подчеркнуть. Если у вас нет ученика, обладающего сверхспособностями к решению задач чудодейственного слова, вашим ученикам понадобится ОЧЕНЬ много практики.Студентам нужны непосредственные инструкции всего класса, время с партнером, самостоятельные занятия для практики, веселые игры «вставай и двигайся», центры карточек с заданиями и домашние задания. Да, вам нужно привлечь родителей ваших учеников к тому, чтобы помочь их детям справиться с этими трудными проблемами. Разнообразие важно для того, чтобы ваши ученики продолжали практиковаться и улучшать свои навыки.
Обучайте, переучивайте, а затем, по прошествии некоторого времени, переучивайте снова. Иногда детям нужно время, чтобы усвоить все трюки, которым вы их научили.Поэтому после первого вводного урока подождите немного и повторите его с помощью короткого мини-урока, чтобы освежить их сознание. Повторяйте мини-уроки столько раз, сколько нужно.
Ох, ох! Я сказал это. И да, я имел это в виду. От этого никуда не деться. Судя по моему опыту, да, у меня его более 18 лет, студентам нужно много-много практики, чтобы справиться с задачами со словом. Иногда, просто иногда, может помочь решить проблему за проблемой. Вы можете мне не поверить, но для детей они действительно воспринимают это как вызов.Поверьте мне!
Вот как я это делаю: сначала я раздаю лист с упражнениями №1 с одной или двумя задачами. Я даю студентам время закончить, и как только они заканчивают, они проверяют его. Если они все поймут правильно, я немедленно даю им страницу №2. Затем я повторяю процесс снова и снова, пока не почувствую, что они устают. Вы узнаете, когда ваш класс достигнет дневного максимума. Они начнут отказываться от задания, не будут работать так усердно, «веселье» больше не витает в воздухе, и вот тогда я понимаю, что пора переходить к следующему занятию.
Еще один способ попрактиковаться – превратить его в игру, чтобы увидеть, сколько задач класс может правильно решить за x минут. Начните со слов: «Мы будем выполнять столько задач, сколько сможем за пять минут. На своей отметке, готовься, ВПЕРЕД! » Ваш класс будет думать, что они играют в игру, а не решают сложные задачи со словами. Вы можете легко отслеживать, сколько задач класс решил правильно в установленные сроки. Если вы повторите эту игру несколько раз, вы увидите, что их общее количество становится все выше и выше по мере роста их навыков.Затем посмотрите, как ваш класс отмечает свои достижения. Они это заслужили!
БЕСПЛАТНАЯ ЗАДАЧА, состоящая из двух слов, которая поможет вашим ученикам начать практиковаться и практиковаться. Я считаю, что наиболее эффективно начинать с одной задачи на странице, а учащиеся работают над тремя задачами на странице.
Да, некоторым детям они нужны. Им нужна система, которой нужно следовать. Я обнаружил, что дать студентам одну простую и понятную стратегию – лучший способ помочь этим студентам.Для них это просто не так запутанно. Убедитесь, что вы выбрали удачную стратегию!
Вот слово «план атаки», которое я использую со своими второклассниками:
- Шаг 1. Прочтите проблему и подумайте: «В чем проблема?»
- Шаг 2. Перечитайте проблему и подумайте: «В чем проблема?»
- Шаг 3. Спланируйте «атаку» и подумайте: «Как лучше всего решить эту проблему?»
- Шаг 4. Решите проблему и подумайте: «Какую операцию мне следует использовать?»
- Шаг 5: Проверьте свой ответ и подумайте: «Имеет ли мой ответ смысл? Моя математика верна? ”
Да, мы учителя и должны учить, но иногда дети просто не понимают, что мы говорим или как мы что-то объясняем.Это не делает нас плохими учителями; считайте это тайной юного ума. Все, что вам нужно сделать, это разделить студентов на пары, которые борются с кем-то, кто пытается справиться с проблемами. Прежде чем вы это узнаете, каждый с легкостью справится с этими проблемами со словами!
Попросите учащихся написать свои собственные задачи со словами, а затем попросите друга решить их. Как только ваши ученики научатся решать задачи со словами, вы увидите, как их понимание этих задач будет расти.
Поговорите о том, что есть много разных способов решить словесную проблему, и что это на 100% нормально решать проблему с помощью стратегии, отличной от чьей-либо другой.Примите эту идею и скажите своим ученикам, что все наши умы уникальны и решение этих проблем просто должно иметь смысл для вас.
Итак, вот и все. Я искренне надеюсь, что вы сможете найти несколько идей, которые сможете сразу же реализовать в своем собственном классе. Для большинства студентов проблемы со словами являются сложной задачей, но они никуда не денутся. Итак, давайте просто сделаем их чем-то, над чем мы будем работать вместе. Если у вас есть какие-либо советы и приемы, которые сработали для ваших учеников, я хотел бы услышать о них в комментариях ниже.
Джо-Эллен Фуди преподает более 18 лет в классах K-3. Она замужем, у нее двое маленьких мальчиков. Джо-Эллен увлечена мотивацией студентов выходить за рамки того, что, по их мнению, было возможным. Ее магазин Teachers Pay Teachers называется Love Believe Teach with Jo-Ellen Foody и ориентирован на класс K-3. Вы можете найти ее в Facebook, Instagram, Pinterest, Twitter или по электронной почте. .

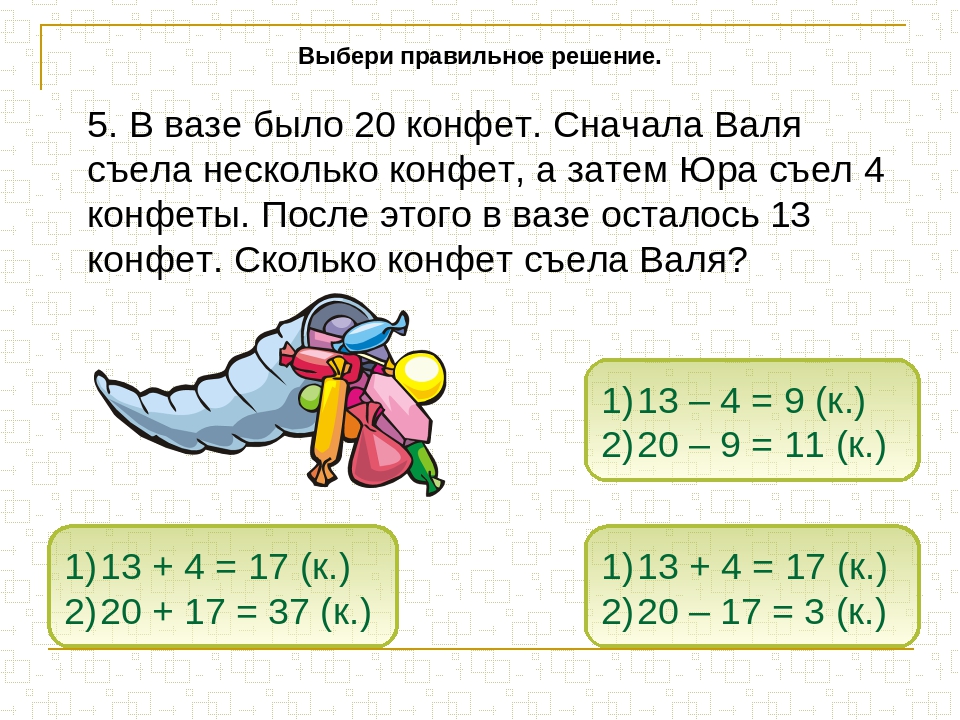 (таблица – подсказка, вспомни как делать краткую
запись. Помни НА (+ / -), В ( Х / : )
(таблица – подсказка, вспомни как делать краткую
запись. Помни НА (+ / -), В ( Х / : ) )
) .
.

 1.Целеполагание
1.Целеполагание