Как решать ребусы с буквами и цифрами: Как решать ребусы? | Развивающие игры для детей — онлайн занятия для детей
Ребусы с буквами
Метки
Головоломки Досуг Загадки Ребусы Смекалка ХоббиКто из нас не любит ребусы с буквами и цифрами? Слова в них зашифрованы при помощи картинок и разных символов. А разгадывать эти загадочные послания нам помогает целый свод правил. Вроде бы всё просто: сколько запятых стоит после слова, столько букв нужно убрать с его конца.
© Pixabay
Предмет нарисован в перевернутом виде — читай его название справа налево. Если, например, цифра 7 нарисована внутри буквы «О», читай «в-о-семь». Стоп, но с таким же успехом это можно прочитать, как «семь-в-о».
© Depositphotos
Вот и тут начинаются сложности. Ведь называть и комбинировать слова и символы на картинках можно десятками способов. Поэтому, чтобы найти правильный ответ, читателям понадобятся зоркий взор и недюжинная смекалка!
Ребусы с буквами
- Начнем с самого простого.
- Тот случай, когда не мудрено запутаться даже в двух буквах.
- Что ж, с правилами мы уже знакомы. Сколько запятых стоит перед словом, столько букв нужно убрать. В результате получается что-то типа «автомат-вал-а-елка»? Ничего не понимаю!
- Хоть и спрятал глаза за очками, но явно на что-то намекает. И физиономия, прошу заметить, глумливая, как у одного гражданина с Патриарших.
- Любители русского рока, ваш выход. Сумеете прочитать зашифрованное в рисунке название популярной песни?
Ответы с объяснением
- Ясно-понятно, что нужно как-то состыковать «к» и «ч». Но иногда проще сказать, чем сделать. «Ка-и-ч», «ка-в-ч» или «ка-на-ч»? Нужно иметь развитое воображение, чтобы представить, что буквы «ка» вроде как идут по «ч». Получаем «по-ч-ка» или почка!
- Имеем букву «о» и какое-то ведро с буквой «а». Другими словами, рядом с «о» стоит бак с буквой «а». Остается лишь отбросить лишнее, чтобы получить «с-о-бак-а» — собака!
- Тот случай, когда для изображенных предметов приходится искать другие названия. Кто-то скажет «автомат», кто-то — «оружие», а самые смекалистые произнесут всего две буквы — АК! Та же история и с елочкой. Но тут логическая цепочка чуть подлиннее: елка — украшения — Новый год — НГ! Остается сложить одно с другим, чтобы прочитать слово акваланг!
- Мужчина за «е» или «е» перед ногами? Не будем томить читателя и сразу назовем правильный ответ. Как видно, буква нашему гражданину ровно по колени. Иными словами «по колени е» — поколение!
- Уверен, что поклонники группы «ДДТ» ответили не задумываясь. Ведь на картинке буквально «плачущее небо по ногами»!
А замечательная песня, откуда мы взяли эту фразу, называется, конечно,
Остается лишь отбросить лишнее, чтобы получить «с-о-бак-а» — собака!Такие вот несложные ребусы, с которыми, мы уверены, ты легко справился. Но даже от такой простой тренировки можно извлечь немало пользы.
Или же пищу для размышлений о том, что тебе стоило бы поработать над собой, чтобы в следующий раз решить все задачки, не заглядывая в ответы.
Поделиться
Вопрос Видео: решение криптоарифметических головоломок
Стенограмма видео
Каждая буква в этой криптоарифметической задаче представляет собой отдельную цифру, и ни в одной из цифр нет ведущих нулей. Найдите значение каждой буквы в головоломке, чтобы составить правильную сумму.
Мы собираемся решить эту головоломку, используя логику и исключение. Во-первых, я просто собираюсь передвинуть это, чтобы освободить место. А затем мы собираемся перечислить каждую из букв C, R, O, S, A, D, N, G, E. Мы перечислим все цифры, которые может представлять каждая из этих букв.
Почти сразу мы можем посмотреть на этот D и определить, какое число он должен представлять. Чтобы найти значение D, нам нужно сложить C и R. Но даже если бы C и R были самыми большими из цифр, например, девять и восемь, в сумме они давали бы 17.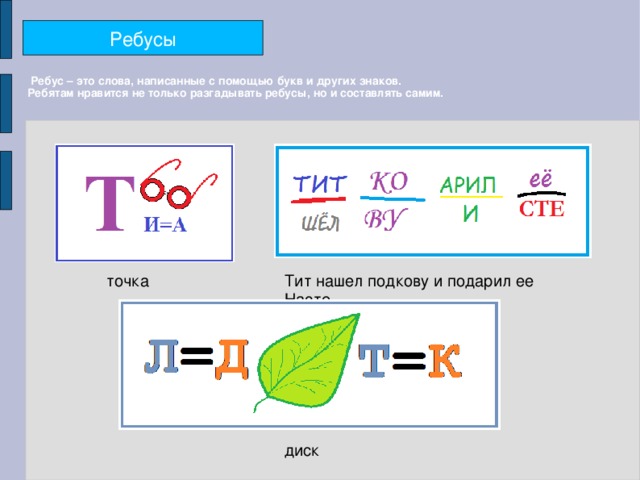
Так что неважно, какая цифра D представляет должен быть равен единице. Оно не может быть больше единицы.
Мы также знаем, что ведущих нулей нет, а это значит, что D не может быть равно нулю. D должен быть равен единице. А это значит, что D не равно ни одному из этих других чисел. Это также означает, что ни одна из других букв не может быть равна единице.
Отличное начало. Но, к сожалению, это действительно единственное, что сразу очевидно для нас. Но я признаю, что S плюс S равно R. И мы можем сделать из этого некоторые выводы. Если мы знаем, что что-то плюс само по себе равно R, мы можем исключить некоторые значения. Поскольку R — одна цифра, S должно быть меньше пяти. Пять плюс пять будет равно 10. А 10 имеет более одной цифры.
Мы не знаем, что такое S, но мы знаем некоторые вещи, которыми S не может быть. Оно не может быть больше пяти. Но как насчет нуля? Может ли S быть равно нулю? Нет, это невозможно. Ноль плюс ноль будет равно нулю. Тогда оператор должен будет сказать, что S плюс S равно S.
У нас есть три варианта для нашего значения S. И поскольку у нас есть три варианта значения S, это также означает, что у нас есть три варианта значения R.
Наш первый вариант: два плюс два равно четырем. Это означает, что R может быть равно четырем. Три плюс три равно шесть. R может быть равно шести. А четыре плюс четыре равняется восьми. Это единственные три варианта для R. И мы можем исключить все остальные цифры. Опять же, мы не знаем, что такое R, но мы знаем некоторые вещи, которыми R не является.
Переходим к S плюс D равно E, S плюс D равно E, и мы уже знаем, что D равно единице. Здесь мы снова не знаем, что такое S, но знаем три его варианта. Один вариант — это два плюс один равно Е. Е может быть равно трем, или три плюс один равно Е. В этом случае Е будет четыре. Последний вариант для E — четыре плюс один. Е может быть равно пяти. Е не может быть равно нулю, двум, шести, семи, восьми или девяти.
В начале мы говорили кое-что о C плюс R, но сейчас мы более подробно рассмотрим C плюс R.
C плюс R равняется единице в десятках. Если мы посмотрим на R, мы исключим все возможные варианты, кроме трех. R будет равно четырем, шести или восьми. Если R равно четырем, чему может быть равно C? Попробуем шесть. C равно шести. Шесть плюс четыре равно 10.
Хорошо, в этом сценарии C равно шести, а A равно нулю. Но если А равно нулю, тогда у нас проблема, потому что все, что плюс ноль, равно самому себе. Что произошло бы, если бы буква O плюс ноль были бы равны букве O, а не букве G. О чем это говорит нам?
Прежде всего, это говорит нам о том, что A не может быть равно нулю. Это также говорит нам, что C не может быть равно шести. Хорошо, но это не единственный случай, когда R равно четырем, не так ли? Как насчет семи? Может ли C равняться семи?
Итак, семь плюс четыре равняется 11. И поскольку мы знаем, что D представляет единицу, семь плюс четыре будет равно DD, а это означает, что C не может быть равно семи. Есть ли что-нибудь еще, что мы можем добавить к четырем? Мы могли бы попробовать восемь.
Восемь плюс четыре равно 12. И пока у нас нет причин исключать эти два варианта. Таким образом, мы можем обвести C, возможно, равному восьми, а A, возможно, равному двум.
У нас есть еще один случай, если R равно четырем. Это тот случай, когда C равно девяти. Девять плюс четыре равняется 13, и мы обведем девять для варианта С и три для варианта А. Итак, мы только что сказали, что если R равно четырем, C может быть равным восьми или девяти, а A может быть равным двум или трем.
Теперь мы хотим рассмотреть случаи, когда R равно шести. Начиная с четырех, четыре плюс шесть равно 10. Но мы уже видели, что А не может быть равно нулю. А это значит, что C не может быть равно четырем. Это неверный вариант.
Можно попробовать пять. Пять плюс шесть равно 11. Мы уже видели, что А не может быть равно единице. И если А не может быть равно единице, С не может быть равно пяти. Мы уже исключили C = семь. C равно восьми все еще кажется, что это может работать. Восемь плюс шесть равно 14.
Если C равно восьми, а R равно шести, то A будет равно четырем. Это все случаи, когда R равно шести.
Теперь мы хотим рассмотреть случай, когда R равно восьми. Если C равно двум, два плюс восемь равно 10. Мы знаем, что A не равен нулю. Следовательно, C не равно двум. Три плюс восемь равно 11, а А не может быть равно единице. Следовательно, С не может быть равно трем. Мы уже исключили четыре, пять, шесть и семь вариантов для C.
Следующим вариантом будет восемь. Восемь плюс восемь равно 16, но вы заметили здесь проблему? Если R равно восьми, то C не может быть равно восьми, а значит, это не наш вариант. Последний случай был бы C равным девяти. Девять плюс восемь равно 17. Если C равно девяти, R равно восьми, то A будет равно семи. И что теперь?
Если мы присмотримся, то увидим, что действительно пропустили одну из наших пар. Мы видели случай, когда C равно восьми, а R равно шести. Как насчет случая, когда C равно девяти? Если C равно девяти, то A будет равно 15. Итак, теперь у нас есть пятый вариант того, каким может быть A.
В этот момент может показаться, что мы получаем все больше и больше возможностей, а не все меньше и меньше. Но мы идем дальше и вычеркиваем то, что, как мы знаем, А не может быть. В моем списке буква С мы видим, что у нас может быть ноль, восемь или девять.
Рассмотрим случай, когда C равно нулю. Если бы C было равно нулю, а R могло быть только четыре, шесть или восемь, мы бы никогда не получили единицу вместо D. И это помогает нам исключить ноль как вариант для C.
В этот момент я хотите взять все маленькие задачи на сложение и записать их горизонтально. А потом я попробую все случаи, когда С равно восьми, а С равно девяти. Вот так.
C равно восьми и R равно четырем. Там у нас 12. Если R равно четырем, мы снова ставим четыре. Мы не знаем О; мы не знаем N; мы не знаем О; но А было бы равно двум, и мы все равно не знали бы G. В этом случае S должно быть равно двум. Два плюс один равняется трем. Е будет равно трем. А два плюс два равно четырем. Этот набор не помог нам ничего исключить, поэтому мы просто оставим его там.
И затем мы перейдем к тому, что C — девять, а R — четыре.
Девять плюс четыре равно 13. Четыре плюс О равно N; О плюс А равно G, но мы знаем, что А равно трем. В этом случае S равно двум, а D равно единице. Два плюс один равняется трем. Но посмотрите, что произошло. В этом случае и A, и E отображаются как три. А мы знаем, что повторяющихся цифр быть не может. А не может быть равно трем.
На этот раз мы выберем C равно восьми, а R равно шести. Восемь плюс шесть равно 14. Шесть плюс О равно N. Мы не можем решить это. О плюс четыре равно G. S плюс D, три плюс один равно четырем. И мы столкнулись с проблемой, потому что теперь у нас есть A и E, отображаемые как четыре. Мы можем исключить A, равное четырем.
Следующий раунд, C равняется девяти, а R равняется шести. Девять плюс шесть равно 15. Шесть плюс О равно N. Мы ничего не можем сказать об этом. О плюс пять равно G. Три плюс один равно четырем, а три плюс три равно шести.
Сейчас я хочу записать, какие цифры мы использовали в обоих этих случаях.
Пока я все это записываю, я замечаю, а может быть, и у вас тоже, ошибку в этом наборе. Посмотрите, сколько раз используется двойка. Это потому, что мы использовали значение два для A и S в этом примере. А не может быть равно двум, и этот вариант недействителен.
Теперь, когда мы подошли к розовому набору, я хочу записать все цифры, которые мы уже использовали. Мы использовали значения один, три, четыре, пять, шесть и девять, что означает, что нам все еще нужны значения два, семь и восемь. У нас пропущены три буквы: O, E и G. Есть ли способ использовать два, семь и восемь и сделать все эти утверждения верными?
Если я подставлю два вместо О, то в итоге я получу шесть плюс два равно Е. Два, кажется, работают. Шесть плюс два равняется восьми. И последний вопрос: «Два плюс пять равно семи?» Это. Теперь кажется, что мы заполнили все эти пробелы. Давайте проверим и убедимся, что мы не сделали ошибок.
Мы сказали, что C равно девяти, а это значит, что никакое другое значение не может быть равно девяти.
Мы сделали R равным шести. Все идет нормально. Мы уже определили, что D равно единице. Теперь у нас А равно пяти. Затем O равно двум, G равно семи, N равно восьми, S равно трем и Е равно четырем. C равно девяти; R равно шести; О равно двум; S равно трем; А равно пяти; D равно единице; N равно восьми; G равно семи; Е равно четырем.
Если вы дошли до конца, вы, вероятно, задаетесь вопросом: «Это единственный способ решить эту проблему? Это лучший способ решить эту проблему?» Это способ, которым вы решаете подобную проблему вручную. Сегодня чаще всего люди используют компьютерные программы, чтобы сократить время, необходимое для решения чего-то подобного. Компьютеры способны выполнять процесс, который мы только что завершили, но быстрее и эффективнее. Однако, если вы когда-нибудь окажетесь на необитаемом острове и вам нужно решить криптоарифметическую головоломку, это будет способ сделать это.
How To Solve a Word Sum
| T | H | R | E | E | |
| T | H | R | E | E | |
| + | F | O | U | R | |
| E | L | E | V | E | N |
Сможете ли вы найти цифры, которыми можно заменить буквы, чтобы эта сумма была правильной?
Примечание для учителя.
Если вы представляете эту головоломку своему классу с помощью проектора, вы можете медленно прокручивать пошаговое руководство ниже, давая подсказки, которые могут помочь вашим ученикам решить головоломку самостоятельно.
Решение
Не существует стандартного способа решения подобной проблемы. Каждый из них совершенно отличается по структуре и будет иметь свои собственные подсказки; но, сказав это, вот пример того, как решить эту конкретную задачу, которая может дать вам идеи для решения других.
Мы должны предположить, что каждая буква обозначает другую цифру.
1. Первое, на что следует обратить внимание, это то, что в нижней строке шесть цифр. Когда две T складываются вместе, ответ приводит к переносу цифры. Эта переносимая цифра, скорее всего, является единицей, хотя есть небольшая вероятность, что это может быть 2. Давайте возьмем единицу и вернемся сюда, если это не сработает.
| T | H | R | 1 | 1 | |
| T | H | R | 1 | 1 | |
| + | F | O | U | R | |
| 1 | L | 1 | V | 1 | N |
2.
Глядя на столбец десятков, чтобы получить цифру один в нижней строке, U должен быть девяткой, если нет цифры, перенесенной из столбца единиц . Пойдем с девяткой и вернемся сюда, если не получится.
| T | H | R | 1 | 1 | |
| T | H | R | 1 | 1 | |
| + | F | O | 9 | R | |
| 1 | L | 1 | V | 1 | N |
It may be useful to keep a record of the letters involved in the головоломка и возможные цифры, которые они могут обозначать:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| T | ✗ | ✗ | ||||||||
| H | ✗ | ✗ | ||||||||
| R | ✗ | ✗ | ||||||||
| E | ✗ | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| F | ✗ | ✗ | ||||||||
| O | ✗ | ✗ | ||||||||
| U | ✗ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | ✓ |
| L | ✗ | ✗ | ||||||||
| В | ✗ | ✗ | ||||||||
| N | ✗ | ✗ |
3.
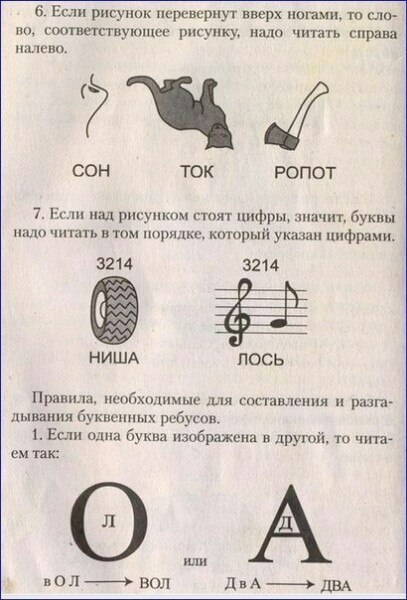Теперь немного сложнее обнаружить какие-либо уверенности, хотя мы можем видеть, что если R четно, то N также четно (и наоборот).
Давайте сделаем предположение и посмотрим, как далеко оно нас заведет. Мы начнем со столбца единиц измерения, так как не нужно беспокоиться о переносимых числах.
Мы предполагаем, что R будет наименьшей возможной цифрой, ноль. Если это неверно и мы застряли дальше, мы всегда можем вернуться к этой точке и изменить наше предположение на следующую наименьшую цифру и так далее.
Если R равно нулю, то N должно быть равно 2.
Здесь будьте осторожны, чтобы не перепутать букву O и цифру ноль. Мы будем использовать ноль с косой чертой, Ø, чтобы избежать путаницы.
| T | H | Ø | 1 | 1 | |
| T | H | Ø | 1 | 1 | |
| + | F | O | 9 | Ø | |
| 1 | L | 1 | V | 1 | 2 |
Эта информация обновлена в таблице.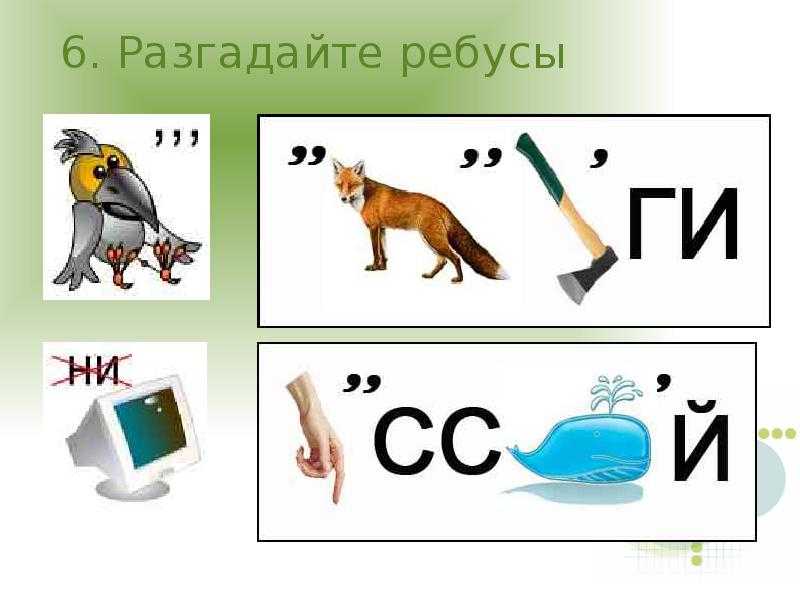
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| T | &крест; | &крест; | ✗ | |||||||
| H | ✗ | &крест; | &крест; | ✗ | ||||||
| R | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| E | ✗ | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| F | ✗ | &крест; | &крест; | ✗ | ||||||
| O | ✗ | &крест; | &крест; | ✗ | ||||||
| U | ✗ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | ✓ |
| L | ✗ | &крест; | &крест; | ✗ | ||||||
| V | ✗ | &крест; | &крест; | ✗ | ||||||
| N | ✗ | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
Работая по столбцам справа налево, мы можем работать с переносимыми числами по мере их появления.
4. Сделаем еще одно предположение. На этот раз для буквы O. Из таблицы видно, что наименьшая цифра, которая может быть, — это тройка. Если это неверно и мы застряли дальше, мы всегда можем вернуться к этой точке и изменить наше предположение на следующую наименьшую цифру и так далее.
Если O равно 3, то V должно быть равно четырем, так как единица переносится из столбца 10.
| T | H | Ø | 1 | 1 | |
| T | H | Ø | 1 | 1 | |
| + | F | 3 | 9 | Ø | |
| 1 | L | 1 | 4 | 1 | 2 |
The table is updated with this information.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| T | ✗ | &крест; | &крест; | &крест; | &крест; | ✗ | ||||
| H | ✗ | &крест; | &крест; | &крест; | &крест; | ✗ | ||||
| R | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| E | ✗ | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| F | ✗ | &крест; | &крест; | &крест; | &крест; | ✗ | ||||
| O | ✗ | &крест; | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| U | ✗ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | ✓ |
| Л | &крест; | &крест; | &крест; | &крест; | &крест; | ✗ | ||||
| V | ✗ | &крест; | &крест; | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; |
| N | &крест; | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
5.
Давайте сделаем еще одно предположение. На этот раз для буквы H. Из таблицы видно, что наименьшей цифрой, которая может быть, является пятерка.
Если H равно пяти, F должно быть равно единице, чтобы получить заданную сумму столбца, но мы уже присвоили цифру один, поэтому H не может быть пятью. Давай отступим.
Из таблицы видно, что следующей наименьшей цифрой может быть шестерка.
Если H равно шести, F должно быть равно девяти, чтобы получить заданную сумму столбца, но мы уже присвоили цифру девять, поэтому H не может быть шестью. Давай отступим.
Из таблицы видно, что следующей наименьшей цифрой может быть семерка.
Если H равно семи, F также должно быть равно семи, чтобы получить заданную сумму столбца, но мы не можем присвоить одну и ту же цифру двум разным буквам. Давай отступим.
Из таблицы видно, что единственным другим возможным выбором буквы H является восемь.
If H is eight, F would have to be five:
| T | 8 | Ø | 1 | 1 | |
| T | 8 | Ø | 1 | 1 | |
| + | 5 | 3 | 9 | Ø | |
| 1 | L | 1 | 4 | 1 | 2 |
Эта информация обновлена.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| T | ✗ | &крест; | &крест; | &крест; | &крест; | &крест; | ✗ | &крест; | ||
| H | ✗ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | ✓ | &крест; |
| R | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| E | ✗ | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| F | ✗ | &крест; | &крест; | &крест; | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; |
| O | ✗ | &крест; | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
| У | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | ✓ |
| L | ✗ | &крест; | &крест; | &крест; | &крест; | &крест; | ✗ | &крест; | ||
| V | ✗ | &крест; | &крест; | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; |
| N | ✗ | &крест; | ✓ | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; | &крест; |
6.
Давайте теперь угадаем букву T. Из таблицы видно, что наименьшая цифра, которая может быть, это шестерка.
Две шестерки с двумя, вынесенными из столбца тысяч, составляют 14, но L не может быть четырем, так как эта цифра уже назначена. Давай отступим.
Единственная оставшаяся возможность состоит в том, что T равно семи, что делает L равным шести.
| 7 | 8 | Ø | 1 | 1 | |
| 7 | 8 | Ø | 1 | 1 | |
| + | 5 | 3 | 9 | Ø | |
| 1 | 6 | 1 | 4 | 1 | 2 |
Здесь некоторые другие догадки найдены в процессе принятия решений выше. Можете ли вы найти какие-либо другие?
| 8 | 4 | Ø | 1 | 1 | |
| 8 | 4 | Ø | 1 | 1 | |
| + | 3 | 5 | 9 | Ø | |
| 1 | 7 | 1 | 6 | 1 | 2 |
| 7 | 4 | 6 | 1 | 1 | |
| 7 | 4 | 6 | 1 | 1 | |
| + | 2 | Ø | 9 | 6 | |
| 1 | 5 | 1 | 3 | 1 | 8 |
| 4 | 6 | 5 | 1 | 1 | |
| 4 | 6 | 5 | 1 | 1 | |
| + | 8 | 2 | 9 | 5 | |
| 1 | Ø | 1 | 3 | 1 | 7 |
.
Вот некоторые из них.0004 Рок + Ролл = Музыка
Четыре + Четыре + Четыре = Три
Девять Девять Девять
Наконец, вот URL-адрес, который приведет вас к действию по взлому кода.
Transum.org/go/?to=Code
Идеи рождественских подарков
Часто бывает очень трудно выбрать рождественские подарки для семьи и друзей, но вот некоторые сезонные подарки, связанные с математикой, выбранные и рекомендованные Transum Математика.
Настольная игра EquateОтличная настольная игра, которая подарит массу удовольствия любой семье с детьми школьного возраста. Рождество — время настольных игр, но и эта пригодится в любое время года. Игры могут быть адаптированы к различным уровням математических способностей. Для репетиторов по математике, работающих только с одним или небольшими группами учеников, эта игра оказалась отличным учебным пособием. Выбор лучших ходов может вызвать уместные дискуссии о математических концепциях. Equate немного похожа на Scrabble — для начинающих математиков. Разработанная настоящим математиком, она работает следующим образом: вы кладете плитки на доску и зарабатываете баллы, правильно выполняя простые уравнения. Ваши девять плиток содержат как числа, так и математические символы; вы можете добавлять к предыдущим играм как по вертикали, так и по горизонтали. подробнее… | |||||
Как не ошибиться Математика, которую мы изучаем в школе, может показаться абстрактным набором правил, установленных древними и не подлежащих сомнению. На самом деле, Джордан Элленберг показывает нам, что математика касается всего, что мы делаем, и немного математических знаний раскрывает скрытые структуры, лежащие под грязной и хаотичной поверхностью мира. В книге «Как не ошибиться» Элленберг исследует математический метод анализа жизни, от повседневной до космической, показывая нам, какие числа защищать, какие игнорировать и когда полностью изменить уравнение. Чего еще любознательному взрослому желать на Рождество? Эту книгу приятно и интересно читать у камина холодными зимними вечерами. подробнее… | |||||
Попутно он объясняет исчисление на одной странице, описывает теорему Гёделя, используя только односложные слова, и показывает, как рано вам на самом деле нужно добраться до аэропорта.Калькулятор графического дисплея Это портативное устройство и сопутствующее программное обеспечение предназначены для создания возможностей для исследования в классе и способствуют лучшему пониманию основных концепций в классе математики и естественных наук. Технология TI-Nspire была разработана в результате тщательного исследования в классе, которое показывает, что «связанное множественное представление имеет решающее значение для развития концептуального понимания, и это возможно только с использованием такой технологии, как TI-Nspire, которая обеспечивает одновременное, динамически связанное представление графиков. Для молодых людей в вашей жизни это отличное вложение. Купленный в качестве рождественского подарка, но полезный на долгие годы, поскольку молодой человек превращается в кандидата A-level, а затем учится в университете. подробнее… | |||||
, уравнения, данные и словесные пояснения, так что изменение одного представления немедленно отражается на других9.0005Apple iPad ProАналитика показывает, что все больше и больше людей получают доступ к Transum Mathematics через iPad, поскольку он настолько портативный и отзывчивый. У iPad так много других применений, помимо решения головоломок и задач Transum, и он станет отличным подарком для всех. Модернизированный дисплей Retina так же великолепен как на вид, так и на ощупь. Все это поставляется с iOS, самой передовой мобильной операционной системой в мире. Айпад Про. Все, что вы хотите, чтобы современные компьютеры были. подробнее… Прежде чем подарить iPad на Рождество, вы можете добавить ссылку на iPad Maths на главный экран. | |||||
Советы Крейга Бартона для учителейОбучение сложное. Но есть простые идеи, которые мы можем применить, чтобы сделать наше обучение более эффективным. В этой книге более 400 таких идей.” далее… «Идеи исходят из двух источников. Во-первых, от замечательных гостей в его подкасте «Советы учителям» — таких тяжеловесов в области образования, как Дилан Вильям, Дейзи Христодулу и Том Шеррингтон, а также от талантливых учителей, имена которых не всем известны, но которые обладают такой мудростью. чем поделиться. А вот и то, чему он научился, работая с замечательными учителями и учениками в сотнях школ по всему миру. | |||||
История математики [DVD] Фильмы этой амбициозной серии предлагают четкие и доступные объяснения важных математических идей, но также полны увлекательных анекдотов, увлекательных биографических подробностей и ключевых эпизодов из жизни великих математиков. Замечательные программы Маркуса дю Сотуа станут прекрасным рождественским подарком подробнее… | |||||
Увлекательный, поучительный и развлекательный сериал дает зрителям новое и часто неожиданное понимание центральной важности математики, превращая эту дисциплину в одно из величайших культурных достижений человечества. Этот DVD содержит все четыре программы из сериала BBC.Рождественская математикаВ этой книге собрано множество веселых заданий на рождественскую тему. Каждый фотокопируемый рабочий лист соответствует Стратегии счета и совместим с Шотландскими рекомендациями 5-14. Эта серия предназначена для занятых учителей в конце осеннего семестра, которые отчаянно нуждаются в актуальных и интересных материалах, которые можно заполнить с минимальным контролем. Все задания подходят для использования классными руководителями, учителями снабжения, учителями SEN и классными помощниками и охватывают такие темы, как «Сколько куропаток подарила настоящая любовь?» и «Наполнить сани подарками, бросив кости!». Отличный источник идей и еще один недорогой наполнитель для чулок. подробнее… | |||||
Дети получат массу удовольствия, работая над рождественскими темами по математике, а также приобретут ценные навыки.Сборник математических методовСколько различных способов решения одновременных уравнений вы знаете? Чтобы умножить десятичные дроби? Чтобы найти n-й член последовательности? Сборник математических методов объединяет более ста различных подходов, применяемых в классах со всего мира, что дает любознательным математикам возможность исследовать увлекательные методы, с которыми они никогда раньше не сталкивались. Если вы обучаете математике любую возрастную группу в любой стране, вы гарантированно узнаете много нового из этой восхитительной книги. Это углубит ваши предметные знания и улучшит ваше преподавание, независимо от вашего существующего уровня знаний. Это вдохновит вас на изучение новых подходов со своими учениками и даст ценные рекомендации по объяснениям и неправильным представлениям. | |||||
подробнее…Математика с плохими рисункамиЯ обучал замечательную Бетси пять лет. Когда настал день нашей последней совместной сессии перед окончанием ее 13-го класса, я получил эту прекрасную книгу в качестве благодарственного подарка. Это очень читаемая книга Бена Орлина. Я действительно наслаждаюсь юмором в письме, и рисунки великолепны. Бен Орлин отвечает на три главных вопроса математики: зачем мне это учить? Когда я когда-нибудь буду его использовать? Почему это так сложно? Ответы приходят в самых разных формах: карикатуры, рисунки, шутки, рассказы и идеи чуткого учителя, который считает, что математика должна принадлежать всем. больше… | |||||
Нажмите на изображения выше, чтобы увидеть все детали этих идей подарков и купить их в Интернете.
Математические футболки
Математические футболки на Amazon. эта страница. Ниже ссылка на Амазон.