Как расписать пример по математике 3 класс: Примеры по математике 3 класс – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Примеры по математике 3 класс

Задачи для 3 класса

Математические диктанты
Комбинаторные задачи
Нестандартные задачи
Множество и его элементы
Способы задания множеств
Пустое множество
Диаграмма Венна
Диаграмма Венна. Часть 2
Подмножество
Множество. Задачи
Скорость, время, расстояние

Числа от 1 до 100

Сложение и вычитание
Буквенные выражения
Единицы длины

Контрольные работы

Умножение и деление

Итоговая контрольная работа

Контрольная работа 1

Контрольная работа 2

Контрольная работа 3

Контрольная работа 1

Контрольная работа 2

Контрольная работа 1

Контрольная работа 1

Контрольная работа 2

Тесты.

3 класс.

Тесты по математике 3 класс
Табличное умножение и деление чисел
Особые случаи умножения и деления

Примеры, уравнения

Примеры
Уравнения
Кроссворды

Математика 3 класс ->> Примеры

Первое полугодие

Второе полугодие

46 + 14 = 60	56 : 7 = 8	31 + 37 = 68	6 : 2 = 3	40 + 38 = 78	18 : 3 = 6
57 – 14 = 43	4 * 5 = 20	80 – 57 = 23	9 * 2 = 18	80 – 69 = 11	27 + 52 = 79
24 : 6 = 4	36 + 63 = 99	56 : 8 = 7	7 + 42 = 49	81 : 9 = 9	51 + 37 = 88
5 * 3 = 15	82 – 23 = 59	4 * 2 = 8	5 – 1 = 4	4 * 2 = 8	80 – 71 = 9
34 + 51 = 85	72 : 9 = 8	3 + 36 = 39	24 : 8 = 3	64 + 9 = 73	14 : 2 = 7
41 + 21 = 63	3 * 9 = 27	95 – 76 = 19	9 * 5 = 45	93 – 87 = 6	8 * 4 = 32
50 + 34 = 84	24 : 4 = 6	50 + 32 = 82	12 : 3 = 4	10 + 64 = 74	36 : 9 = 4
65 – 3 = 62	6 * 2 = 12	55 – 36 = 19	4 * 6 = 24	92 – 78 = 14	4 * 9 = 36
7 : 1 = 7	61 + 28 = 89	45 : 5 = 9	25 + 7 = 32	8 : 2 = 4	73 + 16 = 89
4 * 3 = 12	83 – 79 = 4	5 * 4 = 20	98 – 24 = 74	7 * 6 = 42	94 – 9 = 85
21 + 1 = 22	9 * 2 = 18	2 + 55 = 57	40 : 8 = 5	67 + 27 = 94	50 : 510
73 – 32 = 41	7 * 4 = 28	58 – 38 = 20	6 * 4 = 24	76 – 29 = 47	2 * 4 = 8
8 : 2 = 4	33 + 45 = 78	28 : 4 = 7	14 + 9 = 23	56 : 7 = 8	24 + 53 = 77
3 * 2 = 6	44 – 20 = 24	9 * 9 = 81	74 – 63 = 11	1 * 5 = 5	94 – 50 = 44
16 + 37 = 53	8 : 8 = 1	1 + 34 = 35	63 : 7 = 9	54 + 27 = 81	32 : 4 = 8
44 – 4 = 40	3 * 5 = 15	89 – 33 = 56	4 * 5 = 20	66 – 35 = 31	3 * 7 = 21
6 * 8 = 48	16 – 12 = 14	3 * 6 = 18	83 – 78 = 5	8 * 7 = 56	38 – 15 = 23
19 + 17 = 36	30 : 6 = 5	49 + 32 = 81	6 : 3 = 2	34 + 30 = 64	18 * 9 = 2
42 : 7 = 6	31 + 59 = 90	16 : 8 = 2	79 + 7 = 86	30 : 5 = 6	26 + 42 = 68
2 * 6 = 12	80 – 60 = 20	5 * 8 = 40	70 – 44 = 26	4 * 5 = 20	77 – 33 = 44
23 + 71 = 94	14 : 7 = 2	8 + 38 = 46	56 : 7 = 8	27 + 22 = 49	24 : 8 = 3
24 – 18 = 6	7 * 2 = 14	83 – 0 = 83	3 * 3 = 9	97 – 38 = 59	6 * 2 = 12
10 : 2 = 5	37 + 51 = 88	18 : 6 = 3	36 + 27 = 63	20 : 5 = 4	82 + 6 = 88
6 * 5 = 30	43 – 28 = 25	2 * 4 = 8	77 – 20 = 57	4 * 5 = 20	83 – 54 = 29
42 + 30 = 72	35 : 7 = 5	17 + 48 = 65	36 : 9 = 4	64 + 12 = 76	36 : 6 = 6
96 – 47 = 49	5 * 3 = 15	93 – 65 = 28	7 * 4 = 28	85 – 66 = 19	7 * 7 = 49
42 : 7 = 6	31 + 67 = 98	49 + 8 = 57	39 + 1 = 40	18 : 2 = 9	4 + 24 = 28
2 * 7 = 14	99 – 84 = 15	8 * 1 = 8	64 – 21 = 43	5 * 9 = 45	97 – 32 = 65
46 + 9 = 55	36 : 4 = 9	2 + 49 = 51	54 : 9 = 6	16 + 56 = 72	28 : 4 = 7
94 – 32 = 62	2 * 8 = 16	58 – 38 = 20	5 * 2 = 10	25 – 24 = 1	3 * 6 = 18
_______________	_______________	_______________	_______________	_______________	_______________

Сложение и вычитание чисел от 1 до 100.

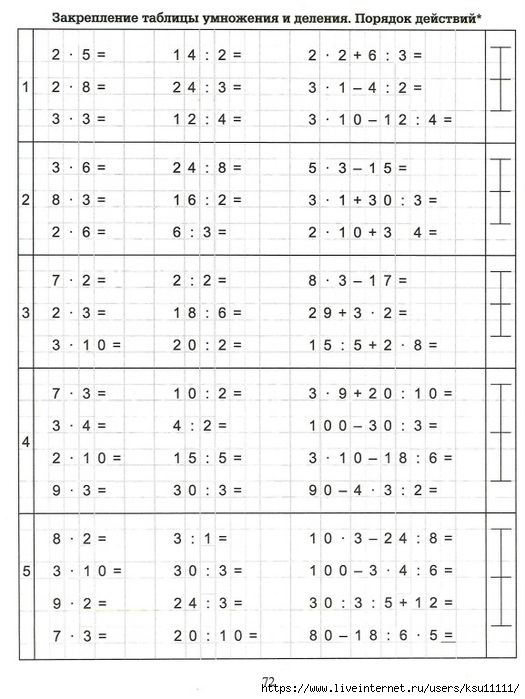
2 + 9	3 + 9	4 + 9	3 + 8
4 + 8	5 + 8	4 + 7	5 + 7
6 + 7	5 + 6	6 + 6	8 + 6
8 + 6	9 + 5	3 + 9	7 + 4
12 – 4	16 – 8	15 – 7	13 – 4

18 + 0	32 + 7	57 + 6	32 – 8	20 + 65	24 + 69
26 – 0	49 – 4	28 + 4	56 – 9	70 – 38	84 – 57

98 + 2	30 – 1	70 – 30	30 + 70
10 + 7	28 – 8	9 + 60	96 – 90

48 + 17	45 + 29	92 – 36	100 – 65
68 + 16	82 – 65	83 – 75	90 – 72
56 + 34	15 + 78	63 + 29	54 + 16
21 + 49	90 – 24	77 + 18	88 + 12

82 – 36	53 + 29	100 – 75	64 + 16	46 + 36	82 – 29
25 + 75	80 – 16	93 – 85	66 + 18	90 – 82	77 + 23
8 + 85	84 – 18	8 + 82	100 – 23	56 + 39	61 – 49
95 – 39	12 + 49	82 – 28	19 + 74	54 + 28	93 – 74
49 + 44	47 + 13	93 – 44	60 – 13	34 – 23	49 + 12

38 + 6 + 4	13 + 8 + 27 + 2	54 + 16 + 6 + 14
47 + 8 + 3	47 + 13 + 9 + 1	71 + 15 + 5 + 9

38 + 59 + 2	30 + 18 – 30	100 – (38 + 12
60 + 37 + 3	60 – 56 + 16	100 – (59 + 12)
79 – (16 + 24)	95 – 80 + 67	100 – (29 + 31)
79 – 16 + 24	82 – 72 + 35	100 – (79+ 21)

90 – 73 + 8	25 + 73 – 8	34 + 36 – 9	61 – 36 + 9	84 – 58 – 7	19 + 58 + 7
93 – (46 + 9)	38 + 46 + 9	(28 + 33) – 8	53 + 8 – 33	54 – (42 – 7)	19 + 42 – 7

46 + 11 – 8	85 – 24 + 9	100 – (34 + 26)	80 – (42 – 12)	39 – (45 – 28)
62 + 38 – 8	62 + (38 – 8)	80 – 42 + 12	50 – 39 + 18	70-(12 + 3)
19 + 80 – 3	44 + 36 – 20	50 – (30 – 2)	50 + (30 + 2)	50 – 30 + 2

2 + 9 = 11 3 + 9 = 12 4 + 9 = 13 3 + 8 = 11
4 + 8= 12 5 + 8 = 13 4 + 7 = 11
5 + 7 = 12
6 + 7 = 13 5 + 6 = 11 6 + 6 = 12 8 + 6 = 14
8 + 6 = 14 9 + 5 = 14 3 + 9 = 12 7 + 4 =
12 – 4 = 16 16 – 8 = 8 15 – 7 = 8 13 – 4 = 9
18 + 0 = 18 32 + 7 = 39 57 + 6 = 63 32 – 8 = 24 20 + 65 = 85 24 + 69 = 93
26 – 0 = 26 49 – 4 = 45 28 + 4 = 32 56 – 9 = 47 70 – 38 = 32 84 – 57 = 27
98 + 2 = 100 30 – 1 = 29 70 – 30 = 40 30 + 70 = 100
10 + 7 = 17 28 – 8 = 20 9 + 60 = 69 96 – 90 = 6
48 + 17 = 65 45 + 29 = 74 92 – 36 = 100 – 65 = 35
68 + 16 = 84 82 – 65 = 147 83 – 75 = 158 90 – 72 = 18
56 + 34 = 90 15 + 78 = 93 63 + 29 = 92 54 + 16 = 70
21 + 49 = 70 90 – 24 = 114 77 + 18 = 95 88 + 12 = 100
82 – 36 = 46 53 + 29 = 82 100 – 75 = 25 64 + 16 = 80 46 + 36 = 82 82 – 29 = 53
25 + 75 = 100 80 – 16 = 64 93 – 85 = 8 66 + 18 = 84 90 – 82 = 8 77 + 23 = 100
8 + 85 = 93 84 – 18 = 66 8 + 82 = 90 100 – 23 = 77 56 + 29 = 85 61 – 49 = 12
95 – 39 = 56 12 + 49 = 61 82 – 28 = 54 19 + 74 = 93 54 + 38 = 92 93 – 74 = 19
49 + 44 = 93 47 + 13 = 60 93 – 44 = 49 60 – 13 = 47 34 – 23 = 11 49 + 12 = 61
38 + 6 + 4 = 48 13 + 8 + 27 + 2 = 50 54 + 16 + 6 + 14 =90
47 + 8 + 3 = 58 47 + 13 + 9 + 1 = 70 71 + 15 + 5 + 9 = 100
38 + 59 + 2 = 99 30 + 18 – 30 = 18 100 – (38 + 12) = 50
60 + 37 + 3 = 100 60 – 56 + 16 = 20 100 – (59 + 12) = 29
79 – (16 + 24) = 39 95 – 80 + 67 = 82 100 – (29 + 31) = 40
79 – 16 + 24 = 87 82 – 72 + 35 = 45 100 – (79 + 21) = 0
90 – 73 + 8 = 25 25 + 73 – 8 = 90 34 + 36 – 9 = 61 61 – 36 + 9 = 34 84 – 58 – 7 = 19 19 + 58 + 7 = 84
93 – (46 + 9) = 38 38 + 46 + 9 = 93 (28 + 33) – 8 = 53 53 + 8 – 33 = 28 54 – (42 – 7) = 19 19 + 42 – 7 = 54
46 + 11 – 8 = 49 85 – 24 + 9 = 70 100 – (34 + 26) = 40 80 – (42 – 12) = 50 39 – (45 – 28) = 22
62 + 38 – 8 = 92 62 + (38 – 8) = 92 80 – 42 + 12 = 50 50 – 39 + 18 = 29 70-(12 + 3) = 55
19 + 80 – 3 = 96 44 + 36 – 20 = 60 50 – (30 – 2) = 22 50 + (30 + 2) = 82 50 – 30 + 2 = 22

Табличное умножение и деление.

9 * 7 =	5 : 1 =	1 * 2 =	3 : 1 =	7 * 3 =	4 : 1 =
9 * 3 =	9 : 9 =	2 * 5 =	3 : 3 =	3 * 7 =	2 : 1 =
1 * 6 =	8 : 2 =	2 * 1 =	5 : 6 =	4 * 1 =	4 : 2 =
8 * 8 =	5 : 5 =	9 * 0 =	4 : 4 =	0 * 6 =	7 : 1 =
0 * 8 =	5 : 1 =	2 * 2 =	3 : 1 =	3 * 9 =	6 : 3 =
3 * 8 =	4 : 2 =	9 * 4 =	9 : 3 =	8 * 0 =	8 : 6 =
5 * 1 =	6 : 2 =	6 * 0 =	8 : 2 =	7 * 6 =	9 : 3 =
6 * 7 =	6 : 6 =	4 * 0 =	4 : 4 =	6 * 5 =	8 : 1 =
1 * 7 =	8 : 4 =	4 * 1 =	9 : 9 =	6 * l =	2 : 1 =
2 * 4 =	4 : 2 =	3 * 3 =	5 : 1 =	7 * 6 =	2 : 1 =
0 * 8 =	3 : 1 =	9 * 1 =	3 : 3 =	9 * 1 =	8 : 2 =
4 * 9 =	5 : 5 =	0 * 2 =	8 : 1 =	3 * 2 =	8 : 2 =
1 * 5 =	5 : 5 =	2 * 5 =	2 : 1 =	9 * 4 =	4 : 4 =
4 * 1 =	7 : 1 =	1 * 3 =	9 : 3 =	9 * 6 =	4 : 2 =
2 * 0 =	9 : 9 =	6 * 2 =	1 : 1 =	4 * 1 =	1 : 1 =
5 * 9 =	4 : 2 =	3 * 6 =	4 : 2 =	4 * 7 =	7 : 7 =

9 * 7 = 63 5 : 1 = 5 1 * 2 = 2 3 : 1 = 3 7 * 3 = 21 4 : 1 = 4
9 * 3 = 27 9 : 9 = 81 2 * 5 = 10 3 : 3 = 9 3 * 7 = 21 2 : 1 = 2
1 * 6 = 6 8 : 2 = 16 2 * 1 = 2 5 : 6 = 30 4 * 1 = 4 4 : 2 = 8
8 * 8 = 64 5 : 5 = 25 9 * 0 = 0 4 : 4 = 16 0 * 6 = 0 7 : 1 = 7
0 * 8 = 0 5 : 1 = 5 2 * 2 = 4 3 : 1 = 3 3 * 9 = 27 6 : 3 = 18
3 * 8 = 24 4 : 2 = 2 9 * 4 = 36 9 : 3 = 3 8 * 0 = 0 8 : 6 = 48
5 * 1 = 5 6 : 2 = 3 6 * 0 = 0 8 : 2 = 4 7 * 6 = 42 9 : 3 = 27
6 * 7 = 42 6 : 6 = 1 4 * 0 = 0 4 : 4 = 1 6 * 5 = 30 8 : 1 = 8
1 * 7 = 7 8 : 4 = 2 4 * 1 = 4 9 : 9 = 1 6 * l = 6 2 : 1 = 2
2 * 4 = 8 4 : 2 = 2 3 * 3 = 9 5 : 1 = 5 7 * 6 = 42 2 : 1 = 2
0 * 8 = 0 3 : 1 = 3 9 * 1 = 9 3 : 3 = 1 9 * 1 = 9 8 : 2 = 16
4 * 9 = 36 5 : 5 = 1 0 * 2 = 0 8 : 1 = 8 3 * 2 = 6 8 : 2 = 16
1 * 5 = 5 5 : 5 = 1 2 * 5 = 10 2 : 1 = 2 9 * 4 = 36 4 : 4 = 16
4 * 1 = 4 7 : 1 = 7 1 * 3 = 3 9 : 3 = 3 9 * 6 = 54 4 : 2 = 8
2 * 0 = 0 9 : 9 = 1 6 * 2 = 12 1 : 1 = 1 4 * 1 = 4 1 : 1 = 1
5 * 9 = 45 4 : 2 = 2 3 * 6 = 36 4 : 2 = 8 4 * 7 = 28 7 : 7 = 49

Простые задачи

Задачи на умножение

Задачи на деление по содержанию и на равные части

Задачи на увеличение и уменьшение числа в несколько раз

Задачи на кратное сравнение

Задачи на приведение к единице

Задачи на цену количество стоимость

Составные задачи

Задачи на нахождение суммы

Задачи на нахождение уменьшаемого, вычитаемого, разности

Задачи на разностное и кратное сравнение

Задачи на деление суммы на число и числа на сумму

Задачи на цену, количество, стоимость

Задачи на разностное и кратное сравнение

Задачи на нахождение суммы двух произведений

Задачи на нахождение неизвестного слагаемого

Задачи на цену, количество, стоимость

Порядок действий

В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.

Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.

Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:

10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1

Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто как 2 + 2 или 9 − 3.

Для подобных выражений принято соблюдать так называемый порядок действий. Суть в том, что выражение вычисляется кусочками по определённому порядку.

Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:

Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!

Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1

Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:

1. Сначала вычислить то, что находится в скобках!

2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!

3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!

Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:

Осталось простейшее выражение 11 + 3, которое вычисляется легко:

11 + 3 = 14

Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14

10 − 1 + 2 + 3 = 14

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 10 − 1 = 9

2) 9 + 2 = 11

3) 11 + 3 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:

Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.

Пример 2. Найти значение выражения (3 + 5) + 2 × 3

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.

Сначала вычислить то, что находится в скобках!

Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:

8 + 2 × 3

Снова читаем первое правило:

Сначала вычислить то, что находится в скобках!

Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:

Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!

Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3

8 + 6

Осталось простейшее выражение 8 + 6, которое вычисляется легко:

8 + 6 = 14

Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14

(3 + 5) + 2 × 3 = 14

Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:

И далее можно выполнить действия по отдельности, что очень удобно:

1) 3 + 5 = 8

2) 2 × 3 = 6

3) 8 + 6 = 14

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Но опять же, используя такой способ, нужно быть очень внимательным.

Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1

Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:

1) 5 − 3 = 2

2) 5 × 2 = 10

3) 2 : 2 = 1

4) 10 + 1 = 11

5) 11 + 1 = 12

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.

Пример 4. Найти значение выражения (3250 − 2905) : 5

Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым

1) 3250 − 2905 = 345

2) 345 : 5 = 69

В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.

Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.

В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.

В результате будем иметь следующий порядок:

1) 6 411 × 8 = 51 288

2) 51 288 − 40 799 = 10 489

3) 10 489 × 6 = 62 934

Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)

Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.

1) 50 377 + 20 338 = 70 715

2) 1 657 974 : 822 = 2 017

3) 2 017 × 106 = 213 802

4) 213 802−70 715 = 143 087

Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)

Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.

В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:

1) 96 : 4 = 24

2) 24 + 3 680 = 3 704

3) 14026 − 3 704 = 10 322

Задание 1. Найдите значение выражения:

5 + 2 − 2 − 1

Решение

Показать решение

Задание 2. Найдите значение выражения:

14 + (6 + 2 × 3) − 6

Решение

Показать решение

Задание 3. Найдите значение выражения:

486 : 9 − 288 : 9

Решение

Показать решение

Задание 4. Найдите значение выражения:

756 : 3 : 4 × 28

Решение

Показать решение

Задание 5. Найдите значение выражения:

807 : 3 − (500 − 58 × 4)

Решение

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Урок математики в 3-м классе по теме “Деление двузначного числа на однозначное”

Цели:

Научить делить двузначное число на однозначное (внетабличные способы)
Развивать навыки устных вычислений, логическое мышление, внимание, речь учащихся.
Воспитывать культуру общения.

Ход урока

1. Приветствие

Долгожданный дан звонок

Начинается урок.

2. Актуализация опорных знаний.. Ситуация успеха.

Решите примеры и соберите слово.

6 • 8
30 • 3

80 : 4

3 • 15

600 : 2

– Что такое успех? (хорошие результаты в работе)

– Что нужно для достижения успеха?

– Я желаю вам всем успеха. А вы мысленно пожелайте успеха мне.

Индивидуальная работа у доски.

(40 + 16) : 7 =

(30 + 12) : 3 =

(40 + 24) : 4 =

(13 + 14) : 3 =

(24 + 28) : 6 =

3.Ситуация затруднения. Устный счёт (с обратной связью)

– Найдите разность чисел в треугольниках, разделите полученный результат на число, записанное в квадрате, результат умножьте на число в круге, прибавьте число в четырёхугольнике, разделите на число в четырёхугольнике.

– Покажите результат. (20)

– Произведение чисел в кругах разделите на разность чисел в треугольниках, результат увеличьте на число, записанное в квадрате.

– Покажите результат. (53)

– Из суммы чисел в прямоугольниках вычтите произведение чисел в кругах, результат разделите на число в пятиугольнике. (У детей возникает затруднение 72 : 6)

– В чём проблема? (не умеем решать такие примеры)

– Вот сегодня на уроке мы должны этому научиться.

В верхнем левом углу доски появляется запись

4. Тема урока

Назовите тему урока.

Деление двузначного числа на однозначное.

– Как вы думаете, какие знания нам для этого понадобятся? (табличное деление, деление суммы на число, алгоритм)

– Хорошо, давайте вспомним всё, что мы уже знаем.

а) Деление за 1 минуту

(На доску вывешиваю таблицу с примерами на табличное деление. Дети на листочках записывают только ответы в течении 1 минуты. Подаю команду “Стоп!” и все сдают листочки. Сразу же выявляю победителя по количеству решённых примеров, а к концу урока проверяю правильность решения и утверждаю победителя или выявляю нового)

б) Проверка индивидуального задания у доски.

– Ребята, проверьте.

(вопрос к ученику, работавшему у доски)

– Объясни, какими способами ты пользовался?

– Какой из этих способов нам сегодня пригодится?

5. Работа над решением проблемы.

а) Работа в тетради. Каллиграфическая минутка.

– Пропишите число 63.

– На какие однозначные числа делится число 63? (7 и 9)

– Так какая у нас сегодня задача на уроке? (Научиться делить двузначное число на однозначное)

б) Представьте число 63 в виде суммы двух слагаемых, каждое из которых делится на 3.

Запишите выражение

63 : 3 = (60 + 3) : 3 = 60 : 3 + 3 : 3 =

– Каким способом деления суммы на число воспользовались?

(Каждое слагаемое разделили на число и результаты сложили)

Вывод: Для того, чтобы разделить число 63 что нам пришлось с ним сделать?

(Заменить суммой разрядных слагаемых)

– А затем? (разделить каждое слагаемое на 3)

– Потом? (результаты сложить)

– Вернёмся к нашей проблеме.

– Какая проблема возникла в устном счёте?

(72 : 6)

– Давайте решим по такому же плану.

(не получается)

– Как же быть?

– Представьте число 72 в виде суммы двух слагаемых, каждое из которых делится на 6.

72 : 6 = (60 + 12) : 6 = 60 : 6 + 12 : 6 = 10 + 2 = 12

Вывод: В первом случае заменили суммой разрядных слагаемых, а во втором – суммой удобных слагаемых.

в) – Давайте составим план наших действий

АЛГОРИТМ

– Что мы делали сначала?

– Потом?

– А потом?

Заменили …удобных

Разделили…

Результаты сложили

– Сравните с алгоритмом умножения двузначного числа на однозначное

Заменили…разрядных

Умножили…

Результаты сложили

(алгоритмы похожи)

6. Физминутка

7. Первичное закрепление новых знаний.

Используя составленный алгоритм найдём значения нескольких выражений.

(работа у доски с подробным объяснением и развёрнутой записью)

72 : 4 =

72 : 3 =

72 : 2 =

7. Работа с учебником

С.13 №2 1 столбик с места с комментированием

Вывод.

– Какая проблема возникла у нас на уроке?

– Удалось нам её решить?

8. Первичный контроль и оценка.

1) Запишите выражение и найдите его значение

36 : 2 =

2) Составьте задачу по этому выражению.(дети составляют задачи разных видов и решают их устно)

3) Дополните условие задачи так, чтобы она стала составной.

Решите задачу в тетради.

9. Итог урока.

– Какую проблему решали на уроке?

– Научились выполнять внетабличное деление двузначного числа на однозначное?

– Хотите себя проверить?

Рефлексия (Каждому ученику выдаётся карточка, на которой примеры трёх уровней сложности.

Ученик имеет право выбрать любой из этих уровней.)

1уровень	2 уровень	3 уровень
1. 86 : 2 =	1. 39 : 3 =	1. 78 : 3 =
2. 93 : 3 =	2. 69 : 3 =	2. 90 : 5 =
3. 68 : 2 =	3. 48 : 2 =	3. 75 : 3 =
4. 96 : 3 =	4. 75 : 5 =	4. 42 : 3 =
5. 88 : 4 =	5. 60 : 4 =	5. 96 : 6 =

Вывешиваю правильные ответы. Дети проверяют и оценивают свою работу.

1 уровень
43

31

34

32

22

2 уровень

13

23

24

15

15

3 уровень

39

18

25

14

16

– Каждый правильный ответ 1 балл

– Покажите (карточкой) сколько баллов заработали.

Закончите предложение.

Сегодня на уроке я…..

– Спасибо, дети, за урок.

Контрольные работы, самостоятельные, тесты, задания, карточки, задачи для 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 классов за 1, 2, 3, 4 четвертей.

МАТЕМАТИКА В ШКОЛЕ

Номер свидетельства СМИ ЭЛ № ФС 77 – 63677 зарегистрировано Роскомнадзором

Задачи и примеры по темам:

Округление Сравнение Сложение Вычитание Сложение и вычитание Умножение Деление Умножение и деление Нумерация Уравнения Дроби Общие темы

Задачи и примеры по классам:

Детский сад 1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 9 класс 10 класс

Уроки и презентации по классам:

1 класс 2 класс 3 класс 4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Тесты и тренажеры по классам

Детский сад 1 класс 2 класс 3 класс 4 класс

Контрольные работы:

1 класс: Входная   Моро М. И.    Петерсон Л.Г.   Итоговая
2 класс: Входная   Моро М.И.    Петерсон Л.Г.   Итоговая
3 класс: Входная   Моро М.И.    Петерсон Л.Г.   Итоговая
4 класс: Входная   Моро М.И.    Итоговая

Самостоятельные работы:

1 класс: Петерсон Л.Г. Моро М.И. 2 класс: Моро М.И. 3 класс: Моро М.И. 4 класс: Моро М.И. 5 класс: Виленкина Н.Я. 6 класс: Виленкина Н.Я. 7 класс: Мордковича А.Г. Атанасяна Л.С.

Домашние задания:

1 класс: Моро М.И. 2 класс: Моро М.И. 3 класс: Моро М.И. 4 класс: Моро М.И. 5 класс: Виленкина Н.Я. 6 класс: Виленкина Н.Я. 7 класс: Мордковича А.Г.

Дата публикации: 12 апреля 2017.

1 КЛАСС

Задачи и примеры для 1 класса по математике по всем темам.
Математика – 1 класс, контрольные работы по Моро М.И.
Домашние задания по математике – 1 класс по учебнику Моро. М.И. Темы: Числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10; Сравнение; Сложение и вычитание; Решение текстовых задач; Числа от 10 до 20; Сложение чисел до 10, 20, до 50.
Математика – 1 класс, итоговые контрольные работы
Тренажеры для 1 класса. Содержание
Самостоятельные работы по математике для 1 класса по учебнику Моро
Карточки по математике – 1 класс по учебнику Моро М.И.
Уроки по математике для 1 класса. Обзор
Математика – 1 класс, контрольные работы по учебнику Петресон Л.Г.
Тесты по математике для 1 класса по учебнику Моро

2 КЛАСС

Математика – 2 класс, контрольные работы по учебникам Моро М.И., на темы: “Сложение, вычитание, длина, сравнение чисел”
Домашние задания по математике – 2 класс за 3 и 4 четверти по темам: “Умножение и деление”, “Сложение и вычитание в пределах от 1 до 100”, “Скобки, порядок выполнения действий”, “Отрезок, угол, прямоугольник”
Математика – 2 класс, задачи и примеры для самостоятельной работы за 1 четверть
Задачи для 2 класса по всем темам
Интерактивные тесты и тренажеры. 2 класс
Математика 2 класс, контрольные работы по Петерсон
Математика 2 класс, карточки за весь год
Тесты по математике – 2 класс, по Моро
Математика 2 класс, математические диктанты
Олимпиада по математике 2 класс

3 КЛАСС

Контрольные работы по математике – 3 класс по учебнику Моро
Самостоятельные работы по математике – 3 класс, по учебнику Моро
Задачи для 3 класса по всем темам
Итоговые контрольные работы по математике 3 класс, по учебнику Моро
Математика 3 класс, урок на тему “Периметр и площадь прямоугольника”
Контрольные работы по математике 3 класс, по учебнику Петерсон, для уроков 1-15, 16-25, 26-33
Тренажеры для 3 класса, содержание
Карточки по математике 3 класс
Домашние задания для 3 класса, по учебнику Моро. Умножение и деление чисел от 0 до 100; Решение текстовых задач; Сложение и вычитание числе от 1 до 1000 и др. за 1, 2, 3, 4 четверти
Тесты по математике 3 класс, онлайн, бесплатно скачать

4 КЛАСС

Контрольные по математике 4 класс, Моро, скачать. Важное
Самостоятельные работы по математике 4 класс по учебнику Моро. Важное
Математика для 4 класс, итоговая контрольная работа за 1 и 2 полугодия и годовая
Математические диктанты 4 класс
Тесты по математике 4 класс 3 и 4 четверть, скачать, моро
Математика 4 класс, карточки по Моро
Входная контрольная работа по математике 4 класс
Математика 4 класс, уроки, обзор
Домашние задания по математике 4 класс по Моро. за 1, 2, 3 и 4 четверти. Важное
Математика 4 класс, урок на тему: “Величины, мера длины, массы, площади, скорости, времени”

5 КЛАСС

Математика – 5 класс, контрольные работы по учебнику Н. Я. Виленкина
Самостоятельные работы по математике – 5 класс, к учебнику Виленкина. Темы: Натуральные числа и их обозначения; Сложение и вычитание натуральных чисел; Сравнение натуральных чисел; Отрезок, прямая, луч; Умножение натуральных чисел; Деление натуральных чис
Задачи и примеры для 5 класса_обзор
Математика 5 класс, тесты по Виленкину
Математика 5 класс, уроки на разные темы, обзор
Математика в 5 классе, урок на тему: “Площадь, формула площади, как найти площадь треугольника, прямоугольника, квадрата, фигуры”
Математика – 5 класс, домашние задания по учебнику Виленкина
Математика 5 класс, урок на тему: “Проценты, задачи на проценты”
Математика 5 класс, урок на тему: “Уравнение, решение уравнений”
Математика 5 класс, урок на тему: “Плоскость, прямая, луч”, по учебнику Виленкина

6 КЛАСС

Математика 6 класс, контрольные за 1 четверть на темы: “Признаки делимости, простые и составные числа, общий делитель, общее кратное”
Самостоятельная работа по математике – 6 класс за 1, 2, 3 и 4 четверти по Виленкину
Задачи и задания для 6 класса, обзор
Математика 6 класс, тесты за 4 четверть на темы: “Умножение и деление положительных и отрицательных чисел”, “Рациональные числа и их свойства”, “Скобки”, “Коэффициент”, “Подобные слагаемые”, “Решение уравнений с дробями”, “Прямые”, “Координатная плоскость
Математика 6 класс, уроки и презентации. Обзор
Задачи для 6 класса на темы: “Отношение чисел, пропорции”
Задачи для 6 класса на темы: “Умножение дробей”
Задачи и примеры для 6 класса на темы:”Деление дробей”
Задачи и задания для 6 класса на темы: “Сравнение дробей, сокращение дробей, основное свойство дробей_1”
Математика 6 класс, урок: “Отношение чисел и пропорции”

Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением

Занимательная математика

Дошкольнику | 1 класс | 2 класс | 3 класс | 4 класс

Упражнения на сложение и вычитание, умножение и деление, логические задачи можно подать совершенно по-разному. Мы знаем, как увлечь ребёнка математикой!

Попробуйте развивающий курс ЛогикЛайк!

Выберите возраст для старта

Дошкольник

1 класс

2 класс

3 класс

Почему дети и родители выбирают ЛогикЛайк?

2 варианта занятий, выбор сложности

Пройдите 3 стартовые главы курса логики – и откройте доступ к разным категориям. Попробуйте «Закономерности», «Логические задачи», «Умный счёт» и другие.
Попробуйте задания разного уровня сложности: «Новичок», «Опытный», «Эксперт».

Начать занятия! Начать занятия!

На LogicLike.com дети учатся рассуждать, развивают логику, способности к математике и познавательный интерес.

Занятия логикой и математикой онлайн

В 1-2 классе особенно важно заинтересовать детей решением задач. Чтобы помочь родителям и учителям, команда опытных методистов и педагогов «ЛогикЛайк» регулярно создает новые уроки, упражнения и тесты.

Наши арифметические, логические и другие задачи повышают интерес к математике и успеваемость в школе.

У нас есть всё, что вы искали

Попробуйте полный курс ЛогикЛайк!

Математические задачи и задания

Задачи на логику

Числовые и предметные закономерности

Фигуры и развёртки, геометрические задачи

Начать курс!

В разминке будут простые вопросы. Постепенно сложность нарастает, открываются новые интересные задания.

Текстовые задачи

Вы можете начать занятия онлайн или просто посмотреть примеры заданий по математике для 2 класса.

Задача 1. Арифметика и логика

Для праздника Профессор купил голубые, красные и жёлтые воздушные шары. Всего — 39 штук. Жёлтых и голубых вместе — 20.
Красных и голубых — 31.

Сколько красных шаров купил Профессор?

Показать ответ

Ответ:

19.

Решение
Использовать все данные можно, но решение окажется длинным, нерациональным.
На самом деле, достаточно от общего количества шаров отнять количество жёлтых и голубых:
39 – 20 = 19.

Взять подсказку

В задаче есть небольшая «ловушка» — лишние данные.

Задача 2. На сравнение количества

На летних каникулах ребята делали фото насекомых. Витя сделал на 8 фото больше, чем Ян, а Сергей на 5 фото больше, чем Витя.

НА сколько больше фото сделал Сергей, чем Ян?

Узнать ответ

Ответ:

13.

Задача 3.

Составная на вычитание или деление

У Профессора на столе лежали упаковки батареек. В каждой по 12 штук. Когда Профессор взял по 9 батареек из каждой упаковки, на столе осталось всего 15 батареек.

Сколько упаковок с батарейками было на столе?

Узнать ответ

Ответ:

Решение
Когда Профессор взял из каждой упаковки по 9 батареек, осталось по 3 батарейки в каждой (12 – 9 = 3).

Вариант 1: Так как всего осталось 15 батареек, то упаковок было 5 (15 – 3 – 3 – 3 – 3 – 3 = 0).

Вариант 2: Можно решать делением: 15 ÷ 3 = 5.

Посмотрите примеры олимпиадных заданий для 2 класса или начинайте занятия.

Попробуйте полный курс занимательной математики и логики от ЛогикЛайк

Гибкий ум и уверенность! Когда дети решают задачи и головоломки на LogicLike, они тренируют «извилины» и развивают смекалку.
Фундамент для IT! Алгоритмы, закономерности, логика — всё это у нас есть. Мы учим работать с информацией, тренируем память и мышление — формируем потенциал успеха в IT-профессиях.
Повышаем успеваемость! Регулярные занятия по 20-30 минут развивают логические и математические способности. Как следствие – высокие оценки в школе, призовые места на олимпиадах и в конкурсах, повышается интерес к учёбе вообще.

Начать занятия!

Примеры в картинках

Восстанови равенство

Чтобы решать задачи, нажмите Начать занятия!

За звездочкой может быть спрятана любая цифра.

Восстанови пример, чтобы равенство стало верным.

Узнать ответ

Ответ:

58-27=31.

Решение
8-7=1
Какое число нужно отнять от 58, чтобы получить 31? Число 27.

Взять подсказку

От какого числа надо отнять 7, чтобы получить 1?

Ребус в таблице

Чтобы решать задачи, нажмите «Начать занятия»!

Одинаковые предметы имеют одинаковую цену.
Число обозначает общую стоимость предметов в столбце или в строке.

Догадайся, какое число нужно указать вместо знака вопроса.

Узнать ответ

Ответ:

180.

Решение
Кукуруза и тыква стоят столько же, сколько кукуруза и три луковицы.
Cледовательно, 3 луковицы стоят столько же, сколько 1 тыква.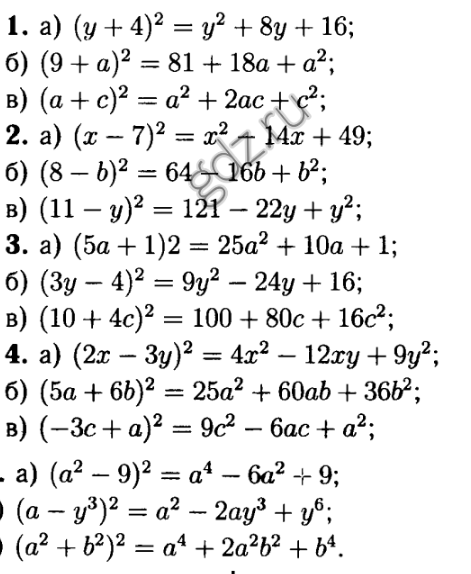

Представь теперь, что в таблице вместо 3 луковиц нарисована 1 тыква и увидишь, что в нижней строке тыква и перец вместе стоят 180, а во втором столбике также стоит воображаемая тыква и тот же перец.

Сколько они будут стоить вместе — и считать не нужно.

Взять подсказку

Посмотри внимательно на картинку и определи, какие наборы овощей стоят одинаково.

Можно посмотреть примеры других арифметических ребусов на сложение и вычитание или приступить к занятиям на сайте.

Предложенные задания — часть образовательной платформы LogicLike.

Задачи на площадь и периметр

Задача 4. Ломаная линия

Чтобы решать задачи, нажмите «Начать занятия»!

Отрезки одинакового цвета имеют одинаковую длину. Какая ломаная линия самая длинная?

Узнать ответ

Ответ:

Задача 5. Периметр

Чтобы решать задачи, нажмите «Начать занятия»!

Профессор сделал 3 рамки из проволоки: треугольную, пятиугольную и прямоугольную. И попросил робота Клапана выбрать самую длинную.

Помоги Клапану справиться с задачей.

Узнать ответ

Ответ:

прямоугольник (10+2+10+2=24 см).

Задача 6. Площадь

Чтобы решать задачи, нажмите «Начать занятия»!

Иришка вырезала два одинаковых (по площади) треугольника, два одинаковых круга и два одинаковых четырёхугольника.

На какую фигуру Иришка израсходовала меньше всего бумаги?

Смотреть ответ

Ответ:

Четырёхугольники полностью помещаются и в круг, и в треугольник. Значит, площадь четырёхугольника самая маленькая.

Здесь лишь малая часть заданий, доступных ученикам образовательной платформы ЛогикЛайк.

Какой формат занятий вы ищете?

Если ваша единственная цель — отработка навыков счета, найдите арифметический тренажер в формате журнала или онлайн.

Для кого мы создали и постоянно развиваем сайт LogicLike?

Для тех, кто хочет научиться думать, рассуждать, мыслить нестандартно.
Для детей, чьи родители понимают что математика — это не только примеры и задачи (подробнее — в статье о пользе от занятий математикой).
Для всех, кто хочет научиться принимать решения не только на уроках математики, но и преуспевать в разных областях жизни.

Понравился материал? Поделитесь с друзьями!

Подключайтесь к ЛогикЛайк!

Более 150 000 ребят со всего мира уже занимаются математикой и логикой с удовольствием

Начать обучение! Начать обучение!

Мы научим ребёнка

Рассуждать и принимать решения

Решать любые логические задачи

Мыслить гибко и нестандартно

Другие категории заданий

по возрасту

Математика для детей 5 – 6 лет

Задачи для 1 класса

Задачи для 3 класса

Задачи для 4 класса

ГДЗ по математике 3 класс Башмаков, Нефедова ответы к учебнику 1, 2 часть

Часть 1.

(Страницы с 6 по 121)
Страница 6, Считаем до тысячи:1; 2; 3;
Страница 7:4; 5; 6; 7; 8;
Страница 8, Разрядные слагаемые:1; 2; 3; 4;
Страница 9:5; 6; 7; 8; 9;
Страница 10, Складываем и вычитаем по разрядам:1; 2; 3; 4;
Страница 11:5; 6; 7; 8;
Страница 12, Меняем одну цифру:1; 2; 3; 4;
Страница 13:5; 6; 7; 8;
Страница 14, Переходим через десяток:1; 2; 3;
Страница 15:4; 5; 6; 7;
Страница 16, Складываем и вычитаем десятки:1; 2; 3;
Страница 17:4; 5; 6;
Страница 18, Вычисляем по разрядам:1; 2; 3; 4; 5; 6; 7; 8;
Страница 20, Решаем задачи:1; 2; 3; 4;
Страница 21:5; 6; 7; 8; 9;
Страница 22, Проверяем, чему мы научились:1; 2; 3; 4; 5;
Страница 22, Математический тренажер:1; 2;
Страница 23:3; 4; 5; 6; 7;
Страница 24, Умножаем и делим на 2:1; 2; 3; 4;
Страница 25:5; 6; 7; 8; 9;
Страница 26, Умножаем и делим на 4:1; 2; 3; 4;
Страница 27:5; 6; 7; 8;
Страница 28, Умножаем и делим на 3:1; 2; 3; 4;
Страница 29:5; 6; 7; 8;
Страница 30, Умножаем на 6:1; 2; 3; 4;
Страница 31:5; 6; 7; 8; 9;
Страница 32, Умножаем на 5:1; 2; 3; 4;
Страница 33:5; 6; 7; 8; 9;
Страница 34, Умножаем на 7:1; 2; 3; 4;
Страница 35:5; 6; 7; 8;
Страница 36, Умножаем на 8 и на 9:1; 2; 3; 4;
Страница 37:5; 6; 7; 8;
Страница 38, Делим и умножаем числа:1; 2; 3; 4; 5;
Страница 39:6; 7; 8;
Страница 40, Решаем задачи, вычисляем, сравниваем:1; 2; 3; 4; 5; 6;
Страница 41:7; 8; 9;
Страница 42, Проверяем, чему мы научились:1; 2; 3; 4;
Страница 42, Математический тренажер:1; 2;
Страница 43:3; 4; 5; 6; 7; 8; 9; 10;
Страница 44, Периметр многоугольника:1; 2;
Страница 45:3; 4; 5; 6;
Страница 46, Единицы длины:1; 2; 3;
Страница 47:4; 5; 6; 7; 8; 9;
Страница 48, Дециметр:1; 2; 3; 4;
Страница 49:5; 6; 7; 8; 9;
Страница 50, Вычисляем площадь:1; 2; 3;
Страница 51:4; 5; 6; 7; 8;
Страница 52, Увеличиваем и уменьшаем фигуры:1; 2; 3;
Страница 53:4; 5; 6; 7; 8; 9;
Страница 54, Строим фигуры из кубиков:1; 2; 3; 4;
Страница 55:5; 6; 7; 8;
Страница 56, Проектируем сад:1; 2;
Страница 57:Практическая работа; 3; 4; 5;
Страница 59, О симметрии:1; 2;
Страница 60, Проверяем, чему мы научились:1; 2; 3;
Страница 60, Математический тренажер:1; 2; 3;
Страница 61:4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14;
Страница 63:15; 16; 17; 18; 19; 20; 21; 22; 23;
Страница 64, Играем с кенгуру:1; 2; 3; 4;
Страница 65:5; 6; 7; 8; 9; 10;
Страница 68, Переставляем слагаемые:1; 2; 3;
Страница 69:4; 5; 6; 7; 8;
Страница 70, Переставляем множители:1; 2; 3;
Страница 71:4; 5; 6; 7;
Страница 72, Складываем и вычитаем:1; 2; 3; 4;
Страница 73:5; 6; 7; 8; 9; 10;
Страница 74, Умножаем и делим:1; 2; 3; 4; 5; 6;
Страница 75:7; 8; 9; 10;
Страница 76, Группируем слагаемые:1; 2; 3; 4;
Страница 77:5; 6; 7;
Страница 78, Умножаем и делим на 10, 100, 1000:1; 2; 3;
Страница 79:4; 5; 6; 7; 8;
Страница 80, Группируем множители:1; 2; 3; 4;
Страница 81:5; 6; 7; 8; 9; 10;
Страница 82, Проверяем, чему мы научились:1; 2; 3; 4;
Страница 82, Математический тренажер:1; 2;
Страница 83:3; 4; 5; 6; 7; 8; 9; 10;
Страница 84, Умножаем сумму:1; 2; 3; 4;
Страница 85:5; 6; 7; 8;
Страница 86, Умножаем и складываем:1; 2; 3;
Страница 87:4; 5; 6;
Страница 88, Делим сумму:1; 2; 3; 4; 5;
Страница 89:6; 7; 8; 9;
Страница 90, Повторяем все правила:1; 2; 3; 4; 5;
Страница 91:6; 7; 8; 9; 10;
Страница 92, Используем правила вычислений:1; 2; 3; 4; 5;
Страница 93:6; 7; 8; 9; 10; 11;
Страница 94, Размышления о нуле:1; 2; 3;
Страница 95:4; 5; 6; 7;
Страница 96, Идем за покупками:1; 2; 3;
Страница 97:4; 5; 6;
Страница 98, Проверяем, чему мы научились:1; 2; 3; 4;
Страница 98, Математический тренажер:1; 2; 3;
Страница 99:4; 5; 6; 7; 8; 9;
Страница 100, Числа и величины:1; 2; 3; 4;
Страница 101:5; 6; 7; 8;
Страница 102, Минуты в часы и обратно:1; 2; 3;
Страница 103:4; 5; 6; 7;
Страница 104, Сутки, месяц, год:1; 2; 3; 4;
Страница 105:5; 6; 7; 8;
Страница 106, Вычисляем длину пути:1; 2; 3; 4;
Страница 107:5; 6;
Страница 108, Рисуем схемы движения:1; 2; 3;
Страница 109:4; 5; 6;
Страница 110, Скорость:1; 2; 3; 4;
Страница 111:5; 6; 7;
Страница 112, Исследуем зависимость:1; 2; 3;
Страница 113:4; 5; 6; 7; 8;
Страница 116, Проверяем, чему мы научились:1; 2; 3;
Страница 116, Математический тренажер:1; 2;
Страница 117:3; 4;
Страница 118:5; 6; 7; 8; 9; 10; 11; 12;
Страница 119:13; 14; 15; 16; 17; 18; 19;
Страница 120, Играем с кенгуру:1; 2; 3; 4; 5;
Страница 121:6; 7; 8; 9; 10; 11;
Часть 2.

(Страницы с 6 по 139)
Страница 6, Как составляют выражения:1; 2; 3; 4;
Страница 7:5; 6; 7; 8;
Страница 8, Вычисляем значение выражения:1; 2; 3; 4;
Страница 9:5; 6; 7;
Страница 10, Неизвестное число в равенстве:1; 2; 3; 4;
Страница 11:5; 6; 7; 8;
Страница 12, Преобразуем выражения:1; 2; 3;
Страница 13:4; 5; 6; 7;
Страница 14, Решаем задачи:1; 2; 3;
Страница 15:4; 5; 6;
Страница 16, Проверяем, чему мы научились:1; 2; 3; 4;
Страница 16, Математический тренажер:1; 2; 3; 4;
Страница 17:5; 6; 7; 8; 9;
Страница 18, Что такое масса:1; 2; 3;
Страница 19:4; 5; 6; 7; 8; 9;
Страница 20, Записываем сложение в столбик:1; 2; 3; 4;
Страница 21:5; 6; 7; 8;
Страница 22, Встречаем сложение чисел на практике:1; 2; 3; 4;
Страница 23:5; 6; 7;
Страница 24, Перепись населения:1; 2; 3;
Страница 25:4; 5; 6; 7;
Страница 26, По дорогам России:1; 2; 3;
Страница 27:4; 5; 6;
Страница 28, Проверяем, чему мы научились:1; 2; 3;
Страница 28, Математический тренажер:1; 2; 3; 4;
Страница 29:5; 6; 7; 8; 9; 10;
Страница 30, Играем в шахматы:1; 2; 3;
Страница 31:4; 5; 6; 7; 8;
Страница 32, Путешествуем по городам Европы:1; 2; 3;
Страница 33:4; 5; 6;
Страница 34, Работаем с таблицами и схемами:1; 2; 3; 4;
Страница 35:5; 6;
Страница 36, Решаем задачи на клетчатой бумаге:1; 2; 3; 4;
Страница 37:5; 6; 7;
Страница 38, Площадь квадрата:1; 2; 3;
Страница 39:4; 5; 6; 7;
Страница 41, Разворот истории:1; 2;
Страница 42, Математический тренажер:1; 2; 3; 4;
Страница 43:5; 6; 7; 8; 9;
Страница 44, Вспоминаем, что мы умеем:1; 2; 3; 4; 5; 6;
Страница 45:7; 8; 9; 10;
Страница 46, Записываем вычитание в столбик:1; 2; 3;
Страница 47:4; 5; 6; 7;
Страница 48, Считаем сдачу:1; 2; 3; 4;
Страница 49:5; 6; 7; 8; 9;
Страница 50, По железной дороге:1;
Страница 51:2; 3; 4; 5;
Страница 52, Как вычесть сумму из числа:1; 2; 3;
Страница 53:4; 5; 6; 7;
Страница 54, Знаменательные даты:1; 2; 3; 4; 5;
Страница 55:6; 7; 8; 9;
Страница 56, Подводим итоги:1; 2; 3; 4; 5; 6;
Страница 57:7; 8; 9; 10;
Страница 58, Проверяем, чему мы научились:1; 2; 3;
Страница 58, Математический тренажер:1; 2; 3;
Страница 59:4; 5; 6; 7;
Страница 60:8; 9; 10; 11;
Страница 61:12; 13; 14; 15; 16; 17; 18;
Страница 62, Играем с кенгуру:1; 2; 3; 4; 5;
Страница 63:6; 7; 8; 9; 10; 11;
Страница 68, Записываем умножение в столбик:1; 2; 3; 4;
Страница 69:5; 6; 7; 8; 9;
Страница 70, Откуда берутся нули:1; 2; 3; 4; 5;
Страница 71:6; 7; 8; 9; 10;
Страница 72, Считаем устно и письменно:1; 2; 3; 4;
Страница 73:5; 6; 7; 8;
Страница 74, Пять пишем, три в уме:1; 2; 3; 4; 5;
Страница 75:6; 7; 8; 9;
Страница 76, Вычисляем массу:1; 2; 3;
Страница 77:4; 5; 6; 7;
Страница 78, Измеряем емкости:1; 2; 3; 4;
Страница 79:5; 6; 7; 8; 9;
Страница 80, Шестидесятеричная система счисления:1; 2;
Страница 81:3; 4;
Страница 82, Проверяем, чему мы научились:1; 2; 3;
Страница 82, Математический тренажер:1; 2;
Страница 83:3; 4; 5; 6; 7; 8; 9; 10; 11;
Страница 84, Вспоминаем, что мы знаем и умеем:1; 2; 3; 4; 5;
Страница 85:6; 7; 8; 9;
Страница 86, Делится – не делится:1; 2; 3;
Страница 87:4; 5; 6; 7; 8; 9;
Страница 88, Подбираем наибольшее произведение:1; 2; 3;
Страница 89:4; 5; 6; 7; 8;
Страница 90, Что в остатке?:1; 2; 3;
Страница 91:4; 5; 6; 7; 8;
Страница 92, Записываем деление уголком:1; 2; 3;
Страница 93:4; 5; 6; 7;
Страница 94, Продолжаем осваивать деление:1; 2; 3; 4; 5;
Страница 95:6; 7; 8; 9;
Страница 96, Проверяем, чему мы научились:1; 2; 3;
Страница 96, Математический тренажер:1; 2;
Страница 97:3; 4; 5; 6; 7; 8; 9; 10; 11;
Страница 98, Находим неизвестное:1; 2; 3; 4; 5;
Страница 99:6; 7; 8; 9; 10;
Страница 100, Делим на круглое число:1; 2; 3; 4; 5;
Страница 101:6; 7; 8; 9;
Страница 102, Собираемся в путешествие:1; 2; 3; 4;
Страница 103:5; 6; 7; 8;
Страница 104, Учимся находить ошибки:1; 2; 3; 4;
Страница 105:5; 6; 7; 8;
Страница 106, Проверяем результаты деления:1; 2; 3;
Страница 107:4; 5; 6; 7; 8;
Страница 108, Проверяем, чему мы научились:1; 2; 3;
Страница 108, Математический тренажер:1; 2; 3; 4;
Страница 109:5; 6; 7; 8; 9; 10;
Страница 110, Окружность и круг:1; 2; 3;
Страница 111:4; 5; 6; 7;
Страница 112, Делим на равные части:1; 2; 3; 4;
Страница 113:5; 6; 7; 8; 9; 10;
Страница 114, Рисуем схемы и делим числа:1; 2;
Страница 115:3; 4; 5; 6; 7;
Страница 116, Вычисляем доли:1; 2; 3; 4; 5;
Страница 117:6; 7; 8; 9; 10;
Страница 118, Рисуем схемы и решаем задачи:1; 2; 3; 4;
Страница 119:5; 6; 7; 8; 9;
Страница 120, Проверяем, чему мы научились:1; 2; 3;
Страница 120, Математический тренажер:1; 2; 3; 4; 5;
Страница 121:6; 7; 8; 9; 10; 11; 12;
Страница 122, Полет на луну:1; 2; 3;
Страница 123:4; 5; 6; 7;
Страница 124, Ворота Мории:1; 2;
Страница 125:3; 4; 5; 6;
Страница 126, Золотое руно:1; 2;
Страница 127:3; 4; 5; 6;
Страница 128, Возвращение аргонавтов:1; 2; 3;
Страница 129:4; 5; 6;
Страница 130, Математический тренажер:1; 2; 3; 4; 5;
Страница 131:6; 7; 8; 9; 10;
Страница 132:11; 12; 13; 14; 15; 16; 17; 18; 19;
Страница 133:20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 30;
Страница 134:31; 32; 33; 34; 35; 36; 37; 38; 39; 40;
Страница 135:41; 42; 43; 44; 45; 46; 47; 48; 49; 50;
Страница 136, Умеешь ли ты.

..:1; 2; 3; 4; 5; 6; 7;
Страница 137:8; 9; 10; 11;
Страница 138, Играем с кенгуру:1; 2; 3; 4; 5;
Страница 139:6; 7; 8; 9; 10; 11;

Предыдущее Следующее

Онлайн решебник и гдз по математике за 3 класс к учебнику Башмакова, Нефедовой с ответами к номерам.

Чтобы новые знания не казались детям тяжелыми, родители помогают им, пользуясь гдз по математике 3 класс к учебнику Башмакова. Такая помощь намного действенней, чем самостоятельно считать задачки со своим сыном или дочерью. В решебнике присутствуют интересные примеры, помогающие третьекласснику учить уроки в увлекательной форме. В учебнике можно смотреть упражнения, которые проходили в школе или задали на дом. Кроме решенных примеров ГДЗ предоставляет:

возможность проверить свои знания при помощи интересных тестов;
поиграть в увлекательные арифметические игры;
списать правильные ответы на любые номера;
легко освоить таблицу умножения / деления.

Правильные ответы по математике за 3 класс Башмаков можно смотреть в любое время на нашем ресурсе. Логическое мышление, хорошие отметки, желание осваивать новую науку – то, что приобретают дети, пользуясь эффективным помощником.

Предыдущее Следующее

Bribbing for Math Strength — 3 класс

Формирующее оценивание и упражнения по формированию моста

Grade 3

Эти материалы были разработаны совместно учителями, тренерами и воспитателями учителей математики и являются частью повторяющегося процесса разработки. Мы продолжаем совершенствовать и улучшать ресурсы для учителей. Обратная связь приветствуется и принимается по ссылке ниже.
* Поделиться отзывом о модулях 3 класса ↗

Примечание: Ссылки, отмеченные знаком ↗, откроются в новой вкладке

Standard 3.4a *↗

Standard 3. 4b *↗

Standard 3.4c *↗

Standard 3.4d ↗

Standard 3.5 * ↗

Стандарт 3.6a *↗

Стандарт 3,6B *↗

Стандарт 3,6C *↗

Стандарт 3.7a *↗

3.7a *↗

0004 Standard 3.7b * ↗

Standard 3.8a ↗

Standard 3.8b ↗

Standard 3.9a * ↗

Стандарт 3. 9B ↗

Стандарт 3.9C ↗

Стандарт 3.10 * ↗

Стандарт 3.11 * ↗

3.11 0009 ↗

Standard 3.12abc ↗

Standard 3.13 ↗

Standard 3.14 ↗

Standard 3.15a ↗

Standard 3.15b * ↗

Стандарт 3,16 * ↗

Стандарт 3,17 * ↗

*Эти стандарты являются промежуточными. Стандарты считаются связующим звеном, если они: функционируют как связующее звено, к которому подключается другой контент в рамках уровня/курса; служить в качестве необходимых знаний для содержания, которое будет рассматриваться в будущих классах/курсах; или обладать выносливостью, выходящей за пределы одной единицы обучения в рамках уровня/курса.

Стандарт 3.1A

S стандарт 3 .1a Чтение, запись и определение места и значения каждой цифры в шестизначном целом числе с моделями и без них.

(Потяните вниз, чтобы узнать больше)

Понимание траектории обучения

Большие идеи:

Структура чисел основана на объединении сумм в сотни, единицы и группы. эти группы могут быть реорганизованы таким образом, что числа могут быть представлены несколькими способами. Например, 2560 может равняться 2 тысячам, 5 сотням, 6 десяткам или 25 сотням и 6 десяткам.
Значение разряда относится к значению каждой цифры и зависит от позиции цифры в числе.
Числа располагаются в точках, и места в этих точках повторяются.

Важная оценка Искать:

Учащиеся могут успешно определять несколько способов определения данного числа.
Учащиеся могут использовать значения и различные представления для создания заданного числа.
Учащиеся могут поставить 0 (ноль) заполнителей, если это применимо, и использовать запятую в соответствующем месте.
Учащиеся умеют различать значение и место цифры.

Наводящие вопросы:

Объясните, почему вы написали это число именно так?
Как вы определили цифру в (единицы, десятки, сотни и т. д.) место? Каково значение цифры в разряде ( единиц, десятков, сотен и т.д. )?
Прочтите это число вслух. Соответствует ли это тому, что в вопросе?
Как можно представить это число по-другому?

Сильные стороны учащихся

Учащиеся умеют читать, писать и определять место и значение каждой цифры в трехзначном числе с моделями и без них

Основные понятия

Учащиеся понимают систему счисления с основанием десять (т. е. значение каждого разряда в 10 раз превышает значение цифры справа).

Учащиеся понимают, что значение цифры определяется ее местом в числе.

Стандарт 3 . 1A

Учащиеся могут читать, писать, представлять и определять место и значение каждой цифры в шестизначном числе с моделями и без них.

Полный модуль с инструктом Ional Tips & Resources:

Оценки:

. Время. Математика. Математика Quick проверка # 3.1a (PDF) ↗
Как раз во времени математика быстрое чек # 3.1a (desmos) ↗

Проценан:

7
0005

Богатые задачи:

Игры/ Tech :

Glate Game Of Splash Learn↗
. UP 3,1a Polygraph: PV Models↗

Вернуться к вершине ↗

Стандарт 3.1B

S Tandard 3 . 1B Круглая целые номера, 3 .1b .,999 или меньше, с точностью до десяти, сотен и тысяч.

(Потяните вниз, чтобы узнать больше)

Понимание траектории обучения

Большие идеи:

Понимание структуры десятичной системы счисления основано на простом понимании где каждое место в десять раз больше места справа от него.
При округлении до ближайших 10, 100 или 1000 цель состоит в том, чтобы приблизить число к ближайшему числу без единиц, десятков и единиц или сотен, десятков и единиц (Common Core Standards Writing Team , 2019).
В математике с помощью числовой прямой можно найти заданное число и определить ближайшее число, кратное десяти, сотням или тысячам.

Важная оценка Искать:

Учащиеся могут точно написать число с соответствующим количеством цифр.
Учащиеся понимают систему счисления с основанием 10 и могут определять разряды десятков, сотен и тысяч для округления.
При округлении учащихся используйте заполнители после округленного разряда.
Учащиеся могут определить ближайшее число, кратное десяти, сотням или тысячам для заданного числа.

Наводящие вопросы:

Откуда вы узнали, что ________ округлить до ________? ( от 224 до 220 )
Какая цифра стоит в ( десятки, сотни, тысячи) разряда? Почему оно округлилось до _______?
Объясните, почему вы выбрали _________ для округления до 3670.

Сильные стороны учащихся

Учащиеся могут читать, писать и определять место и значение каждой цифры в трехзначном числе с моделями и без них.

Учащиеся могут округлять двузначные числа до ближайших десяти.

Объединяющие понятия

Учащиеся понимают значение разряда в десятичной системе счисления.

Учащиеся используют оценку, чтобы найти ориентиры и ориентиры.

Стандарт 3 .1 B

Учащиеся могут округлять целые числа до ближайших десятков, сотен и тысяч.

Полный модуль с подсказками:

Формативное оценивание:
0005
Как раз во времени математика Quick check 3. 1b PDF↗
Сейчас по математике.
Загадочное число↗
Практика округления в числовой строке↗

Богатая задача 915 6 5 50004 округление до 50 или 500↗
Игры/Технология:
Закругление номеров.

Back to top ↗
Standard 3.1C
S tandard 3. 1c Compare and order whole numbers, each 9999 или меньше.
(Чтобы узнать больше, потяните вниз)
Понимание траектории обучения
Большие идеи:
десятки, а единицы представлены трехзначным числом.
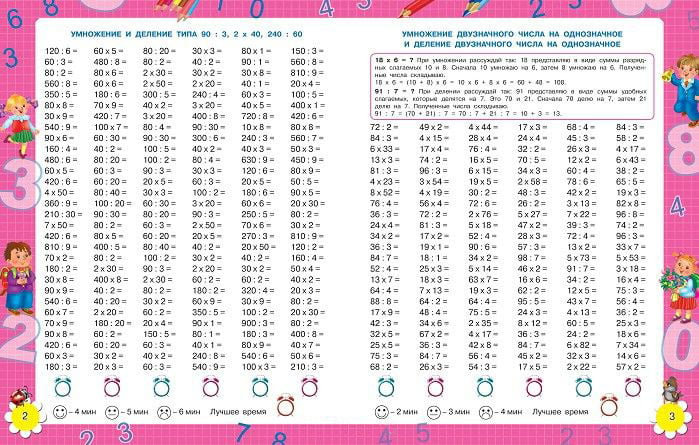
Четырехзначные числа сначала сравниваются путем проверки разряда тысяч, затем разряда сотен и так далее.
Целые числа можно сравнивать, анализируя соответствующие разрядные значения (Чарльз, 2005, стр. 14).
Числа можно сравнивать по их относительным значениям (Чарльз, 2005, стр. 14). Например, эталонные числа — это важные числа, по которым можно оценивать и сравнивать другие числа или количества. Контрольные числа обычно кратны 10 или 100.
0216
Учащийся правильно использует символы >, <,= и .
Учащийся правильно использует термины «наиболее» и «наименее».
Учащийся составляет число, которое меньше, больше или равно заданному числу, используя соответствующий разряд.
Учащийся использует понимание разрядности при сравнении чисел.
Наводящие вопросы:
Как узнать, какое число больше/меньше?
Почему вы расположили номера таким образом?
Почему это число больше/меньше/равно заданному числу?
Сильные стороны учащихся
Учащиеся могут сравнивать и упорядочивать целые числа от 0 до 999.
Стандарт 3.1 с
Учащиеся могут сравнивать и упорядочивать целые числа от 0 до 9999.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.1c↗ (START HERE)

Formative Assessments:
Быстрая проверка Just in Time Mathematics 3. 1c (Word)↗
Быстрая проверка Just in Time Mathematics 3.1c (PDF)↗
Just in Time Mathematics Quick Check 3.1c (Desmos)↗

Routines:
Mystery Number Riddles↗
Target Number Practice↗
Расширенные задачи:
Заказ четырехзначных чисел↗
Достичь ядра↗
Кто это может быть?0219

Games:
Fill the Stairs↗

Back to top ↗
Standard 3. 2a
S tandard 3. 2 a Назовите и запишите дроби и смешанные числа, представленные моделью.
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Дроби представляют равные части целого, часть группы или часть длины (модель числовой линии).
В знаменателе указано общее количество частей в целом или группе, а в числителе указано количество частей.
Смешанные числа записываются из двух частей: целое число и правильная дробь.
Важные оценки:
Учащиеся называют и пишут числители и/или знаменатели в соответствии с моделью.
Студент представляет знаменатель как общее количество частей в целом, группе или на числовой прямой, а не количество частей, которые не указаны.
Ученик различает правильную и неправильную дробь.
Учащийся определяет смешанные числа как целое число и правильную дробь.
Наводящие вопросы:
Объясните, откуда вы знаете, что ваши числитель и знаменатель верны.
Как вы определили, что представленная дробь является правильной дробью или неправильной дробью/смешанным числом?
Можете ли вы записать смешанное число в виде неправильной дроби? Откуда вы знаете, что они представляют одинаковую сумму?
Сильные стороны учащихся
Учащиеся могут называть и записывать дроби с половинными, четвертыми, восьмыми, третьими и шестыми частями.
Объединение понятий
Учащиеся могут различать числитель и знаменатель.
Учащиеся понимают, что в знаменателе указано общее количество частей в целом или группе, а в числителе указано количество частей.
Стандарт 3. 2 а
Учащиеся могут называть и записывать дроби и смешанные числа, представленные моделью.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.2a↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3.2a Word↗
VDOE Just in Time Mathematics Quick Check 3. 2a PDF↗
Vdoe как раз во времени математика Quick check 3.2a desmos↗

Процедуры:
.
Rich Tasks:
Fraction Match↗

Games/Tech:
Fun with Fractions Game↗
Desmos 3.2a Polygraph: Fractions and Mixed Numbers 3.2a Polygraph: Fraction Circles↗

Back to top ↗
Standard 3. 2b
S tandard 3. 2b Представление дробей и смешанных чисел с помощью моделей и символов.
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Дроби — это числовое представление части целого или множества.
Дроби единиц являются основными строительными блоками дробей и многократно повторяются для представления других дробей. (Common Core Progressions, p.7)
Смешанные числа и неправильные дроби больше одного целого.
Важная оценка:
Учащийся делит модель площади на соответствующее количество частей одинакового размера, чтобы представить знаменатель данной дроби.
Учащийся складывает дроби единиц, чтобы определить и назвать более крупную дробь.
Учащийся рисует более одного целого (множества или модели площади) для представления смешанных чисел и неправильных дробей.
Ученик называет модель, представляющую более 1 целого в виде смешанного числа или неправильной дроби.
Учащийся находит неправильные дроби в числе, стоящем больше 1 целого числа.
Наводящие вопросы:
Почему вы так представили эту фракцию?
Как еще можно представить эту дробь?
Можете ли вы создать дополнительное предложение, которое было бы эквивалентно вашему представлению дроби?
Сильные стороны учащихся
Учащиеся могут представлять с помощью моделей и символов дробные части целого числа половин, четвертей, восьмых, третей и шестых частей.
Объединение понятий
Учащиеся могут определить неправильную дробь как дробь, числитель которой больше знаменателя.
Учащиеся могут определить смешанные числа как целое число и правильную дробь.
Учащиеся могут соединить представления неправильной дроби со смешанным числом.
Стандарт 3. 2b
Учащиеся могут представлять дроби и смешанные числа с помощью моделей и символов.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.2b↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3. 2b (Word)↗
Vdoe как раз во времени, математика быстрый чек 3.2b (pdf) ↗
Vdoe. Время математика.
То же самое, но разные
Фракция разговора
Богатые задачи:
0005

Игры/Технологии:
Игра Fun with Fractions 3,2B Использование эталонных фракций на численной линии

Верхний ↗
Стандарт 3.2C
S. 9999. 99. 9 9 9 9 9 9 9 999.99.99. 9 9 9 9 97. и в отличие от знаменателей, используя слова и символы (>, <, = или ≠), с моделями
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Две дроби с одинаковым размером, поэтому знаменатели одинаковые больший числитель больше, потому что он состоит из большего количества дробей (Common Core Progressions, p.9).
Для единичных дробей та, у которой больший знаменатель, меньше, например, исходя из того, что для того, чтобы большее количество (идентичных) частей составляло одно и то же целое, части должны быть меньше. Для двух дробей с одинаковым числителем дробь с меньшим знаменателем больше, потому что части больше (Common Core Progressions, стр. 9).).
Дроби можно сравнивать, рассуждая об относительном размере дробей, предполагая одинаковый размер целого.
Эталонные дроби 0, 1 и ½ используются для сравнения дробей.
Важные критерии оценки:
Учащиеся должным образом используют слова (больше, меньше или равно) и символы (>, <, =).
Учащийся рисует модели одинакового размера при сравнении дробей.
Учащийся обращает внимание как на числитель, так и на знаменатель при сравнении дробей, а не только на сравнение числителей (например, 1/4 < 2/12, потому что 1 меньше 2).
Учащийся использует эталоны 0, ½ и 1 при сравнении дробей.
Ученик использует для определения других дробей, эквивалентных 1/2 (3/6, 4/8 и т. д.).
Целевые вопросы:
Откуда вы знаете, что эта дробь больше или меньше другой дроби? (т. е. как 2/5 меньше 4/10?)
Где на числовой строке вы бы поставили эти дроби? Как можно использовать числовую прямую для сравнения дробей?
Как эта дробь соотносится с эталоном 1/2 (или 0 или 1)?
Можете ли вы нарисовать модель для сравнения этой дроби с 1/2?
Сила учащихся
Учащиеся могут сравнивать дроби единиц половин, четвертей, восьмых, третей и шестых, используя слова (больше, меньше или равно) и символы (>, <, = ), с моделями.
Объединение понятий
Учащиеся могут сравнивать дроби по размеру частей, а не только по числам.
Учащиеся могут использовать эталоны, чтобы рассуждать и сравнивать дроби (при необходимости).
Стандарт 3. 2c
Учащиеся могут сравнивать дроби с одинаковыми и разными знаменателями, используя слова и символы (>, <, = или ≠) с моделями.
Полный модуль с учебными советами и ресурсами:
Стандартный мост математики 3,2C↗ (начало здесь)

СОЗДАНИЯ ВСЕГДА ВСЕГДА ВОЗДА. ↗
VDOE Just in Time Mathematics Quick Check 3.2c (PDF)↗
VDOE Just in Time Mathematics Quick Check 3.2c (Desmos)↗
50228
9 6 Routines:
Would You Rather↗
Rich Tasks:
Comparing Fractions↗

Games/Tech:
Сравнение дробей↗
Сравнение дробей↗
Desmos-3. 2c Сравнение дробей↗

880186
Вернуть к вершине ↗
Стандарт 3.3a
S Tandard 3. 3 A Оценка и определение суммы или разница в двух целых номерах.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Свойства операций позволяют разбивать однозначные числа на одноразрядные для вычислений (сложения и/или вычитания). (Common Core Progressions, стр. 3)
Для нахождения сумм и разностей можно использовать конкретные модели, чертежи и символические изображения.
Оценка является формой округления. Округление слагаемых перед нахождением суммы или разности позволяет учащимся оценить ответ и определить обоснованность окончательного ответа на их вычисление. (Округ Принц Уильям, руководство по разделу 1 для 3 класса).
Важная оценка:
Учащийся использует разрядное значение, чтобы разбить числа для вычислений с многозначными числами.
Учащийся представляет многозначные числа с помощью конкретных предметов и/или абстрактных рисунков.
Студент делает разумные оценки.
Учащийся находит оценку или определяет сумму или разность двух многозначных чисел.
Наводящие вопросы:
Какие шаги необходимы для получения оценки? Какую стратегию вы использовали?
Как разрядное значение помогает вам при определении суммы или разности?
Какую стратегию вы использовали для определения суммы или разницы? Как вы докажете свой ответ?
Сильные стороны учащихся
Учащиеся могут продемонстрировать свободное владение сложением и вычитанием.
Объединение понятий
Учащиеся могут оценить сумму или разницу в пределах 20.
Стандарт 3. 3 a
Учащиеся могут оценить и определить сумму или разность двух целых чисел.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.3a↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3.3a (Word)↗
Vdoe как раз во времени, математика быстрый чек 3. 3a (PDF) ↗
VDOE. Время математика.
Open Middle↗
Rich Tasks:
Base Ten Block Addition↗

Games/Tech:
Domino Addition and Subtraction↗
Desmos-3.3ab Biggest, Smallest, Closest↗

Back to top ↗
Standard 3.3b
S tandard 3. 3b Создание и решение одношаговых и многошаговых практических задач на суммы или разности двух целых чисел, каждое из которых не превышает 9999
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Гибкие методы вычислений включают разделение (разложение) и объединение (составление) чисел различными способами (Van de Walle et al, 8). .
Чтобы разобраться в проблеме, нужно сосредоточиться на мышлении и рассуждениях, а не на ключевых словах.
Знакомство и возможность заниматься различными типами задач укрепят способность учащихся решать новые задачи. Для получения дополнительной информации о типах задач на сложение/вычитание см. Стандарты обучения VDOE для 3-го класса, стр. 15.
Сложение и вычитание являются обратными операциями. Обратные операции связаны между собой и могут гибко использоваться для решения задач.
Для определения обоснованности ответа следует использовать оценку.

Обучающее видео по математике 3.3b↗
Важные критерии оценки:
Учащийся понимает задачу и способен определить неизвестное.
Учащийся использует соответствующую операцию для решения задачи.
Учащийся использует эффективную стратегию для решения задачи и может объяснить свои рассуждения.
Учащийся определяет, разумен ли его ответ.
Наводящие вопросы:
Что неизвестно?
Откуда вы узнали, какую операцию использовать для решения проблемы?
Есть ли другой способ решить эту проблему?
Как вы можете обосновать или доказать правильность своего ответа?
Сильные стороны учащихся
Учащиеся могут создавать и решать одноэтапные и многоэтапные практические задачи на суммы или разности двух целых чисел, каждое из которых не превышает 99.
Учащиеся концептуально понимают сложение/вычитание (сложение/разделение) и могут решать двузначные уравнения.
Объединение понятий
Учащиеся умеют правильно применять сложение/вычитание и могут решать многоэтапные задачи.
Учащиеся могут решать задачи с 3- и 4-значными целыми числами.
Стандарт 3. 3b
Учащиеся могут создавать и решать одноэтапные и многоэтапные практические задачи на суммы или разности двух целых чисел, каждое из которых не превышает 9999.
Полный модуль с учебными советами и ресурсами:
Bridging for Math Strengths Standard 3.3b↗ (START HERE)
Math Strength Instructional Video 3.3b↗

Formative Assessments:
Быстрая проверка по математике Just in Time 3. 3b Word↗
Быстрая проверка по математике Just in Time 3.3b PDF↗
Быстрая проверка по математике Just in Time 3.3b Desmos↗

Routines:
Numberless Word Problems↗
Rich Tasks:
Downsizing Tomatoes↗
Games/Tech :
Desmos-3.3ab Самый большой, самый маленький, ближайший↗

Наверх 59
5
80186 Стандарт 3.
4a
S Tandard 3,4a Представляют умножение и деление на 10 × 10, используя различные подходы и модели
(понижение для большего количества)
Большие идеи:
Стратегии раннего подсчета и сложения, такие как пропуск счета и использование двойников, обеспечивают основу для решения задач на умножение. Умножение и деление являются обратными операциями. Умножение и деление могут быть представлены в различных подходах и моделях, таких как группы одинакового размера, массивы, модель длины (числовая линия), коммутативное свойство.
Модель равных множеств или равных групп подходит для сортировки множества конкретных объектов на равные группы и усиливает концепцию умножения как способа найти общее количество элементов в наборе групп с одинаковыми сумму в каждой группе, а общее количество элементов можно найти путем повторного сложения или пропуска счета. Модель массива, состоящая из строк и столбцов (например, четыре строки по шесть столбцов для массива 4 на 6), помогает понять свойство коммутативности.
При умножении один множитель представляет количество равных групп, а другой множитель представляет количество или размер каждой группы. Произведение — это общее число во всех группах. Модели умножения могут включать в себя повторяющиеся сложения и наборы подобных наборов, частичные произведения и модели площадей или массивов.
Деление — это операция по созданию равных групп или долей. Когда исходная сумма и количество долей известны, разделите их, чтобы определить размер каждой доли. Когда первоначальная сумма и размер каждой доли известны, разделите, чтобы определить количество акций. Обе ситуации могут быть смоделированы с помощью десятичных манипуляторов. Деление обратное умножению. При делении используются следующие термины: делимое, делитель и частное. Учащиеся извлекают пользу из опыта работы с различными методами деления, такими как повторное вычитание и частичное частное.
Обучающее видео по математике 3.4a↗
Важная оценка Искать:
Ученик связывает счет с пропусками и умножением.
Учащийся использует многократное сложение/вычитание и соотносит его с умножением/делением.
Учащийся решает задачи разными способами, демонстрирующими одну и ту же идею.
Учащийся использует манипуляции, чтобы представить проблему и перевести ее в точную картину.
Целевые вопросы:
Расскажите мне о своем ответе. Что представляет собой ваш ответ?
Как ваш рисунок представляет проблему? Объясните, почему вы выбрали именно это представление.
Есть ли другое представление, которое вы могли бы использовать? Как это будет выглядеть на числовой прямой?
Какое число является целым (произведение/деленное) и какие числа являются частями (множители/делитель/частное) в ваших связанных фактах?
Какое выражение (или уравнение) подойдет для этой задачи? (Например, у Сью 5 пеналов по 8 карандашей в каждом. Сколько у нее карандашей?).
Имеет ли значение, в каком порядке расположены факторы? Почему или почему нет?
Сильные стороны учащихся
Учащиеся могут пропускать счет двойками, пятерками и десятками и определять закономерности чисел.
Учащиеся умеют вычислять суммы и разности.
Соединительные понятия
Учащиеся могут связать счет с пропусками (равные группы) с умножением и связать повторяющееся сложение/вычитание с умножением/делением.
Учащиеся понимают умножение/деление концептуально (понимают, что составляют равные группы или доли).
Стандарт 3.4a
Учащиеся умеют представлять умножение и деление до 10 × 10.
Полный модуль с учебными советами и ресурсами:
Bridging for Math Strengths Standard 3.4a↗ (START HERE)
Math Strength Instructional Video 3.4a↗

Formative Assessments:
Quick Проверка 3.4a Word↗
Быстрая проверка 3.4a Pdf↗
Быстрая проверка 3.4a desmos↗

.0009
Number Talk Array Photos↗
Same but Different Math↗
Same & Different: Dog Treat Packs↗
Rich Tasks:
Amara’s Плитки↗
Вечеринка с коалами↗
«Сколько карандашей?» Иллюстративная математика↗

Игры /Технологии:
Сколько строк? Youcubed↗
Bunny Times from NCTM ↗
Desmos 3. 4a Polygraph Arrays 3.4a Polygraph: Dot Arrays 3.4a Multiplication with Arrays↗
Mathigon Multiplication Cards↗
Vertical Connection: 4.4a

Наверх ↗
Стандарт 3.4b
S Tandard 3,6C Создание и решает одноэтапные практические задачи, которые включают умножение и деление на 10 x 10
(понижение для большего)
Некоторые основные факты умножения можно найти, разбив неизвестный факт на известные факты. Затем ответы на известные факты объединяются, чтобы получить окончательное значение (Чарльз, стр. 22).
Некоторые реальные задачи, связанные с объединением равных групп, разделением равных групп, сравнением или комбинациями, могут быть решены с помощью умножения; другие можно решить с помощью деления (Чарльз, стр. 21).
Существует несколько различных типов задач на умножение и деление. Есть три основные категории задач: задачи равных групп, задачи мультипликативного сравнения и задачи массива.
Важные оценки:
Учащийся пишет соответствующее выражение или уравнение, представляющее задачу
Учащийся точно решает уравнение, которое он составил для представления задачи.
Учащийся использует стратегию, которая лучше всего подходит для него, чтобы определить правильное произведение или частное.
Ученик понимает, к чему относится слово «задача», и может определить, что он решает (результат, начальное количество и т. д.).
Наводящие вопросы:
Откуда вы узнали, что нужно умножать/делить для этой задачи?
Как вы получили этот продукт/коэффициент, когда решили проблему?
Какую стратегию вы использовали для решения проблемы?
Сильные стороны учащихся
Учащиеся могут считать двойками, пятерками и десятками до 120, начиная с числа, кратного 2, 5 и 10.
Учащиеся могут создавать и решать одноэтапные и двухэтапные задачи на сложение и вычитание.
Основные понятия
Учащиеся понимают принципы умножения и деления.
Учащиеся могут использовать различные представления умножения и деления, включая основные факты (0, 1, 2, 5 и 10), для решения задач на умножение и деление.
Стандарт 3. 4b
Учащиеся могут создавать и решать одноэтапные задачи на умножение и деление на 10 x 10.
Полный модуль с учебными советами и ресурсами:
Bribbing for Math Strengths Standard 3.4b↗ (НАЧАТЬ ЗДЕСЬ )

Формирующее оценивание:
Just in Time Mathematics Quick Check 3. 4b Word↗
5 00004 Как раз во времени математика Quick проверка 3.4b PDF↗
Сразу по времени математика быстрый проверка 3.4b desmos↗

9000 1011111111111111111111111111111111111 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000 9000
.
Богатые задачи:

Peach Picker↗
Fruit and Nut Bar↗

9 9058

9 9 9 9 9 9

9 7
. 0009
Desmos 3.4b Equal Groups Multiplication 3.4b Multiplicative Comparison: Result Unknown↗

Back to top ↗
Standard 3.4C
S tandard 3. 4 c Продемонстрируйте свободное владение фактами умножения 0, 1, 2, 5 и 10
(Чтобы узнать больше, потяните вниз)
Понимание траектории обучения
Большие идеи:
Некоторые основные факты умножения можно найти, разбив неизвестный факт на известные факты. Затем ответы на известные факты объединяются, чтобы получить окончательное значение (Чарльз, стр. 22).
В этих фактах существуют закономерности и взаимосвязи, и эти взаимосвязи можно использовать для изучения и сохранения фактов.
Изучая закономерности и взаимосвязи, можно построить основу для свободного владения фактами умножения и соответствующими фактами деления.

Обучающее видео по математике 3.4c↗
Важная оценка Искать:
Ученик использует различные стратегии для решения фактов (массивы, равные группы и т. д.).
Студент применяет тождественное свойство умножения, которое утверждает, что любое число, умноженное на 1, является тем же самым числом.
Студент применяет нулевое свойство умножения.
Студент использует свойство коммутативности для умножения, когда это необходимо.
Наводящие вопросы:
Какую стратегию вы использовали, чтобы найти произведение _________?
Откуда вы знаете, что ______ является продуктом ________?
Есть еще один факт, который поможет вам с этим?
Что вы сделали, чтобы решить эту проблему?
Сильные стороны учащихся
Учащиеся могут пропускать счет двойками, пятерками и десятками до 120.
Учащиеся могут находить разницу между двузначными числами.
Основные понятия
Учащиеся могут определить стоимость монет.
Учащиеся могут найти разницу между двумя трехзначными числами.
Стандарт 3. 4c
Учащиеся могут внести сдачу на сумму 5 долларов США или меньше.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.4c↗ (START HERE)
Math Strength Instructional Video 3.4c↗

Формирующее оценивание:
Just in Time Mathematics Quick Check 3.4c Word↗
Just in Time Mathematics Quick Check 3.4c PDF↗
Just in Time Mathematics Quick Check 3.4c Desmos↗

Routines:
Rich Tasks:
Building Arrays↗

Игры/Технология:
Quick Draw↗
Умножение Маниа 40005
DESMOS 3. 4C Polygraph: Умножение.0005

Верхний ↗
Стандарт 3.4d
Tandard 3,0009 Solving . 3. где один фактор равен 99 или меньше, а второй фактор равен 5 или меньше.
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Некоторые основные факты умножения можно найти, разбив неизвестный факт на известные факты. Затем ответы на известные факты объединяются, чтобы получить окончательное значение (Charles, 2005).
Учащиеся должны изучить и применить свойства умножения и сложения в качестве стратегии решения задач на умножение и деление с использованием различных представлений (например, манипуляций, диаграмм и символов). (Учебная программа VDOE 3 класса).
Свойства операций — это «правила» о том, как работают числа и как они соотносятся друг с другом. Учащимся на этом уровне не нужно использовать формальные термины для этих свойств, но они должны использовать эти свойства для дальнейшего развития гибкости и беглости при решении задач. (Учебная программа VDOE 3 класса).
Стратегии решения задач, связанных с умножением или делением, могут включать ментальные стратегии, частичные произведения, стандартный алгоритм, а также коммутативные, ассоциативные и дистрибутивные свойства. (Учебная программа VDOE 3 класса)
Учащиеся должны решить различные типы задач на умножение и деление. (VDOE Grade 3 Curriculum Framework)
Важные критерии оценки:
Учащийся может объяснить, как найти произведение или частное.
Учащийся может использовать различные стратегии и представления.
Работа учащегося показывает, что он понимает контекст, указанный в задаче, и может использовать его для определения операции, необходимой для решения.
Наводящие вопросы:
Как вы представляли свое мышление?
Откуда вы знаете, что ваш ответ правильный?
Можете ли вы показать свое мышление, используя другую стратегию?
Как вы можете использовать то, что вы знаете, чтобы найти продукт с двузначным числом в качестве одного из его факторов?
Сильные стороны учащихся
Учащиеся могут создавать и решать одноэтапные и двухэтапные задачи на сложение и вычитание.
Объединение понятий
Учащиеся понимают понятия умножения и деления как группы одинакового размера, переходы или массивы.
Учащиеся умеют находить произведения и частные.
Стандарт 3. 4d
Учащиеся могут решать одноэтапные практические задачи на умножение целых чисел, где один множитель равен 99 или меньше, а второй множитель равен 5 или меньше.
Полный модуль с учебными советами и ресурсами:
Стандарт математики. Быстрая проверка по математике 3.4d Word↗
Быстрая проверка по математике Just in Time 3.4d PDF↗
Быстрая проверка по математике Just in Time 3. 4d Desmos↗

Routines:
Which One Doesn’t Belong: Color Array↗
Same and Different: Broken Rectangles↗
Numberless Word Problems↗
Богатые задачи:
Продажа выпекания

Games/Tech:
9
0005

Верхний ↗
Стандарт 3. 5
S Tandard 3,5 Solve Практику
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Понимание того, как складываются дроби, позволяет учащимся увидеть, как складываются дроби.
Предварительные знания о сложении и вычитании целых чисел позволяют составлять и разлагать дроби с одинаковым знаменателем.
Целые числа могут быть представлены в виде эквивалентной дроби, что поддерживает вычисления сложения и вычитания с целыми числами и дробями.
Важная оценка Искать:
Учащийся узнает дроби, представленные моделями.
Учащийся использует соответствующую операцию для решения задачи.
Ученик складывает/вычитает только числители, а знаменатель остается неизменным.
Учащийся распознает, когда сумма является неправильной дробью, и может преобразовать ее в смешанное число.
Наводящие вопросы:
Имеет ли смысл ваш ответ? Откуда вы знаете?
Почему вы прибавили/вычли числители, а не знаменатели?
Зачем вы складывали/вычитали числители и знаменатели?
Как вы получили эту дробь для своего ответа?
Сильные стороны учащихся
Учащиеся могут называть и записывать дроби, представленные моделью, состоящей из половин, четвертей, восьмых, третей и шестых частей.
Учащиеся могут создавать и решать одношаговые практические задачи на сложение и вычитание целых чисел.
Объединение понятий
Учащиеся могут применять стратегии целых чисел для сложения и вычитания (т. е. складывать/разбирать) для сложения и вычитания дробей с одинаковыми знаменателями.
Стандарт 3.5
Учащиеся могут решать практические задачи на сложение и вычитание с правильными дробями, имеющими одинаковые знаменатели, равные 12 или меньше, используя конкретные и графические модели, представляющие площадь/регионы.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.5↗ (START HERE)

Formative Assessments:
VDOE Быстрая проверка по математике Just in Time 3. 5 Word↗
VDOE Быстрая проверка по математике Just in Time 3.5 PDF↗
VDOE Быстрая проверка по математике Just in Time 3.5 Desmos↗

Routines:
Rich Tasks:
Decomposing Fractions – Jelly Beans Activity↗

Games/Tech:
Draw or Play↗ (цифровая версия)↗
Desmos 3.5 Сложение и вычитание дробей, подобных знаменателям

Back to Top ↗
Стандарт 3. 6a
S Tandard 3,6 A Определите стоимость сбора счетов и coins, чье значение составляет 5,00 $ 000
40004 40004 40004 40004 40004 4000449 (Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Предыдущий опыт идентификации монет и ценностей поможет учащимся определить ценность коллекции монет и банкнот.
Стратегии определения стоимости коллекции, на которые рассчитывают, начиная с монеты или купюры самой высокой стоимости, группируя подобные монеты или «составляя совместимые комбинации». (Ван де Валле, 2019, стр. 495)
Свойства операций позволяют вычислять (складывать и/или вычитать) значение коллекции. (Common Core Progressions, стр. 3)
Важные критерии оценки:
Учащиеся группируются, как монеты, и используют многократное сложение или пропуск счета для определения ценности коллекции.
Учащиеся группируют монеты, чтобы можно было использовать эталонные числа для более эффективного счета (т. е. комбинируют четвертак и пятицентовик, чтобы получить 30 центов, а затем могут добавлять оставшиеся десятицентовики).
Учащийся использует стратегии подсчета или сложения, чтобы определить стоимость коллекции купюр и монет.
Учащийся рисует эффективную коллекцию долларов и монет, представляющих стоимость (используя комбинации, отличные от одних пенни).
Наводящие вопросы:
Какую стратегию вы использовали? Есть ли другая стратегия, которую можно использовать?
Какие монеты вы могли бы объединить для получения эталонных показателей?
Сколько стоит самая старшая монета? Или счет?
Сколько четвертаков, десятицентовиков, пятаков, пенни или купюр?
Сильные стороны учащихся
Учащиеся могут правильно определить стоимость отдельных купюр и монет.
Учащиеся могут определить эквивалентность монет (например, 5 пятицентовых монет равны четверти).
Соединяющие концепции
Учащиеся могут определить стоимость коллекции банкнот и монет, общая стоимость которых составляет 2 доллара США или меньше.
Стандарт 3.6 a
Учащиеся могут определить стоимость коллекции банкнот и монет, общая стоимость которых не превышает 5 долларов США.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.6a↗ (START HERE)

Formative Assessments:
VDOE Быстрая проверка по математике Just in Time 3. 6a Word↗
VDOE Быстрая проверка по математике Just in Time 3.6a PDF↗
VDOE Быстрая проверка по математике Just in Time 3.6a Desmos↗

Routines:
Same and Different↗
Rich Tasks:
3 Act Task: It All Adds Up↗

Игры/Технология:
Деньги TIC-TAC-TO↗
Сделайте деньги много способов.0005

Верхний ↗
Стандарт 3,6B
Tandard 3,6 TANDARD 3,6 9000 и счета.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Стоимость монет и/или купюр определяет ценность монет и/или коллекций, а не их количество. /или счета.
При подсчете коллекций монет и банкнот учащиеся расширяют стратегии сопоставления, используемые для сравнения коллекций предметов в более ранних начальных классах.
Термины больше, меньше и равно используются для описания отношения наборов монет/банкнот.
Важная оценка Искать:
Учащийся определяет монеты/банкноты и их номинал.
Студент определяет стоимость каждого набора монет/купюр.
Учащийся сравнивает общее значение ИЛИ использует стратегию сопоставления для сравнения значений наборов.
Учащийся обосновывает свой выбор термина больше, меньше или равно.
Наводящие вопросы:
Какую стратегию вы использовали для определения ценности коллекции (коллекций)?
Что означает выражение «больше, меньше или равно»? Какой символ используется для обозначения «больше, меньше или равно?»
Нашли ли вы монеты и купюры эквивалентной стоимости? Если да, то какие?
Можете ли вы создать набор монет/банкнот, стоимость которого «больше» или «меньше» этого набора?
Сила учащихся
Учащиеся могут пропускать счет двойками, пятерками и десятками до 120.
Учащиеся могут найти разницу между двузначными числами.
Основные понятия
Учащиеся могут определить стоимость монет.
Учащиеся могут найти разницу между двумя трехзначными числами.
Стандарт 3.6 b
Учащиеся могут внести сдачу на сумму не более 5 долларов США.
Полный модуль с учебными советами и ресурсами:
Стандартный мостовой для математики 3,6B↗ (начало здесь)

Оценки:
VDOE. Just in Time Mathematics Quick Check3 .6b PDF↗
VDOE Just in Time Mathematics Quick Check 3. 6b Desmos↗

Подпрограммы9:
005
Rich Tasks:
Who has more money?↗

Games:
“Heads or Tails”↗
Ordering Деньги – Balloon Pop – Ранняя математическая игра – математическая игра

Верхне к вершине ↗
Стандарт 3,6C
S Tandard
S Tandard 9000. 0009 3.6c Внесите сдачу на сумму от 5 долларов США или меньше.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Предыдущий опыт работы с купюрами и идентификация монет поддерживает навыки учащихся в поиске монет.
Стратегии расчета сдачи включают: начиная с общей суммы покупок и заканчивая подсчетом потраченной суммы; вычитание суммы покупки из потраченной суммы; и найти следующий целый доллар. Числовая линия и диаграмма сотен помогают учащимся учиться вносить изменения.
Свойства операций позволяют вычислять (складывать и/или вычитать) значение изменения.
Важная оценка Искать:
Учащийся определяет монеты/банкноты и их номинал.
Учащийся использует манипуляторы или другие тактильные объекты для решения задач, связанных с внесением изменений.
Учащийся использует различные стратегии для решения задач, связанных с внесением изменений (т. е. «часть-часть-целое», подсчет, числовой ряд или вычитание).
Учащиеся используют стоимость доступных денег и купленных предметов, чтобы определить подходящую стратегию внесения сдачи.
Наводящие вопросы:
Какую стратегию вы использовали для решения изменений? Можете ли вы объяснить больше?
Какие монеты и/или купюры вы выбрали для сдачи?
Есть ли другой способ и/или стратегия решения этой проблемы?
Сильные стороны учащихся
Учащиеся могут пропускать счет двойками, пятерками и десятками до 120.
Учащиеся могут находить разницу между двузначными числами.
Основные понятия
Учащиеся могут определить стоимость монет.
Учащиеся могут найти разницу между двумя трехзначными числами.
Стандарт 3.6c
Учащиеся могут внести сдачу на сумму не более 5 долларов США.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.6c↗ (START HERE)

Formative Assessments:
Быстрая проверка по математике Just in Time 3. 6c Word↗
Быстрая проверка по математике Just in Time 3.6c PDF↗
Быстрая проверка по математике Just in Time 3.6c Desmos↗

Routines:
Convince Me That…↗
Rich Tasks:
Making Change↗

Игры/Технологии:
Cash Out – Онлайн-игра↗
Take it to the Bank↗
About the MoneyMaking 9 About Desmos 3.0005

Вверх фут, ярд, сантиметр и метр
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Измерение длины или расстояния состоит из двух аспектов измерять и подразделять (мысленно и физически) объект на эту единицу, помещая эту единицу встык (повторяя) рядом с объектом (Common Core Progressions, стр. 4).
Длина объекта — это количество единиц, необходимое для итерации от одного конца объекта до другого без пробелов или перекрытий (Common Core Progressions, стр. 4).
Наличие «эталонов» в реальном мире полезно. Предварительное понимание концепций измерения и масштаба улучшает оценку измерения объекта (Common Core Progressions, стр. 14-15).
Важная оценка:
Студент правильно делит дюймы пополам.
Ученик правильно пользуется линейкой, ставя нулевую отметку на одном конце объекта и заканчивая измерение на конце объекта.
Учащийся точно измеряет длину/ширину объектов, используя правильные единицы измерения.
Студент использует соответствующий измерительный инструмент для каждого вопроса.
Целевые вопросы:
Как вы узнали, что измерения верны?
Можете ли вы показать мне, как вы нашли это измерение? Объясните, откуда вы знаете, что это правильно.
Куда вы положили линейку, чтобы измерить этот предмет?
Что, если бы у нас была сломанная линейка? Можем ли мы по-прежнему использовать его для измерения объектов?
Сила учащихся
Учащиеся могут использовать нестандартные единицы измерения длины.
Учащиеся выбирают подходящий измерительный инструмент (линейку, рулетку) для измерения длины.
Ученики должным образом пользуются линейкой или рулеткой.
Объединение понятий
Учащиеся могут использовать линейку или рулетку для измерения различных предметов с точностью до дюйма.
Учащиеся могут использовать контрольные точки для получения значимых оценок длины.
Стандарт 3. 7a
Учащиеся могут оценивать и измерять длину с точностью до дюйма, ½ дюйма, фута, ярда, сантиметра и метра.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.7a↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3.7a (Word)↗
VDOE Just in Time Mathematics Quick Check 3.7a (PDF)↗
VDOE Just in Time Mathematics Quick Check 3.7a (Google Slides)↗

Процедуры:
. Задачи:
Группа измерений Действия↗

Игры:
95
Matching/Go Fish↗

Back to top ↗
Standard 3.7b
S tandard 3. 7b Estimate and measure liquid volume in чашки, пинты, кварты, галлоны и литры.
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Измерения объема могут быть оценены с использованием соответствующих известных эталонов (Charles, pg. 2les).
Контрольные точки общих объектов должны быть установлены для каждой из указанных единиц измерения (стакан, пинта, кварта, галлон, литр). (VDOE Curriculum Framework)
Измерение жидкости можно представить с помощью одномерных шкал. Задачи могут быть представлены с помощью рисунков или диаграмм, таких как измерения на стакане со шкалой измерения в миллилитрах (Common Core Progressions, стр. 19).
Важные оценки:
Ученик распознает и использует весы на контейнерах (при необходимости).
Студент измеряет объем жидкости, используя соответствующую единицу измерения.
Учащийся понимает, что в больших емкостях содержится больше воды, чем в емкостях меньшего размера.
Наводящие вопросы:
Почему вы выбрали именно эту единицу объема жидкости для этого конкретного контейнера?
Объясните, как вы получили ______ за объем жидкости в этом контейнере.
Какова шкала (если применимо) для контейнера? Объясните откуда вы знаете.
Сильные стороны учащихся
Учащиеся могут использовать нестандартные единицы измерения объема жидкости.
Основные понятия
Учащиеся могут выбрать подходящие инструменты для измерения объема жидкости.
Учащиеся могут использовать ориентиры для получения точных оценок объема жидкости.
Стандарт 3. 7b
Учащиеся могут оценить и измерить объем жидкости в чашках, пинтах, квартах, галлонах и литрах.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3. 7b↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3.7b (Word)↗
Vdoe как раз во времени, математика быстрый чек 3.7b (pdf) ↗
Vdoe. Время математика.
Совместные оценки объема↗
Вы бы предпочли: Время слизи↗
Математика в нашем мире: полив цветов↗
9 Богатые задачи 9:0
009
Liquid Volume Sort↗

Games:
Matching/Go Fish↗

Back to top ↗
Standard 3. 8a
S tandard 3. 8a Измерьте расстояние вокруг многоугольника, чтобы определить его периметр, используя общепринятые в США и метрические единицы.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Измерение включает сравнение атрибута, имеющего тот же атрибут, с единицей измерения или ситуацией. Длины сравниваются с единицами длины, а площади с единицами площади. Прежде чем что-либо можно будет осмысленно измерить, необходимо понять атрибут, который нужно измерить. (Ван де Валле и др., 2018)
Осмысленное измерение и оценка измерений зависят от личного знакомства с используемой единицей измерения. (Van de Walle et al., 2018)
Чтобы что-то измерить, нужно определиться с измеряемым атрибутом, выбрать единицу измерения с этим атрибутом, а затем сравнить единицы измерения с атрибутом измеряемого объекта. (Van de Walle et al., 2018)
Периметр — это путь или расстояние вокруг любой плоской фигуры. (Учебная программа VDOE 3 класса)
Единица измерения, используемая для нахождения периметра, указывается вместе с числовым значением при выражении периметра фигуры (например, периметр обложки книги составляет 38 дюймов). (3 класс VDOE Curriculum Framework)
Возможности для изучения концепции периметра должны включать практический опыт (например, размещение зубочисток (единиц) вокруг многоугольника и подсчет количества зубочисток для определения его периметра. (3 класс VDOE) Учебная программа)
Важная оценка Искать:
Учащийся правильно вычислил периметр.
Ученик точно измеряет расстояние линейкой.
Ученик правильно сложил длины всех сторон.
Учащийся измеряет все стороны фигуры при измерении сторон вогнутой фигуры.
Целенаправленных вопросов:
Что мы подразумеваем под периметром?
Что такое периметр многоугольника и как он определяется?
Как измерить периметр многоугольника?
Как можно оценить размеры периметра?
Почему при измерении периметра важно измерять все стороны многоугольника?
Сила учащихся
Учащиеся оценивают, а затем измеряют длину различных отрезков и объектов с точностью до дюйма с помощью линейки.
Объединение понятий
Учащиеся имеют опыт использования линейки с точностью до дюйма для измерения линий. Учащиеся могут описывать плоские фигуры.
Стандарт 3. 8a
Учащиеся могут измерить расстояние вокруг многоугольника, чтобы определить его периметр, используя общепринятые в США и метрические единицы.
Полный модуль с учебными советами и ресурсами:
Стандартный мостовой для математики 3,8A↗ (старт здесь)

Оценки:
VDOE. Just in Time Mathematics Quick Check 3.8a PDF↗
VDOE Just in Time Mathematics Quick Check 3.8a Google Slides↗

Подпрограммы:
Одинаковые, но разные: прямоугольники↗
Одинаковые и разные: сравнение форм↗
Какой из них не принадлежит? Colorful Calculations↗
Rich Tasks:
Ladybugs Garden↗

Games:
3. 8ab Desmos Area and Perimeter↗
Area or Perimeter↗

Back to top ↗
Standard 3.8b
S tandard 3. 8b Count the number of square units needed покрыть заданную поверхность, чтобы определить ее площадь.
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Измерение включает сравнение атрибута предмета или ситуации с единицей, имеющей тот же атрибут. Длины сравниваются с единицами длины, а площади с единицами площади. Прежде чем что-либо можно будет осмысленно измерить, необходимо понять атрибут, который нужно измерить. (Van de Walle et al., 2018)
Площадь — это мера пространства внутри региона или того, сколько требуется, чтобы покрыть регион. Как и в случае с другими атрибутами, учащиеся должны сначала понять атрибут площади перед измерением. (Ван де Валле и др., 2018 г.)
Площадь — это количество итераций двухмерной единицы, необходимое для покрытия поверхности. Двумерная единица обычно представляет собой квадрат, но может быть и другой формы, например прямоугольника или равностороннего треугольника. (3 класс VDOE Curriculum Framework)
Единица измерения, используемая для нахождения площади, указывается вместе с числовым значением при выражении площади фигуры (например, площадь обложки книги составляет 90 квадратных дюймов). (Учебная программа VDOE 3 класса)
Возможности изучения концептуальной области должны включать в себя практический опыт (например, заполнение или покрытие многоугольника плитками (квадратами) и подсчет плиток для определения его площади). (Структура учебной программы VDOE для 3-го класса)
Задачи площадей, в которых области разделены квадратными единицами, являются важной основой для модели площадей, используемой в стратегиях умножения и деления (Common Core Standards Writing Team, 2019).
Важные критерии оценки:
Учащийся может различать площадь и периметр.
Учащийся правильно считает только заштрихованные части фигуры.
Ученик закрывает всю фигуру без промежутков между плитками.
Ученик создает фигуры правильной площади.
Целевые вопросы:
Что такое площадь?
Как можно измерить площадь ____?
Почему площадь измеряется в квадратных единицах?
Почему важна площадь?
Когда вы могли бы использовать площадь в реальном мире?
Чем он похож и чем отличается от периметра?
Как можно определить площадь поверхности в квадратных единицах?
Сильные стороны учащихся
Учащиеся могут определять и описывать плоские фигуры (круги, квадраты и прямоугольники) в соответствии с их характеристиками (количеством сторон, вершин и углов). Квадраты и прямоугольники имеют четыре прямых угла.
Объединение понятий
Учащиеся могут разбивать многоугольники на более мелкие.
Стандарт 3. 8b
Учащиеся могут подсчитать количество квадратных единиц, необходимых для покрытия заданной поверхности, чтобы определить ее площадь.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.8b↗ (START HERE)

Formative Assessments:
VDOE Быстрая проверка по математике Just in Time 3. 8b Word↗
VDOE Быстрая проверка по математике Just in Time 3.8b PDF↗
VDOE Быстрая проверка по математике Just in Time 3.8b Google Slides↗

Процедуры:
То же самое, но разные: прямоугольные.
Математика в нашем мире: Планирование сада

Игры:
3,8.
3.8b Area of Rectangles↗
Area Builder↗
Area or Perimeter↗

Back to top ↗
Standard 3. 9a
S стандартный 3.9a Определение времени с точностью до минуты с помощью аналоговых и цифровых часов
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Определение времени — это способность читать приборы (аналоговые и цифровые часы). (Ван де Валле, 2019, стр. 493.)
Для определения времени используются часы и минуты.
Пропустить счет пятерками и десятками поддерживает навык чтения аналоговых часов.
Время абстрактно, его нельзя увидеть или почувствовать. (Ван де Валле, 2019 г., стр. 492)
Важные критерии оценки:
Учащийся демонстрирует взаимосвязь между работой часовой и минутной стрелок.
Студент узнает часы и минуты, указанные по положению стрелок на аналоговых часах.
Студент говорит и сопоставляет время с часами, получасами и ближайшей минутой на аналоговых и цифровых часах (и наоборот).
Целевые вопросы:
Что означает число, когда на него указывает часовая стрелка? Минутная стрелка?
Сколько времени показывают эти часы? Объясните откуда вы знаете.
Можете ли вы показать время _____ на этих часах?
Можете ли вы написать время на этих часах?
Сильные стороны учащихся
Учащиеся могут определять время с точностью до часа или получаса с помощью аналоговых и цифровых часов.
Учащиеся могут различать часовую и минутную стрелки.
Объединение понятий
Учащиеся могут определять время с точностью до пяти минут, используя аналоговые и цифровые часы.
Стандарт 3.9a
Учащиеся могут определять время с точностью до минуты, используя аналоговые и цифровые часы.
Полный модуль с учебными советами и ресурсами:
Bribbing for Math Strength Standard 3.9A↗ (Начало здесь)

Оценки:
VDOE. 3.9a (pdf) ↗
ВДО. Сразу во времени математика быстрый чек 3.9a (desmos) ↗

Руководство:
.0005
Каково время?
DESMOS-3,9A Polygraph: раскрытие времени на ближайшую минуту
3,9C Эк Низ. Периоды времени ↗

Back Back ↗ 9000

Back Back ↗ 9000

Back Back ↗ 9000

.b
S tandard 3. 9b Решайте практические задачи, связанные с прошедшим временем с шагом в один час в течение 12-часового периода.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Время измеряется так же, как и другие атрибуты. Время можно рассматривать как продолжительность события от его начала до конца. Для измерения времени единицы времени измеряются с самого начала и подсчитываются до завершения действия. (Ван де Валле и др., 2018 г.)
Время — это продолжительность события от начала до конца, а прошедшее время — это количество времени, которое прошло между двумя заданными моментами времени. (VDOE Curriculum Framework, 2016)
Прошедшее время должно быть смоделировано и продемонстрировано с помощью аналоговых часов и временных шкал. (VDOE Curriculum Framework, 2016)
Прошедшее время можно найти, отсчитывая время от начала или обратно от времени окончания. (Учебная программа VDOE, 2016 г.)
Важные оценочные номера:
Учащийся может читать время, отображаемое на аналоговых или цифровых часах.
Учащийся использует стратегию для определения прошедшего времени.
Учащийся может понять из задачи, что ему было дано либо время начала, либо время окончания, и может найти подходящее время окончания или начала.
Целенаправленные вопросы:
Сколько времени показывают часы? Откуда вы знаете?
Что за проблема просит вас найти? Время начала? Время окончания? Пройденное время? Откуда вы знаете?
Какую стратегию можно использовать для определения времени начала (время окончания или прошедшее время)?
Чем нахождение времени начала отличается от нахождения времени окончания? Как это похоже?
Сильные стороны учащихся
Учащиеся могут определять время с точностью до часа или получаса, используя аналоговые и цифровые часы.
Учащиеся могут различать часовую и минутную стрелки.
Основные понятия
Учащиеся могут точно определять время по цифровым и аналоговым часам.
Они могут считать часы вперед в хронологическом порядке, начиная с двенадцати.
Стандарт 3. 9b
Учащиеся могут решать практические задачи, связанные с прошедшим временем, с шагом в один час в течение 12-часового периода.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.9b↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3. 9b (Word)↗
VDOE Just in Time Mathematics Quick Check 3.9b (PDF)↗
VDOE Just in Time Mathematics Quick Check 3.9b (Desmos)↗

Routines:
Same but Different: Clocks↗
Rich Tasks:
A Day at the Park

Games/Tech:
Tic-Tac-Time↗

Back to top ↗
Standard 3. 9c
S tandard 3. 9c Определение эквивалентных периодов времени и решение практических задач, связанных с эквивалентными периодами времени.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Использование календаря для понимания взаимосвязей между месяцами, днями и временем между неделями, днями и днями и годы, и месяцы, и годы. (Учебная программа VDOE 3 класса)
Учащиеся должны понимать, что время прошло или будет проходить с равными приращениями (т. е. секунды, минуты или часы). (3 класс VDOE Curriculum Framework)
Использование аналоговых часов облегчает понимание временных соотношений между минутами и часами, часами и днями. (Структура учебного плана VDOE для 3 класса)
Важные критерии оценки:
Учащийся понимает, что в одном часе 60 минут.
Учащийся понимает, что в сутках 24 часа.
Учащийся понимает, что в неделе 7 дней.
Учащийся понимает, что в месяце около 30 дней.
Учащийся может гибко складывать, вычитать, умножать или делить на 60, 24, 7 и 30, чтобы найти эквивалентное время.
Целевые вопросы:
Как связаны разные единицы времени?
Почему важно (или полезно) знать, сколько дней в неделе, дней в месяце, дней в году?
Какую стратегию вы бы использовали, чтобы найти число:
У нас одинаковое количество дней в году? Месяц? Почему или почему нет?
Сильные стороны учащихся
Учащиеся могут определить количество дней в неделе, дней в месяце и месяцев в году.
Учащиеся знают количество минут в часе и количество часов в сутках.
Объединение понятий
Учащиеся могут использовать предыдущий опыт чтения и интерпретации календарей и часов для определения эквивалентных периодов времени.
Учащиеся могут составлять предложения на сложение или умножение для представления эквивалентных периодов времени.
Стандарт 3. 9c
Учащиеся могут определять эквивалентные периоды времени и решать практические задачи, связанные с эквивалентными периодами времени.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.9c↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3. 9c (Word)↗
VDOE Just in Time Mathematics Quick Check 3.9c (PDF)↗
VDOE Just in Time Mathematics Quick Check 3.9c (Desmos)↗

Процедуры:
Вы бы предпочли? Practice Time↗
Rich Tasks:
Math in Our World: Julio’s After-School Schedule↗

Games/Tech:
Desmos 3.9c Эквивалентные периоды времени↗
Календарная игра↗

Верхний ↗
Стандарт 3. 10
S Tandard 3,109 Читайте температуру к ближайшей степени.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Навыки, используемые при чтении термометра, могут помочь в чтении показаний с числовой шкалы или линейки.
Соотношения между числами (и отметками) на термометре представляют шкалу и используются при определении температуры.
Температура может отображаться на термометре в градусах Цельсия и/или Фаренгейта.
Важная оценка Искать:
Учащийся читает шкалу термометра и использует шкалу для определения температуры.
Студент различает градусы Цельсия и Фаренгейта на термометре.
Учащийся отмечает температуру на термометре.
Учащийся измеряет вертикальный и круговой термометры.
Целевые вопросы:
Как вы узнали, что температура ______________?
Что считает этот термометр? Как вы определили, что представляет собой каждая галочка?
Шкалы Фаренгейта и Цельсия одинаковы? Откуда вы знаете?
Сильные стороны учащихся
Учащиеся могут считать двойками, пятерками и десятками до 120, начиная с разного. числа, кратные 2, 5 и 10.
Объединяющие понятия
Учащиеся могут определять и использовать шаблоны счета с пропусками.
Учащиеся могут определять температуру с точностью до десяти градусов.
Стандарт 3.10
Учащиеся могут измерять температуру с точностью до градуса на различных термометрах.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.10↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check 3.10 (Word)↗
VDOE Just in Time Mathematics Quick Check 3.10 (PDF)↗
VDOE Just in Time Mathematics Quick Check 3. 10 (Desmos)↗

Routines:
Choral skip counting by 2, 5, or 10↗
Rich Tasks:
Temperature Task↗

Игры:
Соответствие температуры

БАК КАПА №

к верхней части

.0185
Standard 3. 11
S tandard 3. 11 Определение и рисование точек, линий, отрезков, лучей и углов.
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Изучение геометрии помогает учащимся представить и осмыслить мир. Учащиеся приобретают знания о том, как геометрические фигуры соотносятся друг с другом, и начинают использовать математические рассуждения для анализа и обоснования свойств и отношений между фигурами. (Учебная программа VDOE 3 класса)
Учащиеся узнают об этих отношениях, строя, рисуя, измеряя, сравнивая и классифицируя геометрические фигуры. Исследования должны включать исследования предметов повседневного обихода и других физических материалов. (VDOE Grade 3 Curriculum Framework)
Упражнения, в которых учащимся предлагается визуализировать, рисовать и сравнивать фигуры, помогут им не только развить понимание взаимосвязей, но и развить пространственное чувство. В процессе определения обретают смысл, отношения между фигурами становятся понятными, и учащиеся готовятся использовать эти идеи для разработки неформальных аргументов. (Учебная программа VDOE 3 класса)
В математике основными атрибутами космических объектов являются точка, линия, отрезок линии и плоские фигуры. Чтобы подумать об этих атрибутах, можно использовать ситуации реального мира (Charles, 2005).
Важная оценка Искать:
Учащийся определяет и описывает точки, прямые, отрезки прямых, лучи и углы.
Ученик рисует точки, прямые, отрезки, лучи и углы.
Учащийся может идентифицировать и обозначать конечные точки и вершины.
Наводящие вопросы:
Откуда вы знаете, что это ____?
Какая связь между точками, прямыми, отрезками, лучами и углами?
Как можно использовать модель для представления точек, прямых, отрезков, лучей и углов?
Сколько точек на линии?
Чем похожи линии и отрезки? Насколько они разные?
Чем похожи лучи и углы? Насколько они разные?
Сильные стороны учащихся
Учащиеся могут определять и описывать плоские фигуры (круги, квадраты и прямоугольники) в соответствии с их характеристиками (количество сторон, вершин и углов). Квадраты и прямоугольники имеют четыре прямых угла.
Объединение концепций
Учащиеся могут связать свои знания о сторонах, вершинах и углах, составляющих плоские фигуры, с точками, прямыми, отрезками, лучами и углами.
Стандарт 3.1 1
Учащиеся могут определять и рисовать изображения точек, прямых, отрезков, лучей и углов.
Полный модуль с учебными советами и ресурсами:
Bribbing for Math Strengths Standard 3.11↗ (Начало здесь)

Оценки:
VDOE Прямо по математике. ↗
VDOE Сразу по времени математика быстрое чек 3.11 (desmos) ↗

Рутины:
, что не является одному.0005
Same and Different: Big Square, Small Square↗
Same but Different: Geometric Figures↗
Rich Tasks:
Geometric Design↗

Игры:
Playcard.io- Геометрия четырех-дюйма

Back Back op

к верхней части

. 0185
Standard 3.12abc
S tandard 3.1 2abc Учащийся:
;
б) определять и называть многоугольники с 10 и менее сторонами; и
c) объединить и разделить многоугольники с тремя или четырьмя сторонами и назвать полученный(ые) многоугольник(и).
(Потяните вниз, чтобы увидеть больше)
Понимание траектории обучения
Большие идеи:
Изучение геометрии помогает учащимся представлять и понимать мир. Учащиеся приобретают знания о том, как геометрические фигуры соотносятся друг с другом, и начинают использовать математические рассуждения для анализа и обоснования свойств и отношений между фигурами. Учащиеся обнаруживают эти взаимосвязи, строя, рисуя, измеряя, сравнивая и классифицируя геометрические фигуры. (VDOE Grade 3 Curriculum Framework)
Исследования должны включать исследования предметов повседневного обихода и других физических материалов. Упражнения, которые просят студентов визуализировать, рисовать и сравнивать фигуры, помогут им не только развить понимание отношений, но и развить их пространственное чувство. В процессе определения обретают смысл, отношения между фигурами становятся понятными, и учащиеся готовятся использовать эти идеи для разработки неформальных аргументов. (Учебная программа VDOE 3 класса)
Теория понимания геометрии Ван Хиле описывает, как учащиеся изучают геометрию, и обеспечивает основу для структурирования студенческого опыта, который должен привести к концептуальному росту и пониманию.
Уровень 0: Предварительное распознавание. Геометрические фигуры не распознаются. Например, учащиеся не могут различать трехсторонние и четырехсторонние многоугольники.
Уровень 1: Визуализация. Геометрические фигуры распознаются как объекты без какого-либо понимания частей фигур или взаимосвязей между компонентами фигуры. Учащиеся должны узнавать и называть фигуры и отличать данную фигуру от других, которые выглядят примерно так же. (Это ожидаемый уровень успеваемости учащихся в детском саду и в первом классе).
Уровень 2: Анализ. Свойства воспринимаются, но изолированы и не связаны. Учащиеся должны узнавать и называть свойства геометрических фигур. (Ожидается, что учащиеся перейдут на этот уровень во втором и третьем классах.) (Структура учебного плана VDOE, 3 класс)
Многоугольник — это замкнутая плоская фигура, состоящая как минимум из трех непересекающихся отрезков. (Структура учебного плана VDOE Grade 3)
Многоугольники могут быть описаны их атрибутами (например, сторонами и вершинами). Отрезки линий образуют стороны многоугольника, а углы образованы двумя отрезками прямых, сходящимися в вершине многоугольника. (Учебная программа VDOE 3 класса)
Важные оценочные номера:
Многоугольники на рисунках учащихся содержат замкнутые фигуры без кривых или пересеченных сегментов.
Учащийся понимает, что вогнутые или неправильные фигуры являются многоугольниками.
Учащийся может считать стороны многоугольника, включая вогнутые многоугольники.
Учащийся может распознать новую фигуру, созданную путем объединения меньших фигур.
Учащийся может определить и назвать меньшие фигуры при разложении большей фигуры.
Целевые вопросы:
Что такое многоугольник?
Почему эта фигура многоугольник?
Почему круг не является многоугольником?
Как можно использовать свойства определенных многоугольников для их определения и классификации?
Что значит объединять полигоны?
Что значит разделить полигоны?
Что происходит, когда мы объединяем или разделяем фигуры на другие фигуры?
На сколько способов можно разделить квадрат? Ромб? Трапеция? Прямоугольник?
Способности учащихся
Находить и описывать плоские фигуры (круги, треугольники, квадраты и прямоугольники) в соответствии с их характеристиками (количеством сторон, вершин и углов). Квадраты и прямоугольники имеют четыре прямых угла.
Основные понятия
Учащиеся уже имеют опыт работы с многоугольниками, изучая треугольники, квадраты и прямоугольники.
Учащиеся узнают, что корневые слова могут изменять значение слова (например, три- означает 3, как в словах трехколесный велосипед, трицератопс, треугольник)
Стандартный 3.1 2abc
Учащиеся могут
a) определить полигон;
б) определять и называть многоугольники с 10 и менее сторонами; и
c) объединить и разделить многоугольники с тремя или четырьмя сторонами и назвать получившийся многоугольник(и).
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3. 12abc↗ (START HERE)

Formative Assessments:
VDOE JiT QC Standard 3.12a Word↗ PDF↗ Desmos↗
VDOE JiT QC Standard 3.12b Word↗ PDF↗ Desmos↗
VDOE JIT QC Стандарт 3.12C Word↗ PDF↗ Google Slide↗

Проценан:
6
, что не принадлежит? Видеть формы
Угадайте мое правило: стороны и углы.
Polygon Picture Task↗

Games:
Desmos 3. 12b Polygraph: Identifying Polygons↗
Guess My Rule↗
Fill the Hexagons↗

Назад к вершине ↗
Стандарт 3.13
S TANDARD 3,1 3 Идентифицируйте и описывают Congruent и Noncong Figures.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Конгруэнтные фигуры имеют одинаковый размер и форму. Неконгруэнтные фигуры не имеют одинакового размера и формы. Возможности исследования конгруэнтных и/или неконгруэнтных фигур лучше всего реализовать с помощью физических моделей. (VDOE Grade 3 Curriculum Framework)
Конгруэнтные плоские фигуры остаются конгруэнтными, даже если они находятся в разных пространственных ориентациях. (Учебная программа VDOE 3 класса)
Конгруэнтные или неконгруэнтные рисунки можно идентифицировать с помощью процедур прямого сравнения и/или отслеживания. (VDOE Grade 3 Curriculum Framework)
Важные критерии оценки:
Учащиеся могут определять фигуры одинаковой формы и одинакового размера.
Учащиеся могут распознавать формы как конгруэнтные, когда их ориентация различна.
Учащиеся могут описать, что делает фигуры конгруэнтными друг другу.
Целевые вопросы:
Как определить, конгруэнтны или неконгруэнтны две фигуры?
Что вы заметили в конгруэнтных фигурах?
Что вы заметили в неконгруэнтных фигурах?
Какие атрибуты фигур вам нужно было сравнить, чтобы определить, конгруэнтны они или неконгруэнтны?
Как можно доказать, что конгруэнтные фигуры конгруэнтны, если их ориентации различны?
Как можно доказать, что неконгруэнтные фигуры не конгруэнтны, если их ориентации различны?
Сильные стороны учащихся
Учащиеся могут определять, отслеживать, описывать и сортировать плоские фигуры по вершинам и углам, независимо от ориентации формы.
Сопоставление понятий
Учащиеся могут использовать атрибуты плоских фигур, чтобы определить, имеют ли две фигуры одинаковую форму.
Учащиеся имеют опыт оценки и измерения, чтобы различать, имеют ли числа одинаковый размер.
Стандарт 3.1 3
Ученики умеют определять и описывать конгруэнтные и неконгруэнтные фигуры.
Полный модуль с учебными советами и ресурсами:
Bribbing for Math Strengths Standard 3.13↗ (НАЧАТЬ ЗДЕСЬ)
5 5 8019
81
Формирующие оценки:
Vdoe Сразу по математике. Проверка 3.13 (Desmos) ↗

Процедуры:
Математика в нашем мире: Street Art↗
Math в нашем мире: Blobers↗
Math в нашем мире: Blobers↗
.0005
Rich Tasks:
Street Art Task
Block Tower Task

Games:
Desmos 3.13: Congruent Figures↗

Верхне к вершине ↗
Стандарт 3. 14
S Tandard 3.1 4 Исследуйте и опишите концепцию вероятности как измерения случайности и перечислите возможные исходы для отдельного события.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Учащиеся должны активно участвовать в исследованиях и экспериментах, где должны быть возможности для исследования и экспериментирования. использовать манипуляторы. (Учебная программа VDOE 3 класса)
Шанс не имеет памяти. Результат одного испытания простого эксперимента не влияет на результат будущих испытаний. (Van de Walle, 2018)
Когда в вероятностном эксперименте очень мало испытаний, результаты могут вводить в заблуждение. Чем больше раз проводится эксперимент, тем ближе экспериментальная вероятность к теоретической вероятности (например, монета падает решкой вверх в половине случаев). (VDOE Grade 3 Curriculum Framework)
Вероятность будущего события может быть определена в диапазоне от невозможного до определенного. (Ван де Валле, 2018)
Важные варианты оценки:
Учащийся может описать, что делает результат маловероятным, но не невозможным.
Учащийся может описать, что делает результат невозможным.
Учащийся демонстрирует, что он понимает, что размер разделов определяет вероятность того, что стрелка может попасть на определенное число.
Учащийся может точно описать вероятность определенного результата, используя термины: невозможно, маловероятно или наверняка.
Целевые вопросы:
Что такое вероятность?
Как можно описать степень вероятности наступления события?
Какими способами мы можем организовать все возможные результаты эксперимента?
Каковы возможные результаты подбрасывания двухцветной фишки (или вращения спиннера, или броска кубика со случайными числами)?
Какова вероятность получить определенный цвет (или номер)?
Что может произойти сегодня? Определенный? Невозможно?
Чем подбрасывание монеты похоже на подбрасывание двухцветной фишки? Насколько они разные?
Как можно спланировать эксперимент и сделать определенный результат определенным (невозможным, вероятным, маловероятным, равновероятным)?
Сильные стороны учащихся
Учащиеся могут читать и интерпретировать данные, отображаемые в таблицах, графических изображениях и графических объектах, используя термины больше, меньше, меньше, больше, меньше и равно.
Объединение понятий
Учащиеся могут использовать ключ для интерпретации пиктограммы.
Учащиеся могут читать и интерпретировать данные, отображаемые в гистограммах, используя термины больше, меньше, меньше, больше, меньше и равно.
Стандарт 3.15b
Учащиеся могут читать и интерпретировать данные, представленные в виде пиктограмм и гистограмм.
Полный модуль с учебными советами и ресурсами:
Стандарт мостики математики 3,13↗ (начало здесь)

СОЗДАНИЯ ВСЕГДА:
9029 .
VDOE Just in Time Mathematics Quick Check 3.14 (PDF)↗
VDOE Just in Time Mathematics Quick Check 3.14 (Desmos)↗

8
80186 Процедуры:
Вы бы предпочли? Scoreboard Strategy↗
Rich Tasks:
What’s in the Bag↗
Likely and Unlikely↗

Games:
Stop or Dare↗
Tricky Track↗

назад к вершине ↗
Стандарт 3. 15A
S TANDARD 3,15 A Соберите, организуйте и представляют данные на пиктографах или на барных графиках.
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
На некоторые вопросы можно ответить, собирая и анализируя данные.
Категориальные данные отображаются в виде пиктограмм и гистограмм (Common Core Progressions, стр. 2)
Пиктограммы и гистограммы снабжены точными названиями, ключом или масштабом и соответствующими категориями (Common Core Progressions, стр. 7).
Данные могут быть представлены визуально с помощью объектов, таблиц, диаграмм и графиков. Тип собираемых данных часто определяет наилучший выбор визуального представления.
Важная оценка Искать:
Учащийся правильно маркирует все части гистограммы, включая каждую ось и категорию, и дает соответствующие названия.
Учащийся правильно маркирует все части пиктограммы, создает соответствующий ключ для данных и дает графику название.
Учащийся использует шкалу и/или ключ для правильной записи данных.
Целевые вопросы:
Зачем мы собираем данные?
Как собираются и систематизируются данные?
Каковы характеристики гистограмм и пиктограмм?
Как создаются гистограммы и пиктограммы для представления данных?
Как читаются и интерпретируются гистограммы и пиктограммы?
Как данные представлены на графике?
Как вы решили, какой должна быть тональность или шкала?
Какие вопросы вы могли бы задать, исходя из данных на графике?
Какие заявления вы можете сделать, чтобы объяснить представленные данные?
Как могут измениться данные, если большее количество учащихся будет опрошено с вопросами, представленными на графике?
Сильные стороны учащихся
Учащиеся могут читать и интерпретировать данные, отображаемые в таблицах, графических изображениях и графических объектах, используя термины больше, меньше, меньше, больше, меньше и равно.
Объединение понятий
Учащиеся могут использовать ключ для интерпретации пиктограммы.
Учащиеся могут читать и интерпретировать данные, отображаемые на гистограммах, используя термины больше, меньше, меньше, больше, меньше и равно.
Стандарт 3.15 a
Учащиеся могут читать и интерпретировать данные, представленные в виде пиктограмм и гистограмм.
Полный модуль с учебными советами и ресурсами:
Bribbing for Math Strengths Standard 3.15a↗ (НАЧАТЬ ЗДЕСЬ)

Формирующие оценки:
VDOE JIT Математика Quick 3,15A (Word) ↗
6 9000 4 В. Математика Quick проверка 3.15a (desmos) ↗

Рутины:
То же самое и разные: что в моем робот? Мы видим ракушки↗
Вы бы предпочли? Предпочтения на игровой площадке ↗
Медленное раскрытие График- Desmos↗
Богатые задачи:
График.
Desmos 3.15 Изменение графика↗

Наверх ↗
Стандарт 3.15b
S Tandard 3,15b Читать и интерпретировать данные, представленные на пиктограммах и гистограммах
(понижение для большего количества)
Категориальные данные отображаются в виде пиктограмм и гистограмм (Common Core Progressions, стр. 2).
Данные на пиктограммах и гистограммах сравниваются в контексте «насколько больше…» и/или «на сколько меньше…» (Common Core Progressions, стр. 7).
Данные могут быть представлены визуально с помощью объектов, таблиц, диаграмм и графиков. Тип собираемых данных часто определяет наилучший выбор визуального представления.
Пиктограммы и гистограммы снабжены точными названиями, ключом или масштабом и соответствующими категориями (Common Core Progressions, стр. 7).

Обучающее видео по математике 3.15b↗
Важные оценки:
Студент использует термины больше, меньше, меньше, больше, меньше и равно в полном предложении при анализе графиков.
Учащийся использует клавишу или шкалу для чтения графика.
Учащийся использует соответствующие заголовки и метки для категорийных данных на диаграмме.
Студент делает соответствующую интерпретацию данных на графике.
Целевые вопросы:
Глядя на (пиктограмму или гистограмму), какая категория имеет наименьшее количество? Самая большая сумма?
Глядя на (пиктограмму или гистограмму), есть ли варианты с «нулем» в качестве суммы? Если да, то что это значит?
Что такое ключ пиктограммы? Каков масштаб гистограммы? Объясните откуда вы знаете.
Какую информацию представляет (показывает) таблица или график?
Что вы замечаете или удивляетесь данным?
Сильные стороны учащихся
Учащиеся могут читать и интерпретировать данные, отображаемые в таблицах, графических изображениях и графических объектах, используя термины больше, меньше, меньше, больше, меньше и равно.
Объединение понятий
Учащиеся могут использовать ключ для интерпретации пиктограммы.
Учащиеся могут читать и интерпретировать данные, отображаемые в гистограммах, используя термины больше, меньше, меньше, больше, меньше и равно.
Стандарт 3.15b
Учащиеся могут читать и интерпретировать данные, представленные в виде пиктограмм и гистограмм.
Полный модуль с учебными советами и ресурсами:
Стандарт математической силы 3.15B↗ (Start здесь)
.
Формирующее оценивание:
VDOE Сразу по времени математика Quick проверка 3. 15B (Word) ↗
VDOE. 3.15b (desmos) ↗

Процедуры:
Slow Sceep Graph↗
BAR и пиктографы.0228
Rich Tasks:
Class Graph↗

Games/Tech:

Back to top ↗
Standard 3.16
S tandard 3.16 Идентификация, описание, создание и расширение паттернов, обнаруженных в объектах, изображениях, числах и таблицах
(Потяните вниз, чтобы узнать больше)
Понимание траектории обучения
Большие идеи:
Можно описывать отношения и делать обобщения для математических ситуаций, в которых числа или объекты повторяются предсказуемым образом.
Структура системы счисления с основанием десять создает множество числовых моделей.
Некоторые последовательности геометрических объектов изменяются предсказуемым образом. (Чарльз, стр. 23)
Важная информация для оценки:
Ученик использует предметы, картинки, числа или таблицы для расширения шаблонов.
Учащийся использует предметы, картинки, числа или таблицы, чтобы найти недостающие части узоров.
Учащийся находит правило для числового шаблона, используя отношения между числами в шаблоне.
Учащийся создает правило для шаблона и расширяет шаблон в соответствии со своим правилом.
Целевые вопросы:
Опишите этот шаблон. Каково правило узора?
Эта модель растет или повторяется? Откуда вы знаете?
Какую стратегию вы использовали?
Какое действие (сложение, вычитание, умножение или деление) вы использовали, чтобы продолжить эту схему или заполнить пропущенный термин? Как вы узнали, что нужно использовать эту операцию?
Сильные стороны учащихся
Учащиеся могут сортировать и классифицировать предметы по атрибутам/категориям.
Учащиеся могут определять закономерности.
Объединение понятий
Учащиеся могут расширять шаблоны.
Учащиеся могут определить правило шаблонов.
Стандарт 3. 16
Учащиеся могут идентифицировать, описывать, создавать и расширять закономерности, встречающиеся в объектах, изображениях, числах и таблицах.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.16↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check SOL 3.16 (Word)↗
VDOE Just in Time Mathematics Quick Check SOL 3.16 (PDF)↗
VDOE Just in Time Mathematics Quick Check 3.16 (Desmos)↗

Процедуры:
До и после узоров
Что придет следующее? Тротуарная последовательность↗; Что будет дальше? Действительно Rad Robots↗
Богатые задачи:
3 Задача: Кард -хаус
Desmos Растущие Паттерны.
Racing Buck Tocking Touss (государственные школы Henrico) ↗

Игры/Технология:
. Game↗
Desmos 3.16 Exploring Patterns

Back to top ↗
Standard 3.17
S tandard 3.1 7 Создание уравнений для представления эквивалентных математических отношений
(понижение для большего количества)
Понимание траектории обучения
Большие идеи:
Кличественные отношения представлены по равным и не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны, а не равны. знаки. (Ван де Валле, 2019, стр. 318)
Знак равенства означает, что обе части числового предложения эквивалентны или сбалансированы. (Ван де Валле, 2019 г., п. 318)
Свойства операций позволяют выполнять вычисления (сложение и/или вычитание) для балансировки выражений. (VDOE, Структура учебного плана, стр. 35)
Важные критерии оценки:
Учащийся различает символы равенства и неравно и использует их надлежащим образом.
Учащийся использует стратегии сложения и вычитания, чтобы найти неизвестное в выражении и сбалансировать уравнение.
Студент рассматривает каждую часть уравнения как независимое выражение, а не правую часть знака равенства как ответ на левую часть.
Студент описывает отношения между величинами.
Целевые вопросы:
Что означает знак равенства? Не равен знак означает?
Какую стратегию вы использовали для решения проблемы равенства?
Есть ли другое возможное решение/ответ? Если так, то, что это?
Как можно доказать, что два выражения равны или не равны друг другу, используя представления или модели?
Сильные стороны учащихся
Учащиеся понимают разницу между равными и не равными.
Учащиеся могут создавать наборы одинаковой стоимости.
Объединение понятий
Учащиеся демонстрируют понимание равенства, используя символ равенства.
Стандарт 3. 17
Учащиеся могут создавать уравнения для представления эквивалентных математических отношений.
Full Module with Instructional Tips & Resources:
Bridging for Math Strengths Standard 3.17↗ (START HERE)

Formative Assessments:
VDOE Just in Time Mathematics Quick Check SOL 3.17 (Word)↗
Vdoe как раз во времени, математика быстрый проверка Sol 3.17 (PDF) ↗
VDOE. Время математика. Допустимые равенства?↗
Какой из них не принадлежит? Дополнительная миссия↗
Сегодняшний номер↗
Богатые задачи:
Dog Walking↗
Equality Possibilities↗ Adapted from VDOE Rich Task 4. 16↗

Games:

Back to top ↗
Grade 3 Математическая лексика: определение и простое объяснение
Какие есть словарные слова по математике для 3 класса? Как помочь математике в 3 классе? Какую математику должен знать 3-классник? В третьем классе математика становится сложнее, и рядом появляется столько чудес – родителей. Настоящим мы представим список математических навыков и словарного запаса с определениями и примерами, советами, классными обучающими играми, которые помогут 3-х классам изучать их с удовольствием.
Какими математическими навыками должен обладать трехклассник или восьмилетний ребенок?
Число и смысл числа
Измерение и геометрия
Расчеты и оценка
Вероятность и статистика
Паттерны, функции и алгебра
Число и смысл числа
Числовая строка
Спросите детей, есть ли числа «растут» (становятся больше) по мере того, как вы перемещаетесь вправо или влево по строке чисел . Обсудите идею о том, что чем больше вы двигаетесь вправо, тем выше число . Если вы переместитесь влево (назад по числовой строке ), чисел станут меньше
Равен
Место Значение Позиция
Числитель/знаменатель
Правильная дробь
Неправильная дробь
Смешанный номер
Интересным способом выражения неправильной дроби является использование смешанного числа

Смешанное число представляет собой комбинацию целого числа и правильной дроби. Давайте еще раз посмотрим на последний пример.
Сколько целых квадратов вы раскрасили? Вот так! У вас есть 2 целых квадрата окрашены .
Какой дробью можно представить третий квадрат? Вот так! 3 из 4 деталей окрашены в цвет . значит 3/4 третьего квадрата окрашены.
Если объединить целое число и дробную часть , получится смешанное число !
Вот как пишется смешанное число 2 3/4 .
Это части смешанного числа:
Вычисление и оценка – математический словарь 3 класса
Перегруппировать/переименовать
Умножить: Продукт
Умножение: модель набора
Умножение: модель массива
Умножение: Площадь (массив) Модель
Умножение: числовая линия Модель
Вас может заинтересовать: Классные математические игры для детей от 8 лет
Разделить : Частное
Раздел: модели числовых линий и массивов
Связанные факты: сложение/вычитание
Связанные факты: Умножение/Деление
Уравнение: Числовое предложение
Дробь: Дополнение
Фракция: вычитание
Измерение и геометрия
Измерение – математический словарь для 3 класса
Линейка: сантиметр и дюйм
Кубок
Пинта
Кварта
Галлон
Литр — лучший способ обучения — использовать материалы для дома, чтобы показать их вот так
Площадь: квадратные единицы
Периметр: Единицы
Часы: минуты, полчаса, час
Истекшее время
Календарь
Геометрия – математический словарь для 3 класса
Термометр
Фигурки самолетов
Многоугольники: Треугольники
Многоугольники: Четырехугольники
Многоугольники: пятиугольник, шестиугольник, семиугольник и восьмиугольник
Многоугольники: Nonagon и Decagon
Подраздел
Комбинат
Прямоугольник: Прямоугольный
Квадрат: Прямой угол
Треугольник: сторона и вершина
Конгруэнтность
Неконгруэнтность
Линейный сегмент
Точка – Угол – Линия – Луч
| >>> Узнайте больше: Геометрические фигуры для детей с четкостью и милыми иллюстрациями!
Вероятность и статистика
Гистограмма
Пиктограмма
Некоторые
Вероятно
Маловероятно
Равновероятно
Невозможно
Образцы, функции и алгебра
Равенство
Не равно
Шаблон
: рост и таблица ввода/вывода
Выражение
Калькулятор
Подобные темы математических словарей Статьи:
| >>> Математический словарь для 2 класса: определение и простое объяснение

| >>> Математический словарь для первоклассников: определения и пояснения для детей
О SKIDOS
Интерактивные обучающие игры SKIDOS для детей разработаны для детей в возрасте от 2 до 11 лет и соответствуют их академическим целям. С помощью наших обучающих игр помогите своим детям стать уверенными учениками в математике, программировании и чтении. Познакомьте их с навыками 21 века, которые помогут им подготовиться к светлому будущему. Благодаря легкодоступным еженедельным отчетам вы также можете следить за их прогрессом.
С SKIDOS Pass вы получаете лучшее соотношение цены и качества:
48+ обучающих игр
1000+ увлекательных занятий для ваших детей
6 игроков в 1 аккаунте
Отмена в любое время
Отслеживание прогресса в обучении19 И 7 no 904 сторонняя реклама
Рекомендуемый
Годовой абонемент
7-дневная бесплатная пробная версия
Стоимость в месяц $5
Самые популярные
Четверть прохода
7-дневная бесплатная пробная версия
Стоимость в месяц 6,66 $
Ввод в эксплуатацию
Месячный абонемент
3-дневная бесплатная пробная версия
Стоимость в месяц $8
Помогите своему ребенку развить ранние математические навыки
До того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного общения. Узнайте, какие неформальные занятия дают детям преимущество в раннем развитии математических навыков, когда они идут в школу.
Дети используют ранние математические навыки в своей повседневной жизни и деятельности. Это хорошая новость, так как эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимание калькулятора во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет одного. После того, как Томас поделится одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, стр. 201). Другие математические навыки вводятся через ежедневные занятия, которыми вы делитесь со своим ребенком — например, подсчет шагов, когда вы поднимаетесь или спускаетесь. Неформальные занятия, подобные этому, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие знания по математике потребуются вашему ребенку позже в начальной школе? К ранним математическим концепциям и навыкам, на которых строится учебная программа по математике в первом классе, относятся: (Bowman et al. , 2001, стр. 76).
Понимание размера, формы и узоров
Умение считать устно (сначала вперед, потом назад)
Распознавание цифр
Идентификация большего и меньшего количества
Понимание однозначного соответствия (т. е. сопоставление наборов или знание того, в какой группе четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на раннем математическом «фундаменте» — точно так же, как дом строится на прочном фундаменте. В дошкольном возрасте вы можете помочь своему ребенку начать развивать ранние математические навыки, познакомив его с такими идеями, как: (Из Diezmann & Yelland, 2000, и Fromboluti & Rinck, 1999.)
Чувство числа
Это способность точно считать — первый вперед. Затем, в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, такие как сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он считал с папой: «Раз, два, три, четыре, пять, шесть…»
Представление
Превращение математических идей в реальность с помощью слов, изображений, символов и объектов (например, кубиков). Кейси (3 года) устраивала воображаемый пикник. Он аккуратно разложил четыре пластиковых тарелки и четыре пластиковых стаканчика: «Чтобы вся наша семья могла приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к количеству выбранных им тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. 902:10 Азиз (28 месяцев) хихикал внизу слайда. — Что смешного? — удивилась его тетя. «Я поднялся, — сказал Азиз, — потом я спустился!»
Измерение
Технически это определение длины, высоты и веса объекта с использованием таких единиц измерения, как дюймы, футы или фунты. Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою бабушку: «Сделать печенье? Я сделаю это!» Ее бабуля показала ей, как наполнить мерный стаканчик сахаром. «Нам нужно две чашки, Габи. Наполните его один раз и положите в чашу, а затем снова наполните».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это очень трудно сделать. Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным бубликом, другой был мини-бубликом. Его папа спросил: «Какой бы ты хотел?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот бублик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак!»
Узоры
Узоры — это вещи — числа, формы, изображения — которые повторяются логическим образом. Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на луну: «Луна. Солнце идет ночь-ночь. Ее дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце и уходит луна. Ночью солнце засыпает, а луна выходит играть. А вот Аве пора спать, прямо как солнцу.
Решение проблем
Способность обдумывать проблему, осознавать, что существует более одного пути к ответу. Это означает использование прошлых знаний и навыков логического мышления, чтобы найти ответ. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с 3 отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на коренастые фигуры на полу. Он взял треугольник. Он положил его в свой месяц, а затем стукнул им об пол. Он коснулся края пальцами. Затем он попытался засунуть его в каждое из отверстий новой игрушки. Сюрприз! Он упал в треугольную дыру! Карл потянулся за другим блоком, на этот раз круглым…
Математика: одна часть целого
Математические навыки — это лишь часть большой сети навыков, которые дети развивают в раннем возрасте, включая языковые навыки, физические навыки и социальные навыки. Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала кубики. Она положила два квадратных блока один на другой, а затем еще один треугольный. Она обнаружила, что на вершине треугольного блока больше не будет балансировать ни один блок. Она посмотрела на своего отца и показала ему блок, который она не могла поднять, чтобы остаться на вершине, фактически говоря ему своим жестом: «Папа, мне нужна помощь, чтобы понять это». Ее отец показал ей, что, если она уберет треугольный блок и вместо него возьмет квадратный, она сможет сложить больше сверху. Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Папа, ок! Хорошо!»
В этом обычном взаимодействии вы можете увидеть, как все области развития Трины работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности, чтобы выполнить свой план по строительству башни. Она использует свой язык и социальные навыки, когда просит отца о помощи. Ее эффективное общение позволяет папе реагировать и оказывать ей необходимую помощь (еще больше улучшая ее социальные навыки, поскольку она считает себя важным и хорошим коммуникатором). Затем это еще больше развивает ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
What You Can Do
В приведенных ниже советах рассказывается о том, как вы можете помочь своему ребенку освоить ранние математические навыки, опираясь на его природное любопытство и весело проводя время вместе. (Примечание. Большинство этих советов предназначены для детей старшего возраста — от 2 до 3 лет. Детей младшего возраста можно знакомить с рассказами и песнями, используя повторения, рифмы и числа.)
Приготовьтесь.
Поиграйте с формовщиками. Поговорите с ребенком о каждой фигуре — посчитайте стороны, опишите цвета. Сделайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «запрыгнуть на круг» или «прыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Сортируйте их по размеру, цвету или тому, что они делают (т. е. все машины в одну кучу, все животные в другую).
Позвоните.
Вместе с 3-летним ребенком начните учить его адресу и номеру телефона вашего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и что их дом или квартира является одним из ряда, каждый со своим номером.
Какой это размер?
Обратите внимание на размеры предметов в окружающем вас мире: этот розовый бумажник самый большой. Синий бумажник самый маленький. Попросите ребенка подумать о своем размере относительно других предметов («Ты помещаешься под столом? Под стулом?»).
Теперь ты готовишь!
Даже маленькие дети могут помочь наполнить, перемешать и налить. Благодаря этим занятиям дети совершенно естественно учатся считать, измерять, складывать и оценивать.
Уходи.
Прогулка дает детям много возможностей сравнить (какой камень больше?), оценить (сколько желудей мы нашли?), отметить сходства и различия (есть ли у утки мех, как у кролика?) и классифицировать (см. если вы можете найти несколько красных листьев). Вы также можете говорить о размере (делая большие и маленькие шаги), оценивать расстояние (близко ли парк от нашего дома или далеко?) и практиковаться в счете (давайте посчитаем, сколько шагов, пока мы не дойдем до угла).
Время изображения.
Используйте песочные часы, секундомер или таймер для выполнения коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что некоторые вещи занимают больше времени, чем другие.
Подготовьтесь.
Укажите на различные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть желтый знак в форме треугольника. Внутри магазина вы можете увидеть прямоугольную вывеску красного цвета.
Прочитайте и спойте свои номера.
Пойте песни, которые рифмуются, повторяются или содержат числа. Песни укрепляют шаблоны (что также является математическим навыком). Они также являются интересным способом практиковать язык и развивать социальные навыки, такие как сотрудничество.
Начните сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари укрепляют счет, последовательности и закономерности. Развивайте навыки логического мышления, рассказывая о холодной погоде и спрашивая ребенка: что мы носим, когда холодно? Это побуждает вашего ребенка установить связь между холодной погодой и теплой одеждой.
Передайте это всем.
Попросите ребенка помочь вам в раздаче таких предметов, как закуски, или раскладывании салфеток на обеденном столе. Помогите ему дать по одному крекеру каждому ребенку. Это помогает детям понять переписку один на один. Когда вы раздаете предметы, подчеркивайте концепцию числа: «Один для тебя, один для меня, один для папы». Или: «Обуваемся: раз, два».
Большие блоки.
Дайте ребенку возможность поиграть с деревянными кубиками, пластмассовыми блоками, пустыми коробками, пакетами из-под молока и т. д. Складывание этих игрушек и манипулирование ими помогает детям узнать о формах и взаимосвязях между ними (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Туннельное время.
Откройте большую картонную коробку с каждой стороны, чтобы превратить ее в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Короче говоря.
Отрежьте несколько (3–5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Вместе с ребенком расположите их в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры с открытыми глазами, а затем с закрытыми.
Игра по шаблону.
Развлекайтесь с узорами, предлагая детям раскладывать сухие макароны, крупные бусины, разные виды сухих хлопьев или кусочки бумаги с разными узорами или рисунками. Внимательно следите за своим ребенком во время этого занятия, чтобы предотвратить удушье, и уберите все предметы, когда закончите.
Обучение стирке.
Превратите работу по дому в удовольствие. Пока вы сортируете белье, попросите ребенка сделать стопку из рубашек и стопку из носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрим, сможет ли он сделать пары носков. Можете ли вы взять два носка и положить их в отдельную стопку? (Не волнуйтесь, если они не совпадают! Это упражнение больше связано со счетом, чем с сопоставлением.)
Математика на игровой площадке.
Пока ваш ребенок играет, сравнивайте его по росту (высокий/низкий), положению (больше/меньше) или размеру (большой/маленький).
Платье для успехов в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти что-нибудь в своей комнате, что тоже желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры в его одежде — полоски, цвета, формы или рисунки: Я вижу узор на вашей рубашке. Есть полосы, которые идут красный, синий, красный, синий. Или: Твоя рубашка покрыта пони — большой пони рядом с маленьким пони, по всей твоей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, сделайте таблицу, куда ваш ребенок будет приклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе оценить, в какой колонке больше или меньше наклеек, и сосчитать, сколько их, чтобы быть уверенным.
Ссылки
Боуман, Б.Т., Донован, М.С., и Бернс, М.С., (ред.). (2001). Стремление учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, NJ (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении специалистов дошкольного возраста. (стр. 47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С., и Ринк, Н. (июнь 1999 г.). Раннее детство: с чего начинается обучение. Министерство образования США, Управление образовательных исследований и усовершенствований, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. с https://www2.ed.gov/pubs/EarlyMath/title.html 9.0005

Примеры текстовых задач по математике для 3-го класса с решениями
В этом посте мы рассмотрим подборку задач по математике для 3-го класса в Smartick.
Начнем с объяснения, что такое словесная проблема.
Что такое словесная задача?
Словесная задача — это вопрос или подход, на который нельзя ответить, используя одну конкретную операцию, а скорее комбинацию предыдущих знаний, математических или нет.
Решение математической задачи является когнитивно сложным , поскольку оно включает в себя понимание ситуации, представленной в словесной задаче, а также понимание сообщения и слов, используемых в словесной задаче. Следовательно, сначала столкнуться с математической задачей — значит столкнуться с проблемой лингвистического понимания . Как только слово «проблема» будет понято, вы должны выбрать, какие или какие процедуры вы собираетесь использовать для достижения решения (математическое понимание).
Этот вид деятельности помогает ребенку связать математику с окружающим миром и таким образом применить полученные знания в повседневной жизни. Чтобы решить проблему, необходимо не только овладеть специфическими знаниями, связанными с проблемой, но также спланировать и выполнить некоторые процедуры для достижения решения.
Задачи по математике для 3-го класса
Для оценки математической компетентности в задачах по математике для 3-го класса, необходимо помнить о некоторых когнитивных процессах, которые можно разделить на следующие три группы:
Знать и производить . Это относится к знанию основного математического языка, основных математических свойств и фактов, а также к повторению практикуемых алгоритмов вычислений, связывая их со знакомыми математическими процессами и задачами, которые включают основные операции. Это требуется даже для самых простых упражнений.
Применение и анализ . Включает в себя знание того, как использовать различные математические инструменты и устанавливать отношения между различными ситуациями в относительно хорошо известных контекстах, выбирать стратегии решения проблем, выполнять вычисления и получать решения. Это необходимо для упражнений, которые немного сложнее.
Рассуждать и размышлять . Это требует способности логически и систематически мыслить и включает в себя анализ результатов, полученных при решении проблемы, и размышление об используемом процессе. Это относится к интерпретации результатов в соответствии с контекстом, сообщению об использованном методе и полученном результате надлежащим образом. Это подразумевает более высокую степень конкурентного приобретения.
Прежде чем приступить к занятиям, я бы порекомендовал вам попробовать решить задачи по математике 3-го класса самостоятельно, не глядя на решения. Попробуйте!
Словесная задача 1
Решение 1
После прочтения словесной задачи нам нужно убедиться, что мы поняли предоставленную информацию.
Лазанья будет разрезана на кусочки одинакового размера.
Кэтрин и Ной будут есть порции разного размера.
Ной съест на 1/4 больше, чем Кэтрин.
Поскольку мы знаем, что Кэтрин съест порцию 1 1/2 (1 полный кусок и один 1/2 кусок), нам просто нужно выяснить, насколько большой будет порция Ноя. Давайте посмотрим на дробь, сколько раз 1/4 может перейти в 1/2? Два раза, потому что в целом 2 половины, а в целом 4 четверти, поэтому 1/2 = 2/4. Теперь, когда мы знаем, что Кэтрин съест 1 2/4, а Ной съест еще 1/4, 2/4 + 1/4 = 3/4.
Ной съест 1 3/4 кусочка лазаньи .
Словесная задача 2
Решение 2
Нас попросили изменить только одно число в словесной задаче так, чтобы количество карточек, которые есть у Александра в конце первой части игры, равнялось 6. Мы сказал, что выиграл 17 карт во второй половине и закончил игру с 28 картами. Чтобы узнать, сколько карт было у него в первой части, мы должны вычесть то, что он выиграл во второй части, из общего количества карт, с которыми он закончил игру, другими словами, 28 – 17 = 11. Поскольку мы попросили убедиться, что ответ равен 6 и можно изменить только одни данные, у нас есть два допустимых варианта.
Измените количество карт, которые он выиграл во второй части, если он выиграл 17 и мы добавим 5, 17 +5 = 22. Затем, когда мы вычтем это число из общего числа, 28 – 22 = 6 , это дает нам число, необходимое для решения задачи со словами. В конце первой части игры у Александра было 6 карт.
Измените количество карт, которые у него были в конце игры, вычтя 5 из 28 карт, 28 – 5 = 23 . Затем вычтите количество карт, которые он выиграл во второй части, 17, из общего количества, 9.0007 23 – 17 = 6 . В конце первой части игры у Александра было 6 карт.
Иногда математические задачи имеют несколько решений.
Задача Word 3
Решение 3
Эта задача очень проста, поскольку в приведенной таблице содержится вся информация.
Первое, что нам нужно знать, это общее количество бутербродов всех видов, подаваемых вчера днем и ночью. Проще говоря, нам нужно добавить 16 + 54 = 70 бутербродов .
Далее нам нужно заполнить пустое место для бутерброда Fisherman’s . Чтобы узнать, сколько было сервировано вечером , нам нужно вычесть количество бутербродов , поданных в течение дня из всего .
54 – 27 = 27 Бутерброды рыбака мы подавали вчера вечером в столовой, где работает Кэтрин.
Задача 4
Решение 4
Прежде всего, мы хотим узнать общее количество детей в автобусе. Для этого нам достаточно выполнить очень простую операцию. Мы знаем, что в автобусе 6 детей и автобус совершает 4 поездки, поэтому мы можем сделать 6 x 4 = 24 . Теперь мы знаем, что всего в автобусе в течение дня детей находится 24 ребенка. Далее нам нужно определить, сколько детей высаживают в каждой школе. Слово задача говорит нам о том, что одинаковое количество детей высаживают в каждой школе , школ две, делим на 2!
24 / 2 = 12 , автобус доставляет 12 детей в каждую школу.
Если вы хотите продолжить практиковать математические задачи для 3-го класса и другие темы из начальной математики, адаптированные к вашему уровню, зарегистрируйтесь в Smartick и попробуйте бесплатно!
Подробнее:
Автор
Последние сообщения
Smartick
Группа создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения Smartick (посмотреть все)
Математические навыки в 3-м классе, чему будет учиться ваш ребенок
Образование
Математические советы
3-й
Третий класс — важный год для изучения математики! Дети узнают об умножении и делении, погружаются в дроби и даже начинают вычислять площади и периметры. Узнайте, как поддержать своего ребенка, изучив, что будет происходить в третьем классе по математике.
В третьем классе ваш ребенок научится:
1. Умножение и деление в пределах 100
Теперь, когда ваш ребенок освоил сложение и вычитание, пришло время перейти к умножению и делению. Третьеклассники начнут с использования изображений и предметов для изучения каждой операции, а затем перейдут к решению более абстрактных задач на умножение и деление.
Дома: Придумайте несколько задач из реальной жизни, которые должен решить ваш третьеклассник, например: «В нашей семье четыре человека. Если каждый из нас получит по пять вишен, сколько всего будет вишен?» Когда дети изучают умножение и деление, использование рисунков и реальных предметов может быть хорошей визуальной поддержкой.

2. Понимать взаимосвязь между умножением и делением
Точно так же, как сложение и вычитание являются обратными операциями (одно противоположно другому), третьеклассники узнают, как умножение и деление связаны одинаковым образом.
Помогите ребенку изучить связанные факты, например, 24 разделить на 8 равно 3, а 3 умножить на 8 равно 24. , они готовы использовать все четыре операции для решения текстовых задач. Студенты научатся читать задачи и решать, какую операцию им следует использовать. Они также будут работать над решением двухшаговых задач самостоятельно.
Дома дайте ребенку словесные задачи для решения. Обсудите, как ваш ребенок может решить, какую операцию использовать при решении задач. Пусть ваш ребенок напишет числовое предложение, чтобы показать, как была решена проблема.
4. Дроби на числовой оси
У детей уже есть базовые знания о дробях, но в третьем классе они еще больше углубят это понимание. Учащиеся учатся отображать дроби на числовой прямой и сравнивать различные дроби.
Поддержите своего ребенка, нарисовав числовую линию, чтобы показать взаимосвязь между различными дробями. Поговорите о том, какие дроби больше или меньше, и предложите ребенку задавать вопросы. Дроби могут быть сложными для понимания, поэтому дайте третьекласснику достаточно времени для их изучения.
5. Время с точностью до минуты
В предыдущих классах ваш ребенок научился определять время с точностью до пяти минут. Третьеклассники готовы освоить часы и научатся определять время с точностью до минуты.
Дома: спрашивайте ребенка «Который час?» в течение дня и попросите его напомнить вам, когда пора что-то делать — у детей будет больше мотивации тщательно определять время, когда он отмечает то, что они должны делать. с нетерпением жду!
6. Масштабированные гистограммы и графические изображения
В третьем классе учащиеся учатся создавать масштабированные изображения и гистограммы. Это означает, что вместо того, чтобы одна картинка или квадрат представляли один ответ, они могут представлять несколько ответов. Ваш третьеклассник должен будет использовать сложение и/или умножение при чтении графиков.
Дома: пройдите опрос! Подсчитайте количество красных, синих, зеленых или других цветных вещей в корзине для белья и поместите данные в масштабированное изображение или гистограмму. Выясните, какой масштаб имеет смысл использовать.
7. Понимание площади и периметра
В третьем классе дети знакомятся с понятиями площади и периметра. Они используют свои знания об умножении для решения задач с площадями, вычисляя длину x ширину. Дети также будут использовать сложение, чтобы вычислить периметр различных фигур.
Дайте ребенку сантиметровую ленту и дайте задание определить периметр предметов домашнего обихода. Поощряйте ребенка измерять и вычислять площадь квадратов или прямоугольников, например, поверхности книги или листа бумаги.
Математика в третьем классе полна более сложных и интересных тем. Приготовьтесь к веселой поездке, пока вы погружаетесь в обучение со своим ребенком!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике для классов от детского сада до 5-го класса
Написано Лили Джонс . Она работала воспитателем в детском саду и начальных классах, педагогическим тренером, разработчиком учебных программ и тренером для учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Разработанный для детей от 5 до 11 лет для использования дома, Komodo использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в занятую семейную рутину. Komodo помогает пользователям развивать беглость и уверенность в математике — , не заставляя их долго сидеть за экраном .
Узнайте больше о Komodo и о том, как он ежегодно помогает тысячам детей лучше успевать по математике — вы даже можете попробовать Komodo бесплатно.
Снова в школу — 5 советов, которые помогут вам вернуться к рутине
Вот несколько шагов, которые вы можете предпринять, чтобы вывести детей из режима полных каникул, чтобы первая неделя в школе не сбила вас с толку.

2 + 9 = 11	3 + 9 = 12	4 + 9 = 13	3 + 8 = 11
4 + 8= 12	5 + 8 = 13	4 + 7 = 11	5 + 7 = 12
6 + 7 = 13	5 + 6 = 11	6 + 6 = 12	8 + 6 = 14
8 + 6 = 14	9 + 5 = 14	3 + 9 = 12	7 + 4 =
12 – 4 = 16	16 – 8 = 8	15 – 7 = 8	13 – 4 = 9

18 + 0 = 18	32 + 7 = 39	57 + 6 = 63	32 – 8 = 24	20 + 65 = 85	24 + 69 = 93
26 – 0 = 26	49 – 4 = 45	28 + 4 = 32	56 – 9 = 47	70 – 38 = 32	84 – 57 = 27

98 + 2 = 100	30 – 1 = 29	70 – 30 = 40	30 + 70 = 100
10 + 7 = 17	28 – 8 = 20	9 + 60 = 69	96 – 90 = 6

48 + 17 = 65	45 + 29 = 74	92 – 36 =	100 – 65 = 35
68 + 16 = 84	82 – 65 = 147	83 – 75 = 158	90 – 72 = 18
56 + 34 = 90	15 + 78 = 93	63 + 29 = 92	54 + 16 = 70
21 + 49 = 70	90 – 24 = 114	77 + 18 = 95	88 + 12 = 100

82 – 36 = 46	53 + 29 = 82	100 – 75 = 25	64 + 16 = 80	46 + 36 = 82	82 – 29 = 53
25 + 75 = 100	80 – 16 = 64	93 – 85 = 8	66 + 18 = 84	90 – 82 = 8	77 + 23 = 100
8 + 85 = 93	84 – 18 = 66	8 + 82 = 90	100 – 23 = 77	56 + 29 = 85	61 – 49 = 12
95 – 39 = 56	12 + 49 = 61	82 – 28 = 54	19 + 74 = 93	54 + 38 = 92	93 – 74 = 19
49 + 44 = 93	47 + 13 = 60	93 – 44 = 49	60 – 13 = 47	34 – 23 = 11	49 + 12 = 61

38 + 6 + 4 = 48	13 + 8 + 27 + 2 = 50	54 + 16 + 6 + 14 =90
47 + 8 + 3 = 58	47 + 13 + 9 + 1 = 70	71 + 15 + 5 + 9 = 100

38 + 59 + 2 = 99	30 + 18 – 30 = 18	100 – (38 + 12) = 50
60 + 37 + 3 = 100	60 – 56 + 16 = 20	100 – (59 + 12) = 29
79 – (16 + 24) = 39	95 – 80 + 67 = 82	100 – (29 + 31) = 40
79 – 16 + 24 = 87	82 – 72 + 35 = 45	100 – (79 + 21) = 0

90 – 73 + 8 = 25	25 + 73 – 8 = 90	34 + 36 – 9 = 61	61 – 36 + 9 = 34	84 – 58 – 7 = 19	19 + 58 + 7 = 84
93 – (46 + 9) = 38	38 + 46 + 9 = 93	(28 + 33) – 8 = 53	53 + 8 – 33 = 28	54 – (42 – 7) = 19	19 + 42 – 7 = 54

46 + 11 – 8 = 49	85 – 24 + 9 = 70	100 – (34 + 26) = 40	80 – (42 – 12) = 50	39 – (45 – 28) = 22
62 + 38 – 8 = 92	62 + (38 – 8) = 92	80 – 42 + 12 = 50	50 – 39 + 18 = 29	70-(12 + 3) = 55
19 + 80 – 3 = 96	44 + 36 – 20 = 60	50 – (30 – 2) = 22	50 + (30 + 2) = 82	50 – 30 + 2 = 22

9 * 7 = 63	5 : 1 = 5	1 * 2 = 2	3 : 1 = 3	7 * 3 = 21	4 : 1 = 4
9 * 3 = 27	9 : 9 = 81	2 * 5 = 10	3 : 3 = 9	3 * 7 = 21	2 : 1 = 2
1 * 6 = 6	8 : 2 = 16	2 * 1 = 2	5 : 6 = 30	4 * 1 = 4	4 : 2 = 8
8 * 8 = 64	5 : 5 = 25	9 * 0 = 0	4 : 4 = 16	0 * 6 = 0	7 : 1 = 7
0 * 8 = 0	5 : 1 = 5	2 * 2 = 4	3 : 1 = 3	3 * 9 = 27	6 : 3 = 18
3 * 8 = 24	4 : 2 = 2	9 * 4 = 36	9 : 3 = 3	8 * 0 = 0	8 : 6 = 48
5 * 1 = 5	6 : 2 = 3	6 * 0 = 0	8 : 2 = 4	7 * 6 = 42	9 : 3 = 27
6 * 7 = 42	6 : 6 = 1	4 * 0 = 0	4 : 4 = 1	6 * 5 = 30	8 : 1 = 8
1 * 7 = 7	8 : 4 = 2	4 * 1 = 4	9 : 9 = 1	6 * l = 6	2 : 1 = 2
2 * 4 = 8	4 : 2 = 2	3 * 3 = 9	5 : 1 = 5	7 * 6 = 42	2 : 1 = 2
0 * 8 = 0	3 : 1 = 3	9 * 1 = 9	3 : 3 = 1	9 * 1 = 9	8 : 2 = 16
4 * 9 = 36	5 : 5 = 1	0 * 2 = 0	8 : 1 = 8	3 * 2 = 6	8 : 2 = 16
1 * 5 = 5	5 : 5 = 1	2 * 5 = 10	2 : 1 = 2	9 * 4 = 36	4 : 4 = 16
4 * 1 = 4	7 : 1 = 7	1 * 3 = 3	9 : 3 = 3	9 * 6 = 54	4 : 2 = 8
2 * 0 = 0	9 : 9 = 1	6 * 2 = 12	1 : 1 = 1	4 * 1 = 4	1 : 1 = 1
5 * 9 = 45	4 : 2 = 2	3 * 6 = 36	4 : 2 = 8	4 * 7 = 28	7 : 7 = 49

Примеры по математике 3 класс

Первое полугодие

Второе полугодие

Сложение и вычитание чисел от 1 до 100.

Табличное умножение и деление.

Порядок действий

Урок математики в 3-м классе по теме “Деление двузначного числа на однозначное”

Контрольные работы, самостоятельные, тесты, задания, карточки, задачи для 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 классов за 1, 2, 3, 4 четвертей.

МАТЕМАТИКА В ШКОЛЕ

Задачи и примеры по темам:

Задачи и примеры по классам:

Уроки и презентации по классам:

Тесты и тренажеры по классам

Контрольные работы:

Самостоятельные работы:

Домашние задания:

1 КЛАСС

2 КЛАСС

3 КЛАСС

4 КЛАСС

5 КЛАСС

6 КЛАСС

Задачи по математике для 2 класса, 3500 занимательных заданий с ответами и решением

Занятия логикой и математикой онлайн

У нас есть всё, что вы искали

Популярные категории заданий

Текстовые задачи

Задача 1. Арифметика и логика

Задача 2. На сравнение количества

Задача 3.

Примеры в картинках

Восстанови равенство

Ребус в таблице

Задачи на площадь и периметр

Задача 4. Ломаная линия

Задача 5. Периметр

Задача 6. Площадь

Какой формат занятий вы ищете?

Мы научим ребёнка

Другие категории заданий

ГДЗ по математике 3 класс Башмаков, Нефедова ответы к учебнику 1, 2 часть

Онлайн решебник и гдз по математике за 3 класс к учебнику Башмакова, Нефедовой с ответами к номерам.

Bribbing for Math Strength — 3 класс

Формирующее оценивание и упражнения по формированию моста

0005

80186 Стандарт 3.

. Богатые задачи:

.
Богатые задачи: