Как определить знак больше и меньше: Больше, меньше, равно — урок. Математика, 1 класс. – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Метод интервалов – материалы для подготовки к ЕГЭ по Математике

Метод интервалов – простой способ решения дробно-рациональных неравенств. Так называются неравенства, содержащие рациональные (или дробно-рациональные) выражения, зависящие от переменной.

1. Рассмотрим, например, такое неравенство

Метод интервалов позволяет решить его за пару минут.

В левой части этого неравенства – дробно-рациональная функция. Рациональная, потому что не содержит ни корней, ни синусов, ни логарифмов – только рациональные выражения. В правой – нуль.

Метод интервалов основан на следующем свойстве дробно-рациональной функции.

Дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует.

Найдем нули функции в левой части нашего неравенства. Для этого разложим числитель на множители. (Если вы не помните, что такое нули функции и знак функции на промежутке – смотрите статью «Исследование графика функции»).

Напомним, как раскладывается на множители квадратный трехчлен, то есть выражение вида .

, где и — корни квадратного уравнения .

Получим:

Рисуем ось и расставляем точки, в которых числитель и знаменатель обращаются в нуль.

Нули знаменателя и – выколотые точки, так как в этих точках функция в левой части неравенства не определена (на нуль делить нельзя). Нули числителя и – закрашены, так как неравенство нестрогое. При и наше неравенство выполняется, так как обе его части равны нулю.

Эти точки разбивают ось на промежутков.

Определим знак дробно-рациональной функции в левой части нашего неравенства на каждом из этих промежутков. Мы помним, что дробно-рациональная функция может менять знак только в тех точках, в которых она равна нулю или не существует. Это значит, что на каждом из промежутков между точками, где числитель или знаменатель обращаются в нуль, знак выражения в левой части неравенства будет постоянным – либо “плюс”, либо “минус”.

И поэтому для определения знака функции на каждом таком промежутке мы берем любую точку, принадлежащую этому промежутку. Ту, которая нам удобна.
. Возьмем, например, и проверим знак выражения в левой части неравенства. Каждая из “скобок” отрицательная. Левая часть имеет знак .

Следующий промежуток: . Проверим знак при . Получаем, что левая часть поменяла знак на .

. Возьмем . При выражение положительно – следовательно, оно положительно на всем промежутке от до .

При левая часть неравенства отрицательна.

И, наконец, . Подставим и проверим знак выражения в левой части неравенства. Каждая “скобочка” положительна. Следовательно, левая часть имеет знак .

Мы нашли, на каких промежутках выражение положительно. Осталось записать ответ:

Ответ: .

Обратите внимание: знаки на промежутках чередуются. Это произошло потому, что при переходе через каждую точку ровно один из линейных множителей поменял знак, а остальные сохранили его неизменным.

Мы видим, что метод интервалов очень прост. Чтобы решить дробно-рациональное неравенство методом интервалов, приводим его к виду:

, или , или , или .

(в левой части – дробно-рациональная функция, в правой – нуль).

Затем – отмечаем на числовой прямой точки, в которых числитель или знаменатель обращаются в нуль.
Эти точки разбивают всю числовую прямую на промежутки, на каждом из которых дробно-рациональная функция сохраняет свой знак.
Остается только выяснить ее знак на каждом промежутке.
Мы делаем это, проверяя знак выражения в любой точке, принадлежащей данному промежутку. После этого – записываем ответ. Вот и всё.

Но возникает вопрос: всегда ли знаки чередуются? Нет, не всегда! Надо быть внимательным и не расставлять знаки механически и бездумно.

2. Рассмотрим еще одно неравенство.

Снова расставляем точки на оси . Точки и – выколотые, поскольку это нули знаменателя. Точка – тоже выколота, поскольку неравенство строгое.

При числитель положителен, оба множителя в знаменателе отрицательны. Это легко проверить, взяв любое число с данного промежутка, например, . Левая часть имеет знак :

При числитель положителен; первый множитель в знаменателе положителен, второй множитель отрицателен. Левая часть имеет знак :

При ситуация та же! Числитель положителен, первый множитель в знаменателе положителен, второй отрицателен. Левая часть имеет знак :

Наконец, при все множители положительны, и левая часть имеет знак :

Ответ: .

Почему нарушилось чередование знаков? Потому что при переходе через точку “ответственный” за неё множитель не изменил знак. Следовательно, не изменила знак и вся левая часть нашего неравенства.

Вывод: если линейный множитель стоит в чётной степени (например, в квадрате), то при переходе через точку знак выражения в левой части не меняется. В случае нечётной степени знак, разумеется, меняется.

3. Рассмотрим более сложный случай. От предыдущего отличается тем, что неравенство нестрогое:

Левая часть та же, что и в предыдущей задаче. Та же будет и картина знаков:

Может, и ответ будет тем же? Нет! Добавляется решение Это происходит потому, что при и левая, и правая части неравенства равны нулю – следовательно, эта точка является решением.

Ответ: .

В задаче на ЕГЭ по математике такая ситуация встречается часто. Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!

4. Что делать, если числитель или знаменатель не удается разложить на линейные множители? Рассмотрим такое неравенство:

Квадратный трехчлен на множители разложить нельзя: дискриминант отрицателен, корней нет. Но ведь это и хорошо! Это значит, что знак выражения при всех одинаков, а конкретно – положителен. Подробнее об этом можно прочитать в статье о свойствах квадратичной функции.

И теперь мы можем поделить обе части нашего неравенства на величину , положительную при всех . Придём к равносильному неравенству:

– которое легко решается методом интервалов.

Обратите внимание – мы поделили обе части неравенства на величину, о которой точно знали, что она положительна. Конечно, в общем случае не стоит умножать или делить неравенство на переменную величину, знак которой неизвестен.

5. Рассмотрим еще одно неравенство, на вид совсем простое:

Так и хочется умножить его на . Но мы уже умные, и не будем этого делать. Ведь может быть как положительным, так и отрицательным. А мы знаем, что если обе части неравенства умножить на отрицательную величину – знак неравенства меняется.

Мы поступим по другому — соберём всё в одной части и приведём к общему знаменателю. В правой части останется нуль:

И после этого – применим метод интервалов.

Что означает знак больше или меньше. Какие знаки есть на клавиатуре. Какие часто используемые знаки есть на клавиатуре

Ни один пользователь компьютера или ноутбука не обойдется без буквенных знаков на клавиатуре, вводимых с помощью соответствующих клавиш. Почти на каждой клавише обозначены 2 буквы – английская вверху и русская внизу, т.е. на клавиатуре есть 26 букв английского алфавита и 33 буквы русского. Причем это могут быть как строчные буквы, так и прописные, которые печатаются с помощью клавиши Shift.

Прямой ввод с экранной клавиатурой для конкретной страны

И найдите нужный символ в соответствующем шрифте. Во-первых, установите желаемый язык в строке схемы ввода. Вы можете вводить символы иностранного языка непосредственно с клавиатуры, как если бы вы были греком перед греческой клавиатурой, например. Затем вы можете вводить символы непосредственно над этой виртуальной клавиатурой или над реальной клавиатурой. Здесь приводятся символы за пределами первых примерно 1000 символов. В конце концов, при переключении происходит преобразование шестнадцатеричных кодов.

Знаки препинания есть и в английской, и в русской раскладке, хотя и находятся в разных местах клавиатуры. Удобно при работе с русским текстом, что точка и запятая – это одна и та же клавиша, которая находится в нижнем ряду буквенных клавиш самой последней. Только запятая печатается в комбинации с клавишей с Shift. А в английской раскладке точка – клавиша с русской буквой Ю, а запятая – Б. Так что для ввода данных знаков препинания не нужно переключаться с одного шрифта на другой.

В версии 9 вы найдете ответ на это решение, но его внешний вид и функциональность довольно необычны. Инструменты для издателей. Здесь вы найдете обзор специальных символов, которые всегда нужны, отсортированы по предметной области. У символов также всегда есть описание, если имя неизвестно. Таким образом, описание знаков не является формальным, но интуитивным. Если вы ищете конкретный символ, используйте функцию поиска вашего браузера.

Это выбор. Если вы пропустите знак, вы можете написать комментарий в нижней части страницы. Выбор персонажа постоянно расширяется. Специальные специальные символы, используемые в математике. Различные логические и алгебраические операторы. Специальные персонажи из категории Физика.

Цифровые знаки или цифры мы используем не только для вычислений, но и в тексте для обозначения различных числовых данных. При этом можно пользоваться как верхним цифровым рядом клавиатуры, так и дополнительным цифровым блоком (малая цифровая клавиатура), находящимся у клавиатуры справа.

Основные знаки арифметических действий (плюс «+», минус «-», умножение «*», деление «/»), расположенные на малой цифровой клавиатуре по аналогии с привычным калькулятором, поэтому ими удобно пользоваться при расчетах. А вот если Вам нужно именно напечатать знак равно «=», а не узнать результат вычислений, то такого знака Вы там не найдете. Он находится в верхнем цифровом ряду после цифры 0 через одну клавишу.

Специальные специальные символы из категории валюты, торговли и денег. Специальные знаки препинания, которые не всегда так легко найти на клавиатуре. Специальные специальные символы из количественной теории. Вам не хватает персонажа или вы нашли ошибку?

Какие часто используемые знаки есть на клавиатуре

Не стесняйтесь и напишите комментарий! Кодовая страница предоставляет текстовые символы определенного языка на компьютере. Кодовая страница представляет собой таблицу символов, которая создает связь между ключом на клавиатуре компьютера, с одной стороны, и текстовым символом, с другой стороны, который отображается на экране. На кодовой странице указывается, какой символ отображается на экране при нажатии определенной клавиши. Изменение кодовой страницы изменяет раскладку клавиатуры, то есть назначение клавиш текстовым символам.

Если внимательно посмотреть на клавиатуру, то можно увидеть, что многие знаки скрываются в цифровом ряду и с правой стороны буквенных рядов, последние клавиши. Для ввода при печати знаков вместо букв или цифр нужно переключить верхний регистр клавишей Shift.

Если идти по порядку, начиная с цифры 1, то таким способом при печати русских текстов вводится:

В кодовой странице каждый текстовый символ имеет уникальный код; уникальный номер. Байт используется для кодирования каждого символа. Байт – наименьшая единица чувств. Каждый байт состоит из восьми бит. Каждый бит имеет одно из двух возможных значений: нуль или один. Поскольку байт состоит из восьми бит, каждый из которых имеет одно из двух возможных состояний, 2 8 – возможные комбинации восьми бит в одном байте. Таким образом, байт состоит из одной из 256 возможных комбинаций нулей и единиц. Каждая из этих различных комбинаций имеет определенное числовое значение между 0 и эти числовые значения также называются кодовыми точками.

1) восклицательный знак «!»;
2) открывающиеся и закрывающиеся кавычки в начале и конце фразы «…»;
3) затем при необходимости знак номера «№»;
4) точка с запятой «;»;
5) знак процента «%»;
6) двоеточие «:»;
7) вопросительный знак «?»;

8) знак звездочка «*», который используется и как знак умножения при компьютерных вычислениях;
9) круглая открывающаяся скобка «(»;
10) круглая закрывающаяся скобка «)» на клавише с цифрой 0;
11) дефис и знак «-» – в компьютерном варианте выглядят одинаково. Знак тире (более длинный) появляется автоматически с использование пробелов до и после этого знака в текстовых программах или же вводится с помощью специального кода.

12) знак равно «=» и знак «+» в верхнем регистре, т.е. в комбинации с клавишей Shift.

Вместо этих символов обычно отображаются пустые поля. Чтобы написать большинство западноевропейских языков, «Американский стандартный код для обмена информацией» недостаточен. Необходимы специальные символы и диакритические знаки. Код номера символа соответствует его порядковому номеру, то есть номер его кодовой точки, с предшествующим нулем.

Выбор случайного примера выборки из случаев, выбор области конкретного случая, выбор переменной записи в качестве критерия фильтра для определения того, должны ли быть отфильтрованы или удалены случаи, которые не были выбраны. Большую часть времени вы только фильтруете, потому что данные, как правило, позже отображаются и анализируются дальше. Слева вы увидите список доступных переменных набора данных. Критерии ложного выбора записываются в поле в правом верхнем углу; это происходит частично через клавиатуру, частично также со встроенной клавиатурой оператора.

Примечательно, что восклицательный знак, %, *, круглые скобки находятся как в русской, так и в английской раскладке клавиатуры на одних и тех же клавишах.

Но некоторые знаки существуют только в английской раскладке. Например, квадратные […] и фигурные {…} скобки, которые находятся на клавишах с русскими буквами Х (открывающиеся) и Ъ (закрывающиеся), знак больше «>» (клавиша с русской буквой Ю) и меньше «Редко используемые знаки на клавиатуре

Математические и логические функции можно выбрать в поле внизу справа. Такой выбор полезен, когда, например, исследование должно проводиться только для конкретной целевой группы. Формула для выбора случаев может быть довольно сложной. Далее описываются операторы и наиболее важные функции, а затем описываются некоторые примеры для более сложных определений выбора.

Следует выбирать случаи, когда респондентами были мужчины в возрасте до 26 лет или женщины старше 24 лет. «Выбрать случаи» часто используется для сужения расследования в конкретных случаях, Отвечал на конкретный пол и возраст, возможно, в сочетании с другими характеристиками, такими как занятие или политические предпочтения. В случае анализа контента, для дальнейшего анализа могут быть выбраны единицы измерения со специальными характеристиками, Взносы, в которых встречаются Ангела Меркель и Герхард Шредер, а Зеленые имеют плохую оценку.

В повседневной жизни обычному пользователю редко приходится пользоваться знаками, существующими только в английской раскладке: разные варианты кавычек “…”, ‘…’, `…`, черточек «|», прямой «/» и обратный «\» слеш, тильда «~». А вот знак параграфа «§» или градуса «°» не помешал бы , но на клавиатуре их нет. Приходится вводить в текст некоторые символы другим способом.

Другое приложение – очистка данных. Примечание: мы будем использовать. для представления десятичной точки. Например, мы напишем 3 для обозначения двух запятых три. Вещественные числа, \\, – это те, которые образуют реальную строку. Стрелки указывают, что линия продолжается бесконечно с обеих сторон.

Все реальные числа сортируются, например. В математике не писать «меньше» или «больше, чем», мы используем символы.

Мы можем переписать предыдущий пример как. Когда мы помещаем два числа на линию, то справа справа больше, чем слева. Когда мы используем этот символ, мы оставляем слева слева число, которое меньше и справа от того, которое больше.

Где знак умножения на клавиатуре , знак деления, проценты, минус, равно, т.д. – про эти кнопки и другие функции, вызываемые кнопками, смотрите здесь.
Красным цветом обведены кнопки, которыми ставим знаки. Смотрим эти кнопки:
Знак «Равно» расположен на кнопке, где написано «+ и =». Нажимать нужно только на эту кнопку.
Знак сложения – нажимаем эту же кнопку, но предварительно нажимаем кнопку «Shift», удерживаем её нажатой, затем «+».
Знак вычитания расположен на кнопке, расположенной слева от кнопки «=». Нажимать нужно только на эту кнопку.
Знак умножения расположен на кнопке с цифрой 8. Это звездочка (*). Но предварительно нажимаем кнопку «Shift», удерживаем нажатой, затем (*).

Знак деления – это черточка (/).

Это кнопка справа на клавиатуре, там нарисовано 4 черточки с разным наклоном.
Чтобы поставить нужную черточку, нажимаем кнопку «Shift», удерживаем нажатой, затем «/».
Знак “больше” (>) – нажимаем на английскую раскладку клавиатуры, нажимаем кнопку “Shift” и, удерживая её нажатой, нажимаем кнопку “>”. Эта кнопка находится на кнопке руссой буквы “Ю”.
Знак “меньше” (- устанавливаем английскую раскладку на клавиатуре, нажимаем на кнопку”Shift” и, удерживая её, нажимаем на кнопку знака ” Но на ноутбуке есть еще одна клавиатура числовая, которая включается, когда нажимаете кнопку «Fn», она обведена желтым. Тогда кнопки знаков будут другие. Лучше эту кнопку не нажимать, чтобы не путаться. Это для общей информации, если нечаянно нажмете кнопку.
Чтобы вызвать функцию , часто нужно воспользоваться сочетание кнопок (нажать не одну, а несколько – 2 или 3 кнопки).
Сначала нажимаем первую кнопку, которая указана в сочетании, и, удерживая её нажатой, нажимаем следующую кнопку. Сочетания кнопок нужно нажимать на английской раскладке клавиатуры . В скобках указаны кнопки на русской раскладке клавиатуры.
Например, такое сочетание кнопок: « Ctrl+C (С) ». Сначала нажимаем кнопку «Ctrl», удерживаем её нажатой, и нажимаем кнопку с буквой «С», (на русской раскладке это тоже кнопка с буквой «С»). Эта функция копирования, поэтому сначала нужно выделить тот фрагмент, который будем копировать.
Копировать кнопками так. Сначала ставим курсор на первую ячейку диапазона, который будем копировать. Затем нажимаем кнопку «Shift», и передвигаем курсор на последнюю ячейку диапазона. Всё, диапазон выделен.
Другие сочетания кнопок.
Ctrl + X (Ч) – вырезать.
Ctrl + V (М) – вставить
Ctrl + Z – отмена
Ctrl + В – полужирный шрифт
Ctrl + U – подчеркивание
Ctrl + I – курсив.
Вызвать контекстное меню можно нажав сочетание кнопок «Shift + F10».
Перемешаться по контекстному меню стрелками.
Кнопка «Delete»– удалить.
В Excel можно вызвать функцию, нажав функциональную клавишу на клавиатуре или сочетание клавиш. Читайте статью о функциональных клавишах ” Горячие клавиши Excel ” .
Можно нажимать несколько клавиш одновременно, тогда подключаются определенные функции. Смотрите разные сочетания кнопок клавиатуры в статье ” Сочетание клавиш в Excel ” .
Раскладку клавиатуры ноутбука, ПК можно настроить на несколько языков, кроме русского и английского. Как это сделать, смотрите в статье “Раскладка клавиатуры “.
В Word некоторые сочетания отличаются от сочетаний в Excel, п.ч. функции в Word другие. О сочетаниях клавиш в Word читайте в статье “Горячие клавиши Word”.
Как сохранить таблицу, читайте в стать “

Мнемоника: левая часть символа меньше правой. Когда мы используем этот символ, мы пишем слева от него число, которое больше, а справа – меньшее. Мнемоническое правило: правая часть символа меньше левой. В этом упражнении вы должны выбрать символ, чтобы соотношение между числами выполнялось.

Символы \\

\\ меньше или равно \\

\\ больше или равно \\. Разница в том, что \\ и \\ можно также использовать для обозначения равенства. Тест – это операция, целью которой является оценка значения выражения. Это выражение может просто быть чем-то, или это может быть предложение.

ТЕМА: «Больше, меньше». | План-конспект занятия по математике (подготовительная группа) на тему:

ТЕМА: «Больше, меньше».

ЦЕЛЬ:

1) закрепить умение сравнивать группы предметов по количеству с помощью составления пар, определять на предметной основе, на сколько в одной группе предметов больше или меньше, чем в другой, использовать знаки «>» и «

2) уточнить представления о числовом ряде, закрепить умение соотносить числа с символами, сравнивать числа с помощью определения порядка их следования в числовом ряду, определять на предметной основе, на сколько одно число больше (меньше) другого;

3) тренировать умение ориентироваться по элементарному плану, решать простейшие примеры на сложение и вычитание;

4) сформировать опыт преобразования способа решения задачи (проблемы) в зависимости от ситуации, опыт самопроверки по образцу, обоснования своего суждения, выполнения действий с комментированием.

МАТЕРИАЛЫ К ЗАНЯТИЮ

Демонстрационный:

образец выполнения задания 2.4;

образец выполнения задания 2.5.

ХОД ЗАНЯТИЯ

Введение в ситуацию.

Дидактические задачи: мотивировать детей на включение в игровую деятельность.

Воспитатель собирает детей около себя и предлагает вспомнить сказку «Гуси-лебеди».

-Чему учит эта сказка?

Воспитатель предлагает детям отправиться в гости к героям этой сказки и помочь вернуть братца.

-Хотите?

Игровая деятельность.

2.1. Работа в учебнике-тетради («Игралочка — ступенька к школе», ч. 4(1).

Дидактические задачи:

2) уточнить представление о сравнении чисел на предметной основе и определять, на сколько одно число больше или меньше другого;

3)сформировать опыт проговаривания алгоритма перед выполнением задания.

№ 1. с. 51.

«Каких яблок на дереве больше — красных или желтых? На сколько?

Прибей к забору слева от яблоньки 3 дощечки, а справа — на 2 дощечки

больше».

Воспитатель предлагает детям рассмотреть картинку и рассказывает, что яблонька обещала рассказать девочке, куда полетели гуси-лебеди, если девочка скажет, каких яблок на яблоньке больше — красных или желтых и на сколько.

Как вы будете выполнять задание? (Соединим ниточками попарно красные и желтые яблоки. Те яблоки, которым не хватило пары, покажут, каких яблок больше и на сколько.)

Дети проводят ниточки и делают вывод:

«Без пары остались 2 красных яблока, значит, красных яблок на 2 больше, чем желтых».

Воспитатель говорит, что у яблоньки есть просьба: чтобы зайцы не обгрызали ее нежную кору, яблонька просит детей огородить ее.

Слева от яблоньки «приколотите» (нарисуйте) 3 дощечки, а справа — на 2 дощечки больше.

-Как вы будете выполнять задание? (Нарисуем слева и справа по 3 дощечки, а затем справа нарисуем еще 2 дощечки. )

После выполнения задания всеми детьми воспитатель задает вопрос:

-Сколько дощечек слева (справа) от яблоньки? (Слева — 3 (справа — 5).)

2.2Игра «Кислое яблоко».

Дидактические задачи: организовать активный отдых детей. Яблонька предлагает детям отведать ее яблочка. Дети «берут в руку яблоко, кусают его, жуют». Яблоко оказывается кислым. Дети должны мимикой показать это.

2.3Работа в учебнике-тетради («Игралочка — ступенька к школе», ч. 4(1). Дидактические задачи:

1) закрепить представление о смысле сложения и вычитания, сравнении нисел с помощью определения порядка их следования в числовом ряду;

2) тренировать умение ориентироваться по элементарному плану, решать простейшие примеры на сложение и вычитание;

3) сформировать опыт преобразования способа решения задачи (проблемы) в зависимости от ситуации.

№2. с. 51.

«Нарисуй дорогу к домику с номером 5. Какие примеры решать не надо?»

5 + 4

Воспитатель говорит, что яблонька рассказала о том, что гуси-лебеди полетели к домику Бабы-яги. На этом доме написано выражение, значение которого равно 5.

-Как вы будете искать этот дом?

Как правило, дети предлагают решать все примеры.

Воспитатель предлагает детям подойти к домику с красной крышей. Дети должны проговорить свой путь: «Иду прямо, поворачиваю направо».

-Прочитайте, что написано на доме. (5 — 3.)

– Как вы думаете, надо ли решать этот пример для того, чтобы определить, является ли ответом число 5? (Нет. В этом примере от 5 надо отнять 3 поэтому получится число меньшее, чем 5.)

-Подчеркните те домики, примеры на которых решать не нужно.

После самостоятельного выполнения задания воспитатель предлагает

детям назвать цвет крыш тех домиков, которые они подчеркнули. Это домика с голубой, оранжевой и синей крышей.

-Объясните, почему примеры на этих домиках не нужно решать, для тоге чтобы убедиться, что ответ не равен 5? (Потому что во всех этих примерах от 5 надо отнять или к 5 надо прибавить число. В результате получится числе меньшее или большее, чем 5. )

-Сколько примеров вам надо решить? (4 примера.)

Дети самостоятельно решают примеры.

-В каком домике живет Баба-яга? (В домике с зеленой крышей.)

-Нарисуйте дорогу к этому домику и расскажите, как вы шли.

2.4. Работа в учебнике-тетради («Игралочка — ступенька к школе», ч. 4(1

Дидактические задачи:

1) закрепить представление о смысле сложения и вычитания;

2)тренировать умение соотносить числа с символами, сравнивать числа с помощью определения порядка их следования в числовом ряду, использовать знаки «>» и «

3)сформировать опыт самопроверки по образцу, обоснования своего суждения.

№ 3. с. 52

«Сравни с помощью знаков ».

Воспитатель рассказывает, что Баба-яга согласилась отдать братца, есл.- дети выполнят ее задания.

-Сможете выполнить задания Бабы-яги?

Воспитатель предлагает рассмотреть рамку слева и напоминает, что одинаковые числа обозначаются одинаковыми значками.

-В каком мешке число больше — в первом или во втором? Почему” (Число больше в первом мешке, потому что в нем к числу, обозначенном, месяцем, прибавляется единица и число увеличивается. Во втором мешке ■ этому же числу ничего не прибавляется.)

Дети пишут нужный знак между мешками.

Воспитатель предлагает рассмотреть вторую пару мешков в этой же рамке.

— В каком мешке число больше — в первом или во втором? Почему? (В первом мешке число больше, потому что в первом мешке с числом ничего не происходит , а во втором из этого же числа отнимают 3, поэтому оно уменьшиться)

Дети пишут нужный знак между мешками.

проверки воспитатель помещает на доску образец:

Задание в правой рамке дети выполняют самостоятельно с последующей самопроверкой по образцу:

2.5 Работа в учебнике-тетради («Игралочка — ступенька к школе», ч. 4(1).

Дидактические задачи:

1)тренировать умение сравнивать группы предметов по количеству с помощью составления пар, использовать знаки «>» и «

2) закрепить умение сравнивать числа с помощью определения порядка их следования в числовом ряду, определять на предметной основе, на сколько одно число больше (меньше) другого;

3)сформировать опыт самопроверки по образцу, обоснования своегосуждения, выполнения действий с комментированием.

«Сравни, используя знаки . На сколько больше? На сколько меньше?»

Воспитатель предлагает детям рассмотреть картинку и рассказывав Баба-яга отдаст братца, если дети наведут порядок в ее кладовке.

Сможете?

Воспитатель предлагает детям рассмотреть мешки слева.

Как вы будете определять, каких грибов больше или меньше сколько?

Дети рассказывают, проделывая названные действия:

«Считаем мухоморы и записываем их количество с помощью цифры 4

– считаем белые грибы и записываем их количество с помощью цифры 5

ставим знак «

проводим ниточки, соединяя между собой мухоморы и белые грибы обводим белые грибы, у которых нашлась пара».

На сколько мухоморов меньше, чем белых грибов? Почему? – потому что одному белому грибу не хватило пары.)

Воспитатель предлагает детям рассмотреть мешки справа.

Какое число больше? Почему? (Число 3 больше, потому что при с оно идет после числа 1.)

Дети записывают знак между числами.

Как узнать, на сколько 3 больше 1? (Надо в первом мешке нарисовать 3 предмета, а во втором — 1.)

Воспитатель предлагает в один мешок положить орехи (коричневые круги), а в другой мешок — ягоды (красные круги.)

Далее детям предоставляется самостоятельность. Для проверки воспитатель помещает на доску образец:

2.6. Работа в учебнике-тетради («Игралочка — ступенька к школе”. – –

Дидактические задачи:

закрепить представление о порядке следования чисел в числовом ряду;

тренировать умение соотносить числа с символами на основе представления о порядке следования чисел в числовом ряду;

закрепить умение сравнивать числа с помощью определения п их следования в числовом ряду;

сформировать опыт выполнения действий с комментированием

№ 5. с. 52.

«С помощью знаков > и

бубликов и печений. Используй для сравнения числовой ряд».

Воспитатель говорит, что осталось последнее задание Бабы-яги.

Воспитатель задает детям вопрос:

Как меняются числа при движении влево по числовому ряду? (Числа уменьшаются. )

Как меняются числа при движении вправо по числовому ряду? (Числа увеличиваются.)

В какой тарелке больше всего угощения? (Больше всего угощения в голубой тарелке, т.к. число, обозначенное кольцом, стоит в числовом ряду правее других чисел, которые обозначают количество угощения в тарелках.)

В какой тарелке меньше всего угощения? (В розовой тарелке, потому что число, обозначенное месяцем, стоит в числовом ряду левее других чисел, которые обозначают количество угощения в тарелках.)

Воспитатель предлагает детям сравнить количество пирожков и булочек.

Какое из чисел — кольцо или бантик — стоит правее? (Кольцо.)

Что можно сказать об этих числах? (Кольцо больше, чем бантик.)

Чего больше — пирожков или булочек? (Булочек.)

На сколько булочек больше, чем пирожков? Почему? (На 1, потому что каждое следующее число на 1 больше предыдущего.)

Второе задание дети выполняют с комментированием.

«Ромбик в числовом ряду стоит правее месяца. При движении по числовому ряду вправо числа увеличиваются, поэтому ромбик больше месяца, т. е. бубликов больше, чем печений».

На сколько бубликов больше, чем печений? (На 1.)

Все задания Бабы-яги выполнены. Братец спасен.

3. Осмысление (итог) занятия.

Дидактические задачи: сформировать первичный опыт осмысления собственной деятельности, фиксации достижения запланированного результата и условий, которые позволили его достичь.

Воспитатель собирает детей около себя.

Где вы сегодня побывали?

Какие знания и умения вам помогли спасти братца?

Примеры по математике больше меньше или равно 1 класс распечатать: Attention Required!

Содержание

Математические знаки и символы — Карточки и Задания для детей

Большое значение в математике имеют математические знаки и символы, благодаря которым выполняются различные действия: сложения, вычитания, деления, умножения, равенства и сравнения. Для детей достаточно и этих знаков, хотя в математике их гораздо больше. Но так как мы разрабатываем материалы для детей, то ограничимся самыми основными знаками и действиями математической науки.

Здесь вы найдете массу полезных математических заданий на сравнение чисел, а также счет до 10, примеры в картинках, раскраски и множество других развивающих заданий для детей, которые учатся в 1 классе, и для тех, которые только готовятся к поступлению в школу.

Математические знаки и символы — Карточки распечатать и вырезать

Очень удобно проводить учебные занятия по математике с детьми, используя математические знаки и символы в виде карточек. Их нужно распечатать, вырезать и использовать для составления примеров или заданий.

С распечатанным материалом можно придумывать самостоятельно различные задания. Например, положить на стол цветные карандаши, затем разделить их на две части. Попросить ребенка, чтобы он посчитал и сказал, в какой части карандашей больше (или меньше). Пусть положит между ними соответствующий математический знак. То же самое задание можно выполнять и с цифрами.

Но если ребенку с цифрами работается еще трудно, то лучше разнообразьте задания различными предметами. Пусть сравнивает количество маленьких и больших монет, ложек, конфет и любых других мелких предметов. Передайте инициативу по выбору предметов ребенку. Попробуйте с ним составить пример с помощью предметов. Попросите ребенка самого составить любой пример, используя различные предметы и вырезанные математические знаки.

Скачать математические знаки и символы в виде карточек для вырезания вы можете во вложениях.

Посчитай и поставь подходящие математические знаки

В этих новогодних картинках от ребенка требуется правильно расставить математические знаки, а также закончить примеры.

Для этого необходимо сначала посчитать количество предметов с левой стороны в обоих квадратах и вписать количество предметов в одном квадрате, во втором квадрате и их сумму в пустые клетки для примера под квадратами. То же самое нужно проделать и с левой стороны. После сравнения обеих сторон — поставить между ними подходящий знак.

Скачать учебный бланк с математическими знаками вы можете во вложениях.

Поставь нужный знак — Больше, меньше, знак равенства, плюс или минус

Здесь вы можете скачать еще одно упражнение, в котором нужно правильно составить и дорешать примеры с математическими знаками. Чтобы выполнить задания, ребенок должен свободно владеть счетом от 1 до 10. Опять же, для привлечения внимания ребенка задания представлены в красочном оформлении.

В первом задании нужно посчитать предметы в каждом прямоугольнике и вписать соответствующее число под ним. Между числами нужно поставить нужный математический знак, сравнивая эти числа между собой — одно число больше другого, меньше или они равны.

Во втором задании даны примеры, в которых складываются и вычитаются различные геометрические фигуры. Вот только в этих примерах отсутствуют математические знаки «+» и «-«. Ребенок должен написать эти знаки вместо звездочек, чтобы ответ примера получился верным.

Скачать задания — Поставь нужный знак — вы можете во вложениях внизу страницы

Задания для детей — Раскрась, найди соседей, подбери знаки, составь примеры

В этом упражнении несколько интересных заданий, для выполнения которых детям понадобятся не только знания математических знаков, но и умение считать, составлять примеры, а также находить соседей чисел (руководствуясь порядковым счетом от 0 до 10).

В первом задании нарисованы медведи. Ребенку нужно раскрасить такое количество медведей (можно в разные цвета), которое соответствует числу 10. Вопрос ребенку нужно задавать именно так, как написано на картинке.
Во втором задании каждая строчка — это порядковый ряд чисел от 0 до 10 или от 10 до 0. Ребенку нужно по вписанным числам определить, какой порядок чисел у каждой строки (на увеличение или на уменьшение), а затем вписать в пустые клетки недостающие числа. В последней строке совсем отсутствуют числа, поэтому ребенку нужно будет ориентироваться по начальной клетке (она состоит из двух квадратиков, значит в ней написано двузначное число, т. е. 10). Но не подсказывайте ребенку — он должен додуматься до этого самостоятельно!
В третьем задании нужно сравнить указанные числа между собой и поставить нужный математический знак или символ.
В четвертом задании нужно решить примеры в картинках, отнимая или прибавляя предметы. Ответы нужно вписывать не числами, а овалами (какое число, столько овалов и нужно вписать в клетки. В каждой клетке — 1 овал). Затем можно попросить ребенка записать в числовом виде все примеры (можно на отдельном листе).

Скачать 4 задания с раскрасками, счетом и примерами вы можете во вложениях.

Задания на математическое сравнение количества предметов

Тренируемся дальше в освоении математического сравнения, используя основные математические знаки «>» — больше, «» — меньше и «=» — знак равенства. Скачайте и распечатайте картинку с заданиями, подготовьте простой карандаш, ластик и, при желании, цветные карандаши.

В первом задании даны уже готовые примеры на сравнение. Но количество нарисованных геометрических фигур не соответствует знаку между ними — каких-то предметов не хватает. Ребенку нужно дорисовать недостающее количество справа или слева, чтобы знак оказался верным.
Во втором задании нужно не дорисовать предметы (как в первом задании), а зачеркнуть лишние. Так как здесь математические знаки тоже проставлены неверно.

Скачать учебный бланк с фигурами и предметами для сравнения вы можете во вложениях.

Веселые задания на сравнение с героями мультфильмов

В этих веселых задания для детей вы можете проверить не только умение ребенка ставить математические знаки между числами, но и его память — ведь ему придется вспомнить имена всех героев мультфильмов и сказок, нарисованных ка картинке.

В первом задании ребенок сначала должен сказать название двух сказок, героев которых он видит на картинке. Слева — одна сказка, а справа — другая. Затем ему нужно хорошо подумать и вспомнить, какие еще герои были в этих сказках — кого забыли нарисовать художники? Пусть ребенок дорисует недостающих персонажей. После этого ему нужно пересчитать отдельно персонажей одной сказки и другой, поставив между ними соответствующий математический знак.
Во втором задании ребенку нужно назвать всех персонажей известных мультфильмов, пересчитать их с левой и с правой стороны, а затем поставить необходимый математический знак между ними. Некоторые персонажи встречаются на картинке несколько раз. Пусть ребенок назовет их и посчитает, сколько раз каждый из них повторяется.

Скачать учебный бланк с героями мультфильмов вы можете во вложениях.

Задачи для детей на сравнение — Больше и меньше

В этих красочных заданиях с примерами на сравнение для детей встречается и счет до 10, и четные и нечетные числа, и математические знаки, и вопрос на развитие логического мышления. Скачайте и распечатайте картинку во вложениях и прочитайте ребенку условия заданий.

В первом задании ребенок должен пересчитать все предметы в прямоугольниках, а затем обвести карандашом соответствующее слово над картинками. После этого нужно сравнить количество предметов справа и слева, подумать, где предметов больше (или меньше), и поставить между прямоугольниками нужный математический знак.
Во втором задании также необходимо пересчитать в обоих прямоугольниках всех мультяшных зверей и обвести карандашом соответствующее число. Затем ребенок должен ответить на вопрос, в каком прямоугольнике четное число зверей, а в каком нечетное? Поставить между двумя прямоугольниками правильный математический знак.
В третьем задании нарисованы сладости — мороженые и пирожные. Все сладости ждут своих гостей, которые должны прийти к девочке на день рождения. Известно, что для каждого гостя заготовлены 1 мороженое и 1 пирожное. Задача ребенка — подумать и сказать, сколько гостей придет?

Скачать красочные задания с математическими знаками вы можете во вложениях.

Составь примеры с математическими знаками по картинкам

Очень полезно для дошкольников, как и для учеников младших классов, умение составлять примеры с математическими знаками по картинкам. С помощью данных заданий дети потренируются в этом нелегком деле, заодно повторяя счет до 10.

В первом задании нужно составить пример с математическим знаком, который покажет кого больше (или меньше) — бабочек или пчелок.
Во втором задании ребенок должен посчитать и сказать, на сколько больше лягушек, чем божьих коровок. Затем пусть ребенок подумает и ответит: что нужно сделать, чтобы их стало поровну (убрать одну лягушку)? После этого нужно подумать, сколько станет божьих коровок, если прилетит еще одна? — Записать это в виде примера.

В третьем задании нужно посчитать, сколько останется божьих коровок, если несколько из них перелетели на ветку. — Записать это в виде примера.

Скачать примеры с математическими знаками по картинкам вы можете во вложениях.

Изучаем математические знаки — плюс, минус и знак равенства

С помощью следующих заданий можно научить дошкольника писать математические знаки — плюс, минус и знак равенства, а также познакомят его с простыми примерами в картинках на сложение и вычитание. Выполнять такие задания можно уже с 4-5 лет.

Задание №1

Посмотри на самый добрый знак — плюс, который похож на крестик. Почему он добрый? — Потому что всегда что-то прибавляет. Посмотри на картинке, как плюс прибавил к двум яблокам еще одно, а к двум конфетам — еще две. Обведи математические знаки в больших квадратах.

Задание №2

А теперь познакомься со знаком минус. Минус — очень жадный. Он всегда у всех что-то отнимает. Внимательно посмотри на картинку и ты увидишь, как он отнял от торта целых три кусочка! А от двух воздушных шариков отнял один шарик. Обведи минус в больших квадратах под картинками.

Задание №3

А теперь ты увидишь знак равенства — он самый дружественный. Потому что уравнивает все предметы и числа, так, что никто ни на кого не в обиде. Справа и слева от этого знака всегда находится одинаковое количество предметов. Обведи по точкам знак равенства в квадратах.

Также вам пригодятся и другие материалы для распечатки, в которых встречаются математические знаки:

Примеры по математике — 1 класс — Распечатать в картинках

Здесь вы можете найти примеры по математике (1 класс), распечатать на принтере и использовать в качестве учебного материала на уроках математики или в детских садах.

Учимся считать до 20 с героями мультфильмов

В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.

Счет геометрических фигур — Картинки с заданиями

Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.

Устный счет в пределах 10 — Картинки с заданиями

Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.

А еще вы можете встретить математические знаки в математических играх от лисенка Бибуши:

Игра «Сложение и вычитание до 10» — Задачки в картинках

Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши, в которой малыш сможет решить восемь новых задачек на счет до 10.

Задачи-примеры для малышей в картинках

Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10. В трех уровнях игры ребенок будет решать задачи на вычитание, а в пяти — складывать заданные предметы.

Таблица математических знаков (символов): значения, распечатать

Ниже представлена таблица с основными математическими символами и знаками: корень (√), больше (>), меньше (<), равенство (=) и др. Также приведено их краткое описание и примеры для лучшего понимания.


Символ / знак	Название	Значение / описание	Пример
=	равно	равенство	<img src=’/800/600/https/ds04.infourok.ru/uploads/ex/03e5/000497c4-58b4cd91/img11.jpg’ /> е. 4 плюс 3 равно 7</nobr>» data-order=»<nobr>7 = 4 + 3,</nobr><br><nobr>т.е. 4 плюс 3 равно 7</nobr>»>7 = 4 + 3,<br/>т.е. 4 плюс 3 равно 7</td></tr><tr><td data-cell-id=” a3=”” data-order=”≠”>≠	не равно	неравенство	7 ≠ 10, 7 не равно 10
≈	приблизительно равно	приближенное равенство/округление	равно 0,36</nobr>” data-order=”<nobr>0,35765 ≈ 0,36,</nobr><br><nobr>0,35765 прибл. равно 0,36</nobr>”>0,35765 ≈ 0,36, 0,35765 прибл. равно 0,36
>	больше	A больше, чем B	15 > 10, 15 больше 10
<	меньше	A меньше, чем B	6 < 8, 6 меньше 8
≥	больше или равно	A больше или равно B	10 ≥ 4, 10 больше или равно 4
≤	меньше или равно	A меньше или равно B	3 ≤ 7, 3 меньше или равно 7
( )	круглые скобки	сначала считается выражение внутри скобок	3 ⋅ (4 + 6) = 30
[ ]	квадратные скобки	сначала считается выражение внутри скобок	[(1 + 3) ⋅ (2 + 4)] = 24
+	плюс	знак сложения	1 + 2 = 3
−	минус	знак вычитания	3 − 2 = 1
±	плюс-минус	выполняются оба действия: и сложение, и вычитание	4 ± 6 = 10 или -2
±	минус-плюс	выполняются оба действия: и вычитание, и сложение	5 ∓ 8 = -3 или 13
*	звездочка	умножение	3 * 3 = 9
×	икс	умножение	3 × 3 = 9
⋅	точка	умножение	3 ⋅ 3 = 9
÷	обелюс	деление	8 ÷ 2 = 4
/	косая черта	деление	8 / 2 = 4
:	двоеточие	деление	8 : 2 = 4
—	горизонтальная линия	дробь (деление)	1/2
mod	modulo	остаток от деления	7 mod 2 = 1, 7 : 2 = 3 (остаток 1)
<img src=’/800/600/https/mypresentation.ru/documents_6/bc8400e580744cc264c41b89112a6e50/img5.jpg’ /> » data-order=».»>.</td><td data-cell-id=” b23=”” data-order=”точка”>точка	десятичный разделитель	3.45 = 3 + 45/100
,	запятая	десятичный разделитель	6,12 = 6 + 12/100
a^b	степень	число А в степени B	3² = 9
a^b	циркумфлекс	число А в степени B	4^3 = 64
√a	квадратный корень	√a ⋅ √a = a	√16 = ±4
³√a	кубический корень	³√a ⋅ ³√a ⋅ ³√a = a	³√27 = 3
ⁿ√a	корень n-й степени		ⁿ√8 = 2 для n=3
%	процент	1% = 1/100	10% × 50 = 5
‰	промилле	<img src=’/800/600/https/ds04.infourok.ru/uploads/ex/01c1/00044780-e4b213f7/hello_html_754b7909.jpg’ /> 1%</nobr>» data-order=»<nobr>1‰ = 1/1000 = 0.1%</nobr>»>1‰ = 1/1000 = 0.1%</td><td data-cell-id=” d31=”” data-order=”<nobr>5‰ × 40 = 0.2</nobr>”>5‰ × 40 = 0.2

microexcel.ru

Математика 1 класс «Знаки больше, меньше, равно»

Слайды и текст этой онлайн презентации

Слайд 1

1 класс. Математика
Знаки: «>» (больше), «

Слайд 2

Разминка
Назови четыре различных цвета.

Слайд 3

Разминка
Кого Колобок встретил вторым?

Слайд 4

Разминка
Сколько дней в неделе?

Слайд 5

Разминка
Какие цифры находятся рядом с цифрой 4?
4

Слайд 6

Разминка
Как называется фигура, имеющая три угла?

Слайд 7

2 + 3 = 5
5 – 1 = 4
5 – 1 = 4
4 – 2 = 2
3 + 2 = 5
1 + 3 = 4

Слайд 8

2
3
2

Слайд 9

Знак «

Слайд 10

5
9
4
8
3
6
2
5
МЕНЬШЕ

Слайд 11

2
1
2 > 1

Слайд 12

Знак «>» — больше.

Слайд 13

5
2
БОЛЬШЕ
4
3
7
4
9
6

Слайд 14

Знак ставится так, чтобы большее число находилось с той стороны, где расстояние между концами больше.

Слайд 15

3
1

Слайд 16

4
5

Слайд 17

7
7

Слайд 18

Слайд 19

Слайд 20

Солнце глянуло в кроватку… Раз, два, три, четыре, пять. Все мы делаем зарядку, Надо нам присесть и встать. Руки вытянуть пошире, Раз, два, три, четыре, пять. Наклониться — три, четыре, И на месте поскакать. На носок, потом на пятку. Все мы делаем зарядку.
Физкультминутка.

Слайд 21

3 + 1 = 4
3

Слайд 22

4 – 1 = 3
4 > 3

Слайд 23

3 + 1 = 4 3 4 – 3 = 1 4 > 3

Слайд 24

Слайд 25

Слайд 26

Cтр. 47

Слайд 27

5 =

Слайд 28

Разминка для глаз

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Какое время показывают часы? Допиши нужные цифры.
5
3
1
4

Слайд 33

Слайд 34

Спасибо за урок!

Знаки: «>» больше, «

Однажды решили Белочка и Ёжик проверить, что птицы любят есть больше всего: пшеничные зерна или крошки белого хлеба. На один пень насыпали зерна, а на другой крошки хлеба и стали наблюдать.

— Ежик, ну что ты там видишь?

— Пока ничего.

— О, теперь вижу. Два воробья прилетели. Сейчас зерна будут клевать.

— А крошки клюют?

— Пока нет.

— Ой. Ко второму пню, ну там где крошки, сорока наша прилетела.

— Так где птиц больше?

— На пне с зернышками птиц больше, чем около пня с крошками.

— Белочка, кажется дядя Филя прилетел.

— Ну, и где сейчас птиц стало больше?

— Теперь птиц стало одинаково.

— Любик, а ты знаешь, что в математике, чтобы сравнивать объекты или предметы используют специальные математические знаки: больше, меньше и равно.

Например, вот у нас одно яблоко и одна груша, т. е. яблок столько же сколько и груш. Значит между ними можно поставить знак равно. А записать это можно так: два равно двум.

Теперь мы сравним грибы: три боровика и две лисички. Что больше?

— Три боровика больше, чем две лисички.

— Правильно. В этом случае мы между грибами поставим знак больше. А записать это можно так: три больше чем два.

— А сейчас сравним жёлуди и орехи. Чего меньше?

— Ага… Желудей у нас три, а орехов пять. Значит желудей меньше, чем орехов.

— Правильно, в этом случае мы поставим знак меньше. А записать это можно так: пять меньше чем три.

А теперь мы посмотрим, как пишутся эти знаки.

— Я помню как пишется знак равно. Он состоит из двух палочек, которые пишутся друг под другом. Вот.

— Правильно. Знаки больше и меньше тоже состоят из двух палочек. В знаке больше палочки расходятся к большему числу, а записывается этот знак так.

В знаке меньше палочки сходятся к меньшему числу и записывается он так.

— Ежик, допиши пожалуйста знаки в строчку, в пустые клеточки.

— Ага… Сейчас, сейчас. Сначала допишу знак равно, теперь больше и меньше.

А чтобы ты не запутался, запомни: левая рука, согнутая в локте даст нам знак меньше, а правая рука согнутая в локте даст нам знак больше.

Если между двумя числами поставить знак равно, то получится числовое равенство. А если между двумя числами поставить знаки больше или меньше, то получится числовые неравенства.

Ежик, а теперь проверь пожалуйста, верные ли равенства и неравенства.

Так, так, так. Ага. Два больше чем один – все верно, три больше, чем четыре…ага…

что-то не так, три обозначает большее количество предметов, чем четыре и при счете

идет раньше, чем четыре значит это неравенство не верное. Мы его зачеркнем.

— А давай лучше исправим, чтобы у нас не было ошибок.

— Давай. Значит здесь надо поставить знак меньше. Вот.

— Так-так. Пять равно пяти. Все верно.

— Ага, а здесь совсем сложно.

— Ничего сложного. Смотри, чтобы проверить, надо сначала посчитать, сколько будет два да один.

— Это будет три.

— А сколько будет два да три.

— Пять. Значит три меньше пяти. Здесь опять ошибка. Надо поставить знак меньше.

— Ну молодец Ежик. Ты все правильно выполнил. Итак, ты должен запомнить:

1. Чтобы сравнить числа в математике используют знаки больше, меньше или равно.

2. Знак больше, расходится палочками к большему числу. И если согнуть правую руку в локте, то получится знак больше. Выражение, в котором стоит знак больше называется неравенство.

3. Знак меньше, сходится палочками к меньшему числу. И если согнуть левую руку в локте, то получится знак меньше. Выражение, в котором стоит знак меньше тоже называется неравенство.

4. Знак равно состоит из двух палочек, которые пишутся друг под другом, а выражение, в котором стоит знак равно называется числовым равенством.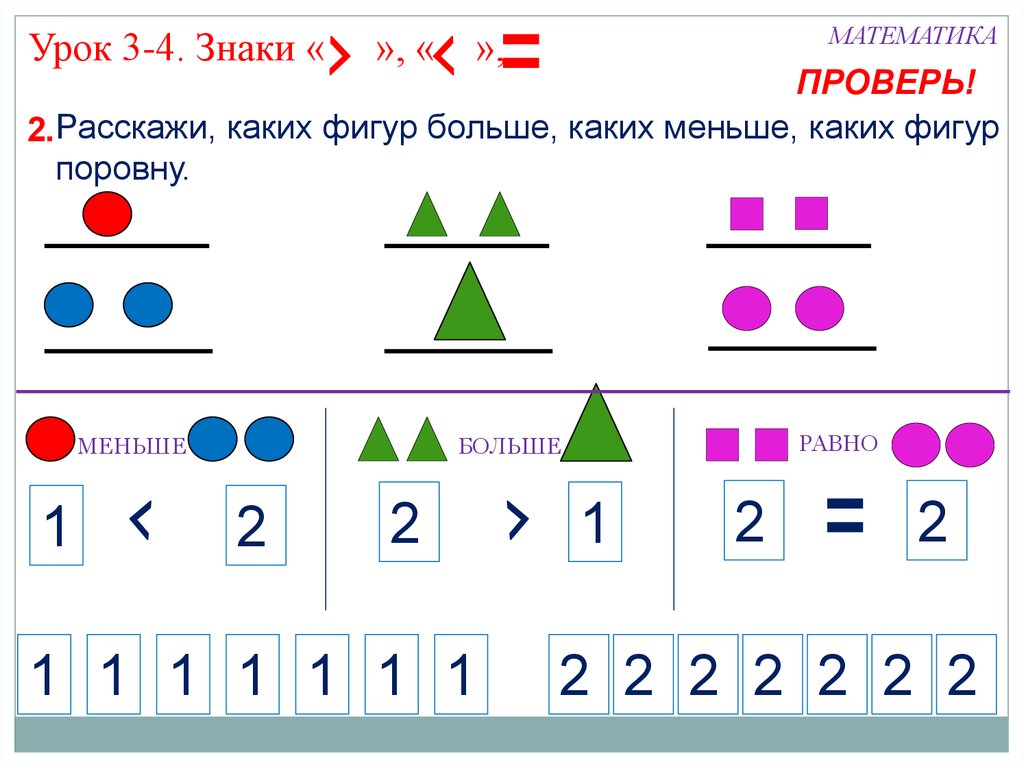

— Белочка, а давай посмотрим, что там наши птицы делают?

— Все склевали и улетели. Да, теперь мы не сможем определить, что же птицы любят больше. Ничего не осталось.

— Наверное, Ежик, одни птицы больше любят есть зерна, а другие хлебные крошки.

Конспект урока «Знаки > (больше),

Конспект урока по математике в 1 классе

« Знаки > (больше), < (меньше), = (равно) »

УМК «Школа России», автор учебника М.И. Моро

Тип урока: изучение нового материала.

Цель урока: в ходе практической работы и наблюдений познакомить

со знаками >, <, =; научить выполнять записи с этими знаками; закреплять

знания состава чисел, развивать умение рассуждать.

Планируемые результаты: учащиеся научатся сравнивать любые два

числа и записывать результат сравнения, используя знаки >, <, =; читать

записи; выполнять мыслительные операции анализа и синтеза и делать

умозаключения; применять полученные ранее знания в измененных

условиях; слушать собеседника и вести диалог; слушать учителя и выполнять

его требования; оценивать себя, границы своего знания и незнания; работать

в паре и оценивать товарища.

Познавательные УУД:

1. Ориентироваться в учебнике.

2. Понимать информацию, представленную в виде текста, рисунка,

схем.

3. Сравнивать предметы, объекты: находить общее и различие.

4. Классифицировать предметы, объекты по заданным критериям.

Регулятивные УУД:

1. Организовывать свое рабочее место.

2. Осуществлять контроль в форме сличения своей работы с

заданным эталоном..

3. Вносить дополнения, исправления в свою работу.

Коммуникативные УУД:

1. Соблюдать нормы речевого этикета.

2. Вступать в диалог.

3. Сотрудничать с товарищами при выполнении заданий в паре:

устанавливать и соблюдать очередность действий, корректно

сообщать товарищу об ошибках.

4. Участвовать в коллективном обсуждении учебной проблемы.

Оборудование: для учителя — интерактивная доска или проектор;

магнитный набор цифр и знаков, геометрических фигур; учебник

«Математика, 1 класс»; рабочая тетрадь с печатной основой;

для учащихся – геометрический набор; большие карточки с цифрами;

учебник; рабочая тетрадь, пенал.

больше, меньше, равно», 1 класс

Технологическая карта по учебному предмету «Математика»
Тема урока	«Знаки: больше, меньше, равно»
Класс	1
Место урока в разделе	13 урок в разделе «Нумерация»
Тип урока	ОНЗ
Цели урока	создание условий для знакомства с математическими знаками: больше, меньше, равно.
Задачи урока	обучающая: научить писать знаки, научить выполнять записи с этими знаками, научить сравнивать числа, используя знаки, читать неравенства; развивающая: развивать внимание, память, мышление, навык устного счета; воспитывающая: воспитывать усидчивость, выдержку, терпение, интерес к изучению предмета.
Планируемые результаты изучения темы
Предметные		Метапредметные						Личностные
Учащийся научится: использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи, измерения, прикидки, умение распознавать и изображать геометрические фигуры.		Учащийся научится: Познавательные УУД Учащийся получит возможность научиться: самостоятельное выделение и формулирование познавательной цели; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; постановка и формулирование проблемы, создание алгоритмов деятельности при решении проблем; установление причинно-следственных связей; построение логической цепи рассуждений. Регулятивные УУД Учащийся получит возможность научиться: целеполагание — как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно; планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, оценивание качества и уровня усвоения. Коммуникативные УУД Учащийся получит возможность научиться: планирование учебного сотрудничества с учителем и сверстниками – определение целей, функций участников, способов взаимодействия; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.						Учащийся получит возможность формирования: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения, формирование эстетических потребностей, ценностей и чувств, развитие навыков сотрудничества со взрослыми, сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций.
Ресурсы
Учебно-методическое сопровождение				Дидактические материалы		ИКТ, ЦОР
Учебник, авторы: М.И. Моро, С.И. Волкова, С.В. Степанова. Тетрадь на печатной основе, авторы: М.И. Моро, С.И. Волкова.				Числовой веер		Компьютер Монитор Мышь Клавиатура Проектор Интерактивная доска Учебная презентация
Межпредметные связи	Окружающий мир, «Зимующие и перелетные птицы».
Организация пространства	Расстановка парт в традиционной форме – двухместные парты в три ряда, так же компьютерный стол и интерактивная доска.
Этапы урока
Название этапа	Деятельность учителя		Деятельность учащихся		Планируемые результаты
					Предметные		УУД
Мотивационный	Приветствие, проверка готовности.		Приветствуют учителя, проверяют готовность к уроку.		—		Личностные: принятие и освоение социальной роли обучающегося.
Актуализации знаний	Организует устный счет (проводится фронтально): — увеличение или уменьшение числа на …; — состав числа.		Демонстрируют ответы на числовом веере.		использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи, измерения, прикидки.		Познавательные: контроль и оценка процесса и результатов деятельности.
Выявление затруднения	Организует аналитическую деятельность обучающихся: сравнение предметов, показанных на доске (работа фронтально). Создает проблемную ситуацию Педагог останавливается на варианте «поровну, равное количество», знак «=». — А теперь сравните количество предложенных предметов. — Каких больше? — Как можно записать это? — Можем воспользоваться знаком =? — Почему? — Тогда нам нужен новый знак?		Сравнивают количество предметов, показанных на доске, отвечают по поднятой руке. Высказывают свои предположения по ее решению. Кораблей больше, чем машин. Высказывают предположения. Да Потому что предметов не равное количество.		использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи, измерения, прикидки,		Познавательные: постановка и формулирование проблемы, создание алгоритмов деятельности при решении проблем; установление причинно-следственных связей; построение логической цепи рассуждений. Регулятивные: оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками – определение целей, функций участников, способов взаимодействия; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Личностные: развитие мотивов учебной деятельности и формирование личностного смысла учения, развитие навыков сотрудничества со взрослыми, сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций.
Разработка проекта, плана	Постановка цели урока совместно с учителем – что узнаем, чему научимся. Построение плана урока вместе с учителем.		Отвечают на вопросы учителя, исходя из ответов формулируют цель урока, план урока.		овладение основами математической речи, измерения, прикидки.		Познавательные: самостоятельное выделение и формулирование познавательной цели; создание алгоритмов деятельности при решении проблем; установление причинно-следственных связей. Регулятивные: целеполагание — как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно; планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий; планирование — определение последовательности промежуточных целей с учетом конечного результата; составление плана и последовательности действий. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками – определение целей, функций участников, способов взаимодействия; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Личностные: формирование личностного смысла учения.
Разрешение затруднения	Введение нового знака «больше», вопросы на ассоциацию этого знака с другими предметами – на что похож? Возвращение к заданию с машинами и кораблями. Преобразование рисунка в математическую запись. — Сколько кораблей? — Сколько машин? — Какой знак ставим? — Прочитаем выражение – 5 больше 3. Тренировка в сравнении чисел с использованием уже известных знаков (больше, равно). Создание новой проблемной ситуации: сравнение предметов, где нельзя поставить знаки больше и равно, понадобится новый знак, чтобы сравнить предметы. Введение нового математического знака «меньше». Вопросы на ассоциацию этого знака с другими предметами – на что похож? Возвращение к предыдущему «проблемному» заданию. Оформление записи с использованием нового знака. Тренировка в сравнении чисел с использованием уже известных знаков (больше, равно, меньше). Работа у доски.		Знакомятся с новым математическим знаком «больше». Делятся своими ассоциациями. 5 3 Знак больше. Читают. Обучающиеся фронтально сравнивают предметы, преобразуя в математическую запись и вставляют уже известные знаки неравенств. Сталкиваются с новой проблемной ситуацией – не могут сравнить предметы, потому что не хватает знаний. Знакомятся с новым знаком «меньше». Делятся своими ассоциациями, приводят примеры. Совместно с учителем устно оформляют и проговаривают неравенство. Учащиеся сравнивают предметы, выходят к доске и преобразуют устный ответ в математическую запись. остальные обучающиеся осуществляют взаимооценку.		использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи, измерения, прикидки, умение распознавать и изображать геометрические фигуры.		Познавательные: самостоятельное выделение и формулирование познавательной цели; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; построение логической цепи рассуждений. Регулятивные: определение последовательности промежуточных целей с учетом конечного результата. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками – определение целей, функций участников, способов взаимодействия; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Личностные: развитие мотивов учебной деятельности и формирование личностного смысла учения; развитие навыков сотрудничества со взрослыми, сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций.
Первичное закрепление	Работа с учебником на с. 46. Чтение по очереди обучающимися неравенств. Работа с рисунками: анализ действий, показанных на рисунках, организует контроль ответов обучающихся при преобразовании в математическую запись. Организует аналогичный разбор рисунков с ягодами. Проводит беседу о зимующих и перелетных птицах. Физ. минутка.		Читают неравенства, предложенные в учебнике по цепочке, остальные обучающиеся осуществляют взаимооценку. Выполняют следующее задание аналогично совместно с учителем. Актуализируют свои знания о перелетных и зимующих птицах. Выполняют физ. минутку.		использование полученных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи, измерения, прикидки.		Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; установление причинно-следственных связей; построение логической цепи рассуждений. Регулятивные: выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, оценивание качества и уровня усвоения. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками – определение целей, функций участников, способов взаимодействия; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Личностные: развитие навыков сотрудничества со взрослыми, сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций.
Самостоятельная работа и проверка по эталону	Инструктаж о выполнении самостоятельной работы в тетради на печатной основе с.18. Первое задание выполняется совместно с учителем, второе задание обучающиеся выполняют самостоятельно. Контроль и выявление неуспевающих обучающихся. Педагог задает домашнее задание, и комментирует его.		Вспоминают правила индивидуальной работы, слушают инструктаж, разбирают вместе с учителем задание 1. Выполнят совместно с учителем. Выполняют задание 2 самостоятельно. Выполнение самопроверки и самооценки обучающимися выполненной работы. Выявляют возможные затруднения при выполнении домашнего здания, осуществляют запись домашнего задания в дневник.		использование полученных математических знаний для описания и характристики окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи, измерения, прикидки, умение распознавать и изображать геометрические фигуры.		Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. Регулятивные: оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, оценивание качества и уровня усвоения. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Личностные: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения, развитие навыков сотрудничества со взрослыми, сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций.
Рефлексия	Устный опрос о достижении цели урока, деятельности на уроке. Учитель организует самооценку обучающихся, используя прием «Лестница успеха».		Отвечают на вопросы учителя, формулируют выводы по изученной теме. Осуществляют самоконтроль освоения знаний.		использование полученных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, оценке их количественных и пространственных отношений, овладение основами математической речи.		Познавательные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности; построение логической цепи рассуждений. Регулятивные: оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, оценивание качества и уровня усвоения. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Личностные: принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения, развитие навыков сотрудничества со взрослыми, сверстниками в разных социальных ситуациях, умения не создавать конфликтов и находить выходы из спорных ситуаций.

Урок 11. равенство. неравенство. знаки «>», «

Математика, 1 класс

Урок 11. Равенство. Неравенство. Знаки «>», «<», «=»

Перечень вопросов, рассматриваемых на уроке:

1. Определять место знаков больше, меньше, равно

2. Писать знаки >,<,=

3. Называть равенство, неравенство.

Глоссарий

Равенство – это когда одно количество равно другому.

Неравенство – это когда одна сторона выражения не равна второй.

Если носик галочки смотрит направо — это знак больше (>).

Если носик галочки смотри налево – это знак меньше (<).

Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя одинаковыми по своему значению выражениями.

Ключевые слова

Знак >; знак <; знак =

Основная литература:

1.Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. М.: Просвещение, 2017.

Дополнительная литература:

1. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 1 кл. В 2 ч. пособие для общеобразовательных организаций. — М.: Просвещение, 201 с.

Основное содержание урока

1. Сегодня мы отправляемся в магазин, чтобы купить Оле и Ане к уроку технологии все учебные принадлежности.

Для урока понадобится 1 пачка пластилина и две пачки картона.

По сколько пачек пластилина получили девочки? ( по одной пачке)

Можно сказать, что девочки получили одинаковое количество пластилина.

2. Для технологии необходимо две пачки картона.

По сколько пачек картона получили девочки? (по две пачки)

Можно сказать, что девочки получили одинаковое количество картона.

3. В математике используется специальный значок, чтобы записать, что число предметов одинаковое.

Можно записать цифрами и использовать для слов «одинаково», «равно» специальный значок «=»,1 = 1

2 = 2 (аналогично)

Две палочки напишут дети,

И что получится в ответе,

Ведь каждый выучил давно,

Как пишется тот знак: РАВНО!

Такие записи называются равенствами.

Это равенства. Записать равенства можно с помощью знака «=».

Докажем, что одинаковое количество предметов с помощью стрелочек образует пары.

На схеме каждый предмет обозначим кружочком и образуем пары. Покажем стрелочкой.

Оля Аня

Лишних фигур не осталось. Значит, поровну, одинаково.

Можно записать 1 = 1

6. 2 + 1 = 3

Как можно прочитать эту запись?

(Числовое равенство)

Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака « =».

Обе части записи равны между собой.

В каком количестве нужно было для урока картона? А пластилина?

Чтобы узнать, каких предметов потребовалось больше или меньше, используют специальные значки «>», « <».

Если с какой- то стороны больше или меньше, то запись будет называться «неравенство».

Два больше одного.

Картон Пластилин

Если слева больше число, чем справа, то используют знак «>».

2 > 1

А если число слева меньше, чем справа, то ставим знак меньше «<».

1 < 2

Такие записи называются неравенства:

4 > 3, 4 < 5

Разбор типового тренировочного задания

Выберите нужный знак и распределите на две группы.

Дополните каждую группу своими записями.

6 (=, >, <) 9

1 (=, >, <) 3

2 (=, >, <) 2

3 (=, >, <) 3

Правильный ответ:

Равенства: 2 = 2, 3 = 3

Неравенства: 6 < 9, 1 < 3

Больше, чем меньше, чем Рабочий лист

Добро пожаловать в «Математические саламандры» «Больше чем меньше, чем рабочие листы» для 1-го класса, где сравниваются числа до 100. Здесь вы найдете широкий спектр бесплатных распечатываемых листов по математике, которые помогут вашему ребенку научиться сравнивать и упорядочивать пары чисел до 100. а также правильно использовать символы>,

Хороший визуальный способ описать, как использовать символы больше и меньше, — это изобразить пасть крокодила.

Крокодил — существо жадное и всегда будет пытаться съесть как можно больше, поэтому его рот всегда сталкивается с наибольшим числом.

В приведенном выше случае 15 больше 12, поэтому он поворачивается, чтобы съесть число 15, показывая нам знак больше, чем .

В приведенном выше случае большее из двух чисел — 24, поэтому он поворачивается, чтобы съесть это число, показывая нам знак меньше, чем .

На этой странице есть несколько рабочих листов, которые помогут вашему ребенку научиться сравнивать и заказывать числа.

Это также отличное и простое введение в использование символов «больше» (>) и «меньше» (

Листы располагаются в порядке сложности, сначала самые простые.

Самые простые листы включают в себя затенение большего из двух чисел, а затем использование правильного символа для сравнения чисел.

Более сложные листы включают в себя оценку таких выражений, как 30 + 5, и использование правильного символа:>,

Использование этих листов поможет вашему ребенку:

сравните числа со 100;
используйте символы> и
сравнивает числа и простые выражения друг с другом.

Взгляните на еще несколько наших рабочих листов, похожих на эти.

Вот наш генератор для создания ваших собственных листов больше, чем меньше.

Наш генератор создаст следующие рабочие листы:

номера до 8 цифр
номеров до 3dp.
положительные и отрицательные числа

Здесь вы найдете наш ассортимент рабочих листов по метательной стоимости.

Использование этих листов поможет вашему ребенку:

узнать значение разряда до 100;
Номера для заказа до 100;
рассчитывают и возвращаются на единицы.

Все бесплатные листы математики в этом разделе поддерживают тесты Elementary Math Benchmarks.

Вот наша подборка рабочих листов для 1 класса.

Использование этих листов поможет вашему ребенку:

часов отсчета до половины;
преобразовать часы и полупрошедшие часы в цифровые;
нарисуйте стрелки часов правильно, чтобы отметить время и половину прошедшего.

Листы в этом разделе помогут вашему ребенку научиться определять время.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

Больше, чем Листы

Оживите обучение с помощью наших распечатываемых рабочих листов «больше чем», «меньше чем», заполненных красочными изображениями и увлекательными упражнениями в сочетании с манипуляторами, чтобы помочь детям дошкольного и детского сада и детям 1 класса. Будь то веселые действия по вырезанию и склеиванию, подсчет изображений и сравнение наборов с помощью и =, или просто сравнение чисел, эти рабочие листы по сравнению чисел до 10 с их максимальной универсальностью — верный способ улучшить навыки субитизации ваших детей.Наши бесплатные рабочие листы больше, чем меньше — хорошее место для начала вашей практики.

Сравнение однозначных чисел | Картинки

С учетом привлекательности дошкольников красочных изображений, эти печатные таблицы для сравнения однозначных чисел побуждают их подсчитывать картинки в каждом наборе и сравнивать их.

Сравнение чисел до 10

Попробуйте сравнить числа с этими числами для сравнения до 10 рабочих листов в формате PDF.Дети из детского сада и первого класса сравнивают числа с обеих сторон и определяют, больше ли одно из них, меньше или равно другому.

Группы сравнения

Пусть ваши дошкольники считают числами кошек и собак, рубашек и платьев, крабов и осьминогов и сравнивают числа, используя соответствующий символ сравнения.

Подсчет и сравнение

Кусочки джунглей в этих больших, меньше, чем рабочие листы PDF-файлов достаточно, чтобы привлечь детей к развитию навыков, поскольку они подсчитывают и сравнивают популяцию животных и насекомых каждого вида и определяют, каких больше, а каких мало.

Сравнение десяти кадров

Практикуйте дивергентное мышление и используйте десять фреймов в качестве манипулятора для сравнения чисел. Попросите детей вычислить количество счетчиков в каждых десяти кадрах и сравнить пару кадров, используя и =.

Сравнение игральных костей

Сравнение очков на кубиках — еще один отличный способ побудить детей в детском саду еще больше инвестировать в сравнение чисел. Попросите детей подсчитать количество очков на каждой кубике и сравнить их.

Сравнение сторон и углов

Посмотрите, как дети 1-го класса переходят между развлечениями и обучением, поскольку они подсчитывают количество ребер и вершин каждой 2D-формы, сравнивают фигуры на основе заданных атрибутов и определяют форму в этих PDF-файлах больше или меньше.

Жевать большее число

Аллигатор Snappy, когда ему предлагается выбор между двумя корзинами с рыбой, всегда выбирает ту, в которой больше. Поразмыслите и выясните, какой набор защелкивается аллигатором, и приклейте его мордочку, открытую к нему.

Кормление лягушки

Чем больше, тем веселее мантра лягушки-гурмана Хупера. Дети сабитируют и сравнивают количество элементов, решают, что больше; правильно вырежьте и приклейте рот Хуперу и помогите ему выбрать тот, в котором больше еды.

Сравнение чисел

Вырежьте клюв Птички Визг, сравните червей и насекомых и приклейте открытый клюв к набору, в котором их больше, и помогите ей сделать правильный выбор в этих печатных листах «Больше, чем, меньше, чем».

, ≤, ≥ — Сделано легко

Смотреть
Видео

Старт
Практика

Показать
Рабочие листы

Оцените это видео

Ø 5.0 / 1 оценок

Вы должны войти в систему, чтобы оценить это видео.

Вау, Спасибо!
Дайте нам свою оценку в Google! Мы были бы счастливы.

Гуглить

Автор

Юджин Ли

Описание

Символы неравенства: , ≤, ≥

Символы неравенства — это сокращенное обозначение, используемое для сравнения различных величин. Есть четыре символа неравенства: «больше», «меньше чем», «больше или равно» и «меньше или равно». Так, например, предложение «5 больше 2» можно записать как 5> 2. Хороший способ запомнить, какое число больше, — представить каждый символ как рот; рот всегда будет есть большее из двух сравниваемых чисел.Узнайте о символах неравенства, помогая вампиру Кристоферу упаковать максимальное количество припасов, необходимых ему для поездки в Калифорнию. Ссылка на Common Core: CCSS.MATH.CONTENT.6.EE.B.8

Стенограмма

Символы неравенства: , ≤, ≥

Вампир Кристофер — гурман, и ему нужна свежая, новая история для его блога: Вампир-вегетарианец. Он работает над новым произведением, поэтому он хочет отправиться в место, где растет его любимый фрукт: красный апельсин.В «Вампедии» он читал, что в Калифорнии растут кровавые апельсины, и это прекрасно, потому что он всегда хотел посетить там подземные сады. Чтобы помочь ему собрать вещи, он использует свои знания символов неравенства . И все его припасы разложены в постели? Накидки, проверьте. Гель для волос, проверьте. Кровавый апельсиновый сок, проверьте. Но сколько из этих вещей ему разрешено брать с собой в самолет? Давайте посмотрим на числовую линию.

Использование неравенства

Путешествие Кристофера Вампира продлится на меньше, чем 15 дней.Для неравенств с ‘меньше’ мы используем этот знак больше, чем 1000 мл сока кровавого апельсина. Для неравенств типа « меньше или равно » мы используем этот символ: ≤. Нашему гурману-вампиру также нужно упаковать более 1 бутылки геля для волос, так как он закончился во время последнего отпуска. Нарисуем это на числовой прямой. Для неравенств с «больше чем» мы используем символ « больше ».Еще ему нужно упаковать не менее 16 накидок, по одной на каждый день и две на всякий случай. Для неравенств с « не менее » мы используем символ « больше или равно ».

Сводка по неравенствам — Представьте себе рот

Давайте еще раз посмотрим на различные символы неравенства . Хороший способ запомнить, какое число больше, — представить каждый знак как рот . Рот всегда будет съесть большее из двух сравниваемых чисел.Например, сравним 2 и 4. Так как 2 меньше 4, рот съест 4. Если рот открывается вправо, читается: «a» на меньше, чем «b». Однако, если рот открывается влево, читается: «а» на больше, чем «b». Как мы видели ранее, символы «больше» и «меньше» также можно комбинировать со знаком равенства . Когда мы говорим « столько же, сколько» или «не более », мы имеем в виду «меньше или равно», что означает, что а может быть меньше или равно b.Но когда мы говорим « минимум », мы имеем в виду «больше или равно». Здесь a может быть больше b или равно b. Посмотрим, как вампир Кристофер наслаждается отпуском. О НЕТ! Нет больше кровавых апельсинов?!? Это может усложнить его отпуск …

Символы неравенства:

, ≤, ≥ Упражнение

Хотели бы вы применить на практике то, что вы только что узнали? Практические задачи для этого видео Символы неравенства: , ≤, ≥ помогут вам попрактиковаться и повторить свои знания.

Объясните символы неравенства.
Подсказки
Здесь вы видите числовую строку для $> 65 $.
$ \ ge ~ $ совпадает с $ ~> ~ $, включая отношение $ ~ = ~ $.
Здесь вы видите числовую строку для $ \ le 55 $.
Обратите внимание на кружок.
Решение
Чтобы различать символы неравенства:
- $ меньше . Вы видите соответствующую числовую строку рядом.Тот факт, что Кристофер проводит в своей поездке на меньше, чем 15 дней, представлен пустым кружком.
- $ \ le $ для отношения меньше или равно . Разница между этим символом и символом $
- $> $ для отношения больше . Аналогично отношению $
- $ \ ge $ для отношения больше или равно .Он также включает знак $ = $, который может отображаться закрашенным кружком.
Найдите символ, который правильно описывает отношения.
Подсказки
Взгляните на этот пример:
$ 4 $ больше, чем $ 2 $.
Вы можете записать это как $ 4> 2 $.
Или вы можете написать это как $ 2
Не менее означает больше или равно.
Запомните знаки отношения:
- $
- $ \ le $ меньше или равно
- $> $ больше
- $ \ ge $ больше или равно
Решение
Кристофер уже знает, что его поездка занимает менее 15 дней. Меньше указывает на символ $
Количество красного апельсина, которое он может взять с собой, ограничено сверху на 1000 ~ мл $, включая это количество. Это указывает на символ $ \ le $ — или меньше или равно: $ \ le 1000 $. Здесь вы используете закрашенный кружок.
Кристофер знает, сколько геля для волос ему нужно. Поэтому он приходит к выводу, что нужно упаковать более одной бутылки геля для волос. Это указывает на $> $ — или больше чем-символ: $> 1 $.Снова вы используете пустой кружок.
И последнее, но по крайней мере, он собирает несколько накидок: по крайней мере, один на каждый день и один запасной, всего 16. Не менее обозначает символ $ \ ge $ — или больше или равно: $ \ ge 16 $. Здесь вы используете закрашенный кружок на числовой прямой.
Но что это? Прибыв в сад кровавых апельсинов, Кристофер обнаруживает табличку: Извините! Никаких кровяных апельсинов.
Определите соответствующее математическое неравенство, соответствующее числовой прямой.
Подсказки
Эта числовая прямая представляет собой неравенство $ x \ le 7 $.
- Стрелка слева указывает на $
- Закрашенный кружок означает меньше или равно.
Эта числовая строка означает $ x> -20 $.
Символ $ \ ge $ можно исключить, так как кружок пустой.
Решение
Сначала рассмотрим числовые прямые в целом.
- Стрелка слева указывает на отношение $
- Стрелка вправо указывает на отношение $> $ или $ \ ge $.
Вы можете решить, использовать ли вам $$ или $ \ ge $ в зависимости от круга.
- Пустой кружок означает $ $ в зависимости от направления стрелки.
- Закрашенный кружок означает $ \ le $ или $ \ ge $.
Таким образом, мы можем определить соответствующее неравенство слева направо:
- $ x \ le 8 $
- долл. США x
- долл. США x> 4 долл. США
- $ х \ ge 4 $
Изучите неравенство по разным задачам со словами.
Подсказки
Не менее означает больше или равно.
Более обозначают символ $> $.
Различать меньше или равно ($
Решение
Вы можете запомнить различные ключевые слова, которые указывают на символ неравенства:
- Больше чем означает больше, чем $> $.
- Не менее означает, что $ \ ge $ больше или равно.
Ограничение скорости Конечно, ограничение скорости не означает, что вы должны ехать быстрее этого ограничения. Получаем неравенство $ x \ le 45 $.
День рождения Вы хотите пригласить менее 10 друзей. Получаем $ x
Наушники Более обозначают символ $> $. Это дает нам $ x> 25 $.
Решите, какой символ неравенства использовать.
Подсказки
Обратите внимание
Если вы измените знак чисел, вам также придется изменить символ неравенства.
Позаботьтесь об использовании $> $ или $ \ ge $:
- $ 7 \ ge 7 $, но $ 7 \ not> 7 $
- $ 7> 4 $ а так же 7 $ \ ge 4 $
Решение
Вы можете представить себе символ «больше чем» в виде рта.
Чем большее число съедает, тем большее число.
- Например, $ 4> 2 $. Вы также можете использовать знак $ \ ge $.
- Аналогично $ 2
Обратите внимание на знак чисел:
- $ -2> -4 $, а также $ -2 \ ge -4 $.
- И наоборот, мы можем заключить, что $ -4
Определите соответствующее неравенство.
Подсказки
Обратите внимание на кружок:
- Пустые кружки обозначают $> $ или $
- Закрашенные кружки обозначают $ \ ge $ или $ \ le $.
Кружок указывает число, которое вы должны использовать в неравенстве.
Кружок указывает, с одной стороны, на число 65 долларов США, а с другой — на то, что 65 долларов США принадлежат неравенству.
Стрелка справа указывает $> $ или $ \ ge $.
Вместе мы можем заключить следующее неравенство для этой числовой прямой:
$ x \ ge 65 $.
Решение
Вы используете числовые линии для обозначения неравенства.
Сначала вы рисуете круг точно на месте соответствующего числа.
В зависимости от символа неравенства кружок заполнен или пуст:
- Пусто: $> $ или $
- Заполнено: $ \ ge $ или $ \ le $
Вы можете выбрать $$ или $ \ ge $ в зависимости от направления стрелки.
Здесь вы видите четыре разные числовые линии, сверху вниз:
- $ x> -6 $
- $ х \ ле -2
- долл. США x
- $ х \ ge 2 $

Больше видео в Решение уравнений

Номера для сравнения и заказа — Рабочие листы

Сравнение и номера для заказа

Однозначные числа: сравнение

Сравните однозначные числа с математическими символами. Также включает в себя рабочие листы по использованию слов больше и меньше .Иллюстрации на многих листах требуют подсчета.

2-значные числа: сравнение и заказ

На этой странице вы найдете большой выбор таблиц по сравнению и упорядочиванию 2-значных чисел. Научите учащихся использовать математические символы больше, чем , , меньше, чем , и , равные математическим символам. Включает в себя пару математических игр и учебных центров, а также рабочие листы.

Трехзначные числа: сравнение и заказ

На этой странице есть печатные формы для заказа и сравнения трехзначных чисел.Включает в себя рабочие листы, карточки с заданиями, классные игры, задание «вырезать и склеить» с аллигатором и многое другое.

4-значные числа: упорядочивание и сравнение

Узнайте о « больше », « меньше » и « равно » с помощью этих печатных учебных материалов. Все включают числа до четырех цифр.

5-значные числа: сравнение и упорядочивание

Загрузите карточки задач, классные игры, рабочие листы для обучения студентов порядку и сравнению значений пятизначных чисел.

6-значные числа: сравнение и порядок

Используйте математические символы для «равно», «меньше чем» и «больше чем» для сравнения чисел. Также порядковые номера от наименьшего к наибольшему.

Дроби, деньги, десятичные сравнения

Дроби: сравнение и упорядочение

Загрузите эти упражнения, если вы учите свой класс упорядочиванию и сравнению дробей и смешанных чисел.

Десятичные дроби: сравнение и порядок

На этих распечатках ученики будут использовать символы и = для сравнения десятичных значений.

Деньги: сравнение

Сравните пары денежных сумм. (пример: $ 1,56

Place Value

Вот наша основная страница с размеченными значениями, на которой есть множество ресурсов, которые могут помочь учащимся узнать о числовых значениях, блоках разнесенных значений, чтении чисел и развернутой форме.

Округление

Этот набор учебных ресурсов будет помогите учащимся узнать об округлении до ближайших десяти, сотен, тысяч, десятых и сотых

Inequalities

На этой индексной странице представлены рабочие листы по неравенству для средней школы.

Математика аллигатора (больше, меньше и равно)

Сводка

Учитель объяснит на доске понятие «больше чем», «меньше чем» и «равно», а также соответствующие знаки для этих сравнений. В парах учащиеся затем используют карточки со знаками аллигатора, чтобы сначала показать неравенства с числами, представленными точками, а затем с записанными числами от 1 до 10.Затем учащиеся продемонстрируют свои знания, выполнив рабочий лист с графическим и числовым представлением чисел.

Материалы

магнитные счетчики
маркер для доски / белой доски
zipolc bag для каждой пары учеников, который содержит 1 набор ламинированных знаков из кожи аллигатора, набор точечных карточек 1-10 (всего 10) и набор номерных карточек 1-10 (всего 20)
двусторонних рабочих листов со сравнением изображений с одной стороны и числовыми сравнениями с другой для каждого ученика.
карандашей

Фон для учителей

Учителю необходимо понимать числа и их количественные значения. Им также необходимо понимать, когда числа больше, меньше или равны друг другу, а также знать соответствующие символы для этих сравнений.

Предыдущие знания учащихся

Студентам необходимо уметь понимать числа и счет.Важно, чтобы они понимали, как числовые символы представляют реальные величины. Им нужно будет особенно хорошо разбираться в числах от 1 до 10 и их хронологическом порядке. Базовые знания числовых линий будут полезны для понимания этого урока.

Предполагаемые результаты обучения

1. Учащиеся смогут правильно определить, какое число больше или меньше, или равны ли два числа, когда им представлены два числа.

2. Учащиеся смогут использовать правильный символ ( или =) для определения отношений между числами.

Инструкционные процедуры

Вся группа (я): 8-10 минут

1. Учитель объяснит концепцию на белой доске, показывая 4 фишки с одной стороны и шесть с другой.

2. Учитель предлагает классу вслух пересчитывать счетчики, указывая на каждую при подсчете

3.Учитель спрашивает, кто больше

4. Учитель объясняет . и = знаки

5. Учителя показывают другие примеры (1 и 3, 6 и 10, 7 и 4, 3 и 3) и объясняют, что знак похож на аллигатора и указывает на большее количество (аллигаторы ОЧЕНЬ голодны, поэтому они хотят большее количество)

6. Учитель использует приемы вопросов и показывает, как ученики понимают концепцию.

7. Выполняя эти упражнения, учитель может попросить ученика создать знаки «больше, чем» и «равно», используя свои руки.

Пары (делаем): 10 минут

1. С напарником ученикам будет предложена игра в аллигатора.

2. Студенты будут практиковаться в создании большего, меньшего и равного сравнению с использованием точечных представлений. Они сделают это, взяв две карты из стопки и положив их рядом.

3. Используя знаки аллигатора, они поместят правильного аллигатора между ними так, чтобы пасть аллигатора указывала на карту с большим количеством точек.Например, если карта с 5 точками и карта с 7 точками размещены рядом, ученик поместит меньшее, чем крокодил между двумя картами, так, чтобы он указывал на карту с 7 точками.

4. Затем оба ученика произнесут изображение вслух. Например, «пять меньше семи».

5. Учащиеся будут повторять этот процесс, пока они не изучат точечные карточки (около 5 минут).

6. Затем ученики повторяют процесс с карточками с цифрами (около 5 минут).

7. Если некоторые ученики заканчивают так рано, учитель может попросить их попрактиковаться с комбинацией карточек с точками и цифрами.

8. Учитель ходит по всему занятию и помогает ученикам, когда это необходимо.

Индивидуальный (вы делаете): 5-10 минут

1. Учитель раздаст двусторонний рабочий лист по одному каждому ученику

2. Учащиеся напишут правильный знак ( или +) между каждым изображением с одной стороны и каждым числовым изображением с другой.

3. Учитель ходит на протяжении всего занятия, наблюдая за учениками и помогая учащимся, которые борются.

Стратегии для разнообразных учащихся

Для этого задания учитель может объединить учеников, которые не говорят по-английски, но говорят на другом родном языке, вместе для поддержки со стороны сверстников и дать им возможность считать на своем родном языке. Для более успешных учеников учитель может попросить их поработать над более высокими двузначными числами, если они полностью усвоят концепцию. Учитель может сосредоточить больше индивидуального внимания на учащихся, которые испытывают трудности, и может начинать их только с цифр 1-5, пока они не усвоят концепцию. Учащиеся с ограниченными возможностями смогут иметь учителя специального образования, который будет помогать им в занятиях.

Расширения

Учитель пошлет домой письмо родителям о том, что они узнали в классе в тот день, включая информацию о задании по математике.Также будет дополнительное задание, которое не требуется, но если оно будет завершено, они получат небольшой приз, такой как наклейка или цветной карандаш. Это задание поможет повторить урок дома. На следующем уроке учитель повторно рассмотрит принципы, изложенные в этом упражнении.

План оценки

1. Учитель попросит учеников показывать большие пальцы вверх, если они понимают, и большие пальцы вниз, если они все еще сбиты с толку во время группового обучения.Учитель также может попросить учеников продемонстрировать свое понимание, заставив их правильно жестами обозначить неравенство, проводимое всей группой.

2. Наблюдение: Учитель будет наблюдать за учениками в парах во время прогулки по комнате. Учитель будет наблюдать, кто борется с концепцией, и при необходимости помогать ученикам. Учитель может делать заметки об учащихся, испытывающих трудности, в частности,

3. Формирующее оценивание: Учитель соберет индивидуальный рабочий лист, чтобы оценить понимание учащимся.

Библиография

FREE Dice games!

http://cleverlearner.com/number-activities/greater-than-less-than-preschool-worksheet. html

http://www.pinsdaddy.com/less-than-greater-or-equal-to-and_tcwvhJcXFxBaAzOWzzZcURDOSHV*E7nDqdt*2kIlbniijLIz8FsfyPM1EsVJHL*iw9b5WDa7hvyuZ9ogQPKNQg/jyU5Ac6pnunN5RqQl%7C6u627sTvO*NjT2trzOqFZHM*SX%7ChU5lRNZmbgtZUXw%7CDZi0FpbYY9ovTFLbBfgk4gNSzmOmGv%7CKj6Rq8DnX*nRiY6UAR09awkkM5aCXyty*WklzBX9wwqRNNgx5I2QIxwMWQRNjhYJfTBn5cRKoXmzGbM/

https: // www. pinterest.com/pin/3812579246432/

https://www.uen.org/core/core.do?courseNum=5100#71383

Больше / Меньше / Равно

Целей IEP: (Подсчет для демонстрации однозначного соответствия) 1. Получив предметы для подсчета до ____ (10/12/15/20), СТУДЕНТ продемонстрирует однозначное соответствие, самостоятельно подсчитав правильное количество предметов с точностью 80% в 4 из 5 возможных МЕСЯЦ ГОД.

2. Получив записанное число, СТУДЕНТ будет отсчитывать такое же количество предметов с точностью 80% в 4 из 5 возможных вариантов по МЕСЯЦУ, ГОДУ.

(Что такое распознавание чисел) 1. Получив число от _____ (0-3, 4-7, 8-10 и т. Д.), СТУДЕНТ произнесет название числа и напишет номер с правильным построением, с точностью 80%, в 4 из 5 возможных вариантов, по МЕСЯЦ, ГОД.

2. Учитывая визуальную таблицу номеров или карточки с цифрами и запрос учителя (прикоснуться к номеру / произнести номер / указать на устройстве вывода голоса), СТУДЕНТ выполнит запрос с точностью 80% в 4 из 5 возможности, по МЕСЯЦУ, ГОДУ.

3. Получив числа от 0 до 30 для трассировки, СТУДЕНТ будет отслеживать каждое одно- и двузначное число, отслеживая данные пунктирными числами с точностью 80% в 4 из 5 возможных вариантов, по МЕСЯЦУ, ГОДУ.

(Дополнение) 1. Имея два набора объектов для подсчета с суммой до ___ (15.10.20), СТУДЕНТ будет подсчитывать каждый набор и записывать число для каждого слагаемого и складывать, чтобы определить «сколько» (сумма), с 80% точность, в 4 из 5 возможностей, по МЕСЯЦУ, ГОДУ.

2.Учитывая три набора объектов для подсчета, СТУДЕНТ напишет «сколько» для каждого слагаемого, чтобы определить сумму трех чисел с точностью 80% в 4 из 5 возможных вариантов, по МЕСЯЦУ, ГОДУ.

(вычитание) 1. Учитывая набор объектов, СТУДЕНТ будет «убирать» или вычитать вычитаемое (заранее определенное или по выбору студента), чтобы решить и записать разницу с точностью 80% в 4 из 5 возможных вариантов путем МЕСЯЦ ГОД.

(больше / меньше: больше / меньше / равно) 1.Учитывая два набора объектов, один набор которых имеет больше или меньше, СТУДЕНТ будет подсчитывать количество объектов, чтобы определить, какой набор имеет больше / меньше / или равны ли они, с точностью 80%, в 4 из 5 возможностей, по МЕСЯЦУ, ГОД.

Равно, меньше и больше символов

Помимо знакомого знака равенства (=), он также очень полезен, чтобы показать, не равно ли что-то (≠) больше чем (>) или меньше (

Это важные знаки, которые необходимо знать :

=	Когда два значения равны , мы используйте знак «равно»	пример: 2 + 2 = 4
≠	Когда два значения определенно не равны , мы используйте знак «не равно»	пример: 2 + 2 ≠ 9
	Когда одно значение меньше другого , мы используйте знак «меньше»	пример: 3
>	Когда одно значение больше другого , мы используйте знак «больше»	пример: 9> 6

меньше и больше

Знаки «меньше» и «больше» выглядят как буква «V» на своей стороне, не так ли?

Чтобы запомнить, в какую сторону идут знаки «», просто запомните:

«Маленький» конец всегда указывает на меньшее число, например:

Символ больше: БОЛЬШОЙ> маленький

Пример:

10> 5

«10 это больше 5″

Или наоборот:

«5 это меньше 10″

Вы видите, как символ «указывает» на меньшее значение?

… Или равно …

Иногда мы знаем, что значение меньше, но также может быть равно !

Например, кувшин вмещает до 4 чашек воды.

Так сколько в нем воды?

Это может быть 4 чашки или меньше 4 чашек: Итак, пока мы не измерим, все, что мы можем сказать, это «меньше или равно » 4 чашки.

Чтобы показать этот , мы добавляем дополнительную строку внизу символа «меньше» или «больше», например:

Знак «меньше или равно »:		≤

Знак «больше или равно »:		≥

Все символы

Вот краткое изложение всех символов:

Символ	слов	Пример использования
=	равно	1 + 1 = 2
≠	не равно	1 + 1 ≠ 1

>	больше	5> 2
	менее	7

≥	больше или равно	мрамора ≥ 1
≤	меньше или равно	собаки ≤ 3

Зачем они нужны?

Потому что есть вещи, которые мы, , не знаем точно, …

… но все же может сказать что-то о .

Итак, у нас есть способы сказать то, что мы знаем (что может быть полезно!)

Пример: у Джона было 10 шариков, но он потерял несколько. Сколько у него сейчас?

Ответ: У него должно быть меньше 10:

Мрамор 10

Если у Джона все еще есть шарики, мы также можем сказать, что у него больше нуля шариков:

Мраморы > 0

Но если бы мы думали, что Джон мог бы иметь потерять всех своих шариков, мы бы сказали

Мрамор ≥ 0

Другими словами, количество шариков больше или равно нулю.

Объединение

Иногда мы можем сказать две (или более) вещи в одной строке:

Пример: Бекки начинает с 10 долларов, что-то покупает и говорит: «У меня тоже есть сдача». Сколько она потратила?

Ответ: Что-то больше, чем 0 долларов США, но меньше 10 долларов США (но НЕ 0 или 10 долларов США):

«На что тратит Бекки»> 0
«На что тратит Бекки»

Это можно записать одной строкой:

$ 0

Это говорит о том, что 0 долларов меньше, чем «То, что Бекки тратит» (другими словами, «То, что Бекки тратит» больше, чем 0 долларов), а то, что Бекки тратит, также меньше 10 долларов.

Обратите внимание на то, что «>» перевернулось на « перед , что тратит Бекки. Всегда проверяйте малый конец указывает на малое значение .

Смена сторон

В предыдущем примере мы видели, что когда мы меняем стороны, мы также переворачиваем символ.

Это:		Бекки тратит> $ 0		(Бекки тратит более $ 0)
то же самое, что это:		$ 0		(0 долларов меньше, чем тратит Бекки)

Просто убедитесь, что маленький конец указывает на маленькое значение!

Вот еще один пример использования «≥» и «≤»:

Пример: у Бекки 10 долларов, и она идет за покупками.Сколько она

потратит (без использования кредита)?

Ответ: что-то большее или возможное равное 0 долларов США и меньшее или, возможно, равное 10 долларам США:

Бекки тратит ≥0 долларов
Бекки тратит ≤ 10 долларов

Это можно записать одной строкой:

0 долл. США ≤ Бекки тратит ≤ 10 долл. США 90 148

Длинный пример: перерезание каната

Вот интересный пример, о котором я подумал:

Пример: Сэм разрезает 10-метровую веревку на две части.Какова длина более длинного куска? Какова длина более короткого отрезка?

Ответ: Назовем более длинной длиной веревки « L », а более короткой длиной « S »

L должен быть больше 0 м (иначе это не кусок веревки), а также меньше 10 м:

L> 0
L

Итак:

Это говорит о том, что L (большая длина веревки) находится между 0 и 10 (но не 0 или 10)

То же самое можно сказать и о более короткой длине « S «:

~~Но я сказал, что есть «короче» и «длиннее», поэтому мы также знаем:~~

(Вы видите, насколько изящна математика? Вместо того, чтобы говорить «меньшая длина меньше, чем большая длина», мы можем просто написать « S »)

~~Мы можем объединить все это так:~~

~~Это говорит о многом:~~

~~0 меньше короткой длины, короткой длины меньше длинной, длинной меньше 10.~~

~~Если читать «задом наперед», то можно увидеть:~~

~~10 больше длинной длины, длинная длина больше короткой длины, короткая длина больше 0.~~

~~Это также позволяет нам увидеть, что «S» меньше 10 («перепрыгивая» через «L»), и даже что 0~~

Устойчивая красота и гигиена: действительно ли это хороший выбор или всего лишь обещание производителей

Представитель Национального центра общественного здравоохранения Регина Бурбене сказала, что люди, которые пользуются продуктами быстрой моды, являются потребителями “новинок”, не задумываясь о их реальной ценности, включая загрязнение во время производства.

“Думаю, что сегодня мы вынуждены понимать, что такая модель “бери → используй → выбрось” – не только дорого стоит, но и вредит окружающей среде, здоровью, экономике и всей нашей планете. Если мы от этого не откажемся, то лишим возможности нормальной жизни людей последующих поколений”, – сказала Бурбене.

Однако она заметила, что даже те, кто думает об устойчивости, иногда попадаются на крючок “зеленых обещаний”.

~~Устойчивость – это не исключение, а норма~~

Чтобы рационально использовать ресурсы и восстановить равновесие отношений человека и природы, по словам Бурбене, по инициативе Еврокомиссии были подготовлены стратегические документы, предусматривающие такое развитие промышленности в Европе и поведение потребителей, чтобы устойчивые продукты были не исключением, а нормой.

“Касается ли это косметики? Да. ПО своей природе косметика химического происхождения: это натуральные или синтетические вещества и смеси, которые как при производстве, так и при использовании оставляют экологический след”, – сказала Бурбене.

Не менее важно, по ее словам, влияние продуктов на окружение в ходе всего цикла их существования. Согласно регламенту ЕК по предложениям устойчивых продуктов EK, производители должны обеспечить доступность информации всем покупателям.

“У всех регулируемых продуктов будет цифровой паспорт. Это облегчит их переработку, будет легче отследить вызывающие озабоченность химические вещества в цепи поставок продукта. Также может быть введено соответствующее обозначение”, – рассказала Бурбене.

~~Ищите на товарах следующие знаки~~

Поисл экологических товаров, по словам Бурбене, облегчает введенный в 1992 году знак EU Ecolabel, которым помечают товары и услуги 24 разных категорий, в их числе: шампуни, детская одежда, бытовая химия, стротельная краска и другие стройматериалы, бытовая техника, услуги проживания и др.

“Чтобы изделие было помечено этим логотипом, оно должно отвечать установленным требованиям”, – рассказала специалист.

Кроме того, есть и национальные логотипы, отмечающие экологические товары: в Северных странах “Северный лебедь”, в Германии “Голубой ангел”, во Франции Ecocert, в США USDA organic.

~~Потребителей вводит в заблуждение “зеленая промывка мозгов”~~

Бурбене рассказала, что часть поставщиков, чтобы привлечь клиентов экологией, применяет “зеленый” маркетинг. Вместе с ним появилась и “зеленая промывка мозгов”, т.е. потребителей вводят в заблуждение в вопросе экологических качеств продукта, пытаются убедить в его экологичности, даже если это не так.

“Каждая организация, предоставляющая знак экокачества, на своих сайтах сообщает список критериев, которым отвечают производители и произведенная ими продукция, поэтому несложно проверить, заслуженно ли на этикетке появился тот или иной логотип. Рядом с ним должен быть и номер организации, которая выдала сертификат”, – сказала Бурбене.

Указание знаков экологичности совсем необязательно, это добровольный акт, выделяющий изделие. Однако, если добавить в рецептуру продукта из 20 составляющих 0,0001% экстракта из экологического хозяйства и самовольно укажем, что продукт экологический, то это будет преступным введением потребителей в заблуждение.

Однако есть группа знаков, которые с юридической точки зрения обязательны. Они предупреждают потребителя о том, что в составе продукта есть пластик, о том, каким способом нельзя избавляться о предмета.

“С 3 июля 2021 г. на упаковках с влажными салфетками, гигиеническими пакетами, тампонами требуется указывать, что они приносят вред при неправильной утилизации”, – заметила Бурбене.

~~Ženklinimas~~

~~Создание устойчивого продукта~~

Создание устойчивого продукта, по словам Бурбене, охватывает несколько шагов. Выбор сырья ручной работы или экосырья – первый шаг, но потом нужно делать и другие шаги.

“Это и создание экологической формулы, и биологически расщепляемые, многоразовые или перерабатываемые упаковки, и действенные процессы производства, если возможно, снижающие потребление энергии и воды, а также выбросов вредных веществ”, – рассказала специалист.

Создатель ботанической косметики Эрика Симутене сказала, что крема, серумы и гидролаты из натуральных веществ она производит только по заказу, благодаря этому они не застаиваются на прилавках, нет эффекта избыточного потребления. Кроме того, такие средства, как гидролат из лаванды, эфирное масло из лаванды и гель из алоэ – очень универсальные средства, решающие сразу несколько проблем.

“Главное – не навредить человеку и окружению. Я вижу много маркетинга. Неужели столько всего нужно, это риторический вопрос, видимо, каждый, выбирает по себе. Тот же принцип касается и состава косметики. Я думаю, меньше значит больше”, – сказала она.

По словам Симутене, ботаническая косметика рождается из природы: растительных масел, цветочной воды, натуральной глины, пчелиного воска, эфирных масел.

“Летом много растений, я сама их собираю. Для меня это как терапия. Из многих растений я делаю гидролат. Другие сушу и использую для сухих шампуней, чаев”, – рассказала создатель ботанической косметики.

~~Многоразовая гигиена – устойчивость и прогресс~~

Устойчивое потребление прогрессивно и полезно для здоровья, окружающей среды и кошелька, сказала создатель электронного магазина, в котором продают многоразовые продукты Айсте Самулене.

Согласно подсчетам, за свою жизнь одна женщина выбрасывает 11 400 одноразовых прокладок, которые обходятся в 60 евро в год. Это больше чем в два раза превышает стоимость многоразовых решений.

“Женщина может выбирать устойчивые средства в зависимости от своего желания и образа жизни: сегодня на рынке есть менструальные чаши, трусики, многоразовые прокладки и даже специальные купальные плавки”, – заметила Самулене.

Идея продавать такие вещи у нее появилась, поскольку появилась личная потребность в таких вещах. Казалось бы, на дворе XXI век, есть много удобных одноразовых средств, но отказаться от них заставляет забота о здоровье и окружении.

“Я шире взглянула на это тогда, когда долго не могла забеременеть, но выяснилось, что никаких медицинских причин нет. Пришлось пересмотреть, что я ем, какие кремы использую. Один менструальный цикл я находилась дома и увидела, сколько отходов остается, я пришла в ужас – ведь, казалось бы, прокладки продают в таких небольших упаковках. И это были отходы только одной женщины за один цикл”, – рассказала Самулене.

Это было 15 лет назад, когда многоразовые средства гигиены не пользовались популярностью в Литве, но и тогда ей удалось найти выход, а сейчас выбор больше, а новые средства удобнее и дешевле.

Гороскоп на 28 сентября для всех знаков зодиака

~~Новини~~

~~28.09.2022~~

~~3 хв. на прочитання~~

Сегодня, 28 сентября, Луна в Скорпионе. Этот день несет двойственную энергетику. С одной стороны, он прекрасно подходит для саморазвития и творчества. Сегодня можно решить накопившиеся проблемы. С другой стороны, день категорически не подходит для групповой работы, опрометчивых или интуитивных решений.

♈ Овен

Настройтесь на волну своего сердца. Начните диалог с самим собой о важных вещах. Спросите себя, как вы на самом деле относитесь к определенному человеку или ситуации. В минуты тишины ответы откроются совершенно случайным образом. Примите то, что приносит радость и пробуждает страсть.

Космический совет: скажи «да» тому, что приносит тебе радость.

♉ Телец

Этот период связан с новыми начинаниями. Вы призваны определить наши намерения, посеять семена и предпринять необходимые действия. Обратите внимание на то, что стремится родиться в вашей душе. Ваши желания священны и продвигают вас в правильном направлении.

Космический совет: посадите семена в своей душе.

♊ Близнецы

Честность — лучшая политика. Где бы вы ни находились и через что бы вы ни проходили, говорите всю правду. Она может сблизить вас с окружающими на многих уровнях. В то же время помните, что в каждом разговоре участвуют два человека.

Космический совет: говорите правду.

♋ Рак

Энергия растущей луны пробуждает вас. Вы начинаете понимать, что ваша цель намного больше, чем кажется на первый взгляд. Обратите внимание на мысли, импульсы, видения, знаки и символы. Радость, которую вы чувствуете глубоко внутри себя, является признаком того, что вы на правильном пути и продвигаетесь в правильном темпе. Но это не значит, что в вашем мире всегда будет радуга и солнце. Проблемы также являются частью вашей жизни.

Космический совет: чувство радости приведет вас на правильный путь.

♌ Лев

Жизнь нельзя уместить в таблицу Excel, презентацию PowerPoint и дедлайны. Пришло время порвать с этим навязчивым подходом и необходимостью быть продуктивным всегда. Вспомните, когда вы искренне радовались. В ваше уравнение нужно вернуть элемент радости.

Космический совет: жизнь должна быть праздником.

♍ Дева

Разрешение конфликтов — большая тема для вас прямо сейчас. Растущая луна приносит с собой возможность принести мир туда, где была война. Так что действуйте на совесть. Убедитесь, что вы активно слушаете других и уделяете внимание их историям. В сфере любви и романтики дела обстоят гораздо лучше. Будьте открыты многим возможностям.

Космический совет: пришло время заключить мир.

♎ Весы

Вселенная хочет дать вам именно то, о чем вы просили, и именно так, как вы просили. Но верите ли вы, что заслуживаете этого? Сегодня звезды призывают вас пробудиться ото сна и немножко поверить в чудеса.

Космический совет: вы легко дотянетесь до желаемого.

♏ Скорпион

В период ретроградного Меркурия возвращение в прошлое является главной темой. Воспринимайте эту ностальгию как знак того, что вам нужно восстановить связь с определенными людьми в вашей жизни. Просто не тратьте слишком много времени на размышления о том, почему все пошло именно так. Иногда оставить прошлое в прошлом — единственный выход.

Космический совет: пришло время написать другу, о котором вы недавно вспоминали.

♐ Стрелец

У некоторых вещей есть шанс сработать, когда вы меньше всего этого ожидаете. На этой неделе вас просят ожидать неожиданного и верить в невозможное. Также в этот день вы сможете легко преодолевать все возникающие трудности.

Космический совет: ждите сюрпризов от судьбы.

♑ Козерог

В этот день вам понадобится надежное плечо, наставник и учитель. Вполне вероятно, что вы не получите помощи на стороне и вам придется искать мудрого гуру внутри себя. Обратитесь к своему прошлому, чтобы вспомнить похожие ситуации, которые уже происходили. Опыт поможет вам преодолеть любые преграды.

Космический совет: вам нужно найти мудрого наставника.

♒ Водолей

Доверяйте знакам и тому, куда они вас ведут. Поток толкает вас к новой жизни. Жизнь, которую вы представляете для себя в течение некоторого времени. Обращайте внимание на импульсы и реагируйте на происходящее.

Космический совет: примите своевременные меры.

♊ Рыбы

Учитывая траекторию вашей жизни, для вас будет естественным чувствовать, что все, что вам близко, может быть отнято у вас в любой момент. Но это — лишь паранойя. В ближайшие дни вы вступаете в период стабильности.

Космический совет: вам есть за что быть благодарным.

Читай наші новини в Google News, Telegram, Facebook та Twitter

Підписка на кращі новини тижня
Не бійтеся. Ми ніколи не надсилаємо спам!
Символы «больше» и «меньше» Определение, приемы
Математические статьи
Символы больше и меньше сравнивают любые два числа. Когда число больше или меньше другого, используются знаки больше или меньше. Знак «больше» (>) используется, когда первое число больше второго. Если первое число меньше второго, то используется знак меньше (<). Математика — это тот язык, где есть свои правила и формулы.
Символы, используемые в математике, уникальны для всех дисциплин и общеприняты. Использование математических символов требует меньше времени и места. Это позволяет человеку обмениваться информацией через символику. В этой статье мы узнаем определение символов «больше» и «меньше», их символы и примеры сравнения двух чисел с использованием знаков «меньше» и «больше».
Содержание
Символы «больше» и «меньше» Определение
Символ больше
Примеры символов «больше чем»
Меньше символа
Примеры символов меньше чем
равно символу
Сравнение чисел
Уловка, чтобы запомнить больше, чем меньше, чем знак
Аллигаторный метод
L Метод
Символы, используемые в математике
Применение символов больше и меньше в алгебре
Решенные примеры
Часто задаваемые вопросы (FAQ)
Символы «больше» и «меньше» представляют собой неравенство между двумя значениями. Символ, используемый для обозначения «больше» — «>», а для обозначения «меньше» — «<».
Больше символа
Знак «больше» в математике ставится между двумя значениями, в которых первое число больше второго. Например, 11 > 6. Здесь 11 больше 6.
В неравенстве знак «больше» всегда указывает на большее значение, а символ состоит из двух штрихов одинаковой длины, соединяющихся под острым углом справа (>).
Примеры символов больше, чем
3 > 1: 3 больше 1
0,1 > 0,01: В системе счисления, состоящей из десятичных чисел, где значение 0,1 больше 0,01
8/2 > 6/3: 8/2 равно 4, а 6/3 равно 2. Итак, 4 > 2, что означает, что 8/2 больше, чем 6/3.
Меньше символа
Между двумя числами ставится знак меньше, если первое число меньше второго. Например, меньше символа неравенства 4 < 8. Это означает, что 4 меньше 8.
В неравенстве символ «меньше» всегда указывает на маленькое значение, где две черты одинаковой длины соединяются под острым углом слева (<).
Символ «больше чем меньше» уменьшает временную сложность и упрощает понимание читателем.
Меньше, чем Примеры символов
4 < 6: Рассмотрим целое число, где 4 меньше 6
22 < 23: Здесь 22 записывается как 2 × 2 = 4, а 23 записывается как 2 × 2 × 2 = 8. Таким образом, 4 меньше 8. Также мы можем сказать, что 22 меньше 23.
0,002 < 0,1: десятичное значение 0,002 меньше 0,1
Символ “равно”
Символ «равно» показывает равенство между двумя значениями или числами. Этот символ равенства противоречит как больше, так и меньше, чем символ. Даже в терминах уравнений мы обычно используем аналогичный символ. Он представлен как ‘=.’
Пример: если a = 6 и b = 6, то a = b.
Сравнение номеров
Всякий раз, когда мы сравниваем числа, мы обычно говорим о размерах чисел.
Например,
11 больше 8, 3 меньше 5
Вместо того, чтобы писать словами, мы будем использовать знак «больше чем» или символ «больше чем» и знак «меньше чем»
11>8 и 3<5
Уловка, чтобы помнить больше, чем меньше, чем знак
Как правило, для запоминания символов больше и меньше используются два метода. Они
Аллигаторный метод
Л-метод
Аллигаторный метод
Мы знаем, что аллигатор (или крокодил) всегда хочет съесть большое количество рыбы. Таким образом, пасть аллигатора всегда открывается в сторону наибольшего количества рыбы. Теперь предположим, что числа с обеих сторон представляют собой количество рыб. Возьмем пример, 9> 4
Здесь пасть аллигатора указывает на 9. Это означает, что 9 больше, чем 4.
Это означает, что 4 меньше 9. Это также записывается с использованием символа меньше, чем 5 < 8.
L-метод
Буква «L» похожа на знак «меньше» «<. «Теперь вы можете запомнить первую букву слова меньше, чем символ. Пример: 20 < 40
Символы, используемые в математике
Символ Описание Обозначение символов Пример
Знак больше > 8 > 4
Знак меньше < 4< 8
Равно знаку = 4 + 1 = 5
Не равно знаку ≠ 5 + 2 ≠ 4 + 2
Применение символов больше и меньше в алгебре
Как мы знаем, математические задачи не всегда заканчиваются равенством. Иногда он должен иметь неравенства, такие как больше или меньше символа. Утверждение может быть представлено с помощью математических выражений.
Например, «у» — это количество учеников в школе. Если в школе более 100 учеников и еще 20 учеников присоединились к вашей школе, то в школе больше 120 учеников. Это утверждение математически выражается как y + 20 > 120.
В математике решение неравенств похоже на решение уравнений. При работе с проблемами неравенства всегда обращайте внимание на направление неравенства. Некоторые приемы не влияют на направление неравенств в задаче. их
Умножить или разделить неравенства в обе стороны на одно и то же положительное число
Вычитание или добавление одного и того же числа к обеим сторонам выражения неравенства
Решенные примеры
Q1. У бриджеша 14 бананов, а у манси 20 бананов. Узнай, у кого больше бананов.
Ответ. Дано,
У Бриджеша 14 бананов.
У манси 20 бананов.
Итак, 20 больше 14, 20 >14
Поэтому у манси бананов больше, чем у бриешей.
Q2. Каран спит 30 минут, а Рохит спит 45 минут каждый день днем. Узнайте, кто спит меньше времени.
Ответ. Дано,
Каран спит 30 минут
Рохит спит 45 минут
Мы знаем, что 30 минут меньше 45 минут, поэтому мы можем записать это как 30<45
Поэтому Каран спит меньше времени.
Часто задаваемые вопросы (FAQ)
Q1. Запишите различные символы неравенства.
Ответ. Различные символы неравенства:
Больше чем (>)
Менее (<)
Не равно (≠)
Больше или равно (≥)
Меньше или равно (≤)
Q2. Как можно сказать, какое число больше?
Ответ. Чем дальше справа, тем больше число.
Q3. Что означает ≥?
Ответ. Символ ≥ означает больше или равно.
Q4. Ноль больше любого отрицательного числа?
Ответ. Ноль больше любого отрицательного целого числа.
Q5. Напишите больше или равно символу.
Ответ. Символ ≥ означает больше или равно
Символы неравенства | Что?, История, Больше, Меньше
ЧТО ТАКОЕ НЕРАВЕНСТВО?
Неравенство — это отношение между двумя числами или алгебраическим выражением, которое не равно. Неравенства иногда могут быть представлены либо как вопрос, который может быть решен, либо как констатация факта в форме теорем. Есть четыре термина неравенства, которые мы можем использовать для сравнения двух величин, а именно: больше, больше или равно, меньше и меньше или равно.
ИСТОРИЯ СИМВОЛОВ НЕРАВЕНСТВА
Неравенство как математическое понятие не было чуждым понятием древним математикам (Bagni, 2005), поскольку они уже знали неравенство треугольника как геометрический факт и среднее арифметико-геометрическое неравенство (Fink, 2000). Тем не менее, в 1631 году символы больше и меньше, чем в книге «Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas» или Аналитические искусства в применении к решению алгебраических уравнений Томаса Хэрриота был впервые представлен. Харриот, британский математик, умер в 1621 году, и его книга была опубликована через 10 лет после его смерти. Пьер Бугер, французский математик, поставил черту под символами неравенства, чтобы обозначить больше или равно и меньше или равно. Затем в 1734 году были введены символы < и >.
БОЛЬШЕ, ЧЕМ
Больше, чем одно из неравенств, используемых, когда количество больше или больше, чем другое количество или количества. На рисунке ниже показан символ, используемый для обозначения больше чем.
Обозначение a > b означает, что a больше, чем b. Например, 2 > 1.
Обратите внимание на приведенный ниже рисунок. Просто взглянув, можно легко заметить, что на левой стороне есть цветы, чем на правой. Поэтому можно сказать, что 7 цветков больше, чем 4 цветка.
Другой пример — сравнение стоимости денег.
В левой части у нас общая стоимость 110 долларов, а в правой части общая стоимость 70 долларов. Следовательно, мы можем сказать, что 110 долларов > 70 долларов.
БОЛЬШЕ ИЛИ РАВНО
Больше или равно — это термин, который используется для отображения взаимосвязи в линейных неравенствах. Больше или равно предполагает, что значение переменной может быть больше или равно определенному числу. Использование термина «по крайней мере» также может означать «больше или равно». Как показано на рисунке ниже, разница между символами «больше чем» и «больше или равно» заключается в дополнительной строке под символом «больше чем».
В таблице ниже показано, как мы можем использовать символ больше или равно и как мы его определяем.
EXAMPLE MEANING
$x\geq 7$ The inequality means that the value of x can be equal to 7 or any number greater than 7 such as 8, 20 и т. д.
$-1\geq x\geq3$ В данном примере это означает, что значение может быть равно 3 или -1 или любому числу от -1 до 3, например 0 и 1. Следовательно, мы можем сказать, что значение x включительно находится между -1 и 3.
МЕНЬШЕ
Когда первое указанное значение меньше второго значения, мы используем термин меньше чем. Меньше используется, чтобы показать отношение между меньшим и большим значением. Символ, используемый для обозначения меньше, чем показан на рисунке ниже.
Обозначение a < b означает, что a меньше, чем b. Например, 1 < 2.
Возьмем другой пример ниже. Мы можем ясно видеть, что на левой стороне меньше манго, чем на правой. Итак, мы можем сказать, что 3 манго меньше, чем 5 манго.
МЕНЬШЕ ИЛИ РАВНО
Как следует из названия, меньше или равно означает, что переменная либо меньше, либо равна другому числу, выражению или термину. Использование терминов «самое большее», «не более», «максимум» и «не превышающий» также означает меньше или равно. На рисунке ниже показан символ, используемый для выражения меньше или равно. Вы можете заметить линию под символом «меньше чем», которая отличает их друг от друга.
В таблице ниже показано, как мы можем использовать символ больше или равно и как мы его определяем.
EXAMPLE MEANING
$x\leq 1$ The value of x can be equal to 1 or any number less than 1 such as 0, -1, – 5 и т. д. Это неравенство также означает, что наибольшее возможное число для x равно 1.
$-4\leq x\leq 4$ Это неравенство означает, что значение x должно лежать между -4 и 4, например -2, 0 и 1, включая -4 и 4.
ИСПОЛЬЗОВАНИЕ НЕРАВЕНСТВА ПРИ СРАВНЕНИИ ЧИСЕЛ
При сравнении чисел мы используем символы > и <, чтобы показать их отношения друг к другу. Всегда имейте в виду, что более широкий рот указывает на большее число.
ПРИМЕР #1
Какой символ неравенства будет показывать отношение между 35__21?
Поскольку 35 больше 21, мы будем использовать >. Следовательно, 35 > 21.
ПРИМЕР #2
Изучите рисунок ниже и определите соответствующий символ неравенства.
Глядя на фото, можно сказать, что на правой стороне больше мороженого, чем на левой. Поэтому мы будем использовать <, так как 2 мороженого меньше, чем 4 мороженого.
СВОЙСТВА НЕРАВЕНСТВА
ЗАКОН ТРИХОТОМИИ
Закон трихотомии для действительных прямых утверждает, что для любых действительных чисел a и b верно только одно из 𝑎 < 𝑏, 𝑎 = 𝑏 > .
Предположим, у нас есть утверждения, 8 < 9, 8 = 9, 8 > 9, только из них верно. Поскольку мы знаем, что 9больше 8, то мы можем сказать, что единственно верное утверждение 8 < 9.
ОБРАЩАЕМОЕ СВОЙСТВО
Обратное свойство неравенства утверждает, что < и >, ≤ и ≥ являются обратными друг другу. Это означает, что для любых действительных чисел a и b 𝑎 < 𝑏 и 𝑏 > 𝑎 и 𝑎 ≤ 𝑏 и 𝑏 ≥ 𝑎 эквивалентны, или мы можем просто сказать, что:
𝑎 < 𝑎 700 ↔ 𝑔
𝑎 ≤ 𝑏 ↔ 𝑏 ≥ 𝑎
Предположим, что у нас есть 3 < 7. По обратному свойству неравенства 3 < 7 равно 7 > 3.
ПЕРЕХОДНОЕ СВОЙСТВО
Для любых действительных чисел a , b и c ,
Если 𝑎 < 𝑏 и 𝑏 < 𝑐, то 𝑐.
Если 𝑎 > 𝑏 и 𝑏 > 𝑐, то 𝑎 > 𝑐.
Предположим, что 21 > 19 и 19 > 8, тогда по транзитивному свойству неравенства 21 > 8. тогда для любого действительного числа a , b и c :
если 𝑎 < 𝑏, то 𝑎 + 𝑐 < 𝑏 + 𝑐.
если 𝑎 ≤ 𝑏, то 𝑎 + 𝑐 ≤ 𝑏 + 𝑐.
Например,
Если в неравенстве 13 > 9 прибавить 19, используя свойство сложения неравенства, то получится:
13 + 19 > 9 + 19
32 > 28 свойство неравенства гласит, что если к обеим частям неравенства вычесть общий постоянный член c , то для любого действительного числа A , B и C :
, если 𝑎 <𝑏, то 𝑎 - 𝑐 <𝑏 - 𝑐
Если 𝑎 ≤ ≤ 𝑎 𝑐 ≤ ≤ 𝑐 𝑐 𝑐 𝑐 𝑐 𝑐 𝑐 𝑐 ≤ ≤ ≤ ≤. если вычесть 3 из неравенства 6 < 12, то по свойству вычитания неравенства следует, что: b , и $c\neq 0$,
если 𝑎 < 𝑏 и 𝑐 > 0, то 𝑎𝑐 < 𝑏𝑐
если 𝑎 < 𝑏 и 𝑐 < 0, то 𝑎𝑐 > 𝑏𝑐
если 𝑎 ≤ 𝑏 и 𝑐 > 0, то 𝑎𝑐 ≤ 𝑏𝑐.
Если 𝑎 ≤ 𝑏 и 𝑐 < 0, то 𝑎𝑐 ≥ 𝑏𝑐.
Предположим, что неравенство 4 < 7 и 𝑐 = 9. По свойству умножения неравенства
4 × 9 < 7 × 9
36 < 63
Другой пример: 1 < 3 и 𝑐 = −1. Если умножить -1 на неравенство 1 < 3, то получится:
1 × -1 < 3 × -1
-1 > -3
Обратите внимание, что каждый раз, когда вы умножаете неравенство на отрицательное число, вы должен перевернуть знак неравенства.
СВОЙСТВО ДЕЛЕНИЯ
Для любых действительных чисел a , b и $c\neq 0$,
если 𝑎 < 𝑏 и 𝑐 > 0, то $\frac{a}{c}< \ frac{b}{c}$
, если 𝑎 < 𝑏 и 𝑐 < 0, то $\frac{a}{c}> \frac{b}{c}$
Предположим, что 21 < 51 и 𝑐 = 3 , то по свойству деления неравенства
$\frac{21}{3}< \frac{51}{3}$
$7 < 17$
Возьмем другой пример, если у нас есть неравенство 20 > 10 и 𝑐 = −5, то применение свойства деления неравенства приведет к:
$\frac{20}{-5}> \frac{10}{-5}$
$-4 < -2$
Помните, каждый раз, когда вы делите отрицательное число на неравенство, символ неравенства будет наоборот.
АДДИТИВНОЕ ОБРАТНОЕ СВОЙСТВО
Аддитивное обратное свойство неравенства утверждает, что для любых действительных чисел a и b ,
, если 𝑎 < 𝑏, то −𝑎 > −𝑏.
, если 𝑎 ≤ 𝑏, то −𝑎 ≥ −𝑏.
МУЛЬТИПЛИКАТИВНОЕ ОБРАТНОЕ СВОЙСТВО
Мультипликативное обратное свойство неравенства утверждает, что если для любых действительных чисел a и b , оба положительные или оба отрицательные,
, если a < b, то $\frac{1}{a}> \frac{1}{b}$.
если a > b, то $\frac{a}{c}< \frac{b}{c}$.
НЕРАВЕНСТВО В ЧИСЛОВОЙ РЯДКЕ
ГРАФИК БОЛЬШЕ, ЧЕМ В ЧИСЛОВОЙ РЯДКЕ
Чтобы изобразить неравенство больше чем, используйте открытый кружок, чтобы отметить начальное значение, и направьте стрелку в сторону положительной бесконечности. На рисунке ниже показано, как легко обнаружить неравенство, обозначающее больше.
ПРИМЕР
График x > 3.
РЕШЕНИЕ
На приведенном ниже графике показано числовое значение. Вы можете видеть незакрашенный круг, расположенный над цифрой 3, поскольку он простирается до положительной бесконечности.
Чтобы обозначить множество решений данного выше неравенства, мы используем символы ( и ), чтобы указать, что конечная точка линии не включена. Этот символ используется, когда вы видите график, который представляет собой открытый круг. Следовательно, мы можем обозначить множество решений $x>3$ как $(3, +\infty )$.
ГРАФИК БОЛЬШЕ ИЛИ РАВНО В ЧИСЛОВОЙ ЛИНИИ
Чтобы изобразить неравенство больше или равно, используйте замкнутый круг, чтобы отметить начальное значение, и направьте стрелку в сторону положительной бесконечности или вправо. На рисунке ниже показано, как легко обнаружить неравенство, которое означает больше или равно.
ПРИМЕР
График $x\geq 3$.
РЕШЕНИЕ
Чтобы представить график в виде числовой прямой, начните с того, что поместите замкнутый круг поверх числа 3, а затем продлите линию до положительной бесконечности. На рисунке ниже показан график для $x\geq 3$.
Чтобы записать набор решений $x\geq 3$ , используйте символы [ и ], чтобы указать, что конечные точки линии также включены. Этот символ используется, когда вы видите график с конечными точками, которые являются замкнутым кругом. Таким образом, мы можем обозначить множество решений $x\geq 3$ как [$ 3, +\infty $).
ИЗОБРАЖЕНИЕ МЕНЬШЕ ЧИСЛОВОЙ ЛИНИИ
Чтобы изобразить меньше неравенства, отметьте начальное значение незаштрихованным кружком и направьте стрелку в сторону отрицательной бесконечности или влево. На рисунке ниже показано, как легко определить неравенство, обозначающее меньше чем.
ПРИМЕР
График $x<3$.
РЕШЕНИЕ
Чтобы нарисовать график для в виде числовой прямой, используйте открытый кружок для обозначения начальной точки, равной 3. Затем продлите линию до отрицательной бесконечности. График ниже представляет неравенство $x<3$.
Представление множества решений $x<3$ даст нам $(-\infty,3)$. Помните, что при обозначении набора решений всегда нужно начинать с наименьшего возможного значения. Поскольку на графике изображен незакрашенный кружок, мы используем символ ( и ) для обозначения его набора решений.
ИЗОБРАЖЕНИЕ МЕНЬШЕ ИЛИ РАВНО В ЧИСЛОВОЙ ЛИНИИ
Чтобы построить график меньше или равно неравенству, используйте тесный кружок, чтобы отметить начальное значение, и направьте стрелку в сторону отрицательной бесконечности или влево. На рисунке ниже показано, как легко определить неравенство, которое обозначает меньше или равно.
ПРИМЕР
График $x\leq 3$.
РЕШЕНИЕ
Чтобы изобразить график числовой прямой, нарисуйте замкнутый круг, от которого начинается линия. В этом случае заданное значение равно 3. Затем удлините линию от 3 до отрицательной бесконечности. На рисунке ниже показан график для $x\leq 3$.
Чтобы записать набор решений $x\leq 3$, мы используем символы [ и ], чтобы указать, что значение 3 включено. Таким образом, множество решений $x\leq 3$ равно ($-\infty,3$].
ЦЕПОЧНАЯ ОБОЗНАЧЕНИЕ
Когда мы видим такие обозначения, как a ≤ b ≤ c или a ≤ b < c , это означает, что у нас есть цепная запись. Если мы разобьем цепную запись a ≤ b ≤ c , это будет означать a ≤ b и b ≤ c . Эта запись описывает двойное неравенство, которое имеет нижнее и верхнее предел числа б . По транзитивному свойству неравенства также следует, что a ≤ c .
ПРИМЕР #1
Какое множество решений задано -1 < x < 10 ?
РЕШЕНИЕ
Чтобы обозначить набор решений -1 < x < 10 , мы начнем с определения наименьшего и наибольшего возможного значения x . В этом неравенстве -1 будет нижним пределом, а 10 – верхним пределом. Так как неравенство показывает оба обозначения с использованием <, то мы будем использовать ( и ). Следовательно, набор решений равен (-1, 10).
ПРИМЕР #2
Какое множество решений задано -4 < x ≤ 5 ?
РЕШЕНИЕ
Если мы разберем цепочку обозначений, это даст нам неравенства −4 < 𝑥 и 𝑥 ≤ 5 . По обратному свойству неравенства −4 < 𝑥 эквивалентно 𝑥 > −4 . Следовательно, мы имеем 𝑥 > −4 и 𝑥 ≤ 5 . Тогда мы можем сказать, что -4 — это нижний предел, а 5 — верхний предел. Поскольку у нас есть , это означает, что в набор решений входит только 5. Таким образом, множество решений определяется формулой (−4,5].
Перевод математических утверждений в неравенство иногда может быть запутанным и трудным. Тем не менее, это методы, которые нужно помнить, чтобы избежать путаницы.
Иногда синонимы слов больше и меньше могут сбить вас с толку.
Например, вы видите утверждения « x больше 7» и « x больше 7». Хотя они могут иметь одинаковое значение, « x больше 7» относится к значению x больше 7. Следовательно, перевод его в символы приведет к х > 7 . Однако утверждение « x больше, чем 7» относится к добавлению 7 к значению x . Таким образом, если мы переведем это в алгебраические выражения, это станет x + 7 .
Не путайте с утверждениями «максимум» и «минимум». Утверждение «максимум» просто означает, что значение переменной меньше или равно, а «по крайней мере» означает, что значение переменной больше или равно.
ПРИМЕР #1
Перевести 7 больше 5.
РЕШЕНИЕ
Если мы переведем 7 больше 5 в алгебраическое выражение, будет 7 > 5.
ПРИМЕР #2
x составляет не менее 10 дюймов.
РЕШЕНИЕ
Ключевым термином в этом утверждении является «не более». «Не более» при переводе в алгебраические термины означает «меньше или равно». Следовательно, x ≤ 10 .
ПРИМЕР #3
Джеймс моложе Райана. Как можно перевести это утверждение в алгебраическое выражение?
РЕШЕНИЕ
Учитывая, что Джеймс старше Райана, мы можем сказать, что возраст Джеймса меньше, чем у Райана. Таким образом, если мы представим возраст Джеймса как x , а возраст Райана как y , мы получим неравенство x < y .
ПРИМЕР #4
Алиссе необходимо получить минимум 83 балла в следующей четверти, чтобы сдать предмет по математике. Как перевести в алгебраическое выражение?
РЕШЕНИЕ
Чтобы перевести данное утверждение, отметьте ключевой термин «минимальный уровень». Минимальная оценка 83 означает, что самая низкая возможная оценка, которую она должна получить, равна 83. Кроме того, мы должны принять к сведению, что максимально возможная оценка равна 100. Таким образом, перевод этого утверждения даст нам выражение 83 ≤ x ≤ 100 .
Решение текстовых задач на линейные уравнения и линейные неравенства Рабочие листы по математике для 7-го класса
Рабочие листы по неравенствам с одной переменной (временная тематика)
Понимание и решение неравенств с одной переменной Рабочие листы по математике для 6-го класса
Просмотреть все рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Больше или равно в Excel
«Больше или равно» — это сравнение или логический оператор, помогающий сравнивать две ячейки данных одного типа. Обозначается символом «>=» и возвращает следующие значения:
«Истина», если первое значение больше или равно второму значению
«Ложь», если первое значение меньше второго значения
Как правило, «больше или равно» оператор используется для значений даты и времени и чисел. Его также можно использовать для текстовых данных.
Например, если ячейка C1 содержит слово «роза», а ячейка D1 содержит слово «лотос», формула «=C1>=D1» возвращает значение «истина». Это потому, что первая буква «р» больше, чем буква «л». Значения «a» и «z» считаются самым низким и самым высоким текстовыми значениями соответственно.
Содержание
«Больше или равно» (>=) в Excel
Логические и арифметические операторы
Как использовать «больше чем» (>) и «больше или равно» (> знак равно
Пример №1 – «Больше» и «Больше или равно»
Пример №2 – «Больше или равно» с функцией ЕСЛИ
Пример №3 – «Больше или равно» с функцией Функция СЧЁТЕСЛИ
Пример № 4. «Больше или равно» с функцией СУММЕСЛИ
Часто задаваемые вопросы
Рекомендуемые статьи
Логические и арифметические операторы
Символ «равно» (=), используемый в математических операциях, помогает определить, равны ли два значения или нет. Аналогичным образом, каждый логический операторЛогический операторЛогические операторы в Excel также известны как операторы сравнения, и они используются для сравнения двух или более значений, возвращаемый результат, предоставляемый этими операторами, является либо истинным, либо ложным, мы получаем истинное значение, когда условия соответствуют критериям. и false в результате, когда условия не соответствуют критериям. Читать далее служит определенной цели. Поскольку логические операторы возвращают только логические значения «истина» или «ложь», их также называют логическими операторами. 9) символы используются в формулах. Эти операторы используются в вычислениях для создания числового вывода.
Звездочка, косая черта и знак вставки используются для умножения, деления и возведения в степень соответственно.
Как использовать «больше чем» (>) и «больше или равно» (>=)?
Давайте рассмотрим несколько примеров, чтобы понять использование данных операторов сравнения в Excel.
Вы можете скачать этот шаблон больше или равно Excel здесь — Шаблон больше или равно Excel
Пример №1 — «Больше» и «Больше или равно»
В следующем списке показаны пять числовых значений из ячеек с A2 по A6. Мы хотим проверить, больше ли каждое число 50 или нет.
Шаги для проверки большего числа перечислены ниже:
Введите знак «равно» (=) в ячейку B2.

Выберите ячейку A2 для проверки.

Поскольку мы хотим проверить, больше ли значение в ячейке A2 50 или нет, введите оператор сравнения (>), а затем число 50.

Нажмите клавишу «Ввод», чтобы получить результат . Скопируйте и вставьте или перетащите формулу в остальные ячейки. Ячейки желтого цвета содержат число больше 50. Следовательно, результат «истинный».

Значение ячейки A4 (50) не больше числа 50. Следовательно, результат в ячейке B4 — «ложь».
Чтобы включить 50 в тест, нам нужно изменить оператор сравнения на «больше или равно» (>=).
Оператор «больше или равно» возвращает значение «истина» в ячейке B4. Это означает, что значение ячейки A4 либо больше, либо равно 50.
Пример 2. «Больше или равно» с функцией ЕСЛИ
Давайте воспользуемся оператором сравнения «больше или равно» с функцией ЕСЛИ условиеЕСЛИ Функция ЕСЛИ в Excel оценивает, выполняется ли заданное условие, и возвращает значение в зависимости от того, является ли результат «истинным» или «ложным». Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев. читать далее.
В следующей таблице показаны общие продажи (в долларах) за разные месяцы. Ежемесячные поощрения рассчитываются путем сравнения продаж с эталоном в 6500 долларов. Возможны следующие варианты:
Если общий объем продаж> 6500 долларов, поощрения рассчитываются по ставке 10%.
Если общий объем продаж <6500 долларов, поощрения равны 0.
Шаг 1: Откройте функцию ЕСЛИ. Функция ЕСЛИ помогает оценить критерий и возвращает «истина» или «ложь» в зависимости от того, выполнено условие или нет.
Шаг 2: Применение логического тестаЛогический тестЛогический тест в Excel приводит к аналитическому выводу, который может быть либо истинным, либо ложным. Оператор равенства «=» является наиболее часто используемым логическим тестом. Подробнее, B2>6500.
Шаг 3: Условие состоит в том, что если логический тест «верен», мы рассчитываем поощрения как B2*10%. Итак, набираем этот критерий.
Шаг 4: Если логическая проверка «ложь», поощрения равны 0. Итак, мы вводим ноль в конце формулы.
В ячейке C2 формула возвращает результат 0. Это означает, что значение в ячейке B2 меньше 6500 долларов США.
Шаг 5: Перетащите формулу в оставшиеся ячейки, как показано на следующем рисунке.
Поскольку значения в ячейках B5, B11, B12 и B13 превышают 6500 долларов США, мы получаем соответствующие суммы поощрений в столбце C.
Давайте воспользуемся оператором сравнения «больше или равно» с функцией СЧЁТЕСЛИФункция СЧЁТЕСЛИ в Excel подсчитывает количество ячеек в диапазоне на основе заранее заданных критериев. Он используется для подсчета ячеек, содержащих даты, числа или текст. Например, СЧЁТЕСЛИ(A1:A10,”Козырь”) подсчитает количество ячеек в диапазоне A1:A10, содержащих текст “Козырь”. читать дальше функция.
В следующей таблице показаны даты и суммы счетов, отправленных покупателю. Мы хотим подсчитать количество счетов, отправленных 14 ^th марта 2019 года или после этой даты.
Шаг 1: Откройте функцию СЧЁТЕСЛИ. Функция COUNTIF помогает подсчитывать ячейки в определенном диапазоне на основе критерия.
Шаг 2: Выберите столбец даты (столбец A) в качестве диапазона (A2:A13).
Шаг 3: Поскольку критерий равен или больше 14 ^th March 2019, его можно представить как «>=14-03-2019». Введите символ «>=» в двойных кавычках.
Примечание: Операторы сравнения в аргументе «критерии» должны быть заключены в двойные кавычки.
Шаг 4: Введите знак амперсанда (&). Мы предоставляем дату с помощью функции DATEФункция DATEФункция даты в Excel — это функция даты и времени, представляющая число, предоставленное в качестве аргументов в коде даты и времени. Отображаемый результат представлен в формате даты, но аргументы представлены как целые числа. Подробнее. Это связано с тем, что мы не используем ссылку на ячейку ReferencesCell ReferencesCell в Excel ссылаемся на другие ячейки в ячейку, чтобы использовать ее значения или свойства. Например, если у нас есть данные в ячейке A2 и мы хотим использовать их в ячейке A1, используйте =A2 в ячейке A1, и это скопирует значение A2 в A1. Подробнее о значениях даты.
Шаг 5: Закройте скобки формулы и нажмите клавишу «Ввод».
Результат равен 7, что означает, что 14 ^th марта 2019 года или после этой даты было создано семь счетов. оператор сравнения «больше или равно» с СУММЕСЛИМНФункция СУММЕСЛИ Excel вычисляет сумму диапазона ячеек на основе заданных критериев. Критерии могут включать даты, числа и текст. Например, формула «=СУММЕСЛИ(B1:B5, «<=12»)» складывает значения в диапазоне ячеек B1:B5, которые меньше или равны 12. читать дальше функция.
В следующей таблице показаны ежемесячные продажи организации. Данные о продажах указаны в тысячах долларов. Мы хотим выяснить, превышает ли общий объем продаж 20 000 долларов или равен ему.
Шаг 1: Откройте функцию СУММЕСЛИ. Функция СУММЕСЛИ суммирует ячейки на основе заданного критерия.
Шаг 2: Выберите столбец продаж (столбец B) в качестве «диапазона» ($B$2:$B$13). Это помогает суммировать ежемесячные значения продаж.
Шаг 3: Введите «критерии» как «>=»&20. Поместите оператор сравнения в двойные кавычки.
Шаг 4: Выберите «sum_range» так же, как аргумент «диапазон», т. е. $B$2:$B$13.
Результат: 132 000 долларов. Следовательно, общий объем продаж превышает 20 000 долларов.
Часто задаваемые вопросы
Определение оператора «больше или равно» в Excel.
«Больше или равно» (>=) — это один из шести логических операторов сравнения Excel. Он возвращает «true», если первое число больше или равно второму числу; в противном случае возвращает «ложь».
Остальные операторы сравнения: «равно» (=), «не равно» (<>), «больше» (>), «меньше» (<) и «меньше или равно» ( <=). Все операторы сравнения помогают сравнивать две ячейки данных. Их можно использовать с числами, текстом, значениями даты и времени.
Например, формула «=C2>=СУММ(F2:h21)» возвращает «истина», если значение в ячейке C2 больше или равно сумме значений в диапазоне F2:h21. Если обратное верно, возвращается «false».
Когда следует использовать оператор «больше или равно» в Excel?
Данный оператор сравнения следует использовать в следующих ситуациях:
• Чтобы найти, какая из двух величин больше или меньше
• Чтобы определить, равна ли одна величина другой
• Чтобы оценить две величины относительно заданному критерию
• Для сравнения двух отдельных величин с третьей величиной
Примечание: Две величины можно сравнивать, только если обе имеют один и тот же тип данных.
Как записывается символ «больше или равно» в Excel?
Символ «больше или равно» (>=) записывается в Excel путем ввода знака «больше» (>), за которым следует оператор «равно» (=).
Оператор «>=» помещается между двумя сравниваемыми числами или ссылками на ячейки. Например, введите формулу «=A1>=A2» в Excel.
Символ «>=» помещается в двойные кавычки при вводе в аргумент «критерии» функций СУММЕСЛИ и СЧЁТЕСЛИ. Например, введите формулу «=СУММЕСЛИ(B2:B11»>=100″)» в Excel.
Примечание: Две формулы Excel (в предыдущих примерах) следует вводить без пробелов и без начальных и конечных кавычек.
Рекомендуемые статьи
Это было руководство по «больше или равно» в Excel. Здесь мы обсудим, как использовать «больше чем» и «больше или равно» (>=) с формулами ЕСЛИ, СУММЕСЛИ и СЧЁТЕСЛИ, а также примеры и загружаемые шаблоны Excel. Вы также можете посмотреть на эти полезные функции в Excel —
«Не равно» в VBA
Формула Excel для СЧЁТЕСЛИ
Не равно в Excel
Список функций Excel
Как ☝️Использовать «Если больше» и «Меньше» 05 «Больше» 9 0 9 0 9 01081 9 Функция Than and Less Than
в Microsoft Excel — это логическая функция, которая возвращает одно значение, если условия выполняются, и другое значение, если условия не выполняются. Эта функция полезна для принятия решений на основе данных в электронной таблице.
Как использовать, если больше и меньше чем в Excel
Символы больше и меньше в Excel используются для сравнения двух значений. Если вы хотите узнать, больше или меньше число другого числа, вы можете использовать символы Больше ( > ) и Меньше ( < ).
Вы также можете использовать символ больше или равно , который представлен цифрой 9.0005 >= символов. Это вернет TRUE , если число, которое вы тестируете, больше или равно числу, с которым вы его сравниваете. Для меньше или равно используйте символы <= .
Вы также можете использовать символ Not Equal To , который представлен символами <> . Это вернет TRUE , если число, которое вы тестируете, не равно числу, с которым вы его сравниваете.
Вот несколько примеров использования этих символов в Excel.
Использование функции ИЛИ
Функция ИЛИ – это логическая функция в Excel, которая возвращает ИСТИНА , если любой из аргументов условия равен ИСТИНА и ЛОЖЬ , если все 900 6 ЛОЖЬ
аргументы равны
.
Давайте посмотрим, как настроить функцию ИЛИ с символами Больше и Меньше .
1. Нажмите на ячейку, где вам нужен результат.
2. Перейдите к строке Formula и введите =OR(A2<5, B2<5) . Здесь A2 и B2 — это ячейки с нашими значениями, а 5 — это число для условия, с которым вы сравниваете свои значения.
3. Нажмите клавишу Enter на клавиатуре.
4. Перетащите ячейку вниз, чтобы применить формулу к остальным ячейкам.
Ну вот!
Использование функции И
Функция И представляет собой логическую функцию, которая возвращает ИСТИНА , если все условия выполнены, и ЛОЖЬ , если какое-либо из условий не выполняется, даже если некоторые из них выполняются.
Чтобы использовать эту функцию, выполните следующие действия:
1. Выберите ячейку, в которой вы хотите получить результат.
2. В строке Formula введите =И(A2<10, B2<10) , где A2 и B2 — это ячейки с вашими значениями, а 10 — это условие, с которым вы сравниваете числа.
3. Нажмите клавишу Enter на клавиатуре.
4. Перетащите ячейку с формулой вниз через остальные ячейки, чтобы скопировать формулу в другие ячейки.
Вуаля! В этом примере вы эффективно использовали символов меньше .
Использование функции ЕСЛИ с символами больше или меньше
Функция ЕСЛИ в Excel — это логическая функция, которая используется для принятия решений. Функция проверяет, выполняется ли определенное условие, и если оно выполняется, то возвращает конкретное значение; в противном случае возвращается другое значение. Указанное вами условие сравнивается с вашими значениями с помощью оператора больше чем ( > ), меньше ( < ) или равно ( = ) символов.
Давайте погрузимся и посмотрим, как вы можете его использовать! Вот один из примеров функции ЕСЛИ с символами больше или меньше :
1. Щелкните ячейку, в которой вы хотите получить результат.
2. Перейдите к строке Формула и введите =ЕСЛИ(B2>3, «ИСТИНА», «ЛОЖЬ») . B2 — это ячейка с вашим значением, а 3 — это ваше состояние, с которым вы сравниваете свое значение. Если условие выполнено, оно покажет TRUE. Если условие не выполнено, оно покажет FALSE.
3. Нажмите Введите .
4. Скопируйте эту формулу в оставшиеся ячейки, перетащив начальную ячейку с формулой вниз через остальные.
Вот и результат!
ПРИМЕЧАНИЕ. Вы можете заменить термины «ИСТИНА» и «ЛОЖЬ» на любые, соответствующие вашим потребностям (например, «ДА» и «НЕТ»). Просто убедитесь, что в формуле заключены кавычки вокруг слов, которые вы хотите использовать.
Вы также можете опустить одно из значений в формуле, если хотите оставить ячейку пустой. См. пример ниже:
Использование функции СУММЕСЛИ
Функция СУММЕСЛИ в Excel используется для суммирования ячеек, соответствующих определенным критериям. Например, вы можете использовать функцию СУММЕСЛИ для суммирования всех ячеек в диапазоне, которые больше или меньше определенного значения.
1. Выберите ячейку, в которой вы хотите получить результат.
2. В строке Formula введите =СУММЕСЛИ(A2:A5, «>8», B2:B5) . Здесь A2:A5 и B2:B5 представляют диапазон ваших ячеек. 8 — условное число, с которым вы будете сравнивать значения.
3. Нажмите клавишу Enter на клавиатуре.
Здесь видно, что требование не выполнено, поэтому результат нулевой.
Использование функции СЧЁТЕСЛИ
Функция СЧЁТЕСЛИ в Excel — это логическая функция, которая определяет, сколько ячеек соответствует заданным вами критериям.
Давайте посмотрим, как это применить.
1. Выберите ячейку, в которой вы хотите получить результат.
2. Перейдите к строке Formula и введите =СЧЁТЕСЛИ(A2:B5,<>”) , где A2:B5 — это диапазон ячеек, к которым будет применяться формула.
3. Нажмите клавишу Enter .
4. Перетащите ячейку вниз, чтобы применить формулу к остальным ячейкам.
Полегче!
Символы больше и меньше в Excel используются для сравнения значений и возврата результата. Вы можете использовать эти символы, чтобы вычислить, больше или меньше значение, чем другое значение, или для сравнения двух диапазонов значений.
равно, не равно, больше, меньше
Многие задачи, выполняемые в Excel, включают сравнение данных в разных ячейках. Для этого в Microsoft Excel предусмотрено шесть логических операторов, которые также называются операторами сравнения. Этот учебник призван помочь вам понять суть логических операторов Excel и написать наиболее эффективные формулы для анализа данных.
Логические операторы Excel
Равен
Не равно
Больше / меньше / больше или равно / меньше или равно
Распространенное использование логических операторов в Excel
Логические операторы Excel — обзор
Логический оператор используется в Excel для сравнения двух значений. Логические операторы иногда называют булевыми операторами, потому что результат сравнения в любом конкретном случае может быть либо ИСТИНА, либо ЛОЖЬ.
В Excel доступно шесть логических операторов. В следующей таблице объясняется, что делает каждый из них, и иллюстрируется теория примерами формул.
Состояние Оператор Пример формулы Описание
Равен = =А1=В1 Формула возвращает значение ИСТИНА, если значение в ячейке A1 равно значению в ячейке B1; ЛОЖЬ в противном случае.
Не равно <> =А1<>В1 Формула возвращает значение ИСТИНА, если значение в ячейке A1 не равно значению в ячейке B1; ЛОЖЬ в противном случае.
Больше > =А1>В1 Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше, чем значение в ячейке B1; в противном случае возвращается ЛОЖЬ.
Менее < =А1<В1 Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше, чем в ячейке B1; ЛОЖЬ в противном случае.
Больше или равно >= =А1>=В1 Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.
Меньше или равно <= =А1<=В1 Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.
На приведенном ниже снимке экрана показаны результаты, возвращаемые логическими операторами Равно , Не равно , Больше и Меньше :
Может показаться, что приведенная выше таблица охватывает все, и говорить больше не о чем. о. Но на самом деле у каждого логического оператора есть свои особенности, и знание их может помочь вам использовать настоящую мощь формул Excel.
Использование логического оператора “Равно” в Excel
Логический оператор “Равно ” (=) может использоваться для сравнения всех типов данных – чисел, дат, текстовых значений, логических значений, а также результатов, возвращаемых другими приложениями Excel. формулы. Например:
=A1=B1 Возвращает ИСТИНА, если значения в ячейках A1 и B1 совпадают, в противном случае — ЛОЖЬ.
=A1=”апельсины” Возвращает ИСТИНА, если ячейки A1 содержат слово «апельсины», в противном случае — ЛОЖЬ.
=A1=ИСТИНА Возвращает ИСТИНА, если ячейки A1 содержат логическое значение ИСТИНА, в противном случае возвращает ЛОЖЬ.
=А1=(В1/2) Возвращает ИСТИНА, если число в ячейке A1 равно частному от деления B1 на 2, в противном случае — ЛОЖЬ.
Пример 1. Использование оператора “Равно” с датами
Возможно, вы удивитесь, узнав, что логический оператор “Равно ” не может сравнивать даты так же легко, как числа. Например, если в ячейках А1 и А2 указана дата «1.12.2014», формула =A1=A2 вернет TRUE, как и должно быть.
Однако, если вы попробуете либо =A1=12/1/2014 , либо =A1="12/1/2014" , вы получите ЛОЖЬ в результате. Немного неожиданно, а?
Дело в том, что Excel хранит даты как числа, начинающиеся с 1-янв-1900, что сохраняется как 1. Дата 1/12/2014 хранится как 41974. В приведенных выше формулах Microsoft Excel интерпретирует «12/1/ 2014″ как обычную текстовую строку, а так как “12. 01.2014″ не равно 41974, возвращает ЛОЖЬ.
Чтобы получить правильный результат, вы всегда должны заключать дату в функцию ДАТАЗНАЧ, например: =A1=ДАТАЗНАЧ("1/12/2014")
Примечание. Функцию DATEVALUE также необходимо использовать с другим логическим оператором, как показано в следующих примерах.
Тот же подход следует применять при использовании оператора равенства Excel в логической проверке функции ЕСЛИ. Вы можете найти больше информации, а также несколько примеров формул в этом руководстве: Использование функции Excel IF с датами.
Пример 2. Использование оператора “Равно” с текстовыми значениями
Использование оператора Excel “Равно ” с текстовыми значениями не требует никаких дополнительных поворотов. Единственное, что вы должны иметь в виду, это то, что логический оператор Equal to в Excel нечувствителен к регистру , что означает, что различия в регистре игнорируются при сравнении текстовых значений.
Например, если ячейка A1 содержит слово “ апельсинов “, а ячейка B1 содержит “ апельсинов “, формула =A1=B1 вернет ИСТИНА.
Если вы хотите сравнить текстовые значения с учетом их различия в регистре, вы должны использовать функцию EXACT вместо оператора равно . Синтаксис функция EXACT так же проста, как:
EXACT(text1, text2)
Где text 1 и text2 — это значения, которые вы хотите сравнить.Если значения совпадают, включая регистр, Excel возвращает TRUE, в противном случае он возвращает ЛОЖЬ. Вы также можете использовать функцию ТОЧНОЕ в формулах ЕСЛИ, когда вам нужно сравнение текстовых значений с учетом регистра, как показано на снимке экрана ниже:
Примечание. Если вы хотите сравнить длину двух текстовых значений, вы можете вместо этого использовать функцию ДЛСТР, например, =ДЛСТР(A2)=ДЛСТР(B2) или =ДЛСТР(A2)>=ДЛСТР(B2) .
Пример 3. Сравнение логических значений и чисел
Существует распространенное мнение, что в Microsoft Excel логическое значение ИСТИНА всегда равно 1, а ЛОЖЬ – 0. Однако это верно лишь отчасти, и ключевое слово здесь ” всегда” или точнее “не всегда” 🙂
При написании логического выражения “равно” для сравнения логического значения и числа необходимо специально указать для Excel, что нечисловое логическое значение должно рассматриваться как число. Вы можете сделать это, добавив двойной знак минус перед логическим значением или ссылкой на ячейку, например. грамм. =A2=--ИСТИНА или =A2=--B2 .
Знак минус 1 ^st, который технически называется унарным оператором, приводит ИСТИНА/ЛОЖЬ к -1/0 соответственно, а второй унарный инвертирует значения, превращая их в +1 и 0. Это, вероятно, будет проще чтобы понять глядя на следующий скриншот:
Примечание. Вы должны добавить двойной унарный оператор перед логическим значением при использовании других логических операторов, таких как не равно , больше или меньше , чтобы правильно сравнивать числовые и логические значения.
При использовании логических операторов в сложных формулах вам также может понадобиться добавить двойное унарное выражение перед каждым логическим выражением, которое возвращает ИСТИНА или ЛОЖЬ в качестве результата. Вот пример такой формулы: СУММПРОИЗВ и СУММЕСЛИМН в Excel.
Использование логического оператора «Не равно» в Excel
Вы используете оператор Excel Не равно (<>), когда хотите убедиться, что значение ячейки не равно указанному значению. Использование оператора Not equal to очень похоже на использование оператора Equal to , которое мы только что обсуждали.
Результаты, возвращаемые оператором Not equal to , аналогичны результатам, полученным функцией НЕ Excel, которая инвертирует значение своего аргумента. В следующей таблице приведены несколько примеров формул.
Не равно оператору функция НЕ Описание
=А1<>В1 = НЕ(А1=В1) Возвращает TRUE, если значения в ячейках A1 и B1 не совпадают, иначе FALSE.
=A1<>“апельсины” = НЕ(A1=”апельсины”) Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме «апельсинов», и ЛОЖЬ, если она содержит «апельсины», или «АПЕЛЬСИНЫ», или «апельсины» и т. д.
=A1<>ИСТИНА = НЕ (A1 = ИСТИНА) Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме ИСТИНА, в противном случае – ЛОЖЬ.
=А1<>(В1/2) = НЕ(А1=В1/2) Возвращает ИСТИНА, если число в ячейке A1 не равно частному от деления B1 на 2, в противном случае – ЛОЖЬ.
=A1<>ДАТАЗНАЧ(“1/12/2014”) = НЕ(A1=ДАТАЗНАЧ(“1/12/2014”)) Возвращает ИСТИНА, если A1 содержит какое-либо значение, кроме даты 1 декабря 2014 года, независимо от формата даты, в противном случае — ЛОЖЬ.
Больше, меньше, больше или равно, меньше или равно
Эти логические операторы используются в Excel для проверки сравнения одного числа с другим. Microsoft Excel предоставляет 4 операции сравнения, имена которых говорят сами за себя:
Больше, чем (>)
Больше или равно (>=)
Меньше чем (<)
Меньше или равно (<=)
Чаще всего операторы сравнения Excel используются с числами, значениями даты и времени. Например:
=А1>20 Возвращает ИСТИНА, если число в ячейке A1 больше 20, в противном случае — ЛОЖЬ.
=А1>=(В1/2) Возвращает ИСТИНА, если число в ячейке A1 больше или равно частному от деления B1 на 2, в противном случае — ЛОЖЬ.
=A1<ДАТАЗНАЧ("1/12/2014") Возвращает ИСТИНА, если дата в ячейке A1 меньше 1 декабря 2014 г., в противном случае — ЛОЖЬ.
=A1<=СУММ(B1:D1) Возвращает ИСТИНА, если число в ячейке A1 меньше или равно сумме значений в ячейках B1:D1, в противном случае — ЛОЖЬ.
Использование операторов сравнения Excel с текстовыми значениями
Теоретически вы также можете использовать операторы больше , больше или равно , а также их аналоги меньше с текстовыми значениями. Например, если ячейка A1 содержит « яблока », а ячейка B1 содержит « банана », угадайте, какая формула =A1>B1 вернется? Поздравляю тех, кто сделал ставку на ЛОЖЬ : )
При сравнении текстовых значений Microsoft Excel игнорирует их регистр и сравнивает значения посимвольно, при этом “a” считается наименьшим текстовым значением, а “z” – наибольшим текстовым значением.
Итак, при сравнении значений « яблок » (A1) и « бананов » (B1) Excel начинается с их первых букв «a» и «b» соответственно, а так как «b» больше чем “а”, формула =A1>B1 возвращает ЛОЖЬ.
Если первые буквы совпадают, то сравниваются 2 ^и буквы, если они тоже совпадают, то Excel попадает в 3 ^rd , 4 ^th буквы и так далее. Например, если A1 содержит “ яблока “, а B1 содержит “ агавы “, формула =A1>B1 вернет TRUE, поскольку “p” больше, чем “g”.
На первый взгляд кажется, что использование операторов сравнения с текстовыми значениями имеет очень мало практического смысла, но никогда не знаешь, что тебе может понадобиться в будущем, так что, возможно, эти знания кому-то пригодятся.
Обычное использование логических операторов в Excel
В реальной работе логические операторы Excel редко используются сами по себе. Согласитесь, булевы значения TRUE и FALSE, которые они возвращают, хоть и очень истинны (извините за каламбур), но не очень значимы. Чтобы получить более разумные результаты, вы можете использовать логические операторы как часть функций Excel или правил условного форматирования, как показано в приведенных ниже примерах.
1. Использование логических операторов в аргументах функций Excel
Что касается логических операторов, то Excel очень либерален и позволяет использовать их в параметрах многих функций. Одно из наиболее распространенных применений находится в функции ЕСЛИ в Excel, где операторы сравнения могут помочь построить логический тест, а формула ЕСЛИ вернет соответствующий результат в зависимости от того, оценивается ли тест как ИСТИНА или ЛОЖЬ. Например:
=ЕСЛИ(A1>=B1, "ОК", "Неверно")
Эта простая формула ЕСЛИ возвращает значение ОК, если значение в ячейке A1 больше или равно значению в ячейке B1, “Неверно ” в противном случае.
А вот еще пример:
=ЕСЛИ(A1<>B1, СУММ(A1:C1), "")
Формула сравнивает значения в ячейках A1 и B1, и если A1 не равно B1 , возвращается сумма значений в ячейках A1:C1, в противном случае — пустая строка.
Логические операторы Excel также широко используются в специальных функциях ЕСЛИ, таких как СУММЕСЛИ, СЧЁТЕСЛИ, СРЗНАЧЕСЛИ и их эквивалентах во множественном числе, которые возвращают результат на основе определенного условия или нескольких условий.
Вы можете найти множество примеров формул в следующих руководствах:
Использование функции ЕСЛИ в Excel
Как использовать СУММЕСЛИ в Excel
Excel СУММЕСЛИМН и СУММЕСЛИ с несколькими критериями
Использование СЧЁТЕСЛИ в Excel
Excel COUNTIFS и COUNTIF с несколькими критериями
2. Использование логических операторов Excel в математических расчетах
Конечно, функции Excel очень эффективны, но не всегда их нужно использовать для достижения желаемого результата. Например, результаты, возвращаемые следующими двумя формулами, идентичны:
Функция ЕСЛИ: =ЕСЛИ(B2>C2, B2*10, B2*5)
Формула с логическими операторами: =(B2>C2)*(B2*10)+(B2<=C2)* (B2*5)
Думаю, формулу ЕСЛИ легче интерпретировать, верно? Он говорит Excel умножить значение в ячейке B2 на 10, если B2 больше, чем C2, иначе значение в ячейке B1 умножается на 5.
Теперь давайте проанализируем, что формула 2 ^nd с больше, чем и меньше или равно логических операторов. Полезно знать, что в математических вычислениях Excel приравнивает логическое значение ИСТИНА к 1, а ЛОЖЬ к 0. Имея это в виду, давайте посмотрим, что на самом деле возвращает каждое из логических выражений.
Если значение в ячейке B2 больше, чем значение в C2, то выражение B2>C2 является ИСТИНА и, следовательно, равно 1. С другой стороны, B2<=C2 является ЛОЖЬ и равно 0. Итак, учитывая что B2>C2, наша формула претерпевает следующее преобразование:
Поскольку любое число, умноженное на ноль, дает ноль, мы можем отбросить вторую часть формулы после знака плюс. И поскольку любое число, умноженное на 1, является этим числом, наша сложная формула превращается в простую =B2*10, которая возвращает произведение умножения B2 на 10, что и делает приведенная выше формула ЕСЛИ: )
Очевидно, что если значение в ячейке B2 меньше, чем в C2, то выражение B2>C2 оценивается как FALSE (0), а B2<=C2 как TRUE (1), что означает, что произойдет обратное описанному выше.
3. Логические операторы в условном форматировании Excel
Логические операторы также часто используются в условном форматировании Excel, что позволяет быстро выделить наиболее важную информацию в электронной таблице.
Например, следующие простые правила выделяют выбранные ячейки или целые строки на вашем листе в зависимости от значения в столбце A:
Меньше (оранжевый): =A1<5
Больше (зеленый): =A1>20
Подробные пошаговые инструкции и примеры правил см. в следующих статьях. :
Формулы условного форматирования Excel
Как изменить цвет строки на основе значения ячейки
Два способа изменить цвет фона на основе значения ячейки
Как выделить каждую вторую строку в Excel
Как видите, использование логических операторов в Excel интуитивно понятно и просто. В следующей статье мы изучим азы логических функций Excel, которые позволяют выполнять более одного сравнения в формуле. Пожалуйста, оставайтесь с нами и спасибо за чтение!
Вас также может заинтересовать
Значение, символ, способы использования, примеры
Больше или равно означает, что значение больше или равно заданному пределу. Для любой переменной, сущности или выражения значение больше или равно не дает определенного значения. Вместо этого он указывает диапазон значений, которые больше или равны указанному элементу.
В этой статье мы увидим значение больше или равно с его символом, использованием, решенными примерами и часто задаваемыми вопросами
Узнайте также, как представлять дроби в числовой строке.
Что больше или равно в математике?
Больше или равно означает, что нечто больше или равно числу. Знак «≥» означает «больше или равно». Рассмотрим следующий сценарий. Термин y ≥ 19 обозначает значение y, которое больше или равно 19.
Больше или равно также может быть представлено на числовой прямой. Чтобы показать неравенства на числовой прямой, мы используем следующее:
Незакрашенные кружки используются для чисел, которые меньше или больше (< или >).
Закрытые кружки используются для чисел, которые меньше или равны или больше или равны (≤ или ≥).
Условие больше равно неприменимо для двух известных чисел. Мы никогда не можем сказать, что 13 ≥ 4, потому что мы знаем, что 13 > 4. Однако, если есть неизвестная переменная, скажем, v, и нам нужно узнать ее значение, то ≥ — это возможный случай. Мы можем сказать, что v ≥ 3 означает, что v больше 3, но есть вероятность, что это может быть 3.
Значение и символ больше или равно
В математике мы часто используем термины больше, меньше и равно для описания отношения между двумя математическими выражениями, переменными или объектами. Мы используем символы, чтобы изобразить случай, чтобы облегчить его понимание.
Рассмотрим две переменные a и b.
Если нам нужно сказать, что a больше, чем b, мы пишем a > b. С другой стороны, если нам нужно сказать, что а меньше у, мы пишем а < b. Точно так же мы можем показать, что a и b равны, написав a = b.
Иногда нам нужно показать два условия, например больше или равно. Как упоминалось выше, больше или равно означает, что что-либо либо больше, либо равно числу. Символ «≥» означает больше или равно.
Итак, если мы должны сказать, что x больше или равно y, мы пишем это как x ≥ y.
Узнайте о типах чисел здесь.
Использование
Знак больше или равно используется следующим образом:
Знак больше или равно в основном используется для обозначения неравенства между двумя объектами.
Задачи линейного программирования используют знак больше или равно для максимизации функций.
Как использовать больше или равно символу?
«Больше», «меньше», «больше или равно» и «меньше или равно» — четыре символа неравенства. Сокращенное обозначение для сравнения двух величин представлено символами неравенства. Предложение «9 больше 4», например, может быть записано как 9>4. Рассматривайте каждый знак как рот, который всегда будет глотать большее из двух сравниваемых чисел. Это эффективный метод запоминания того, какое число больше.
Чтобы лучше понять это, давайте рассмотрим пример, когда вы отправляетесь в отпуск. Ваше путешествие займет менее 20 дней. Мы используем знак < для неравенства «меньше чем». Кроме того, вам разрешено брать с собой в самолет только 1000 мл яблочного сока. Мы используем символ ≤ для таких неравенств, как «меньше или равно». Это противоположно больше или равно значению не больше или равно. Также необходимо упаковать не менее 3 пар одежды. Таким образом, мы можем использовать здесь знак больше или равно, то есть 3 ≥ одежды.
Прочтите эту статью о среднем арифметическом.
Решенные примеры больше или равно
Вот несколько решенных примеров больше или равно для подготовки к экзамену.
Решено Пример: Если x больше или равно 25, а y меньше или равно 40, то какое из следующих утверждений всегда верно?
x больше y
(y – x) больше 15
(y – x) меньше или равно 15
(x – y) больше или равно 65
Решение:
Давайте сначала запишем сравнение с оператором больше или равно.
x ≥ 25
y ≤ 40 или -y ≥ -40
Сложение обоих неравенств,
(x – y) ≥ 25 – 40
(x – y) ≥ -4y – 15 900 900 ≤ 15
Правильный ответ: 3.
Решено Пример: Каково решение квадрата х больше или равного 3? 92≥0 \)
$ (x – \sqrt{3}) (x +\sqrt{3}) ≥0 $
$ ⟹x∈(−∞,−\sqrt{3}]∪ [\sqrt{3},∞) $
Решено Пример: Найдите решение линейного неравенства. у ≥ 4х – 5 (1, 1) б. (2, 1) в. (3, 4) д. (3, 0)
Решение:
y ≥ 4x – 5
y – 4x ≥ – 5
Подставим вместо x и y значения из вариантов и проверим неравенство.
x = 1 , y = 1
y – 4x = 1 – 4(1) = -3 ≥ – 5
Следовательно, условие неравенства выполнено.
x = 2 , y = 1
y – 4x = 1 – 4(2) = -7 ≤ – 5
Следовательно, условие неравенства не выполняется.
x = 3 , y = 4
y – 4x = 3 – 4(4) = -13 ≤ – 5
Следовательно, условие неравенства не выполняется.
x = 3, y = 0
y – 4x = 0 – 4(3) = -12 ≤ – 5
Следовательно, условие неравенства не выполняется.
Следовательно, правильный вариант 1.
Надеюсь, что эта статья о больше или равно была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Больше или равно Часто задаваемые вопросы
В.1 Что означает этот символ ≥?
Ответ 1 Символ «≥» означает больше или равно. Больше или равно означает, что что-либо больше или равно числу.
В.2 Чему больше и равно?
Ответ 2 Больше или равно — это один из способов отображения неравенства в выражении. Как следует из названия, «больше или равно» означает, что что-то либо больше, либо равно числу. Символ «≥» означает больше или равно.
Q.3 Что такое использование больше или равно в математике?
Ответ 3 Иногда нам нужно показать два условия, например больше или равно. Больше или равно — это один из способов отображения неравенства в выражении. Он не дает нам фиксированного значения для какой-либо переменной, объекта или выражения. Он скорее определяет диапазон значения, которое больше или равно конкретному фиксированному объекту.
В.4 Как использовать больше или равно в примере?
Ответ 4 Допустим, вам нужно упаковать минимум 3 пары одежды. Таким образом, мы можем использовать здесь знак больше или равно, то есть 3 ≥ одежды.
В.5 Как научить ребенка лучше, чем меньше?
Ответ 5 Например, фраза «5 больше 2» может быть представлена как 5>2.

Символ Описание	Обозначение символов	Пример
Знак больше	>	8 > 4
Знак меньше	<	4< 8
Равно знаку	=	4 + 1 = 5
Не равно знаку	≠	5 + 2 ≠ 4 + 2

EXAMPLE	MEANING
$x\geq 7$	The inequality means that the value of x can be equal to 7 or any number greater than 7 such as 8, 20 и т. д.
$-1\geq x\geq3$	В данном примере это означает, что значение может быть равно 3 или -1 или любому числу от -1 до 3, например 0 и 1. Следовательно, мы можем сказать, что значение x включительно находится между -1 и 3.

EXAMPLE	MEANING
$x\leq 1$	The value of x can be equal to 1 or any number less than 1 such as 0, -1, – 5 и т. д. Это неравенство также означает, что наибольшее возможное число для x равно 1.
$-4\leq x\leq 4$	Это неравенство означает, что значение x должно лежать между -4 и 4, например -2, 0 и 1, включая -4 и 4.

Состояние	Оператор	Пример формулы	Описание
Равен	=	=А1=В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 равно значению в ячейке B1; ЛОЖЬ в противном случае.
Не равно	<>	=А1<>В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 не равно значению в ячейке B1; ЛОЖЬ в противном случае.
Больше	>	=А1>В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше, чем значение в ячейке B1; в противном случае возвращается ЛОЖЬ.
Менее	<	=А1<В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше, чем в ячейке B1; ЛОЖЬ в противном случае.
Больше или равно	>=	=А1>=В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.
Меньше или равно	<=	=А1<=В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.

=A1=B1	Возвращает ИСТИНА, если значения в ячейках A1 и B1 совпадают, в противном случае — ЛОЖЬ.
=A1=”апельсины”	Возвращает ИСТИНА, если ячейки A1 содержат слово «апельсины», в противном случае — ЛОЖЬ.
=A1=ИСТИНА	Возвращает ИСТИНА, если ячейки A1 содержат логическое значение ИСТИНА, в противном случае возвращает ЛОЖЬ.
=А1=(В1/2)	Возвращает ИСТИНА, если число в ячейке A1 равно частному от деления B1 на 2, в противном случае — ЛОЖЬ.

Не равно оператору	функция НЕ	Описание
=А1<>В1	= НЕ(А1=В1)	Возвращает TRUE, если значения в ячейках A1 и B1 не совпадают, иначе FALSE.
=A1<>“апельсины”	= НЕ(A1=”апельсины”)	Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме «апельсинов», и ЛОЖЬ, если она содержит «апельсины», или «АПЕЛЬСИНЫ», или «апельсины» и т. д.
=A1<>ИСТИНА	= НЕ (A1 = ИСТИНА)	Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме ИСТИНА, в противном случае – ЛОЖЬ.
=А1<>(В1/2)	= НЕ(А1=В1/2)	Возвращает ИСТИНА, если число в ячейке A1 не равно частному от деления B1 на 2, в противном случае – ЛОЖЬ.
=A1<>ДАТАЗНАЧ(“1/12/2014”)	= НЕ(A1=ДАТАЗНАЧ(“1/12/2014”))	Возвращает ИСТИНА, если A1 содержит какое-либо значение, кроме даты 1 декабря 2014 года, независимо от формата даты, в противном случае — ЛОЖЬ.

=А1>20	Возвращает ИСТИНА, если число в ячейке A1 больше 20, в противном случае — ЛОЖЬ.
=А1>=(В1/2)	Возвращает ИСТИНА, если число в ячейке A1 больше или равно частному от деления B1 на 2, в противном случае — ЛОЖЬ.
=A1<ДАТАЗНАЧ("1/12/2014")	Возвращает ИСТИНА, если дата в ячейке A1 меньше 1 декабря 2014 г., в противном случае — ЛОЖЬ.
=A1<=СУММ(B1:D1)	Возвращает ИСТИНА, если число в ячейке A1 меньше или равно сумме значений в ячейках B1:D1, в противном случае — ЛОЖЬ.

Метод интервалов – материалы для подготовки к ЕГЭ по Математике

Что означает знак больше или меньше. Какие знаки есть на клавиатуре. Какие часто используемые знаки есть на клавиатуре

Прямой ввод с экранной клавиатурой для конкретной страны

Какие часто используемые знаки есть на клавиатуре

Символы \\

\\ меньше или равно \\

ТЕМА: «Больше, меньше». | План-конспект занятия по математике (подготовительная группа) на тему:

Примеры по математике больше меньше или равно 1 класс распечатать: Attention Required!

Математические знаки и символы — Карточки и Задания для детей

Математические знаки и символы — Карточки распечатать и вырезать

Посчитай и поставь подходящие математические знаки

Поставь нужный знак — Больше, меньше, знак равенства, плюс или минус

Задания для детей — Раскрась, найди соседей, подбери знаки, составь примеры

Задания на математическое сравнение количества предметов

Веселые задания на сравнение с героями мультфильмов

Задачи для детей на сравнение — Больше и меньше

Составь примеры с математическими знаками по картинкам

Изучаем математические знаки — плюс, минус и знак равенства

Таблица математических знаков (символов): значения, распечатать

Математика 1 класс «Знаки больше, меньше, равно»

Слайды и текст этой онлайн презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25

Слайд 26

Слайд 27

Слайд 28

Слайд 29

Слайд 30

Слайд 31

Слайд 32

Слайд 33

Слайд 34

Знаки: «>» больше, «

Конспект урока «Знаки > (больше),

больше, меньше, равно», 1 класс

Урок 11. равенство. неравенство. знаки «>», «

Больше, чем меньше, чем Рабочий лист

Больше, чем Листы

, ≤, ≥ — Сделано легко

Описание

Стенограмма

Использование неравенства

Сводка по неравенствам — Представьте себе рот

Символы неравенства:

Объясните символы неравенства.

Найдите символ, который правильно описывает отношения.

Определите соответствующее математическое неравенство, соответствующее числовой прямой.

Изучите неравенство по разным задачам со словами.

Решите, какой символ неравенства использовать.

Определите соответствующее неравенство.

Номера для сравнения и заказа — Рабочие листы

Сравнение и номера для заказа

Дроби, деньги, десятичные сравнения

Математика аллигатора (больше, меньше и равно)

Сводка

Материалы

Фон для учителей