Как определить четная или нечетная: Чётные и нечётные функции — урок. Алгебра, 9 класс.
Четность и нечетность функции | Онлайн калькулятор
Данный калькулятор предназначен для определения четности и нечетности функции онлайн. Четность и нечетность функции определяет ее симметрию.
Функция y=f(x) является четной, если для любого значения x∈X выполняется следующее равенство: f(-x)=f(x). Область определения четной функции должна быть симметрична относительно ноля. Если точка b принадлежит области определения четной функции, то точка –b также принадлежит данной области определения. График четной функции также будет симметричен относительно центра координат.
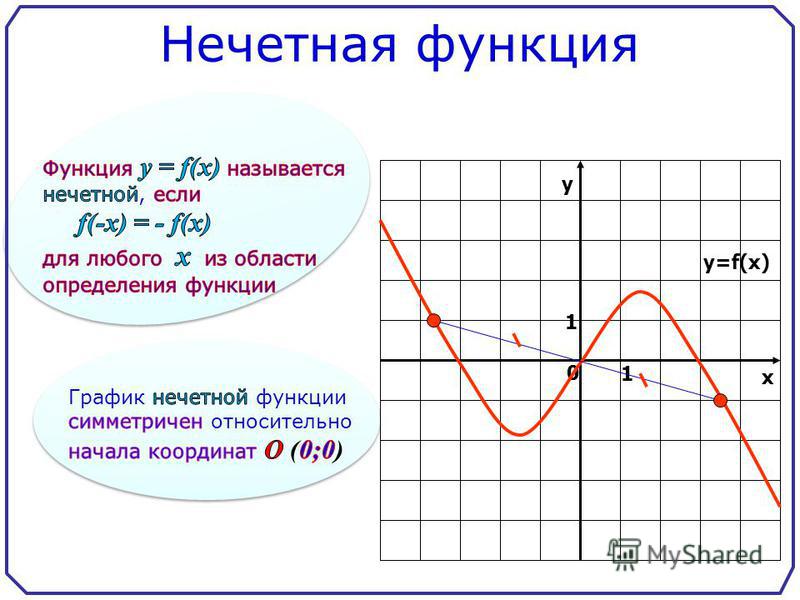
Нечетной называется функция y=f(x) при условии выполнения равенства f(-x)=-f(x).
x
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
Скачать калькулятор
Select rating12345
Рейтинг: 3.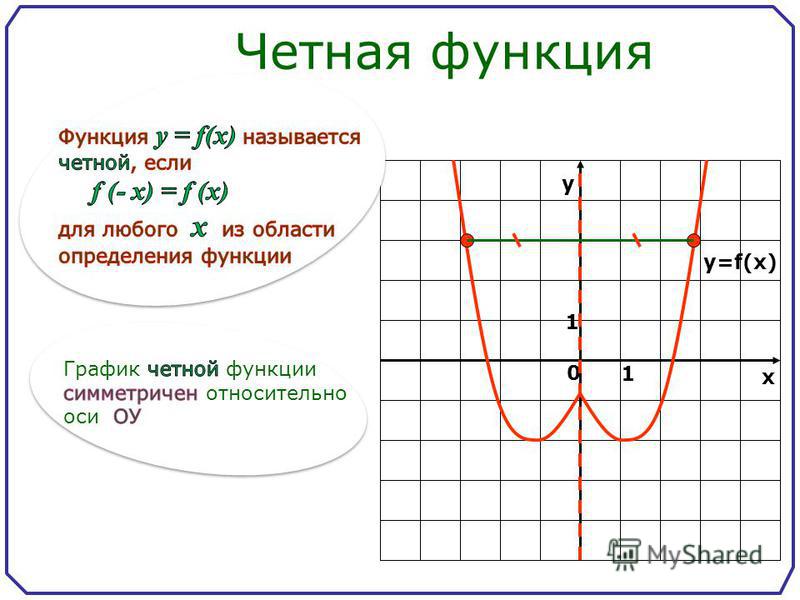
1 (Голосов 111)
Сообщить об ошибке
Смотрите также
Четные и нечетные функции
Цели:
- сформировать понятие чётности и нечётности функции, учить умению определять и использовать эти свойства при исследовании функций, построении графиков;
- развивать творческую активность учащихся, логическое мышление, умение сравнивать, обобщать;
- воспитывать трудолюбие, математическую культуру; развивать коммуникативные качества.
Оборудование: мультимедийная установка, интерактивная доска, раздаточный материал.
Формы работы: фронтальная и групповая с элементами поисково-исследовательской деятельности.
Информационные источники:
1.Алгебра9класс А.Г Мордкович. Учебник.
2.Алгебра 9класс А.Г Мордкович. Задачник.
3.
Алгебра 9 класс. Задания для обучения и развития учащихся. Беленкова Е.Ю. Лебединцева Е.А
ХОД УРОКА
1. Организационный момент
Постановка целей и задач урока.
2. Проверка домашнего задания
№10.17 (Задачник 9кл. А.Г. Мордкович).
а) у = f(х), f(х) =
б) f (–2) = –3; f (0) = –1; f(5) = 69;
в) 1. D(f) = [– 2; + ∞)
2. Е(f) = [– 3; + ∞)
3. f(х) = 0 при х ~ 0,4
4. f(х) >0 при х > 0,4 ; f(х)
< 0 при – 2 < х < 0,4.
5. Функция возрастает при х € [– 2; + ∞)
6. Функция ограничена снизу.
7. унаим = – 3, унаиб не
существует
8. Функция непрерывна.
(Вы использовали алгоритм исследования
функции?) Слайд.
2. Таблицу, которую вам задавалась, проверим по слайду.
| Заполните таблицу | |||||
Функция |
Область определения |
Нули функции |
Промежутки знакопостоянства |
Координаты точек пересечения графика с Оу | |
у > 0 |
у < 0 |
||||
х ≠ –3 |
х = –5, |
х € (–5;3) U |
х € (–∞;–5) U |
( 0;) |
|
х ∞ –5, |
х = –3 |
х € (–5;3) U |
х € (–∞;–5) U |
( 0;) |
|
х ≠ –5, |
нет |
х € (–∞; –5) U U (2; ∞) |
х € (–5; 2) |
( 0;) |
|
3.
Актуализация знаний
– Даны функции.
– Указать область определения для каждой
функции.
– Сравнить значение каждой функции для каждой
пары значения аргумента: 1 и – 1; 2 и – 2.
– Для каких из данных функций в области
определения выполняются равенства f(– х)
= f(х), f(– х) = – f(х)? (полученные
данные занести в таблицу) Слайд
D (f) |
f |
f(2) и f(– 2) | графики | f(– х) = –f(х) | f(– х) = f(х) | |
| 1. f(х) = | R |
2 и 2 |
Г |
|
+ |
|
2. f(х) = х3 |
R |
1 и 1 |
8 и – 8 |
А |
+ |
|
| 3. f(х) = | х | | R |
1 и – 1 |
2 и 2 |
Б |
|
+ |
| 4. f(х) = 2х – 3 | R |
– 1 и – 5 |
1 и – 7 |
Е |
|
|
5. f(х) = |
х ≠ 0 |
6 и – 6 |
3 и – 3 |
В |
+ |
|
| 6. f(х)= | х > –1 | и 0 |
и не опред. |
З |
|
|
4. Новый материал
– Выполняя данную работу, ребята мы выявили ещё
одно свойство функции, незнакомое вам, но не
менее важное, чем остальные – это чётность и
нечетность функции. Запишите тему урока: «Чётные
и нечётные функции», наша задача – научиться
определять чётность и нечётность функции,
выяснить значимость этого свойства в
исследовании функций и построении графиков.
Итак, найдём определения в учебнике и прочитаем (стр. 110). Слайд
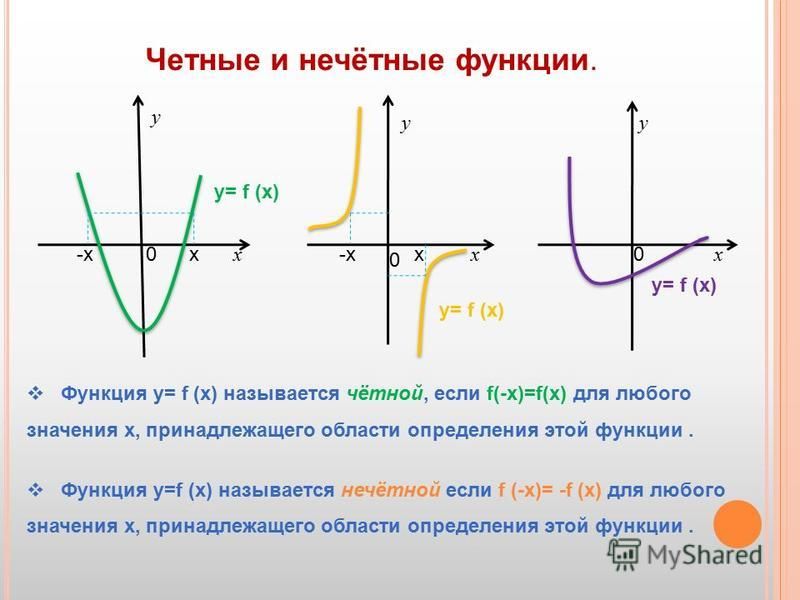
Опр. 1 Функция у = f (х), заданная на множестве Х называется чётной, если для любого значения х Є Х выполняется равенство f(–х)= f(х). Приведите примеры.
Опр. 2 Функция у = f (х), заданная на множестве Х называется нечётной, если для любого значения х Є Х выполняется равенство f(–х)= –f(х). Приведите примеры.
Где мы встречались с терминами «четные» и
«нечётные»?
Какие из данных функций будут чётными, как вы
думаете? Почему? Какие нечётными? Почему?
Для любой функции вида у = хn, где n
– целое число можно утверждать, что функция
нечётна при n – нечётном и функция чётна при n
– чётном.
к. не выполняются
равенства f(– х) = – f(х), f(–
х) = f(х)Изучение вопроса о том, является ли функция чётной или нечётной называют исследованием функции на чётность. Слайд
В определениях 1 и 2 шла речь о значениях функции при х и – х, тем самым предполагается, что функция определена и при значении х, и при – х.
Опр 3. Если числовое множество вместе с каждым своим элементом х содержит и противоположный элемент –х, то множество Х называют симметричным множеством.
Примеры:
(–2;2), [–5;5]; (∞;∞) – симметричные множества, а [0; ∞), (2;–2], [–5;4] – несимметричные.
– У чётных функций область определения –
симметричное множество? У нечётных?
– Если же D(f) – несимметричное множество, то
функция какая?
– Таким образом, если функция у = f(х)
– чётная или нечётная, то её область определения
D(f) – симметричное множество.
А верно ли
обратное утверждение, если область определения
функции симметричное множество, то она чётна,
либо нечётна?
– Значит наличие симметричного множества
области определения – это необходимое условие,
но недостаточное.
– Так как же исследовать функцию на четность?
Давайте попробуем составить алгоритм.
Слайд
Алгоритм исследования функции на чётность
1. Установить, симметрична ли область определения функции. Если нет, то функция не является ни чётной, ни нечётной. Если да, то перейти к шагу 2 алгоритма.
2. Составить выражение для f(– х).
3. Сравнить f(– х).и f(х):
- если f(– х).= f(х), то функция чётная;
- если f(– х).= – f(х), то функция нечётная;
- если f(– х) ≠ f(х) и f(–
х) ≠ –f(х), то функция не является ни
чётной, ни нечётной.
Примеры:
Исследовать на чётность функцию а) у = х5 +; б) у = ; в) у= .
Решение.
а) h(х) = х5 +,
1) D(h) = (–∞; 0) U (0; +∞), симметричное множество.
2) h (– х) = (–х)5 + – х5 –= – (х5 +),
3) h(– х) = – h (х) => функция h(х) = х5 + нечётная.
б) у = ,
у = f(х), D(f) = (–∞; –9)? (–9; +∞), несимметричное множество, значит функция ни чётная, ни нечётная.
в) f(х) = , у = f (х),
1) D(f) = (–∞; 3] ≠ [3; +∞), симметричное множество.
2)f (– х) == ;
3) f (– х) = f (х) => функция f(х) = чётная.
Итак, по аналитической записи можно определить
четность функции? Но кроме аналитического
способа задания функции есть другие.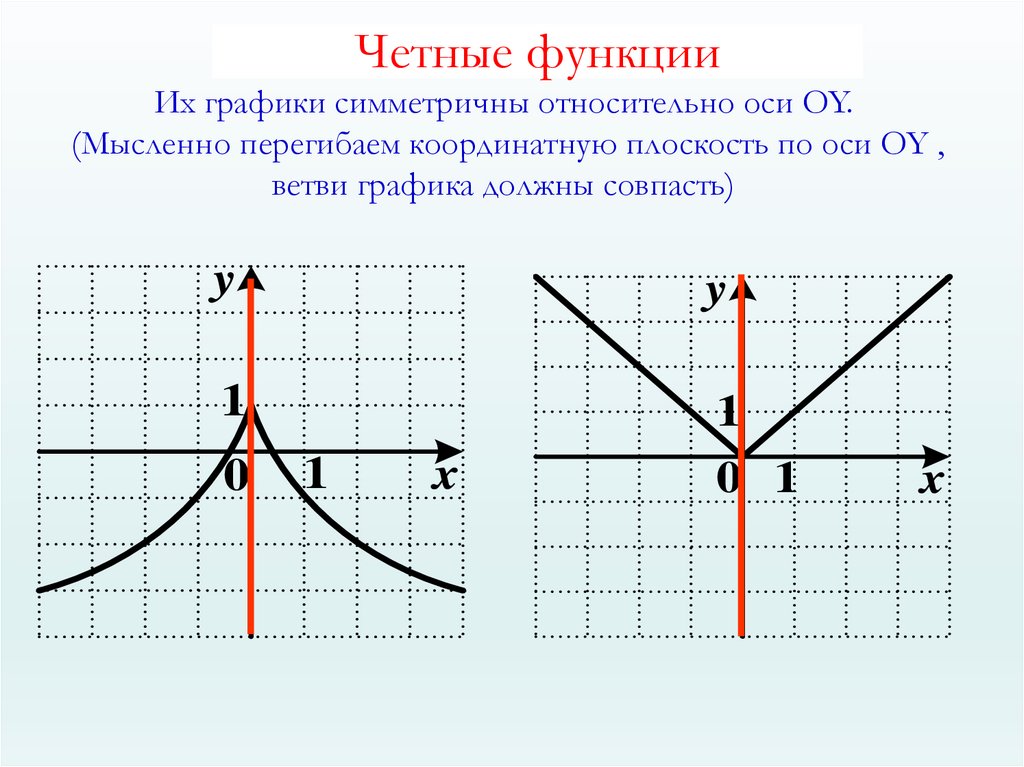
Какие? Можно
ли по графику функции выявить её четность?
Давайте вернёмся к заданию, которое мы выполняли
в начале урока, найдём соответствие между
аналитически заданными функциями и их
графиками (изображёнными на доске), что вы
находите примечательного в расположении
графиков чётных функций? Нечётных?
Слайд.
Вывод:
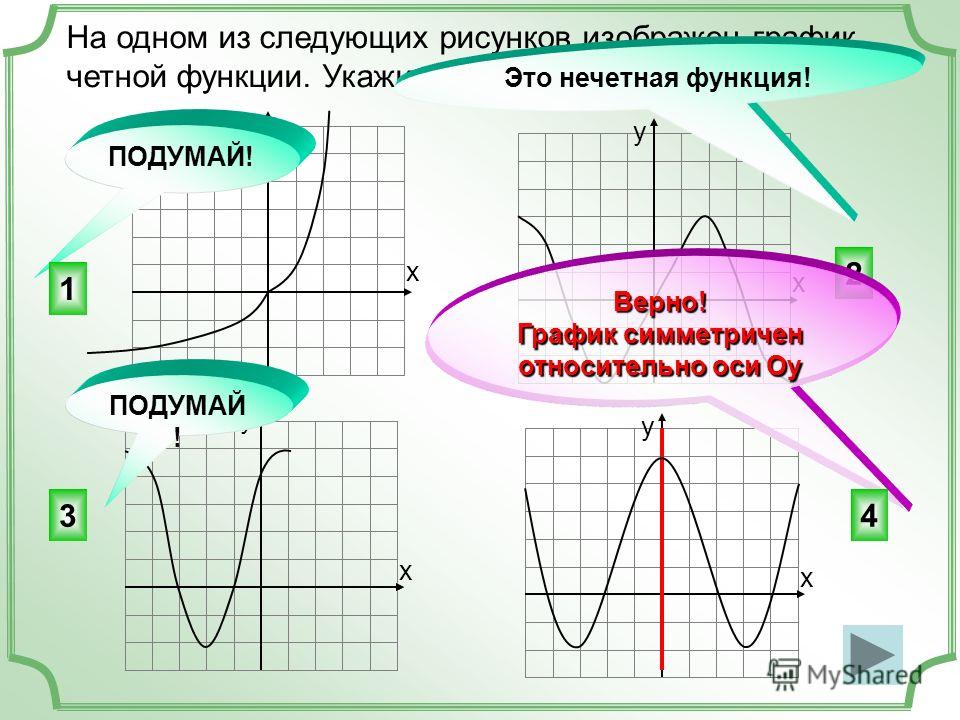
- График чётной функции симметричен относительно оси у.
- График нечётной функции симметричен относительно начала координат.
– Верны ли обратные утверждения?
- Если график функции у = f(х) симметричен относительно оси ординат, то у = f(х) – чётная функция.
- Если график функции у = f(х) симметричен
относительно начала координат, то у = f(х)
– нечётная функция.
Доказательство данных утверждений разобрать дома самостоятельно по учебнику и записать в тетрадь.
– Какова же значимость свойства четности или
нечётности функции? Зачем нужно изучать
свойство чётности функций .В план свойств
функций свойство чётности вы поставили бы на
какое порядковое место
5. Первичное закрепление
Самостоятельная работа
Вариант 1 1. Является ли симметричным заданное множество: а) [–7;7]; б) (∞; –2), (–4; 4]? |
Вариант 2 1. Является ли симметричным заданное множество: а) [–2;2]; б) (∞; 0], (0; 7) ? |
| 2. Исследуйте на чётность функцию: а); б) у = х· (5 – х2).  |
2. Исследуйте на чётность функцию: а) у = х2 · (2х – х3), б) у = |
| 3. На рис. построен график у = f(х),
для всех х, удовлетворяющих условию х?
0. Постройте график функции у = f(х), если у = f(х) – чётная функция.
|
3. На рис. построен график у = f(х),
для всех х, удовлетворяющих условию х ? 0. Постройте график функции у = f(х), если у = f(х) – нечётная функция.
|
Взаимопроверка по слайду.
6. Задание на дом: №11.11, 11.21,11.22;
Доказательство геометрического смысла
свойства чётности.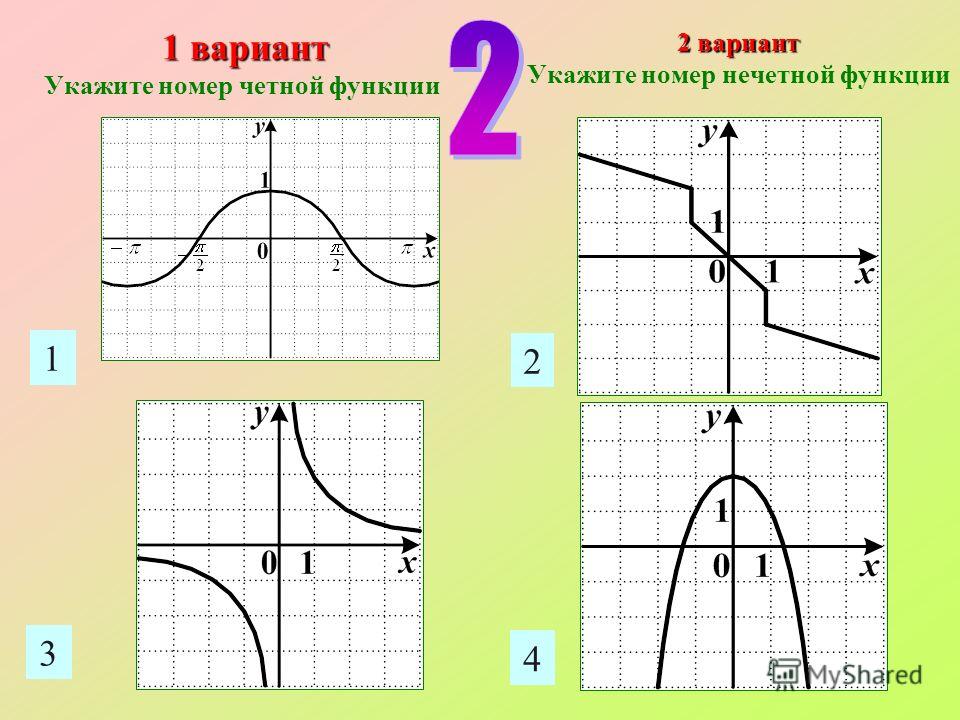
***(Задание варианта ЕГЭ ).
1. Нечётная функция у = f(х) определена на всей числовой прямой. Для всякого неотрицательного значения переменной х значение этой функции совпадает со значением функции g(х) = х(х + 1)(х + 3)(х – 7). Найдите значение функции h(х) = при х = 3.
7. Подведение итогов
Приложения
Как определить, является ли функция четной или нечетной? [Решено]
Функция определяется как изменение выходного значения по отношению к входному, где выходная переменная зависит от входной переменной.
Ответ: Для четной функции f(-x) = f(x) для всех x, для нечетной функции f(-x) = -f(x) для всех x. Если f(x) ≠ f(-x) и -f(x) ≠ f(-x) для некоторых значений x, то f не является ни четным, ни нечетным.
Давайте разберемся с решением.
Объяснение:
(а) Давайте разберемся с четными функциями.
Если заданная функция симметрична относительно оси Y, она называется четной функцией.
Функция четная, если f(x) = f(−x) для всех значений x
Для четной функции f(x), если мы подставим −x вместо x, тогда значение f( −x) равно значению f(x).
Таким образом, формула для проверки четности функции выглядит следующим образом:
f(x) = f(−x)
Давайте рассмотрим пример, чтобы понять четные функции.
Пример: f(x) = x 2
f(-x) = (-x) 2 = x 2
Таким образом, мы видим, что f(x) = f(-x)
Следовательно, заданная функция f(x) = x 2 является четной функцией.
Проверим графически.
Мы видим, что график y = x 2 симметричен относительно оси y и, следовательно, является четной функцией.
(b) Рассмотрим нечетные функции:
Функция, в которой одна сторона оси X инвертирована по знаку по отношению к другой стороне или графически симметрична относительно начала координат, называется нечетной функцией.
Функция является нечетной, если f(-x) = – f(x) для всех значений x
Для нечетной функции f(x), если мы подставим −x вместо x, тогда значение f (−x) равно значению – f(x).
Таким образом, формула для проверки нечетности функции имеет следующий вид:
f(-x) = – f(x)
Давайте рассмотрим пример, чтобы понять нечетные функции.
Пример: f(x) = x 3
f(-x) = (-x) 3 = – x 3
Кроме того, – f(x) = – x 3
Таким образом, f(x) = x 3 является нечетной функцией, поскольку f(-x) = – f(x).
Проверим графически.
График выглядит симметричным относительно начала координат, поэтому это нечетная функция.
(c) Давайте разберемся с функцией, которая не является ни четной, ни нечетной
Функция f(x), в которой f(x) ≠ f(−x) и −f(x) ≠ f(−x) для любого значение x не является ни четной, ни нечетной функцией.
Графически эти функции не симметричны ни относительно начала координат, ни относительно оси Y.
Давайте рассмотрим пример, чтобы понять это.
Пример: f(x) = 2x 5 + 3x 2 + 1
f(-x) = – 2x 5 + 3x 2 = + 1
– 90 5 – 3x 2 – 1
Таким образом, мы видим, что f(x) ≠ f(−x) и −f(x) ≠ f(−x) для заданной функции. Следовательно, это ни четная, ни нечетная функция.
Посмотрим на график этой функции.
Мы видим, что график не симметричен ни относительно начала координат, ни относительно оси Y. Таким образом, это не четная и не нечетная функция.
Итак, мы поняли про четные, нечетные и ни четные, ни нечетные функции.
Определение четных и нечетных функций (видео)
Когда мы думаем о «четных и нечетных», обычно на ум приходят четные и нечетные числа. Но что такое четные и нечетные функции? В сегодняшнем видео мы определим четные и нечетные функции и обсудим, как их идентифицировать.
Начнем с четных функций. Если функция \(f(x)\), вычисленная в \(-x\), дает нам то же самое \(f(x)\), с которого мы начали, эта функция четна.
Официально написано, когда 9{2}+1\). Обратите внимание, что он по-прежнему имеет ту же форму и по-прежнему является четной функцией. Он только что был перемещен на одну единицу вверх по координатной плоскости.
Теперь давайте поговорим о том, на что похожи нечетные функции. Рассмотрим другую функцию \(f(x)\), которую мы снова будем вычислять в \(-x\). Но на этот раз вместо поиска того же \(f(x)\), с которого мы начали, мы хотим посмотреть, меняет ли \(f(-x)\) знак всех членов функции. Другими словами, если \(f(-x)=-f(x)\), то функция 9{3}\)
Итак, если вы заметили, \(f(x)\) противоположно \(f(-x)\). Каждое слагаемое, которое в данном случае у нас только одно, меняется с положительного на отрицательное. Значит, эта функция нечетная.
Обратите внимание: если бы мы добавили к этой функции константу, она перестала бы быть нечетной. Помните, что для нечетных функций каждый член должен менять знак при вычислении в \(-x\). Этот постоянный член не мог бы изменить знак, и мы бы увидели на графике, что функция больше не проходит через начало координат.
{2}+1\) по-прежнему четная. Как видите, четная функция будет иметь четные степени .
Неудивительно, что нечетных функций также будут иметь нечетные показатели степени ! Помните, что для того, чтобы функция была нечетной, все члены должны менять знак, когда мы вычисляем \(-x\).
Ясно, что любой член с \(x\) в первой степени изменит знак, когда мы подставим отрицательное значение \(x\). Таким же образом \(x\) в третьей степени, в пятой степени и т. д. все меняют знак, когда мы подставляем отрицательное значение для \(x\). Как мы упоминали ранее, когда член имеет четную степень \(x\), он не меняет знак. Это означает, что нечетная функция не может содержать членов с четными степенями \(x\) и не может иметь констант.
Вы сможете распознавать четные и нечетные функции позже в исчислении, когда дело дойдет до разложения Тейлора.
Время для некоторых практических задач!
Основываясь на этом графике, определите, является ли эта функция четной, нечетной или ни одной?
Ни то, ни другое.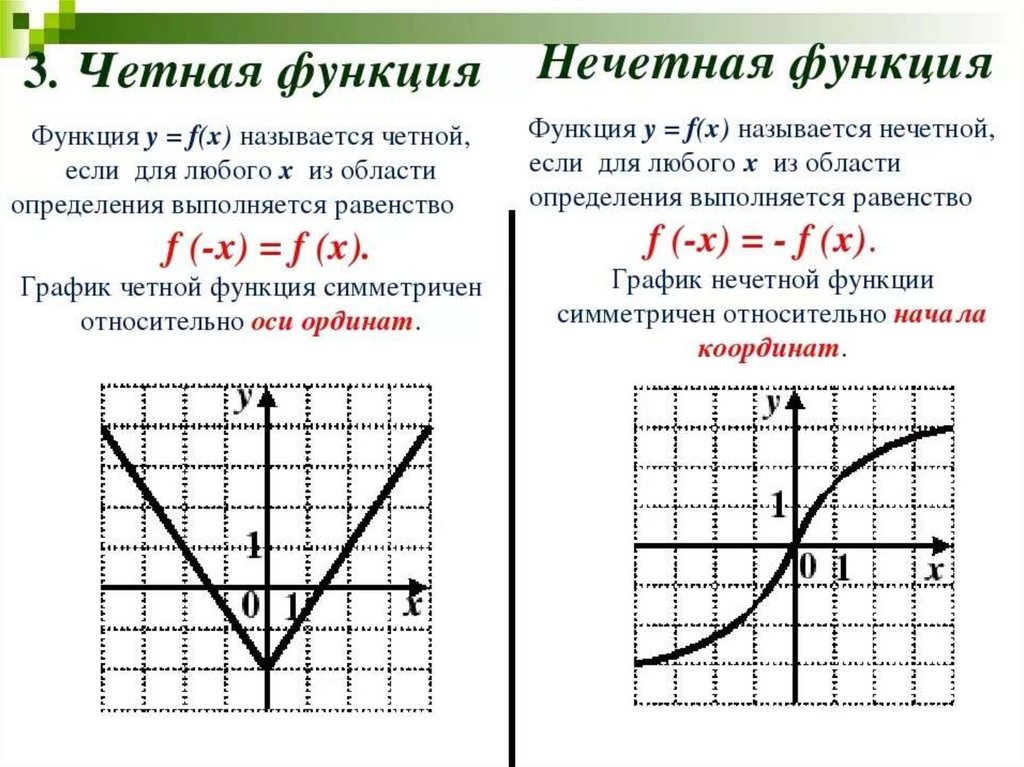
Эта функция не симметрична относительно оси \(y\), поэтому она не является четной. И хотя он проходит через начало координат, он не является странным, потому что он не выглядел бы таким же, если бы мы повернули изображение на 180°.
Давайте закончим более концептуальным вопросом.
Мы знаем, что некоторые функции могут быть ни четными, ни нечетными, но может ли функция быть и четной, и нечетной?
Удивительно, но ответ положительный, но только для одной функции. Вы представляете, что это за функция? Помните, что для четных функций \(f(-x)=f(x)\), а для нечетных функций \(f(-x)=-f(x)\). Единственный способ удовлетворить оба этих требования — это когда \(f(x)=0\).
\(f(-x)=f(x)\)
\(и\)
\(f(-x)=-f(x)\)
В качестве краткого обзора, мы можем определить четные и нечетные функции следующим образом:
Графически четные функции симметричны относительно оси \(y\).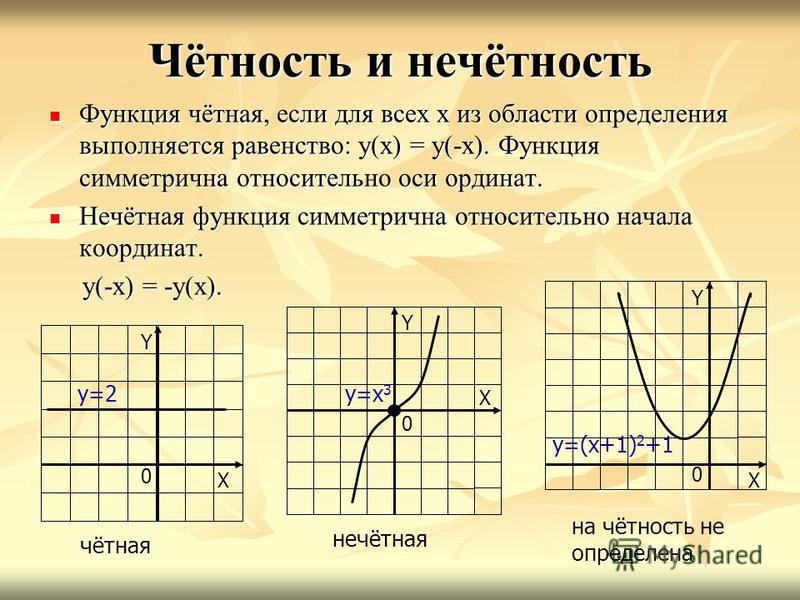
И они не должны проходить через источник. Однако нечетные функции должны проходить через начало координат, и они будут выглядеть одинаково при повороте на 180°.
Алгебраически четные функции одинаковы, когда мы оцениваем в точках \(+x\) и \(-x\). Нечетные функции будут менять знаки во всех терминах при оценке в \(-x\).
Короче говоря, если функция содержит только четные показатели степени \(x\) (и может иметь или не иметь константы), то она четная. Если функция не имеет констант и имеет только нечетные показатели \(х\), то она нечетная.
Теперь, когда мы рассмотрели все и пробежались по некоторым примерам, вам должно быть достаточно удобно определять четные и нечетные функции.
Спасибо за просмотр и удачной учебы!
Вопрос №1:
График функции \(y=f(x)\) показан на координатной плоскости ниже.
Основываясь на графике, какое из следующих утверждений верно?
Функция четная.
Нечетная функция.
Функция не является ни четной, ни нечетной функцией.
Функция одновременно четная и нечетная.
Показать Ответ
Ответ:
График функции является четным, если он имеет симметрию относительно оси \(y\). График будет отражаться относительно оси \(y\). Другими словами, отражение части графика функции, лежащей справа от оси \(у\), дает часть графика, лежащую на левой стороне оси \(у\). Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,y)\), которая также находится на графике функции. Ниже приведен график функции и ее отражение относительно оси \(y\), показанное красным цветом.
Обратите внимание, что отраженный график \(y=f(x)\) относительно оси \(y\) дает совершенно другой график. Таким образом, график \(y=f(x)\) не имеет симметрии относительно оси \(y\), поэтому он не является четной функцией.
График функции является нечетным, если он имеет симметрию относительно начала координат.
График будет таким же, если его повернуть на 180° вокруг начала координат. Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,-y)\), которая также находится на графике функции. Ниже приведен график функции и ее отражение относительно начала координат, показанное красным цветом.
Обратите внимание, что отраженный график \(y=f(x)\) относительно начала координат дает совершенно другой график. Таким образом, график \(y=f(x)\) не имеет симметрии относительно начала координат, поэтому не является нечетной функцией. Кроме того, еще одно условие, которое следует учитывать при определении того, является ли график функции нечетным, заключается в том, что он должен проходить через начало координат.
Следовательно, график \(y=f(x)\) не является ни четной, ни нечетной функцией.
Скрыть ответ
Вопрос №2: 93\)?
Функция четная.
Нечетная функция.
Функция не является ни четной, ни нечетной функцией.
Функция одновременно четная и нечетная.
Показать ответ
Ответ:
Функция \(y=f(x)\) является четной функцией при замене значения \(x\) в функции на \(-x\) не меняет значения функции. То есть \(y=f\left(-x\right)=f(x)\). Заменяя \(x\) на \(-x\) для нашей функции и упрощая, мы получаем: 93\right)=-f(x)\)
Так как \(f\left(-x\right)=-f(x)\), значение функции меняет знак при замене на \(-x \), поэтому функция не является четной.
Функция \(y=f(x)\) является нечетной функцией, когда замена значения \(x\) в функции на \(-x\) изменяет значение функции. То есть \(y=f\left(-x\right)=-f(x)\). Как мы видели выше, замена \(x\) на \(-x\) для нашей функции дает \(f\left(-x\right)=-f(x)\), поэтому наша функция является нечетной функцией . 92+1\)?
Функция четная.
Нечетная функция.
Функция не является ни четной, ни нечетной функцией.
Функция одновременно четная и нечетная.
Показать ответ
Ответ:
Функция \(y=f(x)\) является четной функцией при замене значения \(x\) в функции на \(-x\) не меняет значения функции. То есть \(y=f\left(-x\right)=f(x)\). Заменяя \(x\) на \(-x\) для нашей функции и упрощая, мы получаем: 92+1=f(x)\)
Так как \(f\left(-x\right)=f(x)\), значение функции не меняет знак при замене на \(-x\ ), поэтому функция является четной функцией.
Функция \(y=f(x)\) является нечетной функцией, когда замена значения \(x\) в функции на \(-x\) изменяет значение функции. То есть \(y=f\left(-x\right)=-f(x)\). Как мы видели выше, замена \(x\) на \(-x\) для нашей функции дает \(f\left(-x\right)=f(x)\), поэтому наша функция не является нечетной функцией .
Таким образом, функция является только четной функцией.
Скрыть ответ
Вопрос № 4:
Фотография поперечного сечения чашеобразной рампы для скейтборда, сделанная в скейтпарке, показана на координатной плоскости ниже.
Пусть поперечное сечение криволинейной формы пандуса есть функция \(y=f(x)\).
Если мы смотрим на дно чашеобразного пандуса, какое из следующих утверждений о графике функции, представляющей поперечное сечение пандуса, кажется верным?
Функция четная.
Нечетная функция.
Функция не является ни четной, ни нечетной функцией.
Функция одновременно четная и нечетная.
Показать Ответ
Ответ:
График функции является четным, если он имеет симметрию относительно оси \(y\). График будет отражаться относительно оси \(y\). Отражение части графика функции, лежащей справа от оси \(у\), дает часть графика, лежащую слева от оси \(у\). Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,y)\), которая также находится на графике функции. Ниже приведен график рампы и ее отражения относительно оси \(y\).
Обратите внимание, что отражение стороны графика справа от оси \(y\) относительно оси \(y\) дает часть наклона, которая находится слева от \(y\) )-ось.
Одна такая точка на графике рампы подтверждает это, и это верно для всех точек на графике рампы. Таким образом, график функции \(y=f(x)\), представляющий рампу конька, имеет симметрию относительно оси \(y\), поэтому это четная функция.
График функции является нечетным, если он имеет симметрию относительно начала координат. График будет таким же, если его повернуть на 180° вокруг начала координат. Это означает, что любая точка \((x,y)\) на графике функции отражает точку \((-x,-y)\), которая также находится на графике функции. Ниже приведен график рампы и ее отражения относительно начала координат.
Обратите внимание, что отраженный график рампы вокруг начала координат дает совершенно другой график. Таким образом, график рампы не имеет симметрии относительно начала координат, поэтому не является нечетной функцией.
Таким образом, график \(y=f(x)\), представляющий рампу для коньков, является только четной функцией.
Скрыть ответ
Вопрос № 5:
Радиоволны — это электромагнитные волны, которые распространяются со скоростью света или близкой к ней.
Существует много типов радиоволн, встречающихся в природе, таких как световые волны, и те, которые искусственно генерируются машинами. Одна такая искусственная волна, называемая радиоволной FM (частотная модуляция), передает несущий сигнал от радиостанции, которая передает информацию на антенну вашего радиоприемника, в которой амплитуда несущего сигнала постоянна, но частота модулируется или изменяется. Ниже приведен пример 2 циклов или периодов модулированной несущей FM.
Согласно графику сигнала, FM-радиоволна:
Четная функция
Нечетная функция
Ни четная, ни нечетная функция
И четная, и нечетная функция
Показать ответ
Ответ:
График функции является четным, если он имеет симметрию относительно оси \(y\). График будет отражаться относительно оси \(y\). Отражение части графика функции, лежащей справа от оси \(у\), дает часть графика, лежащую слева от оси \(у\).