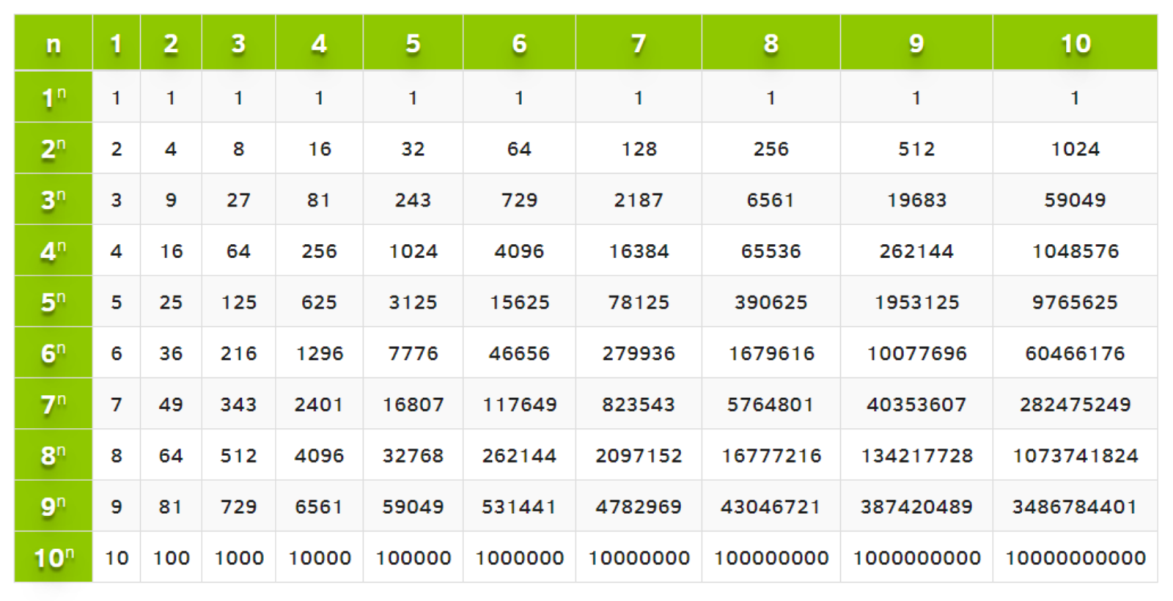
Как быстро выучить таблицу квадратов: Квадраты чисел. Легкий способ вычисления
Быстрое возведение чисел от 1 до 100 в квадрат
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
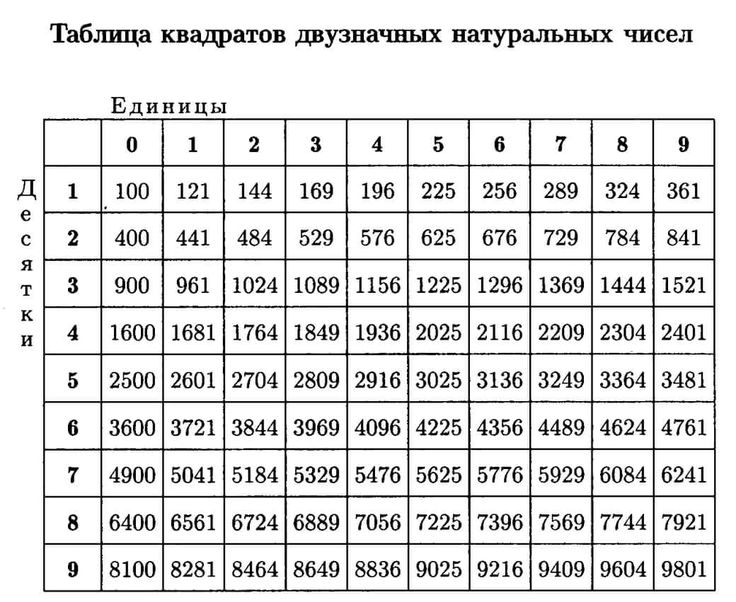
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
75 * 75 = 7 * 8 = 56 … 25 = 5625.
В таблице отмечены зеленым.
2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Автор: LysoSutriN
Источник
Таблица квадратов натуральных чисел. Формулы сокращенного умножения
Как научиться считать быстро и без калькулятора? Ведь и на ЕГЭ, и на ОГЭ по математике пользоваться калькулятором вы не можете.
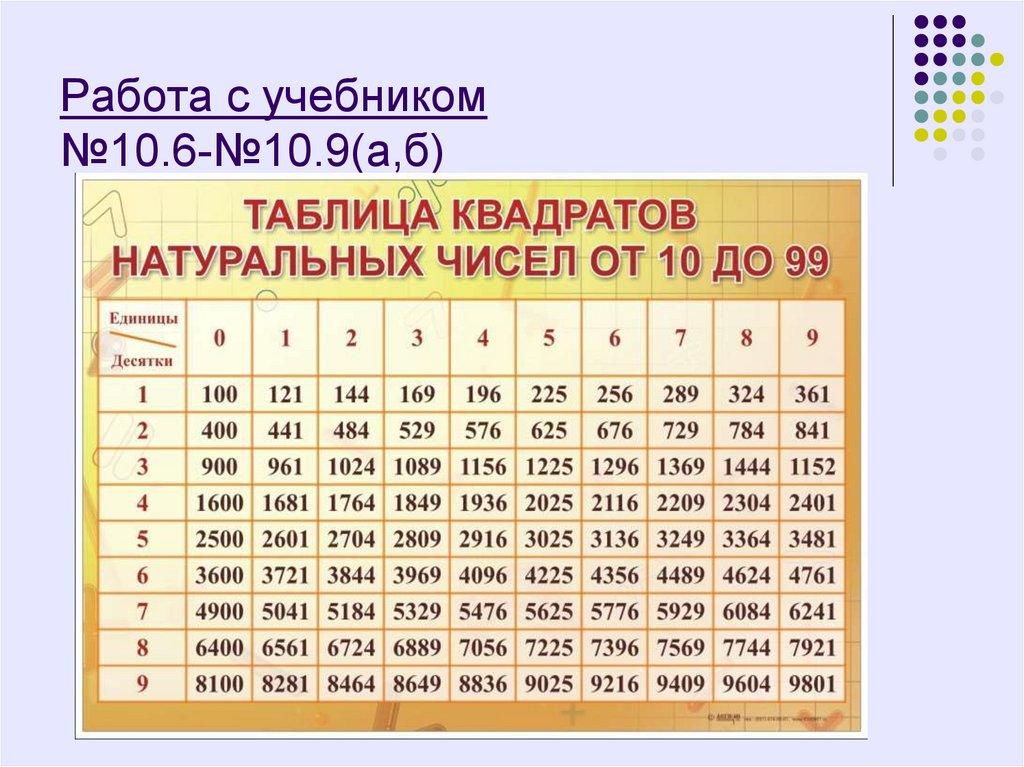
Первое, что вам поможет, – это знание таблицы квадратов натуральных чисел.
Учите наизусть, как таблицу умножения!
Все мы изучали в средней школе формулы сокращенного умножения. Правда, тогда мы не вполне понимали, зачем нам это надо. Все эти квадраты суммы и разности квадратов… А нужны они для того, чтобы быстро считать. И когда на ЕГЭ по математике на решение варианта у вас всего 3 часа 55 минут, а успеть надо очень много, – эти формулы просто незаменимы.
Как применять эти формулы на практике?
Например,
;
.
И более сложная ситуация. Она может вам встретиться в задании 7 Профильного ЕГЭ по математике, если вдруг придется считать площадь криволинейной под графиком функции как разность первообразных.
Правда, есть и более простое решение этой задачи. И в нем тоже используется одна из формул сокращенного умножения.
А вот и еще один полезный лайфхак:
Числа, оканчивающиеся на 5, в квадрат возводятся мгновенно.
Чтобы найти квадрат числа ( – не обязательно цифра, любое натуральное число), умножаем на и к результату приписываем 25.
)
Например,
.
Разберем еще несколько примеров на формулы сокращенного умножения.
1. Вычислите:
Решение:
Применим формулу разности кубов для выражения в числителе.
Ответ: 123.
2. Вычислите
Решение:
Конечно, мы не будем отдельно вычислять значения выражений в числителе и знаменателе дроби.
Применим формулы сокращенного умножения. В числителе – квадрат разности. В знаменателе – разность квадратов.
Ответ: 1,25.
Такие задания могут встретиться в первой части ЕГЭ по математике. А вычисления этого типа – в «экономической» задаче из второй части.
3. Найдите значение выражения если a = 47, b = 999.
Решение:
Числитель дроби является полным квадратом;
Знаменатель дроби преобразуем к виду:
Получим:
Если a = 47, b = 999, получаем:
4. Найдите значение выражения:
Решение:
Сделаем замену переменной: тогда
Запишем выражение в виде:
Квадратный трехчлен имеет корни и поэтому
Ответ: 2.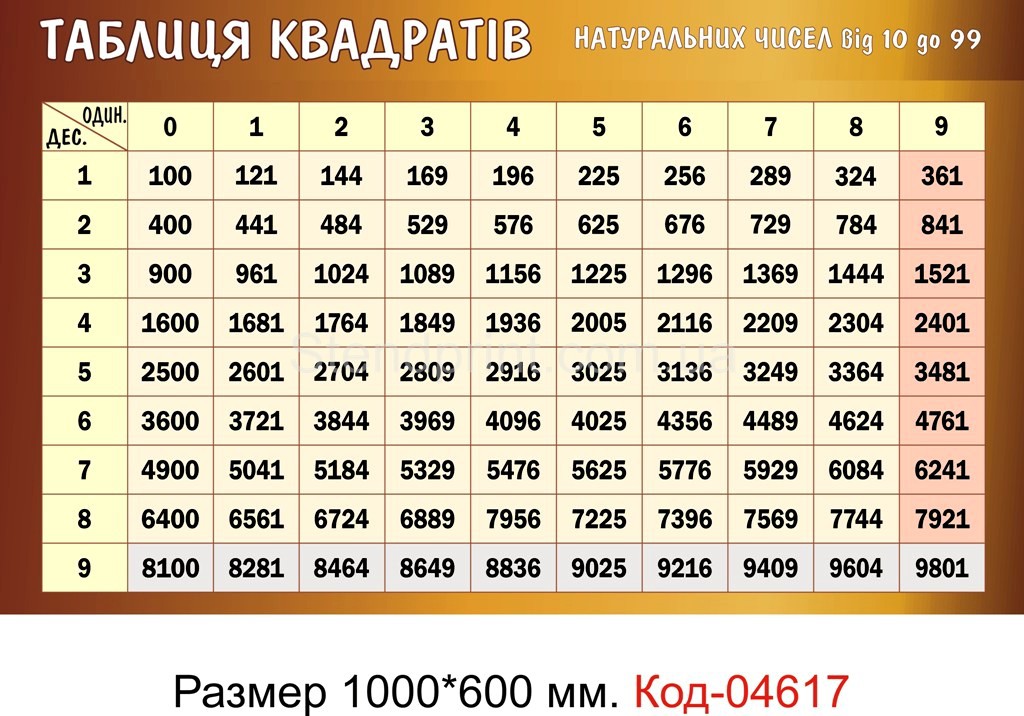
Рассмотрим задачи по теме: разложение на множители. Здесь мы тоже применяем формулы сокращенного умножения: разность квадратов, квадрат суммы и квадрат разности, разность кубов, сумма кубов… Все это может пригодиться, например, при решении задач с параметрами, а также уравнений и неравенств на ЕГЭ по математике.
Разложите на множители:
5.
Решение:
Применим формулу разности квадратов.
6.
Каждое из слагаемых содержит m в целой степени. Вынесем за скобки Также за скобки можно вынести 12. Получим:
Здесь мы применили формулу квадрата суммы.
7.
Решение:
Представим выражение в виде:
Выражение в скобках – это квадрат суммы. Получим:
Это разность квадратов. Применяем формулу:
разложили на множители.
8.
Такое выражение может встретиться в задаче с параметрами. Разложим его на множители:
9.
Решение:
Первые три слагаемые образуют полный квадрат:
Следовательно,
10.
Решение. Последние три слагаемые после вынесения знака минус образуют полный квадрат:
Тогда
Воспользуемся формулой разности квадратов и получим:
Тогда
Ответ:
Формулы сокращенного умножения помогут также при решении уравнений.
11. Решите уравнение:
Решение: По формуле разности кубов,
Тогда
Подставив в наше уравнение, получим:
Ответ: 2
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Таблица квадратов натуральных чисел. Формулы сокращенного умножения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.
01.2023
Найдите мысленно идеальные квадраты с помощью этого трюка | Бретт Берри | Математические лайфхаки
Математика в уме, часть 6
Математические трюки в уме. Разве они не великолепны? Маленькие хитрости и ярлыки, которые помогут вам добраться до места назначения быстрее и проще. А у меня для вас есть еще один! Это позволит вам вычислить в уме любой двузначный совершенный квадрат.
Мы говорили о совершенных квадратах однажды в Уроке 2: Десятичная система, экспоненты и несколько совершенных чисел . Проверьте это, если вам нужно освежить знания!
К этому моменту вам должно быть удобно работать с идеальными квадратами до двенадцати квадратов.
А если вы отличник, то можете даже знать до шестнадцати в квадрате. (✋Виновен.)
Замечательно, но что, если бы вы могли вычислить эти двузначные квадраты одним простым методом?
Готовы к этому изящному трюку?
Давайте решим пятнадцать в квадрате с помощью фокуса.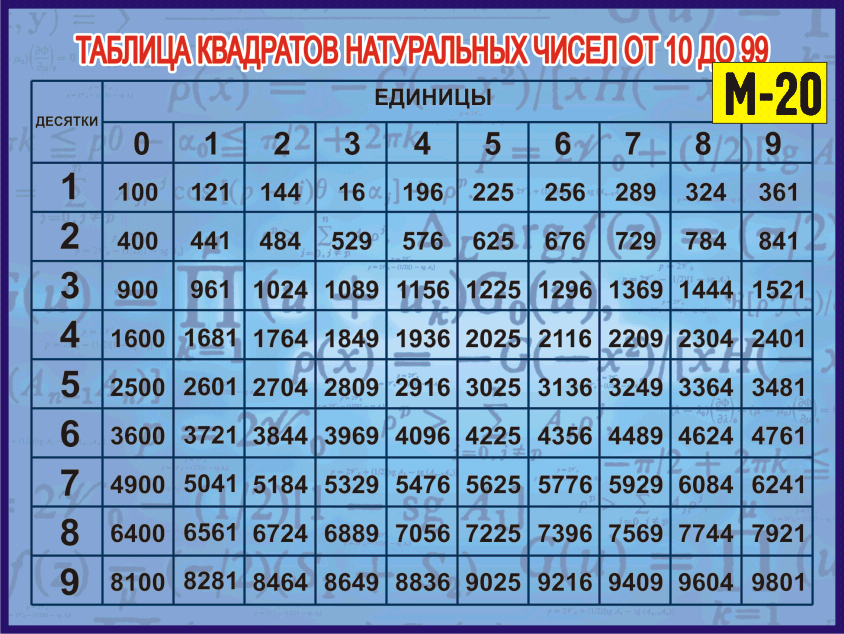
Шаг первый: Определите расстояние 15 от 10, что равно 5. Следовательно, прибавьте и вычтите 5 из 15.
Шаг 2 : Перемножьте результаты.
Шаг 3: Возьмите 5, возведите его в квадрат и прибавьте к 200.
Вот диаграмма, иллюстрирующая весь процесс.
Попробуем другой пример.
Начните с прибавления и вычитания 6 из 16.
Затем умножьте результаты.
И прибавьте к этому шесть в квадрате.
Следовательно, ответ на шестнадцать в квадрате равен 256. Опять же, вот обзор.
А теперь самое сложное.
В этой задаче прибавьте и вычтите 3, так как это дает нам эталонное значение 80.
Поскольку 80 x 86 — это большой продукт, я разделил 86 на 80 + 6, чтобы распределить 80 по всем частям.
(Помните, что при умножении на числа, кратные 10, просто перемножьте ненулевые цифры и добавьте к результату равное количество нулей.)
После распределения 80 у меня есть следующее:
Следовательно, ответ:
К настоящему моменту вы, возможно, задаетесь вопросом , какого черта это работает? Давайте рассмотрим теорию, почему это работает, на примере пятнадцать в квадрате.
Напомним, что пятнадцать в квадрате эквивалентны:
Чтобы упростить умножение, мы вычитаем 5, чтобы получить 15 до эталонного числа 10. Чтобы учесть вычитание 5, прибавьте 5 к остальным 15.
В этот момент, мы вычли 25 из нашего продукта. Чтобы увидеть это, умножьте два термина вместе.
Мы будем использовать метод под названием FOIL для умножения терминов , , что означает Первый, Снаружи, Внутри, Последний.
Первые относятся к умножению первых членов каждого двучлена.
Снаружи относится к перемножению самого первого и самого последнего членов.
Внутри относится к умножению второго и третьего членов.
примечание: положительное число, умноженное на отрицательное число, всегда отрицательно.Последнее относится к умножению последних членов в обеих скобках.
примечание: положительное число, умноженное на отрицательное число, всегда отрицательно.
Объедините продукты вместе.
Так как + 75 – 75 = 0, мы имеем:
Мы можем заключить, что наше сложение и вычитание 5 привело к дефициту 25. Вот почему мы должны добавить пять в квадрате к уравнению.
Примечание: Умножение крест-накрест из прошлого урока работает и с двузначными квадратами, если хотите!
Следующий урок: Отрицательные показатели и десятичная система счисления
Спасибо за чтение!
Подпишитесь сейчас!! Math Hacks уже на YouTube!
Присоединяйтесь ко мне, пока мы вместе решаем математические задачи. Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
www.youtube.com
Изучите таблицы умножения с первого взгляда с помощью 100 Square
В сегодняшнем посте мы собираемся представить результаты таблицы умножения на «100 квадратных» .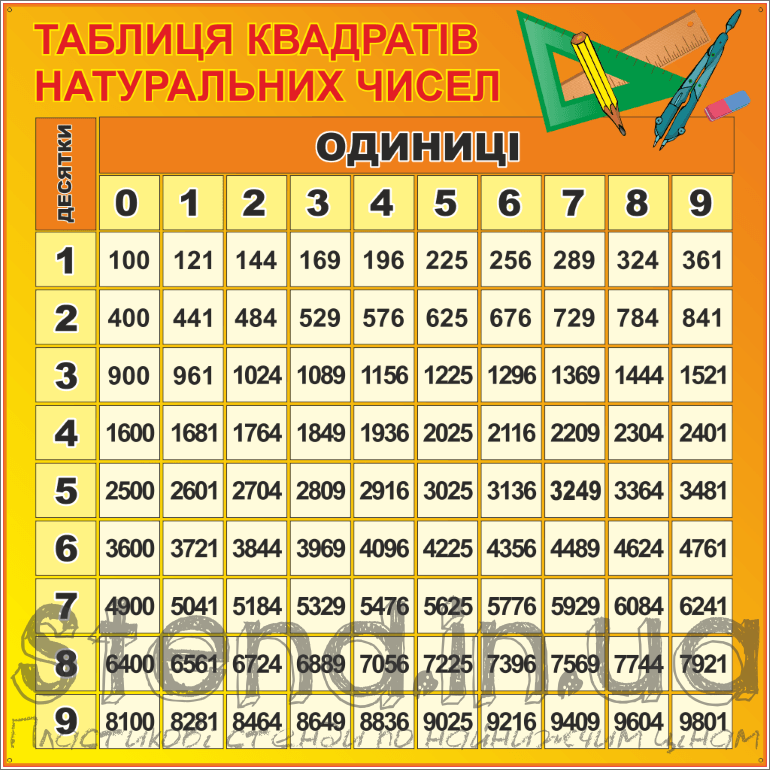
С этим наглядным пособием изучение таблицы умножения станет намного проще!
«Квадрат 100» — это не что иное, как таблица чисел от 1 до 100, расположенных в ряды 10 на 10, например: в таблице, если мы выделим результаты таблицы умножения. Это то, что вы можете попробовать сами с этой таблицей, которую вы можете скачать здесь.
Это занятие облегчает изучение таблиц умножения , потому что помогает понять их поведение и строение.
В рамках наших занятий Smartick мы часто включаем упражнения, в которых показана подобная таблица, и учащиеся могут выбирать числа в ней, например, чтобы выбрать кратные числа:
Таблица умножения на 2
Мы начну с таблицы 2 раз. Чтобы представить его, сначала мы должны вычислить все умножения в таблице и записать результаты:
2 x 1 = 2 , 2 x 2 = 4 , 2 x 3 = 6 , 2 x 4 = 8 , 2 x 5 = 10 , 2 x 6 = 12 , 2 x 7 = 14 , 2 x 8 = 16 , 2 x 9 = 18 , 2 x 10 = 20
Затем мы выделяем эти результаты в квадрате 100:
5
2 Как видите, начиная с цифры 2 мы выделили одну цифру, а следующую оставили пустой.
Мы выделили числа в «прыжках 2».Таким образом, без вычислений мы можем отметить все результаты «расширенной» таблицы умножения на 2, пока не достигнем 100, просто наблюдая закономерность.
Мы нашли шаблон для таблицы умножения 2 ! Это выглядит так:
Вы могли заметить, что таблица умножения на 2 представляет собой очень простую схему. Очень легко увидеть все пары, выделенные на 100-м квадрате.
Это облегчает запоминание результаты и выучите одну из своих таблиц умножения!
Таблица умножения на 3
Мы продолжим работу с таблицей умножения на 3. Опять же, чтобы представить это, посчитайте все умножения в таблице и запишите результаты:
3 x 1 = 3 , 3 x 2 = 6 , 3 x 3 = 9 , 3 x 4 = 12 , 3 x 5 = 15 , 3 x 6 = 18 , 3 x 7 = 21 , 3 x 8 = 24 , 3 x 9 = 27 , 3 x 10 = 30
Как и прежде, выделите эти результаты в квадрате 100:
Еще раз, если мы будем следовать созданному шаблону, мы можем выделить все результаты «расширенной» 3-кратной таблицы, пока не достигнем 100.
Мы нашли шаблон для таблицы 3 умножения ! Вот как это выглядит:
Красиво, не правда ли? Как и прежде, вы можете легко запомнить результаты и выучить таблицу умножения на 3.
Таблица умножения на 4
Теперь ваша очередь представлять таблицу умножения на 4. Вы можете сделать это с квадратом 100, который можно скачать здесь.
Если вам это покажется слишком сложным, сначала выполните таблицу умножения на 5, а затем попробуйте еще раз, это будет намного проще!
Вам понравилась идея представить таблицу умножения на 100-м квадрате? Как вы думаете, полезно ли это для запоминания, понимания и изучения таблиц умножения?
Если вам понравился этот пост, поделитесь им, чтобы другие тоже могли насладиться этими упражнениями по визуализации!
