Изучаем математику тетрадь с заданиями для развития детей: Тетрадь с заданиями для развития детей. Изучаем математику. Часть 2
Изучаем математику часть 1. Тетрадь с заданиями для развития детейMOBILE
Аннотация
Уважаемые родители и педагоги! Предлагаем вашему вниманию серию тетрадок для дошкольного образования . Перед вами тетрадь, занимаясь по которой вы поможете детям младшего дошкольного возраста развить процессы внимания
Дополнительная информация
| Регион (Город/Страна где издана): | Москва |
| Тираж: | 30000 |
| Страниц: | 32 |
| Ширина издания: | 170 |
| Высота издания: | 205 |
Вес в гр. : : | 41 |
| Язык публикации: | Русский |
| Тип обложки: | Мягкий / Полужесткий переплет |
| Цвета обложки: | Оранжевый, Белый |
| Иллюстрирована: | Да |
| Тип иллюстраций: | Чёрно-белые иллюстрации |
Нет отзывов о товаре
С этим товаром покупают
Изучаем математику часть 2. Тетрадь с заданиями для развития детей, | ISBN: Д-717
Аннотация
Уважаемые родители и педагоги! Предлагаем вашему
вниманию серию тетрадок для дошкольного образования . Перед вами тетрадь, занимаясь по которой вы поможете
детям младшего дошкольного возраста развить процессы
внимания
Перед вами тетрадь, занимаясь по которой вы поможете
детям младшего дошкольного возраста развить процессы
внимания
Дополнительная информация
| Регион (Город/Страна где издана): | Москва |
| Тираж: | 15000 |
| Страниц: | 32 |
| Ширина издания: | 170 |
| Высота издания: | 205 |
| Вес в гр.: | 41 |
| Язык публикации: | Русский |
| Тип обложки: | Мягкий / Полужесткий переплет |
| Цвета обложки: | Оранжевый, Белый |
| Иллюстрирована: | Да |
| Тип иллюстраций: | Чёрно-белые иллюстрации |
Изучаем математику. Рабочая тетрадь с заданиями. Часть 2 | 2000000002835
Стоимость товара может отличаться от указанной на сайте!Наличие товара уточняйте в магазине или по телефону указанному ниже.
г.
8 (473) 277-16-90
г. Липецк, проспект Победы, 19А
8 (4742) 22-00-28
г. Воронеж, ул. Маршака, д.18А
8 (473) 231-87-02
г. Липецк, пл.Плеханова, д. 7
8 (4742) 47-02-53г. Богучар, ул. Дзержинского, д.4
8 (47366) 2-12-90
г. Воронеж, ул. Г. Лизюкова, д. 66 а
8 (473) 247-22-55
г. Воронеж, ул. Плехановская, д. 33
8 (473) 252-57-43
 Воронеж, ул. Ленинский проспект д.153
Воронеж, ул. Ленинский проспект д.1538 (473) 223-17-02
г. Нововоронеж, ул. Ленина, д.8
8 (47364) 92-350
г. Воронеж, ул. Хользунова, д. 35
8 (473) 246-21-08
г. Россошь, Октябрьская пл., 16б8 (47396) 5-29-29
г. Россошь, пр. Труда, д. 26А
8 (47396) 5-28-07
г. Лиски, ул. Коммунистическая, д.7
8 (47391) 2-22-01
8 (4722) 42-48-42
г. Курск, пр. Хрущева, д. 5А
Курск, пр. Хрущева, д. 5А
8 (4712) 51-91-15
г. Губкин, ул. Дзержинского,д. 115
8 (47241) 7-35-57
г.Воронеж, ул. Жилой массив Олимпийский, д.1
8 (473) 207-10-96
г. Калач, пл. Колхозного рынка, д. 21
8 (47363) 21-857
г. Воронеж, ул.Челюскинцев, д 88А
8 (4732) 71-44-70
г. Старый Оскол, ул. Ленина, д.22
8 (4725) 23-38-06
г. Воронеж, ул. Ростовская, д,58/24 ТЦ «Южный полюс»
8 (473) 280-22-42
г. Воронеж, ул. Пушкинская, 2
Воронеж, ул. Пушкинская, 2
8 (473) 300-41-49
г. Липецк, ул.Стаханова,38 б
8 (4742) 78-68-01
г. Курск, ул.Карла Маркса, д.6
8 (4712) 54-09-50
г.Старый Оскол, мкр Олимпийский, д. 62
8 (4725) 39-00-10
г. Воронеж, Московский пр-т, д. 129/1
8 (473) 269-55-64
ТРЦ «Московский Проспект», 3-й этаж
г. Курск, ул. Щепкина, д. 4Б
8 (4712) 73-31-39
|
1 2 |
||
ШРР «Академия веселых наук»
Дидактическое обеспечение
Дидактические игры:
– Лабиринты букв. Развивает интеллект. Совершенствуются процессы внимания, памяти, логического мышления. Подготовка к обучению чтения. Запоминаются буквы. Анализируются слова по звуковому составу, тренируются навыки чтения. Подготовка руки к письму. Создается моторный образ буквы, развивается умение сохранять плавное и неотрывное движение руки в соответствии с изображением буквы.
Развивает интеллект. Совершенствуются процессы внимания, памяти, логического мышления. Подготовка к обучению чтения. Запоминаются буквы. Анализируются слова по звуковому составу, тренируются навыки чтения. Подготовка руки к письму. Создается моторный образ буквы, развивается умение сохранять плавное и неотрывное движение руки в соответствии с изображением буквы.
– Лабиринты цифр.Развивает познавательные способности: внимание, память, мышление (умение анализировать, сравнивать). Способствует освоению математического содержания: обозначение количества цифрой; независимость количества от формы и расположения предметов; выстраивание ряда чисел в порядке убывания и возрастания; умение находить и исправлять ошибки, представлять целое по фрагментам. Подготовка руки к письму: умение сохранять направление движения руки (плавного и неотрывного) в соответствии с изображением цифры.
– Лото по различным темам.
Таблицы:
– Цифры от 1 до 9.
– Как правильно писать цифры.
– Геометрические фигуры (квадрат, треугольник, круг, овал, прямоугольник).
– Алфавит в картинках.
Картины:
– Времена года.
– Животные и их детеныши.
– Дорожные знаки.
– Сюжетные картины по темам.
– Сказки.
Раздаточный материал:
– карточки со слогами;
– карточки с цифрами;
– карточки с буквами;
– наборы геометрических фигур.
Учебно – методическое обеспечение (на каждого ученика)
1. Тетрадь с заданиями для развития детей. Изучаем грамоту. В двух частях.
Издательство: ИП Бурдина С.В. г.Киров
2. Тетрадь с заданиями для развития детей. Изучаем математику. В двух частях.
Издательство: ИП Бурдина С.В. г.Киров
3. Рабочая тетрадь дошкольника. 30 занятий для успешной подготовки к школе.6 лет. Серия «Мои первые тетрадки» Гаврина С.Е., Кутявина Н.Л. и др. Издательство: ИП Бурдина С.В., г.Киров
4. Тетрадь с заданиями для развития детей. Окружающий мир. В двух частях.
В двух частях.
Издательство: ИП Бурдина С.В. г.Киров
5. Тетрадь с заданиями для развития детей. Рисуем по клеточкам. В двух частях.
Издательство: ИП Бурдина С.В. г.Киров
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Рабочая тетрадь «Изучаем математику». Часть 1
Хотите, чтоб ваш малыш на голову опережал сверстников в своём развитии? Индивидуальные занятия с ребёнком не только в школе, но и дома быстро дадут свои результаты. Рабочая тетрадь “Изучаем математику” ч.1 – поможет каждому родителю в обучении своего малыша.
Интересная подача материала, красивая обложка, качественная офсетная печать – вот достоинства представленного товара. Приобретая его в «» вы экономите время и деньги.
| Основная | |
| Вес | 44 г. |
| Вид | Рабочие тетради |
| Возраст | От 5 лет |
| Доставка | Бесплатная |
| Количество в боксе | 250 |
| Количество страниц | 32 |
| Количество товара в упаковке | 1 |
| Количество товара, помещяющегося в бокс | 200 |
| Материал | бумага |
| Материалы из которых произведен товар | Бумага |
| Минимальная партия | 1 |
| Набор | Нет |
| Объем бокса | 13.94 |
| Объем продукта | 0. 0697 0697 |
| Объем упаковки | 0.070 |
| Размеры товара | 0,2 см × 20,5 см × 17 см |
| Размеры упаковки | 0.2 см × 20.5 см × 17 см |
| Сертификат | ЕАС |
| Склад | КИУ 2 |
| Страна | Россия |
| Тема обучения | Цифры, счёт, математика |
| Тематика | Подготовка к школе |
| Товар партнёра | Нет |
| Упаковано в | Без упаковки |
Математических журналов
Математические журналы
Математические журналы или записные книжки для решения проблем, как их иногда называют, – это книги, в которых студентов часто просят записывать свою стратегию и мыслительные процессы, а также решения. Пока
студенты учатся “делать” математику, они также должны научиться артикулировать
что они изучают. Важно предоставить много возможностей
для студентов, чтобы организовать и записать свою работу без структуры
рабочий лист.Математические журналы поддерживают обучение студентов
потому что, чтобы воплотить свои идеи в жизнь, дети должны организовывать,
прояснить и поразмыслить над их мышлением. Первоначально многие студенты будут
нуждаются в поддержке и поощрении, чтобы доносить свои идеи и
ясно мыслит на бумаге, но, как и в случае с любым другим навыком, чем больше они практикуются
тем легче станет. Математические журналы также являются бесценным
ресурсы для оценки, которые могут быть полезны для обучения в классе. Требование к учащимся сообщать о своих процессах мышления дает полезное представление о том, что ребенок
понимает, как он подходит к идеям и какие у него заблуждения. Датируя записи, журнал обеспечивает хронологическую запись развития математического мышления учащихся в течение года.
Задач
которые просят студентов применять заученные процедуры к рутинным задачам, требуют одного
вид мышления. Нетипичные или открытые задачи, которые просят учащихся взаимодействовать с концепциями и
для установления связи между идеями и представлениями требуется совсем другое
вид мышления.Хотя применяя
заученные процедуры важны для развития беглости речи и не должны
уволен, размышления и рассуждения на более высоком уровне необходимы, чтобы
развивать навыки решения проблем. Пока
рутинные или закрытые задания могут использоваться для оценки понимания учащимися
числовые факты, стратегии точного решения алгоритмов или знание других
математические факты, открытые задания включают следственные ответы, которые стимулируют
математические рассуждения и способствовать пониманию того, что математика
творческое начало.Некоторые бессрочные задачи
может иметь более одного правильного ответа, но максимум правильных ответов, в то время как
у других может быть бесконечное количество правильных ответов. Например, задание В миски нужно положить 16 яблок. В каждой чаше должно быть одинаковое количество
яблоки. Сколько разных способов
яблоки в миски? »У есть несколько правильных ответов, в то время как у задачи « Я решил историю с номерами деления и получил
частное 7. Каким может быть число
story be? » предоставляет практически безграничные возможности приемлемых ответов.Другие нестандартные задачи, такие как «Был бы
вы предпочитаете 1/3 или 2/8 тарелки брокколи? Используйте математику для обоснования
ваши рассуждения. “ нет ни одного правильного
ответьте, но вместо этого сосредоточьтесь на том, чтобы ученик выбирал вариант и обосновывал свое
выбор с использованием математических рассуждений. Важно учитывать, когда
выбор или написание задачи математического журнала зависит от того, предоставляете ли вы
возможности для студентов регулярно участвовать в разнообразных повседневных делах и
нестандартные задачи для развития концептуального понимания и
процедурная беглость.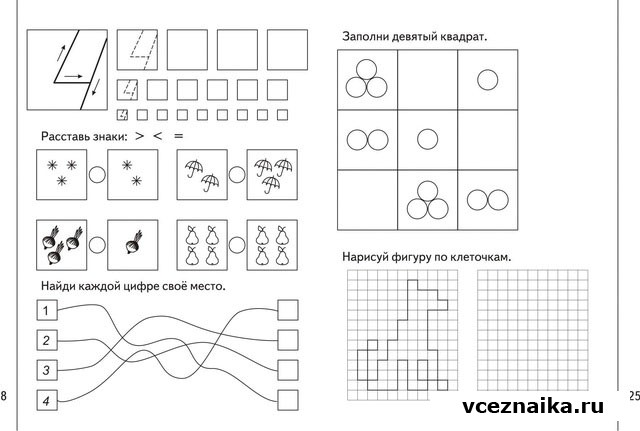
Хороший вопрос из журнала по математике….
- создает дифференциацию, позволяя использовать несколько точек входа и методов записи, тем самым позволяя всем учащимся работать на своем индивидуальном уровне мышления,
- предоставляет учащимся возможность учиться, выходя за рамки того, что они уже знают, отвечая на вопрос , и для того, чтобы учитель узнал о каждом ученике с его попытки,
- может иметь более одного решения или множество возможных путей решения, которые варьируются от простого к сложному,
- требует некоторой степени когнитивных усилий (больше, чем просто запоминание факт или воспроизведение навыка),
- предоставляет учащимся возможность представить свои математические идеи с помощью моделей и письменного языка,
- предоставляет учащимся возможности обосновать свои рассуждения и оценить рассуждения других,
- дает четкие, краткие указания .
Повторение или повторное посещение задач позволяет
учащиеся могут заниматься задачами на более глубоком уровне. В первый раз
студент может быть сосредоточен на том, «как выполнить» задание. Последующие посещения дают учащимся возможность более ясно выразить свое математическое мышление и рассуждения. Внесение небольших изменений в задачу (например, изменение чисел, контекста или используемых материалов) поможет поддерживать интерес, пока учащиеся развивают навыки и концепции.Некоторым учителям нравится представлять задачи всему классу, а затем размещать их в центрах, чтобы дети могли повторно их посещать в другое время в течение года. Другие учителя выбирают одно задание из дневника и повторяют его с небольшими вариациями несколько раз в течение года в качестве отчета о развитии математических навыков и понимания для портфолио учащихся.
Методы
которые дети используют для представления своего мышления, со временем изменится.
год. Повторение задания дает учителям запись этого роста,
родители и ученики. Например, в детском саду открытый
дополнительная задача (см. примеры работ ниже) может быть изучена в начале года
прежде, чем дети начнут писать числовые предложения. В начале года больше всего
Воспитанники детского сада будут записывать свое мнение по этому поводу
проблема графически и может записывать только одно или два решения
проблема. По мере прохождения года постепенно начнутся символические представления.
появиться и представления станут более подробными. Образец работы ниже слева показывает попытку учеников детского сада записать свои мысли в начале учебного года в ответ на задание « Ванесса съела 5 кексов».Некоторые были шоколадными. Некоторые были ванильными. Сколько было шоколада? Сколько было ванили ? ‘ Три месяца спустя этот студент выполнил аналогичную задачу: «У Cameron было 6 кнопок. Некоторые были зелеными. Некоторые были пурпурными. Сколько было зеленых? Сколько было пурпурных? ‘ В этом случае письменное изображение ребенка (внизу справа) более детально и ясно демонстрирует ее развивающееся понимание сложения. Хотя она повторяет некоторые числовые предложения, на ее рисунках показаны все возможные комбинации шести кнопок.
Например, в детском саду открытый
дополнительная задача (см. примеры работ ниже) может быть изучена в начале года
прежде, чем дети начнут писать числовые предложения. В начале года больше всего
Воспитанники детского сада будут записывать свое мнение по этому поводу
проблема графически и может записывать только одно или два решения
проблема. По мере прохождения года постепенно начнутся символические представления.
появиться и представления станут более подробными. Образец работы ниже слева показывает попытку учеников детского сада записать свои мысли в начале учебного года в ответ на задание « Ванесса съела 5 кексов».Некоторые были шоколадными. Некоторые были ванильными. Сколько было шоколада? Сколько было ванили ? ‘ Три месяца спустя этот студент выполнил аналогичную задачу: «У Cameron было 6 кнопок. Некоторые были зелеными. Некоторые были пурпурными. Сколько было зеленых? Сколько было пурпурных? ‘ В этом случае письменное изображение ребенка (внизу справа) более детально и ясно демонстрирует ее развивающееся понимание сложения. Хотя она повторяет некоторые числовые предложения, на ее рисунках показаны все возможные комбинации шести кнопок.
Некоторые учителя используют несколько заданий в неделю в качестве разминки перед уроком математики.
Другие учителя выделяют один период в неделю для журналов, выбирают задачу, которая коррелирует с текущей единицей обучения, и дают учащимся больше времени, чтобы поделиться своими мыслями друг с другом. Задания также можно использовать для оценки или в качестве домашнего задания. Важно обеспечить, чтобы учащимся регулярно давали
возможность в течение года представлять свое математическое мышление
способами, которые имеют для них смысл.
Наш опыт в многочисленных классах K-5 показал, что тетрадь с пустыми страницами дает наилучшие результаты.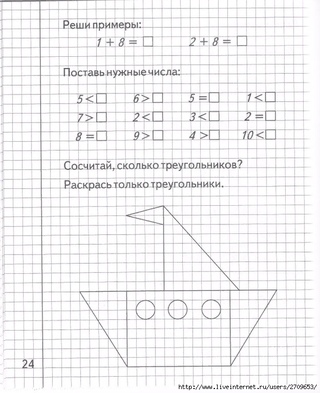 Хотя они не всегда доступны так же легко, как записные книжки в линейку (и часто стоят дороже), они имеют явное преимущество в том, что учащиеся не ограничены линиями и имеют место для выбора, использовать ли изображения, числа, слова или их комбинацию. записывать их мысли.Щелкните по ссылкам ниже, чтобы посетить страницы нашей галереи, чтобы увидеть примеры типов письменных ответов, которые дают учащиеся детского сада – учащиеся 5-го класса, когда им предлагается принять собственное решение о том, как записывать свое мышление.
Хотя они не всегда доступны так же легко, как записные книжки в линейку (и часто стоят дороже), они имеют явное преимущество в том, что учащиеся не ограничены линиями и имеют место для выбора, использовать ли изображения, числа, слова или их комбинацию. записывать их мысли.Щелкните по ссылкам ниже, чтобы посетить страницы нашей галереи, чтобы увидеть примеры типов письменных ответов, которые дают учащиеся детского сада – учащиеся 5-го класса, когда им предлагается принять собственное решение о том, как записывать свое мышление.
Сделать математику значимой для детей младшего возраста
Дети – прирожденные математики. Они толкают и тянут игрушки, складывают блоки, наполняют и опорожняют чашки водой в ванне. Все эти действия позволяют маленьким детям познавать математические концепции, экспериментируя с пространственным восприятием, измерением и решением проблем (ETFO 2010; NAEYC 2010).Маленькие дети легко учатся, когда они описывают, объясняют и рассматривают идеи из своего непосредственного окружения. Я такой же высокий, как Янси? Как я могу узнать? Я знаю! Мы оба можем стоять рядом друг с другом перед зеркалом.
Ранняя математика – это не заучивание наизусть отдельных фактов, например, сколько равно 5 + 7. Скорее, речь идет о детях, активно осмысляющих окружающий их мир. В отличие от упражнений или рабочих листов с одним правильным ответом, открытое, игровое исследование побуждает детей решать проблемы в реальных ситуациях.Поскольку ситуации значимы, дети могут получить более глубокое представление о количестве, количестве, размере, структуре и управлении данными (Grossman 2012). Например, легче понять, что означает шесть, применительно к реальной задаче, такой как поиск шести бусин, которые можно нанизать на ожерелье, или размещение по одному крекеру на каждой из шести пластин.
Создание класса с богатой математикой
Исследования показывают, что дошкольные классы могут быть идеальной средой для изучения математики (ETFO 2010). Дети сортируют материалы по соответствующим корзинам во время уборки, исследуют узоры и формы, создавая за столом для рисования, определяют время, используя визуальный график, чтобы предсказать, какие действия будут следующими, и измеряют, когда они протискиваются через альпиниста на игровой площадке (ETFO 2010).
Дети сортируют материалы по соответствующим корзинам во время уборки, исследуют узоры и формы, создавая за столом для рисования, определяют время, используя визуальный график, чтобы предсказать, какие действия будут следующими, и измеряют, когда они протискиваются через альпиниста на игровой площадке (ETFO 2010).
Дошкольные классы также отмечают любопытство и риск, поскольку дети участвуют в исследовательских исследованиях в различных учебных центрах и на открытом воздухе. Интересные предметы в окружающей среде побуждают детей находить ответы на свои вопросы и решать проблемы во всех областях учебной программы.Дети измеряют, хлопая в такт музыке. Во время танца они повторяют ритмические узоры. Они описывают, сортируют и подсчитывают предметы в научном центре открытий и ищут закономерности во время прогулки на природе. Они считают ступеньки, поднимаясь по лестнице на чердак. Многие знакомые детские песни, рассказы и стихи содержат математические сообщения, которые помогают приучить детей к счету, измерению и построению паттернов. Например, дети могут сосчитать «Раз, два, пристегни мою обувь» и «Десять маленьких обезьянок прыгают на кровати».”
Помимо того, что учителя предлагают блоки, кнопки и другие разрозненные материалы, которые можно потрогать и изучить, они могут задавать открытые вопросы, которые способствуют решению проблем, исследуют и бросают вызов математическому мышлению и рассуждению детей (Министерство образования Онтарио, 2010). Такие вопросы предназначены не для получения правильных ответов, а, скорее, для вовлечения детей в открытые беседы, способствующие высокоуровневому мышлению, например, . Что вы замечаете в этих объектах? Как мы можем отсортировать игрушки? Одна из основ игрового обучения заключается в том, что учитель активен в игре, задавая вопросы и добавляя знания и идеи.Педагог учится вместе с детьми на протяжении всего процесса исследования.
Каждый дошкольный класс должен быть богат материалами, которые поощряют изучение и изучение математики. В хорошо укомплектованном центре математики и манипуляций есть найденные предметы, такие как ракушки, камни, хлебные жетоны и палочки, а также купленные материалы. Центр может включать в себя фотографии завершенных творений геобордов или детей, сортирующих монеты в театральном игровом центре. Это могут быть рассказы об обучении детей, такие как стенограммы детских комментариев и разговоров, а также рисунки, изображающие исследование узоров или форм.Учителя могут публиковать документы об обучении математике, чтобы побудить детей задуматься о прошлом опыте и побудить их планировать и пересматривать будущий. Эти визуальные эффекты могут вдохновить на еще более глубокое и связное обучение. Они помогают детям сосредоточиться на определенной теме, уточнять и расширять свои идеи, передавать полученные знания другим и размышлять над своим опытом, прежде чем строить новые планы.
В хорошо укомплектованном центре математики и манипуляций есть найденные предметы, такие как ракушки, камни, хлебные жетоны и палочки, а также купленные материалы. Центр может включать в себя фотографии завершенных творений геобордов или детей, сортирующих монеты в театральном игровом центре. Это могут быть рассказы об обучении детей, такие как стенограммы детских комментариев и разговоров, а также рисунки, изображающие исследование узоров или форм.Учителя могут публиковать документы об обучении математике, чтобы побудить детей задуматься о прошлом опыте и побудить их планировать и пересматривать будущий. Эти визуальные эффекты могут вдохновить на еще более глубокое и связное обучение. Они помогают детям сосредоточиться на определенной теме, уточнять и расширять свои идеи, передавать полученные знания другим и размышлять над своим опытом, прежде чем строить новые планы.
Поощряйте детей к математической игре
Маленькие дети должны видеть себя способными математиками.Исследования, ориентированные на детей и ориентированные на них, и математические задания под руководством учителя помогают детям практиковать и закреплять полученные знания. Это помогает им быть уверенными в том, что они знают и умеют. Хотя многие дошкольники изучают некоторые математические понятия самостоятельно, учителям важно включать математику в аутентичный опыт, что приведет к более глубокому пониманию детьми (ETFO 2010).
Помимо создания богатого центра изучения математики и манипуляций, учителя могут поощрять детей использовать математические инструменты и стратегии во всех областях в классе.Дети могут использовать набор пластиковых звеньев для измерения своих зданий в центре квартала, использовать игровые деньги для оплаты билета на поезд в театральном игровом центре и использовать линейки для измерения роста весенних лампочек в научном центре открытий. Возьмите весы на улицу, чтобы дети могли выяснить, кто нашел самый тяжелый камень. Использование математических инструментов для решения реальных задач позволяет учителям и детям действовать спонтанно, что приводит к более богатому общению и более спокойной учебной среде (Wien 2004).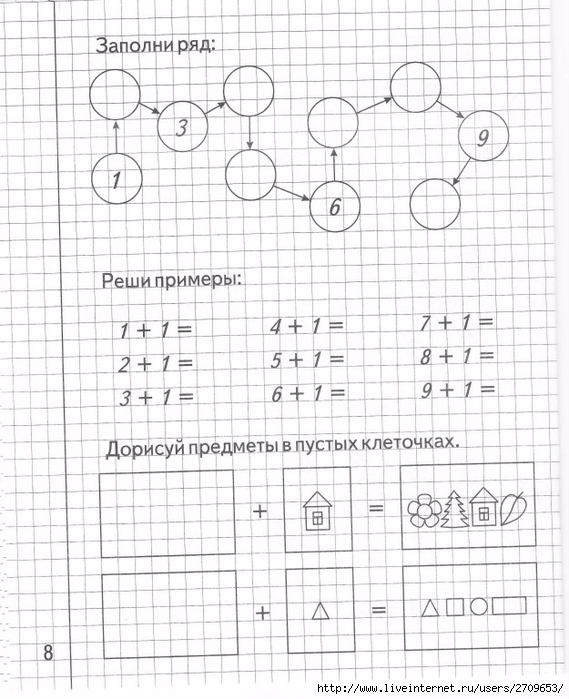
Помимо свободы использовать материалы аутентичным образом, детям также нужна свобода времени и пространства, чтобы глубоко погрузиться в математику. В дошкольном расписании должно быть достаточно времени для непрерывных игр, чтобы у детей было время, необходимое для работы над постоянными интересными задачами. Это позволяет детям тщательно изучать материалы, что со временем часто приводит к более сложному и развитому опыту. Если ребенок проводит все свое время в одном учебном центре, он не упускает возможности обучения в другом месте.Напротив, его глубокая связь с центром часто свидетельствует о богатых знаниях. Учителя могут смоделировать использование других материалов в центре, например, использовать письменные принадлежности, чтобы нарисовать планы строящейся структуры, или ставить задачи, которые побуждают ребенка думать за пределами своей игры, например Какую высоту вы можете построить эту башню прежде чем он упадет?
Для поддержки обучения важно побуждать детей делиться своими исследованиями и открытиями. Учителя могут установить распорядок, в котором дети делятся своим опытом во время групповых занятий.Например, ребенок может объяснить, как он построил конструкцию из блоков, танцевал с повторяющимися шагами или поделился фотографией сложного узора, сделанного из разноцветных пуговиц. Проходя по комнате, учитель может заметить качественную работу и предложить ребенку поделиться ею со своими сверстниками во время группового занятия. Ребенок, проводящий презентацию, становится увереннее, и зрители могут захотеть испытать это на себе.
Вывод
Большинство детей поступают в дошкольные учреждения, хорошо разбираясь в математике.В безопасном и благоприятном классе они будут чувствовать себя комфортно, рискуя и участвуя в самостоятельном решении проблем. Включение математики во все области учебной программы улучшит игровой опыт детей и позволит всем учащимся добиться успеха. Дети скоро увидят себя способными математиками, которые применяют свои навыки разными способами. Их растущие математические навыки, уверенность в себе и интересы хорошо послужат им в школе и в жизни.
Их растущие математические навыки, уверенность в себе и интересы хорошо послужат им в школе и в жизни.
Поддержка изучающих два языка
Дети, которые являются библиотеками DLL, могут изучать математические понятия и навыки, не владея своим вторым языком свободно.Значительная часть смысла содержится в правильных материалах. Если семьи пришлют в класс знакомые предметы из дома, дети будут знать названия и функции предметов на их родном языке. Они могут использовать эти предварительные знания в качестве основы для изучения математики. Например, маленькие дети могут не понимать, как сортировать пластмассовые формы, но они уже знают, как важно сортировать носки ребенка и папы в отдельные стопки – математическое задание, имеющее реальное значение на любом языке.
Каталожные номера
ETFO (Федерация учителей начальной школы Онтарио). 2010. Продумывая: преподавание и обучение в классе детского сада . Торонто, Онтарио: ETFO.
Гроссман, С. 2012. «Дилемма рабочего листа: преимущества игровых программ». Новости раннего детства . www.earlychildhoodnews.com/earlychildhood/article_view.aspx?ArticleID=134.
NAEYC. 2010. «Математика для детей младшего возраста: содействие хорошему началу.Заявление о совместной позиции NAEYC и Национального совета учителей математики (NCTM). www.naeyc.org/files/naeyc/file/positions/psmath.pdf.
Министерство образования Онтарио. 2010. Программа полного дня дошкольного образования для детского сада (черновая версия). Торонто, Онтарио: Королевский принтер для Онтарио. www.edu.gov.on.ca/eng/curriculum/elementary/kindergarten_english_june3.pdf.
Wien, C.A. 2004. «От полицейской службы к участию: отмена правил и создание дружелюбных классных комнат».» Дети младшего возраста 59 (1): 34–40. www.naeyc.org/files/yc/file/200401/Wien.pdf.
Где математика? Книги, игры и упражнения для пробуждения мышления детей
Этот замечательный ресурс не только поддерживает учителей, которые развивают математическое мышление в увлекательных и подходящих для развития способах, он делает это, естественным образом привнося насыщенные беседы и начальные навыки грамотности! Обязательное дополнение к любому классу для детей младшего возраста.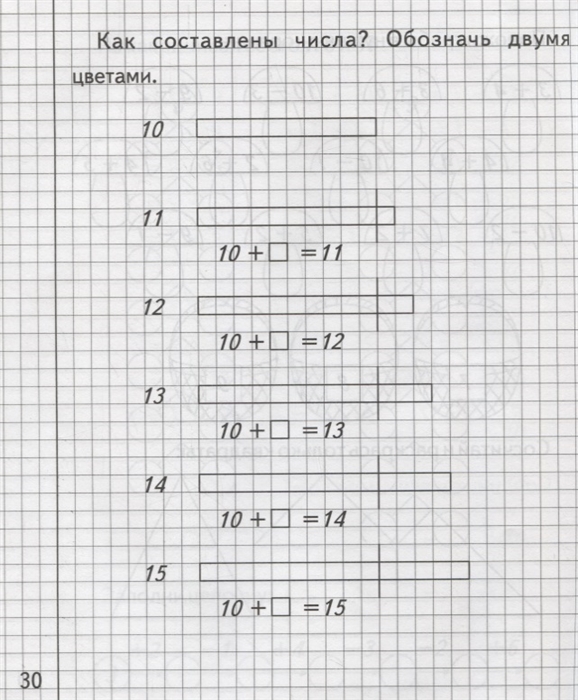
– Джессика Мерсер Янг, Старший научный сотрудник, Центр развития образования
Эта книга – содержательное руководство, которое поможет детям открыть для себя математику, которая их окружает, извлечь из нее уроки и полюбить ее.Несмотря на то, что он явно основан на ранних исследованиях математики, он написан в стиле, который делает тему доступной, незамедлительно полезной и убедительной.
– Эрик Диринг, профессор прикладной психологии развития и педагогической психологии, Бостонский колледж
Где математика? показывает вам, как поддержать математическое мышление детей. и вдохновляют вас взглянуть на повседневный опыт через математическую призму. Используя этот ресурс, вы можете намеренно сформировать свой «математический разговор», чтобы помочь детям понять взаимосвязь между их игрой и важными математическими идеями.
– Кейт Хероман, Консультант и автор по вопросам детей младшего возраста, Cate Heroman, LLC
Эта книга – гораздо больше, чем просто набор упражнений – это увлекательный набор исследований, которые учителя могут адаптировать, чтобы вовлечь молодых учеников в поиск математики, которая нас окружает.
– Джи-Ци Чен, старший вице-президент по академическим вопросам и основатель сотрудничества по ранней математике, Институт Эриксона.
Наконец! В этой хорошо написанной книге приводятся конкретные примеры того, как использовать чудеса природы и любопытство детей к миру и , чтобы поддержать их изучение математики. Где математика? – ценный ресурс для любого педагога дошкольного образования.
– Кристен Э. Рид, Старший директор проекта, Центр развития образования
В каждой главе этого ресурса, который необходимо прочитать, описываются практические занятия в классе, направленные на развитие у детей математического мышления и усвоения концепций посредством реальных исследований и ситуаций, связанных с решением проблем.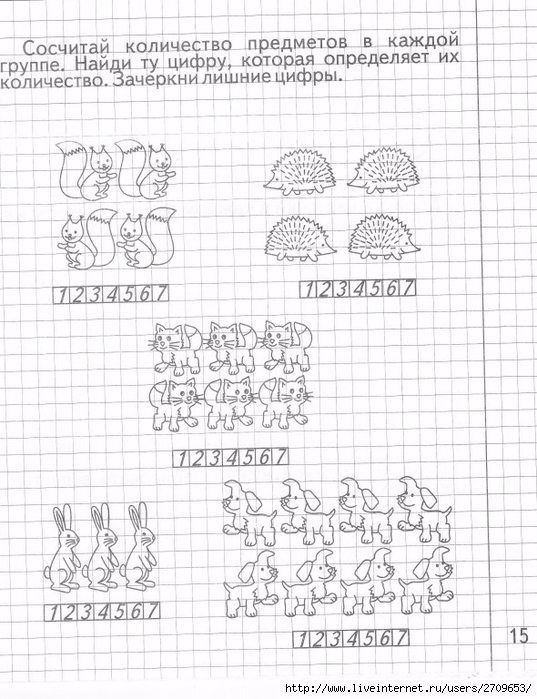
– Даниэль Дэвис, учитель дошкольного образования, государственные школы Метро Нэшвилл.
Авторы этой важной книги убедительно доказывают, что математика присутствует повсюду в жизни всех маленьких детей.Это ценный ресурс для педагогов дошкольного образования, приверженных математике.
– Дэнни Бернард Мартин, профессор, факультет математики, статистики и информатики, Иллинойсский университет в Чикаго.
5 эффективных способов помочь детям развить мышление роста в математике – Big Life Journal
ЭТА СТАТЬЯ ВКЛЮЧАЕТ БЕСПЛАТНУЮ ПЕЧАТЬ
«Я плохо разбираюсь в математике».
«Я не математик.”
«Я не родился с математическим геном».
К сожалению, как преподавателю математики, эти фразы мне слишком знакомы. Дети учатся в школе, а жизнь засыпают сообщениями, которые подразумевают, что некоторые люди хорошо разбираются в математике, а некоторые – нет.
Для некоторых из нас математика просто «кликает». Но что, если он не сразу «щелкнет» для вас? Что ж, можешь сдаться. Ты просто не математик. Проблема с этими сообщениями, явными или подразумеваемыми, заключается в том, что они содержат ложных .
Этот «культурный багаж», который у нас есть по отношению к математике, не основан на истине о том, как устроен наш мозг. Он основан на том, что родители и учителя за годы непонимания или ненависти к математике передали эти негативных взглядов и убеждений своим детям.
Однако хорошая новость заключается в том, что все больше и больше исследований доказывают, что эти сообщения ложны, поскольку мы узнаем, как работает наш мозг и как стили преподавания математики могут влиять на мышление и достижения.
Прежде чем двигаться дальше, не забудьте подписаться на наши БЕСПЛАТНЫЕ еженедельные печатные издания , тщательно разработанные, чтобы научить ваших детей мышлению роста, устойчивости и многому другому. Зарегистрируйтесь ниже, чтобы убедиться, что вы в списке!
Зарегистрируйтесь ниже, чтобы убедиться, что вы в списке!
После регистрации вы сразу же получите наше популярное «Руководство для родителей по установке на рост» .
Почему так важно иметь растущее мышление в отношении математики?Чем больше исследователей изучают и корректируют то, как учителя думают о математике и как ее преподают, тем больше доказательств показывает связь между установкой на рост и успехом в математике.
Мы все хотим, чтобы дети чувствовали себя уверенно и успешно изучали математику.Дети, у которых есть установка на рост в отношении своих математических способностей, показывают на результаты лучше по стандартным тестам и более активны в классе.
В своей исследовательской статье Кэрол Двек «Мышление и достижения в математике / науке» глубоко углубляется в различные исследования, подтверждающие эту корреляцию. И хотя мы видим доказательства преимуществ установки на рост, она также заявляет:
«Учащиеся с установкой на данность, но хорошо подготовленные и не сталкивающиеся с трудностями, могут отлично справиться.Однако, когда они сталкиваются с препятствиями или препятствиями , они могут оказаться в невыгодном положении ».
И в этом-то и проблема. В какой-то момент для каждого из нас математика превратится в сложных . Для некоторых это может быть во втором классе, когда они сталкиваются с вычитанием при перегруппировке. Для других это может не стать трудным до исчисления.
Каждый ребенок в какой-то момент столкнется с математическими препятствиями, и подготовка к встрече с ними с установкой на рост и здоровым отношением к математике придаст им стойкости, чтобы выстоять и преодолеть трудности.
Как помочь детям развить мышление роста в математике?Вот несколько практических идей для начала.
1. Научите детей способности к росту Если необходимо, сначала нам нужно изменить взгляд детей на математику и свои математические способности. Есть много детей, которые считают, что они никогда не будут хороши в математике, , как бы они ни старались .
Есть много детей, которые считают, что они никогда не будут хороши в математике, , как бы они ни старались .
Показывая им , как работает наш мозг , , мы даем им надежду на то, что их мозг может расти и меняться по мере того, как они продолжают изучать математику.
Вот некоторые предлагаемые действия:
- Для детей младшего возраста покажите забавные видеоролики на YouTube, такие как «Песня о нейронах», чтобы они узнали о нейропластичности.
- Детям постарше покажите этот короткий отрывок из документального фильма BBC «Человеческое тело», который демонстрирует, как создание новых нейронных путей между клетками мозга похоже на строительство моста, ведущего через овраг.
- Проведите своих детей или студентов через бесплатный онлайн-курс от Джо Болер из Стэнфордского университета.Этот курс объяснит текущие исследования мозга и представит математику так, как многие никогда раньше не видели и не думали. Кроме того, исследования показали, что студенты, проходящие этот курс, более позитивно относятся к математике, больше занимаются математикой и лучше справляются со стандартными тестами.
- Пусть ваши дети или ученики создадут свой собственный плакат Brain Poster (входит в наш комплект Growth Mindset Printables Kit ) и продемонстрируют свое творение, чтобы оно служило напоминанием об огромной силе их мозга.
Еще один важный аспект развития установки на рост – положительный взгляд на ошибки.
Дети должны понимать , наш мозг узнает больше, когда мы делаем ошибки . Если мы правильно решим все домашние задания по математике, мы ничего не узнаем без всяких усилий. Мы совсем не напрягали и не укрепляли свой мозг.
Согласно Джо Боулер в своей книге «Математическое мышление», наш мозг реагирует на ошибки одним из двух способов. Во-первых, через реакцию ERN, которая представляет собой повышенную активность нашего мозга, которая происходит, когда существует «конфликт между правильным ответом и ошибкой».
Во-первых, через реакцию ERN, которая представляет собой повышенную активность нашего мозга, которая происходит, когда существует «конфликт между правильным ответом и ошибкой».
Второй – это реакция Ре, которая возникает, когда мозг осознает, что была сделана ошибка. Удивительно, но наш мозг вспыхивает и растет вместе с ответом ERN. Мы можем растягивать и развивать наш мозг, совершая ошибки, даже если мы не осознаем этого или работаем над их исправлением. Какое невероятное воодушевление – знать это!
Чтобы помочь детям увидеть и оценить свои ошибки, мы можем помочь им увидеть ошибки такими, какие они есть: возможности для развития мозга .
Вот некоторые предлагаемые действия:
- Модель ошибок на глазах у детей. Покажите им, что вы тоже ошибаетесь, и это хорошо.
- Проанализируйте ошибок вместе, чтобы увидеть, чему и как мы учимся на них. Отличным примером для классных учителей является включение фразы «мое любимое нет», которая позволяет всему классу вместе обсуждать ошибки и находить в них ценность.
- Прочтите вместе сработавшие ошибки Шарлотты Фольц Джонс.
- Создайте дом или класс , приветствующий ошибку , украсив его вдохновляющими плакатами и графикой. Используйте наши плакаты «Наш дом – это…» (или «Наш класс – это…»), доступные в комплекте материалов для печати «Рост мышления».
- Попросите вашего ребенка прочитать стихотворение об ошибках и показать его где-нибудь, где он может часто его видеть (доступно в комплекте печатных форм для мышления роста).
3. Обеспечьте
разнообразных открытых математических задачХотя изменение отношения детей к математике и языку, который они используют, важно, никаких реальных изменений или прогресса не произойдет, если математику и дальше преподавать по методике .
Поскольку математика часто преподается как закрытый, фиксированный предмет с одной целью – получить правильный ответ, – дети часто боятся ошибиться, потому что это кажется неудачей. Их единственная мысль – найти это единственное правильное решение, а когда они этого не делают, они закрываются и уходят.
Но правда в том, что математика – это гораздо больше, чем просто получение правильного ответа. Речь идет об изучении важных идей, установлении связей и умении творчески решать проблемы.
Вместо того, чтобы сосредотачиваться на запоминании фактов или воспроизведении математических процедур, родители и учителя должны предлагать сложные и содержательные задания, которые побуждают детей мыслить нестандартно.
Как это выглядит? Что ж, как говорит Джо Булер, значимые математические задачи сочетают в себе 5C: любопытство, установление связей, вызов, творчество и сотрудничество.
Когда детям будут предложены задания такого типа, они будут больше увлечены математикой и будут более вовлечены в обучение.
Заставить детей задуматься о том, что они делают и ПОЧЕМУ это работает, более продуктивно, чем просто выполнить 20 задач из учебника.
Вот некоторые предлагаемые действия:
- Попробуйте вместе с детьми выполнить задания из YouCubed .Эти задания выполняются детьми со всего мира и пробуждают еще большую любовь к математике. Узнайте больше о неделе вдохновляющей математики здесь.
- Возьмите традиционные закрытые задачи и превратите их в сложных задач . Например, ваши дети могут работать над проблемой 18 x 5. Это может быть простая задача с единственным решением. Но что, если вместо этого вы попросите детей решить эту проблему двумя разными способами? Или дать наглядное подтверждение своего решения и объяснить свой ответ?
- Используйте еще одно увлекательное задание от Булера – , задание «четыре четверки» .В этой задаче детям (или родителям и учителям) предлагается найти все числа от 1 до 20, используя 4 четверки и любую математическую операцию. Например, 4 + 4 + 4 + 4 = 16, 4 + 4 – 4 + 4 = 8 и т. Д. После некоторых основных операций эта задача становится намного сложнее и увлекательнее!
- Поднимите планку для детей, которые справились с заданной проблемой или задачей. Один из простых способов сделать это – предложить им создать свою собственную задачу . Попросите их написать новый аналогичный вопрос, но посложнее.Это дает детям шанс проявить творческий подход и вдохновляет их бросать вызов своим сверстникам.
Пока ваши дети работают над математическими задачами, поощряйте их использовать 5-этапных карточек для решения задач , которые доступны в наборе для действий «Рост мышления».
4. Убрать акцент на скоростиКак я уже упоминал, у детей часто создается впечатление, что математика – это одно и только одно: быстро получить правильный ответ .Но если бы изучение и преподавание математики сводилось только к тому, чтобы получить правильный ответ, в этом не было бы никакого смысла, потому что калькуляторы могут сделать эту работу за нас.
Факты свидетельствуют о том, что рассчитанных на время теста по математике усиливают у детей тревогу и ненависть к математике. Давление, связанное с завершением в установленные сроки, может быть настолько стрессовым, что у некоторых детей возникает серьезная математическая тревога, которая остается с ними на всю жизнь.
Таким образом, вместо того, чтобы сосредоточиться на скорости, сосредотачивается на процессе .
Вот некоторые предлагаемые действия:
- Научите детей стратегиям , которые они используют, а также тому, как они говорят о больших математических идеях , на важнее, чем на окончательный ответ.И скажите им, что ведущие математики мира часто проводят годы, сосредотачиваясь на ОДНОЙ проблеме, доказательстве или идее.
- Если вы работаете в классе, вы можете задавать меньше задач по математике . Когда дети видят лист или задание с 20 или 30 задачами, они могут быть более склонны найти способ быстро все это решить. Но если вместо этого вы назначите меньше проблем и убедитесь, что они оправдывают своих ответов, или поищите нескольких решений , они с большей вероятностью замедлят ход и задумаются над процессом.
- Замените набор практических задач рефлексивными вопросами , например: «Какую большую идею мы узнали сегодня?» или «С чем вы боролись сегодня?» или «Из какой ошибки вы узнали сегодня?» [источник]
- Используйте для начала беседы с установкой на рост , чтобы рассказать об их процессе и усилиях за обеденным столом или во время поездки на машине (доступно в комплекте печатных форм для установки на рост).
Наконец, и, вероятно, самое главное, я хочу призвать вас особенно внимательно относиться к своим собственным взглядам на математику и к языку , который вы используете, чтобы говорить об этом перед своими детьми. Дети смотрят, слушают и учатся на нашем примере (осознаем мы это или нет), и даже малозаметные послания с установкой на данность будут понятны детям.
Недавно авторы одного исследования пришли к выводу, что вмешательство в установление мышления неэффективно и является пустой тратой денег в математическом образовании.Проблема с их исследованием, однако, заключается в том, что оно игнорирует ключевой компонент успешного вмешательства в образ мышления: изменения в преподавателе и преподавании математики.
Если единственное усилие – это изменение языка, например, использование таких слов, как «пока» или «ошибки помогают нашему мозгу развиваться», но мышление учителя и стиль преподавания не меняются, настоящих изменений в детях не произойдет.
Вместо этого мы должны увидеть эффект «просачивания вниз» : он начинается с того, что родители и учителя меняют свое мышление в сторону математики.Это, в свою очередь, влияет на то, как мы говорим и представляем математику детям. Затем это меняет образ мышления детей с фиксированного на рост и начинает влиять на их успеваемость в классе математики и на стандартных тестах.
Вот несколько предложений для вас:
- Продолжайте узнайте и изучите важность и влияние установки на рост для себя. Это не только поможет вам развить установку на рост в математике, но и станет ярким примером для ваших детей, поскольку вы покажете им, как проявлять настойчивость.
- S p end time вместе как семья обсуждают некоторые из открытых математических задач , описанных выше. Вы можете вместе изучить новые стратегии и весело провести время, обсуждая важные идеи. Вы будете проводить время вместе и одновременно заниматься осмысленным изучением математики! Это беспроигрышный вариант.
- Если вас беспокоит собственное отношение к математике, пройдите бесплатный курс от Джо Болер. Вам также может понравиться этот бесплатный мини-курс для учителей по созданию сложных математических задач (даже если вы не учитель).
- Следуйте бесплатному 4-недельному руководству «Как научить детей менталитету роста», в нем приведены конкретные примеры того, как моделировать установку на рост и обучать ей своих детей.
При наличии времени и преднамеренности, даже самое фиксированное мышление в отношении математики может быть изменено, и самые трудные ученики могут добиться успеха, преуспеть и будут любить изучать математические идеи.
Последствия, характеристики и причины неспособности к математической обучаемости и устойчивой низкой успеваемости по математике
Резюме
Цель
Обзор преследует три цели; а) выявить последствия слаборазвитых математических компетенций для образования и трудоустройства; б) обзор характеристик детей со стабильно низкими успеваемостями по математике; и c) предоставить учебник по исследованиям в области когнитивных наук, которые направлены на выявление когнитивных механизмов, лежащих в основе этих нарушений обучаемости и связанных с ними когнитивных вмешательств.
Метод
Литература, посвященная образовательным и экономическим последствиям плохой успеваемости по математике, была проанализирована и объединена с обзорами эпидемиологических, поведенческих генетических и когнитивных исследований плохой успеваемости по математике.
Результаты
Плохие математические способности являются обычным явлением среди взрослых и приводят к трудностям при приеме на работу и трудностям во многих повседневных делах. Среди студентов около 7% детей и подростков имеют математическую неспособность к обучению (MLD), а еще 10% демонстрируют устойчиво низкие достижения (LA) по математике, несмотря на средние способности в большинстве других областей.Дети с MLD и их сверстники из LA имеют проблемы с пониманием и представлением числовых величин, трудности с извлечением основных арифметических фактов из долговременной памяти и задержки в обучении математическим процедурам. Эти недостатки и задержки не могут быть связаны с интеллектом, но связаны с дефицитом рабочей памяти у детей с MLD, но не у детей из Лос-Анджелеса. Вмешательства, направленные на этот когнитивный дефицит, находятся в стадии разработки, и предварительные результаты многообещающие.
Заключение
Нарушения в обучении по математике и трудности в обучении, связанные со стойкими низкими достижениями по математике, являются обычным явлением и не связаны с интеллектом.У этих людей есть определенное количество, а также задержки и дефициты памяти, которые, по-видимому, характерны для обучения математике. Наиболее многообещающими являются вмешательства, направленные на эти конкретные дефициты, и, кроме того, для детей с MLD вмешательства, направленные на их низкий объем рабочей памяти.
Ключевые слова: нарушение обучаемости, нарушение математической обучаемости, низкие достижения, математические познания, рабочая память
Мало кто сомневается в важности грамотности для работы и повседневной жизни в современном мире, но многие недооценивают важность арифметических и других базовых математических навыков (например,г., простая алгебра, измерение) 1 . Фактически, социальные и индивидуальные затраты на плохо развитые математические навыки могут быть выше, чем затраты, связанные с плохими навыками чтения, отчасти потому, что больше людей испытывают трудности с математикой, чем с чтением, и из-за постоянного увеличения количественных знаний, необходимых для функционирования во многих странах. рабочие места сегодня, в том числе многие рабочие места для синих воротничков 1, 2, 3, 4, 5 . Последствия подробно описаны в первом разделе, а во втором – обзор характеристик детей с математической неспособностью к обучению (MLD) и их сверстников, у которых постоянно низкие математические достижения по математике (LA), несмотря на средние способности в большинстве других областей. .В последнем разделе представлен учебник по исследованиям в области когнитивных наук с акцентом на выявление механизмов, лежащих в основе MLD и LA, и попытках разработать меры, нацеленные на них.
ПОСЛЕДСТВИЯ
Последствия плохо развитой математической компетенции были задокументированы в обзоре крупномасштабных национальных исследований чтения и математических навыков детей и взрослых в Великобритании 1 . Неудивительно, что их результаты показали, что плохие навыки чтения уменьшают возможности трудоустройства и заработной платы, но было удивительно, что плохие математические навыки привели к еще более плачевным перспективам даже для людей с хорошими навыками чтения 2, 4 .Суть иллюстрируется результатами крупномасштабного лонгитюдного исследования около 17000 человек от рождения до взрослого возраста, при котором у 10% из них в возрасте 37 2 были полностью оценены навыки чтения, математики, трудоустройства и трудовой стаж. В экзаменах по чтению и математике основное внимание уделялось повседневным навыкам. Тест по чтению включал в себя вопросы, начиная от способности понимать рекламу и заканчивая выводами о технической газетной статье, а вопросы по математике варьировались от определения правильной суммы сдачи после покупки до определения связи между повышением заработной платы и повышением стоимости жизни.Все вопросы по математике можно было легко решить с помощью базовых арифметических, измерительных и простых алгебраических навыков. Чтобы избежать недоразумений, основное внимание было уделено людям, которые не пошли в колледж после окончания средней школы, и сравнения проводились в двух группах: одна со средними навыками чтения и математики, а другая – со средним уровнем чтения, но ниже среднего.
Как для мужчин, так и для женщин плохие математические навыки были связаны с более низким уровнем полной занятости, более высоким уровнем занятости на низкооплачиваемых рабочих местах, более частыми периодами безработицы и более низкой способностью воспользоваться преимуществами обучения, предлагаемого работодателем. и, следовательно, более низкие показатели продвижения по службе.Многие женщины в этой группе в конечном итоге покинули рынок труда на условиях полной занятости, и, хотя 4 из 5 мужчин были заняты полный рабочий день, 50% из них имели низкий годовой доход по сравнению с 26% мужчин в группе сравнения. Эти данные не ограничиваются Великобританией, поскольку аналогичные отношения обнаруживаются в Соединенных Штатах 4 .
Эти результаты и результаты других крупномасштабных исследований, проведенных в Соединенных Штатах и Канаде, также указывают на то, что математические способности ниже среднего в начале обучения связаны с повышенным риском плохих математических навыков в конце обучения, сверх того, что влияние семейного происхождения, социального и эмоционального функционирования ребенка, его интеллекта и способностей к чтению 1, 6 .Раннее выявление детей, подверженных риску длительных трудностей в математике, имеет решающее значение. Без вмешательства эти ранние дефициты, вероятно, выльются в пожизненную борьбу на рабочем месте и в удовлетворении повседневных потребностей современного мира.
ХАРАКТЕРИСТИКИ
ОПРЕДЕЛЕНИЕ
Диагностическое и статистическое руководство по психическим расстройствам Американской психиатрической ассоциации определяет MLD с точки зрения несоответствия между результатами тестов по математике и ожидаемыми результатами, основанными на возрасте, интеллекте и годах образования и для взрослых существенно мешает их повседневной деятельности 7 .Однако не было установлено, что дети (или взрослые) с низкими показателями успеваемости по математике и с низким интеллектом имеют разные формы дефицита математического познания, чем дети с низкими достижениями по математике и средним интеллектом. Некоторые результаты, описанные в статье CAUSES , предполагают, что математические недостатки могут быть одинаковыми, но механизмы, вызывающие эти недостатки, могут отличаться. На этом этапе подразумевается, что уровень интеллекта может не иметь значения при выявлении математических недостатков, но для детей с более высоким или более низким интеллектом могут потребоваться различные подходы к исправлению.
Среди исследователей в этой области появляется консенсус относительно полезности различения детей с MLD и их сверстников из Лос-Анджелеса, с ограничением, что показатели интеллекта выше 15 -го процентиля 8, 9 . Дети, набравшие 10 -й процентиль или ниже по стандартизированным тестам на успеваемость по математике в течение как минимум двух последовательных академических лет, обычно классифицируются как MLD в исследовательских исследованиях, а дети, набирающие от 11 -го до 25 -го процентилей, включительно, минимум два года подряд относятся к категории LA.Реакция на вмешательство также может быть использована для выявления и лечения детей с MLD и LA и описана в COGNITIVE INTERVENTIONS .
ЗАБОЛЕВАЕМОСТЬ
На основе нескольких проспективных исследований населения и многих более мелких исследований около 7% детей и подростков будут диагностированы как MLD по крайней мере в одной области математики до окончания средней школы, а также в дополнительных 10% детей и подростков будут идентифицированы как LA 10, 11, 12 .Анализ более чем 340 000 11-летних детей в период с 1998 по 2007 год включительно показал, что от 5% до 7% в каждом учебном году отстают от 3-4 классов по математике, что соответствует уровню дефицита, соответствующему MLD 1 .
В любой год 10% детей будут иметь баллы по математике на уровне или ниже 10 -го процентиля по определению, но не все из них будут набирать баллы в этом диапазоне через несколько лет, и, таким образом, оценочная заболеваемость MLD в 7% составляет ниже, чем предлагаемое пороговое значение 10 -го процентиля; то же самое касается оценок в диапазоне LA.Критерии нескольких лет важны, потому что многие дети, получившие низкие баллы в течение одного учебного года, получают более высокие баллы в последующие годы, и у этих детей нет когнитивных нарушений, характерных для детей, которые постоянно набирают в диапазонах MLD и LA 13, 14 . Наконец, крупномасштабные исследования, проведенные в Великобритании, показали, что около 23% взрослых не имеют достаточного числа людей, то есть не обладают математическими способностями, необходимыми для многих повседневных повседневных дел.
Причина, по которой этот процент выше, чем объединенные оценки MLD и LA, неизвестна, но может быть связана с исключением детей с низким IQ из исследований MLD и LA, потерей базовых математических навыков при неиспользовании или некоторой их комбинацией 15 .Какими бы ни были причины, у детей и взрослых часто бывают слаборазвитые математические способности. Как мы рассмотрим в ПРИЧИН, для некоторых из этих людей трудности с математикой связаны не с обучением или интеллектом, а скорее с одним или несколькими конкретными когнитивными задержками или недостатками.
ЭТИОЛОГИЯ
Исследования близнецов и семей выявили генетический и экологический вклад в индивидуальные различия в успеваемости по математике, а также в MLD и LA 16, 17, 18 .Исследование близнецов в начальной школе выявило генетический, а также общий (между парой близнецов) и уникальный вклад окружающей среды в индивидуальные различия в успеваемости по математике и в MLD, причем последний определяется порогами в 5 th и 15 th процентиля на тесте успеваемости по математике. В зависимости от класса и используемого теста по математике от 50% до 67% индивидуальных различий в успеваемости по математике были связаны с генетической изменчивостью, а оставшаяся часть – с общим и уникальным опытом 16 .
Те же генетические факторы, которые способствовали MLD, способствовали индивидуальным различиям на всех уровнях производительности 16, 19 . Не существует конкретных генов MLD, скорее генетическое влияние на MLD такое же, как и те, которые влияют на успеваемость по математике по всему диапазону баллов. Примерно 33% генетических влияний на достижения в математике перекрывали генетические влияния, способствующие изменчивости интеллекта, 33% перекрывали генетические влияния, способствующие изменчивости способностей к чтению независимо от интеллекта, а 33% были уникальными для математики.
Умеренное генетическое влияние на MLD не следует приравнивать к ограничению возможностей устранения этих недостатков, потому что изменения в окружающей среде человека могут изменить относительную степень этих генетических и средовых влияний. В любом случае генетические исследования также указывают на важное влияние окружающей среды на изучение математики и MLD. Учеба в школе влияет на успеваемость по математике в целом, а новые вмешательства для MLD ( COGNITIVE INTERVENTIONS ) улучшают успеваемость этих детей по математике сверх влияния общего образования, даже если они не устраняют различия в математических результатах 20 .
КОМОРБИДНЫЕ ЗАБОЛЕВАНИЯ
Генетические факторы, влияющие на успеваемость в академических областях, могут объяснить, почему многие дети с MLD имеют неспособность читать (RD) или другие трудности, мешающие обучению в школе, такие как синдром дефицита внимания и гиперактивности (ADHD) 10, 12, 21 . Barbaresi et al. обнаружено, что от 57% до 64% студентов с MLD также имели RD, в зависимости от диагностических критериев, используемых для определения MLD. Ранее отмеченное крупномасштабное исследование 11-летних детей в Великобритании показало, что 6% этих детей показали уровень успеваемости, соответствующий MLD, и 2 из 3 из них также плохо читали 1 .
Исследования детей, выявленных в их школах с особыми трудностями в обучении, показывают, что эти дети часто страдают множеством социальных недостатков и что дети, направленные на обследование из-за серьезных эмоциональных или поведенческих проблем в школе, часто классифицируются как неспособные к обучению 22, 23 . Хотя большинство этих исследований сосредоточено на РД, они все еще могут иметь отношение к MLD. Один метаанализ показал, что в группе и по сравнению с детьми с обычными достижениями (ТА) дети, которые классифицируются как неспособные к обучению (чтению, математике или обоим), испытывают большее социальное отторжение, имеют плохие навыки решения социальных проблем и другие сообщают, что они, помимо прочего, являются агрессивными и незрелыми.
В то же время многочисленные крупномасштабные проспективные исследования, отслеживающие взаимосвязь между семейным происхождением, социально-эмоциональными факторами, контролем внимания, интеллектом и академическими навыками при поступлении в школу (т. Е. В возрасте от пяти до шести лет) и длительном обучении. зачетные результаты по математике и чтению не находят связи между социально-эмоциональными проблемами и плохими результатами по математике 6 . Лучшим показателем успеваемости по математике в школе были математические навыки на начальном уровне.Ранние навыки внимания также предсказывали более поздние достижения, но величина этого эффекта была менее 25% от величины эффекта для математических навыков начального уровня. Проблемы интернализации (например, тревоги) и экстернализации (например, агрессии) при поступлении в школу не были связаны с более поздними достижениями и не были более общими показателями социальных навыков. Этот анализ предполагает, что ранний социальный и поведенческий профиль детей не связан с их долгосрочными достижениями в математике.
Несоответствующие результаты указывают на то, что в этой области предстоит проделать большую работу, особенно в отношении детей с MLD.На этом этапе можно сделать предварительный вывод о том, что социально-эмоциональное функционирование не оказывает причинного влияния на обучение детей математике, но у детей с MLD может быть множество сопутствующих социальных и поведенческих проблем.
ПРИЧИНЫ
Ученые-когнитивисты и нейропсихологи провели подробные исследования количества, счета и арифметических способностей детей с MLD и LA, а также детей и взрослых с приобретенными (после черепно-мозговой травмы) математическими трудностями, пытаясь найти решение. определить источник или источники их плохих достижений по математике 24, 25, 26, 27, 28, 29 .Многие из этих исследований также включают оценку общих способностей – интеллекта, рабочей памяти и скорости обработки данных – которые влияют на обучение в академических областях. Цель состоит в том, чтобы определить, есть ли когнитивные дефициты, характерные для изучения математики, и являются ли эти дефициты независимыми или взаимодействуют с общими способностями предметной области во время математического обучения или успеваемости. Поведенческие генетические исследования предполагают как совпадение генетических механизмов и механизмов окружающей среды, влияющих на математику и другие формы обучения в школе, так и механизмы, которые уникальны для математики.Рассмотренные здесь результаты когнитивных исследований согласуются с этими выводами.
Прежде чем перейти к этому обсуждению, важно проиллюстрировать серьезность дефицита математических достижений у детей с MLD и их сверстников из Лос-Анджелеса. показывает эти дефициты в сравнении с детьми ТА и группой детей с показателями интеллекта ниже 10 -го процентиля (низкий IQ, средний IQ = 78). Эти данные взяты из Миссурийского лонгитюдного исследования математического развития и инвалидности и показывают траектории успеваемости детей в этих группах с первого по пятый класс включительно 30, 31 .В группу MLD вошли дети, которые попали в нижние 10 процентов выборки по тесту на успеваемость по математике со второго по пятый класс включительно, тогда как группа LA включала детей с баллами между 11 -м и 25 -м процентилями включительно. У детей в группе MLD были низкие средние оценки IQ ( M = 91) и средние оценки детей LA ( M = 101) и TA ( M = 103).
Необработанная математика Успеваемость с первого по пятый класс включительно.Скобки – стандартные ошибки. LIQ = низкий IQ, MLD = математическая неспособность к обучению, LA = низкий уровень успеваемости, TA = обычно достигаемый.
Наиболее поразительные результаты заключаются в том, что достижения детей с MLD по математике отстают от детей с низким IQ после третьего класса, а достижения групп LA и Low-IQ частично совпадают, несмотря на разницу в 23 балла в среднем IQ ( средние показатели интеллекта в группах с низким IQ и LA составляли 7 -й и 53 -й процентили соответственно).В разных классах преимущество детей с ТА по математике увеличивается, но разрыв в чтении сокращается. Ясно, что плохие достижения по математике в группах MLD и LA нельзя объяснить низким интеллектом или способностями к чтению.
Когнитивные и нейропсихологические исследования сосредоточены на выявлении недостатков, лежащих в основе этих моделей достижений. Последовательные результаты предполагают дефицит способности формировать представления числовой величины, формировать в памяти представления основных арифметических фактов или извлекать эти факты после того, как воспоминания сформированы, а также задержки в развитии в обучении арифметическим процедурам.
НОМЕР
Имеются данные о наличии базовой системы взаимосвязанных количественных навыков, которые могут способствовать изучению детьми формальной математики в школе. 32 Человеческие младенцы, дошкольники, а также люди из многих других видов могут отличать меньшее от большего количества (например, 8 предметов против 16 предметов), упорядочивать ряд относительных количеств (например, 2, 3, 4, предметы), а некоторые (включая младенцев и дошкольников) обладают элементарной способностью считать и заниматься простым сложением и вычитанием 33, 34, 35, 36 .Эти основные способности составляют основу раннего детского чувства числа, которое проявляется в их способности (а) воспринимать количество наборов из 3-4 предметов или действий, не считая 37, 38, 39 ; (b) использовать невербальные процессы или счет для количественной оценки небольших наборов объектов, а также для добавления и вычитания небольших количеств из этих наборов 40, 41 ; и (c) оценить относительную величину наборов объектов и результаты простых числовых операций 42 .Баттерворт и его коллеги предположили, что MLD является результатом недостатков в двух из этих фундаментальных систем определения чисел, одна из которых поддерживает представление и неявное понимание точного количества небольших наборов объектов и символов (например, арабских цифр), которые представляют их. количества (например, ‘3’ = ▪▪▪), а другой для представления приблизительной звездной величины больших количеств 27, 43 .
В соответствии с этой гипотезой, дети с MLD и, в меньшей степени, дети LA могут иметь дефицит или задержку развития в обеих этих основных системах представления и обработки чисел 44, 45, 46, 47 .В качестве примера Кунц и Берч попросили учащихся третьего и четвертого классов с MLD и их сверстников по TA определить, совпадают ли комбинации арабских цифр (например, 3–2), числовых наборов (▪▪-▪▪) или цифр и наборов. (2-▪▪) или разные (3-▪▪) 46 . Это простое задание предусматривало оценку репрезентативной системы детей для точных небольших количеств. Подтверждая более ранние выводы 48 , дети ТА обрабатывали представления трех (например, 3, ▪▪▪) так же быстро, как они обрабатывали представления двух.Дети с MLD также могли быстро обрабатывать представления двух, но, похоже, полагались на счет для определения количества трех. Результаты показывают, что некоторые дети с MLD могут не иметь врожденного представления для числа три или точная система представления не позволяет надежно различать два и три.
Последующие исследования, в которых детей просили мысленно комбинировать наборы предметов (например, ▪▪▪▪) и арабские цифры, чтобы соответствовать целевому числу (например, ▪▪▪▪ + 2 = 5), подтверждают медленную обработку чисел для группы детей МЛД и ЛА 8, 31, 49 .Баллы беглости показывают скорость и точность, с которой дети получают доступ к этим небольшим числовым величинам и комбинируют их, и иллюстрируют пятилетние тенденции для тех же групп, представленных в 31 . Беглость обработки чисел у детей с MLD находится на том же уровне или немного ниже, чем у детей из группы с низким IQ. К пятому классу успеваемость обеих групп сопоставима с уровнем учеников третьего класса ТА. Дети из Лос-Анджелеса примерно на год отстают от своих сверстников из ТА.Не менее важно, что тенденции не показывают, что группы MLD и LA догоняют своих коллег по TA; во всяком случае, после третьего класса разрыв увеличивается.
Показатели беглости для определения и комбинирования величин, связанных с наборами предметов (например, ▪▪▪) и арабскими цифрами (например, ▪▪▪ + 2 = 5) с первого по пятый класс включительно. Скобки – стандартные ошибки. LIQ = низкий IQ, MLD = математическая неспособность к обучению, LA = низкий уровень успеваемости, TA = обычно достигаемый.
Стандартная математическая числовая строка (вверху), сжатая числовая строка (в центре) и очень сжатая числовая строка для детей с MLD.Две последние линии отображают мысленное расстояние между величинами, представленными в системе представления приблизительных величин, и чем больше понимание, тем труднее различать большие величины.
Размещение детьми цифр на физической числовой прямой использовалось для того, чтобы сделать выводы о природе их приблизительной системы представления величин. Размещение, соответствующее натуральному логарифму чисел, может отражать зависимость от потенциально внутренней системы, которая представляет приблизительные величины 50, 51 .Эти размещения отражают расширение числовой линии для меньших значений, как показано в средней части рисунка 4, и сокращение для более крупных. «Умственное расстояние» между единицей и двумя намного больше, чем расстояние между восемью и девятью, и, таким образом, детям легче различать разницу в величинах между единицей и двумя, чем между восемью и девятью, даже несмотря на то, что фактическая разница такая же. . С помощью обучения дети в конечном итоге выучивают математическую числовую линию; расстояние между двумя последовательными числами одинаково независимо от положения в строке.Какой бы ни была лежащая в основе репрезентативная система, точность линейного размещения предопределяет более поздние достижения в математике 52 .
В одном из наших исследований мы сравнили размещение учеников первого и второго классов MLD, LA и TA по числовой строке от 0 до 100 44 . Групповые различия выявлялись с использованием групповых медиан, с оценкой проб за следом, соответствовало ли размещение логарифмическому (предполагая использование приблизительной системы величин) или линейному (предполагающему изучение математической числовой линии) мысленному представлению положения по числу. линии и с несколькими мерами абсолютной погрешности.Общая картина предполагала, что дети с MLD в большей степени зависели от приблизительной репрезентативной системы – они не учили математическую числовую линию так же легко, как другие дети – и в соответствии с гипотезой Баттерворта, их представление величины оказалось более сжатым, чем у LA. и дочерние элементы TA, представленные нижней числовой строкой в. Другими словами, детям с MLD трудно различать величины, представленные даже маленькими цифрами, возможно, из-за недостатка или задержки в системе для представления приблизительных величин.Последующее наблюдение за этими детьми до пятого класса показало, что дети с низким IQ (не оцениваемые в первом исследовании) догнали своих сверстников ТА по этой задаче к третьему классу, дети из Лос-Анджелеса – к четвертому, но дети с MLD все еще имели не догнали пятую, хотя и сократили разрыв 31 .
Хотя и неубедительные, эти исследования показывают, что многие дети с MLD и, в меньшей степени, их сверстники из Лос-Анджелеса не имеют сильного интуитивного ощущения числовой величины, что этот дефицит не связан с интеллектом или способностями к чтению.Необходимы последующие исследования, но тенденции развития, показанные на рисунке, предполагают, что эти трудности распространятся далеко за пределы начальной школы. Являются ли они результатом ранних нарушений развития нервной системы в фундаментальных системах для представления малых, точных величин и приблизительных величин, как предположил Баттерворт, еще предстоит определить. В любом случае, низкая успеваемость в этих простых числовых задачах свидетельствует о достижениях ниже среднего по математике, помимо влияния интеллекта, рабочей памяти или навыков чтения 49 .
АРИФМЕТИКА
Типичное развитие
К тому времени, когда они начинают формальное обучение, большинство детей координируют свои знания чисел и навыки счета с неявным пониманием сложения и вычитания, и в результате могут начать использовать числовые слова и арабские цифры для решения формальные задачи сложения и вычитания (например, «Сколько будет 3 + 2?») 53, 54, 55 . Хотя дети этого возраста будут использовать сочетание различных стратегий решения проблем, наиболее распространенные подходы включают счет, иногда с использованием пальцев, а иногда и без них. 56 .Процедуры min и sum – это два распространенных способа подсчета детьми 57 . Процедура min включает в себя указание слагаемого с большим значением, а затем подсчет количества раз, равный значению меньшего слагаемого; например, сказать «пять», а затем считать «шесть, семь, восемь», чтобы решить «5 + 3 =?». Процедура суммирования включает в себя подсчет обоих слагаемых, начиная с 1. Использование подсчета результатов в развитии долговременной памяти, репрезентации основных фактов 56 . После формирования эти представления поддерживают использование процессов, основанных на памяти; в частности, прямой поиск арифметических фактов и разложение.Последний включает в себя восстановление ответа на основе поиска частичной суммы; например, 6 + 7 можно решить, получив ответ на 6 + 6 и затем прибавив 1 к этой частичной сумме.
Развитие, однако, – это не просто переход от использования менее сложных методов подсчета к более сложным стратегиям поиска 58 . Скорее, в любое время дети могут использовать любую из множества известных им стратегий для решения различных задач; они могут получить ответ на 3 + 1, но считают, чтобы решить 5 + 8.Что меняется, так это сочетание стратегий: сложные используются чаще, а менее сложные – реже 59 .
Дети с MLD и LA
Те же методы, которые были разработаны для изучения арифметических способностей детей TA, были применены к исследованию детей с MLD и LA и выявили сходства и несколько заметных различий 8, 13, 60, 61 , 62, 63 . Дети с MLD и LA используют те же подходы к решению проблем, что и их сверстники TA, но отстают в развитии процедурных навыков и имеют более стойкие трудности с запоминанием основных арифметических фактов.
Процессуальная компетенция
Дети с MLD и их сверстники из Лос-Анджелеса совершают больше процедурных ошибок, чем дети того же класса, когда они решают простые (например, 4 + 3) и сложные (например, 745–198) арифметические задачи (4 + 3) , а также текстовые задачи 8, 60, 64, 65 . Распространенная ошибка первоклассников с MLD – занижение счета при использовании процедуры min; для задачи «5 + 3 =?» они скажут «пять, шесть, семь». Они правильно считают три числовых слова, минимальное слагаемое, но не используют «пять» для обозначения кардинального значения большего слагаемого.Даже когда эти дети не совершают ошибок, они склонны использовать незрелые процедуры 60, 62, 66 . К первому классу большинство детей ТА могут считать молча («в уме») и использовать процедуру min для решения простых задач сложения, но первоклассники с MLD используют свои пальцы, чтобы следить за счетом, и чаще используют процедуру суммирования. чем их коллеги по ТА. Дети LA также чаще используют пальцы, чем дети TA, но используют процедуру min чаще, чем дети с MLD 8, 62, 67, 68 .Для простой арифметики это означает задержку в развитии примерно на два-три года для детей с MLD и примерно на один год для детей из Лос-Анджелеса.
Недостатки и задержки детей с MLD и LA при решении простых задач становятся более очевидными, когда они пытаются решить более сложные 69, 70 . Во время решения многоступенчатых арифметических задач, таких как 45 × 12 или 126 + 537, четвероклассники с MLD совершали больше ошибок, чем их сверстники ТА 64 , соответствующие IQ.Ошибки включают несовпадение цифр при записи частичных ответов или при переносе или заимствовании из одного столбца в другой. Распространенные ошибки вычитания включали вычитание большего числа из меньшего (например, 83–44 = 41), невозможность уменьшения после заимствования из одного столбца в следующий (например, 92–14 = 88; 90 не уменьшалось до 80) и заимствование через 0 (например, 900–111 = 899) 66 . Эти закономерности были обнаружены для детей с MLD и LA, независимо от их успехов в чтении.Опять же, ошибки – это в основном задержки в развитии, а не постоянные проблемы; они совершаются младшими детьми ТА 71 , и дети с MLD и LA в конечном итоге осваивают правильные процедуры, хотя и на несколько лет позже, чем их сверстники из TA.
Память для основных фактов
Наиболее последовательный результат исследования состоит в том, что большинство детей с MLD и подмножество детей из Лос-Анджелеса постоянно испытывают трудности с сохранением основных арифметических фактов в долговременной памяти или их извлечением после того, как они усвоены 14, 60, 62 .Дело не в том, что эти дети не могут запоминать или извлекать какие-либо основные факты, они скорее демонстрируют стойкие различия в частоте, с которой они правильно извлекают их, и в структуре ошибок извлечения. Было предложено три различных механизма в качестве потенциального источника этих трудностей поиска.
Первый – это недостаток способности формировать фонетические, языковые и звуковые репрезентации в долговременной памяти 24 . Эта гипотеза вытекает из того, что дети с самого начала полагались на счет, когда они впервые учатся решать арифметические задачи, поскольку счет зависит от фонетических и семантических систем языковой области.Любое нарушение способности представлять или извлекать информацию из этих систем теоретически должно приводить к трудностям в формировании ассоциаций проблема / ответ для арифметических задач во время процесса подсчета, а также приводить к сопутствующим проблемам с поиском слов во время акта чтения. . Исследования арифметических нарушений после травмы головного мозга показывают, что извлечение дополнительных фактов действительно поддерживается системой нейронных структур, которые, по-видимому, поддерживают фонетические и семантические представления и задействованы во время возрастающих процессов, таких как счет 72, 73 .Однако эти результаты следует интерпретировать с осторожностью, поскольку они основаны на исследованиях взрослых, а мозг и когнитивные системы, поддерживающие раннее обучение, во многом отличаются от тех, которые поддерживают такую же компетенцию во взрослом возрасте 74, 75 .
Второй механизм – это недостаток способности препятствовать поступлению нерелевантных ассоциаций в рабочую память в процессе извлечения фактов 76 . Эти вторжения часто оцениваются, прося детей только попытаться запомнить ответ и не использовать счет или любую другую процедуру для решения проблемы 26 .Если вторжение мешает детям получить правильный ответ, тогда соответствующие ошибки поиска должны быть связаны с цифрами в представленной задаче. Примеры включают получение 36 при попытке решить 6 × 5 или 8 при попытке решить 4 + 7. Первая называется ошибкой, связанной с таблицей, потому что это правильный ответ на аналогичную задачу (6 × 6) в таблице умножения, а вторая называется ошибкой счетной строки, потому что полученный ответ следует за одним из слагаемых в счетная строка (8 следует за 7) 77, 78 .Оба типа вторжений происходят для детей ТА, как и вторжения между операциями; например, напоминая 40 для 8 + 5 79 . Все эти типы вторжений более распространены и устойчивы в большем количестве классов для детей с MLD и некоторых детей из Лос-Анджелеса. Подростки с MLD часто сталкиваются с вторжениями, связанными с таблицами, когда они решают простые задачи умножения, а в начальной школе вторжения со счетными строками являются обычным явлением для поиска сложения. 14, 76 .
Третий предложенный механизм – это недостатки или задержки в системах счисления, которые поддерживают точное представление малых величин и приблизительное представление больших величин 27 .Обоснование этого состоит в том, что раннее обучение детей арифметике может зависеть от этого интуитивного понимания числа: их способность оценивать приблизительные ответы при первом обучении решать арифметические задачи может частично зависеть от системы представления приблизительных величин. Другими словами, предполагается, что эти базовые системы счисления обеспечивают часть основы для изучения вышеуказанных чисел (например, система с основанием 10) и арифметики в школе. С этой точки зрения, дефицит поиска вторичен по отношению к более фундаментальному дефициту в приблизительной репрезентативной системе.Эмпирическая оценка потребует проведения лонгитюдных исследований, чтобы определить, существует ли связь между дефицитом обработки чисел в дошкольном возрасте и дефицитом поиска в начальной школе. Хотя этот тип лонгитюдного исследования еще предстоит провести, анализ связи между показанным дефицитом беглости речи и дефицитом извлечения у детей с MLD и детей LA с частыми ошибками вторжения предполагает, что эти два дефицита не связаны. Например, у некоторых детей из Лос-Анджелеса медленная обработка чисел обнаруживается при отсутствии дефицита поиска 80 .
В целом очевидно, что трудности с изучением или извлечением основных арифметических фактов – обычная и постоянная проблема для детей с MLD и для подгруппы детей из Лос-Анджелеса. Из предложенных механизмов наиболее убедительными доказательствами являются ошибки вторжения, то есть дефицит поиска частично связан с проникновением связанной, но не относящейся к делу информации в рабочую память, когда эти дети пытаются запомнить арифметические факты. Не все их ошибки происходят из-за вторжений, однако можно предположить, что в них может быть задействовано несколько механизмов и что у разных детей могут быть проблемы с извлечением по разным причинам.Остается определить, связаны ли эти альтернативные механизмы с языковой системой и недостатками обработки чисел.
Прежде чем перейти к Общие дефициты домена , я отмечу, что ошибки поиска сами по себе не могут использоваться для определения наличия у ребенка MLD. Это связано с тем, что во многих учебных программах по математике, используемых в Соединенных Штатах, не акцентируется внимание на изучении основных фактов, и поэтому многие дети не знают их всех. Дети с MLD и многие из их сверстников из Лос-Анджелеса совершают больше этих ошибок, чем дети TA, и, как уже отмечалось, больше из них являются ошибками вторжения.Доказательства того, что у этих детей трудности с поиском фактов – это реальный дефицит, а не результат ограниченной практики, получены из исследований, проведенных в странах, которые делают упор на запоминание основных фактов. Дети в Гонконге, где упор делается на запоминание, имеют те же процедурные задержки и дефицит поиска для групп детей из MLD и LA, что и в США и многих других странах 81 . Обычные учебные программы по математике в Соединенных Штатах не вызывают этих трудностей, но затрудняют их выявление.
ОБЩИЕ ДЕФИЦИТЫ ДОМЕНА
По определению, неспособность к обучению определяется успеваемостью ребенка в тестах на успеваемость и в школе в целом, а для взрослых – влиянием плохого чтения и математических навыков на их повседневное функционирование, в том числе их занятость 1 . Поэтому как для детей, так и для взрослых важно оценивать не только конкретные недостатки (например, в обработке чисел), но и другие когнитивные факторы, которые предсказывают успеваемость в школе и производительность на работе.Эти общие способности к обучению включают подвижный интеллект, рабочую память и скорость обработки данных. Хотя измерения этих различных способностей обычно коррелируют друг с другом, все они оценивают уникальные компетенции, которые потенциально важны для академического обучения 82, 83, 84, 85 .
Полезной эвристикой является иерархическая организация этих компетенций Кэрролла 86 . Гибкий интеллект находится на вершине и представляет процессы, которые влияют на обучение в разных контекстах и содержании, особенно на простоту изучения новых и сложных концепций 83, 87, 88 .Рабочая память и скорость обработки находятся на втором уровне и представляют собой широкие возможности, влияющие на обучение во многих, но не во всех областях. На третьем уровне находятся более узкие области компетенции, включая математику. Исследования результатов по широкому кругу тестов с бумагой и карандашом выявили по крайней мере две основные математические области: Числовые возможности, которые оценивают компетентность в арифметике, а для маленьких детей – их количество и умение считать, и Математическое мышление, которое оценивает более абстрактные математические знания. 89 .
Интеллект
Гибкий интеллект – лучший индивидуальный показатель академической успеваемости 90, 91 . В качестве одного примера, пятилетнее проспективное исследование более 70 000 студентов показало, что интеллект в возрасте 11 лет объясняет почти 60% отклонений в национальных тестах по математике, проводимых в возрасте 16 лет 92 . Интеллект также передается по наследству, и, похоже, существуют общие гены, способствующие корреляции между интеллектом и математическими достижениями 93 .Одна из возможностей состоит в том, что медленный математический рост детей с MLD и их сверстников из Лос-Анджелеса и частичная наследственность этих расстройств могут быть связаны с интеллектом.
Хотя это может быть фактором, способствующим развитию детей с MLD, он, по-видимому, не является основным. Как отмечено в CAUSES и возвращаясь к этому, успеваемость детей с MLD по математике значительно ниже, чем у детей с гораздо более низкими показателями интеллекта. Во всяком случае, дети с MLD должны иметь более высокие баллы по математике, чем они, если бы интеллект был основным источником их неспособности к обучению.Интеллект вообще не может быть фактором для детей из Лос-Анджелеса, учитывая, что их интеллект средний. Это не означает, что дети или взрослые с более низкими показателями интеллекта не испытывают трудностей при изучении математики. Действительно, контроль интеллекта сократил разрыв в математических достижениях по сравнению с группами TA и Low-IQ, показанными в, но не внес свой вклад в разрыв между группами TA и MLD; то есть результативность детей с низким IQ соответствовала их показателям интеллекта, но показатели детей с MLD были ниже ожидаемых.Дело в том, что есть много детей и, предположительно, взрослых, которые борются с некоторыми областями математики по причинам, не связанным с их интеллектом.
Рабочая память
Рабочая память – это способность использовать фокусировку внимания для удержания информации в уме при выполнении других умственных действий; отфильтровать информацию, не имеющую отношения к поставленной задаче; и переключаться с одной задачи на другую. Когнитивные ученые определили, что рабочая память зависит от трех основных систем.Центральный исполнительный орган, обеспечивающий нисходящий контроль над информацией, которая активна (т. Е. Осознает ее) в двух репрезентативных системах 94, 95 . Это языковой фонологический цикл и визуально-пространственный блокнот 96, 97 . Существует четвертая система, эпизодический буфер, который способствует интеграции языковой и зрительно-пространственной информации и вызывает воспоминания о личных переживаниях, но об этой системе известно не так много, как о трех других 98 .
Связь между объемом рабочей памяти и результатами тестов на успеваемость по математике и математических познавательных задач четко установлена 8, 99 . Независимо от того, оценивались ли они одновременно или на один или несколько лет раньше, чем выше возможности центрального исполнительного органа, тем лучше показатели успеваемости по математике и математических познаний 100, 101, 102 . Важность фонологической петли и визуально-пространственного блокнота для рисования зависит от содержания оцениваемой математики 8, 100 .Фонологический цикл, по-видимому, поддерживает процессы, которые включают в себя артикуляцию чисел, например, счет, решение математических задач со словами и может быть связан с поиском арифметических фактов 24, 99, 102 . Блокнот для визуально-пространственных эскизов поддерживает обучение в более широком количестве математических областей, таких как числовая линия и аспекты перевода текстовых задач в математические уравнения 104, 105 .
Дети с MLD и LA дети
Дети с MLD имеют дефицит рабочей памяти в каждой из трех основных систем, что, в свою очередь, способствует их медленному прогрессу в изучении математики помимо вклада интеллекта и скорости обработки данных 8, 67, 100, 106, 107 .Их скомпрометированный центральный исполнительный орган особенно важен 8, 108, 109 , но это отношение осложняется по крайней мере тремя подкомпонентами центрального исполнительного органа, каждый из которых может влиять на математическое обучение по-разному. К ним относятся умение сохранять информацию в рабочей памяти, переключение задач и запрещение поиска нерелевантной информации 9, 110, 111, 112 .
В любом случае, трудности, препятствующие активации нерелевантной информации в рабочей памяти, были независимо связаны с плохими математическими достижениями несколькими исследовательскими группами 110, 111, 112 .Как отмечено в документе Память основных фактов , дефицит этого компонента центральной исполнительной власти может объяснять детям с высокой частотой вторжений MLD во время акта поиска арифметических фактов и может быть фактором, способствующим сопутствующей патологии MLD и RD. у некоторых детей; плохие читатели менее способны подавлять не относящиеся к контексту значения двусмысленных слов (например, берег реки, кассир в банке), значения похожих по звучанию слов (например, пациенты, терпение) и извлекать больше контекстной информации, чем это необходимо для прочитанного отрывка 113 .Хотя содержание арифметики и чтения различается, основные причины некоторых (но не всех) трудностей в обучении в этих областях могут быть одинаковыми. Ошибки вторжения, которые возникают у некоторых детей из Лос-Анджелеса, также соответствуют такому дефициту, но их центральные исполнительные баллы обычно находятся в среднем диапазоне. Тем не менее, центральные исполнительные меры, использованные в этих исследованиях, в первую очередь оценивали компоненты обслуживания и переключения задач, а не компонент тормозящего контроля 8, 106 .Таким образом, еще предстоит установить прямую связь между компонентом тормозящего контроля центральной исполнительной власти и ошибками вторжения, которые способствуют плохому поиску фактов у детей с MLD и их сверстников из LA.
Мы обнаружили, что дети из Лос-Анджелеса имеют средние баллы по измерениям фонологической петли и зрительно-пространственного блокнота 8 , но у некоторых из этих детей могут быть тонкие зрительно-пространственные дефициты 106 . Как уже отмечалось, у детей с MLD есть недостатки в обеих этих системах рабочей памяти, что, в свою очередь, может способствовать их медленному прогрессу в определенных областях математики 8, 44 .Например, плохая зрительно-пространственная рабочая память детей с MLD может способствовать их медленной обработке чисел и низкой производительности в задаче числовой линии по сравнению с детьми LA с IQ-соответствием. Потенциальный вклад зрительно-пространственной рабочей памяти в эти специфические недостатки интригует, потому что считается, что точные и приблизительные системы представления величины расположены в той области мозга, которая также способствует способности формировать зрительно-пространственные представления. Напротив, частые ошибки, совершаемые детьми с MLD, когда они используют счет для решения простых задач сложения, связаны с их плохой фонологической рабочей памятью, то есть их способностью сохранять языковые звуки (например,g., числовые слова) в уме, когда занят другой задачей (например, отслеживает процесс подсчета).
Очевидно, что еще многое предстоит узнать о связи между несколькими компонентами рабочей памяти и индивидуальными различиями в обучении в разных областях математики в целом и о вкладе этих систем рабочей памяти в плохие достижения детей с MLD и их сверстники из Лос-Анджелеса. На этом этапе мы можем сделать вывод, что у детей с MLD есть повсеместный дефицит по всем системам рабочей памяти, которые были оценены, но наше понимание отношений между конкретными компонентами рабочей памяти и конкретными дефицитами математического познания находится в зачаточном состоянии.Многие дети с ЛА, напротив, имеют нормальную фонологическую рабочую память, особенно если успеваемость по чтению средняя или выше, а также нормальную способность использовать функции контроля внимания центральной исполнительной власти для сохранения информации в рабочей памяти. У многих из этих детей, по-видимому, также имеется нетронутая система зрительно-пространственной рабочей памяти, но у некоторой их части могут быть более тонкие недостатки. Наиболее многообещающие результаты предполагают, что у детей с ЛП наблюдается незначительный дефицит тормозящего компонента управления центральной исполнительной властью 8, 9 , но мы ждем подтверждения.
Скорость обработки
Более высокая скорость обработки связана с более высокими оценками достижений, хотя сила этих отношений меньше, чем между интеллектом, рабочей памятью и достижением 87, 88 . Когнитивные ученые в настоящее время обсуждают, вызваны ли индивидуальные различия в рабочей памяти более фундаментальными различиями в скорости когнитивной обработки и принятия решений, или фокус внимания, связанный с центральным исполнительным директором, ускоряет обработку информации 114, 115 .Независимо от направления взаимосвязи, скорость обработки имеет несколько подкомпонентов, которые не зависят от рабочей памяти 86 , и иногда оказывается, что она лучше предсказывает математические результаты, чем рабочая память или независимый предсказатель после контроля рабочей памяти и интеллекта 116 , 117 . В процессе развития скорость обработки данных быстро увеличивается для многих простых задач в первые годы начальной школы, а затем асимптотически приближается к уровням, близким к взрослым, в подростковом возрасте 118 .Механизмы, лежащие в основе этого паттерна, не до конца понятны, но могут включать в себя существенные улучшения в компоненте фокуса внимания центральной исполнительной системы и быстрое увеличение нейронального белого вещества (которое ускоряет нейронную передачу) в этом возрастном диапазоне 119 .
Дети с MLD и LA Дети в среднем тратят больше времени на решение задач, чем их сверстники из TA 120 , но это не обязательно указывает на более низкую скорость основной обработки данных 24 .Их медленная скорость решения задач частично объясняется трудностями поиска фактов у многих из этих детей, что приводит к тому, что они полагаются на более медленные процедуры решения проблем; например, при попытке решить простые задачи сложения на подсчет уходит больше времени, чем на извлечение. Математическое моделирование можно использовать для разделения скорости обработки на составляющие, такие как скорость кодирования чисел в рабочую память и скорость неявного подсчета. Использование этих методов позволило получить более детальную картину скорости обработки информации у детей с MLD и их сверстников из Лос-Анджелеса 13, 120, 121 .Исследования иногда показывают, что дети с MLD медленнее в неявном счете, чем их сверстники TA, но иногда нет различий. Более последовательный вывод состоит в том, что маленькие дети с MLD медленнее справляются с более простыми процессами, такими как кодирование чисел в рабочую память.
Использование быстрого автоматизированного именования (RAN), при котором детей просят как можно быстрее назвать серию хорошо выученных букв или цифр, является лучшим подходом к вопросу о том, имеют ли дети с MLD и LA более медленные основы. скорость кодирования и обработки информации 122 .Поскольку обрабатываемая информация очень проста, результаты не искажаются различными стратегическими подходами (например, подсчет или поиск). Более низкая производительность при выполнении задач RAN постоянно связана с более низкими показателями успеваемости по чтению, что может быть связано с простотой кодирования и представления звуков языка в фонологическом цикле 123, 124 . В наших исследованиях мы обнаружили, что дети с MLD начинают школу с гораздо более медленной скоростью обработки чисел, чем их сверстники TA, с детьми в группах LA и с низким IQ между ними, но разрыв быстро сокращается.Для некоторых детей ЛА их медленная обработка может быть связана с компонентом контроля внимания центральной исполнительной власти, а не с более фундаментальной разницей в скорости обработки как таковой. Для детей с MLD, напротив, может быть более фундаментальное различие в механизмах (например, развитие белого вещества), которые поддерживают скорость обработки информации, но любое такое различие, по-видимому, является скорее задержкой в развитии, чем стойким дефицитом. Чтобы определить, так ли это, потребуются исследования головного мозга.
КОГНИТИВНЫЕ ВМЕШАТЕЛЬСТВА
К сожалению, существует несколько научно обоснованных программ лечения, направленных на устранение дефицита математического познания у детей с MLD и их сверстников из Лос-Анджелеса. На основе нескольких в широком смысле высококачественных вмешательств по математике для учащихся с ограниченными возможностями в обучении Национальная консультативная группа по математике определила, что прямое, управляемое учителем подробное обучение тому, как решать определенные типы математических задач, было наиболее эффективным вмешательством 20 .Эффективные вмешательства всегда включали несколько занятий, продолжавшихся от нескольких недель до шести месяцев, и приводили к значительному улучшению способности студентов решать математические задачи со словами, вычислительные арифметические задачи и новые задачи со словом и арифметикой. Однако, как правило, многие из этих эффектов вмешательства не подлежат обобщению, а это означает, что улучшение вычислительных навыков, например, требует прямого вмешательства в вычислительные навыки, а не вмешательств для решения общих задач или даже других математических компетенций.Тем не менее, обобщение может произойти, если навык, который был целью вмешательства, является компонентом более сложной математической задачи.
Вмешательства, разработанные для устранения определенных когнитивных задержек или нарушений, определенных в ПРИЧИНЫ в настоящее время разрабатываются и оцениваются 125, 126 . Одно вмешательство фокусируется на частоте и точности, с которой дети с MLD используют процедуру подсчета мин для решения задач сложения и соответствующую процедуру для решения задач вычитания 126 .Сопутствующее исследование включало индивидуальные занятия в течение 48 занятий по 20–30 минут. Обучение включало подробные инструкции о том, как использовать подсчет мин, проиллюстрированные числовой линией. Для некоторых детей наставления сопровождались осознанной практикой; в частности, если ребенок не мог правильно ответить на простую задачу сложения или вычитания в течение одной минуты, ему предлагалось использовать подсчет мин для решения задачи. Другим детям давали те же инструкции, но потом они читали цифры, вместо того, чтобы заниматься осознанной практикой.Сочетание явных инструкций и осознанной практики подсчета минут привело к повышению компетентности в решении простых задач сложения и вычитания и более сложных задач, в которые были встроены простые.
Также разрабатываются вмешательства для улучшения рабочей памяти, которые будут особенно полезны для детей с MLD 127, 128, 129, 130, 131 . Типичное вмешательство заключается в том, чтобы просить детей выполнять задачи, требующие нагрузки на их объем рабочей памяти, то есть задачи, требующие одновременной обработки и манипулирования информацией, близкой к максимальной, с которой они могут эффективно справиться.В одном недавнем исследовании было продемонстрировано, что дети, которые участвовали в вмешательстве, которое соответствовало сложности задачи их текущему объему рабочей памяти, но не более легкому вмешательству, показали значительное улучшение фонологических и зрительно-пространственных компонентов рабочей памяти после примерно 20 тренировок ( По 35 минут). Важно отметить, что они сохранили эти успехи в течение шести месяцев наблюдения и продемонстрировали умеренный прирост на математическом тесте при последующем наблюдении. Источник или источники этих достижений до конца не изучены, но могут включать улучшенный контроль внимания сверху вниз через центральную исполнительную власть; это улучшит способность помнить вербальную и зрительно-пространственную информацию во время решения проблем.
Некоторые из этих вмешательств также были сосредоточены на компоненте тормозящего контроля рабочей памяти. К сожалению, результаты исследований этих вмешательств неоднозначны; Напомним, что подкомпонент управления вниманием центрального исполнительного органа участвует в учете нескольких вещей во время решения проблем и может быть отделен от подкомпонента тормозящего управления центрального исполнительного органа. На данный момент эти вмешательства, и особенно те, которые, по-видимому, улучшают контроль внимания, открывают большие перспективы для устранения недостатков и задержек у детей с MLD и их сверстников из Лос-Анджелеса.Следующим шагом является объединение вмешательств на рабочую память с вмешательствами, нацеленными на критические математические навыки.
В конечном подходе есть многоуровневый ответ на вмешательство (RtI) 132 . Первый уровень включает скрининг всех детей на предмет риска MLD или LA. Учащиеся, отнесенные к группе риска, затем будут участвовать в общем математическом образовании (первый уровень) и в мероприятиях в малых группах (второй уровень), нацеленных на области риска. Учащиеся, не добившиеся улучшения в рамках вмешательства второго уровня, переходят к более интенсивному, часто индивидуальному вмешательству третьего уровня (подробности см. В справке 132 ).В настоящее время неизвестно, сколько детей с MLD и LA «устойчивы к лечению» с этим подходом, и является ли резистентность к лечению или необходимость вмешательства третьего уровня хорошим подходом к диагностике MLD.
РЕЗЮМЕ И ПОСЛЕДСТВИЯ ДЛЯ КЛИНИЧЕСКОЙ ПРАКТИКИ И БУДУЩИХ ИССЛЕДОВАНИЙ
В нашем понимании когнитивных задержек и дефицитов, лежащих в основе медленного изучения математики, примерно 7% детей с MLD и 10% детей со стойким низким уровнем развития достигли значительного прогресса. успеваемость по математике, несмотря на средний интеллект и умение читать 1, 10 .Хотя многие из основных недостатков могут быть одинаковыми, хотя и в разной степени, исследователи в этой области движутся к различию между MLD и LA с диагностическим порогом для MLD на уровне или ниже 10 -го процентиля в тесте успеваемости по математике для более одного класса и диапазон между 11 -м и 25 -м процентилями включительно для LA и снова для более чем одного класса 8, 9 . Перед постановкой любого такого диагноза важно учитывать успеваемость по классам, так как многие дети с оценками в этих диапазонах в одном классе будут средними в следующем.У этих детей, в свою очередь, нет когнитивных задержек и нарушений, которые были выявлены в исследованиях MLD и LA 13 .
Различие между MLD и LA важно, потому что первая группа имеет обширный дефицит рабочей памяти, который обычно не встречается во второй группе – единственное возможное исключение – плохой тормозящий контроль, который имеет последствия для исправления. В частности, детям с MLD будут полезны вмешательства на рабочую память, а также вмешательства, нацеленные на конкретные математические области, в которых они демонстрируют задержки или недостатки.Дети с ЛА также получат пользу от последнего, но большинству из них не потребуется вмешательство в рабочую память. Подмножество детей ЛА с ошибками вторжения в процессе извлечения фактов может выиграть от вмешательств рабочей памяти, нацеленных на тормозящий контроль, после того, как эти вмешательства будут отрегулированы и последовательно продемонстрированы как эффективные.
Поскольку вмешательства наиболее эффективны, когда они нацелены на конкретные, четко определенные области дефицита, исследования когнитивных наук на этих детях имеют решающее значение.Эти исследования выявили несколько основных недостатков и задержек. У детей с MLD и, в меньшей степени, у детей LA наблюдается недостаток или задержка в обработке чисел, обучении арифметическим процедурам и запоминанию основных арифметических фактов. Эти трудности в обучении частично связаны с низким средним интеллектом (например, 90–95) и объемом рабочей памяти ниже среднего у детей с MLD, но это еще не все. У этих детей также есть проблемы с представлением чисел и обработкой, которые, по-видимому, не связаны с интеллектом или рабочей памятью, и хотя мы знаем, что рабочая память способствует их процедурным задержкам и может способствовать их дефициту поиска, это не может быть единственным причинным механизмом. .
Ни интеллект, ни широкий дефицит рабочей памяти не могут объяснить плохие достижения в математике у детей из Лос-Анджелеса. Эти дети в большинстве своем обладают способностями ниже среднего в работе с числами (например, прибавляют ●●● + 2 =?), Используют незрелые арифметические процедуры, и их часть испытывает особые трудности с извлечением основных фактов из долговременной памяти 8 , 14, 26 . Какими бы ни были основные причины, обработка чисел и процедурные трудности, по-видимому, больше связаны с задержкой в развитии (улучшается по классам), чем с дефицитом (показывает небольшое улучшение от класса к классу), при этом дети из Лос-Анджелеса отстают от своих сверстников и детей ТА с MLD на два-три года позади 117 .Трудности с запоминанием арифметических фактов более устойчивы для детей с MLD и для подгруппы детей с LA 62 . Эти недостатки могут быть связаны с плохой способностью препятствовать вторжению нерелевантной информации в рабочую память во время процесса поиска, хотя это вряд ли будет единственным источником дефицита информации.
Одной из областей, в которой был небольшой прогресс или если он вообще был достигнут, является социальное и эмоциональное функционирование детей с MLD и их сверстников из Лос-Анджелеса.Исследования детей с РЗ предполагают повышенный риск сопутствующих социальных и эмоциональных проблем, но в остальном мы мало знаем об этих проблемах. Последняя задача на ближайшие десятилетия – более полно изучить источники коморбидности MLD, RD и других расстройств, влияющих на обучение. Мы знаем, что у этих детей часто встречаются коморбидные расстройства, но не понимаем, почему это так.
Суть для практикующего педиатра состоит в том, чтобы (а) регулярно получать оценки успеваемости своих пациентов по математике (и чтению) и (б) направлять детей, которые набрали 25 -й национальный процентиль или ниже в более чем одном классе для образовательная оценка; (c) оценка должна включать тесты интеллекта и рабочей памяти, а также тесты, оценивающие определенные математические навыки (они доступны во многих стандартизированных тестах).Местные школы должны предоставлять мероприятия, которые включают характеристики (например, подробное обучение), описанные в КОГНИТИВНЫЕ ВМЕШАТЕЛЬСТВА.
Интерактивная тетрадь с номерами 1–20 для заданий по математике для дошкольных и детских учреждений
Описание
Наша интерактивная записная книжка с номерами 1–20 – увлекательный и увлекательный способ выучить математику! Каждому номеру соответствует 4 страницы, за которыми легко следить. Когда дети поймут, как заполнять каждую страницу, они смогут работать независимо.Отлично подходит для дошкольных учреждений и детских садов! Студенты весело учатся числам и счету! Они также работают над мелкой моторикой, собирая каждую страницу.
Об интерактивной записной книжке с номерами 1-20
Это задание представляет собой цифровой PDF-файл, скачать . Для доступа к этому занятию вам потребуется установленная программа просмотра PDF-файлов. После завершения процесса оформления заказа вы получите ссылку для его загрузки по электронной почте и / или на странице заказа. Для получения дополнительной помощи свяжитесь с нами здесь.
В этот товар входят:
→ 87 страниц всего
- Следующие действия для номеров 1-20:
- Нахождение числа, которое соответствует фокусному числу, с помощью забавной мазки для бинго
- Отделка основания 10 рамы
- Показаны различные способы определения числа фокусировки (с помощью объектов, меток, пальцев, игральных костей)
- Написание цифрового и письменного числа
- Подсчет и сортировка объектов, которые складываются с числом фокуса, и объектов, которые не соответствуют
- Вращайте, чтобы выиграть игру, чтобы узнать, какое число выиграет
- Нахождение числа фокусировки на числовой строке
Приготовиться легко! Просто распечатайте это задание, возьмите мелки, карандаши / цветные карандаши, ножницы, клей и готово!
Дополнительные продукты, которые мы рекомендуем для этого занятия:
Этот продукт содержит партнерские ссылки.
Бумага
Мелки / маркеры
Цветные карандаши
Ножницы
Клей
Этот продукт дает вам одну лицензию, которая дает право одному человеку использовать продукт. Если вы хотите поделиться нашими продуктами с другими учителями, друзьями или семьей, вам необходимо приобрести дополнительные лицензии. Пожалуйста, ознакомьтесь с нашими полными Условиями использования здесь.
Другие продукты, которые вам понравятся:
Учебный план по письму и фонетической грамотности
Полная программа по математике для дошкольников
Учебное пособие для занятий с номерами
Рабочие листы с числами 1-20 с уроками
Формы для лепки с цифрами
Snap Cube Числа
8 простых заданий по математике для малышей, которые стоит попробовать сегодня – чтение яиц
Вернуться к статьямПомогать ребенку развить основные математические навыки должно быть весело! Изучите сотни онлайн-заданий по математике для малышей с Mathseeds.Бесплатная пробная версия
Родители обычно проводят много времени, разговаривая со своими детьми о буквах, звуках и словах. Это часто происходит естественно, когда мы садимся вместе читать книгу по вечерам или указываем на слова, когда мы в пути, например, на рекламных щитах и уличных знаках.
Но исследования показывают, что говорить о числах и использовать математический язык с нашими малышами не менее важно. Фактически, многие исследования показывают, что это ключевой фактор, предсказывающий успехи ребенка в математике, когда он пойдет в школу.
Часто родители уделяют меньше внимания «цифрам» со своими детьми, чем понятиям ранней грамотности. Интересно, что матери говорили с мальчиками о числовых концепциях в два раза чаще, чем с девочками.
Чтобы начать развивать ключевые математические навыки, родителям рекомендуется регулярно говорить со своими малышами о числах с раннего возраста. Занятия – прекрасный способ научиться говорить с числами и помочь вашему ребенку развить понимание математического языка и понятий в увлекательной и увлекательной форме!
Вот восемь математических заданий для малышей, которые помогут вам включить разговор с числами в повседневную деятельность и побудят вашего ребенка развивать ключевые математические навыки.
Изучите сотни математических заданий для малышей с Mathseeds!
Созданная опытными учителями начальной школы программа по математике , удостоенная множества наград, предназначена для развития основных навыков математики и решения задач у детей в возрасте от 3 до 9 . Mathseeds предлагает сотен заданий по математике для малышей , индивидуальных уроков для самостоятельного изучения и веселых игр, в которых каждая новая математическая концепция представлена по-разному – ваш ребенок даже не узнает, что они учатся! А также получите полный доступ к удостоенной множества наград онлайн-программе чтения для детей младшего возраста Reading Eggs.
8 простых заданий по математике для малышей
1. Считать каждый день
Вы можете легко превратить счет в веселое повседневное занятие, куда бы вы ни пошли. Подсчитайте, сколько птиц вы заметите на послеобеденной прогулке. Или сколько красных машин ждут на светофоре. Сколько стульев в приемной у врача и сколько журналов или книг? Поднимите пальцы, когда будете считать, и произнесите числа вслух. Вы даже можете держать наготове блокнот и ручку, чтобы вести подсчет.
2. Развлекайтесь, решая головоломки
Настольные игры и головоломки – это увлекательный и интересный способ познакомить вашего малыша с математическим языком. Семейные настольные игры, такие как Chinese Checkers , Chutes and Ladders и Candy Land , – все это отличные способы научить вашего малыша понимать числа. Каждый раз, когда вы бросаете кости, читайте число вслух и считайте квадраты, перемещая игровую фишку по доске. Головоломки (например, головоломки с деревянными формами) могут помочь малышам научиться распознавать формы и понимать пространственные концепции.Поощряйте своего малыша называть разные формы во время игры и сообщайте вам, является ли определенная форма «слишком большой» или «слишком круглой», чтобы соответствовать ей.
3. Ролевые игры
Игра с воображением дает множество образовательных преимуществ. Вашему ребенку может понравиться притворяться продавцом и просить вас покупать товары в его «магазине». Или они могут притвориться ученым или волшебником, готовящим секретные зелья в своей скрытой лаборатории. Куда бы ни привело их воображение вашего ребенка, обязательно найдется возможность использовать математический язык.Вы можете создать или купить реквизит для своего ребенка, например игровые деньги для покупок, пластиковые фрукты для имитации продуктов или простой мерный стакан для смешивания зелий. Если они приглашают вас принять участие, посоветуйте им сказать вам, сколько фруктов они продают, могут ли они дать вам по три каждого овоща или сколько жидкости нужно добавить в их секретное зелье.
4. Сортировать объекты
Поощряйте ребенка замечать сходства и различия между объектами, чтобы классифицировать и отсортировать их по категориям.Например, если вы помогаете им складывать игрушки, попросите их отсортировать все игрушки по таким категориям, как «игрушечные машинки», «мягкие игрушки» или «кубики». Вы также можете сделать это во время уборки. Попросите ребенка собрать предметы, которые нужно убрать, и отсортировать их по категориям (например, «бумага» или «пластик»). Спросите их, сколько предметов они собрали для каждой группы, или укажите на группу с определенным количеством предметов. Это может быть даже хорошей возможностью использовать пространственный язык, например, «поставьте красные машины рядом с синими машинами» или «поместите маленькую чашку внутрь большой чашки».
5. Используйте линейку, измерительную ленту и мерную чашку
Весело проведите время с вашим ребенком, измеряя предметы вокруг дома и считывая или записывая результаты измерений. Веселое занятие во время купания включает в себя сбор фляг, чашек и контейнеров разного размера, чтобы научить вашего ребенка, что такое «полный» и «пустой», и сравнить вместимость. Говорите о том, что происходит во время игры. Например, «Моя чашка полна, в мою чашу больше не поместится вода» или «Давай нальем воды из моей маленькой чаши в твою большую и посмотрим, станет ли она полной».
6. Указывайте числа, куда бы вы ни пошли
Укажите числа на уличных знаках или номерных знаках, когда вы сидите с ребенком в пробке. Укажите на них и попросите назвать числа или зачитайте их сами. Вы также можете попросить ребенка показать числа пальцами и по-разному поощрять его делать это. Например, для показа числа пять можно поднять два пальца на одной руке и три – на другой.
7. Не забывайте регулярно использовать «разговор по номерам»
Попробуйте решать задачи по математике на глазах у ребенка, чтобы помочь им установить связь между математикой и повседневной жизнью.Например, когда вы готовите, читайте вслух каждый шаг и соответственно измеряйте количество, чтобы ваш ребенок мог их видеть. Используйте числа, когда говорите о времени, датах и температуре. Сколько часов и минут до ужина? Сколько недель и дней до школы? Будет ли температура на выходных выше или ниже?
8. Ресурсы для онлайн-обучения
Онлайн-обучение стало важной частью современного образования за последнее десятилетие, а технологические устройства могут стать интересным, интерактивным и ценным инструментом раннего обучения для малышей.Многие онлайн-ресурсы по математике разработаны так, чтобы быть очень интересными и простыми в использовании для детей дошкольного возраста и знакомить их с концепциями раннего обучения в увлекательной игровой форме. Mathseeds разработан, чтобы научить детей в возрасте от 3 до 6 лет считать, определять закономерности и формы и понимать основные концепции решения проблем.
Изучите сотни математических заданий для малышей с Mathseeds!
Созданная опытными учителями начальной школы программа по математике , удостоенная множества наград, предназначена для развития основных навыков математики и решения задач у детей в возрасте от 3 до 9 .
 Эти пособия не только интересны и разнообразны, но и отличаются очень доступной ценой. Мы рекомендуем обратить внимание на эти книжки не только родителей, но и воспитателей детских садов.
Эти пособия не только интересны и разнообразны, но и отличаются очень доступной ценой. Мы рекомендуем обратить внимание на эти книжки не только родителей, но и воспитателей детских садов.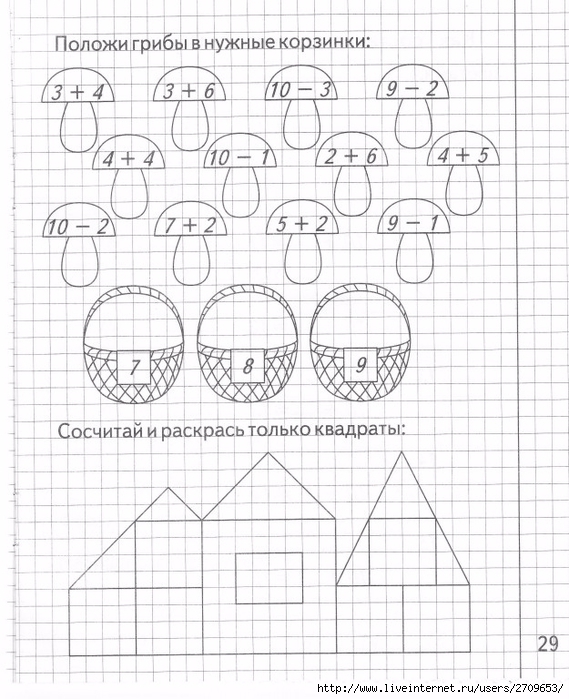 Белорецк муниципального района Белорецкий район Республики Башкортостан
Белорецк муниципального района Белорецкий район Республики Башкортостан
