Геометрия для детей: Знакомство с геометрией для детей 4-6 лет. Задания и игры.

Геометрия для детей: janemouse — LiveJournal

Геометрия для детей: janemouse — LiveJournal ?

Category:

• Дети
• Cancel

Когда-то у меня была книжка Шеврина и Житомирского “Геометрия для малышей”, с путешествием Точки по стране Геометрии, и всякими играми, приключениями и экспериментами.
Мы с мамой читали по главе в день, делали отвесы, привязывая тяжёлую гайку на прочную нитку,
измеряли длины линейками и портновским сантиметром.
Это было 40 лет назад, но эти занятия с экспериментами я помню до сих пор.
И моё убеждение в том, что надо сперва пощупать, потом узнать теорию, ничуть не изменилось.
Мы в любое занятие с детьми стараемся отвести заметное время под манипуляцию с предметами, под свои эксперименты.
Мы недавно со вторым и третьим классом говорили про углы и измерения.

Принесли им транспортиры – и предложили ряд экспериментов.


У нас есть набор стыкующихся палочек, AngLegs, с кнопочками по краям,
(есть более удобные, GeoSticks, но у меня таких нет)

Все красные палочки одинаковой длины, самые длинные.
Синие покороче, зелёные ещё короче.
И мы просили собрать треугольники из палочек заданных оттенков, и потом измеряли углы в получившихся треугольниках.

Дети сами в какой-то момент обнаружили, что если взять треугольник из 3 одинаковых палочек, то все 3 угла получаются одинаковые.
И у треугольника из трёх красных палочек такие же углы, как у треугольника из трёх фиолетовых палочек!
Это было такое открытие!

А ещё некоторые заметили, что у равнобедренных треугольников, у которых 2 палочки одного цвета, тоже всегда 2 равных угла!

Потом я им нарезала произвольные треугольники из бумаги, дети измеряли все 3 угла – и считали сумму углов в разных треугольниках.

записывали, измеряли следующий угол

и сами обнаружили, что сумма всех трёх углов получается почти одинаковая (с точностью до измерения)
Мне кажется, если бы в школе тоже начинали изучение углов в треугольниках с эксприментов, детям было бы намного интереснее!
А у вас в школе были какие-нибудь практические работы по математике?

Tags: геометрические игры, кружок, математика, мышематика, школа

Subscribe

• Звери по клеточкам – новый урок-квест

  Недавно опробовали с нашими группами второго и третьего класса урок-квест про площади – со смешными зверушками. Сначала определяли высоту…

• Танграм: вырезаем и по ходу собираем картинки из деталей

  Танграм – любимая головоломка, и я люблю к ней возвращаться. В этом году мы начали со всеми с того, что вырезали из квадратика свой танграм.…

• Математика 1 класс. Что остаётся от сказки потом, после того, как её рассказали?

  Иногда к концу дня даже жалко стирать с доски то, что там накопилось за несколько уроков. Вот, например, какая красота. У нас по-прежнему есть…

• Кубики Никитина “Сложи узор”. Мышематика сент 22

  Даже интересно, были ли у вас в детстве такие кубики? У меня были, мне моя мама самодельные делала, прочитав статью Бориса Никитина. Мама отклеивала…

• Мышематика Беляево. Геометрические игры

  В этом году у нас в Беляево на удивление полные группы пятилеток, но некоторые из этих прекрасных деточек ещё почти не знакомы с миром чисел, цифры…

• ЦДО 6 октября. Танграм

  Вырезали сегодня со всеми школьниками танграм. И вот, что интересно: одинаково сложно многим и в первом классе, и в третьем. Причём в каждой…

• Шестилетки. сент 22. ЦДО. Скоростные колпачки как геометрический материал

  У нас есть набор цветных стаканчиков, 5 штук разного цвета, от игры “скоростные колпачки”, и мы из этих стаканчиков собираем иногда башенки по…

• Школьники. ЦДО. Цифры и числа.

  Головоломка на проекции

  Спросили в четверг у школьников 2 и 3 класса, чем отличаются цифры и числа. Оказалось, что это очень сложный вопрос. Кто-то считает, что…

• Уроки-квесты. Блок-схемы в первом классе

  Мы подготовили за август 5 уроков-квестов, и планируем в этом году давать квесты не только дошкольникам, но и школьникам. Вот, например, сделали…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

12 comments

• 12 comments

• Звери по клеточкам – новый урок-квест

  Недавно опробовали с нашими группами второго и третьего класса урок-квест про площади – со смешными зверушками. Сначала определяли высоту…

• Танграм: вырезаем и по ходу собираем картинки из деталей

  Танграм – любимая головоломка, и я люблю к ней возвращаться. В этом году мы начали со всеми с того, что вырезали из квадратика свой танграм. …

• Математика 1 класс. Что остаётся от сказки потом, после того, как её рассказали?

  Иногда к концу дня даже жалко стирать с доски то, что там накопилось за несколько уроков. Вот, например, какая красота. У нас по-прежнему есть…

• Кубики Никитина “Сложи узор”. Мышематика сент 22

  Даже интересно, были ли у вас в детстве такие кубики? У меня были, мне моя мама самодельные делала, прочитав статью Бориса Никитина. Мама отклеивала…

• Мышематика Беляево. Геометрические игры

  В этом году у нас в Беляево на удивление полные группы пятилеток, но некоторые из этих прекрасных деточек ещё почти не знакомы с миром чисел, цифры…

• ЦДО 6 октября. Танграм

  Вырезали сегодня со всеми школьниками танграм. И вот, что интересно: одинаково сложно многим и в первом классе, и в третьем. Причём в каждой…

• Шестилетки. сент 22. ЦДО. Скоростные колпачки как геометрический материал

  У нас есть набор цветных стаканчиков, 5 штук разного цвета, от игры “скоростные колпачки”, и мы из этих стаканчиков собираем иногда башенки по…

• Школьники.

  ЦДО. Цифры и числа. Головоломка на проекции

  Спросили в четверг у школьников 2 и 3 класса, чем отличаются цифры и числа. Оказалось, что это очень сложный вопрос. Кто-то считает, что…

• Уроки-квесты. Блок-схемы в первом классе

  Мы подготовили за август 5 уроков-квестов, и планируем в этом году давать квесты не только дошкольникам, но и школьникам. Вот, например, сделали…

Консультация для родителей «Геометрия для малышей: как выучить фигуры» | Консультация (младшая группа):

Консультация для родителей

«Геометрия для малышей: как выучить фигуры»

Сегодня мы поговорим об увлекательнейшей теме – геометрии для малышей. По нормам к 2 годам ребёнок должен знать 3 геометрические фигуры – это квадрат, круг и треугольник. К 3-м годам количество узнаваемых фигур увеличивается до 6-7.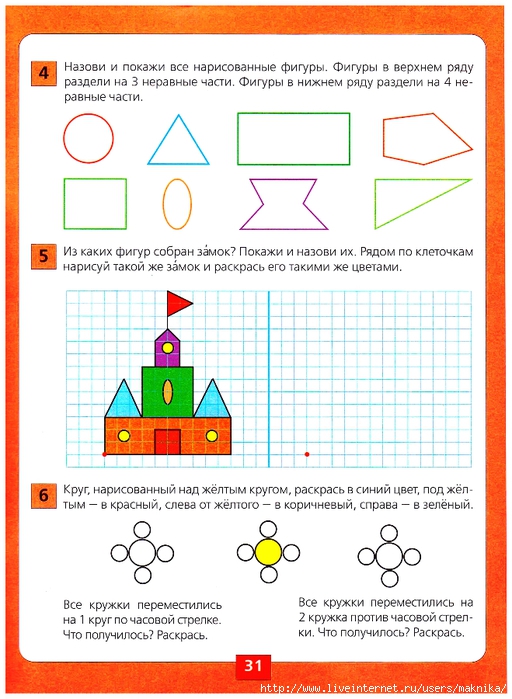 Добавляются овал, прямоугольник, ромб и высший пилотаж – трапеция. Как научить ребёнка их различать?

Изучаем геометрические фигуры

С самых ранних лет используйте в разговоре с ребёнком такие понятия как круглый (мяч), квадратный (табурет), овальный (стол) и т.д. Данный метод особенно эффективно работает, когда ребёнок видит несколько предметов с одинаковым названием, но разной формы и ему нужно выбрать один конкретный предмет. Делать это нужно ненавязчиво. Например, накрывая на стол можно попросить ребёнка дать Вам квадратную тарелку. Или перед сном предложить принести почитать круглую книжку. Вначале, когда ребёнок ещё не умеет самостоятельно определять формы и теряется перед кучей книжек покажите ему какая, из них круглая.
Следующий этап (1,5-2 года) – вырезаем из цветного картона фигуры квадрат, круг и треугольник 3-5 штук каждой, все одного цвета (чтобы цвет не отвлекал) и играем с ребёнком в игру «Собери фигуры», т.е. хаотично раскладываем фигуры на столе и просим ребёнка собрать все кружочки, затем квадраты и т.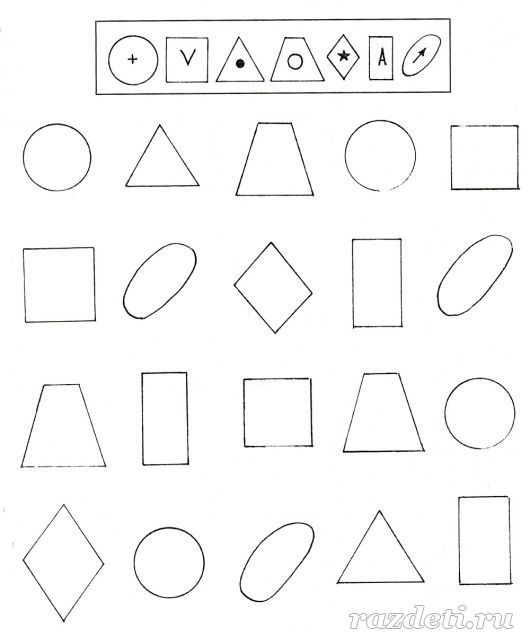 д. При необходимости помогаем ему. Если ребёнок справляется с заданием легко, то снова вырезаем из картона те же фигуры, но уже разных цветов. Берите для начала 4 основных цвета – красный, жёлтый, синий и зелёный. И снова играем в ту же игру.
Бывает, что разный цвет фигур сбивает ребёнка, помогите ему, уточнив задание: «Собери кружочки всех цветов: и жёлтые, и красные, и синие, и зелёные». Когда ребёнок начинает легко справляться с заданием, добавляем фигуры разных размеров и используем в игре фигуры разного цвета и разного размера.
После 2-х лет, если ребёнок хорошо усвоил все вышеперечисленные навыки, можно добавлять новые фигуры – овал, прямоугольник, ромб и по желанию – трапецию. После этого переходим к следующему этапу.
Если ребёнок хорошо владеет цветами и размером, то можно усложнить игру – просить собрать определённые фигуры конкретного цвета, например жёлтые треугольники. Или конкретного размера – маленькие кружочки.
И верхом мастерства для Вашего ребёнка будет успешное выполнение задания из 3-х составляющих: собрать определённые фигуры, конкретного цвета и размера. Например, синие большие треугольники или красные маленькие овалы.
Самое главное не спешите, переходите к следующему этапу только тогда, когда видите, что ребёнок легко справляется с заданием сам.

Учимся разделять предмет на фигуры. Пространственное воображение

После 2-х лет у ребёнка начинает формироваться воображение. Ребёнок начинает видеть в различных очертаниях тот или иной образ. В этом возрасте ребёнок может запросто сказать Вам, что вот этот странной формы узор похож на лягушку или собаку. И действительно, приглядевшись, Вы найдёте это сходство.
Используйте данный период для развития пространственного воображения. Обсуждайте с ребенком, на какие фигуры похож тот или иной предмет. С помощью цветных карандашей, красок или аппликации из цветной бумаги «превращайте» обычный прямоугольник в замечательную картину, кружочки и овалы – в милую кошку, а из прямоугольника и треугольников «постройте» космическую ракету.
Выкладывайте из вырезанных цветных картонных фигур различные предметы: домики, машины, корабли и просто красивые узоры.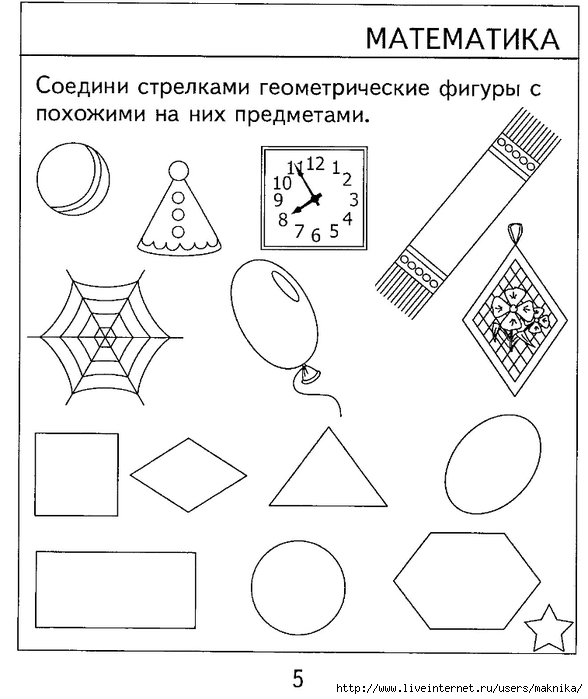
Акцентируйте внимание ребёнка на том, какую форму имеет та или иная часть предмета – что кузов у грузовика прямоугольный, колёса – круглые, а крыша у домика треугольная.

Развиваем объёмное мышление

Все родители знают, что маленькие дети просто обожают прятаться «в» и «под» различные объёмные предметы. Куда только они не залезут: в коробки и шкафы, под кровати и столы, строят домики и «штабики» из стульев и покрывал. Такие акробатическо-строительные занятия развивают у ребёнка объёмное мышление. Доказано, что дети, которым родители запрещают играть в такие игры сталкиваются в дальнейшем с трудностями в школе при изучении объёмной геометрии.
Дело в том, что сидя, например, в домике ребёнок воспринимает объёмность предмета изнутри, осознаёт тот факт, что у предмета есть внутреннее пространство.
Любая игра, подчёркивающая объёмность предмета добавит плюсик к развитию объёмного мышления Вашего ребёнка. Например, игра «Игрушечные прятки». Вы прячете несколько игрушек, а ребёнок их ищет. А затем наоборот. Главное – прятать игрушки в «правильные» места: шкафы, коробки, кастрюли, в закрывающийся кузов машины и т.д. Для маленьких детей оставляйте «подсказки» – высунутая из шкафа лапка у зайчика или выглядывающая из кастрюли голова любимого мишки.
Стройте из кубиков. Обязательно используйте конструктор – это вообще универсальная развивающая игрушка. Игра с конструктором развивает у ребёнка мелкую моторику и координацию движений, цветовое восприятие и логическое мышление, фантазию и конечно пространственно-объёмное мышление

Ершова Н.В.

Геометрия для детей: практическое образование ресурс

от Maryanne Kochenderfer / 16 сентября 2020 г. 17 сентября 2020 г.

35 акций

• . обучающие идеи, которые вы можете использовать для обучения геометрии детей всех возрастов. Ресурс для родителей и учителей.

  Некоторые ссылки на этом сайте являются партнерскими ссылками, и как партнер я могу получать небольшую комиссию бесплатно для вас. Нажмите на изображения и синий текст, чтобы перейти к ссылкам. Спасибо! Учить больше.

  Что вы найдете на этой странице

  Геометрия — это часть математики, которую дети буквально никогда не будут слишком маленькими для изучения! Простые детские игрушки, такие как сортировщики фигур и деревянные блоки, обучают наших младенцев основам геометрии задолго до того, как они начнут ходить и говорить.

  Почему-то до сих пор в наших головах крутится мысль, что геометрия — это какой-то ужасный предмет, который нельзя трогать до 10-го класса. Это настоящий позор! Сегодня я поделюсь некоторыми действительно забавными геометрическими идеями для детей, которые помогут им учиться в игре на протяжении всей жизни.

  Что такое геометрия?

  Геометрия — это часть математики, изучающая точки, линии, формы и пространство.

  Поскольку наша жизнь полна точек, линий, форм и пространства, это означает, что геометрия очень актуальна в нашей жизни! Таким образом, мы все выигрываем, когда начинаем узнавать об этом в более раннем возрасте и продолжаем изучать это на протяжении всей жизни.

  Геометрические фигуры Упражнения для дошкольников

  Дошкольники очарованы формами, поэтому на них сосредоточено большинство занятий по геометрии для дошкольников.

  Изучаем геометрию с помощью блоков узоров

  Блоки узоров — моя любимая игрушка для обучения дошкольников геометрии. Вот несколько забавных способов использования этой практической математической игрушки:

  • Рассортируйте фигуры. Это явно воспитательная деятельность.
  • Используйте блоки, чтобы создать мозаику на стене. Мои дети делали это снова и снова, когда они были маленькими!
  • Свободная игра с блоками шаблонов. Раньше моих детей раздражало то, как блоки скользят, поэтому я придумал это решение для игры с блоками без разочарований.
  • Сопоставление с шаблонами блоков шаблонов. Их можно купить или распечатать в интернете и заламинировать дома.
  • Смешивание блоков для выкройки с пластилином. Очевидно, что блоки так не работают. Но в этом и суть! Это позволяет детям видеть формы под разными углами, чем они обычно появляются в повседневной жизни. Этот опыт готовит их к изучению различных геометрических плоскостей в дальнейшей жизни.

  Строительные изображения с геометрическими фигурами

  Создание изображений из фигур — отличный способ закрепить названия фигур, а также узнать об углах и площади поверхности. Вот несколько забавных заданий по сборке геометрических фигур с помощью печатных форм:

  • Поезд
  • Лодка
  • Грузовик
  • Замок

  Дети также могут многое узнать о фигуре, используя одну и ту же фигуру снова и снова для создания другая форма. Например, дошкольники могут использовать точечные маркеры, чтобы написать свое имя, или стикеры в виде кружков, чтобы создать картинку.

  Практические занятия по геометрии для детей

  Поскольку мир полон форм, линий и точек, найти для детей практические занятия по геометрии несложно. Мне очень понравилось составлять этот список из идей со всего мира блогов.

  Слишком часто я слышу, как люди говорят, что они слишком артистичны для математики. Знаете ли вы, что научиться использовать перспективу в искусстве — это фантастическое занятие по геометрии?

  Не забывайте играть с математикой. Занятия, которые не кажутся суперобразовательными, как, например, эта раскраска весеннего дерева, вдохновленная числом пи, все же помогают развивать математическую осведомленность.

  Геометрия и пространственное восприятие

  Геометрия также может помочь детям развить пространственное мышление, поскольку они узнают, как различные формы взаимодействуют в физическом мире. Эти знания могут даже помочь детям стать лучшими спортсменами!

  Оригами — это простое занятие на геометрическую тематику, которое помогает детям открыть взаимосвязь между двухмерными и трехмерными фигурами.

  Какие ваши любимые ресурсы по геометрии для детей?

  Поделитесь комментариями и отзывами ниже, на на мою страницу в Facebook или по номеру , отметив меня в Instagram . Подпишитесь на мою рассылку , чтобы еженедельно получать на почту рекомендации по книгам, поделкам, мероприятиям и советам для родителей.

  МэриЭнн Кохендерфер

  Веб-сайт

  МэриЭнн Лайвс — любящий свое дело педагог, музыкант, фотограф и писатель, которая живет в Силиконовой долине со своим мужем Майком и четырьмя детьми.

  35 акций

  • Поделиться
  • Твитнуть

  Факты о геометрии для детей

  Уроки геометрии в 20 веке

  Геометрия — это разновидность математики, изучающая размер, форму и положение вещей. В геометрии есть плоские (2D) формы и твердые (3D) формы. Квадраты, круги и треугольники — одни из самых простых фигур в плоской геометрии. Кубы, цилиндры, конусы и сферы — простые фигуры в объемной геометрии.

  Содержание

  • Применение
  • Происхождение
  • Примеры
  • Важные понятия геометрии
    • Аксиомы
    • Очки
    • строк
    • Самолеты
    • Уголки
    • Кривые
    • Поверхности
    • Коллекторы
    • Топологии и метрики
    • Конструкции компаса и линейки
    • Размер
    • Симметрия
    • Неевклидова геометрия
  • Связанные страницы
  • Картинки для детей

  Использование

  Геометрия может использоваться для измерения площади и периметра плоской формы. Его также можно использовать для измерения объема и площади поверхности твердого тела.

  Геометрия может быть использована для расчета размера и формы многих вещей. Например, геометрия может помочь людям найти:

  • площадь дома, чтобы они могли купить нужное количество краски
  • объем коробки, чтобы узнать, достаточно ли она велика, чтобы вместить литр еды
  • площадь фермы, поэтому ее можно разделить на равные части
  • расстояние по краю пруда, чтобы знать, сколько ограждения купить.

  Истоки

  Геометрия зародилась как искусство измерения формы земли, чтобы ее можно было справедливо разделить между людьми. Слово «геометрия» означает «измерять землю». Из этого она выросла и стала одной из важнейших частей математики. Греческий математик Евклид написал первую книгу по геометрии. Геометрия — один из древнейших разделов математики.

  Примеры

  Геометрия начинается с нескольких простых идей, которые считаются истинными и называются аксиомами. Например:

  • Точку изображают на бумаге, касаясь ее карандашом или ручкой без каких-либо боковых движений. Мы знаем, где находится точка, но она не имеет размера.
  • Прямая — это кратчайшее расстояние между двумя точками. Например, Софи тянет веревку из одной точки в другую. Прямая линия между двумя точками будет следовать по пути натянутой струны.
  • Плоскость представляет собой плоскую поверхность, которая не останавливается ни в каком направлении. Например, представьте себе стену, бесконечно простирающуюся во всех направлениях.

  Важные понятия геометрии

  Ниже приведены некоторые из наиболее важных понятий геометрии.

  Аксиомы

  Иллюстрация постулата Евклида о параллельности. Евклид ввел некоторые аксиомы или постулаты, выражающие первичные или самоочевидные свойства точек, прямых и плоскостей. Он приступил к строгому выводу других свойств с помощью математических рассуждений. Характерной чертой подхода Евклида к геометрии была его строгость, и он стал известен как

  аксиоматическая или синтетическая геометрия. В начале XIX века открытие неевклидовых геометрий Николаем Ивановичем Лобачевским (1792–1856), Яношем Бойяи (1802–1860), Карлом Фридрихом Гауссом (1777–1855) и другими привело к возрождению интереса к этой дисциплины, а в 20 веке Дэвид Гильберт (1862–1943) использовал аксиоматические рассуждения, пытаясь заложить современную основу геометрии.

  Точки

  Главная страница: Точка (геометрия)

  Точки считаются фундаментальными объектами в евклидовой геометрии. Они были определены различными способами, включая определение Евклида как «то, что не имеет частей», а также с помощью алгебры или вложенных множеств. Во многих областях геометрии, таких как аналитическая геометрия, дифференциальная геометрия и топология, все объекты считаются построенными из точек. Однако некоторые исследования геометрии проводились без привязки к точкам.

  Линии

  Главная страница: Линия (геометрия)

  Евклид описал линию как «длину без ширины», которая «равномерна по отношению к точкам на самой себе». В современной математике, учитывая множество геометрий, понятие линии тесно связано со способом описания геометрии. Например, в аналитической геометрии линия на плоскости часто определяется как множество точек, координаты которых удовлетворяют заданному линейному уравнению, но в более абстрактных условиях, таких как геометрия инцидентности, линия может быть независимым объектом, отличным от множество точек, лежащих на нем. В дифференциальной геометрии геодезическая — это обобщение понятия линии на искривленные пространства.

  Плоскости

  Плоскость (геометрия)

  Плоскость — это плоская двумерная поверхность, простирающаяся бесконечно далеко. Плоскости используются во всех областях геометрии. Например, плоскости можно изучать как топологическую поверхность без привязки к расстояниям или углам; его можно изучать как аффинное пространство, где можно изучать коллинеарность и отношения, но не расстояния; его можно изучать как комплексную плоскость с использованием методов комплексного анализа; и так далее.

  Уголки

  Основная страница: Угол

  Евклид определяет плоский угол как наклон друг к другу в плоскости двух прямых, которые пересекаются и не лежат прямо относительно друг друга. Говоря современным языком, угол — это фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла.

  Острый (а), тупой (б) и прямой (в) углы. Острые и тупые углы также известны как косые углы.

  В евклидовой геометрии углы используются для изучения многоугольников и треугольников, а также как самостоятельный объект изучения. Изучение углов треугольника или углов единичной окружности составляет основу тригонометрии.

  В дифференциальной геометрии и исчислении углы между плоскими кривыми, пространственными кривыми или поверхностями можно вычислить с помощью производной.

  Кривые

  Кривая — это одномерный объект, который может быть прямым (как линия) или нет; кривые в 2-мерном пространстве называются плоскими кривыми, а кривые в 3-мерном пространстве называются пространственными кривыми.

  В топологии кривая определяется функцией от интервала действительных чисел до другого пространства. В дифференциальной геометрии используется то же определение, но определяющая функция должна быть дифференцируемой. Алгебраическая геометрия изучает алгебраические кривые, которые определяются как алгебраические многообразия размерности один.

  Поверхности

  Сфера — это поверхность, которую можно задать параметрически (через x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ ) or implicitly (by x ² + y ² + z ² − r ² = 0.)

  Поверхность — это двумерный объект, такой как сфера или параболоид. В дифференциальной геометрии и топологии поверхности описываются двумерными «участками» (или окрестностями), которые собираются диффеоморфизмами или гомеоморфизмами соответственно.

  В алгебраической геометрии поверхности описываются полиномиальными уравнениями.

  Многообразия

  Главная страница: Многообразие

  Многообразие является обобщением понятий кривой и поверхности. В топологии многообразие — это топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную евклидову пространству. В дифференциальной геометрии дифференцируемое многообразие — это пространство, каждая окрестность которого диффеоморфна евклидову пространству.

  Многообразия широко используются в физике, в том числе в общей теории относительности и теории струн

  Топологии и метрики

  Главная страница: Топология

  Визуальная проверка теоремы Пифагора для треугольника (3, 4, 5), как в Zhoubi Suanjing 500–200 г. до н.э. Теорема Пифагора является следствием евклидовой метрики.

  Топология — это математическая структура множества, которая сообщает, как элементы множества пространственно соотносятся друг с другом. Самые известные примеры топологий происходят из метрик, которые представляют собой способы измерения расстояний между точками. Например, евклидова метрика измеряет расстояние между точками на евклидовой плоскости, а гиперболическая метрика измеряет расстояние на гиперболической плоскости. Другие важные примеры метрик включают метрику Лоренца специальной теории относительности и полуриманову метрику общей теории относительности.

  Конструкции компаса и линейки

  Главная страница: Конструкции компаса и линейки

  Классические геометры уделяли особое внимание построению геометрических объектов, которые были описаны другим способом. Классически единственными инструментами, разрешенными в геометрических построениях, являются циркуль и линейка. Кроме того, каждое построение должно было быть завершено за конечное число шагов. Однако некоторые задачи оказалось трудно или невозможно решить только этими средствами, и были найдены остроумные конструкции с использованием парабол и других кривых, а также механических устройств.

  Размер

  Главная страница: Размер

  Снежинка Коха с фрактальной размерностью = log4/log3 и топологической размерностью = 1

  Там, где традиционная геометрия допускала измерения 1 (линия), 2 (плоскость) и 3 (наш окружающий мир, воспринимаемый как трехмерное пространство), математики использовали более высокие измерения в течение почти двух столетий. Измерение прошло через этапы превращения в любое натуральное число n , возможно бесконечное с введением гильбертова пространства, и в любое положительное действительное число во фрактальной геометрии. Теория размерности — это техническая область, изначально входящая в общую топологию, в которой обсуждаются определений ; как и большинство математических идей, размерность теперь определяется, а не интуиция. Связные топологические многообразия имеют четко определенную размерность; это теорема (инвариантность домена), а не что-то

  априорное .

  Вопрос размерности по-прежнему важен для геометрии, несмотря на отсутствие полных ответов на классические вопросы. Измерения 3 пространства и 4 пространства-времени являются частными случаями в геометрической топологии. Размерность 10 или 11 — ключевое число в теории струн. Исследования могут дать удовлетворительный результат геометрическая причина значимости 10 и 11 измерений.

  Симметрия

  Главная страница: Симметрия

  Мозаика гиперболической плоскости

  Тема симметрии в геометрии почти так же стара, как и сама геометрическая наука. Симметричные формы, такие как круг, правильные многоугольники и платоновые тела, имели большое значение для многих древних философов и подробно исследовались еще до Евклида. Симметричные узоры встречаются в природе и были художественно воспроизведены во множестве форм, в том числе в графике М. К. Эшера. Тем не менее, только во второй половине 19 в.века, когда была признана объединяющая роль симметрии в основаниях геометрии. Эрлангенская программа Феликса Кляйна провозгласила, что в очень точном смысле симметрия, выраженная через понятие группы преобразования, определяет, какая геометрия

  есть . Симметрия в классической евклидовой геометрии представлена ​​конгруэнциями и жесткими движениями, тогда как в проективной геометрии аналогичную роль играют коллинеации, геометрические преобразования, переводящие прямые в прямые. Однако именно в новых геометриях Бойяи и Лобачевского, Римана, Клиффорда и Клейна и Софуса Ли идея Клейна «определить геометрию через ее группу симметрии» оказалась наиболее влиятельной. И дискретные, и непрерывные симметрии играют заметную роль в геометрии, первая — в топологии и геометрической теории групп, вторая — в теории Ли и римановой геометрии.

  Другим типом симметрии является принцип двойственности в проективной геометрии (см. Двойственность (проективная геометрия)) среди других областей. Это метафеномен можно примерно описать так: в любой теореме поменяйте местами точку с плоскостью , соедините с и , лежит в , а содержит , и вы получите столь же истинную теорему. Аналогичная и тесно связанная форма двойственности существует между векторным пространством и его дуальным пространством.

  Неевклидова геометрия

  Дифференциальная геометрия использует инструменты исчисления для изучения проблем, связанных с кривизной.

  За почти две тысячи лет после Евклида, в то время как круг геометрических вопросов, задаваемых и ответов, неизбежно расширялся, основное понимание пространства оставалось в основном тем же самым. Иммануил Кант утверждал, что существует только одна абсолютная геометрия, истинность которой известна априорно внутренней способностью ума: евклидова геометрия была априорно синтетической. Этот господствующий взгляд был опрокинут революционным открытием неевклидовой геометрии в работах Бойяи, Лобачевского и Гаусса (так и не опубликовавшего свою теорию). Они продемонстрировали, что обычное евклидово пространство — лишь одна из возможностей развития геометрии. Широкое видение предмета геометрии было затем выражено Риманом в его инаугурационной лекции 1867 г. Über die Hypothesen, welche der Geometrie zu Grunde liegen ( О гипотезах, на которых основана геометрия ), опубликовано только после его смерти.