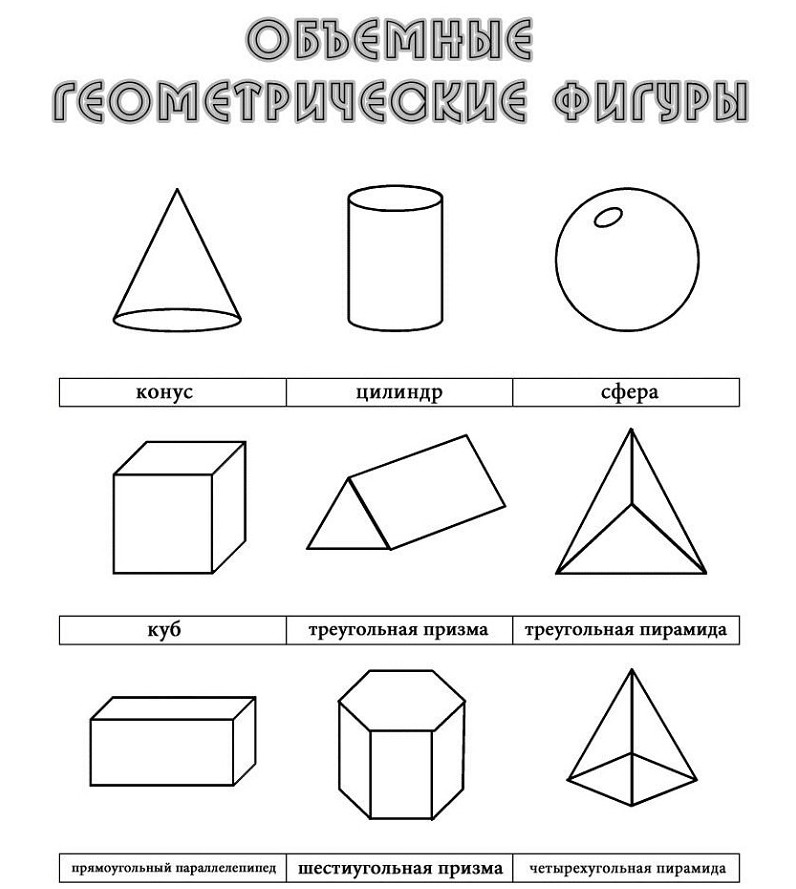
Геометрических фигур: Основные геометрические фигуры 🟢🟨🔺 и их названия – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Формирование пространственного мышления школьников на занятиях по «3D-моделированию геометрических фигур». — ЦНППМ

Интеграция деятельности школьного информационно-библиотечного центра и Центра цифрового и гуманитарного профилей Точка роста.

Коллегам, прошедшим обучение в ФГАОУ ДПО Академия Минпросвещения России

Июн 16

Опубликовано в Образовательный Workshop «Педагогический диалог»

Формирование пространственного мышления школьников на занятиях по «3D-моделированию геометрических фигур».

Сидорова Екатерина Яковлевна,

учитель математики

МОУ захаровская СОШ

С. Захарово Красночикойский район

Аннотация: С открытием на базе МОУ Захаровская СОШ Центра цифрового и гуманитарного профилей Точка роста и получением новейшего оборудования разработана и реализуется программа дополнительного образования «3D-моделирование геометрических фигур».

При проведении уроков геометрии часто возникает проблема несформированности у обучающихся пространственного мышления. Это вызывает определенные трудности при построении чертежей, решении различных задач. Поэтому было принято решение об интеграции уроков геометрии и занятий по «3D-моделированию геометрических фигур».

Применение 3D технологий на уроках геометрии – это возможность по новому взглянуть на предмет геометрия в школе. 3D-моделирование на уроках геометрии позволяет развивать пространственное воображение. А развитие пространственного воображения, мышления, в свою очередь, – одна из основных задач, которая позволяет создавать пространственные образы и оперировать ими в процессе решения практических и теоретических задач.

В рамках интеграции внеурочной и урочной деятельности по предмету геометрия и кружка «3D- моделирование геометрических фигур» были внесены изменения календарно-тематическое планирование рабочей программы по предмету геометрия 7-11 класс.

Теперь мы не только знакомимся, учимся чертить, изучаем свойства, но и моделируем геометрические фигуры и тела, и с помощью 3D печати можем получить наглядный материал.

Важнейшей отличительной чертой трехмерных моделей является то, что при работе с ними можно в любой момент произвольно изменить ракурс изображения. Появляется возможность по-новому ставить и решать задачи на построение в пространстве, причем проверить правильность решения можно, взглянув на конструкцию с разных сторон.

На этапе идеи учащийся ставит перед собой определённую цель, что он будет делать, как он будет делать и для чего. Определяет практическую значимость проекта.

На этапе проекта учащийся устанавливает взаимосвязь элементов геометрической фигуры.

На этапе 3D-моделирования при помощи программы «blender» создается трехмерная модель будущего объекта. Происходит визуальный анализ, вносятся коррективы.

На этапе 3D-печати происходит создание физического объекта из виртуальной модели.

И заключительный этап применения, когда учащийся использует результат своей деятельности.

3D моделирование в совокупности с новыми технологиями 3D-печати – это уже целый комплекс по развитию учащегося, который позволяет пройти путь от идеи до реального применения.

Равенство геометрических фигур / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Начальные геометрические сведения
Равенство геометрических фигур

Самой малой геометрической фигурой является точка. Остальные геометрические фигуры – это множество точек, которые обладают определенным свойством

, характерным только для этой фигуры. Существует множество геометрических фигур, которые мы можем сравнивать друг с другом, и равными в геометрии считаются те, которые имеют одинаковую форму и размеры.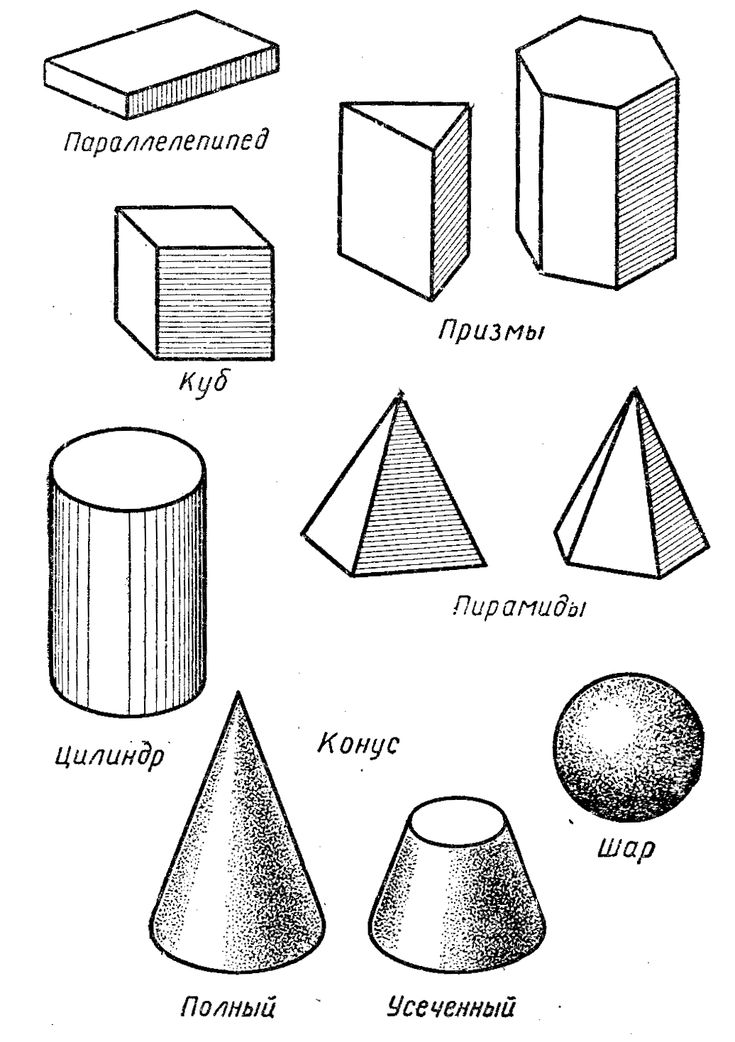

Простые геометрические фигуры мы можем сравнивать на практике с помощью измерительных инструментов, например: отрезки сравнивают с помощью линейки, углы с помощью транспортира. Но чаще всего фигура имеет более сложную форму, и поэтому чтобы ее сравнить с другой фигурой, мы не можем использовать измерители, поэтому для сравнения геометрических фигур используют метод наложения.

Метод наложения:

Пусть у нас даны две фигуры: Ф1 и Ф2.

Для того чтобы узнать равны ли фигуры друг другу, переведем на кальку (прозрачную бумагу) одну из фигур (в данном случае Ф2). А затем, вращая кальку, пробуем совместить копию фигуры Ф2 и фигуру Ф1.

Если их удалось совместить, то фигуры равны.

Свойства равенства геометрических фигур:

Каждая фигура равна самой себе.
Если первая фигура равна второй фигуре, то вторая фигура равна первой фигуре.
Если каждая из двух фигур равна третьей фигуре, то первые две фигуры равны.
Если первая фигура равна второй фигуре, а вторая фигура равна третьей фигуре, то первая фигура и третья фигура также равны между собой.
Если фигуры равны, то их площади и периметры равны (обратное утверждение не верно, то есть, если площадь и периметр одинаковы у двух фигур, это не значит, что они равны).

Равными фигурами в геометрии считаются те, которые имеют одинаковую форму
и размеры
Две геометрические фигуры называются равными, если их можно совместить наложением.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 18, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 19, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 813, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1157, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 13, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 2, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1293, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Geometric Shape – Etsy.

Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.

Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.

Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.

(более 1000 релевантных результатов)

Геометрические фигуры и формулы в объемной геометрии

Базовый калькулятор

Капсула

Калькулятор капсул

Объем = πr ² ((4/3)r + a)
Площадь поверхности = 2πr(2r + а)
Окружность = 2πr

Также называется стадион революции.

Круглый конус

Круглый конус Калькулятор

Объем = (1/3)πr ² ч
Наклонная высота = √(r ² + h ² )
Площадь боковой поверхности = πrs = πr√(r ² + h ² )
Площадь базовой поверхности = πr ²
Общая площадь поверхности
= L + B = πrs + πr ² = πr(s + r) = πr(r + √(r ² + h ² ))

Круглый цилиндр

Круглый цилиндр Калькулятор

Объем = πr ² ч
Площадь боковой поверхности = 2πrh
Площадь верхней поверхности = πr ²
Площадь нижней поверхности = πr ²
Общая площадь поверхности
= L + T + B = 2πrh + 2(πr ² ) = 2πr(h+r)

Conical Frustum

Conical Frustum Calculator

Volume = (1/3)πh (r ₁ ² + r ₂ ² + (r ₁ * r ₂ ))
Наклонная высота = √((r ₁ – r ₂ ) ² + h ² )
Площадь боковой поверхности
= π(r ₁ + r ₂ )s = π(r ₁ + r ₂ )√((r ₁ – r ₂ ) ² + h ² )
Площадь верхней поверхности = πr ₁ ²
Площадь базовой поверхности = πr ₂ ²
Общая площадь поверхности
= π(r ₁ ² + r ₂ ² + (r ₁ + r ₂ ) * s)
= π[ r ₁ ² + r ₂ ² + (r ₁ + r ₂ ) * √((r ₁ – r ₂ ) ² + h ² ) ]

Куб

Куб Калькулятор

Объем = a ³
Площадь поверхности = 6a ²
Диагональ лицевой стороны (f) = a√2
Диагональ (d) = a√3

Полушарие

Калькулятор полушария

Объем = (2/3)πr ³
Окружность = 2πr
Площадь криволинейной поверхности = 2πr ²
Площадь базовой поверхности = πr ²
Общая площадь поверхности = (2πr ² ) + (πr ² ) = 3πr ²

Пирамида: Квадрат

Калькулятор пирамиды

Объем = (1/3)а ² ч
Наклонная высота (s) = √(h ² + (1/4)a ² )
Площадь боковой поверхности = a√(a ² + 4h ² )
Площадь базовой поверхности = a ²
Общая площадь поверхности
= Л + В = ² + а√(а ² + 4ч ² ))
= а(а + √(а ² + 4h ² ))

Прямоугольная призма

Прямоугольная призма Калькулятор

Объем = lwh
Площадь поверхности = 2(lw + lh + wh)
Диагональ (d) = √(l ² + w ² + h ² )

Сфера

Калькулятор сферы

Объем = (4/3)πr ³
Окружность = 2πr
Площадь поверхности = 4πr ²

Сферическая крышка

Сферическая крышка Formulas

Объем
= (1/6)πh(3a ² + h ² )
= (1/3)πh ² (3R – h)
Радиус базовой окружности = √h(2R – h)
Окружность Базовая окружность = 2π√h(2R – h)
Площадь поверхности = 2πRh = π(а ² + ч ² )

Сферический сегмент

Формулы сферического сегмента

Объем = (1/6)πh(3a ² + 3b ² + h ² )
Площадь верхней поверхности = πb ²
Площадь нижней поверхности = πa ²
Площадь боковой поверхности = 2πRh
Где R = радиус сферы и
R = √{ [[(a-b) ² + h ² ] [(a+b) ² + h ² ] ] / 4h ² }

Треугольная призма

Треугольная призма Формулы

Объем = (1/4)h √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
Площадь верхней поверхности = (1/4) √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
Площадь нижней поверхности = (1/4) √[(a+b+c)(b+c-a)(c+a-b)(a+b-c)]
Площадь боковой поверхности = h(a+b+c)
Общая площадь поверхности = Площадь верхней поверхности + Площадь нижней поверхности + Площадь боковой поверхности

Трубка

Калькулятор трубки (полый цилиндр)

Окружность, C:
- С ₁ = 2πr ₁
- С ₂ = 2πr ₂
Площадь боковой поверхности, л, для цилиндр:
- L ₁ = 2πr ₁ h, площадь внешней поверхности
- L ₂ = 2πr ₂ h, площадь внутренней поверхности
Площадь, А, для торцевого поперечного сечения трубы:
- А ₁ = πr ^{₁ 2} для области, ограниченной C ₁
- А ₂ = πr ^{₂ 2} для области, ограниченной C ₂
- А = А ₁ – А ₂ = π(r ^{₁ 2} – r ^{₂ 2} ) для площади сплошного сечения трубы, конца, кольцо.