Геометрические веселые фигуры: Непосредственно-образовательная деятельности с детьми средней группы «Геометрические фигуры»
Веселая геометрия
Личностные, метапредметные и предметные результаты изучения курса
Личностными результатами изучения данного курса являются:
- развитие любознательности, сообразительности при выполнении разнообразных заданий проблемного и поискового характера;
- развитие внимательности, настойчивости, целеустремленности, умения
- преодолевать трудности – качеств весьма важных в практической деятельности любого человека;
- воспитание чувства справедливости, ответственности;
- развитие самостоятельности суждений, независимости и нестандартности мышления.
Метапредметные результаты:
- Умение сравнивать разные приемы действий, выбирать удобные способы для выполнения конкретного задания.
- Анализировать правила игры. Действовать в соответствии с заданными правилами.
- Включаться в групповую работу. Участвовать в обсуждении проблемных вопросов, высказывать собственное мнение и аргументировать его.
- Выполнять пробное действие, фиксировать индивидуальное затруднение в пробном действии.
- Аргументировать свою позицию в коммуникации, учитывать разные мнения, использовать критерии для обоснования своего суждения.
- Сопоставлять полученный (промежуточный, итоговый) результат с заданным условием.
- Контролировать свою деятельность: обнаруживать и исправлять ошибки.
Предметные результаты:
- Ориентироваться в понятиях «влево», «вправо», «вверх», «вниз».
- Ориентироваться на точку начала движения, на стрелки указывающие направление движения.
· Иметь представление:
– о линиях: прямой, кривой, ломанной, луче, отрезке;
– о замкнутых и незамкнутых линиях;
-о взаимном расположении линий и точек на плоскости;
– об углах и их видах: прямом, остром и тупом – о соотношении между ними;
– о многоугольниках и их классификации по числу углов;
– о разнице между плоскими и объемными предметами;
– об объёмных телах: шаре, цилиндре, конусе, призме, пирамиде
· Уметь:
– чертить прямые, лучи, отрезки, ломанные, углы, многоугольники;
– строить отрезки, находить их длину при помощи чертежной линейки;
– находить в окружающем мире предметы похожие на геометрические фигуры и тела.
· Моделировать объёмные фигуры из различных материалов (проволока, пластилин и др.) и из развёрток на бумаге.
Этикет. Сравнения. Геометрические фигуры. Цвета.
Ирина Гурина
Весёлый этикет
Хорошие манеры
Медвежонок за столом
Занимался мишка с папой:
– Ложку держим правой лапой,
Зачерпни тихонько мед
И отправь всю ложку в рот.
Папа мед налил в тарелку.
Мишка вдруг увидел белку.
Он за белкой побежал,
Мед, конечно, расплескал!
Папа сердится на мишку:
– Непослушный ты мальчишка!
Надо ровненько сидеть
И в окошко не глядеть!
Медвежонок ровно сел,
Ложкой сладкий мед доел!
Да так быстро, аккуратно!
Просто посмотреть приятно!
Вежливый зайчик
На заре зайчишка встал.
– С добрым утром,- всем сказал,
Солнышку и кочкам,
Маленьким цветочкам.
Маме и братишкам,
Елочкам и шишкам.
Ветру, небу, облакам,
Разноцветным мотылькам.
На дорожку вышел,
А навстречу – мыши!
– Здравствуйте, сестренки!-
Говорит он звонко.
Здравствуйте, лисята,
Здравствуйте, лосята!
Он здоровался с друзьями:
С кабанами, муравьями,
С рыбками, стрекозами,
Белками и козами.
А навстречу страшный волк,
Лес испуганно примолк!
Бедный зайка задрожал,
Хвостик маленький поджал.
А потом закрыл глаза,
Тихо «Здравствуйте» сказал.
Даже волк его не съел,
Улыбнулся, подобрел.
Говорит ему в ответ:
– И тебе, косой, привет!
Чистюли
Солнце катится над лесом.
Смотрит солнце с интересом:
Что за пыль стоит под горкой?
У зверей идет уборка!
Из берлоги мишки
Выметают шишки.
Мыли белочки дупло,
В нем и чисто, и светло!
Зайка веником метет,
Лось с ведром воды идет.
Тряпку еж несет на спинке:
Лисы вымоют тропинки.
А веселые кроты,
Хоть не видят чистоты,
От души стараются,
В норках убираются.
Даже крошки-мышки
Чистили домишки,
Наводили красоту!
Звери любят чистоту!
Волшебное слово
На крыльце высоком кошка
Ела спелую морошку.
Подошел утенок к ней:
– Дай мне ягод поскорей!
Рассердилась очень кошка:
– Будь повежливее, крошка!
Ягод я тебе не дам.
Почему? Подумай сам!
К ним барашек подошел:
– Так просить нехорошо!
Ты, утенок, не спеши!
Ты «пожалуйста» скажи!
– Да! – мычит корова:
– Без такого слова
Не получишь ничего,
Ведь оно важней всего!
Подбежал утенок к кошке:
– Дай, пожалуйста, немножко.
Кошка подобрела:
– Вот, другое дело!
Угощайтесь все, друзья!
Не жалею ягод я.
За такое слово
Все отдать готова!
Послушные стихи
Если в лужу наступить,
Можно ноги промочить
И, конечно, простудиться.
В лужи лазать не годится!
Если утром не умыться,
Мама может удивиться,
Не узнать и испугаться.
Лучше буду умываться!
Если скатерть потянуть,
Можно всё перевернуть,
Разобьётся вся посуда.
Скатерть трогать я не буду.
Если вдруг перед едой
Руки не помыть водой,
Заболит живот тогда.
Руки мою я всегда!
Если в книге накалякать,
Будет книга горько плакать,
Будем мы без сказок жить!
Лучше с книгами дружить!
Если влезть, куда не надо,
Мама вряд ли будет рада.
Если мама запретила,
Значит, это нужно было!
Если кто-то любит врать,
Я не буду с ним играть.
Сам не вру, и мне вруны
Рядом вовсе не нужны!
Если незнакомый кто-то
Или в гости позовёт,
Не пойду без спроса.
Вот!
Весёлые противоположности (сравнения)
Большой-маленький
Слон большой ушами машет,
Муха маленькая пляшет.
Слон большой, почти огромный,
А размер у мухи – скромный!
Мелко-глубоко
Лягушонку в луже мелко:
Эта лужа – как тарелка!
В синем море, далеко
Дна не видно – глубоко!
Чистый-грязный
На крыльце котенок чистый,
Белый, маленький, пушистый.
Поросенок в луже грязный
Вид имеет безобразный!
Высокий-низкий
На холме стоит сосна.
Ах, высокая она!
А к сосне прижавшись близко
Задремал пенечек низкий.
Головой до звёзд достав,
Гордо смотрит вниз жираф.
Он высокий, словно дом.
Рядом бродит низкий гном.
Светло-темно
Солнце яркое взошло,
Стало в комнате светло.
Ночью спать уйдет оно,
Будет в комнате темно!
Длинный-короткий
По траве ползет питон:
Словно поезд длинный он.
Рядом розовый и кроткий
Червячок ползет короткий.
Мокро-сухо
Шепчет окунь из пруда:
– Мокро тут, везде вода!
Потирает лапки муха:
– Вылезай, у нас здесь сухо!
Толстый-худой
Ходит толстый добрый мишка,
Рядом – худенький зайчишка.
Мишка пухленький такой,
А дружок его – худой!
В тёплом озере живёт
Очень толстый бегемот.
Возвышаясь над водой,
Аист бродит там худой.
Тихо-громко
Под застенчивой луной
Тихо пел сверчок ночной!
На заре петух встает,
Громко-громко он поет!
Веселый-грустный
Шел веселый медвежонок,
Меда съел медведь бочонок,
А навстречу ежик грустный:
Ежик съел сухарь невкусный!
Старый-молодой
Старый дед с клюкой идет,
Внука за руку ведет.
Старый дед совсем седой,
А внучок-то молодой!
Легкий-тяжелый
На весах тяжёлый слон:
Очень много весит он.
Лёгкий пёстрый мотылёк
Даже взвеситься не смог!
Вот тяжелый пароход
По седым волнам плывет.
Рыбка легкая играет,
Пароходик догоняет!
Горький-сладкий
Как-то лось сказал грачу,
– Мухомор я не хочу!
Горький он, совсем не сладкий,
Подкреплюсь я шоколадкой!
Быстро-медленно
Быстро бегает гепард,
У него хороший старт!
Черепаха еле-еле
Доползёт с трудом до цели!
Узкий-широкий
По широкой, по дороге
Шли слона большие ноги,
А по узкой, по тропинке
Шли мартышкины ботинки!
copyright: текст Ирина Гурина © копирование с сайта gurinairina.ru запрещено
Весёлая геометрия
Треугольник
Треугольный треугольник
Угловатый своевольник.
Он похож на крышу дома
И на шапочку у гнома.
И на острый кончик стрелки,
И на ушки рыжей белки.
Угловатый очень с виду
Он похож на пирамиду!
Круг
Круглый круг похож на мячик,
Он по небу солнцем скачет.
Круглый словно диск луны,
Как бабулины блины,
Как тарелка, как венок,
Как веселый колобок,
Как колеса, как колечки,
Как пирог из теплой печки!
Полукруг
Если круг разломишь вдруг,
То получишь полукруг.
Это месяц в облаках
И пол-яблока в руках.
Это шляпка у грибочка,
На болоте мокром кочка.
Разноцветным полукругом
Встала радуга над лугом.
Квадрат
Словно стол стоит квадрат.
Он гостям обычно рад.
Он квадратное печенье
Положил для угощенья.
Он – квадратная корзина
И квадратная картина.
Все четыре стороны
У квадратика равны.
Прямоугольник
Как окно прямоугольник,
Аккуратный, словно школьник.
Он похож дверь, на книжки,
И на ранец у мальчишки.
На автобус, на тетрадку,
На большую шоколадку.
На корыто поросенка
И на фантик у ребенка.
Ромб
Слон квадратик повернул,
Присмотрелся и вздохнул.
Сверху сел, чуть-чуть примял,
И квадратик ромбом стал!
Овал
С высоты кружок упал.
Он теперь не круг – овал!
Он овальный, как жучок,
Он похож на кабачок,
На глаза и на картошку,
А еще похож на ложку,
На орех и на яйцо,
На овальное лицо!
Трапеция
Если влезть с пилой повыше,
Отпилить у дома крышу,
То хозяев мы обидим,
Но трапецию увидим!
А потом мы все починим
И из шкафа юбку вынем.
Мы увидим: юбка тоже
На трапецию похожа!
copyright: текст Ирина Гурина ©
Цвета
Картинка
Я рисую летний луг
За моим окошком.
Все зеленое вокруг,
Желтого немножко.
Крашу в желто-золотой
Солнце и дорожку,
Золотистый зверобой
И цыпленка-крошку.
Брызну красным на листок:
Это земляника.
Вот коричневый мосток
За осокой дикой.
Нарисую голубым
Быструю речушку,
Небо, легкое, как дым,
Васильков веснушки.
Крашу белым облака,
Лепестки ромашки,
Ножку белого грибка,
Мотыльков и кашки.
Дорисую яркий луг,
И картинка эта
Среди белых зимних вьюг
Мне подарит лето.
Цветной лес
По коричневой тропинке,
На коричневой, на спинке,
Косолапый медвежонок
Нес коричневый бочонок!
Ярко-рыжая лисица
К рыжей белке в гости мчится.
Собрала она в лукошко
Рыжих рыжиков немножко.
Светит красный мухомор
Словно строгий светофор.
Дятел в красненькой беретке
Ел рябину с тонкой ветки.
Солнце желтое катилось,
Да за елку зацепилось,
Одуванчиками вдруг
Разлилось оно на луг!
Ветер травку щекотал,
В яркой зелени летал,
А зеленая лягушка
В мох легла, как на подушку!
Из далёка-далека
Плещет синяя река.
Отражает гладь озер
Неба синего шатер.
Цвета с куклой
Что за белые шары
Посреди такой жары?
Сладко-вкусный белый ком
Таял в вазе молоком.
Это с куклой мы сидели
И мороженое ели.
Но она не успевала,
Так что съела очень мало.
А потом мы рисовали,
Только белый выбирали:
Вот черемухи цветок,
Вот ромашки лепесток.
Словно первый снег несмелый
Лист лежал альбомный белый.
========
Это самый летний цвет.
Веселее просто нет!
С куклой мы в цвета играли
И зеленый цвет искали:
Юбка, кофта, босоножки,
И травинки у дорожки,
У сосны и пышной ёлки
Изумрудные иголки.
Огурец, горох и лук,
За деревней дальней луг,
Мох, пушистый, как подушка,
И кузнечик, и лягушка,
Огород и даже дом
Утонули в цвете том!
===================
Смотрит строгий светофор
Словно спелый помидор.
С куклой мы моей вначале
Очень сильно заскучали.
Красный свет, придется ждать.
Но ведь можно поиграть!
Мы искали красный цвет:
Вот ведро, велосипед,
Сумка, куклин сарафан,
На моих штанах карман,
Земляника, мухомор,
И, конечно, светофор!
===================
Мы поехали на юг.
У меня был синий круг,
В синей сумке кукла, сок,
Синий зонтик, кошелёк.
С куклой мы позагорали,
Искупались, поиграли,
Синий камушек нашли,
Маме с папой принесли.
Неба синего шатёр,
Пляжа теплого ковёр
В синем море синий кит
На тугих волнах лежит.
=====================
Кукла в садике сидела.
Нет у нас сегодня дела.
Жаркий полдень, знойный день.
Нам идти на речку лень.
Желтый день, как лютик летний,
Это лета день последний.
Солнце желтое танцует
И подсолнухи целует.
Завтра осень, листопад,
Пожелтеет летний сад.
Только осень бродит где-то,
А сегодня просто лето!
Кукла вертит головой –
На макушке бант живой.
Ярко-желтый мотылёк
В завитках ее прилёг.
Copyright: текст Ирина Гурина © Копирование с сайта gurinairina.ru запрещено
Лэпбук «Веселая геометрия» для детей старшего дошкольного возраста
Лэпбук «Веселая геометрия» составлен для ознакомления и закрепления знаний старших дошкольников о гоеметрических фигурах.
Содержаит следующие разделы: Книжка-малышка “Знакомимся с геометрическими фигурами”, “Загадки о геометрических фигурах”, “Загадки о геометрических телах”, “Геометрические сказки”, “Геометрические раскраски”, дидактической игры “Подбери предмет”, “Игротека”. Данное пособие составлено совместно с воспитателем Басовой О.Н. Лэпбук может быть полезен для работы воспитателям, учителям начальных классов. В лэпбуке использованы материалы Сети Интернет.
СКАЗКИ О ГЕОМЕТРИЧЕСКИХ ФИГУРАХ
«Самый важный».
«В одной прекрасной стране, которая называется «Геометрия» жили не тужили разные геометрические фигуры. Жители этой страны всегда друг другу помогали, друг друга выручали, поэтому жили дружно и весело. Но, в одно прекрасное летнее утро треугольник сидел рядом со своим домиком на завалинке (Педагог ставит на наборное полотно геометрическую фигуру треугольник).
Сидел он сидел, думал, думал и решил вдруг, что он самая нужная и важная из геометрических фигур. Обрадовался, вскочил и побежал к другу квадрату (Педагог ставит на наборное полотно геометрическую фигуру квадрат). Стучит в дверь: «Квадрат, открывай. У меня для тебя новость». Посмотри, я самый важный и нужный из фигур. У меня есть три угла. Вот я какой красивый. Квадрат посмотрел на треугольник и сказал: «Нет брат, я самый важный и нужный из фигур. У тебя три угла, а у меня четыре. Спорили, спорили треугольник с квадратом, но так и не о чем не договорились. Решили пойти к прямоугольнику (Педагог ставит на наборное полотно геометрическую фигуру прямоугольник). Подошли они к домику прямоугольника, стучат к нему в дом и просят его: «Рассуди нас, кто главнее»? Треугольник говорит:«Я главный, у меня три угла». Квадрат говорит: «Я главней. У меня четыре угла». Выслушал их прямоугольник и сказал: «Нет ребята, Вы не правы. Я самый главный. У меня четыре угла, я самый высокий и красивый». Пуще прежнего друзья рассорились.
Никто друг другу уступать не хотел. Мимо проходил круг, услышал он спор и сказал: «Друзья, не надо спорить и ссориться. Каждая из Вас нужная и важная фигура (Педагог ставит на наборное полотно геометрическую фигуру круг). С давних времен в нашей стране, которая называется «Геометрия», споров и ссор не было. И с тех пор в этой замечательной стране все фигуры стали жить дружно.
«Как треугольник и круг познакомились с квадратом».
– Стоит на опушке леса вот такой необычный дом. (Рассматривание, узнавание и называние фигур.)
– Как вы думаете, кто его жители? (Обобщая ответы детей, воспитатель продолжает рассказывать сказку.)
– Жили-были вот в таком доме круг и треугольник. И выглядели они так. (показываем картинку).
Однажды пошли друзья погулять и встретили вот такую фигуру. Узнаете, кто это? (показываем картинку квадрата).
А наши друзья незнакомца не узнали, поэтому испугались, спрятались за куст и думают: «Кто он такой? Стали рассуждать:
– На круг похож? (Нет.
) Почему? (У него углы есть.)
– На треугольник похож? (Нет.) Посчитайте углы. (Их четыре.)
Думали-гадали, а потом круг предложил: «Подойдем, спросим, как его зовут и познакомимся».
– Здравствуй, я – круг, у меня нет углов. Я похож на колесо, на солнышко, на тарелку. Я умею катиться.
– А я – треугольник, у меня три угла и я похож на колпак гнома, на крышу домика.
– Здравствуйте, друзья, я очень рад с вами познакомиться и подружиться. Меня зовут квадрат. Смотрите, какой я красивый, все мои стороны одинаковы. А на что я похож, догадайтесь сами. ( Дети предлагают свои варианты.)
– Родом я из большого и дружного семейства четырехугольников, у меня много братьев и сестер. Но сегодня я ушел гулять один и вот заблудился. Не могли бы вы меня приютить на время в своем домике. (Воспитатель подводит детей к мысли, что нужно сконструировать для троих друзей новый домик.)
«Барон Квадрат».
Давным – давно в мире было много разных волшебных стран.
И особым волшебством отличалась страна – Всезнаек! В ней правила мудрая царица Геометрия. В то время из одной страны в другую бродил Лист. Его края были неровными, с множеством загибов, потому что его вырвал из тетради мальчик по имени Веня, и уже долгое время Лист находился в пути. А нашему герою очень хотелось, чтобы все его стороны стали вновь ровными.
Собравшись с силами, Лист отправился к царице Геометрии. Только она могли ему помочь. Лист целых пять дней провел в пути, потому что двигаться он мог только с помощью ветра, а ветреная погода была не каждый день. На шестой день своего пути Лист оказался у дворца самой царицы. Она ласково встретила его, выслушала его просьбу и сказала:
– Хорошо, я помогу тебе, только мне нужны помощники: Карандаш, Линейки и Ножницы.
Хлопнула царица в ладоши три раза и перед ней явились её слуги: Карандаш, Линейки и Ножницы.
– Ну, теперь ты будешь квадратом! – спросила царица Геометрия
– Квадратом? – удивился Лист.
– Да! Да! Квадратом! – убедительно ответила царица Геометрия.
– А что это такое? – спросил Лист.
– Это прямоугольник, у которой все стороны не только ровные, но и равные, – объяснила царица Геометрия.
– Да, мне это подходит, – ответил Лист.
– Тогда все принимайтесь за работу, – сказала царица.
Карандаш чертил ровно. Линейка замеряла стороны так, чтобы все они были одинаковой длины, а ножницы ровно отрезали лишние части. Когда работа была сделана, царица Геометрия объявила:
– Теперь ты превратился в настоящий Квадрат.
Лист обрадовался. Он поблагодарил Карандаша, Линейку и Ножницы, а царица Геометрия велела принести ему зеркало. Он долго смотрелся в него, а потом закричал:
– Квадрат! Квадрат! Ура! У меня теперь все стороны равны!!!
Лист – квадрат поблагодарил царицу Геометрия, а она присвоила ему звание – барона.
Барон квадрат пошёл гулять по странам с высоко поднятой головой. Ему очень понравился его внешний вид и звание.
«Купец Круг».
У царицы Геометрии в её дворце была потайная комната. И каждый вечер она уединялась в ней для того чтобы… посмотреть в своё волшебное зеркало. В нём она видела всех своих жителей. Но каждый день она подолгу наблюдала за бароном Квадратом. Ей было его очень жалко – он всегда гулял один. У него не было друзей. В её стране он был единственной фигурой.
Однажды вечером царица Геометрия, после наблюдений за бароном Квадратом, вышла погулять в сад. Погода была чудесная! На небе ярко сияла луна и звёзды. Царица Геометрия была очарована видом Луны, и тогда её осенило: а ведь Луна похожа на квадрат, только углы закруглены. Она в один миг достала циркуль и нарисовала круг. Позвала к себе ножницы, велела вырезать фигуру по контуру и нарекла его купцом
«Граф Треугольник».
Жизнь в стране Всезнаек шла своим чередом. В ней происходили и хорошие и плохие события. Царица Геометрия следила за всем, но однажды…
Проказник Фокус – Покус решил пошутить над бароном Квадратом. Он притворился его другом и во время очередной встречи разделил его с угла на угол пополам! Квадрат испугался. Он не знал, что ему делать. Но вдруг раздался голос царицы Геометрии:
Не бойся барон Квадрат. Новую фигуру с тремя углами и тремя сторонами я нареку графом треугольником, а ты как был бароном квадратом, так им и останешься. Царица Геометрия наказала Фокуса – Покуса за его злую шутку, но в тоже время была довольна тем, что в её стране появился новый житель.
«Полезный прямоугольник».
Прямоугольник все время завидовал Квадрату.
– Я такой неуклюжий, – жаловался он. – Если поднимусь во весь рост, то стану длинным и узким. А если лягу на бок, то буду низким и толстым.
– А ты всегда остаешься одинаковым, – продолжал он, обращаясь к Квадрату. – И стоя, и сидя, и лежа!
– Да уж, – с гордостью говорил важный Квадрат. – У меня все стороны равны. Не то, что у некоторых: то дылда-дылдой, а то блин-блином.
И Квадрат переворачивался с боку на бок, но его рост и ширина от этого не менялись.
А однажды случилось вот что. Один Человек заблудился в лесу. Он шел наугад сквозь чащу и встретился с Квадратом и Прямоугольником. Поскольку у Квадрата был очень важный вид, то Человек обратился за помощью именно к нему.
– Можно, я заберусь на вас и погляжу, где мой дом? – спросил он у Квадрата.
Человек залез сначала на одну сторону Квадрата. Но ничего не увидел, потому что ему мешали макушки деревьев.
Тогда Человек попросил Квадрат перевернуться и залез на другую сторону. Но, как известно, все стороны у Квадрата одинаковые. Поэтому и на сей раз Человек ничего не увидел из-за деревьев.
– Гражданин Квадрат! – взмолился Человек. – Помогите мне хотя бы через речку перебраться!
Квадрат подошел к речке и попытался дотянуться до другого берега.
Но… плюх! Плюхнулся в воду.
– Может, я смогу помочь вам? – предложил Человеку скромный Прямоугольник.
Он встал во весь свой рост. Человек забрался на него и оказался выше деревьев.
Вдалеке он увидел свой дом и наконец понял, куда ему надо идти. Тогда Прямоугольник лег на бок и стал мостом.
Человек перебрался по Прямоугольнику через речку, помог ему подняться и, горячо поблагодарив, отправился домой.
А Квадрат, который сушился на берегу после вынужденного купания, сказал Прямоугольнику:
– Вы, оказывается, полезная фигура!
– Ну, что вы! – скромно улыбнулся Прямоугольник. – Просто мои стороны разной длины: две – длинные, а две – короткие. Иногда это бывает очень удобно.
«Треугольник и Квадрат».
Жил-был Треугольник. Хотя, по правде сказать, он не столько жил, сколько скучал. Вот так…
С ним по соседству скучал и Квадрат. После того, как ему не удалось помочь Человеку выбраться из леса, он уверовал в свою полную бесполезность.
Теперь Квадрат валялся в каком-то овраге и чувствовал себя никому не нужным и ужасно одиноким. Вот таким…
Скучал он, скучал и решил послать письмо Треугольнику. «Дорогой Треугольник! Поодиночке мы ни на что не годимся, – писал он. – А вместе мы уже имеем смысл. Что вы об этом думаете?»
Треугольник ответил ему так: «Уважаемый Квадрат! От скуки я разучился думать. Поэтому почти ничего не думаю. Но мне кажется, что надо жить со смыслом».
И стали они жить со смыслом, то есть вместе. И что же получилось?
«Белочка и геометрические фигуры».
Наступила зима. Белочка нашла пустое дупло и решила жить в нем вместе с бельчатами. Но им было холодно в дупле, потому что оно было всегда открыто. В этом же лесу жили два мастера, фигуры Круг и Треугольник. Треугольник был злой и думал о себе, что он самый главный в лесу мастер, а Круг был добрый и веселый. Пошла белочка к фигурам и попросила их сделать для дупла двери.
Треугольник сделал дверь треугольную, потому что считал, что самые лучшие двери – треугольные, а все остальные совсем никому не нужны. Поставила белочка треугольную дверь. Но она не закрывала дупло хорошо, так как оно было круглое. Ветер дул в щели, и бельчатам было холодно. Тогда белочка опять пошла к фигурам и попросила сделать другую дверь. Треугольник нахмурился и обиделся. А Круг сделал круглую дверь, которая подошла к дуплу, и всем было тепло. С тех пор Треугольник понял, что все фигуры важны.
Однажды Квадрат и Прямоугольник отправились на прогулку и попали в один двор. Там сидел мальчик и грустил. «Ты почему грустишь?» — спросил его Прямоугольник. «Просто у нас во дворе негде играть», — ответил мальчик.
И тогда Квадрат и Прямоугольник построили горку.
Мальчик обрадовался и стал кататься.
«Я понял! — сказал Прямоугольник. — Неважно, какой ты внешне, главное — быть кому-нибудь полезным!»
ГЕОМЕТРИЧЕСКИЕ РАСКРАСКИ
ЗАГАДКИ О ГЕОМЕТРИЧЕСКИХ ТЕЛАХ
ЗАГАДКИ О ГЕОМЕТРИЧЕСКИХ ФИГУРАХ И ФОРМАХ
КНИЖКА-МАЛЫШКА «Знакомимся с геометрическими фигурами»
Круг
Посмотрите-ка вокруг!
Пальчиком рисуем круг.
Куклы были вместе в ряд,
А теперь в кругу сидят.
Наше солнышко в окне –
Золотой круг в вышине.
Круглый мячик здесь лежит,
В ручки к вам он поспешит.
Треугольник
Треугольник – три угла,
Посмотрите детвора:
Три вершины очень острых –
Треугольник – «остроносый».
Стороны в нем тоже три:
Раз, два, три – ты посмотри.
Треугольник мы рисуем,
Знать теперь его мы будем.
Квадрат
Познакомьтесь, вот квадрат!
Он знакомству очень рад!
В нём угла уже четыре,
Нет его ровнее в мире:
Стороны четыре в нём,
Две скрепляются углом.
Круг в нем может разместиться,
В куб он сможет превратиться.
Ромб
Ромб – фигура непростая,
Две в себе объединяет:
Треугольник раз и два –
Фигура стала вдруг одна.
Четыре в ромбе стороны.
Между собой они равны.
Четыре в ромбе и угла,
Равны между собой по два.
Прямоугольник
Как окно прямоугольник,
Аккуратный, словно школьник.
Он похож дверь, на книжки,
И на ранец у мальчишки.
На автобус, на тетрадку,
На большую шоколадку.
На корыто поросенка
И на фантик у ребенка.
Овал
Вот овальный огуречик,
Из него и человечек
Получиться может ловко:
Ручки, ножки и головка.
Наш овал нам сделать просто:
Круг растянем – больше роста.
Нет углов и нет сторон,
Очень вытянутый он.
ИГРОТЕКА
Задание: Посмотри на картинку. Из каких фигур состоят предметы, изображенные предметы. Из представленных фигур найди подходящие и закрой пустые окошки.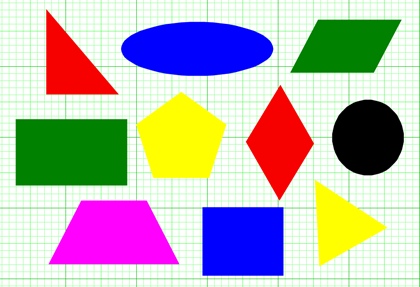
Задание: Посмотри на картинку. Из каких геометрических фигур она составлена? Попробуй составить такую же картинку.
Задание: Посмотри внимательно на фигуры в верхней части карточки. Запомни их цвет. Закрой верхнюю часть карточки и раскрась фигуры в нижней части, также как на верхней.
ДИДАКТИЧЕСКАЯ ИГРА
Игра «Подбери предмет».
Цель: упражнять в умении находить предметы похожие на определенные геометрические фигуры – круг, квадрат, треугольник, овал, ромб, прямоугольник. Из представленных ниже картинок с геометрическими фигурами, необходимо вырезать и заламинировать предметы для игры.
КАРТИНКИ ДЛЯ ОФОРМЛЕНИЯ ОБЛОЖКИ
Развивающие лэпбуки, созданные педагогами-практиками, в магазине на «Уроке»!
Конспект НОД для старшей группы “Веселые геометрические фигуры” (Нетрадиционная техника рисования)
Конспект НОД
по ОО «Художественно – эстетическое развитие»
Рисуем по шаблону «Веселые геометрические фигуры»
Старшая группа
Цель занятия: познакомить детей с новой техникой рисования – шаблонография.
Задачи:
– учить детей рисовать, используя шаблоны геометрических фигур;
– расширять представление детей о строении сложных предметов;
– Развивать воображение, координацию движений, мелкую моторику.
Материалы для занятий: альбомный лист, шаблоны геометрических фигур разного размера (деревянные кубики: треугольник, квадрат, круг, прямоугольник), простой карандаш, цветные карандаши.
Предварительная работа: создание из геометрических фигур объектов на фланелеграфе, из цветного картона, из счетных палочек.
Ход занятия.
Воспитатель: наш мир состоит из множества предметов, вещей, и если внимательно на них посмотреть, можно увидеть, что все они имеют определенную форму. Какие вы знаете геометрические формы?
Дети: круг, квадрат, треугольник, прямоугольник, овал.
Воспитатель предлагает детям отгадать загадки: назвать отгадку и определить форму предмета, о котором идет речь.
Квадрат.
В нашей комнате есть волшебное окно, в том окошечке – кино.
(Телевизор)
Набита пухом, лежит под ухом…
(Подушка)
В доме есть оно, называется …
(Окно)
Круг.
На небе круглая она, ночью в окно к нам светит…
(Луна)
Круглый бок, румяный бок, покатился …
(Колобок)
Любит он на солнце греться, в полосатое одеться, и, как сахар, он на вкус, а зовут его …
(Арбуз)
Треугольник.
Уступая ветру в споре, увлекает судно в море.
(Парус)
Крыльев нет у этой птицы, но нельзя не подивиться: лишь распустит птица хвост – и поднимется до звезд.
(Ракета)
Подними глаза повыше, антенну увидишь ты на нашей…
(Крыша)
Прямоугольник.
Она ни в город, ни во двор не просится гулять, на миг заглянет в коридор и в комнату опять.
(Дверь)
Много, много окон в нем, это большой и красивый наш…
(Дом)
Не куст, а с листочками, не рубашка, а сшита, не человек, а рассказывает.
(Книга)
Разгадывание загадок подкрепляется рисунками – разгадками, где хорошо просматривается геометрическая форма.
Воспитатель. А вот некоторые предметы имеют сложное строение, они могут состоять сразу из нескольких и разных геометрических фигур.
Приводится пример: домик, снеговик, машина, светофор, шкаф и др. Предлагается детям привести свои примеры.
Физкультминутка.
Покажу вам треугольник, будем весело шагать,
Вы увидели квадрат, будем дружно приседать,
А вот это вот кружок, прыгай веселей дружок.
Воспитатель показывает фигуры, а дети выполняют движения. Далее показывает фигуры без слов, в другом порядке, дети выполняют движения соответствующие каждой фигуре.
Воспитатель. Мы с вами убедились, что все предметы вокруг нас в своем строении имеют одну или несколько разных геометрических форм. Сегодня мы с вами будем составлять изображение объектов из готовых геометрических фигур – шаблонов.
А послужат нам шаблонами ваши кубики. Отберите 4 формы – треугольник, квадрат, прямоугольник, круг, но только мы не будем с ними играть, а будем их обводить, и в результате у вас должно получиться изображение целой фигуры.
Практическая часть.
Воспитатель. Давайте пофантазируем над вашими будущими рисунками, какие они у вас будут, из каких объектов будут состоять, а эти объекты из каких геометрических форм будут состоять.
Дети продумывают содержание рисунка, если дети затрудняются, педагог помогает определиться с сюжетом.
Воспитатель показывает и объясняет последовательность выполнения работы.
- Начинать создание объекта в следующей последовательности: вначале нужно обрисовать основную форму, самую крупную, и только потом переходить к деталям.
- Простым карандашом обрисовать геометрические формы – составляющие персонажа или предмета – таким образом, чтобы готовое изображение представляло единое целое.
- Каждый шаблон необходимо как можно ближе прикладывать к нарисованному контуру предыдущей формы, не оставляя между ними промежутков. Одной рукой плотно придерживать кубик на поверхности листа, а другой рукой карандашом обводить его вокруг.
- Готовую композицию выполнить в цвете цветными карандашами.
Одной рукой плотно придерживать кубик на поверхности листа, а другой рукой карандашом обводить его вокруг.Заключительная часть.
Педагог вместе с детьми рассматривает рисунки, отмечает наиболее интересные по содержанию, по сложности строения и расположению объектов в композиции и еще раз подводит детей к тому, что, если внимательно приглядеться, можно увидеть, что все предметы , окружающие нас, по форме на что – то похожи.
Используемая литература
Давыдова Г.Н. 22 занятия по рисованию для дошкольников. Нетрадиционные техники. – М.: Издательство СКРИПТОРИЙ 2003, 2018 – 112с.
ФОТООТЧЕТ
Автор: Е.В. Куницкая
Познавательно-творческий проект «В стране геометрических фигур» для детей старшей логопедической группы
Статья:
Вид проекта
Познавательно-исследовательский.
Возраст детей:
Старшая группа (5 – 6 лет)
Участники проекта:
Дети, родители воспитанников, воспитатели.
Продолжительность проекта:
Краткосрочный (2 недели)
Актуальность:
Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.
В. Произволов.
Современные ученые отмечают большое значение геометрии для развития пространственного мышления и воображения ребенка, для его способности видеть мир в целостных образах. Следовательно, становится актуальным изучение и закрепление знаний о геометрических фигурах, как одного из важнейших показателей развития пространственного мышления и воображения ребенка.
Анализ проведенных занятий, бесед, игр, наблюдений за детьми в свободной деятельности, выявил проблему – поверхностный уровень знаний о геометрических фигурах. Дети очень любознательны и хотят все знать, поэтому мы решили провести углубленную работу по данной теме через познавательно-исследовательскую деятельность.
Цели проекта:
Формирование знаний, умений, навыков по теме «геометрические фигуры», создание условий для развития математических и творческих способностей детей в процессе реализации проекта.
Задачи проекта:
– Закреплять знания о геометрических фигурах, формировать мыслительные операции, умение классифицировать по разным признакам (форма, цвет, размер, соотносить форму предметов с геометрическими фигурами, называть и показывать элементы геометрических фигур, преобразовывать одни фигуры в другие (путем складывания, разрезания).
– Развивать речь, внимание, память, воображение, мелкую моторику рук, творческие способности, формировать познавательные интересы в различных видах деятельности.
– Формировать интерес к математике, воспитывать самостоятельность, инициативность, умение трудиться в коллективе, доводить начатое дело до конца.
Предполагаемый результат:
Формирование у детей первичных представлений об объектах окружающего мира, познавательных и творческих способностей, развитие воображения, любознательности, активности.
В процессе реализации проекта
– Разработана система знаний о геометрических фигурах;
– Повысился интерес к математике;
– Дети проявили коммуникативные, познавательные и творческие способности;
– Пополнился словарный запас детей математической терминологией;
-Дети, в сотворчестве со взрослым, умеют ставить цели задачи и самостоятельно реализовывать работу в различных видах деятельности;
– Дети научились представлять результат своего труда;
– Родители получили необходимые знания по теме проекта.
Основные методы и формы реализации проекта:
1. Определение темы, постановка цели и задачи.
2. Определение методов и приемов работы.
3. Создание презентаций на тему «Угадай фигуру», «Веселая геометрия».
4. Подбор методической и художественной литературы, физкультминуток, пальчиковых игр, дидактического материала.
5. Подбор обучающих мультфильмов.
6. Подбор материалов, игрушек, атрибутов для игровой деятельности.
7. Подбор материала для конструирования и творческого труда.
8. Изготовление атрибутов для игр (маски, схемы, карты и т. д.)
9. Составление перспективного плана.
Продукт проектной деятельности:
– коллаж «Город геометрических фигур»
– рисунки и аппликация на тему: «Волшебные превращения»
– выставка поделок «Веселый квадрат» (оригами)
– альбом «Стихи и загадки о геометрических фигурах»
– цикл НОД на тему «В стране геометрических фигур»
– фотографии всех видов деятельности
– презентация «Как мы изучали геометрические фигуры».
Обеспечение:
– интерактивная доска
-компьютер
– художественные произведения и энциклопедии
-методическая литература по теме,
– презентации и обучающие мультфильмы для детей
– демонстрационный и наглядный материал (иллюстрации, схемы, карточки с заданиями и др.)
-дидактические и развивающие игры с математическим содержанием (геометрическое лото, геометрическая мозаики, цветные палочки Кюизенера и др.
)
-трафареты для свободного рисования фигур
-наборы конструкторов и строительных материалов
– пеналы с набором геометрических фигур
– магнитная доска с набором геометрических фигур
– настольно – печатные игры.
Этапы работы над проектом:
1. Подготовительный этап:
Воспитатели.
– Составление с детьми плана работы. (Что мы знаем? Что мы хотим узнать? Как мы это будем делать)
– Подбор материала и оборудования для занятий, бесед, игр с детьми.
Сотрудничество с родителями:
– Анкетирование родителей, изучение возможности участия родителей в реализации проекта.
– Беседы с родителями об актуальности, о целях и задачах проекта, привлечение к участию в проекте
– Оформление наглядного материала.
2. Основной этап:
Мероприятия по работе с детьми:
– Чтение художественной литературы –
– Просмотр мультфильмов и презентаций
– Беседы
– НОД –
– Рассматривание альбомов и иллюстраций.
– Экспериментирование
-Конструирование
– Рисование
– Аппликация
-Лепка
– Дидактические игры
– Пальчиковые игры
– Физкультминутки
– Подвижные игры
– Театрализованные игры и инсценировки.
Сотрудничество с родителями:
– Участие родителей в выставке рисунков и работ по аппликации «Волшебные превращения»;
– разучивание с детьми стихов, загадок;
– помощь в оформлении коллажа «Город геометрических фигур»;
– помощь в изготовлении альбома «Стихи о геометрических фигурах».
3. Заключительный этап:
– оформление выставки «Геометрический вернисаж»
– изготовление альбома «Стихи и загадки о геометрических фигурах»
– коллаж «Город геометрических фигур»
– презентация «Как мы изучали геометрические фигуры»
– фотоотчет по проекту.
Отчет о реализации проекта.
Проект был направлен на формирование знаний, умений, навыков по теме «геометрические фигуры», на развитие познавательно – творческих способностей, любознательности, пытливости ума.
Участниками реализации проекта являлись дети старшей логопедической группы, воспитатели, родители воспитанников. Перспективный план был составлен с интеграцией всех образовательных областей, работа строилась с учетом предметно – развивающей среды.
В ходе реализации проекта удалось создать положительный эмоциональный фон, вызвать интерес к познавательной и мыслительной деятельности детей. Систематизированы и расширены знания детей о геометрических фигурах. Дети проявляли интерес ко всем видам деятельности, творческую активность.
В совместной продуктивной деятельности с педагогом и родителями были созданы: дидактическая игра «Часть и целое», набор фигур для геометрической мозаики, коллаж «Город геометрических фигур», альбом «Стихи и загадки о геометрических фигурах». Были оформлены выставки рисунков и поделок из бумаги в технике «оригами». В последний день работы проекта было проведено итоговое занятие «Путешествие в страну геометрических фигур. Закончился проект просмотром презентации «Как мы изучали геометрические фигуры» и обсуждением, что нового они узнали, чему научились, что сделали своими руками.
С результатами проекта также были познакомлены родители детей.
Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста,
напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.
Нужны ли геометрические фигуры для детей?
Зачем маленького ребенка обучать геометрическим фигурам? Наверняка, многие родители даже не задумываются над этим вопросом, просто отдавая дань моде и обучая кроху математике чуть ли не с рождения. Между тем, геометрические фигуры для детей, их своевременное изучение играют большую роль в познании окружающего, знакомя с одним из основных свойств предметов – формой. Это необходимо для развития логического мышления, пространственных представлений, совершенствования математических способностей. Вот почему важно начинать ознакомление с геометрическими фигурами как можно раньше, подкрепляя знания ребятишек увлекательными заданиями в повседневной жизни.
Что должен знать ребенок о геометрических фигурах
Важно: Геометрические фигуры – общепринятые эталоны, меры измерения формы предметов. Поэтому домашнее ознакомление ребенка с формами должно проходить не отдельно, а в системе сенсорного (чувственного) воспитания. Лучше всего кроха запомнит форму, когда параллельно рассматривает цвет, величину, назначение предмета, так как в разнообразной деятельности знания активно используются и лучше запоминаются.
- Специалисты утверждают, что целенаправленно обучать ребенка геометрическим фигурам в домашних условиях надо начинать на третьем году жизни. В это время у деток появляется двигательный и осязательный опыт изучения окружающего мира. Они умеют говорить, отличаются любознательностью и желанием все исследовать, стремятся к новому. Именно поэтому для дальнейшего формирования знаний у детей нужна работа в пополнении представлений о геометрических фигурах: круге, квадрате, треугольнике. В увлекательной игре (не специально!) кроха знакомится с шариком (шар), кубиком (куб).
- Четырех – пятилетние детки кроме треугольных, квадратных, круглых форм узнают прямоугольные и овальные. Считается, что в 5 лет дети уже осваивают геометрию, поэтому к следующему возрастному этапу они должны четко называть круг, овал, треугольник, квадрат, ромб, различать их и находить вокруг себя. Дошколята должны уметь анализировать и обобщать форму предметов, отмечая основные свойства, и даже решать логические задачи, сравнивая фигуры. Например, в популярной игре “Чем похожи и не похожи круг и квадрат, квадрат и прямоугольник, круг и овал?”.
- Старшие дошколята уже хорошо знают названия всех фигур, их знакомят с новыми: плоскостными (многоугольник, трапеция) и объемными (шар, куб, цилиндр и конус). Для школьного обучения детям нужно научиться делить и собирать фигуры разными способами (разрезанием и складыванием), решать задачи – головоломки, например, “Знаете ли вы, как составить из двух частей квадрат, прямоугольник, треугольник?”, “Сколько квадратов (кругов, прямоугольников) на рисунке?”.
В увлекательной игре (не специально!) кроха знакомится с шариком (шар), кубиком (куб).
Учим геометрические фигуры с малышами: главные правила
Важно: Как научить ребенка называть и различать геометрические фигуры легко и быстро! Для этого нужно придерживаться определенных правил. При хаотичном, непоследовательном обучении малыш может путать фигуры, не видеть их похожесть и различность.
- Педагоги настаивают, при домашнем обучении сделать главными правилами систематичность, последовательность, доступность. Не надо истязать себя и ребенка какими-либо заумными заданиями и пособиями, достаточно использовать развивающие книжки, игрушки (конструкторы, кубики, машинки, кукольную посуду) и привычную окружающую обстановку (предметы мебели, быта, посуду).
- Знакомство с новыми фигурами обязательно проводить в исследовательской деятельности: предложить крохе ощупать, обвести пальчиком контур, “прорисовать” в воздухе, сложить фигуры вместе, прокатывать, просовывать в отверстия.
- Ребенок быстро освоит новый материал, если будет практически действовать с ним в играх, творческой деятельности, рассматривании и чтении книжек, бытовых процессах. Например, при знакомстве малыша с квадратом можно предложить ему найти квадратные предметы в окружающей обстановке: сиденье у детского стульчика, носовой платочек, грань кубика, салфетка. Во время прогулки спросить, какой формы скамейка в сквере, стена дома, сумка у мамы, мячик, в который играют старшие ребята. При этом сам взрослый четко и понятно называет все геометрические фигуры, которые встречаются малышу.
- Хорошо, если при обучении взрослые будут использовать стишки, сказки, загадки, мультики, героями которых становятся геометрические фигуры. Можно не только читать их, но и рисовать под ритмику стиха. Эти приемы сделают обучение увлекательным, помогут активизировать процессы внимания, мышления, речи.
Например, при знакомстве малыша с квадратом можно предложить ему найти квадратные предметы в окружающей обстановке: сиденье у детского стульчика, носовой платочек, грань кубика, салфетка. Во время прогулки спросить, какой формы скамейка в сквере, стена дома, сумка у мамы, мячик, в который играют старшие ребята. При этом сам взрослый четко и понятно называет все геометрические фигуры, которые встречаются малышу.Загадки в стихах
Нет углов у меня и похож на блюдце я, на тарелку и на крышку, на кольцо и колесо. Кто же я такой, друзья? Назовите вы меня (круг).
Он давно знакомый мой, каждый угол в нем прямой. Все четыре стороны одинаковой длины. Вам его представить рад.
Как зовут его? (квадрат).
На фигуру посмотри и в альбоме начерти, три угла, три стороны меж собой соедини. Получился не угольник, а красивый (треугольник).
Вот такая есть окружность – очень странная наружность. Круг приплюснутым стал, получился вдруг (овал).
Растянули мы квадрат и представили на взгляд. На кого он стал похожим или с чем-то очень схожим?
Ни кирпич, ни треугольник – стал квадрат (прямоугольник).
Сказка “Два брата” (взрослый рисует под ритмику стиха)
Давным-давно в темном лесу в фигурной избушке жили-были два брата, два квадрата. И были они близнецами. Убедитесь сами:
Видите на картинке – у каждого 4 стороны, 4 угла и 4 вершинки.
Гулял как-то первый квадрат между кустами, стучал по дорожке четырьмя уголками.
А звери говорят: «Кто это? Первый квадрат или его брат, второй квадрат? Как же они похожи!
Помните на картинке: 4 стороны, 4 угла и 4 вершинки.
Надоело квадрату, что его путают с братом, и решил он измениться, в другую фигуру превратиться.
Взял он ножницы и срезал себе четыре уголка. В круг превратился и по дорожке покатился.
И живется теперь братьям чудно, перепутать теперь братьев трудно:
Один катается по дорожкам, другой ходит на четырех уголках – четырех ножках.
До сих пор дружат два брата – круг с квадратом!
Важно: Особенности восприятия детьми геометрических фигур совсем не такие, как у взрослых. Например, взрослый видит предметы сообразно формам (кастрюля – цилиндр, окно – прямоугольник). Ребенок, наоборот, сначала форму опредмечивает (квадрат – воздушный змей, треугольник – крыша дома, круг – мячик, несколько кругов – очки, бусы). При правильном обучении он начинает абстрагироваться от предметов и воспринимать в окружающем знакомую фигуру, например, стакан как цилиндр (цилиндрической формы), крыша как треугольник (треугольной формы), мяч как шар (круглой формы).
Играем с геометрическими формами!
Педагоги напоминают, что основные знания о геометрических фигурах дошкольники получают в детском саду, а домашние занятия направлены на закрепление изучаемого.
Поэтому самым лучшим средством дома будет игра, как основная деятельность малышей. Именно в игре ненавязчиво, легко и быстро ребенок выучит все названия фигур, научится их сравнивать и различать. Среди развивающих игр на обучение геометрическим формам первенство принадлежит настольным играм. В них можно играть по вечерам, во время семейного досуга, сделать частью любого домашнего занятия, развлечения.
«Что спряталось»
Классическая игра понятна и доступна даже двухлетнему крохе. Взрослый раскладывает перед ребенком изображения знакомых фигур: круг, квадрат, треугольник. Так как карточек должно быть не меньше пяти, для количества используются фигуры разных цвет и размеров, например, два квадрата – большой и маленький, два треугольника – синий и желтый, один круг. Рассмотреть их с ребенком, обсудить, убедиться, что понимает, какие фигуры перед ним и может их правильно назвать. Затем малыш закрывает глаза, взрослый прячет одну из фигур и спрашивает, что спряталось. С возрастом количество фигур увеличивается, к старым добавляются новые.
«Одним словечком»
Игра “геометрические фигуры” направлена на формирование у детей обобщения однотипных фигур. Взрослому нужно подготовить круги, квадраты и треугольники разного размера и цвета. Дошкольник должен распределить по группам представленные фигуры независимо от цвета и размера, назвать их обобщающим словом, например, все квадраты. Как вариант, можно усложнять задания, предлагая сгруппировать фигуры только по цвету или размеру.
«Чудесный мешочек»
Игры по типу “чудесного мешочка” хорошо знакомы ребятишкам детсадовского возраста. Они полезны тем, что дают представление о контурах предметов, обучают обследованию на ощупь и упражняют в различении форм. Взрослый готовит мешочек с предметами разных форм, например, кубик, шарик, мячик, кирпичик, конусная пирамидка. Игрок обследует их и называет форму игрушки, которую хочет достать. Для усложнения задания старшим деткам предлагается найти какую-либо конкретную форму, например, “Найди круглую игрушку”.
«Волшебные очки»
Предварительно готовятся импровизированные очки из плотной бумаги разной формы: круглые, квадратные. Игра интересна всем ребяткам, помогает расширить представления о геометрических фигурах, находить предметы определенной формы в окружающем пространстве. Например, ребенок надевает круглые очки и ищет все круглое вокруг себя: тарелка, дно у вазы, плафон у люстры, ковер, бабушкины очки. За каждый правильный подбор игрок награждается фишкой, а затем получает поощрительный приз в конце игры.
«Латки – заплатки»
Для занятия по закреплению представлений о геометрических фигурах нужна подборка картинок с изображением различных предметов, в которых есть “дырки” – незакрашенные места разной формы, например, у платья круглая дырка, в сапожке – квадратная. Среди разных “заплаток” ребенок выбирает нужную и соединяет с предметом. Интересно будет, если взрослый сам приготовит для игры изображения, например, вырежет из бумаги вещи (свитер, юбка, брюки, сапожки, шапочку).
Как вариант игры в “латки – заплатки”, можно приобрести дидактическую игру в “липучки”, которые очень похожи правилами и содержанием
«Что сломалось»
Такое задание поможет приучить детей замечать, какой формы не хватает в изображенном предмете, развивает внимание. Для игры можно использовать картинки, аппликацию из вырезанных деталей, строительный материал. Главное – предмет должен состоять из частей геометрической формы. Например, взрослый выкладывает аппликацию “дом”, где деталями являются треугольник – крыша, прямоугольник – стена, квадрат – окошко, маленький прямоугольник – дверь, круг – окошко в чердаке, четырехугольник – труба. Ребенок внимательно рассматривает изображение и закрывает глаза, взрослый убирает какую-либо деталь, смешивая ее с любыми другими. Нужно отгадать, что сломалось у домика и “починить”, отыскав недостающую часть. В дальнейшем можно усложнить задание, сразу же не добавляя определенную форму или убирая две формы одновременно.
Если это нарисованное изображение, то ребенок подрисовывает недостающие детали, например, круг – колесо у машины, прямоугольники – окошки у башенки.
«Игра с палочками»
Интересное задание для средних и старших дошкольников, одновременно развивает моторику и умение составлять геометрические фигуры. Если нет счетных палочек, можно использовать спички или зубочистки, предварительно их подготовить, обрезать серную головку или острые концы, чтобы малыш не поранился. Такое задание можно провести в виде соревнования во время семейного досуга, “кто быстрее всех составит фигуру?”, “у кого самая сложная фигура?”. Затем отметить призом победителя. Обязательно в какой-то момент им должен стать ребенок. Взрослый, например, может отметить его оригинальное решение или тщательно и аккуратно выложенную фигуру.
«Что пригодилось художнику в картине»
Для старших дошколят можно использовать оригинальное задание на рассматривание картин, которое не только закрепляет название фигур, но и развивает зрительное восприятие, умение видеть разные формы в необычной обстановке.
Взрослый подбирает иллюстрации соответствующего содержания, которые художник рисует при помощи геометрических форм. Затем предлагает дошкольнику рассмотреть картинку м найти знакомые формы. Если какие-либо из них пока еще незнакомы дошколенку, обязательно обратить на них внимание и рассказать, как они называются, какие предметы похожи на них. Усложняя игру, можно посчитать, сколько геометрических фигур понадобилось для изображения картины.
«Геометрическое лото»
Классическое задание на ознакомление детей с геометрическими фигурами учит сравнивать форму предмета с геометрической фигурой, подбирать изображения в опоре на эталон. Чтобы получился соревновательный момент, интересный ребятишкам, играть лучше всей семьей. Правило классическое: на больших карточках – изображения разных фигур, например, овал, круг, треугольник. Ведущий произносит название предмета на маленькой карточке, например, яблоко, огурец, платок, телевизор. Игроки ищут на своей карточке форму названого предмета и закрывают ее соответствующей картинкой.
Выигрывает игрок, который быстро и правильно закроет карточку.
«Геометрическая мозаика»
Такая развивающая игра поможет ребятишкам закреплению представлений о геометрических фигурах. Кроме того, научит дошколят преобразовывать их, ориентируясь на эталон (образец), поможет творческому воображению. Правила игры просты и доступны ребяткам любого возраста, для старших – количество деталей увеличивается, усложняются сюжеты. Игроки должны собрать из нескольких геометрических фигур какие-либо предметы. Для малышей это могут быть домики разной величины и конфигурации, машины, башенки, мостики, солнышко, цветы, узоры; для старших ребятишек – фигурки сказочных или мультяшных персонажей, сюжетные картинки: ваза с цветами, улица, дорога, ковер, животные, люди разных профессий. Обязательно отметить творчество дошколенка, похвалить его. Возможно, оставить выложенную картинку на некоторое время, чтобы показать всем близким. Главное, что такую развивающую мозаику можно приобрести в специальном магазине, а можно сделать своими руками по типу игрушек Монтессори.
Первые геометрические фигуры для детей – прекрасный повод провести весело время
Думаете, сложно изучать геометрические фигуры с ребятней? Или считаете, что этому научат их учителя в начальной школе? На самом деле, изучение цифр и ассоциативных образов можно уже начать с того момента, когда малышу исполнился один год. Но для начала настройтесь на то, что первые геометрические фигуры для детей – это прекрасный повод провести весело время. Мы подготовили для вас несколько полезных советов, которыми вы обязательно воспользуйтесь в ближайшее время.
Зачем нужны знания о фигурах?
Понятия круга, квадрата или овала нужны не только для решения математических задач, но также для общего развития:
- образы мы встречаем повсюду: мяч, которым играют во дворе, тарелка, в которую выкладываем котлеты, книга, которую читаем на ночь, и так далее. Анализируя схожесть окружающих предметов с очертаниями, ребятня развивает в себе пространственное и ассоциативное мышление. Эти знания чрезвычайно важны для развития других навыков и способностей;
- когда дитя постепенно осваивает новую информацию, ему приходится значительно проще воспринимать получаемые сведения;
- понимание различий очертаний позволяет крошкам успешно осваивать другие игры, например, лего, мозаику, конструктор и другие.
Анализируя схожесть окружающих предметов с очертаниями, ребятня развивает в себе пространственное и ассоциативное мышление. Эти знания чрезвычайно важны для развития других навыков и способностей;Овладение новыми знаниями – прекрасная возможность тренировать мозг. А активное обучение формирует в вашем чаде гармоничную и креативную личность. Если с первого года жизни давать детям шанс беспрепятственно развиваться, регулярно узнавать что-то занимательное, то через несколько лет рядом с вами окажутся разносторонне развитые люди, имеющие собственный взгляд на окружающее. Разве не такая цель стоит перед заботливыми родителями?!
Как объяснить материал дошкольникам?
С чего начать занятие – первостепенный вопрос, которым задаются родители.
Мы подготовили для вас несколько простых игровых уроков, с помощью которых вы быстро сориентируетесь, какие методы вам полезны сейчас, а какими стоит воспользоваться немного позднее:
- Рассматриваем картинки, изображения всегда и везде. Обсуждаем и учим названия. Пусть в часто кроха будет путаться и забывать названия, а вы будете снова напоминать ему их. Если читаете книгу, увидели знакомые очертания, обязательно обговорите это. Интересно, что старинные литеры во многих языках были схожи с какими-то предметами. Их было много, но люди их запоминали благодаря ассоциативной памяти. Сейчас подобные литеры остались только китайских иероглифах. Неудивительно, что они так привлекают нас.
- Отменная игра, которой вам нужно непременно воспользоваться – лото с красочными изображениями. Уверены, подобные развлечения были и в вашем детстве. Большое преимущество игры в том, что дети смогут играть в нее независимо от взрослых. Кроме них, можно изучать животных, цифры, цвета, овощи и растения. Если не знаете, где купить лото, сделайте его сами. Распечатайте на цветном принтере два экземпляра картинок, разрежьте их на части и играйте.
- Прекрасное развлечение – сортер. Это идеальный вариант для дитя до года-полутора лет. Каждое очертание подходит только для одного отверстия. Поэтому чадо методично подбирает игрушку, которая смогла бы поместиться в отверстие. В этот момент мамы и папы могут проговаривать действия детей. Например, “эта игрушка имеет округлости, поэтому не может пройти в квадрат. Но если ты попробуешь другое отверстие, то у тебя может все получиться”.
- Другой вариант сортера – рамка-вкладыш с фигурками. Такие развлечения часто можно встретить в продаже, особенно актуальны варианты с буковками.
- Сортировать штучки согласно их форме. Например, кукле достанутся округлые объекты, а мячику – квадратные. Позвольте детям самостоятельно выбирать предпочтения для своих любимых игрушек.
- Рисование – волшебный процесс, которому практически нет равных для развития чад. Можно рисовать карандашами, красками, ручками и маркерами, использовать различные линеечки и кухонные приборы, которые можно обводить по контуру. Находите вместе с крохой схожести с образами, пусть он называет их.
- Подготовьте заранее квадраты, треугольники, круги и овалы, прямоугольники и ромбы из цветной бумаги. Предоставьте ребенку самостоятельно создать собственную картину из этих материалов. Но не забывайте обсуждать с ним, что он использует, с какой целью и как называются штуки.
Если не знаете, где купить лото, сделайте его сами. Распечатайте на цветном принтере два экземпляра картинок, разрежьте их на части и играйте.
Можно рисовать карандашами, красками, ручками и маркерами, использовать различные линеечки и кухонные приборы, которые можно обводить по контуру. Находите вместе с крохой схожести с образами, пусть он называет их.Каждое чадо имеет свой путь развития. Задача родителей дать уверенность ему в действиях, мыслях, рассуждениях. В первые годы жизни кроха готов ежедневно совершать интеллектуальные подвиги, не забывайте об этом. Занимайтесь детьми, получайте от совместного времяпровождения удовольствие!
Вы можете убедиться в этом, пройдя по данной ссылке и выполнив задания:
https://alimok.com/ru/disciplina/matematika
или ознакомиться с другими статьями:
https://alimok.
com/ru/sovety-psihologa
11 крутых форм, о которых вы не знали
В природе, в архитектуре или в товарах, которые мы используем, крутые формы встречаются повсюду.
Фактически, формы образуют строительные блоки любого дизайна. И хотя мы можем этого не осознавать, каждая форма может заставить нас чувствовать себя определенным образом.
Бренды и визуальные коммуникаторы по всему миру могут использовать формы в дизайне, чтобы делиться определенными ценностями и сообщениями со своей аудиторией. Формы могут использоваться в фирменном стиле, например в логотипах, дизайне веб-сайтов и визитных карточек, или в дизайне продукта в практических или эмоциональных целях.
Но формы не ограничиваются только кругами, квадратами и треугольниками. Есть несколько интересных фигур, о которых вы, вероятно, не узнали в школе. И, как и все другие формы и символы в мире, эти классные формы также имеют свои собственные значения и эмоции.
Вот 11 интересных форм, которые помогут вам создавать значимые дизайны и лучше взаимодействовать с вашей аудиторией.
Вы можете просмотреть визуальную инфографику этого сообщения ниже или пропустить его, чтобы прочитать подробное описание и историю каждой крутой формы.
11 крутых форм, о которых вы не знали1 Гептаграмма
Гептаграмма – это семиконечная звезда, нарисованная семью прямыми штрихами.
Он использовался в различных религиях мира для обозначения чего-то священного. Например, в христианстве эта форма использовалась для обозначения семи дней творения.
Это был также символ богини Бабалон в Телеме.
Однако в последнее время форма в значительной степени ассоциировалась с религией Викка – современной религией, основанной на древних традициях колдовства.Для виккан, которые поклоняются природе и следуют традиции Фей, гептаграмма является священным символом и известна как Эльфийская или Фэйри-звезда.
Источник изображения
Помимо религии, гептаграмма также используется в алхимии; Семигранная звезда, обозначающая семь планет, известных древним алхимикам.
Обладая такой яркой историей, гептаграмма, безусловно, представляет собой форму, которую нельзя игнорировать.
Гептаграмму также можно увидеть на флагах различных стран, в первую очередь на флагах Австралии и Иордании.Он также используется в логотипе известной транспортно-логистической компании Maersk.
Источник изображения
Говорят, что Петер Мэрск Мёллер, основатель Maersk, был глубоко религиозным христианином. После того, как его жена вылечилась от болезни, он прикрепил синий флаг с белой семиконечной звездой – гептаграммой – на своем пароходе «Лаура», который позже стал эмблемой Maersk Group.
В письме к жене в 1886 году Петр объяснил: «Маленькая звезда на дымоходе – это воспоминание о ночи, когда я молился за вас и просил знамения: если звезда появится на сером и облачном небе, она будет означать, что Господь отвечает на молитвы.«
Визуальные коммуникаторы могут использовать эту классную форму для представления совершенства или для создания глубокого чувства принадлежности к своей аудитории. Компании могут использовать гептаграмму в своих проектах для иллюстрации различных разделов, отделов или основных ценностей.
2 Triquetra
Буквальное значение слова «трикетра» – «треугольник».
Эта крутая треугольная форма симметрична и образована перекрытием трех дуг. Он использовался для различных целей в истории, особенно в религии.
В христианстве три края трикетры представляют Святую Троицу Отца, Сына и Святого Духа. Вот почему эту форму также называют «узлом Троицы».
Трикетра часто изображается с кругом – кругом Троицы – переплетенным между тремя дугами, что символизирует единство. Форма также появляется в кельтском искусстве, а также в раннем христианском искусстве.
Источник изображения
Выше показано, как трикетра использовалась в оконном искусстве в католической церкви Непорочного Сердца Марии в Уилмингтоне, Делавэр.
Трикетра также можно увидеть в американском телешоу «Зачарованные».
Хотя шоу было о трех ведьмах, сражающихся с демонами и колдунами, никакого религиозного значения трикетра не подразумевалось.
Источник изображения
Triquetra – отличная форма для использования в визуальном дизайне и брендинге для всех типов визуальных коммуникаторов. Его можно использовать для иллюстрации объединения трех элементов, таких как ценности, личности или другие аспекты.
3 звезды Лакшми
Звезда Лакшми – это особая октаграмма – восьмиугольный многоугольник, состоящий из двух равных квадратов с одним и тем же центром, расположенных под углом 45 °.
Происхождение этой крутой формы восходит к индуистской религии.
В индуизме Лакшми – богиня богатства – имеет восемь форм проявления, известных как Ашталакшми. Они представлены двумя переплетенными квадратами, образующими октаграмму.
Каждое проявление представляет собой определенную форму богатства: деньги, способность к транспорту, бесконечное процветание, победу, терпение, здоровье и питание, знания и семью.
Эта крутая форма также используется в центральном вестибюле здания парламента в Лондоне.
Сегодня форма чаще встречается в архитектурном дизайне, коврах, плитке, ювелирных изделиях и других украшениях.
Он даже появляется на сайте американской рок-группы Faith No More.
Источник изображения
Звезда Лакшми, безусловно, очень уникальная форма с глубоким символизмом. Это отличный выбор для духовных и целительных брендов, стремящихся создать новый фирменный стиль.
4 Лемниската
Лемниската похожа на кривую в виде восьмерки и напоминает символ бесконечности.
Происхождение лемнискаты восходит к 5 веку нашей эры. Его нашел греческий философ-неоплатоник Прокл, который назвал эту фигуру оковами для лошади, так как она напоминала два соединенных вместе копыта.
В графическом дизайне эта классная форма часто используется в типографике. Обратите внимание на логотип Coursera, известной платформы онлайн-обучения.
Источник изображения
Символ бесконечности олицетворяет непрерывность и бессмертие. В случае с Coursera, приведенным выше, он явно используется, чтобы показать, что обучение и рост – это бесконечный процесс.
Предстоящий чемпионат мира по футболу 2022 года также использует форму лемнискаты в своем официальном логотипе.
Источник изображения
5 Весика Писцис
Vesica Piscis очень похожа на диаграмму Венна, но имеет гораздо более глубокий смысл.
Эта крутая форма образована пересечением двух кругов с одинаковым радиусом, где центр каждого круга лежит на окружности другого.
Дословный перевод слова Vesica Piscis – «пузырь рыбы».”Он считается священным числом, потому что отношение его ширины к его высоте считалось 165: 153 или 1,73203, что считалось священным числом.
Один из витражей церкви Святой Марии и Всех Святых в Честерфилде демонстрирует Vesica Piscis, созданную еще в 1947 году.
Источник изображения
Эту крутую форму также можно увидеть в Чаши Колодца в графстве Сомерсет, Англия.
Vesica Piscis также используется в современном ювелирном дизайне. Многие организации по всему миру так или иначе использовали эту форму.
Mastercard, одна из самых известных финансовых компаний в мире, использует эту классную форму в своем логотипе.
Источник изображения
Причина, по которой Vesica Piscis использовалась в их логотипе, может заключаться в том, что Mastercard была образована в результате объединения множества различных банков и финансовых учреждений.
Они также придумали слоган: «Mastercard, сердце коммерции». в 2006 году, что делает логотип похожим на символ центрального источника энергии, такого как сердце.
Визуальные коммуникаторы и бренды могут использовать эту форму для обозначения союза двух сил или источника. Его также можно использовать для обозначения созидания, рождения и плодородия, так как он напоминает женский репродуктивный орган.
6 Треугольник Рело
Треугольник Рело (произносится как «ру-лос») – изогнутый треугольник, образованный пересечением трех круговых дисков.
Вы, наверное, видели эту классную форму в медиаторах, карандашах, архитектуре, монетах и даже сверлах.
Треугольник Рело назван в честь немецкого инженера 19 века Франца Рёло, который был известен тем, что использовал этот дизайн в своей работе.
Вы также можете найти эту форму в корпоративных логотипах и вывесках по всему миру. Например, Национальная система троп и система велосипедных маршрутов США отмечают маршруты треугольниками Рило на своих указателях.
Источник изображения
Эта форма также использовалась в архитектуре, например, в этой башне в Барселоне, в которой использовался треугольник Рило, чтобы создать легкую и максимально просторную конструкцию.
Источник изображения
7 Эннеаграмма
Эннеаграмма (произносится как «любой-грамм») – это девятиугольная фигура, обычно заключенная в круг.
Если эта классная форма кажется вам знакомой, вы, вероятно, поклонник Slipknot.
Источник изображения
Происхождение этой крутой формы неясно. Некоторые говорят, что его можно проследить до сакральной геометрии пифагорейских математиков, в то время как другие полагают, что он, возможно, проник в иудаизм и представляет Древо жизни в Каббале.
Чаще эннеаграмма используется в системе анализа для представления спектра возможных типов личности, где числа 1-9 используются для обозначения части личности. Вы можете пройти тест здесь.
Источник изображения
В визуальной идентичности вы можете использовать эннеаграмму для описания нескольких личностей или аспектов вашего бренда.
8 Nonagon
Нонагон, также известный как эннеагон, представляет собой многоугольник с девятью сторонами.
Все стороны правильного шестиугольника имеют одинаковую длину, а углы составляют 140 градусов каждая.Однако неправильный шестиугольник не имеет равных сторон или углов.
Эту классную форму можно увидеть в различных зданиях по всему миру. Например, вершина стального здания США в Питтсбурге, штат Пенсильвания, представляет собой неправильный шестиугольник.
Источник изображения
Похоже на треугольник, но на самом деле у него девять сторон. Идите и сосчитайте их.
Эта крутая форма также связана с религией Веры Бахаи – все их Дома Поклонения должны иметь девять сторон. Вот видео, которое показывает собрание храмов бахаи мира.
У фигурки даже есть своя детская песенка. Так круто!
Нонагон также широко используется в дизайне интерьеров, ювелирных изделиях, искусстве и даже в брендинге и логотипах. Поскольку число 9 считается священным в большинстве религий, эта форма идеально подходит для обозначения магии, силы и мудрости в ваших рисунках.
9 кольцевое пространство
Кольцо напоминает объект в форме кольца, центральная часть которого заключена в два концентрических круга.Эта крутая форма обычно используется при строительстве нефтяных и водяных скважин, насосно-компрессорных труб и обсадных труб.
Помимо производственного и архитектурного использования, эта классная форма также может использоваться в фирменном стиле, корпоративных презентациях, презентациях и даже логотипах для обозначения цели, цели или направления вашего бизнеса.
Кольцо также используется в логотипе Target, восьмого по величине ритейлера в США.
Источник изображения
10 Лента Мебиуса
Лента Мебиуса, или лента Мебиуса, представляет собой трехмерную фигуру с одной сплошной стороной.
Эта форма названа в честь Августа Фердинанда Мёбиуса, немецкого математика, который также был поклонником необычных форм.
Вы, должно быть, видели эту фигуру как символ утилизации.
Источник изображения
Лента Мебиуса символизирует непрерывность, что объясняет, почему она используется в качестве всемирно признанного символа вторичной переработки.
Это также символ инноваций и постоянных изменений, поэтому он также используется в логотипе Google Диска.
Источник изображения
Ленту Мебиуса можно использовать для передачи различных ценностей и эмоций.Эта классная форма также может использоваться для обозначения единства, баланса, реинкарнации и других подобных значений в ваших проектах.
Эта форма часто встречается в обручальных кольцах и символизирует бесконечность и вечную любовь. Он также используется дизайнером Арихиро Мияке в своей подвесной лампе Kepler.
Источник изображения
11 Сквиркл
Белка – это уникальная форма, которая находится где-то между квадратом и кругом.
Возможно, это не так, но эта милая маленькая фигурка на самом деле имеет математическое происхождение.Это часто встречается в дизайне обеденных тарелок, оптики, монет и многого другого.
Даже в старых телефонах Nokia в сенсорные панели встроен блокнот.
Эту классную форму теперь можно найти на значках приложений вашего iPhone, а также на задней панели iPhone 11 Pro Max от Apple.
Источник изображения
Несколько лет назад сквиркллы были в моде в автомобильном дизайне. Его можно было найти буквально повсюду – от фар до интерьера.
Отчасти сквиркл так популярен из-за того, что он практичен, а также выглядит гладким и утонченным.Например, круглая обеденная тарелка может вместить больше еды, чем круглая или квадратная тарелка.
Бьюсь об заклад, вы никогда этого не осознавали, но даже Instagram использует squircle в качестве своего логотипа!
Источник изображения
В качестве бренда или средства визуальной коммуникации вы можете использовать сквиркл, чтобы символизировать инновации и творчество в своих проектах. Этот символизм проистекает из того, что эта классная форма органично объединяет две правильные формы, создавая более красивую и функциональную.
Создавайте уникальный дизайн с этими крутыми формами
Каждый хороший визуальный коммуникатор должен знать «почему», стоящий за использованием определенного символа или формы в своем дизайне.Это поможет вам создавать не только более красивые дизайны, но и более мощные и эффективные.
Использование крутых креативных форм может превратить скучный или простой дизайн в значимые визуальные эффекты, которые находят отклик у вашей аудитории и приближают их к вашему бренду.
Начните использовать эти классные формы в своих проектах, чтобы сформировать уникальные и запоминающиеся ассоциации с вашим брендом. В Visme вы можете создавать всевозможные визуальные эффекты, такие как инфографика, изображения в социальных сетях, презентации, материалы для идентификации бренда и многое другое.
Зарегистрируйтесь и получите бесплатную учетную запись прямо сейчас и пройдите тест-драйв!
|
Видео для детей, обучающие геометрии
Дети часто очень наглядны, когда дело доходит до обучения, что делает включение видео в ваши уроки забавным и простым инструментом, который отвечает их визуальным потребностям. Особенно по математике! Ваши ученики могут не ожидать, что вы будете воспроизводить видео во время обучения математике, что придаст вашему уроку неожиданный поворот! Этот элемент неожиданности и того, чтобы застать их врасплох, поделившись различными видео, связанными с геометрией, – отличный способ полностью заинтересовать ваших маленьких учеников! Кроме того, математические видеоролики очень увлекательны и часто очень интерактивны.
В следующем списке видеороликов представлены разнообразные энергичные песни, отличная графика и простые объяснения геометрии. Поскольку эти видео в совокупности затрагивают различные учебные классы и подтемы геометрии, у вас не должно возникнуть проблем с поиском идеального места в ваших инструкциях по математике для использования одного (или нескольких) из этих развлекательных и образовательных видео по геометрии.
Введение в симметрию: все о симметрии для детей (2:35)Некоторым ученикам может быть трудно понять симметрию – но не тогда, когда вы им показываете это видео! Он предлагает идеальное введение в концепцию симметрии! Мне очень нравится, как это видео не только показывает и объясняет симметрию с точки зрения форм и рисунков, но и использует реальные объекты в качестве примеров.Это действительно помогает детям задуматься о симметрии, существующей в окружающем их мире! Несмотря на то, что в этом видео нет броской мелодии, привлекательная графика и невероятно четкое объяснение симметрии делают его отличным ресурсом для знакомства с концепцией базовой симметрии.
Симметрия для детей (3:48)
Ваши дети будут в восторге от изучения симметрии с этим веселым видео! В него входит веселая рок-н-ролльная песня, которая поможет вашим ученикам расширить свои знания о симметрии далеко за пределы основ! Используя яркие формы и красочную графику в сочетании с простыми текстовыми пояснениями и запоминающейся мелодией, песня и видео работают вместе, чтобы эффективно раскрыть множество различных аспектов симметрии.Это отличное видео для расширения этой концепции, поскольку в нем исследуются различные варианты симметрии, такие как двусторонняя и вращательная симметрия.
Видео с песней Polygon (4:02)
Ваши дети полностью поймут, что такое многоугольник, послушав запоминающуюся песню из этого видео. Определение многоугольника объясняется сразу же и продолжает показывать изображения различных многоугольников, а также объясняет, как они получили свои названия.Он четко исследует и обсуждает трех-, четырех-, пятиугольные формы вплоть до десятиугольника. После объяснения каждой формы видео принимает интерактивный вид: зрителей просят нарисовать различные фигуры в воздухе, подпевая их видео. Вашим детям это понравится!
Они многоугольник Песня (3:18)
Эта очаровательная песня помогает ясно показать разницу между «скучным квадратом» и другими формами, такими как пятиугольники, шестиугольники, семиугольники, восьмиугольники, неугольники и десятиугольники.Хотя припев песни немного монотонен с текстами о скучном квадрате, он отлично показывает, сколько сторон имеет каждая форма и чем каждая из них отличается от квадрата. Слово многоугольник на самом деле не упоминается в этом видео, поэтому показ ролика № 3 перед этим был бы отличным способом сначала представить многоугольники, а затем усилить их суть, продемонстрировав это.
Узнайте о двухмерных фигурах с поездом Choo-Choo – Часть 1 (9:35)
Хотя это видео длиннее и не содержит запоминающихся тематических песен, это действительно эффективный инструмент для обучения двухмерных фигур младшим школьникам.Красочно анимированный говорящий поезд поможет заинтересовать ваших маленьких учеников, в то время как четкие и простые для понимания объяснения не оставят места для путаницы в отношении двумерных фигур. Если вас беспокоит длина видео, вы можете пропустить первую минуту видео – в основном это просто вступительная музыка. Яркая анимация и подробные объяснения различных характеристик двумерных фигур гарантируют, что ваши ученики полностью усвоят эту базовую концепцию геометрии и получат от этого удовольствие! Им понравится интерактивный характер этого видео, поскольку говорящий поезд задает вопросы аудитории на протяжении всего видео.
Изучение трехмерных фигур (геометрические тела) с поездом Choo-Choo – Часть 2 (12:05)
Часть 2 серии видеороликов Choo-Choo Train основывается на предыдущем видеоролике, переходя от двухмерных к трехмерным фигурам. Тот же говорящий поезд из предыдущего видео поможет вашим ученикам понять различные трехмерные формы и то, что делает их трехмерными. Опять же, если вы беспокоитесь о времени, вы можете перейти к минуте 2:55, чтобы перейти к реальной сути видео, где полностью исследуется каждая трехмерная форма и каждая из них соотносится с двухмерной формой.Как и двухмерное видео, это видео предлагает интерактивный компонент, так как он задает вопросы зрителям, исследуя различные трехмерные формы – предлагая вам прекрасную возможность остановиться и обсудить концепции со своими учениками! (Убедитесь, что ваши дети понимают, что такое многоугольник, прежде чем смотреть видео, поскольку он относится к многоугольникам без подробного объяснения.)
Двухмерные геометрические формы для лепки (6:12)
https://www.youtube.com/watch?v=yXRv8RPHJjc
Хотя в этом видео нет слов, его все же невероятно полезно использовать в качестве наглядного примера создания двухмерных фигур.Выполнение упражнения, показанного в видео, с вашим классом было бы отличным способом предложить учащимся практический опыт формирования фигур. Вы также можете использовать это видео в качестве подсказки для вопросов в классе о геометрии или пространственных отношениях. Например, какую форму вы видите над пятиугольником и т. Д. Видео короткое, но все же ясно показывает детям, как формировать двумерные формы, используя маленькие шарики из пластилина и зубочистки! Если вы собираетесь выполнить это задание со своим классом, используйте это видео в качестве введения или на заднем плане класса, пока учащиеся лепят различные формы для лепки.
Трехмерные фигуры с пластилином (9:06)
https://www.youtube.com/watch?v=Fy5abut63Qk
Очень похоже на предыдущий, это еще одно видео без слов, которое просто показывает детям этапы создания трехмерных фигур с помощью Play Dough и зубочисток. Вы можете легко использовать это видео сразу же после предыдущего, чтобы по-настоящему подчеркнуть разницу между двухмерными и трехмерными формами для ваших учеников. Его также можно легко использовать в качестве введения к этому заданию или в качестве справочной информации, пока ваши ученики создают трехмерные фигурки из теста для лепки.Если вас беспокоит длина этого видео, вы можете легко перемотать некоторые этапы построения фигур, когда увидите, что ваши дети уловили концепцию.
Как легко рисовать треугольники с Евклидом (3:47)
Не обманывайте себя заголовком – это видео не только учит детей рисовать треугольник. Главный герой, древнегреческий математик Евклид, дает зрителям краткое введение в несколько различных геометрических тем, включая линии, углы и треугольники.Он предлагает объяснения взаимосвязи между линиями, различных видов линий и того, как они пересекаются или не пересекаются, и в конечном итоге связывает эти идеи, показывая нам, как нарисован треугольник, соединяя три точки тремя линиями, а затем образуя три угла. Детям понравится, как рассказчик иллюстрирует Евклида во время разговора, а его британский акцент – дополнительный бонус! Это видео о гораздо большем, чем просто рисование треугольников, является отличным дополнением к любому уроку геометрии о линиях, углах И треугольниках.
Песня о полигонах для детей Рэп-видео: геометрия, четырехугольники, шестиугольники и т. Д. (1:57)
https://youtu.be/meaGjrKWGFQ
Ваши дети будут в восторге от запоминающегося ритма в этой рэп-песне, поскольку в ней подробно объясняются различные предварительные исправления форм и их влияние на количество сторон формы. В этом видео замечательно то, что во время воспроизведения песни изображения каждой обсуждаемой формы отображаются в реальных ситуациях. Например, на видео показан треугольник в парусе лодки и четырехугольник в двери дома.Это поможет вашим ученикам увидеть, что формы можно найти повсюду вокруг нас, а также послужит отличным введением в потенциальное занятие по поиску формы.
Песня о параллельных, перпендикулярных и пересекающихся линиях | NUMBEROCK (2:21)
https://youtu.be/P3AOoLbA3us
Если вы рассказываете своим детям о различных типах линий и о том, как они взаимодействуют друг с другом, вы обязательно должны поделиться этим видео со своим классом! С запоминающимся ритмом, припевом, который вы не забудете скоро, и четкой графикой – это видео и песня помогут вашим детям быстро понять концепцию геометрических линий! Припев побуждает зрителей поднимать руки вверх и формировать руками различные линии во время постукивания в видео.Повторение в этом видео действительно помогает донести мысль о параллельных, перпендикулярных и пересекающихся линиях в веселой и приятной форме!
Песня о трехмерных фигурах для детей | Видео 3-D формы от NUMBEROCK (2:04)
https://youtu.be/uZ8Jy1xgqPU
Еще одно отличное видео от NUMBEROCK, эта живая рэп-песня отлично объясняет зрителям трехмерные формы. Если некоторые из ранее упомянутых видеороликов, посвященных трехмерным фигурам, покажутся вашим ученикам слишком юными, это будет большим успехом у старших детей – и даже у самых маленьких! Хор помогает напомнить учащимся о характеристиках трехмерных форм, в то время как остальная часть песни объясняет конкретные трехмерные формы и места, где зрители могут видеть эти формы в повседневной жизни.Ваши дети не только лучше поймут трехмерные формы после просмотра этого видео, но и будут напевать мелодию в течение нескольких дней, показывая трехмерные формы вокруг себя!
Колин Доддс – Геометрические преобразования (3:15)
Понимание различных способов перемещения или трансформации фигур кажется достаточно простым, но некоторым ученикам может быть сложно полностью понять их. Хотя в этом видео не самая впечатляющая графика, мелодия запоминается, а объяснения различных способов движения фигур очень легко понять.Хор повторяет ключевые термины, касающиеся геометрических преобразований, таких как поворот, перевод и отражение, и полностью объясняет, что означает каждый термин. Это видео может быть лучше для студентов старшего возраста, поскольку в нем вводится более сложный термин, мозаика, а также много текстовых отображений определений. По этой причине может быть полезно показать это видео учащимся, которые умеют читать, хотя это не обязательно для того, чтобы оно было эффективным.
Песня Shapes: Shapes Rap / Chant – Песня формы робота (3:36)
Отличное введение в основные формы, это видео сочетает в себе простой фоновый рисунок с простыми объяснениями различных форм, таких как круги, треугольники, четырехугольники, параллелограммы и т. Д.После демонстрации визуального представления каждой формы в видео используется простая анимация, чтобы показать, как на самом деле создается каждая форма, и четко указать, сколько у нее сторон. Хотя графика довольно проста и бит не получит Грэмми в ближайшее время, это видео предлагает очень простые для понимания объяснения и введение в основные формы. Идеально подходит для младших школьников!
Triangle Song ⋆ Типы треугольников для детей от NUMBEROCK (1:55)
https: // youtu.be / JQUTVgT9RXY
Можете ли вы сказать, что я большой поклонник этих видео NUMBEROCK? Я думаю, что они действительно отличное дополнение к любому уроку геометрии, потому что все они содержат разные, но одинаково запоминающиеся ритмы и мелодии в сочетании с понятными объяснениями данной концепции. Мне также нравится, как все они показывают реальные примеры геометрических концепций и геометрических фигур. В этом конкретном видео отлично исследуются все виды треугольников – концепция, с которой, как я обнаружил, многие мои ученики испытывают затруднения.В песне не только объясняются и показаны примеры различных треугольников, но и подчеркиваются различные характеристики, которые отличают эти треугольники друг от друга. Быстро, запоминающе и по делу – это видео станет отличным дополнением к любому уроку геометрии треугольников.
Другие ресурсы для обучения геометрии
Нельзя отрицать, что некоторые видео действительно могут дать вашим ученикам возможность познакомиться с различными математическими концепциями, если вы включите их в свои уроки математики, но давайте не будем забывать обо всех других замечательных ресурсах, которые также могут помочь обогатить ваши инструкции по математике! Включение следующих ресурсов по геометрии от Lucky Little Learners в ваши инструкции по математике определенно поможет повысить вовлеченность учащихся и углубить их понимание различных геометрических концепций! Ознакомьтесь со всеми этими невероятными продуктами, перейдя по ссылкам ниже.
Блокнот по интерактивной геометрии для 1 класса по математике
Блокнот по интерактивной геометрии для 2-го класса по математике
Набор интерактивных тетрадей по математике для 2-х классов: время, деньги, геометрия
Карты задач с QR-кодом Geometry
Карты задач на геометрию (без QR-кодов)
Гостевой пост Марго Кармайкл из Carmichael’s Class
«Четыре года преподавания в 4-м классе помогли мне стать учителем, который увлечен созданием класса, который увлекает и вдохновляет моих учеников, объединяет обучение на основе технологий, предлагает реальный опыт и способствует творчеству.Я преподавал очень разные классы с большим количеством изучающих английский как иностранный язык, изучающих специальное образование и учащихся с проблемами поведения, что дало мне глубокое понимание важности индивидуального подхода к обучению для каждого ученика. Как учитель, я постоянно учусь и развиваюсь, но одна постоянная – всегда ставить учеников на первое место! »
Спасибо за регистрацию. Нажмите на ссылку ниже, чтобы подтвердить подписку, и вы уже в путь.
занятий по геометрии, которые нравятся студентам! | Снимки высшего образования
tw Когда дело доходит до математики, кажется, что геометрия находится в совершенно другой лиге.Некоторые дети влюбляются в это мгновенно, в то время как другим детям это кажется сложным. Одна из замечательных особенностей геометрии заключается в том, что мы можем предложить своим ученикам так много практических занятий, что делает их очень увлекательными!Вот некоторые из моих любимых занятий по геометрии:
1. Начните с фигур
Мне нравится, когда ученики начинают с фигур, которые они знают с тех пор, как они были крошечными, таких как треугольники, квадраты и круги. Мы рисуем их на классных досках целым классом.Затем мы рисуем более сложные формы, такие как пятиугольники, шестиугольники, восьмиугольники, трапеции и даже ромб! Это подводит нас к обсуждению многоугольников, и таким образом мы можем классифицировать формы.
Помимо белых досок, есть много способов для детей работать с формами, например, палочки для мороженого (которые также отлично подходят для иллюстрации параллельных, пересекающихся и перпендикулярных линий), LEGOS, геодоски и даже прищепки, которые можно соединить вместе.
2.Marshmallow Geometry
Мне нравится это занятие, потому что каждый раз, когда вы добавляете еду, дети уже готовы! Используя зефир и зубочистки, дети могут создавать простые двухмерные фигуры, а также трехмерные фигуры. Кроме того, это упражнение – идеальное место для выделения вершин, поскольку каждый раз, когда вы добавляете зефир, вы кладете его в угол. Если у вас пищевая аллергия или школьные правила запрещают еду, вы можете заменить зефир пластилином.
3. Используйте анкерную диаграмму
После того, как учащиеся провели много времени для исследования форм, пришло время обсудить их атрибуты.Мне нравится делать эту диаграмму привязки с помощью детей. Объясняю, как это будет организовано, от наименьшего количества сторон до наибольшего. Мы также замечаем паттерны сторон и вершин по мере их создания. Я прошу детей привести примеры форм, и иногда они проявляют в этом настоящий творческий подход!
4. Отправляйтесь на охоту за мусорщиком формы
Это занятие, которое отлично подойдет для некоторых родительских помощников, если они у вас есть. Я люблю присылать камеры iPad с каждой группой, планшеты, карандаши и протокол.Дети записывают форму, которая была найдена, тип объекта и место его обнаружения. Действительно весело наблюдать, какие формы они могут найти, прогуливаясь по школьному кампусу!
5. Добавьте немного искусства
Я большой сторонник искусства, поэтому добавляю искусство везде, где оно подходит. Геометрия – прекрасное время для создания геометрических животных, роботов или людей. Я обычно выбираю одну из этих категорий, но на самом деле вы тоже можете сделать это широко открытым проектом!
Я поделился другим забавным занятием с геометрическим искусством в своем блоге под названием «Включение искусства в класс».Это от компании «Любит грамотность». В продолжение уроков по геометрии линий и углов я вырезал многоугольники из белого картона для каждого ребенка. У меня есть дети, которые используют линейки и фломастеры и следуют моим пошаговым указаниям, рисую линии, а затем находят тупые углы, прямые углы, перпендикулярные линии и т. По окончании урока дети добавляют к ним цвет, превращая его в действительно забавное произведение искусства.
6. Добавьте немного кинестетического обучения
Детям нужно движение, и с помощью этого модуля легко добавить немного движения.В этом упражнении учащиеся будут на полу, работая с партнером, чтобы строить различные виды линий (параллельные, пересекающиеся и перпендикулярные), формы и углы (прямые, острые и тупые), используя свое тело. В качестве альтернативы можно попросить детей встать и использовать руки, чтобы проиллюстрировать эти геометрические концепции.
Еще одно кинестетическое занятие – это сбор китайских скакалок или пакетов с резинками. Если вы используете резинку, одной упаковки хватит на небольшую группу из 5-6 детей. Идея состоит в том, чтобы ученики использовали резинку как группу для создания фигур, которые вы называете (особенно хороши типы треугольников) или типов углов.Если две группы работают вместе, можно создать разные виды линий.
7. Добавьте несколько карточек задач и игр
Карточки задач – один из моих любимых инструментов! Детям нравится игровой формат, и я знаю, что они действительно сосредоточены на изучении любой математической концепции, над которой мы работаем. Я использовал их в качестве центров / станций, на протяжении всего урока по математике, для индивидуальных занятий и в качестве выходных листов.
Если вам нужны готовые карточки с математическими задачами специально для геометрии, щелкните здесь;
Набор для геометрии 3-го класса
Набор для геометрии 4-го класса
Набор для геометрии 5-го класса
8.Прочтите текст наставника
Мне нравится, когда я могу связать чтение с математикой! Приведенные выше книги – одни из моих любимых текстов для наставников по геометрии. Мне нравятся все включенные наглядные примеры.
9. Используйте музыку
Я только что нашел эти песни от Numberock на YouTube, и они идеально подходят для этого устройства! Действительно отличные картинки и запоминающиеся мелодии:
Параллельные, перпендикулярные и пересекающиеся линии
Углы
Типы треугольников
10. Практика углов
Серьезно, после деления в столбик, измерение углов, вероятно, является самым сложным математическим навыком, с которым ученики столкнутся в начальной школе. годы! Не помогает и то, что он вводится в четвертом классе в общем ядре, а затем даже не упоминается в стандартах пятого класса.Ну что ж!
Одно из полезных занятий – попросить детей использовать миллиметровую бумагу и написать свое имя заглавными печатными буквами. Учащиеся могут измерить любые углы, образованные пересечением линий буквы.
Еще одно любимое занятие для отработки углов – это взять ленту и провести различные линии, которые создают углы на столе, столе или даже на листах мясной бумаги. Дети используют транспортиры для измерения углов, а затем пишут экспозицией (или маркерами на мясной бумаге) прямо на партах / столах! Отличный способ добавить немного веселья к этой сложной концепции!
Надеюсь, вы нашли хотя бы несколько идей, которые можно использовать для своего геометрического блока! Я действительно хотел сообщить вам, что у меня есть комплекты карточек с заданиями по математике для каждого класса с 3-го по 5-й.В каждом наборе 30 наборов из 32 карточек задач, охватывающих ВСЕ СТАНДАРТЫ (CCSS) для этих классов. Я люблю готовить их в начале года, а затем беру любую концепцию, над которой мы работаем, для дополнительной практики.
Если вы хотите взглянуть на:
Комплект карточек заданий по математике для 3-х классов
Комплект карточек заданий по математике для 4-х классов
Комплект карточек заданий по математике для 5-х классов
Спасибо, что заглянули! Если вам понравился этот пост, я был бы рад, если бы вы прикрепили его или поделились с другом-учителем!
Чтобы узнать больше об идеях и стратегиях для старших классов начальной школы, не забудьте подписаться на бесплатную рассылку новостей The Teacher Next Door по электронной почте прямо ЗДЕСЬ.
Я хотел бы с вами связаться!
9 необычных форм, названия которых вы, вероятно, не знали
Вот несколько необычных форм с фантастическими названиями, которые вы почти наверняка не изучали в школе геометрии.
1. Тор Изображение любезно предоставлено Wikimedia Commons.
Подождите, это же просто пончик, да? Собственно, сама фигура называется тором.Хотя, наверное, все равно было бы вкусно в глазури.
Для шутливого анекдота: пожалуйста, один «торчащий из желе» тор.
2. Треугольник Рело Изображение любезно предоставлено Wikimedia Commons.Этот изогнутый треугольник, который может напомнить медиаторы, называется треугольником Рело в честь немецкого инженера Франца Рило.
Он образован перекрытием трех кругов или заполнением правильного треугольника слишком большим количеством гелия.
3. Гиперболоид Изображение любезно предоставлено Wikimedia Commons.Эта трехмерная форма напоминает по форме песочные часы или сплющенный цилиндр. Это называется гиперболоидом, не путать с гиперболой, величайшим словом всех времен.
4. Аполлонийская прокладка Изображение любезно предоставлено Wikimedia Commons.Аполлоническая прокладка была обнаружена греческим философом Аполлонием. Что касается необычных форм, то этот особенно упрощен, он состоит из одного круга с кругами все меньшего размера, заполняющими пространство внутри него.
5.Балбис Фото любезно предоставлено Wikimedia Commons. К счастью,H – это одна буква, которая тоже может быть формой. Это называется балбис от древнегреческого слова βαλβίς, что означает веревку между двумя столбами, обозначающую начало и конец гонки.
6. Лента Мебиуса Изображение любезно предоставлено Wikimedia Commons.Одна полоса трехмерной сферы называется лентой Мёбиуса или лентой Мёбиуса. Он назван в честь немецкого математика и любителя необычных форм Августа Фердинанда Мебиуса и, вероятно, его можно найти на запястьях на ближайшем концертном зале.
Для шутливого анекдота: «Не могли бы вы защитить мою ленту Мебиуса?»
7. Vesica Piscis Изображение любезно предоставлено Wikimedia Commons.Хотя эти пересекающиеся круги могут напоминать олимпийские кольца или диаграммы Венна, правильное название миндалевидной формы, созданной двумя перекрывающимися кругами, – vesica piscis.
Как ни странно, на латыни это слово буквально переводится как «пузырь рыбы», предположительно потому, что он похож на пузырь рыбы, и, надеюсь, не потому, что он использовался в качестве древнего футбольного мяча.
8. Лемниската Изображение любезно предоставлено Wikimedia Commons.Нет, это не просто символ бесконечности или цифра 8. Это уместно причудливое название – лемнискат, что переводится с латыни как «украшенный лентами», хотя сначала в Древней Греции он был известен как «конские оковы» за то, что он напоминал лемнискат. предмет, который скрепляет копыта.
За (действительно) вызывающую уловку шутку: «Чтобы лемнискатировать и не только».
9. Hemihilex, одна из новейших необычных форм
Обнаруженная в 2014 году, эта необычная форма определяется повторяющимися изгибами усиков – спиральным шнуром, который меняет направление скручивания по своей длине.
Для реального, реального научного применения: исследователи из Гарварда надеются, что его можно уменьшить до наноразмеров для использования в качестве крошечных пружин, управляющих светом.
Что, вы ждали еще одной шутки? Вам, вероятно, следует более серьезно отнестись к необычным формам.
Предсказание необычных форм дает новые
В 2018 году системный биолог использовал компьютерное моделирование, чтобы спрогнозировать оптимальную форму плотной упаковки клеток. Результатом стала Скутоид, совершенно новая форма, которую никогда раньше не предсказывали и не наблюдали.
Имея в руках предсказание формы, ученые искали примеры из реального мира и нашли их в щитках некоторых насекомых. В сообщениях о новой форме говорится, что она может быть характерна для каждого из нас.
Обновлено
10 исследований геометрического искусства для изучения математики
В следующих упражнениях учащиеся используют словарный запас геометрии и изучают математические понятия, в том числе: измерение, площадь и периметр, дроби и закономерности!
1.Спиральные треугольникиСоздайте спиральный дизайн из равносторонних треугольников! Чтобы создать дизайн, начните с большого треугольника. Затем вырежьте треугольник, длина стороны которого равна высоте большого треугольника. Вставьте сторону треугольника по центру большего треугольника так, чтобы она покрывала половину большого треугольника. Продолжайте создавать меньшие треугольники со сторонами, соответствующими высоте предыдущего треугольника, чтобы получилась спираль!
2.Квадратный стек Это художественное задание принадлежит Lucky To Be In First. Студенты отмеряют , вырезают и вставляют квадраты в порядке убывания. Каждый квадрат на 1/2 дюйма меньше предыдущего.
Примечание. Вы также можете попросить детей вычислить площадь и периметр каждого квадрата на отдельном листе бумаги.
Пример
1. Площадь = 25, периметр = 20
2. Площадь = 20,25, периметр = 18
3. Площадь = 16, периметр = 16
4. Площадь = 12,25, периметр = 14
5.площадь = 9, периметр = 12
6. площадь = 6,25, периметр = 10
7. площадь = 4, периметр = 8
8. площадь = 2,25, периметр = 6
9. Площадь = 1, периметр = 4
Объедините математику и искусство, создав линейный рисунок. Дети используют линейку и рисуют на бумаге случайные линии. Затем они становятся исследователями полигонов! Они рассматривают свои изображения и цвета в многоугольниках с одинаковым количеством сторон.
4. МногоугольникиИсследуйте вершины и диагонали, ища узоры в многоугольниках! Попросите детей угадать количество диагоналей треугольника, квадрата, пятиугольника, шестиугольника, семиугольника и восьмиугольника. Разделите детей на команды. Затем попросите их решить проблему, нарисовав диагонали на контурах фигуры. Убедитесь, что дети используют маркеры разного цвета для каждой диагонали (чтобы они могли их сосчитать).Также попросите товарища по команде подсчитать каждую нарисованную диагональ. Могут ли они найти выкройку ?! Сколько диагоналей у шестиугольника ?!
5. Квадратный взрывПодарите детям ножницы и бумажный квадратик и посмотрите, что они могут создать!
6.Frac-Geo-BotFrac-Geo-Bot – это увлекательная математическая игра, позволяющая детям проявить творческий подход. Они конструируют робота из различных полигонов. Затем они вычисляют дробь для каждой формы и цвета. Дети постарше могут создавать более сложных ботов, подобных приведенному выше. Дети младшего возраста могут создавать более простых ботов, используя простые формы.
7.Передайте статью: сотрудничествоЭтот совместный проект в области математического искусства создан Incredible Art! Дети демонстрируют свои знания геометрических терминов , создавая искусство! Каждому ребенку дается листок бумаги. Им дается инструкция (например, сделать 3 точки). Затем они передают свой лист бумаги. Дается еще одна инструкция (например: используйте циркуль, чтобы создать 3 круга из 3 точек). Студенты рисуют на бумаге своих сверстников. Затем они передают бумагу. Бумаги распространяются, пока не достигнут своего «хозяина».”Владелец украшает линейный рисунок, чтобы создать уникальное произведение искусства!
8. Формы коллекционных карточек Дети рисуют форму и заполняют обратную сторону карточек. Щелкните здесь, чтобы распечатать.Примечание. Не обрезайте по центральной линии.Карта складывается пополам, так что есть лицевая и оборотная стороны.
9. Асимметричный звездообразование Студенты изучают геометрию и искусство, создавая асимметричные рисунки со вспышками звезд!
1. Нарисуйте отрезок линии длиной от 3 до 5 дюймов в центре листа.
2. Нарисуйте точки вокруг отрезка линии. (Без точек на горизонтальной линии)
10 точек (5 вверху, 5 внизу для младших школьников / 15-20 точек для старших учеников)
3.Соедините точки! – но, в узор. (Соедините один конец линейного сегмента с точкой, обратно к другому концу линейного сегмента) – повторите (конец линейного сегмента-точка-другой конец линейного сегмента) – используйте линейку
Примечание: Чтобы упростить это попросите детей сделать их горизонтальную линию другим цветом или добавить яркие цветные точки в конце отрезка линии. Тогда они смогут увидеть, куда они проводят свои линии.
Math Connection: Посетите I Love That Teaching Idea, чтобы задать вопросы детям, пока они конструируют!
10.Математическое оп-арт
Студенты используют свои математические навыки для создания оп-арта! Во-первых, попросите учащихся измерить расстояние между параллельными линиями. В примере между каждой линией есть зазор в 1/2 дюйма. После того, как учащиеся проведут свои параллельные линии с помощью линейки, они выбирают пять многоугольников для включения в свою композицию. Они рисуют свои формы с помощью линейки. После того, как их формы нарисованы, они создают узор AB, используя два маркера разного цвета, раскрашивая их формы.Затем они возвращаются и раскрашивают свои формы, чтобы создать оптическую иллюзию! (см. пример).